Effect of quantum correction of electron–ion collision frequency on ion temperature and expansion energy in laser-driven fusion

Abstract

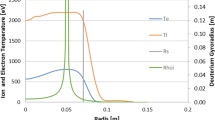
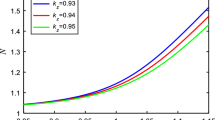
The nonlinear heat conduction equation can be solved by quantum modified heat transfer coefficient in deuterium–tritium (DT) plasma driven by laser above the critical electron temperature. As a result, the electron profile temperature and the heat flux solutions are improved. In this paper, we have studied the subsequent modification of ion temperature due to ion heating by energy transfer between electrons and ions through electron–ion collisions. The differential equation between T_e and T_i, expansion energy of plasma as well as the threshold energy of the laser beam for plasma ignition are renewed by considering quantum modification in electron–ion collision frequency. The achieved results improve the values of the ion temperature and the threshold energy for plasma ignition compared with the values obtained from the calculations using the classical electron–ion collision frequency.

Appendix: Expansion energy of plasma electrons with quantum modified EICF consideration

1.1 The expansion energy of the electrons due to ordinary Zeldovich solution for T _e

The basic formula associated with the expansion energy of plasma has been obtained in [7] as follows:

$$w_{{{\text{expansion}}}} = \frac{4}{3}T\frac{\partial u}{{\partial x}}.$$

(42)

Here, T and u are the electron temperature and local velocity of fluid in plasma, respectively. The velocity u can be related to temperature T via the following formula:

$$u = C\sqrt {\frac{{k_{b} T}}{{m_{e} }}}$$

(43)

where C is another constant which can be calculated by comparison. However, depending on the solution of nonlinear heat transfer equation, T_e(x, t), we can obtain the relation of expansion energy with respect to the electron temperature. First, as a review, we have derived the expansion energy of the electrons which satisfy the nonlinear heat transfer equation due to the Chu's solution.

As we see in [17], Chu’s solution can be presented as follows:

$$T_{e} (x,t) = \left( {Q^{2} /{\text{at}}} \right)^{\frac{2}{9}} f(\xi ) = \left( {Q^{2} /{\text{at}}} \right)^{\frac{2}{9}} \left[ {\frac{5}{18}\left( {\xi_{o}^{2} - \xi^{2} } \right)} \right]^{\frac{2}{5}}$$

(44)

where is defined as. Considering Ref. [7], the expansion energy of the hot electrons can be obtained by

$$w_{{{\text{expansion}}}} = \frac{4}{3}T\frac{\partial u}{{\partial x}} = C\frac{4}{3}T\frac{\partial }{\partial x}\left( {\sqrt {\frac{{k_{b} T}}{{m_{e} }}} } \right) = C\frac{1}{2}\frac{4}{3}T\sqrt {\frac{{k_{b} }}{{m_{e} T}}} \frac{\partial T}{{\partial x}} = C\frac{2}{3}\sqrt {\frac{{k_{b} T}}{{m_{e} }}} \frac{\partial T}{{\partial x}}.$$

(45)

Substituting T_e from Chu's solution, we can establish a relation as derived in Ref. [17]. After some calculations for getting the derivative of temperature T_e with respect to x, we have:

$$\begin{aligned} w_{{{\text{expansion}}}} & = \frac{4}{3}T\frac{\partial u}{{\partial x}} = C\frac{2}{3}\sqrt {\frac{{k_{b} T}}{{m_{e} }}} \frac{\partial T}{{\partial x}} = C\frac{2}{3}\sqrt {\frac{{k_{b} T}}{{m_{e} }}} \frac{\partial \xi }{{\partial x}}\frac{\partial T}{{\partial \xi }} \\ w_{{{\text{expansion}}}} & = C\frac{2}{3}\sqrt {\frac{{k_{b} T}}{{m_{e} }}} \frac{\partial \xi }{{\partial x}}\frac{\partial T}{{\partial \xi }} = C\frac{2}{3}\sqrt {\frac{{k_{b} T}}{{m_{e} }}} \left( {Q^{2} /{\text{at}}} \right)^{\frac{2}{9}} \times \frac{x}{{\left( {Q^{5/2} {\text{at}}} \right)^{\frac{4}{9}} }}\left( \frac{2}{5} \right)\left( { - \frac{10}{{18}}} \right)\left[ {\frac{5}{18}\left( {\xi_{o}^{2} - \xi^{2} } \right)} \right]^{{ - \frac{3}{5}}} \\ \end{aligned}.$$

(46)

Here, we use the chain rule as ξ is a function of x:

$$w_{{{\text{expansion}}}} = \frac{4x}{{27}}C\sqrt {\frac{{k_{b} T_{e} }}{{m_{e} }}} \frac{{\left( {Q^{2} /{\text{at}}} \right)^{\frac{2}{9}} }}{{\left( {Q^{5/2} {\text{at}}} \right)^{\frac{4}{9}} }}\left[ {\left( {\frac{{T_{e} }}{{\left( {Q^{2} /{\text{at}}} \right)^{\frac{2}{9}} }}} \right)^{\frac{5}{2}} } \right]^{{ - \frac{3}{5}}} = \frac{4}{27}\frac{1}{a}\left( \frac{x}{t} \right)C\sqrt {\frac{{k_{b} T_{e} }}{{m_{e} }}} T_{e}^{{ - \frac{3}{2}}} = \frac{4}{27}C^{2} \frac{1}{a}\frac{{k_{b} }}{{m_{e} }}T_{e}^{{ - \frac{1}{2}}}$$

(47)

$$w_{{{\text{expansion}}}} = \frac{8}{9}\frac{1}{a}\frac{{k_{b} }}{{m_{e} }}\frac{1}{{T_{e}^{\frac{1}{2}} }} = \frac{4}{27}C^{2} \frac{1}{a}\frac{{k_{b} }}{{m_{e} }}T_{e}^{{ - \frac{1}{2}}}.$$

(48)

Comparing the derived equation with the expansion energy term presented in Ref. [17] and equating it to Eq. (48), we obtain:

$$C^{2} = 6$$

(49)

1.2 The expansion energy of the electrons via Mayer solutions modified by quantum consideration to heat transfer equation coefficient T _e

In Ref. [21], the solution of the nonlinear heat equation with quantum consideration in the ion–electron collision frequency has been derived as:

$$T_{e} (x,t) = \frac{{T_{{{\text{oe}}}} }}{{\left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{2/7} }} \times \left[ {1 - \frac{{x^{2} }}{{\frac{4}{3}L_{o}^{2} \left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{4/7} }}} \right],^{2/3}$$

(50)

where T_oe is the initial temperature of electron and is determined by the total absorbed energy of laser at t = 0. Since we select neodymium glass laser as the driver laser, $L_{o} \approx 1.06 \times 10^{ - 4} \;{\text{cm}}$. The quantity $a_{{{\text{qu}}}}$ is defined in $\chi = a_{{{\text{qu}}}} T_{e}^{3/2}$, where $\chi$ is the quantum modified heat transfer coefficient. Again, by applying Eq. (45) and substituting T_e from (48), we have:

$$\begin{aligned} & w_{{{\text{expansion}}}} = C\frac{2}{3}\sqrt {\frac{{k_{b} T_{e} }}{{m_{e} }}} \frac{{\partial T_{e} }}{\partial x} = \\ & \quad C\frac{2}{3}\sqrt {\frac{{k_{b} T_{e} }}{{m_{e} }}} \frac{\partial }{\partial x}\left[ \begin{gathered} \frac{{T_{{{\text{oe}}}} }}{{\left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{2/7} }} \times \hfill \\ \left[ {1 - \frac{{x^{2} }}{{\frac{4}{3}L_{o}^{2} \left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{4/7} }}} \right]^{2/3} \hfill \\ \end{gathered} \right] \\ \end{aligned}.$$

(51)

Taking the derivative into account with respect to x gives:

$$w_{{{\text{expansion}}}} = C\frac{2}{3}\sqrt {\frac{{k_{b} T_{e} }}{{m_{e} }}} \frac{{T_{{{\text{oe}}}} }}{{\left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{2/7} }} \times \left[ { - \frac{2x}{{\frac{4}{3}L_{o}^{2} \left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{4/7} }}} \right] \times \left[ {1 - \frac{{x^{2} }}{{\frac{4}{3}L_{o}^{2} \left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{4/7} }}} \right]^{ - 1/3}.$$

(52)

Consequently, we have:

$$w_{{{\text{expansion}}}} = C\frac{2}{3}\sqrt {\frac{{k_{b} T_{e} }}{{m_{e} }}} \left( { - 2x} \right)\frac{{T_{{{\text{oe}}}} }}{{\frac{4}{3}L_{o}^{2} \left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{6/7} }} \times \left[ {1 - \frac{{x^{2} }}{{\frac{4}{3}L_{o}^{2} \left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{4/7} }}} \right]^{ - 1/3}.$$

(53)

Considering Eq. (50), we conclude that:

$$\left[ {1 - \frac{{x^{2} }}{{\frac{4}{3}L_{o}^{2} \left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{4/7} }}} \right] = \left[ {\frac{{T_{e} }}{{T_{{{\text{oe}}}} }}\left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{2/7} } \right].$$

(54)

Therefore, we have:

$$w_{{{\text{expansion}}}} = C\frac{2}{3}\sqrt {\frac{{k_{b} T_{e} }}{{m_{e} }}} \left( { - 2x} \right)\frac{{T_{{{\text{oe}}}} }}{{\frac{4}{3}L_{o}^{2} \left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{6/7} }} \times \left[ {\frac{{T_{e} }}{{T_{{{\text{oe}}}} }}\left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{2/7} } \right]^{ - 1/2}.$$

(55)

As it can be seen from the numerical computations, we are able to use the following equation in Eq. (54) with sufficient accuracy:

$$\left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{2/7} \cong \left( {\left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right)^{2/7}.$$

(56)

Finally, we have:

$$w_{{{\text{expansion}}}} = C\frac{2}{3}\sqrt {\frac{{k_{b} T_{e} }}{{m_{e} }}} \left( { - 2x} \right)\frac{{T_{oe} }}{{\frac{4}{3}L_{o}^{2} \left[ {1 + \left( \frac{7}{2} \right)\frac{{a_{{{\text{qu}}}} T_{{{\text{oe}}}}^{3/2} }}{{L_{o}^{2} }}t} \right]^{6/7 + 1/7} }} \times \left[ {\frac{{T_{e} }}{{T_{{{\text{oe}}}} }}} \right]^{ - 1/2}$$

(57)

$$w_{{{\text{expansion}}}} = C\frac{2}{3}\sqrt {\frac{{k_{b} T_{e} }}{{m_{e} }}} \left( { - 2x} \right)\frac{{T_{oe}^{3/2} T_{e}^{ - 1/2} }}{{\frac{4}{3}L_{o}^{2} \left[ {\left( \frac{7}{2} \right)\frac{{a_{qu} T_{oe}^{3/2} }}{{L_{o}^{2} }}t} \right]}}.$$

(58)

By substituting $C^{2} = 6$ in Eq. (58) and assuming, we obtain:

$$w_{{{\text{expansion}}}} = - C\frac{2}{7}\frac{1}{{a_{{{\text{qu}}}} }}\sqrt {\frac{{k_{b} }}{{m_{e} }}} \left( \frac{x}{t} \right) = - C\frac{2}{7}\frac{1}{{a_{{{\text{qu}}}} }}\sqrt {\frac{{k_{b} }}{{m_{e} }}} \left( {C\sqrt {\frac{{k_{b} T_{e} }}{{m_{e} }}} } \right) = - \frac{{2C^{2} }}{7}\frac{1}{{a_{{{\text{qa}}}} }}\left( {\frac{{k_{b} }}{{m_{e} }}} \right)T_{e}^{\frac{1}{2}}$$

(59)

$$w_{{{\text{expansion}}}} = - \frac{12}{7}\frac{1}{{a_{{{\text{qa}}}} }}\left( {\frac{{k_{b} }}{{m_{e} }}} \right)T_{e}^{\frac{1}{2}}.$$

(60)