Dynamic brain effective connectivity analysis based on low-rank canonical polyadic decomposition: application to epilepsy

Abstract

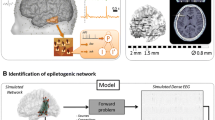
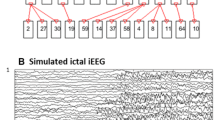
In this paper, a new method to track brain effective connectivity networks in the context of epilepsy is proposed. It relies on the combination of partial directed coherence with a constrained low-rank canonical polyadic tensor decomposition. With such combination being established, the most dominating directed graph structures underlying each time window of intracerebral electroencephalographic signals are optimally inferred. Obtained time and frequency signatures of inferred brain networks allow respectively to track the time evolution of these networks and to define frequency bands on which they are operating. Besides, the proposed method allows also to track brain connectivity networks through several epileptic seizures of the same patient. Understanding the most dominating directed graph structures over epileptic seizures and investigating their behavior over time and frequency plans are henceforth possible. Since only few but the the most important directed connections in the graph structure are of interest and also for a meaningful interpretation of obtained signatures to be guaranteed, the low-rank canonical polyadic tensor decomposition is prompted respectively by the sparsity and the non-negativity constraints on the tensor loading matrices. The main objective of this contribution is to propose a new way of tracking brain networks in the context of epileptic iEEG data by identifying the most dominant effective connectivity patterns underlying the observed iEEG signals at each time window. The performance of the proposed method is firstly evaluated on simulated data imitating brain activities and secondly on real intracerebral electroencephalographic signals obtained from an epileptic patient. The partial directed coherence-based tensor has been decomposed into space, time, and frequency signatures in accordance with the expected ground truth for each consecutive sequence of the simulated data. The method is also in accordance with the clinical expertise for iEEG epileptic signals, where the signatures were investigated through a simultaneous multi-seizure analysis.

Appendix A

1.1 A.1 Technical materials on the minimization of $\boldsymbol {{\mathscr{L}}}_{1}$ defined in Eq. 14

As mentioned in Section 3.2.1, solving the minimization problem defined in Eq. 13 is possible by minimizing its associated augmented Lagrangian function ${\mathscr{L}}_{1}$ given by:

$$ \begin{array}{@{}rcl@{}} \mathcal{L}_{1}&=&{{\alpha}_{\mathbf{S}} \left\| \mathbf{S} \right\|}_{2,1}+{\delta}{\left\| \mathbf{Y} \right\|}_{1}+{\alpha}_{\mathbf{T}}{\left\| \mathbf{T} \right\|}_{2,1}+{\alpha}_{\mathbf{F}}{\left\| \mathbf{F} \right\|}_{2,1}\\ &&+ vec(\mathbf{W})^{\top} vec(\mathbf{Y}-\mathbf{S})+\frac{\rho}{2} \left\| \mathbf{Y}-\mathbf{S} \right\|^{2}_{F}\\ &&+\lambda{\left\| \boldsymbol{\mathcal{P}}-\sum\limits_{r=1}^{R} \mathbf{s}_{r} \circ \mathbf{t}_{r} \circ \mathbf{f}_{r} \right\|}_{F}^{2} \end{array} $$

(23)

$$ \begin{array}{@{}rcl@{}} &=&{\alpha}_{\mathbf{S}} Tr\left( \mathbf{S}^{\top}\boldsymbol{\Gamma}_{S}\mathbf{S}\right)+{\delta}{\left\| \mathbf{Y} \right\|}_{1}+{\alpha}_{\mathbf{T}} Tr\left( \mathbf{T}^{\top}\boldsymbol{\Gamma}_{T}\mathbf{T}\right)+{\alpha}_{\mathbf{F}}Tr\left( \mathbf{F}^{\top}\boldsymbol{\Gamma}_{F}\mathbf{F}\right) \end{array} $$

$$ \begin{array}{@{}rcl@{}} &&+ vec(\mathbf{W})^{\top} vec(\mathbf{Y}-\mathbf{S})+\frac{\rho}{2} \left\| \mathbf{Y}-\mathbf{S} \right\|^{2}_{F}+\lambda{\left\| \boldsymbol{\mathcal{P}}-\sum\limits_{r=1}^{R} \mathbf{s}_{r} \circ \mathbf{t}_{r} \circ \mathbf{f}_{r} \right\|}_{F}^{2}\\ \end{array} $$

(24)

with respect to its variable matrices S, T, F. This minimization is possible by looking for the stationary points of ${\mathscr{L}}_{1}$ in these variable matrices, as shown hereafter. Note that according to Definition 3, we can write P₍₁₎ = S(F ⊙T)^⊤, P₍₂₎ = T(S ⊙F)^⊤, and P₍₃₎ = F(T ⊙S)^⊤. For mathematical convenience, derivation of the update rules will be expressed in a vector form.

1.1.1 A.1.1 Update of S

The stationary point of ${\mathscr{L}}_{1}$ defined in Eq. 14 in S is computed by solving the equation $\frac {\partial \boldsymbol {{\mathscr{L}}}_{1}}{\partial vec({\mathbf {S})}}=\mathbf {0}$. Then according to Eq. 24, we can write:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_{1}}{\partial vec({\mathbf{S})}}=& \alpha_{\mathbf{S}} \frac{\partial Tr\left( \mathbf{S}^{\top} \boldsymbol{\Gamma}_{\mathbf{S}} \mathbf{S}\right)} {\partial vec({\mathbf{S})}} +\frac{\partial vec(\mathbf{W})^{\top} vec(\mathbf{Y}-\mathbf{S})} {\partial vec({\mathbf{S})}}+\frac{\rho}{2} \frac{\partial \left\| \mathbf{Y}-\mathbf{S} \right\|^{2}_{F}} {\partial vec(\mathbf{S})}+\lambda \frac{\partial \left\| \mathbf{P}_{(1)}-\mathbf{S}(\mathbf{F}\odot\mathbf{T})^{\top} \right\|^{2}_{F}} {\partial vec({\mathbf{S})}} \end{array} $$

(25)

Now, based on the properties of matrix trace, Kronecker product [46], and [16], we obtain:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_1}{\partial vec(\mathbf{S})}&=& -2\lambda((\mathbf{F}\odot\mathbf{T})\otimes \mathbf{I}_{{N}_v^2-N_v})^{\top} vec(\mathbf{P}_{(1)})-vec(\mathbf{W})-\rho vec(\mathbf{Y})\\ && +(2\alpha_{\mathbf{S}} \mathbf{I}_R \otimes \boldsymbol{\Gamma}_{\mathbf{S}}+2\lambda((\mathbf{F}\odot\mathbf{T})^{\top} (\mathbf{F}\odot\mathbf{T}) )\otimes \mathbf{I}_{{N}_v^2-N_v}+\rho \mathbf{I}_{R({N}_v^2-N_v})) vec(\mathbf{S}) \end{array} $$

(26)

Then, by solving $\frac {\partial \boldsymbol {{\mathscr{L}}}_{1}}{\partial vec({\mathbf {S})}}=\mathbf {0}$ with respect to vec(S), we get:

$$ \begin{array}{@{}rcl@{}} vec(\mathbf{S})&=&(\alpha_{\mathbf{S}} \mathbf{I}_R \otimes \boldsymbol{\Gamma}_{\mathbf{S}} + \lambda ((\mathbf{F}\odot\mathbf{T})^{\top} (\mathbf{F}\odot\mathbf{T}) )\otimes \mathbf{I}_{{N}_v^2-N_v}+\rho \mathbf{I}_{R({N}_v^2-N_v)})^{-1} \\ && \times((\lambda (\mathbf{F}\odot\mathbf{T})^{\top} \otimes \mathbf{I}_{{N}_v^2-N_v}) vec(\mathbf{P}_{(1)})+\frac{vec(\mathbf{W})}{2}+\frac{\rho}{2} vec(\mathbf{Y})) \end{array} $$

(27)

1.1.2 A.1.2 Update of T

Similarly, the stationary point of ${\mathscr{L}}_{1}$ defind in Eq. 14 in T is computed by solving the equation $\frac {\partial \boldsymbol {{\mathscr{L}}}_{1}}{\partial vec({\mathbf {T})}}=\mathbf {0}$. Then according to Eq. 24, we can write:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_1}{\partial vec({\mathbf{T})}}= \alpha_{\mathbf{T}} \frac{\partial Tr(\mathbf{T} \boldsymbol{\Gamma}_{\mathbf{T}} \mathbf{T}^{\top})} {\partial vec({\mathbf{T})}} +\lambda \frac{\partial \left\| \mathbf{P}_{(2)}-\mathbf{T}(\mathbf{S}\odot\mathbf{F})^{\top} \right\|^2_F} {\partial vec({\mathbf{T})}} \end{array} $$

(28)

Based also on the properties of matrix trace, Kronecker product [46], and [16], we obtain:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_1}{\partial vec({\mathbf{T})}}&=& 2\lambda ((\mathbf{S} \odot \mathbf{F})\otimes \mathbf{I}_{N_w})^{\top} vec(\mathbf{P}_{(2)})\\ &&+\left( 2\alpha_{\mathbf{S}} \mathbf{I}_{R}\otimes \boldsymbol{\Gamma}_{T}+2\lambda((\mathbf{S} \odot \mathbf{F})(\mathbf{S} \odot \mathbf{F})^{\top}\right)\otimes \mathbf{I}_{N_w})vec(\mathbf{T}) \end{array} $$

(29)

Then, by solving $\frac {\partial {\mathscr{L}}_{1}}{\partial vec(\mathbf {S})}=\mathbf {0}$, we get:

$$ \begin{array}{@{}rcl@{}} vec(\mathbf{T})=&(\alpha_{\mathbf{T}} \mathbf{I}_R \otimes \boldsymbol{\Gamma}_{\mathbf{T}} +\lambda ((\mathbf{S}\odot\mathbf{F})^{\top} (\mathbf{S}\odot\mathbf{F}) )\otimes \mathbf{I}_{{N_w}})^{-1}(\lambda(\mathbf{S}\odot\mathbf{F})^{\top}\otimes \mathbf{I}_{{N_w}})vec(\mathbf{P}_{(2)}) \end{array} $$

(30)

1.1.3 A.1.3 Update of F

Similarly, the stationary point of ${\mathscr{L}}_{1}$ defined in Eq. 14 in F is computed by solving the equation $\frac {\partial \boldsymbol {{\mathscr{L}}}_{1}}{\partial vec({\mathbf {F})}}=\mathbf {0}$. Then according to Eq. 24, we can write:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_1}{\partial vec({\mathbf{F})}}= \alpha_{\mathbf{F}} \frac{\partial Tr(\mathbf{F} \boldsymbol{\Gamma}_{\mathbf{F}} \mathbf{F}^{\top})} {\partial vec({\mathbf{F})}} +\lambda \frac{\partial \left\| \mathbf{P}_{(3)}-\mathbf{F}(\mathbf{T}\odot\mathbf{S})^{\top} \right\|^2_F} {\partial vec({\mathbf{F})}} \end{array} $$

(31)

Based also on the properties of matrix trace, Kronecker product [46], and [16], we obtain:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_1}{\partial vec({\mathbf{F})}}&=& 2\lambda ((\mathbf{T} \odot \mathbf{S})\otimes \mathbf{I}_{N_f})^{\top} vec(\mathbf{P}_{(3)})\\ &&+(2\alpha_{\mathbf{F}} \mathbf{I}_{R}\otimes \boldsymbol{\Gamma}_{F}+2\lambda((\mathbf{T} \odot \mathbf{S})(\mathbf{T} \odot \mathbf{S})^{\top})\otimes \mathbf{I}_{N_f})vec(\mathbf{F}) \end{array} $$

(32)

Then, by solving $\frac {\partial {\mathscr{L}}_{1}}{\partial vec(\mathbf {F})}=\mathbf {0}$, we get:

$$ \begin{array}{@{}rcl@{}} vec(\mathbf{F})&=&(\alpha_{\mathbf{F}} \mathbf{I}_R \otimes \boldsymbol{\Gamma}_{\mathbf{F}}+\lambda ((\mathbf{T}\odot\mathbf{S})^{\top}\\&& \times(\mathbf{T}\odot\mathbf{S}) )\otimes \mathbf{I}_{{N_f}})^{-1}(\lambda(\mathbf{T}\odot\mathbf{S})^{\top}\otimes \mathbf{I}_{{N_f}})vec(\mathbf{P}_{(3)}) \end{array} $$

(33)

1.1.4 A.1.4 Update of Y

The update rule of the dual variable Y is given by:

$$ \mathbf{Y} \leftarrow \mathbf{Y}+{prox}_{\phi,\frac{\delta}{\rho}}\left( \mathbf{S}+\frac{\mathbf{W}}{\rho}\right) $$

(34)

where ${prox}_{\phi ,\frac {\delta }{\rho }}$ is a proximal operator dealing with non smooth function (here, $\phi =\left \| . \right \|_{1}$) initially proposed in [20] and $\frac {\delta }{\rho }$ denotes the shrinking threshold.

1.1.5 A.1.5 Update of W

The update rule of the Lagrange multiplier W is given by:

$$ \mathbf{W} \leftarrow \mathbf{W} +\rho (\mathbf{S}-\mathbf{Y}) $$

(35)

1.2 A.2 Technical materials on the minimization of $\boldsymbol {{\mathscr{L}}}_{2}$ defined in Eq. 17

As mentioned in Section 3.2.2, solving the minimization problem defined in Eq. 16 is possible by minimizing its associated augmented Lagrangian function ${\mathscr{L}}_{2}$ given by:

$$ \begin{array}{@{}rcl@{}} \mathcal{L}_{2}&=&{{\alpha}_{\mathbf{S}} \left\| \mathbf{S} \right\|}_{2,1}+{\delta}{\left\| \mathbf{Y} \right\|}_{1}+{\alpha}_{\mathbf{T}}{\left\| \mathbf{T} \right\|}_{2,1}+{\alpha}_{\mathbf{F}}{\left\| \mathbf{F} \right\|}_{2,1}\\ &&+{\alpha}_{\mathbf{C}}{\left\| \mathbf{C} \right\|}_{2,1}+ vec(\mathbf{W})^{\top} vec(\mathbf{Y}-\mathbf{S})+\frac{\rho}{2} \left\| \mathbf{Y}-\mathbf{S} \right\|^{2}_{F}\\ &&+\lambda{\left\| \boldsymbol{\mathcal{Q}}-{\sum}_{r=1}^{R} \mathbf{s}_{r} \circ \mathbf{t}_{r} \circ \mathbf{f}_{r} \circ \mathbf{c}_{r} \right\|}_{F}^{2} \end{array} $$

(36)

$$ \begin{array}{@{}rcl@{}} &=&{\alpha}_{\mathbf{S}} Tr(\mathbf{S}^{\top}\boldsymbol{\Gamma}_{S}\mathbf{S})+{\delta}{\left\|\mathbf{Y} \right\|}_{1}+{\alpha}_{\mathbf{T}} Tr(\mathbf{T}^{\top}\boldsymbol{\Gamma}_{T}\mathbf{T})\\ &&+{\alpha}_{\mathbf{F}}Tr(\mathbf{F}^{\top}\boldsymbol{\Gamma}_{F}\mathbf{F})+{\alpha}_{\mathbf{C}}Tr(\mathbf{C}^{\top}\boldsymbol{\Gamma}_{C}\mathbf{C})\\ &&+ vec(\mathbf{W})^{\top} vec(\mathbf{Y}-\mathbf{S})+\frac{\rho}{2} \left\|\mathbf{Y}-\mathbf{S} \right\|^{2}_{F}\\&&+\lambda{\left\| \boldsymbol{\mathcal{Q}}-{\sum}_{r=1}^{R} \mathbf{s}_{r} \circ \mathbf{t}_{r} \circ \mathbf{f}_{r} \circ \mathbf{c}_{r} \right\|}_{F}^{2} \end{array} $$

(37)

with respect to its variable matrices S, T, F, and C. This minimization is possible by looking for the stationary points of ${\mathscr{L}}_{2}$ in these variable matrices, as shown hereafter. Note that according to Definition 3, the unfolding matrices associated with the first, the second, the third, and the fourth direction of the 4rd-order tensor $\boldsymbol {\mathcal {Q}}$ are given, respectively, by: Q₍₁₎ = S(C ⊙F ⊙T)^⊤, Q₍₂₎ = T(S ⊙C ⊙F)^⊤, Q₍₃₎ = F(T ⊙S ⊙C)^⊤, and Q₍₄₎ = C(F ⊙T ⊙S)^⊤. For mathematical convenience, derivation of the update rules will be expressed in a vector form.

1.2.1 A.2.1 Update of S

The stationary point of ${\mathscr{L}}_{2}$ defined in Eq. 17 in S is computed by solving the equation $\frac {\partial \boldsymbol {{\mathscr{L}}}_{2}}{\partial vec({\mathbf {S})}}=\mathbf {0}$. Then according to Eq. 36, we can write:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_{2}}{\partial vec({\mathbf{S})}}&=& \alpha_{\mathbf{S}} \frac{\partial Tr(\mathbf{S}^{\top} \boldsymbol{\Gamma}_{\mathbf{S}} \mathbf{S})} {\partial vec({\mathbf{S})}} +\frac{\partial vec(\mathbf{W})^{\top} vec(\mathbf{Y}-\mathbf{S})} {\partial vec({\mathbf{S})}}\\&&+\frac{\rho}{2} \frac{\partial \left\| \mathbf{Y}-\mathbf{S} \right\|^{2}_{F}} {\partial vec(\mathbf{S})} +\lambda \frac{\partial \left\| \mathbf{Q}_{(1)}-\mathbf{S}(\mathbf{C} \otimes \mathbf{F}\odot\mathbf{T})^{\top} \right\|^{2}_{F}} {\partial vec({\mathbf{S})}} \end{array} $$

(38)

Now based on the properties of matrix trace, Kronecker product [46], and [16], we obtain:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_2}{\partial vec(\mathbf{S})}&=& -2\lambda((\mathbf{F}\odot\mathbf{T})\otimes \mathbf{I}_{{N}_v^2-N_v})^{\top} vec(\mathbf{Q}_{(1)})-vec(\mathbf{W})-\rho vec(\mathbf{Y})\\ &&+(2\alpha_{\mathbf{S}} \mathbf{I}_R \otimes \boldsymbol{\Gamma}_{\mathbf{S}}+2\lambda((\mathbf{F}\odot\mathbf{T})^{\top} (\mathbf{F}\odot\mathbf{T}) )\otimes \mathbf{I}_{{N}_v^2-N_v}\\ &&+\rho\mathbf{I}_{R({N}_v^2-N_v)}) vec(\mathbf{S}) \end{array} $$

(39)

Then, by solving $\frac {\partial \boldsymbol {{\mathscr{L}}}_{2}}{\partial vec({\mathbf {S})}}=\mathbf {0}$ with respect to vec(S), we get:

$$ \begin{array}{@{}rcl@{}} vec(\mathbf{S})&=&(\alpha_{\mathbf{S}} \mathbf{I}_R \otimes \boldsymbol{\Gamma}_{\mathbf{S}} + \lambda ((\mathbf{C} \otimes \mathbf{F}\odot\mathbf{T})^{\top} (\mathbf{C} \otimes \mathbf{F}\odot\mathbf{T}) )\otimes \mathbf{I}_{{N}_v^2-N_v}+\rho \mathbf{I}_{R({N}_v^2-N_v)})^{-1}\\ &&\times\left( \left( \lambda (\mathbf{C} \otimes \mathbf{F}\odot\mathbf{T})^{\top}\otimes \mathbf{I}_{{N}_v^2-N_v}\right)vec(\mathbf{Q}_{(1)})+\frac{vec(\mathbf{W})}{2}+\frac{\rho}{2} vec(\mathbf{Y})\right) \end{array} $$

(40)

1.2.2 A.2.2 Update of T

Similarly, the stationary point of ${\mathscr{L}}_{2}$ defined in Eq. 17 in T is computed by solving the equation $\frac {\partial \boldsymbol {{\mathscr{L}}}_{2}}{\partial vec({\mathbf {T})}}=\mathbf {0}$. Then according to Eq. 36, we can write:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_2}{\partial vec({\mathbf{T})}}= \alpha_{\mathbf{T}} \frac{\partial Tr(\mathbf{T} \boldsymbol{\Gamma}_{\mathbf{T}} \mathbf{T}^{\top})} {\partial vec({\mathbf{T})}} +\lambda \frac{\partial \left\| \mathbf{Q}_{(2)}-\mathbf{T}(\mathbf{S}\odot\mathbf{F})^{\top} \right\|^2_F} {\partial vec({\mathbf{T})}} \end{array} $$

(41)

Based also on the properties of matrix trace, Kronecker product [46], and [16], we obtain:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_2}{\partial vec({\mathbf{T})}}& =& 2\lambda ((\mathbf{S} \odot \mathbf{F})\otimes \mathbf{I}_{N_w})^{\top} vec(\mathbf{Q}_{(2)})\\ &&+(2\alpha_{\mathbf{S}} \mathbf{I}_{R}\otimes \boldsymbol{\Gamma}_{T}+2\lambda((\mathbf{S} \odot \mathbf{C} \odot \mathbf{F})(\mathbf{S} \odot \mathbf{C} \odot \mathbf{F})^{\top})\otimes \mathbf{I}_{N_w})vec(\mathbf{T}) \end{array} $$

(42)

Then, by solving $\frac {\partial {\mathscr{L}}_{2}}{\partial vec(\mathbf {S})}=\mathbf {0}$, we get:

$$ \begin{array}{@{}rcl@{}} vec(\mathbf{T})&=&(\alpha_{\mathbf{T}} \mathbf{I}_R \otimes \boldsymbol{\Gamma}_{\mathbf{T}} +\lambda ((\mathbf{S}\odot\mathbf{C} \odot\mathbf{F})^{\top}\\ &&\times (\mathbf{S}\odot\mathbf{C} \odot\mathbf{F}) )\otimes \mathbf{I}_{{N_w}})^{-1}(\lambda(\mathbf{S}\odot\mathbf{C} \odot\mathbf{F})^{\top}\otimes \mathbf{I}_{{N_w}})vec(\mathbf{Q}_{(2)}) \end{array} $$

(43)

1.2.3 A.2.3 Update of F

The stationary point of ${\mathscr{L}}_{2}$ defined in Eq. 17 in F is computed by solving the equation $\frac {\partial \boldsymbol {{\mathscr{L}}}_{2}}{\partial vec({\mathbf {F})}}=\mathbf {0}$. Then, according to Eq. 24, we can write:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_1}{\partial vec({\mathbf{F})}}= \alpha_{\mathbf{F}} \frac{\partial Tr(\mathbf{F} \boldsymbol{\Gamma}_{\mathbf{F}} \mathbf{F}^{\top})} {\partial vec({\mathbf{F})}} +\lambda \frac{\partial \left\| \mathbf{Q}_{(3)}-\mathbf{F}(\mathbf{T}\odot\mathbf{S})^{\top} \right\|^2_F} {\partial vec({\mathbf{F})}} \end{array} $$

(44)

Based also on the properties of matrix trace, Kronecker product [46], and [16], we obtain:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_2}{\partial vec({\mathbf{F})}}&=& 2\lambda ((\mathbf{T} \odot \mathbf{S}\odot \mathbf{C})\otimes \mathbf{I}_{N_f})^{\top} vec(\mathbf{Q}_{(3)})\\ &+&(2\alpha_{\mathbf{F}} \mathbf{I}_{R}\otimes \boldsymbol{\Gamma}_{F}+2\lambda((\mathbf{T} \odot \mathbf{S}\odot \mathbf{C})(\mathbf{T} \odot \mathbf{S}\odot \mathbf{C})^{\top})\otimes \mathbf{I}_{N_f})vec(\mathbf{F}) \end{array} $$

(45)

Then, by solving $\frac {\partial {\mathscr{L}}_{2}}{\partial vec(\mathbf {F})}=\mathbf {0}$, we get:

$$ \begin{array}{@{}rcl@{}} vec(\mathbf{F})&=&(\alpha_{\mathbf{F}} \mathbf{I}_{R} \otimes \boldsymbol{\Gamma}_{\mathbf{F}} +\lambda ((\mathbf{T}\odot\mathbf{S}\odot \mathbf{C})^{\top} (\mathbf{T}\odot\mathbf{S}\odot \mathbf{C}) )\otimes \mathbf{I}_{{N_{f}}})^{-1}\\ &&\times (\lambda(\mathbf{T}\odot\mathbf{S}\odot \mathbf{C})^{\top}\otimes \mathbf{I}_{{N_{f}}})vec(\mathbf{Q}_{(3)}) \end{array} $$

(46)

1.2.4 A.2.4 Update of C

Similarly, the stationary point of ${\mathscr{L}}_{2}$ defined in Eq. 17 in C is computed by solving the equation $\frac {\partial \boldsymbol {{\mathscr{L}}}_{2}}{\partial vec({\mathbf {C})}}=\mathbf {0}$. Then according to Eq. 24, we can write:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_2}{\partial vec({\mathbf{C})}}= \alpha_{\mathbf{C}} \frac{\partial Tr(\mathbf{C} \boldsymbol{\Gamma}_{\mathbf{C}} \mathbf{C}^{\top})} {\partial vec({\mathbf{C})}} +\lambda \frac{\partial \left\| \mathbf{Q}_{(4)}-\mathbf{C}(\mathbf{F}\odot\mathbf{T}\odot\mathbf{S})^{\top} \right\|^2_F} {\partial vec({\mathbf{C})}} \end{array} $$

(47)

Based also on the properties of matrix trace, Kronecker product [46], and [16], we obtain:

$$ \begin{array}{@{}rcl@{}} \frac{\partial \boldsymbol{\mathcal{L}}_2}{\partial vec({\mathbf{C})}}&=& 2\lambda ((\mathbf{F}\odot\mathbf{T}\odot\mathbf{S})\otimes \mathbf{I}_{N_c})^{\top} vec(\mathbf{Q}_{(4)})\\ &&+(2\alpha_{\mathbf{C}} \mathbf{I}_{R}\otimes \boldsymbol{\Gamma}_{C}+2\lambda((\mathbf{F}\odot\mathbf{T}\odot\mathbf{S})(\mathbf{F}\odot\mathbf{T}\odot\mathbf{S})^{\top})\otimes \mathbf{I}_{N_c})vec(\mathbf{C}) \end{array} $$

(48)

Then, by solving $\frac {\partial {\mathscr{L}}_{2}}{\partial vec(\mathbf {C})}=\mathbf {0}$, we get:

$$ \begin{array}{@{}rcl@{}} vec(\mathbf{C})&=&(\alpha_{\mathbf{C}} \mathbf{I}_R \otimes \boldsymbol{\Gamma}_{\mathbf{C}} +\lambda ((\mathbf{F}\odot\mathbf{T}\odot\mathbf{S})^{\top} (\mathbf{F}\odot\mathbf{T}\odot\mathbf{S}) )\otimes \mathbf{I}_{{N_c}})^{-1}\\ &&\times (\lambda(\mathbf{F}\odot\mathbf{T}\odot\mathbf{S})^{\top}\otimes \mathbf{I}_{{N_c}})vec(\mathbf{Q}_{(4)}) \end{array} $$

(49)

1.2.5 A.2.5 Update of Y

The update rule of the dual variable Y is given by:

$$ \mathbf{Y} \leftarrow \mathbf{Y}+{prox}_{\phi,\frac{\delta}{\rho}}\left( \mathbf{S}+\frac{\mathbf{W}}{\rho}\right) $$

(50)

1.2.6 A.2.6 Update of W

The update rule of the Lagrange multiplier W is given by:

$$ \mathbf{W} \leftarrow \mathbf{W} +\rho (\mathbf{S}-\mathbf{Y}) $$

(51)