Constraint multi-objective optimal design of hybrid renewable energy system considering load characteristics

Abstract

Finding the optimal size of a hybrid renewable energy system is certainly important. The problem is often modelled as an multi-objective optimization problem (MOP) in which objectives such as annualized system cost, loss of power supply probability etc. are minimized. However, the MOP model rarely takes the load characteristics into account. We argue that ignoring load characteristics may be inappropriate when designing HRES for a place with intermittent high load demand. For example, in a training base the load demand is high when there are training tasks while the demand decreases to a low level when there is no training task. This results in an interesting issue, that is, when the loss of power supply probability is determined at a specific value, say 15%, then it is very likely that most of loss of power supply would occur right in the training period which is unexpected. Therefore, this study proposes a constraint multi-objective model to deal with this issue—in addition to the general multi-objective optimization model, the loss of power supply probability over a critical period is set as a constraint. Correspondingly, the non-dominated sorting genetic algorithm II with a relaxed $\epsilon$ constraint handling strategy is proposed to address the constraint MOP. Experimental results on a real world application demonstrate that the proposed model and algorithm are both effective and efficient.

Introduction

Electricity in remote places, e.g., islands, are generally supplied by fossil fuel based generation systems. However, due to the depletion of fossil fuels and harmful emissions, renewable energies which are sustainable and environment-friendly have received increasing attentions in recent years. Nevertheless, their intermittence and unpredictable characteristics have brought challenges for their applications. In order to resolve this issue, multi-energy complementary hybrid renewable energy systems (HRES) have become increasingly popular [1, 2].

In this context, optimal sizing components of a HRES, i.e., determining the capacity of system components on the premise of certain optimization objectives, is a key factor to attain a low cost and reliable HRES. In general, the problem can be formulated as an multi-objective optimization model, see Eq. (1).

$$\begin{aligned} \begin{aligned} \text {Min}&F(\mathbf {x}) = \{f_1(\mathbf {x}),f_2(\mathbf {x}),\ldots , f_m(\mathbf {x}) \} \\ \text {S.T.}&\mathbf {x} = (x_1,x_2,\ldots ,x_i,\ldots , x_k) \in \Omega \end{aligned} \end{aligned}$$

(1)

where $f_1(\mathbf {x}),f_2(\mathbf {x}),\ldots , f_m(\mathbf {x})$ represent optimization objectives such as the annualized system cost (ASC), loss of power supply probability (LPSP) [3], and $\mathbf {x}$ is the decision vector which determines the HRES size such as the number of photovoltaic (PV) panels, wind turbines, the installation angle of PV panels. Besides, m and $\Omega$ in Eq. (1) denote the number of objectives and the search space, respectively. With the MOP model, an optimization solver such as evolutionary multi-objective algorithm [4] can then be applied to find a set of Pareto optimal solutions. These solutions effectively present different trade-offs amongst optimization objectives [5, 6]. To this end, a decision-maker can select his/her preferred solution, i.e., HRES size. The above method presents a basic process of sizing a HRES. For a specific application scenario, the method, especially the MOP model, needs to be further refined.

In this paper, the research of optimal sizing of HRES focuses on places whose load demand has intermittent characteristics. For example, in a training base, when there are training tasks the load demand is high, however, when the training completes, the load demand becomes very low. In addition, the annual training tasks and training period are usually fixed. Therefore, while sizing a HRES for such places, the load characteristics are suggested to be taken into account. That is, in addition to the commonly used optimization criteria, an additional constraint that measures the power supply reliability over the training period must be included. This is also to ensure an appropriate use of the criterion of LPSP. Generally, LPSP at about 10–15% is acceptable in an HRES. However, for the above scenario, it is very likely that the loss of power supply would mostly occur during the training period, which is clearly not expected.

Therefore, this study proposes a constraint multi-objective optimization model for the optimal sizing of HRES in places with intermittent high load demand. Specifically, the annualized system cost (ASC), loss of power supply probability (LPSP) are used as optimization objectives, the LPSP of a specific period, denoted as LPSP-T, is considered as a constraint. Correspondingly, an effective and efficient constraint multi-objective evolutionary algorithm, i.e., NSGA-II with an $\epsilon$ relaxed constraint handling strategy, is proposed to address the constraint MOP, searching for the best HRES size, i.e., the number of PV panels and their installation angle ($N_\mathrm{pv}$ and $\alpha$), the number of wind turbines and their installation height ($N_\mathrm{wt}$ and H), the number of diesel generators ($N_\mathrm{dg}$), the number of battery banks ($N_\mathrm{bat}$). Lastly, a case study on Chang-Shan island ($122^\circ 44' N$, $37\circ 55' E$) demonstrates the effectiveness of the proposed model and algorithm.

The rest of this paper is organized as follows. Section 3 reviews recent studies with respect to optimal sizing of HRES. Section 4 presents mathematical models of the main components in HRES. Section 5 elaborates the proposed constraint MOP model and optimizer for optimal sizing of HRES. This is then followed by a case study in Sect. 6. Section 7 concludes the paper, and identifies future studies.

Literature review

The optimal sizing of HRES has been intensively studied as shown in Fig. 1. These studies have mainly investigated the following two issues—(i) various combinations of optimization objectives while sizing a HRES such as the loss of power supply probability, loss of load probability, annualized system cost, energy production and environmental emissions, and (ii) development of different problem solvers including linear programming, heuristics, hybrid methods and software tools. This section briefly reviews some representative studies. Readers can refer to [7,8,9] for more comprehensive surveys.

Fig. 1

The number of publications in Web of Science with respect to “multi-objective optimal sizing (design) of hybrid renewable energy system”

In [10] the optimal sizing of a PV-wind-battery system is conducted. A single objective constraint optimization model is built in which the annualized system cost is minimized while a pre-defined LPSP is satisfied. The design variables include the number of PV panels, the slope angle of PV panels, the number of wind turbines and their installation height, and the capacity of batteries. In [11], the optimal energy storage size of a PV-based standalone system under different time scales is studied in which the optimization criterion is the lifetime system cost. In [3] the optimal size of a PV-wind-battery-diesel system is studied where ASC, LPSP and greenhouse gas emission are minimized. Interestingly, this study takes both the type of and capacity of HRES components as decision variables. With respect to the studies of models in the optimal sizing of HRES, the authors of [8] reviewed the latest studies and found that the PV-Wind-Diesel-Battery is the most frequent configuration. Also, in [12] a systematic framework integrated with techno-economic optimization analysis for the design of HRES is provided. The study examined different hybridizations of system components, i.e., solar photovoltaic, wind turbines, diesel generators, batteries and converters. It is found that the hybrid PV-wind-diesel-battery-converter system is the most feasible and reliable solution in terms of minimizing the system cost and pollutant emissions.

Due to the model complexity of optimal sizing of HRES, various algorithms have been developed to solve the model. In [13] the socio-techno-economic optimal design of HRES is studied where the effect of different hybridizations of wind turbines, PV panels, diesel generators, biomass and batteries is examined. Also, performance of several representative evolutionary algorithms on this problem is analyzed. In [14], the grey wolf optimization algorithm is proposed to find the optimal size of HRES in terms of minimizing the system cost. In [15] a multi-objective hybrid particle swarm optimization-grey wolf optimizer is applied to find the optimal size of HRES while minimizing the total cost and emissions in a 20-years lifetime. Note that in this study the HRES is grid-connected and is integrated with a reverse osmosis desalination plant. It uses PV modules and wind turbines as the main source of energy, and uses battery banks and hydrogen storage systems as to store energy. Diesel generators are used as backup energy sources. In [16] the HRES is composed of only PV panels and diesels. Multi-objective crow search algorithm (MOCSA) is applied to solve the sizing model where the total net present cost, $\mathrm{CO}_2$ emission and LPSP are taken as optimization objectives. Experimental results show that MOCSA outperforms multi-objective particle swarm optimization on this problem. In [17] four heuristics, i.e., lion optimizer algorithm , grey wolf optimizer algorithm, krill herd algorithm and JAYA algorithm, are applied to minimizing the unit energy cost of HRES for a specified LPSP. Experimental results show that JAYA is the most effective. Besides, this study also investigated the effect of different energy storage technologies in solar-wind hybrid system, i.e., PV/Wind/Ni-Cd, PV/Wind/Li-ion and PV/Wind/LA, and found that PV/Wind/Ni-Cd and PV/Wind/Li-ion are more effective than PV/Wind/LA. Lastly, as reviewed in [7], HRES sizing methods also include classical methods and software tools. For example, dynamic programming is used in [18], the HOMER software is applied in [19, 20].

To make the sizing model more applicable, uncertainties such as renewable resources availability and load demand have gradually received attentions in the design of HRES. For example, the study [21] proposed a probabilistic simulation-based multi-objective optimization method for sizing HRES under various uncertainties. Experimental results show that the system cost with the same LPSP under uncertain environment is a bit higher than that under deterministic condition. In [22] uncertainties of wind speed and solar radiation are considered in the design of HRES. The NSGAII algorithm integrated with a chance constrained programming method is applied to solve the model. In [23] the particle swarm optimization algorithm integrated with Monte Carlo simulation method is applied to sizing HRES under uncertainties. Very recently, the authors of [24] proposed a two-stage method to handle the optimal sizing of HRES under uncertainties for seaports. In the first stage, the capacity of system components, i.e., the PV panels, diesels, is optimized by minimizing the investment cost. In the second stage, the stochastic characteristics of wind energy and load demand in the seaports are further considered to minimize the operation cost and to satisfy the capacity and emission constraints.

Overall there have been a large number of studies with respect to multi-objective optimal sizing of HRES. However, these studies rarely take the characteristics of load demand into account. As is previously mentioned, the load demand of some places may have intermittent characteristics. That is, the load demand is high during a specific period while is relatively low at the rest of time. In such case we argue that load characteristics cannot be ignored while sizing HRES. Thus, this study proposes a novel constraint multi-objective model and an effective constraint multi-objective evolutionary algorithm to sizing HRES.

Modelling

This study focuses on stand-alone hybrid renewable energy system as shown in Fig. 2. The HRES in specific contains PV panels, wind turbines, battery banks, diesel generators as well as other accessory devices and cables. Next we describe mathematical models of these HRES components.

Fig. 2

Illustration of a typical stand-alone hybrid solar and wind system [25]

PV panels

The solar energy is utilized through PV panels. The power output by PV panels is mainly determined by solar radiation (sr), the number (size) of panels ($N_\mathrm{pv}$) and the installation angle of panels ($\alpha$). Specifically, the model described in [26] is adopted, see Eq. (2).

$$\begin{aligned} \begin{aligned} P_\mathrm{pv}(t)&= I_\mathrm{SC}(t)\cdot V_\mathrm{OC}(t) \cdot \eta _\mathrm{pv}\\ I_\mathrm{SC}(t)&= [I_\mathrm{SC,STC}+ K_I\left( T_C(t)-25\right) ]\frac{sr_p(t)}{1000}\\ V_\mathrm{OC}(t)&= V_\mathrm{OC,STC}+K_V \cdot T_C(t)\\ T_C(t)&= T_A(t) + \frac{T_\mathrm{CSTC}-20}{800} \mathrm{sr}_p(t) \end{aligned} \end{aligned}$$

(2)

where $P_\mathrm{pv}(t)$ denotes power output by a single PV panel at time step t, which equals to the product of short-circuit current, $I_\mathrm{SC}(t)$(A), the open-circuit voltage, $V_\mathrm{OC}(t)$(V), and the coefficient of efficiency of PV panels, $\eta _\mathrm{pv}$. Note that $\eta _\mathrm{pv}$ accounts for the power loss caused by the cable resistance, the diffused and reflected solar radiation and the accumulative dust, and is set to 0.95 [26]. Both $I_\mathrm{SC}$ and $V_\mathrm{OC}$ are determined by the short-circuit current $I_\mathrm{SC,STC}$ and open-circuit voltage $V_\mathrm{OC,STC}$ under standard condition (STC), the cell temperature $T_C$ ($^\circ$C), $K_I$ (the coefficient of the short-circuit current temperature, $A/^\circ C$) and $K_V$ (the coefficient of open-circuit voltage temperature $V/^\circ C$). The parameter $\mathrm{sr}_p$ denotes solar radiation perpendicular to PV panels, which affects both $I_\mathrm{SC}$ and $T_C$. $T_C$ is also affected by the ambient temperature $T_A$($^\circ$C) and the nominal cell operating temperature $T_\mathrm{CSTC}$($^\circ$C). Lastly, $\mathrm{sr}_p$ is determined by the solar radiation (sr), the installation angle of panels ($\alpha$), and the geography of the latitude ($\phi$), see Eq. (3) [27].

$$\begin{aligned} \begin{aligned} \mathrm{sr}_p(t)&= \frac{\mathrm{sr}(t)}{\sin \beta }\cdot \sin (\alpha +\beta )\\ \sin \beta&= \sin \phi \sin \delta + \cos \phi \cos \delta + \cos \tau \\ \delta&= \theta \times \left( \frac{360\times (284+d)}{365}\right) \\ \tau&= \frac{360\times (12-t_\mathrm{loc})}{24} \\ \theta&= 23.44^\circ \\ \end{aligned} \end{aligned}$$

(3)

where d denotes the cumulative days with January 1st as 1, and $t_\mathrm{loc}$ denotes the local time ($0\le t_\mathrm{loc} \le 23$). In the equation, $\delta$ and $\beta$ denote the solar declination and the angle between the sun and the horizon over a day, respectively. $\theta = 23.44^\circ$ indicates the angle between the equatorial plane and the earth axis.

One advantage of the PV model is that the latitude of the place, the change of solar elevation angle over a day and the installation angle $\alpha$ are all considered for the measurement of solar radiation which enables the calculation of power output to be more accurate. Certainly, the model also has shortcomings, for example, the diffused and reflected solar radiation are neglected though they have little effect.

Wind turbine

The output power of wind turbines is determined by the wind speed (v), the cut-in ($V_\mathrm{in}$), cut-off wind speed ($V_\mathrm{off}$), and can be described using a piecewise linear function. In specific, wind turbines generate power when the wind speed v is larger than $V_\mathrm{in}$. The output power linearly increases as v increases to the rated wind speed ($V_r$). When $V_r<v<V_\mathrm{off}$, the output power equals to the rated power $P_\mathrm{wtr}$. Lastly, when $v < V_\mathrm{in}$ or $v > V_\mathrm{off}$ wind turbines are shut down for safety reasons. Mathematically, Eq. (4) presents the power output by a single wind turbine.

$$\begin{aligned} P_\mathrm{wt} = {\left\{ \begin{array}{ll} 0, &{} v< V_\mathrm{in} \\ P_\mathrm{wtr} \cdot \frac{v-V_\mathrm{in}}{V_r-V_\mathrm{in}} &{} V_\mathrm{in}\le v< V_r \\ P_\mathrm{wtr} &{} V_r \le v < V_\mathrm{off} \\ 0, &{} v > V_\mathrm{off} \end{array}\right. } \end{aligned}$$

(4)

In general, given the wind speed record of a place ($V_\mathrm{ref}$) at a reference height $H_\mathrm{ref}$, the wind speed v of height H can be refined by Eq. (5).

$$\begin{aligned} v = V_\mathrm{ref}\left( \frac{H_\mathrm{ref}}{H} \right) ^\gamma \end{aligned}$$

(5)

where $\gamma$ is usually set as $\frac{1}{7}$ for relatively flat surfaces.

Battery banks

In a HRES battery banks store excess power generated by PV panels and wind turbines, and output power when there is a load-supply gap. The working process of battery banks can be described using the parameter state-of-charge (SOC), see Eq. (6)

$$\begin{aligned} \begin{aligned}&\mathrm{SOC}(t+1) = \mathrm{SOC}(t)\cdot (1-\delta _\mathrm{bat}) \\&\qquad \qquad \qquad \qquad + sign \cdot \frac{\eta _\mathrm{bat} \cdot E_\mathrm{bat}(t) \cdot \Delta _t}{Cap_\mathrm{bat}}\cdot \frac{1}{N_\mathrm{bat}}\\&sign = 1~~\text {charging mode}\\&sign = -1~~\text {discharging mode}\\ \end{aligned} \end{aligned}$$

(6)

where SOC of the $(t+1)$ step, $\mathrm{SOC}(t+1)$, is determined by $\mathrm{SOC}(t)$ and the total power ($E_\mathrm{bat}(t)$) charged or discharged at time step t. Parameters $\delta _\mathrm{bat}$ and $\mathrm{Cap}_\mathrm{bat}$ denote the self-discharging coefficient and the nominal capacity of the battery, respectively. $\eta _\mathrm{bat}$ denotes the round-trip efficiency of batteries. Lastly, $\mathrm{SOC}(t)$ of batteries is always restricted within $\mathrm{SOC}_\mathrm{min}$ and $\mathrm{SOC}_\mathrm{max}$ for safety reasons.

Fig. 3

Simulation of HRES workflow over a year’s time [3]

Diesel generator

When the power demand cannot be met by both renewable energies and battery banks, diesel generators start working. The output power of a single diesel generator can be calculated as follows [25].

$$\begin{aligned} \begin{aligned} P_\mathrm{dg} = P_\mathrm{rdg} \cdot \eta _\mathrm{dg} \end{aligned} \end{aligned}$$

(7)

where $P_\mathrm{rdg}$ denotes the nominal output power of a diesel generator, and $\eta _\mathrm{dg}$ is a coefficient describing the efficiency of diesel generator.

Constrained Multi-objective optimal sizing model of HRES

Prior to introducing the optimization model of HRES, the workflow of HRES is presented in Fig. 3. Assuming that the hourly load demand, the wind speed and the solar radiation are known beforehand, first power generated by renewable energies is used to meet the load demand. Note that efficiencies of inverter ($\mathrm{in}_e$) and rectifier ($\mathrm{re}_e$) are set to 0.9 [10]. After satisfying the load demand, excess power is used to charge battery banks till they reach the maximum SOC. On the other hand, if the load demand cannot be met by renewable energies, then battery banks discharge their power till they reach the minimum SOC. If the load demand still cannot be met, then diesel generators start working to fill in the demand-supply gap. Accordingly, the cost of fuel consumption and the associated gas emissions are calculated. Note that when the fuel is also used up while the load demand is still unmet, then some load will be cut off. This accounts for a loss of power supply.

Next we present the constraint multi-objective optimal model proposed for sizing HRES with load characteristics. The optimization objectives are minimization of the loss of power supply probability, $F_\mathrm{LPSP}$ and minimization of the annualized system cost, $F_\mathrm{ASC}$, and the constraint $C_\mathrm{LPSP}$ is that the loss of power supply probability during a specific period must be lower than a specified level. Assuming that the overall number of simulation steps is a year’s time, i.e., $T = 8760$, next we describe how to calculate $F_\mathrm{LPSP}$, $F_\mathrm{ASC}$ and $C_\mathrm{LPSP}$.

• $F_\mathrm{ASC}$ is the annualized system cost which is composed of the investment cost ($C_\mathrm{ini}$) of HRES distributed to each year, the operation and maintenance cost ($C_\mathrm{aom}$) per year, the battery replacement cost per year, the fuel consumption and emission cost.

  $$\begin{aligned} \begin{array}{ll} F_\mathrm{ASC} &{}= C_\mathrm{ini} + C_\mathrm{om} + C_\mathrm{rep}+ C_\mathrm{fuel}\\ &{}= C_\mathrm{ini}(\mathrm{PV} + \mathrm{WT} + \mathrm{Bat} + \mathrm{DG}) +\\ &{} C_\mathrm{om}(\mathrm{PV} + \mathrm{WT} + \mathrm{Bat} + \mathrm{DG})+\\ &{} C_\mathrm{rep}(\mathrm{Bat})+\\ &{} C_\mathrm{fuel} \end{array} \end{aligned}$$

  (8)

  where $C_\mathrm{fuel}$ accounts for the cost of fuel consumption and the cost of greenhouse gas emission.

  $$\begin{aligned} \begin{array}{ll} C_\mathrm{fuel}&{}= C_\mathrm{emi} + C{cosp}\\ &{}= \sum _{i=0}^{T} Q_\mathrm{fuel}(t)* \mathrm{fuel}_c +\\ &{}= \sum _{i=0}^{T} Q_\mathrm{fuel}(t)* \mathrm{emi}_{\alpha }*fac_\mathrm{emi}\\ Q_\mathrm{fuel}(t) &{}= P_\mathrm{rdg}* dg_1 + P_\mathrm{dg}(t)*\mathrm{dg}_2 \end{array} \end{aligned}$$

  (9)

  where $Q_\mathrm{fuel}(t)$(L) denotes the fuel consumption at time step t and $fuel_c$ is the fuel price. $\mathrm{fac}_\mathrm{emi} \in$ [2.4kg/L, 2.8kg/L] is diesel generator related parameter that measures the emission coefficient. $\mathrm{emi}_{\alpha }$ is the coefficient of emission-to-cost. Besides, $\mathrm{dg}_1=0.08145$1/kWh and $\mathrm{dg}_2=0.246$1/kWh are parameters, describing the curve of fuel consumption [28].

  Given the life time of HRES is designed for 20 years, it is necessary to consider the nominal interest rate (nir) and the inflation rate (ir). Specifically, the real annual interest rate (rair), the capital recovery factor (crf) and the sinking fund factor (sff) are calculated as follows.

  $$\begin{aligned} \begin{aligned}&\mathrm{rair} = \frac{\mathrm{nir-ir}}{1_\mathrm{ir}}\\&\mathrm{crf} = \frac{\mathrm{rair}(1+r \mathrm{air})^{ly}}{(1+\mathrm{rair})^{\mathrm{ly}}-1}\\&\mathrm{sff} = \frac{\mathrm{rair}}{(1 + \mathrm{rair})^{lbat}-1}\\&\mathrm{ly} = 25,~~lbat = 5,~~\mathrm{nir} = 3.75\%,~~ir = 1.5\% \end{aligned} \end{aligned}$$

  (10)

  where lhres and lbat denote the life time of HRES and batteries, respectively.

  Moreover, Eq. (11) calculates the $C_\mathrm{ini}$, $C_\mathrm{rep}$ and $C_\mathrm{om}$.

  $$\begin{aligned} \begin{aligned}&C_\mathrm{ini}(\mathrm{PV} + \mathrm{WT} + \mathrm{Bat} + \mathrm{DG}) \\&\quad = \mathrm{crf} \cdot (N_\mathrm{pv}C_\mathrm{ipv}+N_\mathrm{wt}C_\mathrm{iwt}+N_\mathrm{bat}C_\mathrm{ibat}+N_\mathrm{dg}C_\mathrm{idg})\\&C_\mathrm{om}(PV+WT+Bat+DG)\\&\quad = N_\mathrm{pv}C_\mathrm{mpv}+N_\mathrm{wt}C_\mathrm{mwt}\\&\qquad +N_\mathrm{bat}C_\mathrm{mbat}+N_\mathrm{dg}C_\mathrm{mdg} C_\mathrm{rep}(Bat)\\&= sff \cdot (N_\mathrm{bat}C_\mathrm{rbat}) \end{aligned} \end{aligned}$$

  (11)

  where $C_\mathrm{ipv}, C_\mathrm{iwt}, C_\mathrm{ibat}$ and $C_\mathrm{idg}$ denote the initial investment cost of PV panels, wind turbines, battery banks and diesel generators distributed in each year, respectively. $C_\mathrm{mpv},C_\mathrm{mwt}$ $,C_\mathrm{mbat}$ and $C_\mathrm{mdg}$ denote the operation and maintenance cost of these components per year. $C_\mathrm{rbat}$ denotes the battery replacement cost per year.

• $F_\mathrm{LPSP}$ measures the overall loss of power supply probability, which is calculated as follows.

  $$\begin{aligned} F_\mathrm{LPSP} = \frac{\sum _{i=0}^{T} t_i}{T} \end{aligned}$$

  (12)

  where $t_i=1$ when the supplied power $P_\mathrm{supply}(t)$ at time t is smaller than the load demand $P_\mathrm{load}(t)$, otherwise $t_i=0$.

• $C_\mathrm{LPSP}$ describes the loss of power supply probability during a specific period, and is defined in Eq. (13).

  $$\begin{aligned} C_{\mathrm{LPSP}_T} = \frac{\sum _{i\in \Omega _t} t_i}{|\Omega _t|} \end{aligned}$$

  (13)

  where $\Omega _t$ denotes a specific period. For example, $\Omega _t$ can be an interval $[t_1,t_2]$ where $t_1$ and $t_2$ denote the beginning and end simulation steps, respectively.

Overall, the two-objective constraint optimization model is described as follows.

$$\begin{aligned} \begin{array}{rl} \text {Min} F(\mathbf {x}) = &{} \{F_\mathrm{LPSP}, F_\mathrm{ASC}\} \\ \mathbf {x} = &{} (N_\mathrm{pv},\alpha ,N_\mathrm{wt},H, N_\mathrm{bat}, N_\mathrm{dg})\\ S.T.~~ &{}\\ &{} C_{\mathrm{LPSP}_T} \le \mathrm{LPSP}_v\\ &{} H \in [10,30]\\ &{} \alpha \in (0^\circ , 90^\circ ) \\ &{} N_\mathrm{pv}, N_\mathrm{wt},N_\mathrm{bat},N_\mathrm{dg}\in [0,50] \end{array} \end{aligned}$$

(14)

where $\mathrm{LPSP}_v$ is a pre-specified constraint value.

Remark

in general the optimal sizing of HRES is solved using an multi-objective model. However, we argue that for places that have intermittent high load demand, it is necessary to introduce the constraint, i.e., $C_{\mathrm{LPSP}_T} \le \mathrm{LPSP}_v$ into the model so as to find more appropriate HRES designs. For example, when we design a HRES for a training base, the load of such place features significant characteristics. That is, when there are training tasks, the load demand is high while when there is no training task, the load demand is low. Moreover, the training only occurs at a fixed period of a year, e.g., summer or winter holidays. It is surprising to see that in literature this issue is rarely discussed. Without introducing the $C_{\mathrm{LPSP}_T}$ constraint, it is very likely that when $F_\mathrm{LPSP}$ is specified at certain level, e.g., 10%, then the loss of power supply occurs mostly during the training period. Besides, at the rest of time the power output by renewable energies could be redundant. By introducing the constraint, it is explicitly guaranteed that the loss of power supply probability at a specific (or preferred) period meet the practical demand (or preference of decision-makers).

Algorithm

In literature, the optimal sizing of HRES design is generally solved by an unconstrained evolutionary multi-objective (EMO) algorithm . For example, in [29], PICEAg [30] is applied to sizing a standalone HRES in which the annualized cost, system reliability and emissions are minimized. In addition to PICEAg, other EMO algorithms, e.g., SPEA [31], NSGAII [32], MOEA/D [33, 34] have also been used, see [3, 25, 35]. Based on these studies, this section proposes an effective EMO algorithm to solve the constraint multi-objective optimization model.

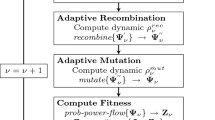
The well-known NSGAII is taken as the base EMO algorithm due to its effectiveness and robustness on various real world problems [32]. As is shown in Fig. 4, NSGAII is an $(N+N)$ elitist algorithm. That is, the offspring solutions of size $\mu$ are combined with their parents, the combined solutions compete with each other to obtain the next N parent solutions. Readers are referred to [32] for more details about NSGA-II.

Fig. 4

Illustration of the $(N+N)$ elitist framework

In order to handle the constraint multi-objective model, we integrate a relaxed $\epsilon$ constraint handling technique into NSGAII, the derived algorithm is denoted as $\epsilon$-CNSGAII. Prior to elaborating the $\epsilon$-CNSGAII, we describe the relaxed $\epsilon$ technique. The idea is simple—if the constraint violation of a solution is less than the value of $\epsilon$, then the solution is taken as feasible, otherwise it is infeasible. In principle the setting of $\epsilon$ is related to the trade-off between feasible and infeasible solutions. At the beginning of the search, $\epsilon$ is set as a large value, which enables most of solutions to be feasible. As the search progresses, $\epsilon$ changes based on the generation number and the ratio of feasible solutions. Specifically, $\epsilon$ is changed according to the following rule. When most of solutions are infeasible, then $\epsilon$ is exponentially decreased so as to effectively push the search towards feasible regions. If most of solutions become feasible, then $\epsilon$ is increased such that the exploration in the infeasible regions is strengthened. The adaptive $\epsilon$ is helpful in making use of both feasible and infeasible information, and thus, leading to a good algorithm performance. The relaxed $\epsilon$ strategy is described as follows.

$$\begin{aligned} \begin{aligned} \epsilon _k= {\left\{ \begin{array}{ll} \phi (\mathbf {x}^i),&{}k=1\\ (1-\tau )\epsilon _{k-1},&{}1<k<G_c\hbox { and }r_k\le \delta \\ (1+\tau )\phi _\mathrm{max},&{}1<k<G_c\hbox { and }r_k>\delta \\ 0,&{}k\ge G_c \end{array}\right. } \end{aligned} \end{aligned}$$

(15)

where k is the generation number and $r_k$ is the ratio of feasible solutions in the k-th generation. $G_c$ is the total generation number that allows for the constraint relaxation, and $\delta$ is the parameter used to control the searching preference between the feasible and infeasible regions. $G_c$ and $\delta$ are set to be 80% of the maximum generation number and 0.95, respectively [36]. Additionally, $\mathbf {x}^i$ is the ith solution amongst the initial population which is ranked in descending order according to the constraint violation value, with $\phi (\mathbf {x}^i)$ being the constraint violation of $\mathbf {x}^i$. $\tau$ is a scaling factor and $\tau \in [0,1]$. $\phi _\mathrm{max}$ is the so-far-found maximum constraint violation value.

From Eq. (15), we can observe that (i) when $k< G_c$, $\epsilon _k$ is dynamically adjusted to balance the search in the feasible and infeasible regions, and (ii) when $k\ge G_c$, $\epsilon _k=0$ is applied to exert strong selection pressure towards feasible regions, thus the feasibility of the finally obtained solutions can be ensured.

The pseudo-code of $\epsilon$-CNSGAII is shown in Algorithm (1). The algorithm starts with a set of N randomly generated parent solutions (Line 1). After the objective vectors and the constraint violation values are calculated, the initial solution archive $A_s$, the level of relaxation $\epsilon$ and the maximum constraint violation $\phi _\mathrm{max}$ can be determined (Lines 2–6). Note that if all solutions in the initial population are infeasible, then $A_s=\emptyset$. At each iteration, the same number of offspring solutions are generated through selection, crossover and mutation operators (i.e., simulated binary crossover (SBX) and polynomial mutation (PM) [37]). Then the parent solutions and their offspring are combined to form a joint population (Lines 9–11). Correspondingly, $\phi _\mathrm{max}$ can be updated by comparing the constraint violation values of newly-generated solutions with the original $\phi _\mathrm{max}$, and the maximum one selected (Line 12). As for the joint population $S_\mathrm{joint}$, they are compared based on $\epsilon _k$-level relaxation. That is, for any solution, e.g. $\mathbf {x}^i$, if the constraint violation is less than $\epsilon _k$, then it is considered to be $\epsilon _k$-feasible. Here, we label each $\epsilon _k$-feasible solution in the joint population with “0”. Otherwise, the solutions whose constraint violation is larger than $\epsilon _k$ are labelled with “1”. During the environmental selection phase, the solutions in $S_\mathrm{joint}$ are ranked, based on their Pareto dominance levels, $\epsilon _k$-feasible labels, and the crowding distances. The former two indicators are used in ascending order while the latter one is used in descending order. Based on the ranking results, the best N solutions survive into the next generation, which forms the new parent population S (Lines 13–15). Finally, the solution archive $A_s$ is updated by new feasible solutions. That is, a total number of N solutions are selected from the archive population when its size exceeds N. (Lines 16–19).

The computational complexity of $\epsilon$-CNSGAII is similar to that of NSGA-II, i.e., $O(mN^2)$. Although $\epsilon$-CNSGAII needs to update the parameter $\epsilon _k$, the additional computation is minor.

Case study

This section presents a case study to demonstrate the effectiveness of the proposed model and algorithm. A standalone hybrid renewable energy system is designed for Chang-Shan island of Shandong province, China ($122^\circ 44'N$, $37^\circ 55'E$). The input data of load demand, solar radiation, temperature and wind speed is collected from the site of http://data.cma.cn/, and is illustrated in Fig. 5.

Input data, model and algorithm parameters

Fig. 5

Illustration of load demand, solar radiation, temperature and wind speed for a year’s time horizon (i.e., $T=8760$ hours)

It can be observed from Fig. 5 that the load demand is relatively high during April and May, specifically, $T \in [2191,3650]$, while at the rest of time the load demand is low. Effectively, this accords with the fact that there is extensive training in April and May while little training during the remaining months. As is repeatedly mentioned, this phenomenon raises an interesting issue, that is, although a low LPSP is pre-specified, say 10%, most of the loss of power supply may occur in April and May, which is unexpected.

Parameters of HRES components and the proposed $\epsilon$-CNSGAII are listed in Table 1. Note that parameters of $\epsilon$-CNSGAII are configured based on the results in [38, 39].

Table 1 Related parameter settings of HRES model and the $\epsilon$-CNSGAII algorithm

Results and analysis

In this section we first demonstrate that unconstrained multi-objective sizing model used in most of studies (e.g., [9, 25, 29, 40]) is not appropriate when the load has intermittent characteristics. Second we show that by the proposed constraint multi-objective model and the $\epsilon$-CNSGAII algorithm, the optimal sizing of HRES for this typical case can be successfully tackled. Note that for the unconstrained model, we only consider minimizing the annualized system cost ($F_\mathrm{LPSP}$) and the loss of power supply probability ($F_\mathrm{ASC}$) in Eq. (14). The NSGAII algorithm is adopted as the problem solver.

Sizing HRES with unconstrained model

Figure 6 presents non-dominated solutions of the unconstrained model obtained by NSGAII. The non-dominated solutions correspond to different trade-offs between $F_\mathrm{LPSP}$ and $F_\mathrm{ASC}$. Assuming that a decision maker requires $F_\mathrm{LPSP}\le 15\%$, then solution $\mathbf {x}_A$ that satisfies this requirement while minimizes $F_\mathrm{ASC}$ is identified. In this case, $F_\mathrm{ASC}=7327.9$.

Fig. 6

Non-dominated solutions of the unconstrained multi-objective model obtained by NSGAII

Next we investigate the performance of $\mathbf {x_A}$. The simulation results of the loss of power supply over the whole year is plotted in Fig. 7. The load demand is plotted as a reference. From the results we can find that the loss of power supply frequently occurs during the training period (i.e., April and May). Specifically, when $F_\mathrm{LPSP} = 15\%$, $C_{\mathrm{LPSP}_T}$ is as high as $42.1\%$. This implicitly indicates that the HRES does not really solve the power shortage issue, and thus, we argue that the unconstrained sizing model is not applicable for places having such load characteristics.

Fig. 7

Illustration of loss of power supply labels ( ) over a year’s horizon. The load demand servers as a reference

Sizing HRES with constrained model

In this experiment we introduce $C_{\mathrm{LPSP}_T} \le \mathrm{LPSP}_v$ into the unconstrained model, and for illustration $\mathrm{LPSP}_v$ is set as 30%. This means that the decision-maker expects the loss of power supply probability over the training period to be less than 30%. Figure 8 presents non-dominated solutions of the constrained model obtained by $\epsilon$-CNSGAII. For the easy of comparison, again, the optimal solution satisfying $F_\mathrm{LPSP} \le 15\%$ while minimizing $F_\mathrm{ASC}$ is identified, denoted as $\mathbf {x_B}$. By comparing $\mathbf {x_A}$ and $\mathbf {x_B}$, it is found that $F_\mathrm{ASC}$ of $\mathbf {x_B}$ is 7103.2 which is smaller than that of $\mathbf {x_A}$. Moreover, $\mathbf {x_B}$ satisfies the constraint $C_{\mathrm{LPSP}_T} \le 30\%$ which is better than $\mathbf {x_A}$ with $C_{\mathrm{LPSP}_T} = 42.1\%$. Such results clearly indicate the superiority of the proposed constrained model.

Fig. 8

Non-dominated solutions of the constrained multi-objective model obtained by $\epsilon$-CNSGAII

Next the operation performance of HRES with $\mathbf {x_B}$ as the optimal size is plotted over a year’s time. The hourly power output of PV panels, wind turbines, batteries and diesel generators is shown in Fig. 9.

Fig. 9

Illustration of operation performance of HRES under the optimal size

From Fig. 9 it is observed that (i) when the load demand is low, the power output by PV panels and wind turbines can sufficiently meet the demand, that is, the results in Fig. 9d is positive, and (ii) when the load demand is high in the training period, the demand-supply gap is large. Then, battery banks and diesel generators will start working to fill in the demand-supply gap.

The effectiveness of $\epsilon$-CNSGAII

To effectively solve the constrained multi-objective model, a tailored algorithm, $\epsilon$-CNSGAII is proposed. Alternatively, we can also first ignore the constraint in Eq. (14), and directly apply NSGAII to solve the unconstrained model, obtaining a set of well-spread non-dominated solutions. Then, we filter out solutions that satisfy the constraint from those obtained solutions. However, such approach is not as effective as the $\epsilon$-CNSGAII.

Fig. 10

Non-dominated solutions obtained by $\epsilon$-CNSGAII and NSGAII

For illustration, $\mathrm{LPSP}_v$ is set to 30%, i.e., $C_{\mathrm{LPSP}_T} \le 30\%$ is set as constraint. The obtained non-dominated solutions are shown in Fig. 10. Qualitatively, it can be observed from Fig. 10 that a much richer set of solutions is found by $\epsilon$-CNSGAII than NSGAII. Also, the solutions are more evenly distributed. Furthermore, the hypervolume metric, a widely used indicator for performance assessment of non-dominated solution set, is employed to quantitatively compare the results. The hypervolume metric measures the volume enclosed by non-dominated solutions and a reference point [31]. The larger the hypervolume, the better the solution set. Prior to calculating the hypervolume metric, solutions are normalized within [0,1] by the ideal point (0,0) and the nadir point. Note that in this case study the nadir point is approximated by the maximum objective values of each objective amongst all solutions. The reference point is then set as [1.1, 1.1]. The hypervolume values for the two sets of solutions are 0.7956 and 0.8464, respectively, which indicates that $\epsilon$-CNSGAII outperforms NSGAII.

Conclusion

Due to the environmental degradation and depletion of fossil energy, renewable energies have attracted increasing attentions in recent years. However, their stochastic and intermittent characteristics have greatly jeopardized their applications, which instead popularized hybrid renewable energy systems (HRES). The optimal sizing of HRES is a critical issue while designing a HRES. In general a multi-objective optimization (MOP) model is formulated where economic, environment and reliability related objectives are simultaneously optimized. However, this study argues that this ordinary method is not applicable for places having intermittent high load demand. In such places, the load demand is very high during the training period while is relatively low at the rest of time. Without introducing an additional constraint into the MOP model to handle this issue, the obtained optimal HRES size may result in frequent loss of power supply during the high load demand period. Therefore, this study proposes a constrained multi-objective optimal sizing model in which the loss of power supply probability during a specific period is introduced as a constraint. Accordingly, NSGAII with a relaxed $\epsilon$ constraint handling strategy, $\epsilon$-CNSGAII, is presented to solve the model. Experimental results have justified the necessity of the constrained multi-objective model, and the effectiveness of the $\epsilon$-CNSGAII.

With respect to future studies, first this study has only discussed sizing a HRES. Effectively, the HRES size and its operation strategies could be optimized integratively which therefore deserves further study. Second, we have only considered the power demand on sizing a HRES, in fact the combined heat and power (CHP) system based on renewable energies is also widely used [41]. Thus, the proposed method could be extended to CHP system. Third, sizing a HRES involves the optimization of mixed variables, more effective algorithms are therefore required [42,43,44,45,46,47,48]. Lastly, in addition to those frequently used optimization objectives like ASC, LPSP, new criteria in the view of reliability, economic and environment can be disseminated.