Crack identification with incomplete boundary data in linear elasticity by the reciprocity gap method

Abstract

This paper proposes and studies three methods for the identification of cracks in linear elastic bodies. They are based on the reciprocity gap principle which they extend to the case of partially redundant boundary data. The methods are all assessed on an academic 2D case, then the most appealing is more deeply analysed and illustrated on a 3D test-case.

A Brief study of the Petrov-Galerkin formulation

This “Appendix” aims at providing some theoretical ground to the formulation used in Sects. 4 and 5. For simplicity reasons, we focus on the case of identifying a crack with fully known boundary conditions. The extra terms needed for more general cases do not change the main properties of the system.

We recall that the system to be solved takes the form (for simplicity reason, we drop the subscript r, and the bracket notations for the displacement jump):

$$\begin{aligned} \begin{aligned}&\text {Find }{\underline{u}}\in H^{1/2}_{00}(\omega ), \text { such that }\forall {\underline{v}}\in {\mathcal {V}}, \\&\langle \underline{{\underline{\sigma }}}({\underline{v}})\cdot {\underline{n}}, {\underline{u}}\rangle _{H^{1/2}(\omega )} = \int _{\partial \varOmega } \underline{{\widehat{f}}}\cdot {\underline{v}}- \underline{{\widehat{u}}}\cdot \underline{{\underline{\sigma }}}({\underline{v}}) \cdot {\underline{n}}\, dS \end{aligned} \end{aligned}$$

(30)

with

$$\begin{aligned} {\mathcal {V}}= \left\{ {\underline{v}}\in H^1(\varOmega ), \underline{{\underline{\sigma }}}({\underline{v}})\in H_{div}(\varOmega ), {\text {div}}(\underline{{\underline{\sigma }}}({\underline{v}})) = 0 \right\} \end{aligned}$$

(31)

In the formulation, we make use of the duality bracket in the Hilbert space $H^{1/2}_{00}$. ${\mathcal {V}}$ is a closed subspace of $H^{1}(\varOmega )$, it inherits its Hilbert space structure. Fields in ${\mathcal {V}}$ have enough regularity for the trace and normal flux to be well-defined and continuous on the boundary and on $\omega$, so that all operations are well posed and the (bi)linear forms are continuous. In practice, we use polynomial approximation in ${\mathcal {V}}$ and Lagrange finite element in $H^{1/2}_{00}$, granting sufficient regularity to replace the duality bracket by a classical integral on $\omega$.

Formulation (30) makes use of different search ($H^{1/2}_{00}$) and test (${\mathcal {V}}$) spaces, which is the playground of the Banach-Necas-Babǔska theorem [17], also known as inf-sup theorem.

One first precaution must be taken. For a given plane surface $\omega$, we can define ${\mathcal {V}}_\omega$, the space of the ${\underline{v}}$ such that $\underline{{\underline{\sigma }}}({\underline{v}})\cdot {\underline{n}}|_{\omega } = 0$. Let us define ${\underline{v}}\in {\mathcal {V}}_\omega ^\perp$, the subspace of ${\mathcal {V}}$ that is orthogonal to ${\mathcal {V}}_\omega$. ${\mathcal {V}}_\omega$ is a closed space, which means in particular that it is not dense in ${\mathcal {V}}$, and ensures that ${\underline{v}}\in {\mathcal {V}}_\omega ^\perp$ is not empty. In order to avoid inconsistency, the formulation must be studied with ${\underline{v}}\in {\mathcal {V}}_\omega ^\perp$.

For the formulation to be stable, the following quantity should be bounded from below by a positive number:

$$\begin{aligned} \inf _{{\underline{u}}\in H^{1/2}_{00}(\omega )} \sup _{{\underline{v}}\in {\mathcal {V}}_{\omega }^\perp } \dfrac{\langle \underline{{\underline{\sigma }}}({\underline{v}})\cdot {\underline{n}}, {\underline{u}}\rangle }{\Vert {\underline{u}}\Vert _{H^{1/2}(\omega )}\Vert {\underline{v}}\Vert _{{\mathcal {V}}}} \end{aligned}$$

(32)

Unfortunately, this is not possible. Indeed, we have the following property:

$$\begin{aligned} \inf _{{\underline{u}}\in H^{1/2}_{00}(\omega )} \sup _{{\underline{\tau }}\in H^{-1/2}(\omega )} \dfrac{\langle {\underline{\tau }},{\underline{u}}\rangle }{\Vert {\underline{u}}\Vert _{H^{1/2}(\omega )}\Vert {\underline{\tau }}\Vert _{H^{-1/2}(\omega )}} = 1 \end{aligned}$$

(33)

and more precisely, for a given ${\underline{u}}\in H^{1/2}_{00}$, the ${\underline{\tau }}$ which realizes the upper bound is the image of ${\underline{u}}$ by Riesz’ isomorphism which we note ${\underline{\tau }}_{{\underline{u}}}$. The problem is then to find ${\underline{v}}\in {\mathcal {V}}$ such that $\underline{{\underline{\sigma }}}({\underline{v}})\cdot {\underline{n}}= {\underline{\tau }}_{{\underline{u}}}$; this is the subject of Proposition 2. Unfortunately, its proof appeals to a Cauchy problem, which is unstable. Thus we can not control $\Vert {\underline{v}}\Vert _{{\mathcal {V}}}$ from above with $\Vert {\underline{\tau }}_{{\underline{u}}}\Vert _{H^{-1/2}}=\Vert {\underline{u}}\Vert _{H^{1/2}_{00}}$.

In the end, the lack of stability is caused by fields ${\underline{u}}\in H^{1/2}_{00}(\omega )$ aligned with high energy test fields ${\underline{v}}\in {\mathcal {V}}_\omega ^\perp$. This justifies the use of gradient-based regularization.

Proposition 2

Let $\omega$ be a surface that cuts the domain $\varOmega$. For any ${\underline{\tau }}\in H^{-1/2}(\omega )$, there exists ${\underline{v}}\in {\mathcal {V}}_{\omega }^\perp$ such that $\underline{{\underline{\sigma }}}({\underline{v}})\cdot {\underline{n}}_{\varPi }= {\underline{\tau }}$ on $\omega$.

Proof

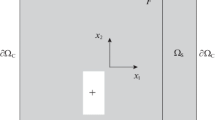
The surface $\omega$ splits $\varOmega$ into two open sets, denoted by $\varOmega _1$ and $\varOmega _2$ (Fig. 29). For any ${\underline{u}}_1\in H^{1/2}(\partial \varOmega _1)$, one can solve a direct problem on $\varOmega _1$ in order to build ${\underline{v}}_1\in H^1(\varOmega _1)$ such that the equilibrium s verified and $\underline{{\underline{\sigma }}}({\underline{v}}_1)\cdot {\underline{n}}_{\varPi }= {\underline{\tau }}$ on $\omega$.

Fig. 29

Splitting of the domain

${\underline{v}}_1$ and ${\underline{\tau }}$ are compatible data for a Cauchy problem set on $\varOmega _2$, and it is possible to build the field ${\underline{v}}_2\in H^1(\varOmega _2)$ such that the equilibrium is also verified and $\underline{{\underline{\sigma }}}({\underline{v}}_2)\cdot {\underline{n}}_{\varPi }= {\underline{\tau }}$ on $\omega$.

The traces on $\omega$ of the fields ${\underline{v}}_1$ and ${\underline{v}}_2$ are the same, and consequently, the field ${\underline{v}}$, that is equal to ${\underline{v}}_1$ on $\varOmega _1$ and ${\underline{v}}_2$ on $\varOmega _2$, and that is extended by continuity on $\omega$, is in ${\mathcal {V}}_{\omega }^\perp$ and is such that $\underline{{\underline{\sigma }}}({\underline{v}})\cdot {\underline{n}}_{\varPi }= {\underline{\tau }}$ on $\omega$. $\square$