Theoretical determination of asymmetric rolling amplitude in irregular beam seas

Abstract

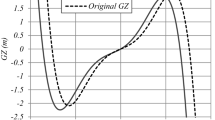
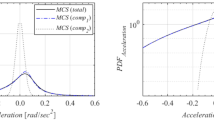
A methodology for predicting the probability density function of roll motion for irregular beam seas is developed in the author’s previous research. In this paper, two methods for the prediction of the probability density function (PDF) of the rolling amplitude are examined. One of these methods is an approach based on a non-Gaussian PDF with the use of the equivalent linearization and the moment method, which has been used by Maki in the field of naval architecture. In the framework of this method, the instantaneous joint PDF of the roll and roll rate can be calculated. Thereby, the transformation from the joint PDF to the PDF of the total energy H is necessary. In this paper, the transformation from the joint PDF of instantaneous roll and rate to the PDF of H was conducted. The other method is the energy-based stochastic averaging method, whereby the PDF of the total energy H is determined from which the roll amplitude is calculated. It is noteworthy that the proposed theory aims to predict the PDF of the amplitude of the vessel due to wind or flooding. For such conditions, the restoring curve (GZ curve) has asymmetricity. To take into account this asymmetricity, a new theory for the transform of the PDF of the total energy H to the PDFof amplitude is proposed. The obtained theoretical results show almost complete agreement, and both of the two theoretical methods i.e., the energy-based stochastic averaging method and the non-Gaussian PDF method with the use of the equivalent linearization and moment method, show equivalent prediction performance even in the asymmetric condition.

Appendix

The numerical calculation of drift and diffusion is shown below.

$$\begin{gathered} m\left( H \right) = \frac{1}{T\left( H \right)}\int_{0}^{T\left( H \right)} {\left[ {\dot{\phi }_{H}^{2} \left( { - \alpha \dot{\phi }_{H} - \beta \dot{\phi }_{H} \left| {\dot{\phi }_{H} } \right.} \right)} \right]} + \int_{ - \infty }^{0} {R\left( \tau \right)} \frac{{\dot{\phi }_{H} \left( {t + \tau } \right)}}{{\dot{\phi }_{H} \left( t \right)}}dt \hfill \\ \sigma^{2} \left( H \right) = \frac{1}{T\left( H \right)}\int_{0}^{T\left( H \right)} {\int_{ - \infty }^{ + \infty } {R\left( \tau \right)\dot{\phi }_{H} \left( t \right)} } \dot{\phi }_{H} \left( {t + \tau } \right)d\tau dt \hfill \\ \end{gathered}$$

(38)

Dostal has proposed the analytical expressions of these integrals for the system having cubic restoring term. However, for a general restoring case, we need to rely on numerical computation since the analytical form of the solution cannot be necessarily obtained. From this point of view, we need to consider an accurate numerical integration method. The numerical calculation of drift is not straightforward in Eq. 38 since there is a singularity in the integration with respect to time t. This singularity looks very simple, but to keep a high numerical accuracy and save computational costs, a suitable integration scheme has to be used. Of course, the biggest problem appears at $\dot{\phi }_{\,H} = 0$. This singularity is very easy to avoid as follows. First, in the vicinity of the singular point, $\dot{\phi }_{\,H}$ is approximated as

$$\left\{ \begin{gathered} \dot{\phi }_{\,H} \left( {t + \tau } \right) \approx a_{2} t^{2} + a_{1} t + a_{0} \hfill \\ \dot{\phi }_{\,H} \left( t \right) \approx b_{2} t^{2} + b_{1} t \hfill \\ \end{gathered} \right..$$

(39)

It is assumed that $\dot{\phi }_{\,H} \left( t \right) = 0$ at time zero, which can be easily established by shifting the coordinate system. Then, we consider the numerical integration scheme of the following part:

$$\int_{0}^{T\left( H \right)} {\frac{{\dot{\phi }_{H} \left( {t + \tau } \right)}}{{\dot{\phi }_{H} \left( t \right)}}dt} ,$$

(40)

which is included in the drift. Apparently, it has a singularity at t equals zero. However, this singularity can be easily excluded as follows. In the vicinity of the singular point, the integration to be evaluated becomes as follows:

$$\int_{\alpha }^{\beta } {\frac{{\dot{\phi }_{H} \left( {t + \tau } \right)}}{{\dot{\phi }_{H} \left( t \right)}}dt} \approx \int_{\alpha }^{\beta } {\frac{{a_{2} t^{2} + a_{1} t + a_{0} }}{{b_{2} t^{2} + b_{2} t^{2} }}dt} \,\,\,\,\,\,where\,\,\left| \alpha \right| \ll 1\,\,and\,\,\left| \beta \right| \ll 1.$$

(41)

Notice that $\tau$ is constant here, and $\dot{\phi }_{\,H} \left( t \right) = 0$ is satisfied. Now, we introduce some new coefficients for simplicity.

$$\frac{{a_{2} }}{{b_{2} }}\int_{\alpha }^{\beta } {\frac{{t^{2} + a_{4} t + a_{3} }}{{t^{2} + b_{4} t}}} dt,\,\,\,\,\,\,where\,\,a_{4} = \frac{{a_{1} }}{{a_{2} }},\,\,a_{3} = \frac{{a_{0} }}{{a_{2} }},\,\,b_{4} = \frac{{b_{0} }}{{b_{2} }}.$$

(42)

Then, we get

$$\begin{gathered} dr = dt \cdot \left( {n_{1} \cdot r + n_{3}^{{}} \cdot r^{3} \, + K \cdot u} \right) + \sigma^{2} \left( r \right) \cdot dW, \hfill \\ u = - G \cdot r. \hfill \\ \end{gathered}$$

$$\begin{gathered} \frac{{a_{2} }}{{b_{2} }}\int_{\alpha }^{\beta } {\frac{{t^{2} + a_{4} t + a_{3} }}{{t^{2} + b_{4} t}}} dt = \frac{{a_{2} }}{{b_{2} b_{4} }}\int_{\alpha }^{\beta } {\left( {\frac{{t^{2} + a_{4} t + a_{3} }}{t} - \frac{{t^{2} + a_{4} t + a_{3} }}{{t + b_{4} }}} \right)dt} , \\ = \frac{{a_{2} }}{{b_{2} b_{4} }}\int_{\alpha }^{\beta } {\left( {t + a_{4} + \frac{{a_{3} }}{t} - \frac{{t^{2} + a_{4} t + a_{3} }}{{t + b_{4} }}} \right)dt} , \\ = \frac{{a_{2} }}{{b_{2} b_{4} }}\left[ {\int_{\alpha }^{\beta } {\left( {t + a_{4} } \right)dt + a_{3} \int_{\alpha }^{\beta } \frac{1}{t} dt} } \right], \\ - \frac{{a_{2} }}{{b_{2} b_{4} }}\left[ {\int_{{\alpha + b_{4} }}^{{\beta + b_{4} }} {\left( {s + a_{4} - 2b_{4} } \right)ds + \left( {b_{4}^{2} - a_{4} b_{4} + a_{3} } \right)} \int_{{\alpha + b_{4} }}^{{\beta + b_{4} }} {\frac{1}{s}ds} } \right]. \\ \end{gathered}$$

(43)

Notice, that even in the case of $\alpha < 0 < \beta$, the following relation is definitely fulfilled since the negative and positive singular values cancel.

$$\int_{\alpha }^{\beta } {\frac{1}{t}dt} \to \ln \left| \beta \right| - \ln \left| \alpha \right|.$$

(44)

Therefore, the calculation of the singular term can be completed.

On the other hand, in the wider region around the singular points, the numerical behavior is not suitable for computation. For instance, we should not directly approximate the integrand as follows:

$$\frac{{\dot{\phi }_{\,H} \left( {t + \tau } \right)}}{{\dot{\phi }_{\,H} \left( t \right)}} \approx a_{2} t^{2} + a_{1} t + a_{0} .$$

(45)

This kind of approximation of the integrand could deteriorate the numerical accuracy. Therefore, again, we separately introduce the polynomial approximation for both, the denominator and the numerator of the integrand as

$$\int_{\alpha }^{\beta } {\frac{{\dot{\phi }_{H} \left( {t + \tau } \right)}}{{\dot{\phi }_{H} \left( t \right)}}dt} \approx \int_{\alpha }^{\beta } {\frac{{a_{2} t^{2} + a_{1} t + a_{0} }}{{b_{2} t^{2} + b_{1} t + a_{0} }}dt} .$$

(46)

Since there is not a singularity in the region which we are considering now, this numerical integration can be calculated as follows:

$$\begin{gathered} \int_{\alpha }^{\beta } {\frac{{a_{2} t^{2} + a_{1} t + a_{0} }}{{b_{2} t^{2} + b_{1} t + b_{0} }}} dt = \frac{{a_{2} }}{{b_{2} }}\left( {\beta - \alpha } \right) \\ + \frac{{b_{2} \left( {2a_{0} b_{2} - a_{0} b_{1} } \right) + a_{2} \left( {b_{1}^{2} - 2b_{0} b_{2} } \right)}}{{2b_{2}^{2} \sqrt {4b_{0} b_{2} - b_{1}^{2} } }}\left[ {2\tan^{ - 1} \left( {\frac{{b_{1} + 2b_{2} x}}{{\sqrt {4b_{0} b_{2} - b_{1}^{2} } }}} \right)} \right]_{\alpha }^{\beta } \\ + \frac{1}{{2b_{2}^{2} }}\left[ {\left( {a_{1} b_{2} - a_{2} b_{1} } \right)\log \left( {b_{2} x^{2} + b_{1} x + b_{0} } \right)} \right]_{\alpha }^{\beta } . \\ \end{gathered}$$

(47)

Notice that the square root included in the above expression becomes imaginary in general, and the inside of the arctangent function becomes also imaginary. Therefore, in programming, this point should be taken into account. However, in the outer region of the singular point, the above approximate integration method should be applied. Please see the literature [25] for further numerical techniques.

Furthermore, to save computational time, the discretized trajectory and period $T\left( H \right)$ of the Hamiltonian system should be obtained before carrying out the numerical integration. Here, to retain numerical accuracy, the Newton method is applied for the determination of the discretized trajectory and period $T\left( H \right)$ e.g., [26]. Thereby, the unknown variable is $T\left( H \right)$. Now, the equation of motion of the Hamiltonian system is as follows:

$$\frac{d}{dt}{\mathbf{x}} = {\mathbf{F}}\left( {\mathbf{x}} \right),$$

(48)

where

$${\mathbf{x}} \equiv \left( {\phi ,\,\,p} \right)^{T} ,\,\,{\mathbf{F}}\left( {\mathbf{x}} \right) \equiv \left( \begin{gathered} p \hfill \\ - G\left( \phi \right) \hfill \\ \end{gathered} \right).$$

(49)

Here, we introduce the non-dimensional time $\tilde{t}$ as

$$\tilde{t} = \frac{t}{T\left( H \right)}.$$

(50)

Then, the period of this system becomes one.

$$\frac{d}{{d\,\tilde{t}}}{\mathbf{x}} = T\left( H \right) \cdot {\mathbf{F}}\left( {\mathbf{x}} \right).$$

(51)

The solution trajectory of this system in the time domain is defined as

$${\mathbf{x}}\,\left( {\tilde{t}} \right) = {\mathbf{\varphi }}\,\left( {\tilde{t},\,\,{\mathbf{x}}_{0} } \right).$$

(52)

Thereby, ${\mathbf{x}}_{0}$ is the initial condition. We define the Poincare map as

$$P:\,\,R^{2} \to R^{2} ;\,\,{\mathbf{x}} = {\mathbf{\varphi }}\,\left( {n \cdot T\left( H \right),\,\,{\mathbf{x}}_{0} } \right),$$

(53)

where, n is an arbitrary integer. The condition of the periodic solution is

$${\mathbf{f}}\left( {{\mathbf{x}}_{0} } \right) \equiv P\,\left( {{\mathbf{x}}_{0} } \right) - {\mathbf{x}}_{0} = {\mathbf{\varphi }}\,\left( {t,\,\,{\mathbf{x}}_{0} } \right) - {\mathbf{x}}_{0} .$$

(54)

Therefore, the above condition should be solved with the Newton method. Again, the unknown value to be obtained is $T\left( H \right)$.