Abstract
This paper presents a novel compensator-critic structure-based event-triggered decentralized tracking control of modular robot manipulators (MRMs). On the basis of subsystem dynamics under joint torque feedback (JTF) technique, the proposed tracking error fusion function, which includes position error and velocity error, is utilized to construct performance index function. By analyzing the dynamic uncertainties, a local dynamic information-based robust controller is designed to engage the model uncertainty compensation. Based on adaptive dynamic programming (ADP) algorithm and the event-triggered mechanism, the decentralized tracking control is obtained by solving the event-triggered Hamilton–Jacobi–Bellman equation (HJBE) with the critic neural network (NN). The tracking error of the closed-loop manipulators system is proved to be ultimately uniformly bounded (UUB) using the Lyapunov stability theorem. Finally, experimental results illustrate the effectiveness of the developed control method.
Similar content being viewed by others
Introduction
The modular robot manipulators (MRMs) [1, 2] equipped with standard modules adapt to severe working conditions through changing their configurations and increasing/reducing modules. Since the modularization and light weight of MRMs, they are potential in numerous unmanned and complex environments, such as aerospace explorations, search-rescue operations, and medical assistance. Thus, the effective control strategies are expected to ensure the security and low consumption.
The tracking control strategies of MRMs can be classified into centralized control [3, 4], distributed control [5, 6], and decentralized control [7,8,9] according to the recent literature. The centralized control and distributed control are designed by employing the information of all subsystems or its neighbors, which violates the original intention of mechanical design of the MRMs and leads to increasing communication exchange. Indeed, the primary characteristic of MRMs is that the joint module can be added, deleted, and replaced without redesigning the controller. Thus, it is better to develop a controller contains the information of the corresponding subsystem only in the “modularization” point of view. Fortunately, the decentralized control method, which is reasonable to MRMs, has aroused many scholars’ interests. In addition, most robot control strategies rely on the accurate model dynamics. However, it is impossible to obtain the complete dynamics of MRMs, since their intrinsic mechanical characteristic that the configurations are changing with increasing/reducing the modules for various task environments. To mitigate the influence induced by the model uncertainties, Zhu et al. [10] introduced a first-order Takagi–Sugeno fuzzy logic system to approximate the unknown dynamics, and proposed a decentralized adaptive fuzzy sliding mode control scheme for MRMs. Zhou et al. [11] developed a torque sensorless force/position decentralized control by utilizing the radial basis function neural networks (RBFNNs). The other feasible selection is to adopt the joint torque feedback (JTF) technique [12, 13] to reduce the complexity of the dynamics and to improve the generality in practice. Zhang et al. [14] presented a modular distributed control technique for MRMs that the model uncertainties associated with link and payload masses were compensated using joint torque sensor measurement. Nevertheless, the drawback of mentioned methods lies in ignoring the comprehensive optimization of the control performance and power consumption, as well as the high-energy cost caused by the long-time computation and communication, simultaneously. To the best of our knowledge, there are very few attempts on developing the decentralized optimal tracking control methods for robots, especially, the decentralized tracking control integrating adaptive dynamic programming (ADP) and event-triggered algorithm for MRMs.
Optimal control scheme has been received widespread attentions from both researchers and engineers since the mid-1950s. As an effective way to solve optimal control problems of nonlinear systems, ADP algorithm, which was first proposed by Werbos [15], can avoid the difficulties of “curse of dimensionality”. Recently, ADP-based methods are utilized to design optimal controllers for continuous-time [16, 17] and discrete-time [18, 19] nonlinear systems with input/output constraints [20, 21], external disturbances [22, 23], and mismatched interconnections [24, 25]. Since the optimal control problems of nonlinear systems are solved gradually, the ADP-based optimal control approaches [26] are applied to various fields [27, 28]. Nevertheless, all the aforementioned control methods were developed based on the time-triggered mechanism, which neglected the huge amount of unnecessary computation, communication, and energy cost in a long working time. In the last few years, the event-triggered mechanism [29, 30] is employed to address above problems. Kyriakos et al. [31] proposed a novel optimal adaptive event-triggered control algorithm for nonlinear continuous-time systems. Yang et al. [32] tackled the optimal event-triggered control problem of nonlinear continuous-time systems subject to asymmetric control constraints. Considering the interconnected systems, Vignesh et al. [33] presented an approximate optimal distributed control scheme for nonzero-sum games. He et al. [34] designed a decentralized event-triggered control method for nonlinear systems with matched interconnections. For the MRM systems, Dong et al. [35] proposed the time-triggered decentralized robust optimal control for MRMs via critic-identifier structure-based ADP approach. Zhao et al. [36] developed an event-triggered decentralized tracking optimal control approach by employing a local NN observer to estimate unknown model dynamics. In general, since the composed components for each module of MRMs are basically identical in practice, the dynamics of MRMs is usually partially known, such as the specification of actuators, the reduction ratio, etc. Besides, the training of NN needs a large amount of online or offline data, which wastes computation, communication, and energy resource. Thus, they should be taken into account to extend their service time. Unfortunately, a few ADP-based event-triggered decentralized tracking control approaches for MRMs were investigated, especially, considering the model-based real-time compensation of model uncertainties.
Inspired by the above literature, this paper presents an event-triggered decentralized tracking control approach with compensator-critic structure for MRMs. First, the dynamic model of MRMs, which is described as the integration of all subsystems associated with coupling dynamics, is formulated based on JTF technique. Then, a model-based real-time robust compensator is implemented to deal with the model uncertainties. Second, the performance index function which contains the tracking error and control torque is defined, and the system state is sampled according to the event-triggering condition. Based on the ADP algorithm, the event-triggered HJBE can be solved by the critic NN, and then, the event-triggered approximate decentralized optimal tracking control policy can be obtained. By utilizing the Lyapunov stability theorem, the tracking error of the closed-loop manipulators system is proved to be UUB under the proposed control method. Finally, the effectiveness of the proposed compensator-critic structure-based event-triggered decentralized optimal tracking control method is verified via the experimental results.
The main contributions of this paper are summarized as follows.
-
1.
We address the ADP-based event-triggered decentralized tracking control problem of MRMs with compensator-critic structure. On the basis of JTF technique, the model-based robust compensator and the critic NN are designed to mitigate model uncertainties in real time and to approximate the optimal compensation tracking control policy, respectively.
-
2.
Unlike existing time-triggered control methods [37, 38] which ignored the conservation of limited energy resource, in this paper, a novel compensator-critic structure-based event-triggered decentralized tracking control method for MRMs is proposed. It does not only make the actual trajectory of each joint module follow its desired one, but also reduce the computational burden, save the communication, and energy consumption simultaneously.
The remainder of this paper is arranged as follows. “Dynamic model and preliminaries” sketches the dynamic model and preliminaries of MRM subsystems. In “Compensator-critic structure-based event-triggered decentralized tracking control”, the compensator-critic structure-based event-triggered decentralized tracking control of MRMs is proposed, and the stability analysis is given. In “Experimental results”, experiments verify the effectiveness of the developed method. “Conclusion” summarizes this paper.
Dynamic model and preliminaries
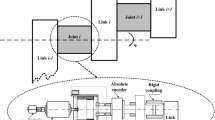
We consider a n-degree of freedom (DOF) serial MRM, whose each module consists of a rotary joint with a direct current (DC) motor, a speed reducer, and a joint torque sensor, as shown in Fig. 1. Based on the JTF technique [39], the dynamics of the ith joint subsystem can be modeled as:
where \(I_{ri}\) denotes rotor moment of inertia related to the axis of rotation, \({\gamma _i}\) refers to the reduction ratio of the speed reducer, \({q_i}\) is the vector of the joint movements, \({{\dot{q}}_i}\) and \({\ddot{q}_i}\) are the joint velocity and acceleration, respectively, \({\tau _{ti}}\) represents the measurement of the joint torque sensor, \({f_{ri}}\left( {{q_i},{{\dot{q}}_i}} \right) \) means the joint friction torque, \({Z_i}\left( {q,\dot{q},\ddot{q}} \right) \) indicates the dynamic coupling torque among the subsystems, and \({\tau _i}\) is the control input torque, also the motor output torque.
The joint friction torque \({f_{ri}}\left( {{q_i},{{\dot{q}}_i}} \right) \) mainly reflects the friction of the motor and speed reducer. Motivated by [40, 41], it is assumed to be a function of the joint position and joint velocity as:
where \({f_{bi}}\) represents the viscous friction coefficient, \({f_{si}}\) is the static friction, \(f_{\tau i}\) denotes a positive parameter corresponding to the Stribeck effect, \(f_{ci}\) reflects the Coulomb friction, \({f_{pi}}\left( {{q_i},{{\dot{q}}_i}} \right) \) denotes the position dependency of friction and other friction modeling errors, and \(sgn(\cdot )\) is a classical sign function.
Supposing the nominal values of \({f_{bi}}, {f_{si}}, {f_{\tau i}}\) and \({f_{ci}}\) are closed to their actual values, then according to the linearization scheme [41], the friction model (2) can be approximated by:
where \({{\hat{f}}_{bi}}, {{\hat{f}}_{si}}, {{\hat{f}}_{\tau i}}\), and \({{\hat{f}}_{ci}}\) are the approximate values of \({f_{bi}}, {f_{si}}, {f_{\tau i}}\), and \({f_{ci}}\), respectively, and
Remark 1
In practice, the joint friction torque \({f_{ri}}\) is always constant and bounded, which is affected slightly by temperature and lubrication. Thus, it is reasonable to assume that the estimated error term \({{\tilde{F}}_{ri}}\) is also bounded as \(|{{\tilde{F}}_{ri}}| \le {\beta _{Fbi}}\), where \({\beta _{Fbi}}\) is a positive constant vector with \(b = 1,2,3,4\). The non-parametric friction term \({f_{pi}}\left( {{q_i},{{\dot{q}}_i}} \right) \) has an upper bound as \(|| {{f_{pi}}\left( {{q_i},{{\dot{q}}_i}} \right) } || \le {\beta _{pi}}\) with \({\beta _{pi}}\) a positive constant.
On the basis of the dynamic model in [42], the dynamic coupling torque \({Z_i}\left( {q,\dot{q},\ddot{q}} \right) \) can be obtained by:
where \(c_{ri}\), \(c_{j}\), and \(c_{k}\) represent unit vectors along the rotation axis of the ith, the jth and the kth joint, respectively. Accordingly, we define \(\varPhi _j^i=c_{ri}^T{c_j}\) and \(\varPsi _{kj}^i = c_{ri}^T\left( {{c_k} \times {c_j}} \right) \). Moreover, we have \(\varPhi _j^i = {\hat{\varPhi }} _j^i + {\tilde{\varPhi }} _j^i\) and \(\varPsi _{kj}^i = {\hat{\varPsi }} _{kj}^i + {\tilde{\varPsi }} _{kj}^i\), where \({\hat{\varPhi }} _j^i\) and \({\hat{\varPsi }} _{kj}^i\) are the estimates of the vectors \(\varPhi _j^i\) and \(\varPsi _{kj}^i\), \({\tilde{\varPhi }} _j^i\) and \({\tilde{\varPsi }} _{kj}^i\) indicate the alignment errors, respectively.
Remark 2
From the dynamic coupling torque (4), we know the terms \(c_{ri}\), \({c_j}\) and \({c_k}\) are bounded as \(||{\varPhi _j^i} ||\mathrm{{ = }}|| {c_{ri}^T{c_j}} || \le 1\), \(|| {\varPsi _{kj}^i} ||= || {c_{ri}^T\left( {{c_k} \times {c_j}} \right) } || \le 1\), respectively. Moreover, we also conclude that if the jth and the kth \((1<j,k<i-1)\) joints are assembled lower, then the dynamic coupling term \({Z_i}\left( {q,\dot{q},\ddot{q}} \right) \) is bounded as \(|| {{Z_i}\left( {q,\dot{q},\ddot{q}} \right) } || \le {\beta _{Zi}}\) with \({\beta _{Zi}}\) a positive constant. Accordingly, the MRM can be controlled “joint by joint”, such that the lower joints are all controlled when the current joint is controlled.
According to (1) and (3), the dynamic model of the MRM subsystem is described by:
where \({x_i} = {\left[ {\begin{array}{*{20}{c}} {{x_{1i}}}&{{x_{2i}}} \end{array}} \right] ^T} = {\left[ {\begin{array}{*{20}{c}} {{q_i}}&{{{\dot{q}}_i}} \end{array}} \right] ^T} \in {{{\mathbb {R}}}^{2}}\), \({D_i} = {\left( {{I_{ri}}{\gamma _i}} \right) ^{ - 1} \in {{{\mathbb {R}}}^+}}\), \({\varGamma _{fi}}= -{D_i}\) \(\left( {{{{\hat{f}}}_{bi}}{x_{2i}} + \left( {{{{\hat{f}}}_{si}}{e^{\left( { - {{{\hat{f}}}_{\tau i}}{{\left( {{x_{2i}}} \right) }^2}} \right) }} + {{{\hat{f}}}_{ci}}} \right) {\mathrm{sgn}} \left( {{x_{2i}}} \right) }+{\frac{{{\tau _{ti}}}}{{{\gamma _i}}}}\right) \), \(u_{i}=\tau _{i}\) represents the ith joint control torque, and the model uncertainty which includes the friction model error and the interconnection joint coupling can be given as:
Assumption 1
The nonlinear system dynamics (5) is Lipschitz continuous for the state \({x_i} \in \varOmega \), and each subsystem is controllable, and \({x_i}\left( 0 \right) = 0\) with a equilibrium of system.
In this paper, we propose a compensator-critic structure-based event-triggered decentralized tracking control of MRMs based on ADP algorithm. The aim is to find a decentralized near-optimal control policy \(u_i\) to guarantee the stability of the closed-loop MRM subsystem. For the subsystem (5), the improved infinite horizon performance index function is defined as:
where \({\vartheta _i}\left( {{x_i}} \right) = {x_{2i}} - {x_{2di}} + {a_{ei}}\left( {{x_{1i}} - {x_{1di}}} \right) \) is the hybrid error function including the position error and velocity error with \({\vartheta _{i0}}\left( {{x_i}\left( 0 \right) } \right) = {\vartheta _i}\left( 0 \right) \), \({a_{ei}}\) is a positive constant, \({x_{1di}}\) and \({x_{2di}}\) denote the desired position and velocity trajectories, respectively, \({Q_i}\) and \({R_i}\) are the positive definite matrices, \({N_i}\left( {{\vartheta _i},{u_i}\left( {\vartheta _i} \right) } \right) = \vartheta _i^T{Q_i}{\vartheta _i} + u_i^T\left( {{\vartheta _i}} \right) R{u_i}\left( {{\vartheta _i}} \right) \ge 0\) is the utility function with \({N_i}\left( {0,0} \right) = 0\), where \({u_i}\left( {{\vartheta _i}} \right) ={u_i}\left( {\vartheta _i}\left( {{x_i}\left( t \right) } \right) \right) \) is designed to realize the decentralized tracking control by transforming \({u_i}\left( {{x_i}} \right) \) into \({u_i}\left( {{\vartheta _i}} \right) \).
Then, we develop the time-triggered HJBE for subsystem (5) as:
where \(\nabla {\varXi _i}\left( {{\vartheta _i}} \right) \) shows the partial derivative of \({\varXi _i}\left( {{\vartheta _i}} \right) \) with respect to \({\vartheta _i}\), i.e., \(\nabla {\varXi _i}\left( {{\vartheta _i}} \right) = \partial {\varXi _i}\left( {{\vartheta _i}} \right) /\partial {\vartheta _i}\) and \({\upsilon _i}= - {x_{2di}} + {a_{ei}}\left( {{{x}_{1i}} - {{ x}_{1di}}} \right) \). The optimal performance index function is described by:
Substituting (9) into the HJBE (8), we obtain:
Kalman [43] strictly demonstrated that if the optimal performance index function \(\varXi _i^*\left( {{\vartheta _i}} \right) \) is continuously differential and satisfies (10), the solution of HJBE \(u_i^*\left( {{\vartheta _i}} \right) \) exists as the optimal control policy of the corresponding nonlinear continuous system, which can be formulated as:
Then, the HJBE can be presented as:
To mitigate the subsystem dynamics, by utilizing the partly known model information, we can rewrite the optimal control \(u_i^*\) as:
which is used to deal with dynamic model term \({\varGamma _{fi}}\), \({\varTheta _i}\) and to realize the optimal tracking control, respectively. Thus, combining (12) with (13), and through simple transformation, we have
Remark 3
On the basis of optimization theory and the dynamic model analysis, in this paper, the decentralized tracking control problem of MRMs is transformed into an optimal compensation control problem (13), which consists of model-based robust control \(u_{1i}\left( {\vartheta _i}\right) \) and ADP-based optimal control \(u_{2i}^*\left( {\vartheta _i}\right) \). Inspired by the previous works [41, 44], the decentralized optimal tracking control is developed with a compensator-critic structure, which can not only mitigate model uncertainties in real time but also realize the satisfactory tracking performance for MRMs.
According to [38, 45], the HJBE (8) can be solved by time-triggered ADP algorithm. However, as mentioned in [46], the time-triggered optimal control strategies do not only suffer from heavy computational burden and communication, but also waste limited energy resource. To address above shortcomings, a compensator-critic structure-based event-triggered decentralized tracking control is designed for MRMs as follows.
Compensator-critic structure-based event-triggered decentralized tracking control
In this section, the detailed design procedure of compensator-critic structure-based event-triggered decentralized tracking control for MRMs is described.
The model-based robust compensator
In practice, the dynamics of each joint module is partially known. Inspired by [13, 47, 48], we present a robust compensator \({u_{1i}}\), which consists of the model-based measurable term \(u_{1mi}\) and compensation term for dynamic uncertainties \(u_{1ui}\), can be expressed by:
where the compensation term \(u_{1ui}\) is designed to deal with the approximated friction model error term \({{\tilde{F}}_{ri}}\) and the dynamic coupling term \({Z_i}\left( {x,\dot{x},\ddot{x}} \right) \). Based on our previous works [49, 50], \(u_{fi}\) and \(u_{zi}\) are presented to compensate \({{\tilde{F}}_{ri}}\) and \({Z_i}\left( {x,\dot{x},\ddot{x}} \right) \), respectively. The robust compensator \(u_{fi}\) can be designed as:
where \({\kappa _{fi}}\) and \({\kappa _{fib}}\) are positive parameters with \(b = 1,2,3,4\). To facilitate the analysis of the dynamic coupling term \({Z_i}\left( {x,\dot{x},\ddot{x}} \right) \), one can rewrite the term as:
The robust compensator \(u_{zi}=u_{z1i}+u_{z2i}\) is developed to compensate the terms \(\sum \nolimits _{j = 1}^{i - 1} {{\bar{\varPhi }} _j^iU_j^i}\) and \( \sum \nolimits _{j = 2}^{i - 1} {\sum \nolimits _{k = 1}^{j - 1} {{\bar{\varPsi }} _{kj}^iZ_{kj}^i} }\) in (19) as:
where \({\kappa _{1i}}\), \({\kappa _{2i}}\), \({\kappa _{z1oi}}\), \({\kappa _{z2oi}}\), \({\xi _{1oi}}\), and \({\xi _{2oi}}\) are positive parameters with \(o=1,2\). According to (15), (16), (17), (18), (20) and (21), the robust compensator \(u_{1i}\) can be presented as:
Theorem 1
Consider a MRM working in free space, the subsystem dynamics (5) with model uncertainties as (3) and (4). The tracking errors are ensured to be UUB under the robust compensation control law (22).
Proof
Choose the Lyapunov function candidate for the MRM subsystem as:
where
In (24), the actual terms \({{\tilde{F}}_{ri}}\), \( {U_j^i}\), and \( {Z_{kj}^i} \) are all constants. Therefore, the time derivative of (23) is expressed as:
According the robust compensator \(u_{1i}\) in (15), \(u_{1mi}\) and \(u_{1ui}\) are employed to deal with the known dynamics and uncertainties correspondingly. Through (16) and (22), we obtain
Combining (18), (20) and (21) with (26), we have
By the simple transformation, assuming that \(\left\| {{A_i}\left( {{x_{2i}}} \right) A_i^T\left( {{x_{2i}}} \right) } \right\| \le {A_{Mi}}\) and \(\left\| {{\upsilon _i}} \right\| \le {\upsilon _{Mi}}\), we rewrite (27) as:
According to the Lyapunov’s direct method, the tracking error \({\vartheta _i}\) can be guaranteed to be UUB, if \({\vartheta _i}\) lies outside the compact set:
This completes the proof. \(\square \)
Decentralized tracking control based on event-triggered mechanism
The event-triggered mechanism is effective to reduce the computational burden and energy cost. Based on event-triggered mechanism, the decentralized tracking control input is updated when the triggering condition is violated. Suppose that \(\left\{ {{t_l}} \right\} _{l = 0}^{ + \infty }\) is a monotonically increasing sequence consisting of triggering instants, where \(t_{l}\) satisfies \(0< {t_l} < {t_{l + 1}}\) and \(\mathop {\lim }\nolimits _{l \rightarrow \infty } {t_l} = \infty \) for \(l \in \left\{ {0,1,2, \ldots } \right\} \). The sampled state is presented as:
where \({{\hat{\vartheta }} _{li}}\left( {{{{\hat{x}}}_{li}}} \right) \) is the sampled data for \(t \in \left[ {{t_l},{t_{l + 1}}} \right) \). To obtain the proper event-triggering condition, the gap function between the sampled state and the actual state is defined as:
Based on the event-triggering mechanism, the control policy is updated \({\vartheta _i}\left( {{x_i}} \right) = \left\{ \begin{array}{l} {{{\hat{\vartheta }} }_{li}}\left( {{{{\hat{x}}}_{li}}} \right) , t \in \left[ {{t_l},{t_{l + 1}}} \right) \\ {\vartheta _i}\left( {{x_i}} \right) , t=t_{l+1} \end{array} \right. \). In this situation, the decentralized tracking control input becomes a piece-wise continuous-time signal by a zero-order hold, which is formulated as:
during the time interval \([t_l,t_{l+1})\). Based on (11), the event-triggered decentralized optimal control can be formulated by:
However, \(u_i^*\left( {{{{\hat{\vartheta }} }_{li}}\left( {{{{\hat{x}}}_{li}}} \right) } \right) \) is the discrete value of aperiodic sampling and by introducing the zero-order hold, the control signal becomes continuous.
Substituting (32) into (14), we establish the event-triggered HJBE as:
Assumption 2
The decentralized tracking control \(u_i^*\) is Lipschitz continuous for every state \({\vartheta _i}\), \({{\hat{\vartheta }} _{li}} \in \varOmega \), i.e., there exists a positive constant \({m_{li}}\), such that
Remark 4
In the event-triggered decentralized tracking control policy (32), the subsystem error function \({\vartheta _i}\left( {{x_i}} \right) \) is substituted by \({{\hat{\vartheta }} _{li}}\left( {{{{\hat{x}}}_{li}}} \right) \) to determine the triggering time instant \(t_{l}\), and the decentralized tracking control policy is updated by \(u_i^*\left( {{\vartheta _i}\left( {{x_i}\left( {{t_l}} \right) } \right) } \right) = u_i^*\left( {{{{\hat{\vartheta }} }_{li}}\left( {{{{\hat{x}}}_{li}}} \right) } \right) \) within \(t \in \left[ {{t_l},{t_{l + 1}}} \right) \).
Critic-based event-triggered decentralized tracking control
To solve the event-triggered HJBE, the neural network (NN) which has powerful learning ability, is utilized to approximate the performance index function \(\varXi _i^*\left( {{\vartheta _i}} \right) \) as:
where \({W_{ci}} \in {\mathbb {R}}{^K}\) is the desired weight vector, K is the number of neurons in the hidden layer, \({\delta _{ci}}\left( {{\vartheta _i}} \right) \) is the activation function, and \({\varepsilon _{ci}}\left( {{\vartheta _i}} \right) \) is the critic NN approximation error. Thus, the partial derivative of \(\varXi _i^*\left( {{{{\hat{\vartheta }} }_{li}}} \right) \) is:
where \(\nabla \delta _{ci}\left( {{{{\hat{\vartheta }} }_{li}}}\right) = {\left. {\frac{{\delta _{ci}\left( {{\vartheta _i}} \right) }}{{\partial {\vartheta _i}}}} \right| _{{\vartheta _i}= {{{\hat{\vartheta }} }_{li}}}}\) and \(\nabla {\varepsilon _{ci}}\left( {{{{\hat{\vartheta }} }_{li}}} \right) = {\left. {\frac{{\varepsilon _{ci}\left( {{\vartheta _i}} \right) }}{{\partial {\vartheta _i}}}} \right| _{{\vartheta _i}= {{{\hat{\vartheta }} }_{li}}}}\). According to [51], it is reasonable to assume \(||\nabla \delta _{ci}\left( {{{{\hat{\vartheta }} }_{li}}}\right) ||\le {\delta _{cid}}\) and \(||\nabla {\varepsilon _{ci}}\left( {{{{\hat{\vartheta }} }_{li}}} \right) ||\le {\varepsilon _{cid}}\) with \({\delta _{cid}}\) and \({\varepsilon _{cid}}\) positive constants. Through Assumption 2, we have \(\left\| \nabla \delta _{ci}\left( {{{ \vartheta }_{i}}}\right) -\nabla \delta _{ci}\left( {{{{\hat{\vartheta }} }_{li}}}\right) \right\| \) \(\le P_{i}\left\| E_{li}\right\| \). Combining (32) with (36), we can obtain
Therefore, the event-triggered HJBE can be rewritten as:
where \({u_i^*\left( {{{{\hat{\vartheta }} }_{li}}} \right) } = u_{1i} + u_{2i}^*\left( {{{{\hat{\vartheta }} }_{li}}} \right) \) is the ideal control torque. Since the desired weight vector \(W_{ci}\) is unavailable, the critic NN can be approximated by:
and the partial derivative of \({{\hat{\varXi }} _i}\left( {{{{\hat{\vartheta }} }_{li}}} \right) \) can be expressed by \(\nabla {{\hat{\varXi }} _i}\left( {{{{\hat{\vartheta }} }_{li}}} \right) \) \( = \nabla \delta _{ci}^T\left( {{{{\hat{\vartheta }} }_{li}}} \right) \) \({{\hat{W}}_{ci}}\). The event-triggered approximate decentralized tracking control strategy \({{\hat{u}}_{i}}\left( {{{{\hat{\vartheta }} }_{li}}} \right) \) is presented as:
Remark 5
Different from the traditional ADP-based optimal control approaches that rely on actor NNs, critic NNs, and even model NNs, in this paper, the compensator-critic structure-based event-triggered decentralized tracking control method, which consist of model-based robust compensator and only critic NNs-based approximated optimal controller, is proposed for MRMs.
Through (38), (39) and (40), the approximate event-triggered Hamiltonian is:
Comparing (38) with (41), the NN weight approximation error can be defined as \({{\tilde{W}}_{ci}} = {W_{ci}} - {{\hat{W}}_{ci}}\), and the residual error \({\varepsilon _{cHi}}\) is:
where \({\varepsilon _{cHi}}\) is bounded as \(||{\varepsilon _{cHi}} ||\le {\varepsilon _{cHiM}}\) with \({\varepsilon _{cHiM}}\) a positive constant, and \({\varepsilon _{ZiM}}\) is the upper bound of \({\varepsilon _{Zi}}\) as:
with \(\varepsilon _{ui}={{{{\hat{u}}}_i}\left( {{{{\hat{\vartheta }} }_{li}}} \right) - {u_i}\left( {{{{\hat{\vartheta }} }_{li}}} \right) }= -\frac{1}{2}R_i^{ - 1}D_i^T\left( {{\nabla {\delta ^T _{ci}}}\left( {{{{\hat{\vartheta }} }_{li}}} \right) \tilde{W}_{ci}}+{\nabla \varepsilon ^T _{ci}}\left( {{{{\hat{\vartheta }} }_{li}}} \right) \right) \).
To adjust the critic NN weight vector \({ {{\hat{W}}}}_{ci}\), we minimize the objective function \({E_{ci}} = \frac{1}{2}\varepsilon _{cHi}^T{\varepsilon _{cHi}}\) by the gradient decent algorithm, and it should be updated by:
where \({\sigma _{ci}}{=} \nabla {\delta _{ci}}\left( {{\vartheta _i}} \right) \left( {{\varGamma _f}\left( {{x_i}} \right) {+} {D_i}{{{\hat{u}}}_i}\left( {{{{\hat{\vartheta }} }_{li}}} \right) {+} {\varTheta _i}\left( x \right) {+} {\upsilon _i}} \right) \). Therefore, the weight approximation error can be updated by:
Remark 6
The critic NN is constructed to approximate the decentralized optimal compensation control based on the powerful learning ability of NNs. Note that the critic NN weight learning law (44) is designed using the local joint modular state without relying on the event-triggered conditions.
Thus, the event-triggered approximate decentralized tracking control policy \({{{\hat{u}}}_i}\left( {{{{\hat{\vartheta }} }_{li}}} \right) \) which is applied to MRM as the control torque is given as (40). The structural diagram of the proposed compensator-critic structure-based event-triggered decentralized tracking control strategy of MRM systems is illustrated in Fig. 2.
Theorem 2
Considering the n-DOF MRM whose subsystem dynamics described as (5), the weight estimation error \( {\tilde{W}}_{ci}\) of the critic NN can be guaranteed to be UUB with the weight updating law (44).
Proof
Select the Lyapunov function candidate as:
Supposed that \({{{\sigma _{ci}}\sigma _{ci}^T} \le \lambda _{\max }}\left( {{\sigma _{ci}}\sigma _{ci}^T} \right) \buildrel \varDelta \over = {\sigma _{ciM}}\) with a positive constant \({\sigma _{ciM}}\), where \({\lambda _{\max }}\left( \cdot \right) \) denotes the maximal eigenvalue of matrix. Then, according the critic NN weight updating law (44) and Young’s inequality, the time derivative of (46) is calculated as:
Thus, the weight approximation error \( {\tilde{W}}_{ci}\) can be proved to be UUB with \({\alpha _{ci}} > \frac{1}{2}\), if \( {\tilde{W}}_{ci}\) lies outside the compact set:
\(\square \)
Remark 7
Unlike existing works which presented time-triggered tracking controllers [37, 38], in this paper, the event-triggered mechanism is introduced to develop the compensator-critic structure-based decentralized tracking control strategy based on the ADP approach with considering the optimal performance, reducing computational burden, and saving communication and energy consumption.
Stability analysis of the closed-loop MRM system
In this part, the stability analysis of the closed-loop MRM system under the developed compensator-critic structure-based event-triggered decentralized tracking control is provided using the Lyapunov stability theorem.
Theorem 3
Considering the n-DOF MRM whose subsystem dynamics described as (5), and Assumptions 1 and 2, the closed-loop MRM system is UUB via the approximate compensator-critic structure based event-triggered decentralized tracking control law (40) if the following condition is satisfied:
Proof
Select the Lyapunov function candidate for the MRM subsystem as:
(1) The events are not triggered, i.e., \(t \in \left[ {{t_l},{t_{l + 1}}} \right) \). Calculating the time derivative of (49) \({\dot{V}_{i}}={\dot{V}_{1i}}+{\dot{V}_{2i}}\), the first term is:
\(\square \)
In light of the time-triggered HJBE (14) and optimal control law (32), we obtain:
and
Then, substituting (51) and (52) into \({\dot{V}_{1i}}\), we have
According to Theorem 1 and Assumption 2, through Young’s inequality, (53) becomes:
For the second term \(\dot{V}_{2i}\), we have \({\dot{V}_{2i}} = \nabla \varXi _i^*\left( {{{{\hat{\vartheta }} }_{li}}} \right) = 0\).
Applying (49) and (54), we obtain the time derivative of the Lyapunov function candidate \( \dot{V} \left( t \right) \) of the MRM system as:
Hence, (55) implies that \(\dot{V}(t)\le 0\) if the triggering condition (48) is satisfied when \(\vartheta _i\) lies outside the compact set \({\varOmega _{ui}} = \left\{ {\vartheta _i}:\left\| {{\vartheta _i}} \right\| \le \frac{{\upsilon _{Mi}}}{ {\lambda _{\min }}\left( {{Q_i}} \right) -1}\right\} \).
(2) When the events are triggered, i.e., \(\forall t = {t_{l + 1}}\), the difference of (49) is presented as:
where \({{\hat{\vartheta }} _{li}}\left( {t_{l + 1}^ - } \right) = \mathop {\lim }\nolimits _{{\rho _i} \rightarrow 0} \left( {{{{\hat{\vartheta }} }_{li}}\left( {{t_{l + 1}} - {\rho _i}} \right) } \right) \) and \({\rho _i}\) is a small positive constant. From (49), (55), and (56), we obtain that \({\dot{V}_i}\left( t \right) \le 0\) when the events are not triggered \(t \in \left[ {{t_l},{t_{l + 1}}} \right) \). Then, we have
where \({O_i}\left( \cdot \right) \) is class-k function [52], and \({E_{\left( {l + 1} \right) i}}\left( {{t_l}} \right) = {{\hat{\vartheta }} _{\left( {l + 1} \right) i}} - {{\hat{\vartheta }} _{li}}\). Then, (56) becomes
Therefore, if event-triggered condition (48) holds, the closed-loop MRM system is UUB. This completes the proof.
Exclusion of Zeno behaviors
In general, the MRM system is a continuous-time system that the minimum trigger interval \({t_{\min }} = \min \left\{ { {{t_{l + 1}} - {t_l}} } \right\} \) is possible to be zero, i.e., the so-called Zeno behavior. Thus, it is necessary to prove that \({t_{\min }}\) has a positive lower bound.
Theorem 4
Considering the dynamics of the MRM subsystem (5), the triggering condition (48) and the compensator-critic structure-based event-trigger-ed decentralized tracking control strategy (40), the minimum trigger interval \({t_{\min }}\) has a positive lower bound by:
where \({\varPi _{l,\min }} = \min \left( {\left\| {{E_{li}}\left( {{{{\hat{\vartheta }} }_{li}}\left( {t_{l + 1}^ - } \right) } \right) } \right\| /\left( {{{{\hat{\vartheta }} }_{li}}} \right) + {\varpi _i}} \right) > 0\) and \({\varpi _i}\) is a positive constant.
Proof
The time derivative of the event-triggered error (30) is:
According to Assumptions 1 and 2, the upper bound of \({{\dot{\vartheta }} _i}\left( {{x_i}} \right) \) is derived as:
Combining (30), (62) with (63), we can obtain:
When \(t = {t_{l + 1}}\), the event-triggered condition satisfies:
According to (64) and (65), the lth triggering interval \(\varDelta {t_l}\) has the lower bound by:
It can be seen from (66) that the minimum triggering interval \({t_{\min }} = \left\| {{E_{Li}}} \right\| \) \(/ \left( \left\| {{{{\hat{\vartheta }} }_{li}}} \right\| + {\varpi _i} \right) \) which increases from zero to the positive value \({\varPi _{l,\min }} {=} \min \) \(\left( {\left\| \! {{E_{li}}\left( {{{{\hat{\vartheta }} }_{li}}\left( {t_{l + 1}^ - } \right) } \right) } \right\| \!/\left( {{{{\hat{\vartheta }}}_{li}}} \right) \! {+}\! {\varpi _i}} \right) ,\) \(\forall t \in \left[ {{t_l},{t_{l{+}1}}} \right) \). Therefore, the minimum triggering interval \({t_{\min }}\) satisfies the condition (61), such that \({t_{\min }}\) has a positive lower bound for arbitrary state \({\vartheta _i}\left( {{x_i}} \right) \). \(\square \)
Experimental results
Establishment of experimental platform
A 2-DOF MRM experimental platform has been established, which is composed of two sets of joint modules and connecting rods, as shown in Fig. 3. Each joint module contains a motor, an incremental encoder, a speed reducer, an absolute encoder, and a torque sensor. The DC Brush motor selected from Maxon Inc. is the power to drive the MRM and each joint motor is driven by a linear power amplifier (LPA). The incremental encoder and the absolute encoder are utilized to measure the displacement of the motor and the position of the link module, correspondingly. The speed reducer is connected to increase the motor output torque through reducing motor speed with the gear ratio 100:1. The joint torque sensor is equipped between the link module and the joint module to measure the joint torque. The experimental data acquisition and processing depend on the QPIDe data acquisition device and Matlab/Simulink software installed in the host–computer, respectively. The designed control system is built by Simulink, and the packaged QUARC module is utilized to establish the communication between the host–computer and the QPIDe device to realize the real-time control of the 2-DOF MRM.
In this paper, the experiments of a 2-DOF MRM with tracking task are established to verify the effectiveness of the proposed compensator-critic structure-based event-triggered decentralized tracking control strategy. We select the desired trajectories for each joint as \( {q_{1d}} = \frac{{\pi }}{{4}}\sin \left( {\frac{\pi }{{45}}} \right) t+0.05\), \({q_{2d}} = \frac{{\pi }}{{2}}\sin \left( {\frac{\pi }{{45}}} \right) t+0.1\). For the critic NN, we choose the radial basis function neural network (RBFNN) to approximate the optimal performance index function. The 1-5-1 NN structure is selected with 1 input neuron, 5 hidden neurons, and 1 output neuron for each joint. The NN weights are defined as \({{\hat{W}}_{ci}} = {\left[ {{{{\hat{W}}}_{1ci}},{{{\hat{W}}}_{2ci}},{{{\hat{W}}}_{3ci}},{{{\hat{W}}}_{4ci}},{{{\hat{W}}}_{5ci}}} \right] ^T}\) with \({{\hat{W}}_{0ci}} = {\left[ {0.3,0.1,0.3,0.1,0.3} \right] ^T}\). The activation function is chosen as the radial basis function \({\delta _{jci}}\left( {{\vartheta _i}} \right) = \exp \left( { - \frac{{{{\left\| {{\vartheta _i} - {c_i}} \right\| }^2}}}{{2b_j^2}}} \right) \), \(b_{j}=1.5\), \(j=1,2,3,4,5\). And, \(c_{1}= [-1, -0.5,0,0.5,1]^T\) and \(c_{2}= [-2, -1,0,1,2]^T\). Other model parameters, control parameters, and upper bound parameters are listed in Table 1. Note that the real-time state of MRMs can only be obtained by sensor sampling; therefore, we choose the sampled state from the time-triggered mechanism method as the system state in the event-triggered control.
Experimental results and analysis
Experimental results under the proposed control method are shown in Figs. 4, 5, 6, 7 and 8, which compared with the ADP-based time-triggered decentralized tracking control method [37].
Figure 4 shows the position tracking curves of each joint under the proposed control method. The red and blue dashed lines present desired tracking trajectory and actual tracking trajectory, respectively. From this figure, one observes that the asymptotic tracking between the actual and the desired trajectories can be realized in a very short time. Through Fig. 5, the position tracking errors of each joint keep within an acceptable range (less than \( \pm \mathrm{{5}}\times 10^ {- 3}\)rad) under the proposed event-triggered tracking control approach, and it illustrates the effectiveness of the presented control scheme intuitively.
Figure 6 presents the joint control torque curves of MRMs under the conventional and the proposed control methods. The red and blue lines show that of the time-triggered control method [37] and the proposed event-triggered control method, respectively. We can see the proposed joint control torques only updated when the event-triggered condition is satisfied, and thus, it has a lower updating frequency. Figure 7 illustrates the triggering error \(\left\| E_{li}\right\| \) and the triggering threshold \(\left\| E_{Li} \right\| \). In Figs. 6 and 7, we can see that the control torque curve within time interval [20,30] is a piece-wise one depending on the zero-order hold.
The cumulative numbers of sample states used in the time-triggered control method [37] and the proposed event-triggered control method are shown in Fig. 8. It shows that the updating time of the time-triggered control method is near five times as that of the event-triggered one.
From the experimental results, the developed compensator-critic structure-based event-triggered decentralized tracking control is effective to MRMs. It cannot only maintain the satisfactory control accuracy, but also effectively reduce the computational burden, save the communication, and energy consumption.
Conclusion
This paper addresses the event-triggered decentralized tracking control problem for MRMs with a compensator-critic structure-based ADP algorithm. With the help of the JTF technique, the subsystem dynamic model of MRM is established. The model-based robust compensator is utilized to avoid the influence of dynamic uncertainties. The performance index function is constructed to reflect the position error, the velocity error, and the control torque. Thus, the event-triggered decentralized tracking control is obtained including the model-based robust controller and the ADP-based optimal compensation controller. Then, a critic NN is constructed to solve the improved event-triggered HJBE, and the event-triggered approximate decentralized optimal compensation tracking control torque can be derived directly. The Lyapunov stability theorem is utilized to prove UUB of the tracking error of the closed-loop MRM system. In contrast to the time-triggered optimal controller, the proposed compensator-critic structure-based event-triggered decentralized tracking control method cannot only maintain the satisfactory control accuracy, but also effectively reduce the computational burden, save the communication, and energy cost, simultaneously.
References
Yun A, Moon D, Ha J (2020) ModMan: an advanced reconfigurable manipulator system with genderless connector and automatic kinematic modeling algorithm. IEEE Robot Autom Lett 99:1–1
Machi Z, Jacek S (2018) Transformations of arm-z modular manipulator with particle swarm optimization. Adv Eng Softw 126:147–160
Jin L, Li S, Yu J (2018) Robot manipulator control using neural networks: a survey. Neurocomputing 285:23–24
Liang Y, Shi H, Tian G (2018) A reduced-order approach to the adaptive fuzzy sliding mode control of the constrained manipulator. Adv Mech Eng 10(7):1–12
Yang Y, Liu Z, Ma G (2019) Adaptive distributed control of a flexible manipulator using an iterative learning scheme. IEEE Access 7:145934–145943
Fareh Raouf (2014) Saad: distributed control strategy for flexible link manipulators. Robotica 33(04):768–786
Ham S, Lee J (2015) Decentralized neural network control for guaranteed tracking error constraint of a robot manipulator. Int J Control Autom 13(4):906–915
Ramon Garcia-Hernandez (2013) Jose: decentralized neural backstepping control applied to a robot manipulator. Int J Adv Rob Syst 10(78):1–10
Fareh R, Saad M (2019) Trajectory tracking and stability analysis for mobile manipulators based on decentralized control. Robotica 37(10):1732–1749
Zhu M, Zhao B, Li Y (2010) Decentralized adaptive fuzzy sliding mode control for reconfigurable modular manipulators. Int J Robust Nonlin 20(4):472–488
Zhou F, Dong B, Li Y (2017) Torque sensorless force/position decentralized control for constrained reconfigurable manipulator with harmonic drive transmission. Int J Control Autom 15(4):2364–2375
Kosuge K, Takeuchi H (1990) Motion control of a robot arm using joint torque sensors. IEEE Trans Rob 6(2):258–263
Imura J, Sugie T, Yokokohji Y (2002) Robust control of robot manipulators based on joint torque sensor information. In: International workshop on intelligent robots a systems 91 intelligence for mechanical systems, Osaka, Japan
Zhang H, Ahmad S, Liu G (2017) Torque estimation for robotic joint with harmonic drive transmission based on position measurements. Int J IEEE Trans Robot 31(2):322–330
Werbos P (1992) Approximate dynamic programming for real time control and neural modeling. In: White DA, Sofge DA (eds) Handbook of intelligent control: neural, fuzzy, and adaptive approaches. Van Nostrand Reinhold, New York
Zhao B, Liu D, Alippi Cesare (2020) Sliding mode surface-based approximate optimal control for uncertain nonlinear systems with asymptotically stable critic structure. IEEE Trans Cybern (Early access). https://doi.org/10.1109/TCYB.2019.2962011
Huang Y, Liu D (2014) Finite-horizon neuro-optimal tracking control for a class of discrete-time nonlinear systems using adaptive dynamic programming approach. Neurocomputing 125(11):46–56
Wei Q, Liu D (2015) Value iteration adaptive dynamic programming for optimal control of discrete-time nonlinear systems. IEEE Trans Cybern 46(3):840–853
Yang X, Liu D, Wei Q (2016) Guaranteed cost neural tracking control for a class of uncertain nonlinear systems using adaptive dynamic programming. Neurocomputing 198:80–90
Jiang Y, Jiang Z (2013) Robust adaptive dynamic programming with an application to multimachine power system. IEEE Trans Neural Netw Learn 24(7):1150–1156
Zhao B, Liu D, Luo C (2019) Reinforcement learning-based optimal stabilization for unknown nonlinear systems subject to inputs with uncertain constraints. IEEE Trans Neural Netw Learn 31(10):4330–4340
Wang D, Liu D, Li H (2016) An approximate optimal control approach for robust stabilization of a class of discrete-time nonlinear systems with uncertainties. IEEE Trans Syst Man Cybern Syst 46(5):713–717
Zhu Y, Zhao D (2020) Online minimax Q network learning for two-player zero-sum Markov games. IEEE Trans Neural Netw Learn Syst (Early access). https://doi.org/10.1109/TNNLS.2020.3041469
Zhao B, Wang D, Shi G, Liu D, Li Y (2018) Decentralized control for large-scale nonlinear systems with unknown mismatched interconnections via policy iteration. IEEE Trans Syst Man Cybern Syst 48(10):1725–1735
Zhao B, Luo F, Lin H, Liu D (2021) Particle swarm optimized neural networks based local tracking control scheme of unknown nonlinear interconnected systems. Neural Netw 134:54–63
Liu D, Xue S, Zhao B, Luo B, Wei Q (2021) Adaptive dynamic programming for control: a survey and recent advances. IEEE Trans Syst Man Cybern Syst 51(1):142–160
Zhu Y, Zhao D, He H (2020) Optimal feedback control of pedestrian flow in heterogeneous corridors. IEEE Trans Auto Sci Eng (Early Access). https://doi.org/10.1109/TASE.2020.2996018
Zhou W, Shi J, Yin G, He W, Yi J (2020) Optimal control for aluminum electrolysis process using adaptive dynamic programming. IEEE Access 8:220374–220383
Nguyen LT (2019) Event-triggered distributed h constrained control of physically interconnected large-scale partially unknown strict-feedback systems. IEEE Trans Syst Man Cybern Syst 20:1–13
Zhang Q, Zhao D, Wang D (2018) Event-based robust control for uncertain nonlinear systems using adaptive dynamic programming. IEEE Trans Neural Netw Learn Syst 29:37–50
Vamvoudakis KG, Ferraz H (2018) Model-free event-triggered control algorithm for continuous-time linear systems with optimal performance. Automatica 87:412–420
Yang X, He H (2019) Decentralized event-triggered control for a class of nonlinear-interconnected systems using reinforcement learning. IEEE Trans Cybern 99:1–14
Vignesh Narayanan Avimanyu (2018) Approximate optimal distributed control of nonlinear interconnected systems using event-triggered nonzero-sum games. IEEE Trans Neural Netw Learn Syst 30(5):1512–1522
Yang X, He H (2018) Adaptive critic designs for event-triggered robust control of nonlinear systems with unknown dynamics. IEEE Trans Cybern 49(6):2255–2267
Dong B, Zhou F, Li Y (2020) Decentralized robust optimal control for modular robot manipulators via critic-identifier structure-based adaptive dynamic programming. Neural Comput Appl 32:3441–3458
Zhao B, Liu D (2019) Event-triggered decentralized tracking control of modular reconfigurable robots through adaptive dynamic programming. IEEE Trans Ind Electron 67(4):3054–3064
Dong B, An T, Zhou F, Yu W (2019) Model-free optimal decentralized sliding mode control for modular and reconfigurable robots based on adaptive dynamic programming. Adv Mech Eng 11(12):1–12
Zhao B, Li Y (2018) Model-free adaptive dynamic programming based near-optimal decentralized tracking control of reconfigurable manipulators. Adv Mech Eng 16:478–490
Chen M, Yang G (1998) Automatic model generation for modular reconfigurable robot dynamics. J Dyn Syst Meas Control 120(3):346
Liu G (2002) Decomposition-based friction compensation of mechanical systems. Int J Mechatron 12(5):755–769
Dong B, Zhou F, Liu K, Li Y (2018) Decentralized robust optimal control for modular robot manipulators via critic-identifier structure-based adaptive dynamic programming. Neural Comput Appl 32:3441–3458
Liu G, Abdul S, Andrew A (2008) Distributed control of modular and reconfigurable robot with torque sensing. Robotica 26(1):75–84
Kalman RE (1960) Contribution to the theory of optimal control. Bol Soc Matem Mex 20:102–110
Ma B, Dong B, Zhou F, Li Y (2020) Adaptive dynamic programming-based fault-tolerant position-force control of constrained reconfigurable manipulators. IEEE Access 8:183286–183299
Mu C, Sun C, Wang D (2018) Decentralized adaptive optimal stabilization of nonlinear systems with matched interconnections. Soft Comput 22:2705–2715
Yang X, He H (2019) Adaptive critic learning and experience replay for decentralized event-triggered control of nonlinear interconnected systems. IEEE Trans Syst Man Cybern Syst 99:1–13
Spong MW (1992) On the robust control of robot manipulators. IEEE Trans Autom Contr 37(11):1782–1786
Liu G, Goldenberg A (1997) Robust control of robot manipulators based on dynamics decomposition. IEEE Trans Robot Autom 1(5):783–789
Dong B, An T, Zhou F, Li Y (2019) Decentralized robust zero-sum neuro-optimal control for modular robot manipulators in contact with uncertain environments: theory and experimental verification. Nonlinear Dyn 97(13):503–524
Li Y, Jin W, Ma B, Dong B (2020) Adaptive dynamic programming-based decentralized guaranteed cost control for reconfigurable manipulators with uncertain environments. J Electr Eng Technol 20:1–16
Wang D, Liu D (2018) Neural robust stabilization via event-triggering mechanism and adaptive learning technique. Neural Netw 102:27–35
Khalil H (2002) Nonlinear systems (third edition). Prentice-Hall, Upper Saddle River
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant no. 61773075 and 61703055), the Scientific Technological Development Plan Project in Jilin Province of China (Grant nos. 20200801056GH and 20190103004JH), and the Science and Technology project of Jilin Provincial Education Department of China during the 13th Five-Year Plan Period (JJKH20200672KJ, JJKH20200673KJ, and JJKH20200674KJ).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ma, B., Li, Y. Compensator-critic structure-based event-triggered decentralized tracking control of modular robot manipulators: theory and experimental verification. Complex Intell. Syst. 8, 1913–1927 (2022). https://doi.org/10.1007/s40747-021-00359-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-021-00359-0