An Analytical Study in Multi-physics and Multi-criteria Shape Optimization

Abstract

A simple multi-physical system for the potential flow of a fluid through a shroud, in which a mechanical component, like a turbine vane, is placed, is modeled mathematically. We then consider a multi-criteria shape optimization problem, where the shape of the component is allowed to vary under a certain set of second-order Hölder continuous differentiable transformations of a baseline shape with boundary of the same continuity class. As objective functions, we consider a simple loss model for the fluid dynamical efficiency and the probability of failure of the component due to repeated application of loads that stem from the fluid’s static pressure. For this multi-physical system, it is shown that, under certain conditions, the Pareto front is maximal in the sense that the Pareto front of the feasible set coincides with the Pareto front of its closure. We also show that the set of all optimal forms with respect to scalarization techniques deforms continuously (in the Hausdorff metric) with respect to preference parameters.

1 Introduction

The design of a mechanical component requires choosing a material and a shape. Often, a component serves a primary objective, but also requires a certain level of endurance. Material damage is caused by the loads that are imposed during service. The quest for an optimal design in the majority of cases therefore is at least a bi-criteria optimization problem and in many cases a multi-criteria one [22].

In mechanical engineering, multi-criteria optimization often comes along with coupled multi-physics simulations. If we take the design of turbine blades as an example, the simulation of external flows and cooling air flows inside a blade have to be combined with a thermal and a mechanical simulation inside the blade [53].

Mathematical optimization is widely used in mechanical engineering; see, e.g., [41, 44]. On the other hand, some directions of contemporary mathematical research—like topology optimization (we refer, e.g., to [3, 8])—were initiated by mechanical engineers [24]. While the given field is interdisciplinary, from the mathematical point of view one would not only like to propose and analyze new optimization algorithms, but also to understand the existence and the properties of optimal solutions. While for mono-criteria optimization such a framework has been established [3, 17, 20, 26, 34], a general framework for multi-criteria optimization is still missing; see however [18, 21, 34] for numerical studies addressing the topic.

Component life models from materials science are used to judge the mechanical integrity of a component after a certain number of load cycles; see, e.g., [5]. These models often use deterministic life calculation which predicts failure at the point of the highest mechanical loading and thus involves the non-differentiable formation of a minimum life over all points on the component or component’s surface, depending on whether we have a volume or a surface-driven damage mechanism. In recent time, such models have been extended by probabilities of failure [4, 25, 31, 32, 35, 40, 47, 48], which involve integrals over local functions of the stress tensor in the component or on the component’s surface, respectively. This approach makes it possible to compute shape derivatives and gradients [10, 16, 29, 50] and therefore places component reliability in the context of shape optimization. However, as remarked in [31], the probability of failure as an objective functional requires more regular solutions as provided by the usual weak theory based on $H^1$ Sobolev spaces [23]. As we find here, this is also the case for simplistic models of fluid dynamical efficiency. As in previous works [9, 13, 31], we therefore apply a framework based on Hölder continuous classical solution spaces and extend it to multi-criteria optimization.

Within this general framework, we prove the existence of Pareto optimal designs; see also [21] for a related result in a different setting requiring less regularity. Here, however, we show how to use the graph compactness property [34, Subsection 2.4] along with the lower semi-continuity of all objective functionals to prove certain maximality properties of the non-dominated feasible points: Namely that the Pareto front in the set of feasible points [22] coincides with the Pareto front of the closure of the feasible points. Put in other words, each dominated design is also dominated by at least one Pareto optimal design.

We give a simplistic multi-physical system as an example that fits the general framework. This mathematical model couples a potential flow with structural mechanics and is motivated from gas turbine engineering. We define two (rather singular) objective functionals, namely a aerodynamic loss based on the theory of boundary layers [45] and furthermore, the probability of failure after a certain number of load cycles [31, 40]. Each of these models includes nonlinear functions that depend on second derivatives of the solution after restriction to the boundary of the underlying PDE’s domains. For this system, we prove that the assumptions of the general framework are fulfilled and we conclude that a maximal Pareto front exists in this case.

Multi-criteria optimization relates to preferences of a decision maker [22, 41]. Here, we are interested in continuity properties of Pareto optimal shapes, when the preference is expressed by a parameter in a merit function, which, e.g., could be the weights in a weighted sum approach. The stability of the optimal solutions to such scalarization techniques in dependence of a parameter is already investigated in the literature; see, e.g., [7, 33, 51, 52], for finite-dimensional and infinite-dimensional spaces. Here, we show that our general framework is indeed suitable to prove certain continuity properties of the ${\mathrm{arg\,min}}$ sets of scalarized multi-criteria optimization problems in the Hausdorff distance as a function of the scalarization—or preference—parameter. Such structural properties of the Pareto front for the first time are applied in the context of shape optimization.

As this work is focused on the existence and the mathematical properties of the Pareto front in shape optimization, it does not contain any numerical and algorithmic contributions. However, numerical implementations for the computation of the reliability of failure can be found in [39, 46]. The adjoint method for computing the shape derivatives for such objective functionals has been applied in [12, 29, 30]. In [21, 49], numerical studies of multi-criteria shape optimization are presented and Pareto fronts are explored. While the objective functionals in these two works fit into our general framework, they do not (yet) include aerodynamic losses (see however [37]). The results we present here on the continuity properties of Pareto optimal solutions under a change of scalarization can be seen as a theoretical underpinning of the Pareto tracing method presented in [11].

Our paper is organized as follows: We introduce the physical systems, which underlie the multi-criteria shape optimization problem we consider in Sect. 2. Afterward, in Sect. 3, we describe our framework for multi-criteria shape optimization. By deriving uniform bounds for the solution spaces of the physical systems in Sect. 4, we prove the well posedness of the shape optimization problem. Up to here we considered optimality in terms of Pareto optimality. In Sect. 5, we apply scalarization techniques to transform the problem into an univariate shape problem and investigate the dependency of the optimal shapes on the specific used technique. In Sect. 6, we give a resume and an outlook on future research direction. Some technical details on Hölder functions and solutions of elliptic partial differential equations are found in Appendix A.

2 A Simple Multi-physics System

We intend to optimize the shape of some component, e.g., a turbine vane, in terms of reliability and efficiency. Reliability depends on surface and volume forces acting on the component. In our setting, the component lies in a shroud and within the shroud a fluid is flowing past the component. Due to static pressure, the fluid imposes a surface force on the component. Hence, it is indispensable to include the fluid flow field into the optimization process. At the same time, the component leads to frictional loss in the fluid that diminishes the efficiency of the design.

In the following, we describe a simple model, which approximates the fluid flow in a simple way as potential flow and model frictional loss via a post-processing step to the solution that is based on a simple model for the boundary layer. We also consider the effect of the fluid’s mechanical loads to the component. As the static pressure takes the role of a boundary condition for the partial differential equation of linear elasticity, the internal stress fields of the component depend on the flow field, too. The component’s fatigue life that results in the probability of failure, i.e., the formation of a fatigue crack, as a second objective functional.

2.1 Potential Flow Equation

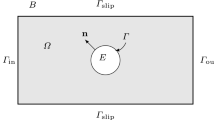
As component we consider a compact domain ${\varOmega }\subset {\mathbb {R}}^3$ with $C^{k,\alpha }$ boundary —where we always have that $k \in {\mathbb {N}}_{0}$ and $\alpha \in \, ]0,1]$ unless we specify further— that is partially contained in some larger compact domain $D\subset {\mathbb {R}}^3$ representing a shroud with $C^{k,\alpha }$ boundary as well. With $\mathrm {int}({\varOmega })$ and $\mathrm {cl}({\varOmega })$ we shall denote the topological interior and closure of a set ${\varOmega }$, respectively. We assume that $\mathrm {int}(D\backslash {\varOmega })$ is simply connected, has $C^{k,\alpha }$ boundary, and that there exists a open ball $B := B_\epsilon$ with $\epsilon > 0$ such that $\mathrm {cl}(B) \subset \mathrm {int}({\varOmega }\backslash D)$. The shroud D has an inlet and outlet where the fluid flows in and out, respectively. At the remaining boundary part the fluid cannot leak. In this work, we consider an incompressible and rotation-free perfect fluid in a steady state. The assumption of zero shearing stresses in a perfect fluid—or zero viscosity—simplifies the equation of motion so that potential theory can be applied. The resulting solution still provides reasonable approximations to many actual flows. The viscous forces are limited to a thin layer of fluid adjacent to the surface, and therefore, in favor of simplicity, we leave these effects out since they have little effect on the general flow pattern.¹

A fundamental condition is that no fluid can be created or destroyed within the shroud D. The equation of continuity expresses this condition. Consider a three-dimensional velocity field v on $D\subset {\mathbb {R}}^3$, then the continuity equation is given by

$$\begin{aligned} \nabla \cdot v = 0. \end{aligned}$$

If we assume that the velocity field v is rotation free, $\nabla \times v=0$, then there exists a velocity potential or flow potential $\phi$ such that

$$\begin{aligned} v = \nabla \phi . \end{aligned}$$

Hence, under the assumption that v is divergence free and rotation free, there is a velocity potential $\phi$ that satisfies the Laplace equation

$$\begin{aligned} {\varDelta }\phi =\nabla \cdot \nabla \phi = 0. \end{aligned}$$

Let n be the unitary outward normal of the boundary $\partial D$. By applying suited Neumann boundary conditions g, that correspond with our assumptions for a conserved flow through the inlet and outlet of the shroud, we get the potential flow equation

(1)

Here, we assume that g is only nonzero in the inlet and outlet regions and is continued to be zero on the upper and lower wall of the shroud. Therefore, no discontinuities occur where $\partial {\varOmega }$ meets $\partial D$ (Fig. 1).

Fig. 1

A turbine blade ${\varOmega }$ within a shroud D. We note that this representation of the domains ${\varOmega }$ and D is only a sketch. In particular, every visible edge has to be sufficiently rounded in order to ensure the Hölder continuity of the boundaries

The following lemma ensures the existence of a solution to the potential equation. It also gives a Schauder estimate that leads to a uniform bound for the solution space we investigate in Sect. 4.1. This uniform bound is crucial for the existences of solutions to the multi-criteria optimization problem we consider in this work and which we introduce in Sect. 3.

Lemma 2.1

(Schauder Estimate for Flow Potentials) We consider the potential flow Eq. (1). Let $g \in C^{1,\alpha }(D, {\mathbb {R}})$ and assume that the boundaries described above are all of class $C^{k, \alpha }$ with $k \ge 2$. If $\int _{\partial D} g\, \hbox {d}A = 0$, then (1) possesses at least one solution $\phi \in C^{2,\alpha }(\mathrm {cl}(D\backslash {\varOmega }), {\mathbb {R}})$. To obtain uniqueness, we fix $u(x_{0}) = 0$ at some point $x_0 \in \mathrm {int}(D\backslash {\varOmega })$. This solution satisfies

$$\begin{aligned} \Vert \phi \Vert _{C^{2,\alpha }(D\backslash {\varOmega })} \le C\left( \Vert \phi \Vert _{C^{0,\alpha }(D\backslash {\varOmega })} + \Vert g \Vert _{C^{1,\alpha }(\partial D\backslash \partial (D \cap {\varOmega }))} \right) , \end{aligned}$$

(2)

with constant $C=C({\varOmega })$.

Proof

By assumption (and by definition), $D\backslash {\varOmega }$ has a Hölder continuous boundary of class $C^{k, \alpha }$, with $k \ge 2,\, \alpha \in ]0,1]$. Additionally, the Neumann boundary condition holds $\int _{\partial (D \backslash {\varOmega })} g + 0 \, \hbox {d}A = 0$, and thus the assertion follows directly out of [42, Theroem 3.1 and Theorem 4.1]$\square$

2.2 Elasticity Equation

One of the most crucial demands on the component ${\varOmega }$ is the reliability. Fatique failure is the most appearing type of failure for, e.g., gas turbines where the event of failure for a component as, e.g., a blade or vain is the appearance of the first crack. For this purpose, we consider the elasticity equation, which models the deformation of a component under given surface and volume forces and allows us to calculate the stress fields that drive crack formation.

We denote with n the unitary outward normal of the boundary $\partial {\varOmega }$ and let $\partial ({\varOmega }\backslash B) = \partial {\varOmega }\cup \partial B$ such that $\partial B$ is clamped, and on $\partial {\varOmega }$ a force surface density $g_{|\partial {\varOmega }}$ is imposed. Then according to [23] the mixed problem of linear isotropic elasticity, or the elasticity equation, is described by

(3)

Here, $\lambda > 0$ and $\mu > 0$ are the Lamé constants (also called coefficients) and $u:{\varOmega }\backslash B \rightarrow {\mathbb {R}}^3$ is the displacement field on ${\varOmega }\backslash B$. I is the $3\times 3$ identity matrix. The linearized strain rate tensor $\epsilon (u):{\varOmega }\backslash B \rightarrow {\mathbb {R}}^{3\times 3}$ is defined as $\epsilon (u) = \frac{1}{2}(\nabla u + \nabla u^\top )$. Approximate numerical solutions can be computed by a finite element approach (see, e.g., [23] or [36]).

The potential Eq. (1) gives the velocity field at the part of the component’s boundary $\partial {\varOmega }$ that lies within the shroud D. Assuming that the total energy density, also denoted as stagnation pressure $p_{\text {st}}$, is constant at the inlet, we can derive the static pressure $p_\text {s}$ from Bernoulli’s law

$$\begin{aligned} p_{\text {st}} = \frac{1}{2}\rho |\nabla \phi |^2 + p_{\text {s}} \Leftrightarrow -p_{\text {s}} = \frac{1}{2}\rho |\nabla \phi |^2 - p_{\text {st}}, \end{aligned}$$

(4)

where $\rho$ denotes the density of the fluid. We consider the static pressure $p_{\text {s}}$ as surface load on the component ${\varOmega }$. Therefore, by continuously extending $p_{\text {s}}$ to be zero on $\partial {\varOmega }\backslash D$, the surface load $g_{\text {s}}$ is given by

$$\begin{aligned} g_{\text {s}} = - p_{\text {s}}n = \left( \frac{1}{2}\rho |\nabla \phi |^2 - p_{\text {st}}\right) n. \end{aligned}$$

This yields as boundary condition on ${\varOmega }$ for (3)

$$\begin{aligned} \sigma (u) n = {g_{\text {s}}} \quad \Leftrightarrow \quad \sigma (u) n = \left( \frac{1}{2}\rho |\nabla \phi |^2 - p_{\text {st}}\right) n. \end{aligned}$$

(5)

Hence, the displacement vector u to the elasticity equation not only depends on the shape ${\varOmega }$ but also on the solution $\phi$ to the potential equation (1).

Assuming the boundary of ${\varOmega }$ is of class $C^{k, \alpha }$, with $k \ge 1$ and $\alpha \in \, ]0,1]$, the unitary outward normal n is a function in $C^{k-1, \alpha }(\partial {\varOmega }, {\mathbb {R}}^{3})$. Further, let $\phi$ be in $C^{k, \alpha }(\mathrm {\partial {\varOmega },} {\mathbb {R}})$. Since we model an incompressible flow, the fluid density $\rho$ is constant as well as, by assumption, the stagnation pressure $p_{\mathrm {st}}$. Therefore, the static pressure $g_{\mathrm {s}}$ lies in $C^{k-1, \alpha }(\partial {\varOmega }, {\mathbb {R}}^3)$ and the following lemma provides, for $k \ge 2$, existence and uniqueness of a solution u along with a Schauder estimate.

Lemma 2.2

(Schauder estimate for displacement fields, [10]) Consider the elasticity Eq. (3). Let ${\varOmega }\subset {\mathbb {R}}^3$ be a compact domain that possesses $C^{k,\alpha }$-boundary. As volume load we consider $f \in C^{k,\alpha }({\varOmega },{\mathbb {R}}^3)$ and as surface load $g_{\text {s}} \in C^{k+1,\alpha }(\partial {\varOmega },{\mathbb {R}}^3)$. Then, the disjoint displacement-traction problem given by

has a unique solution $u \in C^{k+2,\alpha }(\mathrm {cl}({\varOmega }\backslash B), {\mathbb {R}}^3)$, which satisfies

$$\begin{aligned} \Vert u \Vert _{C^{k+2,\alpha }({\varOmega }\backslash B)} \le C\left( \Vert f \Vert _{C^{k,\alpha }({\varOmega })} + \Vert g_{\text {s}} \Vert _{C^{k+1,\alpha }(\partial {\varOmega })} + \Vert u \Vert _{C^{0,\alpha }({\varOmega }\backslash B)} \right) , \end{aligned}$$

(6)

with constant $C({\varOmega })>0$.

2.3 Optimal Reliability and Efficiency

Low cycle fatigue (LCF)-driven surface crack initiation is particularly important for the reliability of highly loaded engineering parts as turbine components [38, 46]. The design of such engineering parts therefore requires a model that is capable of accurately quantify risk levels for LCF crack initiation, crack growth and ultimate failure. Here we refer to the model introduced in [40] that models the statistical size effect but also includes the notch support factor by using stress gradients arising from the elasticity Eq. (3):

$$\begin{aligned} J_R({\varOmega }, u_{\varOmega }):= \int _{\partial {\varOmega }\cap D} \left( \frac{1}{N_\text {det} (\nabla u_{{\varOmega }},\nabla ^2 u_{\varOmega }(x))} \right) ^m \hbox {d}A. \end{aligned}$$

(7)

${\varOmega }$ represents the shape of the component, $u_{\varOmega }$ is the displacement field and the solution to the elasticity equation on ${\varOmega }\backslash B$, $N_\text {det}$ is the deterministic number of life cycles at each point of the surface of ${\varOmega }$ and m is the Weibull shape parameter. The proability of failure (PoF) after t load cycles is then given as $PoF(t)=1-e^{-t^m J_R({\varOmega },u_{\varOmega })}$. Minimizing the probability of failure thus clearly is equivalent to minimizing $J_R({\varOmega },u_{\varOmega })$.

For a detailed discussion including experimental validation we refer to [39]. We can apply this model as cost functional in order to optimize the component ${\varOmega }$ with respect to reliability.

Another primary objective of the component is the efficiency that is connected with the viscosity of the fluid flowing through the shroud. Viscosity is a measure which describes the internal friction of a moving fluid. In a laminar fluid the effect of viscosity is limited to a thin layer near the surface of the component. The fluid does not slip along the surface, but adheres to it. In the case of potential flow, there is a transition from zero velocity at the surface to the full velocity which is present at a certain distance from the surface. The layer where this transition takes place is called the boundary layer or frictional layer. The thickness of the boundary layer is not constant but (roughly) proportional to the square root of the kinematic viscosity $\nu$ and is growing from the leading edge, the location where the fluid first impinge on the surface of the component. Friction of the fluid on the surface leads to energy dissipation. A coefficient for the inflicted local wall shear stress is given by

$$\begin{aligned} \tau _w(x) = \frac{0.322\cdot \mu |v|^\frac{3}{2}}{\sqrt{\nu \cdot \text {dist}_{\text {LE}}(x)}}, \end{aligned}$$

(8)

where we denote with $|\cdot |$ the Euclidean norm, $\mu$ is the viscosity, and $\text {dist}_{\text {LE}}$ the distance to the leading edge along the component’s surface $\partial {\varOmega }$. For a detailed introduction to boundary layer theory one can see, e.g., [14, 45]. With this coefficient, one can derive an estimate for the loss of power due to friction given by

$$\begin{aligned} J_E({\varOmega }, \phi _{\varOmega }) := \int _{\partial {\varOmega }\cap D} |v_{{\varOmega }} |\tau _w\, \hbox {d}A. \end{aligned}$$

(9)

For the multi-physics and multi-criteria shape optimization problem we introduce in the next chapter, we realize above, objective functionals that contain boundary integrals of second-order derivatives of the solutions of second-order elliptic BVPs. This can only be realized if one considers regular shapes and strong solutions. Further, we have to apply additional assumptions on our shapes, i.e., a fixed and unique leading edge for all shapes in the shape space. This, however, changes very little in our general analysis.

3 A Multi-criteria Optimization Problem

In this section, we introduce the multi-criteria shape optimization problem, which is based on the above boundary value problems and cost functionals, investigated in this work. But before we introduce our multiphysics shape problem, we present a general approach to shape optimization problems and provide conditions for the existences of optimal shapes (see [34, Section 2.4]). Afterward, we apply our model.

3.1 General Definitions

We denote a family of admissible shapes with $\tilde{{\mathcal {O}}}$ and for every shape ${\varOmega }\in \tilde{{\mathcal {O}}}$ we denote with $V_1({\varOmega }),\dots ,V_n({\varOmega }),\, n\in {\mathbb {N}}$ state spaces of real-valued functions on ${\varOmega }$. Consider a sequence of shapes $({\varOmega }_m)_{m\in {\mathbb {N}}}$ in $\tilde{{\mathcal {O}}}$, and let ${\varOmega }\in \tilde{{\mathcal {O}}}$. Assuming a topology on the shape space $\tilde{{\mathcal {O}}}$ is given, the convergence of ${\varOmega }_m$ against ${\varOmega }$ is denoted by ${\varOmega }_m \overset{\tilde{{\mathcal {O}}}}{\longrightarrow } {\varOmega }$ as $m \rightarrow \infty$. For a sequence of functions $({\varvec{y}}_m)_{m\in {\mathbb {N}}}$, with for all $m \in {\mathbb {N}}$, we denote the convergence against some with ${\varvec{y}}_m \rightsquigarrow {\varvec{y}}$ as $m \rightarrow \infty$. We assume that for every ${\varOmega }\in \tilde{{\mathcal {O}}}$ one can solve uniquely a given set of state problems, e.g., a set of PDEs or a variational inequalities. By associating the corresponding unique solutions $v_{i,{\varOmega }}\in V_i({\varOmega })$ with ${\varOmega }\in \tilde{{\mathcal {O}}}$, one obtains the map $v_i: {\varOmega }\mapsto v_{i,{\varOmega }} \in V_i({\varOmega })$. Let ${\mathcal {O}}$ be a subfamily of $\tilde{{\mathcal {O}}}$, then ${\mathcal {G}} = \{ ({\varOmega },{\varvec{v}}_{\varOmega })\, :\, {\varOmega }\in {\mathcal {O}} \}$ is called the graph of the mapping ${\varvec{v}} := (v_1,\dots , v_n)$. A cost functional J on $\tilde{{\mathcal {O}}}$ is given by a map $J:({\varOmega },{\varvec{y}}) \mapsto J({\varOmega },{\varvec{y}}) \in {\mathbb {R}}$, where ${\varOmega }\in \tilde{{\mathcal {O}}}$ and . Then, a vector of l cost functionals is defined by ${\varvec{J}}:= (J_1,\dots , J_l)$, and the image of ${\mathcal {O}}$ (or ${\mathcal {G}}$) under ${\mathbf {J}}$ is denoted with ${\mathcal {Y}} \subset {\mathbb {R}}^l$. For the sake of convenience, we shall write ${\varvec{J}}({\varOmega },{\varvec{v}}_{{\varOmega }}) := (J_1({\varOmega },{\varvec{v}}_{{\varOmega }}),\dots , J_l({\varOmega },{\varvec{v}}_{{\varOmega }}))$, and, in addition, we make use of the notation $\nabla {\varvec{v}}_{{\varOmega }} := (\nabla v_{1,{\varOmega }}, \dots , \nabla v_{n,{\varOmega }})$.

Definition 3.1

(Pareto optimality) Consider a subfamily ${\mathcal {O}}$ of $\tilde{{\mathcal {O}}}$ with corresponding graph ${\mathcal {G}}$ to given state spaces ${\varvec{V}} = (V_1, \dots ,V_n)$. We call a point $({\varOmega }^*,{\varvec{v}}_{{\varOmega }^*}) \in {\mathcal {G}}$ Pareto optimal with respect to cost functionals ${\varvec{J}} = (J_1,\dots , J_l)$, if there is no $({\varOmega },{\varvec{v}}_{{\varOmega }})\in {\mathcal {G}}$ such that $J_k({\varOmega },{\varvec{v}}_{{\varOmega }}) \le J_k({\varOmega }^*,{\varvec{v}}_{{\varOmega }^*})$ for all $1\le k \le l$ and $J_i({\varOmega },{\varvec{v}}_{{\varOmega }}) < J_i({\varOmega }^*,{\varvec{v}}_{{\varOmega }^*})$ for some $i \in \{1,\dots ,l\}$. The associated value ${\mathbf {J}}({\varOmega }^*,{\varvec{v}}_{{\varOmega }^*})$ is called nondominated.

Let ${\mathcal {Y}}:= {\mathbf {J}}({\mathcal {G}}) = \{ {\mathbf {J}}({\varOmega }, {\varvec{v}}_{{\varOmega }})\, :\, ({\varOmega }, {\varvec{v}}_{{\varOmega }}) \in {\mathcal {G}} \}$ denote the image of the graph ${\mathcal {G}}$ under the objective functionals mapping ${\mathbf {J}}$. For a set of Pareto optimal points, we can define ${\mathcal {Y}}_N:= \{{\mathbf {J}}({\varOmega }, {\varvec{v}}_{{\varOmega }}) \in {\mathcal {Y}}\, :\, {\mathbf {J}}({\varOmega }, {\varvec{v}}_{{\varOmega }}) \text { is nondominated in } {\mathcal {Y}}\}$, i.e., the corresponding Pareto front which lies by definition on the boundary of ${\mathcal {Y}}$.

Definition 3.2

(Multi-criteria shape optimization problem) Consider a subfamily ${\mathcal {O}}$ of $\tilde{{\mathcal {O}}}$ and for every ${\varOmega }\in {\mathcal {O}}$ let ${\varvec{v}}_{\varOmega }= (v_{1,{\varOmega }},\dots ,v_{n,{\varOmega }})$ be the unique solutions to given state problems on ${\varOmega }$, and let ${\varvec{J}}= (J_1,\dots , J_l)$ be cost functionals on $\tilde{{\mathcal {O}}}$. We define an optimal shape design problem by

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{ll} \text {Find } {\varOmega }^* \in {\mathcal {O}} \text { such that}\\ ({\varOmega }^*,{\varvec{v}}_{{\varOmega }^*})\text { is Pareto optimal with respect to } {\varvec{J}}. \end{array} \right. \end{aligned} \end{aligned}$$

(10)

The next theorem gives us conditions for the existence of a solution to the optimal shape design problem (10). Afterward, in subsection 3.2, we define our shape optimization problem and use this theorem to prove the existence of a solution to it.

Theorem 3.1

Let $\tilde{{\mathcal {O}}}$ be a family of admissible domains and ${\mathcal {O}}$ a subfamily. Consider cost functionals ${\varvec{J}} = (J_1,\dots , J_l)$ on $\tilde{{\mathcal {O}}}$ and assume for each ${\varOmega }\in \tilde{{\mathcal {O}}}$ we have state problems with state spaces ${\varvec{V}}({\varOmega }) = (V_1({\varOmega }),\dots ,V_n({\varOmega }))$ such that each state problem has a unique solution $v_{k,{\varOmega }}\in V_k({\varOmega })$, $1\le k \le n$. When the following both assumptions hold true

• (i) Compactness of ${\mathcal {G}} =\{({\varOmega },{\varvec{v}}_{\varOmega })\, :\, {\varOmega }\in {\mathcal {O}} \}$:

  Every sequence $({\varOmega }_m,{\varvec{v}}_{{\varOmega }_m})_{m\in {\mathbb {N}}}$ has a subsequence $({\varOmega }_{m_k}, {\varvec{v}}_{{\varOmega }_{m_k}})_{k\in {\mathbb {N}}}$ that satisfies

  $$\begin{aligned} \begin{aligned} {\varOmega }_{m_k} \overset{\tilde{{\mathcal {O}}}}{\longrightarrow } {\varOmega }, \quad&k \rightarrow \infty \\ {\varvec{v}}_{{\varOmega }_{m_k}} \rightsquigarrow {\varvec{v}}_{\varOmega }, \quad&k\rightarrow \infty , \end{aligned} \end{aligned}$$

  for some $({\varOmega },{\varvec{v}}_{\varOmega }) \in {\mathcal {G}}$.

• (ii) Lower semicontinuity of $J_k$:

  Let $({\varOmega }_m)_{m\in {\mathbb {N}}}$ be a sequence in $\tilde{{\mathcal {O}}}$ and $({\varvec{y}}_m)_{m\in {\mathbb {N}}}$ be a sequence such that ${\varvec{y}}_m \in {\varvec{V}}({\varOmega }_m)$ for all $m \in {\mathbb {N}}$. Consider some elements ${\varOmega },\, {\varvec{y}}$ in $\tilde{{\mathcal {O}}}$ and ${\varvec{V}}({\varOmega })$, respectively. Then,

  $$\begin{aligned} \left. \begin{array}{rl} {\varOmega }_m \overset{\tilde{{\mathcal {O}}}}{\longrightarrow } {\varOmega }, &{}\quad m\rightarrow \infty \\ {\varvec{y}}_m \rightsquigarrow {\varvec{y}}, &{}\quad m\rightarrow \infty \end{array} \right\} \Longrightarrow \liminf _{n\rightarrow \infty }J_k({\varOmega }_n,{\varvec{y}}_n) \ge J_k({\varOmega },{\varvec{y}}), \end{aligned}$$

  for all $1\le k \le l$.

Then, the multi-criteria shape design problem (10) possesses at least one solution and the Pareto front covers all nondominated points in $\mathrm {cl}({{\mathcal {Y}}})$, i.e., ${\mathcal {Y}}_N = \mathrm {cl}({{\mathcal {Y}}})_N$, the set of non-dominated points in the closure of ${\mathcal {Y}}$.

Proof

First, we prove the existence of an optimal shape. [34, Theorem 2.10, p. 46] shows that, in this setting, a lower semicontinuous cost functional possesses at least one minimal solution. We apply this theorem, without loss of generality, to cost functional $J_1$ and minimize it on ${\mathcal {G}}$. Due to the compactness of ${\mathcal {G}}$ and the lower semicontinuity of $J_1$, the resulting set of arguments of the minimum $\mathop {\mathrm{arg\,min}}\limits _{({\varOmega },{\varvec{v}}_{\varOmega })\in {\mathcal {G}}}J_1$ is also compact. Hence, we can again apply [34, Theorem 2.10, p. 46] to the next cost functional $J_2$ and minimize it on $\mathop {\mathrm{arg\,min}}\limits _{({\varOmega },{\varvec{v}}_{\varOmega })\in {\mathcal {G}}}J_1$. We continue this procedure until we minimized each cost functional on its preceding cost functionals set of arguments of the minimum. The last set then contains at least one Pareto optimal point.

For the second assertion, we recall that ${\mathcal {Y}}_N$ lies on the boundary of ${\mathcal {Y}}$ and it follows directly that ${\mathcal {Y}}_N \subseteq \mathrm {cl}({{\mathcal {Y}}})_N$. Conversely, let ${\mathbf {J}}({\varOmega }^*, {\varvec{v}}_{{\varOmega }^*}) \in \mathrm {cl}({{\mathcal {Y}}})_N$. Consider a sequence $({\mathbf {J}}({\varOmega }_n, {\varvec{v}}_{{\varOmega }_n}))_{n\in {\mathbb {N}}} \subset {\mathcal {Y}}$ with ${\mathbf {J}}({\varOmega }_n, {\varvec{v}}_{{\varOmega }_n}) \rightarrow {\mathbf {J}}({\varOmega }^*, {\varvec{v}}_{{\varOmega }^*})$ as $n\rightarrow \infty$. We assume that the corresponding sequence $({\varOmega }_{n}, {\varvec{v}}_{{\varOmega }_{n}})_{n \in {\mathbb {N}}} \subset {\mathcal {G}}$ converges to some $({\varOmega }, {\varvec{v}}_{{\varOmega }}) \in {\mathcal {G}}$ as well (since ${\mathcal {G}}$ is compact we can always find a subsequence). Due to the lower semicontinuity of ${\varvec{J}}$, we have

$$\begin{aligned} J_i({\varOmega },{\varvec{v}}_{\varOmega }) \le \lim _{n\rightarrow \infty }J_i({\varOmega }_n,{\varvec{v}}_{{\varOmega }_n}) = J_i({\varOmega }^*, {\varvec{v}}_{{\varOmega }^*}), \quad \text {for all } 1\le i \le l. \end{aligned}$$

The Pareto optimality of ${\mathbf {J}}({\varOmega }^*, {\varvec{v}}_{{\varOmega }^*})$ gives that ${\mathbf {J}}({\varOmega }, {\varvec{v}}_{{\varOmega }}) = {\mathbf {J}}({\varOmega }^*, {\varvec{v}}_{{\varOmega }^*})$, and since ${\mathbf {J}}({\varOmega }, {\varvec{v}}_{{\varOmega }}) \in {\mathcal {Y}}$, it follows that ${\mathbf {J}}({\varOmega }^*, {\varvec{v}}_{{\varOmega }^*}) \in {\mathcal {Y}}$ and therefore $\mathrm {cl}({{\mathcal {Y}}})_N \subseteq {\mathcal {Y}}_N$. $\square$

3.2 Multi-physics Shape Optimization

In the previous subsection, we introduced a general framework of multi-criteria shape optimization. We now state a class of shape optimization problems that includes the multi-physics shape optimization problem given by the coupled potential and elasticity equation as introduced in Sect. 2. As we will see, in Sect. 4, multi-criteria shape optimization problems from this class fulfill the required assumption of Theorem 3.1 to ensure us the existence of the Pareto front.

We consider shapes with Hölder continuous boundaries. This assumptions ensures, in this setting, strong regularity for the solutions of the physical problems which enables us to deal with cost functionals, defined on the boundaries of the shapes, containing first and second derivatives as motivated in Sect. 2.3. In the following, $C^{k,\alpha }$ stands for the real valued functions with k-th derivatives being Hölder continuous with exponent $\alpha$; see the appendix.

Definition 3.3

Let ${\varOmega },\, {\varOmega }^\prime$ be bounded domains in ${\mathbb {R}}^{d}$.

• (i) A $C^{k,\alpha }$-diffeomorphism from ${\varOmega }$ to ${\varOmega }^{\prime }$ is a bijective mapping $f: {\varOmega }\rightarrow {\varOmega }^\prime$ such that $f \in \left[ C^{k,\alpha }({\varOmega }) \right] ^d$ and $f^{-1} \in \left[ C^{k,\alpha }({\varOmega }^\prime ) \right] ^d$.

• (ii) The set of $C^{k,\alpha }$-diffeomorphisms is denoted by ${\mathcal {D}}^{k,\alpha }({\varOmega },{\varOmega }^\prime )$ or ${\mathcal {D}}^{k,\alpha }({\varOmega })$ if $f: {\varOmega }\rightarrow {\varOmega }$.

Definition 3.4

Consider a bounded domain ${\varOmega }\subset {\mathbb {R}}^d$. The boundary of ${\varOmega }$ is of class $C^{k,\alpha }$, with $k\in {\mathbb {N}}_{0}$ and $0 < \alpha \le 1$, if at each point $x_0 \in \partial {\varOmega }$ there is an open ball $B=B(x_0)$ and a $C^{k,\alpha }$-diffeomorphism T of B onto $G \subset {\mathbb {R}}^d$ such that:

$$\begin{aligned} (i)\ T(B \cap {\varOmega }) \subset {{\mathbb {R}}_{\ge 0}^d}; \quad (ii)\ T(B \cap \partial {\varOmega }) \subset \partial {{\mathbb {R}}^d_{\ge 0}}; \quad \end{aligned}$$

We shall say that the diffeomorphism T straightens the boundary near $x_0$ and call it hemisphere transform. Note that by this definition ${\varOmega }$ is of class $C^{k,\alpha }$ if each point of $\partial {\varOmega }$ has a neighbourhood in which $\partial {\varOmega }$ is the graph of a $C^{k,\alpha }$ function of $d-1$ of the coordinates $x_1,\dots ,x_n$. The converse is true if $k\ge 1$; see, e.g., [20, Chapter 2, Theorem 5.5].

Definition 3.5

Let $K>0$ be a positive constant and ${\varOmega }_0 \subset {\varOmega }^{\text {ext}} \subset {\mathbb {R}}^{3}$ be compact $C^{k,\alpha }$ domains. The elements of the set

$$\begin{aligned} U_{k,\alpha }^{\text {ad}}({\varOmega }^{\text {ext}})&:= \left\{ \psi \in {\mathcal {D}}^{k,\alpha }({\varOmega }^{\text {ext}}) \, : \, \psi |_{\mathrm {cl}({\varOmega }\backslash D)} \,= \text {id}, \, \Vert \psi \Vert _{\left[ C^{k,\alpha }({\varOmega }^{\text {ext}}) \right] ^{3}} \le K,\right. \\&\qquad \left. \Vert \psi ^{-1} \Vert _{\left[ C^{k,\alpha }({\varOmega }^{\text {ext}}) \right] ^{3}} \le K \right\} \end{aligned}$$

are called design-variables. These design variables induce, in a natural way, the set of admissible shapes

$$\begin{aligned} {{\mathcal {O}}_{k,\alpha }} := {\mathcal {O}}_{k,\alpha }({\varOmega }_0,{\varOmega }^{\text {ext}}) := \left\{ \psi ({\varOmega }_0)\, : \, \psi \in U_{k,\alpha }^{\text {ad}}({\varOmega }^{\text {ext}}) \right\} , \end{aligned}$$

assigned to ${\varOmega }_0$. Note that due to the Hölder continuity, every ${\varOmega }\in {\mathcal {O}}_{k,\alpha }$ is compact.

Lemma 3.1

Let $k \ge 0$ and $\alpha \in \, ]0,1]$, then the shape space ${\mathcal {O}}_{k, \alpha }$ satisfies a uniform cone condition.

Proof

As $k \ge 1$, the shape ${\varOmega }_0$ is a domain with Lipschitz boundary and therefore fulfills a uniform cone condition. Since every transform $\psi \in U_{k,\alpha }^{\text {ad}}({\varOmega }^{\text {ext}})$ is a $C^{k, \alpha }$-diffeomorphism with $\Vert \psi \Vert _{\left[ C^{k,\alpha }({\varOmega }^{\text {ext}}) \right] ^{3}}\le K$ and $\Vert \psi ^{-1} \Vert _{\left[ C^{k,\alpha }({\varOmega }^{\text {ext}}) \right] ^{3}}\le K$, we have

$$\begin{aligned} \frac{1}{K} |x - y| \le |\psi (x) - \psi (y)| \le K |x - y|, \quad \text {for all } x,y \in {\varOmega }_0. \end{aligned}$$

(11)

Let C(x) be the cone associated with the cone condition satisfied by ${\varOmega }_0$, where $x \in \partial {\varOmega }_0$ denotes the vertex. Further, we denote with $C_{K}(x)$ the cone where we decreased the radius of C with factor $\frac{1}{K}$. Then, by the lower bound in (11), we can always place the shrinked cone $C_{K}$ within the transformed cone $\psi (C(x))$ at the boundary point $\psi (x)$ for every $\psi \in U_{k,\alpha }^{\text {ad}}({\varOmega }^{\text {ext}})$ and $x \in \partial {\varOmega }_0$. Therefore, the cone $C_K$ provides the uniform cone condition for ${\mathcal {O}}_{k, \alpha }$. $\square$

On the space of admissible domains we can define the Hausdorff distance as metric. Note that in general the Hausdorff distance is no metric because in general the identity of indiscernibles is not given. Here, however, the compactness of the shapes ensures us this property.

Definition 3.6

For two non-empty subsets ${\varOmega }$, ${\varOmega }^\prime$ of a metric space (M, d) we define their Hausdorff distance by

$$\begin{aligned} d_H ({\varOmega },{\varOmega }^\prime ) := \max \{ \sup _{x\in {\varOmega }} \inf _{y\in {\varOmega }^\prime } d(x - y), \, \sup _{y\in {\varOmega }^\prime } \inf _{x\in {\varOmega }} d( x - y ) \} \end{aligned}$$

If we equip the set F(M) of all closed subsets of a metric space (M, d) with the Hausdorff distance, then we obtain another metric space. Since the shapes in ${\mathcal {O}}_{k,\alpha }$ are compact, the Hausdorff distance defines a metric on ${\mathcal {O}}_{k,\alpha }$. By the following Lemma, we see in chapter 4, that $({\mathcal {O}}_{k,\alpha },\, d_H)$ is additionally compact.

Theorem 3.2

(Blaschke’s Selection Theorem [6]) Let (M, d) be a metric space, where M is a compact subset of a Banach space B. Then, the set F(M) of all closed subsets of M is compact with respect to the Hausdorff distance $d_H$.

Definition 3.7

(Local Cost Functionals) Let ${\mathcal {O}}\subset {\mathcal {P}}({\mathbb {R}}^3)$ denote a shape space with corresponding state spaces $V_1({\varOmega }),\dots , V_n({\varOmega }), \, {\varOmega }\in {\mathcal {O}}$ and graph ${\mathcal {G}} := \{({\varOmega },{\varvec{v}}_{{\varOmega }})\,:\, {\varOmega }\in {\mathcal {O}}\}$. Assuming that $V_i({\varOmega }) \subseteq C^k({\varOmega },{\mathbb {R}}^3)$ for all $1\le i\le n$, the local cost functional on ${\mathcal {G}}$ is given by

$$\begin{aligned} \begin{aligned} J({\varOmega },{\varvec{v}}_{{\varOmega }}) :=&\int _{\varOmega }{\mathcal {F}}_{\text {vol}}\, (x,{\varvec{v}}_{{\varOmega }},\nabla {\varvec{v}}_{{\varOmega }},\dots , \nabla ^k {\varvec{v}}_{{\varOmega }})\,\hbox {d}x \\&+ \int _{\partial {\varOmega }} {\mathcal {F}}_{\text {sur}} \, (x,{\varvec{v}}_{{\varOmega }},\nabla {\varvec{v}}_{{\varOmega }},\dots , \nabla ^k {\varvec{v}}_{{\varOmega }})\,\hbox {d}A, \end{aligned} \end{aligned}$$

(12)

where ${\mathcal {F}}_{\text {vol}}$, ${\mathcal {F}}_{\text {vol}}: {\mathbb {R}}^d\rightarrow \mathrm {cl}({{\mathbb {R}}}_{\ge 0})$ and $d = 3 + n\sum _{j=0}^k 3^{j+1} = 3+\frac{3n}{2}(3^{k+1}-1)$. We denote the volume integral and surface integral with

$$\begin{aligned} \begin{aligned}&J_{\text {vol}}({\varOmega },{\varvec{v}}_{{\varOmega }}) := \int _{\varOmega }{\mathcal {F}}_{\text {vol}}\, (x,{\varvec{v}}_{{\varOmega }},\nabla {\varvec{v}}_{{\varOmega }},\dots , \nabla ^k {\varvec{v}}_{{\varOmega }})\,\hbox {d}x, \\&J_{\text {sur}}({\varOmega },{\varvec{v}}_{{\varOmega }}) := \int _{\partial {\varOmega }} {\mathcal {F}}_{\text {sur}}\, (x,{\varvec{v}}_{{\varOmega }},\nabla {\varvec{v}}_{{\varOmega }},\dots , \nabla ^k {\varvec{v}}_{{\varOmega }})\,\hbox {d}A. \end{aligned} \end{aligned}$$

Definition 3.8

(Multi-physics Shape Optimization Problem) We consider the space $({\mathcal {O}}_{k,\alpha }, d_H)$ of admissible shapes and let $J_1, \dots , J_l$ be local cost functionals on the Graph ${\mathcal {G}} := \{ ({\varOmega }, u_{\varOmega }, \phi _{\varOmega }) \, : \, {\varOmega }\in {\mathcal {O}}_{k,\alpha },\, u_{\varOmega }\text { solves } (3)\text { on } {\varOmega }, \phi _{\varOmega }\text { solves } (1) \text { on } {\varOmega }\backslash D \}$. The multi-physics shape optimization problem is given by:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{ll} \text {Find } {\varOmega }^* \in {\mathcal {O}}_{k,\alpha } \text { such that}\\ ({\varOmega }^*,u_{{\varOmega }^*},\phi _{{\varOmega }^*})\text { is Pareto optimal with respect to } {\varvec{J}}. \end{array} \right. \end{aligned} \end{aligned}$$

(13)

Before this section ends, we note that our choice of state problems here is only exemplary. In the next section, we see that we can include an arbitrary amount of physical models in this multi-physics shape optimization problem as long as they provide a unique solution with sufficient regularity and a compact solution space on the shape space ${\mathcal {O}}_{k,\alpha }$.

4 Existence of Pareto Optimal Shapes

In this section, the approach outlined in Thoerem 3.1 will be followed in order to show the existence of an optimal shape for the multi physics shape optimization problem. This approach includes the compactness of the Graph ${\mathcal {G}}$ which requires bounded solution spaces on ${\mathcal {O}}_{k,\alpha }$. We first derive such uniform bounds based on the Schauder estimates given in Sect. 2.

4.1 Uniform Bounds for Solution Spaces

Lemma 4.1

Let $\phi _{{\varOmega }}$ be the unique solution to (1) on ${\varOmega }\in {\mathcal {O}}_{k,\alpha }$ with $k\ge 2$. Then, there exists a constant $K>0$ independent of ${\varOmega }$ such that

$$\begin{aligned} \Vert \phi _{{\varOmega }} \Vert _{C^{2,\alpha }(D\backslash {\varOmega })} \le K. \end{aligned}$$

Proof

This estimate is based on Lemma 2.1:

$$\begin{aligned} \Vert \phi _{{\varOmega }} \Vert _{C^{2,\alpha }(D\backslash {\varOmega })} \le {\tilde{C}}\left( \Vert \phi _{{\varOmega }} \Vert _{C^{0,\alpha }(D\backslash {\varOmega })} + \Vert g \Vert _{C^{1,\alpha }(\partial D\backslash \partial (D \cap {\varOmega })} \right) , \end{aligned}$$

where the constant ${{\tilde{C}}}$ possibly depends on the shape ${\varOmega }$. First, we outline that the constant ${\tilde{C}}$ can be chosen independently of the shape ${\varOmega }\in {\mathcal {O}}_{k,\alpha }$. A full proof is provided in [28] (or [9]). In order to prove estimate (2), one straightens the boundary $\partial {\varOmega }$ piecewise with hemisphere transforms. The dependence of the constant ${{\tilde{C}}}$ is through the ellipticity of the differential operator and hence depends on the bounds of the hemisphere transform that is used to straightens the boundary. Let T be such a hemisphere transform for ${\varOmega }_0$. For every shape $\psi ({\varOmega }_0)\in {\mathcal {O}}_{k,\alpha }$ we can construct a hemisphere transform by pulling $\psi ({\varOmega }_0)$ back to ${\varOmega }_0$ and apply T afterward, i.e., $T_{\psi ({\varOmega }_0)} := T \circ \psi ^{-1}$. Due to the definition of design variables, $\psi$ is uniformly bounded w.r.t. $\Vert \cdot \Vert _{C^{k,\alpha }({\varOmega }^\text {ext})}$, and since $k \ge 2$, also lies in $C^{k-1, 1}({\varOmega }^{\text {ext}})$. Therefore, it follows that $T_{\psi ({\varOmega }_0)}$ is a function of class $C^{k, \alpha }$ and uniformly bounded in ${\mathcal {O}}_{k,\alpha }$ w.r.t. $\Vert \cdot \Vert _{C^{k, \alpha }({\varOmega }^{\text {ext}})}$ as well.

Next, we note that $\Vert g \Vert _{C^{1,\alpha }(\partial D\backslash \partial (D \cap {\varOmega })}$ is obviously uniformly bounded by $\Vert g \Vert _{C^{1,\alpha }(\partial D)}$, and it remains to further estimate $\Vert \phi _{{\varOmega }} \Vert _{C^{0,\alpha }(D\backslash {\varOmega })}$. Since ${\mathcal {O}}_{k, \alpha }$ satisfies a uniform cone condition (see Lemma 3.1), [31, Lemma 5.5] implies that for every $\epsilon > 0$ there is a constant $C(\epsilon ) > 0$ such that

$$\begin{aligned} \Vert \phi _{{\varOmega }} \Vert _{C^{0,\alpha }(D\backslash {\varOmega })} \le \epsilon \Vert \phi _{{\varOmega }} \Vert _{C^{1,\alpha }(D\backslash {\varOmega })} + C(\epsilon ) \int _{D\backslash {\varOmega }} |\phi _{{\varOmega }} |\, \hbox {d}x. \end{aligned}$$

We choose $\epsilon < 1/{{\tilde{C}}}$ and get

$$\begin{aligned} \begin{aligned} \Vert \phi _{{\varOmega }} \Vert _{C^{2,\alpha }(D\backslash {\varOmega })} \le \,&{{\tilde{C}}}\left( \Vert \phi _{{\varOmega }} \Vert _{C^{0,\alpha }(D\backslash {\varOmega })} + \Vert g \Vert _{C^{1,\alpha }(\partial D)} \right) ,\\ \le \,&\frac{1}{1 - \epsilon {{\tilde{C}}}} \left( C(\epsilon ) \int _{D\backslash {\varOmega }} \phi _{{\varOmega }}\, \hbox {d}x + {{\tilde{C}}} \Vert g \Vert _{C^{1,\alpha }(\partial D)} \right) \\ \le \,&\frac{1}{1 - \epsilon {{\tilde{C}}}} \left( C(\epsilon ) \Vert \phi _{{\varOmega }} \Vert _{H^1(D\backslash {\varOmega })} + {{\tilde{C}}} \Vert g \Vert _{C^{1,\alpha }(\partial D)} \right) . \end{aligned} \end{aligned}$$

One can easily verify the a-priori estimate $\Vert \phi _{{\varOmega }} \Vert _{H^1(D\backslash {\varOmega })} \le C_p |D |\Vert g \Vert _{C^{1,\alpha }(\partial D)}$ holds for a constant $C_p >0$ originating from the Poincaré inequality (see, e.g., [23, Lemma B.61]). This yields

$$\begin{aligned} \begin{aligned} \Vert \phi _{{\varOmega }} \Vert _{C^{2,\alpha }(D\backslash {\varOmega })} \le \,&\frac{1}{1 - \epsilon {{\tilde{C}}}} \left( C(\epsilon ) \Vert \phi _{{\varOmega }} \Vert _{H^1(D\backslash {\varOmega })} + {{\tilde{C}}} \Vert g \Vert _{C^{1,\alpha }(\partial D)} \right) \\ \le \,&\frac{C(\epsilon )C_p|D |+ {{\tilde{C}}}}{1 - \epsilon {{\tilde{C}}}} \Vert g \Vert _{C^{1,\alpha }(\partial D)} =: K. \end{aligned} \end{aligned}$$

$\square$

We recall that the elasticity Eq. (3) describes with $g_{\text {s}}$, given by the static pressure $p_{\text {s}}$, the surface force that the fluid exerts on the component ${\varOmega }$ (see (5)). Hence, in our framework, the surface force $g_{\text {s}}$ is given by Bernoulli’s equation and we have

$$\begin{aligned} \sigma (u_{{\varOmega }})n = g_{\text {s}} \quad \Leftrightarrow \quad \sigma (u_{{\varOmega }}) n = \left( \frac{1}{2}\rho |\nabla \phi _{{\varOmega }} |^2 - p_{\text {st}}\right) n, \end{aligned}$$

(14)

where we contiuously extends $g_{\text {s}}$ to be zero on $\partial {\varOmega }\backslash D$. The solution $u_{{\varOmega }}$ of the elasticity equation not only depends on the shape ${\varOmega }\in {\mathcal {O}}_{k,\alpha }$ but on the solution $\phi _{{\varOmega }}$ of potential equation (1) as well. We can derive a uniform bound for $u_{{\varOmega }}$, as we have for $\phi _{{\varOmega }}$, from estimate (6) which already provides an uniform bound in ${\mathcal {O}}_{k,\alpha }$ if the surface load $g_{\text {s}}$ is independent of $\phi _{{\varOmega }}$. However, in our framework $g_{\text {s}}$ depends on $\phi _{{\varOmega }}$, and thus we have to further estimate the surface force $g_{\text {s}}$ in ${\mathcal {O}}_{k,\alpha }$.

Lemma 4.2

Let $u_{{\varOmega }}$ be the unique solution to (3) on ${\varOmega }\in {\mathcal {O}}_{k,\alpha }$ with $k \ge 2$. Then, there exists a constant $K>0$ independent of ${\varOmega }$ such that

$$\begin{aligned} \Vert u \Vert _{C^{2,\alpha }({\varOmega }\backslash B)} \le K, \end{aligned}$$

Proof

We consider estimate (6) given by

$$\begin{aligned} \Vert u_{{\varOmega }} \Vert _{C^{2,\alpha }({\varOmega }\backslash B)} \le {\tilde{C}}\left( \Vert f \Vert _{C^{0,\alpha }({\varOmega })} + \Vert g_{\text {s}} \Vert _{C^{1,\alpha }(\partial {\varOmega })} + \Vert u_{{\varOmega }} \Vert _{C^{0,\alpha }({\varOmega }\backslash B)} \right) , \end{aligned}$$

where the constant ${\tilde{C}}>0$ potentially depends on the domain ${\varOmega }$. However, as we described above, due to the construciton of ${\mathcal {O}}_{k,\alpha }$, C can be choosen independently of ${\varOmega }\in {\mathcal {O}}_{k,\alpha }$. Further, $\Vert f \Vert _{C^{0,\alpha }({\varOmega })}$ is bounded by $\Vert f \Vert _{C^{0,\alpha }({\varOmega }^{\text {ext}})}$, and $\Vert g_{\text {s}} \Vert _{C^{1,\alpha }(\partial {\varOmega })}$ depends on the potential $\phi _{{\varOmega }}$ in terms of (5). In the proof to Lemma 4.1, we have shown for the bounded domains ${\varOmega }\in {\mathcal {O}}_{k,\alpha }$ that the diffeomorphisms, which describe the boundary of the domains, are uniformly bounded in ${\mathcal {O}}_{k,\alpha }$ with respect to $\Vert \cdot \Vert _{C^{k,\alpha }}$. As we can use these diffeomorphism as chart mapping to describe the two-dimensional submanifold $\partial {\varOmega }$, we can conclude that the unitary normal vector n of $\partial {\varOmega }$ is uniformly bounded in ${\mathcal {O}}_{k,\alpha }$ by some constant $M>0$ with respect to $\Vert \cdot \Vert _{C^{k, \alpha }(\partial {\varOmega })}$. Hence, we can estimate

$$\begin{aligned} \begin{aligned} \Vert g_{\text {s}} \Vert _{C^{1,\alpha }(\partial {\varOmega })} = \,&\left\Vert \left( \frac{1}{2}\rho |\nabla \phi _{{\varOmega }} |^2 - p_{\text {st}}\right) n \right\Vert _{C^{1,\alpha }(\partial {\varOmega })} \\ \le \,&p_{\text {st}}M + \frac{1}{2}\rho \Vert \nabla \phi _{\varOmega }^2 n \Vert _{C^{1, \alpha }(\partial {\varOmega })}. \end{aligned} \end{aligned}$$

Equation (1) models an incompressible fluid and therefore the fluid density $\rho$ is constant as well as $p_{\text {st}}$ by assumption. Since n is uniformly bounded in ${\mathcal {O}}_{k, \alpha }$, we have by Lemma 4.1 that $\Vert \nabla \phi _{\varOmega }^2 n \Vert _{C^{1, \alpha }(\partial {\varOmega })}$ is also uniformly bounded in ${\mathcal {O}}_{k, \alpha }$. Thus, we get that

$$\begin{aligned} \Vert g_{\text {s}} \Vert _{C^{1,\alpha }(\partial {\varOmega })} \le {\tilde{M}}, \end{aligned}$$

with some constant ${\tilde{M}}>0$ which is independent of ${\varOmega }\in {\mathcal {O}}_{k,\alpha }$.

Now, by [31, Lemma 5.5], for $\epsilon > 0$ one can estimate

$$\begin{aligned} \Vert u_{{\varOmega }} \Vert _{C^{0,\alpha }({\varOmega }\backslash B)} \le \epsilon \Vert u_{{\varOmega }} \Vert _{C^{1,\alpha }({\varOmega }\backslash B)} + C(\epsilon ) \int _{{\varOmega }\backslash B} |u_{{\varOmega }} |\, \hbox {d}x, \end{aligned}$$

with constant $C(\epsilon ) > 0$ which is independent of ${\varOmega }\in {\mathcal {O}}_{k,\alpha }$. Applying this with $\epsilon < 1/{\tilde{C}}$ on (6) and estimating $\int _{{\varOmega }\backslash B} |u_{{\varOmega }} |\, \hbox {d}x \le \Vert u_{{\varOmega }} \Vert _{H^1({\varOmega }\backslash B)}$ yields

$$\begin{aligned} \begin{aligned} \Vert u_{{\varOmega }} \Vert _{C^{2,\alpha }({\varOmega }\backslash B)} \le \frac{1 + {\tilde{C}}}{1-\epsilon {\tilde{C}}}\left( \Vert f \Vert _{C^{0,\alpha }({\varOmega }^{\text {ext}})} + \Vert g_{\text {s}} \Vert _{C^{1,\alpha }(\partial {\varOmega })} + C(\epsilon )\Vert u_{{\varOmega }} \Vert _{H^1({\varOmega }\backslash B)}\right) \end{aligned} \end{aligned}$$

Let $V_{DN} = \{ v \in [H^1({\varOmega }\backslash B)]^3\, :\, v=0 \text { a.e. on } \partial B\}$, and consider the weak formulation of (3) given by

$$\begin{aligned} \int _{{\varOmega }\backslash B} \text {tr}(\sigma (u_{{\varOmega }})\epsilon (v))\, \hbox {d}x = \int _{{\varOmega }\backslash B} fv\, \hbox {d}x + \int _{\partial {\varOmega }}g_{\text {s}}v\, \hbox {d}A, \quad \text {for all } v \in V_{DN}. \end{aligned}$$

One can see that for all $v\in V_{DN}$ we have

$$\begin{aligned} C^{-1}\Vert \epsilon (v) \Vert ^2_{L_2({\varOmega }\backslash B)}\le \int _{{\varOmega }\backslash B} \text {tr}(\sigma (v)\epsilon (v))\, \hbox {d}x, \end{aligned}$$

with constant $C>0$. We can choose C such that, due to the uniform boundedness of f and $g_{\text {s}}$, we also have

$$\begin{aligned} \left|\int _{{\varOmega }\backslash B} fv\, \hbox {d}x + \int _{\partial {\varOmega }}g_{\text {s}}v\, \hbox {d}A \right|\le C\Vert v \Vert _{H^1({\varOmega }\backslash B)}, \end{aligned}$$

where C is additionally uniform with respect to ${\mathcal {O}}_{k,\alpha }$. Korn’s second inequality (A.2) then implies

$$\begin{aligned} \begin{aligned} q\Vert \epsilon (u_{{\varOmega }}) \Vert ^2_{L_2({\varOmega }\backslash B)} \le \,&C\Vert u_{{\varOmega }} \Vert _{H^1({\varOmega }\backslash B)} \le \, C_K \Vert \epsilon (u_{{\varOmega }}) \Vert _{L_2({\varOmega }\backslash B)} \\ \Rightarrow \,&\Vert u_{{\varOmega }} \Vert _{H^1({\varOmega }\backslash B)} \le \,C_K^2, \end{aligned} \end{aligned}$$

where the constant $C_{K} > 0$, which originates from Korn’s second inequality, may depends on the domain ${\varOmega }$. Examining the proof to Korn’s second inequality (see, e.g., [43]), one can see that the constant $C_K$ depends on ${\varOmega }$ through the cone associated to the uniform cone condition to ${\varOmega }$. Since ${\mathcal {O}}_{k, \alpha }$ satisfies a uniform cone condition, the constant $C_K$ is uniform with respect to ${\mathcal {O}}_{k, \alpha }$. Thus, the previous inequality is uniform in ${\mathcal {O}}_{k,\alpha }$ and the assertion is proven. $\square$

4.2 Pareto Optimality

In order to prove the existence of an optimal shape to the multi physics shape optimization problem (13), we want to make use of Theorem 3.1. Therefore, we show that the local cost functionals from Definition 3.7 are lower semicontinuous—we even show that they are continuous—and that the graph from Definition 3.8 is compact. The continuity is given and discussed in Lemma 4.7. First, we denote with ${\mathcal {P}}_{k,\alpha }:= \{ \phi _{\varOmega }\,:\, \phi _{{\varOmega }} \text { solves } (1) \text { with } {\varOmega }\in {\mathcal {O}}_{k,\alpha } \}$ and ${\mathcal {E}}_{k,\alpha }:= \{ u_{\varOmega }\,:\, u_{{\varOmega }} \text { solves } (1) \text { with } {\varOmega }\in {\mathcal {O}}_{k,\alpha } \}$ the spaces of solutions to (1) and (3) on admissible shapes, respectively. We equip these spaces with the metric that is induced by the Hölder norm. The solutions in these spaces are defined on different and distinct domains and therefore are not comparable with respect to $\Vert \cdot \Vert _{C^{k,\alpha }}$. We give our solution to this problem in the following first definition of this subsection:

Definition 4.1

($C^{k,\alpha }$-Convergence of Functions with Varying Domains) By recalling the sets ${\mathcal {O}}_{k,\alpha }$ and ${\varOmega }^{\text {ext}}$ from Definition 3.5, we denote with $p_{\varOmega }: [C^{k,\alpha }({\varOmega }\backslash B)]^{3n} \rightarrow [C^{k,\alpha }_0({\varOmega }^{\text {ext}}\backslash B)]^{3n}$ be the extension operator that can be derived from Lemma A.1. For ${\varvec{v}} \in [C^{k,\alpha }({\varOmega }\backslash B)]^{3n}$ set ${\varvec{v}}^{\text {ext}} = p_{\varOmega }{\varvec{v}}$. For $({\varOmega }_n)_{n\in {\mathbb {N}}} \subset {\mathcal {O}}_{k,\alpha },\ {\varOmega }\in {\mathcal {O}}_{k,\alpha }$ and $({\varvec{v}}_n)_{n\in {\mathbb {N}}}$ with ${\varvec{v}}_n \in [C^{k,\alpha }({\varOmega }_n\backslash B)]^{3n},\ n\in {\mathbb {N}}$, the expression ${\varvec{v}}_n \rightsquigarrow {\varvec{v}}$ as $n \rightarrow \infty$ is defined by ${\varvec{v}}_n^{\text {ext}} \rightarrow {\varvec{v}}^{\text {ext}}$ in $[C^{k,\alpha }_0({\varOmega }^{\text {ext}}\backslash B)]^{3n}$.

Remark 4.1

Obviously, in the same way as above, we can extend a Hölder continuous functions p on $\mathrm {cl}(D\backslash {\varOmega })$ to the whole domain D for all ${\varOmega }\in {\mathcal {O}}_{k,\alpha }$.

With this definition of convergence, we can prove the compactness of ${\mathcal {G}}$. We show that the metric spaces $({\mathcal {O}}_{k,\alpha },d_H) ,\ ({\mathcal {P}}_{k,\alpha }, \Vert \cdot \Vert _{C^{k,\alpha ^\prime }})$, and $({\mathcal {E}}_{k,\alpha }, \Vert \cdot \Vert _{C^{k,\alpha ^\prime }})$ are each compact, where $0< \alpha ^\prime< \alpha < 1$, and that ${\mathcal {G}}$ is a closed subset of ${\mathcal {O}}_{k,\alpha }\times {\mathcal {P}}_{k,\alpha }\times {\mathcal {E}}_{k,\alpha }$.

Lemma 4.3

The space of admissible shapes ${\mathcal {O}}_{k,\alpha }({\varOmega }_0,{\varOmega }^{\text {ext}})$ equipped with the Hausdorff distance $d_H$ is a compact metric space.

Proof

We prove that ${\mathcal {O}}_{k,\alpha }$ is sequentially compact. First, we show that the space of design variables $U_{k,\alpha }^{\text {ad}}({\varOmega }^{\text {ext}})$ is compact. Then, the compactness of ${\mathcal {O}}_{k,\alpha }({\varOmega }_0,{\varOmega }^{\text {ext}})$ follows out of it. By definition, $U_{k,\alpha }^{\text {ad}}({\varOmega }^{\text {ext}})$ is a bounded subspace of $C^{k,\alpha }({\varOmega }^{\text {ext}})$ and thus precompact in $C^{k,\alpha ^\prime }({\varOmega }^{\text {ext}})$ for any $0< \alpha ^\prime < \alpha$ (see Lemma A.3). Hence, for every sequence $(\psi _n)_{n\in {\mathbb {N}}}\subset U_{k,\alpha }^{\text {ad}}({\varOmega }^{\text {ext}})$ there exists a subsequence that converges in $C^{k,\alpha ^\prime }({\varOmega }^{\text {ext}})$. For the compactness of $U_{k,\alpha }^{\text {ad}}({\varOmega }^{\text {ext}})$ it remains to show that the limit of $(\psi _n)_{n\in {\mathbb {N}}}$ lies in $U_{k,\alpha }^{\text {ad}}({\varOmega }^{\text {ext}})$. Since $U_{k,\alpha }^{\text {ad}}({\varOmega }^{\text {ext}})$ is precompact in the Banach space $C^{k,\alpha ^\prime }({\varOmega }^{\text {ext}})$, that sequence has a subsequence $(\psi _{n_l})_{l\in {\mathbb {N}}}$ with $\psi _{n_l} \rightarrow \psi$ in $\Vert \cdot \Vert _{C^{k,\alpha ^\prime }}$ for some $\psi \in C^{k,\alpha ^\prime }({\varOmega }^{\text {ext}})$. First, we note that since $\Vert \psi _{n_l} \Vert _{C^{k,\alpha }}\le K$ we have for any $\gamma \in {\mathbb {N}}^3$ with $0 \le |\gamma |\le k$

$$\begin{aligned} \left|\frac{\partial ^{|\gamma |}\psi _{n_l}(x)}{\partial ^{\gamma } x} -\frac{ \partial ^{|\gamma |}\psi _{n_l}(y)}{\partial ^{\gamma } x}\right|\le \left( K - \max _{|\gamma |= k} \left\Vert \frac{\partial ^{|\gamma |}\psi _{n_l}}{\partial x^\gamma } \right\Vert _{\infty } \right) |x - y |^\alpha \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\max _{|\gamma |= k}\left[ \frac{\partial ^{|\gamma |}\psi _{n_l}}{\partial x^\gamma } \right] _{0,\alpha } \le K - \max _{|\gamma |\le k}\left\Vert \frac{\partial ^{|\gamma |} \psi _{n_l}}{\partial x^\gamma } \right\Vert _\infty ,\\&\max _{|\gamma |\le k}\left\Vert \frac{\partial ^{|\gamma |} \psi _{n_l}}{\partial x^\gamma } \right\Vert _\infty \longrightarrow \max _{|\gamma |\le k}\left\Vert \frac{\partial ^{|\gamma |} \psi }{\partial x^\gamma } \right\Vert _\infty \le K. \end{aligned} \end{aligned}$$

We apply these estimates to show that $\psi \in C^{k,\alpha }$ and $\Vert \psi \Vert _{C^{k,\alpha }}\le K$:

$$\begin{aligned} \left|\frac{\partial ^{|\gamma |}\psi (x)}{\partial ^{\gamma } x} - \frac{\partial ^{|\gamma |}\psi (y)}{\partial ^{\gamma } x}\right|\le&\, \left|\frac{\partial ^{|\gamma |}\psi (x)}{\partial ^{\gamma } x} - \frac{\partial ^{|\gamma |}\psi _{n_l}(x)}{\partial ^{\gamma } x}\right|\\&+ \, \left|\frac{\partial ^{|\gamma |}\psi _{n_l}(x)}{\partial ^{\gamma } x} - \frac{\partial ^{|\gamma |}\psi _{n_l}(y)}{\partial ^{\gamma } x}\right|\\&+ \, \left|\frac{\partial ^{|\gamma |}\psi _{n_l}(y)}{\partial ^{\gamma } x} - \frac{\partial ^{|\gamma |}\psi (y)}{\partial ^{\gamma } x}\right|\\ \le&\, \left|\frac{\partial ^{|\gamma |}\psi (x)}{\partial ^{\gamma } x} - \frac{\partial ^{|\gamma |}\psi _{n_l}(x)}{\partial ^\gamma x}\right|\\&+ \, \left( K - \max _{|\gamma |\le k}\left\Vert \frac{\partial ^{|\gamma |} \psi _{n_l}}{\partial x^\gamma } \right\Vert _\infty \right) |x - y |^\alpha \\&+ \, \left|\frac{\partial ^{|\gamma |}\psi _{n_l}(y)}{\partial ^{\gamma } x} - \frac{\partial ^{|\gamma |}\psi (y)}{\partial ^\gamma x}\right|\end{aligned}$$

For the second term we used the Hölder continuity of $\psi _{n_l}$. The first and third term converge to zero since $\Vert \psi _{n_l} \Vert _{C^{k,\alpha }} \rightarrow \Vert \psi \Vert _{C^{k,\alpha }}$. Overall we get

$$\begin{aligned} \begin{aligned} \left|\frac{\partial ^{|\gamma |}\psi (x)}{\partial ^{\gamma } x} - \frac{\partial ^{|\gamma |}\psi (y)}{\partial ^{\gamma } x}\right|\le&\left|\frac{\partial ^{|\gamma |}\psi (x)}{\partial ^{\gamma } x} - \frac{\partial ^{|\gamma |}\psi _{n_l}(x)}{\partial ^\gamma x}\right|\\&+ \left( K - \max _{|\gamma |\le k}\left\Vert \frac{\partial ^{|\gamma |} \psi _{n_l}}{\partial x^\gamma } \right\Vert _\infty \right) |x - y |^\alpha \\&+ \, \left|\frac{\partial ^{|\gamma |}\psi _{n_l}(y)}{\partial ^{\gamma } x} - \frac{\partial ^{|\gamma |}\psi (y)}{\partial ^\gamma x}\right|\\ \longrightarrow&\ \left( K - \max _{|\gamma |\le k}\left\Vert \frac{\partial ^{|\gamma |} \psi }{\partial x^\gamma } \right\Vert _\infty \right) |x - y |^\alpha . \end{aligned} \end{aligned}$$

This gives $\psi \in C^{k,\alpha }({\varOmega }^{\text {ext}})$ and $\Vert \psi \Vert _{C^{k,\alpha }}\le K$. Further, by the same arguments we can show that the sequence of inverse $(\psi _{n_l}^{-1})_{l\in {\mathbb {N}}}$ converges to some function ${\tilde{\psi }} \in C^{k,\alpha }({\varOmega }^{\text {ext}})$ with respect to $\Vert \cdot \Vert _{C^{k,\alpha ^\prime }}$ (we can always find a subsequence) and with $\Vert {\tilde{\psi }} \Vert _{C^{k,\alpha }({\varOmega }^{\text {ext}})} \le K$. Now, it is straightforward to show that any bounded subset of $C^{k,\alpha }({\varOmega }^{\text {ext}})$ is uniformly equicontinuous, which implies that ${\tilde{\psi }} = \psi ^{-1}$ and thus $\psi \in U_{k,\alpha }^{\text {ad}}({\varOmega }^{\text {ext}})$. Therefore, $U_{k,\alpha }^{\text {ad}}({\varOmega }^{\text {ext}})$ is closed and with that compact.

We use the compactness of $U_{k,\alpha }^{\text {ad}}({\varOmega }^{\text {ext}})$ with respect to $\Vert \cdot \Vert _{C^{k,\alpha ^\prime }({\varOmega }^{\text {ext}})}$ to show the compactness of $({\mathcal {O}}_{k,\alpha }, d_{\mathcal {O}})$. Consider a sequence $({\varOmega }_n)_{n\in {\mathbb {N}}} \subset {\mathcal {O}}_{k,\alpha }$. By the definition of ${\mathcal {O}}_{k,\alpha }$, there is a corresponding sequence $(\psi _n)_{n\in {\mathbb {N}}} \subset U^{\text {ad}}_{k,\alpha }({\varOmega }^{\text {ext}})$ with $\psi _n({\varOmega }_0) = {\varOmega }_n$ for all $n\in {\mathbb {N}}$. Since $U^{\text {ad}}_{k,\alpha }({\varOmega }^{\text {ext}})$ is compact, there exists a subsequence $(\psi _{n_l})_{l\in {\mathbb {N}}}$ that converge to some $\psi \in U^{\text {ad}}_{k,\alpha }({\varOmega }^{\text {ext}})$ in $\Vert \cdot \Vert _{C^{k,\alpha ^\prime }}$. We show that the corresponding subsequence of shapes $({\varOmega }_{n_l}) = \psi _{n_l}({\varOmega }_0)$ converge to ${\varOmega }= \psi ({\varOmega }_0)$ by using the convergence of $\psi _{n_l} \rightarrow \psi$ in $\Vert \cdot \Vert _{C^{k,\alpha \prime }}$:

$$\begin{aligned} \begin{aligned} d_{\mathcal {O}}({\varOmega }_{n_l}, {\varOmega }) = \,&\max \{\underset{x\in {\varOmega }_{n_l}}{\sup } \ \underset{y\in {\varOmega }}{\inf }|x - y |,\, \underset{y\in {\varOmega }}{\sup } \ \underset{x\in {\varOmega }_{n_l}}{\inf }|x - y |\}\\ = \,&\max \{\underset{x\in {\varOmega }_0}{\sup } \ \underset{y\in {\varOmega }_0}{\inf }|\psi _{n_l}(x) - \psi (y) |,\, \underset{y\in {\varOmega }_0}{\sup } \ \underset{x\in {\varOmega }_0}{\inf }|\psi _{n_l}(x) - \psi (y) |\} \\ \le \,&\max \{\underset{x\in {\varOmega }_0}{\sup }|\psi _{n_l}(x) - \psi (x) |,\, \underset{y\in {\varOmega }_0}{\sup } |\psi _{n_l}(y) - \psi (y) |\} \\ \underset{l\rightarrow \infty }{\longrightarrow } \&0. \end{aligned} \end{aligned}$$

Hence, each sequence in ${\mathcal {O}}_{k,\alpha }$ has a convergent subsequence that converge in ${\mathcal {O}}_{k,\alpha }$ w.r.t. the Hausdorff distance. Therefore, $({\mathcal {O}}_{k,\alpha }, d_{\mathcal {O}})$ is sequentially compact. $\square$

Lemma 4.4

Let $0< \alpha ^\prime < \alpha \le 1$ and $k \ge 2$. Then, the solution space ${\mathcal {P}}_{k,\alpha }^{\mathrm {ext}}$, i.e., the space consisting of extensions from Definition 4.1 to the solutions $\phi _{\varOmega }\in {\mathcal {P}}_{k,\alpha }$, is compact in $C^{2,\alpha ^\prime }(D)$.

Proof

First, Lemma 2.1 gives that ${\mathcal {P}}_{k,\alpha }$ consists of Hölder continuous functions. We denote the extension from $\phi _{\varOmega }\in {\mathcal {P}}_{k,\alpha }$ on D with $\phi ^{\text {ext}}_{\varOmega }$. With Lemma 4.1 and (17) the following estimate holds

$$\begin{aligned} \Vert \phi ^{\text {ext}}_{\varOmega }\Vert _{C^{2,\alpha }(D)} \le C\Vert \phi _{{\varOmega }} \Vert _{C^{2,\alpha }(D\backslash {\varOmega })} \le CK, \end{aligned}$$

where K is uniform in ${\mathcal {O}}_{k,\alpha }$. In [9] it is shown that the constant C can also be chosen uniformly with respect to ${\mathcal {O}}_{k,\alpha }$ which yields an uniform bound for $\phi ^{\text {ext}}_{\varOmega }$. Hence, ${\mathcal {P}}^\text {ext}_{k,\alpha }$ is a bounded subset of $C^{k,\alpha ^\prime }(D)$ and therefore precompact in $C^{k,\alpha ^\prime }(D)$ (see Lemma A.3). Since $C^{k,\alpha ^\prime }(D)$ is a Banach space, it remains to show that ${\mathcal {P}}^\text {ext}_{k,\alpha }$ is closed. For this, let $(\phi _{{\varOmega }_n}^\text {ext})_{n\in {\mathbb {N}}}\subset {\mathcal {P}}^\text {ext}_{k,\alpha }$ be a sequence that converge to some function $\phi$ with respect to $\Vert \cdot \Vert _{C^{k,\alpha }({\varOmega }^{\text {ext}})}$ and let $({\varOmega }_n)_{n\in {\mathbb {N}}}\subset {\mathcal {O}}_{k,\alpha }$ be the corresponding sequence of shapes. As ${\mathcal {O}}_{k,\alpha }$ is compact, we can find a subsequence of shapes $({\varOmega }_{n_l})_{l\in {\mathbb {N}}}$ that converge against some ${\varOmega }\in {\mathcal {O}}_{k,\alpha }$. Now, consider the corresponding subsequence of solutions $(\phi _{{\varOmega }_{n_l}}^\text {ext})_{l\in {\mathbb {N}}}$. This subsequence also converge against $\phi$. Since the convergence is in $\Vert \cdot \Vert _{C^{2,\alpha }({\varOmega }^{\text {ext}})}$ and we have additionally seen in the proof of Lemma 4.3 that $\phi \in C^{2,\alpha }(D)$, it follows that $\phi$ is the extension to a solution $\phi _{\varOmega }$ for (1) and therefore lies in ${\mathcal {P}}^\text {ext}_{k,\alpha }$. $\square$

Lemma 4.5

Let $0< \alpha ^\prime < \alpha \le 1$ and $k \in {\mathbb {N}}_0$. The solution space ${\mathcal {E}}_{k,\alpha }^\mathrm {ext}$, i.e., the space consisting of extensions from Definition 4.1 to the solutions $u_{\varOmega }\in {\mathcal {E}}_{k,\alpha }$, is compact in $C^{2,\alpha ^\prime }({\varOmega }^{\text {ext}})$.

Proof

The proof follows the exact same arguments as in Lemma 4.4 and therefore is omitted. $\square$

Lemma 4.6

Consider the multi-physics shape optimization problem (13) with boundary regularity $C^{k,\alpha },\, k \ge 2$ and $\alpha \in \, ]0,1]$. Then, the Graph ${\mathcal {G}}$ is compact with respect to the corresponding maximum product metric.

Proof

By applying LemmaS 4.3, 4.4, and 4.5 we have that ${\mathcal {O}}_{k,\alpha }\times {\mathcal {P}}_{k,\alpha }^{\mathrm {ext}}\times {\mathcal {E}}_{k,\alpha }^{\mathrm {ext}}$ is compact. Let $({\varOmega }_n)_{n\in {\mathbb {N}}} \subset {\mathcal {O}}_{k,\alpha }$ and ${\varOmega }\in {\mathcal {O}}_{k,\alpha }$ with ${\varOmega }_n \rightarrow {\varOmega }$ in $d_H$. Then, one can see that due to the compactness of ${\mathcal {O}}_{k,\alpha }\times {\mathcal {P}}_{k,\alpha }^{\mathrm {ext}}\times {\mathcal {E}}_{k,\alpha }^{\mathrm {ext}}$ that $\phi _{{\varOmega }_n}^{\text {ext}} \rightarrow \phi ^{\text {ext}}$ and $u_{{\varOmega }_n}^{\text {ext}} \rightarrow u^{\text {ext}}$ in $\Vert \cdot \Vert _{C^{2,\alpha ^\prime }({\varOmega }^{\text {ext}})}$ with $\phi ^{\text {ext}}_{|{\varOmega }}$ solves (1) on ${\varOmega }$ and $u^{\text {ext}}_{|{\varOmega }}$ solves (3) on ${\varOmega }$. Hence, ${\mathcal {G}}$ is a closed subspace of a compact metric space and therefore compact as well. $\square$

Lemma 4.7

(Continuity of Local Cost Functionals [31]) We consider ${\mathcal {F}}_{\text {vol}},\, {\mathcal {F}}_{\text {sur}} \in C^0({\mathbb {R}}^d)$ (with d as in Definition 3.7 with $r=3$) and let ${\mathcal {O}}_{k,\alpha }$ only consists $C^0$-admissible shapes. For ${\varOmega }$ and ${\varvec{v}} \in [C^k(\mathrm {cl}({\varOmega }))]^{3n}$ consider the volume integral $J_{\text {vol}}({\varOmega },{\varvec{v}})$ and the surface integral $J_{\text {sur}}({\varOmega },{\varvec{v}})$. Let ${\varOmega }_n\subset {\mathcal {O}}_{k,\alpha }$ with ${\varOmega }_n \overset{\tilde{{\mathcal {O}}}}{\longrightarrow }{\varOmega }$ as $n\rightarrow \infty$ and let $({\varvec{v}}_n)_{n\in {\mathbb {N}}}\subset [C^k(\mathrm {cl}({\varOmega }_n))]^{3n}$ be a sequence with ${\varvec{v}}_n \rightsquigarrow {\varvec{v}}$ as $n\rightarrow \infty$ for some ${\varvec{v}}\in [C^k(\mathrm {cl}({\varOmega }_n))]^{3n}$. Then,

• (i) $J_{\text {vol}}({\varOmega }_n,{\varvec{v}}_n) \longrightarrow J_{\text {vol}}({\varOmega },{\varvec{v}})$ as $n\rightarrow \infty$.

• (ii) If the set ${\mathcal {O}}_{k,\alpha }$ only consists of $C^1$-admissible shapes one obtains $J_{\text {sur}}({\varOmega }_n,{\varvec{v}}_n)$ $\longrightarrow J_{\text {sur}}({\varOmega },{\varvec{v}})$ as $n\rightarrow \infty$ as well.

Proof

(i) First, we apply the characteristic function on the volume integral and obtain

$$\begin{aligned} J_{\text {vol}}({\varOmega }_n,{\varvec{v}}_n) := \int _{{\varOmega }^\text {ext}} \chi _{{\varOmega }_n}\cdot {\mathcal {F}}_{\text {vol}}\, (x,{\varvec{v}}^\text {ext}_n,\nabla {\varvec{v}}^\text {ext}_n,\dots , \nabla ^k {\varvec{v}}^\text {ext}_n)\,\hbox {d}x. \end{aligned}$$

Because of ${\mathcal {F}}_{\text {vol}} \in C^0(\mathbb {R^d})$ and ${\varvec{v}}_n \rightsquigarrow {\varvec{v}}$ as $n\rightarrow \infty$ there exist a constant $C>0$ such that $|\chi _{{\varOmega }_n}\cdot {\mathcal {F}}_{\text {vol}}\, (x,{\varvec{v}}^\text {ext}_n,\nabla {\varvec{v}}^\text {ext}_n, \dots , \nabla ^k {\varvec{v}}^\text {ext}_n)|\le C$ is valid for all $n\in {\mathbb {N}}$ almost everywhere in ${\varOmega }_{\text {ext}}$. Moreover, ${\varOmega }_n \overset{\tilde{{\mathcal {O}}}}{\longrightarrow } {\varOmega }$ and ${\varvec{v}}_n^{\text {ext}} \rightarrow {\varvec{v}}^{\text {ext}}$ in $[C_0^k({\varOmega }^\text {ext})]^{3n}$ ensure the existence of

$$\begin{aligned} \begin{aligned}&\lim _{n\rightarrow \infty }\chi _{{\varOmega }_n}\cdot {\mathcal {F}}_{\text {vol}} \, (x,{\varvec{v}}^\text {ext}_n, \nabla {\varvec{v}}^\text {ext}_n,\dots , \nabla ^k {\varvec{v}}^\text {ext}_n) \\&\quad = \chi _{{\varOmega }}\cdot {\mathcal {F}}_{\text {vol}}\, (x,{\varvec{v}}^\text {ext}, \nabla {\varvec{v}}^\text {ext},\dots , \nabla ^k {\varvec{v}}^\text {ext}), \end{aligned} \end{aligned}$$

for all $x\in {\varOmega }^{\text {ext}}$. Therefore, we can apply Lebesgue‘s dominated convergence theorem:

$$\begin{aligned} \begin{aligned} \lim _{n\rightarrow \infty } J_{\text {vol}}({\varOmega }_n,{\varvec{v}}_n)&= \lim _{n\rightarrow \infty } \int _{{\varOmega }^\text {ext}} \chi _{{\varOmega }_n}\cdot {\mathcal {F}}_{\text {vol}}\, (x,{\varvec{v}}^\text {ext}_n,\nabla {\varvec{v}}^\text {ext}_n,\dots , \nabla ^k {\varvec{v}}^\text {ext}_n)\,\hbox {d}x \\&= \ \int _{{\varOmega }^\text {ext}} \lim _{n\rightarrow \infty } \chi _{{\varOmega }_n}\cdot {\mathcal {F}}_{\text {vol}}\, (x,{\varvec{v}}^\text {ext}_n,\nabla {\varvec{v}}^\text {ext}_n,\dots , \nabla ^k {\varvec{v}}^\text {ext}_n)\,\hbox {d}x \\&= \ \int _{{\varOmega }^\text {ext}} \chi _{{\varOmega }}\cdot {\mathcal {F}}_{\text {vol}}\, (x,{\varvec{v}}^\text {ext},\nabla {\varvec{v}}^\text {ext},\dots , \nabla ^k {\varvec{v}}^\text {ext})\,\hbox {d}x \\&= \ J_{\text {vol}}({\varOmega },{\varvec{v}}) \end{aligned} \end{aligned}$$

(ii) The second assertion can be analogously proven as in [9] and we only state the main ideas here.

First, we note that every shape ${\varOmega }\in {\mathcal {O}}_{k,\alpha }$, by its definition, can be considered as two-dimensional submanifold and therefore is locally embeddable into ${\mathbb {R}}^2$. Let $A_n^i \subset \partial {\varOmega }$, $1\le i \le m$ with $\cup _{i=1}^m A_i = \partial {\varOmega }$ and $A_i \cap A_j = \emptyset$ for $i\ne j$. We can find in i and n uniformly bounded chart mappings $h_n^i:A_n^i \rightarrow {\tilde{A}}_i$ with ${\tilde{A}}_i\subset {\mathbb {R}}^2$. We use them to straighten the boundary of ${\varOmega }_n$ to obtain a volume integral, e.g.,

$$\begin{aligned} \begin{aligned} J_{\text {sur}}({\varOmega }_n,{\varvec{v}}_n)&= \ \int _{\partial {\varOmega }_n} {\mathcal {F}}_{\text {sur}}\, (x,{\varvec{v}}_n,\nabla {\varvec{v}}_n,\dots , \nabla ^k {\varvec{v}}_n)\,\hbox {d}A \\&= \ \sum _{i=1}^{m} \int _{A_n^i} {\mathcal {F}}_{\text {sur}}\, (x,{\varvec{v}}_n,\nabla {\varvec{v}}_n,\dots , \nabla ^k {\varvec{v}}_n)\,\hbox {d}A \\&= \ \sum _{i=1}^{m} \int _{{\tilde{A}}_i} {\mathcal {F}}_{\text {sur}}\, \left( h_n^i(s),{\varvec{v}}_n(h_n^i(s)), \nabla {\varvec{v}}_n(h_n^i(s)),\dots , \nabla ^k {\varvec{v}}_n(h_n^i(s))\right) \\&\quad \sqrt{g^{h_n^i}(s)}\,ds, \end{aligned} \end{aligned}$$

where ds indicates the Lebesgue measure on ${\tilde{A}}_i$ and corresponding Gram determinants $g^{h_n^i}$. Due to the fact that the chart mappings $h_n^i$ are uniform bounded and since ${\tilde{A}}_i$ is independent of n, one can see that, similarly to (i), we can apply Lebesgue’s Theorem and the assertion is proven. $\square$

Remark 4.2

The continuity assumption of Lemma 4.7 ensures the existence of an integrable majorant for ${\mathcal {F}}_{\text {vol}}$ and ${\mathcal {F}}_{\text {sur}}$. Example (9) does not fulfil this assumption. However, (8) is integrable on compact sets and one can easily find an integrable majorant by applying the uniform bound of Lemma 4.1.

Theorem 4.1

Assuming $k \ge 2$, the multi-physics shape optimization problem (13) possesses at least one Pareto optimal solution $({\varOmega }^*, \phi _{{\varOmega }^*}, u_{{\varOmega }^*}) \in {\mathcal {G}}$ and covers all nondominated points in ${\mathcal {Y}}$, i.e., ${\mathcal {Y}}_N = \mathrm {cl}({{\mathcal {Y}}})_N$.

Proof

Lemma 4.6 provides the compactness of ${\mathcal {G}}$ and Lemma 4.7 the continuity of the local cost functionals. Then, Theorem 3.1 gives the existence of an optimal shape and the closeness of the set of optimal shapes. $\square$

5 Scalarization and Multi-physics Optimization

Scalarizing is the traditional approach to solving a multicriteria optimization problem. This includes formulating a single objective optimization problem that is related to the original Pareto optimality problem by means of a real-valued scalarizing function typically being a function of the objective function, auxiliary scalar or vector variables, and/or scalar or vector parameters. Additionally scalarization techniques sometimes further restrict the feasible set of the problem with new variables or/and restriction functions. In this section, we investigate the stability of the parameter-dependent optimal shapes to different types of scalarization techniques with underlying design problem (13).

First, let us define the scalarization methods we consider. This involves a certain class of real-valued functions $S_\theta : {\mathbb {R}}^l\rightarrow {\mathbb {R}}$, referred to as scalaraization function that possibly depends on a parameter $\theta$ which lies in a parameter space ${\varTheta }$. The scalarization problem is given by

$$\begin{aligned} \begin{aligned} \begin{array}{ll} \min S_\theta \left( {\mathbf {J}}({\varOmega },u_{{\varOmega }},\phi _{{\varOmega }})\right) \\ \,\text { subject to } ({\varOmega },u_{{\varOmega }},\phi _{{\varOmega }}) \in {\mathcal {G}}_\theta , \end{array} \end{aligned} \end{aligned}$$

(15)

where ${\mathcal {G}}_\theta \subseteq {\mathcal {G}}$. For the sake of notational convenience, we sometimes identify an element $({\varOmega }, u_{\varOmega }, \phi _{\varOmega })\in {\mathcal {G}}_\theta$ only by its distinct shape ${\varOmega }$. If we assume that ${\mathcal {G}}_\theta$ is closed and the scalarization $S_\theta ({\mathbf {J}})$ is lower semicontinuous on ${\mathcal {G}}_\theta \times \{ \theta \}$, then, by the results of Sect. 4, (15) obviously has an optimal solution for $\theta \in {\varTheta }$. For a fixed $\theta \in {\varTheta }$ we shall denote the space of all optimal shapes to an achievement function problem with $\zeta _\theta =\mathop {\mathrm{arg\,min}}\limits _{{\varOmega }\in {\mathcal {G}}_\theta }S_\theta \left( {\mathbf {J}}({\varOmega },u_{{\varOmega }},\phi _{{\varOmega }})\right)$. We assume that ${\varTheta }\subset {\mathbb {R}}^l$ is closed and equip the space ${\mathcal {Z}}:= \{\zeta _\theta \, :\, \theta \in {\varTheta }\}$ with the Hausdorff distance, which in this setting defines, due to the closeness of the optimal shapes sets, a metric (see Lemma 5.1 and Corollary 5.1).

In the following, we gather some definitions and assertion from chapter 4 of [7]. We define the optimal set mapping $\chi : {\varTheta }\rightrightarrows {\mathcal {Z}}$, the optimal value mapping $\tau :{\varTheta }\longrightarrow {\mathbb {R}}$, and the graph mapping $G:{\varTheta }\rightrightarrows 2^{\mathcal {G}}$ which maps a parameter $\theta \in {\varTheta }$ to the corresponding set of optimal shapes $\zeta _\theta$, the corresponding optimal value $\min _{{\varOmega }\in {\mathcal {G}}_\theta } S_\theta ({\mathbf {J}})$, and the corresponding graph ${\mathcal {G}}_\theta$, respectively. With these definitions in hand, we can describe the stability of the optimal shapes for a wide range of scalarization methods. First, we state a lemma that shows that $({\mathcal {Z}}, d_H)$ is indeed a metric space.

Lemma 5.1

The optimal set mapping $\chi$ is closed if $\tau$ is upper semicontinuous and $S_\theta ({\mathbf {J}})$ is lower semicontinuous on ${\mathcal {G}}\times \{ \theta \}$.

Corollary 5.1

If the scalarization function $S_\theta$ is lower semicontinuous on ${\mathbb {R}}^l \times \{ \theta \}$ and uniform continuous on $\{ r \} \times {\varTheta }$, for $r\in {\mathbb {R}}^l$, then the Hausdorff distance $d_H$ defines a metric on ${\mathcal {Z}}$.

Proof

Due to the continuity of ${\mathbf {J}}$ (see Lemma 4.7) and the uniform continuity of $S_\theta$ on $\{ r \} \times {\varTheta }$, the optimal value maping $\tau$ is upper semicontinuous and therefore, by Lemma 5.1, the optimal set mapping $\chi$ is closed. Since $d_H$ defines a metric on $F({\mathcal {G}})$ (the set of all closed subsets of ${\mathcal {G}}$), $({\mathcal {Z}}, d_H)$ defines a metric space. $\square$

Since the sclarization solution is not necessarly unique, we need some sort of continuity property of point-to-set mappings in order to discuss the stability of sets of optimal shapes. The literature describes serveral definitions which vary in the statement. We investigate the stabilty according to Hausdorff and Berge (for Berge see [7]) which, in this setting, are equivalent.

Definition 5.1

(Upper semicontiniuity according to Hausdorff) Let $({\varTheta }, d_{\varTheta })$ and $(X, d_x)$ be metric spaces. A point-to-set mapping of ${\varTheta }$ into X is a function ${\varGamma }$ that assigns a subset ${\varGamma }(\theta )$ of X to each element $\theta \in {\varTheta }$. This function is called upper semicontinuous in $\theta ^*$ if for each sequence $(\theta _n)_{n\in {\mathbb {N}}} \subseteq {\varTheta }$ with $\theta _n \longrightarrow \theta ^*$, for $n \rightarrow \infty$, we have

$$\begin{aligned} \sup _{x\in T(\theta _n)} \inf _{x^\prime \in T(\theta ^*)} d_X(x, x^\prime ) \longrightarrow 0. \end{aligned}$$

(16)

${\varGamma }$ is called upper semicontinuous if ${\varGamma }$ is upper semicontinuous in each $\theta \in {\varTheta }$. For this type of continuity we simply write u.s.c.-H.

The next theorem states stability conditions for scalarization function problems.

Theorem 5.1

([7]) Assume that G is u.s.c.-H at $\theta ^*$ and $G(\theta ^*)$ is compact. Further, let $\tau$ be upper semicontinuous at $\theta ^*$ and $S_{\theta ^*}$ lower semicontinuous on $G(\theta ^*)\times \{ \theta ^* \}$. Thenm the optimal set mapping $\chi$ is u.s.c.-H at $\theta ^*$.

The following two corollaries demonstrate continuity properties of shapes under change of preferences for two commonly used scalarization techniques. In particular, the results apply to the shape optimization problem introduced in Sect. 3.2.

Corollary 5.2

(Weighted Sum Method) Consider cost functionals ${\mathbf {J}} = (J_1,\dots , J_l)$ and let ${\varTheta }\subset {\mathbb {R}}^l$ be a closed subset. Then, the weighted sum scalaraization method, which is given by

$$\begin{aligned} \begin{aligned} \begin{array}{ll} \min \sum _{i=1}^l \theta _i J_i(({\varOmega },u_{{\varOmega }},\phi _{{\varOmega }}))\\ \,\text { subject to } ({\varOmega },u_{{\varOmega }},\phi _{{\varOmega }}) \in {\mathcal {G}}, \end{array} \end{aligned} \end{aligned}$$

fulfills all conditions of Theorem 5.1 due to the compactness of ${\mathcal {G}}$ (see Lemma 4.6) and the continuity of ${\mathbf {J}}$ (see Lemma 4.7).

Corollary 5.3

($\epsilon$-Constraint Method) Let ${\mathbf {J}} = (J_1,\dots , J_l)$ be cost functionals. We optimize cost functional $J_j$ and constrain the other functionals by $J_i \le \epsilon _i \in {\mathbb {R}}$, for $1 \le i \le n$ and $i\ne j$. If each $\epsilon _i$ converges monotonically decreasing to some $\epsilon _i^*$, then the $\epsilon$-Constraint Method

$$\begin{aligned} \begin{aligned} \begin{array}{ll} \min J_j(({\varOmega },u_{{\varOmega }},\phi _{{\varOmega }}))\\ \,\text { subject to } J_i \le \epsilon _i, \end{array} \end{aligned} \end{aligned}$$

fulfills all conditions of Theorem 5.1.

Proof

Let $\epsilon = (\epsilon _1, \dots , \epsilon _l)$ and ${\mathcal {G}}_\epsilon = \{ {\varOmega }\in {\mathcal {G}} \ : \ J_i({\varOmega }) \le \epsilon _i,\, i\ne j\}$. The u.s.c.-H of G is given due to the continuity of ${\mathbf {J}}$. The continuity of $J_j$, the u.s.c.-H of G, and the fact that ${\mathcal {G}}_\epsilon \subseteq {\mathcal {G}}_{\epsilon ^\prime }$ for all $\epsilon ^*\le \epsilon ^\prime \le \epsilon$ gives that $\tau (\epsilon )$ converge continuously against $\tau (\epsilon ^*)$ for $\epsilon \searrow \epsilon ^*$. Hence, the optimal sets $\chi (\epsilon )$ converge against $\chi (\epsilon ^*)$ for $\epsilon \searrow \epsilon ^*$ in the sense of u.s.c.-H. $\square$

Remark 5.1

Whenever the scalarized problem (15) possesses a unique solution $\zeta _\theta =\{{\varOmega }_\theta \}$ for all $\theta$ in some neighborhood of $\theta ^*\in {\varTheta }$, then ${\varOmega }_{\theta _n}\longrightarrow {\varOmega }_{\theta ^*}$ in the Hausdorff distance (for subsets in ${\mathbb {R}}^d$) if $\theta _n\rightarrow \theta ^*$.

6 Conclusions

In this work, we extended the well-known framework of the existence of optimal solutions in shape optimization [17, 34] to a multi-criteria setting. We formulated conditions for the existence and completeness of Pareto optimal points. Multiple criteria in design are often related to simulations that include different domains of physics. We presented a coupled fluid-dynamic and mechanical system, which is motivated by gas turbine design and fits to the given framework. The objective functions in this case are given by fluid losses and mechanical durability expressed by the probability of failure under low cycle fatigue. Both objectives require classical solutions to the underlying partial differential equations and therefore can only be formulated on sufficiently regular shapes such that elliptic regularity theory applies [1, 2, 28]. We presented a formulation of the family of admissible shapes that implied the existence of such classical solutions and thereby provided a non-trivial example for the general framework.

In multi-criteria optimization [22], the Pareto front contains points which are optimal with respect to different preferences of a decision maker. An interesting point is, if a small variation of the preference also leads to a small variation in the design. This question however is ill-posed, if Pareto optimal solutions need not to be unique. We therefore presented a study, where we went over to the sets of Pareto optimal shapes for a given preference and studied the variation of these sets in the Hausdorff-metric. In this setting, certain continuity properties in the preference parameters were derived.

It will be of interest to develop multi-criteria shape optimization also from an algorithmic standpoint, using the theory of shape derivatives and gradient-based optimization; see, e.g., [11, 21] for some first steps in that direction. For a rigorous analysis of numerical schemes of shape optimization, it will be of interest, if (a) the optima of the discretized problem are close to the optima of the continuous problem and, if (b) the same holds for shape gradients for non-optimal solutions, as e.g., used in multi-criteria descent algorithms. In particular, this should be true for the objective values of discretized and continuous solutions, respectively. Potentially, iso-geometric finite elements [19, 27, 54] could be a useful numerical tool to not spoil the domain regularity that is built into our framework by the need of $C^{k,\alpha }$-classical solutions needed for the evaluation of the objectives in multi-criteria shape optimization problems like the one presented here.

Appendix

Definition A.1

(Hölder continuity) Let $U \subseteq {\mathbb {R}}^d$ be open. A function $f:U \rightarrow {\mathbb {R}}$ is called Hölder continuous if there exist non-negative real constants ${C > 0,\, \alpha \in \, ]0,1]}$, such that

$$\begin{aligned} |f(x) - f(y) |\le C |x - y |^\alpha , \quad {\text {for all } x,y \in U.} \end{aligned}$$

With $C^{k,\alpha }(U)$ we denote the space consisting of function on U having Hölder continuous derivatives up to order ${k \in {\mathbb {N}}_{0}}$ with exponent $\alpha$. If the function f and its derivatives up to order k are bounded on the closure of U, then we can assign the norm

$$\begin{aligned} \Vert f \Vert _{C^{k,\alpha }\left( U\right) } = \max _{|\gamma |\le k}\left\Vert \frac{\partial ^{|\gamma |} f}{\partial x^\gamma } \right\Vert _\infty + \max _{|\gamma |= k}\left[ \frac{\partial ^{|\gamma |}f}{\partial x^\gamma } \right] _{0,\alpha }, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&\Vert f \Vert _{\infty } = \sup _{x\in U} |f(x) |\\&[f]_{0,\alpha } = \sup _{\begin{array}{c} x,y \in U \\ x \ne y \end{array}} \frac{|f(x) - f(y) |}{|x - y |^\alpha }. \end{aligned} \end{aligned}$$

We note that $(C^{k,\alpha }(U), \Vert \cdot \Vert _{C^{k,\alpha }(U)})$ is a Banach space. A vector field $f:U \rightarrow {\mathbb {R}}^n$ is Hölder continuous with exponent $\alpha$ if each component of f is Hölder continuous with exponent $\alpha$.

Lemma A.1

([28], Lemma 6.37) Let ${\varOmega }$ be a $C^{k,\alpha }$ domain in ${\mathbb {R}}^d$ with $k\ge 1, \, \alpha \in \, ]0,1]$ and let ${\varOmega }^\prime$ be an open set containing $\mathrm {cl}({{\varOmega }})$. Suppose $u\in C^{k,\alpha }(\mathrm {cl}\left( {{\varOmega }}\right) )$. Then, there exist a function $w\in C_0^{k,\alpha }({\varOmega }^\prime )$ such that $w = u$ in ${\varOmega }$ and

$$\begin{aligned} \Vert w \Vert _{C^{k,\alpha }({\varOmega }^\prime )} \le C\Vert u \Vert _{C^{k,\alpha }({\varOmega })}, \end{aligned}$$

(17)

where $C=C(k,{\varOmega }, {\varOmega }^\prime )$.

Lemma A.2

(Korn’s Second Inequality, [15]) Let ${\varOmega }\subset {\mathbb {R}}^3$ be an open bounded set with piecewise smooth boundary. In addition, suppose ${\varGamma }_0 \subset \partial {\varOmega }$ has positive two-dimensional measure. Then, there exist a positive number $c^\prime = c^\prime ({\varOmega }, {\varGamma }_0)$ such that

$$\begin{aligned} \Vert \epsilon (u_{{\varOmega }}) \Vert ^2_{L_2({\varOmega })} = \int _{\varOmega }\mathrm {tr}(\epsilon (v)^2)\, \hbox {d}x \ge c^\prime \Vert v \Vert _{H^1({\varOmega })}, \quad \text {for all } v\in H^1_{\varGamma }({\varOmega }). \end{aligned}$$

Here, $H^1_{\varGamma }({\varOmega })$ is the closure of $\{ v \in [C^\infty ({\varOmega })]^3 \, :\, v(x) = 0 \text { for } x\in {\varGamma }_0 \}$ with respect to the $\Vert \cdot \Vert _{H^1({\varOmega })}$-norm.

Lemma A.3

([28], Lemma 6.36) Let ${\varOmega }$ be a $C^{k,\alpha }$ domain in ${\mathbb {R}}^d$ with $k\ge 1, \, \alpha \in \, ]0,1]$ and let S be a bounded set in $C^{k,\alpha }(\mathrm {cl}\left( {{\varOmega }}\right) )$. Then, S is precompact in $C^{j,\beta }(\mathrm {cl}\left( {{\varOmega }}\right) )$ if $j+\beta \le k + \alpha$.