1 Introduction

In recent years, the structural health monitoring of buildings has attracted considerable attention and many monitoring systems have become commercially available. Most monitoring systems estimate the overall behavior of the building by measuring the acceleration response, such as the natural period, attenuation, and inter-story drift, to represent the structural performance and integrity [1,2,3,4]. Kaloop et al. [5] proposed a structural health monitoring method based on statistical and wavelet analysis of the measured acceleration, which they applied to an actual building. The results showed that the roof vibration was more obvious and dominant during shaking. However, such indices are not sensitive enough to directly measure structural damage to individual structural elements. Furthermore, even if one of the structural elements in a building is severely damaged (e.g., fractured), the overall behavior of the building will not change enough to change global indices such as the dominant frequency or damping. For example, in a large-scale shaking table test using an 18-story steel moment frame specimen [6, 7], even when many of the beam ends in the structure yielded, the dominant frequency of the system did not change as long as the beams and columns did not fracture. Meanwhile, the dominant frequency and damping may change even if the building suffers little or no structural damage [1, 8]. Many attempts have been made to develop advanced techniques for analyzing small changes in the acceleration response to identify damaged members and their locations. Bernal [9], Reynders and De Roeck [10] and Hann et al. [11] proposed mathematical methods based only on acceleration records. However, many cases are very difficult to solve, because they are ill-posed, and such advanced techniques are difficult to apply to complex structures such as real buildings.

Alternatively, a better measurement index for determining the state of individual structural members may be the strain. Kurata et al. [12] and Matarazzo et al. [13] proposed the use of piezoelectric sensors to measure the strain at the bottom flanges of the beam ends; section area reduction due to crack extension or fracture can be detected by comparing the strain amplitude before and after earthquake loading. Iyama et al. [14, 15] applied a similar method to shaking table tests and defined “local stiffness” using the strain recorded by the strain gauges attached to the beam flanges and the displacement recorded by the displacement meter; they confirmed that this method is effective for fracture location. For civil infrastructure such as bridges and dams, structural health monitoring has long been of interest; many attempts have been made to use strain gauges and optical fiber sensors to measure the strain for such structures. The strain measured in bridge girders is used to measure the traffic load (i.e., weigh-in-motion) [16] and detect damage, defined as the root mean square of the traffic load, to structural members based on changes in the strain and stress distributions [17,18,19,20,21,22,23,24,25]. For building structures, however, there have been very few examples of strain measurement. This may be because the daily strain on the structural frame of a building is extremely small and difficult to measure, and data acquisition systems for dynamic strain are expensive. In addition, local strains are likely to be affected by the measurement location and the surrounding environment, and converting the measured value to a more understandable index that represents the structural conditions may be difficult. Thus, methods for analyzing and utilizing strain measurements have not been established.

In recent years, high-precision semiconductor strain gauges have become available that make it possible to measure strain amplitudes caused by small earthquakes or microtremors. Such measurement devices and dynamic data acquisition systems are still expensive, and the cost needs to be further reduced for widespread use. Moreover, it is necessary to carry out measurements in actual buildings and accumulate data to determine the usefulness and potential applications of such data. The authors have installed high-precision semiconductor strain gauges and accelerometers in several steel structure buildings for continuous monitoring. The present study focuses on one of these buildings, which is currently being occupied as well as measurements being conducted [26]. In this paper, the recorded data are organized and presented using the concept of “local stiffness” discussed in a previous paper [14]. The consistency of the recorded data with the analysis results, the amplitude dependence, and the long-term tendency were investigated to examine the possibility of damage evaluation based on strain measurement.

2 Measurement method

2.1 Target structure

Figure 1 shows a photograph of the target structure. It is a three-story steel moment frame building in Fukushima Prefecture, Japan. This area is close to the epicenter of the 2011 Tohoku earthquake and experiences more earthquakes than other areas in Japan. The target structure was constructed with web-clamp-type beam–column rigid joints [27,28,29] in June 2018 and has been in use since its construction. Figure 2a–d shows the floor plan of the second floor, X2 axis structural frame, floor slab detail, and details of the outer walls. Table 1 presents the list of cross sections of the structural frame. Some beam–column joints are pin joints, wherein only the beam web were connected to the column with high-strength bolts. As shown in Fig. 2c, the floor is a composite slab with a concrete thickness of 80 mm; it is connected to the beam through headed studs. The distance between the centroids of the steel beam and concrete slab is 409 mm.

Fig. 1
figure 1

Photograph of the building

Full size image
Fig. 2
figure 2

Structural frame of the target building

Full size image
Table 1 Section list
Full size table

2.2 Measurements

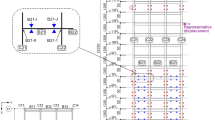
This study used KPSB series semiconductor strain gauges manufactured by Kyowa Electronic Instruments Co., Ltd. (Tokyo, Japan). The semiconductor strain gauges were attached to the columns and beams, depicted within the dashed lines in Fig. 2a, b. Figure 3 shows details of the measurement positions. To measure the axial force and bending moment, four KSN-2-120-E4-11 semiconductor strain gauges (Kyowa Electric Instruments) were installed on the back of the H-shaped steel flange at each cross section: four beams and four columns. The measured beams and columns are designated as LB (left beam), RB (right beam), UC (upper column), and LC (lower column). In addition, two ASQ-2D accelerometers (Kyowa Electric Instruments) each were installed at the ground (1F), second floor (2F), and roof (RF); measurements were conducted in both the short (X) and long (Y) axes of the building. The strain gauges and accelerometers were connected to an NTB-500A data logger (Kyowa Electric Instruments) and synchronized to a sampling frequency of 100 Hz. The sensors were set up simultaneously with the construction of the building by June 2018. Thereafter, measurements have been performed continuously, without any special triggering since December 2018. For this study, the data during each earthquake were isolated from the continuous recorded data and analyzed.

Fig. 3
figure 3

Locations of strain gauges [26]

Full size image

The analysis included 198 small earthquakes recorded between December 2, 2018 and April 20, 2020. The largest earthquake that occurred during this time was an M6.4 earthquake with the epicenter off Fukushima Prefecture at 19:23 JST on August 4, 2019. The maximum seismic intensity at the site, as reported by the Japan Meteorological Agency, was 4, and the maximum acceleration in the Y-direction, measured by the 1F accelerometer, was 1.02 m/s2. The maximum horizontal displacement at roof level, calculated using the double-integral of the acceleration, was 0.018 m.

2.3 Calculated structural characteristics of the building

A 3D frame analysis was performed using the commercial structural analysis software SuperBuild SS-3, developed by Union System Inc. (Osaka, Japan). For the structural analysis, the stiffness is assumed to be constant over the entire length of the composite beam and equal to the average of the stiffness values under positive and negative bending, calculated based on the current Japanese design code [30]. The exposed-type column base was modeled as a rotational spring whose rotational stiffness is as described in the product manual of the column base [31]. Figure 4 shows the distributions of the horizontal displacement and bending moment under the seismic load obtained via structural analysis in the design stage. The numerical values for the horizontal displacement chart in Fig. 4a represent the horizontal displacements at each floor, and the values in parentheses are normalized by the RF horizontal displacement (59.6 and 49.7 mm in the Y- and X-direction, respectively). Meanwhile, the values in Fig. 4b are the bending moments in the measurement target range (unit: kN-m), and the values in parentheses are divided by the RF horizontal displacement (unit: kN-m/mm). Because this value represents the bending moment of each member when a unit deformation is applied to the building, it is called the “local bending stiffness” in this paper and is used as an index for the behavior of structural members. Figure 5 shows the natural frequencies and mode shapes of the building, obtained through an eigenvalue analysis. The eigenmode shape was normalized by the maximum displacement of the stories. The primary natural frequencies in the Y- and X-direction were 1.05 and 1.16 Hz, respectively. The first-mode shape almost matched the deformation shape when the seismic load in Fig. 4 was considered a static load.

Fig. 4
figure 4

Structural analysis for a horizontal seismic load [26]

Full size image
Fig. 5
figure 5

Eigenvalue analysis [26]

Full size image

3 Measurement results

3.1 Recorded time history and frequency characteristics

In this section, the largest seismic record measured is used as an example. Its time history and frequency characteristics are presented, and details of the data analysis method are described.

3.1.1 Acceleration

Figure 6 shows examples of the time histories of the accelerations measured on RF and 2F relative to the acceleration measured on the ground; it also depicts the Fourier amplitude spectra for these relative accelerations. Figure 6(a1) and (b1) shows the time history of the recorded acceleration. Figure 6(a2) and (b2) shows the Fourier amplitude spectra of acceleration \(\left| {\hat{a}_{i} \left( f \right)} \right|\). Figure 6(a3) and (b3) shows the pseudo-displacement spectra \(\left| {\hat{d}_{i} \left( f \right)} \right|\), and Fig. 6(a4) and (b4) shows the phase difference between the Fourier transforms of the accelerations measured on 2F and RF. These are calculated as follows:

$$\hat{a}_{i} \left( f \right) = \frac{1}{L}\int {a_{i} \left( t \right)e^{{ - 2i\pi ft}} } dt$$
(1)
$$\hat{d}_{i} \left( f \right) = \frac{{\hat{a}_{i} \left( f \right)}}{{4\pi^{2} f^{2} }}$$
(2)
$$\Delta \phi \left( f \right) = {\text{arg }}\hat{a}_{2F} \left( f \right) - {\text{arg}} \hat{a}_{RF} \left( f \right)$$
(3)
Fig. 6
figure 6

Relative acceleration recorded for the RF earthquake that occurred at 2019-08-04T19:23+0900

Full size image

Here, \(a_{i} \left( t \right)\) is the floor response relative acceleration at time t. The subscript i indicates the location (2F or RF). L is the time duration of the target acceleration record. \(\hat{ \cdot }\left( f \right)\) represents the Fourier transform at frequency f; according to this definition, \(\hat{a}_{i} \left( f \right)\) and \(\hat{d}_{i} \left( f \right)\) have dimensions of acceleration and displacement, respectively.

Figure 6(a2) shows the acceleration spectrum in the Y-direction; a peak frequency can be observed at 1.96 Hz. However, Fig. 6(a3) shows the pseudo-displacement spectrum obtained by dividing by ω2; here, the peak frequency is 1.73 Hz. For both frequencies, 2F and RF vibrated in the same phase, as shown in Fig. 6(a4). Moreover, the ratios between the displacement amplitudes of 2F and RF were almost the same (0.357 and 0.353) for these two frequencies. Regardless of the frequency selected, the mode shape of the structure could be obtained. In the following sections, these two peak frequencies are considered, and the effect of the peak selection is discussed.

3.1.2 Mode shape

Figure 7 shows the vibration mode shape obtained from the spectra depicted in Fig. 6. The horizontal axis represents the ratio of the displacement amplitude at a given floor to that at RF at the peak frequency. As shown in Fig. 6, because different peaks were observed in both the acceleration and displacement spectra, the measured data are provided for both frequencies (1.73 and 1.96 Hz). Figure 7 also includes the displacement distribution obtained by the eigenvalue and static analyses described above. Because this was not measured on 3F, only the values on 2F can be compared, which can be seen to match roughly. Thus, although the frequency differed, the calculated vibration mode shapes were almost the same.

Fig. 7
figure 7

Mode shape

Full size image

3.1.3 Bending moment and axial force of beams

This section presents the bending moment and axial force calculated from the strain measurements. In the target structure, four strain gauges were pasted on one section. The axial force and bending moment in the steel beams are calculated from the measured strains as follows:

$$N_{s} \left( t \right) = EA_{s} \frac{{\varepsilon_{1} \left( t \right) + \varepsilon_{2} \left( t \right) + \varepsilon_{a} \left( t \right) + \varepsilon_{b} \left( t \right)}}{4}$$
(4)
$$M_{s} \left( t \right) = EZ_{s}^{*} \frac{{\varepsilon_{1} \left( t \right) - \varepsilon_{2} \left( t \right) + \varepsilon_{a} \left( t \right) - \varepsilon_{b} \left( t \right)}}{4}$$
(5)
$$M_{ys} \left( t \right) = EZ_{sy}^{*} \frac{{\varepsilon_{1} \left( t \right) - \varepsilon_{a} \left( t \right) + \varepsilon_{2} \left( t \right) - \varepsilon_{b} \left( t \right)}}{4}$$
(6)

where \(N_{s}\) and \(M_{s}\) are the axial force and the bending moment, respectively, of the steel section. The subscript “s” indicates that the section property belongs to the steel section. The additional subscript “y” indicates that the property is along the weak axis. \(\varepsilon_{1}\), \(\varepsilon_{2}\), \(\varepsilon_{a}\), and \(\varepsilon_{b}\) are the strains measured at time t, and the subscripts indicate the gauge locations, as shown in Fig. 3. E is Young’s modulus and As is the cross-sectional area. \(Z_{s}^{*}\) and \(Z_{sy}^{*}\) are the section moduli along the strong and weak axes, respectively, which are calculated by dividing the moment of inertia of the steel section by half of the vertical distance between strain gauges. The axial force is positive in tension, and the bending moment is positive when the upper flange or outer edge is in tension.

Figure 8(a1)–(a4) shows the recorded data of the bending moment. MI and MJ represent the bending moments at sections I and J, respectively, of the right beam, which are calculated with Eq. (5). Figure 8(a1) shows the time histories of MI, MJ, and the relative acceleration in the Y-direction. The phases of MI and MJ were opposite to each other, and the phases of MJ and the relative acceleration were the same. This indicates that the bending moments and acceleration were almost proportional. Figure 8(a2) shows the spectra of MI, MJ, and the relative displacement. The values at 1.73 and 1.96 Hz (i.e., the peak frequencies of the relative acceleration and relative displacement spectra, respectively) are shown. The ratios of the values (0.923 / 0.263 and 0.857 / 0.200, respectively) are similar yet slightly different, which implies that the estimated bending moment distribution may differ slightly for different peak frequencies. In this paper, as the bending moment distribution is considered proportional to the displacement (not the acceleration), the frequency at which the displacement spectrum peaks (i.e., 1.73 Hz) is used hereinafter. Figure 8(a3) shows the phase differences of MI and MJ with the relative acceleration in the Y-direction. The phase difference between MI and the relative acceleration was very stable at \(\pi\) around the peak frequencies, which indicates that they were almost proportional but with opposite signs. The phase difference of MJ was not as stable as that of MI, but the value was close to zero at the peak frequencies; this indicates that MJ and the displacement were also proportional. Figure 8(a4) shows the phase differences of MI and MJ with the relative acceleration in the X-direction. These plots show large scatter, which indicates that MI and MJ were not proportional to the displacement in the X-direction. These figures show that MI and MJ were mostly proportional to the relative displacement in the Y-direction but not to that in the X-direction. In addition, although the peak frequencies for the relative acceleration and relative displacement were different, the bending moment and local stiffness distributions did not change regardless of the peak frequency. Similarly, the axial force shown in Fig. 8b shows the same properties as the bending moment in Fig. 8a. Figure 8c shows the spectrum of the weak-axis bending moment; the phase difference in Fig. 8(c3) is not as stable as those in Fig. 8(a3) and (b3), but it is about 0 or π near the peak frequency. This indicates that the weak-axis bending moment of the beam also oscillated approximately in proportion to the displacement in the Y-direction. The above analysis indicates that not only the strong-axis bending moment but also the axial force and weak-axis bending moment are proportional to the displacement in the Y-direction. It is considered that the axial force was generated by the composite effect with the floor slab. The exact cause of the weak-axis bending cannot be determined using the data obtained in this study; however, given that the measured beams faced the outer wall, we can speculate that the unsymmetrical geometry of the slab and wall may have generated the weak-axis bending moment according to the strong-axis bending moment.

Fig. 8
figure 8

Time history and frequency characteristics of the section forces for RB

Full size image

To investigate the magnitude of stress due to the strong-axis bending moment, axial force, and weak-axis bending moment, Fig. 9 shows the strain distributions of the beam sections at a vibration frequency of 1.73 Hz. These were calculated from the values shown in Fig. 8a, b based on the Bernoulli–Euler theory. The values for the bending moment and axial force without parentheses are for the steel beam sections. The axial force value in parentheses is for the concrete floor slab, which was estimated using the effective width of the slab (1045 mm) as calculated from the design formula in the current Japanese design code [30]. Figure 9a shows that the steel beams were subjected to a considerable amount of axial force, which was undoubtedly the effect of the concrete slab. Thus, calculations of the bending moment of a composite beam including a concrete slab need to consider the effect of this axial force. It also shows that the estimated axial force of the concrete slab (984 N in I-section) was much smaller than that of the steel beam (2451 N), and the two forces were not balanced. This indicates that more axial force was transferred by the slab in the section measured under this small earthquake than estimated from the design formula. Figure 9b shows the estimated bending moment around the weak axis. In general, the bending moment along the weak axis was much less than that along the strong axis. For section I, the weak-axis bending moment was only 3% of the strong-axis bending moment. However, the maximum strain caused by the weak-axis bending moment (0.2 µ) was up to 11% of that caused by the strong-axis bending moment (1.71 µ). This indicates that the strain owing to the weak-axis bending moment should not be neglected even if this moment is small.

Fig. 9
figure 9

Estimated strain amplitude distribution in RB at the dominant frequency

Full size image

As described above, the axial force and weak-axis bending moment were observed in addition to the strong-axis bending moment. These forces are considered to be caused by the floor slabs attached to the beams and the inner and outer walls. RN and RY are two indices defined to represent the contributions of the axial force and weak-axis bending moment, respectively:

$$R_{N} = \frac{{\sigma_{{{\text{axial}}}} }}{{\sigma_{{{\text{axial}}}} + \sigma_{{{\text{bending}}}} }} = \frac{{\varepsilon_{{{\text{axial}}}} }}{{\varepsilon_{{{\text{axial}}}} + \varepsilon_{{{\text{bending}}}} }} = \frac{{\frac{{N_{s} }}{{A_{s} }}}}{{\frac{{N_{s} }}{{A_{s} }} + \frac{{M_{s} }}{{Z_{s} }}}}$$
(7)
$$R_{Y} = \frac{{\sigma_{{{\text{bending}},y}} }}{{\sigma_{{{\text{bending}},y}} + \sigma_{{{\text{bending}}}} }} = \frac{{\varepsilon_{{{\text{bending}},y}} }}{{\varepsilon_{{{\text{bending}},y}} + \varepsilon_{{{\text{bending}}}} }} = \frac{{\frac{{M_{sy} }}{{Z_{sy} }}}}{{\frac{{M_{sy} }}{{Z_{sy} }} + \frac{{M_{s} }}{{Z_{s} }}}}$$
(8)

Here, \(\sigma_{{{\text{axial}}}}\) and \(\sigma_{{{\text{bending}}}}\) are the stresses owing to the axial force and bending moment, respectively. The strains \(\varepsilon_{{{\text{axial}}}}\) and \(\varepsilon_{{{\text{bending}}}}\), corresponding to the axial force and bending moment, respectively, are proportional to \(\sigma_{{{\text{axial}}}}\) and \(\sigma_{{{\text{bending}}}}\) under the assumption that the material is in the elastic state. The value of \(R_{N}\) is between 0 and 1, where 0 indicates that the stress is only owing to the bending moment and 1 indicates that the stress is only owing to the axial force. When the stress in the floor slab increases, the stress in the beam element also increases, which in turn increases \(R_{N}\). For example, from Fig. 9, one can calculate \(R_{N}\) as 0.64/1.72 = 0.372 for section I. The estimated value according to the Japanese design code [30] and considering the slab’s effect is 0.242, which is less than the values in Fig. 9. This indicates that the slab’s effect is larger than expected.

3.1.4 Bending moment and axial force of columns

Figure 10 shows the time histories for the bending moment and axial force, the Fourier amplitude spectrum, and the phase spectrum of the LC. For the bending moments shown in Fig. 10a, the phases at the I- and J-sections of the column were opposite to each other; this indicates that the bending moment distribution was antisymmetric. In contrast, for the axial forces in Fig. 10b, the phases at the peak frequency were the same, suggesting that the axial force inside the column was constant. The phase of the axial force was also almost the opposite of that of the Y-direction acceleration, which indicates that the axial force vibration was proportional to the displacement vibration in the Y-direction (i.e., strong-axis bending direction). It is seen in Fig. 10c that the phase of the weak-axis bending moment almost matches that of the X-direction acceleration, indicating that the weak-axis bending moment of the column accompanies the vibration in the X-direction.

Fig. 10
figure 10

Time history and frequency characteristics of the section forces for the LC

Full size image

3.2 Local stiffness

3.2.1 Definition

As discussed in Sect. 3.1.1, the acceleration amplitude was obtained from the response acceleration recorded on RF. As discussed in Sect. 3.1.3, the axial force and bending moment amplitudes were obtained from the measurement cross-sections. The local stiffness can be obtained by dividing the stress amplitude (i.e., axial force amplitude or bending moment amplitude) by the displacement amplitude. Specifically, the local bending stiffness is calculated as follows:

$$K_{S,i} = \frac{{\hat{S}_{i} \left( {f_{{{\text{peak}}}} } \right)}}{{\hat{d}_{r} \left( {f_{{{\text{peak}}}} } \right)}},$$
(9)

where \(f_{{{\text{peak}}}}\) is the peak frequency in the relative displacement spectrum and \(\hat{S}_{i}\) is the amplitude of an internal section force at section i. \(\hat{d}_{r}\) is the Fourier transform of the displacement at RF:

$$\hat{d}_{r} \left( f \right) = \frac{{\hat{a}_{r} \left( f \right)}}{{4\pi^{2} f^{2} }},$$
(10)

where \(\hat{a}_{r} \left( f \right)\) is the Fourier transform at frequency f of \(a_{r} \left( t \right)\). For the internal section force Si, any section force can be used. In this study, the bending moment and axial force were used for the following calculations.

3.2.2 Bending moment distribution along the Y-direction

Equation (9) calculates the local bending stiffness for only a certain section, where the strain is measured. However, if the bending moment distribution is assumed to be linear over the entire length of the member, then the local bending stiffness is also linear over the entire length of the member. Therefore, the local bending stiffness can be calculated over the entire length of the member by linear interpolation and extrapolation.

For the local bending stiffness of the beam, the additional bending moment by the composite effect of the floor slab should be considered. Assuming that the observed axial force in the steel beam is balanced with that in the concrete floor slab, the bending moment of a beam is calculated as follows:

$$M = M_{s} + 409\,{\text{mm}} \times N_{s}$$
(11)

where 409 mm is the distance between the centroids of the steel beam section and concrete floor slab. This equation does not consider the bending moment in the slab section as its effect is small enough to be neglected.

Figure 11 shows the local stiffness distribution when calculated as explained above. The values represent the local stiffness at the beam and column ends extrapolated from the measured section data. The locations of the measured sections are indicated by the transversal lines in the diagram. The broken line in Fig. 11 shows the local bending stiffness distribution obtained from the structural calculations shown in Fig. 4.

Fig. 11
figure 11

Local stiffness distribution [kN-m/mm] of the bending moment in frame X2 measured during an earthquake that occurred at 2019-08-04T19:23+0900

Full size image

Because the local bending stiffness is proportional to the bending moment, the sum of the local bending stiffness values of the column and the sum of the local bending stiffness values of the beam should theoretically match at the beam–column joint. However, the sum of the measured values of the column was approximately 1.6 times that of the beam. Although the cause cannot be determined solely from the current measurement results, one hypothesis is that some unidentified members bore the stress in parallel to the beam. Figure 12 illustrates a very simple example of this hypothesis. For this measurement, the strain gauge was attached only to the two sections of the column and beam. Only the stress (axial force and bending moment) could be measured at these sections. For this reason, the stress at the beam–column joint was estimated by linearly extrapolating the stresses of the two cross sections. However, if some unidentified elements parallel to the beam also bore stresses (as shown in Fig. 12), then the stress would be transferred to the column but not captured by these measurements. As shown in Fig. 2d, the target building has autoclaved lightweight concrete panels attached outside the beams via vertical furring strips of H-section steel (H-100 × 100 × 6 × 8) at 800 mm intervals. These furring strips are quite rigid and may have transferred some stress to the columns.

Fig. 12
figure 12

Presumed cause of unbalanced local stiffness values for the beam and column

Full size image

3.2.3 Bending moment distribution along the X-direction

Figure 13 shows the local stiffness distribution calculated from the bending moment along the weak axis of the column. The amplitudes of the weak-axis bending moments for sections I and J (0.374 and 0.286 kN-m, respectively) at the dominant frequency in the X-direction (i.e., 1.86 Hz, as shown in Fig. 10c) were divided by the displacement amplitude (0.373 mm, as shown in Fig. 6b) to obtain the local stiffness values. These were then extrapolated to the edges of the column elements under the assumption of a linear distribution. The measured local stiffness was greater than the analytical value. In addition, the transmitted bending moment was larger than expected. The analytical results also indicated that the shear forces of the columns between 1 and 2F were in opposite directions; however, the measurement results did not indicate such a reversal of the shear force. One explanation is that the analysis assumed that the beam was pin-jointed to the column, such that the bending moment is not transmitted; however, some bending moment was indeed transmitted in the actual building.

Fig. 13
figure 13

Measured local stiffness distribution [kN-m/mm] in frame Y3 (X-direction loading)

Full size image

3.3 Amplitude dependency and long-term trends

3.3.1 Dominant frequency and mode shape

Figure 14a shows the dominant frequency and displacement amplitude for the 198 small earthquakes measured during the study period. The horizontal axis represents the pseudo-displacement amplitude obtained by Eq. (2). The solid line represents the regression straight line, although it appears as a curve, because the horizontal axis is logarithmic. CHG indicates the amount of change in the displayed regression line from start (left) to end (right); %CHG represents the ratio of the CHG value to the value of the regression line at the start (left); and R2 indicates the coefficient of determination (i.e., square of the correlation coefficient). The dominant frequency tended to decrease as the displacement amplitude increased. When the displacement amplitude was small, the dominant frequency was approximately 2.6 Hz. However, it decreased to approximately 1.8 Hz as the displacement amplitude increased. The coefficient of determination was approximately 0.27, which indicates a certain degree of correlation. The rate of change was approximately -34%; if the mass was constant and the dominant frequency was simply calculated as the square root of the change in stiffness, then the stiffness would have dropped by approximately half. Figure 14b shows the long-term changes in the dominant frequency over the entire measurement period. Although the variation is not small, the regression lines indicate a downward trend, with a coefficient of determination of 0.268 and 0.193 for the Y- and X-direction, respectively.

Fig. 14
figure 14

Dominant frequency

Full size image

To visualize the amplitude dependency of the mode shape, the ratio of the displacement amplitudes at 2F and RF is shown in Fig. 15a. For the Y-direction, although a slight downward trend is observed, many earthquakes show stable values between 0.37–0.38, which indicates that the structure vibrated in the primary mode shape obtained by analysis. Figure 15b shows the long-term changes in the mode shape. The coefficient of determination (shown as “R2” in the figures) is very small, and few long-term trends could be observed. This indicates that the mode shape hardly changed during the study period.

Fig. 15
figure 15

Mode shape

Full size image

3.3.2 Local stiffness for the bending moment

Figures 16a and 17a show the relationship between the response displacement amplitude at RF and the calculated local bending stiffness at the beam–column joints for all measured seismic responses. The solid line, CHG, %CHG, and R2 have the same meanings as for Figs. 14 and 15. The local stiffness of the beam was calculated with Eq. (2) to include the additional bending moment by the floor slab. As the displacement amplitude increased, the local bending stiffness tended to increase for the beams and decrease for the columns. The regression lines in Figs. 16a and 17a indicate that the ratio of the sum of the local bending stiffness values for UC and LC to the sum of those values for LB and RB was approximately 2.1 when the amplitude was small and 1.4 when the amplitude was large. This indicates that the difference between the local bending stiffness values of the beam and column decreased as the displacement amplitude increased. This may indicate that the effect of unidentified members parallel to the beam bearing some bending moment would decrease as the displacement increases. The average rate of decrease in the local bending stiffness of the columns was approximately -13%. This change is considerably smaller than the change in local stiffness estimated from the change in the dominant frequency, as mentioned in Sect. 3.3.1. This implies that the change in the dominant frequency did not occur only because of the change in the local bending stiffness of the columns. Another reason may be that the effective mass of nonstructural members and equipment contributed to building vibration changes, depending on the amplitude. However, the cause could not be determined within the scope of the measurements performed in this study; further detailed measurements are needed.

Fig. 16
figure 16

Ki values for bending moment of beams

Full size image
Fig. 17
figure 17

Ki values for bending moment of columns in the Y-direction

Full size image

Figures 16b and 17b show the long-term changes in the local bending stiffness of the beam and column at the beam–column joint. The coefficient of determination for the beams is less than 0.1, which indicates no clear correlation between the time and local stiffness of the beams. On the other hand, the coefficients of determination for the columns are approximately 0.27 and 0.13, which indicates a slight correlation. The change ratio was approximately 5%, corresponding to the decrease in the dominant frequency by approximately 2.5%. The estimated value was smaller than the observed value by 10%, as shown in Fig. 13. This result shows that column stiffness change may be a factor for the change in the dominant frequency but is not the only cause. Other causes may not have been captured by these measurements.

Figure 18 shows the amplitude dependency and long-term trend for the local stiffness of the bending moment along the weak axis of the column. Little correlation can be observed for the time and weak-axis bending moment with the column displacement.

Fig. 18
figure 18

Ki values for bending moment of columns in the X-direction

Full size image

3.3.3 Ratio between the moment and axial force

Figure 19 shows the amplitude dependency and long-term trend of RN. Figure 19(a1)–(a4) shows little amplitude dependency. Figure 19(b1) and (b2) shows a slight time dependency in the beams. Considering that the axial force in the beams is mainly owing to the effect of the floor slab, this trend may be attributed to any damage or aging of the floor slab. However, the reason why LB exhibits a decreasing tendency, while RB exhibits an increasing tendency cannot be explained. Therefore, further long-term observation is necessary. Figure 19(b3) and (b4) shows almost no dependency in the columns. These figures indicate that the ratio of the axial stress to the total stress has little dependency on the displacement amplitude, but there may be some time dependency in the beams.

Fig. 19
figure 19

RN values

Full size image

3.3.4 Ratio between the weak-axis and strong-axis bending moments

Figure 20 shows the amplitude dependency and long-term trend of RY. Figure 20(a1) and (a2) shows a strong relationship between RY and the displacement amplitude. Considering that the weak-axis bending moment may originate from walls, slabs, and other nonstructural elements, the amplitude dependency may also originate from such elements. The effect may decrease when the displacement amplitude increases. For small earthquakes, RY was as high as 0.5; however, RY decreased significantly for strong earthquakes. This indicates that the weak-axis bending moment is a less significant concern for structural integrity against stronger earthquakes. Figures 20(b1) and (b2) show a small and gradual variation over time, but R2 is smaller than 0.1 and the trend is not clear. A seasonal variation can be observed, wherein RY decreased during the summer; however, the study period was not long enough to clarify the reason. Continuous measurement is required to observe more long-term tendencies; however, the results of the current study indicate that RY does not have a strong time dependency.

Fig. 20
figure 20

RY values

Full size image

4 Conclusion

Structural monitoring has been used in actual buildings to estimate the natural frequency, damping, maximum inter-story deformation angle, and other phenomena. In many cases, the main measurement target is the acceleration response of the floors of the building. However, it is difficult to identify structural damage to individual structural elements from these indices. The strain is a physical quantity that can be directly measured to clarify the stress transmission mechanism, verify structural calculations, quantify the structural performance degradation due to deterioration or damage by earthquakes, and identify damaged parts. However, there have been few cases, where the strain has been measured for an actual building frame, and it is not clear whether strain measurements match the analytical calculations or whether they can be used to evaluate the structural performance. In this study, the dynamic strain of an actual building under small earthquakes was measured and used to evaluate the stress distribution, amplitude dependency, and long-term changes in the beams and columns.

The measurement results are presented for the motion of the largest earthquake. The measured dominant frequency was much greater than the result obtained analytically. However, the local stiffness based on the strain measurement coincided with the analytical value. The local stiffness directly indicates the stress transmission state of each structural element; therefore, the performance can be verified by continuously measuring and comparing the local stiffness with the analytical results. The dominant frequency, mode shape, amplitude dependency of the local stiffness, and temporal changes were investigated. For the dominant frequency, a clear dependency on the displacement amplitude was observed; the rate of change was approximately − 34%, whereas the maximum horizontal displacement observed on RF was approximately 0.018 m. If this change is attributed solely to the change in building stiffness, the stiffness should have decreased to half. However, the maximum decrease in the local stiffness of the column was approximately 16%, which is not large enough to account for the change in the dominant frequency. Therefore, the decrease in the dominant frequency was strongly influenced by factors other than the stiffness of the frame. For the beam–column joint, the sum of the local stiffness values of the columns was larger than that of the beams. Theoretically, the two values should match, so this result suggests that additional members such as slabs and walls may transmit stress to some extent. This difference decreased as the displacement amplitude increased, which indicates that the effect of such additional members decreased. For this building, rigid furring was joined to the beam and attached to the outer wall; this may have transmitted some stress and consequently reduced the stress amplitude of the beam under small earthquakes; this effect may decrease under stronger earthquakes.

Thus, the measured strain data were approximately consistent with the analysis results. Although there were some inconsistencies in the measurements of the amplitude dependency and long-term transitions, these could be attributed to the influence of slabs, walls, and other nonstructural members. Some of the fluctuations could be considered seasonal, but the measurement period was too short to determine the reason for this. Because there was no severe earthquake during the measurement period, the data presented in this paper corresponds to a condition, wherein the structural frame is not damaged. However, if a large earthquake occurs in the future, it will be possible to clarify whether damage has occurred through a comparison with these trends. To study the change in local stiffness of structural elements during severe earthquakes, the measurements need to continue and trends for longer periods need to be monitored. It is also necessary to perform similar strain measurements for various other buildings to investigate and improve the applicability of the results.