Skip to main content
SpringerLink
Log in

Far field geometric structures of 2D flows with localised vorticity

  • Published:
Mathematische Annalen Aims and scope Submit manuscript

Abstract

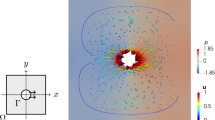
We show that 2D Navier–Stokes and Euler flows with localised vorticity always feature regular structures in the far field. The level lines of each component of the velocity, at large distances, tend to have the symmetries of a regular polygon: a digon if the total circulation is non-zero; a square for flows with zero total circulation and non-integrable velocity; an hexagon for flows with integrable velocity and, exceptionally, a polygon with more than six sides.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Ben-Artzi, M.: Global solutions of two-dimensional Navier–Stokes and Euler equations. Arch. Rational Mech. Anal. 128(4), 329–358 (1994)

    Article  MathSciNet  Google Scholar 

  2. Brandolese, L.: Space-time decay of Navier–Stokes flows invariant under rotations. Math. Ann. 329(4), 685–706 (2004)

    Article  MathSciNet  Google Scholar 

  3. Brandolese, L.: Concentration–diffusion effects in viscous incompressible flows. Indiana Univ. Math. J. 58(2), 789–806 (2009)

    Article  MathSciNet  Google Scholar 

  4. Brandolese, L.: Hexagonal structures in 2D Navier–Stokes flows. https://hal.archives-ouvertes.fr/hal-03125332/document, (2021)

  5. Brandolese, L., Vigneron, F.: New asymptotic profiles of nonstationary solutions of the Navier–Stokes system. J. Math. Pures Appl. (9) 88(1), 64–86 (2007)

    Article  MathSciNet  Google Scholar 

  6. Brezis, H.: Remarks on the preceding paper by M. Ben-Artzi: “Global solutions of two-dimensional Navier–Stokes and Euler equations”. Arch. Rational Mech. Anal. 128(4), 329–358 (1994). [Arch. Rational Mech. Anal. 128(4), 359–360 (1994)]

  7. Carlen, E.A., Loss, M.l: Optimal smoothing and decay estimates for viscously damped conservation laws, with applications to the \(2\)-D Navier–Stokes equation. Duke Math. J. (1995) 81(1), 135–157 (1996)

  8. Duoandikoetxea, J., Zuazua, E.: Moments, masses de Dirac et décomposition de fonctions. C. R. Acad. Sci. Paris Sér. I Math 315(6), 693–698 (1992)

    MathSciNet  MATH  Google Scholar 

  9. Gamblin, P., Iftimie, D., Sideris, T.: On the evolution of compactly supported planar vorticity. Comm. Part. Diff. Eq. 24(9–10), 1709–1730 (1999)

    MathSciNet  MATH  Google Scholar 

  10. Giga, Y., Miyakawa, T., Osada, H.: Two-dimensional Navier–Stokes flow with measures as initial vorticity. Arch. Rational Mech. Anal. 104(3), 223–250 (1988)

    Article  MathSciNet  Google Scholar 

  11. Kato, T.: The Navier–Stokes equation for an incompressible fluid in \({ R}^2\) with a measure as the initial vorticity. Differ. Integral Equ. 7(3–4), 949–966 (1994)

    MATH  Google Scholar 

  12. Kukavica, I., Reis, E.: Asymptotic expansion for solutions of the Navier–Stokes equations with potential forces. J. Differ. Equ. 250(1), 607–622 (2011)

    Article  MathSciNet  Google Scholar 

  13. Lemarié-Rieusset, P. G.: Recent developments in the Navier–Stokes problem. Chapman & Hall/CRC Research Notes in Mathematics, 431, Chapman & Hall/CRC, Boca Raton, FL, xiv+395 (2002)

  14. Majda, A.J., Bertozzi, A.L.: Vorticity and Incompressible Flow. Cambridge Texts in Applied Mathematics, 27, Cambridge University Press, Cambridge, xii+545 (2002)

  15. Marshall, J.S.: Inviscid Incompressible Flows. Wiley, New York (2001). ISBN 0-471-37566-7

    Google Scholar 

  16. McOwen, R., Topalov, P.: Spatial asymptotic expansions in the incompressible Euler equation. Geom. Funct. Anal. 27(3), 637–675 (2017)

    Article  MathSciNet  Google Scholar 

  17. McOwen, R., Topalov, P.: Perfect fluid flows in \(\mathbb{R}^d\) with growth/decay conditions at infinity (2021). arXiv:2102.05622

  18. Sultan, S., Topalov, P.: On the asymptotic behavior of solutions of the 2d Euler equation. J. Differ. Equ. 269(6), 5280–5337 (2020)

    Article  MathSciNet  Google Scholar 

  19. Xu, Y.: Orthogonal polynomial of several variables. arXiv:1701.02709 (2017)

Download references

Acknowledgements

The author would like to thank the referees for their careful reading and useful remarks. Their suggestions are incorporated in the present version.

Author information

Authors and Affiliations

  1. Institut Camille Jordan, Université de Lyon, Université Lyon 1, 43 bd. du 11 Novembre, 69622, Villeurbanne Cedex, France

    Lorenzo Brandolese

Authors
  1. Lorenzo Brandolese
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lorenzo Brandolese.

Ethics declarations

Data availability statement

The present paper has no associated data.

Additional information

Communicated by Y. Giga.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Brandolese, L. Far field geometric structures of 2D flows with localised vorticity. Math. Ann. 383, 699–714 (2022). https://doi.org/10.1007/s00208-021-02177-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00208-021-02177-8

Search

Navigation