Introduction

Graphene has emerged as a promising platform for developing alternative electronic devices with higher performance and even microelectronics because of its exceptional properties such as high intrinsic mobility, high electrical conductivity, and ballistic transport at micron scales under ambient temperatures1. Great progress has been made in developing functional devices such as Dirac fermion microscopes, electron waveguides, splitters and inductors both theoretically2,3, and experimentally4,5,6,7,8,9. Graphene ballistic electrons bear a close analogy to light since they share a linear dispersion relation. This similarity has inspired the development of quantum electron optics in graphene by applying enlightening ideas in optics to two-dimensional materials. The behaviours of graphene electrons and light can be understood within the same theoretical framework10,11,12, and similar phenomena13,14 can be observed experimentally. Over the past decades, metaoptics has attracted tremendous interest owing to the extraordinary phenomena that are not available in naturally occurring materials15,16,17,18,19. Extending these manipulation methods to graphene is natural because it is a promising candidate for breaking the limitation of conventional electron manipulation methods, as has been done in optics. Negative refraction, a peculiar behaviour in optical metamaterials, has been reported in graphene theoretically20 and experimentally21,22 with the demonstration of a Dirac fermion Veselago lens. However, metagratings for Dirac fermions have not yet been studied. Metagratings have exhibited great application potential in beam steering23,24,25,26,27 and metaholography28,29 by guiding light to the desired diffraction order. In this paper a Dirac fermion metagrating is illustrated with the extraordinary wave beam manipulation abilities, theoretically realized by a linear array of gate-bias-controlled quantum dots (QDs).

The metagrating channels electron waves into the -1st-order transmission direction and thus enables the arbitrary large-angle beam deflection. Steering electron beams to an arbitrary large deflection angle remains a challenge in graphene. This can be partly attributed to the Klein tunnelling which is one of the characteristic features of ballistic electrons in graphene30. Near-normal-incidence electrons can pass through arbitrarily high potential barriers with no damping by undergoing a transition between electron-like and hole-like states. This rules out all possibilities of reflecting electron waves at the near-normal incidence and hence hinders the large-angle deflection of reflected electron beams. Opening a complete bandgap, explored both in theory31,32,33,34 and experiments35, is one of the options to break this limitation. However, one has to take on the risk of loss of high intrinsic mobility of electrons, which is an advantage of graphene over conventional semiconductor materials. Another option demonstrated experimentally is to manipulate electron waves at the neutrality point where the conductivity drops with a power-law temperature dependence36. However, the operating bandwidth is restricted to only the Dirac point with the requirement of extremely low temperatures. In addition, a bent waveguide was proposed theoretically. Only when the deflection angle is below 120° can high-efficiency deflection be attainable37. In addition to the limited deflection angle, a smooth and sufficiently long transition region is required in such a waveguide to ensure high transmission through the bends, which prevents downsizing of electron units. In contrast to these approaches, the metagrating steers electron beams without the requirement of opening a complete bandgap or extremely low temperatures and simultaneously caters to the desire for miniaturization.

The metagrating eliminates the dependency on reflection and produces abrupt changes in the electron propagation direction by transmission at a negative angle. This means that the transmitted wave lies on the same side of the normal as the incident wave. Compared with conventional reflection, negative transmission avoids the Klein tunnelling, which comes into play for reflection. This is achieved when the induced particular electron whispering-gallery modes (WGM) within the QDs under the strong inter-QD interaction focus the scattering fields of the QDs into the negative-transmission direction. Recently, electron WGMs in graphene has received special attention in experimental research38,39,40,41,42 on quasi-bound states where the electrons are predicted to be able to be trapped for a finite time43,44,45,46. Unlike these works, we focus on their radiative properties. These WGMs do not radiate electrons in the ordinary and -1st-order reflection directions at the arbitrary incidence and thus enable perfect large-angle beam deflection along the -1st-order transmission direction.

Results and discussion

Perfect large-angle beam deflection

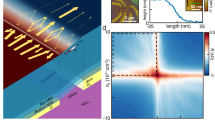
QDs are circular potential steps that can be tuned by applying a desired bias. The steps are smooth on the scale of the lattice constant of graphene such that the intervalley scattering is neglected and the low-energy electron dynamics can be described by the single-valley Hamiltonian46,47,48,49,50,51,52

$$H=-i\nabla \sigma +V{{\Theta }}({R}_{s}-r),$$
(1)

where Θ(Rs − r) is the Heaviside step function, Rs is the radius of the circular QD, V is the bias and σ = (σx, σy) are Pauli matrices. We use reduced units with ℏ = 1 and a Fermi velocity vF = 1. At the same time, the steps are sharp on the scale of the de Broglie wavelength. The transition of potentials from the background to the QDs occurs over a distance ΔRs. This distance should be smaller than 0.5Rs to ensure that the scattering behaviour can be well approximated by the step function53. The electron scattering problem of such a single QD can be rigorously calculated by the Mie scattering method46,51,52 which helps predict the excited WGMs in experiments54. Strong inter-QD interactions may occur in a linear QD array and dramatically alter the WGMs and thus electron scattering behaviour of QDs. Consequently, the array produces negative transmission with the distribution probability of the scattered electrons concentrated primarily in the -1st-order transmission direction. The configuration of the linear array and the propagation of the electron wave are schematically shown in Fig. 1a, where the blue circular dots represent the QDs and the angle θWA is the angle made by the incident wave with the linear array. Figure 1b shows the phase diagram of the -1st-order transmittance versus the bias V applied on the QDs and the angle θWA in reduced units with fixed incident-electron energy E = 0.8. The QD radius is Rs = 1 and the quantities with dimensions of length, including the lattice constant and wavelength, are in units of Rs, namely, wavelength λ = 2πRs/0.8 and lattice constant \(d=\lambda /(2\cos {\theta }_{WA})\). Note that the lattice constant varies with θWA (as in Figs. 1b and 2) such that the metagratings only support the zeroth and -1st diffraction orders, and simultaneously, the angle of transmission into the -1st diffraction order equals the angle of incidence. Thus once Rs is known in real units, the incident-electron energy in real units can be achieved by E = 0.8ℏvF/Rs. Moreover, according to the definition of “refractive index” N = (V − E)/E, the bias is V = (1 + N)E. Our calculation for multiple QD systems exploits rigorous multiple-scattering theory12,55 (“Methods”), which takes into account the interaction between all the QDs, not just the neighbour interactions. By controlling the QD bias V, negative transmission with unity efficiency can be achieved for θWA ranging from 0° to 45°, which corresponds to a perfect wide-angle deflection from 90° to nearly 180°. Figure 2 presents the bending of Gaussian beams at three different angles θWA, simulated by using nanoscale QDs. Very recently, such nanoscale QDs with atomically sharp boundaries have been obtained in experiments56,57,58. The fabrication techniques of high-precision QDs54,56,57,58 make it possible to demonstrate negative transmission in experiments.

Fig. 1: The -1st-order transmittance.
figure 1

a Schematic view of the abrupt change in the propagation direction of the electron beam by a metagrating realized by a one-dimensional array of quantum dots on graphene. b Phase diagram of the -1st-order transmittance as a function of the bias applied on the QDs and angle θWA between the incident wave and the array. The calculation assumes QDs with radius Rs = 1 and incident energy E = 0.8, in reduced units. The bias V is controllable in practical applications. The black dotted line indicates unity efficiency.

Full size image
Fig. 2: Simulation of negative transmission.
figure 2

Negative-transmission-based deflection of electron beams at (a) θWA = 5°, (b) θWA = 20°, and (c) θWA = 45°. The bias and the lattice spacing are (a) V = 977 meV and d = 14 nm, (b) V = 970 meV and d = 15 nm, and (c) V = 940 meV and d = 20 nm. In all the cases, the QD radius is Rs = 3.5 nm and the incident electrons have a fixed energy E = 148 meV. The Gaussian beam has a waist radius w = 3λ.

Full size image

The role of WGM in beam deflection

Obviously, the theory for bulk materials is not appropriate for a linear QD array. We thus have to turn our attention to individual QDs, which play a crucial role in negative transmission. To this end, we investigate the modes excited in a QD in the presence of other QDs. Due to the inter-QD coupling interaction, this case differs significantly from the case of an isolated QD. We use Mie scattering theory to analyse the modes because its expansion terms correspond one-to-one with the various modes. The scattered field is expressed as

$$\begin{array}{lll}{\psi }_{s}&=&\left(\begin{array}{l}{\psi }_{s}^{A}\\ {\psi }_{s}^{B}\end{array}\right)\\ &=&\frac{1}{\sqrt{2}}\mathop{\sum }\limits_{n=-\infty }^{+\infty }{i}^{n+1}{a}_{n}\left(\begin{array}{l}-i{H}_{n}^{(1)}({k}_{0}r){e}^{in\phi }\\ \alpha {H}_{n+1}^{(1)}({k}_{0}r){e}^{i(n+1)\phi }\end{array}\right)\end{array}$$
(2)

where an is the scattering-field coefficient in the nth angular-momentum channel, α is the “band index”, and Jn and \({H}_{n}^{(1)}\) are the nth order Bessel function and Hankel function of the first kind, respectively. The band index in the background is α = sgn(E) and in the QD region is \(\alpha ^{\prime}\) = sgn(E − V). Applying the reduced units, the wavenumbers in the two regions are k0 = αE and ks = \(\alpha ^{\prime} (E-V)\). In this work, the QD radius is much less than the electron wavelength. The dominant scattering contributions come from the isotropic monopole, dipole, and quadrupole modes, corresponding to the terms n = 0, n = ± 1 and n = ± 2, respectively.

For an isolated QD, the scattering coefficients follow a−n = an−1 and a−n ≠ an. This is different from an isolated isotropic homogeneous dielectric rod in electromagnetism, for which a−n = an. a−1 and a1 correspond to clockwise and counterclockwise circular dipole modes, respectively, and their interaction in a dielectric rod leads to a linear-oscillating dipole mode due to a−1 = a1. Clearly, a linear dipole mode cannot be induced in an isolated QD. However, the inter-QD coupling significantly alters the symmetry of the scattering coefficients, with the relation a−n ≠ an−1. Figure 3 illustrates ∣an∣ for a QD in an array for unity efficiency cases [black dotted line in Fig. 1b] at a deflection angle ranging from 90° to 180°. We can see that a1 = a−1 when 0° < θWA < 20°. Thus, the output will be a standard dipole mode. Meanwhile, the impact of the isotropic mode related to a0 gradually increases with increasing θWA, although, its contribution is much less than that of the dipole mode for θWA < 20°. The coefficient a−2, which represents a quadrupole mode, is nearly zero for θWA < 20°. As a result, the total scattering field from a QD in the linear QD array, calculated on a circle of radius ρ = 60 and in a square region at θWA = 5° (20°), exhibits clear linear-oscillating dipolar characteristics [see Fig. 4a, b (Fig. 4c, d), respectively].

Fig. 3: Contribution from different multipole modes.
figure 3

Scattering coefficients of a QD for the four dominant angular-momentum channels as a function of θWA. The contribution from other angular momentum channels is negligible. The channels n = −2, n = − 1 (n = 1) and n = 0 correspond to circular quadrupole, circular dipole, and isotropic modes, respectively. The QD is located in a linear array and inter-QD coupling is considered.

Full size image
Fig. 4: Scattering from a QD in a linear array.
figure 4

a ∣Re\(\{{\psi }_{s}^{A}\}|\) around a circle with radius ρ = 60, and (b) Re\(\{{\psi }_{s}^{A}\}\) in a square region for θWA = 5°. Re\(\{{\psi }_{s}^{A}\}\) is the real part of the first spinor component [see Eq. (2)] of the field scattered by a QD located in the linear array. c, d [(e) and (f)] correspond to θWA = 20° (θWA = 45°). In the ordinary and -1st-order reflection directions, Re\(\{{\psi }_{s}^{A}\}\) is zero, which leads to the disappearance of the two diffraction orders. This is also the case at θWA = 5° (see Supplementary Fig. 1). The scattered fields are calculated for the QD located at the origin of the coordinates. The presence of many QDs in (b), (d) and (f) implies that inter-QD coupling has been considered.

Full size image

However, even though the linear dipole mode excited at θWA = 5° is nearly standard, with a−1 = a1, its radiation is not ordinary. First, it propagates transversely to the incident wave. However, in electromagnetism, it generally propagates parallel to the incident direction. Second, its radiation field has a definite and interesting phase relation with the radiation field obtained from the isotropic mode. The comparison between Fig. 5a, b shows that the scattering components of both modes are in phase and strengthen each other on the transmission side, whereas they are out of phase and interfere destructively on the reflection side. Accordingly, the total scattering probability is enhanced and spans the entire transmission region. However, it becomes weaker and more confined to the centre of the reflection region as θWA increases. Although the radiation from the isotropic mode is much weaker than that from the linear dipole mode, the superposition of them makes the total scattering probability zero, especially in the directions of the ordinary and -1st-order reflection indicated in Fig. 4a, c by arrows R0 and R−1, respectively. The null scattering probability in the two directions at θWA = 5° is also explicitly illustrated in Supplementary Fig. 1 in Supplementary Note 1. As a result, the ordinary and -1st-order reflections do not appear because they arise from the interference between scattering from all QDs.

Fig. 5: Elimination of the ordinary and -1st-order reflections at θWA = 5° and 45°.
figure 5

The scattered field distribution contributed (a) by the channel n = 0 correspondings to an isotropic mode and (b) by the channels n = − 1 and 1 corresponding to a standard dipole mode at θWA = 5°. The scattered field distribution contributed (c) by the channels n = −2 and −1 and (d) by the channels n = 0 and 1 at θWA = 45°. The calculation is performed for the same QD with the inter-QD interaction considered as in Fig. 4. Ki and R0 denote the incident and ordinary reflection directions, respectively.

Full size image

When θWA > 20°, a0 and a−2 begin to play more important roles. At θWA = 45°, the scattering on the reflection side remains well suppressed, and the scattering probability nearly vanishes, as shown in Fig. 4e, f. This can be understood as resulting from the interaction between the four modes. Considering that ∣a−2∣ is nearly equal to ∣a−1∣, as are ∣a0∣ and ∣a1∣, at θWA = 45°, as shown in Fig. 3, we give the scattering contributed by a−2 and a−1 in Fig. 5c and that by a0 and a1 in Fig. 5d. The phases of the fields in Fig. 5c, d are compared at two points selected arbitrarily in the ordinary and -1st-order reflection directions. This figure shows that they are always out of phase and have nearly the same amplitude and thus will interfere destructively with each other, which means that the ordinary and -1st-order reflections are not supported by the linear array. Consequently, the metagrating does not support the ordinary and -1st-order reflection for arbitrary θWA between 0° and 45°.

Moreover, the propagation probabilities in the ordinary transmission direction are also inhibited in this range of incident angles. The ordinary transmission is the superposition of the incident wave and the total scattered wave and differs from the diffraction in all the other diffraction orders, which are only determined by the total scattered wave. The null propagation probability in this direction arises from the destructive interference owing to the opposite phases of the incident and scattered waves (see Supplementary Fig. 2 in Supplementary Note 2). Consequently, neither ordinary reflection and transmission nor -1st-order reflection are supported by the metagrating. Therefore, the unique nonzero propagation probability appears in the -1st-order transmission direction. This leads to negative transmission and large-angle deflection of the incident electron beam.

Despite the details of the interaction between the four scattering coefficients, direct and deep insight into the beam deflection can be gained from the resultant WGMs within the QDs. As shown in Fig. 4b, d, f, the WGM is similar to a standard dipole when θWA approaches zero, then becomes asymmetric with increasing θWA, and finally turns into a rainbow-like mode near 45°. For the cases of near-zero θWA, the standard dipole mode in Fig. 4b does not radiate electrons into the ordinary and -1st-order reflection directions which are nearly parallel to the linear array. The WGM evolves into a rainbow-like mode on the transmission side, completely suppressing the radiation on the reflection side, near 45°, although the two reflected diffraction orders are very close to the vertical line of the particle array. Meanwhile, the WGMs can always give rise to radiation into the ordinary transmitted order, which is out of phase with the incident wave and these waves cancel each other at arbitrary incidence. The WGMs produce full inhibition of the other diffraction orders and enable the metagratings to realize perfect negative transmission into the -1st transmitted diffraction order. This implies that the WGMs, the localized nature of the metagrating, are the underlying physics behind the negative transmission. In addition, what WGMs are excited in the scattering process depends on the dimension of the QDs, the applied bias, the spacing and the wavelength, not on the shape of the QDs. Therefore it is not necessary to fabricate circular QDs in experiments. A striking example is that negative transmission has been obtained not only by circular rods but also by square rods in optics17. Negative transmission is also to some extent robust against the structure disorder (see Supplementary Fig. 3 in Supplementary Note 3).

Merits of metagrating-based beam deflection

Note that we actually obtain sharp changes in the direction of electron propagation by using the metagrating. First, the linear QD array is only one-QD-diameter thick, which is less than the electron wavelength. In Fig. 2, the wavelength of electrons (27.9 nm) is nearly four times the diameter (2Rs = 7 nm) of the QDs. Second, the transition distance necessary for high transmission (a larger bend radius than the wavelength) in bent waveguides becomes dispensable since the electron beam is bent immediately after passing through the QD array. In addition, the opening of a bandgap in graphene requires a structure thicker than the wavelength. Therefore, we use a subwavelength structure to realize the bending of electron waves. The electron beam indeed undergoes a drastic change in the propagation direction, namely, a sharp bend.

In the simulation, we assumed that graphene is suspended in a vacuum or air. In actual experiments, graphene is usually supported on a substrate, and the impacts of the substrate on the electrical properties of graphene must be considered. Therefore, we should give preference to the substrate that has as little impact as possible on graphene mobility. To this end, a substrate with a larger dielectric constant, such as HfO2, is preferred.

In summary, we illustrate a Dirac fermion metagrating that enables the deflection of electron beams in graphene at a near-180° angle with unity efficiency by engineering the incident electrons into the -1st-order transmission direction. The mechanism based on transmission rather than reflection breaks the restriction of Klein tunnelling and avoids the possible loss of the high intrinsic mobility of electrons in graphene due to the opening of a complete bandgap. The extraordinary capabilities of the linear arrays benefit from the excitation of various whispering gallery modes. The deflection occurs over a distance much smaller than electron wavelengths and no transition distance is required. Such an approach may be used to fabricate compact graphene devices with dramatically improved integration based on the abrupt change in the propagation direction. The one-dimensional design also allows precise control over the performance of individual QDs and the spacing between them. Finally, by controlling the bias applied to the QDs, unity efficiency can be ensured for a wide range of deflection angles.

Methods

Mie scattering method

Firstly, we solve the scattering problem of a single gate-controlled QD based on Mie scattering method in graphene46,51,52. The incident and scattered waves are expanded as follows:

$${\psi }_{in}=\frac{1}{\sqrt{2}}\mathop{\sum }\limits_{m=-\infty }^{+\infty }{i}^{m+1}\left(\begin{array}{l}-i{p}_{m}^{A}{J}_{m}({k}_{0}r){e}^{im\phi }\\ \alpha {p}_{m}^{B}{J}_{m+1}({k}_{0}r){e}^{i(m+1)\phi }\end{array}\right),$$
(3)
$${\psi }_{s}=\frac{1}{\sqrt{2}}\mathop{\sum }\limits_{m=-\infty }^{+\infty }{a}_{m}{i}^{m+1}\left(\begin{array}{l}-i{H}_{m}^{(1)}({k}_{0}r){e}^{im\phi }\\ \alpha {H}_{m+1}^{(1)}({k}_{0}r){e}^{i(m+1)\phi }\end{array}\right),$$
(4)

where m is an integer angular momentum quantum number, \({p}_{m}^{A}={e}^{-i(m+\frac{1}{2}){\phi }_{inc}}\), \({p}_{m}^{B}={e}^{-i(m-\frac{1}{2}){\phi }_{inc}}\), Jm and \({H}_{m}^{(1)}\) are, respectively, the mth order Bessel function and Hankel function of the first kind, ϕinc is the incident angle. Similarly, the inner field inside the dot can be written as

$${\psi }^{ins}=\frac{1}{\sqrt{2}}\mathop{\sum }\limits_{m=-\infty }^{+\infty }{d}_{m}{i}^{m+1}\left(\begin{array}{l}-i{J}_{m}({k}_{s}r){e}^{im\phi }\\ \alpha ^{\prime} {J}_{m+1}({k}_{s}r){e}^{i(m+1)\phi }\end{array}\right),$$
(5)

where k0 and ks are respectively the wave vector in the background region and the QD, the index α = 1 represents the conduction band and \(\alpha ^{\prime} =-1\) represents the valence band, and ks = Nk0 with the refractive index N = ∣V − E∣/E. After imposing the boundary condition at the surface of the QD with its radius Rs, the size parameter ρ = k0Rs is introduced and the scattering coefficient am is given

$${a}_{m}=-\frac{{J}_{m}(\rho ){J}_{m+1}(N\rho ){p}_{m}^{A}-\alpha \alpha ^{\prime} {J}_{m+1}(\rho ){J}_{m}(N\rho ){p}_{m}^{B}}{{J}_{m+1}(N\rho ){H}_{m}^{(1)}(\rho )-\alpha \alpha ^{\prime} {J}_{m}(N\rho ){H}_{m+1}^{(1)}(\rho )},$$
(6)
$${a}_{-m}=-\frac{{J}_{m}(\rho ){J}_{m-1}(N\rho ){p}_{-m}^{A}-\alpha \alpha ^{\prime} {J}_{m-1}(\rho ){J}_{m}(N\rho ){p}_{-m}^{B}}{{J}_{m-1}(N\rho ){H}_{m}^{(1)}(\rho )-\alpha \alpha ^{\prime} {J}_{m}(N\rho ){H}_{m-1}^{(1)}(\rho )}.$$
(7)

The relation between the scattering coefficients a and the incident coefficients \(\left(\begin{array}{c}{p}^{A}\\ {p}^{B}\\ \end{array}\right)\) in Eqs. (6) and (7) can also be expressed as a = Sp by a scattering matrix S.

Multiple scattering method

In a linear QD array, the incident wave that strikes the surface of QD j consists of two parts: (1) the initial incident wave \({\psi }_{inc}^{0}(j)\) and (2) the scattered waves of all other QDs according to multiple scattering theory12,55 (also known in solid-state physics as the K.K.R. method59,60). Thus it can be written as

$${\psi }_{inc}(j)={\psi }_{inc}^{0}(j)+\sum _{l\ne j}{\psi }_{s}(l).$$
(8)

By the translational addition theorem, the scattered wave from any other potential l (with l ≠ j) can be expanded as follows,

$$\begin{array}{lll}{\psi }_{s}(l)&=&\frac{1}{\sqrt{2}}\mathop{\sum }\limits_{n=-\infty }^{+\infty }{a}_{n}^{(l)}{i}^{n+1}\left(\begin{array}{l}-i{H}_{n}^{(1)}({k}_{0}r){e}^{in\phi }\\ \alpha {H}_{n+1}^{(1)}({k}_{0}r){e}^{i(n+1)\phi }\end{array}\right)\\ &=&\frac{1}{\sqrt{2}}\mathop{\sum }\limits_{m=-\infty }^{+\infty }{i}^{m+1}\left(\begin{array}{l}-i{p}_{m}^{(l,j)}{J}_{m}({k}_{0}r){e}^{im\phi }\\ \alpha {p}_{m}^{(l,j)}{J}_{m+1}({k}_{0}r){e}^{i(m+1)\phi }\end{array}\right),\end{array}$$
(9)

where

$${p}_{m}^{(l,j)}=\sum _{n}{i}^{(m-n)}{H}_{m-n}^{(1)}(k{d}_{lj}){e}^{-i(m-n){\phi }_{lj}}{a}_{n}^{(l)},$$
(10)

and dlj = dljcos\({\phi }_{lj}{\hat{e}}_{x}\)+dljsin\({\phi }_{lj}{\hat{e}}_{y}\) is the vector extending from the centre of QD l to that of QD j. In the main text, the linear QD array is placed along the x axis, so the angle θWA between the incident wave and the array equals the angle of incidence ϕinc.

Substituting (9) into Eq. (6) and a(j) = Sp(j), one will yield a set of linear equations that contains the iterative scattering coefficients. In our practical numerical calculation, the series expansion was truncated at some n = nc. With the equations, we can compute the scattering field at any position and the transmittance(reflectivity) of any order diffraction wave. To ensure the accuracy of the results in our paper, the minimum nc should be larger than 2. Physically, the minimum nc is determined by the wavelength, the radius of the QD and the bias voltage applied to the QD. The larger the ratio of the radius to wavelength or the bias voltage is, the larger the minimum nc is.

In a linear QD array placed along the x direction, the transmittance in the vth transmitted order can be expressed as

$${T}_{v}=| {t}_{v}{| }^{2}=| \frac{2{a}_{m}^{(0)}}{d{k}_{yv}}\mathop{\sum }\limits_{m=-\infty }^{+\infty }\frac{{({k}_{xv}+i{k}_{yv})}^{m+\frac{1}{2}}}{{k}^{m+\frac{1}{2}}}+{\delta }_{v0}{| }^{2}$$
(11)

where d is the separation between adjacent QDs, kxv and kyv respectively denote the propagation constants in the x and y directions with kxv = kx + 2πv/d, \({k}_{yv}=\sqrt{{k}^{2}-{k}_{xv}^{2}}\) for \({k}^{2}\ge {k}_{xv}^{2}\).