1 Introduction

In recent years, with the gradual popularization of wireless sensor technology, smart environment sensing-based applications [1–4] have gradually become an indispensable part of people’s daily life, and the wireless sensing technology [5–9] has been widely used in the places where people gather, such as shopping malls and airports.

Extracting parameters of information contained in wireless signal accurately is the basis of human detection, behavior recognition, and other applications [10–15]. The existing parameter estimation algorithms mainly include parameter estimation algorithm based on subspace decomposition [16, 17] and maximum likelihood estimation [18]. Schmidt proposed multiple signal classification (MUSIC) [19] algorithm, which decomposes wireless signal into signal subspace and noise subspace by eigen decomposition and estimates the angle of arrival (AoA) by using the orthogonality of signal subspace and noise subspace. Wang et al. estimated the AoA and then trained the AoA estimation results by using neural network to realize target localization [20]. Chen et al. proposed channel state information (CSI) forward/backward smoothing algorithm to improve the performance of AoA estimation, which effectively alleviates the decline of AoA estimation accuracy under low signal-noise ratio (SNR) and can obtain higher localization accuracy [21]. However, when two or more targets are in the same incident direction, the AoA parameter estimation algorithm mentioned above cannot separate multiple signals, resulting in misjudgment. Therefore, some scholars improve the classic algorithms, such as MUSIC, and estimate AoA and time of flight (ToF) or Doppler frequency shift (DFS) parameters jointly, so that when the AoAs of multiple targets are close, the target can be distinguished by other parameters. Li et al. used CSI information to construct CSI image, which contains AoA, ToF, and amplitude information, and then put the image into convolutional neural network (CNN) for training to locate the target [22]. Xu et al. combined received signal strength (RSS), AoA, and time of arrival (ToA) to achieve single static target location [23]. Xu et al. proposed a 3D joint parameter estimation algorithm, which uses the time difference of arrival (TDoA) and AoA of three receivers to locate the target in non-line-of-sight (NLOS) scene [24]. By improving the expectation maximization (EM) algorithm, the space alternating generalized expectation maximization (SAGE) algorithm proposed in widar2.0 [25] can estimate AoA, ToF, DFS, and signal amplitude, and its parameter estimation accuracy can reach Cramer-Rao lower bound (CRLB) in theory. However, the SAGE algorithm depends on the selection of initial value and estimates each parameter separately, which easily makes the parameter estimation result fall into the local optimal value and affects the parameter estimation accuracy. Moreover, in order to improve the accuracy of parameter estimation, the SAGE algorithm needs to go through and compare the value of each parameter to find the parameters which are closest to the true value. In addition, the SAGE algorithm needs to iterate continuously to improve the accuracy of parameter estimation, which leads to the high computational complexity. Bazzi et al. proposed a deterministic maximum likelihood estimation algorithm based on the SAGE algorithm [26], which introduces three JADE estimators to the partially relaxed model, namely a deterministic maximum likelihood, a weighted subspace fitting, and a covariance fitting estimator to estimate parameters, but this method also has some problems such as local convergence. Whether AoA is estimated alone or AoA, ToF, and other parameters are estimated jointly, the receiving antenna array must satisfy the spatial sampling theorem; otherwise, there will be more false peaks in the estimation results, which will lead to misjudgment. However, most of the existing algorithms for parameter estimation are based on the uniform linear array or uniform plane array which satisfies the spatial sampling theorem. Therefore, the existing parameter estimation algorithms cannot accurately estimate the parameters of the wireless signal received by the service antenna array, which does not meet the spatial sampling theorem.

For service antenna array, in order to achieve spatial diversity and reduce the interference between antennas in the communication process, the spacing between array antennas is set to be larger and does not satisfy the spatial sampling theorem. If the existing parameter estimation method is used to estimate the signal parameters, there will be more pseudo peaks in the estimation results, and the correct signal parameters cannot be obtained. However, for the sparse array with antenna spacing greater than half wavelength, some existing researches use the matrix filling theory to fill the sparse array [27], recover the signal received by the sparse array into the complete array received signal, and then estimate the parameter of the received signal by the whole array to achieve accurate target AoA estimation. But the matrix filling theory requires that the matrix is of low rank. Only when the dimension of the matrix, the number of rows and columns of the objective matrix, and the rank of the objective matrix satisfy m>lr(n1+n2−r), [27] where m is the number of known array elements, n1 and n2 are the number of rows and columns of the objective matrix, r is the rank of the target matrix, and l is a constant, the target signal can be recovered accurately by using the matrix filling theory. For the service antenna array, when the MUSIC algorithm is used to estimate the parameters of the signal received by the array, the matrix of the array must be full rank, that is, r= max{n1,n2} ; therefore, lr(n1+n2−r)=l× max{n1,n2}× min{n1,n2}=l×n1n2, m is the number of known array elements and n1 and n2 are the number of rows and columns of the objective matrix, so n1n2>m. Therefore, the condition m>lr(n1+n2−r) is not satisfied, and the matrix filling theory cannot be used to fill the service antenna for accurate parameter estimation.

Therefore, in view of the problems existing in the existing systems, this paper analyzes the CSI signal and antenna array which does not meet the spatial sampling theorem, and proposes a three-dimensional joint parameter estimation method of AoA, DFS, and ToF by using the service antenna. This method maps the service antenna array to a virtual linear array and uses the virtual linear array to estimate the three-dimensional parameters of the signal, and then the parameters of the signal incident on the service antenna are obtained by using the geometric relationship between the two arrays. This method solves the problem that the existing parameter estimation algorithms can not estimate the parameters of the wireless signal received by the service antenna which does not satisfy the spatial sampling theorem, making the service antenna array can be used not only for communication but also for smart environments sensing and other wireless sensing applications.

2 Methods

2.1 System model

Assuming that the receiving antenna is a uniform array and the number of antennas are M=I×J, I and J are the number of elements in the x-axis and y-axis direction respectively. As shown in Fig. 1, the spacing between antennas is d, the number of subcarriers are N, and the antenna array receives P packets from the transmitter.

Fig. 1
figure 1

Planar array

Full size image

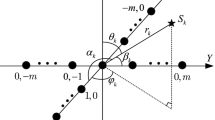
The I antennas in each row of the antenna array constitute a subarray with J rows in total. There are K(M>K) incident signals with the same center frequency F incident to the array at azimuth θ1,θ2,⋯,θK and elevation ϕ1,ϕ2,⋯,ϕK, where θk,0≤θk≤360∘ and ϕk,0≤ϕk≤360∘ are the azimuth and elevation angles of the kth incident signal. The signal sources incident to the space array is shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram of the direction of arrival

Full size image

Assuming that the antenna at the origin is the reference, the kth signal incident on the antenna array, the wave path difference between the mi,j,(1≤i≤I,1≤j≤J) array antenna and the reference antenna in the space is

$$ {\beta_{k}} = 2\pi \left({x_{{m_{i,j}}}}\cos {\phi_{k}} \sin {\theta_{k}} + {y_{{m_{i,j}}}}\sin {\phi_{k}} \sin {\theta_{k}} + {z_{{m_{i,j}}}}\cos {\theta_{k}} \right)/\lambda $$
(1)

where \(\left ({x_{{m_{i,j}}}},{y_{{m_{i,j}}}},{z_{{m_{i,j}}}}\right)\) are the coordinate of the mi,j antenna, and the array exists in the x−y plane, \({z_{{m_{i,j}}}} = 0\). At time t, for subarray in plane array, taking the antenna of coordinate origin as reference, the steering vector of the kth signal incident on subarray 1 is

$$ {a_{k}}(t,1,I) = \left[ {\begin{array}{ccc} 1\\ {{e^{- j2\pi d\cos {\phi_{k}}\sin {\theta_{k}}/\lambda }}}\\ \vdots \\ {{e^{- j2\pi d({I} - 1)\cos {\phi_{k}}\sin {\theta_{k}}/\lambda }}} \end{array}} \right] $$
(2)

The steering matrix of K signals incident on subarray 1 is

$$ \mathbf{A}(t,1,I) = \left[ {a_{1}(t,1,I)\;a_{2}(t,1,I)\; \ldots \;a_{K}(t,1,I)} \right] $$
(3)

The steering matrix A(t,j,I),(1≤j≤J) of the other jth subarray is the offset of subarray 1 along the y-axis, where the wave path difference of each antenna relative to the reference antenna is equal to that of the antenna of subarray 1 plus −2πd(j−1) sinϕk sinθk/λ. Therefore, the steering matrix of the signal incident on the planar array along the angle (θk,ϕk) is

$$ \mathbf{A}(t) = {\left[ {\mathbf{A}(t,1,I)\;\mathbf{A}(t,2,I) \ldots \mathbf{A}(t,J,I)} \right]^{T}} $$
(4)

where

$$ \mathbf{A}(t,j,I) = \mathbf{A}(t,1,I) \cdot {e^{- j2\pi d(j - 1)\sin {\phi_{k}} \sin {\theta_{k}} /\lambda }} $$
(5)

Then, kth signal of the signal source sk(t) is incident on the array antenna mi,j, and the output of the array is as follows:

$$ {x_{k}}\left(t,j,i\right) = {a_{k}}\left(t,j,i\right){s_{k}}(t) + {n_{k}}(t) $$
(6)

where ak(t,j,i) is channel impulse response and nk(t) is additive white gaussian noise (AWGN). The output of K signals incident on the antenna array is as follows:

$$ \mathbf{X}(t) = \mathbf{A}(t)\mathbf{S}(t) + \mathbf{N}(t) $$
(7)

where \(\mathbf {X}(t) = \left (\sum \limits _{k = 1}^{K} {x_{k}}\left (t,j,i\right)\right)_{M \times 1}, (1 \le i \le I,1 \le j \le J)\) is the received signal on antenna array, \(\mathbf {A}(t) = \left (\sum \limits _{k = 1}^{K} {a_{k}}\left (t,j,i\right)\right)_{M \times 1}, (1 \le i \le I,1 \le j \le J)\) is the array manifold of antenna array.

When the signals pass through different subcarriers and are incident on different antennas in the array, there will be different channel impulse responses. Due to the different frequencies of different subcarriers, the wave path difference will be generated when the signals are transmitted through different subcarriers, resulting in phase difference. Assuming that there are N subcarriers and the interval between the subcarriers is Δf, the phase difference between different signals transmitted to antenna mi,j through the n(1≤n≤N) subcarrier relative to that transmitted to antenna mi,j through the first subcarrier is e−j2π(n−1)Δfτ, and the steering matrix is A(t,j,i,n); for convenience, it is abbreviated as A(j,i,n), so

$$ \mathbf{A}\left(j,i,n\right) = \mathbf{A}(j,i,1) \cdot {e^{- j2\pi (n - 1)\Delta f\tau }} $$
(8)

where A(j,i,n)J×I×N,(1≤i≤I,1≤j≤J,1≤n≤N).

Through analysis, it is found that when the target is moving, the Doppler frequency offset caused by the moving speed of the target will be reflected between the received packets at different times. Supposing that the sampling interval is ts, the phase difference between the pth packet transmitted by the nth subcarrier received by the array antenna mi,j with respect to the first packet is \({e^{- j2\pi (p - 1)\frac {{v{t_{s}}}}{c}}}\), and the steering matrix is A(j,i,n,p)

$$ \mathbf{A}(j,i,n,p) = \mathbf{A}(j,i,n,1) \cdot {e^{- j2\pi (p - 1)\frac{{v{t_{s}}}}{c}}} $$
(9)

where A(j,i,n,p)P×J×I×N,(1≤i≤mx,1≤j≤my,1≤n≤N,1≤p≤P). Therefore, by analyzing the three-dimensional matrix AP×J×I×N composed of multiple data packets received by the antenna array, the parameters of AoA, ToF, and DFS can be obtained.

2.2 Proposed 3D parameter estimation algorithm based on service antenna array

When wireless signals are transmitted to antenna array, the phase difference between different antennas is only related to the spatial position of the antennas and the incident angle of the signal. When an antenna in the array moves along a certain direction for a certain distance, the wave path difference between the position of the signal incident on the antenna after displacement and the position before the displacement can be calculated by the spatial position. Therefore, the wave path difference of the signal incident to the position after the antenna displacement can be calculated by the wave path difference of the signal incident to the position before the displacement and the distance between the two positions. The wave path difference of the antenna moving to a certain position along a certain direction is determined, as long as the distance between the positions before and after the displacement of the antenna and the geometric relationship between the two positions are known; we can calculate the signal of another position and the related parameters of the signal through the signal of any position before or after the displacement. Therefore, this paper analyzes the geometric characteristics of the service antenna and the wave path difference of the signal incident at different positions of the array and combines MUSIC algorithm to estimate the three-dimensional parameters of the signal.

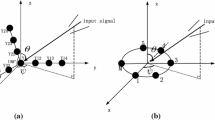
When positioning the target, we only need to determine the geometric position of the target on the two-dimensional plane of the ground. In order to simplify the calculation, we estimate the parameters of the signal in the same horizontal plane as the receiving antenna array, that is, we do not estimate the elevation angle of the signal. Assuming that there are K signals and N subcarriers in wireless system, and in practical applications, service antenna array is mostly rectangular arrays composed of four antennas; therefore, the number of service antennas in a single AP of indoor wireless equipment is usually 4; these antennas receive CSI information in P packets from signal source, and the distance between antennas is λ, which does not satisfy the space sampling theorem. As shown in Fig. 3, the four antennas are numbered as antennas 1, 2, 3, and 4 from top to bottom and from left to right. θk is the incident angle of k∈{1,2,⋯,K} signal sources, and the incident angle vectors of different signal sources can be expressed as Θ={θ1,θ2,⋯,θK}. Some antennas in the plane array are mapped to the remaining antenna lines along the incident direction of the signal. The mapped virtual antenna and the remaining antennas form a new virtual linear array with the numbers of 1′,2′,3′, and 4′, and then the parameters of the incident signal are estimated by the virtual linear array.

Fig. 3
figure 3

Service antenna array mapping diagram

Full size image

Since the virtual antenna array is different when the signal is incident from different directions, the plane of array is divided into eight blocks according to the signal incident direction, and the signal incident angle θk(1≤k≤K) is divided into 0∼45∘,46∼90∘,91∼135∘,136∼180∘,181∼225∘,226∼270∘,271∼315∘, and 316∼360∘; the signal incidence in each area is analyzed respectively.

Firstly, for area I, the signal is incident on the array from the direction θk, and the range of θk is 0∼45∘. Antenna 2 and antenna 3 are projected on the line of antenna 1 and antenna 4 along the direction of signal incidence. After projection, the virtual antenna and antenna 1 and antenna 4 form a non-uniform virtual linear array. The number of virtual linear array is 1′,2′,3′,4′.

The steering vector of the signal incident on the service antenna array from area I is as follows:

$$ {\mathbf{\mathrm{A}}_{\mathrm{I}}}\left({{\theta_{k}},{\tau_{k}},{\nu_{k}}} \right)={{\mathrm{e}}^{- j2\pi Ft}} \otimes {\boldsymbol{\Phi}_{{{\mathrm{I}},s}}}\left({{\theta_{k}}} \right) \otimes {\boldsymbol{\Phi}_{c}}\left({{\tau_{k}}} \right) \otimes {\boldsymbol{\Phi}_{p}}\left({{v_{k}}} \right) $$
(10)

where ⊗ is the Kronecker product and

$$\begin{array}{*{20}l} {\boldsymbol{\Phi}_{{\mathrm{I}},s}}\left({{\theta_{k}}} \right)=&{\left[ {\begin{array}{c} {\mathrm{1}}\\ {{e^{- j2\pi F(- \lambda \cos {\theta_{k}})}}}\\ {{e^{- j2\pi F(\lambda \sin {\theta_{k}})}}}\\ {{e^{- j2\pi F(- \sqrt 2 \lambda \cos ({\theta_{k}} + {{45}^ \circ }))}}} \end{array}} \right]^{T}} \end{array} $$
(11)
$$\begin{array}{*{20}l} {\boldsymbol{\Phi}_{c}}\left({{\tau_{k}}} \right)&=&{\left[ {1\;{e^{- j2\pi {\Delta f}{\tau_{k}}}}\; \ldots \;{e^{- j2\pi (N - 1){\Delta f}{\tau_{k}}}}} \right]^{\mathrm{T}}} \end{array} $$
(12)
$$\begin{array}{*{20}l} {\boldsymbol{\Phi}_{p}}\left({{v_{k}}} \right)&=&{\left[ {1\;{e^{- j2\pi F\frac{{{v_{k}}{t_{s}}}}{c}}}\; \ldots \;{e^{- j2\pi (P - 1)F\frac{{{v_{k}}{t_{s}}}}{c}}}} \right]^{\mathrm{T}}} \end{array} $$
(13)

ΦI,s(θk) represents the phase difference caused by the spacing between antennas when the signal is incident on the sparse array at an angle of θk, and the angle θk is in area I, Φc(τk) is the phase difference caused by the transmission of different subcarriers, Φp(vk) is the phase difference between different packets, and F is the signal center frequency.

Taking antenna 1 as the reference antenna, the distances between antenna 1′,2′,3′, and 4′ of non-uniform line virtual array antenna are

$$ {\mathbf{d}_{\mathrm{I}}} = \left[ {0\;\frac{{\lambda \sin {\theta_{k}}}}{{\sin \left({{45}^ \circ} + {\theta_{k}}\right)}}\;\sqrt 2 \lambda - \frac{{\lambda \sin {\theta_{k}}}}{{\sin \left({{45}^ \circ} + {\theta_{k}}\right)}}\;\sqrt 2 \lambda} \right] $$
(14)

When the signal is incident on the virtual non-uniform linear array at angle θk, the phase difference \({\overline {\boldsymbol {\Phi }}_{{\mathrm {I}},v}}\left ({{\theta _{k}}} \right)\) caused by the spacing between virtual antennas is

$$ {\overline{\boldsymbol{\Phi}}_{{\mathrm{I}},v}}\left({{\theta_{k}}} \right)={\left[ {\begin{array}{ccc} {\mathrm{1}}\\ {{e^{- j2\pi F\left(\frac{{\lambda \sin {\theta_{k}}}}{{\sin \left({{45}^ \circ} + {\theta_{k}}\right)}}\right)\sin {\theta_{k}}}}}\\ {{e^{- j2\pi F\left(\sqrt 2 \lambda - \frac{{\lambda \sin {\theta_{k}}}}{{\sin \left({{45}^ \circ} + {\theta_{k}}\right)}}\right)\sin {\theta_{k}}}}}\\ {{e^{- j2\pi F(\sqrt 2 \lambda)\sin {\theta_{k}}}}} \end{array}} \right]^{T}} $$
(15)

When the incident angle is θk, the phase difference between the sparse array and the mapped non-uniform virtual linear array is

$$ \boldsymbol{\Delta}{\boldsymbol{\Phi}_{\mathrm{I}}}({\theta_{k}},{\tau_{k}},{\nu_{k}}) = \boldsymbol{\Delta }{\boldsymbol{\Phi }_{{\mathrm{I}},{s \to v}}}({\theta_{k}}) \otimes {\boldsymbol{\Phi }_{c}}\left({{\tau_{k}}} \right) \otimes {\boldsymbol{\Phi }_{p}}\left({{v_{k}}} \right) $$
(16)

where

$$ \boldsymbol{\Delta }{\boldsymbol{\Phi}_{{{\mathrm{I}},{s \to v}}}}({\theta_{k}})=\left[ {1\;{e^{- j2\pi \frac{{\lambda \sin {{45}^ \circ }}}{{\sin \left({{45}^ \circ} + {\theta_{k}}\right)}}}}\;{e^{- j2\pi \left(\frac{{ - \lambda \sin {{45}^ \circ }}}{{\sin \left({{45}^ \circ} + {\theta_{k}}\right)}}\right)}}\;1} \right] $$
(17)

ΔΦI,s→v(θk) represents the phase difference caused by the spatial position between the sparse array and the non-uniform virtual linear array when the AoA θk is incident from area I.

Since the incident angle θk is unknown, and the phase difference ΔΦI(θk) between the plane array and the linear array is related to the incident angle, we change the incident angle θk from 0∼45∘ in steps of 1∘. Every time the angle changes, we get a corresponding phase difference ΔΦI(θk). By multiplying the steering vector of the sparse array with the phase difference between the sparse array and the non-uniform virtual linear array, the steering vector \({\overline {\mathbf {A}}_{\mathrm {I}}}{({\theta _{k}})}\) of the signal incident on the virtual non-uniform linear array at the angle of θk is obtained.

$$ {\overline{\mathbf{A}}_{\mathrm{I}}}{({\theta_{k}}) = }{\mathbf{A}_{\mathrm{I}}}{({\theta_{k}})} \times \boldsymbol{\Delta }{\boldsymbol{\Phi}_{\mathrm{I}}}({\theta_{k}}) $$
(18)

Therefore, when the incident signal is incident to the antenna array from the direction of area I, in the pth packet, the steering vector of the signal incident to the virtual non-uniform array along the n subcarrier at angle θk is

$$ {\overline{\mathbf{A}}_{\mathrm{{I}}}}{({\theta_{k}}{{,}}{\tau_{k}},{v_{k}})} = e{}^{- j2\pi Ft} \otimes {\overline{\boldsymbol{\Phi}}_{{\mathrm{I}},v}}\left({{\theta_{k}}} \right) \otimes {\boldsymbol{\Phi}_{c}}\left({{\tau_{k}}} \right) \otimes {\boldsymbol{\Phi}_{p}}\left({{v_{k}}} \right) $$
(19)

The kth signal received by virtual linear array is as follows:

$$ \overline{\mathbf{X}} {({\theta_{k}}{{,}}{\tau_{k}},{v_{k}}{{;}}t) = }{\overline{\mathbf{A}}_{\mathrm{I}}}{({\theta_{k}}{{,}}{\tau_{k}},{v_{k}}{{;}}t)}{S_{k}}(t) + {\mathbf{N}_{k}}(t) $$
(20)

Therefore, the array output of K signal sources incident on the antenna array is

$$\begin{array}{@{}rcl@{}} \overline{\mathbf{X}} {(\Theta {,}\mathrm{T},V{;}t)}& =& \sum\limits_{k = 1}^{K} {\overline{\mathbf{X}} {({\theta_{k}}{{,}}{\tau_{k}},{v_{k}}{{;}}t)}} \\ &=&\sum\limits_{k = 1}^{K} {{{\overline{\mathbf{A}} }_{\mathrm{I}}}{({\theta_{k}}{{,}}{\tau_{k}},{v_{k}}{{;}}t)}{S_{k}}(t) + {\mathbf{N}_{k}}(t)} \\ &= &\overline{{\mathbf{A}}_{\mathrm{I}}} (\Theta {,}\mathrm{T},V{;}t)\mathbf{S}(t) + \mathbf{N}(t) \end{array} $$
(21)

where Θ=[θ1,θ2,…,θK],T=[τ1,τ2,…,τK], and V=[ν1,ν2,…,νK].

Assuming that the incidence angle of the kth signal incident on the virtual linear array is φk, the geometric relationship between the angle φk of the signal incident on the virtual linear array and the angle θk of the signal incident on the service antenna can be obtained through the geometric relationship between the signal incident on the service antenna and the virtual linear array in Fig. 3

$$ {\theta_{k}} = {\varphi_{k}} - 45^{\circ} $$
(22)

Assuming that the service antenna array receives the signal X(t), then through multiplying the received signal by the phase difference between the service antenna and the virtual linear array, the signal \(\overline {\mathbf {X}} (t)\) which is incident on the virtual linear array can be obtained. MUSIC algorithm is used to decompose the received signal \(\overline {\mathbf {X}} (t)\) to solve the noise subspace and signal subspace, and then the signal parameters incident on the virtual antenna array can be obtained. MUSIC algorithm first calculates the covariance matrix S of the matrix \(\overline {\mathbf {X}} \), then the matrix S is decomposed into NMP eigenvalues. Among them, NMP−K smaller eigenvalues are equal to the variance of noise σ2, and these NMP−K eigenvalues are only related to noise, and their corresponding eigenvectors constitute noise subspace. Because all the minimum eigenvectors of the covariance matrix S are orthogonal to the column vectors of the steering matrix \({\overline {\mathbf {A}}_{\mathrm {I}}}\). Therefore, orthogonal noise subspace and signal subspace can be obtained. By constructing a noise eigenvector matrix EN with NMP−(NMP−K) dimensions from the eigenvectors in the noise subspace, the spectral function can be solved and the estimated parameters can be obtained.

$$ f(\Psi,\mathrm{T},V) = \frac{1}{{{\rho^{\mathrm{H}}}(\Psi,\mathrm{T},V){E_{N}}E_{N}^{\mathrm{H}}\rho (\Psi,\mathrm{T},V)}} $$
(23)

where ρ(Ψ,T,V) is the steering vector which has the same array manifold with \(\overline {\mathrm {Y}} \) and Ψ,T, V is the parameter to be estimated, where Ψ=[φ1,φ2,…,φK] is the incident angle of the signal incident on the virtual linear array. T and V are ToF and DFS of incident signal respectively, and H is conjugate transpose. By changing the value of the parameter to be estimated in the spectral function, the corresponding parameter estimation value can be obtained by searching the peak value of the spectral function.

At this time, the estimated AoA Ψ is the angle of the signal incident on the virtual linear array, the angle of signal incident from area I to service antenna can be obtained by formula (22)

$$ \Theta = \Psi - 45^{\circ} $$
(24)

For area II, the signal is incident on the array from the direction θk, and the range of θk is 46∼90∘. Antenna 2 and antenna 3 are projected on the line of antenna 1 and antenna 4 along the direction of signal incidence. After projection, the virtual antenna and antenna 1 and antenna 4 form a non-uniform virtual linear array. The number of virtual linear array is 1′,3′,2′,4′.

The steering vector of the signal incident on the service antenna array from area II is as follows:

$$ {\mathbf{\mathrm{A}}_{\text{II}}}\left({{\theta_{k}},{\tau_{k}},{\nu_{k}}} \right)={{\mathrm{e}}^{- j2\pi Ft}} \otimes {\boldsymbol{\Phi}_{{{\text{II}},s}}}\left({{\theta_{k}}} \right) \otimes {\boldsymbol{\Phi}_{c}}\left({{\tau_{k}}} \right) \otimes {\boldsymbol{\Phi}_{p}}\left({{v_{k}}} \right) $$
(25)

where

$$ {\boldsymbol{\Phi}_{{{\text{II}},s}}}\left({{\theta_{k}}} \right) = {\left[ {\begin{array}{*{20}{c}} 1\\ {{e^{- j2\pi F(\lambda \sin {\theta_{k}})}}}\\ {{e^{- j2\pi F(- \lambda \cos {\theta_{k}})}}}\\ {{e^{- j2\pi F(- \sqrt 2 \lambda \cos ({\theta_{k}} + {{45}^ \circ }))}}} \end{array}} \right]^{T}} $$
(26)

ΦII,s(θk) represents the phase difference caused by the spacing between antennas when the signal is incident on the sparse array at an angle of θk.

Taking antenna 1 as the reference antenna, the distances between antenna 1′,3′,2′, and 4′ of non-uniform line virtual array antenna are

$$ {\mathbf{d}_{\text{II}}} = \left[ {0\;\sqrt 2 \lambda - \frac{{\lambda \sin {\theta_{k}}}}{{\sin \left({{45}^ \circ} + {\theta_{k}}\right)}}\;\frac{{\lambda \sin {\theta_{k}}}}{{\sin \left({{45}^ \circ} + {\theta_{k}}\right)}}\;\sqrt 2 \lambda} \right] $$
(27)

When the signal is incident on the virtual non-uniform linear array at angle θk, the phase difference \({\overline {\boldsymbol {\Phi }}_{{\text {II}},v}}\left ({{\theta _{k}}} \right)\) caused by the spacing between virtual antennas is

$$ {\overline{\boldsymbol{\Phi}}_{{{\text{II}},v}}}\left({{\theta_{k}}} \right)={\left[ {\begin{array}{ccc} 1\\ {{e^{- j2\pi F\left(\sqrt 2 \lambda - \frac{{\lambda \sin {\theta_{k}}}}{{\sin \left({{45}^ \circ} + {\theta_{k}}\right)}}\right)\sin {\theta_{k}}}}}\\ {{e^{- j2\pi F\left(\frac{{\lambda \sin {\theta_{k}}}}{{\sin \left({{45}^ \circ} + {\theta_{k}}\right)}}\right)\sin {\theta_{k}}}}}\\ {{e^{- j2\pi F(\sqrt 2 \lambda)\sin {\theta_{k}}}}} \end{array}} \right]^{T}} $$
(28)

When the incident angle is θk, the phase difference between the sparse array and the mapped non-uniform virtual linear array is

$$ \boldsymbol{\Delta }{\boldsymbol{\Phi}_{\text{II}}}({\theta_{k}},{\tau_{k}},{\nu_{k}}) = \boldsymbol{\Delta }{\boldsymbol{\Phi}_{{{\text{II}},{s \to v}}}}({\theta_{k}}) \otimes {\boldsymbol{\Phi}_{c}}\left({{\tau_{k}}} \right) \otimes {\boldsymbol{\Phi}_{p}}\left({{v_{k}}} \right) $$
(29)

where

$$ \boldsymbol{\Delta }{\boldsymbol{\Phi}_{{{\text{II}},{s \to v}}}}({\theta_{k}})=\left[ {1\;{e^{- j2\pi \left(\frac{{ - \lambda \sin {{45}^ \circ }}}{{\sin \left({{45}^ \circ} + {\theta_{k}}\right)}}\right)}}\;{e^{- j2\pi \frac{{\lambda \sin {{45}^ \circ }}}{{\sin \left({{45}^ \circ} + {\theta_{k}}\right)}}}}\;1} \right] $$
(30)

ΔΦII,s→v(θk) represents the phase difference caused by the spatial position between the sparse array and the non-uniform virtual linear array when the AoA θk is incident from area II.

Let the incident angle θk change from 46∼90∘ in steps of 1∘, every time θk changes, a corresponding phase difference ΔΦII(θk) is obtained. By multiplying the steering vector of the sparse array with the phase difference between the sparse array and the non-uniform virtual linear array, the steering vector of the signal incident on the virtual non-uniform linear array at angle θk is obtained

$$ {\overline{\mathbf{A}}_{\text{II}}}{({\theta_{k}}) = }{\mathbf{A}_{\text{II}}}{({\theta_{k}})} \times \boldsymbol{\Delta }{\boldsymbol{\Phi}_{\text{II}}}({\theta_{k}}) $$
(31)

Therefore, when the incident signal is incident to the antenna array from the direction of area II, in the pth packet, the steering vector of the signal incident to the virtual non-uniform array along the n subcarrier at angle θk is

$$ {\overline{\mathbf{A}}_{\text{II}}}{({\theta_{k}}{,}{\tau_{k}}{,}{v_{k}})} = e^{- j2\pi Ft} \otimes {\overline{\boldsymbol{\Phi}}_{{{\text{II}},v}}}\left({{\theta_{k}}} \right) \otimes {\boldsymbol{\Phi}_{c}}\left(\tau_{k} \right) \otimes {\boldsymbol{\Phi}_{p}}\left(v_{k} \right) $$
(32)

The signal of area II received by virtual linear array is

$$ \overline{\mathbf{X}} {({\theta_{k}}{{,}}{\tau_{k}},{v_{k}}{{;}}t) = }{\overline{\mathbf{A}}_{{\text{II}}}}{({\theta_{k}}{{,}}{\tau_{k}},{v_{k}}{{;}}t)}{S_{k}}(t) + {\mathbf{N}_{k}}(t) $$
(33)

By analyzing the signal, we can get the AoA, ToF, and DFS of the signal incident on the virtual linear array. According to the geometric relationship between the signal incident on the service antenna and the virtual linear array in Fig. 3, the geometric relationship between the angle φk of the signal incident on the virtual linear array and the angle θk of the signal incident on the service antenna is same as formula (22).

For area III, the signal is incident on the array from the direction θk, and the range of θk is 91∼135∘. Antenna 1 and antenna 4 are projected on the line of antenna 2 and antenna 3 along the direction of signal incidence. After projection, the virtual antenna and antenna 2 and antenna 3 form a non-uniform virtual linear array. The number of virtual linear array is 3′,1′,4′,2′.

The steering vector of the signal incident on the service antenna array from area III is as follows:

$$ {\mathbf{\mathrm{A}}_{\text{III}}}\left({{\theta_{k}},{\tau_{k}},{\nu_{k}}} \right)={{\mathrm{e}}^{- j2\pi Ft}} \otimes {\boldsymbol{\Phi}_{{{\text{III}},s}}}\left({{\theta_{k}}} \right) \otimes {\boldsymbol{\Phi}_{c}}\left({{\tau_{k}}} \right) \otimes {\boldsymbol{\Phi}_{p}}\left({{v_{k}}} \right) $$
(34)

where

$$ {\boldsymbol{\Phi}_{{{\text{III}},s}}}\left({{\theta_{k}}} \right)={\left[ {\begin{array}{*{20}{c}} {{e^{- j2\pi F(\lambda \sin {\theta_{k}})}}}\\ 1\\ {{e^{- j2\pi F\left(- \sqrt 2 \lambda \cos \left({\theta_{k}} + {{45}^ \circ }\right)\right)}}}\\ {{e^{- j2\pi F\left(- \lambda \cos {\theta_{k}}\right)}}} \end{array}} \right]^{T}} $$
(35)

ΦIII,s(θk) represents the phase difference caused by the spacing between antennas when the signal is incident on the sparse array at an angle of θk.

Taking antenna 3 as the reference antenna, the distances between antenna 3′,1′,4′, and 2′ of non-uniform line virtual array antenna are

$$ {\mathbf{d}_{\text{III}}} = \left[ {0\;\frac{{\lambda \sin ({\theta_{k}} - {{90}^ \circ })}}{{\sin \left({\theta_{k}} - {{45}^ \circ }\right)}}\;\sqrt 2 \lambda - \frac{{\lambda \sin ({\theta_{k}} - {{90}^ \circ })}}{{\sin \left({\theta_{k}} - {{45}^ \circ }\right)}}\;\sqrt 2 \lambda} \right] $$
(36)

When the signal is incident on the virtual non-uniform linear array at angle θk, the phase difference \({\overline {\boldsymbol {\Phi }}_{{{\text {III}},v}}}\left ({{\theta _{k}}} \right)\) caused by the spacing between virtual antennas is

$$ {\overline{\boldsymbol{\Phi}}_{{{\text{III}},v}}}\left({{\theta_{k}}} \right)={\left[ {\begin{array}{*{20}{c}} 1\\ {{e^{- j2\pi F\left(\frac{{\lambda \sin ({\theta_{k}} - {{90}^ \circ })}}{{\sin \left({\theta_{k}} - {{45}^ \circ }\right)}}\right)\sin \theta }}}\\ {{e^{- j2\pi F\left(\sqrt 2 \lambda - \frac{{\lambda \sin \left({\theta_{k}} - {{90}^ \circ }\right)}}{{\sin \left({\theta_{k}} - {{45}^ \circ }\right)}}\right)\sin \theta }}}\\ {{e^{- j2\pi F\left(\sqrt 2 \lambda \right)\sin {\theta_{k}}}}} \end{array}} \right]^{T}} $$
(37)

When the incident angle is θk, the phase difference between the sparse array and the mapped non-uniform virtual linear array is

$$ \boldsymbol{\Delta }{\boldsymbol{\Phi}_{\text{III}}}({\theta_{k}},{\tau_{k}},{\nu_{k}}) = \boldsymbol{\Delta }{\boldsymbol{\Phi}_{{{\text{III}},{s \to v}}}}({\theta_{k}}) \otimes {\boldsymbol{\Phi}_{c}}\left({{\tau_{k}}} \right) \otimes {\boldsymbol{\Phi}_{p}}\left({{v_{k}}} \right) $$
(38)

where

$$ \boldsymbol{\Delta }{\boldsymbol{\Phi}_{{{\text{III}},{s \to v}}}}({\theta_{k}})=\left[ {1\;{e^{- j2\pi \frac{{\lambda \sin {{45}^ \circ }}}{{\sin \left({\theta_{k}} - {{45}^ \circ }\right)}}}}\;{e^{- j2\pi \left(\frac{{ - \lambda \sin {{45}^ \circ }}}{{\sin \left({\theta_{k}} - {{45}^ \circ }\right)}}\right)}}\;1} \right] $$
(39)

ΔΦIII,s→v(θk) represents the phase difference caused by the spatial position between the sparse array and the non-uniform virtual linear array when the AoA θk is incident from area III.

Let the incident angle θk change from 91∼135∘ in steps of 1∘, every time θk changes, a corresponding phase difference ΔΦIII(θk) is obtained. By multiplying the steering vector of the sparse array with the phase difference between the sparse array and the non-uniform virtual linear array, the steering vector of the signal incident on the virtual non-uniform linear array at angle θk is obtained

$$ {\overline{\mathbf{A}}_{\text{III}}}{({\theta_{k}}) = }{\mathbf{A}_{\text{III}}}{({\theta_{k}})} \times \boldsymbol{\Delta }{\boldsymbol{\Phi}_{\text{III}}}({\theta_{k}}) $$
(40)

Therefore, when the incident signal is incident to the antenna array from the direction of area III, in the pth packet, the steering vector of the signal incident to the virtual non-uniform array along the n subcarrier at angle θk is

$$ {\overline{\mathbf{A}}_{\text{III}}}{({\theta_{k}}{,}{\tau_{k}}{,}{v_{k}})} = e^{- j2\pi Ft} \otimes {\overline{\boldsymbol{\Phi}}_{{{\text{III}},v}}}\left({{\theta_{k}}} \right) \otimes {\boldsymbol{\Phi}_{c}}\left({{\tau_{k}}} \right) \otimes {\boldsymbol{\Phi}_{p}}\left({{v_{k}}} \right) $$
(41)

The signal of area II received by virtual linear array is

$$ \overline{\mathbf{X}} {({\theta_{k}}{{,}}{\tau_{k}},{v_{k}}{{;}}t) = }{\overline{\mathbf{A}}_{\text{III}}}{\left({\theta_{k}}{{,}}{\tau_{k}},{v_{k}}{{;}}t\right)}{S_{k}}(t) + {\mathbf{N}_{k}}(t) $$
(42)

The geometric relationship between the angle φk of the signal incident on the virtual linear array and the angle θk of the signal incident on the service antenna is

$$ {\theta_{k}} = {\varphi_{k}} + 45^{\circ} $$
(43)

For area IV, the signal is incident on the array from the direction θk, and the range of θk is 136∼180∘. Antenna 1 and antenna 4 are projected on the line of antenna 2 and antenna 3 along the direction of signal incidence. After projection, the virtual antenna and antenna 2 and antenna 3 form a non-uniform virtual linear array. The number of virtual linear array is 3′,4′,1′,2′.

The steering vector of the signal incident on the service antenna array from area IV is as follows:

$$ {\mathbf{\mathrm{A}}_{\text{IV}}}\left({{\theta_{k}},{\tau_{k}},{\nu_{k}}} \right)={{\mathrm{e}}^{- j2\pi Ft}} \otimes {\boldsymbol{\Phi}_{{{\text{IV}},s}}}\left({{\theta_{k}}} \right) \otimes {\boldsymbol{\Phi}_{c}}\left({{\tau_{k}}} \right) \otimes {\boldsymbol{\Phi}_{p}}\left({{v_{k}}} \right) $$
(44)

where

$$ {\boldsymbol{\Phi}_{{{\text{IV}},s}}}\left({{\theta_{k}}} \right) = {\left[ {\begin{array}{*{20}{c}} {{e^{- j2\pi F(- \lambda \cos {\theta_{k}})}}}\\ 1\\ {{e^{- j2\pi F\left(- \sqrt 2 \lambda \cos \left({\theta_{k}} + {{45}^ \circ }\right)\right)}}}\\ {{e^{- j2\pi F(\lambda \sin {\theta_{k}})}}} \end{array}} \right]^{T}} $$
(45)

ΦIV,s(θk) represents the phase difference caused by the spacing between antennas when the signal is incident on the sparse array at an angle of θk.

Taking antenna 3 as the reference antenna, the distances between antenna 3′,4′,1′, and 2′ of non-uniform line virtual array antenna are

$$ {\mathbf{d}_{\text{IV}}} = \left[ {0\;\sqrt 2 \lambda - \frac{{\lambda \sin ({\theta_{k}} - {{90}^ \circ })}}{{\sin \left({\theta_{k}} - {{45}^ \circ }\right)}}\;\frac{{\lambda \sin ({\theta_{k}} - {{90}^ \circ })}}{{\sin \left({\theta_{k}} - {{45}^ \circ }\right)}}\;\sqrt 2 \lambda} \right] $$
(46)

When the signal is incident on the virtual non-uniform linear array at angle θk, the phase difference \({\overline {\boldsymbol {\Phi }}_{{{\text {IV}},v}}}\left ({{\theta _{k}}} \right)\) caused by the spacing between antennas is

$$ {\overline{\boldsymbol{\Phi}}_{{{\text{IV}},v}}}\left({{\theta_{k}}} \right)={\left[ {\begin{array}{ccc} 1\\ {{e^{- j2\pi F\left(\sqrt 2 \lambda - \frac{{\lambda \sin ({\theta_{k}} - {{90}^ \circ })}}{{\sin \left({\theta_{k}} - {{45}^ \circ }\right)}}\right)\sin \theta }}}\\ {{e^{- j2\pi F\left(\frac{{\lambda \sin ({\theta_{k}} - {{90}^ \circ })}}{{\sin \left({\theta_{k}} - {{45}^ \circ }\right)}}\right)\sin \theta }}}\\ {{e^{- j2\pi F\left(\sqrt 2 \lambda\right)\sin {\theta_{k}}}}} \end{array}} \right]^{T}} $$
(47)

When the incident angle is θk, the phase difference between the sparse array and the mapped non-uniform virtual linear array is

$$ \boldsymbol{\Delta }{\boldsymbol{\Phi}_{\text{IV}}}({\theta_{k}},{\tau_{k}},{\nu_{k}}) = \boldsymbol{\Delta }{\boldsymbol{\Phi}_{{{\text{IV}},{s \to v}}}}({\theta_{k}}) \otimes {\boldsymbol{\Phi}_{c}}\left({{\tau_{k}}} \right) \otimes {\boldsymbol{\Phi}_{p}}\left({{v_{k}}} \right) $$
(48)

where

$$ \boldsymbol{\Delta }{\boldsymbol{\Phi}_{{{\text{IV}},{s \to v}}}}({\theta_{k}})=\left[ {1\;{e^{- j2\pi \left(\frac{{ - \lambda \sin {{45}^ \circ }}}{{\sin \left({\theta_{k}} - {{45}^ \circ }\right)}}\right)}}\;{e^{- j2\pi \frac{{\lambda \sin {{45}^ \circ }}}{{\sin \left({\theta_{k}} - {{45}^ \circ }\right)}}}}\;1} \right] $$
(49)

ΔΦIV,s→v(θk) represents the phase difference caused by the spatial position between the sparse array and the non-uniform virtual linear array when the AoA θk is incident from area IV.

Let the incident angle θk change from 136∼180∘ in steps of 1∘, every time θk changes, a corresponding phase difference ΔΦIV(θk) is obtained. By multiplying the steering vector of the sparse array with the phase difference between the sparse array and the non-uniform virtual linear array, the steering vector of the signal incident on the virtual non-uniform linear array at angle θk is obtained

$$ {\overline{\mathbf{A}}_{\text{IV}}}{({\theta_{k}}) = }{\mathbf{A}_{{\text{IV}}}}{({\theta_{k}})} \times \boldsymbol{\Delta }{\boldsymbol{\Phi}_{\text{IV}}}({\theta_{k}}) $$
(50)

Therefore, when the incident signal is incident to the antenna array from the direction of area IV, in the pth packet, the steering vector of the signal incident to the virtual non-uniform array along the n subcarrier at angle θk is

$$ {\overline{\mathbf{A}}_{\text{IV}}}{({\theta_{k}}{,}{\tau_{k}}{,}{\nu_{k}})} = e^{- j2\pi Ft} \otimes {\overline{\boldsymbol{\Phi}}_{{{\text{IV}},v}}}\left({{\theta_{k}}} \right) \otimes {\boldsymbol{\Phi}_{c}}\left({{\tau_{k}}} \right) \otimes {\boldsymbol{\Phi}_{p}}\left({{v_{k}}} \right) $$
(51)

The signal of area IV received by virtual linear array is

$$ \overline{\mathbf{X}} {({\theta_{k}}{{,}}{\tau_{k}},{v_{k}}{{;}}t) = }{\overline{\mathbf{A}}_{\text{IV}}}{({\theta_{k}}{{,}}{\tau_{k}},{v_{k}}{{;}}t)}{S_{k}}(t) + {\mathbf{N}_{k}}(t) $$
(52)

The geometric relationship between the angle φk of the signal incident on the virtual linear array and the angle θk of the signal incident on the service antenna is same as formula (42).

For areas V, VI, VII, and VIII, the mapping directions of signals from these areas to the antenna array are completely opposite to the mapping directions of signals from areas I, II, III, and IV, respectively.

3 Results and discussion

In this section, we will verify the performance of our system through simulation experiments and compare it with TWPalo [28]. Compared with other parameter estimation algorithms, the proposed algorithm can estimate the signal parameters without false peaks when the antenna array does not satisfy the spatial sampling theorem. Therefore, the simulation experiment compares the proposed algorithm with the existing advanced parameter estimation algorithm to illustrate this phenomenon. Then, for the simulation experiment, the performance of the proposed algorithm will be analyzed and explained. Firstly, the influence of the antenna spacing on the proposed algorithm is illustrated by increasing the spacing between the antennas in the antenna array. Then, the influence of noise on the performance of the algorithm is illustrated by simulation under different SNR. Finally, whether the accuracy of parameter estimation is affected by the signal incident on the array from different angles will be explained.

The simulation parameter settings are shown in Table 1.

Table 1 Parameter setting
Full size table

The service antenna array is mostly composed of four antennas. Assuming that the spacing of the receiving antenna array is λ=c/F, c is the speed of light, the signal is a far-field source signal, the center frequency of the signal is F=5.7×109, and the spacing of the subcarriers is Δf=1.26×106. There are 30 subcarriers in the OFDM system. The bandwidth is 40 MHz. Assuming that the target is stationary, its Doppler velocity is v=0 m/s, the transmission delay from the transmitter to the receiver is 20 ns, and the angle of the signal incident to the array is 30∘. The simulation is carried out when the SNR is 0 dB.

Firstly, the algorithm proposed in this paper is compared with the existing advanced algorithm TWPalo, the two algorithms are simulated 500 times, and the simulation results are statistically analyzed to illustrate that the proposed algorithm can also accurately estimate the signal parameters when the array antenna spacing does not meet the spatial sampling theorem, while the existing advanced parameter estimation algorithms will produce false peaks and result in misjudgment.

It can be seen from Fig. 4 that TWPalo algorithm and the parameter estimation algorithm proposed in this paper can accurately estimate the time delay and Doppler velocity of the signal in time and frequency dimensions. However, in the spatial dimension, because the spacing between array antennas is greater than half wavelength, it does not meet the spatial sampling theorem; therefore, TWPalo produces pseudo peaks when estimating AoA, which interferes with the judgment of parameters and leads to misjudgment. For the algorithm proposed in this paper, because the geometric relationship between the service antenna array and the mapped virtual linear array is unique, the AoA parameters of the signal can be uniquely obtained through the geometric relationship between the two arrays through the specific angle mapping virtual linear array.

Fig. 4
figure 4

Parameter estimation comparison between the existing algorithm and the algorithm proposed

Full size image

The accuracy of the simulation results of AoA, ToF, and DFS of TWPalo and the parameter estimation algorithm proposed in this paper are statistically analyzed, as shown in Fig. 5. For AoA estimation, it can be seen from Fig. 4a that when the angle search range is within − 90 to 90∘, there are 30∘ true angle and − 30∘,90∘, and − 90∘ pseudo peaks in the parameter estimation results. These pseudo peaks are caused by the spacing between antennas that does not meet the spatial sampling theorem. If these pseudo peaks are not removed and treated as correct parameter estimation results, the accuracy of parameter estimation will be greatly affected. As shown in Fig. 5a, due to the existence of − 90∘ pseudo peak, the statistical parameter estimation error can reach 120∘. As can be seen from Fig. 4b, there will be no false peaks in AoA estimation by using the parameter estimation algorithm proposed in this paper, so the accuracy of parameter estimation is high. As shown in Fig. 5a, the AoA estimation accuracy of the proposed algorithm is within 3∘.

Fig. 5
figure 5

Comparison of cumulative distribution of parameter estimation errors between two algorithms

Full size image

For the parameters of ToF and DFS, the estimation error is statistically analyzed, as shown in Fig. 5b and c. It can be seen that the accuracy of the proposed algorithm for ToF and DFS estimation is also better than that of TWPalo, because in the proposed algorithm, only when the relationship between the estimated angle and the mapped angle is equal to the geometric relationship between the service antenna and the virtual linear array, the angle of ergodic mapping is equal to the real incident angle of signal, and so as to determine the angle value to be estimated. Therefore, based on the three-dimensional parameter estimation algorithm proposed in TWPalo, the algorithm proposed in this paper further limits the estimated parameters, so as to improve the accuracy of parameter estimation. It can be seen from Fig. 5 that the AoA estimation error of the proposed parameter estimation algorithm is within 3∘ while the error of ToF and DFS parameter estimation is within 1 ns and 1 m/s.

Then, we carry out simulation under different SNR to calculate the influence of SNR on parameter estimation accuracy of the proposed algorithm, as shown in Fig. 6. It can be seen from Fig. 6 that when the SNR is 0 dB, − 10 dB, and − 20 dB, the change of SNR has little effect on the estimation accuracy of AoA, ToF, and DFS. Although there are some pseudo peaks in the process of parameter estimation due to the presence of noise, we can obtain the correct signal parameters by finding out whether there is an angle in the estimated result that satisfies the geometric relationship between the service antenna and the non-uniform linear array, which shows that the proposed algorithm is robust when the SNR is greater than − 30 dB. However, when the SNR is − 30 dB or − 40 dB, the angle estimation error is too large to find the correct angle, which leads to the wrong AoA estimation. The reason of the large error of the AoA estimation is that the noise has a great influence on the estimation of signal parameters when SNR is too low. When we use virtual linear array to estimate parameters, the number and the amplitude of pseudo peaks will increase due to the existence of noise. When the AoA of the pseudo peak satisfies the geometric relationship between the service antenna array and the non-uniform linear array, the pseudo peak will be judged as the true peak, which leads to the decrease of the accuracy of parameter estimation. Moreover, because AoA, ToF, and DFS are estimated at the same time, when AoA cannot be correctly estimated, the corresponding correct ToF and DFS cannot be found through the correct peak value, resulting in the error of ToF and DFS becoming larger.

Fig. 6
figure 6

Comparison of parameter estimation accuracy of the proposed algorithm in different SNR

Full size image

Through the simulation under different packet sending rates, the influence of packet sending rate on parameter estimation is discussed. As shown in Fig. 7, when the packet rate is less than 400 packets per second, the Doppler velocity estimation accuracy is within 2 m/s, and different packet rates will not affect the Doppler velocity estimation results. When the packet rate is greater than 400 packets per second, the estimation accuracy of Doppler velocity decreases with the increase of packet rate. This is because the phase of the received signal is \({e^{- j2\pi F\frac {{v{t_{s}}}}{c}}}\), and it has a periodicity of 2π, when the sending rate is large, the phase difference \({e^{- j2\pi F\frac {{v{t_{s}}}}{c}}}\) will increase, which will lead to the phase exceeding 2π period, resulting in multiple solutions, and the accuracy of parameter estimation will decline.

Fig. 7
figure 7

Estimation accuracy of DFS with different packet sending rates

Full size image

For the bandwidth and subcarrier spacing, when the bandwidth is fixed, the larger the distance between subcarriers, the smaller the number of subcarriers. When the distance between subcarriers is fixed, the larger the bandwidth, the greater the number of subcarriers. Therefore, the number of subcarriers is affected by the bandwidth and subcarrier spacing.

As can be seen from Fig. 8, with the decrease of the number of subcarriers, the accuracy of ToF estimation becomes lower and lower.

Fig. 8
figure 8

Estimation accuracy of ToF with different number of subcarriers

Full size image

Then, in the case of the same incident signal, SNR, and the number of snapshots, the spacing between the array antennas is increased, and the parameter estimation is carried out under different antenna spacing to explore whether the antenna spacing has restrictions on the algorithm. When the antenna spacing is one wavelength, two wavelengths, three wavelengths, and four wavelengths, the accuracy of parameter estimation under different antenna spacing is counted.

As can be seen from Fig. 9, with the increase of antenna spacing, the parameter estimation accuracy of AoA, ToF, or DFS is not affected, because the estimation of ToF and DFS is only related to the spacing between subcarriers and the sampling time between packets, and has nothing to do with the arrangement between antennas. Although AoA estimation is related to the spacing and arrangement of antennas, the parameter estimation method proposed in this paper maps the service antenna array into a virtual linear array, estimates the signal parameters by using the virtual linear array, and then uses the geometric relationship between the service antenna array and the virtual linear array to calculate the angle of signal incident on the service antenna array. Because of the unique geometric relationship between the virtual linear array and the service antenna array, there will be no pseudo peak due to the large array spacing when estimating the angle.

Fig. 9
figure 9

Three-dimensional parameter estimation under different antenna spacing

Full size image

However, because the array is a square array composed of four antennas, at some special angles, such as perpendicular to the line of adjacent antennas or perpendicular to the line of two antennas on the diagonal line, the mapped virtual antenna array overlaps with the antenna after mapping, the amount of information in the array is reduced, and the array aperture is reduced. The accuracy of AoA estimation using virtual linear array will decrease, as shown in Fig. 10

Fig. 10
figure 10

Schematic diagram of signal incident to service antenna array from different directions

Full size image

In Fig. 10, when the far-field source signal is incident on the array from the line perpendicular to the two adjacent antennas in direction 1, the second and third antennas are mapped to the positions of antennas 1 and 3 respectively, resulting in the number of effective antennas being only 2, and the angles of signal incident on the mapped virtual linear array and service antenna are equal, so the angle of signal incident to the service antenna cannot be obtained by the angle of signal incident on the virtual linear array and the geometric relationship between the virtual linear array and the service antenna. Similarly, the signal incident from direction 2 to service antenna array is the same as that from direction 1. When the signal is incident on the array from direction 3, antenna 2 and antenna 3 are mapped to the same position on the connecting line of antenna 1 and antenna 4, and the effective number of antennas is 3. Although the signal angle can be accurately estimated by the three antennas, when the signal is perpendicular to the line of antennas 1 and 4, the angle of signal incident on the service antenna and virtual linear array is equal, and the angle of signal incident to the service antenna cannot be obtained by the angle of signal incident on the virtual linear array and the geometric relationship between the virtual linear array and the service antenna similarly. Therefore, the parameter estimation algorithm proposed in this paper cannot estimate the parameters of the signal incident from any edge and diagonal line of the rectangle which is perpendicular to the array antenna.

4 Conclusion

In this paper, a multi-dimensional joint parameter estimation algorithm based on the AoA, ToF, and DFS of service antenna array is proposed. The algorithm maps the antenna in the service antenna array which does not meet the spatial sampling theorem from the incident direction of the signal to the virtual linear array, and estimates the signal parameters through the virtual linear array. Finally, the true signal parameter is obtained through the geometric relationship between the plane array and the virtual linear array. The simulation results show that the proposed algorithm can accurately estimate the AoA when the antenna array spacing does not meet the spatial sampling theorem, and is not affected by the pseudo peak. However, when the SNR is very low, which is lower than − 30 dB, the accuracy of signal parameter estimation will be reduced due to the excessive influence of noise. Therefore, how to remove the influence of noise on the algorithm is the focus of the next step.