1 Introduction

Linear inverse problems are ubiquitous in many applications in science and engineering. Starting with the seminal works of Candès et al. [10], as well as Donoho [15], a new paradigm in their analysis became an active area of research in the last decades. Namely, rather than considering the linear model as entirely given by the application, one seeks to actively choose remaining degrees of freedom, often using a randomized strategy, to make the problem less ill-posed. This approach gave rise to a number of recovery guarantees for random linear measurement models under structural data assumptions. The first works considered the recovery of sparse signals; subsequent works analyzed more general union-of-subspaces models [18] and the recovery of low-rank matrices [44], a model that can also be employed when studying phaseless reconstruction problems [11] or bilinear inverse problems [1].

Another line of works following this approach studies manifold models. That is, one assumes that the structural constraints are given by (unions of finitely many) manifolds. While this model is considerably richer than say sparsity, its rather general formulation makes a unified study, at least in some cases, somewhat more involved. The first work to study random linear projections of smooth manifold was [5], the authors show that Gaussian linear dimension reductions typically preserve the geometric structure. In [29], these results are refined and complemented by a recovery algorithm, which is based on the concept of the Geometric Multi-Resolution Analysis as introduced in [3] (cf. Sect. 2.1 below). These results were again substantially improved in [17]; these latest results no longer explicitly depend on the ambient dimension.

Arguably, working with manifold models is better adapted to real-world data than sparsity and hence may allow one to work with smaller embedding dimensions. For that, however, other practical issues need to be considered as well. In particular, to our knowledge there are almost no works to date that study the effects of quantization, i.e., representing the measurements using only a finite number of bits (the only remotely connected work that we are aware of is [39], but this paper does not consider dimension reduction and exclusively focuses on the special case of Grassmann manifolds).

For sparse signal models, in contrast, quantization of subsampled random measurements is an active area of research. On the one hand, a number of works considered the scenario of memoryless scalar quantization, that is, each of the measurements is quantized independently. In particular, the special case of representing each measurement only by a single bit, its sign—often referred to as one-bit compressed sensing—has received considerable attention. In [31], it was shown that one-bit compressed sensing with Gaussian measurements approximately preserves the geometry, and a heuristic recovery scheme was presented. In [42], recovery guarantees for a linear method, again with Gaussian measurements, were derived. Subsequently, these results were generalized to sub-Gaussian measurements [2], and partial random circulant measurements [14]. In [41], the authors provided a recovery procedure for noisy one-bit Gaussian measurements which provably works on more general signal sets (essentially arbitrary subsets of the Euclidean ball). This procedure, however, becomes NP-hard as soon as the signal set is non-convex, a common property of manifolds.

Another line of works studied the so-called feedback quantizers, that is, the bit sequence encoding the measurements is computed using a recursive procedure. These works adapt the Sigma-Delta modulation approach originally introduced in the context of bandlimited signals [22, 40] and later generalized to frame expansions [6, 7] to the sparse recovery framework. A first such approach was introduced and analyzed for Gaussian measurements in [23]; subsequent works generalize the results to sub-Gaussian random measurements [20, 33]. Recovery guarantees for a more stable reconstruction scheme based on convex optimization were proven for sub-Gaussian measurements in [45] and extended to partial random circulant matrices in [21]. For more details on the mathematical analysis available for different scenarios, we refer the reader to the overview chapter [9].

In this paper, we focus on the MSQ approach and leave the study of Sigma-Delta quantizers under manifold model assumptions for future work.

1.1 Contribution

We provide the first tractable one-bit compressed sensing algorithm for signals which are well approximated by manifold models. It is simple to implement and comes with error bounds that basically match the state-of-the-art recovery guarantees in [41]. In contrast to the minimization problem introduced in [41], which does not come with a minimization algorithm, our approach always admits a convex formulation and hence allows for tractable recovery. Our approach is based on the Geometric Multi-Resolution Analysis (GMRA) introduced in [3], and hence combines the approaches of [29] with the general results for one-bit quantized linear measurements provided in [41, 43].

1.2 Outline

We begin by a detailed description of our problem in Sect. 2 and fix notation for the rest of the paper. The section also includes a complete axiomatic definition of GMRA. Section 3 states our main results. The proofs can be found in Sect. 4. In Sect. 5, we present some numerical experiments testing the recovery in practice and conclude with Sect. 6. Technical parts of the proofs as well as adaption of the results to GMRAs from random samples are deferred to the appendix.

2 Problem Formulation, Notation, and Setup

The problem we address is the following. We consider a given union of low-dimensional manifolds (i.e., signal class) \({\mathscr {M}}\) of intrinsic dimension d that is a subset of the unit sphere \({\mathbb {S}}^{D-1}\) of a higher dimensional space \({\mathbb {R}}^D\), \(d \ll D\). Furthermore, let us imagine that we do not know \({\mathscr {M}}\) perfectly, and so instead we only have approximate information about \({\mathscr {M}}\) represented in terms of a structured dictionary model \({\mathcal {D}}\) for the manifold. Our goal is now to recover an unknown signal \({\mathbf {x}}\in {\mathscr {M}}\) from m one-bit measurements

$$\begin{aligned} {\mathbf {y}}= {\text {sign}}A{\mathbf {x}}, \end{aligned}$$
(1)

where \(A \in {\mathbb {R}}^{m\times D}\) has Gaussian i.i.d. entries of variance \(1/\sqrt{m}\), using as few measurements, m, as possible. Each single measurement \({\text {sign}}{\langle {\mathbf {a}}_i,{\mathbf {x}}\rangle }\) can be interpreted as the random hyperplane \(\{{\mathbf {z}}\in {\mathbb {R}}^D:\langle {\mathbf {a}}_i,{\mathbf {z}}\rangle = 0\}\) tessellating the sphere (cf. Fig. 1a). In order to succeed using only \(m \ll D\) such one-bit measurements we will use the fact that \({\mathbf {x}}\) is approximately sparse in our (highly coherent, but structured) dictionary \({\mathcal {D}}\) for \({\mathscr {M}}\) provides structural constraints for signal \({\mathbf {x}}\) to be recovered. Thus the setup connects to recent generalizations of the quantized compressed sensing problem [41] which we will exploit in our proof.

Fig. 1
figure 1

One-bit measurements and GMRA

Full size image

2.1 GMRA Approximations to \({\mathscr {M}}\subset {\mathbb {R}}^D\) and Two Notions of Complexity

Clearly, the solution to this problem depends on what kind of representation, \({\mathcal {D}}\), of the manifold \({\mathscr {M}}\) we have access to. In this paper, we consider the scenario where the dictionary for the manifold is provided by a Geometric Multi-Resolution Analysis (GMRA) approximation to \({\mathscr {M}}\) [3] (cf. Fig. 1b). We will mainly work with GMRA approximations of \({\mathscr {M}}\) characterized by the axiomatic Definition 2.1 below, but we also consider the case of a GMRA approximation based on random samples from \({\mathscr {M}}\) (see Sect. 3 and Appendices D and E for more details).

As one might expect, the complexity and structure of the GMRA-based dictionary for \({\mathscr {M}}\) will depend on the complexity of \({\mathscr {M}}\) itself. In this paper, we will work with two different measures of a set’s complexity: (i) the set’s Gaussian width and (ii) the notion of the reach of the set [19]. The Gaussian width of a set \({\mathscr {M}}\subset {\mathbb {R}}^D\) is defined by

$$\begin{aligned} w({\mathscr {M}}) := {{\mathbb {E}}}_{}\!\left[ \sup _{{\mathbf {z}}\in {\mathscr {M}}} \langle {\mathbf {g}},{\mathbf {z}}\rangle \right] \end{aligned}$$

where \({\mathbf {g}}\sim {\mathcal {N}}({\mathbf {0}},I_D)\). Properties of this quantity are discussed in Sect. 4.1. The notion of reach is, in contrast, more obviously linked to the geometry of \({\mathscr {M}}\) and requires a couple of additional definitions before it can be defined formally.

The first of these definitions is the tube of radius r around a given subset \({\mathscr {M}}\subset {\mathbb {R}}^D\), which is the D-dimensional superset of \({\mathscr {M}}\) consisting of all the points in \({\mathbb {R}}^D\) that are within Euclidean distance \(r \ge 0\) from \({\mathscr {M}}\subset {\mathbb {R}}^D\),

$$\begin{aligned} \mathrm {tube}_r{\mathscr {M}}:= \Bigl \{ {\mathbf {x}}\in {\mathbb {R}}^D :\inf _{{\mathbf {y}}\in {\mathscr {M}}} \Vert {\mathbf {x}}- {\mathbf {y}}\Vert _2 \le r \Bigr \}. \end{aligned}$$

The domain of the nearest neighbor projection onto the closure of \({\mathscr {M}}\) is also needed, and is denoted by

$$\begin{aligned} D({\mathscr {M}}) := \Bigl \{{\mathbf {x}}\in \mathbb {\mathbb {R}}^D :\exists !\, {\mathbf {y}}\in {\overline{{\mathscr {M}}}} \text { such that }\Vert {\mathbf {x}}-{\mathbf {y}}\Vert _2=\inf _{{\mathbf {z}}\in {\mathscr {M}}}\Vert {\mathbf {x}}- {\mathbf {z}}\Vert _2 \Bigr \}. \end{aligned}$$

Finally, the reach of the set \({\mathscr {M}}\subset {\mathbb {R}}^D\) is simply defined to be the smallest distance r around \({\mathscr {M}}\) for which the nearest neighbor projection onto the closure of \({\mathscr {M}}\) is no longer well defined. Equivalently,

$$\begin{aligned}{\text {reach}}{\mathscr {M}}:=\sup {\{r\ge 0:\mathrm {tube}_r{\mathscr {M}}\subseteq D({\mathscr {M}})\}}. \end{aligned}$$

Given this definition one can see, e.g., that the reach of any \(d < D\) dimensional sphere of radius r in \({\mathbb {R}}^D\) is always r, and that the reach of any \(d \le D\) dimensional convex subset of \({\mathbb {R}}^D\) is always \(\infty \).

Definition 2.1

(GMRA approximation to \({\mathscr {M}}\) [29])Let \(J \in {\mathbb {N}}\) and \(K_0,K_1,\dots ,K_J \in {\mathbb {N}}\). Then a Geometric Multi-Resolution Analysis (GMRA) approximation of \({\mathscr {M}}\) is a collection \(\{ ({\mathscr {C}}_j,{\mathscr {P}}_j) \}\), \(j \in [J] := \{0,\dots ,J\}\), of sets \({\mathscr {C}}_j = \{ {\mathbf {c}}_{j,k} \}_{k = 1}^{K_j} \subset {\mathbb {R}}^D\) of centers and

$$\begin{aligned} {\mathscr {P}}_j = \bigl \{ {\mathbb {P}}_{j,k}:{\mathbb {R}}^D \rightarrow {\mathbb {R}}^D \mid k \in [K_j] \bigr \} \end{aligned}$$

of affine projectors that approximate \({\mathscr {M}}\) at scale j, such that the following assumptions (i)–(iii) hold.

  1. (i)

    Affine projections: Every \({\mathbb {P}}_{j,k} \in {\mathscr {P}}_j\) has both an associated center \({\mathbf {c}}_{j,k} \in {\mathscr {C}}_j\) and an orthogonal matrix \(\varPhi _{j,k} \in {\mathbb {R}}^{d \times D}\) such that

    $$\begin{aligned} {\mathbb {P}}_{j,k}({\mathbf {z}}) = \varPhi _{j,k}^T \varPhi _{j,k} ({\mathbf {z}}-{\mathbf {c}}_{j,k}) + {\mathbf {c}}_{j,k}, \end{aligned}$$

    i.e., \({\mathbb {P}}_{j,k}\) is the projector onto some affine d-dimensional linear subspace \(P_{j,k}\) containing \({\mathbf {c}}_{j,k}\).

  2. (ii)

    Dyadic structure: The number of centers at each level is bounded by \(|{\mathscr {C}}_j| = K_j \le C_{{\mathscr {C}}}2^{dj}\) for an absolute constant \(C_{{\mathscr {C}}} \ge 1\). There exist \(C_1 > 0\) and \(C_2 \in (0,1]\), such that following conditions are satisfied:

    1. (a)

      \(K_j \le K_{j+1}\) for all \(j \in [J-1]\).

    2. (b)

      \(\Vert {\mathbf {c}}_{j,k_1} - {\mathbf {c}}_{j,k_2} \Vert _2 > C_1 \cdot 2^{-j}\) for all \(j \in [J]\) and \(k_1 \ne k_2 \in [K_j]\).

    3. (c)

      For each \(j \in [J]\setminus \{ 0 \}\) there exists a parent function \(p_j :[K_j] \rightarrow [K_{j-1}]\) with

      $$\begin{aligned} \Vert {\mathbf {c}}_{j,k} - {\mathbf {c}}_{j-1,p_j(k)} \Vert _2 \le C_2\, \cdot \!\min _{k' \in [K_{j-1}] \setminus \{ p_j(k) \}} \Vert {\mathbf {c}}_{j,k} - {\mathbf {c}}_{j-1,k'}\Vert _2. \end{aligned}$$
  3. (iii)

    Multiscale approximation: The projectors in \({\mathscr {P}}_j\) approximate \({\mathscr {M}}\) at scale j, i.e., when \({\mathscr {M}}\) is sufficiently smooth the affine spaces \(P_{j,k}\) locally approximate \({\mathscr {M}}\) pointwise with error \({\mathscr {O}}( 2^{-2j})\). More precisely:

    1. (a)

      There exists \(j_0 \in [J-1]\) such that \({\mathbf {c}}_{j,k} \in \mathrm {tube}_{C_12^{-j-2}} ({\mathscr {M}})\) for all \(j > j_0 \ge 1\) and \(k\in [K_j]\).

    2. (b)

      For each \(j \in [J]\) and \({\mathbf {z}}\in {\mathbb {R}}^D\) let \({\mathbf {c}}_{j, k_j({\mathbf {z}})}\) be one of the centers closest to \({\mathbf {z}}\), i.e.,

      $$\begin{aligned} k_j({\mathbf {z}}) \in \mathop {\mathrm {arg \, min}}\limits _{k \in [K_j]} \Vert {\mathbf {z}}- {\mathbf {c}}_{j,k} \Vert _2. \end{aligned}$$
      (2)

      Then, for each \({\mathbf {z}}\in {\mathscr {M}}\) there exists a constant \(C_{\mathbf {z}}> 0\) such that

      $$\begin{aligned} \Vert {\mathbf {z}}- {\mathbb {P}}_{j, k_j({\mathbf {z}})} ({\mathbf {z}}) \Vert _2 \le C_{\mathbf {z}}\cdot 2^{-2j} \end{aligned}$$

      for all \(j \in [J]\). Moreover, for each \({\mathbf {z}}\in {\mathscr {M}}\) there exists \({\tilde{C}}_{\mathbf {z}}> 0\) such that

      $$\begin{aligned} \Vert {\mathbf {z}}- {\mathbb {P}}_{j,k'}({\mathbf {z}}) \Vert _2 \le {\tilde{C}}_{\mathbf {z}}\cdot 2^{-j} \end{aligned}$$

      for all \(j \in [J]\) and \(k' \in [K_j]\) satisfying

      $$\begin{aligned} \Vert {\mathbf {z}}- {\mathbf {c}}_{j,k'} \Vert _2 \le 16 \cdot \max {\bigl \{ \Vert {\mathbf {z}}- {\mathbf {c}}_{j,k_j({\mathbf {z}})} \Vert _2, C_1 \cdot 2^{-j-1} \bigr \}}. \end{aligned}$$

Remark 2.2

By property (i), GMRA approximation represents \({\mathscr {M}}\) as a combination of several anchor points (the centers \({\mathbf {c}}_{j,k}\)) and corresponding low-dimensional affine spaces \(P_{j,k}\). The levels j control the accuracy of the approximation. The centers are organized in a tree-like structure as stated in property (ii). Property (iii) then characterizes approximation criteria to be fulfilled on different refinement levels. Note that centers do not have to lie on \({\mathscr {M}}\) (compare Fig. 1b) but their distance to \({\mathscr {M}}\) is controlled by property (iii.a). If the centers form a maximal \(2^{-j}\) packing of a smooth manifold \({\mathscr {M}}\) at each scale j or if the GMRA is constructed from manifold samples as discussed in [38] (cf. Appendix E), the constants \(C_1\) and \({{\tilde{C}}}_{\mathbf {z}}\) are in fact bounded by absolute constants which will become important later on, cf. Remark 3.2.

Fig. 2
figure 2

The closest center \({\mathbf {c}}_{j,k_j({\mathbf {x}})}\) is not identified by measurements. Dotted lines represent one-bit hyperplanes

Full size image

2.2 Additional Notation

Let us now fix some additional notation. Throughout the remainder of this paper we will work with several different metrics. Perhaps most importantly, we will quantify the distance between two points \({\mathbf {z}},{\mathbf {z}}' \in {\mathbb {R}}^D\) with respect to their one-bit measurements by

$$\begin{aligned} d_A({\mathbf {z}},{\mathbf {z}}') := \frac{d_{H }({\text {sign}}A{\mathbf {z}},{\text {sign}}A{\mathbf {z}}')}{m}, \end{aligned}$$

where \(d_{H }\) counts the number of differing entries between the two sign patterns (i.e., \(d_A({\mathbf {z}},{\mathbf {z}}')\) is the normalized Hamming distance between the signs of \(A{\mathbf {z}}\) and \(A{\mathbf {z}}'\)). Furthermore, let \({\mathbb {P}}_{\mathbb {S}}\) denote orthogonal projection onto the unit sphere \({\mathbb {S}}^{D-1}\), and more generally let \({\mathbb {P}}_K\) denote orthogonal (i.e., nearest neighbor) projection onto the closure of an arbitrary set \(K\subset {\mathbb {R}}^D\) wherever it is defined. Then, for all \({\mathbf {z}},{\mathbf {z}}' \in {\mathbb {R}}^D\) we will denote by \(d_{G }({\mathbf {z}},{\mathbf {z}}') = d_{G }({\mathbb {P}}_{\mathbb {S}}({\mathbf {z}}),{\mathbb {P}}_{\mathbb {S}}({\mathbf {z}}'))\) the geodesic distance between \({\mathbb {P}}_{\mathbb {S}}({\mathbf {z}})\) and \(P_{\mathbb {S}}({\mathbf {z}}')\) on \({\mathbb {S}}^{D-1}\) normalized to fulfill \(d_{G }({\mathbf {z}}'',-{\mathbf {z}}'') = 1\) for all \({\mathbf {z}}'' \in {\mathbb {R}}^D\).

Herein the Euclidian ball with center \({\mathbf {z}}\) and radius r is denoted by \({\mathscr {B}}({\mathbf {z}},r)\). In addition, the scale-j GMRA approximation to \({\mathscr {M}}\),

$$\begin{aligned} {\mathscr {M}}_j := \{ {\mathbb {P}}_{j,k_j({\mathbf {z}})}({\mathbf {z}}) :{\mathbf {z}}\in {\mathscr {B}}({\mathbf {0}},2) \} \cap {\mathscr {B}}({\mathbf {0}},2), \end{aligned}$$

will refer to the portions of the affine subspaces introduced in Definition 2.1 for each fixed j, which are potentially relevant as approximations to some portion of \({\mathscr {M}}\subset {\mathbb {S}}^{D-1}\). To prevent the \({\mathscr {M}}_j\) above from being empty we will further assume in our results that we only use scales \(j > j_0\) large enough to guarantee that \(\mathrm {tube}_{C_1 2^{-j-2}} ({\mathscr {M}}) \subset {\mathscr {B}}(0,2)\). Hence we will have \({\mathbf {c}}_{j,k} \in {\mathscr {B}}({\mathbf {0}},2)\) for all \(k \in K_j\), and so \({\mathscr {C}}_j \subset {\mathscr {M}}_j\). This further guarantees that no sets \(P_{j,k} \cap {\mathscr {B}}({\mathbf {0}},2)\) are empty, and that \(P_{j,k} \cap {\mathscr {B}}({\mathbf {0}},2) \subset {\mathscr {M}}_j\) for all \(k \in K_j\).

Finally, we write \(a > rsim b\) if \(a \ge Cb\) for some constant \(C > 0\). The diameter of a set \(K \subset {\mathbb {R}}^D\) will be denoted by \({\text {diam}}K:= \sup _{{\mathbf {z}},{\mathbf {z}}' \in K} \Vert {\mathbf {z}}- {\mathbf {z}}' \Vert _2\), where \(\Vert \,{\cdot }\, \Vert _2\) is the Euclidian norm. We use \(\mathrm {dist}(A,B) = \inf _{{\mathbf {a}}\in A, {\mathbf {b}}\in B} \Vert {\mathbf {a}}- {\mathbf {b}}\Vert _2\) for the distance of two sets \(A,B \subset {\mathbb {R}}^D\) and, by an abuse of notation, \(\mathrm {dist}({\mathbf {0}}, A) = \inf _{{\mathbf {a}}\in A} \Vert {\mathbf {a}}\Vert _2\). The operator norm of a matrix \(A\in {\mathbb {R}}^{n_1\times n_2}\) is denoted by \(\Vert A \Vert =\sup _{{\mathbf {x}}\in \mathbb R^{n_2},\Vert {\mathbf {x}}\Vert _2\le 1}\Vert A{\mathbf {x}}\Vert _2\). We will write \({\mathscr {N}}(K,\varepsilon )\) to denote the Euclidian covering number of a set \(K \subset {\mathbb {R}}^D\) by Euclidean balls of radius \(\varepsilon \) (i.e., \({\mathscr {N}}(K,\varepsilon )\) is the minimum number of \(\varepsilon \)-balls that are required to cover K). And, the operators \(\lfloor r \rfloor \) (resp. \(\lceil r \rceil \)) return the closest integer smaller (resp. larger) than \(r \in {\mathbb {R}}\).

2.3 The Proposed Computational Approach

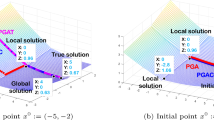
Combining prior GMRA-based compressed sensing results [29] with the one-bit results of Plan and Vershynin in [41] suggests the following strategy for recovering an unknown \({\mathbf {x}}\in {\mathscr {M}}\) from the measurements given in (1): First, choose a center \({\mathbf {c}}_{j,k'}\) whose one-bit measurements agree with as many one-bit measurements of \({\mathbf {x}}\) as possible. Due to the varying shape of the tessellation cells this is not an optimal choice in general (see Fig. 2). Nevertheless, one can expect \(P_{j,k'}\) to be a good approximation to \({\mathscr {M}}\) near \({\mathbf {x}}\). Thus, in the second step a modified version of Plan and Vershynin’s noisy one-bit recovery method using \(P_{j,k'}\) should yield an approximation of \({\mathbb {P}}_{j,k'}({\mathbf {x}})\) which is close to \({\mathbf {x}}\).Footnote 1 See OMS-simple for pseudocode.

figure a

Remark 2.3

The minimization in (3) can be efficiently calculated by exploiting tree structures in \({\mathscr {C}}_j\). Numerical experiments (see Sect. 5) suggest this strategy to yield adequate approximation for the center \({\mathbf {c}}_{j,k_j({\mathbf {x}})}\) in (2), while being considerably faster (we observed differences in runtime up to a factor of 10).

Though simple to understand, the constraints in (4) have two issues that we need to address: First, in some cases the minimization problem (4) empirically exhibits suboptimal recovery performance (see Sect. 5.1 for details). Second, the parameter R in (4) is unknown a priori (i.e., OMS-simple requires parameter tuning, making it less practical than one might like). Indeed, our analysis shows that making an optimal choice for R in OMS-simple requires a priori knowledge about \(\Vert {\mathbb {P}}_{j,k'}({\mathbf {x}}) \Vert _2\) which is only approximately known in advance.

To address this issue, we will modify the constraints in (4) and instead minimize over the convex hull of the nearest neighbor projection of \(P_{j,k'} \cap {\mathscr {B}}({\mathbf {0}},2)\) onto \({\mathbb {S}}^{D-1}\),

$$\begin{aligned} {\text {conv}}{\mathbb {P}}_{\mathbb {S}}(P_{j,k'} \cap {\mathscr {B}}({\mathbf {0}},2)), \end{aligned}$$

to remove the R dependence. If \({\mathbf {0}} \in P_{j,k'}\) one has \({\text {conv}}{\mathbb {P}}_{\mathbb {S}}(P_{j,k'} \cap {\mathscr {B}}({\mathbf {0}},2))=P_{j,k'} \cap {\mathscr {B}}({\mathbf {0}},1)\). If \({\mathbf {0}} \notin P_{j,k'}\) the set \({\text {conv}}{\mathbb {P}}_{\mathbb {S}}(P_{j,k'} \cap {\mathscr {B}}({\mathbf {0}},2))\) is described by the following set of convex constraints which are straightforward to implement in practice. Denote by \({\mathbb {P}}_{\mathbf {c}}\) the projection onto the vector \({\mathbf {c}}= {\mathbb {P}}_{j,k'}({\mathbf {0}})\). Then

$$\begin{aligned} {\mathbf {z}}\in {\text {conv}} {\mathbb {P}}_{\mathbb {S}}(P_{j,k'} \cap {\mathscr {B}}({\mathbf {0}},2))\quad \Longleftrightarrow \quad {\left\{ \begin{array}{ll} \Vert {\mathbf {z}}\Vert _2 \le 1, \\ \varPhi _{j,k'}^T \varPhi _{j,k'} {\mathbf {z}}+ {\mathbb {P}}_{\mathbf {c}}({\mathbf {z}}) = {\mathbf {z}}, \\ \langle {\mathbf {z}},{\mathbf {c}}\rangle \ge \Vert {\mathbf {c}}\Vert _2^2/2. \end{array}\right. } \end{aligned}$$
(5)

The first two conditions above restrict \({\mathbf {z}}\) to \({\mathscr {B}}({\mathbf {0}},1)\) and \({\text {span}}P_{j,k'}\), respectively. The third condition then removes all points that are too close to the origin (see Fig. 3). A rigorous proof of equivalence can be found in Appendix A.

Fig. 3
figure 3

Two views of an admissible set \({\text {conv}}{\mathbb {P}}_{\mathbb {S}}(P_{j,k'}\cap {\mathscr {B}}(\mathbf{0},2))\) from (5) if \(\Vert {\mathbf {c}}\Vert _2 = \Vert {\mathbb {P}}_{j,k'}({\mathbf {0}}) \Vert _2 \!<\! 1\)

Full size image

Our analysis uses that the noisy one-bit recovery results of Plan and Vershynin apply to arbitrary subsets of the unit ball \({\mathscr {B}}({\mathbf {0}},1) \subset {\mathbb {R}}^D\) which will allow us to adapt our recovery approach. Replacing the constraints in (4) with those in (5) we obtain the following modified recovery approach, OMS.

figure b

As we shall see, theoretical error bounds for both OMS-simple and OMS can be obtained by nearly the same analysis despite their differences.

3 Main Results

In this section, we present the main results of our work, namely that both OMS-simple and OMS approximate a signal on \({\mathscr {M}}\) to arbitrary precision with a near-optimal number of measurements. More precisely, we obtain the following theorem.

Theorem 3.1

((uniform) recovery) There exist absolute constants \(E,E',c > 0\) such that the following holds. Let \(\epsilon \in (0,1)\) and assume the GMRA’s maximum refinement level \(J \ge j := \lceil \log (1/\varepsilon ) \rceil \). Further suppose that one has \(\mathrm {dist}({\mathbf {0}},{\mathscr {M}}_j) \ge 1/2\), \(0<C_1 < 2^{j}\), and \(\sup _{{\mathbf {x}}\in {\mathscr {M}}}{\tilde{C}}_{\mathbf {x}}< 2^{j - 2}\). If

$$\begin{aligned} m \ge E C_1^{-6} \varepsilon ^{-6} \max {\bigl \{w({\mathscr {M}}), \sqrt{d\log (e/\varepsilon )} \bigr \}^2}, \end{aligned}$$
(8)

then with probability at least \(1-12e^{-c C_1^2 \varepsilon ^2 m}\), for all \({\mathbf {x}}\in {\mathscr {M}}\subset {\mathbb {S}}^{D-1}\) the approximations \({\mathbf {x}}^*\) obtained by OMS satisfy

$$\begin{aligned} \Vert {\mathbf {x}}- {\mathbf {x}}^*\Vert _2^2 \le E' \bigl ( 1 + {\tilde{C}}_{\mathbf {x}}+ C_1 \max {\{ 1,\log C_1^{-1}\}} \bigr )^2 \varepsilon \log \frac{1}{2\varepsilon }. \end{aligned}$$
(9)

Proof

The proof can be found below Theorem 4.14 in Sect. 4. \(\square \)

Remark 3.2

Let us briefly comment on the assumptions of Theorem 3.1. First, since \({\mathscr {M}}\subset {\mathbb {S}}^{D-1}\), requiring \(\mathrm {dist}({\mathbf {0}},{\mathscr {M}}_j) \ge 1/2\) is a mild assumption. Any GMRA not fulfilling it would imply a worst-case reconstruction error of 1/2 in (9). The constant 1/2 was chosen for simplicity and can be replaced by an arbitrary number in (0, 1). This, however, influences the constants \(E,E',c\). Second, the restrictions on \(C_1\) and \({{\tilde{C}}}_{\mathbf {x}}\) are easily satisfied, e.g., if the centers form a maximal \(2^{-j}\) packing of \({\mathscr {M}}\) at each scale j or if the GMRA is constructed from manifold samples as discussed in [38] (cf. Appendix E). In both these cases \(C_1\) and \({{\tilde{C}}}_{\mathbf {x}}\) are in fact bounded by absolute constants.

Note that Theorem 3.1 depends on the Gaussian width of \({\mathscr {M}}\). For general sets K this quantity provides a quite tight measure of the set complexity which might seem counter-intuitive for non-convex K on first sight. After all the convex hull of K might be considerably larger than the set itself while \(w(K) = w({\text {conv}} K)\). However, the intuition is deceptive in this case. In high-dimensional spaces, the intrinsic complexity of non-convex sets and their convex hull hardly differ. For instance, if K is the set of s-sparse vectors in the D-dimensional Euclidean unit ball, its convex hull, the \(\ell _1\)-ball, is full dimensional but \(w(K) = w({\text {conv}} K) \approx s \log (D/s)\) which differs from the information theoretic lower bound on the complexity of K by at most a log-factor.

In the case of compact Riemannian submanifolds of \({\mathbb {R}}^D\) it might be more convenient to have a dependence on the geometric properties of \({\mathscr {M}}\) instead (e.g., its volume and reach). Indeed, one can show by means of [17] that \(w({\mathscr {M}})\) can be upper bounded in terms of the manifold’s intrinsic dimension d, its d-dimensional volume \({\text {Vol}}{\mathscr {M}}\), and the inverse of its reach. Intuitively, these dependencies are to be expected as a manifold with fixed intrinsic dimension d can become more complex as either its volume or curvature (which can be bounded by the inverse of its reach) grows. The following theorem, which is a combination of different results in [17], formalizes this intuition by bounding the Gaussian width of a manifold in terms of its geometric properties.

Theorem 3.3

Assume \({\mathscr {M}}\subset {\mathbb {R}}^D\) is a compact d-dimensional Riemannian manifold with d-dimensional volume \({\text {Vol}}{\mathscr {M}}\) where \(d \ge 1\). Then one can replace \(w({\mathscr {M}})\) in the above theorem by

$$\begin{aligned} w({\mathscr {M}}) \le C\cdot {\text {diam}}{\mathscr {M}}\cdot \sqrt{d \cdot \max {\biggl \{\log \frac{c\sqrt{d}}{\min {\{1,{\text {reach}}{\mathscr {M}}\}}}, 1 \biggr \}} + \log \max {\{1,{\text {Vol}}{\mathscr {M}}\}}} \end{aligned}$$

where \(C,c > 0\) are absolute constants.

Proof

See Appendix B. \(\square \)

Remark 3.4

Note that in our setting \({\mathscr {M}}\subset {\mathbb {S}}^{D-1}\) implies that \({\text {diam}}{\mathscr {M}}\le 2\) and \({\text {reach}}{\mathscr {M}}\le 1\). As we will see, the Gaussian width of the GMRA approximation to \({\mathscr {M}}\) is also bounded in terms of \(w({\mathscr {M}})\). This additional width bound is crucial to the proof of Theorem 3.1 as the complexity of the GMRA approximation to \({\mathscr {M}}\) also matters whenever one attempts to approximate an \({\mathbf {x}}\in {\mathscr {M}}\) using only the available GMRA approximation to \({\mathscr {M}}\). See, e.g., Lemmas 4.3, 4.5, and 4.6 below for upper bounds on the Gaussian widths of GMRA approximations to manifolds \({\mathscr {M}}\subset {\mathbb {S}}^{D-1}\) in various settings.

Finally, we point out that Theorem 3.1 assumes access to a GMRA approximation to \({\mathscr {M}}\subset {\mathbb {S}}^{D-1}\), which satisfies all of the axioms listed in Definition 2.1. Following the work of Maggioni et al. [38], however, one can also ask whether a similar result will still hold if the GMRA approximation one has access to has been learned by randomly sampling points from \({\mathscr {M}}\) without the assumptions of Definition 2.1 being guaranteed a priori. Indeed, such a setting is generally more realistic. In fact it turns out that a version of Theorem 3.1 still holds for such empirical GMRA approximations under suitable conditions; see Theorem E.7. We refer the interested reader to Appendices D and E for additional details and discussion regarding the use of such empirically learned GMRA approximations.

4 Proofs

This section provides proofs of the main result in both settings described above and establishes several technical lemmas. First, properties of the Gaussian width and the geodesic distance are collected and shown. Then, the main results are proven for a given GMRA approximation fulfilling the axioms.

4.1 Toolbox

We start by connecting slightly different definitions of dimensionality measures similar to the Gaussian width and clarify how they relate to each other. This is necessary as the tools we make use of appear in their original versions referring to different definitions of Gaussian width.

Definition 4.1

(Gaussian (mean) width)   Let \(g\sim {\mathcal {N}}({\mathbf {0}},\mathrm {Id}_D)\). For a subset \(K \subset {\mathbb {R}}^D\) define

  1. (i)

    the Gaussian width: \(w(K) := \mathbb E\bigl [\sup _{{\mathbf {x}}\in K}\langle {\mathbf {g}},{\mathbf {x}}\rangle \bigr ]\),

  2. (ii)

    the Gaussian mean width to be the Gaussian width of \(K-K\), and

  3. (iii)

    the Gaussian complexity: \(\gamma (K)=\mathbb E\bigl [\sup _{{\mathbf {x}}\in K}|\langle {\mathbf {g}},{\mathbf {x}}\rangle |\bigr ]\).

By combining properties 5) and 6) of [41, Prop. 2.1] one has

$$\begin{aligned} w(K-K)\le 2w(K)\le 2\gamma (K)\le 2\biggl (w(K-K)+\sqrt{\frac{2}{\pi }}\,\mathrm {dist}({\mathbf {0}},K)\biggr ). \end{aligned}$$
(10)

Remark 4.2

One can easily verify that \(w(K) \ge 0\) for all \(K \subset {\mathbb {R}}^D\) since \(w(K) := \mathbb E\bigl [\sup _{{\mathbf {x}}\in K}\langle {\mathbf {g}},{\mathbf {x}}\rangle \bigr ] \ge \sup _{{\mathbf {x}}\in K} \mathbb E[\langle {\mathbf {g}},{\mathbf {x}}\rangle ]= 0\). The square \(w(K \cap B(0, 1))^2\) of the Gaussian width of \(K \subset {\mathbb {R}}^D\) is also a good measure of intrinsic dimension. For example, if K is a linear subspace with \(\dim K=d\) then \(w(K \cap {\mathscr {B}}({\mathbf {0}},1)) \le \sqrt{d}\). In this sense, the Gaussian width extends the concept of dimension to general sets K. Furthermore, for a finite set K the Gaussian width is bounded by \(w(K) \le C_f{\text {diam}}(K \cup \{ {\mathbf {0}} \}) \sqrt{\log |K|}\). This can be deduced directly from the definition (see, e.g., [41, Sect. 2]).

Now that we have introduced the notion of Gaussian width, we can use it to characterize the union of the given manifold and a single level of its GMRA approximation \({\mathscr {M}}\cup {\mathscr {M}}_j\) (recall the definition of \({\mathscr {M}}_j\) in Sect. 2).

Lemma 4.3

(a bound on the Gaussian width for coarse scales)   For \({\mathscr {M}}_j\), the subspace approximation in the GMRA of level \(j > j_0\) (cf. the end of Sect. 2) for \({\mathscr {M}}\) of dimension \(d\ge 1\), the Gaussian width of \({\mathscr {M}}\cup {\mathscr {M}}_j\) can be bounded from above and below by

$$\begin{aligned} \max { \{ w({\mathscr {M}}),w({\mathscr {M}}_j) \} }\le & {} w({\mathscr {M}}\cup {\mathscr {M}}_j)\\\le & {} 2w({\mathscr {M}}) + 2w({\mathscr {M}}_j) + 3 \le 2w({\mathscr {M}})+ C\sqrt{dj}. \end{aligned}$$

Remark 4.4

Note that the first inequality holds for general sets, not only \({\mathscr {M}}\) and \({\mathscr {M}}_j\). Moreover, one only uses \({\mathscr {M}}_j \subset {\mathscr {B}}({\mathbf {0}},2)\) to prove the second inequality. It thus holds for \({\mathscr {M}}_j\) replaced with arbitrary subsets of \({\mathscr {B}}({\mathbf {0}},2)\). We might use both variations referring to Lemma 4.3.

Proof

The first inequality follows by noting that

$$\begin{aligned} \max { \{ w({\mathscr {M}}),w({\mathscr {M}}_j) \}}&= \max { \biggl \{ \mathbb E\biggl [{\sup _{{\mathbf {v}}\in {\mathscr {M}}} \langle {\mathbf {v}}, {\mathbf {g}}\rangle }\biggr ], \mathbb E\biggl [{\sup _{{\mathbf {v}}\in {\mathscr {M}}_j} \langle {\mathbf {v}},{\mathbf {g}}\rangle }\biggr ] \biggr \}} \\&\le \mathbb E\biggl [{\sup _{{\mathbf {v}}\in {\mathscr {M}}\cup {\mathscr {M}}_j} \langle {\mathbf {v}},{\mathbf {g}}\rangle }\biggr ] = w({\mathscr {M}}\cup {\mathscr {M}}_j). \end{aligned}$$

To obtain the second inequality observe that

$$\begin{aligned} \begin{aligned} w({\mathscr {M}}\cup {\mathscr {M}}_j)&\le \gamma ({\mathscr {M}}\cup {\mathscr {M}}_j) \le \mathbb E\biggl [{\sup _{{\mathbf {v}}\in {\mathscr {M}}} |\langle {\mathbf {v}},{\mathbf {g}}\rangle |+ \sup _{{\mathbf {v}}\in {\mathscr {M}}_j} |\langle {\mathbf {v}},{\mathbf {g}}\rangle |}\biggr ] \\&= \gamma ({\mathscr {M}})+\gamma ({\mathscr {M}}_j) \\&\le 2w({\mathscr {M}}) + 2w({\mathscr {M}}_j) + \sqrt{\frac{2}{\pi }}{\text {dist}}({\mathbf {0}},{\mathscr {M}}) + \sqrt{\frac{2}{\pi }}{\text {dist}}({\mathbf {0}},{\mathscr {M}}_j) \\&\le 2\biggl ( w({\mathscr {M}}) + w({\mathscr {M}}_j) + 1.5\sqrt{\frac{2}{\pi }} \biggr ), \end{aligned} \end{aligned}$$
(11)

where we used (10), the fact that \({\mathscr {M}}\subset {\mathbb {S}}^{D-1}\), and that \({\mathscr {M}}_j \subset {\mathscr {B}}({\mathbf {0}},2)\). For the last inequality we bound \(w({\mathscr {M}}_j)\). First, note that

$$\begin{aligned} w ({\mathscr {M}}_j)&= \mathbb E\biggl [{\sup _{{\mathbf {v}}\in {\mathscr {M}}_j}\langle {\mathbf {v}},{\mathbf {g}}\rangle }\biggr ] = \mathbb E\biggl [{\sup _{{\mathbf {v}}\in \{ {\mathbb {P}}_{j,k_j({\mathbf {x}})}({\mathbf {x}}) :{\mathbf {x}}\in {\mathscr {B}}({\mathbf {0}},2) \} \cap {\mathscr {B}}({\mathbf {0}},2) } \langle {\mathbf {v}},{\mathbf {g}}\rangle }\biggr ]\\&\le \mathbb E\Biggl [{\sup _{{\mathbf {x}}\in \bigcup _{k \in [K_j]} P_{j,k} \cap {\mathscr {B}}({\mathbf {0}},2)}\langle {\mathbf {x}},{\mathbf {g}}\rangle }\Biggr ]. \end{aligned}$$

For all \(k \in [K_j]\) there exist d-dimensional Euclidean balls \(L_{j,k}\subset P_{j,k}\) of radius 2 such that \(P_{j,k} \cap {\mathscr {B}}({\mathbf {0}},2) \subset L_{j,k}\). Hence, \(\bigcup _{k \in [K_j]} (P_{j,k} \cap {\mathscr {B}}({\mathbf {0}},2)) \subset L_j := \bigcup _{k \in [K_j]} L_{j,k}\). By definition, the \(\varepsilon \)-covering number of \(L_j\) (a union of \(K_j\) d-dimensional balls) can be bounded by \({\mathscr {N}}(L_j,\varepsilon ) \le K_j (6/\varepsilon )^d\) which implies \(\log {\mathscr {N}}(L_j,\varepsilon ) \le dj \log ( 12C_{\mathscr {C}}/\varepsilon )\) by GMRA property (ii). By Dudley’s inequality (see, e.g., [16]) we conclude via Jensen’s inequality that

$$\begin{aligned} w({\mathscr {M}}_j)&\le w(L_j) \le C_\text {Dudley} \int _0^2\! \sqrt{\log {{\mathscr {N}}(L_j,\varepsilon )}}\,\mathrm {d}\varepsilon \\&\le C_Dudley \sqrt{dj} \int _0^2 \!\sqrt{\log 12C_{\mathscr {C}}- \log \varepsilon }\,\mathrm {d}\varepsilon \\&\le C_\text {Dudley} \sqrt{dj} \sqrt{ 2 \log 12C_{\mathscr {C}}- \int _0^2 \log \varepsilon \,\mathrm {d}\varepsilon }\le C' \sqrt{dj}, \end{aligned}$$

where \(C'\) is a constant depending on \(C_\text {Dudley}\) and \(C_{\mathscr {C}}\). Choosing \(C = 2C' + 3\) yields the claim as \(3\sqrt{2/ \pi } \le 3 \sqrt{dj}\). \(\square \)

The following two lemmas concerning width bounds for fine scales will also be useful. Their proofs (see Appendix C), though more technical, use ideas similar to the proof of Lemma 4.3. The first lemma improves on Lemma 4.3 for large values of j by considering a more geometrically precise approximation to \({\mathscr {M}}\), \({\mathscr {M}}^{rel }_j \subset {\mathscr {M}}_j\).

Lemma 4.5

(a bound of the Gaussian width for fine scales) Assume \(j \ge \log _2D\), \(\max { \{ 1, \sup _{{\mathbf {z}}\in {\mathscr {M}}}C_{\mathbf {z}}\}} =: C_{{\mathscr {M}}}<\infty \), and \({\mathscr {M}}^{rel }_j := \{{\mathbb {P}}_{j,k_j({\mathbf {z}})}({\mathbf {z}}):{\mathbf {z}}\in {\mathscr {M}}\} \cap B({\mathbf {0}},2)\). We obtain

$$\begin{aligned} \max { \{ w({\mathscr {M}}),w({\mathscr {M}}^{rel }_j) \} }\le & {} w({\mathscr {M}}\cup {\mathscr {M}}^{rel }_j)\\\le & {} 2w({\mathscr {M}}) + 2w({\mathscr {M}}^{rel }_j) + 3 \le C (w({\mathscr {M}}) + 1)\log D. \end{aligned}$$

It is not surprising that for general \({\mathscr {M}}\in {\mathbb {S}}^{D-1}\) the width bound for \(w({\mathscr {M}}_j)\) (resp. \(w({\mathscr {M}}^{rel }_j)\)) depends on either j or \(\log D\). When using the proximity of \({\mathscr {M}}^{rel }_j\) to \({\mathscr {M}}\) in Lemma 4.5 we only use the information that \({\mathscr {M}}^{rel }_j \subset \mathrm {tube}_{C_{{\mathscr {M}}} 2^{-2j}}\) and a large ambient dimension D will lead to a higher complexity of the tube. In the case of Lemma 4.3, we omit the proximity argument by using the maximal number of affine d-dimensional spaces in \({\mathscr {M}}_j\) and hence do not depend on D but on the refinement level j.

The next lemma just below utilizes even more geometric structure by assuming that \({\mathscr {M}}\) is a Riemannian manifold. It improves on both Lemma 4.3 and 4.5 for such \({\mathscr {M}}\) by yielding a width bound which is independent of both j and D for all j sufficiently large.

Lemma 4.6

(a bound of the Gaussian width for approximations to Riemannian manifolds) Assume \({\mathscr {M}}\subset {\mathbb {S}}^{D-1}\) is a compact d-dimensional Riemannian manifold with d-dimensional volume \({\text {Vol}}{\mathscr {M}}\) where \(d \ge 1\). Furthermore, suppose that for \(\max {\{ 1, \sup _{{\mathbf {z}}\in {\mathscr {M}}}C_{\mathbf {z}}\}} =: C_{{\mathscr {M}}}\), \(j > \max {\{ j_0, \log _2(8 C_{{\mathscr {M}}} / C_1) \}}\), and set \({\mathscr {M}}^{rel }_j := \{{\mathbb {P}}_{j,k_j({\mathbf {z}})}({\mathbf {z}}): {\mathbf {z}}\in {\mathscr {M}}\} \cap {\mathscr {B}}({\mathbf {0}},2)\). Then there exist absolute constants \(C,c > 0\) such that

$$\begin{aligned}&\max { \{ w({\mathscr {M}}),w({\mathscr {M}}^{rel }_j) \} }\le w({\mathscr {M}}\cup {\mathscr {M}}^{rel }_j) \\&\quad \le C \sqrt{ d\biggl (1+\log \frac{c\sqrt{d}}{{\text {reach}}M}\biggr ) + \log \max {\{1,{\text {Vol}}{\mathscr {M}}\}}}. \end{aligned}$$

Here the constants \(C_z\) and \(C_1\) are from properties (iii.b) and (iii.a), respectively.

Finally, the following lemma quantifies the equivalence between Euclidean and normalized geodesic distance on the sphere.

Lemma 4.7

For \({\mathbf {z}}, {\mathbf {z}}'\in {\mathbb {S}}^{D-1}\) one has

$$\begin{aligned} d_{G }( {\mathbf {z}}, {\mathbf {z}}')\le \Vert {\mathbf {z}}- {\mathbf {z}}'\Vert _2\le \pi d_{G }( {\mathbf {z}}, {\mathbf {z}}'). \end{aligned}$$

Proof

First observe that \(\langle {\mathbf {z}}, {\mathbf {z}}'\rangle =\cos \measuredangle ({\mathbf {z}},{\mathbf {z}}')=\cos \pi d_{G }({\mathbf {z}},{\mathbf {z}}')\). This yields

$$\begin{aligned} \Vert {\mathbf {z}}- {\mathbf {z}}'\Vert _2-d_{G }( {\mathbf {z}}, {\mathbf {z}}')=\sqrt{2-2\cos \pi d_{G }({\mathbf {z}},{\mathbf {z}}')}-d_{G }({\mathbf {z}},{\mathbf {z}}')\ge 0 \end{aligned}$$

as the function \(f(x)=\sqrt{2-2\cos \pi x}-x\) is non-negative on [0, 1]. For the upper bound note the relation between the geodesic distance \({{\tilde{d}}}_{G }\) and the normalized geodesic distance \(d_{G }\),

$$\begin{aligned} {{\tilde{d}}}_{G }({\mathbf {z}},{\mathbf {z}}')=\pi d_{G }({\mathbf {z}},{\mathbf {z}}'), \end{aligned}$$

which yields

$$\begin{aligned} \Vert {\mathbf {z}}- {\mathbf {z}}'\Vert _2\le {{\tilde{d}}}_{G }({\mathbf {z}},{\mathbf {z}}')=\pi d_{G }({\mathbf {z}},{\mathbf {z}}'). \square \end{aligned}$$

We now have the preliminary results necessary in order to prove Theorem 3.1.

4.2 Proof of Theorem 3.1 with Axiomatic GMRA

Recall that our theoretical result concerns OMS-simple with recovery performed using (3) and (4). The proof is based on the following idea. We first control the error \(\Vert {\mathbf {c}}_{j,k'} - {\mathbf {x}}\Vert _2\) made by (3) in approximating a GMRA center closest to \({\mathbf {x}}\). To do so we make use of Plan and Vershynin’s result on \(\delta \)-uniform tessellations in [43]. Recall the equivalence between one-bit measurements and random hyperplanes.

Definition 4.8

(uniform tessellation [43, Defn. 1.1])   Let \(K \subset {\mathbb {S}}^{D-1}\) and an arrangement of m hyperplanes in \({\mathbb {R}}^D\) be given via a matrix A (i.e., the j-th row of A is the normal to the j-th hyperplane). Let \(d_A({\mathbf {x}},{\mathbf {y}}) \in [0,1]\) denote the fraction of hyperplanes separating \({\mathbf {x}}\) and \({\mathbf {y}}\) in K and let \(d_{G }\) be the normalized geodesic distance on the sphere, i.e., opposite poles have distance one. Given \(\delta > 0\), the hyperplanes provide a \(\delta \)-uniform tessellation of K if

$$\begin{aligned} | d_A({\mathbf {x}},{\mathbf {y}}) - d_{G }({\mathbf {x}},{\mathbf {y}})| \le \delta \end{aligned}$$

holds for all \({\mathbf {x}}, {\mathbf {y}}\in K\).

Theorem 4.9

(random uniform tessellation, [43], Thm. 3.1]) Consider a subset \(K\subseteq {\mathbb {S}}^{D-1}\) and let \(\delta >0\). Let

$$\begin{aligned} m\ge {\bar{C}}\delta ^{-6}\max {\{w(K)^2, 2/\pi \}} \end{aligned}$$

and consider an arrangement of m independent random hyperplanes in \({\mathbb {R}}^D\) uniformly distributed according to the Haar measure. Then with probability at least \(1-2e^{-c\delta ^2m}\), these hyperplanes provide a \(\delta \)-uniform tessellation of K. Here and later \({{\bar{C}}},c\) denote positive absolute constants.

Remark 4.10

In words, Theorem 4.9 states that if a number of one-bit measurements scale at least linearly in intrinsic dimension of a set \(K \subset {\mathbb {S}}^{D-1}\), then with high probability the percentage of different measurements of two points \(x,y \in K\) is closely related to their distance on the sphere. Implicitly the diameter of all tessellation cells is bounded by \(\delta \). The original version of Theorem 4.9 uses \(\gamma (K)\) instead of w(K). However, note that by (10) we get for \(K\subseteq {\mathbb {S}}^{D-1}\) that \(\gamma (K) \le w(K-K)+\sqrt{2/\pi } \le 3w(K)\) as long as \(w(K) \ge \sqrt{2/\pi }\) which is reasonable to assume. Hence, if \({\bar{C}}\) is changed by a factor of 9, Theorem 4.9 can be stated as above.

Using these results we will show in Lemma 4.13 that the center \({\mathbf {c}}_{j,k'}\) identified in step I of the algorithm OMS-simple satisfies \(\Vert {\mathbf {x}}- {\mathbf {c}}_{j,k'} \Vert _2 \!\le \! 16 \max {\{ \Vert {\mathbf {x}}\!-\! {\mathbf {c}}_{j,k_j({\mathbf {x}})} \Vert _2, C_1 2^{-j\!-\!1} \}}\) in Lemma 4.13. Therefore, the GMRA property (iii.b) provides an upper bound on \(\Vert {\mathbf {x}}-{\mathbb {P}}_{j,k'}({\mathbf {x}}) \Vert _2\). What remains is to then bound the gap between \({\mathbb {P}}_{j,k'}({\mathbf {x}})\) and the approximation \({\mathbf {x}}^*\). This happens in two steps. First, Plan and Vershynin’s result on noisy one-bit sensing (see Theorem 4.11) is applied to a scaled version of (4) bounding the distance between \({\mathbb {P}}_{j,k'}({\mathbf {x}})\) and \({\bar{{\mathbf {x}}}}\) (the minimizer of the scaled version). This argument works by interpreting the true measurements \({\mathbf {y}}\) as a noisy version of the non-accessible one-bit measurements of \({\mathbb {P}}_{j,k'}({\mathbf {x}})\). The rescaling becomes necessary as Theorem 4.11 is restricted to the unit ball in Euclidean norm. Lastly, a geometric argument is used to bound the distance between the minimum points \({\bar{{\mathbf {x}}}}\) and \({\mathbf {x}}^*\) in order to conclude the proof.

Theorem 4.11

(noisy one-bit [41, Thm. 1.3])   Let \({\mathbf {a}}_1,\dots ,{\mathbf {a}}_m\) be i.i.d. standard Gaussian random vectors in \({\mathbb {R}}^D\) and let K be a subset of the Euclidean unit ball in \({\mathbb {R}}^D\). Let \(\delta > 0\) and suppose that \(m \ge C'\delta ^{-6} w(K)^2\). Then with probability at least \(1-8e^{-c\delta ^2 m}\), the following event occurs. Consider a signal \({\tilde{{\mathbf {x}}}} \in K\) satisfying \(\Vert {\tilde{{\mathbf {x}}}} \Vert _2 = 1\) and its (unknown) uncorrupted one-bit measurements \({\tilde{{\mathbf {y}}}} = ({\tilde{y}}_1,\dots ,{\tilde{y}}_m)\) given as

$$\begin{aligned} {\tilde{y}}_i = {\text {sign}}{\langle {\mathbf {a}}_i,{\tilde{{\mathbf {x}}}} \rangle }, \qquad i = 1,2,\dots ,m. \end{aligned}$$

Let \({\mathbf {y}}=(y_1,\dots ,y_m) \in \{ -1,1 \}^m\) be any (corrupted) measurements satisfying \(d_{H }({\tilde{{\mathbf {y}}}},{\mathbf {y}}) \le \tau m\). Then the solution \({\bar{{\mathbf {x}}}}\) to the optimization problem

$$\begin{aligned} {\bar{{\mathbf {x}}}} = \mathop {\mathrm {\arg \, max}}\limits _{\mathbf {z}}\sum {}_{i = 1}^{m} y_i \langle {\mathbf {a}}_i,{\mathbf {z}}\rangle \quad \ \text {subject to}\,\, {\mathbf {z}}\in K, \end{aligned}$$

with input \({\mathbf {y}}\), satisfies

$$\begin{aligned} \Vert {\bar{{\mathbf {x}}}} - {\tilde{{\mathbf {x}}}} \Vert _2^2 \le \delta \sqrt{\log \frac{e}{\delta }} + 11\tau \sqrt{\log \frac{e}{\tau }}\,. \end{aligned}$$

Remark 4.12

Theorem 4.11 yields guaranteed recovery of unknown signals \(\mathbf{x} \in K \subset {\mathscr {B}}(\mathbf{0} ,1)\) up to a certain error by the formulation we use in (4) from one-bit measurements, if the number of measurements scales linearly with the intrinsic dimension of K. The recovery is robust to noise on the measurements. Note that the original version of Theorem 4.11 uses \(w(K-K)\) instead of w(K). As \(w(K-K)\le 2w(K)\) by (10), the result stated above also holds for a slightly modified constant \(C'\).

We begin by proving Lemma 4.13.

Lemma 4.13

If \(m \ge {\bar{C}} C_1^{-6} 2^{6(j+1)} \max {\{ w({\mathscr {M}}\cup {\mathbb {P}}_{\mathbb {S}}({\mathscr {C}}_j))^2, 2/ \pi \}}\) the center \({\mathbf {c}}_{j,k'}\) chosen in step I of Algorithm OMS-simple fulfills

$$\begin{aligned} \Vert {\mathbf {x}}- {\mathbf {c}}_{j,k'} \Vert _2 \le 16 \max { \{ \Vert {\mathbf {x}}- {\mathbf {c}}_{j,k_j({\mathbf {x}})} \Vert _2, C_1 2^{-j-1} \}} \end{aligned}$$

for all \({\mathbf {x}}\in {\mathscr {M}}\subset {\mathbb {S}}^{D-1}\) with probability at least \(1-2e^{-c (C_1 2^{-j-1})^2 m}\).

Proof

By definition of \({\mathbf {c}}_{j,k'}\) in (3) we have that

$$\begin{aligned} d_{H } ( {\text {sign}}A {\mathbf {c}}_{j,k'},{\mathbf {y}}) \le d_{H } ( {\text {sign}}A{\mathbf {c}}_{j,k_j({\mathbf {x}})},{\mathbf {y}}). \end{aligned}$$

As, for all \({\mathbf {z}},{\mathbf {z}}' \in {\mathbb {R}}^D\), \(d_{H }( {\text {sign}}A{\mathbf {z}}, {\text {sign}}A{\mathbf {z}}') = m d_A({\mathbf {z}},{\mathbf {z}}') = m d_A({\mathbb {P}}_{\mathbb {S}}({\mathbf {z}}),{\mathbb {P}}_{\mathbb {S}}({\mathbf {z}}'))\), this is equivalent to

$$\begin{aligned} d_A ( {\mathbb {P}}_{\mathbb {S}}({\mathbf {c}}_{j,k'}),{\mathbf {x}}) \le d_A ( {\mathbb {P}}_{\mathbb {S}}({\mathbf {c}}_{j,k_j({\mathbf {x}})}),{\mathbf {x}}). \end{aligned}$$

Noting that Gaussian random vectors and Haar random vectors yield identically distributed hyperplanes, Theorem 4.9 now transfers this bound to the normalized geodesic distance, namely

$$\begin{aligned} d_{G } ( {\mathbb {P}}_{\mathbb {S}}({\mathbf {c}}_{j,k'}),{\mathbf {x}}) \le d_{G } ( {\mathbb {P}}_{\mathbb {S}}({\mathbf {c}}_{j,k_j({\mathbf {x}})}),{\mathbf {x}}) + 2\delta \end{aligned}$$

with probability at least \(1-2e^{-c\delta ^2m}\) where \(\delta = C_1 2^{-j-1}\). Observe \(d_{G }({\mathbf {z}},{\mathbf {z}}') \le \Vert {\mathbf {z}}- {\mathbf {z}}' \Vert _2 \le \pi d_{G }({\mathbf {z}},{\mathbf {z}}')\) for all \({\mathbf {z}},{\mathbf {z}}' \in {\mathbb {S}}^{D-1}\) (recall Lemma 4.7) which leads to

$$\begin{aligned} \Vert {\mathbb {P}}_{\mathbb {S}}({\mathbf {c}}_{j,k'}) - {\mathbf {x}}\Vert _2\le \pi d_{G }( {\mathbb {P}}_{\mathbb {S}}( {\mathbf {c}}_{j,k_j({\mathbf {x}})}),{\mathbf {x}}) + 2\pi \delta \le \pi \Vert {\mathbb {P}}_{\mathbb {S}}({\mathbf {c}}_{j,k_j({\mathbf {x}})}) - {\mathbf {x}}\Vert _2 + 2\pi \delta . \end{aligned}$$

As by property (iii.a) the centers are close to the manifold, they are also close to the sphere and we have \(\Vert {\mathbb {P}}_{\mathbb {S}}({\mathbf {c}}_{j,k}) - {\mathbf {c}}_{j,k} \Vert _2 < C_1 2^{-j-2}\), for all \({\mathbf {c}}_{j,k} \in {\mathscr {C}}_j\). Hence, we conclude

$$\begin{aligned} \Vert {\mathbf {c}}_{j,k'} - {\mathbf {x}}\Vert _2&\le \Vert {\mathbf {c}}_{j,k'}-{\mathbb {P}}_{\mathbb {S}}({\mathbf {c}}_{j,k'})\Vert _2+\Vert {\mathbb {P}}_{\mathbb {S}}({\mathbf {c}}_{j,k'})-{\mathbf {x}}\Vert _2\\&\le \pi \bigl ( \Vert {\mathbf {c}}_{j,k_j({\mathbf {x}})} - {\mathbf {x}}\Vert _2 + C_1 2^{-j-2} \bigr ) + 2\pi \delta + C_1 2^{-j-2} \\&\le \biggl ( \pi + \frac{\pi }{2} + 2\pi + \frac{1}{2} \biggr ) \max { \{ \Vert {\mathbf {c}}_{j,k_j({\mathbf {x}})} - {\mathbf {x}}\Vert _2, C_1 2^{-j-1} \} }\\&\le 16 \max { \{ \Vert {\mathbf {c}}_{j,k_j({\mathbf {x}})} - {\mathbf {x}}\Vert _2, C_1 2^{-j-1} \}}. \end{aligned}$$

\(\square \)

We can now prove a detailed version of Theorem 3.1 for the given axiomatic GMRA and deduce Theorem 3.1 as a corollary.

Theorem 4.14

(uniform recovery—axiomatic case) Let \({\mathscr {M}}\subset {\mathbb {S}}^{D-1}\) be given by its GMRA for some levels \(j_0 < j \le J\), such that \(C_1 < 2^{j_0 + 1}\) where \(C_1\) is the constant from GMRA properties (ii.b) and (iii.a). Fix j and assume that \(\mathrm {dist}({\mathbf {0}},{\mathscr {M}}_j) \ge 1/2\). Further, let \(d \ge 1\) and

$$\begin{aligned} m \ge 16\max {\{C',{\bar{C}}\}}\cdot C_1^{-6} 2^{6(j+1)} (w({\mathscr {M}}) + C\sqrt{dj})^2, \end{aligned}$$
(12)

where \(C'\) is the constant from Theorem 4.11, \({\bar{C}}\) from Theorem 4.9, and \(C > 3\) from Lemma 4.3. Then, with probability at least \(1 - 12e^{-(C_1 2^{-j-1})^2cm}\) the following holds for all \({\mathbf {x}}\in {\mathscr {M}}\) with one-bit measurements \({\mathbf {y}}= {\text {sign}}A{\mathbf {x}}\) and GMRA constants \({\tilde{C}}_{\mathbf {x}}\) from property (iii.b) satisfying \({\tilde{C}}_{\mathbf {x}}< 2^{j - 1}\): The approximations \({\mathbf {x}}^*\) obtained by OMS fulfill

$$\begin{aligned} \Vert {\mathbf {x}}- {\mathbf {x}}^*\Vert _2\le & {} 2^{-{j}/{2}}\root 4 \of {j}\\&\times \left( 2{\tilde{C}}_{\mathbf {x}}2^{-{j}/{2}} + \sqrt{\frac{C_1}{2}} \root 4 \of {\log \frac{4e}{\min { \{C_1,1\}}}}+ \sqrt{11C'_{\mathbf {x}}} \root 4 \of {\log \frac{2e}{\min { \{C'_{\mathbf {x}}, 1\}}}} \right) . \end{aligned}$$

Here \(C'_{\mathbf {x}}:= 2{\tilde{C}}_{\mathbf {x}}+ C_1\).

Proof of Theorem 3.1

As \(j = \lceil \log (1/\varepsilon ) \rceil \), we know that \(2^{-j} \le \varepsilon \le 2^{-j+1}\). This implies

$$\begin{aligned} m&\ge E C_1^{-6} \varepsilon ^{-6} \max \left\{ w({\mathscr {M}}), \sqrt{d \left( \log \frac{1}{\varepsilon }+ 1 \right) } \right\} ^{\!2}\\&\ge 16\max {\{C',{\bar{C}}\}}\cdot C_1^{-6} 2^{6(j+1)} (w({\mathscr {M}}) + C\sqrt{dj})^2 \end{aligned}$$

for \(E > 0\) chosen appropriately. The result follows by applying Theorem 4.14. \(\square \)

Proof of Theorem 4.14

Recall that \(k'\) is the index chosen by OMS in (6). The proof consists of three steps. First, we apply Lemma 4.13 in (I). By the GMRA axioms this supplies an estimate for \(\Vert {\mathbf {x}}- {\mathbb {P}}_{j,k'}({\mathbf {x}}) \Vert _2\) with high probability. In (II) we use Theorem 4.11 to bound the distance between \({\mathbb {P}}_{j,k'}({\mathbf {x}})/\Vert {\mathbb {P}}_{j,k'}({\mathbf {x}}) \Vert _2\) and the minimizer \({\mathbf {x}}^*\) given by

$$\begin{aligned} x^* = \mathop {\mathrm {arg \, min}}\limits _{\mathbf {z}}\sum _{l = 1}^m (-y_l) \langle {\mathbf {a}}_l,{\mathbf {z}}\rangle \quad \ \ \text {subject to}\ \ {\mathbf {z}}\in K := {\text {conv}}{\mathbb {P}}_{\mathbb {S}}( P_{j,k'} \cap {\mathscr {B}}({\mathbf {0}},2) ) \end{aligned}$$
(13)

with high probability. By a union bound over all events, part (III) then concludes with an estimate of the distance \(\Vert {\mathbf {x}}- {\mathbf {x}}^*\Vert _2\) combining (I) and (II).

(I) Set \(\delta := C_1 2^{-j-1}\). Observing that \(C_1 2^{-j-2} < 1/2\) by assumption, GMRA property (iii.a) yields that all centers in \({\mathscr {C}}_j\) are closer to \({\mathbb {S}}^{D-1}\) than 1/2, i.e., \(1/2 \le \Vert {\mathbf {c}}_{j,k} \Vert _2 \le 3/2\). Hence, by (10)

$$\begin{aligned} \begin{aligned}&0 \,\le w({\mathbb {P}}_{\mathbb {S}}({\mathscr {C}}_j)) \le \gamma ({\mathbb {P}}_{\mathbb {S}}({\mathscr {C}}_j)) \\&\quad \le 2\gamma ({\mathscr {C}}_j) \le 4w({\mathscr {C}}_j) + 2\sqrt{\frac{2}{\pi }} {\text {dist}}({\mathbf {0}}, {\mathscr {C}}_j) \le 4w({\mathscr {C}}_j) + 4. \end{aligned} \end{aligned}$$
(14)

As \({\mathscr {C}}_j \subset {\mathscr {M}}_j\) we know by Lemma 4.3, (14), and Remark 4.4 that

$$\begin{aligned} m&\ge 4 {\bar{C}} \delta ^{-6} (2w({\mathscr {M}}) + 2C\sqrt{dj})^2 \ge 4{\bar{C}} \delta ^{-6} (2w({\mathscr {M}}) + 4w({\mathscr {C}}_j) + 6 )^2 \\&\ge 4{\bar{C}} \delta ^{-6} (2w({\mathscr {M}}) + w({\mathbb {P}}_{\mathbb {S}}({\mathscr {C}}_j)) + 2 )^2 = {\bar{C}} \delta ^{-6} (4w({\mathscr {M}}) + 2w({\mathbb {P}}_{\mathbb {S}}({\mathscr {C}}_j)) + 4 )^2 \nonumber \\&\ge {\bar{C}} \delta ^{-6} (w({\mathscr {M}}\cup {\mathbb {P}}_{\mathbb {S}}({\mathscr {C}}_j)) + 1 )^2 \ge {\bar{C}} \delta ^{-6} \max {\{w({\mathscr {M}}\cup {\mathbb {P}}_{\mathbb {S}}({\mathscr {C}}_j))^2,2/\pi \}}.\nonumber \end{aligned}$$
(15)

Hence, Lemma 4.13 implies that

$$\begin{aligned} \Vert {\mathbf {x}}- {\mathbf {c}}_{j,k'} \Vert _2 \le 16 \max { \{ \Vert {\mathbf {x}}-{\mathbf {c}}_{j,k_j({\mathbf {x}})} \Vert _2, C_1 2^{-j-1} \}} \end{aligned}$$

with probability at least \(1-2e^{-c\delta ^2 m}\). By GMRA property (iii.b) we now get that

$$\begin{aligned} \Vert {\mathbf {x}}- {\mathbb {P}}_{j,k'}({\mathbf {x}}) \Vert _2 \le {\tilde{C}}_{\mathbf {x}}2^{-j} \end{aligned}$$
(16)

for some constant \({\tilde{C}}_{\mathbf {x}}\).

(II) Define \(\alpha := \Vert {\mathbb {P}}_{j,k'}({\mathbf {x}}) \Vert _2\) and note that one has \(1/2 \le \alpha \le 3/2\) as \({\mathbf {x}}\in {\mathbb {S}}^{D-1}\) and \(\Vert {\mathbf {x}}- {\mathbb {P}}_{j,k'}({\mathbf {x}}) \Vert _2 \le {\tilde{C}}_{\mathbf {x}}2^{-j} \le 1/2\) by (16) and assumption. We now create the setting of Theorem 4.11. Define \({\tilde{{\mathbf {x}}}} := {\mathbb {P}}_{j,k'}({\mathbf {x}})/\alpha \in {\mathbb {S}}^{D-1}\), \({\tilde{{\mathbf {y}}}} :={\text {sign}}A{\tilde{{\mathbf {x}}}}= {\text {sign}}A{\mathbb {P}}_{j,k'}({\mathbf {x}})\), \(K = {\text {conv}} {\mathbb {P}}_{\mathbb {S}}( P_{j,k'} \cap {\mathscr {B}}({\mathbf {0}},2) )\), and \(\tau := (2{\tilde{C}}_{\mathbf {x}}+ C_1)2^{-j}\). If successfully applied with these quantities, Theorem 4.11 will bound \(\Vert {\tilde{{\mathbf {x}}}} - {\mathbf {x}}^* \Vert _2\) by

$$\begin{aligned} \begin{aligned} \Vert {\tilde{{\mathbf {x}}}} - {\mathbf {x}}^* \Vert _2&\le \sqrt{\delta \sqrt{\log \frac{e}{\delta }} + 11\tau \sqrt{\log \frac{e}{\tau } }}\\&\le \left( \sqrt{\frac{C_1}{2}} \root 4 \of {\log \frac{4e}{\min { \{C_1,1\}} }} \right. \\&\,\qquad \left. +\, \sqrt{11(2{\tilde{C}}_x + C_1)} \root 4 \of {\log \frac{2e}{\min { \{2{\tilde{C}}_x + C_1, 1\}}}} \right) 2^{-{j}/{2}} \root 4 \of {j}. \end{aligned} \end{aligned}$$
(17)

All that remains is to verify that the conditions of Theorem 4.11 are met so that (17) is guaranteed with high probability. We first have to check \(d_{H }({\tilde{{\mathbf {y}}}},{\mathbf {y}}) \le \tau m\). Recall that \(1/\alpha \le 2\) and for \(\alpha >0\) one has \(\alpha w(K)=w(\alpha K)\). Applying Lemma 4.3 and (10) we have, in analogy to (15), that

$$\begin{aligned} m&\ge {\bar{C}} \delta ^{-6} (4w({\mathscr {M}}) + 4w({\mathscr {M}}_j) + 12)^2 \ge {\bar{C}} \delta ^{-6} \biggl ( 2w({\mathscr {M}}) + 2w\biggl ( \frac{{\mathscr {M}}_j}{\alpha } \biggr ) + 12 \biggr )^{\!2}\\&\ge {\bar{C}} \delta ^{-6} \biggl ( w \biggl ({\mathscr {M}}\cup \frac{{\mathscr {M}}_j}{\alpha } \biggr ) + 7 \biggr )^{\!2} \ge {\bar{C}} \delta ^{-6} \biggl ( w \biggl ( \biggl ( {\mathscr {M}}\cup \frac{{\mathscr {M}}_j}{\alpha } \biggr ) \cap {\mathscr {B}}({\mathbf {0}},1) \biggr ) + 7 \biggr )^{\!2}. \end{aligned}$$

Note that in the third inequality a slight modification of the second inequality in Lemma 4.3 is used. As \({\mathscr {M}}_j/\alpha \subset {\mathscr {B}}(\mathbf{0},4)\), one has \(w({\mathscr {M}}\cup {\mathscr {M}}_j/\alpha ) \le 2w({\mathscr {M}}) + 2w({\mathscr {M}}_j/\alpha ) + 5\) by adapting (11). We can now use Theorem 4.9, Lemma 4.7, and the fact that \(|1 - \alpha | = |\Vert {\mathbf {x}}\Vert _2 - \Vert {\mathbb {P}}_{j,k'}({\mathbf {x}}) \Vert _2 | \le \Vert {\mathbf {x}}- {\mathbb {P}}_{j,k'}({\mathbf {x}}) \Vert _2\) to obtain

$$\begin{aligned} \frac{d_{H }({\tilde{{\mathbf {y}}}},{\mathbf {y}})}{m}&= d_A({\tilde{{\mathbf {x}}}},{\mathbf {x}}) \le d_{G }({\tilde{{\mathbf {x}}}},{\mathbf {x}}) + \delta \le \Vert {\tilde{{\mathbf {x}}}} - {\mathbf {x}}\Vert _2 + \delta \\&\le \Vert {\tilde{{\mathbf {x}}}} - {\mathbb {P}}_{j,k'}({\mathbf {x}}) \Vert _2 + \Vert {\mathbb {P}}_{j,k'}({\mathbf {x}}) - {\mathbf {x}}\Vert _2 + \delta \\&= | 1 - \alpha | + \Vert {\mathbb {P}}_{j,k'}({\mathbf {x}}) - {\mathbf {x}}\Vert _2 + \delta \\&\le 2 \Vert {\mathbb {P}}_{j,k'}({\mathbf {x}}) - {\mathbf {x}}\Vert _2 + \delta \le (2{\tilde{C}}_{\mathbf {x}}+ C_1) 2^{-j} = \tau \end{aligned}$$

with probability at least \(1-2e^{-c\delta ^2 m}\). Furthermore, by a similar argumentation as in (14) one gets

$$\begin{aligned} w(K) = w({\mathbb {P}}_{\mathbb {S}}( P_{j,k'} \cap {\mathscr {B}}({\mathbf {0}},2) )) \le 4w({\mathscr {M}}_j) + 4, \end{aligned}$$
(18)

where one uses invariance of the Gaussian width under taking the convex hull (see [41, Proposition 2.1]), the fact that \(P_{j,k'} \cap {\mathscr {B}}({\mathbf {0}},2) \subset {\mathscr {M}}_j\), and the assumption that \(1/2 \le \mathrm {dist}({\mathscr {M}}_j, {\mathbf {0}}) \le 2\). In combination with Lemma 4.3 we have, in analogy to (15), that

$$\begin{aligned} m \ge 4C'\delta ^{-6} (2w({\mathscr {M}}) + 4w({\mathscr {M}}_j) + 6 )^2 \ge 4C'\delta ^{-6} (w(K) + 2)^2 \ge C' \delta ^{-6} w(K)^2. \end{aligned}$$

Hence, we can apply Theorem 4.11 to obtain with probability at least \(1-8e^{-c \delta ^2 m}\) that

$$\begin{aligned} \Vert {\bar{{\mathbf {x}}}} - {\tilde{{\mathbf {x}}}} \Vert _2^2 \le \delta \sqrt{\log \frac{e}{\delta } } + 11\tau \sqrt{\log \frac{e}{\tau } }; \end{aligned}$$

the estimate (17) now follows.

(III) To conclude the proof we apply a union bound and obtain with probability at least \(1 - 12e^{-c \delta ^2 m}\) that

$$\begin{aligned} \Vert {\mathbf {x}}- {\mathbf {x}}^*\Vert _2&\le \Vert {\mathbf {x}}- {\mathbb {P}}_{j,k'}({\mathbf {x}}) \Vert _2 + \Vert {\mathbb {P}}_{j,k'}({\mathbf {x}}) - {\tilde{{\mathbf {x}}}} \Vert _2 + \Vert {\tilde{{\mathbf {x}}}} - {\mathbf {x}}^* \Vert _2 \\&= \Vert {\mathbf {x}}- {\mathbb {P}}_{j,k'}({\mathbf {x}}) \Vert _2 + |1-\alpha | + \Vert {\tilde{{\mathbf {x}}}} - {\mathbf {x}}^* \Vert _2 \\&\le 2\Vert {\mathbf {x}}- {\mathbb {P}}_{j,k'}({\mathbf {x}}) \Vert _2 + \Vert {\tilde{{\mathbf {x}}}} - {\mathbf {x}}^* \Vert _2. \end{aligned}$$

GMRA property (iii.b) combined with (17) now yields the final desired error bound. \(\square \)

Remark 4.15

For obtaining the lower bounds on m in (12) and (8) we made use of Lemma 4.3 leading to the influence of j which is suboptimal for fine scales (i.e., j large). To improve on this for large j one can exploit the alternative versions of the lemma, namely, Lemmas 4.5 and 4.6. Then, however, some minor modifications become necessary in the proof of Theorem 4.14 as the lemmas only apply to \({\mathscr {M}}^{rel }_j\):

  • In (I), e.g., one has to guarantee that \({\mathscr {C}}_j \subset {\mathscr {M}}^{rel }_j\), i.e., that each center \({\mathbf {c}}_{j,k}\) is a best approximation for some part of the manifold. This is a reasonable assumption especially if the centers are constructed as means of small manifold patches, which is a common approach in empirical applications (cf. Appendix D).

  • Also, when working with \({\mathscr {M}}^{rel }_j\) it is essential in (II) to have a near-best approximation subspace of \({\mathbf {x}}\), i.e., the \(k'\) obtained in (I) has to fulfill \(k' \approx k_j({\mathbf {x}})\) as \({\mathscr {M}}^{rel }_j\) does not include many near-optimal centers for each point on \({\mathscr {M}}\). Here, one can exploit the minimal distance of centers \({\mathbf {c}}_{j,k}\) to each other as described in GMRA property (ii.b) and choose \(\delta \) slightly smaller (in combination with a correspondingly strengthened upper bound in Lemma 4.13) to obtain the necessary guarantees for (I). As we are principally concerned with the case where \(j = {\mathcal {O}}({\log D})\) in this paper, however, we will leave such variants to future work.

We are now prepared to explore the numerical performance of the proposed methods.

5 Numerical Simulation

In this section, we present various numerical experiments to benchmark OMS. The GMRAs we work with are constructed using the GMRA code provided by Maggioni.Footnote 2 We compared the performance of OMS for three exemplary choices of \({\mathscr {M}}\), namely, a simple 2-dim sphere embedded in \({\mathbb {R}}^{20}\) (20000 data points sampled from the 2-dimensional sphere \({\mathscr {M}}\) embedded in \({\mathbb {S}}^{20-1}\)), the MNIST data set [36] of handwritten digits “1” (3000 data points in \({\mathbb {R}}^{784}\)), and the Fashion-MNIST data set [47] of shirt images (2000 data points in \({\mathbb {R}}^{784}\)). Both MNIST data sets have been projected to the unit sphere before taking measurements and computing the GMRA. In each of the experiments 5.1–5.4, we first computed a GMRA up to refinement level \(j_{max } = 10\) and then recovered 100 randomly chosen \({\mathbf {x}}\in {\mathscr {M}}\) from their one-bit measurements by applying OMS. Depicted is the averaged relative error between \({\mathbf {x}}\) and its approximation \({\mathbf {x}}^*\), i.e., \(\Vert {\mathbf {x}}- {\mathbf {x}}^*\Vert _2 / \Vert {\mathbf {x}}\Vert _2\) which is equal to the absolute error \(\Vert {\mathbf {x}}- {\mathbf {x}}^*\Vert _2\) for \({\mathscr {M}}\subset {\mathbb {S}}^{D-1}\). Note the different approximation error ranges of the sphere and the MNIST experiments when comparing both settings. As a benchmark, the average error caused by the best GMRA approximation, i.e., projection of \({\mathbf {x}}\) onto the GMRA, is provided in all plots in the form of a horizontal dashed black line.Footnote 3 Let us mention that the error caused by best GMRA approximation—though being a benchmark for the recovery performance one could expect—is not a strict lower bound to OMS since the algorithm is not restricted to the GMRA but uses convex relaxations of the GMRA subspaces, cf. Fig. 4a.

5.1 OMS-Simple vs. OMS

The first test compares recovery performance of the two algorithms presented above, namely OMS-simple for \(R \in \{0.5, 1, 1.5 \}\) and OMS. The results are depicted in Fig. 4. Note that only \(R = 1.5\) and, in the case of the 2-sphere, \(R = 1\) are depicted as in the respective other cases for each number of measurements most of the trials did not yield a feasible solution in (4), so the average was not well defined. One can observe that for all data sets OMS outperforms OMS-simple which is not surprising as OMS does not rely on a suitable parameter choice. This observation is also the reason for us to restrict the theoretical analysis to OMS. The more detailed approximation of the toy example (2-dimensional sphere) is due to its simpler structure and lower dimensional setting and can also be observed in 5.2–5.4. Figures 5 and 6 depict one specific reconstructed image of Fashion-MNIST, for four different numbers of measurements m. Obviously, OMS shows a better performance having less quantization artifacts. Moreover, the good visual quality of the OMS reconstruction in Fig. 6 for only \(m=100\) suggests that the \(\ell _2\)-error used in Fig. 4 is a rather pessimistic performance measure. Considering that all MNIST-images could be fully coded in \(8\cdot 28 \cdot 28 = 6272\) bits (gray-scale images contain only 8-bit of information per pixel), it is important to point out the potentially overly pessimistic nature of the \(\ell _2\)-errors reported for \(m = 10000\), as well as to note that the visual quality is already much better than one might expect for OMS at compressions of ratios of size \(100/6272<0.02\).

Fig. 4
figure 4

Comparison of OMS-Simple for \(R = 1\) (dotted-dashed, yellow), \(R = 1.5\) (dashed, blue), and OMS (solid, red). Recall from Sect. 5.1 that OMS-Simple for \(R = 1\) does not recover in b and c. The black dotted line highlights average error caused by direct GMRA projection

Full size image
Fig. 5
figure 5

One Fashion-MNIST signal with its OMS-Simple \((R = 1.5)\) reconstructions. The best GMRA approximation is given as a benchmark. Note that the GMRA uses an 11-dimensional subspace at this part of the manifold

Full size image
Fig. 6
figure 6

One Fashion-MNIST signal with its OMS reconstructions. The best GMRA approximation is given as a benchmark. Note that the GMRA uses an 11-dimensional subspace at this part of the manifold

Full size image

5.2 Modifying OMS

Observations in [34] motivate to consider a modification of OMS in which (7) is replaced by

$$\begin{aligned} {\mathbf {x}}^*= \mathop {\mathrm {arg \, min}}\limits _{{\mathbf {z}}\in {\mathbb {R}}^D} \sum _{l=1}^{m} \left[ (-y_l) \langle {\mathbf {a}}_l,{\mathbf {z}}\rangle \right] _+ \quad \ \ \text {subject to }\ \ {\mathbf {z}}\in {\text {conv}}{\mathbb {P}}_{\mathbb {S}}(P_{j,k'} \cap {\mathscr {B}}(\mathbf{0},2)), \end{aligned}$$

where \([t]_+ = \max { \{0,t\}}\) denotes the positive part of \(t \in {\mathbb {R}}\). We tested this approach in some initial numerical experiments, but found that the modification produced ambiguous results with no clear improvement. Let us mention that after the original version of this paper had been finished, the \([\,{\cdot }\,]_+\)-formulation has been thoroughly analyzed for robust one- and multi-bit quantization in a dithered measurement setup in [32], but not in the context of GMRA and with dithering (this explains the ambiguous experimental outcomes in our case, as we do not use dithering in the one-bit measurements). Certainly one could transfer results from [32] to our setting by changing the measurement model to include dithering, cf. [13].

5.3 Are Two Steps Necessary?

One might wonder if the two steps in OMS-simple and OMS are necessary at all. Wouldn’t it be sufficient to use the center \({\mathbf {c}}_{j,k'}\) determined in step I as an approximation for \({\mathbf {x}}\)? If the GMRA is fine enough, this indeed is the case. If one only has access to a rather rough GMRA, the simulations in Fig. 7 show that the second step makes a notable difference in approximation quality. This behavior is not surprising in view of Lemma 4.13. The lemma guarantees a good approximation of \({\mathbf {x}}\) by \({\mathbf {c}}_{j,k'}\) as long as \({\mathbf {x}}\) is well approximated by an optimal center. For both MNIST data sets, one can observe that the second step only improves performance if the number of one-bit measurements is sufficiently high. For a small set of measurements the centers might yield better approximation as they lie close to \({\mathscr {M}}\) by GMRA property (iii.a). On the other hand, only parts of the affine spaces are practical for approximation and a certain number of measurements is necessary to restrict II to the relevant parts.

Fig. 7
figure 7

Comparison of the following: Approximation by step I of OMS when using tree structure (dashed with points, yellow) and when comparing all centers (solid with points, purple); approximation by steps I  &  II of OMS when using tree structure (dashed, blue; this line is mostly hidden behind the solid red curve in the first plot) and when comparing all centers (solid, red). The black dotted line highlights average error caused by direct GMRA projection

Full size image
Fig. 8
figure 8

One Fashion-MNIST signal with OMS reconstructions using tree search or full center search and using only step I or both steps, for \(m=100\). The best GMRA approximation is given as a benchmark. Note that the GMRA uses a 7-dimensional subspace at this part of the manifold

Full size image
Fig. 9
figure 9

One Fashion-MNIST signal with OMS reconstructions using tree search or full center search and using only step I or both steps, for \(m = 1000\). The best GMRA approximation is given as a benchmark. Note that the GMRA uses a 7-dimensional subspace at this part of the manifold

Full size image

5.4 Tree vs. No Tree

In the fourth test, we checked if approximation still works when not all possible centers are compared in step I of OMS but their tree structure is used. More precisely, to find an optimal center one compares on the first refinement level all centers, and then continues in each subsequent level solely with the children of the k best centers (in the presented experiments we chose \(k = 10\)). Of course, the chosen center will not be optimal as not all centers are compared (see Fig. 7). In the simple 2-dimensional sphere setting, step II, however, can compensate the worse approximation quality of I with tree search. Figure 7a hardly shows a difference in final approximation quality in both cases. In both MNIST settings, however, one can observe a considerable difference even when performing two steps. Figures 8 and 9 illustrate the differences in reconstruction using tree search vs. full center comparison, respectively, using only step I of OMS vs. using both steps, for \(m=100\) and \(m = 1000\). This corresponds to a compression ratio of \(100/6272 < 0.02\) resp. \(1000/6272 < 0.2\), cf. the discussion in Sect. 5.1. Comparing c and d with e and f of Fig. 8 one sees that full center search reconstructs more detailed features (shape), comparing c and d with e and f of Fig. 9 one sees that the second step enhances reconstruction of details (neckline).

5.5 A Change of Refinement Level

The last experiment (see Fig. 10) examines the influence of the refinement level j on the approximation error. For small j (corresponding to a rough GMRA) a high number of measurements can hardly improve the approximation quality while for large j (corresponding to a fine GMRA) the approximation error decreases with increasing measurement rates. This behavior is as expected. A rough GMRA cannot profit much from many measurements as the GMRA approximation itself yields an approximate lower bound on the obtainable approximation error. For fine GMRAs the behavior along the measurement axis is similar to above experiments. Note that further increase of j for the same range of measurements did not improve accuracy. Notably, the Fashion-MNIST reconstruction performs quite well even for small choices of j suggesting that the manifold of shirt images is, at least in terms of GMRA approximation, of lower complexity than the manifold of digits “1.” This is in line with the observation that the approximation error for Fashion-MNIST is smaller than for MNIST in the above experiments. The non-monotonous increase of the quality of reconstruction in Fig. 10c—the levels \(j=4,8,10\) perform especially well—is more difficult to explain; it might relate to the fact that Fashion-MNIST is considered to be harder to classify than MNIST—there seem to be features identifying the images (overall shape, detailed contours) on various levels of refinement.

Fig. 10
figure 10

Approximation error of OMS for different refinement levels j and numbers of measurements

Full size image

6 Discussion

In this paper, we proposed OMS, a tractable algorithm to approximate data lying on low-dimensional manifolds from compressive one-bit measurements, thereby complementing the theoretical results of Plan and Vershynin on one-bit sensing for general sets in [41] in this important setting. We then proved (uniform) worst-case error bounds for approximations computed by OMS under slightly stronger assumptions than [41], and also performed numerical experiments on both toy examples and real-world data. As a byproduct of our theoretical analysis (see, e.g., Sect. 4), we have further linked the theoretical understanding of one-bit measurements as tessellations of the sphere [43] to the GMRA techniques introduced in [3], by analyzing the interplay between a given manifold and its GMRA approximation’s complexity measured in terms of the Gaussian mean width. Finally, to indicate applicability of our results we showed that they hold even if there are just random samples from the manifold at hand as opposed to the entire manifold (see, e.g., Appendices D and E). Several interesting questions remain for future research, however.

First, the experiments in Sect. 5.4 suggest a possible benefit from using the tree structure within \({\mathscr {C}}_j\). Indeed, approximation of OMS does still yield comparable results if I is restricted to a tree-based search which has the advantage of being computable much faster than the minimization over all possible centers. It would be desirable to obtain theoretical error bounds even in this case, as well as to consider the use of other related fast nearest neighbor methods from computer science [26].

Second, the attentive reader might have noticed in the empirical setting of Appendices D and E that (A2) in combination with Lemma E.6 seems to imply that II of OMS may be unnecessary. As can be seen from Sect. 5.3 though, the second step of OMS yields a notable improvement even with an empirically constructed GMRA which hints that even with (A2) not strictly fulfilled the empirical GMRA techniques remain valid, and II of OMS of value. Understanding this phenomenon might lead to more relaxed assumptions than (A1)–(A4).

Third, it could be rewarding to also consider versions of OMS for additional empirical GMRA variants including, e.g., those which rely on adaptive constructions [37], GMRA constructions in which subspaces that minimize different criteria are used to approximate the data in each partition element (see, e.g., [27]), and distributed GMRA constructions which are built up across networks using distributed clustering [4] and SVD [30] algorithms. Such variants could prove valuable with respect to reducing the overall computational storage and/or runtime requirements of OMS in different practical situations.

Fourth, it would be illustrative to compare our GMRA approach which can be interpreted as “signal processing”-type convexification (or at least reduction to a convex subproblem) with recent advances on non-convex ADMM [35], i.e., direct application of non-convex optimization techniques. Two approaches seem of special interest: first, one could replace the GMRA manifold model by Generative Adversarial Networks (GANs) and apply ADMM to the resulting non-convex reconstruction problem or, second, stay in the GMRA setting but not restrict the reconstruction procedure to one single subspace.

Finally, it would also likely be fruitful to explore alternate quantization schemes to the one-bit measurements (1) considered herein. In particular, the so-called \(\varSigma \varDelta \) quantization schemes generally outperform the type of memoryless scalar quantization methods considered herein both theoretically and empirically in compressive sensing contexts [25, 33, 45], and initial work suggests that they may provide similar improvements in the GMRA model setting considered here [28]. Nevertheless, one should be aware that feedback quantization schemes like \(\varSigma \varDelta \) quantization might be of limited practicability in recent large-scale applications like massive MIMO [24], where the measurements are collected (and quantized) in a distributed fashion rendering the use of feedback information impossible. In such cases, the just analyzed memoryless quantization model is of particular interest.