Abstract
We consider fully discrete time-space approximations of abstract linear parabolic partial differential equations (PDEs) consisting of an hp-version discontinuous Galerkin (DG) time stepping scheme in conjunction with standard (conforming) Galerkin discretizations in space. We derive abstract computable a posteriori error bounds resulting, for instance, in concrete bounds in  - and
- and  -type norms when I is the temporal and
-type norms when I is the temporal and  the spatial domain for the PDE. We base our methodology for the analysis on a novel space-time reconstruction approach. Our approach is flexible as it works for any type of elliptic error estimator and leaves their choice to the user. It also exhibits mesh-change estimators in a clear and concise way. We also show how our approach allows the derivation of such bounds in the
the spatial domain for the PDE. We base our methodology for the analysis on a novel space-time reconstruction approach. Our approach is flexible as it works for any type of elliptic error estimator and leaves their choice to the user. It also exhibits mesh-change estimators in a clear and concise way. We also show how our approach allows the derivation of such bounds in the  norm.
norm.
Similar content being viewed by others
1 Introduction
Adaptive numerical methods have been shown to provide accurate and efficient numerical treatment of evolution PDEs thanks to their properties for localized mesh resolution especially in the context of moving fronts, interfaces, singularities, or layers (both boundary and interior). Such numerical methods predominantly admit spatial discretizations of variational type, e.g., finite element methods (FEMs), which allow for general, possibly unstructured, dynamic mesh modification. FEMs are also ideally suited for deriving mathematically rigorous a posteriori bounds, owing to their variational nature.
Some of the classical works on adaptive finite element methods for parabolic problems [10,11,12,13,14] are based on discontinuous Galerkin (DG) time stepping combined with FEM in space, and proving a posteriori bounds in various norms using duality techniques. The key motivation in using DG in time, which is also of variational type, is that it naturally allows for spatially-local-time stepping, i.e. different time step sizes in different parts of the spatial domain [10, 15, 21, 25]. This classical, but as of yet undeveloped in full, concept of local adaptivity in both space and time has the potential of delivering substantial computational savings and even complexity reduction.
In addition to the ability of Galerkin time marching schemes to employ locally different time step sizes, their variational character also allows for arbitrary variations in the local approximation orders. They can therefore be cast naturally into the framework of hp-approximation schemes. In the context of parabolic PDEs, hp-version time marching methods can be used, for instance, to resolve an initial layer in the (otherwise smooth) solution at high algebraic or even exponential rates of convergence, see, e.g., the works [33, 34, 39] on linear parabolic PDEs, and also [29, 30] which employ a combination of hp-version time stepping with suitable wavelet spatial discretizations to yield a log-linear complexity algorithm for nonlocal evolution processes involving pseudo-differential operators. Additionally, we note the numerical analysis of high-dimensional parabolic problems using sparse grids in space; see [38].
More recent results on rigorous a posteriori bounds for parabolic problems have focused on extending the paradigm of the reliable and efficient a posteriori error analysis of elliptic problems to the parabolic case [31, 36, 37]. Such works typically involve basic low-order time stepping schemes combined with various types of FEM in space. A posteriori error bounds for DG time-stepping methods have also appeared in the last few years; we point to [22, 27, 35] which are based on the reconstruction technique, to [16, 17] which employ an equilibrated flux approach, or to [19] which presents a provably convergent adaptive algorithm for a residual-type a posteriori estimator.
In this paper, we present a posteriori error bounds for an hp-version DG-in-time and conforming Galerkin discretization in space method for both  - and
- and  -norm errors separately, allowing for what appears to be optimal order in each case. The key idea is the use of suitable reconstruction frameworks to derive a perturbed PDE for the reconstructed error of the numerical method; a posteriori error bounds are then deduced using PDE stability properties, cf. [1, 23, 26, 27]. Our approach is based on new space and space-time reconstructions which are built on the combination of respective ideas for DG-time stepping methods [27, 35] and elliptic reconstruction [23, 26] to the fully-discrete setting. To that end, the key challenge of constructing a globally time-continuous reconstruction in the presence of mesh modification between time-steps is addressed by first reconstructing onto the solution space with respect to the spatial variables via a novel elliptic reconstruction definition, given in (3.14), which is a modification of the one in [23]. In particular, the new proposed elliptic reconstruction takes into account the effect of mesh-change.
-norm errors separately, allowing for what appears to be optimal order in each case. The key idea is the use of suitable reconstruction frameworks to derive a perturbed PDE for the reconstructed error of the numerical method; a posteriori error bounds are then deduced using PDE stability properties, cf. [1, 23, 26, 27]. Our approach is based on new space and space-time reconstructions which are built on the combination of respective ideas for DG-time stepping methods [27, 35] and elliptic reconstruction [23, 26] to the fully-discrete setting. To that end, the key challenge of constructing a globally time-continuous reconstruction in the presence of mesh modification between time-steps is addressed by first reconstructing onto the solution space with respect to the spatial variables via a novel elliptic reconstruction definition, given in (3.14), which is a modification of the one in [23]. In particular, the new proposed elliptic reconstruction takes into account the effect of mesh-change.
Our results are closely related, however, with important departures, to those of [16, 17, 19]. In particular, the new reconstructions defined below allow for the derivation of a posteriori upper error bounds for each of the following norms  (Theorem 4.4) and
(Theorem 4.4) and  (Sect. 6) separately; the Hilbert space
(Sect. 6) separately; the Hilbert space  is the domain of a self-adjoint uniformly elliptic operator
is the domain of a self-adjoint uniformly elliptic operator  (see Sect. 2 for details). A key attribute of our approach is the flexibility in incorporating any a posteriori elliptic error estimators available, as the reconstruction-type approach, allows to separate the challenges in the a posteriori error estimation of elliptic and time-evolution errors. To facilitate a wide range of applications, we will present the theory within a Gelfand-triple-type abstract setting allowing, for instance, both second- and fourth-order spatial operators. This generality comes at the possible expense of different, yet quantitatively analogous, computable constants in the resulting a posteriori error estimators compared to the bounds in [16, 17, 19]. For instance, when the equilibrated flux elliptic error estimators from [3] are used (with
(see Sect. 2 for details). A key attribute of our approach is the flexibility in incorporating any a posteriori elliptic error estimators available, as the reconstruction-type approach, allows to separate the challenges in the a posteriori error estimation of elliptic and time-evolution errors. To facilitate a wide range of applications, we will present the theory within a Gelfand-triple-type abstract setting allowing, for instance, both second- and fourth-order spatial operators. This generality comes at the possible expense of different, yet quantitatively analogous, computable constants in the resulting a posteriori error estimators compared to the bounds in [16, 17, 19]. For instance, when the equilibrated flux elliptic error estimators from [3] are used (with  and
and  ), we recover similar estimators to the upper bounds derived in [16, 17]. Importantly, however, the work [16] shows that these are also lower bounds for the “joint-norm” of
), we recover similar estimators to the upper bounds derived in [16, 17]. Importantly, however, the work [16] shows that these are also lower bounds for the “joint-norm” of  , and the article [17] does the same for the
, and the article [17] does the same for the  under the condition \(h^2<c\tau \), relating the mesh-size h with the time-step \(\tau \) for some constant \(c>0\). Also, in the present work, we are not concerned with the interesting question of convergence of adaptive algorithms as in [19]. Crucially, however, the novel space-time reconstruction, allows for the proof of an a posteriori error bound for the
under the condition \(h^2<c\tau \), relating the mesh-size h with the time-step \(\tau \) for some constant \(c>0\). Also, in the present work, we are not concerned with the interesting question of convergence of adaptive algorithms as in [19]. Crucially, however, the novel space-time reconstruction, allows for the proof of an a posteriori error bound for the  -norm, which appears to be of optimal order; this result, to the best of our reading, is not captured in [16, 17, 19].
-norm, which appears to be of optimal order; this result, to the best of our reading, is not captured in [16, 17, 19].
Outline. The remainder of this work is structured as follows. In Sect. 2 we set up the abstract framework for the paper by introducing the model parabolic PDE problem and its DG-in-time and conforming Galerkin spatial discretization. Furthermore, in Sect. 3, we provide the necessary technical tools for the ensuing analysis, and state their essential properties. In Sect. 4, we derive a posteriori error bounds in the  -norm using a time reconstruction and a novel elliptic reconstruction which includes mesh-change; this technical novelty is revealed to be crucial in our setting. In Sect. 5, upon defining a new space-time reconstruction, we derive a posteriori error bounds in the
-norm using a time reconstruction and a novel elliptic reconstruction which includes mesh-change; this technical novelty is revealed to be crucial in our setting. In Sect. 5, upon defining a new space-time reconstruction, we derive a posteriori error bounds in the  -norm. Finally, in Sect. 6 we briefly discuss an approach to arriving at
-norm. Finally, in Sect. 6 we briefly discuss an approach to arriving at  -type a posteriori error estimates.
-type a posteriori error estimates.
2 Model problem and space-time discretization
We introduce most of the notation and technical background for the paper. In Sect. 2.1 we provide the functional analytic set-up for the abstract heat equation, a related concrete Example 2.2, and we present the fully discrete numerical scheme in Sect. 2.3.
2.1 Abstract setting
Throughout this work, Bochner spaces will be used. To that end, given an interval  , and a real Hilbert space
, and a real Hilbert space  with inner product
with inner product  and induced norm
and induced norm  , we define
, we define

We write  to signify the space of measurable functions
to signify the space of measurable functions  such that the corresponding norm is bounded. Note that
such that the corresponding norm is bounded. Note that  is a Hilbert space with inner product and induced norm given by
is a Hilbert space with inner product and induced norm given by

and  , respectively. We also let
, respectively. We also let  be the Sobolev space of all functions in
be the Sobolev space of all functions in  whose (weak temporal) derivative is bounded in
whose (weak temporal) derivative is bounded in  , with the norm
, with the norm

Finally, the space  consists of all functions that are continuous on
consists of all functions that are continuous on  , the closure of J, with values in
, the closure of J, with values in  , endowed with the standard maximum norm
, endowed with the standard maximum norm

We consider henceforth two (real) Hilbert spaces  and
and  forming a Gelfand triple
forming a Gelfand triple

where  denotes the dual of
denotes the dual of  . The duality pairing
. The duality pairing  of
of  and
and  can be seen as a continuous extension of the inner product
can be seen as a continuous extension of the inner product  . In particular, identifying
. In particular, identifying  , for
, for  and
and  , there holds
, there holds

see, e.g., [32, §7.2] for details.
Moreover, let

be a self-adjoint linear elliptic operator continuous and coercive in the sense that there exist constants \(\beta \ge \alpha >0\) such that

Given an initial value  , a final time \(T>0\), denoting henceforth the time interval
, a final time \(T>0\), denoting henceforth the time interval

and given a source function  , we are interested in a Galerkin-type numerical approximation of the function
, we are interested in a Galerkin-type numerical approximation of the function

which solves uniquely the linear parabolic initial value problem

Incidentally, due to the continuous embedding

it follows that u belongs to  [32, e.g., Lemma 7.3] and the initial condition in (2.11) makes sense.
[32, e.g., Lemma 7.3] and the initial condition in (2.11) makes sense.
2.2 Example
(Concrete elliptic operators) A commonly encountered situation which can be cast in the above framework is the classical linear diffusion equation, i.e.  , where, for a given open, connected, and bounded domain
, where, for a given open, connected, and bounded domain  , \(d=1,2\) or 3, we consider a given symmetric matrix-valued function
, \(d=1,2\) or 3, we consider a given symmetric matrix-valued function  ,
,  , satisfying
, satisfying

for some constant \(\alpha >0\). Here, we choose, e.g.,  ,
,  , and
, and  to be the typical function spaces in the context of second-order linear elliptic PDEs with homogeneous Dirichlet boundary condition \(u=0\) on
to be the typical function spaces in the context of second-order linear elliptic PDEs with homogeneous Dirichlet boundary condition \(u=0\) on  .
.
Another possible choice, e.g., is  ,
,  , and
, and  , for the case of a fourth-order parabolic problem with essential boundary conditions.
, for the case of a fourth-order parabolic problem with essential boundary conditions.
2.2 Time discontinuous and space conforming Galerkin approximation
Given a (real) linear space  , the space of all
, the space of all  -valued polynomials of degree at most r, with \(r\in \mathbb {N}_0\), on
-valued polynomials of degree at most r, with \(r\in \mathbb {N}_0\), on  is defined by
is defined by

In addition, if  , we define
, we define

In order to introduce the discontinuous Galerkin time stepping scheme for (2.11), we consider a finite sequence of time nodes and time steps,

as well as the corresponding time intervals

Thus, we have a partition  of the time interval I given in (2.9).
of the time interval I given in (2.9).
Given a  -piecewise continuous function
-piecewise continuous function  , we define its time jump across
, we define its time jump across  , for given \(g(t_0^-)\), by
, for given \(g(t_0^-)\), by

where we introduce the one-sided limits  Moreover, we associate with the finite sequence of time instants
Moreover, we associate with the finite sequence of time instants  a finite sequence of finite-dimensional conforming subspaces
a finite sequence of finite-dimensional conforming subspaces

For a generic  -conforming Galerkin space
-conforming Galerkin space  , we signify by
, we signify by  the
the  -orthogonal projection from
-orthogonal projection from  onto
onto  :
:

Note that, due to (2.6), for  , we have
, we have

When  is
is  , for some
, for some  , we write
, we write  to indicate
to indicate  .
.
In order to introduce the time semidiscrete and space-time fully discrete spaces, let  ,
,  , be a polynomial degree. Then, consider the time semidiscrete Galerkin space
, be a polynomial degree. Then, consider the time semidiscrete Galerkin space

respectively, the space-time fully discrete Galerkin space

where  are the space-time Galerkin subspaces. The fully discrete time-discontinuous Galerkin and spatially-conforming approximation of (2.11) is then an
are the space-time Galerkin subspaces. The fully discrete time-discontinuous Galerkin and spatially-conforming approximation of (2.11) is then an  -piecewise continuous function
-piecewise continuous function  , such that
, such that

and for  ,
,

 where
where  .
.
3 Reconstructions
We will next introduce some technical essentials. The main tools are the time lifting (Sect. 3.1), the time reconstruction (Sect. 3.3), and a new variant of the elliptic reconstruction from [23] for fully discrete schemes (Sect. 3.6). In Sect. 3.7 we postulate the availability of a posteriori error estimators for elliptic residuals, and we give some pointers to the relevant literature. In addition, we discuss various error estimates that measure the time reconstruction error; in particular, we state two identities which follow directly, respectively, from [35, Theorem 2] and, taking into account the explicit representation of the time reconstruction, from [20, Lemma 1].
3.1 Time lifting
Let us consider, for given  , a linear time lifting operator
, a linear time lifting operator

It is defined, for each  , by the Riesz representation
, by the Riesz representation

3.2 Lemma
(Space invariance under time lifting) For any linear subspace  , the time lifting from (3.1) and (3.2) satisfies
, the time lifting from (3.1) and (3.2) satisfies

In particular, writing  for the indicator function on a generic set A, and assuming
for the indicator function on a generic set A, and assuming  for each
for each  , we have
, we have

Proof
This result is a straightforward consequence of the explicit representation of \(\chi _n\) as described in [35, Lemma 6]. \(\square \)
3.2 Time reconstruction
Let us define the time-reconstruction  of a given time-discrete function
of a given time-discrete function

as follows: for each  , we let
, we let  satisfy
satisfy

Equivalently, we note the following characterization of  in weak form on each
in weak form on each  ,
,

 , with the initial condition
, with the initial condition

for  ; cf. [27, 35]. Evidently, the above construction carries over to any linear subspace
; cf. [27, 35]. Evidently, the above construction carries over to any linear subspace  in an obvious way.
in an obvious way.
3.4 Proposition
(Time-reconstruction error identities) Consider any (real) Hilbert space  , and
, and  ,
,  , with
, with  defined from
defined from  through (3.6). Then, for given
through (3.6). Then, for given  , the following approximation identities hold
, the following approximation identities hold

where

and

Proof
The identity (3.9) was first proved in [27, Lemma 2.2], and extended to this exact form in [35, Theorem 2] accounting for the dependence on the polynomial degree explicitly. The second equality (3.11) follows directly by combining the explicit representation formula derived in [35, Eq. (33)] with [20, Lemma 1]. \(\square \)
3.5 Remark
(Continuity of the time-reconstruction) Owing to [28, Lemma 2.1], the semidiscrete (spatially exact) time-reconstruction (3.6) originally defined in [28] and [35] is a continuous function in time. In particular, the time-reconstruction  of the fully discrete solution
of the fully discrete solution  , defined in (2.24) and (2.25), is still continuous across the time nodes \(t_0,\ldots ,t_{N-1}\), despite having
, defined in (2.24) and (2.25), is still continuous across the time nodes \(t_0,\ldots ,t_{N-1}\), despite having  , on \(I_n\), when the spatial mesh changes across \(t_{n-1}\) in a non-hierarchical fashion.
, on \(I_n\), when the spatial mesh changes across \(t_{n-1}\) in a non-hierarchical fashion.
3.3 Elliptic reconstruction
Let  be a generic conforming Galerkin space. Then, given the elliptic operator
be a generic conforming Galerkin space. Then, given the elliptic operator  from (2.7), we define the discrete elliptic operator
from (2.7), we define the discrete elliptic operator  , for each
, for each  , as
, as  such that
such that

From the ellipticity of  , it follows that
, it follows that  is invertible. Note that the discrete elliptic operator’s domain may be extended from
is invertible. Note that the discrete elliptic operator’s domain may be extended from  to all of
to all of  ; indeed, this may be convenient in some cases where we are ready to give up its invertibility. If
; indeed, this may be convenient in some cases where we are ready to give up its invertibility. If  is one of
is one of  s, for some
s, for some  , we denote
, we denote  by
by  .
.
To optimize on the structure of the mesh-change indicator below, we use a nonstandard elliptic reconstruction on each time interval \(I_n\). To that end, for each \(t\in I_n\), we define the elliptic reconstruction  , by
, by

where  is the time-reconstruction of the fully discrete solution
is the time-reconstruction of the fully discrete solution  from (2.24) and (2.25). It follows that
from (2.24) and (2.25). It follows that  and may be written implicitly, for any
and may be written implicitly, for any  , as the solution of the t-dependent elliptic problem
, as the solution of the t-dependent elliptic problem

The initial value of  is given by
is given by

with  from (2.11).
from (2.11).
Upon restricting the test functions in (3.13) to  , we obtain
, we obtain

cf. (3.12). Evidently this identity implies

for each  ,
,  .
.
3.4 Assumption (elliptic a posteriori error estimates)
For given  , consider the abstract elliptic problem of finding
, consider the abstract elliptic problem of finding  such that
such that  . Moreover, let
. Moreover, let  be a generic
be a generic  -conforming Galerkin space, and let
-conforming Galerkin space, and let  be w’s Galerkin approximation in
be w’s Galerkin approximation in  , defined implicitly as the solution of
, defined implicitly as the solution of  . Then some a posteriori error bound holds, viz.,
. Then some a posteriori error bound holds, viz.,

with a suitable a posteriori error estimator  , which we assume to be available for
, which we assume to be available for  representing any of the spaces
representing any of the spaces  or
or  . Recalling (3.14), assumption (3.18) allows, for instance, to get a posteriori error control of the elliptic reconstruction error in the
. Recalling (3.14), assumption (3.18) allows, for instance, to get a posteriori error control of the elliptic reconstruction error in the  -norm, i.e.
-norm, i.e.

for the selection of spaces  . Details on such a posteriori error estimates can be found, e.g., in [2, 4, 5, 9]. It is worth mentioning that
. Details on such a posteriori error estimates can be found, e.g., in [2, 4, 5, 9]. It is worth mentioning that  does not need to belong to
does not need to belong to  for (3.18) to hold; instead, it is usually enough that
for (3.18) to hold; instead, it is usually enough that  is
is  -orthogonal to
-orthogonal to  in order to derive elliptic a posteriori error estimates.
in order to derive elliptic a posteriori error estimates.
3.5 Pointwise form
For  , we denote by
, we denote by

the time-local fully discrete  -orthogonal projection defined by
-orthogonal projection defined by

and its time-global counterpart

Let  , and note that using Definition 3.3 and identity (3.17), the fully discrete local DG formulation (2.25) transforms into
, and note that using Definition 3.3 and identity (3.17), the fully discrete local DG formulation (2.25) transforms into

Thus, for each  , we have
, we have

noting that  from Fubini’s Theorem. Hence, from the elliptic reconstruction (3.13), we deduce the pointwise form
from Fubini’s Theorem. Hence, from the elliptic reconstruction (3.13), we deduce the pointwise form

3.9 Remark
Upon noting the trivial identity for \(t\in I_n\),

we observe that the above definition of the elliptic reconstruction constitutes a high order extension of the zero-th order version from [6, Definition 6.1].
4
 -norm a posteriori error analysis
-norm a posteriori error analysis
To highlight the potential generality of the reconstruction approach, we first embark on proving a posteriori error bounds in the  -norm. As we will see below, the resulting bounds are qualitatively closely related to the bounds from [16, 17, 19] when
-norm. As we will see below, the resulting bounds are qualitatively closely related to the bounds from [16, 17, 19] when  . A key attribute of the approach presented below is that the resulting a posteriori bounds are flexible with respect to the choice of respective elliptic bounds, such as residual, recovery, or flux-reconstruction ones.
. A key attribute of the approach presented below is that the resulting a posteriori bounds are flexible with respect to the choice of respective elliptic bounds, such as residual, recovery, or flux-reconstruction ones.
4.1 Errors
Introduce the following errors

and the corresponding remainder error

whereby the full error can be decomposed as

Recalling that our ultimate goal is to find a posteriori estimates for e, and noting that such estimates for  and
and  are provided by Proposition 3.4 and Assumption 3.7, respectively, it will suffice to estimate
are provided by Proposition 3.4 and Assumption 3.7, respectively, it will suffice to estimate  , or
, or  , in terms of
, in terms of  or
or  .
.
4.2 Lemma
(Time reconstruction error bounds) For  , we have the explicitly computable bounds
, we have the explicitly computable bounds

and

Proof
The proof follows immediately from Proposition 3.4. \(\square \)
4.3 Lemma
(Space reconstruction error bounds) Assume the availability of elliptic a posteriori error bounds as per Assumption 3.7. Then, for  , we have the explicitly computable bound
, we have the explicitly computable bound

We can now prove the first main result of this work. \(\square \)
4.4 Theorem
( -norm a posteriori error bound) Let Assumption 3.7 hold. Then, for \(n=1,\dots ,N\), and
-norm a posteriori error bound) Let Assumption 3.7 hold. Then, for \(n=1,\dots ,N\), and

we have the following a posteriori error bound

where \(c_{\alpha ,\beta }:=\sqrt{\alpha ^{-1}+\beta ^{-1}}\), with the constants \(\alpha ,\beta \) from (2.8), and  and
and  to signify the data oscillation and initial error indicators, respectively.
to signify the data oscillation and initial error indicators, respectively.
Proof
From (3.25) and the PDE (2.11), on each \(I_n\), we have

Testing (4.9) with  , we deduce
, we deduce

Note that the term  occurring in the above estimator is computable signifying the so-called oscillation error. Thanks to the continuity of
occurring in the above estimator is computable signifying the so-called oscillation error. Thanks to the continuity of  , we can integrate the last identity on \((0,t_n)\), for some \(n=1,\dots ,N\), and through standard arguments, we obtain
, we can integrate the last identity on \((0,t_n)\), for some \(n=1,\dots ,N\), and through standard arguments, we obtain

using the continuity and coercivity of  , cf. (2.8). For any \(\vartheta >0\) observe the identity
, cf. (2.8). For any \(\vartheta >0\) observe the identity

Notice that the last two terms are non-positive for \(\vartheta \) as in (4.7). Then, from (4.11), we infer

Taking square root and using the triangle inequality,  , we deduce
, we deduce

Invoking now Lemmas 4.2 and 4.3, and noting that  , the result already follows. \(\square \)
, the result already follows. \(\square \)
4.5 Remark
For the particular case  ,
,  and
and  , cf. Example 2.2, note that the constants in (2.8) can be chosen to be \(\alpha =\beta =1\). Especially, selecting
, cf. Example 2.2, note that the constants in (2.8) can be chosen to be \(\alpha =\beta =1\). Especially, selecting  , we have \(c_{\alpha ,\beta }\vartheta =1\) in (4.8).
, we have \(c_{\alpha ,\beta }\vartheta =1\) in (4.8).
4.6 Remark
(Mesh change error via elliptic reconstruction) The elliptic reconstruction (3.13) features a mesh-change type term. This is an important departure from the (standard) elliptic reconstruction proposed in [24]; cf. also [6, Definition 6.1]. For instance, if  from (3.18) is the standard residual energy norm a posteriori error estimator, the element residual includes the expression
from (3.18) is the standard residual energy norm a posteriori error estimator, the element residual includes the expression  , which is effectively a mesh-change term. Indeed, from (3.6) we have on \(I_n\):
, which is effectively a mesh-change term. Indeed, from (3.6) we have on \(I_n\):

from the commutativity of the spatial projection  and operations on the time variable. Let now \(\varkappa _n :I_n\rightarrow \mathbb {R}\) be the polynomial of degree \(r_n\) representing the time lifting \(\chi _n\) from (3.2), i.e. such that
and operations on the time variable. Let now \(\varkappa _n :I_n\rightarrow \mathbb {R}\) be the polynomial of degree \(r_n\) representing the time lifting \(\chi _n\) from (3.2), i.e. such that

for all \(t\in I_n\) and  ; we refer to [35, Lemmas 6 & 7] or [20, Remark 1] for an explicit formula for \(\varkappa _n \). Then, we can conclude
; we refer to [35, Lemmas 6 & 7] or [20, Remark 1] for an explicit formula for \(\varkappa _n \). Then, we can conclude

i.e. the arbitrary order DG-analogue to the classical mesh-change indicator. We note that the representation (4.17) is particularly relevant in implementation as it can be used to efficiently realize the space reconstruction error bounds in Lemma 4.3. Finally, observing that \(\varkappa _n\) takes its maximum at \(t_{n-1}\), which follows from [35, Lemma 6], and recalling (3.2), it is possible to compute the maximum value of \(\varkappa _n\) on \(\overline{I}_n\):

Hence

see [35, Proposition 2].
4.7 Remark
(Reconstruction vs direct approach) As noted by one referee, it is possible to spare the use of elliptic reconstruction in the proof of the  -norm a posteriori bound, for particular cases of operators
-norm a posteriori bound, for particular cases of operators  and of Gelfand triples (2.5), as discussed in [16, 17, 19] for the specific case
and of Gelfand triples (2.5), as discussed in [16, 17, 19] for the specific case  ,
,  and
and  ; cf. Example 2.2. As a result, different a posteriori error estimators arise with, possibly, slightly different constants multiplying common terms in the estimator. Elliptic reconstruction, nonetheless, offers the ability to use various elliptic estimators from the literature in the bound: this feature may become important for multiscale operators
; cf. Example 2.2. As a result, different a posteriori error estimators arise with, possibly, slightly different constants multiplying common terms in the estimator. Elliptic reconstruction, nonetheless, offers the ability to use various elliptic estimators from the literature in the bound: this feature may become important for multiscale operators  , e.g., singular perturbations. In general, elliptic reconstruction allows for, crucial in some cases, flexibility in the handling for more complicated spatial operators
, e.g., singular perturbations. In general, elliptic reconstruction allows for, crucial in some cases, flexibility in the handling for more complicated spatial operators  , e.g., nonlinear or singularly perturbed operators [6, 7, 18].
, e.g., nonlinear or singularly perturbed operators [6, 7, 18].
5
 -norm a posteriori error analysis
-norm a posteriori error analysis
We continue by proving an a posteriori error bound in the  -norm, which appears to be of higher order than the
-norm, which appears to be of higher order than the  -norm one presented above. A key difference with respect to the above proof of the
-norm one presented above. A key difference with respect to the above proof of the  -norm bound is the use of a combined space-time reconstruction defined below.
-norm bound is the use of a combined space-time reconstruction defined below.
5.1 Error-residual relation
Set  , i.e. the time reconstruction of the elliptic reconstruction, noting that Definition 3.3 is still valid for functions on
, i.e. the time reconstruction of the elliptic reconstruction, noting that Definition 3.3 is still valid for functions on  in space. Now, introducing the time error
in space. Now, introducing the time error
which is continuous on  , and subtracting the PDE (2.11) from (3.25), we have:
, and subtracting the PDE (2.11) from (3.25), we have:

our aim being to deduce an evolution equation for \(\rho \). To this end, we have

from the linearity of the time reconstruction.
We define  to be the finest common coarsening of the two meshes, with the associated largest common finite element subspace given by
to be the finest common coarsening of the two meshes, with the associated largest common finite element subspace given by  , and a meshsize
, and a meshsize  .
.
5.2 Lemma
(Time reconstruction error bound) Let \( t\in I_n\), \(n=0,1\dots , N\). Then, we have the abstract estimate

with

Assume further that, for every  , there exists a
, there exists a  , such that
, such that

for some \(s>0\), and for generic constants \(C_\mathrm{ap}, C_\mathrm{stab}>0\), independent of v and of  . Then, we also have the bound
. Then, we also have the bound

with

Therefore, setting  , we have the combined estimate
, we have the combined estimate

Proof
Recalling (3.6) and using the fact that the elliptic operator  is time independent, we immediately observe that
is time independent, we immediately observe that

Therefore, by Proposition 3.4 and of Remark 3.9, for  , we conclude that
, we conclude that

which is (5.4). Furthermore, exploit the orthogonality identity

which follows from the definition of  and the properties of
and the properties of  . From the latter, together with Remark 3.9, and the temporal independence of
. From the latter, together with Remark 3.9, and the temporal independence of  , we have
, we have

From (5.6) and the continuity of  , therefore, we deduce
, therefore, we deduce

and the result already follows. \(\square \)
5.3 Remark
(Practical upper bound for \(\eta _{n,1}^\mathrm{time}\)) In standard settings, e.g., in the canonical example of the heat equation, cf. Example 2.2, for which (5.6) holds, we can use \(\eta _{n,2}^\mathrm{time}\) for \(\eta _{n}^\mathrm{time}\); this is particularly pertinent when the dimension of  is comparable to those of
is comparable to those of  and
and  . In cases, however, in which (5.6) may not be effective, or even known, we may be forced to revert to (5.4); see [8] for two such settings, where one involves virtual element methods, and the other incorporates moving mesh methods. The dual norm in \(\eta _{n,1}^\mathrm{time}\) typically requires a global inversion to be evaluated, in the absence of a natural Galerkin orthogonality property like (5.12) above.
. In cases, however, in which (5.6) may not be effective, or even known, we may be forced to revert to (5.4); see [8] for two such settings, where one involves virtual element methods, and the other incorporates moving mesh methods. The dual norm in \(\eta _{n,1}^\mathrm{time}\) typically requires a global inversion to be evaluated, in the absence of a natural Galerkin orthogonality property like (5.12) above.
Although solving an elliptic problem to determine/estimate the time estimator \(\eta _{n,1}^\mathrm{time}\) may appear to be computationally demanding, such global solves may be typically performed in a lower dimensional space than  itself, through an a posteriori error controlled fashion, as we now demonstrate. Let
itself, through an a posteriori error controlled fashion, as we now demonstrate. Let  be the solution to the problem
be the solution to the problem  (with
(with  for instance). Let also an approximation
for instance). Let also an approximation  to \(\varphi \), for some Galerkin space
to \(\varphi \), for some Galerkin space  , be given by
, be given by

Now, the continuity of  implies
implies  In addition, from coercivity, continuity and the Galerkin orthogonality
In addition, from coercivity, continuity and the Galerkin orthogonality  , we have, respectively,
, we have, respectively,

using also the self-adjointness of  . The above, together with the assumed availability of an a posteriori error indicator in the energy norm give the computable bound
. The above, together with the assumed availability of an a posteriori error indicator in the energy norm give the computable bound

or, for the specific case  ,
,

5.4 Lemma
(Space reconstruction error bound) For  ,
,  , we have the bound
, we have the bound

where

with  from (4.16) in Remark 4.6, and the estimator is explicitly computable, via Assumption 3.7.
from (4.16) in Remark 4.6, and the estimator is explicitly computable, via Assumption 3.7.
Proof
Recalling (3.6), on \(I_n\) we have

Hence, with the notation of Remark 4.6, it follows that

Differentiating (3.16) with respect to \(t\in I_n\), and recalling that the elliptic operator  is t-independent, we deduce the Galerkin orthogonality relation
is t-independent, we deduce the Galerkin orthogonality relation

We conclude that  is the Galerkin approximation of
is the Galerkin approximation of  , where
, where

by differentiating (3.14) with respect to t.
Furthermore, from the definition of the elliptic reconstruction (3.14), we have, respectively,

implying, therefore,

This means that  and
and  are the Galerkin approximations of the first and second problem in (5.25), respectively.
are the Galerkin approximations of the first and second problem in (5.25), respectively.
Now, (5.24) together with Assumption 3.7, yield

Similarly, noting that

and combining (5.25) with Assumption 3.7, leads to

The result already follows by inserting the above estimates into (5.22). \(\square \)
We are now ready to present the second main result of this work.
5.5 Theorem
( -norm a posteriori bound) With the notation of §2 and under Assumption 3.7, along with the assumptions of Lemmata 5.2 and 5.4, for each
-norm a posteriori bound) With the notation of §2 and under Assumption 3.7, along with the assumptions of Lemmata 5.2 and 5.4, for each  , we have the bound
, we have the bound

with  and \(\eta ^\mathrm{in}\) as in Theorem 4.4.
and \(\eta ^\mathrm{in}\) as in Theorem 4.4.
Proof
We start from (5.3), which upon testing with \(\rho \) and integrating with respect to t between (0, t), along with the coercivity of  , (2.8), gives
, (2.8), gives

and, thus,

via standard arguments.
Now fix \(n\in \{1,\dots , N\}\) and choose \(t^\star \in [0,t_n]\) such that

Then, letting \(t=t^\star \) in (5.32), and taking the square root, yields

It remains to bound the last term on the right-hand side of (5.33). To that end, applying (3.9), and involving Lemmata 5.2 and 5.4, results in

The triangle inequality now gives

To estimate the second and third term on the right-hand side of (5.35), we apply (3.11), and the triangle inequality, to obtain

Also, with the aid of (3.19),

Combining the last two estimates, we conclude

Combining the above completes the argument. \(\square \)
5.6 Remark
(Alternative ‘short-time’ a posteriori error estimator) Starting from the alternative estimate

the bound (5.31) with \(t=t^\star \) as in the proof of Theorem 5.5 gives

Triangle inequality trivially yields

Now, using Hölder’s inequality, recalling (5.10), and applying Proposition 3.4 and Remark 3.9, we have, respectively,

In addition, an inspection of the proof of Lemma 5.4 reveals the bound

for \(t\in I_m\), where

Combining the above estimates, we arrive at

this, in conjunction with (5.38) now yields an alternative a posteriori error bound which may be superior to the one given in Theorem 5.5 for small final time \(t_n\).
6
 -type a posteriori error estimates
-type a posteriori error estimates
We conclude this work by briefly arguing on how our techniques allow to derive  -type a posteriori error estimates. To this end, for any
-type a posteriori error estimates. To this end, for any  -piecewise sufficiently smooth function z, we define the broken (semi-)norm
-piecewise sufficiently smooth function z, we define the broken (semi-)norm

with  signifying the time partition of \(I=(0,T]\) from (2.17). Then, recalling \(\rho \) from (5.1), the triangle inequality yields
signifying the time partition of \(I=(0,T]\) from (2.17). Then, recalling \(\rho \) from (5.1), the triangle inequality yields

upon noting the continuity of \(\rho \) with respect to the time variable. To control the first term on the right-hand side of (6.2), we start from (5.3), and notice that

with \(\beta \) from (2.8). Furthermore, based on (5.31) with \(t=T\), standard arguments give

Combining the last two bounds, we arrive at

The first term on the right-hand side of (6.5) is bounded trivially by \(\eta ^\mathrm{in}\) (defined in Theorem 4.4), while for the second we use (5.34). To estimate the second term on the right-hand side of (6.2), we consider the splitting

The second term on the right-hand side of the last estimate is a computable quantity, while the first can be immediately bounded using Lemma 5.4, through the linearity of the time reconstruction.
7 Conclusions
In this article we have presented a posteriori error estimates for fully discrete hp-DG-in-time and general Galerkin-in-space discretizations of abstract linear parabolic PDE. Our approach is based on a novel combination of temporal and elliptic reconstructions, the latter allowing for arbitrary elliptic error spatial estimators. Our main results include computable  - and
- and  -a posteriori error estimates; some remarks concerning
-a posteriori error estimates; some remarks concerning  -norm error estimation are given as well. Finally, we note that a series of numerical experiments showcasing the optimality of the a posteriori error estimators derived above are given in [7].
-norm error estimation are given as well. Finally, we note that a series of numerical experiments showcasing the optimality of the a posteriori error estimators derived above are given in [7].
References
Akrivis, G., Makridakis, C., Nochetto, R.H.: A posteriori error estimates for the Crank–Nicolson method for parabolic equations. Math. Comp. 75(254), 511–531 (2006)
Ainsworth, M., Tinsley Oden, J.: A posteriori error estimation in finite element analysis. Pure and Applied Mathematics (New York). Wiley, New York (2000)
Braess, D., Pillwein, V., Schöberl, J.: Equilibrated residual error estimates are p-robust. Comput. Methods Appl. Mech. Eng. 198(13–14), 1189–1197 (2009)
Braess, D.: Finite elements: theory, fast solvers, and applications in elasticity theory, 3rd edn, p. 4. Cambridge University Press, Cambridge (2007)
Brenner, S.C., Scott, L.R.: The mathematical theory of finite element methods. Texts in Applied Mathematics, 3rd edn. Springer, New York (2007)
Cangiani, A., Georgoulis, E.H., Metcalfe, S.: Adaptive discontinuous Galerkin methods for nonstationary convection–diffusion problems. IMA J. Numer. Anal. 34(4), 1578–1597 (2014)
Cangiani, A., Georgoulis, E.H., Sabawi, M.: A posteriori error analysis for implicit-explicit \(hp\)-discontinuous Galerkin timestepping methods for semilinear parabolic problems. J. Sci. Comput. 82(2), 24 (2020)
Cangiani, Andrea, Georgoulis, Emmanuil H., Sutton, Oliver J.: Adaptive non-hierarchical Galerkin methods for parabolic problems with application to moving mesh and virtual element methods. Online preprint arXiv:2005.05661, May (2020)
Destuynder, P., Métivet, B.: Explicit error bounds in a conforming finite element method. Math. Comput. 68(228), 1379–1396 (1999)
Eriksson, K., Johnson, C.: Adaptive finite element methods for parabolic problems. I. A linear model problem. SIAM J. Numer. Anal. 28(1), 43–77 (1991)
Eriksson, K., Johnson, C.: Adaptive finite element methods for parabolic problems. II. Optimal error estimates in \(L_\infty L_2\)and\(L_\infty L_\infty \). SIAM J. Numer. Anal. 32(3), 706–740 (1995)
Eriksson, K., Johnson, C.: Adaptive finite element methods for parabolic problems. IV. Nonlinear problems. SIAM J. Numer. Anal. 32(6), 1729–1749 (1995)
Eriksson, K., Johnson, C.: Adaptive finite element methods for parabolic problems. V. Long-time integration. SIAM J. Numer. Anal. 32(6), 1750–1763 (1995)
Eriksson, K., Johnson, C., Larsson, S.: Adaptive finite element methods for parabolic problems. VI. Analytic semigroups. SIAM J. Numer. Anal. 35(4), 1315–1325 (1998). (electronic)
Eriksson, K., Johnson, C., Thomée, V.: Time discretization of parabolic problems by the discontinuous Galerkin method. RAIRO Modél. Math. Anal. Numér. 19(4), 611–643 (1985)
Ern, A., Smears, I., Vohralík, M.: Guaranteed, locally space-time efficient, and polynomial-degree robust a posteriori error estimates for high-order discretizations of parabolic problems. SIAM J. Numer. Anal. 55(6), 2811–2834 (2017)
Ern, A., Smears, I., Vohralík, M.: Equilibrated flux a posteriori error estimates in \(L^2(H^1)\)-norms for high-order discretizations of parabolic problems. IMA J. Numer. Anal. 39(3), 1158–1179 (2019)
Georgoulis, E.H., Makridakis, C.: On a posteriori error control for the Allen-Cahn problem. Math. Methods Appl. Sci. 37(2), 173–179 (2014)
Gaspoz, F.D., Siebert, K., Kreuzer, C., Ziegler, D.A.: A convergent time-space adaptive \({\rm dG}(s)\) finite element method for parabolic problems motivated by equal error distribution. IMA J. Numer. Anal. 39(2), 650–686 (2019)
Holm, B., Wihler, T.P.: Continuous and discontinuous Galerkin time stepping methods for nonlinear initial value problems with application to finite time blow-up. Numer. Math. 138(3), 767–799 (2018)
Jamet, P.: Galerkin-type approximations which are discontinuous in time for parabolic equations in a variable domain. SIAM J. Numer. Anal. 15(5), 912–928 (1978)
Kyza, I., Metcalfe, S., Wihler, T.P.: \(hp\)-adaptive Galerkin time stepping methods for nonlinear initial value problems. J. Sci. Comput. 75(1), 111–127 (2018)
Lakkis, O., Makridakis, C.: Elliptic reconstruction and a posteriori error estimates for fully discrete linear parabolic problems. Math. Comp. 75(256), 1627–1658 (2006)
Lakkis, Omar: Makridakis, Charalambos: Elliptic reconstruction and a posteriori error estimates for fully discrete linear parabolic problems. Math. Comp. 75(256), 1627–1658 (2006)
Makridakis, C., Babuška, I.: On the stability of the discontinuous Galerkin method for the heat equation. SIAM J. Numer. Anal. 34(1), 389–401 (1997)
Makridakis, C., Nochetto, R.H.: Elliptic reconstruction and a posteriori error estimates for parabolic problems. SIAM J. Numer. Anal. 41(4), 1585–1594 (2003)
Makridakis, C., Nochetto, R.H.: A posteriori error analysis for higher order dissipative methods for evolution problems. Numer. Math. 104(4), 489–514 (2006)
Makridakis, Charalambos, Nochetto, Ricardo H.: A posteriori error analysis for higher order dissipative methods for evolution problems. Numer. Math. 104(4), 489–514 (2006)
Matache, A.-M., Schwab, C., Wihler, T.P.: Fast numerical solution of parabolic integrodifferential equations with applications in finance. SIAM J. Sci. Comput. 27, 369–393 (2005)
Matache, A.-M., Schwab, C., Wihler, T.P.: Linear complexity solution of parabolic integro-differential equations. Numer. Math. 104, 69–102 (2006)
Picasso, M.: Adaptive finite elements for a linear parabolic problem. Comput. Methods Appl. Mech. Engrg. 167(3–4), 223–237 (1998)
Roubíček, T.: Nonlinear partial differential equations with applications. International Series of Numerical Mathematics, 2nd edn. Birkhäuser/Springer Basel AG, Basel (2013)
Schötzau, D., Schwab, C.: Time discretization of parabolic problems by the \(hp\)-version of the discontinuous Galerkin finite element method. SIAM J. Numer. Anal. 38, 837–875 (2000)
Schötzau, D., Schwab, C.: \(hp\)-discontinuous Galerkin time-stepping for parabolic problems. C. R. Acad. Sci. Paris, Série I 333, 1121–1126 (2001)
Schötzau, D., Wihler, T.P.: A posteriori error estimation for \(hp\)-version time-stepping methods for parabolic partial differential equations. Numer. Math. 115(3), 475–509 (2010)
Verfürth, R.: A posteriori error estimates for nonlinear problems \(L^r(0, T;L^\rho (\Omega ))\)-error estimates for finite element discretizations of parabolic equations. Math. Comp. 67(224), 1335–1360 (1998)
Verfürth, R.: A posteriori error estimates for finite element discretizations of the heat equation. Calcolo 40(3), 195–212 (2003)
von Petersdorff, T., Schwab, C.: Numerical solution of parabolic equations in high dimensions. Math. Model. Anal. Numer. 38, 93–127 (2004)
Werder, T., Gerdes, K., Schötzau, D., Schwab, C.: \(hp\)-discontinuous Galerkin time-stepping for parabolic problems. Comput. Methods Appl. Mech. Eng. 190, 6685–6708 (2001)
Acknowledgements
We would like to thank the referees for their thoughtful remarks that have led to relevant improvements of our results. EHG acknowledges financial support by The Leverhulme Foundation (Grant No. RPG-2015-306) and by the Marie Skłodowska–Curie ITN “ModCompShock”. OL’s contribution was partially supported by the Marie Skłodowska–Curie ITN “ModCompShock”. TPW acknowledges the financial support of the Swiss National Science Foundation (SNF), Grant No. 200021_182524.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Georgoulis, E.H., Lakkis, O. & Wihler, T.P. A posteriori error bounds for fully-discrete hp-discontinuous Galerkin timestepping methods for parabolic problems. Numer. Math. 148, 363–386 (2021). https://doi.org/10.1007/s00211-021-01187-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-021-01187-7



 -norm a posteriori error analysis
-norm a posteriori error analysis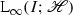 -norm a posteriori error analysis
-norm a posteriori error analysis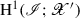 -type a posteriori error estimates
-type a posteriori error estimates