Abstract
The Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) is considered among the most frequently used techniques to deal with multi-criteria group decision-making (MCGDM) conflicts. In this article, we have presented an extended TOPSIS technique in the framework of interval type-2 trapezoidal Pythagorean fuzzy numbers (IT2TrPFN). We first projected a novel approach to evaluate the distance between them using ordered weighted averaging operator and \((\alpha ,\beta )\)-cut. Subsequently, we widen the concept of TOPSIS method formed on the distance method with IT2TrPFNs and applied it on MCGDM dilemma by considering the attitudes and perspectives of the decision-makers. Lastly, an application of solar tracking system and numerous contrasts with the other existing techniques are presented to express the practicality and feasibility of our projected approach.
Similar content being viewed by others
1 Introduction
“Multi-criteria group decision-making” (MCGDM) is a branch of operational research that yields results to rank and assess the optimum alternatives from set of alternatives under multiple criterion regarding multiple decision-maker’s choices and preferences Celik et al. (2015). In the conventional MCGDM techniques, the alternative ratings and criterion weights were articulated using crisp values or natural language was employed by the decision-makers. It has been become complex to state the linguistic terms exactly and accurately by using these terms. Consequently, the “fuzzy set” (FS) theory introduced by Zadeh (1965a) was supposed to be used for coping up with the problems involving subjective uncertainties Chakraborty et al. (2018), Chakraborty et al. (2019), Alamin et al. (2020), [52]. Afterwards, “type-2 fuzzy sets” (T2FS) Mendel et al. (2006), Mendel and John (2002), Mendel (2007), an extension of “type-1 fuzzy sets” (T1FS) were introduced since they can engage with more uncertainties than T1FSs. The most extensively used T2FSs are “interval type-2 fuzzy sets” (IT2FS) Mendel (2007), Mendel and John (2002), Mendel et al. (2006) that is a particular case of frequently used T2FSs.
Later on, Atanassov introduced “intuitionistic fuzzy sets” (IFS) Atanassov (1986) that considers both membership and non-membership grades Phu et al. (2019). Many investigators have declared their uniqueness in decision-making because of their significance in dealing with uncertainty. “Pythagorean fuzzy sets” (PFS) pioneered by Yager (2013) is a generalization of IFS being an innovative tool used for modeling imprecision and ambiguous information occurring in MCGDM problems. PFSs are proved to be adeptly more competent in managing vagueness, imprecision and uncertainties than IFSs in several decision-making processes. The prominent characteristic of the PFSs in comparison to the IFSs is to ease the state that “the sum of membership and non-membership degree is less than or equal to one with the square sum of membership and non-membership degree less than or equal to one”. For handling the uncertainties and impreciseness more accurately, we have introduced “interval type-2 Pythagorean fuzzy sets” (IT2PFS) that are capable to detain the fuzziness more efficiently. If a IT2PFS is convex and defined on a bounded and closed interval then it is called “interval type-2 Pythagorean fuzzy number” (IT2PFN). Decision-making is one of the most widely used phenomena in our day-today life. One of the most powerful theories is that of the multi-attribute decision-making (MADM) also known as multi-criteria decision-making (MCDM) or multi-criteria decision-analysis (MCDA) for handling problems that extensively impact the human real-life problems. In literature, there are various MCGDM techniques including ELECTRE, fuzzy VIKOR, PROMETHEE, fuzzy AHP, fuzzy ANP Celik et al. (2015), Kahraman et al. (2015), Chen (2011), Chen et al. (2012), Touqeer et al. (2020), Touqeer et al. (2020), Touqeer et al. (2020). All these MCGDM techniques engages FSs that are not capable to handle indeterminacy and irregularity involved in MCGDM processes so, in the recent times, few Pythagorean MCGDM strategies have been productively established for dealing with such ambiguities. Many useful tactics have been established to enrich PFS theory. Another approach involving MCGDM problem under fuzzy framework was presented by Yang et al. (2020) where TOPSIS is extended in trapezoidal interval type-2 fuzzy environment using \(\alpha\)-cut.
TOPSIS Mardani et al. (2015) is among the most widely used techniques for dealing with MCGDM setbacks in different fields. The main objective of TOPSIS is: the optimal alternative must possess shortest distance from “Positive Ideal Solution” (PIS) and farthest distance from “Negative Ideal Solution” (NIS). In the presented article, we have broaden the prevailing approach in the context of IT2PFN using the novel notion of \(\left( {\alpha ,\beta } \right)\)-cut. We have proposed an extended TOPSIS approach where OWA operator is utilized to depict the outlook and perspectives of decision-makers. Based on IT2PFN structure, this paper utilizes a well-known Pythagorean fuzzy number having trapezoidal appearance called an IT2TrPFN. The core difference of the anticipated approach is that it utilizes IT2TrPFN and uses \(\left( {\alpha ,\beta } \right)\)-cut to defuzzify the IT2PFNs.
The remaining article is structured in this manner: Sect. 2 recalls some fundamental concepts about PFS, IT2PFS, IT2TrPFN, \(\left( {\alpha ,\beta } \right)\)-cut, OWA operator and TOPSIS method. Section 3 presents a technique to compute distance between two IT2TrPFNs using \(\left( {\alpha ,\beta } \right)\)-cut and OWA operator and also projects an analytical solution of distance between two IT2TrPFNs. Section 4 anticipates thorough methodology of extension of TOPSIS in the framework of IT2TrPFNs using the projected distance approach. Section 5 demonstrates the application of solar tracking system to prove the feasibility of the anticipated approach. Section 6 compares the proposed technique with previous techniques to demonstrate the viability of presented approach. Section 7 sums up the paper and provides conclusion.
2 Preliminaries
Several related definitions and concepts about PFS, IT2PFS, IT2TrPFN, \(\left( {\alpha ,\beta } \right)\)-cut, OWA operator and TOPSIS method used in the subsequent discussions are reviewed in brief in the following section.
2.1 Pythagorean fuzzy set (PFS) and interval type-2 pythagorean fuzzy set (IT2PFS)
Definition 2.1
Yager (2013) A PFS \(\bar{\bar{\mathrm {E}}}\) on universal set \({\mathbf {U}}\) is defined as:
where \(\mu _{\bar{\bar{\mathrm {E}}}}(\varsigma )\) and \(\nu _{\bar{\bar{\mathrm {E}}}}(\varsigma )\) represent the “Pythagorean membership degree and Pythagorean non-membership degree” of \(\bar{\bar{\mathrm {E}}}\) at \(\varsigma\) respectively.
Definition 2.2
Peng and Yang (2015), Rahman et al. (2018) The degree of indeterminacy of \(\varsigma\) to \(\bar{\bar{\mathrm {E}}}\) is defined as:
where \(\pi _{\bar{\bar{\mathrm {E}}}}(\varsigma )\in [0,1]\).
Definition 2.3
Let \(\bar{\bar{\mathrm {E}}}(\varsigma )=[\bar{\bar{\mathrm {E}}}^{U}(\varsigma ),\bar{\bar{\mathrm {E}}}^{L}(\varsigma )]\) be a IT2PFS on universal set \({\mathbf {U}}\) where \(\varsigma \in {\mathbf {U}}\) and \(\bar{\bar{\mathrm {E}}}^{U}:{\mathbf {U}} \rightarrow [0,1]\) and \(\bar{\bar{\mathrm {E}}}^{L}:{\mathbf {U}} \rightarrow [0,1]\) are two type-1 Pythagorean fuzzy sets (T1PFS) known as upper and lower Pythagorean fuzzy sets respectively having the condition \(0\le \bar{\bar{\mathrm {E}}}^{L}(\varsigma )\le \bar{\bar{\mathrm {E}}}^{U}(\varsigma ) \le 1\). If \(\bar{\bar{\mathrm {E}}}\in \varsigma\) is convex and defined on a bounded and closed interval then \(\bar{\bar{\mathrm {E}}}\) is termed as IT2PFN on \({\mathbf {U}}\).
Definition 2.4
The degree of indeterminacy of an IT2PFN is defined as:
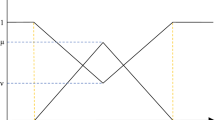
where \(\pi _{\bar{\bar{\mathrm {E}}}}^U(\varsigma ),\pi _{\bar{\bar{\mathrm {E}}}}^L(\varsigma )\in [0,1]\). (Fig. 1)
2.2 Interval type-2 trapezoidal pythagorean fuzzy number (IT2TrPFN)
In this subsection, the concept of IT2TrPFNs along with some of their operations are discussed.
Definition 2.5
Shakeel et al. (2020) Let \(\bar{\bar{\mathrm {E}}}^U=[{\bar{\bar{\mathrm {e}}}_1}^U,{\bar{\bar{\mathrm {e}}}_2}^U,{\bar{\bar{\mathrm {e}}}_3}^U,{\bar{\bar{\mathrm {e}}}_4}^U;\mu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {E}}}}^U]\) and \(\bar{\bar{\mathrm {E}}}^L=[{\bar{\bar{\mathrm {e}}}_1}^L,{\bar{\bar{\mathrm {e}}}_2}^L,{\bar{\bar{\mathrm {e}}}_3}^L,{\bar{\bar{\mathrm {e}}}_4}^L;\mu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {E}}}}^L]\) be the upper and lower trapezoidal Pythagorean fuzzy number (TrPFN) defined on the universal set \({\mathbf {U}}\) where \(0\le {\bar{\bar{\mathrm {e}}}_1}^U \le {\bar{\bar{\mathrm {e}}}_2}^U \le {\bar{\bar{\mathrm {e}}}_3}^U \le {\bar{\bar{\mathrm {e}}}_4}^U \le 1\),\(0\le {\bar{\bar{\mathrm {e}}}_1}^L \le {\bar{\bar{\mathrm {e}}}_2}^L \le {\bar{\bar{\mathrm {e}}}_3}^L \le {\bar{\bar{\mathrm {e}}}_4}^L \le 1\), \(0 \le \mu _{\bar{\bar{\mathrm {E}}}}^L \le \mu _{\bar{\bar{\mathrm {E}}}}^U \le 1\), \(0 \le \nu _{\bar{\bar{\mathrm {E}}}}^L \le \nu _{\bar{\bar{\mathrm {E}}}}^U \le 1\) and \(\bar{\bar{\mathrm {E}}}^L\subset \bar{\bar{\mathrm {E}}}^U\). The Pythagorean membership function \(\mu _{\bar{\bar{\mathrm {E}}}}\) and Pythagorean non-membership function \(\nu _{\bar{\bar{\mathrm {E}}}}\) is defined as follows:
where \(\mu _{\bar{\bar{\mathrm {E}}}}=[\mu _{\bar{\bar{\mathrm {E}}}^U}(\varsigma ),\mu _{\bar{\bar{\mathrm {E}}}^L}(\varsigma )]\)and \(\nu _{\bar{\bar{\mathrm {E}}}}=[\nu _{\bar{\bar{\mathrm {E}}}^U}(\varsigma ),\nu _{\bar{\bar{\mathrm {E}}}^L}(\varsigma )]\)are IT2PFNs.
The number \(\bar{\bar{\mathrm {E}}}\)can be represented as \(\bar{\bar{\mathrm {E}}}=[\bar{\bar{\mathrm {E}}}^U,\bar{\bar{\mathrm {E}}}^L]=([{\bar{\bar{\mathrm {e}}}_1}^U,{\bar{\bar{\mathrm {e}}}_2}^U,{\bar{\bar{\mathrm {e}}}_3}^U,{\bar{\bar{\mathrm {e}}}_4}^U;\mu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {E}}}}^U],[{\bar{\bar{\mathrm {e}}}_1}^L,{\bar{\bar{\mathrm {e}}}_2}^L,{\bar{\bar{\mathrm {e}}}_3}^L,{\bar{\bar{\mathrm {e}}}_4}^L;\mu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {E}}}}^L])\)and is called IT2TrPFN.
2.2.1 Operations on IT2TrPFN
Definition 2.6
Let \(\bar{\bar{\mathrm {E}}}_1=([{\bar{\bar{\mathrm {e}}}_{11}}^U,{\bar{\bar{\mathrm {e}}}_{12}}^U,{\bar{\bar{\mathrm {e}}}_{13}}^U,{\bar{\bar{\mathrm {e}}}_{14}}^U;\mu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {E}}}}^U],[{\bar{\bar{\mathrm {e}}}_{11}}^L,{\bar{\bar{\mathrm {e}}}_{12}}^L,{\bar{\bar{\mathrm {e}}}_{13}}^L,{\bar{\bar{\mathrm {e}}}_{14}}^L;\mu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {E}}}}^L])\) and \(\bar{\bar{\mathrm {E}}}_2=([{\bar{\bar{\mathrm {e}}}_{21}}^U,{\bar{\bar{\mathrm {e}}}_{22}}^U,{\bar{\bar{\mathrm {e}}}_{23}}^U,{\bar{\bar{\mathrm {e}}}_{24}}^U;\mu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {E}}}}^U],[{\bar{\bar{\mathrm {e}}}_{21}}^L,{\bar{\bar{\mathrm {e}}}_{22}}^L,{\bar{\bar{\mathrm {e}}}_{23}}^L,{\bar{\bar{\mathrm {e}}}_{24}}^L;\mu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {E}}}}^L])\) be two IT2TrPFNs and \(\xi \ge {0}\). Then following are the basic operations defined on IT2TrPFNs:
-
1.
Addition:
\(\bar{\bar{\mathrm {E}}}_1\oplus \bar{\bar{\mathrm {E}}}_2= \big \langle \big [\bar{\bar{\mathrm {e}}}_{11}^U+\bar{\bar{\mathrm {e}}}_{21}^U,\bar{\bar{\mathrm {e}}}_{12}^U+\bar{\bar{\mathrm {e}}}_{22}^U,\bar{\bar{\mathrm {e}}}_{13}^U+\bar{\bar{\mathrm {e}}}_{23}^U,\bar{\bar{\mathrm {e}}}_{14}^U+\bar{\bar{\mathrm {e}}}_{24}^U;\sqrt{(\mu _1^U)^2+(\mu _2^U)^2-(\mu _1^U)^2(\mu _2^U)^2},\nu _1^U\nu _2^U\big ], \big [\bar{\bar{\mathrm {e}}}_{11}^L+\bar{\bar{\mathrm {e}}}_{21}^L,\bar{\bar{\mathrm {e}}}_{12}^L+\bar{\bar{\mathrm {e}}}_{22}^L,\bar{\bar{\mathrm {e}}}_{13}^L+\bar{\bar{\mathrm {e}}}_{23}^L,\bar{\bar{\mathrm {e}}}_{14}^L+\bar{\bar{\mathrm {e}}}_{24}^L;\sqrt{(\mu _1^L)^2+(\mu _2^L)^2-(\mu _1^L)^2(\mu _2^L)^2},\nu _1^L\nu _2^L\big ]\big \rangle\)
-
2.
Multiplication:
\(\bar{\bar{\mathrm {E}}}_1\otimes \bar{\bar{\mathrm {E}}}_2= \big \langle \big [\bar{\bar{\mathrm {e}}}_{11}^U\bar{\bar{\mathrm {e}}}_{21}^U,\bar{\bar{\mathrm {e}}}_{12}^U\bar{h }_{22}^U,\bar{\bar{\mathrm {e}}}_{13}^U\bar{\bar{\mathrm {e}}}_{23}^U,\bar{\bar{\mathrm {e}}}_{14}^U\bar{\bar{\mathrm {e}}}_{24}^U;\mu _1^U\mu _2^U,\sqrt{(\nu _1^U)^2+(\nu _2^U)^2-(\nu _1^U)^2(\nu _2^U)^2}\big ], \big [\bar{\bar{\mathrm {e}}}_{11}^L\bar{\bar{\mathrm {e}}}_{21}^L,\bar{\bar{\mathrm {e}}}_{12}^L\bar{\bar{\mathrm {e}}}_{22}^L,\bar{\bar{\mathrm {e}}}_{13}^L\bar{\bar{\mathrm {e}}}_{23}^L,\bar{\bar{\mathrm {e}}}_{14}^L\bar{\bar{\mathrm {e}}}_{24}^L;\mu _1^L\mu _2^L,\sqrt{(\nu _1^L)^2+(\nu _2^L)^2-(\nu _1^L)^2(\nu _2^L)^2}\big ]\big \rangle\)
-
3.
Multiplication by an ordinary number:
\(\xi \bar{\bar{\mathrm {E}}}_1= \big \langle \big [\xi \bar{\bar{\mathrm {e}}}_{11}^U,\xi \bar{\bar{\mathrm {e}}}_{12}^U,\xi \bar{\bar{\mathrm {e}}}_{13}^U,\xi \bar{\bar{\mathrm {e}}}_{14}^U;\sqrt{1-(1-(\mu _1^U)^2)^\xi },(\nu _1^U)^\xi \big ], \big [\xi \bar{\bar{\mathrm {e}}}_{11}^L,\xi \bar{\bar{\mathrm {e}}}_{12}^L,\xi \bar{\bar{\mathrm {e}}}_{13}^L,\xi \bar{\bar{\mathrm {e}}}_{14}^L; \sqrt{1-(1-(\mu _1^L)^2)^\xi },(\nu _1^L)^\xi \big ]\big \rangle\)
-
4.
Exponential:
\({\bar{\bar{\mathrm {E}}}_1}^\xi = \big \langle \big [\bar{\bar{\mathrm {e}}}_{11}^{U^\xi },\bar{\bar{\mathrm {e}}}_{12}^{U^\xi },\bar{\bar{\mathrm {e}}}_{13}^{U^\xi },\bar{\bar{\mathrm {e}}}_{14}^{U^\xi };(\mu _1^U)^\xi ,\sqrt{1-(1-(\nu _1^U)^2)^\xi }\big ], \big [\bar{\bar{\mathrm {e}}}_{11}^{L^\xi },\bar{\bar{\mathrm {e}}}_{12}^{L^\xi },\bar{\bar{\mathrm {e}}}_{13}^{L^\xi },\bar{\bar{\mathrm {e}}}_{14}^{L^\xi };(\mu _1^U)^\xi ;(\mu _1^L)^\xi ,\sqrt{1-(1-(\nu _1^L)^2)^\xi }\big ]\big \rangle\)
2.3 \(\left( {\alpha ,\beta } \right)\)-Cut
Definition 2.7
The \(\left( {\alpha ,\beta } \right)\)-cut of a Pythagorean Fuzzy number labelled by \(\bar{\bar{\mathrm {E}}}_(\alpha ,\beta )\) is defined in this way:
where \(\alpha ,\beta \in [0,1]\) and are fixed numbers.
Definition 2.8
The \(\left( {\alpha ,\beta } \right)\)-cut of an IT2PFN \(\bar{\bar{\mathrm {E}}}\) is represented as follows:
where \(\varsigma \in {{\mathbf {U}}},[\mu _{\bar{\bar{\mathrm {E}}}}^U(\varsigma ),\mu _{\bar{\bar{\mathrm {E}}}}^L(\varsigma )],[\nu _{\bar{\bar{\mathrm {E}}}}^U(\varsigma ),\nu _{\bar{\bar{\mathrm {E}}}}^L(\varsigma )],\alpha ,\beta \in {[0,1]}\)and \(\bar{\bar{\mathrm {e}}}(\alpha )\in [\bar{\bar{\mathrm {e}}}_l(\alpha ),\bar{\bar{\mathrm {e}}}_r(\alpha )],\bar{\bar{\mathrm {f}}}(\alpha )\in [\bar{\bar{\mathrm {f}}}_l(\alpha ),\bar{\bar{\mathrm {f}}}_r(\alpha )], \bar{\bar{\mathrm {e}}}(\beta )\in [\bar{\bar{\mathrm {e}}}_l(\beta ),\bar{\bar{\mathrm {e}}}_r(\beta )],\bar{\bar{\mathrm {f}}}(\beta )\in [\bar{\bar{\mathrm {f}}}_l(\beta ),\bar{\bar{\mathrm {f}}}_r(\beta )]\).
If \(\left( {\alpha ,\beta } \right)\)-cut on \({\bar{\bar{\mathrm {E}}}}^L\)exists, then the intervals \([\bar{\bar{\mathrm {e}}}(\alpha ),\bar{\bar{\mathrm {f}}}(\alpha )]\)and \([\bar{\bar{\mathrm {e}}}(\beta ),\bar{\bar{\mathrm {f}}}(\beta )]\)are divided into three sub-intervals: \([\bar{\bar{\mathrm {e}}}_l(\alpha ),\bar{\bar{\mathrm {e}}}_r(\alpha )],[\bar{\bar{\mathrm {e}}}_r(\alpha ),\bar{\bar{\mathrm {f}}}_l(\alpha )]\)and \([\bar{\bar{\mathrm {f}}}_l(\alpha ),\bar{\bar{\mathrm {f}}}_r(\alpha )]\);\([\bar{\bar{\mathrm {e}}}_l(\beta ),\bar{\bar{\mathrm {e}}}_r(\beta )]\), \([\bar{\bar{\mathrm {e}}}_r(\beta ),\bar{\bar{\mathrm {f}}}_l(\beta )]\)and \([\bar{\bar{\mathrm {f}}}_l(\beta ),\bar{\bar{\mathrm {f}}}_r(\beta )]\)respectively. \(\bar{\bar{\mathrm {e}}}(\alpha )\)and \(\bar{\bar{\mathrm {e}}}(\beta )\)cannot suspect a value larger than \(\bar{\bar{\mathrm {e}}}_r(\alpha )\)and \(\bar{\bar{\mathrm {e}}}_r(\beta )\). Similarly, \(\bar{\bar{\mathrm {f}}}(\alpha )\in [\bar{\bar{\mathrm {f}}}_l(\alpha ),\bar{\bar{\mathrm {f}}}_r(\alpha )]\)and \(\bar{\bar{\mathrm {f}}}(\beta )\in [\bar{\bar{\mathrm {f}}}_l(\beta ),\bar{\bar{\mathrm {f}}}_r(\beta )]\)cannot suspect a value smaller than \(\bar{\bar{\mathrm {f}}}_l(\alpha )\)and \(\bar{\bar{\mathrm {f}}}_l(\beta )\)respectively. However, if \(\left( {\alpha ,\beta } \right)\)-cut on \(\bar{\bar{\mathrm {E}}}^L\)doesn’t exist, then both \(\bar{\bar{\mathrm {e}}}_r(\alpha )\)and \(\bar{\bar{\mathrm {f}}}_l(\alpha )\);\(\bar{\bar{\mathrm {e}}}_r(\beta )\)and \(\bar{\bar{\mathrm {f}}}_l(\beta )\)can suspect values freely in the whole intervals \([\bar{\bar{\mathrm {e}}}_l(\alpha ),\bar{\bar{\mathrm {f}}}_r(\alpha )]\)and \([\bar{\bar{\mathrm {e}}}_l(\beta ),\bar{\bar{\mathrm {f}}}_r(\beta )]\).
2.4 OWA operator
Definition 2.9
Sang and Liu (2014) An OWA operator with n dimension is a mapping \(\bar{\bar{\mathrm {E}}}:{\mathbf {R}}^n\rightarrow {\mathbf {R}}\) associated with an n vector \(\ddot{\text {W}}=(\ddot{\text {w}}_1,\ldots ,\ddot{\text {w}}_n)\) in such a way that \(\ddot{\text {w}}_i\in [0,1]\) and \(\sum _{i=1}^n \ddot{\text {w}}_i=1\). Moreover,
where \(\bar{\bar{\mathrm {f}}}_j\) represents j-th largest element of aggregated objects collection \(\bar{\bar{\mathrm {e}}}_1,\ldots ,\bar{\bar{\mathrm {e}}}_n\).
2.5 TOPSIS method
Assuming a MCGDM problem having n alternatives \((\text {P}_1,\ldots ,\text {P}_n)\) and m criterion \((\text {Q}_1,\ldots ,\text {Q}_n)\). Each alternative is estimated in accordance with n criterion. Decision matrix \(\text {X}=(x_{ij})_{n\times m}\) exhibits all the values designated to alternatives corresponding to each criterion. \(\breve{\text {W}}=(\ddot{\text {w}}_1,\ldots ,\ddot{\text {w}}_m)\) shows the criterion weights satisfying \(\sum _{j=1}^m \ddot{\text {w}}_j=1\).
2.5.1 TOPSIS algorithm
- Step 1::
-
Formulate a normalized decision matrix.
For benefit type criteria:
$$\begin{aligned} \text {n}_{ij}=\frac{x_{ij}}{\max (x_{ij})} \end{aligned}$$(13)For cost type criteria:
$$\begin{aligned} \text {n}_{ij}=\frac{\min (x_{ij})}{x_{ij}} \end{aligned}$$(14)where \(\text {n}_{ij}\) is the normalized value of \(x_{ij}\).
- Step 2::
-
Evaluate weighted normalized decision matrix \(\text {U}=(\breve{\mathrm {u}}_{ij})_{n\times m}\).
$$\begin{aligned} \breve{\mathrm {u}}_{ij}=\ddot{\text {w}}_j\text {n}_{ij} \end{aligned}$$(15)where \(\ddot{\text {w}}_j\) is the j-th criterion weight and \(\sum _{j=1}^m \ddot{\text {w}}_j=1\).
- Step 3::
-
Evaluate the PIS and NIS.
$$\begin{aligned} \text {P}^*= & {} \{\breve{\mathrm {u}}_1^*,\breve{\mathrm {u}}_2^*,\ldots ,\breve{\mathrm {u}}_n^*\}\nonumber \\= & {} \big \{(\max _i \breve{\mathrm {u}}_{ij}|j\in \text {K}_t)(\min _i \breve{\mathrm {u}}_{ij}|j\in \text {K}_c)\big \} \end{aligned}$$(16)$$\begin{aligned} \text {N}^-= & {} \{\breve{\mathrm {u}}_1^-,\breve{\mathrm {u}}_2^-,\ldots ,\breve{\mathrm {u}}_n^-\}\nonumber \\= & {} \big \{(\max _i \breve{\mathrm {u}}_{ij}|j\in \text {K}_c)(\min _i \breve{\mathrm {u}}_{ij}|j\in \text {K}_t)\big \} \end{aligned}$$(17)where \(\text {K}_t\) is the benefit criterion set and \(\text {K}_c\) is the cost criterion set.
- Step 4::
-
Acquire the distances of alternatives from PIS and NIS.
$$\begin{aligned} \text {D}_i^*= & {} \sqrt{\sum _{j=1}^n(\breve{\mathrm {u}}_{ij}-\breve{\mathrm {u}}_j^*)^2} \end{aligned}$$(18)$$\begin{aligned} \text { D}_i^-= & {} \sqrt{\sum _{j=1}^n(\breve{\mathrm {u}}_{ij}-\breve{\mathrm {u}}_j^-)^2} \end{aligned}$$(19) - Step 5::
-
Asses relative closeness to the ideal alternatives.
$$\begin{aligned} \text { RC}_i=\frac{\text {Y}_i^-}{\text {Y}_i^- + \text {Y}_i^*} \end{aligned}$$(20) - Step 6::
-
Rank the alternatives with respect to the relative closeness to ideal alternatives. The larger the relative closeness coefficient the better the alternative is.
3 Method to compute distance between two IT2TrPFNs
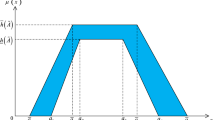
In the following segment, we projected a novel technique to estimate the distance between two IT2TrPFNs using \(\left( {\alpha ,\beta } \right)\)-cut and OWA operator that can be employed to determine the distance of an alternative from PIS and NIS whose ratings of local criterion are represented as IT2TrPFNs. Moreover, we established an analytical solution of the distance between two IT2TrPFNs that can be used for calculating the distance more suitably and easily. (Fig. 2)
The techniques of computing the distance between two IT2TrPFNs are shown as follows:
Firstly, a new assumption is made about the \(\left( {\alpha ,\beta } \right)\)-cuts of a IT2TrNN when \(\alpha\) and \(\beta\) are over the lower membership and non-membership functions i.e. \(\mu _{\bar{\bar{\mathrm {E}}}}^L\) and \(\nu _{\bar{\bar{\mathrm {E}}}}^L\). For a IT2TrPFN \(\bar{\bar{\mathrm {E}}}\) (seen in Fig. 3), it is assumed that when \(\alpha ,\beta >\mu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {E}}}}^L\); \(\bar{\bar{\mathrm {e}}}(\alpha )\) lies freely in the interval \([\bar{\bar{\mathrm {e}}}_l(\alpha ),\bar{\bar{\mathrm {f}}}_r(\alpha )]\) and \(\bar{\bar{\mathrm {f}}}(\alpha )\) lies freely in the interval \([\bar{\bar{\mathrm {e}}}_l(\alpha ),\bar{\bar{\mathrm {f}}}_r(\alpha )]\), which implies that the \(\alpha\)-cuts of a IT2TrPFN are \([([\bar{\bar{\mathrm {e}}}_l(\alpha ),\bar{\bar{\mathrm {f}}}_r(\alpha )]),([\bar{\bar{\mathrm {e}}}_l(\alpha ),\bar{\bar{\mathrm {f}}}_r(\alpha )])]\) when \(\alpha >\mu _{\bar{\bar{\mathrm {E}}}}^L\). Similarly, \(\bar{\bar{\mathrm {e}}}(\beta )\) lies freely in the interval \([\bar{\bar{\mathrm {e}}}_l(\beta ),\bar{\bar{\mathrm {f}}}_r(\beta )]\) and \(\bar{\bar{\mathrm {f}}}(\beta )\) lies freely in the interval \([\bar{\bar{\mathrm {e}}}_l(\beta ),\bar{\bar{\mathrm {f}}}_r(\beta )]\), which implies that the \(\beta\)-cuts of a IT2TrPFN are \([([\bar{\bar{\mathrm {e}}}_l(\beta ),\bar{\bar{\mathrm {f}}}_r(\beta )]),([\bar{\bar{\mathrm {e}}}_l(\beta ),\bar{\bar{\mathrm {f}}}_r(\beta )])]\) when \(\beta >\nu _{\bar{\bar{\mathrm {E}}}}^L\). In order to get rid of the overlapping of right and left intervals of \(\alpha\) and \(\beta\) cuts of IT2TrPFN, we make an amendment in the above assumption that \(\bar{\bar{\mathrm {e}}}(\alpha )\) values freely in the interval \([\bar{\bar{\mathrm {e}}}_l(\alpha ),\frac{x_2^L+x_3^L}{2}]\) and \(\bar{\bar{\mathrm {f}}}(\alpha )\) lies freely in the interval \([\frac{x_2^L+x_3^L}{2},\bar{\bar{\mathrm {f}}}_r(\alpha )]\) when \(\alpha >\mu _{\bar{\bar{\mathrm {E}}}}^L\). Similarly, \(\bar{\bar{\mathrm {e}}}(\beta )\) lies freely in the interval \([\bar{\bar{\mathrm {e}}}_l(\beta ),\frac{x_2^L+x_3^L}{2}]\) and \(\bar{\bar{\mathrm {f}}}(\beta )\) lies freely in the interval \([\frac{x_2^L+x_3^L}{2},\bar{\bar{\mathrm {f}}}_r(\beta )]\) when \(\beta >\nu _{\bar{\bar{\mathrm {E}}}}^L\). In other words, we replace \(\bar{\bar{\mathrm {e}}}_r(\alpha )\) and \(\bar{\bar{\mathrm {f}}}_l(\alpha )\) with \(\frac{x_2^L+x_3^L}{2}\) when \(\alpha >\mu _{\bar{\bar{\mathrm {E}}}}^L\), \(\bar{\bar{\mathrm {e}}}_r(\beta )\) and \(\bar{\bar{\mathrm {f}}}_l(\beta )\) with \(\frac{x_2^L+x_3^L}{2}\) when \(\beta >\nu _{\bar{\bar{\mathrm {E}}}}^L\). Therefore, \(\bar{\bar{\mathrm {e}}}_r(\alpha )\),\(\bar{\bar{\mathrm {f}}}_l(\alpha )\),\(\bar{\bar{\mathrm {e}}}_r(\beta )\) and \(\bar{\bar{\mathrm {f}}}_l(\beta )\) are redefined in the following way:
Figure 3 indicates a novel definition of \((\alpha ,\beta )\)-cut of a IT2TrPFN when \((\alpha ,\beta )>(\mu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {E}}}}^L)\) and \((\alpha ,\beta )<(\mu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {E}}}}^L)\).
3.1 Algorithm for computing distance between two IT2TrPFNs
-
Step 1:
Computing the \(\left( {\alpha ,\beta } \right)\)-cut of the difference between two IT2TrPFNs. For IT2TrPFNs \(\bar{\bar{\mathrm {E}}}\) and \(\bar{\bar{\mathrm {F}}}\)
$$\begin{aligned} \begin{aligned} \bar{\bar{\mathrm {E}}} = &(\bar{\bar{\mathrm {E}}}^U,\bar{\bar{\mathrm {E}}}^L)\\ = &[(\bar{\bar{\mathrm {e}}}_1^U,\bar{\bar{\mathrm {e}}}_2^U,\bar{\bar{\mathrm {e}}}_3^U,\bar{\bar{\mathrm {e}}}_4^U;\mu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {E}}}}^U), (\bar{\bar{\mathrm {e}}}_1^L,\bar{\bar{\mathrm {e}}}_2^L,\bar{\bar{\mathrm {e}}}_3^L,\bar{\bar{\mathrm {e}}}_4^L;\mu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {E}}}}^L)]\\ \bar{\bar{\mathrm {F}}} = &(\bar{\bar{\mathrm {F}}}^U,\bar{\bar{\mathrm {F}}}^L)\\ = &[(\bar{\bar{\mathrm {f}}}_1^U,\bar{\bar{\mathrm {f}}}_2^U,\bar{\bar{\mathrm {f}}}_3^U,\bar{\bar{\mathrm {f}}}_4^U;\mu _{\bar{\bar{\mathrm {F}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U), (\bar{\bar{\mathrm {f}}}_1^L,\bar{\bar{\mathrm {f}}}_2^L,\bar{\bar{\mathrm {f}}}_3^L,\bar{\bar{\mathrm {f}}}_4^L;\mu _{\bar{\bar{\mathrm {F}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L)] \end{aligned} \end{aligned}$$the difference between them can be estimated by using subtraction operation identified as \(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}}\) that is also an IT2TrPFN. The \(\left( {\alpha ,\beta } \right)\)-cut of \(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}}\) is portrayed in Fig. 4 and determined as follows:
$$\begin{aligned} (\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }=\big [[{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_1,{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_2][{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_3,{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_4]\big ] \end{aligned}$$(25)$$\begin{aligned} (\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }=\big [[{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_1,{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_2][{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_3,{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_4]\big ] \end{aligned}$$(26)Now, we have
$$\begin{aligned} {(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_1= & {} \frac{(\bar{\bar{\mathrm {e}}}_2^U-\bar{\bar{\mathrm {f}}}_3^U-\bar{\bar{\mathrm {e}}}_1^U+\bar{\bar{\mathrm {f}}}_4^U)\cdot \alpha }{\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U\big )}+\bar{\bar{\mathrm {e}}}_1^U-\bar{\bar{\mathrm {f}}}_4^U \ \ \alpha \in \bigg [0,\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U\big )\bigg ] \end{aligned}$$(27)$$\begin{aligned} {(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_2= & {} {\left\{ \begin{array}{ll} \frac{(\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L-\bar{\bar{\mathrm {e}}}_1^L+\bar{\bar{\mathrm {f}}}_4^L)\cdot \alpha }{\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^L,\mu _{\bar{\bar{\mathrm {F}}}}^L\big )}+\bar{\bar{\mathrm {e}}}_1^L-\bar{\bar{\mathrm {f}}}_4^L &{}\alpha \in \bigg [0,\min \big ((\mu _{\bar{\bar{\mathrm {E}}}}^L,\mu _{\bar{\bar{\mathrm {F}}}}^L\big )\bigg ]\\ \frac{\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L+\bar{\bar{\mathrm {e}}}_3^L-\bar{\bar{\mathrm {f}}}_2^L}{2} &{}\alpha \in \bigg [\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^L,\mu _{\bar{\bar{\mathrm {F}}}}^L\big ),\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U\big )\bigg ] \end{array}\right. } \end{aligned}$$(28)$$\begin{aligned} {(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_3= & {} {\left\{ \begin{array}{ll} \bar{\bar{\mathrm {e}}}_4^L-\bar{\bar{\mathrm {f}}}_1^L-\frac{(\bar{\bar{\mathrm {e}}}_4^L-\bar{\bar{\mathrm {f}}}_1^L-\bar{\bar{\mathrm {e}}}_3^L+\bar{\bar{\mathrm {f}}}_2^L)\cdot \alpha }{\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^L,\mu _{\bar{\bar{\mathrm {F}}}}^L\big )}&{}\alpha \in \bigg [0,\min \big ((\mu _{\bar{\bar{\mathrm {E}}}}^L,\mu _{\bar{\bar{\mathrm {F}}}}^L\big )\bigg ]\\ \frac{\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L+\bar{\bar{\mathrm {e}}}_3^L-\bar{\bar{\mathrm {f}}}_2^L}{2} &{}\alpha \in \bigg [\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^L,\mu _{\bar{\bar{\mathrm {F}}}}^L\big ),\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U\big )\bigg ] \end{array}\right. } \end{aligned}$$(29)$$\begin{aligned} {(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_4= & {} \bar{\bar{\mathrm {e}}}_4^U-\bar{\bar{\mathrm {f}}}_1^U-\frac{(\bar{\bar{\mathrm {e}}}_4^U-\bar{\bar{\mathrm {f}}}_1^U-\bar{\bar{\mathrm {e}}}_3^U+\bar{\bar{\mathrm {f}}}_2^U)\cdot \alpha }{\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U\big )} \ \ \alpha \in \bigg [0,\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U\big )\bigg ] \end{aligned}$$(30)where \({(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_1<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_2<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_3<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_4\)when \(\alpha \in \bigg [0,\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^L,\mu _{\bar{\bar{\mathrm {F}}}}^L\big )\bigg ]\) and \({(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_1<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_2={(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_3<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_4\) when \(\alpha \in \bigg [\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^L,\mu _{\bar{\bar{\mathrm {F}}}}^L\big ),\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U\big )\bigg ]\). Similarly,
$$\begin{aligned} {(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_1= & {} \frac{(\bar{\bar{\mathrm {e}}}_2^U-\bar{\bar{\mathrm {f}}}_3^U-\bar{\bar{\mathrm {e}}}_1^U+\bar{\bar{\mathrm {f}}}_4^U)\cdot \beta -\bar{\bar{\mathrm {e}}}_2^U+\bar{\bar{\mathrm {f}}}_3^U+(\bar{\bar{\mathrm {e}}}_1^U+\bar{\bar{\mathrm {f}}}_4^U)\cdot \min \big (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U\big )}{\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U\big )-1} \nonumber \\&\quad \beta \in \bigg [0,\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U\big )\bigg ] \end{aligned}$$(31)$$\begin{aligned} {(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_2= & {} {\left\{ \begin{array}{ll} \frac{(\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L-\bar{\bar{\mathrm {e}}}_1^L+\bar{\bar{\mathrm {f}}}_4^L)\cdot \beta -\bar{\bar{\mathrm {e}}}_2^L+\bar{\bar{\mathrm {f}}}_3^L+(\bar{\bar{\mathrm {e}}}_1^L+\bar{\bar{\mathrm {f}}}_4^L)\cdot \min \big (\nu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L\big )}{\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L\big )-1}&{}\beta \in \bigg [0,\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L\big )\bigg ]\\ \frac{\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L+\bar{\bar{\mathrm {e}}}_3^L-\bar{\bar{\mathrm {f}}}_2^L}{2}&{}\beta \in \bigg [\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L\big ),\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U\big )\bigg ] \end{array}\right. } \end{aligned}$$(32)$$\begin{aligned} {(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_3= & {} {\left\{ \begin{array}{ll} \frac{(\bar{\bar{\mathrm {e}}}_4^L-\bar{\bar{\mathrm {f}}}_1^L-\bar{\bar{\mathrm {e}}}_3^L+\bar{\bar{\mathrm {f}}}_2^L)\cdot \beta +\bar{\bar{\mathrm {e}}}_3^U-\bar{\bar{\mathrm {f}}}_2^L-(\bar{\bar{\mathrm {e}}}_4^L-\bar{\bar{\mathrm {f}}}_1^L)\cdot \min \big (\nu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L\big )}{1-\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L\big )}&{}\beta \in \bigg [0,\min \big ((\nu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L\big )\bigg ]\\ \frac{\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L+\bar{\bar{\mathrm {e}}}_3^L-\bar{\bar{\mathrm {f}}}_2^L}{2}&{}\beta \in \bigg [\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L\big ),\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U\big )\bigg ] \end{array}\right. } \end{aligned}$$(33)$$\begin{aligned} {(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_4= & {} \frac{(\bar{\bar{\mathrm {e}}}_4^U-\bar{\bar{\mathrm {f}}}_1^U-\bar{\bar{\mathrm {e}}}_3^U+\bar{\bar{\mathrm {f}}}_2^U)\cdot \beta +\bar{\bar{\mathrm {e}}}_3^U-\bar{\bar{\mathrm {f}}}_2^U-(\bar{\bar{\mathrm {e}}}_4^U-\bar{\bar{\mathrm {f}}}_1^U)\cdot \min \big (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U\big )}{1-\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U\big )}\nonumber \\&\quad \beta \in \bigg [0,\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U\big )\bigg ] \end{aligned}$$(34)where \({(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_1<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_2<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_3<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_4\) when \(\beta \in \bigg [0,\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L\big )\bigg ]\) and \({(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_1<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_2={(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_3<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\beta }}_4\) when
\(\beta \in \bigg [\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L\big ),\min \big (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U\big )\bigg ]\).
-
Step 2:
Calculating the distance between two IT2TrPFNs at \(\alpha\) and \(\beta\) level. Further, the \(\left( {\alpha ,\beta } \right)\)-cut intervals of the difference between two IT2TrPFNs are integrated within the range of \(\alpha\) and \(\beta\) respectively by which the difference between two IT2TrPFNs is converted into type-2 interval, calculated as follows:
$$\begin{aligned} \begin{aligned} \bigtriangleup _\alpha (\bar{\bar{\mathrm {E}}},\bar{\bar{\mathrm {F}}})&=\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_\alpha d\alpha \\&=\bigg [\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_1 d\alpha ,\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_2d\alpha \bigg ]\\&\bigg [\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_3 d\alpha ,\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_4 d\alpha \bigg ] \end{aligned} \end{aligned}$$(35)where
$$\begin{aligned} \int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_1 d\alpha= & {} \frac{\bar{\bar{\mathrm {e}}}_2^U-\bar{\bar{\mathrm {f}}}_3^U-\bar{\bar{\mathrm {e}}}_1^U+\bar{\bar{\mathrm {f}}}_4^U}{2\cdot \min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)} \end{aligned}$$(36)$$\begin{aligned} \int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_2 d\alpha= & {} \frac{\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L-\bar{\bar{\mathrm {e}}}_1^L+\bar{\bar{\mathrm {f}}}_4^L}{2\cdot \min (\mu _{\bar{\bar{\mathrm {E}}}}^L,\mu _{\bar{\bar{\mathrm {F}}}}^L)}+ \frac{\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L+\bar{\bar{\mathrm {e}}}_3^L-\bar{\bar{\mathrm {f}}}_2^L}{2\cdot \min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)} \end{aligned}$$(37)$$\begin{aligned} \int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_3 d\alpha= & {} \frac{\bar{\bar{\mathrm {e}}}_4^L-\bar{\bar{\mathrm {f}}}_1^L-\bar{\bar{\mathrm {e}}}_3^L+\bar{\bar{\mathrm {f}}}_2^L}{2\cdot \min (\mu _{\bar{\bar{\mathrm {E}}}}^L,\mu _{\bar{\bar{\mathrm {F}}}}^L)}+ \frac{\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L+\bar{\bar{\mathrm {e}}}_3^L-\bar{\bar{\mathrm {f}}}_2^L}{2\cdot \min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)} \end{aligned}$$(38)$$\begin{aligned} \int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_4 d\alpha= & {} \frac{\bar{\bar{\mathrm {e}}}_4^U-\bar{\bar{\mathrm {f}}}_1^U+\bar{\bar{\mathrm {e}}}_3^U+\bar{\bar{\mathrm {f}}}_2^U}{2\cdot \min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)} \end{aligned}$$(39)Similarly,
$$\begin{aligned} \begin{aligned} \bigtriangleup _\beta (\bar{\bar{\mathrm {E}}},\bar{\bar{\mathrm {F}}})&=\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_\beta d\beta \\&=\bigg [\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_1 d\beta ,\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_2d\beta \bigg ]\\&\bigg [\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_3 d\beta ,\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\breve{\text {H}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_4 d\beta \bigg ] \end{aligned} \end{aligned}$$(40)where
$$\begin{aligned} \int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_1 d\beta= & {} \frac{\bar{\bar{\mathrm {e}}}_2^U-\bar{\bar{\mathrm {f}}}_3^U-\bar{\bar{\mathrm {e}}}_1^U+\bar{\bar{\mathrm {f}}}_4^U}{2\cdot \big (\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)-1\big )} \end{aligned}$$(41)$$\begin{aligned} \int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_2 d\beta= & {} \frac{\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L-\bar{\bar{\mathrm {e}}}_1^L+\bar{\bar{\mathrm {f}}}_4^L}{2\cdot \min (\nu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L)}+ \frac{\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L+\bar{\bar{\mathrm {e}}}_3^L-\bar{\bar{\mathrm {f}}}_2^L}{2\cdot \big (\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)-1\big )} \end{aligned}$$(42)$$\begin{aligned} \int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_3 d\beta= & {} \frac{\bar{\bar{\mathrm {e}}}_4^L-\bar{\bar{\mathrm {f}}}_1^L-\bar{\bar{\mathrm {e}}}_3^L+\bar{\bar{\mathrm {f}}}_2^L}{2\cdot \big (1-\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)\big )}+ \frac{\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L+\bar{\bar{\mathrm {e}}}_3^L-\bar{\bar{\mathrm {f}}}_2^L}{2\cdot \min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)} \end{aligned}$$(43)$$\begin{aligned} \int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_4 d\beta= & {} \frac{\bar{\bar{\mathrm {e}}}_4^U-\bar{\bar{\mathrm {f}}}_1^U-\bar{\bar{\mathrm {e}}}_3^U+\bar{\bar{\mathrm {f}}}_2^U}{2\cdot \big (1-\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)\big )} \end{aligned}$$(44)As \({(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_1<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_2<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_3<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_4\) when \(\alpha \in \bigg [0,\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^L,\mu _{\bar{\bar{\mathrm {F}}}}^L\big )\bigg ]\) and \({(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_1<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_2={(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_3<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_4\) when \(\alpha \in \bigg [\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^L,\mu _{\bar{\bar{\mathrm {F}}}}^L\big ),\min \big (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U\big )\bigg ]\). It can be concluded that \(\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_1 d\alpha<\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_2 d\alpha<\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_3 d\alpha <\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_4 d\alpha\). Exchanging the position of \(\bar{\bar{\mathrm {E}}}\) and \(\bar{\bar{\mathrm {F}}}\) in Eqs.(35,36,37, 38,39 and 40), we obtain that:
$$\begin{aligned} \begin{aligned} \bigtriangleup _{\alpha }(\bar{\bar{\mathrm {F}}},\bar{\bar{\mathrm {E}}})&=\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{(\bar{\bar{\mathrm {F}}}-\bar{\bar{\mathrm {E}}})}_\alpha d\alpha \\&=\bigg [-\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_4 d\alpha ,-\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_3 d\alpha \bigg ]\\&\bigg [-\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_2 d\alpha ,-\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_1 d\alpha \bigg ] \end{aligned} \end{aligned}$$(45)Similarly,
$$\begin{aligned} \begin{aligned} \bigtriangleup _{\beta }(\bar{\bar{\mathrm {F}}},\bar{\bar{\mathrm {E}}})&=\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{(\bar{\bar{\mathrm {F}}}-\bar{\bar{\mathrm {E}}})}_\beta d\beta \\&=\bigg [-\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_4 d\beta ,-\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_3 d\beta \bigg ]\\&\bigg [-\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_2 d\beta ,-\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_1 d\beta \bigg ] \end{aligned} \end{aligned}$$(46)Thus, it is shown that the difference between \(\bar{\bar{\mathrm {E}}}\) and \(\bar{\bar{\mathrm {F}}}\) at \(\left( {\alpha ,\beta } \right)\) level has an important property i.e. \(\bigtriangleup _{\alpha }(\bar{\bar{\mathrm {F}}},\bar{\bar{\mathrm {E}}})=-\bigtriangleup _{\alpha }(\bar{\bar{\mathrm {E}}},\bar{\bar{\mathrm {F}}})\) and \(\bigtriangleup _{\beta }(\bar{\bar{\mathrm {F}}},\bar{\bar{\mathrm {E}}})=-\bigtriangleup _{\beta }(\bar{\bar{\mathrm {E}}},\bar{\bar{\mathrm {F}}})\). It indicates that it doesn’t satisfy commutativity. However, no matter what the computational order of both is, the absolute values of the endpoints of two intervals are equal.
-
Step 3:
In the following step, we introduce an OWA operator for defuzzifying \(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}}\) at \(\alpha\) and \(\beta\) level. The distance between them is denoted by \(d(\bar{\bar{\mathrm {E}}},\bar{\bar{\mathrm {F}}})\) and can be determined as:
$$\begin{aligned} \begin{aligned} d(\bar{\bar{\mathrm {E}}},\bar{\bar{\mathrm {F}}})&=\big [\text {F}_{\ddot{\text {w}}}(\bigtriangleup _{\alpha }(\bar{\bar{\mathrm {E}}},\bar{\bar{\mathrm {F}}}))\big ]\\&=\bigg [\text {F}_{\ddot{\text {w}}}\bigg (\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_1 d\alpha ,\ldots ,\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_4 d\alpha \bigg )\bigg ]\\ \end{aligned} \nonumber \\ ={\left\{ \begin{array}{ll} \text {F}_{\ddot{\text {w}}}\bigg (\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_1 d\alpha ,\ldots ,\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_4 d\alpha \bigg )&{} \text {if}\ \ \bar{\bar{\mathrm {E}}}>\bar{\bar{\mathrm {F}}}\\ \text {F}_{\ddot{\text {w}}}\bigg (-\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_1 d\alpha ,\ldots ,-\int _0^{\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\mu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_4 d\alpha \bigg )&{} \text {if}\ \ \bar{\bar{\mathrm {E}}}<\bar{\bar{\mathrm {F}}} \end{array}\right. } \end{aligned}$$(47)$$\begin{aligned} \begin{aligned} d(\bar{\bar{\mathrm {E}}},\bar{\bar{\mathrm {F}}})&=\big [\text {F}_{\ddot{\text {w}}}(\bigtriangleup _{\beta }(\bar{\bar{\mathrm {E}}},\bar{\bar{\mathrm {F}}}))\big ]\\&=\bigg [\text {F}_{\ddot{\text {w}}}\bigg (\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_1 d\beta ,\ldots ,\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_4 d\beta \bigg )\bigg ]\\ \end{aligned} \nonumber \\ ={\left\{ \begin{array}{ll} \text {F}_{\ddot{\text {w}}}\bigg (\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_1 d\beta ,\ldots ,\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_4 d\beta \bigg )&{} \text {if}\ \ \bar{\bar{\mathrm {E}}}>\bar{\bar{\mathrm {F}}}\\ \text {F}_{\ddot{\text {w}}}\bigg (-\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_1 d\beta ,\ldots ,-\int _0^{\min (\nu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)}{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\beta }}_4 d\beta \bigg )&{} \text {if}\ \ \bar{\bar{\mathrm {E}}}<\bar{\bar{\mathrm {F}}} \end{array}\right. } \end{aligned}$$(48)where \(\text {F}_{\ddot{\text {w}}}\) is an OWA operator (see Eq 2.4).
The degree of “orness” corresponding to \(\text {F}_{\ddot{\text {w}}}\) is determined as:
If the orness degree related to the OWA operator is greater than \(\frac{1}{2}\), it depicts that the distance between two IT2TrPFNs is overestimated; in contrast, if it is less than \(\frac{1}{2}\), it means the distance is underestimated; further, if the orness degree is equal to \(\frac{1}{2}\), it implies that the distance is average of the endpoints of the difference between them at \(\alpha\) and \(\beta\) level.
We suppose that an OWA operator \(\text {F}_{\ddot{\text {w}}}\) is related to a weighting function \(\ddot{\text {W}}=(\ddot{\text {w}}_1,\ddot{\text {w}}_2,\ddot{\text {w}}_3,\ddot{\text {w}}_4)\). Resulting \({(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_1<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_2<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_3<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_4\) and \({(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_1<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_2={(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_3<{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})_{\alpha }}_4\), distance between \(\bar{\bar{\mathrm {E}}}\) and \(\bar{\bar{\mathrm {F}}}\) can be computed as:
According to Eqs. (27, 28, 29 and 30), we have
\({{(\bar{\bar{\mathrm {F}}}-\bar{\bar{\mathrm {E}}})}_{\alpha }}_1=-{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_4,{{(\bar{\bar{\mathrm {F}}}-\bar{\bar{\mathrm {E}}})}_{\alpha }}_2=-{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_3, {{(\bar{\bar{\mathrm {F}}}-\bar{\bar{\mathrm {E}}})}_{\alpha }}_3=-{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_2,{{(\bar{\bar{\mathrm {F}}}-\bar{\bar{\mathrm {E}}})}_{\alpha }}_4=-{{(\bar{\bar{\mathrm {E}}}-\bar{\bar{\mathrm {F}}})}_{\alpha }}_1\) Therefore, the distance between two IT2TrPFNs \(\bar{\bar{\mathrm {E}}}\) and \(\bar{\bar{\mathrm {F}}}\) can be computed as follows:
By following the same procedure as mentioned above and using Eqs. (31, 32, 33 and 34). We can get
To acquire analytical solution of distance between two IT2TrPFNs, we suppose that \(\bar{\bar{\mathrm {E}}}>\bar{\bar{\mathrm {F}}}\).
where \(\chi _1,\chi _2,\chi _3,\chi _4\) and \(\sigma\) are constant terms calculated as follows:
\(\chi _1=\frac{\bar{\bar{\mathrm {e}}}_2^U-\bar{\bar{\mathrm {f}}}_3^U-\bar{\bar{\mathrm {e}}}_1^U+\bar{\bar{\mathrm {f}}}_4^U}{2}, \chi _2=\frac{\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L-\bar{\bar{\mathrm {e}}}_1^L+\bar{\bar{\mathrm {f}}}_4^L}{2}, \chi _3=\frac{\bar{\bar{\mathrm {e}}}_4^L-\bar{\bar{\mathrm {f}}}_1^L-\bar{\bar{\mathrm {e}}}_3^L+\bar{\bar{\mathrm {f}}}_2^L}{2}, \chi _4=\frac{\bar{\bar{\mathrm {e}}}_4^U-\bar{\bar{\mathrm {f}}}_1^U-\bar{\bar{\mathrm {e}}}_3^U+\bar{\bar{\mathrm {f}}}_2^U}{2}\) and \(\sigma =\frac{\bar{\bar{\mathrm {e}}}_2^L-\bar{\bar{\mathrm {f}}}_3^L+\bar{\bar{\mathrm {e}}}_3^L-\bar{\bar{\mathrm {f}}}_2^L}{2}\).
\(\left( {\alpha ,\beta } \right)\)-cut and OWA operator are the core tools of this approach. Firstly, the difference between two IT2TrPFNs is converted from a IT2TrPFN to a type-2 interval by using \(\left( {\alpha ,\beta } \right)\)-cut. Afterwards, the distance between two IT2TrPFNs is acquired by defuzzifying the difference between them at \(\left( {\alpha ,\beta } \right)\) level using OWA operator. By following this methodology, an analytical solution is attained that can be implemented to TOPSIS for acquiring the distances from alternatives to PIS and NIS.
4 Extension of TOPSIS with IT2TrPFNs
In existent MCGDM circumstances, decision-makers have distinct decision-making outlooks over the losses and gains. Few decision-makers possesses optimistic attitude, few have pessimistic while others have neutral outlook. The presented TOPSIS technique can assist decision-makers having distinct decision-making perspectives to attain the optimal selection. Decision-makers having optimistic outlook tend to grant more concern over the gains than the losses thereby, the gains will be overrated and the losses will be underrated. The contradictory is valid for the decision-makers having pessimistic outlook. Hence, decision-makers with optimistic outlook will overestimate the distance from an alternative to NIS and underestimate the distance from an alternative to the PIS. In contrast, decision-makers holding pessimistic attitude have the opposite. In the presented approach, OWA operator is utilized to depict the outlook of decision-makers that contributes significantly in MCGDM process. In typical TOPSIS method, the performance ratings of the local criterion related to the alternatives are articulated using crisp numbers, on the contrary, we put forward an extended TOPSIS technique in the framework of IT2TrPFNs to tackle with MCGDM conflicts based upon the distance approach introduced in Sect. 3.
4.1 Proposed TOPSIS method algorithm
-
Step 1:
Form a decision matrix. Let \((\text {P}_1,\ldots ,\text {P}_n)\) be n alternatives and \((\text {Q}_1,\ldots ,\text {Q}_m)\) be m criterion. Let \(\delta _1,\ldots ,\delta _m\) be the m weights associated with the criterion such that \(\sum _{j=1}^m \delta _j=1\). Let \(\text {D}[\breve{\text {X}}_{ij}]_{n\times m}\) be the decision matrix, where
$$\begin{aligned} \begin{aligned} \breve{\text {X}}=&(\breve{\text {X}}^U,\breve{\text {X}}^L)\\ =&[(\breve{\text {a}}_1^U,\breve{\text {a}}_2^U,\breve{\text {a}}_3^U,\breve{\text {a}}_4^U;\mu _{\breve{\text {X}}}^U,\nu _{\breve{\text {X}}}^U), (\breve{\text {a}}_1^L,\breve{\text {a}}_2^L,\breve{\text {a}}_3^L,\breve{\text {a}}_4^L;\mu _{\breve{\text {X}}}^L,\nu _{\breve{\text {X}}}^L)]\\ \end{aligned} \nonumber \\ {\text {D}[\breve{\text {X}}_{ij}]}_{n\times m}= \begin{bmatrix} [\breve{\text {X}}_{11}^U,\breve{\text {X}}_{11}^L] &{} [\breve{\text {X}}_{12}^U,\breve{\text {X}}_{12}^L] &{} \cdots &{} [\breve{\text {X}}_{1m}^U,\breve{\text {X}}_{1m}^L] \\ [\breve{\text {X}}_{21}^U,\breve{\text {X}}_{21}^L] &{} [\breve{\text {X}}_{22}^U,\breve{\text {X}}_{22}^L] &{} \cdots &{} [\breve{\text {X}}_{2m}^U,\breve{\text {X}}_{2m}^L] \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ [\breve{\text {X}}_{n1}^U,\breve{\text {X}}_{n1}^L] &{} [\breve{\text {X}}_{n2}^U,\breve{\text {X}}_{n2}^L] &{} \cdots &{} [\breve{\text {X}}_{nm}^U,\breve{\text {X}}_{nm}^L] \\ \end{bmatrix} \end{aligned}$$(55) -
Step 2:
Normalize the decision matrix.
$$\begin{aligned} {\breve{\text {N}}}_{ij}= {\left\{ \begin{array}{ll} \bigg [\bigg (\frac{x_{1ij}^U}{\breve{\text {X}}_j^*},\frac{x_{2ij}^U}{\breve{\text {X}}_j^*},\frac{x_{3ij}^U}{\breve{\text {X}}_j^*}, \frac{x_{4ij}^U}{\breve{\text {X}}_j^*};\mu _{\breve{\text {X}}_{ij}}^{U},\nu _{\breve{\text {X}}_{ij}}^{U}\bigg ), \bigg (\frac{x_{1ij}^L}{\breve{\text {X}}_j^*},\frac{x_{2ij}^L}{\breve{\text {X}}_j^*},\frac{x_{3ij}^L}{\breve{\text {X}}_j^*}, \frac{x_{4ij}^L}{\breve{\text {X}}_j^*};\mu _{\breve{\text {X}}_{ij}}^{L},\nu _{\breve{\text {X}}_{ij}}^{L}\bigg )\bigg ] &\qquad{} \text {if}\ \ j\in \text {K}_t \\ \bigg [\bigg (\frac{\breve{\text {X}}_j^-}{x_{4ij}^U},\frac{\breve{\text {X}}_j^-}{x_{3ij}^U},\frac{\breve{\text {X}}_j^-}{x_{2ij}^U}, \frac{\breve{\text {X}}_j^-}{x_{1ij}^U};\mu _{\breve{\text {X}}_{ij}}^{U},\nu _{\breve{\text {X}}_{ij}}^{U}\bigg ),\bigg (\frac{\breve{\text {X}}_j^-}{x_{4ij}^L},\frac{\breve{\text {X}}_j^-}{x_{3ij}^L}, \frac{\breve{\text {X}}_j^-}{x_{2ij}^L},\frac{\breve{\text {X}}_j^-}{x_{1ij}^L};\mu _{\breve{\text {X}}_{ij}}^{L},\nu _{\breve{\text {X}}_{ij}}^{L}\bigg )\bigg ] &{} \text {if}\ \ j\in \text {K}_c \end{array}\right. } \end{aligned}$$(56)where \(\breve{\text {X}}_j^*=\max \ \breve{\text {X}}_{ij}^U\) (for \(j \in \text {K}_t\)) and \(\breve{\text {X}}_j^- =\min \ \breve{\text {X}}_{ij}^L\) (for \(j \in \text {K}_c\)). The normalized decision matrix is formalized in the following manner:
$$\begin{aligned} {\text {D}[\breve{\text {N}}_{ij}]}_{n\times m}= \begin{bmatrix} [\breve{\text {N}}_{11}^U,\breve{\text {N}}_{11}^L] &{} [\breve{\text {N}}_{12}^U,\breve{\text {N}}_{12}^L] &{} \cdots &{} [\breve{\text {N}}_{1m}^U,\breve{\text {N}}_{1m}^L] \\ [\breve{\text {N}}_{21}^U,\breve{\text {N}}_{21}^L] &{} [\breve{\text {N}}_{22}^U,\breve{\text {N}}_{22}^L] &{} \cdots &{} [\breve{\text {N}}_{2m}^U,\breve{\text {N}}_{2m}^L] \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ [\breve{\text {N}}_{n1}^U,\breve{\text {N}}_{n1}^L] &{} [\breve{\text {N}}_{n2}^U,\breve{\text {N}}_{n2}^L] &{} \cdots &{} [\breve{\text {N}}_{nm}^U,\breve{\text {N}}_{nm}^L] \\ \end{bmatrix} \end{aligned}$$(57)It should be known that normalization is only necessary when the criterion are estimated by using different sets of linguistic variables. Apart from that, it is not mandatory.
-
Step 3:
Deduce the PIS and NIS.
$$\begin{aligned} \begin{aligned} \text {P}^*=&\{\breve{\mathrm {u}}_1^*,\breve{\mathrm {u}}_2^*,\ldots ,\breve{\mathrm {u}}_m^*\}\\&=\big \{(\max _i \breve{\text {N}}_{ij}|j\in \text {K}_t)(\min _i \breve{\text {N}}_{ij}|j\in \text {K}_c)\big \}\\ \breve{\mathrm {u}}_j^*&=\big [(\breve{\mathrm {u}}_{j1}^{*U},\breve{\mathrm {u}}_{j2}^{*U},\breve{\mathrm {u}}_{j3}^{*U},\breve{\mathrm {u}}_{j4}^{*U};\mu _{\breve{\mathrm {u}}_j^*}^U,\nu _{\breve{\mathrm {u}}_j^*}^U), (\breve{\mathrm {u}}_{j1}^{*L},\breve{\mathrm {u}}_{j2}^{*L},\breve{\mathrm {u}}_{j3}^{*L},\breve{\mathrm {u}}_{j4}^{*L};\mu _{\breve{\mathrm {u}}_j^*}^L,\nu _{\breve{\mathrm {u}}_j^*}^L)\big ] \end{aligned} \end{aligned}$$(58)$$\begin{aligned} \begin{aligned} \text {N}^-=&\{\breve{\mathrm {u}}_1^-,\breve{\mathrm {u}}_2^-,\ldots ,\breve{\mathrm {u}}_m^-\}\\&=\big \{(\max _i \breve{\text {N}}_{ij}|j\in \text {K}_c)(\min _i \breve{\text {N}}_{ij}|j\in \text {K}_t)\big \}\\ \breve{\mathrm {u}}_j^-&=\big [(\breve{\mathrm {u}}_{j1}^{- U},\breve{\mathrm {u}}_{j2}^{- U},\breve{\mathrm {u}}_{j3}^{- U},\breve{\mathrm {u}}_{j4}^{- U};\mu _{\breve{\mathrm {u}}_j^-}^U,\nu _{\breve{\mathrm {u}}_j^-}^U), (\breve{\mathrm {u}}_{j1}^{- L},\breve{\mathrm {u}}_{j2}^{- L},\breve{\mathrm {u}}_{j3}^{- L},\breve{\mathrm {u}}_{j4}^{- L};\mu _{\breve{\mathrm {u}}_j^-}^L,\nu _{\breve{\mathrm {u}}_j^-}^L)\big ] \end{aligned} \end{aligned}$$(59)where \(\text {K}_t\) is benefit type criterion set and \(\text {K}_c\) is the cost type criterion set.
-
Step 4:
Acquire the distances among the alternatives from PIS and NIS. According to the definitions of PIS and NIS, the local criterion’s performance ratings of PIS must not be any less than the prevailing alternatives if the criterion are benefit type otherwise the converse is true if the criterion are cost type. Alternatively, for NIS the local criterion’s performance ratings must not be surpassing than that of existent alternatives if the criterion are benefit type however the converse is true if the criterion are cost type. Hence, we have
$$\begin{aligned} \begin{aligned}&\breve{\mathrm {u}}_j^*\ge \breve{\text {N}}_{ij},j\in \text {K}_t;\breve{\text {N}}_{ij}\ge \breve{\mathrm {u}}_j^*,j\in \text {K}_c;\\&\breve{\text {N}}_{ij}\ge \breve{\mathrm {u}}_j^-,j\in \text {K}_t;\breve{\mathrm {u}}_j^-\ge \breve{\text {N}}_{ij},j\in \text {K}_c. \end{aligned} \end{aligned}$$We assume \({\text {F}}_{\ddot{\text {w}}}\) is an OWA operator having the weighting function \(\breve{\text {W}}=(\ddot{\text {w}}_1,\ddot{\text {w}}_2,\ldots ,\ddot{\text {w}}_n)\), the distances from local criterion’s ratings of the prevailing alternatives to that of PIS and NIS can be obtained by Eq. (58, 59) in the following manner:
$$\begin{aligned} d(\breve{\text {N}}_{ij},\breve{\mathrm {u}}_j^*)={\left\{ \begin{array}{ll} \ddot{\text {w}}_4\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^*)}_{\alpha }}_1 d\alpha +\ddot{\text {w}}_3\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^*)}_{\alpha }}_2d\alpha \\ + \ddot{\text {w}}_2\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^*)}_{\alpha }}_3d\alpha + \ddot{\text {w}}_1\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^*)}_{\alpha }}_4 d\alpha &{} \text {if}\ \ j\in \text {K}_c\\ \ddot{\text {w}}_4\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\mathrm {u}}_j^*-\breve{\text {N}}_{ij})}_{\alpha }}_1 d\alpha +\ddot{\text {w}}_3\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\mathrm {u}}_j^*-\breve{\text {N}}_{ij})}_{\alpha }}_2 d\alpha \\ +\ddot{\text {w}}_2\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\mathrm {u}}_j^*-\breve{\text {N}}_{ij})}_{\alpha }}_3d\alpha +\ddot{\text {w}}_1\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\mathrm {u}}_j^*-\breve{\text {N}}_{ij})}_{\alpha }}_4 d\alpha &{} \text {if}\ \ j\in \text {K}_t \end{array}\right. } \end{aligned}$$(60)$$\begin{aligned} d(\breve{\text {N}}_{ij},\breve{\mathrm {u}}_j^*)={\left\{ \begin{array}{ll} \ddot{\text {w}}_4\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^*)}_{\beta }}_1 d\beta +\ddot{\text {w}}_3\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^*)}_{\beta }}_2d\beta \\ + \ddot{\text {w}}_2\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^*)}_{\beta }}_3d\beta + \ddot{\text {w}}_1\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^*)}_{\beta }}_4 d\beta &{} \text {if}\ \ j\in \text {K}_c\\ \ddot{\text {w}}_4\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\mathrm {u}}_j^*-\breve{\text {N}}_{ij})}_{\beta }}_1 d\beta +\ddot{\text {w}}_3\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\mathrm {u}}_j^*-\breve{\text {N}}_{ij})}_{\beta }}_2 d\beta \\ +\ddot{\text {w}}_2\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\mathrm {u}}_j^*-\breve{\text {N}}_{ij})}_{\beta }}_3d\beta +\ddot{\text {w}}_1\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^*}^U)}{{(\breve{\mathrm {u}}_j^*-\breve{\text {N}}_{ij})}_{\beta }}_4 d\beta &{} \text {if}\ \ j\in \text {K}_t \end{array}\right. } \end{aligned}$$(61)where \(0<\)orness\((\ddot{\text {W}})<\frac{1}{2}\) for decision-makers having optimistic attitude, \(\frac{1}{2}<\)orness\((\ddot{\text {W}})<1\) for decision-makers possessing pessimistic attitude and orness \((\ddot{\text {W}})=\frac{1}{2}\) for decision-makers having neutral attitude.
$$\begin{aligned} d(\breve{\text {N}}_{ij},\breve{\mathrm {u}}_j^-)={\left\{ \begin{array}{ll} \ddot{\text {w}}_4\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^-)}_{\alpha }}_1 d\alpha +\ddot{\text {w}}_3\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^-)}_{\alpha }}_2d\alpha \\ + \ddot{\text {w}}_2\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^-)}_{\alpha }}_3d\alpha + \ddot{\text {w}}_1\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^-)}_{\alpha }}_4 d\alpha &{}\text {if}\ \ j\in \text {K}_t\\ \ddot{\text {w}}_4\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\mathrm {u}}_j^--\breve{\text {N}}_{ij})}_{\alpha }}_1 d\alpha +\ddot{\text {w}}_3\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\mathrm {u}}_j^--\breve{\text {N}}_{ij})}_{\alpha }}_2 d\alpha \\ +\ddot{\text {w}}_2\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\mathrm {u}}_j^--\breve{\text {N}}_{ij})}_{\alpha }}_3d\alpha +\ddot{\text {w}}_1\int _0^{\min (\mu _{\breve{\text {N}}_{ij}}^U,\mu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\mathrm {u}}_j^--\breve{\text {N}}_{ij})}_{\alpha }}_4 d\alpha &{}\text {if}\ \ j\in \text {K}_c \end{array}\right. } \end{aligned}$$(62)$$\begin{aligned} d(\breve{\text {N}}_{ij},\breve{\mathrm {u}}_j^-)={\left\{ \begin{array}{ll} \ddot{\text {w}}_4\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^-)}_{\beta }}_1 d\beta +\ddot{\text {w}}_3\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^-)}_{\beta }}_2d\beta \\ + \ddot{\text {w}}_2\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^-)}_{\beta }}_3d\beta + \ddot{\text {w}}_1\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\text {N}}_{ij}-\breve{\mathrm {u}}_j^-)}_{\beta }}_4 d\beta &{}\text {if}\ \ j\in \text {K}_t\\ \ddot{\text {w}}_4\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\mathrm {u}}_j^--\breve{\text {N}}_{ij})}_{\beta }}_1 d\beta +\ddot{\text {w}}_3\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\mathrm {u}}_j^--\breve{\text {N}}_{ij})}_{\beta }}_2 d\beta \\ +\ddot{\text {w}}_2\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\mathrm {u}}_j^--\breve{\text {N}}_{ij})}_{\beta }}_3d\beta +\ddot{\text {w}}_1\int _0^{\min (\nu _{\breve{\text {N}}_{ij}}^U,\nu _{\breve{\mathrm {u}}_j^-}^U)}{{(\breve{\mathrm {u}}_j^--\breve{\text {N}}_{ij})}_{\beta }}_4 d\beta &{}\text {if}\ \ j\in \text {K}_c \end{array}\right. } \end{aligned}$$(63)where \(0<\)orness\((\ddot{\text {W}})<\frac{1}{2}\) for decision-makers possessing pessimistic attitude, \(\frac{1}{2}<\)orness\((\ddot{\text {W}})<1\) for decision-makers holding optimistic outlook and orness\((\ddot{\text {W}})=\frac{1}{2}\) for decision-makers having neutral outlook. It is indicated that OWA operator depicts the perspectives of decision-makers by overestimating or underestimating the distances among the local criterion corresponding to alternatives and their ideal solutions. Further, the distances from alternatives to PIS and NIS can be computed by considering weighted sum aggregations of criterion as follows:
$$\begin{aligned} \text {Y}_i^*=\sum \delta _j d\big (\breve{\mathrm {u}}_j^*,\breve{\text {N}}_{ij}\big ) \end{aligned}$$(64)$$\begin{aligned} \text {Y}_i^-=\sum \delta _j d\big (\breve{\mathrm {u}}_j^-,\breve{\text {N}}_{ij}\big ) \end{aligned}$$(65) -
Step 5:
Compute the relative closeness to ideal alternatives as follows:
$$\begin{aligned} \text { RC}_i=\frac{\text {Y}_i^-}{\text {Y}_i^- + \text {Y}_i^*} \end{aligned}$$(66) -
Step 6:
Rank the alternatives on the basis of their relative closeness to ideal alternatives. The alternative having the largest relative closeness coefficient is considered to be the best or optimal alternative.
5 Example
In the following section, we demonstrate a numerical example involving MCGDM problem to achieve the practicability of our anticipated extended TOPSIS technique in the framework of IT2TrPFNs.
5.1 Solar tracking system
Chandrasekhar et al. (2013) The growing desires of energy have forced the novelty in the domain of solar energy. Although there are a number of sun trackers available but it is quite crucial to discover the optimal one. An idyllic sun tracker would precisely indicate towards the sun’s direction balancing equally the adjustments in altitudinal angle of sun and latitudinal offset of sun. The prerequisite of sun tracker is to exploit the accessible solar energy to the utmost amount and give best possible outcome. The commonly used tracking systems are listed below:
-
Active Tracker (AT).
-
Manual Tracking (MT).
-
Passive Tracker (PT).
On the following few important factors, all of the above mentioned tracking systems are based:
-
Response: The response of a solar tracker is among the most vital constraints of a tracking system. It is the capability of a tracker system to rapidly modify its angle to the requisite degree when sun’s direction changes.
-
Reliability: It is the ability of giving a specific voltage for specific intensity of sun’s energy over a phase of long period of time. This aspect is quite significant as the usage would ultimately decrease if the sun tracker is not consistent for long term.
-
Accuracy: The more the accuracy of solar tracking system the more it can distribute the rated power output. The most exact solar tracker system can deliver up to 90 percent of the rated output power. Therefore it is a fundamental criteria to select the appropriate solar tracker system.
Selection of a solar tracker is a mandatory course as it is essential in attaining the best possible level of energy derived from the sun. There are many existing tracker systems that are insufficient in the assistance of an expert’s acquaintance in opting for the right system for specific context. Hence, in this article an attempt is made to discover a quite appropriate sun tracking system under the support of keen decision-making. The three sun tracking systems namely AT, PT and MT are considered as three alternatives i.e. \(\text {P}_1,\text {P}_2\) and \(\text {P}_3\) respectively. The three criterion are: reliability \((\text {Q}_1)\), response \((\text {Q}_2)\) and accuracy \((\text {Q}_3)\), where where \(\text {Q}_1\) is cost criterion and \(\text {Q}_2\) and \(\text {Q}_3\) are benefit criterion.
In order to pick the best solar tracking system amongst the three, first we rate each of the three alternatives in terms of three criterion and give the local criterion weights. The criterion ratings corresponding to all alternatives are provided in Table 1 and the criterion weights are shown in Table 2.
In this numerical example, ranking results are discussed in three situations: optimistic,pessimistic and neutral. Based upon our anticipated approach, the methodology for choosing the best tracking system is demonstrated as follows:
-
Step 1:
Build a decision matrix based on Table 1 denoted by \({D[X_{ij}]}_{3\times 3}\) and represented as follows:
$$\begin{aligned} {\text {D}[\breve{\text {X}}_{ij}]}_{3\times 3} = \begin{bmatrix} [\breve{\text {X}}_{11}^U,\breve{\text {X}}_{11}^L] &\quad{} [\breve{\text {X}}_{12}^U,\breve{\text {X}}_{12}^L] &\quad{} [\breve{\text {X}}_{13}^U,\breve{\text {X}}_{13}^L] \\ [\breve{\text {X}}_{21}^U,\breve{\text {X}}_{21}^L] &{} [\breve{\text {X}}_{22}^U,\breve{\text {X}}_{22}^L] &\quad{} [\breve{\text {X}}_{23}^U,\breve{\text {X}}_{23}^L] \\ [\breve{\text {X}}_{31}^U,\breve{\text {X}}_{31}^L] &\quad{} [\breve{\text {X}}_{32}^U,\breve{\text {X}}_{32}^L] &\quad{} [\breve{\text {X}}_{33}^U,\breve{\text {X}}_{33}^L] \\ \end{bmatrix} \end{aligned}$$(67) -
Step 2:
Normalize the decision matrix.
Normalization is not necessary as the criterion in this example is assessed using the same set of linguistic variables.
-
Step 3:
Estimate the PIS and NIS respectively by using Eqs. (58, 59).
$$\begin{aligned} \begin{aligned} \text {P}_i^*&=\{\breve{\mathrm {u}}_1^*,\breve{\mathrm {u}}_2^*,\breve{\mathrm {u}}_3^*\}=\{\breve{\text {X}}_{31},\breve{\text {X}}_{12},\breve{\text {X}}_{23}\}\\&=\{[(0.5287,0.5181,0.5005,0.5109;0.8,0.7),(0.4176,0.4070,0.4114,0.4608;0.6,0.5)],\\&[(0.9952,0.9745,0.9952,0.9585;0.8,0.7),(0.8730,0.8523,0.8730,0.8363;0.6,0.5)],\\&[(0.9548,0.9954,0.9259,0.9259;0.8,0.7),(0.7372,0.7443,0.7145,0.7145;0.6,0.5)]\} \end{aligned} \\ \begin{aligned} \text {N}_i^-&=\{\breve{\mathrm {u}}_1^-,\breve{\mathrm {u}}_2^-,\breve{\mathrm {u}}_3^-\}=\{\breve{\text {X}}_{21},\breve{\text {X}}_{22},\breve{\text {X}}_{33}\}\\&=\{[(0.9574,0.9299,0.5895,0.8821;0.8,0.7),(0.0.8463,0.4188,0.4784,0.7710;0.6,0.5)],\\&[(0.7777,0.7926,0.7743,0.8164;0.8,0.7),(0.6215,0.6815,0.6632,0.7053;0.6,0.5)],\\&[(0.5177,0.5070,0.5074,0.5608;0.8,0.7),(0.4065,0.4060,0.4050,0.4040;0.6,0.5)]\} \end{aligned} \end{aligned}$$ -
Step 4:
Acquire the distances of alternatives from PIS and NIS. We allot three OWA operators with different weighting functions given as follows:
$$\begin{aligned} \begin{aligned}&\text {F}_{\ddot{\text {W}}_1}=(0.1,0.1,0.1,0.7),\text {orness}(\breve{\text {W}}_1)=\frac{2}{5}\\&\text {F}_{\ddot{\text {W}}_2}=(0.4,0.3,0.2,0.1),\text {orness}(\breve{\text {W}}_2)=\frac{3}{4}\\&\text {F}_{\ddot{\text {W}}_3}=(0.1,0.2,0.3,0.4),\text {orness}(\breve{\text {W}}_3)=\frac{1}{2} \end{aligned} \end{aligned}$$For decision-maker’s optimistic attitude: the OWA operators for computing distances from local criterion’s ratings to PIS and NIS are allotted with weighting functions \(\ddot{\text {W}}_1\) and \(\ddot{\text {W}}_2\) respectively. For decision-maker’s pessimistic attitude: the OWA operators are appointed with weighting functions \(\ddot{\text {W}}_2\) and \(\ddot{\text {W}}_1\) respectively. For decision-maker’s neutral attitude: the OWA operators are allotted with weighting functions \(\ddot{\text {W}}_3\).
Then, the distances from ratings of local criterion of all alternatives to PIS and NIS can be determined by using Eqs.(60, 61,62 and 63). Further, distances from alternatives to PIS and NIS can be acquired by using Eqs. (64, 65) and the distances in three situations of decision-maker’s attitude are presented in Table 3.
-
Step 5:
Compute the relative closeness of alternatives using Eq.(66) and the outcomes are given in Table 4.
-
Step 6:
Rank the alternatives. They are ranked according to the descending order of their relative closeness coefficients.
Notice that the ranking results of three alternatives varies for different decision-makers having dissimilar decision-making perspective. Coincidentally all the three decision-makers possessing optimistic, pessimistic and neutral attitude have following priorities for the tracking system choice: \(\text {P}_1,\text {P}_3\) and \(\text {P}_2\). In the actual and factual decision-making situation, decision-makers are not normally objective i.e. their decision-making perspective is not neutral. Hence, in such cases where their attitude is optimistic or pessimistic have more realistic importance.
6 Comparative analysis
A comparative revision is executed to verify the consequences of the projected technique with several other approaches. This investigation is based on the same input information presented in Sect. 5.
6.1 Theoretical comparison with other methods
The anticipated extended TOPSIS technique in the framework of IT2TrPFNs is founded on the distance method for IT2TrPFNs presented in Sect. 3 where the (\(\alpha ,\beta\))-cut method and OWA operator plays the vital role. We have chosen two prevailing distance based methods from literature: a signed-distance based approach for TOPSIS and a distance operational rule described as follows:
-
Signed distance-based approach:
The signed distance of a IT2TrPFN \(\bar{\bar{\mathrm {E}}}\) far from \(\breve{0}\) is defined as:
$$\begin{aligned} d(\bar{\bar{\mathrm {E}}},\breve{0}_1)= & {} \frac{1}{8} \bigg [2({\bar{\bar{\mathrm {e}}}_1}^U+{\bar{\bar{\mathrm {e}}}_2}^U+{\bar{\bar{\mathrm {e}}}_3}^U+{\bar{\bar{\mathrm {e}}}_4}^U)+2({\bar{\bar{\mathrm {e}}}_1}^L+{\bar{\bar{\mathrm {e}}}_2}^L+{\bar{\bar{\mathrm {e}}}_3}^L+{\bar{\bar{\mathrm {e}}}_4}^L)\nonumber \\&\quad +3({\bar{\bar{\mathrm {e}}}_2}^L+{\bar{\bar{\mathrm {e}}}_3}^L-{\bar{\bar{\mathrm {e}}}_1}^L -{\bar{\bar{\mathrm {e}}}_4}^L)\nonumber \\&\quad \bigg (\frac{\mu _{\bar{\bar{\mathrm {E}}}}^L}{\mu _{\bar{\bar{\mathrm {E}}}}^U}-\frac{\nu _{\bar{\bar{\mathrm {E}}}}^L}{\nu _{\bar{\bar{\mathrm {E}}}}^U}\bigg )\bigg ] \end{aligned}$$(68)Taking into account the above signed distance, the distance between two IT2TrPFNs \(\bar{\bar{\mathrm {E}}}\) and \(\bar{\bar{\mathrm {F}}}\) can be determined as:
$$\begin{aligned} d(\bar{\bar{\mathrm {E}}},\bar{\bar{\mathrm {F}}})=\big |d(\bar{\bar{\mathrm {E}}},\breve{0}_1)-d(\bar{\bar{\mathrm {F}}},\breve{0}_1)\big | \end{aligned}$$(69) -
Distance operational rule:
The distance between two IT2TrPFNs can be computed as:
$$\begin{aligned} \begin{aligned} d(\bar{\bar{\mathrm {E}}},\bar{\bar{\mathrm {F}}})=&\frac{1}{8}(|\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {E}}}}^U)\times \bar{\bar{\mathrm {e}}}_1^U-\min (\mu _{\bar{\bar{\mathrm {F}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)\times t_1^U|+ |\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {E}}}}^U)\times \bar{\bar{\mathrm {e}}}_2^U-\min (\mu _{\bar{\bar{\mathrm {F}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)\times t_2^U|\\&+|\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {E}}}}^U)\times \bar{\bar{\mathrm {e}}}_3^U-\min (\mu _{\bar{\bar{\mathrm {F}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)\times t_3^U|+|\min (\mu _{\bar{\bar{\mathrm {E}}}}^U,\nu _{\bar{\bar{\mathrm {E}}}}^U)\times \bar{\bar{\mathrm {e}}}_4^U-\min (\mu _{\bar{\bar{\mathrm {F}}}}^U,\nu _{\bar{\bar{\mathrm {F}}}}^U)\times t_4^U|\\&+|\min (\mu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {E}}}}^L)\times \bar{\bar{\mathrm {e}}}_1^L-\min (\mu _{\bar{\bar{\mathrm {F}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L)\times t_1^L|+|\min (\mu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {E}}}}^L)\times \bar{\bar{\mathrm {e}}}_2^L-\min (\mu _{\bar{\bar{\mathrm {F}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L)\times t_2^L|\\&+|\min (\mu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {E}}}}^L)\times \bar{\bar{\mathrm {e}}}_3^L-\min (\mu _{\bar{\bar{\mathrm {F}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L)\times t_3^L|+|\min (\mu _{\bar{\bar{\mathrm {E}}}}^L,\nu _{\bar{\bar{\mathrm {E}}}}^L)\times \bar{\bar{\mathrm {e}}}_4^L-\min (\mu _{\bar{\bar{\mathrm {F}}}}^L,\nu _{\bar{\bar{\mathrm {F}}}}^L)\times t_4^L|) \end{aligned} \end{aligned}$$(70)
Compared with the above two existing distance methods, the main distinctiveness and advantages of the projected extended TOPSIS technique can be accomplished in the following manner:
-
1.
The anticipated technique computes the distances between two IT2TrPFNs by integrating the (\(\alpha ,\beta\))-cuts and establishes an analytical solution of the distances. Moreover, the intended method imparts a more precise and suitable approach to compute the distances between IT2TrPFNs.
-
2.
The widely used TOPSIS technique suspects that the decision- makers are entirely objective that invades the truth that decision-makers frequently have their own subjective decision-making outlook. Some have optimistic decision-making perspective, few have pessimistic and rest of them have neutral outlook. In the anticipated extended TOPSIS technique, the OWA operator is used to depict the outlook of the decision-makers that can provide multiple subjective decisions for distinct decision-makers.
-
3.
The extended TOPSIS technique based on (\(\alpha ,\beta\))-cut has not been yet explored thoroughly in the framework of IT2TrPFNs that are considered to be more sophisticated than other types of FSs. Our reserach fills in the space of (\(\alpha ,\beta\))-cut based extended TOPSIS technique in IT2TrPFN framework.
6.2 Numerical comparison with other methods
The relative closeness coefficients computed by using the signed distance-based approach are given in Table 5 while those computed by using the distance operational rule are given in Table 6 and the comparison of the relative closeness coefficients computed by our proposed approach and other two methods are given in Table 7.
Based on the comparative study, the achieved results reveals that the projected approach is considerably much better than the rest of the two techniques since it can produce several subjective ranking consequences in varying situations where the decision-makers have distinct decision-making outlook while in the two considered approaches, attitude of the decision-makers is not considered that implies the two techniques can merely yield objective ranking outcomes for the decision-makers. Though, in the existent world, the outlook of decision-maker plays a vital role while choosing the best alternative. Therefore, it is presented that our anticipated technique can produce multiple subjective decisions for the decision-makers whilst choosing the best alternative according to their decision-making perspective. Consequently, our presented approach is more suitable and accurate in dealing MCGDM problems as it considers the outlook of decision-makers.
7 Conclusion
TOPSIS is considered among the most widely known approach to deal with MCGDM conflicts. In this article, we have projected an extended TOPSIS approach in the framework of IT2TrPFNs. In contrast with the existing approaches, the major contribution of our work is to anticipate a new distance computation technique for IT2TrPFNs using OWA operator and \((\alpha ,\beta )\)-cut by which a more exact and flexible analytical solution of the distance amongst two IT2TrPFNs is presented. Moreover, we have anticipated a novel TOPSIS technique for coping up with MCGDM problems formed on the distance method which can produce multiple subjective decisions for the decision-makers having distinct decision-making perspectives. Nonetheless, the weighting functions associated with the OWA operators are allocated without making any examination or practice in this research that may manipulate the worth of decisions. At some point in the future, we aim to broaden our research in the other directions and its application in some other fuzzy systems.
References
Akram M, Adeel A (2019) TOPSIS approach for MAGDM based on interval-valued hesitant fuzzy N-soft environment. Int J Fuzzy Syst 21(3):993–1009
Alam Khan N, Abdul Razzaq O, Riaz F, Ahmadian A, Senu N (2020) Dynamics of fractional order nonlinear system a realistic perception with neutrosophic fuzzy number and Allee effect. J Adv Res. https://doi.org/10.1016/j.jare.2020.11.015
Alamin A, Mondal SP, Alam S, Ahmadian A, Salahshour S, Salimi M (2020) Solution and interpretation of neutrosophic homogeneous difference equation. Symmetry 12(2):1091
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Set Syst 20(1):87–96
Atanassov KT (1989) More on intuitionistic fuzzy sets. Fuzzy Set Syst 33:37–46
Atanassov KT, Gargov G (1989) Interval valued intuitionistic fuzzy sets. Fuzzy Set Syst 31(3):343–349
Biswas P, Pramanik S, Giri BC (2016) Value and ambiguity index based ranking method of single-valued trapezoidal neutrosophic numbers and its application to multi-attribute decision making. Neutrosophic Sets Syst 12:127–138
Biswas P, Pramanik S, Giri BC (2018) Distance measure based MADM strategy with interval trapezoidal neutrosophic numbers. Neutrosophic Sets Syst 19(7):40–46
Biswas P, Pramanik S, Giri BC (2018) TOPSIS strategy for multi-attribute decision making with trapezoidal numbers. Neutrosophic Sets Syst 19:29–39
Celik E, Gul M, Aydin N, Gumus AT (2015) A comprehensive review of multi criteria decision making approaches based on interval type-2 fuzzy sets. Knowl Based Syst 85:329–341
Celik E, Gul M, Aydin N, Gumus AT (2015) A comprehensive review of multi-criteria decision making approaches based on interval type-2 fuzzy sets. Knowl Based Syst 85:329–341
Chakraborty A, Mondal SP, Ahmadian A, Senu N, Alam S (2018) Different forms of triangular neutrosophic numbers, de-neutrosophication techniques, and their applications. Symmetry 10:327
Chakraborty A, Mondal SP, Alam S, Ahmadian A, Senu N, De D, Salahshour S (2019) Disjunctive representation of triangular bipolar neutrosophic numbers, de-bipolarization technique and application in multi-criteria decision-making problems. Symmetry 11:932
Chandrasekhar V, Marthuvanan M, Ramkumar MM, Shriram R, Manickavasagam VM, Ramnath BV (2013) MCDM approach for selecting suitable solar tracking system, 7th International Conference on Intelligent Systems and Control (ISCO)
Chen TY (2011) Signed distanced-based TOPSIS method for multiple criteria decision analysis based on generalized interval-valued fuzzy numbers. Int J Inf Tech Decis 10(6):1131–1159
Chen TY (2012) Multiple criteria group decision-making with generalized interval-valued fuzzy numbers based on signed distances and incomplete weights. Appl Math Model 36(7):3029–3052
Chen TY (2013) A signed distance-based approach to importance assessment and multi-criteria group decision analysis based on interval type-2 fuzzy set. Knowl Inf Syst 35:193–231
Chen SM, Yang MW, Lee LW, Yang SW (2012) Fuzzy multiple attributes group decision-making based on ranking interval type-2 fuzzy sets. Expert Syst Appl 39(5):5295–5308
Dan S, Kar MB, Majumder S, Roy B, Kar S, Pamucar D (2019) Intuitionistic type-2 fuzzy set. Symmetry 11(6):01–18
Dubois D, Prade H (1980) Fuzzy sets and systems- theory and applications. Math Sci Eng 144:01–389
Garg H, Singh S (2018) A novel triangular interval type-2 intuitionistic fuzzy sets and their aggregation operators. Iran J Fuzzy Syst 15(5):69–93
Gupta P, Mehlawat MK, Grover N (2019) A generalized TOPSIS method for intuitionistic fuzzy multiple attribute group decision making considering different scenarios of attributes weight information. Int J Fuzzy Syst 21(2):369–387
Kahraman C, Onar SC, Oztaysi B (2015) Fuzzy multicriteria decision-making: a literature review. Int J Comput Intell Syst 8(4):637–666
Mahapatra GS, Roy TK (2013) Intuitionistic fuzzy number and its arithmetic operation with application on system failure. J Uncertain Syst 7:92–107
Mardani A, Jusoh A, Nor KMD, Khalifah Z, Zakwan N (2015) A, Valipour: multiple criteria decision-making techniques and their applications a review of the literature from 2000 to 2014. Econ Res Ekonomska Istrazivanja 28(1):516–571
Mendel JM (2007) Advances in type-2 fuzzy sets and systems. Inf Sci 177:84–110
Mendel JM, John RI (2002) Type-2 fuzzy sets made simple. IEEE T Fuzzy Syst 10(2):117–127
Mendel JM, John RI, Liu FL (2006) Interval type-2 fuzzy logical systems made simple. IEEE T Fuzzy Syst 14(6):808–821
Park JH, Cho HJ, Kwun YC (2011) Extension of the VIKOR method for group decision making with interval-valued intuitionistic fuzzy information. Fuzzy Optim Decis Mak 10(3):233–253
Peng X, Yang Y (2015) Fundamental properties of interval-valued Pythagorean fuzzy aggregation operators. Int J Intell Syst 31:444–487
Peng JJ, Wang JQ, Chen XH (2015) An extension of ELECTRE to multi-criteria decision-making problems with multi-hesitant fuzzy sets. Inf Sci 307:113–126
Phu ND, Ahmadian A, Hung NN, Salahshour S, Senu N (2019) Narrow metric semi-linear space of intuitionistic fuzzy numbers: application to AIDS model. Int J Fuzzy Syst 21:1738–1754
Rahman K, Ali A, Khan MSA (2018) Some intervalvalued Pythagorean fuzzy weighted averaging aggregation operators and their application to multiple attribute decision making. J Math 50(2):113–129
Sang X, Liu X (2014) An analytic approach to obtain the least square deviation OWA operator weights. Fuzzy Set Syst 240:103–116
Shakeel M, Aslam M, Amin NU, Jamil M (2020) Method of MAGDM based on pythagorean trapezoidal uncertain linguistic hesitant fuzzy aggregation operator with Einstein operations. J Intell Fuzzy Syst 38(2):2130–2211
Shaygan A, Testik OM (2019) A fuzzy AHP-based methodology for project prioritization and selection. Soft Comput 23(4):1309–1319
Touqeer M, Salma J, Rida I (2020) A grey relational projection method for multi attribute decision making based on three trapezoidal fuzzy numbers. J Intell Fuzzy Syst 38(5):5957–5967
Touqeer M, Kiran S, Rida I (2020) Evaluation model for manufacturing plants with linguistic information in terms of three trapezoidal fuzzy numbers. J Intell Fuzzy Syst 38(5):5969–5978
Touqeer M, Abid H, Misbah A (2020) Multi-attribute decision making using grey relational projection method based on interval type-2 trapezoidal fuzzy numbers. J Intell Fuzzy Syst 38(5):5979–5986
Wang W, Liu X, Qin Y (2012) Multi-attribute group decision making models under interval type-2 fuzzy environment. Knowl-Based Syst 30:121–128
Weaver W (1948) Science and complexity. Am Sci 36(4):536–544
Wei GW, Wang HJ, Lin R (2011) Application of correlation coefficient to interval-valued intuitionistic fuzzy multiple attribute decision-making with incomplete weight information. Knowl Inf Syst 26(2):337–349
Xu Z (2005) An overview of methods of determining OWA weights. Int J Intell Syst 20(8):843–865
Xu Z (2010) An integrated model-based interactive approach to FMAGDM with incomplete preference information. Fuzzy Optim Decis Mak 9(3):333–357
Xu Z, Yager RR (2006) Some geometric aggregation operators based on intuitionistic fuzzy sets. Int J Gen Syst 35(4):417–433
Yager RR (2013) Pythagorean fuzzy subsets, in proceedings of the 9th joint world congress on fuzzy systems and NAFIPS annual meeting. Edmonton, Canada, IFSA/NAFIPS, pp 57–61
Yang YY, Wang X, Liu F (2020) Trapezoidal interval type-2 fuzzy TOPSIS using alpha-cuts. Int J Fuzzy Syst 22:293–309
Yao JS, Wu K (2000) Ranking fuzzy numbers based on decomposition principle and signed distance. Fuzzy Set Syst 116(2):275–288
Yu D (2013) Intuitionistic trapezoidal fuzzy information aggregation methods and their applications to teaching quality evaluation. J Inf Comput Sci 10(6):1861–1869
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353
Zadeh LA (1965) The concept of a linguistic variable and its application to approximate reasoning. Inf Sci 8:199–249
Zhang X (2016) Multicriteria Pythagorean fuzzy decision analysis: a hierarchical QUAL-IFLEX approach with the closeness index-based ranking methods. Inf Sci 330:104–124
Funding
Open access funding provided by Università degli Studi Mediterranea di Reggio Calabria within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Umer, R., Touqeer, M., Omar, A.H. et al. Selection of solar tracking system using extended TOPSIS technique with interval type-2 pythagorean fuzzy numbers. Optim Eng 22, 2205–2231 (2021). https://doi.org/10.1007/s11081-021-09623-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11081-021-09623-1
Keywords
- Multi-criteria group decision-making (MCGDM)
- Interval type-2 trapezoidal Pythagorean fuzzy numbers (IT2TrPFN)
- Ordered weighted averaging operator (OWA)