Streaming changepoint detection for transition matrices

Abstract

Sequentially detecting multiple changepoints in a data stream is a challenging task. Difficulties relate to both computational and statistical aspects, and in the latter, specifying control parameters is a particular problem. Choosing control parameters typically relies on unrealistic assumptions, such as the distributions generating the data, and their parameters, being known. This is implausible in the streaming paradigm, where several changepoints will exist. Further, current literature is mostly concerned with streams of continuous-valued observations, and focuses on detecting a single changepoint. There is a dearth of literature dedicated to detecting multiple changepoints in transition matrices, which arise from a sequence of discrete states. This paper makes the following contributions: a complete framework is developed for adaptively and sequentially estimating a Markov transition matrix in the streaming data setting. A change detection method is then developed, using a novel moment matching technique, which can effectively monitor for multiple changepoints in a transition matrix. This adaptive detection and estimation procedure for transition matrices, referred to as ADEPT-M, is compared to several change detectors on synthetic data streams, and is implemented on two real-world data streams – one consisting of over nine million HTTP web requests, and the other being a well-studied electricity market data set.

1 Introduction

A data stream is an unbounded sequence of ordered data items, arriving at high frequency, whose distribution evolves over time. Advances in modern technology has allowed data streams to appear in a broad range of applications, e.g., in cyber-security (Bodenham and Adams 2013; Ye et al. 2004), monitoring credit cards for fraudulent activity (Pozzolo et al. 2015) and in sensor networks and web-mining (Gama 2010). Since data streams are becoming ubiquitous providing inference for them is necessary in applications; however, the dynamics of data streams present several challenges to the statistics and machine learning communities. The fast arrival of observations, as well as the sheer amount of data collected, require algorithms to take into account limited storage capabilities and the need to process each datum only once. In addition to computational constraints, changes in distribution, colloquially referred to as drift (Krempl and Hofer 2011; Tsymbal 2004), require estimates to be able to change over time, that is, to be adaptive and aware of unknown temporal changes in the stream. A large portion of existing literature is concerned with detecting changes in drifting data streams; although, it is striking that there is an absence of literature on change detection for discrete data, and in particular, for transition matrices.

A problem associated with streaming inference is changepoint detection – the identification of times where the stream has experienced a change in distribution. Streaming changepoint detection is difficult since only a single pass through the data is possible and no intervention is allowed, i.e., the stream continues unabated when a change is flagged. Traditionally, sequential changepoint detection is well-studied, e.g. see Tartakovsky et al. (2014). However, most classical methods simplify the task by focusing on detecting a single changepoint, and do so by introducing several control parameters that are difficult to set, particularly in streaming contexts. These parameters, which are critical to a change detector’s performance, are usually chosen based on unrealistic assumptions, such as the parameters of the distributions generating the data being known. This paper avoids such assumptions, and is concerned with continuous monitoring (Bodenham and Adams 2016) – the sequential detection of multiple changepoints in a discrete-time, univariate data stream.

The continuous monitoring paradigm has received some attention (Bodenham and Adams 2013, 2016), although it is usually assumed that the observations are continuous-valued. There is a lack of literature on detecting multiple changepoints in a Markov transition matrix arising from a sequence of discrete states. A method that can continuously monitor for multiple changepoints in a transition matrix, in addition to adaptively and sequentially updating its model, would be beneficial in various applications. Two such applications are considered in Sect.  7. One application arises from monitoring a sequence of web requests to a server farm being managed by a scheduler. Any detected changes in the request structure could be indicative of malicious behavior present in the network. The second illustration analyzes the well-known electricity market data set (Harries and Wales 1999).

Detecting changes in Markov processes has been investigated in various contexts, such as, Markov chains with finite state-spaces (Yakir 1994), hidden Markov models (Fuh 2004; Chen and Willett 1997), sensor networks (Raghavan and Veeravalli 2010; Tartakovsky and Veeravalli 2008) and in Markov-modulated time series (Dey and Marcus 1999). Despite this, most existing literature imposes assumptions that make the methodologies ill-suited for the continuous monitoring paradigm. For example, the references just provided develop detection strategies that require the distribution before and after each changepoint to be known. This is nonsensical in the continuous monitoring paradigm, where several changepoints will occur, and prior knowledge about the post change distribution after every changepoint will not exist.

Markov transition matrices can be viewed as weighted adjacency matrices; therefore, change detection in dynamic networks is a closely related topic. See Ranshous et al. (2015) for an excellent survey. A large portion of literature in this area introduces several parameters that are difficult to set, and have no meaningful interpretation in the continuous monitoring paradigm. For instance, Li et al. (2009) introduce several time independent control parameters when developing reward and penalty functions. In Idé and Kashima (2004) a fixed sliding window is used to compute an ‘activity vector’, and all changes in the stream are based on this vector’s departure from normal network behavior. Thus, the detector’s ability to accurately detect changes relies on the length of this sliding window. As outlined in Ranshous et al. (2015), other approaches introduce a fixed and difficult to interpret threshold, and signal a change whenever some quantity monitored from the stream violates the threshold. Setting and adapting the threshold is a difficult task, which is exacerbated by the presence of multiple changepoints.

This paper introduces an ‘adaptive detection and estimation procedure for transition matrices’, referred to as ADEPT-M, which sequentially and adaptively estimates a transition matrix while continuously monitoring a data stream for changepoints. Temporal adaptivity is introduced via forgetting factors (Bodenham and Adams 2016; Anagnostopoulos et al. 2012; Pavlidis et al. 2011), which are a sequence of scalars that continuously down-weights older observations as newer data arrives. The forgetting factors (FFs) can be tuned online without user supervision, which removes the burden of having to subjectively specify their values. ADEPT-M detects changepoints by constructing control limits, which are based on a novel moment matching technique. Additionally, the parameters introduced by ADEPT-M make no assumptions on the distribution’s parameters generating the data, and have meaningful interpretations in the context of multiple changepoint detection. To the best of the author’s knowledge, this is the first work to adaptively and sequentially detect multiple changepoints in Markov transition matrices.

This paper proceeds as follows: Sect.  2 provides a problem definition and develops a transition matrix, based on a FF framework, which can be efficiently monitored on the stream. A way of adaptively tuning the FFs is discussed in Sect.  3. Section 4 introduces ADEPT-M and discusses commonly used change detectors, which ADEPT-M is compared to in subsequent sections. Section 5 discusses performance measures that will be used in the simulation study of Sect.  6. In Sect.  7 ADEPT-M is implemented on two real-world data streams. Section 8 provides conclusions and directions for future work.

2 Background and adaptive estimation

This section introduces the context of the problem followed by the details of our approach. Notation is introduced and challenges that arise are presented. A maximum likelihood approach is adopted, which develops a temporally adaptive estimate for a first-order Markov transition matrix. Temporal adaptation is provided by a parameter, called a FF, which regulates the contribution of older data to the estimate. The problem of choosing values for the FF is deferred to Sect.  3.

2.1 Problem definition

Consider a data stream consisting of a sequence of discrete random variables

$$\begin{aligned} \langle X_0,X_1,\ldots ,X_{t-1},X_t,\ldots \rangle , \end{aligned}$$

where for any ${t\in {\mathbb {Z}}^+}$, the support of $X_t$ is given by ${{\mathcal {S}}=\{1,2,\ldots ,K\}}$. The set ${{\mathcal {S}}}$ is subsequently referred to as the state-space and the cardinality of ${{\mathcal {S}}}$, denoted ${|{\mathcal {S}}|}$, is assumed fixed.

The observations from the stream are assumed to be generated in segments. A set of unknown changepoints define the segments, and the observations are governed by a fixed transition matrix in each one. Specifically, suppose the locations of the changepoints are given by ${\varvec{\tau }=\{\tau _k\}_{k=1}^m}$, where ${\tau _i<\tau _j}$ for every ${i<j}$. The set ${\varvec{\tau }}$ partitions the stream into $(m+1)$ segments, and ${{\varvec{P}}^{(k)}\in {\mathbb {R}}^{K\times K}}$ is used to denote the unknown transition matrix in the $k^{\text {th}}$ segment. Let ${\varvec{P}}_t$ denote the transition matrix currently generating the data. This transition matrix can be defined piecewise as

$$\begin{aligned} {\varvec{P}}_t&= {\varvec{P}}^{(k)} \qquad \forall t\in [\tau _{k-1},\tau _k),\qquad k = 1,\ldots , m+1, \end{aligned}$$

where $\tau _0=0$ and $\tau _{m+1} = \infty$. This is depicted graphically in Fig. 1. The $ij^{\text {th}}$ element of ${\varvec{P}}_t$ is denoted by $p_t^{(j|i)}$, and represents the Markov probability of transitioning from state i to state j at time t, that is,

$$\begin{aligned} p^{(j|i)}_{t}&=\mathbb {P}({X}_{t}=j \mid X_{t-1}=i)\qquad \forall \quad i,j\in {\mathcal {S}}. \end{aligned}$$

Fig. 1

A schematic representation of the assumed data generating process

Consider the problem of updating an estimate for ${\varvec{P}}_t$. While data arrives in discrete-time, the opportunity to update a row ${i\in {\mathcal {S}}}$ only arises after observing a transition from that state. Thus, two separate ‘clocks’ can be recognized in the data generating process. There is the data clock, which generates the sequence of states making up the data stream, and the transition clock that provides the opportunity to update a specific row of the transition matrix. The nature of such updating requires complex notation even though the concept is relatively simple, and is required to handle the different opportunities for updating. The different clocks also create challenges for assessing the performance of a change detector, as discussed in Sect.  5.

In practice one needs to handle the problem of restarting after a detection has been made. The approach adopted here, as well as in Bodenham and Adams (2016) and Plasse and Adams (2019), involves a grace period following each detection. This period is required to estimate the parameters of a new segment prior to a further round of monitoring, and is illustrated in Fig. 2. It is worth mentioning that grace periods cannot be implemented in much existing work, such as Yakir (1994), since restarting would require knowing the number of changepoints, as well as all transition matrices in the segments. Unlike in Bodenham and Adams (2016) and Plasse and Adams (2019), the presence of the data and transition clocks makes interpreting the grace period more difficult. For example, the opportunity to detect a change in a row ${i\in {\mathcal {S}}}$ only occurs when a transition out of this state is observed. This may be a very infrequent event with respect to the data clock. Developing a grace period that is more suitable for monitoring transition matrices for multiple changepoints is considered in Sect.  4.1.

The goal of this paper is to sequentially maintain an accurate estimate of the transition matrices in each segment and, moreover, to accurately identify the changepoints in $\varvec{\tau }$. To maintain accurate estimates across segments requires a method that will adaptively learn to discard data from previous segments. FFs, the topic of the next section, are a useful way of providing such estimation. Furthermore, FFs being temporally adaptive have the potential for being robust to missed detections, since the estimates will quickly adapt despite missing the change.

Fig. 2

A depiction of the grace period, which begins when a method detects a changepoint. The burn-in and grace period regions are discussed more in Sect.  4

2.2 Forgetting factor framework

A way of producing temporally adaptive parameter estimates is by introducing FFs into the estimation process. FFs have been considered in Bodenham and Adams (2016), Anagnostopoulos et al. (2012), Pavlidis et al. (2011) and Haykin (2008), and are scalars in [0, 1] that continuously down-weights older data as newer data arrives. Therefore, if drift occurs older data is ‘washed-out’, allowing the estimation to be driven by newer, more informative observations. In what follows FFs are introduced into the parameter estimation via a maximum likelihood approach. This leads to the development of a temporally weighted log-likelihood function, resulting in an adaptive estimate for a Markov transition matrix; refer to Eq.s (4)-(5). These equations relate to the optimization of the aforementioned likelihood; however, before this likelihood can be fully understood some precise formulations are required.

2.2.1 Formulation

Since a matrix is being monitored there are several ways of introducing FFs into the parameter estimation. In this article a FF is assigned to each row of the transition matrix estimate. Under this construction, if one row of the matrix experiences a change, the appropriate FF can be tuned without affecting the FFs assigned to the other rows. Other formulations are possible, e.g., a single FF or ${K^2}$ FFs could be assigned to monitor the transition matrix. However, a single FF would be tuned to monitor for a change in the entire matrix, and would not be able to react to subtle changes in a subset of the transition probabilities. Similarly, since each row of the transition matrix is constrained to sum to one, ${K^2}$ FFs would have to be aggregated across rows to preserve the constraints. Consequently, assigning a FF to each row is the most sensible, and the other formulations are not pursued further.

Suppose realizations from the random variables ${X_{0:t} = \langle X_0,X_1,\ldots ,X_t\rangle }$, denoted $x_{0:t}$, have been observed from the data stream. To assign a FF to each row $x_{0:t}$ needs to be partitioned into blocks. This block decomposition is necessary since parameter estimation is driven by the transition clock instead of the data clock, as discussed in Sect.  2.1. Define these blocks by the multisets

$$\begin{aligned} B^{(i)}_t = \{x_k: \,\, x_{k-1}=i, \,\, \forall \,\, k=1,\ldots ,t\}. \end{aligned}$$

(1)

The block $B^{(i)}_t$ represents the subset of observations from the Markov chain that were jumped to from a state ${i\in {\mathcal {S}}}$, and is assumed in ascending order according to the time-stamp t. Further, ${B_t^{(i)}[k]}$ is used to denote the $k^{\text {th}}$ element of $B_t^{(i)}$. This notation is essential in developing the non-sequential adaptive estimates that are presented in Sect.  2.2.3.

An example will help clarify the block decompositions. Consider the 3-state chain given in Fig. 3. Then

$B^{(1)}_7=\{x_1,x_2,x_7\}, \qquad B^{(2)}_7=\{x_3,x_5\}, \qquad B^{(3)}_7=\{x_4,x_6\}$,

where $B^{(1)}_7[2]=x_2$, $B^{(2)}_7[1]=x_3$ etc. Using this notation the weighted log-likelihood function can be formulated and optimized.

Fig. 3

A 3-state Markov chain which clarifies the block notation $B_t^{(i)}$

2.2.2 A temporally adaptive likelihood function

For each row ${i\in {\mathcal {S}}}$, consider a weighted log-likelihood function of the form

$$\begin{aligned} {\mathcal {L}}_{\text {FF}}\left( {\varvec{p}}^{(i)} \mid B_t^{(i)}\right)&= \sum \limits _{k=1}^{|B_t^{(i)}|}\left[ \prod \limits _{\ell =k}^{|B_t^{(i)}|-1}\lambda ^{(i)}_\ell \right] {\mathcal {L}}\left( {\varvec{p}}^{(i)}\mid B_t^{(i)}[k]\right) . \end{aligned}$$

(2)

The vector ${{\varvec{p}}^{(i)}\in {\mathbb {R}}^K}$ are the parameters of the multinomial that we are optimizing the likelihood with respect to, ${B_t^{(i)}}$ was defined in Eq. (1), ${{\mathcal {L}}\left( \cdot |\cdot \right) }$ is the multinomial log-likelihood function, and ${\lambda _{\ell }^{(i)}\in [0,1]}$ is a FF associated with the $i^{\text {th}}$ row. When ${k=|B_t^{(i)}|}$ the empty product is, by convention, assumed one.

Unless otherwise specified suppose that ${x_t\in B_t^{(i)}}$. This is equivalent to saying that an update of the $i^{\text {th}}$ row was possible at time t. Since no new information is available for any other row, all the other blocks remain the same, i.e., ${B^{(h)}_{t}= B_{t-1}^{(h)}}$ ${\forall \,\, h\ne i}$. To examine how the FFs introduce temporal adaptivity the recursive version of Eq. (2) is helpful, and is given by

$$\begin{aligned} {\mathcal {L}}_{\text {FF}}\left( {\varvec{p}}^{(i)}\mid B_t^{(i)}\right)&=\lambda _{|B_t^{(i)}|-1}^{(i)}\,\,{\mathcal {L}}_{\text {FF}}\left( {\varvec{p}}^{(i)}\mid B_{t-1}^{(i)}\right) + {\mathcal {L}}\left( {\varvec{p}}^{(i)}\mid x_t\right) . \end{aligned}$$

(3)

Similar to the block decompositions, the FFs associated with the other rows remain unchanged, and are updated with the new time-stamp. This simplifies notation, and allows us to replace the FF in Eq. (3) with ${\lambda _{t-1}^{(i)}}$, and we remark that this subscript does not necessarily imply that the corresponding FF was updated at the last time-step, but represents the most recent FF available. Additionally, the subscript t does not mean that the FF has incorporated t observations in its estimation, since updating them relies solely on the observations in their corresponding block.

The functional form of Eq. (3) highlights how the FFs introduce temporal adaptivity into the estimation. The older terms in the likelihood are smoothly down-weighted, or ‘forgotten’ as newer data arrives. The rate at which data is forgotten is fully determined by the values of the FFs, and is discussed more in Sect.  2.2.4. Also, the newest observation in any block is given full weight in the parameter estimation, that is, weight one. Hence the likelihood, at any time-step, is aware and responsive to changes in the stream.

2.2.3 Adaptive parameter updates

Now that the FF framework has been introduced, the temporally adaptive transition matrix can be discussed. Let ${\tilde{{\varvec{P}}}_t\in {\mathbb {R}}^{K\times K}}$ represent this matrix, whose $ij^{\text {th}}$ element is denoted by ${\tilde{p}}_{t}^{(j|i)}$. Optimization of Eq. (2) results in the non-sequential weighted maximum likelihood estimates

$$\begin{aligned} {\tilde{p}}_{t}^{(j|i)}&=\frac{1}{n_{t}^{(i)}}\sum \limits _{k=1}^{|B_t^{(i)}|}w_k^{(i)} \,\, \mathbb {I}\left( B_t^{(i)}[k]=j\right) \qquad \forall \,\, i,j\in {\mathcal {S}}, \end{aligned}$$

(4)

where

$$\begin{aligned} w_k^{(i)}=\prod \limits _{\ell =k}^{|B_{t}^{(i)}|-1}\lambda ^{(i)}_\ell ,&\qquad n_t^{(i)}=\sum \limits _{k=1}^{|B_t^{(i)}|}w_k^{(i)}, \end{aligned}$$

(5)

and ${\mathbb {I}(\cdot )}$ represents the indicator function. The scalar ${w_k^{(i)}}$ represents the weight assigned to ${B_t^{(i)}[k]}$ and is a function of the FFs assigned to row ${i\in {\mathcal {S}}}$. The scalar ${n_t^{(i)}}$ is referred to as the effective sample size as it weakly characterizes how many observations are contributing to the estimate; refer to Bodenham (2014) for a thorough discussion. Similar to the blocks and FFs, if a transition from state i does not occur the estimate for the $i^{\text {th}}$ row remains unchanged, and is updated with the current time-stamp as it represents the most up-to-date estimate.

The block decomposition is necessary in the batch formulation of the estimates; however, on the stream it is infeasible and unnecessary to store every observation in memory. Moreover, Eq. (3) reveals that we only need to store the FF for row i that was computed the last time a transition out of state i occurred. The formulas in Eq. (4)-(5) can then be recast as the following set of recursive equations:

$$\begin{aligned} n_{t}^{(i)}&=\lambda _{t-1}^{(i)}n_{t-1}^{(i)}+1, \end{aligned}$$

(6)

$$\begin{aligned} \tilde{{p}}_{t}^{(j|i)}&=\left( 1-\frac{1}{n^{(i)}_{t}}\right) \tilde{{p}}_{t-1}^{(j|i)}+\frac{1}{n^{(i)}_{t}} \,\, \mathbb {I}(x_t=j) \quad \forall \,\, j\in {\mathcal {S}}. \end{aligned}$$

(7)

Eqs. (6) and (7) can be implemented whenever a transition from state i occurs, which is in accordance with the transition clock. These equations do not require the storage of any previous observations in memory (besides ${x_{t-1}}$), and implementing them requires ${\mathcal {O}}(1)$ floating point operations at each time-step. This low complexity makes the adaptive updating of the transition matrix suitable for streaming estimation.

In subsequent sections properties of $\tilde{{\varvec{P}}}_t$ will prove useful. First, summing Eq. (4) over ${j\in {\mathcal {S}}}$ shows that $\tilde{{\varvec{P}}}_t$ requires no renormalization, that is, it is a stochastic matrix. Moreover, in Sect.  4 the mean and variance of each element of $\tilde{{\varvec{P}}}_t$ will be required. These are provided in Lemma 1, and can be derived using the fact that conditional on transitioning from a state ${i\in {\mathcal {S}}}$, the elements of ${B_t^{(i)}}$ are realizations from a multinomial distribution. Refer to Plasse (2019) for a proof of the Lemma.

Lemma 1

Consider the $i^{\text {th}}$ row of $\tilde{\varvec{{P}}}_t$. Assume that the true cell probabilities are ${\{p^{(j|i)}_{t}\}_{j=1}^K}$, ${\tilde{p}}_{t}^{(j|i)}$ is a random variable, and a fixed value for the FF is used. Then the mean and variance of ${\tilde{p}}_{t}^{(j|i)}$ are given by

$$\begin{aligned} \mathbb {E}\left( {\tilde{p}}_{t}^{(j|i)}\right) =p^{(j|i)}_{t},&\qquad \text {Var }\left( {{\tilde{p}}_{t}^{(j|i)}}\right) =u^{(i)}_{t}\,\, p^{(j|i)}_{t}\left( 1-p^{(j|i)}_{t}\right) , \end{aligned}$$

where

$$\begin{aligned} u^{(i)}_{t}=m^{(i)}_t \bigg / \left[ n^{(i)}_{t}\right] ^2 ,&\qquad m_t^{(i)}=\sum \limits _{k=1}^{|B_t^{(i)}|}\left[ w_{k}^{(i)}\right] ^2. \end{aligned}$$

The quantity ${m_t^{(i)}}$ can be computed recursively using

$$\begin{aligned} m_t^{(i)} = \left( \lambda ^{(i)}_{t-1}\right) ^2m_{t-1}^{(i)} + 1. \end{aligned}$$

(8)

A fixed FF is assumed in Lemma 1 to allow for the effective sample size and weights to be ‘pulled through’ the expectation and variance calculations. Without this assumption the derivations become intractable, and when adaptive FFs are used it is understood that the means and variances appearing in the Lemma are approximations. Adaptive and fixed FFs are discussed in more detail in the next section.

2.2.4 Interpreting the forgetting factors

Our notation provides the opportunity for the FFs to change their values over time. These are referred to as adaptive forgetting factors. A simpler possibility is to fix the FFs to a constant value for each row (as in Lemma 1). Although adaptive forgetting is more general, fixed forgetting allows for easier interpretation of the FFs, and is assumed throughout this section.

First suppose that a fixed FF ${\lambda = 1}$ is assigned to every row. This refers to a ‘no forgetting’ scenario since all observations are given equal weight in the parameter estimation. In this case Eq. (4) becomes the classical maximum likelihood estimate for the multinomial distribution, and Eqs. (6)–(7) collapse to the sequential version of the estimate. However, due to the presence of changepoints it would be naive to choose ${\lambda =1}$ for each row. This would result in data from previous, non-informative segments contributing equally in the estimation.

Now assume that a fixed FF ${\lambda \in (0,1)}$ has been assigned to each row. The value of ${\lambda }$ directly affects how quickly (or slowly) the estimate disregards historic data. Due to our formulation of forgetting, values closer to one forget data slower than values closer to zero. Since the data generating process is likely to change, there is no reason to assume that fixed values of the FFs will be appropriate at every time-step. Thus developing a method for, in some sense, optimally choosing the values of the FFs is important. The next section details such a method.

3 Adaptively tuning the forgetting factors

The FF for a row ${i\in {\mathcal {S}}}$ is sequentially updated via the stochastic gradient descent method (Benveniste et al. 2012; Duda et al. 2012). In the current context, this method can be expressed as

$$\begin{aligned} \lambda _t^{(i)}&= \lambda _{t-1}^{(i)} - \eta \,\, \nabla \left[ J\left( \lambda _{t-1}^{(i)}\mid \tilde{{\varvec{p}}}^{(i)}_{t-1},x_t\right) \right] , \end{aligned}$$

(9)

where ${J(\cdot \mid \cdot )}$ is a continuous and differentiable cost function, and the gradient is taken with respect to all previous FFs for row i. The vector ${\tilde{{\varvec{p}}}_{t-1}^{(i)}\in {\mathbb {R}}^K}$ represents the $i^{\text {th}}$ row of ${\tilde{{\varvec{P}}}_{t-1}}$, and the scalar ${0<\eta \ll 1}$ is a step-size that dictates the size of the jump taken in the gradient descent step. Equation (9) is implemented whenever a transition from state i occurs, which is seldom at every time-step.

To make Eq. (9) tangible assumptions must be made. The first assumption deals with the computation of the gradient. Since data streams are unbounded it is not possible to store every FF in memory. This, along with the fact that the FFs are recursively defined in terms of one another, makes an exact gradient computation challenging. However, as in Anagnostopoulos et al. (2012), for small step-sizes it can be argued that the FFs are approximately fixed. The gradient of ${J(\cdot \mid \cdot )}$ is then computed by assuming it is a function of a single, fixed, FF $\lambda ^{(i)}$. This may seem counter-intuitive; however, this heuristic argument was verified rigorously in Bodenham and Adams (2016) and leads to adaptive FFs that have desirable properties. Subsequently, the operator ‘$\nabla$’ is used to denote a derivative with respect to the scalar variable $\lambda ^{(i)}$.

The next assumption deals with the choice of cost function. As in Anagnostopoulos et al. (2012), the one-step ahead negative log-likelihood function is chosen. This measures how well the estimates at time $(t-1)$ fit the $t^{\text {th}}$ observation, and is given by

$$\begin{aligned} J\left( \lambda ^{(i)}\mid \tilde{{\varvec{p}}}_{t-1}^{(i)},x_t\right)&=-\sum \limits _{j=1}^K \mathbb {I}(x_t=j)\,\, \log \left( {\tilde{p}}_{t-1}^{(j|i)}\right) . \end{aligned}$$

Observe that the elements of $\tilde{{\varvec{p}}}_{t-1}^{(i)}$ are functions of the effective sample size $n_{t-1}^{(i)}$, which is a function of the FFs for the $i^{\text {th}}$ row. The gradient of the cost function is given by

$$\begin{aligned} \nabla \left[ J\left( \lambda ^{(i)}\mid \tilde{{\varvec{p}}}_{t-1}^{(i)},x_t\right) \right]&=-\sum \limits _{j=1}^K \mathbb {I}(x_t=j) \,\, \left( \frac{\nabla {{\tilde{p}}_{t-1}^{(j|i)}}}{{\tilde{p}}_{t-1}^{(j|i)}}\right) , \end{aligned}$$

where the recursive updates for the gradients can be derived via direct differentiation of Eq. (6)-(7), and are given by

$$\begin{aligned} \nabla n_{t}^{(i)}&= \lambda ^{(i)}_{t-1}\nabla n_{t-1}^{(i)} + n^{(i)}_{t-1}, \end{aligned}$$

(10)

$$\begin{aligned} \nabla \tilde{{p}}_{t}^{(j|i)}&=\left( 1-\frac{1}{n^{(i)}_{t}}\right) \nabla \tilde{{p}}_{t-1}^{(j|i)} -\frac{\nabla n_{t}^{(i)}}{\left( n_{t}^{(i)}\right) ^2}\left( \mathbb {I}(x_t=j)-\tilde{{p}}_{t-1}^{(j|i)}\right) \quad \forall \,\, j\in {\mathcal {S}}. \end{aligned}$$

(11)

When tuning the FFs a constant step-size $\eta$ was introduced. Thus, it appears that choosing values for the FFs has been replaced with choosing a value for the step-size. This is a caveat with adaptively tuning parameters online – in doing so other parameters are inevitably introduced whose values must be specified. The authors have considered tuning $\eta$ online; however, methods either introduce too much variance into the estimation, or require several parameters to be specified. We favor using a fixed step-size ${\eta }$ for each row, as opposed to tuning time-varying step-sizes, which requires the specification of additional parameters. In Sect.  6, a large simulation study is conducted that considers various choices of the step-size, and provides empirical evidence for setting its value in practice. Refer to Ruder (2016) for a detailed discussion on ways of choosing the step-size $\eta$, and variants of the gradient descent algorithm.

4 Change detection methods

The adaptive estimate developed in Sect.  2 is now used in the formulation of an online change detection method. This Adaptive Detection and Estimation Procedure for Transition Matrices (ADEPT-M) sequentially monitors for multiple changepoints in each element of ${{\varvec{P}}}_t$, as well as maintains an adaptive estimate for the transition matrix currently generating the data. This method is discussed in Sect.  4.1, and introduces control parameters that neither depend on how many changepoints are in the stream, nor the magnitudes of the unknown changes. This appears to be the first attempt at developing an online, adaptive, multiple changepoint detector for transition matrices.

In Sect.  4.2control charts that are commonly used in the literature are discussed, namely the cumulative sum (CUSUM) and the exponentially weighted moving average (EWMA) control charts. Moreover, Sect.  4.3 introduces the adaptive sliding window (ADWIN) and pruned exact linear time (PELT) methods. These methods were not developed to monitor a transition matrix for changes; however, they are modified in Sect.  4.4 so they may be compared to ADEPT-M. Due to the lack of literature on the topic, comparing ADEPT-M to this diverse selection of methods is a natural choice.

4.1 ADEPT-M

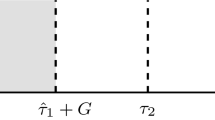
Consider monitoring for a change in ${p}_t^{(j|i)}$. At every time-step ADEPT-M is either in a grace period, or is monitoring the stream for changepoints. When a changepoint is detected, a grace period immediately begins and ADEPT-M does not monitor for subsequent changes while in this period. Control limits are then computed via a function of the parameters estimated at the end of the grace period. The left panel of Fig. 4 illustrates this procedure for a single detection. The scalars $L_1$ and $U_1$ are the control limits before the detection, and $L_2$ and $U_2$ are the control limits obtained after the grace period terminates. This process is repeated every time ADEPT-M detects a changepoint.

Suppose at time ${\hat{\tau }}$ a change is detected in ${p}_t^{(j|i)}$. ADEPT-M immediately enters a grace period, which terminates based on a user defined value $G\in {\mathbb {Z}}^+$. The value of G has several interpretations when monitoring a transition matrix on the stream. One interpretation is that the grace period will end at time ${({\hat{\tau }}+G)}$. However, if ${p_t^{(j|i)}}$ is small after a changepoint the value of G may not be large enough to observe any transitions from state i to state j. To mitigate this problem, the grace period is terminated only when G transitions from state i to state j are observed, that is, a data-adaptive grace period is used. Since G is defined this way, ADEPT-M will have the opportunity to estimate the transition probabilities associated with the new segment. The scalar G also implicitly defines a lower bound on the false positive rate, as G transitions from state i to state j are required before monitoring for further changes.

Fig. 4

An illustration depicting how ADEPT-M resets after a change is detected. The $\times$s denote if a transition occurred at a particular time-step or not. The left figure is provided to help understand the mathematical notation appearing in the right figure

A common way of choosing control limits is to provide guarantees on the false positive rate. Given a significance level ${\alpha \in (0,1)}$ the control limits, denoted $L_t^{(j|i)}$ and $U_t^{(j|i)}$, are typically chosen so that

$$\begin{aligned} {\mathbb {P}}\left( {\tilde{p}}_t^{(j|i)}\in \left[ L_t^{(j|i)},U_t^{(j|i)}\right] \right) \approx 1-\alpha . \end{aligned}$$

Exact $100(1-\alpha )\%$ control limits would require the distribution of ${\tilde{p}}_{t}^{(j|i)}$. This quantity is a weighted sum of Bernoulli random variables whose weights may assume any value in [0, 1], and under this formulation, a known distribution does not appear to exist. There exists some work in learning the distribution of a weighted sum of Bernoulli random variables, e.g. Daskalakis et al. (2015) proposed an algorithm that can learn the distribution in polynomial time for a discrete set of weights. However, this high computational complexity is not suitable for streaming analysis. Raghavan (1986) provided bounds on weighted sums of Bernoulli random variables; however, in practice these bounds are too conservative, frequently not respecting the range of the estimates.

A moment matching technique is used to construct approximate control limits. Such methods have found success in various areas, such as: developing adaptive thresholds for network counts (Lambert and Liu 2006), visual scanning in particle physics (Sanathanan 1972) and in estimating parameters for generalized extreme value distributions (Hosking et al. 1985). Since ${{\tilde{p}}_t^{(j|i)}\in [0,1]}$ a natural distribution to match with is a $\text {Beta}(a,b)$, as it respects the range of our estimate. The mean and variance of a random variable ${Y\sim \text {Beta}(a,b)}$ are

$$\begin{aligned} {\mathbb {E}}(Y) = \frac{a}{a+b}, \qquad \text {Var}(Y) = \frac{ab}{(a+b)^2(a+b+1)}, \qquad a,b>0. \end{aligned}$$

Equating with the mean and variance of ${\tilde{p}}_t^{(j|i)}$ provided in Lemma 1, and using the adaptive transition probability as a plug-in estimate, the following system of equations are obtained

$$\begin{aligned} {\tilde{p}}_t^{(j|i)} = \frac{a}{a+b}, \qquad u_t^{(i)}{\tilde{p}}_t^{(j|i)}\left( 1-{\tilde{p}}_t^{(j|i)}\right) =\frac{ab}{(a+b)^2(a+b+1)}. \end{aligned}$$

Solving for a and b and including appropriate notation results in

$$\begin{aligned} a_t^{(j|i)}&= \left( \frac{1}{u_t^{(i)}} - 1\right) {\tilde{p}}_t^{(j|i)}, \end{aligned}$$

(12)

$$\begin{aligned} b_t^{(j|i)}&= \left( \frac{1}{u_t^{(i)}} - 1\right) \left( 1-{\tilde{p}}_t^{(j|i)}\right) . \end{aligned}$$

(13)

Only the most recent detection made is required to construct the control limits for a new segment. Let ${\hat{\tau }}_{\star }^{(j|i)}$ be the most recent detection made for ${p}_t^{(j|i)}$, and let ${\hat{g}}_\star ^{(j|i)}$ denote the length of the grace period associated with this detection. That is, ${\hat{g}}_\star ^{(j|i)}$ is the number of observations processed until G transitions from state i to state j, following the detection ${\hat{\tau }}_\star ^{(j|i)}$, are observed. Using this notation the grace period will terminate at time $\left( {\hat{\tau }}^{(j|i)}_{\star }+{\hat{g}}_\star ^{(j|i)}\right)$ – refer to the right panel of Fig. 4. For an ${\alpha \in (0,1)}$, when ADEPT-M is leaving a grace period the control limits are computed using

$$\begin{aligned} L_t^{(j|i)}&= {\mathcal {Q}}\left( \alpha /2 \mid a_t^{(j|i)},b_t^{(j|i)}\right) \Big |_{t={\hat{\tau }}^{(j|i)}_\star + {\hat{g}}^{(j|i)}_\star }, \end{aligned}$$

(14)

$$\begin{aligned} U_t^{(j|i)}&= {\mathcal {Q}}\left( 1-\alpha /2 \mid a_t^{(j|i)},b_t^{(j|i)}\right) \Big |_{t={\hat{\tau }}^{(j|i)}_\star + {\hat{g}}^{(j|i)}_\star }, \end{aligned}$$

(15)

where ${{\mathcal {Q}}(\cdot \mid a,b)}$ is the quantile function associated with a ${\text {Beta}(a,b)}$ distribution. The initial confidence limits, ${L_0^{(j|i)}}$ and ${U_0^{(j|i)}}$, are constructed using a burn-in period of length ${B\in {\mathbb {Z}}^+}$. A change is detected whenever the estimate falls outside the control limits, i.e., when

$$\begin{aligned} {\tilde{p}}_t^{(j|i)}\notin \left[ L_t^{(j|i)},U_t^{(j|i)}\right] . \end{aligned}$$

The right hand side of Eq. (14)–(15) use the estimate of ${\tilde{p}}_{t}^{(j|i)}$ obtained immediately after the grace period ends, and these control limits will remain constant until the algorithm detects another change – in which case ADEPT-M will enter a new grace period and the values of ${\hat{\tau }}_{\star }^{(j|i)}$ and ${\hat{g}}_{\star }^{(j|i)}$ would be updated accordingly. Refer to Table 1 for a summary of the notation introduced by ADEPT-M, and to Algorithm 1 for corresponding pseudocode.

Table 1 Notation corresponding to ADEPT-M

4.2 Commonly used control charts

In this section an overview of the CUSUM and EWMA control charts is presented. These methods were developed to detect a single change in the mean of a stochastic process, assuming that in-control and/or out-of-control parameters are known, or efficiently estimated. These control charts are extended to allow for multiple changepoint detection in Sect.  4.4. It is also assumed that $\langle X_0,\ldots ,X_t,\ldots \rangle$ are independent random variables, which have a common in-control mean and variance given by $\mu$, and ${\sigma ^2}$, respectively.

4.2.1 CUSUM

The CUSUM control chart was introduced in Page (1954) and monitors the statistics given by

$$\begin{aligned} C_t^{+}=\max \left\{ 0,C_{t-1}^{+} + z_t - k\right\}&\quad C_0^{+}=0,\\ C_t^{-}=\max \left\{ 0,C_{t-1}^{-}-z_t-k\right\}&\quad C_0^{-}=0, \end{aligned}$$

where $z_t=(x_t-\mu )/\sigma$ are the standardized realizations from the stream, and k is a control parameter referred to as the reference value (Montgomery 2007). CUSUM signals a change whenever $C_t^+$ or $C_t^-$ exceed some threshold h, which is referred to as the decision interval (Montgomery 2007), and is another control parameter that needs to be set by the user.

The tuple (k, h) is difficult to choose in practice, and misspecifying its value can affect the chart’s performance (Ross 2013). The scalar k is commonly chosen to detect a change of some specific magnitude – which assumes prior knowledge of the changepoint is available. The value of h is typically chosen to be proportional to the in-control standard deviation $\sigma$. This assumes $\sigma$ is known, or a reliable estimate is available. In the continuous monitoring paradigm these approaches for choosing the control parameters will be hindered by the presence of multiple changepoints, and restarting the algorithm once a change has been detected is certainly required. In this article, a subset of recommendations made in Hawkins (1993) for choosing the control parameter tuple are used, and are provided in Table 2. It is not obvious which pair of control parameters will perform well in a particular setting; therefore, using multiple choices for (k, h) is essential.

4.2.2 EWMA

The EWMA control chart was proposed in Roberts (1959) and has been investigated in Lucas and Saccucci (1990) and Ross et al. (2012). EWMA monitors a statistic $Z_t$, sequentially defined by the convex combination

$$\begin{aligned} Z_t&=(1-r)Z_{t-1} + rx_t, \end{aligned}$$

for a user defined control parameter ${r\in [0,1]}$. The parameter r has a similar interpretation to a fixed FF and affects how quickly older observations are discarded. In Bodenham (2014) connections between EWMA and the fixed FF case are highlighted. A change is flagged whenever

$$\begin{aligned} Z_t\notin [\mu -L\sigma _{Z_t},\mu +L\sigma _{Z_t}], \end{aligned}$$

for some user defined control limit L, and

$$\begin{aligned} \sigma ^2_{Z_t}&=\sigma ^2\left\{ \frac{r}{2-r}\left[ 1-(1-r)^{2t}\right] \right\} . \end{aligned}$$

The control parameters r and L, as in the case of the CUSUM chart, are difficult to set to guarantee a prescribed false positive rate in the multiple changepoint setting. In the upcoming simulations a subset of parameter values, as suggested in Lucas and Saccucci (1990), are used. These values are provided in Table 2.

Table 2 Control parameters used when implementing CUSUM and EWMA

4.3 Additional detectors

Two other methods are also considered in the simulation study of Sect.  6, and are included to increase the diversity of detectors used for comparison.

4.3.1 ADWIN

The ADaptive sliding WINdow (ADWIN) algorithm (Bifet and Gavalda 2007) is a change detection method based on exponential histograms. ADWIN maintains a variable length sliding window of recent observations, and drops older portions of the window if there is evidence to support that the average of observations in the older portion differs significantly from the rest of the window. The main parameter of ADWIN is a confidence level ${\varDelta \in (0,1)}$, which is used in conjunction with a statistical test to determine if older portions of the window should be discarded. That is, ADWIN tests the null hypothesis that the “average of observations within the window remains constant”, which is sustainable up to confidence level ${\varDelta }$ (Bifet and Gavalda 2007). In Bifet and Gavalda (2007) a Hoeffding-based test is used to determine if older portions of the window are to be dropped.

ADWIN’s time and memory complexity are logarithmic in the length of the largest window being monitored (Bifet et al. 2018), which makes ADWIN more computationally expensive than ADEPT-M, CUSUM and EWMA whose time and memory complexities are constant. Further, ADWIN requires a parameter to be chosen that controls the amount of memory being used, in addition to determining how the sub-windows are chosen. Bifet and Gavalda (2007) mention that this parameter is chosen arbitrarily in practice.

The ADWIN implementation provided in sci-multiflow (Montiel et al. 2018) is used in Sect.  6. The values used for the confidence level are taken as ${\varDelta \in \{0.002, 0.05, 0.10, 0.30\}}$, where 0.002 is the default value provided in sci-multiflow, and 0.05, 0.10, 0.30 are values used in Bifet and Gavalda (2007).

4.3.2 PELT

The Pruned Exact Linear Time (PELT) method was introduced in Killick et al. (2012), is implemented in the R package changepoint (Killick and Eckley 2014), and is a modification of the optimal partitioning algorithm (Jackson et al. 2005). PELT is capable of detecting multiple changepoints, and does so by making several passes over the data. Therefore, PELT is not suitable for streaming data, but in the absence of a state-of-the-art detector for transition matrices provides a good benchmark.

PELT is able to return an optimal segmentation of the data given a user-defined cost function. Under certain assumptions PELT has a linear computational cost; however, if the assumptions fail to hold PELT’s computational complexity becomes quadratic in the length of the data. PELT has a parameter called the ‘minimum segment length’, which dictates the minimum number of observations between changepoints, and is similar to the grace period adopted in this work. Several values for the minimum segment length were considered in Sect.  6; although, the results were similar across all values. Due to this, only one set of simulations is presented for PELT. All other parameters were chosen as the default parameters provided in the R package changepoint.

4.4 Extending to transition matrices

The comparison methods presented in Sect.  4.2–4.3 were not developed to detect multiple changepoints in a transition matrix; hence, modifications are required so that they may be compared to ADEPT-M. To modify the control charts, the stream is transformed into ${K^2}$ streams whose observations are realizations of Bernoulli random variables. Specifically, for each ${i,j\in {\mathcal {S}}}$, the methods are implemented on a stream whose observation at time t is a one if a transition from state i to state j occurred, and zero otherwise. This is sometimes referred to as a binarization of the categorical process (Weiß 2012). It is worth noting that to compare the methods to ADEPT-M, ${K^2}$ runs are required to monitor for changes, while only one run of ADEPT-M is necessary. If the number of states K is large, something common in network analysis (Kolaczyk and Csárdi 2014), this could introduce a great deal of computational burden for the comparison methods.

Lastly, CUSUM and EWMA need to be restarted after they detect a changepoint. Once CUSUM and/or EWMA makes a detection, the methods enter a grace period that terminates according to the control parameter G, as discussed previously.

5 Performance measures

This section introduces four measures that are commonly used to assess online change detectors. These measures will be used in Sect.  6 to compare ADEPT-M with the comparison methods introduced in Sect.  4.2–4.3. In Sect.  5.1, the average run lengths are introduced in terms of the data clock, as they are easier to interpret in this setting. Section 5.2 introduces two other performance measures, which are more suitable for the continuous monitoring paradigm. Adjustments that should be made to the average run lengths are discussed in Sect.  5.3.

5.1 The average run lengths

Two commonly used performance measures are the average run lengths (ARLs) ${ARL}_{0}$ and ${ARL}_1$ introduced in Page (1954). ${ARL}_0$ is defined as the average number of observations that arrive until a false positive is detected, whereas ${ARL}_1$ is defined as the average detection delay (Bodenham and Adams 2016). The ARLs for a change detector are difficult to compute exactly despite the amount of research devoted to the topic, e.g., see Lucas and Saccucci (1990), Brook and Evans (1972), Crowder (1987) and Hawkins (1992). Due to this, Monte Carlo simulations are usually conducted to approximate ${ARL}_0$ and ${ARL}_1$.

Typically, ${ARL}_0$ is estimated by implementing a change detector over multiple streams with no changepoints present and averaging over the first false positive flagged in each stream. To compute $ARL_1$, a change detector is run over multiple streams with one changepoint and the detection delays are averaged over. Detectors exhibiting large values of $ARL_0$ and low values of $ARL_1$ are preferred, although both need to be inspected since either of the ARLs can be improved at the expense of the other.

In the continuous monitoring paradigm the ARLs are not sufficient to assess performance, as they do not take into account how many changepoints a detector flags, nor the number of true changepoints a method did not detect. Because of this, as in Bodenham and Adams (2016), two other performance measures are considered.

5.2 CCD and DNF

When there is more than one changepoint in a stream the ARLs are not complete measures of performance. Due to this, two new measures are introduced, which represent the proportion of changepoints correctly detected (CCD) and the proportion of detections that are not false (DNF). Both CCD and DNF take values in [0, 1], with values closer to one being preferable, and are estimated via Monte Carlo simulations.

The quantities CCD and DNF are analogous to the more familiar quantities of precision and recall used in the classification literature. Thus, to simplify the results presented in Sect.  6, the aggregated ${F_1}$-score

$$\begin{aligned} F_1 = 2\times \dfrac{CCD\times DNF}{CCD+DNF}, \end{aligned}$$

is reported. Although CCD and DNF can be related to precision and recall, it should be noted that not all classification metrics are appropriate in the changepoint detection setting. For example, a change detector not flagging a changepoint when one has not occurred (a true negative) should not be treated the same as a detector correctly flagging a changepoint when one does occur (a true positive). Any metric that treats these quantities equally would be misleading and inappropriate to report.

Since CCD and DNF do not depend on the locations of any detected changepoints, their values are invariant with respect to the data and transition clocks. This is not true for the ARLs, and it is argued in the next section that they should be adjusted in accordance with the transition clock.

5.3 ARL adjustments

Suppose an online detector, in two simulations, flagged its first false positive at times 100 and 200 respectively. The standard definition of $ARL_0$ states that, on average, a false positive is flagged by the detector every 150 time-steps. However, since a transition from state i to state j is not observed at every time-step, this value of $ARL_0$ is an over-estimate for the true $ARL_0$. To see this, suppose that a transition from state i to state j occurred, respectively, 30 and 40 times on the intervals [0, 100] and [0, 200]. Since 30 and 40 transitions occurred over the two simulations, a more accurate $ARL_0$ to report is 35. Any time a transition from state i to state j did not occur should not contribute to the value of $ARL_0$. The same reasoning can be applied to $ARL_1$.

This example makes it clear that the ARLs should be computed with respect to the transition clock, as opposed to the data clock. That is, the number of state i to state j transitions that occur in certain time intervals should be used as opposed to the estimated changepoint locations. Henceforth, when the ARLs are estimated it is understood that these adjustments have been made.

6 Simulation study

In this section a simulation study is considered where ADEPT-M, CUSUM EWMA, ADWIN and PELT are implemented on synthetic data streams.

6.1 Experimental framework

To estimate performance each change detector is implemented on 200 data streams of length $10^5$. In each simulation the number of changepoints assumes a value ${m\in \{0,1,10,50,100\}}$, and the changepoint locations are randomly generated according to a set of rules. If ${m=0}$ there is no changepoint to generate, and if ${m=1}$ a single changepoint is randomly placed near the middle of the stream. When ${m>1}$, the changepoint generation scheme in Bodenham and Adams (2016) is used. This results in the changepoint locations:

$$\begin{aligned} \tau _1&=F + \xi _1,\\ \tau _k&= \tau _{k-1} + (D+F) + \xi _k\qquad k = 2,3,\ldots ,m, \end{aligned}$$

where each ${\xi _k\sim \text {Poisson}(\nu )}$ and ${\nu ,D,F\in {\mathbb {Z}}^+}$. The rate parameter $\nu$ dictates the average length between consecutive changepoints, and D and F are used to ‘pad’ the intervals to give the detectors time to detect a change and undergo a grace period. The scalars $\nu ,$ D and F are not control parameters for any of the change detectors, as they are only used in the generation of the changepoints.

In each segment the data is governed by a fixed probability transition matrix, and ${(m+1)}$ matrices need to be generated. Consider the task of generating ${\varvec{P}}^{(k)}$ in the $k^{\text {th}}$ segment. To simplify the estimation of performance measures, across segments an abrupt change is induced in every element of the matrix. To ensure there has been a noticeable change across consecutive changepoints, a scheme is required to construct ${\varvec{P}}^{(k)}$ from ${\varvec{P}}^{(k-1)}$. This is itself an interesting problem, although not a focal point of the paper. Succinctly, candidate vectors for the rows of ${\varvec{P}}^{(k)}$ are uniformly sampled from the unit simplex, and the vectors that differ most from the rows of ${{\varvec{P}}^{(k-1)}}$ in terms of Euclidean distance are chosen.

A fixed burn-in length ${B=10^3}$ is used, and the scalar that determines the grace period assumes a value ${G\in \{25,50,75,100\}}$. For changepoint generation, ${D=50}$, ${F=20}$ and ${\nu =\lceil {10^5/m}\rceil }$ are chosen. The control parameters used for CUSUM and EWMA were given in Table 2, and the parameters for ADWIN and PELT were discussed in Sect.  4.3.1-4.3.2. For ADEPT-M, ${\alpha =10^{-i}}$ and ${\eta =10^{-j}}$ where ${i\in \{2,3,4\}}$ and ${j\in \{1,2,\ldots ,6\}}$ are chosen. Due to space limitations only ${K=3}$ is considered.

Lastly, since each performance measure is estimated for each component of ${{\varvec{P}}}_t$, they can be represented as ${K\times K}$ matrices. In the next section reporting ${K\times K}$ matrices for every simulation would be too much information to interpret. Therefore, these ‘performance measure matrices’ are averaged over their elements to return a single value that reflects how well a method did overall. These averages are also denoted by ${{ARL}}_0$, ${{ARL}}_1$ and ${F_1}$.

6.2 Results

ADEPT-M’s results are provided in Tables 3 and 6, CUSUM and EWMA’s results in Table 4, and ADWIN and PELT’s results in Table 5. In Table 4 a subscript for CUSUM and EWMA corresponds to the parameter tuple being used. For example, ${\text {CUSUM}_1}$ corresponds to results obtained using ${(k_1,h_1)}$, as given in Table 2. For ADWIN, the values in parentheses appearing in Table 5 are the corresponding values of ${\varDelta }$ used in the simulations.

Consider the ARL results in Tables 3, , 5. Since ${ARL}_0$ is computed by averaging over the first false positive flagged its value is invariant with respect to G. The value of ${ARL}_1$ does depend on G, as any false positives flagged before the changepoint will affect the monitoring periods for ADEPT-M, CUSUM and EWMA. Values of ${\eta \ge 10^{-3}}$ result in poor estimates for the ARLs, which is intuitive since larger values will result in more volatile behaviors of the adaptive estimates. In this case ADEPT-M is likely to flag a false positive earlier due to larger variability in the adaptive transition probabilities. This is also likely to inflate ${{ARL}_1}$, as more false positives will result in ADEPT-M entering grace periods that may overlap with the location of the true changepoint. Conversely, values of ${\eta <10^{-3}}$ result in ARLs which are comparable to the results obtained by the other methods. PELT achieved the highest value of ${ARL_0}$, but ADEPT-M reports lower values for ${ARL_1}$, over all parameter tuples considered, when compared to PELT. For CUSUM and EWMA there are combinations of parameters that report better metrics. However, a priori, the choice of control parameters for CUSUM and EWMA typically depend on information which is unavailable to the analyst. Further, no single set of control parameters for CUSUM or EWMA does well across all columns in Table 4; whereas smaller values of $\eta$ seems to consistently balance the trade-off between the ARLs, resulting in favorable performance for ADEPT-M.

Table 3 ADEPT-M’s ${ARL}_0$ and ${ARL}_1$ values for different choices of ${(G,\alpha ,\eta )}$

Table 4 Performance measures for CUSUM and EWMA

Table 5 Performance measures for PELT and ADWIN

Table 6 ADEPT-M’s $F_1$-scores

Results for the aggregated ${F_1}$-score are provided in Table 6 for ADEPT-M, and in the lower sections of Tables 4,5 for competing methods. The ${F_1}$-scores are computed in the multiple changepoint setting, which is the focal point of this work, and highlights the capability of ADEPT-M. Only values ${\eta < 10^{-3}}$ are considered when investigating the ${F_1}$-scores, as these step-size values were shown to result in favorable values for the ARLs. For ADWIN and PELT, the largest ${F_1}$-score reported, over all values of m, was 0.47; whereas, in 94.4% of ADEPT-M’s simulations the ${F_1}$-score reported exceeded 0.47. For CUSUM and EWMA, Table 4 has combinations of control parameters that result in ${F_1}$-scores similar to ADEPT-M; however, many values are much lower. In fact, 68.1% of CUSUM/EWMA ${F_1}$-scores are under 0.50, and 48.6% of values are under 0.30. For ADEPT-M only 7.4% of simulations had an ${F_1}$-score under 0.5, and no simulations resulted in an ${F_1}$-score below 0.30.

These simulations reinforce the fact that ADEPT-M is able to accurately detect multiple changepoints in a Markov transition matrix in the streaming data setting, and achieves better performance when compared to commonly used change detection algorithms. ADEPT-M requires the parameter tuple ${(G,\alpha , \eta )}$ to be prescribed. Practically, any detector that can effectively detect multiple changepoints would have a parameter similar to G. The scalar $\alpha$ results in approximate ${100(1-\alpha )\%}$ control limits, and Tables 3 and 6 can be used to suggest values that result in a desired trade-off between the performance measures. Empirically we recommend choosing ${\eta <10^{-3}}$, which agrees with existing literature that uses FFs to aid in the detection of changepoints.

7 Real data illustrations

This section analyzes two real-world data sets. Sect.  7.1 investigates a stream consisting of over nine million HTTP web requests, and Sect.  7.2 analyzes the well-studied electricity pricing data set (Harries and Wales 1999).

7.1 HTTP web requests

Morgan (2017) has estimated that cyber-crime will cost the world $6 trillion annually by the year 2021. With cyber-crime continuing to be a major threat, the development of methods to detect attacks in an efficient manner is a pressing concern. A Distributed Denial of Service (DDoS) attack is a common cyber-attack, where a malicious agent overwhelms a service to prevent legitimate access (Mirkovic and Reiher 2004). In this section, a sequence of HTTP web requests to a server farm being managed by a scheduler is considered. Section 7.1.1 introduces the data and discusses a special type of DDoS attack – an HTTP flood attack. Section 7.1.2 manipulates the data to mimic an HTTP flood, and ADEPT-M is shown to successfully detect the attack.

7.1.1 The data

The data consists of a sequence of 9,241,302 HTTP web requests collected on September 7, 2016 from 9am to 3pm, corresponding to approximately 428 observations arriving per second. Web requests include a request type field, and the six appearing in the data stream yields the state-space

$$\begin{aligned} {{\mathcal {S}}=\{\mathtt {DELETE,GET,HEAD,OPTIONS,POST,PUT}\}}. \end{aligned}$$

Briefly, a $\mathtt {GET}$ request pulls information from a server, a PUT request pushes information to a server, and a $\mathtt {POST}$ request sends a client’s data to a server for processing. The other requests have similar meanings; see Gourley and Totty (2002) for more details on HTTP requests.

The data has no ground-truth associated with it, that is, the existence and location of changepoints are unknown. This is typically the case in many real-world data streams, and to circumvent this issue the data is manipulated to mimic an HTTP flood attack – a DDoS attack where an attacker exploits either $\mathtt {POST}$ or $\mathtt {GET}$ requests, typically using ‘botnets’, to generate a high volume of malicious activity (Zargar et al. 2013). These malicious request packets are used to attack a web server by over-allocating its resources, resulting in legitimate users being denied access. Furthermore, the tampered packets are hard to distinguish from genuine traffic since they have legitimate HTTP payloads (Yatagai et al. 2007). For illustration purposes, HTTP $\mathtt {POST}$ floods are considered in the next section.

7.1.2 Results

The simplest way of mimicking an HTTP $\mathtt {POST}$ flood is to choose a time for the attack, and then flood the stream with $\mathtt {POST}$ requests that lasts for a prespecified amount of time. Let ${\tau }$ be the start time of the attack, and let ${\delta \in \{0.25,0.50,1.00,2.00\}}$ be the duration of the attack in minutes. Since approximately 428 observations arrive per second, the number of $\mathtt {POST}$ requests in the flood is taken as ${t_\delta = \delta (428\times 60)}$. Although uncomplicated, this provides a practical way of determining if ADEPT-M can detect such an attack, and is sensible in the absence of ground-truth labeling of malicious activity.

In the cyber-security setting, it is typical to want a detector that raises few false alarms (Turcotte et al. 2017). Therefore, given prior domain knowledge the user could choose the grace period length G to provide a lower bound on the number of detections. We choose ${G=15\times 428}$, resulting in roughly 15 second grace periods (in accordance with the data clock). Since the length of the data stream depends on $\delta$, the burn-in length B is chosen so ADEPT-M is always run on a stream of length 9 million. The significance level $\alpha$ and the step-size $\eta$ assume values in the sets

$$\begin{aligned} \alpha \in \left\{ 10^{-3},10^{-4},10^{-5}\right\} , \qquad \eta \in \left\{ 10^{-4},10^{-5},10^{-6}\right\} . \end{aligned}$$

Table 7 The earliest detection made by ADEPT-M during the interval ${[\tau ,\tau +t_\delta ]}$, in the row of ${\tilde{{\varvec{P}}}_t}$ corresponding to $\mathtt {POST}$ requests

Table 7 displays the earliest detection made by ADEPT-M, in the row corresponding to $\mathtt {POST}$ requests, during the attack period ${[\tau ,\tau +t_\delta ]}$. These values have been scaled to approximate the amount of time (in seconds) that it took ADEPT-M to detect the attack. ADEPT-M was also run over the request data without the HTTP flood present (using the same parameters), and the earliest detection made was roughly 423 seconds after $\tau$, that is, it is reasonable to conclude that ADEPT-M genuinely detected the attack. Inspection of Table 7 also shows that the detection of the HTTP flood is fairly robust to the choice of ${(\alpha ,\eta )}$. Additionally, ADEPT-M took roughly 5 minutes to process the 9 million out of burn-in observations, making ADEPT-M an attractive and practical choice for real-world data streams.

7.2 Electricity pricing

ADEPT-M is now implemented on the publicly available electricity market data set (Harries and Wales 1999), which is well-studied in the streaming literature, and has been used to assess the accuracy of changepoint detectors and classification methods (Bifet and Gavalda 2007; Gama et al. 2004) in the presence of drift. The aim of this section is to show that ADEPT-M can be implemented on data streams comprised of continuous-valued observations, whose state space can be obtained through discretization.

7.2.1 The data

The data was collected from the Australian New South Wales (NSW) electricity market, and consists of 45,312 examples collected from May 7, 1996 to December 5, 1998. Each datum is collected over a 30 minute period and contains a time-stamp, the NSW electricity price and a class label. The sequence of class labels comprise the stream to be analyzed, and makes reference to the change in price when compared to a 24-hour moving average, resulting in the state-space ${{\mathcal {S}} = \{\texttt {UP}, \texttt {DOWN}\}}$. The Markov assumption that, on a given day, the change in electricity price is dependent on the previous day’s price is reasonable, making this data set well-suited for ADEPT-M.

7.2.2 Results

ADEPT-M is now used to detect changes, and is compared to the ADWIN method described in Sect.  4.3.1. The parameters for ADEPT-M are taken as ${(G,\alpha ,\eta ) = (100, 10^{-4}, 10^{-5})}$, with a burn-in period of length ${B=672}$. This burn-in length corresponds to using the first two weeks of the electricity market data to initialize the parameters for ADEPT-M. The default parameters used in sci-multiflow (Montiel et al. 2018) are chosen for ADWIN.

Fig. 5 shows the 24-hour moving average, which was used to compute the state of the electricity price at each time-stamp. The vertical lines depict the detected changepoints by ADEPT-M (dashed line) and ADWIN (dotted line). There is no ground-truth associated with the electricity pricing data; therefore, the conclusions drawn are all based on Fig. 5. The first thing to notice is that ADEPT-M and ADWIN seem to consistently flag changes at similar locations. Furthermore, Fig. 5 shows two large spikes slightly before 30,000 and 40,000, which are detected by ADEPT-M but not by ADWIN. These results are encouraging, and provide empirical evidence to support the claim that ADEPT-M is an attractive choice for real-world data streams. Furthermore, the results of this paper have shown that modeling a data streams dependencies using Markov transition matrices has merit across a broad range of applications.

Fig. 5

Plot of the 24-hour moving average for the NSW electricity price. The vertical lines represent the detections made by ADEPT-M (dashed) and ADWIN (dotted)

8 Conclusions

This article introduced ADEPT-M which, to the best of our knowledge, is the first attempt at developing a streaming change detector for Markov transition matrices in the continuous monitoring paradigm. This problem is especially challenging since common detectors have parameters that are difficult to set in the multiple changepoint setting – an issue that is exacerbated when monitoring a matrix for changes. ADEPT-M has few control parameters, which do not depend on the number of changepoints nor their magnitudes, and empirical evidence shows that the method is fairly robust to the choice of their values.

ADEPT-M requires three values to be specified: the length of the grace period G, the significance level $\alpha$ and the step-size $\eta$. The value G can be specified to provide a lower bound on ADEPT-M’s $ARL_0$, which is an attractive feature. Setting ${\alpha }$ approximates the ${ARL_0}$ of ADEPT-M, which is done using a novel moment matching technique to construct the detector’s control limits. The significance level ${\alpha }$ has a probabilistic interpretation; whereas other methods provide approximations of ${ARL_0}$ by assuming the size of the changepoint they are looking to detect is known. This is a nonsensical assumption in the continuous monitoring setting. Recent literature has investigated ways of tuning ${\eta }$, and empirical evidence shows that a range of values lead to desirable behavior of the FFs.

To conclude, we discuss the limitations of ADEPT-M and provide directions for future research. ADEPT-M places a first-order Markov assumption on the data stream– an assumption that should be checked in practice. Assumptions on the state-space also limit the applicability of ADEPT-M. The state-space is assumed known, is comprised of a discrete set of states, and does not evolve over time. Future work will modify ADEPT-M to handle state-spaces whose cardinality changes over time. That is, in addition to detecting changepoints, ADEPT-M will be able to identify if a state in the chain has expired, or be able to handle the emergence of a new state. Creating a streaming detector for continuous-time Markov chains is also being considered.