Contributions to $ZZV^*$ ($V=\gamma ,Z,Z'$) couplings from CP violating flavor changing couplings

Abstract

The one-loop contributions to the trilinear neutral gauge boson couplings $ZZV^*$ ($V=\gamma ,Z,Z'$), parametrized in terms of one CP-conserving $f_5^{V}$ and one CP-violating $f_4^{V}$ form factors, are calculated in models with CP-violating flavor changing neutral current couplings mediated by the Z gauge boson and an extra neutral gauge boson $Z'$. Analytical results are presented in terms of Passarino-Veltman scalar functions. Constraints on the vector and axial couplings of the Z gauge boson $\left| g_{{VZ}}^{tu}\right| < 0.0096$ and $\left| g_{{VZ}}^{tc}\right| <0.011$ are obtained from the current experimental data on the $t\rightarrow Z q$ decays. It is found that in the case of the $ZZ\gamma ^*$ vertex the only non-vanishing form factor is $f_5^{\gamma }$, which can be of the order of $10^{-3}$, whereas for the $ZZZ^*$ vertex both form factors $f_5^{Z}$ and $f_4^{Z}$ are non-vanishing and can be of the order of $10^{-6}$ and $10^{-5}$, respectively. Our estimates for $f_5^{\gamma }$ and $f_5^{Z}$ are smaller than those predicted by the standard model, where $f_4^{Z}$ is absent up to the one loop level. We also estimate the $ZZ{Z'}^{*}$ form factors arising from both diagonal and non-diagonal $Z'$ couplings within a few extension models. It is found that in the diagonal case $f_{5}^{Z'}$ is the only non-vanishing form factor and its real and imaginary parts can be of the order of $10^{-1}$–$10^{-2}$ and $10^{-2}$–$10^{-3}$, respectively, with the dominant contributions arising from the light quarks and leptons. In the non-diagonal case $f_{5}^{Z^\prime }$ can be of the order of $10^{-4}$, whereas $f_4^{Z'}$ can reach values as large as $10^{-7}$–$10^{-8}$, with the largest contributions arising from the $Z'tq$ couplings.

1 Introduction

Trilinear gauge boson couplings (TGBCs) have long been the subject of considerable interest both theoretically and experimentally. In the experimental area, constraints on the corresponding form factors were first obtained at the LEP [1,2,3] and the Tevatron [4,5,6] colliders, whereas the current bounds were extracted from the LHC data at 8 TeV [7,8,9] and 13 TeV [10,11,12] by the ATLAS and CMS collaborations. Among TGBCs are of special interest the ones involving only neutral gauge bosons, namely, the trilinear neutral gauge boson couplings (TNGBCs) $ZZV^*$ and $Z\gamma V^*$ ($V=Z$,$\gamma$), which can only arise up to the one-loop level in renormalizable theories and have been widely studied within the standard model (SM) and beyond. The SM contributions to TNGBCs were studied in Refs. [13, 14], whereas new physics contributions have been studied within several extension models, such as the minimal supersymmetric standard model (MSSM) [13,14,15], the CP-violating two-Higgs doublet model (2HDM) [16,17,18], models with axial and vector fermion couplings [16], models with extended scalar sectors [19], and also via the effective Lagrangian approach [20]. In the theoretical side, the phenomenology of TNGBCs at particle colliders was widely studied long ago [15, 21,22,23,24,25,26,27] and also has been of interest lately [28,29,30,31]. Even more, study of the potential effects of TNGBCs at future colliders has been the source of renewed interest very recently [32,33,34,35,36]. TNGBCs, which require one off-shell gauge boson at least to be non-vanishing due to Bose statistics, are induced through dimension-six and dimension-eight operators [13, 20, 37, 38] and can be parametrized in a model independent way by two CP-even and two CP-odd form factors. In the SM, only the CP-conserving form factors arise at the one-loop level of perturbation theory, whereas the CP-violating ones are absent at this order and require new sources of CP violation [13, 37]. In the SM, CP violation is generated via the Cabbibo–Kobayashi–Maskawa (CKM) mixing matrix, though the respective amount is not enough to explain the asymmetry between matter and anti-matter in the universe, i.e. the so-called baryogenesis problem. Therefore, new sources of CP violation are required, which is in fact one of the three Sakharov’s conditions to explain the baryon asymmetry of the universe [39]. In this work we are interested in the study of possible CP-violating effects in the TNGBCs via tree-level flavor changing neutral currents (FCNCs) mediated by the Z gauge boson [40], which are forbidden in the SM but can arise in several SM extensions [41, 42]. The possible effects of Z-mediated FCNC couplings on CP-conserving TNGBCs have already been studied [13], nevertheless, possible contributions to the CP-violating ones have not been reported yet to our knowledge. These new contributions are worth studying as they could shed some light in the path to a more comprehensive SM extension.

Possible evidences of new heavy gauge boson have been searched for at the LHC by the CMS collaboration [43], which has been useful to set bounds on the masses of new neutral and charged heavy vector bosons. Such particles are predicted by a plethora of SM extensions with extended gauge sector, for instance, little Higgs models [44, 45], 331 models [46], left-right symmetric models [47], etc. Some of these models allow tree-level FCNCs mediated by a new neutral gauge boson, denoted from now on by $Z^{\prime }$ [48], which means that CP-violating contributions to $VZZ'^*$ couplings ($V=\gamma$, Z) are possible. To our knowledge TNGBCs with new neutral bosons have not received much attention in the literature up to now, though decays of the kind $Z^{\prime }\rightarrow VZ$ ($V=\gamma$,Z) [49] and $Z^{\prime }\rightarrow \gamma A_H$ [50] were already studied. Here $A_H$ stands for a heavy photon.

In this work we present a study of the one-loop contributions to the most general TNGBCs $ZZV^*$ ($V=\gamma$, Z, $Z^{\prime }$) arising from a generic model allowing tree-level FCNCs mediated by the SM Z gauge boson and a new heavy neutral gauge boson $Z'$. The rest of this presentation is as follows. In Sect. 2 we present a short review of the analytical structure of TNGBCs along with the theoretical framework of the FCNCs Z and $Z'$ couplings via a model independent approach. Section 3 is devoted to the calculation of the one-loop contributions to the CP-conserving and CP-violating $ZZV^*$ ($V=\gamma$, Z, $Z^{\prime }$) couplings, for which we use the Passarino-Veltman reduction scheme. In Sect. 4 we present the numerical analysis and discussion, whereas the conclusions and outlook are presented in Sect. 5.

2 Theoretical framework

2.1 Trilinear neutral gauge boson couplings

We now turn to discuss the Lorentz structure of TNGBCs, which are induced by dimension-six and dimension-eight operators. In this work we only focus on the contribution of dimension-six operators as it is expected to be the dominant one. In particular, the TNGBC $ZZV^*$ ($V=\gamma$, Z) coupling can be parametrized by two form factors:

$$\begin{aligned} \varGamma _{ZZV^*}^{\alpha \beta \mu }\left( p_1,p_2,q\right)&= \frac{i (q^2-m_V^2)}{m_Z^2}\Big [f_4^V\left( q^\alpha g^{\mu \beta }+q^\beta g^{\mu \alpha }\right) \nonumber \\&\quad -f_5^V \epsilon ^{\mu \alpha \beta \rho }\left( p_1 -p_2\right) _{\rho } \Big ], \end{aligned}$$

(1)

where we have followed Ref. [13], with the notation for the gauge boson four-momenta being depicted in Fig. 1. From Eq. (1) it is evident that when the $V^*$ gauge boson becomes on-shell ($q^2=m_V^2$), $\varGamma _{ZZV^*}^{\alpha \beta \mu }\left( p_1,p_2,q\right)$ vanishes, which is due to Bose statistics and angular momentum conservation. The general form of this vertex for three off-shell gauge bosons can be found in [20, 37]. The form factor $f_5^V$ is CP-conserving, whereas $f_4^V$ is CP-violating. The former is the only one induced at the one-loop level in the SM via a fermion loop since $W^\pm$ boson loops give vanishing contributions [13]. It was found that $f_5^V$ decreases quickly as $q^2$ becomes large [13]. The current bounds on the form factors $f_4^V$ and $f_5^V$ ($V=Z$, $\gamma$) were obtained by the CMS collaboration at $\sqrt{s}=13$ TeV [12]:

$$\begin{aligned} -0.00066<&f_4^Z<0.0006, \end{aligned}$$

(2)

$$\begin{aligned} -0.00055<&f_5^Z<0.00075, \end{aligned}$$

(3)

$$\begin{aligned} -0.00078<&f_4^\gamma <0.00071, \end{aligned}$$

(4)

$$\begin{aligned} -0.00068<&f_5^\gamma <0.00075. \end{aligned}$$

(5)

Fig. 1

Nomenclature for the TNGBCs $ZZV^*$ ($V=\gamma$, Z, $Z'$)

These constrains are of the order of the SM prediction for the CP-conserving form factors [13]. Thus, corrections to the form factors $f_5^V$ and $f_4^V$ ($V=\gamma$, Z) from models of new physics might play an important role.

As far as TNGBCs with new gauge bosons are concerned, they remain almost unexplored. For our purpose, following Eq. (1), we will parametrize the $ZZ{Z^{\prime }}^*$ coupling as follows

$$\begin{aligned} \varGamma _{ZZ{Z^{\prime }}^*}^{\alpha \beta \mu }\left( p_1,p_2,q\right)&= \frac{i q^2}{m_{Z^{\prime }}^2}\Big [f_4^{Z'}\left( q^\alpha g^{\mu \beta }+q^\beta g^{\mu \alpha }\right) \nonumber \\&\quad -f_5^{Z'} \epsilon ^{\mu \alpha \beta \rho }\left( p_1 -p_2\right) _{\rho } \Big ], \end{aligned}$$

(6)

where we only consider the contributions of the dimension-six operators given in Ref. [37] and have replaced the electromagnetic $F_{\mu \nu }$ tensor by $Z'_{\mu \nu }=\partial _\mu Z'_{\nu } -\partial _\nu Z'_{\mu }$ in the operator basis that induce the $ZZ\gamma ^*$ vertex. We also set the energy scale that corrects the operator dimension to the new physics scale $m_{Z'}$. Of course, the form factor $f_4^{Z'}$ ($f_5^{Z'}$) is CP violating (CP-conserving). We also note in Eq. (6) that this TNGBC does not vanish for an on-shell $Z'$ gauge boson. In fact, the $Z'$ gauge boson can decay into a Z gauge boson pair if kinematically allowed. We will see below that our calculation is consistent with the Lorentz structure presented in Eq. (6).

2.2 FCNCs mediated by the Z and $Z'$ gauge bosons

Beyond the SM, there are some extension theories that allow FCNC couplings mediated by the Z gauge boson [41, 42]. Such an interaction can be expressed by the following Lagrangian

$$\begin{aligned} {\mathcal {L}}&=-\frac{e}{2 s_W c_W}Z^\mu {\overline{F}}_{i}\gamma _\mu \left( {g^{i}_{VZ}}-\gamma ^5g^i_{AZ} \right) F_i \nonumber \\&\quad -\frac{e}{2 s_W c_W}Z^\mu {\overline{F}}_{i}\gamma _\mu \left( {g^{ij}_{VZ}}-\gamma ^5{g^{ij}_{AZ}} \right) F_j {,} \end{aligned}$$

(7)

where $F_{i,j}$ are SM fermions in the mass eigenbasis. Here $g^{i}_{VZ,AZ}$ are the diagonal SM couplings, whereas the non-diagonal couplings $g^{ij}_{VZ,AZ}$ $(i\ne j)$ will be taken as complex since we are interested in the CP-violating contribution. The latter must fulfil $g^{ij*}_{VZ,AZ}=g^{ji}_{VZ,AZ}$ because of their hermiticity. It is also customary to express the Lagrangian of Eq. (7) in terms of the left- and right-handed projectors $P_L$ and $P_R$, with the chiral couplings denoted by $\epsilon ^Z_{L_{ij}, R_{ij}}$, which are given in terms of the vector and vector-axial couplings $g^{ij}_{VZ,AZ}$ as follows

$$\begin{aligned} g^{ij}_{VZ,AZ}= \frac{\epsilon ^Z_{L_{ij}}\pm \epsilon ^Z_{R_{ij}}}{2}. \end{aligned}$$

(8)

Below we will use both the $g^{ij}_{VZ,AZ}$ and $\epsilon ^Z_{L_{ij},R_{ij}}$ parametrizations. The former is useful for the purpose of comparison with previous works, whereas the latter is best suited for our numerical analysis.

Possible phenomenological implications of FCNC couplings mediated by the Z gauge boson have been studied within the SM [51,52,53,54], fourth-generation models [51, 52, 55,56,57], See-Saw models [58], etc. Such FCNC couplings have been constrained via the $b\rightarrow s$ transition [41, 42], Kaon decays [59, 60], $B-{\overline{B}}$ mixing [55], and $B^0$ decays [61, 62]. More, recently constraints on FCNC top quark decays $t\rightarrow q Z$ were reported by the ATLAS Collaboration at $\sqrt{s}=13$ TeV [63].

As for models with FCNC mediated by a new neutral gauge boson, which we generically have denoted by $Z'$, they have been widely studied in the literature [64, 65]. In Table 1 we present a summary of some of the more popular models that predict a new $Z'$ gauge boson.

Table 1 Models in which there is a new neutral gauge boson with FCNC couplings [64]

To describe the FCNC $Z'$ couplings we follow the formalism presented in [48, 64] and introduce an effective Lagrangian analogue to that of Eq. (7) in terms of the chiral couplings $\epsilon ^{Z'}_{L_{ij}, R_{ij}}$, where i and j now run over all the SM fermions $f_{SM}=\nu _i,\ell _i,u_i,d_i$. though there can also be new hypothetical fermions. We thus write

$$\begin{aligned} {\mathcal {L}}^{FCNC}_{Z'}=-g_{Z'} \sum _{i=f_{SM}} Z'_\mu \bar{{\mathbf {F}}}_i \gamma ^\mu \left( {\varvec{\epsilon }}^{Z'}_{L_{i}} P_L + {\varvec{\epsilon }}^{Z'}_{R_{i}} P_R\right) {{\mathbf {F}}}_i, \end{aligned}$$

(9)

where ${{\mathbf {F}}}_i$ is a massive fermion triplet in the flavor basis, ${{\mathbf {F}}}_\ell ^T=(e,\mu ,\tau )$, ${{\mathbf {F}}}_d^T=(d,s,b)$, and ${{\mathbf {F}}}_d^T=(u,c,t)$, with $\varvec{\epsilon }^{Z'}_{L_{i}}$ and $\varvec{\epsilon }^{Z'}_{R_{i}}$ being $3\times 3$ matrices containing the corresponding $Z'$ couplings. We will focus on the quark up-type sector since we expect that the largest contribution to TNGBCs arise from the top quark, which will become evident in Sect. 3. As it was pointed out in Ref. [48], we assume that the $Z'$ couplings to down-type quarks d, charged leptons $\ell$ and neutrinos $\nu$ are flavor-diagonal and family-universal, namely, $\varvec{\epsilon }^{Z'}_{L_{i},R_{i}}=Q^{i}_{L,R}{\mathbf {I}}_{3\times 3}$ for $i=d,\ell ,\nu$, where ${\mathbf {I}}_{3\times 3}$ is the identity matrix and $Q^i_{L,R}$ are the respective chiral charges. As far as the couplings of the $Z'$ gauge boson to up-type quarks are concerned, we assume that they are family non-universal and are given in the flavor basis as

$$\begin{aligned} \varvec{\epsilon }^{Z'}_{L_u}=Q^u_L\left( \begin{array}{ccc}1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} x\end{array}\right) , \quad \varvec{\epsilon }^{Z'}_{R_u}=Q^u_R{\mathbf {I}}_{3\times 3}. \end{aligned}$$

(10)

Thus, non-universal couplings are only induced through left-handed up-type quarks, with x a parameter that characterizes the size of the FCNCs and will be taken as $x\lesssim {\mathcal {O}}(1)$. The chiral $U'(1)$ charges of the up-type quarks $Q^{u}_{L,R}$ differ in each model as shown in Table 2.

Table 2 Chiral charges for the models with a new heavy neutral gauge boson of Table 1. A detailed discussion about the determination of these couplings can be found in Ref. [48]

After rotating to the mass eigenstates, we obtain the left- and right-handed up quark fields in the mass eigenbasis via the ${\mathbf {V}}_{L_u}$ and ${\mathbf {V}}_{R_u}$ matrices respectively. Thus the up-quark term of the Lagrangian of Eq. (9) reads

$$\begin{aligned} {\mathcal {L}}&= -g_{Z'} Z'_\mu \bar{{{\mathbf {F}}}}_u^M \gamma _\mu \Big ({\mathbf {V}}^\dagger _{L_u} \varvec{\epsilon }^{Z'}_{L_{u}}{\mathbf {V}}_{L_u} P_L \nonumber \\&\quad + {\mathbf {V}}^\dagger _{R_u}\varvec{\epsilon }^{Z'}_{R_{u}}{\mathbf {V}}_{R_u} P_R\Big ){{\mathbf {F}}}_u^M, \end{aligned}$$

(11)

where the superscript M denotes the mass eigenbasis. For simplicity we will drop this superscript below and assume that we are referring to the fermions in the mass eigenstate basis. In general ${\mathbf {B}}^u_L\equiv {\mathbf {V}}^\dagger _{L_u}\epsilon ^{Z'}_{L_u} {\mathbf {V}}_{L_u}$ will be non-diagonal. Since no mixing in the down-quark sector is assumed we will have ${\mathbf {V}}_{CKM}={\mathbf {V}}^\dagger _{L_u}{\mathbf {V}}_{L_d}={\mathbf {V}}^\dagger _{L_u}$ [48]. Therefore, the flavor mixing will be determined by the CKM matrix:

$$\begin{aligned} {\mathbf {B}}^u_L&\equiv {\mathbf {V}}_{{CKM}}\varvec{\epsilon }^{Z'}_{L_u} {\mathbf {V}}_{{CKM}}^\dagger \nonumber \\&\approx \left( \begin{array}{c@{\quad }c@{\quad }c}1 &{} (x-1)V_{ub}V^*_{cb} &{} (x-1)V_{ub}V^*_{tb} \\ (x-1)V_{cb}V^*_{ub} &{} 1 &{} (x-1)V_{cb}V^*_{tb} \\ (x-1)V_{tb}V^*_{ub} &{} (x-1)V_{tb}V^*_{cb} &{} x\end{array}\right) , \end{aligned}$$

(12)

where we have used the unitarity conditions of ${\mathbf {V}}_{{CKM}}$. As for the right-handed couplings ${\mathbf {B}}^u_R\equiv {\mathbf {V}}^\dagger _{R_u}\epsilon ^{Z'}_{R_u} {\mathbf {V}}_{R_u}$, it is easy to see that they are flavor-diagonal.

The gauge coupling $g_{Z'}$ is the same as that of the SM for the Z gauge boson in the sequential Z model, namely, $g_{Z'}=e/(2s_Wc_W)$, whereas in the remaining models of Table 1, it is given by

$$\begin{aligned} g_{Z'}=\sqrt{\frac{5}{3}}\frac{e}{c_W}\lambda _g^{1/2}, \end{aligned}$$

(13)

where $\lambda _g\sim {\mathcal {O}}(1)$. Below we will assume that $\lambda _g=1$. Constraints on FCNCs arise from $D^0-\overline{D^0}$ mixing [48, 66], single top-quark production at the LHC [67] and a simple ansatz analysis [68]. Implications of FCNC of a new neutral gauge boson $Z'$ have been studied in leptonic decays of the Higgs boson and the weak bosons [69], $tZ'$ production at the LHC [70], $Z'$ decays [71], $B_s$ and $B_d$ decays [72], etc.

3 Analytical results

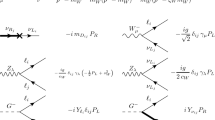
We now turn to present the calculation of the contribution to the TNGBCs $ZZV^*$ ($V=Z$,$\gamma , Z'$) arising from complex FCNC couplings mediated by the SM Z gauge boson and a new neutral heavy gauge boson $Z'$ as shown in Eqs. (7) and (11), respectively. This would allow non-vanishing CP-violating form factors. For our calculation we will assume conserved vector currents and consider Bose symmetry [13]. This last condition will allows us to obtain all the Feynman diagrams contributing to the TNGBCs. We will see, however, that we only need to calculate the three generic Feynman diagrams depicted in Fig. 2 since the amplitudes of the additional diagrams follow easily. For the calculation of the loop amplitudes we use the Passarino–Veltman reduction scheme with the help of the FeynCalc package [73].

Fig. 2

Generic Feynman diagrams required for the contribution of FCNC couplings to TNGBCs $ZZV^*$ and $Z\gamma V^*$ ($V=Z$,$\gamma , Z'$)

3.1 $ZZ\gamma ^*$ coupling

In this case there are 4 contributing Feynman diagrams, but due to gauge invariance we only need to calculate the amplitude of diagram 2a ${\mathcal {M}}^{\alpha \beta \mu }_2$ since the amplitudes of the remaining diagrams are easily obtained as follows. There is an additional diagram that is obtained after the exchange $f_i\leftrightarrow f_j$ so its amplitude follows from ${\mathcal {M}}^{\alpha \beta \mu }_2$ after exchanging the fermion masses ${\mathcal {M}}^{\alpha \beta \mu }_2(f_i\leftrightarrow f_j)$. We also need to add a pair of diagrams where the Z gauge bosons are exchanged, which means that their total amplitude can be obtained from that of the two already described diagrams after the exchange $p_{1\mu }\leftrightarrow p_{2\nu }$ is done. We note that it is not possible to induce CP violation in the $ZZ\gamma ^*$ coupling, which indeed was verified in our explicit calculation. Therefore there are only contributions to the form factor $f_5^\gamma$, which can be written as

$$\begin{aligned} f_{5}^\gamma = -\sum _{i}\sum _{j\ne i}\frac{N_i Q_i e^2 m_Z^2 \mathrm{Re}\left( g_{{AZ}}^{ij*} g_{{VZ}}^{ij} \right) }{8 \pi ^2 s_W^2 c_W^2 \left( q^2-4m_Z^2\right) ^2 q^2} R_{ij}, \end{aligned}$$

(14)

where $m_i$, $N_{i}$ and $Q_i$ are the mass, color number and electric charge of the fermion $f_i$. Note that $Q_j=Q_i$ since we are considering neutral currents. The analytical expression for $R_{ij}$ is somewhat cumbersome and is presented in Appendix A in terms of Passarino–Veltman scalar functions. We have verified that Eq. (14) reduces to that reported in Ref. [13] for real FCNC couplings of the Z gauge boson.

3.1.1 Asymptotic behavior

It is straightforward to obtain the high-energy limit $q^2\gg m_i^2$, $m_j^2$, $m_Z^2$

$$\begin{aligned} f_{5}^{\gamma }\approx -\sum _{i}\sum _{j\ne i} \frac{e^2 Q_i N_i m_Z^2 \mathrm{Re}\left( g_{{AZ}}^{ij*} g_{{VZ}}^{ij} \right) }{4 \pi ^2 q^2 c_W^2 s_W^2}, \end{aligned}$$

(15)

which agrees up to terms of the order $q^{-2}$ with the one reported in [13] for the CP-conserving case ($m_i=m_j$), though we must consider a factor of 1/2 as we are counting twice the number of Feynman diagrams (our results include the contribution of the diagrams with the exchange $f_i \leftrightarrow f_j$). It is evident that $f_{5}^{\gamma }\rightarrow 0$ in the high-energy limit as required by unitarity.

In the scenario where an ultra heavy fermion runs into the loop $m_i^2\gg q^2$, $m_Z^2$, $m_j^2$ must be worked out more carefully as the expansion of the two- and three-point scalar Passarino-Veltman functions around small $m_j$ diverge. This scenario could arise in 331 model [74] or little Higgs models [45], for instance, where new heavy quarks and neutrinos are predicted.

3.2 $ZZZ^*$ coupling

The calculation of this coupling is more intricate than the previous one since there are 36 contributing Feynman diagrams, though we only need to calculate the three generic Feynman diagrams of Fig. 2, which by Bose symmetry must be complemented with the diagrams obtained by performing six permutations of four-momenta and Lorentz indices as well as the exchange of the fermions running into the loops. In this case there are both CP-violating and CP-conserving form factors. The former is due to the fact that the virtual boson is assumed to have complex FCNC couplings. As for the CP-conserving form factor $f^{Z}_{5}$, it can be written as

$$\begin{aligned} f_5^Z&=-\sum _{i}\sum _{j\ne i}\frac{e^2 N_i m_Z^2}{16 \pi ^2 c_W^3 s_W^3 \left( q^2-4 m_Z^2\right) } \nonumber \\&\quad \times \Bigg \{ g^i_{{AZ}} \left( \left| g_{{AZ}}^{ij}\right| ^2+\left| g_{{VZ}}^{ij}\right| ^2\right) \left( R_{1ij}+R_{2ij}\right) \end{aligned}$$

(16)

$$\begin{aligned}&\quad +2g^i_{{VZ}}\mathrm{Re}\left( g_{{AZ}}^{ij*} g_{{VZ}}^{ij} \right) \left( R_{1ij}-R_{2ij}\right) \nonumber \\&\quad +g^i_{{AZ}} \left[ \left| g_{{AZ}}^{ij}\right| ^2-\left| g_{{VZ}}^{ij}\right| ^2\right] R_{3ij}+\left( i \leftrightarrow j\right) \Bigg \}, \end{aligned}$$

(17)

where the $R_{kij}$ ($k=1,2,3$) functions are presented in Appendix A in terms of Passarino–Veltman scalar functions. This results is in agreement with that reported in Ref. [13] for real FCNC couplings of the Z gauge boson.

As for the CP-violating form factor $f_4^Z$, it reads

$$\begin{aligned} f_4^Z&=- \sum _{i}\sum _{j\ne i}\frac{N_i e^2 m_i m_j m_Z^2 }{24\pi ^2 c_W^3 s_W^3 \left( q^2-m_Z^2\right) \left( q^2-4 m_Z^2\right) q^2}\nonumber \\&\quad \times \mathrm{Im}\left( g_{{AZ}}^{ij*} g_{{VZ}}^{ij} \right) g^i_{{AZ}} S_{ij}, \end{aligned}$$

(18)

where $S_{ij}$ is presented in Appendix A. It is easy to see that $f_4^Z$ vanishes for real couplings, which is also true if we consider the same fermion running into the loop ($i=j$). Thus, a non-vanishing $f_{4}^Z$ requires complex FCNC couplings. Furthermore, we can also see that we need different complex phases for $g_{{VZ}}^{ij}$ and $g_{{AZ}}^{ij}$ to obtain a non-vanishing CP-violating form factor. Since $f_{4}^Z$ is proportional to $m_i m_j$ we expect that the main contribution comes from FCNC couplings associated with the top quark. We would like to stress that the result of Eq. (18) has never been reported in the literature.

3.2.1 Asymptotic behavior

As we did it with the $ZZ\gamma ^*$ vertex, we study the high-energy limit $q^2\gg m_i^2$, $m_j^2$, $m_Z^2$

$$\begin{aligned} f_{5}^Z&\approx - \sum _{i}\sum _{j\ne i}\frac{e^2 N_i m_Z^2 }{8 \pi ^2 q^2 c_W^3 s_W^3} \left( g_{{AZ}}^{i}\left( \left| g_{{AZ}}^{ij}\right| ^2 +\left| g_{{VZ}}^{ij}\right| ^2\right) \right. \nonumber \\&\quad \left. +2 g_{{VZ}}^{i} \mathrm{Re}\left( g_{{AZ}}^{ij*} g_{{VZ}}^{ij} \right) \right) . \end{aligned}$$

(19)

Our result for $f_{5}^Z$ also reproduces the one reported in Ref. [13] for the CP-conserving case ($m_i=m_j$), though this time we must consider a factor of 1/6 as we are considering twice the three kinds of Feynman diagrams of Fig. 2 by the exchange $m_i\leftrightarrow m_j$. In ths case we also observe that $f_{5}\rightarrow 0$ in the high-energy limit, which is consistent with unitarity. The same is true for the CP-violating form factor $f_{4}^Z$, which behaves in the high-energy limit as $f_4^Z\sim 1/q^4$, since $S_{ij}\sim q^2$ in this limit.

In the case $m_i^2\gg q^2$, $m_Z^2$, $m_j^2$, both form factors diverge similar as in the case of the $ZZ\gamma ^*$ vertex.

3.3 $ZZZ^{\prime *}$ coupling

For the sake of completeness we now consider a $Z'$ gauge boson with complex FCNCs couplings and calculate the corresponding contributions to the TNGBC $ZZZ^{\prime *}$. We first present the diagonal case, where there is no flavor violation. Since $m_i=m_j$, there is only one independent diagram in Fig. 2 and we only need to add one extra diagram obtained after the exchange $p_{1\mu }\leftrightarrow p_{2\nu }$. After some algebra, the CP-conserving form factor $f_5^{Z'}$ reads

$$\begin{aligned} f_{5}^{Z^\prime }&=-\sum _i\frac{ e N_i m_{Z'}^2}{16 \pi ^2 c_W^2 s_W^2 q^2\left( q^2-4 m_Z^2\right) {}^2}\nonumber \\&\quad \times \Bigg \{g_{{AZ^\prime }}^i\Big [ (g_{{VZ}}^i)^{2}\ L_{1i} + (g_{{AZ}}^i)^2\ L_{2i} \Big ]\nonumber \\&\quad +g_{{VZ^\prime }}^i\ g_{{VZ}}^i\ g_{{AZ}}^i\ L_{3i}\Bigg \}, \end{aligned}$$

(20)

where the $L_{ji}$ ($j=1$, 2, 3) functions are presented in Appendix A. The CP-violating form factor $f_4^{Z'}$ is not induced at the one-loop level in this scenario.

As far as the non-diagonal case with complex FCNCs couplings, it requires more effort. Apart from the three generic Feynman diagram of Fig. 2, we must add those diagrams obtained after the exchanges $p_{1\mu }\leftrightarrow p_{2\nu }$ and $f_1 \leftrightarrow f_2$, so there are 12 contributing Feynman diagrams in total. However, we only need to calculate the amplitudes of the three generic diagrams. In this scenario both $f_{5}^{Z'}$ and $f_{4}^{Z'}$ form factors are non-vanishing. The CP-conserving form factor can be written as

$$\begin{aligned} f_5^{Z^\prime }=&- \sum _{i}\sum _{j\ne i}\frac{e N_i m_{Z'}^2}{16 \pi ^2 c_W^2 s_W^2 q^2 \left( q^2-4 m_Z^2\right) ^2} \nonumber \\&\quad \times \Bigg \{ 2g_{{AZ}}^i\Big [ \mathrm{Re} \left( g_{VZ}^{ij} g_{VZ'}^{ij*} \right) U_{1ij} \nonumber \\&\quad + \mathrm{Re} \left( g_{AZ'}^{ij} g_{AZ}^{ij*} \right) U_{2ij}\Big ]+2g_{VZ'}^i \mathrm{Re} \left( g_{VZ}^{ij} g_{AZ}^{ij*} \right) U_{3ij} \nonumber \\&\quad +2 g_{{VZ}}^i\Big [ \mathrm{Re} \left( g_{VZ}^{ij} g_{AZ'}^{ij*} \right) U_{4ij}+\mathrm{Re} \left( g_{VZ'}^{ij} g_{AZ}^{ij*} \right) U_{5ij} \Big ]\nonumber \\&\quad +g_{AZ'}^i\Big [\left| g_{{AZ}}^{ij}\right| ^2 U_{6ij}+\left| g_{{VZ}}^{ij}\right| ^2 U_{7ij}\Big ]\Bigg \}, \end{aligned}$$

(21)

whereas the CP-violating one reads

$$\begin{aligned} f_4^{Z^\prime }=&\sum _{i}\sum _{j\ne i}\frac{ e N_i m_{Z^\prime }^2}{12 \pi ^2 c_W^2 s_W^2 q^6 \left( q^2-4 m_Z^2\right) } \nonumber \\&\quad \times \Bigg \{ g_{VZ}^{i}\Big [ \mathrm{Im} \left( g_{VZ'}^{ij} g_{VZ}^{ij*} \right) T_{1ij}+ \mathrm{Im} \left( g_{AZ'}^{ij} g_{AZ}^{ij*} \right) T_{2ij}\Big ]\nonumber \\&\quad + g_{{AZ}'}^i\mathrm{Im} \left( g_{VZ}^{ij} g_{AZ}^{ij*} \right) T_{3ij} \nonumber \\&\quad + g_{AZ}^i\Big [ \mathrm{Im} \left( g_{AZ'}^{ij} g_{VZ}^{ij*} \right) T_{4ij} +\mathrm{Im} \left( g_{VZ'}^{ij} g_{AZ}^{ij*} \right) T_{5ij}\Big ] \Bigg \}, \end{aligned}$$

(22)

where the $U_{kij}$ ($k=1\ldots 7$) and $T_{kij}$ ($k=1\ldots 5$) functions are presented in Appendix A. We note that $f_5^{Z^\prime }$ ($f_4^{Z^\prime }$) depends only on the real (imaginary) part of the combinations of products of the vector and axial couplings. We also note that it is not necessary that both Z and $Z'$ gauge bosons have simultaneously complex FCNC couplings to induce the CP-violating form factor.

3.3.1 Asymptotic behavior

In the diagonal case the form factor $f_5^{Z'}$ can be written in the high-energy limit $q^2\gg m_i^2$, $m_j^2$, $m_Z^2$ as

$$\begin{aligned} f_5^{ Z'}&\simeq -\sum _i\frac{e^2 m_{Z'}^2 N_i }{32 \pi ^2 c_W^3 s_W^3 q^2}\Big \{g_{{AZ'}}^i \left( (g_{{AZ}}^i)^2+(g_{{VZ}}^i)^2\right) \nonumber \\&\quad +2 g_{{AZ}}^i\ g_{{VZ}}^i\ g_{{VZ^\prime }}^i\Big \}, \end{aligned}$$

(23)

whereas in the non-diagonal case we obtain

$$\begin{aligned} f_5^{Z'}&\simeq -\sum _{i}\sum _{j\ne i}\frac{e^2 m_{Z'}^2 N_i }{16 \pi ^2 c_W^3 s_W^3 q^2}\nonumber \\&\quad \times \Bigg \{g_{AZ'}^i \left( \left| g_{{AZ}}^{ij}\right| ^2+\left| g_{{VZ}}^{ij}\right| ^2\right) \nonumber \\&\quad +2 \Big [ g_{AZ}^i\Big ( \mathrm{Re}\left( g_{AZ'}^{ij}g_{AZ}^{ij*} \right) +\mathrm{Re}\left( g_{VZ}^{ij}g_{VZ'}^{ij*} \right) \Big )\nonumber \\&\quad +g_{VZ}^i \Big (\mathrm{Re} \left( g_{VZ'}^{ij} g_{AZ}^{ij*} \right) +\mathrm{Re} \left( g_{VZ}^{ij} g_{AZ'}^{ij*} \right) \Big )\nonumber \\&\quad +g_{VZ'}^i \mathrm{Re} \left( g_{VZ}^{ij} g_{AZ}^{ij*} \right) \Bigg ] \Big \} . \end{aligned}$$

(24)

We note that in both scenarios $f_5^{Z'}\sim m_{Z'}^2/q^2$, thereby decreasing quickly when $q^2\geqslant m_{Z'}^2$. However this effect is attenuated for $q^2\lesssim m_{Z'}^2$ due to the mass of the heavy $Z'$ boson. We also note that Eq. (24) reduces to Eq. (23) except by a factor of 6, which is due to the fact that the CP-violating form factor receives the contribution of twelve Feynman diagrams in the diagonal scenario instead of two as in the diagonal case.

On the other hand, the CP-violating form factor $f_4^{Z'}$ is of the order of $m_{Z'}^2/q^4$ in the high energy limit and decreases quickly as $q^2$ increases. The functions $T_{kij}$ behave in this limit as $T_{kij}\sim q^4$, therefore the form factor $f_4^{Z'}$ as functions of $q^2$ has the form $f_4^{Z'}\sim 1/q^4$, which is similar to the vertex $ZZZ^*$ in the high energy limit.

Furthermore, when $m_i^2\gg q^2$, $m_Z^2$, $m_j^2$ both form factors also show the same behavior observed in the case of the vertices $ZZ\gamma ^*$ and $ZZZ^*$.

4 Constraints on FCNC Z couplings

We would like to assess the magnitude of the new contributions to the $f_4^{V}$ and $f_5^{V}$ ($V=\gamma , Z, Z'$) form factors. It is thus necessary to obtain constraints on the FCNC Z couplings to obtain an estimate of the numerical values of such form factors. Since we expect that the main contributions arise from the FCNC couplings of the top quark, we use the current bounds on the branching ratios of the FCNC decays $t\rightarrow qZ$, where $q=c$, u [63] to constrain the $g_{{VZ},{AZ}}^{tq}$ couplings.

4.1 Constraints on the FCNC Z couplings from $t\rightarrow q Z$ decay

A comprehensive compilation of the branching ratios of top FCNC decays within the SM and several extension models can be found in [54]. In the case of tree-level FCNC Z couplings, the decay width $t\rightarrow qZ$ can be written in terms of the vector and axial couplings for negligible $m_q$ as follows

$$\begin{aligned} \varGamma _{t\rightarrow Zq}&=\frac{e^2 m_t^3}{64 \pi c_W^2 m_Z^2 s_W^2}\left( \left| g_{{AZ}}^{tq}\right| ^2+\left| g_{{VZ}}^{tq}\right| ^2\right) \nonumber \\&\quad \times \left( 1-\frac{m_Z^2}{m_t^2}\right) ^2 \left( 1+2 \frac{m_Z^2}{m_t^2}\right) . \end{aligned}$$

(25)

The current upper limits obtained by ATLAS collaboration at $\sqrt{s}=$ 13 TeV are: ${\mathcal {B}}(t\rightarrow uZ)< 1.7\times 10^{-4}$ and ${\mathcal {B}}(t\rightarrow cZ)< 2.4\times 10^{-4}$ with 95% C.L. [63]. Previous results at $\sqrt{s}=7$ TeV are also available [75]. The SM contribution to the $t\rightarrow cZ$ branching ratio is negligible: ${\mathcal {B}}\left( t\rightarrow cZ\right) \simeq 10^{-14}$ [54]. We thus obtain for the contribution of the FCNC couplings of the Z gauge boson:

$$\begin{aligned} {\mathcal {B}}\left( t\rightarrow qZ \right) =0.915699 \left( \left| g_{{AZ}}^{tq}\right| ^2+\left| g_{{VZ}}^{tq}\right| ^2\right) , \end{aligned}$$

(26)

which allows us to obtain the following limits

$$\begin{aligned} \left| g_{{AZ}}^{tu}\right| ^2+\left| g_{{VZ}}^{tu}\right| ^2< 1.8\times 10^{-4}, \end{aligned}$$

(27)

and

$$\begin{aligned} \left| g_{{AZ}}^{tc}\right| ^2+\left| g_{{VZ}}^{tc}\right| ^2<2.6\times 10^{-4}. \end{aligned}$$

(28)

Equations (27) and (28) can also be written in terms of the chiral couplings of Eq. (8).

We show in Fig. 3 the allowed areas on the $\left| g_{{AZ}}^{tq}\right|$ vs $\left| g_{{VZ}}^{tq}\right|$ and $|\epsilon _{R_{tq}}^Z|$ vs $|\epsilon _{L_{tq}}^Z|$ planes. The blue-solid (green-dashed) line corresponds to the $Z{\overline{t}}c$ ($Z{\overline{t}}u$) couplings. We observe that the FCNC couplings of the Z gauge boson can be as large as $10^{-1}$. In fact, if we assume $\left| g_{{AZ}}^{tq}\right| \simeq \left| g_{{VZ}}^{tq}\right|$, we obtain

$$\begin{aligned} \left| g_{{VZ}}^{tu}\right|< 0.0096,\quad \left| g_{{VZ}}^{tc}\right| <0.011, \end{aligned}$$

(29)

which in terms of the chiral coupling read

$$\begin{aligned} |\epsilon _{R_{tu}}^Z|<0.013, \quad |\epsilon _{R_{tc}}^Z|<0.016. \end{aligned}$$

(30)

Thus, our bounds are of the order of $10^{-2}-10^{-3}$, which are similar to the constraints on FCNC couplings of down quarks obtained from B and Kaon meson decays. For instance the constraint on the $\left| g_{{VZ}}^{bd}\right|$ coupling is at the $10^{-2}-10^{-3}$ level [41, 42, 55, 59, 62], whereas the $\left| g_{{VZ}}^{bs}\right|$ coupling is constrained to be below $10^{-1}$ [41]. In some extension models these couplings can be of the order of $10^{-4}-10^{-7}$ [60, 61].

Fig. 3

Allowed area with 95% C.L. in the $\left| g_{{AZ}}^{tq}\right|$ vs $\left| g_{{VZ}}^{tq}\right|$ (left) and $|\epsilon _{R_{tq}}^Z|$ vs $|\epsilon _{L_{tq}}^Z|$ (right) planes from the experimental bounds on $t\rightarrow Zq$ decays, for the $Z{\overline{t}}c$ and (solid-line boundaries) and $Z{\overline{t}}u$ (dashed-line boundaries) couplings

4.2 Constraints on the lepton flavor violating Z couplings from $Z\rightarrow \ell _i\ell _j$

Following the above approach, we now obtain constraints on the lepton flavor violating (LFV) couplings of the Z gauge boson from the experimental limits on the $Z\rightarrow \ell ^{\pm }\ell ^{\mp }$ decays, which have been obtained by the ATLAS and CMS collaborations: ${\mathcal {B}}\left( Z\rightarrow e\tau \right) <5.8 \times 10^{-5}$, ${\mathcal {B}}\left( Z\rightarrow \mu \tau \right) <2.4\times 10^{-5}$ at $\sqrt{s}=14$ TeV [76] and ${\mathcal {B}}\left( Z\rightarrow e\mu \right) < 7.3\times 10^{-7}-7.5\times 10^{-7}$ at $\sqrt{s}=8$ TeV [77, 78]. The decay width $Z\rightarrow \ell _i\ell _j$ is given by

$$\begin{aligned} \varGamma _{Z\rightarrow \ell _i\ell _j}=\frac{e^2 m_Z }{24 \pi c_W^2 s_W^2} \left( \left| g_{{AZ}}^{\ell _i \ell _j}\right| ^2+\left| g_{{VZ}}^{\ell _i \ell _j}\right| ^2\right) , \end{aligned}$$

(31)

and the corresponding branching ratio is

$$\begin{aligned} {\mathcal {B}} \left( Z\rightarrow \ell _i\ell _j \right) = 0.250277 \left( \left| g_{{AZ}}^{\ell _i \ell _j}\right| ^2+\left| g_{{VZ}}^{\ell _i \ell _j}\right| ^2\right) . \end{aligned}$$

(32)

If we assume that $\left| g_{{AZ}}^{\ell _i \ell _j}\right| \simeq \left| g_{{VZ}}^{\ell _i \ell _j}\right|$, we obtain with 95 % C.L.

$$\begin{aligned} \left| g_{{VZ}}^{\tau \mu }\right|<0.0069, \quad \left| g_{{VZ}}^{\tau e}\right|< 0.01, \quad \left| g_{{VZ}}^{\mu e}\right| <0.0012. \end{aligned}$$

(33)

We note that the constraints on $\left| g_{{VZ}}^{\tau e}\right|$ and $\left| g_{{VZ}}^{\mu e}\right|$ are less competitive to those obtained through the $\mu \rightarrow eee$ and $\tau ^{-}\rightarrow e^-\mu ^+\mu ^-$ decays [57], which yield $\left| g_{{VZ}}^{\tau e}\right| < 1.28\times 10^{-3}$ and $\left| g_{{VZ}}^{\mu e}\right| <3.05\times 10^{-6}$. As for the bound on $\left| g_{{VZ}}^{\tau \mu }\right|$, it is of the same order than the one obtained from the $\tau ^-\rightarrow \mu ^-\mu ^+\mu ^-$ decay, namely, $\left| g_{{VZ}}^{\tau \mu }\right| <1.295 \times 10^{-3}$ [57]. In our analysis below we consider the most stringent bounds, thus we will use the values reported in Ref. [57].

As far as the LFV Z couplings to neutrinos are concerned, there are no experimental data to obtain reliable constraints, so to obtain a rough estimate of these contributions we can assume couplings of the same order of magnitude than those used for the charged leptons. Nevertheless, the $f_4^{V}$ and $f_5^{V}$ form factors are mainly dominated by the contribution of the heaviest quarks, whereas the lepton contributions are negligibly.

Finally, in Table 3 we summarize the constraints on the FCNC Z gauge boson couplings that we will use in our numerical analysis, in terms of the corresponding chiral couplings.

Table 3 Bounds on the FCNC couplings of the Z gauge boson, with 95 % C.L., from the current experimental limits on FCNC Z decays. The second row stands for the limit when either $\epsilon _{R_{ij}}^Z$ or $\epsilon _{L_{ij}}^Z$ is taken as vanishing and the other one non-vanishing

5 Numerical analysis

We now turn to present the numerical evaluation of the TNGBCs. For the numerical analysis we evaluate the Passarino–Veltman scalar functions via the LoopTools [79] package and independently by the Collier [80] package, which give a good agreement. We first analyze the case of the $ZZV^*$ ($V=\gamma ,Z$) couplings. As a matter of convenience, we write the complex chiral FCNC Z couplings as

$$\begin{aligned} \epsilon ^{Z}_{L_{ij},R_{ij}}={{\overline{\epsilon }}}^{Z}_{L_{ij},R_{ij}} +i {{\tilde{\epsilon }}}^{Z}_{L_{ij},R_{ij}}, \end{aligned}$$

(34)

where the bar (tilde) denotes the real (imaginary) part of each coupling. The CP-violating phase can then be written as

$$\begin{aligned} \arctan \left( \phi _{L_{ij},R_{ij}}\right) =\frac{{{\tilde{\epsilon }}}^{Z}_{L_{ij},R_{ij}}}{{{\overline{\epsilon }}}^{Z}_{L_{ij},R_{ij}}}. \end{aligned}$$

(35)

We thus can write the real and imaginary terms that enter into the $f_4^{V}$ and $f_5^{V}$ ($V=\gamma , Z, Z'$) form factors [Eqs. (14)-(18)] as follows

$$\begin{aligned} \left| g_{{VZ},AZ}^{ij}\right| ^2= & {} \frac{1}{4}\left( \left( {{\overline{\epsilon }}}^{Z}_{L_{ij}}\pm {{\overline{\epsilon }}}^{Z}_{R_{ij}}\right) ^2 +\left( {{\tilde{\epsilon }}}^{Z}_{L_{ij}}\pm {{\tilde{\epsilon }}}^{Z}_{R_{ij}}\right) ^2 \right) , \end{aligned}$$

(36)

$$\begin{aligned} 2\mathrm{Re}\left( g_{{AZ}}^{ij*} g_{{VZ}}^{ij} \right)= & {} \frac{1}{2}\Big (\left( {{\overline{\epsilon }}}^{Z}_{L_{ij}}\right) ^2 - \left( {{\overline{\epsilon }}}^{Z}_{R_{ij}}\right) ^2+\left( {{\tilde{\epsilon }}}^{Z}_{L_{ij}}\right) ^2\nonumber \\&- \left( {{\tilde{\epsilon }}}^{Z}_{R_{ij}}\right) ^2\Big ), \end{aligned}$$

(37)

$$\begin{aligned} 2\mathrm{Im}\left( g_{{AZ}}^{ij*} g_{{VZ}}^{ij} \right)= & {} \left( {{\overline{\epsilon }}}^{Z}_{L_{ij}} {{\tilde{\epsilon }}}^{Z}_{R_{ij}}-{{\overline{\epsilon }}}^{Z}_{R_{ij}}{{\tilde{\epsilon }}}^{Z}_{L_{ij}} \right) . \end{aligned}$$

(38)

Below we will analyze the behavior of the $f_{4,5}^{V}$ form factors as functions of the ${{\overline{\epsilon }}}^{Z}_{L_{ij},R_{ij}}$ and ${{\tilde{\epsilon }}}^{Z}_{L_{ij},R_{ij}}$ parameters as well as the transfer momentum $q^2$ of the V gauge boson.

5.1 $ZZ\gamma ^*$ coupling

It is convenient to assume small phases of the FCNC Z couplings, namely, we consider that the imaginary parts of the left-handed couplings are smaller than ten percent of their real parts:

$$\begin{aligned} \phi _{L_{ij}}\simeq \frac{{{\tilde{\epsilon }}}^{Z}_{L_{ij}}}{{{\overline{\epsilon }}}^{Z}_{L_{ij}}}\le O\left( 10^{-1}\right) , \end{aligned}$$

(39)

whereas for the right-handed couplings we assume by simplicity that $\phi _{R_{ij}}=0$ (${{\tilde{\epsilon }}}^{Z}_{R_{ij}}=0$). As far as the size of the chiral couplings ${{\tilde{\epsilon }}}^{Z}_{L_{ij},R_{ij}}$ we consider the bounds shown in Table 3 to obtain an estimate of $f_5^\gamma$, which is the only non-vanishing $ZZ\gamma ^*$ form factor.

We show the behavior of the FCNC contributions to $f_5^\gamma$ as a function of the photon transfer momentum $q^2$ in Fig. 4, where we only plot the non-negligible imaginary and real parts arising from each fermion loop as well as their total sum. We find that the only non-negligible contributions arise from the up and down quarks, though the former are the only ones yielding a non-negligible imaginary part, which thus coincides with the total imaginary contribution. We have considered the parameter values of Table 3, but the curves shown in Fig. 4 exhibit a similar behavior for other parameter values: there is a shift upwards (downwards) when the chiral couplings values increase (decrease) as $f_5^\gamma$ is proportional to $\mathrm{Re}\left( g_{{AZ}}^{ij*} g_{{VZ}}^{ij} \right)$. We then conclude that the contributions to $f_5^\gamma$ arising from FCNCs Z couplings are expected to be considerably smaller than the SM contribution, which is of the order of $10^{-2}$.

Fig. 4

Behavior of the FCNC contributions to the $f_5^\gamma$ form factor as a function of the momentum of the photon for $\phi _{L_{ij}}=0.1$, $\phi _{R_{ij}}=0$, $|\epsilon ^{Z}_{R_{ij}}|=0.9|\epsilon ^{Z}_{L_{ij}}|$ and the $|\epsilon ^{Z}_{L_{ij}}|$ values shown in Table 3. Only the non-negligible contributions are shown: up quarks (tc, tu and cu) and down quarks (bs, bd and sd). The total imaginary contribution coincides with the respective up quark contribution since the down quark contribution (not shown in the plot) is negligible

5.2 $ZZZ^*$ coupling

In this case both $f_4^Z$ and $f_5^Z$ are non-vanishing. For our analysis we find it convenient to consider two scenarios:

• Scenario I (left- and right-handed couplings of similar size): $|{{\overline{\epsilon }}}^{Z}_{R_{ij}}|=0.9|{{\overline{\epsilon }}}^{Z}_{L_{ij}}|$, $\phi _{L_{ij}}=0.1$, and $\phi _{R_{ij}}=0$.

• Scenario II (dominating left-handed couplings): $|{{\overline{\epsilon }}}^{Z}_{R_{ij}}| \simeq 10^{-1}\times |{{\overline{\epsilon }}}^{Z}_{L_{ij}}|$, $\phi _{L_{ij}}=0.1$, and $\phi _{R_{ij}}=0$.

We do not consider the scenario with dominating right-handed couplings since there is no substantial change in the magnitude of the $ZZZ^*$ form factors as that observed in Scenario II. We show in Fig. 5 the behavior of the FCNC contributions to $f_5^Z$ as a function of the virtual Z transfer momentum $q^2$ in the two scenarios described above. Again we only show the real and imaginary parts arising from the up and down quarks along with the total contribution, though the imaginary part of the down quark contribution is negligible and is not shown in the plots. We observe that the largest values of $f_5^Z$ are of the order of $10^{-6}$, which are reached for smaller $q^2$ but decrease by one order of magnitude as $q^2$ becomes large. Again, the contribution to $f_5^Z$ from FCNC Z couplings is smaller than the SM contribution.

Fig. 5

Behavior of the FCNC contributions to the $f_5^Z$ form factor as a function of the momentum of the virtual Z gauge boson in the two scenarios discussed in the text. Only the non-negligible contributions are shown: up quarks (tc, tu and cu) and down quarks (bs, bd and sd). The total imaginary contributions coincide with the respective up quark contributions since the down quark contribution (not shown in the plot) is negligible

Fig. 6

Behavior of the $f_4^Z$ form factor as a function of the momentum |q| of the virtual Z gauge boson. We have extracted a factor of $\mathrm{Im}\left( g_{{AZ}}^{tc*} g_{{VZ}}^{qq'} \right)$ from the respective contribution. All other contributions not shown in the plots are well below the $10^{-10}$ level

We now analyze the $f_4^Z$ form factor, which is absent in the SM up to the one-loop level, which means that any sizeable excess can be attributed to new physics effects. We find that the only non-negligible contributions to $f_4^Z$ arise from the loops induced by the Ztc coupling, with the remaining up and down quark contributions being several orders of magnitude smaller. We thus show in the left plot of Fig. 6 the Ztc contribution to the $f_4^Z$ form factor as a function of the virtual Z four-momentum, whereas in the right plot we show the Zbs and Zbd contributions. We have extracted the factor $\mathrm{Im}\left( g_{{AZ}}^{qq'*} g_{{VZ}}^{qq'} \right)$, so for the Ztc contribution $f_4^Z$ is of the order of

$$\begin{aligned} |f_4^Z|\simeq |\mathrm{Im}\left( g_{{AZ}}^{tc*} g_{{VZ}}^{tc} \right) |\times 10^{-5}, \end{aligned}$$

(40)

for relatively small $||q||\sim 200$ GeV, but there is a decrease of up to two orders of magnitude as ||q|| becomes of the order of a few TeVs. All the remaining contributions are considerably suppressed.

5.3 $ZZZ^{'*}$ coupling

We now turn to the analysis of the CP-conserving $f_{5}^{Z'}$ and the CP-violating $f_4^{Z'}$ form factors for an off-shell $Z'$ boson. For the FCNCs couplings mediated by the Z gauge boson we consider the same scenarios analyzed in the case of the $ZZZ^*$ vertex. We thus use the constraints presented in Table 3, which were obtained from the data on $Z{\overline{f}}_if_j$ decays. Furthermore, for the $Z'$ couplings we use the interaction of Eq. (9), with the values of Table 2 for the chiral charges, along with $x=0.1$ and ${\phi _{L^\prime }}_{ij}=0.001$. Here x stands for the parameter characterizing the size of $Z'$ FCNC couplings and ${\phi _{L^\prime }}_{ij}$ is the CP-violating phase of the $Z'$ couplings to left-handed up quarks. Since all the models summarized in Table 2 give rise to similar results, we will only present the numerical results for the $Z_\eta$ model.

Fig. 7

Behavior of the $f_5^{Z^\prime }$ form factor as a function of the transfer momentum |q| (left plot) and the $m_{Z^\prime }$ mass (right plot) in the diagonal case

Fig. 8

Contour lines of the $f_5^{Z^\prime }$ form factor in the |q| vs $m_{Z'}$ plane in the diagonal case

We first analyze the behavior of the CP-conserving form factor $f_5^{Z'}$ in the scenario with no FCNCs (diagonal case). We show in Fig. 7 the behavior of $f_5^{Z^\prime }$ as a function of the heavy $Z'$ gauge boson transfer momentum $q^2$ (left plot) and the $m_{Z^\prime }$ mass (right plot). We observe that the dominant contributions arise from the light quarks and leptons, whereas the top quark contribution is the smaller one as its coupling with the $Z'$ gauge boson is proportional to the x parameter, which is taken of the order of $10^{-1}$. This behavior is also observed in the CP-conserving $ZZZ^*$ form factor in the diagonal case [13]. We also note that $f_5^{Z'}$ decreases for increasing transfer momentum |q|, but it increases for large values of $m_{Z^\prime }$. Since $f_5^{Z'}$ is proportional to $m_{Z^\prime }$ [see Eq. (20)], a similar behavior is expected in the non-diagonal case. In Fig. 8 we present the contour lines of the total real (left plot) and imaginary (right plot) parts of $f_5^{Z^\prime }$ in the |q| vs $m_{Z^\prime }$ plane. It is observed that at high energy, both real and imaginary parts of $f_5^{Z^\prime }$ are considerably small, of the order of $10^{-2}$ and $10^{-3}$, respectively, which is true even if the mass of the heavy boson is very large. For $m_{Z^\prime }\gg$ 3000 GeV and intermediate values of |q|, the value of the real part of $f_5^{Z^\prime }$ can be of the order of O(1), whereas the imaginary part is of the order of $10^{-2}$.

Fig. 9

Behavior of the $f_5^{Z^\prime }$ form factor in the non-diagonal case as a function of the transfer momentum |q| of the $Z'$ gauge boson

Fig. 10

Contour lines in the |q| vs $m_{Z'}$ plane of the real and imaginary parts of the $f_5^{Z^\prime }$ form factor in the non-diagonal case and scenario II

We now show in Fig. 9 the form factor $f_5^{Z^\prime }$ as function of the transfer momentum |q| of the $Z'$ gauge boson in the non-diagonal case. For the FCNCs couplings of the Z gauge boson, we consider both scenario I (left plot) and scenario II (right plot), which were also considered in the analysis of the $ZZZ^*$ vertex. As we are assuming only flavor violation in the up quark sector for the FCNCs mediated by the $Z'$ boson, we only plot this class of contributions. As in the analysis of the $ZZZ^*$ form factor, we only show the non-negligible contributions, which are those where the top quark runs into the loops. We observe that in both scenarios the real parts of the $Z'tc$ and $Z'tu$ contributions are of similar size, although the largest contribution is distinct in each case. We also find that in scenario I the real parts of the $Z'tc$ and $Z'tu$ contributions are of the same sign, but they are of opposite sign in scenario II. Thus, they tend to cancel each other out. As for the imaginary parts of the partial contributions, they exhibit a similar behavior in both scenarios, nevertheless there is a peak in the 600 GeV$<|q|<900$ GeV region, which is present in a distinct contribution in each scenario. We also show in Fig. 10 the contour lines in the |q| vs $m_{Z^\prime }$ plane of the real (left plot) and imaginary (right plot) parts of $f_5^{Z^\prime }$ in scenario II, where it is manifest the cancellation effect between the real parts of the $Z'tc$ and $Z'tu$ contributions for |q| around 900 GeV. In this scenario the form factor $f_5^{Z'}$ can be of the order of $10^{-6}$, though for intermediate |q| and large $m_{Z^\prime }$ it can reach values one order of magnitude larger. As for scenario I, the real and imaginary parts of $f_5^{Z'}$ are of the order $10^{-4}$ in general, but they could be larger for small energies and an ultra heavy $Z^\prime$.

It is also possible to induce the CP-violating form factor $f_4^{Z'}$ via FCNC Z and $Z'$ couplings. We find that the only non-negligible contributions arise from the $Z'tc$ and $Z'tu$ couplings, though the dominant contribution to both real and imaginary parts of $f_4^{Z'}$ is the $Z'tc$ one, which is one order of magnitude larger than the $Z'tu$ contribution. We present in Fig. 11 the form factor $f_4^{Z'}$ as a function of |q|. We observe that the real and imaginary parts behave in a rather similar way. As was the case for the $ZZZ^*$ CP-violating form factor, there is no considerable distinction between the results for scenario I and scenario II of the FCNC Z couplings, thus we only consider scenario I in our analysis. We also show in Fig. 12 the contour lines of the real part of $f_4^{Z'}$ in the |q| vs $m_{Z'}$ plane. The behavior of the imaginary part is similar as already stated. We note that at high energy $f_4^{Z'}$ can be of the order of $10^{-7}-10^{-8}$, though it can be one order of magnitude larger at low energy and for an ultra heavy $Z'$ gauge boson. In our numerical analysis we did not extract the complex phases as in the $ZZZ^*$ case, since the $f_4^{Z'}$ factors depends on five distinct combinations of all of the involved phases [see Eq. (22)].

Fig. 11

Behavior of the $f_4^{Z^\prime }$ form factor as a function of |q| in the non-diagonal case and scenario I

Fig. 12

Contour lines of the real part of $f_4^{Z^\prime }$ in the q vs $m_{Z'}$ plane in the non-diagonal case and scenario I

6 Conclusions and outlook

We have presented a calculation of the TNGBCs $ZZV^*$ ($V=\gamma$, Z, $Z'$) in models where FCNCs couplings mediated by the Z and $Z'$ gauge bosons are allowed. These TNGBCs are given in terms of one CP-conserving form factor $f_5^V$ and another CP-violating one $f_4^V$, for which we present analytical results in terms of Passarino–Veltman scalar functions. Such results reduce to the contributions with diagonal Z couplings already studied in the literature. To asses the behavior of $f_4^V$ and $f_5^V$, for the numerical analysis we obtain constraints on the FCNCs couplings of the Z gauge boson to up quarks, which are the less constrained by experimental data: it is found that the current constraints on the $t\rightarrow qZ$ branching ratios obtained at the LHC translate into the following constraints on the vector and axial Z couplings $\left| g_{{VZ}}^{tu}\right| < 0.0096$ and $\left| g_{{VZ}}^{tc}\right| <0.011$. As far as the $ZZ\gamma ^*$ coupling is concerned, it is found that the only non-vanishing form factor is the CP-conserving one $f_5^{\gamma }$, whose real and imaginary parts are of the order of $10^{-3}$, with the dominant contributions arising from the heavier up and down quarks. On the other hand, as for the $ZZZ^*$ coupling, both the CP-conserving and the CP violating form factors are non-vanishing. We consider two scenarios for the FCNC Z couplings (scenario I and scenario II) and find that the magnitude of the real and imaginary parts of these form factors are of the order of $|f_5^{Z}|\sim 10^{-6}$ and $|f_4^{Z}|\sim |\mathrm{Im}\left( g_{{AZ}}^{tc*} g_{{VZ}}^{tc} \right) |\times 10^{-5}$, with the dominant contributions arising from the non-diagonal top quark couplings. Our estimates for the FCNC contributions to the CP-conserving $f_5^{\gamma }$ and $f_5^{Z}$ form factors are smaller than the prediction of the SM, whereas the $f_4^{Z}$ form factor is not induced in the SM up to the one loop level.

We also consider the case of a new heavy neutral $Z'$ gauge boson with FCNCs and obtain the TNGBC $ZZ{Z'}^{*}$, for which we present analytical results in the case of both diagonal and non-diagonal $Z'$ couplings in terms of Passarino-Veltman scalar functions. In the diagonal case we find the following numerical estimate for the CP-conserving $f_5^{Z'}$ form factor, which is the only non-vanishing, $|\mathrm{Re}f_{5}^{Z'}|\sim 10^{-1}-10^{-2}$ and $|\mathrm{Im} f_{5}^{Z^\prime }|\sim 10^{-2}-10^{-3}$, with the dominant contributions arising from the light quarks and leptons. In the non-diagonal case we also consider two scenarios for the FCNC couplings of the Z gauge boson (scenario I and scenario II). It is found that both the real and imaginary parts of $f_{5}^{Z^\prime }$ are of the order of $10^{-4}$ in scenario I, whereas in scenario II $|\mathrm{Re}f_{5}^{Z'}|\sim 10^{-6}$ and $|\mathrm{Im}f_{5}^{Z'}|\sim 10^{-5}$. In general, in the non-diagonal case the magnitude of both real and imaginary parts of the $f_5^{Z'}$ form factor are one order of magnitude larger for moderate energies and an ultra heavy $Z'$ gauge boson than for high energies, with the dominant contributions arising from the $Z'tu$ and $Z'tc$ couplings. The real (imaginary) part of the non-diagonal contributions to $f_5^{Z'}$ are at least two (one) orders of magnitude smaller than the real (imaginary) parts of the diagonal contributions.

As far as the CP-violating form factor $f_4^{Z'}$ is concerned, we obtain similar estimates for its real and imaginary parts, of the order of $10^{-7}-10^{-8}$ in both scenarios of the FCNC couplings of the Z gauge boson. In closing we would like to stress that FCNC couplings can also yield CP violation in the TNGBCs of a new neutral gauge boson, which may be on interest.

Appendix A: Analytical form of the TNGBCs \(ZZV^*\) (\(V=\gamma , Z, Z'\))

In this appendix we present the analytical expressions for the loop functions appearing in the contributions to the TNGBCs $ZZV^*$ ($V=\gamma , Z, Z'$) arising from the FCNC couplings mediated by the Z gauge boson and a new heavy neutral gauge boson $Z'$. For the calculation we use the Passarino-Veltman reduction scheme.

1.1 Appendix A.1: Passarino-Veltman results

1.1.1 Appendix A.1.1: $ZZ\gamma ^*$ coupling

There are only contribution to the $f_5^\gamma$ form factor, which is given in Eq. (14), where $R_{ij}$ reads

$$\begin{aligned} R_{ij}&=4\left( q^2-m_Z^2\right) \left( m_j^2-m_i^2 \right) \left( B_{ii}\left( q^2 \right) -B_{jj}\left( q^2 \right) \right) \nonumber \\&\quad +2\left( q^2-2m_Z^2 \right) \left( q^2-4m_Z^2 \right) +2m_Z^2\left( q^2+2m_Z^2 \right) \nonumber \\&\quad \times \left( B_{ii}\left( q^2\right) +B_{jj}\left( q^2\right) -2B_{ij}\left( m_Z^2\right) \right) +4\left( q^2-m_Z^2 \right) \nonumber \\&\quad \times \left( m_i^4+m_j^4+m_Z^4-2m_i^2m_j^2-2m_i^2m_Z^2-2m_j^2m_Z^2\right) \nonumber \\&\quad \times \left( C_{iji} \left( q^2 \right) +C_{jij}\left( q^2 \right) \right) \nonumber \\&\quad +2q^2\left( q^2+2m_Z^2\right) \left( m_j^2 C_{iji}\left( q^2 \right) +m_i^2 C_{jij}\left( q^2 \right) \right) , \end{aligned}$$

(A.1)

where we have introduced the shorthand notation

$$\begin{aligned} B_{ij}(c^2)&=B_0\left( c^2,m_i^2,m_j^2 \right) ,\nonumber \\ C_{ijk}\left( q^2\right)&=C_0\left( m_Z^2,m_Z^2,q^2,m_i^2,m_j^2,m_k^2 \right) , \end{aligned}$$

(A.2)

with $B_0$ and $C_0$ being the usual two- and three-point Passarino-Veltman scalar functions. It is useful observe the following symmetry relations

$$\begin{aligned} B_{ij}(c^2)&=B_{ji}(c^2),\nonumber \\ C_{ijk}\left( q^2\right)&=C_{kji}\left( q^2\right) ,\nonumber \\ C_{iij}\left( q^2\right)&= C_{jji}\left( q^2\right) ,\nonumber \\ C_{iji}\left( q^2\right)&=C_{jij}\left( q^2\right) . \end{aligned}$$

(A.3)

In Eq. (A.1) it is evident that ultraviolet divergences cancel out. We have also verified that $R_{ij}$ vanishes for an on-shell photon.

1.1.2 Appendix A.1.2: $ZZZ^*$ coupling

There are contributions to both the CP-conserving form factor $f_5^Z$ and the CP-violating one $f_4^Z$. They are given in Eqs. (18) and (16), with the $R_{kij}$, and $S_{ij}$ functions given in terms of Passarino-Veltman scalar functions as follows

$$\begin{aligned} R_{1ij}&= 1+\frac{2 \left( m_i^2-m_j^2\right) \left( 2 m_Z^2+q^2\right) }{q^2 \left( q^2-4 m_Z^2\right) }\nonumber \\&\quad \times \left( B_{{ij}}\left( m_Z^2\right) -B_{{ii}}\left( m_Z^2\right) \right) -\frac{1}{\left( q^2-4 m_Z^2\right) \left( q^2-m_Z^2\right) }\nonumber \\&\quad \times \Bigg [\frac{1}{q^2}C_{{iij}}\left( q^2\right) \left( -q^4 \left( m_i^2 \left( m_i^2-m_j^2\right) \right. \right. \nonumber \\&\quad \left. -m_Z^2 \left( 7 m_i^2+3 m_j^2-4 m_Z^2\right) \right) \nonumber \\&\quad \left. +4 q^2 m_Z^2 \left( m_i^2 m_j^2-2 m_i^2 m_Z^2-m_j^4+m_Z^4\right) \nonumber \right. \\&\quad \left. +4 m_Z^4 \left( m_i^2-m_j^2\right) ^2-2 q^6 m_i^2\right) -C_{{iji}}\left( q^2\right) \nonumber \\&\quad \times \left( q^2 \left( -3 m_i^2 m_j^2-3 m_i^2 m_Z^2+m_i^4-2 m_j^2 m_Z^2+2 m_j^4+2 m_Z^4\right) \right. \nonumber \\&\quad \left. +2 m_Z^2 \left( m_i^4+2 m_j^2 m_Z^2-m_j^4-m_Z^4\right) +q^4 m_j^2\right) \nonumber \\&\quad +\left( B_{{ii}}\left( q^2\right) -B_{{ii}}\left( m_Z^2\right) \right) \left( \left( m_i^2-m_Z^2\right) \nonumber \right. \\&\quad \times \left. \left( 2 m_Z^2+q^2\right) -2 m_j^2 \left( q^2-m_Z^2\right) \right) \nonumber \\&\quad +\left( B_{{ij}}\left( q^2\right) -B_{{ij}}\left( m_Z^2\right) \right) \left( \left( m_j^2-2 m_Z^2\right) \nonumber \right. \\&\quad \times \left. \left( 2 m_Z^2+q^2\right) -3 m_i^2 \left( q^2-2 m_Z^2\right) \right) \Bigg ], \end{aligned}$$

(A.4)

$$\begin{aligned} R_{2ij}&= \frac{m_i^2}{q^2-m_Z^2} \Big [ \left( m_i^2-m_j^2-m_Z^2\right) \nonumber \\&\quad \times \left( C_{{iij}}\left( q^2\right) -C_{{iji}}\left( q^2\right) \right) +\left( q^2-m_Z^2\right) C_{{iij}}\left( q^2\right) \nonumber \\&\quad +B_{{ii}}\left( q^2\right) -B_{{ii}}\left( m_Z^2\right) +2 \left( B_{{ij}}\left( q^2\right) -B_{{ij}}\left( m_Z^2\right) \right) \Big ], \end{aligned}$$

(A.5)

$$\begin{aligned} R_{3ij}&= \frac{m_i m_j}{q^2-m_Z^2}\Big [ \left( 2 m_i^2-2 m_j^2+q^2\right) \nonumber \\&\quad \times \left[ C_{{iij}}\left( q^2\right) -C_{{iji}}\left( q^2\right) \right] +2\left( q^2-m_Z^2\right) C_{{iji}}\left( q^2\right) \nonumber \\&\quad +2 \left[ B_{{ii}}\left( q^2\right) -B_{{ii}}\left( m_Z^2\right) \right] +4 \left[ B_{{ij}}\left( q^2\right) \right. \nonumber \\&\quad \left. -B_{{ij}}\left( m_Z^2\right) \right] \Big ], \end{aligned}$$

(A.6)

and

$$\begin{aligned} S_{ij}&=\left( 4 m_Z^2-2 q^2\right) \left[ B_{{ii}}\left( m_Z^2\right) - B_{{jj}}\left( m_Z^2\right) \right] \nonumber \\&\quad -2 q^2 \left[ B_{ii}\left( q^2\right) -B_{jj}\left( q^2\right) \right] - \left( 2 m_Z^2-q^2\right) \nonumber \\&\quad \times \left( 2 m_i^2-2 m_j^2+q^2\right) C_{iij}\left( q^2\right) \nonumber \\&\quad -q^2 \left[ q^2-2 \left( m_i^2-m_j^2+m_Z^2\right) \right] C_{iji}\left( q^2\right) \nonumber \\&\quad + \left( q^2-2 m_Z^2\right) \left( 2 m_i^2-2 m_j^2-q^2\right) C_{jji}\left( q^2\right) \nonumber \\&\quad +q^2 \left[ q^2-2 \left( m_j^2-m_i^2+m_Z^2\right) \right] C_{{jij}}\left( q^2\right) . \end{aligned}$$

(A.7)

1.1.3 Appendix A.1.3: $ZZZ^{'*}$ coupling

The contributions to the $f_5^{Z'}$ and $f_4^{Z'}$ form factors are given in Eqs. (20)–(22), with the $L_i$ $T_{kij}$ and $U_{kij}$ functions given as follows

$$\begin{aligned} L_{1i}&=2 m_Z^2 \big (2 \left( q^2 \left( m_i^2+m_Z^2\right) \nonumber \right. \\&\quad \left. -m_Z^2 \left( 4 m_i^2+m_Z^2\right) \right) C_{iii}\left( q^2\right) \nonumber \\&\quad -\left( 2 m_Z^2+q^2\right) \left( B_{{ii}}\left( m_Z^2\right) \nonumber \right. \\&\quad \left. -B_{{ii}}\left( q^2\right) \right) \big )-6 q^2 m_Z^2+8 m_Z^4+q^4, \end{aligned}$$

(A.8)

$$\begin{aligned} L_{2i}&=-4 \left( m_Z-q\right) \left( m_Z+q\right) \nonumber \\&\quad \times \left( m_i^2 \left( q^2-4 m_Z^2\right) +m_Z^4\right) C_{iii}\left( q^2\right) \nonumber \\&\quad -2 \left( 4 m_i^2 \left( q^2-4 m_Z^2\right) +m_Z^2 \left( 2 m_Z^2+q^2\right) \right) \nonumber \\&\quad \times \left( B_{{ii}}\left( m_Z^2\right) -B_{{ii}}\left( q^2\right) \right) -6 q^2 m_Z^2+8 m_Z^4+q^4, \end{aligned}$$

(A.9)

$$\begin{aligned} L_{3i}&=2 \big (2 \left( m_i^2 \left( -6 q^2 m_Z^2+8 m_Z^4+q^4\right) \nonumber \right. \\&\quad \left. -2 m_Z^4 \left( m_Z^2-q^2\right) \right) C_{iii}\left( q^2\right) \nonumber \\&\quad -2 m_Z^2 \left( 2 m_Z^2+q^2\right) \left( B_{{ii}}\left( m_Z^2\right) \nonumber \right. \\&\quad \left. -B_{{ii}}\left( q^2\right) \right) -6 q^2 m_Z^2+8 m_Z^4+q^4\big ). \end{aligned}$$

(A.10)

$$\begin{aligned} U_{1ij}&=-\frac{1}{ q^2} \Big [ B_{{ii}}\left( m_Z^2\right) \big (q^4 \left( 2 m_i \left( m_i-m_j\right) +m_Z^2\right) \nonumber \\&\quad +2 q^2 m_Z^2 \left( m_Z^2-2 \left( m_i-m_j\right) ^2\right) -4 m_Z^4 \left( m_i^2-m_j^2\right) \big )\nonumber \\&\quad +q^2 \left( B_{{ij}}\left( m_Z^2\right) -2 B_{{ij}}\left( q^2\right) \right) \big (q^2 \left( \left( m_i-m_j\right) ^2+m_Z^2\right) \nonumber \\&\quad -4 m_Z^2 \left( m_i-m_j\right) ^2+2 m_Z^4\big )+C_{{iij}}\left( q^2\right) \nonumber \\&\quad \times \big (q^6 m_i \left( m_j-3 m_i\right) +q^4 \big (m_Z^2 \left( m_i(13 m_i-4 m_j)+3 m_j^2\right) \nonumber \\&\quad -2 m_i \left( m_i-m_j\right) ^2 \left( m_i+m_j\right) -4 m_Z^4\big )\nonumber \\&\quad +4 q^2 m_Z^2 \left( \left( m_i-m_j\right) ^3 \left( m_i+m_j\right) \right. \nonumber \\&\quad \left. -4 m_i^2 m_Z^2+m_Z^4\right) +4 m_Z^4 \left( m_i^2-m_j^2\right) ^2\big )\nonumber \\&\quad + \left( 6 q^4 m_Z^2-8 q^2 m_Z^4-q^6\right) \Big ] + (i \leftrightarrow j), \end{aligned}$$

(A.11)

$$\begin{aligned} U_{2ij}&= U_{1ij}(m_j\rightarrow -m_j), \end{aligned}$$

(A.12)

$$\begin{aligned} U_{3ij}&=2 \Big [B_{{ii}}\left( q^2\right) \left( q^2 \left( 2( m_j^2- m_j^2)+m_Z^2\right) \right. \nonumber \\&\quad \left. +2 m_Z^2 \left( m_i^2-m_j^2+m_Z^2\right) \right) \nonumber \\&\quad -m_Z^2 \left( 2 m_Z^2+q^2\right) B_{{ij}}\left( m_Z^2\right) \nonumber \\&\quad +C_{{iji}}\left( q^2\right) \big (2 q^2 \left( m_Z^4-m_Z^2 \left( 2 m_i^2+m_j^2\right) \right. \nonumber \\&\quad \left. +\left( m_i^2-m_j^2\right) ^2\right) -2 m_Z^2 \left( (m_i+m_j)^2-m_Z^2\right) \nonumber \\&\quad \times \left( (m_i-m_j)^2-m_Z^2\right) \nonumber \\&\quad +q^4 m_j^2\big )-3 q^2 m_Z^2+4 m_Z^4+\frac{1}{2}q^4\Big ]+ (i \leftrightarrow j), \end{aligned}$$

(A.13)

$$\begin{aligned} U_{4ij}&=-\frac{1 }{ q^2} \Big [ m_Z^2 B_{{ii}}\left( m_Z^2\right) \left( 2 q^2 \left( 2 m_i^2-2 m_j^2+m_Z^2\right) \nonumber \right. \\&\quad \left. -4 m_Z^2 \left( m_i^2-m_j^2\right) +q^4\right) \nonumber \\&\quad +q^2 \left( m_Z^2 \left( 2 m_Z^2+q^2\right) \left( B_{{ij}}\left( m_Z^2\right) -2 B_{{ij}}\left( q^2\right) \right) \nonumber \right. \\&\quad \left. + \left( 6 q^2 m_Z^2-8 m_Z^4+q^4\right) \right) \nonumber \\&\quad +C_{{iij}}\left( q^2\right) \big (q^6 m_i \left( m_j-m_i\right) \nonumber \\&\quad -q^4 m_Z^2 \left( 8 m_i m_j-m_i^2-3 m_j^2+4 m_Z^2\right) \nonumber \\&\quad -4 q^2 m_Z^2 \left( (m_i-m_j)^2-m_Z^2\right) \left( \left( m_i+m_j\right) ^2+m_Z^2\right) \nonumber \\&\quad +4 m_Z^4 \left( m_i^2-m_j^2\right) ^2\big )\Big ]+ (i \leftrightarrow j), \end{aligned}$$

(A.14)

$$\begin{aligned} U_{5ij}&=U_{4ij}(m_j\rightarrow -m_j), \end{aligned}$$

(A.15)

$$\begin{aligned} U_{6ij}&=-2 \Big [ B_{{ii}}\left( q^2\right) \left( -q^2 \left( 2 m_j \left( m_i+m_j\right) +m_Z^2\right) \nonumber \right. \\&\quad \left. +2 m_Z^2\left( m_i+m_j\right) \left( 3 m_i+m_j\right) -2 m_Z^4\right) \nonumber \\&\quad +B_{{ij}}\left( m_Z^2\right) \left( q^2 \left( \left( m_i+m_j\right) ^2+m_Z^2\right) \right. \nonumber \\&\quad \left. -4 m_Z^2 \left( m_i+m_j\right) ^2+2 m_Z^4\right) \nonumber \\&\quad +C_{{iji}}\left( q^2\right) \big (-q^4 m_j \left( m_i+m_j\right) \nonumber \\&\quad +2 q^2 \left( m_Z^2 \left( 3 m_i m_j+m_i^2+m_j^2\right) \right. \nonumber \\&\quad \left. +m_j \left( m_i^2-m_j^2\right) \left( m_i+m_j\right) -m_Z^4\right) \nonumber \\&\quad -2 m_Z^2 \left( (m_i+m_j)^2-m_Z^2\right) \left( \left( m_i-m_j\right) \left( 3 m_i+m_j\right) \right. \nonumber \\&\quad \left. +m_Z^2\right) \big )+3 q^2 m_Z^2-4 m_Z^4-\frac{1}{2}q^4\Big ] + (i \leftrightarrow j) , \end{aligned}$$

(A.16)

and

$$\begin{aligned} U_{7ij}&=U_{6ij}(m_j\rightarrow -m_j). \end{aligned}$$

(A.17)

$$\begin{aligned} T_{1ij}&= \Big [3 \left( m_i-m_j\right) \big (q^2 \left( m_i+m_j\right) \left( B_{{ij}}\left( q^2\right) \left( q^2-2 m_Z^2\right) \nonumber \right. \\&\quad \left. -m_Z^2 B_{{ij}}\left( m_Z^2\right) \right) +C_{{iij}}\left( q^2\right) \big (q^4 \big (2 m_i^2 \left( m_i+m_j\right) \nonumber \\&\quad -m_Z^2 \left( 3 m_i+m_j\right) \big )-2 q^2 m_Z^2 \left( m_i+m_j\right) \nonumber \\&\quad \times \left( 2 m_i \left( m_i+m_j\right) -m_Z^2\right) +2 m_Z^2 \left( m_i-m_j\right) ^2 \nonumber \\&\quad \times \left( m_i+m_j\right) ^3+q^6 m_i\big )\big )\nonumber \\&\quad +B_{{ii}}\left( m_Z^2\right) \left( q^2 m_Z^2 \left( 12 m_i m_j+7 m_i^2-3 m_j^2-4 m_Z^2\right) \nonumber \right. \\&\left. -6 m_Z^2 \left( m_i^2-m_j^2\right) ^2+q^4 \left( m_Z^2-4 m_i^2\right) \right) \nonumber \\&-2 q^2 B_{{ii}}(0) m_i^2 \left( q^2-4 m_Z^2\right) \Big ]- (i \leftrightarrow j), \end{aligned}$$

(A.18)

$$\begin{aligned} T_{2ij}&=T_{1ij}(m_j\rightarrow -m_j), \end{aligned}$$

(A.19)

$$\begin{aligned} T_{3ij}&=6 q^4 m_i m_j \Big [C_{{iji}}\left( q^2\right) \left( 2 \left( m_i^2-m_j^2+m_Z^2\right) -q^2\right) \nonumber \\&\quad -2 B_{{ii}}\left( q^2\right) \Big ] - (i \leftrightarrow j), \end{aligned}$$

(A.20)

$$\begin{aligned} T_{4ij}&= \Big [3 \left( m_i+m_j\right) \big (C_{{iij}}\left( q^2\right) \nonumber \\&\quad \times \big (q^4 \left( m_Z^2 \left( m_i+m_j\right) +2 m_i m_j \left( m_j-m_i\right) \right) \nonumber \\&\quad -2 q^2 m_Z^2 \left( m_i-m_j\right) \big (2 m_i \left( m_i-m_j\right) -m_Z^2\big )\nonumber \\&\quad +2 m_Z^2 \left( m_i-m_j\right) \left( m_i^2-m_j^2\right) ^2-q^6 m_i\big )\nonumber \\&\quad -q^2 \left( m_i-m_j\right) \big (B_{{ij}}\left( q^2\right) \left( 2 m_Z^2+q^2\right) \nonumber \\&\quad +\left( m_Z^2-q^2\right) B_{{ij}}\left( m_Z^2\right) \big )\big )\nonumber \\&\quad +B_{{ii}}\left( m_Z^2\right) \big (q^4 \left( 2 m_i \left( m_i+3 m_j\right) +m_Z^2\right) \nonumber \\&\quad -q^2 m_Z^2 \left( 12 m_i m_j-7 m_i^2+3 m_j^2+4 m_Z^2\right) \nonumber \\&\quad -6 m_Z^2 \left( m_i^2-m_j^2\right) ^2\big )\nonumber \\&\quad -2 q^2 B_{{ii}}(0) m_i^2 \left( q^2-4 m_Z^2\right) \Big ]- (i \leftrightarrow j) , \end{aligned}$$

(A.21)

$$\begin{aligned} T_{5ij}&=T_{4ij}(m_j\rightarrow -m_j), \end{aligned}$$

(A.22)