INTRODUCTION AND FORMULATION OF THE PROBLEM

Studies of the long-term evolution of orbits in the restricted elliptic three-body problem are generally carried out in the doubly averaged formulation. The integrable case of a circular orbit of the perturbing body is widely used. The studies of this case initiated by the renowned scientists H. von Zeipel (von Zeipel, 1910) and N.D. Moiseev (Moiseev, 1945) were elaborated significantly by M.L. Lidov (Lidov, 1961, 1962) and I. Kozai (Kozai, 1962). These studies are described in detail in the monographs by Shevchenko (2017) and Ito and Ohtsuka (2019). Note that the extensive paper by H. von Zeipel has become deservedly famous and is reflected in the above scientific-historical study by Ito and Ohtsuka (2019) only due to the reference to it in Baily and Emel’yanenko (1996) in connection with the study of the evolution of one of the types of cometary orbits. The works by Moiseev, Lidov, and Kozai performed later were both the results of a qualitative study of the averaged three-body problem and the necessity of investigating the orbital dynamics of artificial satellites of planets and the dynamics of asteroids.

In his extensive paper Zeipel (1910) identified and qualitatively studied three main cases of the orbit location for the perturbed body in the doubly averaged circular problem: the inner one, the outer one, and the case of intersecting, in particular, the so-called linked orbits. The spatial location of linked orbits is characterized by the fact that one of the points of intersection of the orbit of a negligible-mass body with the plane of the orbit of the perturbing body is located inside it, while the other one is outside. Such a classification in the restricted circular doubly averaged three-body problem for uniformly close orbits, along with an analysis of the conditions for their intersection, was proposed by Lidov and Ziglin (1974). The topology of two linked and unlinked Keplerian orbits of all those types was described in detail by Kholshevnikov and Titov (2007).

Note that the phrase “like the rings of a chain” proposed in the monograph by Ito and Ohtsuka (2019) as the English analog of the French term “comme les anneaux d’une shaine” used by von Zeipel (1910) is more sensible and geometrically understandable than the term “linked orbits”. The linked orbits in the restricted elliptic doubly averaged three-body problem are the subject of our study.

Consider the motion of particle Р of negligible mass under the attraction of a central point S of mass m and a perturbing point J of mass m1  \( \ll \) m moving relative to S in an elliptical orbit with a semimajor axis а1 and eccentricity е1. Let us introduce a rectangular coordinate system Oxyz with the origin at point S whose reference plane xOy coincides with the orbital plane of point J. Let the Ox axis be directed to the pericenter of the orbit of point J, the Oy axis be in the direction of its motion from the pericenter in the reference plane, and the Oz axis complements the coordinate system to a right-handed one. The perturbed orbit of point Р is characterized by osculating Keplerian elements: the semimajor axis а, the eccentricity е, the inclination i, the argument of pericenter ω, and the longitude of the ascending node Ω. In the chosen coordinate system the perturbing point J has coordinates x1, y1, and z1 = 0.

The secular part W of the complete perturbing function is used to investigate the orbital evolution of point Р:

$$W\left( {a,e,i,{{\omega }},\Omega ,{{a}_{1}},{{e}_{1}}} \right) = \frac{{f{{m}_{1}}}}{{4{{\pi }^{2}}}}\int\limits_0^{2\pi } {\int\limits_0^{2\pi } {\frac{1}{{\Delta \left( {\lambda ,{{\lambda }_{1}}} \right)}}} } d{{\lambda }_{1}}d\lambda .$$
(1)

Here, \(\Delta = \left| {{\mathbf{r}} - {{{\mathbf{r}}}_{1}}} \right| = \sqrt {{{{\left( {x - {{x}_{1}}} \right)}}^{2}} + {{{\left( {y - {{y}_{1}}} \right)}}^{2}} + {{z}^{2}}} \) is the distance between the perturbed and perturbing points, λ and λ1 are the mean longitudes of these points, and f is the gravitational constant. The absence of low-order commensurabilities between the mean motions of points J and Р is assumed. In the function W a1 and e1 act as parameters of the evolution problem.

The first integrals of the equations of perturbed motion in elements are

$$a = {\text{const}},\,\,\,\,~W(a,e,i,\omega ,\Omega ,{{a}_{1}},{{e}_{1}}) = {\text{const}},$$
(2)

while one more first integral exists in the case of е1 = 0 (Moiseev, 1945):

$$\left( {1 - {{e}^{2}}} \right){{\cos }^{2}}i = {{c}_{1}} = {\text{const}}.$$
(3)

THE AVERAGED PERTURBING FUNCTION AND EVOLUTION EQUATIONS

Another expression, equivalent to (1), for the function W via well-known formulas is also commonly used in analytical studies:

$$\begin{gathered} W = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\left( {1 - e\cos E} \right)} V\left( E \right)dE, \\ V\left( E \right) = \frac{{f{{m}_{1}}}}{{2\pi }}\int\limits_0^{2\pi } {\frac{{d{{\lambda }_{1}}}}{{\Delta \left( {{{\lambda }_{1}},E} \right)}}} , \\ \end{gathered} $$
(4)

where V is the attractive force function of the elliptical Gaussian ring simulating the averaged influence of the perturbing point and Е is the eccentric anomaly of point Р.

Since for the orbits under consideration the distance r can be both less than and greater than r1 as they evolve, the commonly used expansions of the inverse distance 1/Δ into series in Legendre polynomials are inapplicable. Therefore, in this paper we will use the analytical expression for the function V, though with a limited accuracy up to \(e_{1}^{2}\) inclusive, from Vashkov’yak (1986) for a nearly coplanar system of N of weakly elliptical Gaussian rings, but valid for any relation between r and r1. Taking into account the orientation of the introduced coordinate system and assuming that N = 1, i1 = ω1 = Ω1 = k1 = u1 = v1 = 0, and h1 = e1 in Eqs. (6)–(8) of this paper, we will obtain

$$V\left( E \right) = \frac{{f{{m}_{1}}}}{{\sqrt {a_{1}^{2} + {{r}^{2}}} }}\Phi \left( {x,y,z} \right),$$
(5)

and, for coherence, we will permit ourselves to also reproduce the basic simplified computational formulas from this paper by supplementing them with new analytical relations.

The function Ф dependent on the rectangular coordinates x, y, z is expressed via hypergeometric Gaussian functions F:

$$\begin{gathered} \Phi = \left( {1 - \varepsilon + \mu } \right)F\left( {\frac{1}{4},\frac{3}{4};1;\zeta } \right) \\ + \,\,\left( {\nu - \frac{1}{2}\varepsilon } \right)F\left( {\frac{5}{4},\frac{3}{4};2;\zeta } \right), \\ \end{gathered} $$
(6)

Functional series of various structures, depending on the numerical value of the argument ζ (\(\left| \zeta \right| < 1\)), are used for their calculation, so that

$$\Phi = \left\{ \begin{gathered} \mathop \sum \limits_{n = 0}^\infty \left[ {1 + \mu - \frac{{3\left( {2n + 1} \right)}}{{2\left( {n + 1} \right)}}\varepsilon + \frac{{4n + 1}}{{n + 1}}\nu } \right]{{B}_{n}}{{\zeta }^{n}},\,\,\,\,\left| \zeta \right| < {{\zeta }^{*}}; \hfill \\ \frac{1}{{\pi \sqrt 2 }}\sum\limits_{n = 0}^\infty {\left\{ {\left[ {{{H}_{n}} - \ln \left( {1 - \zeta } \right)} \right]\left[ {1 + \mu + 4\left( {4n + 1} \right)\nu - \left( {8n + 3} \right)\varepsilon } \right] + 8\left( {\varepsilon - 2\nu } \right)} \right\}} {{B}_{n}}{{\left( {1 - \zeta } \right)}^{n}},\,\,\,\,\left| \zeta \right| > {{\zeta }^{*}}. \hfill \\ \end{gathered} \right.$$
(7)

Here,

$$\begin{gathered} \varepsilon = \frac{{{{a}_{1}}{{e}_{1}}x}}{{a_{1}^{2} + {{r}^{2}}}},\,\,\,\,\mu = {{\varepsilon }^{2}}\left( {2 + \frac{{a_{1}^{2} + {{z}^{2}}}}{{2{{\rho }^{2}}}}} \right) - \frac{{a_{1}^{2}e_{1}^{2}{{y}^{2}}}}{{\left( {a_{1}^{2} + {{r}^{2}}} \right){{\rho }^{2}}}}, \\ \nu = \frac{3}{2}{{\varepsilon }^{2}} - \frac{{a_{1}^{2}e_{1}^{2}}}{{2\left( {a_{1}^{2} + {{r}^{2}}} \right)}},\,\,\,\,{{r}^{2}} = {{\rho }^{2}} + {{z}^{2}}, \\ {{\rho }^{2}} = {{x}^{2}} + {{y}^{2}},\,\,\,\,\zeta = \frac{{4a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}} \\ \times \,\,\left[ {{{\rho }^{2}} + 2\varepsilon \left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right) + \theta } \right], \\ \theta = e_{1}^{2}\left\{ {a_{1}^{2} - {{x}^{2}}\left[ {\frac{{6a_{1}^{2}\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right)}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}} + \frac{{a_{1}^{2} + {{r}^{2}}}}{{{{\rho }^{2}}}}} \right]} \right. \\ \left. {\frac{{^{{^{{^{{^{{}}}}}}}}}}{{_{{_{{_{{}}}}}}}} + \,\,{{y}^{2}}\left( {\frac{{a_{1}^{2} + {{z}^{2}}}}{{{{\rho }^{2}}}} - \frac{{4a_{1}^{2}}}{{a_{1}^{2} + {{r}^{2}}}}} \right)} \right\}. \\ \end{gathered} $$
(8)

The constant coefficients Bn and Hn are defined by the recurrence relations

$$\begin{gathered} {{B}_{n}} = \frac{{\left( {4n - 3} \right)\left( {4n - 1} \right)}}{{{\text{16}}{{n}^{2}}}}{{B}_{{n - 1}}},\,\,\,\,{{B}_{0}} = 1, \\ {{H}_{n}} = {{H}_{{n - 1}}} + \frac{{2\left( {3 - 8n} \right)}}{{n\left( {4n - 3} \right)\left( {4n - 1} \right)}},\,\,\,{{H}_{0}} = 6{\text{ln}}2, \\ \end{gathered} $$
(9)

while the empirical value of ζ* is taken to be 0.5.

Remark. The function V depends only on the squares of the coordinates y and z, while the coordinate x enters into this function both quadratically and linearly (into the numerator of ε and via it into ζ). The existence of two planar particular solutions, y = 0 and z = 0, in the singly averaged (only over λ1) evolution problem follows from such a double symmetry of the function V with respect to y and z.

The rectangular coordinates x, y, z are expressed via Е by the well-known formulas for unperturbed Keplerian motion

$$\left\| {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right\| = a\left\{ {\left( {{\text{cos}}E - e} \right)\left\| {\begin{array}{*{20}{c}} {{{p}_{1}}} \\ {{{p}_{2}}} \\ {{{p}_{3}}} \end{array}} \right\| + \sqrt {1 - {{e}^{2}}} {\text{sin}}E\left\| {\begin{array}{*{20}{c}} {{{q}_{1}}} \\ {{{q}_{2}}} \\ {{{q}_{3}}} \end{array}} \right\|} \right\},$$
(10)
$$\begin{gathered} {{p}_{1}} = {\text{cos}}\omega {\text{cos}}\Omega - {\text{sin}}\omega {\text{sin}}\Omega {\text{cos}}i, \\ {{p}_{2}} = {\text{cos}}\omega {\text{sin}}\Omega + {\text{sin}}\omega {\text{cos}}\Omega {\text{cos}}i,\,\,\,\,{{p}_{3}} = {\text{sin}}\omega {\text{sin}}i, \\ {{q}_{1}} = - {\text{sin}}\omega {\text{cos}}\Omega - {\text{cos}}\omega {\text{sin}}\Omega {\text{cos}}i, \\ {{q}_{2}} = - {\text{sin}}\omega {\text{sin}}\Omega + {\text{cos}}\omega {\text{cos}}\Omega {\text{cos}}i,\,\,\,{{q}_{3}} = {\text{cos}}\omega {\text{sin}}i{\text{.}} \\ \end{gathered} $$
(11)

Below, it will be convenient to introduce a new independent variable, a “dimensionless time” τ, according to the formula

$$\tau = \frac{{{{m}_{1}}a}}{{m{{a}_{1}}}}n\left( {t - {{t}_{0}}} \right),$$
(12)

where \(n = \frac{{\sqrt {fm} }}{{{{a}^{{3/2}}}}}\) is the mean motion of point Р, and a normalized perturbing function

$$w = \frac{{{{a}_{1}}}}{{f{{m}_{1}}}}W = {\text{const}}{\text{.}}$$
(13)

To describe the evolution of orbits, we will use the Lagrange equations in elements with the function w that is their first and unique integral:

$$\begin{gathered} \frac{{de}}{{d\tau }} = - \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial \omega }},\,\,\,\,\,\frac{{di}}{{d\tau }} = \frac{{{\text{cot}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial \omega }} - \frac{{{\text{cosec}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial \Omega }}, \\ \frac{{d\omega }}{{d\tau }} = \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial e}} - \frac{{{\text{cot}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial i}}, \\ \frac{{d\Omega }}{{d\tau }} = \frac{{{\text{cosec}}i}}{{\sqrt {1 - {{e}^{2}}} }}\frac{{\partial w}}{{\partial i}}. \\ \end{gathered} $$
(14)

The existence of stationary solutions of these equations is possible if the conditions \(\frac{{de}}{{d\tau }} = \frac{{di}}{{d\tau }} = \frac{{d\omega }}{{d\tau }} = \frac{{d\Omega }}{{d\tau }} = 0\) are fulfilled.

PARTIAL DERIVATIVES OF THE NORMALIZED FUNCTION w WITH RESPECT TO THE ELEMENTS

Generally, for arbitrary orbits of point Р a solution of Eqs. (14) can be found apparently only by a numerical method, while the process of calculations can be controlled by the constancy of the function w along this solution. In Vashkov’yak (1986) the partial derivatives of the function w with respect to the elements were calculated by a difference method. Here, we use a combined method, in which the quadratures

$$\begin{gathered} \frac{{\partial w}}{{\partial e}} = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\left[ {\left( {1 - e\cos E} \right)\frac{{\partial \tilde {V}}}{{\partial e}} - \tilde {V}\cos E} \right]} dE, \\ \left\| {\begin{array}{*{20}{c}} {\frac{{\partial w}}{{\partial i}}} \\ {\frac{{\partial w}}{{\partial \omega }}} \\ {\frac{{\partial w}}{{\partial \Omega }}} \end{array}} \right\| = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\left( {1 - e\cos E} \right)} \left\| {\begin{array}{*{20}{c}} {\frac{{\partial \tilde {V}}}{{\partial i}}} \\ {\frac{{\partial \tilde {V}}}{{\partial \omega }}} \\ {\frac{{\partial \tilde {V}}}{{\partial \Omega }}} \end{array}} \right\|dE \\ \end{gathered} $$
(15)

are found numerically by the Gaussian method, while the derivatives of the normalized function

$$\tilde {V} = \frac{{{{a}_{1}}}}{{f{{m}_{1}}}}V = \frac{{{{a}_{1}}}}{{\sqrt {a_{1}^{2} + {{r}^{2}}} }}\Phi \left( {x,y,z} \right)$$
(16)

are found analytically. For the completeness of the set of formulas, we give the necessary expressions to calculate the derivatives of the function \(\tilde {V}\) with respect to the orbital elements:

$$\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \tilde {V}}}{{\partial e}}} \\ {\frac{{\partial \tilde {V}}}{{\partial i}}} \\ {\frac{{\partial \tilde {V}}}{{\partial \omega }}} \\ {\frac{{\partial \tilde {V}}}{{\partial \Omega }}} \end{array}} \right\| = \frac{{\partial \tilde {V}}}{{\partial x}}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial e}}} \\ {\frac{{\partial x}}{{\partial i}}} \\ {\frac{{\partial x}}{{\partial \omega }}} \\ {\frac{{\partial x}}{{\partial \Omega }}} \end{array}} \right\| + \frac{{\partial \tilde {V}}}{{\partial y}}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial y}}{{\partial e}}} \\ {\frac{{\partial y}}{{\partial i}}} \\ {\frac{{\partial y}}{{\partial \omega }}} \\ {\frac{{\partial y}}{{\partial \Omega }}} \end{array}} \right\| + \frac{{\partial \tilde {V}}}{{\partial z}}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial z}}{{\partial e}}} \\ {\frac{{\partial z}}{{\partial i}}} \\ {\frac{{\partial z}}{{\partial \omega }}} \\ {\frac{{\partial z}}{{\partial \Omega }}} \end{array}} \right\|,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \tilde {V}}}{{\partial x}}} \\ {\frac{{\partial \tilde {V}}}{{\partial y}}} \\ {\frac{{\partial \tilde {V}}}{{\partial z}}} \end{array}} \right\| = \frac{{{{a}_{1}}}}{{\sqrt {a_{1}^{2} + {{r}^{2}}} }}\left( {\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \Phi }}{{\partial x}}} \\ {\frac{{\partial \Phi }}{{\partial y}}} \\ {\frac{{\partial \Phi }}{{\partial z}}} \end{array}} \right\| - \frac{\Phi }{{a_{1}^{2} + {{r}^{2}}}}\left\| {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right\|} \right).$$
(17)
$$\begin{gathered} \left\| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial e}}} \\ {\frac{{\partial y}}{{\partial e}}} \\ {\frac{{\partial z}}{{\partial e}}} \end{array}} \right\| = - a\left( {\left\| {\begin{array}{*{20}{c}} {{{p}_{1}}} \\ {{{p}_{2}}} \\ {{{p}_{3}}} \end{array}} \right\| + \frac{{e{\text{sin}}E}}{{\sqrt {1 - {{e}^{2}}} }}\left\| {\begin{array}{*{20}{c}} {{{q}_{1}}} \\ {{{q}_{2}}} \\ {{{q}_{3}}} \end{array}} \right\|} \right),\,\,\,\,\,\,\,\left\| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial i}}} \\ {\frac{{\partial y}}{{\partial i}}} \\ {\frac{{\partial z}}{{\partial i}}} \end{array}} \right\| = a\left[ {\left( {{\text{cos}}E - e} \right){\text{sin}}\omega + \sqrt {1 - {{e}^{2}}} {\text{cos}}\omega {\text{sin}}E} \right]\left\| {\begin{array}{*{20}{c}} {{{r}_{1}}} \\ {{{r}_{2}}} \\ {{{r}_{3}}} \end{array}} \right\|, \\ \left\| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial \omega }}} \\ {\frac{{\partial y}}{{\partial \omega }}} \\ {\frac{{\partial z}}{{\partial \omega }}} \end{array}} \right\| = a\left( {\left( {{\text{cos}}E - e} \right)\left\| {\begin{array}{*{20}{c}} {{{q}_{1}}} \\ {{{q}_{2}}} \\ {{{q}_{3}}} \end{array}} \right\| - \sqrt {1 - {{e}^{2}}} {\text{sin}}E\left\| {\begin{array}{*{20}{c}} {{{p}_{1}}} \\ {{{p}_{2}}} \\ {{{p}_{3}}} \end{array}} \right\|} \right),\,\,\,\left\| {\begin{array}{*{20}{c}} {\frac{{\partial x}}{{\partial \Omega }}} \\ {\frac{{\partial y}}{{\partial \Omega }}} \\ {\frac{{\partial z}}{{\partial \Omega }}} \end{array}} \right\| = a\left( {\left( {{\text{cos}}E - e} \right)\left\| {\begin{array}{*{20}{c}} { - {{p}_{2}}} \\ {{{p}_{1}}} \\ 0 \end{array}} \right\| + \sqrt {1 - {{e}^{2}}} {\text{sin}}E\left\| {\begin{array}{*{20}{c}} { - {{q}_{2}}} \\ {{{q}_{1}}} \\ 0 \end{array}} \right\|} \right), \\ {{r}_{1}} = {\text{sin}}i{\text{sin}}\Omega ,\,\,\,\,{{r}_{2}} = - {\text{sin}}i{\text{cos}}\Omega ,\,\,\,\,{{r}_{3}} = {\text{cos}}i. \\ \end{gathered} $$
(18)
$$\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \Phi }}{{\partial x}}} \\ {\frac{{\partial \Phi }}{{\partial y}}} \\ {\frac{{\partial \Phi }}{{\partial z}}} \end{array}} \right\| = \frac{{\partial \Phi }}{{\partial \varepsilon }}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \varepsilon }}{{\partial x}}} \\ {\frac{{\partial \varepsilon }}{{\partial y}}} \\ {\frac{{\partial \varepsilon }}{{\partial z}}} \end{array}} \right\| + \frac{{\partial \Phi }}{{\partial \zeta }}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \zeta }}{{\partial x}}} \\ {\frac{{\partial \zeta }}{{\partial y}}} \\ {\frac{{\partial \zeta }}{{\partial z}}} \end{array}} \right\| + \frac{{\partial \Phi }}{{\partial \mu }}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \mu }}{{\partial x}}} \\ {\frac{{\partial \mu }}{{\partial y}}} \\ {\frac{{\partial \mu }}{{\partial z}}} \end{array}} \right\| + \frac{{\partial \Phi }}{{\partial \nu }}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial \nu }}{{\partial x}}} \\ {\frac{{\partial \nu }}{{\partial y}}} \\ {\frac{{\partial \nu }}{{\partial z}}} \end{array}} \right\|,$$
(19)
$$\begin{gathered} \frac{{\partial \varepsilon }}{{\partial x}} = \frac{{{{a}_{1}}{{e}_{1}}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left( {a_{1}^{2} - {{x}^{2}} + {{y}^{2}} + {{z}^{2}}} \right),\,\,\,\,\,\,\frac{{\partial \varepsilon }}{{\partial y}} = - \frac{{2{{a}_{1}}{{e}_{1}}xy}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}},\,\,\,\,\frac{{\partial \varepsilon }}{{\partial z}} = \frac{{2{{a}_{1}}{{e}_{1}}xz}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}, \\ \frac{{\partial \mu }}{{\partial x}} = \varepsilon \frac{{\partial \varepsilon }}{{\partial x}}\left( {4 + \frac{{a_{1}^{2} + {{z}^{2}}}}{{{{\rho }^{2}}}}} \right) + \frac{x}{{{{\rho }^{4}}}} \times \,\,\left[ {\frac{{2a_{1}^{2}e_{1}^{2}{{y}^{2}}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left( {a_{1}^{2} + 2{{x}^{2}} + 2{{y}^{2}} + {{z}^{2}}} \right) - {{\varepsilon }^{2}}\left( {a_{1}^{2} + {{z}^{2}}} \right)} \right], \\ \frac{{\partial \mu }}{{\partial y}} = \varepsilon \frac{{\partial \varepsilon }}{{\partial y}}\left( {4 + \frac{{a_{1}^{2} + {{z}^{2}}}}{{{{\rho }^{2}}}}} \right) + \frac{y}{{{{\rho }^{4}}}} \times \,\,\left[ {\frac{{2a_{1}^{2}e_{1}^{2}{{y}^{2}}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left( {a_{1}^{2} + 2{{x}^{2}} + 2{{y}^{2}} + {{z}^{2}}} \right) - {{\varepsilon }^{2}}\left( {a_{1}^{2} + {{z}^{2}}} \right)} \right] \times \,\,\frac{{2a_{1}^{2}e_{1}^{2}y}}{{\left( {a_{1}^{2} + {{r}^{2}}} \right){{\rho }^{2}}}}, \\ \frac{{\partial \mu }}{{\partial z}} = \varepsilon \frac{{\partial \varepsilon }}{{\partial z}}\left( {4 + \frac{{a_{1}^{2} + {{z}^{2}}}}{{{{\rho }^{2}}}}} \right) + \frac{z}{{{{\rho }^{2}}}}\left[ {{{\varepsilon }^{2}} + \frac{{2a_{1}^{2}e_{1}^{2}{{y}^{2}}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}} \right], \\ \left\| {\begin{array}{*{20}{c}} {\frac{{\partial \nu }}{{\partial x}}} \\ {\frac{{\partial \nu }}{{\partial y}}} \\ {\frac{{\partial \nu }}{{\partial z}}} \end{array}} \right\| = 3\varepsilon \left\| {\begin{array}{*{20}{c}} {\frac{{\partial \varepsilon }}{{\partial x}}} \\ {\frac{{\partial \varepsilon }}{{\partial y}}} \\ {\frac{{\partial \varepsilon }}{{\partial z}}} \end{array}} \right\| + \frac{{a_{1}^{2}e_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left\| {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right\|. \\ \end{gathered} $$
(20)
$$\begin{gathered} \frac{{\partial \zeta }}{{\partial x}} = \frac{{4a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left[ {2\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right)\left( {\frac{{\partial \varepsilon }}{{\partial x}} - \frac{{4\varepsilon x}}{{a_{1}^{2} + {{r}^{2}}}}} \right)} \right. + \left. {\,\,2x\left( {1 - 2\varepsilon } \right) - \frac{{4x}}{{a_{1}^{2} + {{r}^{2}}}}\left( {{{\rho }^{2}} + \theta } \right) + \frac{{\partial \theta }}{{\partial x}}} \right], \\ \frac{{\partial \zeta }}{{\partial y}} = \frac{{4a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left[ {2\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right)\left( {\frac{{\partial \varepsilon }}{{\partial y}} - \frac{{4\varepsilon y}}{{a_{1}^{2} + {{r}^{2}}}}} \right)} \right.\left. { + \,\,2y\left( {1 - 2\varepsilon } \right) - \frac{{4y}}{{a_{1}^{2} + {{r}^{2}}}}\left( {{{\rho }^{2}} + \theta } \right) + \frac{{\partial \theta }}{{\partial y}}} \right], \\ \frac{{\partial \zeta }}{{\partial z}} = \frac{{4a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left[ {2\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right)\left( {\frac{{\partial \varepsilon }}{{\partial z}} - \frac{{4\varepsilon z}}{{a_{1}^{2} + {{r}^{2}}}}} \right)} \right.\left. { + \,\,4\varepsilon z - \frac{{4z}}{{a_{1}^{2} + {{r}^{2}}}}\left( {{{\rho }^{2}} + \theta } \right) + \frac{{\partial \theta }}{{\partial z}}} \right], \\ \frac{{\partial \theta }}{{\partial x}} = 2e_{1}^{2}x\left[ \begin{gathered} - \frac{{6a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right)\left( {1 - \frac{{2{{x}^{2}}}}{{a_{1}^{2} + {{r}^{2}}}}} \right) + \frac{{2a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left( {3{{x}^{2}} + 2{{y}^{2}}} \right) \hfill \\ - \frac{{{{y}^{2}}}}{{{{\rho }^{4}}}}\left( {2a_{1}^{2} - {{\rho }^{2}} + 2{{z}^{2}}} \right) - \frac{{{{x}^{2}}}}{{{{\rho }^{2}}}} \hfill \\ \end{gathered} \right], \\ \frac{{\partial \theta }}{{\partial y}} = 4e_{1}^{2}y\left\{ {\frac{{{{x}^{2}}}}{{{{\rho }^{4}}}}\left( {a_{1}^{2} + {{z}^{2}}} \right) + \frac{{a_{1}^{2}}}{{a_{1}^{2} + {{r}^{2}}}}\left[ {\frac{{6x_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right) + \frac{{3{{x}^{2}} + 2{{y}^{2}}}}{{a_{1}^{2} + {{r}^{2}}}} - 2} \right]} \right\}, \\ \frac{{\partial \theta }}{{\partial z}} = 2e_{1}^{2}z\left\{ {\frac{{{{y}^{2}} - {{x}^{2}}}}{{{{\rho }^{2}}}} + \frac{{2a_{1}^{2}}}{{{{{\left( {a_{1}^{2} + {{r}^{2}}} \right)}}^{2}}}}\left[ {2{{y}^{2}} - 3{{x}^{2}} + \frac{{6x_{1}^{2}}}{{a_{1}^{2} + {{r}^{2}}}}\left( {a_{1}^{2} - {{\rho }^{2}} + {{z}^{2}}} \right)} \right]} \right\}. \\ \end{gathered} $$
(21)
$$\begin{gathered} \frac{{\partial \Phi }}{{\partial \varepsilon }} = \left\{ \begin{gathered} - \frac{3}{2}\sum\limits_{n = 0}^\infty {\frac{{2n + 1}}{{n + 1}}} {{B}_{n}}{{\zeta }^{n}},\,\,\,\,\left| \zeta \right| < {{\zeta }^{*}}, \hfill \\ \frac{1}{{\pi \sqrt 2 }}\sum\limits_{n = 0}^\infty {\left\{ {8 - \left( {8n + 3} \right)\left[ {{{H}_{n}} - {\text{ln}}\left( {1 - \zeta } \right)} \right]} \right\}} {{B}_{n}}{{\left( {1 - \zeta } \right)}^{n}},\,\,\,\,\left| \zeta \right| > {{\zeta }^{*}}. \hfill \\ \end{gathered} \right. \hfill \\ \frac{{\partial \Phi }}{{\partial \zeta }} = \left\{ \begin{gathered} \mathop \sum \limits_{n = 1}^\infty \left[ {1 + \mu - \frac{{3\left( {2n + 1} \right)}}{{2\left( {n + 1} \right)}}\varepsilon + \frac{{4n + 1}}{{n + 1}}\nu } \right]n{{B}_{n}}{{\zeta }^{{n - 1}}},\,\,\,\,\left| \zeta \right| < {{\zeta }^{*}}, \hfill \\ \frac{1}{{\pi \sqrt 2 }}\sum\limits_{n = 0}^\infty {\left\{ {\left[ {1 - \left( {8n + 3} \right)\varepsilon + \mu + 4\left( {4n + 1} \right)\nu } \right]\left[ {1 - n\left( {{{H}_{n}} - {\text{ln}}\left( {1 - \zeta } \right)} \right) - 8n\left( {\varepsilon - 2\nu } \right)} \right]} \right\}{{B}_{n}}{{{\left( {1 - \zeta } \right)}}^{{n - 1}}}} ,\,\,\,\,\left| \zeta \right| > {{\zeta }^{*}} \hfill \\ \end{gathered} \right. \hfill \\ \frac{{\partial \Phi }}{{\partial \mu }} = \left\{ \begin{gathered} \sum\limits_{n = 0}^\infty {{{B}_{n}}{{\zeta }^{n}}} ,\,\,\,\,\left| \zeta \right| < {{\zeta }^{*}}, \hfill \\ \frac{1}{{\pi \sqrt 2 }}\sum\limits_{n = 0}^\infty {\left[ {{{H}_{n}} - {\text{ln}}\left( {1 - \zeta } \right)} \right]} {{B}_{n}}{{\left( {1 - \zeta } \right)}^{n}},\,\,\,\,\left| \zeta \right| > {{\zeta }^{*}}, \hfill \\ \end{gathered} \right. \hfill \\ \frac{{\partial \Phi }}{{\partial \nu }} = \left\{ \begin{gathered} \mathop \sum \limits_{n = 0}^\infty \frac{{4n + 1}}{{n + 1}}{{B}_{n}}{{\zeta }^{n}},\,\,\,\,\left| \zeta \right| < {{\zeta }^{*}}, \hfill \\ \frac{4}{{\pi \sqrt 2 }}\mathop \sum \limits_{n = 0}^\infty \left\{ {\left( {4n + 1} \right)\left[ {{{H}_{n}} - {\text{ln}}\left( {1 - \zeta } \right)} \right] - 4} \right\}{{B}_{n}}{{\left( {1 - \zeta } \right)}^{n}},\,\,\,\,\left| \zeta \right| > {{\zeta }^{*}}{\text{.}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$
(22)

Relations (7)–(11) and (15)–(22) represent a complete set of formulas to calculate the right-hand sides of the evolution equations (14).

In view of the properties of the function V (see the remark in the previous section), system (14) has two particular solutions or integrable cases.

Case 1. If sini = 0, then the orbital plane of point Р coincides with the orbital plane of the perturbing point J. By symmetry, it turns out that di/dτ = 0. However, in this planar solution at any а, а1, and e1, in addition to regular orbits, there exist irregular ones intersecting (but not linked) with the orbit of point J (Vashkov’yak, 1982).

Case 2. If cos i = 0 and sinΩ = 0, then in the elliptic problem under consideration the orbital plane of point Р is orthogonal to the orbital plane of the perturbing point J and passes through its line of apsides. By symmetry, it turns out that di/dτ = 0 and dΩ/dτ = 0. The above formulas of the quadratic approximation in е1 allow this to be also verified directly. Indeed, for cosi = 0 and sinΩ = 0 we have

$$\begin{gathered} \delta = {\text{sign}}\left( {\cos \Omega } \right) = \pm 1, \\ {{p}_{1}} = \delta \cos \omega ,\,\,\,\,{{p}_{2}} = 0,\,\,\,\,{{p}_{3}} = \sin \omega , \\ {{q}_{1}} = - \delta \sin \omega ,\,\,\,\,{{q}_{2}} = 0,\,\,\,\,{{q}_{3}} = \cos \omega , \\ {{r}_{1}} = 0,\,\,\,\,{{r}_{2}} = - \delta ,\,\,\,\,{{r}_{3}} = 0, \\ x = a\delta \left[ {\left( {\cos E - e} \right)\cos \omega - \sin \omega \sqrt {1 - {{e}^{2}}} \sin E} \right], \\ y = 0, \\ z = a\left[ {\left( {\cos E - e} \right)\sin \omega + \cos \omega \sqrt {1 - {{e}^{2}}} \sin E} \right], \\ \left\| {\begin{array}{*{20}{c}} {\frac{{\partial w}}{{\partial i}}} \\ {\frac{{\partial w}}{{\partial \Omega }}} \end{array}} \right\| = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\left( {1 - e\cos E} \right)} \left\| {\begin{array}{*{20}{c}} {\frac{{\partial \tilde {V}}}{{\partial i}}} \\ {\frac{{\partial \tilde {V}}}{{\partial \Omega }}} \end{array}} \right\|dE. \\ \end{gathered} $$
(23)

In this case,

$$\begin{gathered} \left\| {\begin{array}{*{20}{c}} {\frac{{\partial \tilde {V}}}{{\partial i}}} \\ {\frac{{\partial \tilde {V}}}{{\partial \Omega }}} \end{array}} \right\| = \frac{{\partial \tilde {V}}}{{\partial y}}\left\| {\begin{array}{*{20}{c}} {\frac{{\partial y}}{{\partial i}}} \\ {\frac{{\partial y}}{{\partial \Omega }}} \end{array}} \right\| = \frac{{\partial \tilde {V}}}{{\partial y}}\left\| {\begin{array}{*{20}{c}} { - \delta z} \\ x \end{array}} \right\| = \frac{{{{a}_{1}}}}{{\sqrt {a_{1}^{2} + {{r}^{2}}} }}\frac{{\partial \Phi }}{{\partial y}}\left\| {\begin{array}{*{20}{c}} { - \delta z} \\ x \end{array}} \right\| \\ = \frac{{{{a}_{1}}}}{{\sqrt {a_{1}^{2} + {{r}^{2}}} }}\left( {\frac{{\partial \Phi }}{{\partial \varepsilon }}\frac{{\partial \varepsilon }}{{\partial y}} + \frac{{\partial \Phi }}{{\partial \zeta }}\frac{{\partial \zeta }}{{\partial y}} + \frac{{\partial \Phi }}{{\partial \mu }}\frac{{\partial \mu }}{{\partial y}} + \frac{{\partial \Phi }}{{\partial \nu }}\frac{{\partial \nu }}{{\partial y}}} \right)\left\| {\begin{array}{*{20}{c}} { - \delta z} \\ x \end{array}} \right\|{\text{.}} \\ \end{gathered} $$
(24)

It is easy to verify that at y = 0 the derivatives of the functions ε, ζ, μ, and ν with respect to y become zero, so that \(\frac{{\partial w}}{{\partial i}} = \frac{{\partial w}}{{\partial \Omega }} = 0\) and \(\frac{{di}}{{d\tau }} = \frac{{d\Omega }}{{d\tau }} = 0.\)

Equations (14) simplified for this case of orthogonal-apsidal orbits take the form

$$\frac{{de}}{{d\tau }} = - \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial \omega }},\,\,\,\,\frac{{d\omega }}{{d\tau }} = \frac{{\sqrt {1 - {{e}^{2}}} }}{e}\frac{{\partial w}}{{\partial e}}.$$
(25)

A general qualitative study of this case by taking into account the possible intersections of the orbits of points Р and J was carried out by a numerical-analytical method in Vashkov’yak (1984) for arbitrary a, а1, and е1. In this paper greater attention is given to linked orbits and, in particular, to the stationary solutions of Eqs. (25) existing at ω0 = 0, π. It can be shown that, in this case, \(\frac{{\partial w}}{{\partial \omega }} = 0\)and the stationary eccentricities themselves are determined as the roots of the transcendental equation

$$\frac{{\partial w\left( {a,{{a}_{1}},{{e}_{1}},{{e}_{0}},{{\omega }_{0}} = 0,\pi ;{{\Omega }_{0}} = 0,\pi } \right)}}{{\partial e}} = 0.$$
(26)

ON THE EVOLUTION OF SOME HYPOTHETICAL AND REAL COMETARY ORBITS IN THE SOLAR SYSTEM MODEL

First we will turn to the linked orbits of point Р highly inclined to the reference plane. In the integrable case of orthogonal-apsidal orbits, a numerical solution of Eq. (26) makes it possible to find the stationary values of the eccentricity е0 at given ω0 = 0°, 180°, Ω0 = 180° and fixed parameters а, а1, е1. In addition, it can be shown that the values of е0 depend on ω0 and Ω0 only through the combination δ1 = sign(cosω0cosΩ0) = ±1. However, the difference in е0 at different signs of δ1 is fairly small and ~\(e_{1}^{2}\).

At an inclination and longitude of the ascending node different from those adopted in case 2, all of the orbital elements will change with time. Our numerical integration of the evolution system (14) by the Runge–Kutta method at а1 = 5.2 AU, е1 = 0.048, and the mass ratio m/m1 in the Sun–Jupiter system makes it possible to estimate such changes for fictitious (or hypothetical) cometary orbits. Tables 1 and 2 give such an estimate in the time interval t* = 500 000 years for orbits with a semimajor axis а = 10а1 = 52 AU, e0(δ1 = 1) = 0.9890, е0(δ1 = –1) = 0.9905. These tables present

$$\begin{gathered} {{\Delta }_{1}} = {\text{max}}\left| {e\left( {t{\text{*}}} \right)-{{e}_{0}}} \right|,\,\,\,\,{{\Delta }_{2}} = {\text{max}}\left| {i(t*)-{{i}_{0}}} \right|, \\ {{\Delta }_{3}} = {\text{max}}\left| {\omega (t*)-{{\omega }_{0}}} \right|,{{\Delta }_{4}} = {\text{max}}\left| {\Omega (t*)-{{\Omega }_{0}}} \right|. \\ \end{gathered} $$
Table 1. Maximum changes of the elements e, i, ω, Ω in a time interval of 500 000 years for i0 = 90°, 90° ± 5°
Full size table
Table 2.   The same as Table 1, but for i0 = 90° ± 30°
Full size table

Table 1 was compiled for three values of i0 = 90°, 85°, 95°. In the exact solution of Eqs. (14)i0 = 90°, Ω0 = 0°, 180° the deviations are zero and, therefore, the corresponding rows are omitted. At Ω0 = 0 and 180° the results for i0 = 95° identical to the corresponding data for i0 = 85° are also omitted.

The initial deviations in i0 and Ω0 from their equilibrium values at t = t* lead to insignificant changes in the shape of the orbit (Δ1, Δ3), but to a noticeable change in its orientation (Δ2 reaches 24°, Δ4 is about 32°).

Table 2 was compiled for more significant initial deviations of the orbit from the orthogonal one, i0 = 90° ± 30°. At Ω0 = 0° and 180° it also contains the results for i0 = 120° identical to the corresponding data for i0 = 60°.

In this case, the inclination also remains close to the initial one, but the deviations of the remaining elements are tens of degrees, reaching approximately 75°.

Below, we will consider the orbits of point Р linked with the orbit of point J, but with an arbitrary spatial orientation. The evolution of such orbits is usually studied using numerical methods even in the integrable doubly averaged circular problem (е1 = 0) due to the absence of a rigorous analytical expression for the averaged perturbing function. The families of phase trajectories in the (еcosω, esinω) plane constructed as equipotential contours of the function W are presented in Ito and Ohtsuka (2019, Section 5.8, Fig. 24). These families correspond to the hypothetical linked orbits of point Р for three pairs of values of the ratio a/a1 and the constant of the integral с1. In all three cases considered

$$\begin{gathered} {\mathbf{I}}\,({a \mathord{\left/ {\vphantom {a {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}} = {\text{ }}0.9,\,\,{{c}_{1}} = {\text{ }}0.4);~\,\,\,\,~{\mathbf{II}}\,({{{{a}_{1}}} \mathord{\left/ {\vphantom {{{{a}_{1}}} a}} \right. \kern-0em} a} = {\text{ }}0.7,\,\,{{c}_{1}} = {\text{ }}0.6); \\ ~{\mathbf{III}}\,({{{{a}_{1}}} \mathord{\left/ {\vphantom {{{{a}_{1}}} a}} \right. \kern-0em} a} = {\text{ }}0.8,\,\,{{c}_{1}} = {\text{ }}0.313) \\ \end{gathered} $$

there exist stationary center-type singular points and closed periodic trajectories enclosing them in the phase plane.

The ellipticity of the orbit of the perturbing point J, naturally, leads to qualitative changes of the families of trajectories in the circular problem. Since the equations for е and ω are not decoupled from the remaining ones, as is the case at е1 = 0, due to the absence of the integral с1 in the elliptic problem, the evolution of these elements can be traced only in projection of the phase trajectory onto the (еcosω, esinω) or (ω, е) plane. In this paper we numerically integrated system (14) for а1 = 5.2 AU, е1 = 0.048, and the mass ratio m/m1 in the Sun-Jupiter system. The difference of this ratio from the one adopted in the calculations by Ito and Ohtsuka (2019) for the Sun–(Earth + Moon) system does not affect the structure of the phase trajectoriesне, but leads only to a change in the time scale.

For a comparison with the results of the circular problem in cases I, II, and III, out of all families of integral curves in the circular problem we chose the trajectories with ω0 = 180° and initial е0 = 0.55, 0.4, and 0.65, respectively. The initial inclinations were calculated from е0 and с1 as \({{i}_{0}} = {\text{arccos}}\sqrt {\frac{{{{c}_{1}}}}{{1 - e_{0}^{2}}}} \), while the initial longitude of the ascending node Ω0 was taken to be zero.

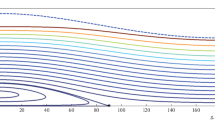
Figures 1–3 show the trajectories for cases I, II, and III, respectively, and fragments of the polar diagrams with plotted numerical values of the angles ω and radii е. The circles and triangles mark the initial and final points, respectively. The time intervals are 100 000 years for cases I, II and 500 000 years for case III. The dashed lines are the so-called “separatrices”, which are not integral curves and correspond to the intersections of the orbits of points P and J. They are defined by the equations

$$\frac{{a\left( {1 - {{e}^{2}}} \right)}}{{{{a}_{1}}\left( {1 \pm {{e}_{1}}} \right)}} \pm e{\text{cos}}\omega - 1 = 0.$$
Fig. 1.
figure 1

Polar diagram or projection of the phase trajectory onto the (еcosω, esinω) plane for case I (е0 = 0.55, i0 = 40°.78).

Full size image
Fig. 2.
figure 2

Same as Fig. 1, but for case II (е0 = 0.4, i0 = 32°.31).

Full size image
Fig. 3.
figure 3

Same as Fig. 1, but for case III (е0 = 0.65, i0 = 42°.59).

Full size image

In all three cases, the closed periodic trajectories of the circular problem are modified and become non-periodic, nevertheless, retaining an oscillatory pattern and remaining in the regions of linked orbits. The amplitude of these oscillations can both decrease (Figs. 1, 3) and increase (Fig. 2) with time.

However, the eccentricity of Jupiter’s orbit can also lead to qualitative changes in the behavior of the trajectory. Figure 4 shows a chaotic trajectory that begins in the ω libration region at ω0 = 180°, then passes into the circulation region, and returns to the libration region, but relative to ω = 0. The initially linked orbit of point Р intersects the orbit of the perturbing point J as it evolves, exiting from one linking region, then traverses the region of unlinked orbits and enters another linking region.

Fig. 4.
figure 4

Example of a chaotic trajectory with a change of the regimes of variations in the argument of perihelion and with intersections of the orbit of the perturbing point in a time interval of 55000 years for case I, but at е0 = 0.475 and i0 = 44°.052.

Full size image

Interestingly, real cometary orbits almost orthogonal to the ecliptic, with the above types of evolution, are also found within the model under consideration (Sun‒Jupiter‒comet). If we make a selection by perihelion distance q < 2 AU and inclination 85° < i < 95° on the set of cometary orbits presented in the JPL database (https://ssd.jpl.nasa.gov/sbdb_query.cgi#x), then only ten orbits remain in this sample. The evolution of seven of them is reduced to successive intersections of Jupiter’s orbit with passages of the linking regions. Figures 5–7 give an idea of the evolution of the remaining three orbits. In contrast to the previous figures, fragments of the (ω, е) plane are shown here not in the polar coordinate system, but in the rectangular one, which is more convenient for highly elliptical orbits. The up-to-date (initial) values of the elements for our numerical integration were taken from the above JPL database. The initial and final values in the (ω – е) plane are marked by the circles and triangles, respectively.

Fig. 5.
figure 5

Variations in the argument of perihelion and orbital eccentricity for comet C/1955 L1 (Mrkos) in a time interval of 1 Myr in a simplified model (Sun–Jupiter–comet).

Full size image
Fig. 6.
figure 6

Same as in Fig. 5, but for comet C/1861 J1 (Great comet) and a time interval of 3 Myr.

Full size image
Fig. 7.
figure 7

Same as Fig. 6, but for comet 122P/de Vico.

Full size image

Figure 5 presents the variations in orbital elements for comet C/1955 L1 (Mrkos) in a time interval of 1 Myr. The motion of the phase point begins in the region of orbital linking and ω libration, while the corresponding stationary value of the eccentricity calculated by solving Eq. (26) is е0 = 0.9818. The phase point has no time to make one revolution relative to the libration center, while the trajectory passes through the “separatrix” corresponding to the intersection of the cometary orbit with Jupiter’s orbit. After the relatively short time interval of ~200 000 years, there occur the second intersection of these orbits and the entry into another linking region with a ω libration center offset by 180° from the initial one. In this case, the initially prograde motion of the comet becomes retrograde already in 100 000 years, while the inclination, increasing monotonically, reaches about 115°.

Figure 6 presents the variations in orbital elements for comet C/1861 J1 (Great comet) in a time interval of 3 Myr. The motion of the phase point begins and remains in the region of orbital linking and ω libration, while the corresponding stationary value of the eccentricity is е0 = 0.9820. In this case, the initially prograde motion of the comet becomes retrograde in 2 Myr, while the inclination reaches about 132° at a minimum of 31°.

Figure 7 presents the variations in orbital elements for comet 122P/de Vico in a time interval of 3 Myr. The motion of the phase point also begins and remains in the region of orbital linking and ω libration, while the corresponding stationary value of the eccentricity is е0 = 0.9630. The motion changes with time from prograde to retrograde and vice versa. The extreme inclinations are 43° and 138°.

In conclusion, it should be recalled that all the above examples of orbital evolution and, in particular, the examples of libration of the argument of perihelion were constructed within the adopted model (Sun‒Jupiter‒comet). However, the real motions of comets in the Solar System can differ from their model motions even qualitatively. These differences are due to the neglect of the influence of the remaining planets, except for Jupiter, and the averaged model of the problem. For example, in the rigorous solution of the complete system of non-averaged differential equations the libration of the argument of perihelion can change to its circulation. The orbit of comet 122P/de Vico is an example of chaotic orbital evolution in a real cometary medium, but this property is found only in the non-averaged Solar System model including both several perturbing bodies (Baily et al. 1992) and one body (Ito and Ohtsuka, 2019; Section 5.8, Fig. 25).

Regarding the methodology of the work described in this paper, note that owing to the studies performed relatively recently and reflected in the monographs and the paper by Kondrat’ev (2007, 2012) and Antonov et al. (2008), the representation of the force function for an elliptical Gaussian ring was obtained in a closed form without expansions in terms of any parameters. However, its practical use involves well-known difficulties and may in future be the subject of a special study.