1 Introduction

Marine autonomous vehicles have been impressively improved during the last decade. Their applications are very extensive ranging from inspection tasks to accomplishing complex underwater explorations. Nowadays, intelligent transportation using the autonomous platforms has become a new research area as state of the art for researcher. In a few years from now, autonomous ships are expected to be used in the sea transportation to carry the goods without assistance of human operator in their navigation. The International Maritime Organization (IMO) specifies four degrees of autonomy for autonomous ships:

ship with automated processes and decision support: seafarers are on board to operate and control shipboard systems and functions. Some operations may be automated.

Remotely controlled ship with seafarers on board: the ship is controlled and operated from another location, but seafarers are on board.

Remotely controlled ship without seafarers on board: the ship is controlled and operated from another location. There are no seafarers on board.

Fully autonomous ship: the operating system of the ship is able to make decisions and determine actions by itself.

As can be seen, the role of human operator is expected to be reduced throughout the development of autonomous ships. It can also be expected that during this process, the exploited ships may fuse two or more degrees of autonomy. The main difference between manned and unmanned ships in terms of control systems is that autonomous ship control system relies on three dependent subsystems which are known as navigation, guidance and control (NGC) systems, while there is no a full decision-making system for the manned ships in particular for the collision avoidance and steering goals.

Designing a high-performance motion control system for these platforms is most significant challenge due to the complexity and nonlinearity of the ship dynamics as well as time-varying external disturbances. There are two groups of perturbations, which affect the autonomous ship’s motion. The first group stems from the uncertainties in autonomous ship’s dynamics caused by parameter variation in the inertia, particularly when there is a variable load carried by ship. Another group is a result of external perturbations including deterministic and time-varying stochastic disturbances, which are induced by the wind, wave and ocean currents. To address these two kinds of perturbations simultaneously a robust-adaptive control approach should be adopted. A brief literature review of related solutions in the marine robotics control area is provided below.

The main author of this paper proposed a perturbation compensating algorithm addressing accurate path tracking of a marine autonomous vehicle in the presence of environmental disturbances—a robust Model Predictive Control (MPC) [1]. In [2], the author presented a robust strategy based on Time-Delay Control (TDC) algorithm and Terminal Sliding Mode (TSM) designed to control an Underwater Vehicle-Manipulator System (UVMS). In this work, TDC was used to estimate some perturbations using a Time-Delay Estimation (TDE) part. In addition, SMC was adopted for withstanding other perturbations, which cannot be estimated by TDC. As for other robust control strategies, which were adopted to address trajectory tracking control of marine robots, some researches upon the underwater robotics were done in [3,4,5,6]. A robust and adaptive controller based on the H-infinity approach was proposed in [7], where some of ship’s parameters were unknown. A related research conducted in [8] by the main author of this paper proposed to use an approximate dynamic programming to optimally adjust the control gains in a super-twisting sliding mode controller for a Maritime Autonomous Surface Ship (MASS). A nonlinear MPC was used for an Unmanned Surface Vehicle (USV) in [9]; however, a conventional MPC was used there and it could not guarantee sufficient robustness. In addition, the environmental disturbances in ocean or sea have not been considered there. In [10], a backstepping control approach combined with sliding mode control algorithm was designed to address the trajectory tracking problem of an underactuated USV. An autonomous robotic boat was presented in [11], and for its controller, a nonlinear model predictive control (NMPC) was adopted. However, the uncertainty effect, resulting from the changes in inertia, was not taken into account there. Another weakness of this work was neglecting the influences due to deterministic and stochastic disturbances. In [12], a nonlinear disturbance observer was designed for an autonomous vessel to estimate unknown parameters and external disturbances. However, this observer was able to estimate only constant disturbances. A control law for path tracking of marine autonomous vessel was adopted in [13], where a singular perturbation method was used to decompose the system into two Lyapunov-based control subsystems. For tuning of gains in a PID controller of USV, a self-regulator PID was designed in [14] in which coefficients have been regulated by the fuzzy rules.

In general, despite significant progress, none of the above-mentioned nonlinear conventional robust control algorithms managed to successfully address internal uncertainties in autonomous ships and time-varying stochastic disturbances upon them with sufficient accuracy. To successfully deal with these perturbations, other algorithms have been proposed as adaptive robust approaches. For this case, a disturbance observer was proposed in [15] for the trajectory tracking of Unmanned Marine Vehicles (UMVs). Researchers in this work adopted an adaptive law to estimate and compensate the disturbance observer error. Following this, by combining a nonlinear disturbance observer, dynamic surface control and adaptive robust backstepping together, they developed a dynamic surface adaptive robust controller. In another robust-adaptive approach [16], a nonlinear tracking differentiator combined with a reduced-order extended state observer (ESO) was adopted to estimate external disturbances and uncertainties with a small estimation error. Another interesting work has been accomplished using the finite-time extended state observer-based distributed formation control for marine surface vehicles with input saturation and external disturbances. The time-varying external disturbances induced by winds, waves, and ocean currents are considered there in the computer simulation [17]. Authors in [18] proposed an MPC approach combined with an adaptive line-of-sight (LOS) guidance for path following of Autonomous Surface Vehicles (ASVs). However, the conventional MPC algorithm is not a robust algorithm inherently. Hence, the robustness analysis should have discussed in aforementioned research. By combining the adaptive continuous sliding mode control with backstepping technique, an adaptive-robust control algorithm was adopted in [19]. Another backstepping-based control algorithm was presented in [20], in which a sliding mode disturbance observer is designed and applied to the path-following system of a container ship to estimate the time-varying environmental disturbances. Concerning some artificial intelligence-based control algorithms for the autonomous marine platforms, an adaptive neural network (NN) controller for fine trajectory tracking of surface vessels with uncertain environmental disturbances was presented in [21]. A novel robust-adaptive formation control scheme based on the Minimal Learning Parameter (MLP) algorithm and the Disturbance Observer (DOB) was presented in [22]. Using the MLP algorithm, a remarkable descent in tunable parameters for the controller and DOB has been achieved, which in turn led to great reduction of the online computational time.

An artificial intelligence-based robust control strategy in the form of a multi-layer neural network was combined with adaptive robust techniques in [23]. This resulted in the control system of great robustness against uncertain nonlinearities and environmental disturbances. The proposed approach efficiently compensated both parametric and non-parametric uncertainties including time-varying disturbances induced by waves and ocean currents.

In this study, we propose an adaptive-robust strategy for path following control of an autonomous ship under deterministic and stochastic disturbances induced by winds, waves and ocean currents. This strategy includes a learning-based algorithm, which is based on the Actor-Critic Approximate Dynamic Programming (ACADP), as an adaptive part and a TDC control algorithm as a robust part. Furthermore, the proposed control algorithm brings an optimal characteristic, which results from solving the Hamilton–Jacobi–Bellman (HJB) equation using Approximate Dynamic Programming (ADP) procedure, for the conventional robust TDC algorithm.

The rest of this paper is organized as follows: an autonomous ship dynamical model associated with all of the time-varying external disturbances including deterministic and stochastic parts as well as uncertainties is described in the next section. The third section is dedicated to describe a time-delay control algorithm. In Sect. 4, the proposed hybrid Actor-Critic Time-Delay Control (AC-TDC) as an adaptive-robust approach is explained. In Sect. 5, the computer simulation results and comparison of them are shown and discussed to confirm high performance of the proposed hybrid control. Finally, the conclusion of this research is provided in Sect. 6.

2 Nonlinear dynamics of autonomous ships

In the control systems designed for the maneuvering control of ships, it is common to consider a 3 DOFs model as a coupled surge–sway–yaw model and thus neglect heave, roll and pitch motions. Therefore, the nonlinear dynamics of an autonomous ship can be described in form of 3 DOFs as follows:

$$\left\{ {\begin{array}{*{20}c} {M\dot{\vartheta } + {\text{C}}\left( \vartheta \right)\vartheta + {\text{D}}\left( \vartheta \right)\vartheta = {\text{U}}_{{\text{c}}} + {\text{MR}}^{{\text{T}}} \left( \psi \right)\Gamma } \\ {\mathop {~\eta }\limits^{} = {\text{R}}\left( \psi \right)\vartheta } \\ \end{array} } \right.$$
(1)

where velocity and position vectors are defined as \({\vartheta }(\mathrm{t})={[u(\mathrm{t}),v(\mathrm{t}),r(\mathrm{t})]}^{\mathrm{T}}\) and \(\upeta (\mathrm{t})={[\mathrm{x}(\mathrm{t}),\mathrm{y}(\mathrm{t}),\uppsi (\mathrm{t})]}^{\mathrm{T}}\), respectively. \(u(\mathrm{t})\) and \(v(\mathrm{t})\) are speed signals of autonomous ship along the \(\mathrm{x}\)- and \(y\)-axes, respectively. In addition, \(r(\mathrm{t})\) is an angular speed of ship around the \(y\)-axis. The respective frames of surge, sway and yaw motions are shown in Fig. 1. In the aforementioned equation, the rotation matrix \(\mathrm{R}\left(\uppsi \right)=\left[\begin{array}{ccc}\mathrm{cos}(\uppsi )& -\mathrm{sin}(\uppsi )& 0\\ \mathrm{sin}(\uppsi )& \mathrm{cos}(\uppsi )& 0\\ 0& 0& 1\end{array}\right]\) is adopted to transfer coordinates from the body-fixed frame to the inertial frame.

Fig. 1
figure 1

Autonomous ship with three degrees of freedom [31]

Full size image

For presenting Eq. (1) in a standard form based on position vector, we can rewrite it using the property of the rotation matrix \(\dot{\upeta }=\mathrm{R}\left(\uppsi \right){\vartheta }\) as

$$\mathrm{M}\left(\upeta \right)\ddot{\upeta }+\mathrm{C}\left(\upeta ,\dot{\upeta }\right)\dot{\upeta }+\mathrm{D}\left(\upeta ,\dot{\upeta }\right)\dot{\upeta }={\mathrm{U}}_{\mathrm{c}}+\Gamma $$
(2)

where all the related components of each matrix in Eq. (2) were presented in [24] analogous to the dynamics of robotic manipulators. \({\mathrm{U}}_{\mathrm{c}}={[{\mathrm{F}}_{\mathrm{x}},{\mathrm{F}}_{\mathrm{y}},{\uptau }_{\uppsi }]}^{\mathrm{T}}\) and \(\Gamma \) are control inputs and external disturbances including deterministic and stochastic disturbances, respectively. These time-varying stochastic disturbances are induced by the winds, waves and ocean currents, which are shown by the vector of \(\Gamma ={[{\Gamma }_{\mathrm{u}},{\Gamma }_{\mathrm{v}},{\Gamma }_{\mathrm{r}}]}^{\mathrm{T}}\). In this research, we consider these disturbances for applying upon the autonomous ship with 3 DOFs, in which each term of \({\Gamma }_{\mathrm{u}}\), \({\Gamma }_{\mathrm{v}}\) and \({\Gamma }_{\mathrm{r}}\) consists of the constant deterministic components and the time-varying stochastic parts [25]. Therefore, we can rewrite them as follows:

$$\left\{\begin{array}{c}{\boldsymbol{\Gamma }}_{u}={\stackrel{-}{\boldsymbol{\Gamma }}}_{u}+{\stackrel{\sim }{\boldsymbol{\Gamma }}}_{u}\\ {\boldsymbol{\Gamma }}_{v}={\stackrel{-}{\boldsymbol{\Gamma }}}_{v}+{\stackrel{\sim }{\boldsymbol{\Gamma }}}_{v}\\ {\boldsymbol{\Gamma }}_{r}={\stackrel{-}{\boldsymbol{\Gamma }}}_{r}+{\stackrel{\sim }{\boldsymbol{\Gamma }}}_{r}\end{array}\right.$$
(3)

where \(\stackrel{-}{*}\) and \(\stackrel{\sim }{*}\) denote deterministic and stochastic components of external disturbances, respectively. Regarding stochastic components, a Wiener process is used to model them as follows [25]:

$$\left\{\begin{array}{c}{\stackrel{\sim }{\boldsymbol{\Gamma }}}_{u}={\Delta }_{1}(t){\dot{w}}_{1}\\ {\stackrel{\sim }{\boldsymbol{\Gamma }}}_{v}={\Delta }_{2}(t){\dot{w}}_{2}\\ {\stackrel{\sim }{\boldsymbol{\Gamma }}}_{r}={\Delta }_{3}(t){\dot{w}}_{3}\end{array}\right.$$
(4)

where \({\Delta }_{1}\), \({\Delta }_{2}\), and \({\Delta }_{3}\) denote time-varying covariance and \({w}_{i}\) is a Wiener process:

$$\mathsf{M}=\left[\begin{array}{ccc}{\mathrm{m}}_{11}& {\mathrm{m}}_{12}& {\mathrm{m}}_{13}\\ {\mathrm{m}}_{21}& {\mathrm{m}}_{22}& {\mathrm{m}}_{23}\\ {\mathrm{m}}_{31}& {\mathrm{m}}_{32}& {\mathrm{m}}_{33}\end{array}\right]\in {\mathbb{R}}^{3}, \mathrm{M}\left(\upeta \right)\in {\mathbb{R}}^{3}, $$

where \(\mathrm{C}\left(\upeta ,\dot{\upeta }\right)\in {\mathbb{R}}^{3}\), \(\mathrm{D}\left(\upeta ,\dot{\upeta }\right)\in {\mathbb{R}}^{3}\) are constant inertia matrix, time-varying inertia matrix, time-varying Coriolis matrix, and time-varying hydrodynamic damping matrix including both linear and nonlinear parts, respectively. Indeed, with taking into account the nonlinear damping parts, the matrix \(\mathrm{D}\left(\upeta \right)\) is changed to the form \(\mathrm{D}\left(\upeta ,\dot{\upeta }\right)\) and nonlinear coefficients (\({\mathrm{d}}_{\mathrm{ij}})\) are dependent on velocity vector \(\dot{\upeta }=\mathrm{R}\left(\uppsi \right){\vartheta }\).

2.1 Time-delay control

Let us assume that the desired paths, which must be followed by the autonomous ship, are denoted by the vector \({\eta }_{d}\). A control strategy of the autonomous ship path following is the adopted to provide a position vector \(\eta \) for following the \({\eta }_{d}\). Let us define the tracking error and its first and second derivatives as

$$e\left(t\right)={\eta }_{d}\left(t\right)-\eta \left(t\right)$$
(5)
$$\dot{e}\left(t\right)={\dot{\eta }}_{d}\left(t\right)-\dot{\eta }\left(t\right)$$
(6)
$$\ddot{e}\left(t\right)={\ddot{\eta }}_{d}\left(t\right)-\ddot{\eta }\left(t\right)$$
(7)

We regard parameters of \({e}_{s}\), \({e}_{sw}\) and \({e}_{y}\) as components of the tracking error vector \(e\left(t\right)\) for an autonomous ship, which are surge, sway and yaw tracking errors, respectively:

$${e}_{s}(t)={x}_{d}(t)-x(t)$$
(8)
$${e}_{sw}(t)={y}_{d}(t)-y(t)$$
(9)
$${e}_{y}(t)={\uppsi }_{d}(t)-\uppsi (\mathrm{t})$$
(10)

where \(\eta \), \({\eta }_{d}\) are supposed to be measurable. In Eq. (2) from the modeling section let \(\mathrm{M}\left(\upeta \right)\) be approximated with \(\stackrel{-}{\mathrm{M}}\) as a constant matrix. Then, Eq. (2) can be rewritten as

$$\stackrel{-}{M}\ddot{\eta }+N\left(\eta ,\dot{\eta }\right)+H\left(\eta ,\dot{\eta },\ddot{\eta }\right)={U}_{c}$$
(11)

where nominal term \(N\left(\eta ,\dot{\eta }\right)\) and perturbation term \(H\left(\eta ,\dot{\eta },\ddot{\eta }\right)\) including uncertainties \({C}_{h}\), \({D}_{h}\) and external deterministic and time-varying stochastic disturbances \(\Gamma \) are expressed as follows:

$$\left\{\begin{array}{c}N\left(\eta ,\dot{\eta }\right)={C}_{n}\left(\eta ,\dot{\eta }\right)\dot{\eta }+{D}_{n}\left(\eta ,\dot{\eta }\right)\dot{\eta } \\ \\ H\left(\eta ,\dot{\eta },\ddot{\eta }\right)=\left[M\left(\eta \right)-\stackrel{-}{M}\right]\ddot{\eta }+\dots \\ {\dots C}_{h}\left(\eta ,\dot{\eta }\right)\dot{\eta }+{D}_{h}\left(\eta ,\dot{\eta }\right)\dot{\eta }- \Gamma \end{array}\right.$$
(12)

Following the control scheme of the Computed Torque Control (CTC) method, the control reads as

$${U}_{c}=\stackrel{-}{M}{u}_{CTC}+ \stackrel{\sim }{H}\left(\eta ,\dot{\eta },\ddot{\eta }\right)$$
(13)
$${u}_{CTC}={\ddot{\eta }}_{d}\left(t\right)+{k}_{d}\dot{e}+{k}_{p}e$$
(14)

where \(\stackrel{\sim }{H}\), \({k}_{d}\) and \({k}_{p}\) are the estimated value of perturbation of \(H\) using Time-Delay Estimation (TDE) part, and the derivative and the proportional gain matrices, respectively. Substituting Eqs. (13) and (14) into Eq. (11), final error dynamics is expressed as

$$\ddot{e}\left(t\right)+{k}_{d}\dot{e}\left(t\right)+{k}_{p}e\left(t\right)=0$$
(15)

In the TDE part of TDC, under the assumption that the time delay (\(L\)) is very small and equal to the simulation step size (\(L=\Delta t\)), \(H(t)\) can be approximated as

$$\stackrel{\sim }{H}(t)\cong {H}_{t-\Delta t}={U}_{c}\left(t-\Delta t\right)-\stackrel{-}{M}\ddot{\eta }(t-\Delta t)$$
(16)

Combining Eqs. (13), (14) and (16), the Time-Delay Control (TDC) law is obtained as

$${u}_{TDC}={u}_{TDC}\left(t-\Delta t\right)-\stackrel{-}{M}\ddot{\eta }\left(t-\Delta t\right)+\stackrel{-}{M}({\ddot{\eta }}_{d}\left(t\right)+{k}_{d}\dot{e}+{k}_{p}e)$$
(17)

In addition, the second derivative for the delayed positions is implemented using the following equation [2]:

$$\ddot{\eta }\left(t-L\right)=\frac{\eta \left(t\right)-2\eta \left(t-\Delta t\right)+\eta (t-2\Delta t)}{{\Delta t}^{2}}$$
(18)

To guarantee that the control system is stable, the constant matrix \(\stackrel{-}{M}\) should be adopted as follows:

$$\stackrel{-}{M}=\gamma I , 0<\gamma <2\Theta $$
(19)

where \(\Theta \) is the minimum bound of eigenvalues \({\lambda }_{i}\) of \(M\left(\eta \right)\) for all \(\eta \).

2.2 Actor-critic TDC and approximate dynamic programming

Although the induced perturbations can be partially estimated by the TDE utility in Eq. (16), this estimation will be inaccurate and bring in large estimation errors when the autonomous ship is encountered with the deterministic and time-varying stochastic disturbances with high amplitudes. Furthermore, if we improperly choose the constant components of the matrix \(\stackrel{-}{M}\), the estimation error of TDC will increase. To address this problem in TDC algorithm, we propose a backpropagation policy algorithm based on approximate dynamic programming and actor-critic learning for compensating of TDE error, particularly when \(\stackrel{-}{M}\) has not been truly tuned.

Let us define TDE error as

$$\varepsilon ={\stackrel{-}{M}}^{-1}\left[\stackrel{\sim }{H}-H\right]$$
(20)

Substituting Eqs. (16) into (17) and considering the above equation, Eq. (17) is rewritten as follows:

$${\mathrm{U}}_{\mathrm{c}}=\stackrel{\sim }{H}+\stackrel{-}{M}\left({\ddot{\eta }}_{d}\left(t\right)+{k}_{d}\dot{e}+{k}_{p}e\right)+$$
$$ {\stackrel{-}{M}}^{-1}\left[\stackrel{\sim }{H}-H\right]$$
(21)

Then, we adopt an optimal guaranteed cost control part \({u}_{AC}\) to incessantly compensate TDE errors and increase convergence speed.

Let us define \({u}_{AC}\) as a compensator signal as

$${u}_{AC}=\stackrel{\sim }{H}-H$$
(22)

where it is optimally generated using an approximate dynamic programming algorithm based on a propagation actor-critic learning approach.

Therefore, combining the TDC technique with optimal control theory, a robust TDC scheme is proposed for path following control of autonomous ships with an inherent uncertain dynamics and under deterministic and time-varying stochastic disturbances. According to Eqs. (16), (21) and (22), the hybrid AC-TDC is designed as

$${\mathrm{u}}_{\mathrm{AC}-\mathrm{TDC}}={u}_{TDC}+{\stackrel{-}{M}}^{-1}{u}_{AC}$$
(23)

where \({\mathrm{u}}_{\mathrm{TDC}}\) is a part of the proposed control law, which is used as a main part of the proposed robust strategy and \({u}_{AC}\) is an optimal guaranteed cost control part. The latter is used to partially compensate time-delay estimation error and attenuate stochastic disturbance effects.

As for the actor-critic network (which will be described in the next section), its reward function and the weights are updated when the autonomous ship encounters deterministic and stochastic disturbances that cannot be suppressed solely by TDC (Inaccurate Matrix \(\stackrel{-}{M}\)).

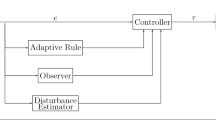
The learning-based part of the proposed control approach can be brought to designing an optimal control strategy. It is responsible for solving the HJB equations using Actor-Critic Approximate Dynamic Programming (ACADP) as a Policy Iteration (PI) algorithm. Figure 2 shows the scheme of this hybrid control approach.

Fig. 2
figure 2

Hybrid control scheme AC-TDC

Full size image

2.3 ACADP strategy

The proposed ACADP algorithm is based on a Heuristic Dynamic Programming (HDP), which is analogous to the formulation of reinforcement learning (RL) using the Temporal Difference (TD) learning methods [26,27,28,29,30,31,32].

Let us define a continuous utility or reward-to-go function as follows:

$$r\left(t\right)={g}_{r}\left(t\right)p{g}_{r}^{T}(t)$$
(24)

where the state-action vector \({g}_{r}\left(t\right)\) is regarded:

$${g}_{r}\left(t\right)=\left[\begin{array}{cc}{q}^{T}(t)& {u}_{AC}^{T}(t)\end{array}\right],$$

and \({u}_{AC}\left(t\right)={\left[\begin{array}{ccc}{u}_{AC}^{surge}& {u}_{AC}^{sway}& {u}_{AC}^{yaw}\end{array}\right]}^{T}\)

is the control law as a compensator part, which is delivered by an actor-critic approximate dynamic programming approach; \({\omega }_{1}\left(t\right)=\left[\begin{array}{cccccc}{e}_{s}(t)& {\dot{e}}_{s}(t)& {e}_{sw}(t)& {\dot{e}}_{sw}(t)& {e}_{y}(t)& {\dot{e}}_{y}(t)\end{array}\right]\), \(p\) is a positive-definite diagonal weighting matrix with a proper dimensions. \(q(t)\) is applied to the backpropagation actor neural network as an input vector in the input layer and its components are as

$${q\left(t\right)=\left[\begin{array}{cc}{\omega }_{1}(t-\Delta t)& {\omega }_{1}\left(t\right)\end{array}\right]}^{T}$$
(25)

where \(\Delta t\) is simulation step size for implementing of ACADP iteration algorithm. We adopt a total cost-to-go function as

$$J\left(q\left(t\right),{u}_{AC}\left(t\right)\right)$$
$$=\sum_{i=0}^{\infty }\zeta r(\left(q\left(t+i\Delta t\right),{u}_{AC}\left(t+i\Delta t\right)\right)$$
(26)

where \(r\left(q\left(t\right),{u}_{AC}\left(t\right)\right)\) is a positive-definite function if \(q(t)\ne 0\) and \({u}_{AC}\left(t\right)\ne 0\) and just equal to zero when \(q\left(t\right)=0\) and \({u}_{AC}\left(t\right)=0\). In above equation, \(\zeta \), \(0<\zeta <1\) is a discount factor. We adopt \({J}^{*}\left(q\left(t\right)\right)\) as a solution of (26). The result of minimization of the mentioned cost-to-go function, which satisfies HJB equation as an optimal solution, can be expressed as

$${J}^{*}\left(q\left(t\right)\right)=\underset{{u}_{\mathit{AC}}\left(t\right)}{\mathrm{min}}\left\{r\left(q\left(t\right),{u}_{AC}\left(t\right)\right)+\zeta {J}^{*}(q\left(t+\Delta t\right))\right\}$$
(27)

For solving Eq. (27), a policy iteration as an iterative method of reinforcement learning is used. In this research, the ACADP approach is used as a policy iteration to approximately solve HJB equation. In other words, \({J}^{*}\left(q\left(t\right)\right)\) is approximated by \(\widehat{J}(q\left(t\right))\), which is the output of the critic neural network. It also means that if estimation error of the TDE part (\(\varepsilon \)) is largely compensated and tracking errors including [\({e}_{s}(t)\), \({\dot{e}}_{s}(t)\), \({e}_{sw}(t)\), \({\dot{e}}_{sw}(t)\), \({e}_{y}(t)\), and \({\dot{e}}_{y}(t)\)] all converge to zero, the ACADP control policy \({u}_{AC}\left(t\right)=0\), \({J}^{*}\left(q\left(t\right)\right)=\widehat{J}\left(q\left(t\right)\right)=0\), and three positions of autonomous ship absolutely track their desired paths with an acceptable deviation in presence of deterministic and stochastic disturbances. In ACADP structure, the critic neural network is trained to appraise the performance of the current control policy, which is composited of actor control policy and TDC control policy.

In our design, the proposed control signal (AC-TDC) is generated by the sum of the TDC and the ACADP control laws. The outputs of the action network (\({\mathrm{u}}_{\mathrm{AC}}\)) are multiplied by the inverse of constant matrix (\({\stackrel{-}{M}}^{-1}\)) and then adaptively compensate perturbation effects, while output of TDC controller (\({\mathrm{u}}_{\mathrm{TDC}}\)) has a large estimation error and is not capable to overcome these stochastic disturbances. The related propagation algorithm of the ACADP strategy is implemented using MATLAB programming environment.

2.4 Critic neural network structure

This network is a function of (\(q\left(t\right)\), \({u}_{AC}\left(t\right)\), \({w}_{c}(t)\)), where \({w}_{c}(t)\) is the critic weight vector and the control law \({u}_{AC}\left(t\right)\) generated by the actor neural network is also the input to the critic neural network [33]. Therefore, critic’s input and output vectors read as

$$\left\{\begin{array}{c}{c}_{i}\left(t\right)={\left[\begin{array}{cc}{q\left(t\right)}^{T}& {{u}_{AC}\left(t\right)}^{T}\end{array}\right]}^{T}\\ {c}_{o}\left(t\right)=\widehat{J}\left(t\right)\end{array}\right.$$
(28)

Using standard algebra, one can derive from Eq. (26):\(\zeta J\left(t\right)+r\left(t\right)-J\left(t-\Delta t\right)=0\), where \(J\left(t\right)=J\left(q\left(t\right),{u}_{AC}\left(t\right)\right)\). Then, we can define an evaluation factor as an error function for the backpropagation critic neural network as follows:

$${e}_{c}\left(t\right)=\zeta \widehat{J}\left(t\right)-[\widehat{J}\left(t-\Delta t\right)-r\left(t\right)]$$
(29)

Regarding weights updating of the critic network, an objective function is minimized in the following equation:

$$\underset{{w}_{c}\left(t\right)}{\mathrm{min}}{E}_{c}\left(t\right)=\underset{{w}_{c}\left(t\right)}{\mathrm{min}}\frac{1}{2}{e}_{c}^{T}(t){e}_{c}(t)$$
(30)

Let us consider \({N}_{ci}\) and \({N}_{ch}\) as number of inputs and number of neurons in hidden layer of critic network, respectively. \({N}_{ci}=n+m\), \(n\) is number of inputs in actor network and \(m\) is number of outputs in actor network. We adopt a hyperbolic tangent threshold activation function for both actor and critic networks as follows:

$$\sigma \left(t\right)=\frac{1-{e}^{-t}}{1+{e}^{-t}}$$
(31)

where \({\sigma }_{c}\left(t\right)={\sigma }_{a}\left(t\right)=\sigma (t)\).

Let us define \({w}_{c1}\) and \({w}_{c2}\) as weights of the critic network for its input layer and its output layer, respectively. In addition, two new variables \({\varnothing }_{cj}(t)\) and \({\theta }_{cj}(t)\) for the jth neuron in hidden layer are expressed as

$${\varnothing }_{cj}\left(t\right)=\sum_{i=1}^{n}{q}_{i}\left(t\right){w}_{c1,ij}\left(t\right)+\sum_{i=1}^{m}{u}_{ACi}(t){w}_{c1,ij}\left(t\right) , j=1,\dots , {N}_{ch}$$
(32)
$${\theta }_{cj}\left(t\right)={\sigma }_{c}\left({\varnothing }_{cj}\left(t\right)\right)=\frac{1-{e}^{-{\varnothing }_{cj}\left(t\right)}}{1+{e}^{-{\varnothing }_{cj}\left(t\right)}} , j=1,\dots , {N}_{ch}$$
(33)
$$\widehat{J}\left(t\right)=\sum_{j=1}^{{N}_{ch}}{w}_{c2,j}\left(t\right){\theta }_{cj}\left(t\right)$$
(34)

We use a gradient-based adaption algorithm for updating the weights of the actor and critic neural networks. Therefore, the weights of the critic network can be calculated using this algorithm as follows:

$$\Delta {w}_{c2,j}\left(t\right)=-{\rho }_{c}\left(t\right)\frac{\partial {E}_{c}\left(t\right)}{\partial \widehat{J}\left(t\right)}.\frac{\partial \widehat{J}\left(t\right)}{\partial {w}_{c2,j}\left(t\right)}$$
(35)
$$\Delta {w}_{c1,ij}\left(t\right)=-{\rho }_{c}\left(t\right)\frac{\partial {E}_{c}\left(t\right)}{\partial \widehat{J}\left(t\right)}.\frac{\partial \widehat{J}\left(t\right)}{\partial {\theta }_{cj}\left(t\right)}.\frac{\partial {\theta }_{cj}\left(t\right)}{\partial {\varnothing }_{cj}\left(t\right)}.\frac{\partial {\varnothing }_{cj}\left(t\right)}{\partial {w}_{c1,ij}\left(t\right)}$$
(36)
$${w}_{c2,j}\left(t+\Delta t\right)={w}_{c2,j}\left(t\right)+\Delta {w}_{c2,j}\left(t\right)$$
(37)
$${w}_{c1,ij}\left(t+\Delta t\right)={w}_{c1,ij}\left(t\right)+\Delta {w}_{c1,ij}\left(t\right)$$
(38)

where \({\uprho }_{\mathrm{c}}\left(\mathrm{t}\right)\) is an adaptive learning rate of the critic neural network.

Suppose that the weights of the input-to-hidden layer are randomly initialized and retained fixed for both the action network (\({w}_{a1,ij})\) and the critic network (\({w}_{c1,ij})\). Based on the universal approximation theorem of neural networks, if the number of hidden-layer neurons is ample enough, then the approximation error can be regarded small. Therefore, we choose the updating strategy for the critic output weights (\({w}_{c})\) as the normalized gradient descent algorithm as in [29]:

$${w}_{c}\left(t+\Delta t\right)={{w}_{c}\left(t\right)-{\rho }_{c}\left(t\right){\sigma }_{c}\left(t\right)\left[\zeta {w}_{c}^{T}\left(t\right){\rho }_{c}\left(t\right)+r\left(t\right)-{w}_{c}^{T}\left(t-\Delta t\right){\sigma }_{c}\left(t-\Delta t\right)\right]}^{\mathrm{T}}$$
(39)

A critic neural network is depicted in Fig. 3, which consists of 3 layers, 15 inputs \({c}_{i}\left(t\right)={\left[\begin{array}{cc}{q\left(t\right)}^{T}& {{u}_{AC}\left(t\right)}^{T}\end{array}\right]}^{T}\) in input layer, 12 neurons in hidden layer and 1 output \({c}_{o}\left(t\right)=\widehat{J}\left(t\right)\) in output layer. As the simulation studies will show, this simple network structure turned out to result in a sufficient accuracy combined with a short update time.

Fig. 3
figure 3

Critic neural network

Full size image

2.5 Actor neural network structure

An actor neural network is a function of (\(q\left(t\right)\), \({w}_{a}(t)\)), whose input and output vectors are defined as follows:

$$\left\{\begin{array}{c}{a}_{i}\left(t\right)=q\left(t\right) \\ {a}_{o}\left(t\right)={u}_{AC}\left(t\right)\end{array}\right.$$
(40)

Let us define\({N}_{ai}\), \({N}_{ah}\) and \({N}_{ao}\) as number of inputs, number of neurons in hidden layer and number of outputs of an actor network, respectively.\({{u}_{AC}}_{k} , k=1\dots {N}_{ao}\). Analogically to the last section (procedure for the critic network design), we adopt three variables\({\varnothing }_{aj}(t)\), \({\theta }_{aj}(t)\) and\({\gamma }_{ak}(t)\). Let us label \({w}_{a1}\) and \({w}_{a2}\) as weights of the actor network for its input layer and its output layer, respectively. Then, the output of actor network \({{u}_{AC}}_{k}(t)\) can be computed as follows:

$${\varnothing }_{aj}\left(t\right)=\sum_{i=1}^{{N}_{ai}}{q}_{i}\left(t\right){w}_{a1,ij}\left(t\right) , j=1,\dots , {N}_{ah}$$
(41)
$${\theta }_{aj}\left(t\right)={\sigma }_{a}\left({\varnothing }_{aj}\left(t\right)\right)=\frac{1-{e}^{-{\varnothing }_{aj}\left(t\right)}}{1+{e}^{-{\varnothing }_{aj}\left(t\right)}} , j=1,\dots , {N}_{ah}$$
(42)
$${\gamma }_{ak}\left(t\right)=\sum_{j=1}^{{N}_{ah}}{w}_{a2,jk}\left(t\right){\theta }_{aj}\left(t\right) , k=1,\dots ,{N}_{ao}$$
(43)
$${{u}_{AC}}_{k}\left(t\right)={\sigma }_{a}\left({\gamma }_{ak}\left(t\right)\right)=\frac{1-{e}^{-{\gamma }_{ak}\left(t\right)}}{1+{e}^{-{\gamma }_{ak}\left(t\right)}} , k=1,\dots ,{N}_{ao}$$
(44)

The action neural network is trained using an iterative evaluation loop, which appraises the error between the desired objective (\({O}_{d}\)) and the approximated cost-to-go function provided by the critic network. Regarding desired objective, \({O}_{d}\) is the objective value of the total cost-to-go and is usually set to 0:

$${e}_{a}\left(t\right)=\widehat{J}\left(t\right)-{O}_{d}$$
(45)

We can express an objective function for the actor neural network as

$$\underset{{w}_{a}\left(t\right)}{\mathrm{min}}{E}_{a}\left(t\right)=\underset{{w}_{a}\left(t\right)}{\mathrm{min}}\frac{1}{2}{e}_{a}^{T}(t){e}_{a}(t)$$
(46)

Following this, we then use a gradient-based adaption approach to update the actor weights adaptively. It is done similarly as for critic network, so we do not repeat this procedure description and the accompanying equations here. Based on mentioned assumption for the critic network in which the weights of the input-to-hidden layer are randomly initialized and retained fixed for both networks, the output weights of the actor neural network are obtained as follows:

$${w}_{a}\left(t+\Delta t\right)={{w}_{a}\left(t\right)-{\rho }_{a}\left(t\right){\sigma }_{a}\left(t\right)[{w}_{c}^{T}\left(t\right)\alpha \left(t\right)][{w}_{c}^{T}(t){\sigma }_{c}(t)]}^{T}$$
(47)

where \(\alpha \left(t\right)\) is a matrix with dimension \({N}_{ch}\times m\) and its elements can be calculated as

$${\alpha }_{jk}\left(t\right)=\frac{1}{2} \left(1-{\sigma }_{cj}^{2}\left(t\right)\right){w}_{cj,n+k}$$
(48)
$$, \left\{\begin{array}{c} j=1,\dots , {N}_{ch}\\ k=1,\dots ,m\end{array}\right.$$

An actor neural network is shown in Fig. 4, which consists of 3 layers, 12 inputs \({{a}_{i}\left(t\right)=\left[\begin{array}{cc}{q}_{1}(t-\Delta t)& {q}_{1}\left(t\right)\end{array}\right]}^{T}\) in input layer, 10 neurons in hidden layer and 3 outputs \({a}_{o}\left(t\right)={\left[\begin{array}{ccc}{u}_{AC}^{surge}& {u}_{AC}^{sway}& {u}_{AC}^{yaw}\end{array}\right]}^{T}\) in output layer.

Fig. 4
figure 4

Actor neural network

Full size image

2.6 Concept of uniformly ultimately bounded

Typically, the presence of bounded deterministic and stochastic disturbances as well as neural network approximation errors lead to a Uniformly Ultimately Bounded (UUB) [32]. The UUB is used in the stability analysis of dynamical systems—particularly those that are based on approximate dynamic programming algorithm. The stability property is developed to guarantee that each of the iterative control laws can make the cost-to-go index function, adaptive weights and tracking errors uniformly ultimately bounded. Based on Eqs. (39) and (47), a dynamical system of estimation errors reads as

$${\stackrel{\sim }{w}}_{a,c}\left(t+\Delta t\right)={\stackrel{\sim }{w}}_{a,c}\left(t\right)-$$
(49)
$$f({w}_{a,c}\left(t-\Delta t\right),{w}_{a,c}\left(t\right),{\sigma }_{a,c}\left(t-\Delta t\right),{\sigma }_{a,c}\left(t\right))$$

where \({\stackrel{\sim }{w}}_{a,c}\left(t\right)={w}_{a,c}-{w}_{a,c}^{*}\). The optimal weights of critic and actor networks are shown by \({w}_{c}^{*}\) and \({w}_{a}^{*}\), respectively. All the weights and activation functions are assumed to be bounded as

$$\left\{\begin{array}{c}\Vert {w}_{c}(t)\Vert \le {w}_{cm}(t)\\ \Vert {w}_{c}^{*}(t)\Vert \le {w}_{cm}(t)\\ \Vert {w}_{a}(t)\Vert \le {w}_{am}(t)\\ \Vert {w}_{a}^{*}(t)\Vert \le {w}_{am}(t)\\ \Vert {\sigma }_{c}(t)\Vert \le {\sigma }_{cm}(t)\\ \Vert {\sigma }_{a}(t)\Vert \le {\sigma }_{am}(t)\end{array}\right.$$
(50)

Definition 1.

A dynamical system is said to be UUB with ultimate bound \(b>0\), if for any \(a>0\) and \({t}_{0}>0\), there exists a positive number \(N=N(a,b)\) independent of \({t}_{0}\), such that \(\Vert \stackrel{\sim }{w}(t)\Vert \le b\) for all \(t\ge N+{t}_{0}\) whenever \(\Vert \stackrel{\sim }{w}({t}_{0})\Vert \le a\).

Theorem 1.

If, for system (49), there exists a function \(L(\stackrel{\sim }{w}\left(t\right),t)\), such that for all \(\stackrel{\sim }{w}({t}_{0})\) in a compact set \(K\), \(L(\stackrel{\sim }{w}\left(t\right),t)\) is positive definite and the first difference, \(L(\stackrel{\sim }{w}\left(t\right),t)<0\) for \(\Vert \stackrel{\sim }{w}({t}_{0})\Vert >b\), for some \(b>0\), such that \(b\)-neighborhood of \(\stackrel{\sim }{w}\left(t\right)\) is contained in \(K\), then the system is UUB and the norm of state is bounded to within a neighborhood of \(b\).

Based on the above theorem and definition, a Lyapunov function can be adopted as follows:

$$\left\{\begin{array}{c}L\left(t\right)={L}_{1}\left(t\right)+{L}_{2}\left(t\right) \\ {L}_{1}\left(t\right)=\left(\frac{1}{{\rho }_{c}}\right)tr({\stackrel{\sim }{w}}_{c}^{T}{\stackrel{\sim }{w}}_{c})\\ {L}_{2}\left(t\right)=\left(\frac{1}{{\rho }_{a}}\right)tr\left({\stackrel{\sim }{w}}_{a}^{T}{\stackrel{\sim }{w}}_{a}\right)\end{array}\right.$$
(51)

With applying the above mentioned theorem and Lyapunov function, presented analysis in [29] showed that errors between the optimal weights of the actor and critic neural networks \({w}_{a}^{*}\), \({w}_{c}^{*}\) and their estimates \({w}_{a}\), \({w}_{c}\), which are approximated using the ACADP algorithm, can be all UUB. The UUB concept is obviously realized in the depicted results of our proposed hybrid algorithm, which are presented in the next section (Table 1).

Table 1 Parameters for Cybership II
Full size table

3 Computer simulations and discussion

In this section, the proposed AC-TDC control algorithm is tasted on a small-scale autonomous surface ship (Cybership II) with the following mass-related and identified parameters, which were calculated using the system identification procedure in [36]:

In the simulation, we consider all the components of matrices \(\mathrm{M}\left(\upeta \right), \mathrm{C}\left(\upeta ,\dot{\upeta }\right),\mathrm{ D}\left(\upeta ,\dot{\upeta }\right)\) given in [24]. Damping matrix \(\mathrm{D}\left(\upeta ,\dot{\upeta }\right)\) includes some nonlinear damping coefficients, which are described as follows [17]:

$${d}_{11}=0.72+1.33\left|u\right|+5.87{u}^{2}$$
$${d}_{22}=0.8896+36.5\left|v\right|+0.805\left|r\right|$$
(52)
$${d}_{23}=7.25+0.8451\left|v\right|+3.45\left|r\right|$$
$${d}_{32}=0.0313+3.96\left|v\right|+0.13\left|r\right|$$
$${d}_{33}=1.9-0.08\left|v\right|+0.75\left|r\right|$$

Other damping coefficients in the damping matrix \(3\times 3\) are assigned to zero. In addition, the constants in the inertia matrix are assigned as follows:

$$\left[\begin{array}{ccc}{\mathrm{m}}_{11}& {\mathrm{m}}_{12}& {\mathrm{m}}_{13}\\ {\mathrm{m}}_{21}& {\mathrm{m}}_{22}& {\mathrm{m}}_{23}\\ {\mathrm{m}}_{31}& {\mathrm{m}}_{32}& {\mathrm{m}}_{33}\end{array}\right]=\left[\begin{array}{ccc}25.8& 0& 0\\ 0& 33.8& 1.0115\\ 0& 1.0115& 2.76\end{array}\right]$$

Furthermore, disturbances are considered for applying upon the Cybership II, in which their respective vectors \(\boldsymbol{\Gamma }={[{\boldsymbol{\Gamma }}_{u},{\boldsymbol{\Gamma }}_{v},{\boldsymbol{\Gamma }}_{r}]}^{T}\) in Eq. (3) can be expressed as follows [17]:

$$\left\{\begin{array}{c}{\boldsymbol{\Gamma }}_{u}=0.1{v}^{3}+0.06u+0.01\mathrm{sin}(t)\\ {\boldsymbol{\Gamma }}_{v}=ur+0.1u+0.01\mathrm{sin}(t)\\ {\boldsymbol{\Gamma }}_{r}=0.4ur+{v}^{2}+0.01\mathrm{sin}(t)\end{array}\right.$$
(53)

In both case studies, we regard the following setting of the coefficients in Table 2 for the critic and actor neural networks:

Table 2 Setting of the neural networks
Full size table

The weighting matrix in Eq. (24) is initialized by \(p=0.1{I}_{nn}\), where \({I}_{nn}\) is an identity matrix with dimension 15 × 15 (The state-action dimension is 15). In the proposed algorithm, we consider an adaptive step size for both neural networks, which are decreased by \(0.01\) in each of the 5 steps \(\Delta t=0.02\). The weights of the critic and actor networks are randomly initialized with values from the range \([-0.2, 0.2]\).

4 Case study 1:

4.1 Tracking of desired paths under stochastic disturbances

The desired paths from which must be followed by the autonomous ship under stochastic disturbances are given by (54). The disturbances themselves are shown in Fig. 5. The simulation time \(t=30 sec.\) is adopted for this tracking:

Fig. 5
figure 5

Stochastic disturbances

Full size image
$$\left\{\begin{array}{c}x=5cos(\frac{1}{15}\pi t)\\ y=5sin(\frac{1}{15}\pi t)\\ \psi =0.01\pi t\end{array}\right.$$
(54)

Regarding parameters of TDC, in the first case study we set them as follows:

\((\stackrel{-}{M}={\left[\begin{array}{ccc}1& 1& 1\end{array}\right]I}_{nn}, n=3\)), \({k}_{d}={k}_{p}=2\) where \({I}_{nn}\) is an identity matrix.

In this case study, we have applied only stochastic disturbances in two stages during the tracking. The results of path following under this condition are shown in Fig. 6, where it is observed that the proposed AC-TDC algorithm is capable of handling disturbances significantly better than standard TDC algorithm. The deviations of TDC from the given path are particularly visible in the bottom part of Fig. 6 and upper part of Fig. 6b, where the TDC algorithm clearly has problems with handling the increased amplitude of stochastic disturbance. In comparison, AC-TDC was able to deal with that and avoid those deviations in both cases (circle path tracking and yaw path tracking).

Fig. 6
figure 6

Path following of autonomous ship under stochastic disturbances

Full size image

The control input signals are depicted in Fig.7, which are in an optimal effort status for the hybrid algorithm toward the conventional TDC. Concerning performance of actor-critic neural network, respective results for the implemented algorithm of ACADP are illustrated in Fig. 8.

Fig. 7
figure 7

Control input signals

Full size image
Fig. 8
figure 8

Adaptive weights and parameters of actor-critic learning algorithm

Full size image

To clearly observe the responses of network weights, we provide some figures with zoom in view depicted in Figs. 9 and dedicated to the actor and critic neural networks, respectively. As it is observed in Fig. 9c, we have uniformly ultimately bounded convergence for the output weights of actor neural network. It means that the actor weights, after their learning, are kept in a variable mode but with bounded amplitudes. Therefore, this variable mode of actor weights leads to the suppression of unexpected stochastic disturbances. Similarly, an exponential convergence is shown in Fig. 10b, c for the output weights of critic neural network.

Fig. 9
figure 9

Zoom in view of actor output adaptive weights

Full size image
Fig. 10
figure 10

Zoom in view of critic output adaptive weights

Full size image

5 Case study 2

5.1 Tracking of desired paths under deterministic and stochastic disturbances

The desired paths, which must be followed by autonomous ship under stochastic disturbances, are given by (55). As for disturbances, they are shown in Fig. 11. The simulation time \(t=30 sec.\) is adopted for this tracking.

Fig. 11
figure 11

Deterministic and stochastic disturbances

Full size image
$$\left\{\begin{array}{c}x=3 (m) \\ y=5sin(\frac{1}{15}\pi t)\\ \psi =0.01\pi t\end{array}\right.$$
(53)

Regarding parameters of TDC in the second case study, we set them as follows:

\((\stackrel{-}{M}={\left[\begin{array}{ccc}0.5& 0.4& 0.6\end{array}\right]I}_{nn}, n=3\)), \({k}_{d}={k}_{p}=2\), where \({I}_{nn}\) is an identity matrix.

In the second case study, we have applied both kinds of disturbances upon the autonomous ships including deterministic and time-varying stochastic disturbances. As shown in Fig. 11, the deterministic disturbances are applied four times, whereas there is for a single 30-s phase of applying the stochastic disturbance. The results of path following under this highly disturbed condition are shown in Fig. 12. It can be observed that the conventional TDC is unable to keep the yaw motion of autonomous ship on the reference values, which is depicted in Fig. 12c. In contrast to the TDC, we have a high-performance responses of the AC-TDC in following the desired paths of surge, sway, and yaw motion with much lower deviations in comparison to the TDC.

Fig. 12
figure 12

Path following of autonomous ship under deterministic and stochastic disturbances

Full size image

The optimal control efforts are depicted in Fig.13. Concerning performance of actor-critic neural network, respective results for the implemented algorithm of ACADP are illustrated in Fig. 14 and some zoom-in-view figures of output weights of actor and critic networks are shown in Figs. 15 and 16.

Fig. 13
figure 13

Control input signals

Full size image
Fig. 14
figure 14

Adaptive weights and parameters of actor-critic learning algorithm

Full size image
Fig. 15
figure 15

Zoom in view of actor output adaptive weights

Full size image
Fig. 16
figure 16

Zoom in view of critic output adaptive weights

Full size image

In this case study, we have chosen smaller values for the components of constant inertia matrix \(\stackrel{-}{M}\) toward the first case study. It leads to an increasing in TDE error. Indeed, with applying the deterministic and stochastic disturbances simultaneously, the perturbation magnitude is increased. Therefore, for overcoming this compelled perturbation, we have to increase the values of \(\stackrel{-}{M}\)’s components in the TDC algorithm. Otherwise, with a decrease in values of \(\stackrel{-}{M}\)’s components, the error of estimating the perturbation by the TDE part is increased. In such a situation (improper values of \(\stackrel{-}{M}\)), the TDC algorithm is no longer capable to follow the path accurately. For instance it is observed in Fig. 12c. For tackling with this problem due to the improper assigning of values to the inertia matrix \(\stackrel{-}{M}\), we have proposed a supplementary control algorithm combined with the TDC. In this proposed AC-TDC control scheme, the TDE error is compensated using an online learning-based part in the proposed control algorithm ACADP. This algorithm generates optimal efforts using an actor neural network as supplementary control inputs in which the output weights of this network are instantly updated, in case of occurring the deterministic disturbances, as shown in Fig. 14d. As it has been depicted in Fig. 14c, with occurring each new deterministic disturbance during of path following, a new learning process is commenced to assign proper weights to the actor network.

Concerning the UUB convergence, the output weights of the actor neural network move toward a bounded variable mode, analogically to the first case study. It is shown in Fig. 15c.

6 Conclusion

In this paper, a hybrid robust-adaptive optimal control structure was developed to address the path following control problem for autonomous ships under deterministic and stochastic disturbances. In the proposed structure, a TDC robust algorithm is combined with an ADP-based algorithm as an adaptive part of the proposed AC-TDC algorithm. This part includes an actor-critic neural network, which is used as a main subsystem to implement an ADP algorithm. Based on the capability of the heuristic ADP procedure in solving the HJB equation with a curse of dimensionality, a supplementary optimal control law is a result of this cost-to-go approximation procedure. This optimal control law was added to the TDC law to address high-performance path following control algorithm for the autonomous ships, particularly when the conventional TDC is unable to track the desired paths in case of facing the deterministic and stochastic disturbances, simultaneously. The robustness of new algorithm has been tested in presence of above-mentioned perturbations for two different case studies. The simulation results depicted that this procedure has significant properties in trajectory tracking with acceptable precision for autonomous ships under deterministic and stochastic disturbances. Concerning the future works, the next step is to implement the presented algorithm upon an underactuated autonomous surface ship equipped with a rudder navigation system. Moreover, the TDC part of the hybrid control algorithm will be enhanced by two structures. First, a Super-Twisting Sliding Mode Control (ST-SMC) strategy will be added to fulfil even greater robustness. Second, the method will feature optimal gain tuning of ST-SMC by means of the ADP part of the proposed control approach.