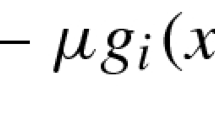Skip to main content
SpringerLink
Log in

An entropic regularized method of centers for continuous minimax problem with semi infinite constraints

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

The purpose of this paper is to focus on continuous minimax problems with semi infinite constraints. We begin by proposing an algorithm for solving this kind of problems. The proposed algorithm combines the parametric approach and the Huard method of centers. That’s we extend the Method of Centers of Roubi for solving minimax fractional programs to continuous minimax problems. On the other hand, calculating the exact optimal solution of the proposed parametric problems, requires an extraordinary computational work per iteration. To overcome this problem we use an iterative entropic regularization method which allows us to solve each auxiliary problem inexactly generating an approximate sequence of optimal values and then the continuous minimax problem is reduced into a sequence of finite minimax problems. Examples for illustration are given to test our algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Lin, J.Y., Sheu, R.L.: Modified Dinkelbach-type algorithm for generalized fractional programs with infinitely many ratios. J Optim Theory Appl. 126, 323–343 (2005). https://doi.org/10.1007/s10957-005-4717-z

    Article  MathSciNet  MATH  Google Scholar 

  2. Sheu, R.L., Lin, J.Y.: Solving continuous min-max problems by an iterative entropic regularization method. J. Optim. Theory Appl. 121, 597–612 (2004). https://doi.org/10.1023/B:JOTA.0000037605.19435.63

    Article  MathSciNet  MATH  Google Scholar 

  3. Roubi, A.: Global convergence and rate of convergence of a methods of centers. Comput. Optim. Appl. 3, 259–280 (1994)

    Article  MathSciNet  Google Scholar 

  4. Roubi, A.: Method of centers for generalized fractional programming. J. Optim. Theory Appl. 107(1), 123–143 (2000). https://doi.org/10.1023/A:1004660917684

    Article  MathSciNet  MATH  Google Scholar 

  5. Roubi, A.: Some properties of methods of centers. Comput. Optim. Appl. 19, 319–335 (2001)

    Article  MathSciNet  Google Scholar 

  6. Roubi, A.: Convergence of prox-regularization methods for generalized fractional programming. RAIRO Oper. Res. 36(1), 73–94 (2002). https://doi.org/10.1051/ro:2002006

    Article  MathSciNet  MATH  Google Scholar 

  7. Hettich, R., Kortanek, K.O.: Semi-infnite programming: theory, methods, and applications. SIAM Rev. (1993). https://doi.org/10.1137/1035089

    Article  MATH  Google Scholar 

  8. Reemtsen, R., Görner, S.: (1998) Numerical Methods for Semi-Infinite Programming: A Survey. In: Reemtsen R., Rückmann J.J. (eds) Semi-Infinite Programming. Nonconvex Optimization and Its Applications, vol 25. Springer, pp. 380–429 (1993) https://doi.org/10.1007/978-1-4757-2868-2_7

  9. Lopez, M., Still, G.: Semi-infinite programming. Eur. J. Operat. Res. 180(2), 491–518 (2007). https://doi.org/10.1016/j.ejor.2006.08.045

    Article  MathSciNet  MATH  Google Scholar 

  10. Qi, L., Ling, C., Tong, X., et al.: A smoothing projected Newton-type algorithm for semi-infinite programming. Comput Optim Appl. 42(4), 1–30 (2009). https://doi.org/10.1007/s10589-007-9117-x

    Article  MathSciNet  MATH  Google Scholar 

  11. Žaković, S., Rustem, B.: Semi-infinite programming and applications to minimax problems. Ann. Oper. Res. 124, 81–110 (2003). https://doi.org/10.1023/B:ANOR.0000004764.76984.30

    Article  MathSciNet  MATH  Google Scholar 

  12. Addoune, S., Boufi, K., Roubi, A.: Proximal bundle algorithms for nonlinearly constrained convex minimax fractional programs. J. Optim. Theory Appl. 179, 212–239 (2018). https://doi.org/10.1007/s10957-018-1342-1

    Article  MathSciNet  MATH  Google Scholar 

  13. Addoune, S., El Haffari, M., Roubi, A.: A proximal point algorithm for generalized fractional programs. Optimization 66(9), 1495–1517 (2017). https://doi.org/10.1080/02331934.2017.1338698

    Article  MathSciNet  MATH  Google Scholar 

  14. Barros, A.I.J., Frenk, B.G., Schaible, S., Zhang, S.: A new algorithm for generalized fractional programs. Math. Program. 72, 147–175 (1996). https://doi.org/10.1007/BF02592087

    Article  MathSciNet  MATH  Google Scholar 

  15. Barros, A.I.J., Frenk, B.G., Schaible, S., Zhang, S.: Using duality to solve generalized fractional programming problems. J. Glob. Optim. 8, 139–170 (1996). https://doi.org/10.1007/BF00138690

    Article  MathSciNet  MATH  Google Scholar 

  16. Bector, C.R., Chandra, S., Bector, M.K.: Generalized fractional programming duality: a parametric approach. J. Optim. Theory Appl. 60(2), 243–260 (1989). https://doi.org/10.1007/BF00940006

    Article  MathSciNet  MATH  Google Scholar 

  17. Boualam, H., Roubi, A.: Dual algorithms based on the proximal bundle method for solving convex minimax fractional programs. J. Ind. Manag. Optim. 15(4), 1897–1920 (2019). https://doi.org/10.3934/jimo.2018128

    Article  MathSciNet  MATH  Google Scholar 

  18. Boualam, H., Roubi, A.: Proximal bundle methods based on approximate Subgradients for solving Lagrangian duals of minimax fractional programs. J. Global Optim. 74(2), 255–284 (2019). https://doi.org/10.1007/s10898-019-00757-2

    Article  MathSciNet  MATH  Google Scholar 

  19. Boufi, K., Roubi, A.: Dual method of centers for solving generalized fractional programs. J. Glob. Optim. 69(2), 387–426 (2017). https://doi.org/10.1007/s10898-017-0523-z

    Article  MathSciNet  MATH  Google Scholar 

  20. Boufi, K., Roubi, A.: Duality results and dual bundle methods based on the dual method of centers for minimax fractional programs. SIAM J. Optim. 29(2), 1578–1602 (2019)

    Article  MathSciNet  Google Scholar 

  21. Boufi, K., Roubi, A.: Prox-regularization of the dual method of centers for generalized fractional programs. Optim. Methods Softw. 34(3), 515–545 (2019). https://doi.org/10.1080/10556788.2017.1392520

    Article  MathSciNet  MATH  Google Scholar 

  22. Méthode, La., des Centres dans un Espace Topologique. : Buì-Trong-Liêũ, Huard, P. Numerische Mathematik 8, 56–67 (1966)

  23. Crouzeix, J.P., Ferland, J.A.: Algorithms for generalized fractional programming. Math. Program. 52, 191–207 (1991). https://doi.org/10.1007/BF01582887

    Article  MathSciNet  MATH  Google Scholar 

  24. Crouzeix, J.P., Ferland, J.A., Nguyen, H.V.: Revisiting Dinkelbach-type algorithms for generalized fractional programs. Opsearch 45, 97–110 (2008). https://doi.org/10.1007/BF03398807

    Article  MathSciNet  MATH  Google Scholar 

  25. Crouzeix, J.P., Ferland, J.A., Schaible, S.: Duality in generalized linear fractional programming. Math. Program. 27, 342–354 (1983). https://doi.org/10.1007/BF02591908

    Article  MathSciNet  MATH  Google Scholar 

  26. Crouzeix, J.P., Ferland, J.A., Schaible, S.: An algorithm for generalized fractional programs. J. Optim. Theory Appl. 47, 35–49 (1985). https://doi.org/10.1007/BF00941314

    Article  MathSciNet  MATH  Google Scholar 

  27. Crouzeix, J.P., Ferland, J.A., Schaible, S.: A note on an algorithm for generalized fractional programs. J. Optim. Theory Appl. 50, 183–187 (1986). https://doi.org/10.1007/BF00938484

    Article  MathSciNet  MATH  Google Scholar 

  28. El Haffari, M., Roubi, A.: Convergence of a proximal algorithm for solving the dual of a generalized fractional program. RAIRO-Oper. Res. 51(4), 985–1004 (2017). https://doi.org/10.1051/ro/2017004

    Article  MathSciNet  MATH  Google Scholar 

  29. El Haffari, M., Roubi, A.: Prox-dual regularization algorithm for generalized fractional programs. J. Ind. Manag. Optim. 13(4), 1991–2013 (2017). https://doi.org/10.3934/jimo.2017028

    Article  MathSciNet  MATH  Google Scholar 

  30. Huard, P.: Programmation Mathématique Convexe. R.I.R.O 7, 43–59 (1968)

    MathSciNet  MATH  Google Scholar 

  31. Jagannathan, R., Schaible, S.: Duality in generalized fractional programming via Farkas’ Lemma. J. Optim. Theory Appl. 41(3), 417–424 (1983). https://doi.org/10.1007/BF00935361

    Article  MathSciNet  MATH  Google Scholar 

  32. Polak, E., He, L.: Unified Steerabale Phase I-Phase II metohd of feasible directions for semi-infinite optimization. Math. Program. 59(1), 83–107 (1991)

    Google Scholar 

  33. Polak, E., Higgins, J.E., Mayne, D.Q.: A barrier function method for minimax problems. Math. Program. 54, 155–176 (1992). https://doi.org/10.1007/BF01586049

    Article  MathSciNet  MATH  Google Scholar 

  34. Stancu-Minasian, I.M.: A ninth bibliography of fractional programming. Optimization 68(11), 2125–2169 (2019). https://doi.org/10.1080/02331934.2019.1632250

    Article  MathSciNet  MATH  Google Scholar 

  35. Dem’yanov, V.F., Malozemov, V.N.: Introduction to Minimax. Wiley, New York (1974)

    MATH  Google Scholar 

  36. Bertsekas, D.P.: Constrained Optimization and Lagrange Multiplier Methods. Academic Press, New York (1982)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratoire Lasad, Ecole Normale Supérieure, Tetouan, Morocco

    Mostafa El Haffari

Authors
  1. Mostafa El Haffari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mostafa El Haffari.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

El Haffari, M. An entropic regularized method of centers for continuous minimax problem with semi infinite constraints. J. Appl. Math. Comput. 68, 637–653 (2022). https://doi.org/10.1007/s12190-021-01524-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-021-01524-x

Keywords

Mathematics Subject Classification

Search

Navigation