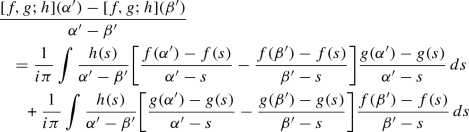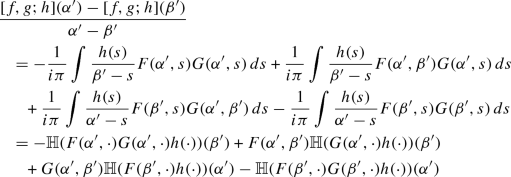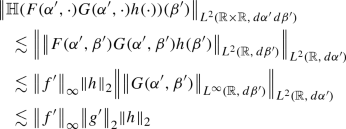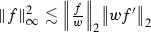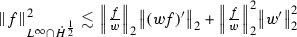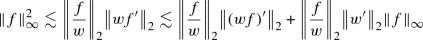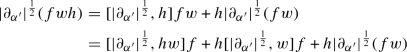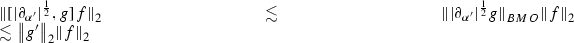Abstract
We consider the capillary–gravity water wave equation in two dimensions. We assume that the fluid is inviscid, incompressible, irrotational and the air density is zero. We construct an energy functional and prove a local wellposedness result without assuming the Taylor sign condition. When the surface tension \(\sigma \) is zero, the energy reduces to a lower order version of the energy obtained by Kinsey and Wu (Camb J Math 6(2):93–181, 2018) and allows angled crest interfaces. For positive surface tension, the energy does not allow angled crest interfaces but admits initial data with large curvature of the order of \(\sigma ^{-\frac{1}{3}+ \epsilon } \) for any \(\epsilon >0\).

Similar content being viewed by others
Notes
The role of gravity will be clarified in a future work.
Here \(K_{-y}\) is the Poisson kernel (3).
For example if we introduce the lower order term
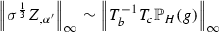 in \(E_{\sigma ,0}\), then it significantly simplifies the proof of the energy estimate and still allows angled crested interfaces for \(\sigma = 0\). However the introduction of this term does not allow the scaling \(\sigma /\epsilon ^\frac{3}{2}\) in Corollary 3.2 and one would then get a weaker result.
in \(E_{\sigma ,0}\), then it significantly simplifies the proof of the energy estimate and still allows angled crested interfaces for \(\sigma = 0\). However the introduction of this term does not allow the scaling \(\sigma /\epsilon ^\frac{3}{2}\) in Corollary 3.2 and one would then get a weaker result.
References
Agrawal, S.: Angled crested like water waves with surface tension II: zero surface tension limit (2020). arXiv:2009.13469
Agrawal, S.: Rigidity of singularities of 2D gravity water waves. J. Differ. Equ. 268(3), 1220–1249 (2020)
Ai, A.: Low regularity solutions for gravity water waves (2017). arXiv:1712.07821
Ai, A.: Low regularity solutions for gravity water waves II: the 2D case. Ann. PDE 6(1), 4 (2020)
Alazard, T., Burq, N., Zuily, C.: On the water-wave equations with surface tension. Duke Math. J. 158(3), 413–499 (2011)
Alazard, T., Burq, N., Zuily, C.: On the Cauchy problem for gravity water waves. Invent. Math. 198(1), 71–163 (2014)
Alazard, T., Burq, N., Zuily, C.: Strichartz estimates and the Cauchy problem for the gravity water waves equations. Mem. Am. Math. Soc. 256(1229), v+108 (2018)
Ambrose, D.M.: Well-posedness of vortex sheets with surface tension. SIAM J. Math. Anal. 35(1), 211–244 (2003)
Ambrose, D.M., Masmoudi, N.: The zero surface tension limit of two-dimensional water waves. Commun. Pure Appl. Math. 58(10), 1287–1315 (2005)
Ambrose, D.M., Masmoudi, N.: The zero surface tension limit of three-dimensional water waves. Indiana Univ. Math. J. 58(2), 479–521 (2009)
Beyer, K., Günther, M.: On the Cauchy problem for a capillary drop. I. Irrotational motion. Math. Methods Appl. Sci. 21(12), 1149–1183 (1998)
Castro, A., Córdoba, D., Fefferman, C., Gancedo, F., Gómez-Serrano, J.: Finite time singularities for water waves with surface tension. J. Math. Phys. 53(11), 115622–115626 (2012)
Castro, A., Córdoba, D., Fefferman, C., Gancedo, F., Gómez-Serrano, J.: Finite time singularities for the free boundary incompressible Euler equations. Ann. Math. (2) 178(3), 1061–1134 (2013)
Christodoulou, D., Lindblad, H.: On the motion of the free surface of a liquid. Commun. Pure Appl. Math. 53(12), 1536–1602 (2000)
Coifman, R.R., McIntosh, A., Meyer, Y.: L’intégrale de Cauchy définit un opérateur borné sur \(L^{2}\) pour les courbes lipschitziennes. Ann. Math. (2) 116(2), 361–387 (1982)
Coutand, D., Shkoller, S.: Well-posedness of the free-surface incompressible Euler equations with or without surface tension. J. Am. Math. Soc. 20(3), 829–930 (2007)
Craig, W.: An existence theory for water waves and the Boussinesq and Korteweg-de Vries scaling limits. Commun. Partial Differ. Equ. 10(8), 787–1003 (1985)
de Poyferré, T.: A priori estimates for water waves with emerging bottom. Arch. Ration. Mech. Anal. 232(2), 763–812 (2019)
Harrop-Griffiths, B., Ifrim, M., Tataru, D.: Finite depth gravity water waves in holomorphic coordinates. Ann. PDE 3(1), 4 (2017)
Hunter, J.K., Ifrim, M., Tataru, D.: Two dimensional water waves in holomorphic coordinates. Commun. Math. Phys. 346(2), 483–552 (2016)
Iguchi, T.: Well-posedness of the initial value problem for capillary–gravity waves. Funkcial. Ekvac. 44(2), 219–241 (2001)
Kato, T., Ponce, G.: Commutator estimates and the Euler and Navier–Stokes equations. Commun. Pure Appl. Math. 41(7), 891–907 (1988)
Kinsey, R.H., Wu, S.: A priori estimates for two-dimensional water waves with angled crests. Camb. J. Math. 6(2), 93–181 (2018)
Lannes, D.: Well-posedness of the water-waves equations. J. Am. Math. Soc. 18(3), 605–654 (2005)
Lemarié, P.G.: Continuité sur les espaces de Besov des opérateurs définis par des intégrales singulières. Ann. Inst. Fourier (Grenoble) 35(4), 175–187 (1985)
Leoni, G.: A First Course in Sobolev Spaces. Graduate Studies in Mathematics, vol. 181, 2nd edn. American Mathematical Society, Providence (2017)
Li, D.: On Kato-Ponce and fractional Leibniz. Rev. Math. Iberoam. 35(1), 23–100 (2019)
Lindblad, H.: Well-posedness for the motion of an incompressible liquid with free surface boundary. Ann. Math. (2) 162(1), 109–194 (2005)
Meyer, Y., Coifman, R.: Wavelets, Cambridge Studies in Advanced Mathematics, vol. 48, Cambridge University Press, Cambridge, 1997, Calderón-Zygmund and multilinear operators, Translated from the 1990 and 1991 French originals by David Salinger
Ming, M., Zhang, Z.: Well-posedness of the water-wave problem with surface tension. J. Math. Pures Appl. (9) 92(5), 429–455 (2009)
Nalimov, V.I.: The Cauchy-Poisson problem, Dinamika Splošn. Sredy (1974), no. Vyp. 18 Dinamika Židkost. so Svobod. Granicami, 104–210, 254
Nguyen, H.Q.: A sharp Cauchy theory for the 2D gravity-capillary waves. Ann. Inst. H. Poincaré Anal. Non Linéaire 34(7), 1793–1836 (2017)
Ogawa, M., Tani, A.: Free boundary problem for an incompressible ideal fluid with surface tension. Math. Models Methods Appl. Sci. 12(12), 1725–1740 (2002)
Pommerenke, Ch.: Boundary Behaviour of Conformal Maps, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 299. Springer, Berlin (1992)
Schweizer, B.: On the three-dimensional Euler equations with a free boundary subject to surface tension. Ann. Inst. H. Poincaré Anal. Non Linéaire 22(6), 753–781 (2005)
Shao, S., Shih, H.-W.: A remark on the two dimensional water wave problem with surface tension. J. Differ. Equ. 266(9), 5748–5771 (2019)
Shatah, J., Zeng, C.: Geometry and a priori estimates for free boundary problems of the Euler equation. Commun. Pure Appl. Math. 61(5), 698–744 (2008)
Shatah, J., Zeng, C.: Local well-posedness for fluid interface problems. Arch. Ration. Mech. Anal. 199(2), 653–705 (2011)
Titchmarsh, E.C.: Introduction to the Theory of Fourier Integrals, 3rd edn. Chelsea Publishing Co., New York (1986)
Wigley, N.M.: Development of the mapping function at a corner. Pac. J. Math. 15, 1435–1461 (1965)
Sijue, W.: Well-posedness in Sobolev spaces of the full water wave problem in 2-D. Invent. Math. 130(1), 39–72 (1997)
Sijue, W.: Well-posedness in Sobolev spaces of the full water wave problem in 3-D. J. Am. Math. Soc. 12(2), 445–495 (1999)
Sijue, W.: Almost global wellposedness of the 2-D full water wave problem. Invent. Math. 177(1), 45–135 (2009)
Wu, S.: Wellposedness and singularities of the water wave equations (2015). arXiv:1503.00549
Sijue, W.: Wellposedness of the 2D full water wave equation in a regime that allows for non-\(C^1\) interfaces. Invent. Math. 217(2), 241–375 (2019)
Yosihara, H.: Gravity waves on the free surface of an incompressible perfect fluid of finite depth. Publ. Res. Inst. Math. Sci. 18(1), 49–96 (1982)
Yosihara, H.: Capillary–gravity waves for an incompressible ideal fluid. J. Math. Kyoto Univ. 23(4), 649–694 (1983)
Zhang, P., Zhang, Z.: On the free boundary problem of three-dimensional incompressible Euler equations. Commun. Pure Appl. Math. 61(7), 877–940 (2008)
Acknowledgements
This work was part of the author’s Ph.D. thesis and he is very grateful to his advisor Prof. Sijue Wu for proposing the problem and for her guidance during this project. The author would also like to thank Prof. Jeffrey Rauch for many helpful discussions. The author was supported in part by NSF Grants DMS-1101434, DMS-1361791 through his advisor.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by A. Ionescu.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Here we will prove all the identities and estimates used in the paper. We will state most of the statements only for functions in the Schwartz class and it can be extended to more general functions by an approximation argument. Let us first recall some of the notation used. Let \(D_t= \partial _t+ b\partial _{\alpha '}\) where \(b\) is given by (11) and recall that  is defined as
is defined as

Proposition 9.1
Let \(f,g,h \in \mathcal {S}(\mathbb {R})\). Then we have the following identities
-
(1)
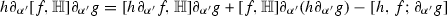
-
(2)
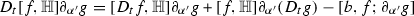
Proof
The second identity is a direct consequence of the first. Now we see that

\(\square \)
Proposition 9.2
Let \(H \in C^1(\mathbb {R}),A_i \in C^1(\mathbb {R}) \) for \(i=1,\cdots m\) and \(F\in C^\infty (\mathbb {R})\). Define

then there exists constants \(c_1,c_2,c_3,c_4\) depending only on F and  so that
so that
-
(1)
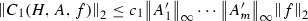
-
(2)
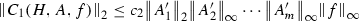
-
(3)
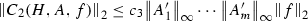
-
(4)
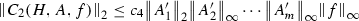
Proof
The first estimate is a theorem by Coifman, McIntosh and Meyer [15]. See also chapter 9 of [29]. Estimate 2 is a consequence of the Tb theorem and a proof can be found in [43]. The third and fourth estimates can be obtained from the first two by integration by parts. \(\quad \square \)
Proposition 9.3
Let \(T:\mathcal {D}(\mathbb {R}) \rightarrow \mathcal {D}'(\mathbb {R})\) be a linear operator with kernel K(x, y) such that on the open set \(\{(x,y):x\ne y\} \subset \mathbb {R}\times \mathbb {R}\), K(x, y) is a function satisfying

where \(C_0\) is a constant. If T is continuous on \(L^2(\mathbb {R})\) with  and if \(T(1) =0\), then T is bounded on \(\dot{H}^s\) for \(0<s<1\) with
and if \(T(1) =0\), then T is bounded on \(\dot{H}^s\) for \(0<s<1\) with 
Proof
This proposition is a direct consequence of the result of Lemarie [25] where only weak boundedness of T on \(L^2\) (in the sense of David and Journe) is assumed. As boundedness on \(L^2\) implies weak boundedness, the proposition follows. See also chapter 10 of [29] for another proof of the result of Lemarie. \(\quad \square \)
Lemma 9.4
Let \(r,s \in \mathbb {R}\), \(k,m\in \mathbb {Z}\). If \(f \in \mathcal {S}(\mathbb {R})\), then we have the following
-
(1)
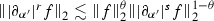 for \(0\le r<s \) with \(1-\theta = \frac{r}{s}\)
for \(0\le r<s \) with \(1-\theta = \frac{r}{s}\) -
(2)
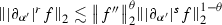 for \(2\le r<s \) with \(1-\theta = \frac{r-2}{s-2}\)
for \(2\le r<s \) with \(1-\theta = \frac{r-2}{s-2}\) -
(3)
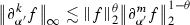 for \(0\le k <m\) with \(1-\theta = \frac{k+\frac{1}{2}}{m}\)
for \(0\le k <m\) with \(1-\theta = \frac{k+\frac{1}{2}}{m}\) -
(4)
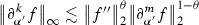 for \(2\le k <m\) with \(1-\theta = \frac{k-\frac{3}{2}}{m-2}\)
for \(2\le k <m\) with \(1-\theta = \frac{k-\frac{3}{2}}{m-2}\)
Proof
The first estimate is a standard interpolation estimate which can be easily proved by using the Fourier transform. We skip its proof. The second one follows from the first by applying it on the function \(f''\) with r, s replaced by \(r-2,s-2\) respectively.
The third estimate is a consequence of the Gagliardo-Nirenberg interpolation estimate (see Theorem 12.87 in [26]). The last one follows from the third estimate by applying it on the function \(f''\) with k, m replaced by \(k-2,m-2\) respectively. \(\quad \square \)
Lemma 9.5
Let \(k,n \in \mathbb {N}\) and \(f_1,f_2, \cdots , f_k \in \mathcal {S}(\mathbb {R})\). Let \(r_1,r_2\cdots , r_k \in \mathbb {Z}\) with \(r_1 + \cdots + r_k = n\) and \( r_i\ge 0\) for all \(1\le i\le k\) and. Let  . Then
. Then
-
(1)
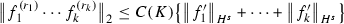 for
for 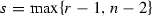
-
(2)
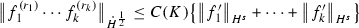 for
for 
with  and C(K) is a constant depending only on K.
and C(K) is a constant depending only on K.
Proof
Let us begin by proving the first estimate. Without loss of generality \(0\le r_1\le r_2 \le \cdots \le r_k\). Clearly the estimate holds if \(k=1\) or \(r=1\). Hence we can now assume that \(k\ge 2\) and \(r\ge 2\). If \(r_1\le \cdots \le r_j \le 1\) for some \(j<k\) with \(r_{j+1} \ge 2\), then we have

Hence without loss of generality we can assume that \(r_1\ge 2\). As \(k\ge 2\) this implies that \(n\ge 4\) and we also have \(r\ge 2\), \(r\le n-2\) and \(s = n-2\). Hence using Lemma 9.4 we have

where \(1-\theta _j = \frac{r_j - \frac{3}{2}}{s-1}\) for \(j<k\) and \(1-\theta _k = \frac{r_k - 2}{s-1}\). Now observe that
Hence by using \(AM-GM\) inequality the estimate follows. The proof of the second estimate is very similar and we skip it. \(\quad \square \)
Corollary 9.6
Let \(f,g \in \mathcal {S}(\mathbb {R})\) and let \(n\in \mathbb {N}\) with \(n\ge 2\). Then
-
(1)
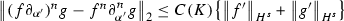 for \(s = n-2\)
for \(s = n-2\) -
(2)
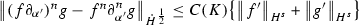 for \(s = n-\frac{3}{2}\)
for \(s = n-\frac{3}{2}\)
where  and C(K) is a constant depending only on K.
and C(K) is a constant depending only on K.
Proof
This follows directly from Lemma 9.5\(\quad \square \)
Proposition 9.7
Let \(f \in \mathcal {S}(\mathbb {R})\). Then we have
-
(1)
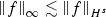 if \(s>\frac{1}{2}\) and for \(s=\frac{1}{2}\) we have
if \(s>\frac{1}{2}\) and for \(s=\frac{1}{2}\) we have 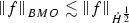
-
(2)
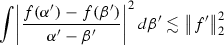
-
(3)
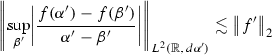
-
(4)
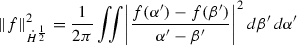
-
(5)

Proof
-
(1)
This is a standard Sobolev embedding result.
-
(2)
This is a consequence of Hardy’s inequality.
-
(3)
We see that
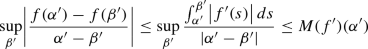
where M is the uncentered Hardy Littlewood maximal operator. As the maximal operator is bounded on \(L^2\), the estimate follows.
-
(4)
Observe that as \(\vert {\partial _{\alpha '}}\vert = i\mathbb {H}\partial _{\alpha '}\) and \(\mathbb {H}(1) =0\) we have
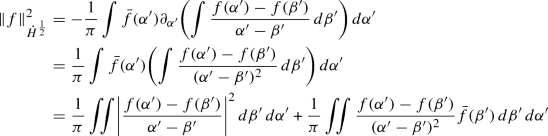
Now observe that
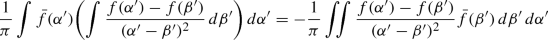
The identity now follows.
-
(5)
We see that

Hence we have
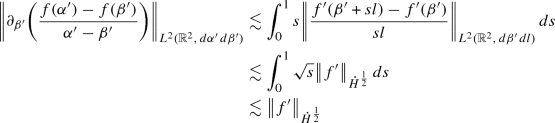
\(\square \)
Proposition 9.8
Let \(f,g \in \mathcal {S}(\mathbb {R})\) with \(s,a\in \mathbb {R}\) and \(m,n \in \mathbb {Z}\). Then we have the following estimates
-
(1)
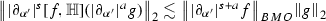 for \(s,a \ge 0\)
for \(s,a \ge 0\) -
(2)
 for \(s\ge 0\) and \(a>0\)
for \(s\ge 0\) and \(a>0\) -
(3)
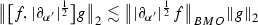
-
(4)
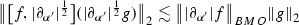
-
(5)
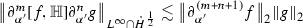 for \(m,n \ge 0\)
for \(m,n \ge 0\) -
(6)
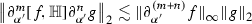 for \(m,n \ge 0\)
for \(m,n \ge 0\) -
(7)
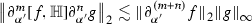 for \(m\ge 0\) and \(n\ge 1\)
for \(m\ge 0\) and \(n\ge 1\) -
(8)
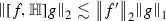
Proof
The first four estimates are all variants of the Kato Ponce commutator estimate and are proved using the paraproduct decomposition. See Lemma 2.1 in [20] for the first two estimates and Theorem 1.2 in [27] for the third and fourth estimates. The fourth estimate is not explicitly stated as part of Theorem 1.2 in [27] however the proof is identical to the proof of estimate 3 with the only change being at the last step where you move half a derivative from g to f.
The \(\dot{H}^\frac{1}{2}\) estimate of the fifth estimate follows from the first estimate. For the \(L^{\infty }\) estimate note that

The estimate now follows from the Cauchy Schwarz inequality. The sixth and seventh estimates follow from the first two estimates. For the last estimate observe that

The estimate now follows from Hardy’s inequality as stated in Proposition 9.7. \(\quad \square \)
Proposition 9.9
Let \(f,g,h \in \mathcal {S}(\mathbb {R})\) with \(s,a\in \mathbb {R}\) and \(m,n \in \mathbb {Z}\). Then we have the following estimates
-
(1)
 for \(s > 0\)
for \(s > 0\) -
(2)
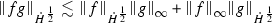
-
(3)
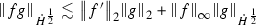
Proof
See [22] for the first estimate. The second one is a special case of the first. For the third one observe that

and hence from Proposition 9.8

\(\square \)
Proposition 9.10
Let \(f,g,h \in \mathcal {S}(\mathbb {R})\) . Then we have the following estimates
-
(1)
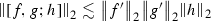
-
(2)
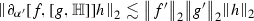
-
(3)
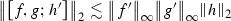
-
(4)
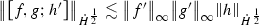
-
(5)
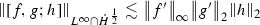
Proof
-
(1)
We see that
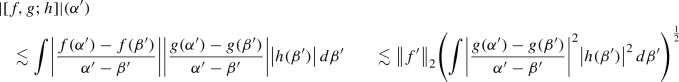
The estimate now follows from Hardy’s inequality.
-
(2)
We see that
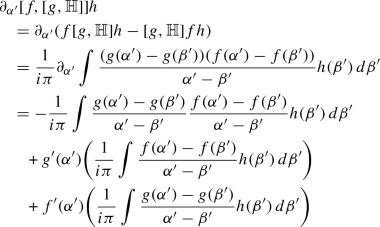
The estimate now follows by previous estimates.
-
(3)
This is a special case of Proposition 9.2
-
(4)
From the third estimate we observe that the operator T defined by the action
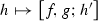 is bounded on \(L^2\). Also we clearly see that \(T(1) =0\). It is also easy to see that the kernel of this operator satisfies the conditions for Proposition 9.3. Hence the operator T is bounded on \(\dot{H}^\frac{1}{2}\).
is bounded on \(L^2\). Also we clearly see that \(T(1) =0\). It is also easy to see that the kernel of this operator satisfies the conditions for Proposition 9.3. Hence the operator T is bounded on \(\dot{H}^\frac{1}{2}\). -
(5)
The \(L^{\infty }\) estimate is obtained easily by an application of Cauchy Schwarz and Hardy’s inequality. Now we use
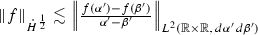 and see that
and see that 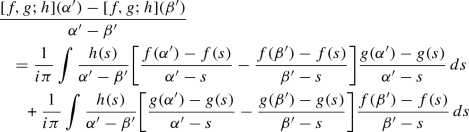
Now we use the following notation to simplify the calculation
$$\begin{aligned} F(a,b) = \frac{f(a) -f(b)}{a-b} \quad \text { and } G(a,b) = \frac{g(a)-g(b)}{a-b} \end{aligned}$$Hence we have
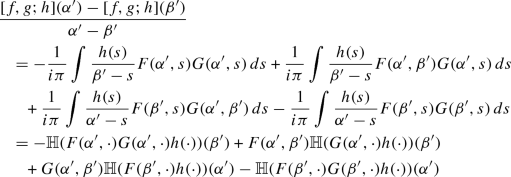
and we see that
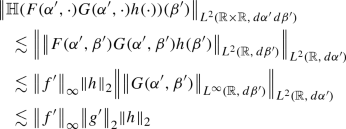
The other terms are handled similarly.\(\quad \square \)
Proposition 9.11
Let \(f \in \mathcal {S}(\mathbb {R})\) and let w be a smooth non-zero weight with \(w,\frac{1}{w} \in L^{\infty }(\mathbb {R}) \) and \(w' \in L^2(\mathbb {R})\). Then
-
(1)
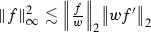
-
(2)
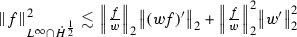
Proof
-
(1)
We see that

Now we integrate and use Cauchy Schwarz to get the estimate.
-
(2)
The \(L^{\infty }\) estimate is obtained from the first estimate by observing that
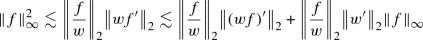
Now use the inequality \(ab \le \frac{a^2}{2\epsilon } + \frac{\epsilon b^2}{2}\) on the last term to obtain the estimate. For the \(\dot{H}^\frac{1}{2}\) estimate, using \(\vert {\partial _{\alpha '}}\vert = i\mathbb {H}\partial _{\alpha '}\) we see that

Now as  we have
we have
Hence using the inequality \(ab \le \frac{a^2}{2} + \frac{b^2}{2}\), we see that

\(\quad \square \)
Proposition 9.12
Let \(f,g \in \mathcal {S}(\mathbb {R})\) and let \(w,h \in L^{\infty }(\mathbb {R})\) be smooth functions with \(w',h' \in L^2(\mathbb {R})\). Then

If in addition we assume that w is real valued then

Proof
-
(1)
We see that
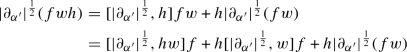
The estimate now follows from the estimate
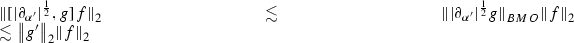
-
(2)
We observe that
$$\begin{aligned} fgw&= (\mathbb {P}_Hf)(\mathbb {P}_Hg)w + (\mathbb {P}_Hf)(\mathbb {P}_Ag)w + (\mathbb {P}_Af)(\mathbb {P}_Hg)w + (\mathbb {P}_Af)(\mathbb {P}_Ag)w \\&= (\mathbb {P}_Hf)\overline{(\mathbb {P}_A\bar{g})}w + (\mathbb {P}_Hf)(\mathbb {P}_Ag)w + (\mathbb {P}_Af)(\mathbb {P}_Hg)w + (\mathbb {P}_Af)\overline{(\mathbb {P}_H\bar{g})}w \end{aligned}$$
We will control only the first term and the other terms are controlled similarly. Now see that

Hence we have

Now observe that as w is real valued we have

Similarly we have

\(\square \)
Proposition 9.13
Let \(f \in C^3([0,T), H^3(\mathbb {R}))\). Then for any \(t\in [0,T)\) we have

Proof
Fix \(s > 0\) satisfying \(t+s \in [0,T)\) and for every \(\epsilon >0\) we find \(a_{\epsilon } \in \mathbb {R}\) such that  . Observe that
. Observe that  and hence we have
and hence we have

Now let \(\epsilon \rightarrow 0\) to get

As \(\partial _t^2 f \in L^{\infty }(\mathbb {R}\times [0,T))\), we take the limit as \(s\rightarrow 0\) to finish the proof. \(\quad \square \)
Lemma 9.14
Let \(K_\epsilon \) be the Poisson kernel from (3). If \(f\in L^q(\mathbb {R})\), then for \(s\ge 0\) an integer we have

Similarly for \(s \in \mathbb {R}, s\ge 0\) we have

Proof
The proof follows from basic properties of convolution. \(\quad \square \)
Rights and permissions
About this article
Cite this article
Agrawal, S. Angled Crested Like Water Waves with Surface Tension: Wellposedness of the Problem . Commun. Math. Phys. 383, 1409–1526 (2021). https://doi.org/10.1007/s00220-020-03934-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00220-020-03934-7





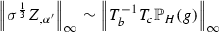 in
in 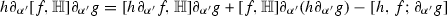
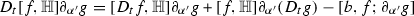
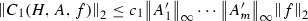
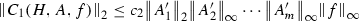
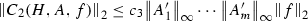
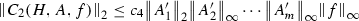
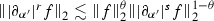 for
for 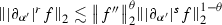 for
for 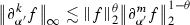 for
for 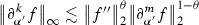 for
for 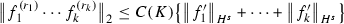 for
for 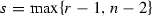
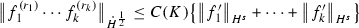 for
for 
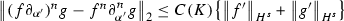 for
for 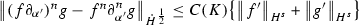 for
for 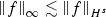 if
if 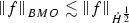
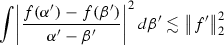
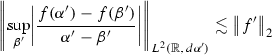
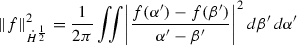

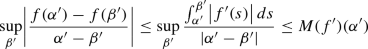
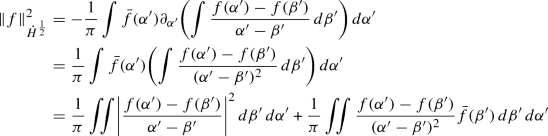
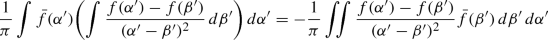

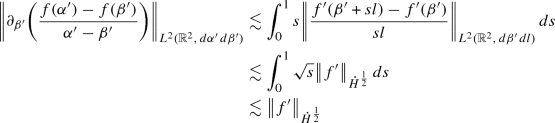
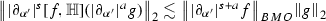 for
for  for
for 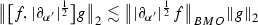
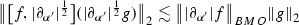
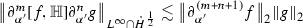 for
for 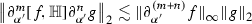 for
for 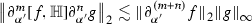 for
for 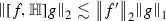
 for
for 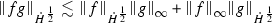
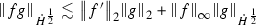
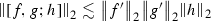
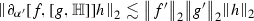
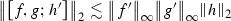
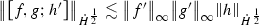
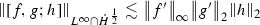
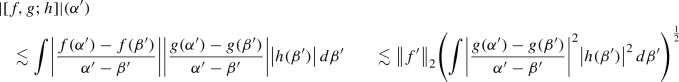
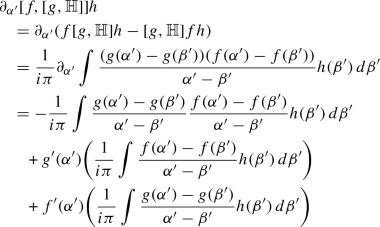
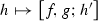 is bounded on
is bounded on 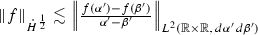 and see that
and see that