A Dynamic Oligopoly with Price Stickiness and Risk-Averse Agents

Abstract

In this paper we present a dynamic discrete-time model that allows to investigate the impact of risk-aversion in an oligopoly characterized by a homogeneous non-storable good, sticky prices and uncertainty. The continuous-time limit of our formulation nests the classical dynamic oligopoly model with sticky prices by Fershtman and Kamien (Econometrica 55:1151–1164, 1987) and extends it by accommodating uncertainty and risk-aversion. We show that in the continuous-time limit of our infinite horizon formulation the optimal production strategy and the consequent equilibrium price are, respectively, directly and inversely related to the degrees of uncertainty and risk-aversion. However, the effect of uncertainty and risk-aversion crucially depends on price stickiness since, when prices can adjust instantaneously, the steady state equilibrium in our model with uncertainty and risk-aversion collapses to Fershtman and Kamien’s analogue.

1 Introduction

How do price stickiness, uncertainty and risk aversion affect the equilibrium outcome of an oligopoly where firms compete over the demand of a homogeneous, non-storable good? We address such a question by extending Fershtman and Kamiem’s differential game for an oligopolistic market with sticky prices and a non-storable good (Fershtman and Kamien 1987) to a formulation with uncertainty and risk-aversion. We derive the optimal (sub-game perfect) production strategy, and the corresponding equilibrium price, and compare it to the Nash equilibria obtained by Fershtman and Kamien (1987). The main contribution of this extension is twofold. Firstly, we shed further light on the quite controversial issue—which has never been investigated in a dynamic oligopoly with sticky prices—of how uncertainty and risk-aversion affect market competition. Secondly, we show that the impact of uncertainty and risk-aversion crucially depends on price stickiness, as the stationary equilibrium collapses to Fershtman and Kamien’s analogue when prices can adjust instantaneously.

We contribute to the literature extending the model developed by Fershtman and Kamien (1987). Dockner (1988) generalizes Fershtman and Kamien (1987) to the case of more than two firms showing that the dynamic oligopoly price converges to the long run (zero profit) competitive price when the number of firms goes to infinity, independent of the assumption of open-loop or feedback strategies. Tsutsui and Mino (1990) introduce the possibility of price ceilings to consider the case of nonlinear feedback strategies finding that, when the price ceiling is not too high, feedback equilibrium prices can be higher than the equilibrium price that arises under the linear feedback strategy assumed by Fershtman and Kamien (1987). Piga (2000) shows that when firms can invest in advertising the nonlinear feedback equilibrium price may be greater than the open-loop equilibrium price, while the latter is above the linear feedback equilibrium price. Other extensions include Dockner and Gaunerdorfer (2001) and Benchekroun (2003) who analyze the profitability of horizontal mergers, Cellini and Lambertini (2007) dealing with the case of firms selling differentiated products, and Wiszniewska-Matyszkiel et al. (2015) focusing on firms’ behavior off the steady state price path.

Our model nests the classical dynamic oligopoly with sticky prices of Fershtman and Kamien (1987) that can be viewed as its continuous-time limit with no uncertainty and no risk aversion. Our analysis starts from a discrete-time formulation of a dynamic oligopolistic market with sticky prices which allows to introduce uncertainty and risk-aversion in a tractable manner by means of a special form of the recursive preferences proposed by Hansen and Sargent (1995). Such preferences are largely used in economics and finance (Hansen et al. 1999; Tallarini 2000; Luo 2004; Luo and Young 2010; Hansen and Sargent 2013) and correspond, under certain conditions, to Epstein–Zin’s recursive preferences (Epstein and Zin 1989; Epstein 1991).

Thus, we derive the optimal (sub-game perfect) production strategy for symmetric firms and, focusing on the continuous-time limit of the infinite time formulation, we obtain several results. Notably, in the presence of demand volatility risk-averse entrepreneurs choose to produce larger quantities of the non-storable good, vis-à-vis their risk-neutral counterparts, since this reduces the variability of their payoffs. Such behavior is exacerbated when demand shocks are more volatile and, as a result, the steady state value of the equilibrium price results to be decreasing in both uncertainty and risk-aversion. Albeit this reaction to a higher degree of uncertainty can appear counter-intuitive from first sight, it is not unprecedented in models where agents strategically act in dynamic contexts. In fact, also in Fershtman and Kamien (1987) the way each firm takes rivals’ reactions to price changes into account brings about a generalized incentive to produce more. In our model, this effect is enhanced as risk-averse agents can reduce the variability of their future payoffs by further increasing their current production.

Other interesting results are derived from the analysis of specific limit cases. Firstly, as it happens for the case without uncertainty and risk-aversion analyzed by Dockner (1988), when the number of firms goes to infinity the steady state price converges to the marginal cost. This is interesting because it shows that his result is robust with respect to the introduction of uncertainty and risk-aversion. Secondly, when the time-discounting factor goes to zero the steady state price converges to the value that would prevail in a static equilibrium with price-taker firms. In this case firms behave as price-takers because they do not take their future profits into account and, given the characterization of price stickiness, their production choices do not affect the current price level either. Thirdly, the steady state price converges to the equilibrium value of a perfectly competitive static market also when prices tend to be infinitely sticky. Obviously, here the result arises because firms’ production choices can affect neither present nor future prices. These limit cases emphasize the important conclusion that uncertainty and risk-aversion do not push firms to produce more when they behave as price-takers and cannot strategically take future outcomes into account. Fourthly, when prices become infinitely flexible the steady state price converges to a limit value which is higher than the price of the static equilibrium with price-taker firms and lower than that of the static Cournot oligopoly. Since in a duopoly such limit case coincides with the deterministic analogue discussed in Fershtman and Kamien (1987), we see that the impact of uncertainty and risk-aversion on a dynamic oligopoly where firms compete over the production of a homogeneous and non-storable good crucially hinges on the presence of price-stickiness. Finally, when we instead consider the special case of a unique firm in the market, we observe that an infinitely flexible price brings about the convergence of the stationary price towards the static Cournot price (coinciding in this case with the monopoly price).

The rest of the paper is organized as follows. In Sect. 2 we first introduce uncertainty and risk-aversion in a discrete-time formulation of a market for a non-storable good with sticky prices, then we consider its continuous-time limit and characterize the equilibrium solutions. In Sect. 3 we concentrate on the stationary solution for the infinite horizon formulation and analyze the impact of risk-aversion and uncertainty. Finally, Sect. 4 investigates the limit cases and Sect. 5 concludes. The proofs of all results discussed in the paper are relegated in a separate Appendix.

2 A Market for a Non-Storable Good with Sticky Prices

We start from a discrete-time formulation of a market for a non-storable good with sticky prices which allows to introduce uncertainty and risk-aversion in a simple, intuitive and tractable manner. We then consider its continuous-time limit and derive several theoretical results. The discrete-time formulation is set out so that its continuous-time limit is consistent with that of Fershtman and Kamien (1987).

Let us assume that production and consumption take place at equally spaced in time moments between time 0 and time T. These moments are $t_1$, $\ldots$,$t_n$, $t_{n+1}$, $\ldots$, $t_N$, where $t_{n+1} = t_n + \Delta$, with $\Delta$ some positive interval of time, while $t_N$ coincides with the final date T in which production is interrupted. By pushing $\Delta$ towards zero our formulation converges to the continuous-time one employed by Fershtman and Kamien (1987). In addition, by pushing T towards infinity we converge towards an infinite horizon formulation which allows to study stationary equilibria.

The discrete-time counterpart of the continuous-time formulation employed by Fershtman and Kamien (1987) for the dynamics of the price of the non-storable consumption good is as follows

$$\begin{aligned} p_{n+1}= & {} \alpha \, s \, \Delta \ + \ (1 - s \Delta ) \, p_n \ - \ s \Delta x_n \ + \ \epsilon _{n+1} \, , \end{aligned}$$

(1)

where $p_n$ is the price of the non-storable good at time $t_n$, $\Delta x_n$ is the corresponding quantity produced and brought to the market, $\epsilon _{n+1}$ is an idiosyncratic shock to its demand function, with $\epsilon _{n+1} \sim N(0,\sigma _{\epsilon }^2 \Delta )$, while $\alpha$ and s are positive constants with s representing a measure of the speed of price adjustment.

The quantity produced and brought to the market $\Delta x_n$ is the product of the time interval $\Delta$ and the output rate/intensity $x_n$ for period n. In oligopoly, where M identical firms produce the non-storable good, $\Delta x_n = \Delta u_{1,n} + \Delta u_{2,n} \ldots + \Delta u_{M,n}$, where $\Delta u_{m,n}$ corresponds to the quantity produced by firm m in period n. This is the product of $\Delta$ and firm m’s output rate/intensity $u_{m,n}$.¹

Equation (1) can be reformulated as

$$\begin{aligned} p_{n+1}-p_n= & {} s \Delta \ ({\hat{p}}_n \ - \ p_n) \ + \ \epsilon _{n+1} \, , \end{aligned}$$

(2)

where ${\hat{p}}_n = \alpha \, - \, x_n$ is the inverse demand function which prevails in a market in which prices adjust immediately to the level determined by the demand function for a given level of output. Because of price stickiness the adjustment process takes time and in fact Eq. (2) indicates that the price variation from period n to period $n+1$ is a linear function of the gap between the price indicated by the demand function for the currently produced quantity and the current market price. The degree of price stickiness depends on the constant parameter s that measures how much of the difference between ${\hat{p}}_n$ and $p_n$ is corrected in a given interval of time. Thus, a larger s would allow a faster convergence of the price to its static equilibrium level with immediate convergence when s goes to infinity. On the other hand, when $s=0$ we have maximum stickiness and changes in the production level do not provoke any variation in prices. Moreover, we note that what firms produce today has an effect on tomorrow price but it does not affect the current price $p_n$ whose level depends, in turn, on production decisions occurred at $t_{n-1}$. This is crucial for the results that we derive.

Note that for $\Delta \downarrow 0$ this discrete-time formulation converges to its continuous-time counter-part. In particular, the continuous-time analogue of Eq. (1) is given by the following expression

$$\begin{aligned} \frac{dp (t)}{dt}= & {} s ( \alpha \ - \ x(t) \ - \ p(t)) \ + \ \epsilon (t) \, , \end{aligned}$$

(3)

where $x(t) = u_1(t) + \cdots + u_M(t)$. Importantly, for $M=2$ and $\epsilon (t) \equiv 0$ we have Eq. (1.2) in Fershtman and Kamien (1987). Given our formulation the condition that no variation in the price is expected is

$$\begin{aligned} E_t \left[ \frac{dp (t)}{dt} \right] = 0 \, . \end{aligned}$$

It can be said that if this condition is met the good market is in steady state in that the good price p(t) adjusts instantaneously to the equilibrium level that would prevail in a static model. Let $p^{*}(t) \equiv \alpha \ - \ x(t)$ be such a price. Substituting it out in Eq. (3) we find that

$$\begin{aligned} \frac{dp (t)}{dt}= & {} - \ s \, ( p(t) \ - \ p^{*}(t)) \ + \ \epsilon (t) \, , \end{aligned}$$

(4)

which is the continuous-time correspondent of Eq. (2) unveiling mean-reverting dynamics toward the static equilibrium price.

We assume the M firms are perfectly symmetrical in that they share the same cost function, while the entrepreneurs which own and run them share the same degree of risk-aversion. Therefore, without loss of generality, let us analyze the optimal production strategy of firm 1. As in Fershtman and Kamien (1987) firm 1 is characterized by quadratic production costs. Specifically, in n the intensity of these costs is $\frac{1}{2} u_n^2$, where for simplicity we write $u_{1,n} = u_n$. The sale of the non-storable good generates a revenue which is linear in the quantity brought to the market. This implies that the intensity of the firm’s revenue in n is $p_n u_n$, while that of the corresponding profits is $p_n u_n - \frac{1}{2} u_n^2$.

The entrepreneur maximizes the discounted value of all the profits her firm generates. As the future prices at which the firm will be able to sell the quantity of the non-storable good it produces are subject to idiosyncratic shocks, this discounted value is uncertain. Therefore, we assume the entrepreneur is risk-averse and is endowed with a special form of recursive preferences proposed by Hansen and Sargent (1995). In particular in period n, with $n=1, 2, \ldots , N$, the entrepreneur solves the following recursive optimization

$$\begin{aligned} \varvec{\mathcal {V}}_n= & {} \min _{u_n} \, \left\{ \Delta c_n \ + \ \frac{2}{\rho } \, \ln \left( E_n \left[ \exp \left( \delta ^{\Delta } \, \frac{\rho }{2} \, \varvec{\mathcal {V}}_{n+1} \right) \right] \right) \right\} \, , \end{aligned}$$

(5)

where $\rho$ (with $\rho >0$) is a risk-enhancement coefficient, $\delta$ (with $0<\delta <1$) is a time-discounting factor, $\Delta c_n$ is the (per-period) loss function, with $c_n = \frac{1}{2} u_n^2 - p_n u_n$, and $\varvec{\mathcal {V}}_{n}$ is the value function (with final condition $\varvec{\mathcal {V}}_{N+1}=0$).

The optimization criterion in (5) accommodates risk-aversion through the curvature of the exponential function. As the convexity of $\ln (E [\exp (\delta ^{\Delta } \, \frac{\rho }{2} \, \varvec{\mathcal {V}}_{n+1} )])$ increases with $\rho$, this coefficient determines the entrepreneur’s degree of risk-aversion. Importantly, for $\rho \downarrow 0$, the recursive optimization in (5) converges to $\varvec{\mathcal {V}}_n = \min _{u_n} E_n [ \Delta c_n + \delta ^{\Delta } {\varvec{\mathcal {V}}}_{n+1} ]$.² As this is the Bellman equation a risk-neutral entrepreneur will solve in our formulation, we conclude that our formulation subsumes that of Fershtman and Kamien, when $\rho =0$, and extends it by allowing for risk-sensitive preferences, when $\rho >0$.

In the Appendix we prove the following Lemma that describes the optimal production strategy when the time interval between two periods converges to zero ($\Delta \downarrow 0$).

Lemma 1

When M identical firms operate in the oligopolistic market for the production of the non-storable good and $\Delta \downarrow 0$, the optimal production strategy of the generic firm converges in t to

$$\begin{aligned} u(t)= & {} \kappa (t) \, p(t) \, - \, 2 \, s \, \vartheta (t), \ \ \text{ with } \ \ \kappa (t) = \left( 1 \, + \, 2 \, s \pi (t) \right) \, \end{aligned}$$

(6)

with $\pi (t)$ and $\vartheta (t)$ satisfying the following differential equations

$$\begin{aligned}&\frac{d \pi (t)}{dt} \, - \, 2 \left( s \pi (t) \, + \, \frac{1}{2} \right) \left( (2M-1) s \pi (t) \, + \, \frac{1}{2} \right) \,\nonumber \\&\quad + \, ( \ln \delta \, - \, 2 s ) \pi (t) \ + \ \rho \sigma _{\epsilon }^2 \pi (t)^2 = 0 \, , \end{aligned}$$

(7)

$$\begin{aligned}&\frac{d \vartheta (t)}{d t} \, + \, \ \biggl (\ln \delta \, - \, (1\, + \, M) s \biggr )\, \vartheta (t) \, \nonumber \\&-\quad \, \left( 2 (2M-1) s^2 \, - \, \rho \sigma _{\epsilon }^2 \right) \, \pi (t) \vartheta (t) \, - \, \alpha s \, \pi (t) = 0 \, , \end{aligned}$$

(8)

with boundary conditions $\pi (T) =0$ and $\vartheta (T) =0$.

Proof

See the Appendix. $\square$

Solving the two differential equations in Lemma 1 is involved. In particular, an explicit solution exists only for the former and hence numerical procedures are called for to describe the dynamics of the equilibrium presented in Lemma 1. However, in the infinite horizon formulation, where the final date T is pushed forward to infinite, we easily characterize the following.

Proposition 1

When M identical firms operate in a oligopolistic market for a non-storable good, $\Delta \downarrow 0$ and $T \uparrow \infty$, the optimal production strategy of the generic firm converges in t to

$$\begin{aligned} u(t) = {\bar{\kappa }} \, p(t) \ - \ 2 \, s \, {\bar{\vartheta }} \end{aligned}$$

(9)

where ${\bar{\kappa }} \, = \, \lim _{t\downarrow - \infty } \kappa (t)$ and ${\bar{\vartheta }} \, = \, \lim _{t\downarrow - \infty } \vartheta (t)$.

Proof

The proof of Proposition 1 as well as the derivation of ${\bar{\kappa }}$ and ${\bar{\vartheta }}$ are in the Appendix. $\square$

3 Comparative Statics: Risk-Aversion and Uncertainty

In a stationary equilibrium the price of the homogeneous non-storable good fluctuates around a steady state value $p^*$. Correspondingly, the quantity produced by a firm in a stationary equilibrium, $u(t)={\bar{\kappa }} p(t) - 2 s {\bar{\vartheta }}$, fluctuates around the steady state value $u^* = {\bar{\kappa }} p^* - 2 s {\bar{\vartheta }}$. Since ${\bar{\kappa }}$ depends positively on both $\rho$ and $\sigma _{\epsilon }$, the first term of $u^*$ is also increasing in $\rho$ and $\sigma _{\epsilon }$. Therefore firms react aggressively to a greater uncertainty by increasing their productions for any given level of price and such behavior is further amplified by higher degrees of risk-aversion. However, if all firms increase their production, in steady state, the price will be smaller, so that the term ${\bar{\kappa }} p^*$ could either increase or decrease. Moreover, ${\bar{\vartheta }}$ depends on $\rho$ and $\sigma _{\epsilon }$ too. This suggests that establishing the overall effect of risk-aversion and uncertainty on the optimal production strategy and on the equilibrium price is a complicated endeavor.

However, the following Proposition allows us to establish that when the risk-adjustment coefficient and the volatility of demand shocks increase, the steady state price decreases and the M firms produce larger quantities of the non-storable good.

Proposition 2

In a stationary equilibrium, for any parametric constellation, the steady state price, $p^{*}$, and the expected quantity produced by an oligopolistic firm in steady state, $u^{*}$, are respectively decreasing and increasing both in $\rho$, the coefficient of risk-aversion, and in $\sigma _{\epsilon }$, the volatility of demand shocks.

Proof

See the Appendix. $\square$

We conclude that uncertainty and risk-aversion affect the strategies of firms producing a homogeneous non-storable good in a dynamic oligopoly market with sticky prices. In particular, we observe that the optimal firms’ reaction to a higher degree of risk-aversion (or a higher level of uncertainty) is to increase their production in order to reduce the variability of their future payoffs. This result is driven by the Epstein and Zin recursive preferences employed in this paper. In fact, as it is discussed in Vitale (2017) and Valentini and Vitale (2019), such preferences imply that relative risk-aversion is greater than the inverse of the inter-temporal elasticity of substitution. Kreps and Porteus (1978) show that under these circumstances agents are pushed towards earlier resolution of uncertainty vis-a-vis the standard case of expected utility. Thus, in our formulation, while it might appear a counter-intuitive response to uncertainty, risk-aversion induces firms to expand production as this reduces the variability of their future profits.

We conclude that risk-aversion exacerbates the effect of the strategic interaction among firms firstly unveiled by Fershtman and Kamien. Indeed, they note that firms know that as they expand their production and cause a fall in price their rivals will be induced to contract their production. Then, such firms find it convenient to expand production to augment their market share and their overall profits. We extend Fershtman and Kamien result by showing that such effect is magnified in the presence of uncertainty and risk-aversion.

Anticipating results we will illustrate extensively in the next section, two comments on the effect of uncertainty and risk-aversion are worth making. Firstly, these effects vanquish when firms do not act strategically and do not consider the impact of their production decisions on prices. Thus, our conclusions crucially hinge on the assumption that firms are not price-takers. Secondly, the apparently surprising effects of uncertainty and risk-aversion are the consequence of the forward-looking behavior of the firms. Indeed, if they were not concerned with the future implications of their current decisions we will not observe an increase in production associated with a larger degree of uncertainty and/or risk-aversion.

Interestingly, the apparently counter-intuitive effects of risk-aversion and uncertainty we find are not novel to models of strategic interaction among agents. Thus, Subrahmanyam (1991) extends Kyle (1985) seminal paper on the strategic interaction of privately informed traders in securities markets to the case in which these agents are risk-averse. Within the static version of Kyle’s model, in which these agents only trade once, Subrahmanyam shows that risk-aversion induces the informed traders to trade less than their risk-neutral counterparts. On the contrary, Holden and Subrahmanyam (1994) introduce risk-aversion in the dynamic, multi-period, version of Kyle’s model and show the opposite result. The reason of the different impact of risk-aversion between the static and dynamic version of Kyle’s model is analogous to that which applies to our model. In the dynamic version the informed traders choose to trade more as this reduces the uncertainty over their future payoffs, while in the static one such consideration dissipates.

4 Some Limit Cases

Here we investigate what happens to the steady-steady of our formulation when the number of firms goes to infinity ($M \uparrow \infty$), time-discounting collapses to zero ($\delta \downarrow 0$) and when prices become either infinitely sticky or perfectly flexible ($s \downarrow 0$ and $s \uparrow \infty$ respectively). These limit scenarios are interesting per se but also because they help unveiling how competitiveness, risk-aversion, time-discounting and price stickiness interact.

The first result pertains to the impact of the number of firms in the oligopolistic market. This is established in the following Proposition.

Proposition 3

When the number of firms goes to infinity the steady state price $p^*$ converges to the firms’ per period marginal production cost.

Proof

See the Appendix. $\square$

The convergence of the steady state price $p^*$ towards the firms’ marginal cost in the limit case of M going to infinity was firstly showed by Dockner (1988) in a dynamic oligopoly without uncertainty. Therefore, Proposition 3 reveals that (i) Dockner’s result is robust to the introduction of uncertainty and risk-aversion and (ii) the degree of uncertainty and risk aversion do not affect the steady state price when the number of firms producing a homogeneous non-storable good in the dynamic market with sticky prices becomes infinity.

We now compare our dynamic formulation with a static one in which prices are always equal to the level dictated by the demand schedule, while entrepreneurs are risk-neutral. In such a static formulation two alternative scenarios can prevail. In the former firms are price-takers and act competitively, while in the latter they act strategically as they take into account the impact that their output has on the equilibrium price.

It is relatively simple to establish that in the former scenario the expected equilibrium price for the homogeneous good, $E[p_t]$, is equal to $p_{{ \text{ comp }}} = \frac{\alpha }{1+M}$, while the production strategy of the individual firm implies that $u_t = \kappa _{{ \text{ comp }}} p_t$, where $\kappa _{{\text{ comp }}}= 1$. When firms act strategically, instead, the expected equilibrium price is equal to $p_{{\text{ stra }}} = \frac{2 \alpha }{2+M}$, while $u_t = \kappa _{{\text{ strat }}} p_t$ with $\kappa _{{\text{ strat }}}= \frac{1}{2}$.

For $\delta \downarrow 0$ the steady state of our dynamic formulation converges to the equilibrium of the static model with price-taker firms, as suggested by the following Proposition.

Proposition 4

When the time-discounting factor falls to zero the steady state price of the stationary equilibrium with M firms converges to the expected price, $E[p_t]$, of the static equilibrium with price-taker firms, in that

$$\begin{aligned} \lim _{\delta \downarrow 0} p^* = p_{{ \text{ comp }}} \, . \end{aligned}$$

Proof

See the Appendix. $\square$

An implication of Proposition 4 is that for $\delta \downarrow 0$ the steady state of our dynamic formulation coincides with the competitive equilibrium of the static formulation of the model presented by Fershtman and Kamien (1987).³ Indeed, in our formulation firms, when choosing their output, know the current price for the homogeneous good, but are uncertain about its future values. Thus, their risk-aversion affects their production strategies insofar they care for future profits. When $\delta \downarrow 0$ they do not take into account future profits and hence their uncertainty about future prices and their risk-aversion become irrelevant.

The steady state of our dynamic formulation manifests similar properties when prices become infinitely sticky. In fact, also when s collapses to zero our steady state converges to the equilibrium of the static model with price-taker firms. This result is posited in the following Proposition.

Proposition 5

When prices become infinitely sticky ($s\downarrow 0$), the steady state price of the stationary equilibrium converges to the expected price, $E[p_t]$, of the static equilibrium with M price-taker firms, in that

$$\begin{aligned} \lim _{s\downarrow 0} p^* = p_{{ \text{ comp }}} \, . \end{aligned}$$

Proof

See the Appendix. $\square$

In this extreme scenario firms are aware that their output does not affect prices. In addition, while they care for future profit opportunities they also know that their current decisions will not bear upon the future. Consequently, firms act as price-taker agents which maximize their expected current profits exactly as in Fershtman and Kamien’s original formulation.

When prices become perfectly flexible the properties of the steady state of our formulation change dramatically, as shown in the following Proposition.

Proposition 6

When prices become perfectly flexible ($s \uparrow \infty$), the steady state price of the stationary equilibrium converges to a limit value which for $M=1$ coincides with the expected price, $E[p_t]$, of the static equilibrium with a strategic monopolist, in that

$$\begin{aligned} \lim _{s \uparrow \infty } p^* = p_{{\text{ strat }}} \, \end{aligned}$$

while for $M\ge 2$ lies between the expected price, $E[p_t]$, of the static equilibrium with price-taker firms and that of the static equilibrium with strategic firms, in that

$$\begin{aligned} p_{{ \text{ comp }}}< \lim _{s \uparrow \infty } p^* < p_{{\text{ strat }}}\, . \end{aligned}$$

Proof

See the Appendix. $\square$

When prices become perfectly flexible they immediately adjust to the level determined by the demand for the homogeneous good. This means that the management of a monopolistic firm will choose its production policy taking into account the immediate and complete impact that this will have on the price of the homogeneous good. More precisely, in t it will select the optimal production quantity u(t) considering its effect through the inverse demand schedule $p(t) = \alpha - u(t)$. In this way the monopolist acts as a single strategic agent and the steady state of the stationary equilibrium converges to the corresponding static equilibrium.

Interestingly, in oligopoly the steady state of the stationary equilibrium does not converge to the corresponding static equilibrium with strategic firms. The steady state price is in fact smaller. Firms find it optimal to eat into their competitors’ market shares and hence choose to increase output above the level consistent with the static equilibrium with strategic firms.

In particular, for $M=2$, when $s \uparrow \infty$ our formulation collapses to the stochastic analogue of the static model discussed by Fershtman and Kamien (1987). Indeed, by substituting $M=2$ in the formula of $\lim _{s \uparrow \infty } p^*$ derived in the Proof of Proposition 6 we can easily verify that

$$\begin{aligned} \lim _{s \uparrow \infty } p^* \ = \ \frac{p_{{ \text{ comp }}} \, + \, 2\frac{\sqrt{2}}{\sqrt{3}} \, p_{{\text{ strat }}} }{1 + 2\frac{\sqrt{2}}{\sqrt{3}}}\, , \end{aligned}$$

where $p_{{ \text{ strat }}} = \frac{1}{2} \alpha$ and $p_{{ \text{ comp }}}= \frac{1}{3} \alpha$. This result coincides with that in Theorem 4 of Fershtman and Kamien (1987) when production costs do not include a linear component, ie. for $c=0$ in their formulation.

This suggests that when prices become perfectly flexible the impact of uncertainty and risk-aversion on the firms’ production strategies and the market equilibrium in our dynamic formulation dissipates. Indeed, this is a general result which we posit in the following Proposition.

Proposition 7

When prices become perfectly flexible ($s\uparrow \infty$), the production strategies of the risk-averse entrepreneurs collapse to those of their risk-neutral counterparts.

Proof

See the Appendix. $\square$

The intuition for this result is immediate. In fact, as prices become perfectly flexible they immediately converge to the level determined by the demand for the homogeneous good. This implies that uncertainty over future prices vanishes and the optimal production strategy of the oligopolistic firms is unaffected by the entrepreneurs’ degree of risk-aversion. We conclude that the impact of risk-aversion and uncertainty on the optimal production strategies of oligopolistic firms crucially hinges on the stickiness of the good price. Only when prices adjust slowly the attitude of the firms’ management and their uncertainty on the dynamics of future prices affect their production decisions.

5 Concluding Remarks

This paper has shown how price stickiness, uncertainty and risk aversion interact in oligopolistic markets of homogeneous and non-storable goods. Such markets are not just a theoretical curiosity. Electricity, for instance, is perfectly homogeneous, difficult to store and typically provided by few firms in retail markets which are characterized by demand uncertainty and prices adjusting very slowly to changes in the wholesale electricity prices.

To analyze these markets we have extended a classical dynamic oligopoly game with sticky prices by developing a discrete-time formulation that allows to introduce uncertainty and risk-aversion via recursive preferences à la Hansen and Sargent (1995). Starting from a discrete-time formulation allows both to move easily to the continuous-time counterpart and shed light on the role of price stickiness and uncertainty. Thus, we have seen that as uncertainty or risk-aversion increases, firms produce more and, consequently, the equilibrium price falls. However, the impact of uncertainty and risk-aversion on production and price levels crucially depends on the presence of price stickiness as it is greater when price stickiness increases and disappears when prices can adjust instantaneously. Indeed, since uncertainty on price dynamics concerns solely next periods, the strategic behavior of risk-averse firms collapses to that of risk-neutral ones when the current price can converge instantaneously to its equilibrium value.

Appendix

The following Lemma is preparatory for the proofs of Lemma 1 and Proposition 1.

Lemma 2

In the discrete-time formulation with M identical firms, in any period n the optimal production strategy of the generic firm is $u_n = \kappa _{p,n} p_n + \kappa _{e,n} (\alpha s \Delta {\tilde{\pi }}_{n+1} - {\tilde{\vartheta }}_{n+1})$, where

$$\begin{aligned}&\kappa _{p,n} = \frac{\frac{1}{2} \, + \, s (1 - s \Delta ) {\tilde{\pi }}_{n+1} }{\frac{1}{2} \, + \, M \,s^2 \Delta {\tilde{\pi }}_{n+1}}\, \ \ \text{ and } \ \ \ \kappa _{e,n} = \, \frac{s}{\frac{1}{2} \, + \, M s^2 \Delta {\tilde{\pi }}_{n+1}}\, \ \ \end{aligned}$$

with ${\tilde{\pi }}_{n+1} = \delta ^{\Delta } \pi _{n+1} (1 - \delta ^{\Delta } \rho \sigma _{\epsilon }^2 \Delta \pi _{n+1})^{-1}$ and ${\tilde{\vartheta }}_{n+1} = \delta ^{\Delta } \vartheta _{n+1} (1 - \delta ^{\Delta } \rho \sigma _{\epsilon }^2 \Delta \pi _{n+1})^{-1}$, while

$$\begin{aligned} \pi _n= & {} \frac{1}{2} \, \Delta \, \kappa _{p,n}^2 \ - \ \Delta \, \kappa _{p,n} \, + \, \left[ (1 - s \Delta ) \, - \, M \, s \, \Delta \, \kappa _{p,n} \right] ^2 \, {\tilde{\pi }}_{n+1}\, \end{aligned}$$

(A.1)

and

$$\begin{aligned} \vartheta _n= & {} [1 \, - \, (M-1) s {\tilde{\pi }}_{n+1} \, \Delta \, \kappa _{e,n} ][ - M s \, \Delta \, \kappa _{p,n} \, + \, (1 \, - \, s \Delta ) ] ({\tilde{\vartheta }}_{n+1} \, - \, \alpha s \Delta {\tilde{\pi }}_{n+1} ) . \nonumber \\ \end{aligned}$$

(A.2)

Proof

Suppose firm 1’s entrepreneur conjectures that in n firms 2, 3, $\ldots$, M will all choose to produce the same quantity $\Delta y_n$. In addition, assume that $\varvec{\mathcal {V}}_{n+1} = \pi _{n+1} \, p_{n+1}^2 - 2 \vartheta _{n+1} p_{n+1} + \nu _{n+1}$, where $\pi _{n+1}$ and $\vartheta _{n+1}$ are some time-variant coefficients. Under this assumption, Lemma 4 in Vitale (2017) shows that solving the recursion in (5) is equivalent to solving the double recursion

$$\begin{aligned} F_n(p_n)= & {} \varvec{\mathcal {L}} \, \widetilde{\varvec{\mathcal {L}}}\, F_{n+1}(p_{n+1})\, , \ \ \text{ where } \ \ F_{n+1} \ \equiv \ \pi _{n+1}\, p_{n+1}^2 \ - \ 2 \vartheta _{n+1} \, p_{n+1} \, , \\ \widetilde{\varvec{\mathcal {L}}} \, \phi (p)= & {} \max _{\epsilon } \, \left[ \delta \pi (p+\epsilon )^2 \ - \ 2 \delta \vartheta (p+\epsilon ) \ - \ \frac{1}{\rho }\, \frac{1}{\sigma _{\epsilon }^2 \Delta } \, \epsilon ^2 \right] \, \ \ \text{ and } \\ \varvec{\mathcal {L}} \, \phi (p)= & {} \min _u \, \biggl [ \Delta c \ + \ \phi \biggl ( \alpha s \Delta \ + \ (1 - s \Delta ) \, p \ - \ s \Delta \, [u + (M-1) y \,] \biggr ) \biggr ]\, . \end{aligned}$$

Applying the $\widetilde{\varvec{\mathcal {L}}}$ operator to $F_{n+1}$ we find that $\widetilde{\varvec{\mathcal {L}}} F_{n+1}(p_{n+1}) = {\tilde{\pi }}_{n+1} \, p_{n+1}^2 - 2 {\tilde{\vartheta }}_{n+1} \, p_{n+1}$ with ${\tilde{\pi }}_{n+1} = \delta ^{\Delta } \pi _{n+1} (1 - \delta ^{\Delta } \rho \, \sigma _{\epsilon }^2 \Delta \, \pi _{n+1})^{-1}$, ${\tilde{\vartheta }}_{n+1} = \delta ^{\Delta } \vartheta _{n+1} (1 - \delta ^{\Delta } \rho \, \sigma _{\epsilon }^2 \Delta \, \pi _{n+1})^{-1}$ and the second order condition that $\delta ^{\Delta } \pi _{n+1} \, - \, \frac{1}{\rho } \, \frac{1}{\sigma _{\epsilon }^2} \, < \, 0$, which will always be satisfied insofar $\pi _{n+1}<0$.

In applying the $\varvec{\mathcal {L}}$ operator to $F_{n+1}(p_{n+1}) = {\tilde{\pi }}_{n+1} \, p_{n+1}^2 - 2 {\tilde{\vartheta }}_{n+1} \, p_{n+1}$ we find the following first order condition

$$\begin{aligned}&\left( \frac{1}{2} \, + \, s^2 \Delta {\tilde{\pi }}_{n+1} \right) \, u_n \, - \, \left( s (1 - s \Delta ) {\tilde{\pi }}_{n+1} + \frac{1}{2} \right) p_n \, \\&\quad + \, (M-1) s^2 \Delta {\tilde{\pi }}_{n+1} y_n - s ( \alpha s \Delta {\tilde{\pi }}_{n+1} - {\tilde{\vartheta }}_{n+1}) = 0 \end{aligned}$$

and hence the optimal production is

$$\begin{aligned} u_n= & {} \frac{\frac{1}{2} \, + \, s (1 - s \Delta ) {\tilde{\pi }}_{n+1} }{\frac{1}{2} \, + \, (M-1) s^2 \Delta {\tilde{\pi }}_{n+1}} \, p_n \, + \, \frac{ (M-1) s \Delta {\tilde{\pi }}_{n+1}}{\frac{1}{2} \, + \, (M-1) s^2 \Delta {\tilde{\pi }}_{n+1}}\, y_{n} \, \nonumber \\&+ \, \frac{ s (\alpha s \Delta {\tilde{\pi }}_{n+1} - {\tilde{\vartheta }}_{n+1})}{\frac{1}{2} \, + \, (M-1) s^2 \Delta {\tilde{\pi }}_{n+1}} \, . \end{aligned}$$

(A.3)

Crucially, firm 1’s conjecture will need to be verified in equilibrium. This is trivially achieved by assuming a symmetric equilibrium in that we posit that $u_n = y_n$. Under such restriction we find that

$$\begin{aligned} u_n= & {} \kappa _{p,n} \, p_n \ + \ \kappa _{e,n} ( \alpha s \Delta {\tilde{\pi }}_{n+1} \, - \, {\tilde{\vartheta }}_{n+1} ) \, , \ \ \text{ with }\\ \kappa _{p,n}= & {} \frac{\frac{1}{2} \, + \, s (1 - s \Delta ) {\tilde{\pi }}_{n+1} }{\frac{1}{2} \, + \, M \,s^2 \Delta {\tilde{\pi }}_{n+1}} \, \ \ \text{ and } \ \ \ \kappa _{e,n} = \, \frac{s}{\frac{1}{2} \, + \, M s^2 \Delta {\tilde{\pi }}_{n+1}}. \end{aligned}$$

Inserting this expression into the argument of the $\varvec{\mathcal {L}}$ operator it is found that

$$\begin{aligned} \pi _n= & {} \frac{1}{2} \, \Delta \, \kappa _{p,n}^2 \ - \ \Delta \, \kappa _{p,n} \, + \, \left[ (1 - s \Delta ) \, - \, M \, s \, \Delta \, \kappa _{p,n} \right] ^2 \, {\tilde{\pi }}_{n+1} \, , \\ \vartheta _n= & {} [1 \, - \, (M-1) s {\tilde{\pi }}_{n+1} \, \Delta \, \kappa _{e,n} ][ - M s \, \Delta \, \kappa _{p,n} \, + \, (1 \, - \, s \Delta ) ] ({\tilde{\vartheta }}_{n+1} \, - \, \alpha s \Delta {\tilde{\pi }}_{n+1} ) \, . \ \end{aligned}$$

$\square$

Proof of Lemma 1

In the limit, for $\Delta \downarrow 0$, $\frac{ (M-1) s \Delta {\tilde{\pi }}_{n+1}}{\frac{1}{2} + (M-1)s^2 \Delta {\tilde{\pi }}_{n+1}} \rightarrow 0$. In addition, for $\Delta \downarrow 0$, as ${\tilde{\pi }}_{n+1} \rightarrow \pi (t)$ (while ${\tilde{\vartheta }}_{n+1} \rightarrow \vartheta (t)$), $\frac{\frac{1}{2} + s (1 - s \Delta ) {\tilde{\pi }}_{n+1}}{\frac{1}{2} + (M-1) s^2 \Delta {\tilde{\pi }}_{n+1}} \rightarrow 1 + 2 s \pi (t)$, while $\frac{ s (\alpha s \Delta {\tilde{\pi }}_{n+1} - {\tilde{\vartheta }}_{n+1})}{\frac{1}{2} \, + \, (M-1) s^2 \Delta {\tilde{\pi }}_{n+1}} \rightarrow -2 s \vartheta (t)$.

Hence, in the limit, the optimal production strategy for firm 1 in t is

$$\begin{aligned} u(t)= & {} \kappa (t) \, p(t) \ - \, 2 \, s \, \vartheta (t)\, , \ \ \text{ with } \ \ \kappa (t) = 1 \ + \ 2 \, s \, \pi (t) \, , \end{aligned}$$

where $\kappa (t) = \lim _{\Delta \downarrow 0} \kappa _{p,n}$, $2 s = \lim _{\Delta \downarrow 0} \kappa _{e,n}$, $\pi (t) = \lim _{\Delta \downarrow 0} \pi _{n}$ and $\vartheta (t) = \lim _{\Delta \downarrow 0} \vartheta _{n}$. To identify the limit functions $\pi (t)$ and $\vartheta (t)$, firstly consider that since

$$\begin{aligned} \left[ (1 - s \Delta ) \, - \, M \, s \Delta \, \kappa _n \right] ^2 = (1 - 2 s \Delta ) \, - \, 2 \, M \, s \, \Delta \, \kappa _n + o(\Delta ^2)\, \end{aligned}$$

it follows that Eq. (A.1) can also be written as

$$\begin{aligned} \pi _n= & {} {\tilde{\pi }}_{n+1} \ + \ \Delta \left( \frac{1}{2} \, \kappa _{p,n}^2 \ - \ \kappa _{p,n} \ - \ 2 s \, {\tilde{\pi }}_{n+1} \ - \ 2\, M\, s \, \kappa _{p,n} \, {\tilde{\pi }}_{n+1} \right) \ + \ o(\Delta ^2) \, , \end{aligned}$$

where $o(\Delta )$ indicates a term of order $\Delta$ or superior. This implies that

$$\begin{aligned} \frac{\pi _n \, - \, \pi _{n+1}}{\Delta }= & {} \frac{{\tilde{\pi }}_{n+1} \, - \, \pi _{n+1}}{\Delta } \ - \ 2 s \, {\tilde{\pi }}_{n+1} \, + \, \kappa _{p,n}\\&\times \left( \frac{1}{2} \, \kappa _{p,n} \ - \ 1 \ - \ 2 \, M\, s \, {\tilde{\pi }}_{n+1} \right) \ + \ o(\Delta ) \, . \end{aligned}$$

Notice, that it can be established that

$$\begin{aligned} \kappa _n \left( \frac{1}{2} \, \kappa _{p,n} \ - \ 1 \ - \ 2 \, M\, s \, {\tilde{\pi }}_{n+1} \right)= & {} - \, \frac{1}{2} \, \left( \frac{\frac{1}{2} \, + \, s {\tilde{\pi }}_{n+1}}{\frac{1}{2} \, + \, M \, s^2 \Delta {\tilde{\pi }}_{n+1}} \right) \,\\&\times \left( \frac{\frac{1}{2} \, + \, (2M-1) \, s {\tilde{\pi }}_{n+1}}{\frac{1}{2} \, + \, M \, s^2 \Delta {\tilde{\pi }}_{n+1}} \right) \ + \ o(\Delta ) \ . \end{aligned}$$

Now, $\lim _{\Delta \downarrow 0} \frac{\pi _n \, - \, \pi _{n+1}}{\Delta } = - \frac{d \pi (t)}{dt}$, $\lim _{\Delta \downarrow 0} \frac{{\tilde{\pi }}_{n+1} \, - \, \pi _{n+1}}{\Delta } = \ln \delta \, \pi (t) + \rho \sigma _{\epsilon }^2 \pi (t)^2$ and $\lim _{\Delta \downarrow 0} {\tilde{\pi }}_{n+1} = \lim _{\Delta \downarrow 0} \pi _{n+1} = \pi (t)$. Given the expression above we also see that $\lim _{\Delta \downarrow 0} \kappa _{p,n} \left( \frac{1}{2} \, \kappa _{p,n} \ - \ 1 \ - \ 2\, M\, s \, {\tilde{\pi }}_{n+1} \right) = - 2 \, (\frac{1}{2} \, + \, s \pi (t) ) (\frac{1}{2} \, + \, (2M-1) \, s \pi (t))$. We conclude that in the limit $\pi (t)$ solves the following differential equation

$$\begin{aligned}&\frac{d \pi (t)}{dt} \ - \ 2 \, \left( s \pi (t) \, + \, \frac{1}{2} \right) \left( (2M-1) s \pi (t) \, + \, \frac{1}{2} \right) \\&\quad - \ 2 s \, \pi (t) \ + \ \ln \delta \, \pi (t) \ + \ \rho \sigma _{\epsilon }^2 \pi (t)^2 = 0 \, . \end{aligned}$$

Similarly, Eq. (A.2) can also be written as follows

$$\begin{aligned} \vartheta _n= & {} {\tilde{\vartheta }}_{n+1} \ - \ \Delta \biggl ( s \, + \, M \, s \, \kappa _{p,n} \ + \ (M-1) \, s \, \kappa _{e,n} \, {\tilde{\pi }}_{n+1} \ + \ o(\Delta ) \biggr ) \, {\tilde{\vartheta }}_{n+1} \\&- \, \Delta ( \alpha \, s \, + \, o(\Delta )) \, {\tilde{\pi }}_{n+1} \, , \end{aligned}$$

so that

$$\begin{aligned} \frac{\vartheta _n \, - \, \vartheta _{n+1}}{\Delta }= & {} \frac{{\tilde{\vartheta }}_{n+1} \, - \, \vartheta _{n+1}}{\Delta } \, \\&- \, \biggl ( s \, + \, M \, s \, \kappa _{p,n} \ + \ (M-1) \, s \, \kappa _{e,n} \, {\tilde{\pi }}_{n+1} \biggr ) \, {\tilde{\vartheta }}_{n+1} \ - \, \alpha \, s {\tilde{\pi }}_{n+1} \, + \, o(\Delta )) \, . \end{aligned}$$

Considering that $\lim _{\Delta \downarrow 0} \frac{\vartheta _n \, - \, \vartheta _{n+1}}{\Delta } = - \frac{d \vartheta (t)}{dt}$, $\lim _{\Delta \downarrow 0} \frac{{\tilde{\vartheta }}_{n+1} \, - \, \vartheta _{n+1}}{\Delta } = \ln \delta \, \vartheta (t) + \rho \sigma _{\epsilon }^2 \pi (t) \vartheta (t)$, $\lim _{\Delta \downarrow 0} {\tilde{\vartheta }}_{n+1} = \lim _{\Delta \downarrow 0} \vartheta _{n+1} = \vartheta (t)$ and that $\lim _{\Delta \downarrow 0} \kappa _{p,n} = 1 + 2 s \pi (t))$ and $\lim _{\Delta \downarrow 0} \kappa _{e,n} {\tilde{\pi }}_{n+1} = 2 s \, \pi (t),$ we conclude that in the limit $\vartheta (t)$ solves the second differential equation

$$\begin{aligned} \frac{d \vartheta (t)}{d t} \, + \, \biggl (\ln \delta \, - \, (1+M) s \biggr )\, \vartheta (t) \, - \, \biggl ( 2 (2M-1) s^2 \, - \, \rho \sigma _{\epsilon }^2 \biggr )\, \pi (t) \vartheta (t) \, - \, \alpha \pi (t) = 0 \, . \ \end{aligned}$$

$\square$

Proof of Proposition 1

We can rewrite (7) as follows

$$\begin{aligned} \frac{d\, \pi (t) }{d\, t} = \frac{1}{2} + \lambda \pi (t) + \gamma \pi (t)^2 \, , \end{aligned}$$

where $\lambda = \bigl (2(1+ M) s - \ln \delta \bigr )$ and $\gamma = 2 (2M -1) s^2 - \rho \sigma _{\epsilon }^2$. This can be transformed into a homogeneous ordinary differential equation of order two,

$$\begin{aligned} \frac{d^2\, z(t)}{d^2\, t} - \lambda \ \frac{d\, z(t)}{d\, t} + \frac{1}{2} \gamma z(t) = 0\, \end{aligned}$$

with $\pi (t) = - \frac{1}{\gamma } \frac{\frac{d\, z(t)}{d\, t}}{z(t)}$. Assume then that $z(t) = m \, \exp (\zeta \,t)$. We have a solution of the ODE iff

$$\begin{aligned}&\zeta ^2 \, m \, \exp (\zeta \,t) \ - \ \zeta \, \lambda \, m \, \exp (\zeta \,t) \ + \ \frac{1}{2} \, \gamma \, m \, \exp (\zeta \,t) \ = \ 0 \, , \\&\quad \text{ ie. } \text{ iff } \ m \, \zeta ^2 \ - \ m \, \lambda \,\zeta \ + \ m \, \frac{1}{2} \, \gamma \ = \ 0 \, . \end{aligned}$$

This admits two roots equal to $\zeta \ = \ \Biggl \{ \begin{array}{c} \zeta _1 = \frac{1}{2} \, \lambda \, + \, \frac{1}{2} \, \mathcal {D} \\ \zeta _2 = \frac{1}{2} \, \lambda \, - \, \frac{1}{2} \, \mathcal {D} \end{array}$, with $\mathcal {D}= [\lambda ^2 - 2 \gamma ]^{1/2}$.

Thus, $z(t) = m_1 \, \exp (\zeta _1 \, t) + m_2 \, \exp (\zeta _2 \, t)$. Given that $\pi (t) = - \frac{1}{\gamma } \, \frac{\frac{d\, z(t)}{d\, t}}{z(t)}$, we can write that

$$\begin{aligned} \pi (t) = - \frac{m_1 \zeta _1 \exp (\zeta _1 t) + m_2 \zeta _2 \exp (\zeta _2 t)}{\gamma \left( m_1 \exp (\zeta _1 t) + m_2 \exp (\zeta _2 \, t)\right) }\, . \end{aligned}$$

We can impose the terminal condition $\pi (T) = 0$ to find that

$$\begin{aligned}&m_1 \, \zeta _1 \, \exp (\zeta _1 \, T) + m_2 \, \zeta _2 \, \exp (\zeta _2 \, T) \ = \ 0 \ \ \Leftrightarrow \ \ m_2 \ = \ - \frac{\zeta _1}{\zeta _2} \, m_1 \, \exp ((\zeta _1 - \zeta _2) \, T) \\&\quad = \ - \frac{\zeta _1}{\zeta _2} \, m_1 \, \exp (\mathcal {D} \, T) \, . \end{aligned}$$

Re-inserting this expression in that for $\pi (t)$ we find that

$$\begin{aligned} \pi (t)= & {} - \, \frac{1}{\gamma } \, \left( \, \frac{\zeta _1 \, \exp (\zeta _1 \, t) \, - \, \zeta _1 \, \exp (\mathcal {D} \, T) \, \exp (\zeta _2 \, t)}{ \exp (\zeta _1 \, t) \, - \, \frac{\zeta _1}{\zeta _2} \, \exp (\mathcal {D} \, T) \, \exp (\zeta _2 \, t)} \, \right) \, \ \\= & {} \ - \, \frac{\zeta _1}{\gamma } \, \left( \, \frac{1 \, - \, \exp (\mathcal {D} \, T) \, \exp (- (\zeta _1 - \zeta _2) \, t)}{1 \, - \, \frac{\zeta _1}{\zeta _2} \, \exp (\mathcal {D} \, T) \, \exp (-(\zeta _1 - \zeta _2) \, t)} \, \right) \, \\= & {} - \ \frac{\zeta _1}{\gamma } \, \left( \, \frac{1 \ - \ \exp (- \, \mathcal {D} \, (t-T) ) }{1 \ - \ \frac{\zeta _1}{\zeta _2} \,\exp (-\mathcal {D} \, (t-T)) } \,\right) \, \ \\= & {} \ - \ \frac{\zeta _1}{\gamma } \, \left( \, \frac{\exp (\, \mathcal {D} \, (T-t) ) \ - \ 1 }{\frac{\zeta _1}{\zeta _2} \, \exp (\mathcal {D} \, (T-t)) \ - \ 1 } \, \right) \, , \end{aligned}$$

as $\zeta _1 - \zeta _2 = \mathcal {D}$. Importantly, we can find the stationary value of $\pi$ pushing t to $-\infty$,

$$\begin{aligned} \lim _{t \downarrow - \infty } \pi (t) \ = \ {\bar{\pi }} \ = \ - \, \frac{\xi _2}{\gamma } \, . \end{aligned}$$

We then immediately see that $\lim _{t \downarrow - \infty } \kappa (t) = 1 + 2 s {\bar{\pi }}$ and that $\lim _{t \downarrow - \infty } \vartheta (t) = \frac{\alpha {\bar{\pi }} s}{\ln \delta - s (1+M) - \gamma {\bar{\pi }}}$. $\Box$

In Lemmas 3–6 we establish a number of results that are important for the economic coherency of our model and/or necessary for the proofs of Propositions 2–7.

Lemma 3

For any parametric constellation ${\bar{\kappa }}$ is positive

Proof

Let w denote $s {\bar{\pi }}$. From the expression solved by ${\bar{\pi }}$ we see that w is a root of the quadratic equation $A w^2 - B w + \frac{1}{2} = 0$, where $A = \left( 2 (2M-1) - \rho \frac{\sigma _{\epsilon }^2}{s^2} \right)$ and $B = \left( 2(1 \, + \, M) - \frac{\ln \delta }{s} \right)$. Now $w > - 1/2$. To verify this inequality notice that it is equivalent to the condition that $\frac{B - \sqrt{B^2 - 2A}}{A} > -1$. This is equivalent to $B+A > \sqrt{B^2 - 2A}$ for $A>0$ and $B+A < \sqrt{B^2 - 2A}$ for $A<0$. In the former case, as we take squared values, we see that $B+A > \sqrt{B^2 - 2A}$ corresponds to $A^2 + 2 A + AB > 0$. This is inequality is obviously satisfied as both A and B are positive. In the latter case, as $A<0$ we notice that $\sqrt{B^2 - 2A}> B > B + A$. Because $w > - \frac{1}{2}$ we conclude that ${\bar{\kappa }} = 1 + 2 w$ is positive.

Lemma 4

For any parametric constellation $p^{*}$ is positive

Proof

In a stationary symmetric equilibrium, $\frac{dp(t)}{d t} = \ \alpha s - s p(t) - s M u(t) + \epsilon (t)$ and $u(t) = {\bar{\kappa }} p(t) - 2 s {\bar{\vartheta }}$. It follows that $\frac{dp(t)}{d t} = \alpha s - A p(t) + 2 s^2 M {\bar{\vartheta }} + \epsilon (t)$, with $A = s \, ( 1 \, + \, M\, {\bar{\kappa }} )$. From this it is immediately to derive that the steady state price is $p^{*} = A^{-1} \, ( \alpha s + \, 2M s^2 {\bar{\vartheta }})$. Consider that from the differential equation (8) it can be concluded that in a stationary equilibrium ${\bar{\vartheta }} = \frac{\alpha {\bar{\pi }} s}{\ln \delta - s (1 + M) - \gamma \,{\bar{\pi }}}$. Substituting the expression for ${\bar{\vartheta }}$ into that for $p^*$ we conclude that $p^{*} = \frac{\alpha s}{A} \left( 1 + \frac{2 M s^2 {\bar{\pi }} }{\ln \delta - s \, (1 + M) - \gamma {\bar{\pi }} } \right)$. Then, notice that we can write $\ln \delta - s (1 + M) - \gamma {\bar{\pi }}=$ $\ln \delta - s (1 + M)+ s (1 + M) - \frac{1}{2} \ln \delta - \frac{1}{2} \mathcal {D} =$ $\frac{1}{2} \left( \ln \delta - \mathcal {D} \right) \equiv Q$. Since both Q and ${\bar{\pi }}$ are negative, while $A= s(1+M {\bar{\kappa }})$ is positive we conclude that $p^{*}$ is positive. $\square$

Lemma 5

In a stationary equilibrium, for any parametric constellation, the expected quantity produced by an oligopolistic firm is positive.

Proof

In a stationary symmetric equilibrium, the expected quantity produced by a generic firm is $u^* = {\bar{\kappa }} p^* - 2 s {\bar{\vartheta }}$. Hence, consider that $p^* = \frac{1}{(1+M {\bar{\kappa }})} \left( \alpha \, + \, 2 M s {\bar{\vartheta }}\right)$. Therefore, $u^* = \frac{1}{1+M {\bar{\kappa }}} \left( {\bar{\kappa }} \alpha - 2 s {\bar{\vartheta }} \right)$, which will be positive if ${\bar{\kappa }} \alpha - 2 s {\bar{\vartheta }} > 0$. Then, consider the expressions for ${\bar{\kappa }}= 1 + 2 s {\bar{\pi }}$ and ${\bar{\vartheta }} = \frac{\alpha {\bar{\pi }} s}{Q}.$ Substituting the expressions for ${\bar{\kappa }}$ and ${\bar{\vartheta }}$ into that for $u^*$, we find that $u^* = \alpha \left[ \frac{1}{2} +\left( \frac{Q - 1}{Q} \right) s {\bar{\pi }}\right]$. Because $0< \frac{Q- 1}{Q}< 1$. Then, since $s {\bar{\pi }} > - \frac{1}{2}$, as seen in the proof of Lemma 3, we see that $u^*$ is positive. $\square$

Lemma 6

In the stationary equilibrium, the production strategy of an oligopolistic firm is more aggressive for a larger $\rho$ and/or larger $\sigma _{\epsilon }$, in that ${\bar{\kappa }}$ is larger.

Proof

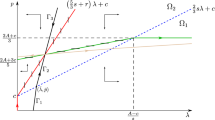
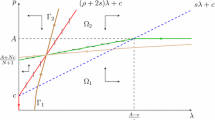
Notice that ${\bar{\pi }}$ corresponds to the root ${\bar{\pi }}_{+} = - \frac{1}{2} \, \frac{\lambda }{\gamma } + \frac{1}{2} \, \frac{\mathcal {D}}{\gamma }$ of the following quadratic equation $\gamma {\bar{\pi }}^2 + \lambda {\bar{\pi }} + \frac{1}{2} = 0$, which is obtained from the differential equation (7) by imposing that $\pi (t) = {\bar{\pi }}$ and $dp(t)/dt=0$. Then, we rely on a graphical argument. In Figs. 1 and 2 we show how the determination of ${\bar{\pi }}_{+}$ changes when either $\rho$ or $\sigma _{\epsilon }^2$ augments. In Fig. 1 we consider the case in which $\gamma$ is positive, while in Fig. 2 that in which it is negative.

Fig. 1

The determination of ${\bar{\pi }}$ for $\gamma > 0$. For any choice of $\rho$ and $\sigma _{\epsilon }^2$ there are two interceptions between the straight line ($-\frac{1}{2} - \lambda \pi$) and the parabola ($\gamma \pi ^2$). That closer to the origin corresponds to ${\bar{\pi }}_{+} = - \frac{1}{2} \, \frac{\lambda }{\gamma } + \frac{1}{2} \, \frac{\mathcal {D}}{\gamma }$. When either $\rho$ or $\sigma _{\epsilon }^2$ rises, so that $\gamma$ falls to $\gamma '$, the parabola moves downward (while the straight line is unaffected given that $\lambda$ is independent of these two parameters) and the stationary value moves up to ${\bar{\pi }}'$

Fig. 2

The stationary value ${\bar{\pi }}$ for $\gamma < 0$. For any choice of $\rho$ and $\sigma _{\epsilon }^2$ there are two interceptions between the straight line ($-\frac{1}{2} - \lambda \pi$) and the parabola ($\gamma \pi ^2$). That smaller one corresponds to ${\bar{\pi }}_{+} = - \frac{1}{2} \, \frac{\lambda }{\gamma } + \frac{1}{2} \, \frac{\mathcal {D}}{\gamma }$. When either $\rho$ or $\sigma _{\epsilon }^2$ rises, so that $\gamma$ falls to $\gamma '$, the parabola moves downward, while the straight line is unaffected since $\lambda$ does not depend on either of these two parameters, and the stationary value moves up to ${\bar{\pi }}'$

Both figures allow to determine what happens when an increase in $\rho$ and/or in $\sigma _{\epsilon }^2$ brings about a reduction in $\gamma$. In both cases graphical inspection shows that for a larger degree of risk-aversion and/or a larger volatility of the demand shocks the stationary value ${\bar{\pi }}$, which is always negative, rises. Then, since ${\bar{\kappa }} \ = \ 1 \, + \, 2 s \, {\bar{\pi }}$ and s is positive we see that ${\bar{\kappa }}$ is increasing in ${\bar{\pi }}$. Then, we conclude that for a larger $\rho$ and/or a larger $\sigma _{\epsilon }^2$ ${\bar{\kappa }}$ is larger. $\square$

Proof of Proposition 2

We have seen in the proof of Lemma 4 that $p^{*} \ = \ \frac{\alpha s}{A} \left( 1 \, \ + \, \frac{2 M \, s^2 \, {\bar{\pi }} }{\ln \delta \, - \, s \, (1 \, + \, M) \, - \, \gamma \, {\bar{\pi }} } \right)$. Then, we notice that in Lemma 6 we proved that ${\bar{\pi }}$ and ${\bar{\kappa }}$ are increasing in $\rho$ and $\sigma _{\epsilon }$. In addition, we notice that $A = s (1+ M {\bar{\kappa }})$ is positive and increasing in ${\bar{\kappa }}$. This implies that $s (1+ M {\bar{\kappa }})$ is increasing in $\rho$ and $\sigma _{\epsilon }$. This means that to establish our result we need to prove that the derivatives of the ratio $\frac{ 2M\, s^2 \, {\bar{\pi }} }{\ln \delta \, - \, s (1 \, + \,M) \, - \, \gamma \, {\bar{\pi }} }$ with respect to $\rho$ and with respect to $\sigma _{\epsilon }$ are negative, so that this ratio is proved to be decreasing in these two parameters. Consider that this ratio can also be written as $\frac{G {\bar{\pi }}}{H \, - \, I {\bar{\pi }}}$, where $G>0$ and $H < 0$. The derivative of this ratio wrt $\rho$ (equivalently with respect to $\sigma _{\epsilon }$) is

$$\begin{aligned}&\frac{1}{(H \, - \, I {\bar{\pi }})^2} \, \left[ \, G (H - I {\bar{\pi }}) \, \frac{d {\bar{\pi }}}{d \rho } \ - \ G {\bar{\pi }} \left( - I \, \frac{d {\bar{\pi }}}{d \rho } \, - \, \frac{d I}{d \rho } \, {\bar{\pi }} \right) \right] \ \\&\quad = \ \frac{G}{(H \, - \, I {\bar{\pi }})^2} \, \left[ H \, \frac{d {\bar{\pi }}}{d \rho } \ + \ {\bar{\pi }}^2 \, \frac{d I}{d \rho }\, \right] \, . \end{aligned}$$

This expression is negative. In fact, $\frac{G}{(H \, - \, I {\bar{\pi }})^2}$ is positive, while $H \, \frac{d {\bar{\pi }}}{d \rho }$ is negative, since H is negative and $\frac{d {\bar{\pi }}}{d \rho }$ is positive. Finally, ${\bar{\pi }}^2 \, \frac{d I}{d \rho }$ is negative because clearly $\frac{d I}{d \rho }$ is negative. An identical argument applies to $\sigma _{\epsilon }$. This proves that $p^*$ is decreasing in both $\rho$ and $\sigma _{\epsilon }$.

Moreover, in the proof of Lemma 5 we have seen that $u^* = \alpha \left[ \frac{1}{2} +\left( \frac{Q - 1}{Q} \right) s {\bar{\pi }}\right]$, where $0< \frac{Q- 1}{Q}< 1$ and $-\frac{1}{2}< s {\bar{\pi }}< 0$. Notice that $\left( \frac{Q - 1}{Q} \right) s {\bar{\pi }}$ is negative. However, in the proof of Lemma 6 we have established that ${\bar{\pi }}$, while negative, is increasing in $\rho$ and $\sigma _{\epsilon }^2$. In addition, Q is negative and decreasing in both $\rho$ and $\sigma _{\epsilon }^2$, while $\frac{Q- 1}{Q}$ is positive and increasing in Q. Combining these results we conclude that when either $\rho$ or $\sigma _{\epsilon }^2$ rises $u^*$ augments. $\square$

Proof of Proposition 3

As $M\uparrow \infty$ both $\lambda$ and $\gamma$ tend to infinity (just recall their definitions) and hence ${\bar{\pi }}$ converges to zero (just consider the graphical inspection of Fig. 1. for $\lambda$ and $\gamma$ raising to infinity). From this it follows that ${\bar{\kappa }} = 1 + 2 s {\bar{\pi }} \rightarrow 1$.

Now recall that $p^{*} \ = \ \frac{\alpha s}{A}\, \left( 1 \, \ + \, \frac{2 M \, s^2 \, {\bar{\pi }} }{\ln \delta \, - \, s \, (1 \, + \, M) \, - \, \gamma \, {\bar{\pi }} } \right)$, where $A \ = \ s (1 \, + \, M {\bar{\kappa }}).$ Using the latter result we see that for $M \uparrow \infty$ A converges to $\infty$. In addition the ratio $\frac{2 M \, s^2 \, {\bar{\pi }} }{\ln \delta \, - \, s \, (1 \, + \, M) \, - \, \gamma \, {\bar{\pi }}}$ can also be written as $\frac{2 s^2 \, {\bar{\pi }} }{\frac{\ln \delta \, - \, s \, - \, \gamma \, {\bar{\pi }}}{M} \, - \, s}$ which clearly converges to zero for $M \uparrow \infty$. From this we conclude that $p^{*}$ converges to zero for $M \uparrow \infty$.

Notice also that for $M \uparrow \infty$ ${\bar{\vartheta }}$ converges to zero too. To see this consider that in an infinite horizon formulation $\pi (t)$ and $\vartheta (t)$ become invariant values, respectively ${\bar{\pi }}$ and ${\bar{\vartheta }}$. This implies that $\frac{d \vartheta (t)}{d t} = 0$ and Eq. (8) simplifies to the following $\biggl (\ln \delta - (1 + \ M) s \biggr ) {\bar{\vartheta }} - \left( 2 (2M-1) s^2 - \rho \sigma _{\epsilon }^2 \right) {\bar{\pi }} {\bar{\vartheta }} - \alpha s \, {\bar{\pi }} = 0$.

We have seen that for $M \uparrow \infty$ ${\bar{\pi }} \downarrow 0$. Then, assume that ${\bar{\vartheta }}$ converges to a value different from zero, say $\vartheta$, for $M \uparrow \infty$. Thence, the first term in the equation rises with M at the same rate (for M large it will be proportional to M). The second term cannot rise with M at the same rate, as ${\bar{\pi }}$ converges to zero when $M \uparrow \infty$ (and hence for M large the second term in the equation will be less than proportional to M). The third term converges to zero. Then, for M large the equation cannot be satisfied. Consequently, we conclude that ${\bar{\vartheta }}$ must also converge to zero.

Now, recall that according to Proposition 1 in a stationary equilibrium $u(t) \ = \ {\bar{\kappa }} \, p(t) \, - \, 2 \, s \, {\bar{\vartheta }}.$ As we have just proved that for $M \uparrow \infty$, $p^{*}$ converges to zero, ${\bar{\kappa }}$ converges to 1 and ${\bar{\vartheta }}$ converges to zero, we conclude that the quantity produced in a steady state by a single firm is zero. As we have quadratic costs the marginal cost for a production level equal to zero is also zero. In brief, we conclude that the marginal cost and the steady state price coincide for $M \uparrow \infty$. $\square$

Proof of Proposition 4

It is sufficient to prove that for $\delta \downarrow 0$ both ${\bar{\pi }}$ and ${\bar{\vartheta }}$ converge to zero, so that the optimal production strategy for the M firms is $u(t) = p(t)$, that is that in the static formulation when the firms’ management takes the good price as given. In addition, the steady state price, $p^*$, converges to $p^* = \frac{\alpha }{1 + M}$, which corresponds to the expected good price, $E_t[p_t]$, in the static formulation when the firms’ management takes such price as given.

In order to prove that $\delta \downarrow 0$ ${\bar{\pi }}$ converges to zero, once again, a graphical argument would suffice. In particular, consider Fig. 3, which, without loss of generality, is drawn under the assumption that $\gamma > 0$ (a similar analysis would apply for $\gamma <0$).

Fig. 3

The stationary value ${\bar{\pi }}$ for $\gamma$ positive. For any choice of M there are two interceptions between the straight line and the parabola. That closer to the origin corresponds to ${\bar{\pi }}_{+} = - \frac{1}{2} \, \frac{\lambda }{\gamma } + \frac{1}{2} \, \frac{\mathcal {D}}{\gamma }$. When $\delta$ falls $\lambda$ rises to $\lambda '$, while $\gamma$ is unaffected. This means that the straight line rotates clockwise, while the parabola does not move. The stationary value moves up to ${\bar{\pi }}'$. For $\delta \downarrow 0$ $\lambda \uparrow \infty$ and the straight line becomes infinitely steep

Notice that as $\delta$ falls $\lambda$ ($\lambda = 2 (1+M)s - \ln \delta$) increases, while $\gamma$ ($\gamma = 2 (2M -1) s - \rho \sigma _{\epsilon }^2$) is unaffected. This implies that as $\delta$ falls the straight line $-\frac{1}{2} - \lambda {\bar{\pi }}$ rotates clock-wise and in the limit becomes vertical. This implies that for $\delta \downarrow 0$ ${\bar{\pi }}$ converges to zero. In the expression for ${\bar{\vartheta }}$ (${\bar{\vartheta }} = \frac{\alpha {\bar{\pi }} s}{\ln \delta \, - \, s\, (1\, + \, M) \, - \, \gamma \,{\bar{\pi }}}$) for $\delta \downarrow 0$ the denominator converges to $-\infty$, while the numerator converges to 0. $\square$

Proof of Proposition 5

As before notice that for $s \downarrow 0$ $\gamma$ ($\gamma = 2 (2M -1) s - \rho \sigma _{\epsilon }^2$) converge to $- \rho \sigma _{\epsilon }^2$, while $\lambda$ ($\lambda = 2 (1+M)s - \ln \delta$) converges to $-\ln \delta$. Thus, ${\bar{\pi }}$ becomes the negative root of $- \rho \sigma _{\epsilon }^2 {\bar{\pi }}^2 \, -\, \ln \delta {\bar{\pi }} \, + \, \frac{1}{2} \, = \, 0$. This implies that both $s {\bar{\pi }}$ and ${\bar{\vartheta }}$ converge to zero for $s\downarrow 0$ and hence that $u(t) = p(t)$, while the stationary price converges to $p^* = \frac{\alpha }{1 + M}$. $\square$

Proof of Proposition 6

Recall from the Proof of Proposition 4 that in the static formulation, if the M firms are price takers, then $p_{{ \text{ com }}} \ = \ \frac{\alpha }{1+M}$. In addition, it is immediate to see that if they are strategic $p_{{ \text{ strat }}} \ = \ \frac{2\alpha }{2+M}$. This implies that $p_{{ \text{ strat }}} = (1 + S) p_{{ \text{ com }}}$, with $S = \frac{M}{2 +M}$. We have seen in the proof of Lemma 3 that $w = s {\bar{\pi }}$ solves equation $A w^2 + B w + \frac{1}{2} = 0$. Given the expressions for A and B, it is immediate to see that for $s\uparrow \infty$ this equation converges to $2 (2M-1) x^2 + 2 (1+ M) x + \frac{1}{2} = \ 0$, which implies that $\lim _{s \uparrow \infty } w = x \equiv - \frac{1 + M - \Gamma }{2 (2M-1)}$, with $\Gamma = [(1+M)^2 - (2M - 1) ]^{1/2} = [M^2 + 2 ]^{1/2}$. In the proof of Proposition 2 we have seen that

$$\begin{aligned} p^{*}= & {} \frac{\alpha }{1 + M {\bar{\kappa }}}\, \left( 1 \, + \, \frac{2 M s \, w}{\ln \delta \, -\, s (1+M) \, - \, 2 (2M - 1) s w \, + \, \rho \sigma _{\epsilon }^2} \right) \, . \end{aligned}$$

For $s \uparrow \infty$ it converges to

$$\begin{aligned} \lim _{s \uparrow \infty } p^{*}= & {} \frac{\alpha }{\lim _{s \uparrow \infty } (1 + M {\bar{\kappa }})}\, \left( \frac{1 \, + \, M \, + \, 2 (M-1) x}{(1+M) \, + \, 2 (2M - 1) x} \right) \, . \end{aligned}$$

Consider that ${\bar{\kappa }} = 1 + 2 s {\bar{\pi }} = 1 + 2 w$. Then $\lim _{s\uparrow \infty } {\bar{\kappa }} = 1 + 2 x$. This implies that $\lim _{s \uparrow \infty } (1 + M {\bar{\kappa }}) = \frac{(1+M)(M-1)}{2M-1} + \frac{M}{2M -1} \Gamma$. In addition, $1 + M + 2 (2M-1) x = \Gamma$ and $1 + M + 2 (M-1) x \ = \ \frac{(1+ M)M}{2M-1} + \frac{M-1}{2M -1} \Gamma$. Substituting in the expression for $\lim _{s \uparrow \infty } p^{*}$ we find that

$$\begin{aligned} \lim _{s \uparrow \infty } p^{*}= & {} \frac{\alpha }{\Gamma }\, \left( \frac{(1 \, + \, M)M \, + \, (M-1) \Gamma }{(1+M)(M-1) \, + \, M \Gamma } \right) \ \\= & {} \ \frac{\alpha }{(1+M) \Lambda }\, \left( \frac{M \, + \, (M-1) \Lambda }{(M-1) \, + \, M \Lambda } \right) , \ \ \ \text{ where } \ \ \Lambda \ = \ \frac{\Gamma }{1+M}. \end{aligned}$$

This implies that $\lim _{s \uparrow \infty } p^{*} = p_{{ \text{ comp }}} \, \left( \frac{M + (M-1) \Lambda }{\Lambda [(M-1) \, + \, M \Lambda ]} \right) = p_{{ \text{ comp }}} ( 1 + R)$ with $R = \frac{M (1 - \Lambda ^2)}{\Lambda [(M-1) \, + \, M \Lambda ]}$. Notice that $0< \Lambda <1$ so that $0<R$. Now for $M=1$ $R=\frac{1}{3} = S$, so that $\lim _{s \uparrow \infty } p^{*} \, = \, \frac{2}{3} \alpha \ = \ p_{{ \text{ strat }}}$, while for $M \ge 2$ $0< R < S$, so that $p_{{ \text{ comp }}} \,< \, \lim _{s \uparrow \infty } p^{*} \, < \, \ p_{{ \text{ strat }}}.$ In fact, consider that for $M =1$ $R = (1 - \Lambda ^2)/\Lambda ^2$, while for $M \ge 2$ $R < (1 - \Lambda ^2)/\Lambda ^2$. In addition, given the expressions for $\Gamma$ and $\Lambda$, we see that $(1 - \Lambda ^2)/\Lambda ^2 = (2M - 1)/(2+M^2)$. The latter is equal to 1/3 and S for $M=1$ and it is not larger than S for $M \ge 2$. In fact, $(2M - 1)/(2+M^2) \le M/(2+M)$ is equivalent to $2(M^2 -1) \le M (M^2-1)$ which holds for $M \ge 2$. $\square$

Proof of Proposition 7

It is sufficient to notice that for $s \uparrow \infty$ ${\bar{\kappa }} \rightarrow 1 + 2 x$, where as shown in the proof of Proposition 6x is function only of the number of firms, M, while ${\bar{\vartheta }} \rightarrow 0$. To prove the latter notice that ${\bar{\vartheta }} = \frac{\alpha w}{Q}$ and that when $s \uparrow \infty$, $w \rightarrow x$, while $Q \uparrow \infty$. In fact, $Q= \frac{1}{2} \mathcal {D}$ with $\mathcal {D} = [\lambda ^2 - 2 \gamma ]^{1/2}$. Given the expression for $\lambda$ and $\gamma$ for s very large $\mathcal {D} \approx 2 s (2 + M^2)^{1/2}$. $\square$