Complex Eigenvalue Splitting for the Dirac Operator

Abstract

We analyze the eigenvalue problem for the semiclassical Dirac (or Zakharov–Shabat) operator on the real line with general analytic potential. We provide Bohr–Sommerfeld quantization conditions near energy levels where the potential exhibits the characteristics of a single or double bump function. From these conditions we infer that near energy levels where the potential (or rather its square) looks like a single bump function, all eigenvalues are purely imaginary. For even or odd potentials we infer that near energy levels where the square of the potential looks like a double bump function, eigenvalues split in pairs exponentially close to reference points on the imaginary axis. For even potentials this splitting is vertical and for odd potentials it is horizontal, meaning that all such eigenvalues are purely imaginary when the potential is even, and no such eigenvalue is purely imaginary when the potential is odd.

1 Introduction

Consider the eigenvalue problem

$$\begin{aligned} P(h)u=\lambda u \end{aligned}$$

(1.1)

on the real line for the Dirac (or Zakharov–Shabat) operator given by the $2\times 2$ non-selfadjoint system

$$\begin{aligned} P(h)=\begin{pmatrix} -hD_x &{} iV(x)\\ iV(x) &{} hD_x\end{pmatrix},\quad D_x=-i\partial /\partial x, \end{aligned}$$

where u is a column vector, h a small positive parameter, $\lambda$ a spectral parameter, and V a real-valued analytic function on ${\mathbb {R}}$. Solving (1.1) constitutes an essential step in the treatment of many important nonlinear evolution equations by means of the inverse scattering transform, including the focusing nonlinear Schrödinger (NLS) equation, the sine-Gordon equation and the modified Korteweg–de Vries equation [7]. Among the numerous applications of these equations are nonlinear wave propagation in plasma physics, nonlinear fiber optics, hydrodynamics and astrophysics.

The operator P(h) is the massless Dirac operator on the real line with anti-selfadjoint potential. In the selfadjoint case, resonances have been studied in various settings by many authors, see for example [17] for a historical account of the massless case, and [18] for the massive case. Certain types of massless Dirac operators have also been shown to be effective models for twistronics, such as in Twisted Bilayer Graphene (TBG), see e.g. [30]. In fact, the twist-angles producing superconductive properties in TBG can be characterized in terms of the spectrum of the related Dirac operator [2, 3], which in this case is highly non-normal.

Here, we shall focus on the connection between P(h) and the NLS equation, which is one of the most fundamental nonlinear evolution equations in physics. In the focusing semiclassical case one is interested in the asymptotic behavior of $\psi =\psi (t,x;h)$ in the semiclassical limit $h\rightarrow 0$, where $\psi$ is the solution to the initial value problem

$$\begin{aligned} ih\frac{\partial \psi }{\partial t}+\frac{h^2}{2}\frac{\partial ^2 \psi }{\partial x^2}+|\psi |^2\psi =0,\quad \psi (0,x)=V(x), \end{aligned}$$

(1.2)

and V is a real-valued function independent of h. In the inverse scattering method the initial data is substituted by the soliton ensembles data, defined by replacing the scattering data for $\psi (0,x)=V(x)$ with their formal WKB approximation. The focusing NLS equation (1.2) is then solved with this new set of h-dependent initial data, and the asymptotic behavior of the obtained approximate solution is analyzed in the limit $h\rightarrow 0$. However, it is a priori not clear how such an h-dependent approximation of initial data affects the behavior of $\psi$ as $h\rightarrow 0$, or if it is even justified at all. For this a rigorous semiclassical description of the spectrum of the corresponding Dirac operator P(h) is required, which has so far only been provided in a few cases such as for periodic potentials by Fujiié and Wittsten [12], and for bell-shaped, even potentials by Fujiié and Kamvissis [9]. Both of the mentioned articles employ the exact WKB method which we describe in Sect. 2 below. For an in-depth discussion on the necessity (as well as effects) of a precise description of the semiclassical spectral data of P(h) in the context of inverse scattering and the focusing NLS equation we refer to the second paper mentioned above.

The interest in the spectrum of the operator P(h) and its relatives dates back to Zakharov and Shabat [27]. Since P(h) is not selfadjoint the eigenvalues are not expected to be real in general. These complex eigenvalues directly determine the energy and speed of the soliton (solitary wave) solutions of (1.2); the energy, or amplitude, given by the imaginary part and the speed by the real part of the eigenvalue. Early on it was realized that there are examples of potentials V(x) for which all the complex eigenvalues are in fact purely imaginary, thus giving rise to soliton pulses with zero velocity in the considered frame of reference. (In the defocusing case, obtained from (1.2) by changing sign of the nonlinear term, no such solutions exist in general. In fact, the corresponding Dirac operator is then selfadjoint, and the first author has shown that it has real spectrum even under small non-selfadjoint perturbations [16].) In 1974, Satsuma and Yajima [26] studied P(h) with $V(x) = V_0{\text {sech}}(x)$, $V_0 > 0$, and solved (1.1) by reducing it to the hypergeometric equation. They found that if $h = h_{N} = V_0/N$, there are exactly N purely imaginary eigenvalues $\lambda _{k}$ given by

$$\begin{aligned} \lambda _{k} = ih_{N}\left( N-k-\frac{1}{2}\right) , \quad k = 0,\ldots , N-1. \end{aligned}$$

For many years thereafter, the literature was filled with erroneous statements about eigenvalues being confined to the imaginary axis whenever the potential V is real-valued and symmetric. In the nonsemiclassical regime ($h=1$) the question was given rigorous consideration in a series of papers by Klaus and Shaw [20,21,22] who established that

• (a) if V is of Klaus–Shaw type, that is, a “single-lobe” potential defined by a non-negative, piecewise smooth, bounded $L^{1}$ function on the real line which is nondecreasing for $x<0$ and nonincreasing for $x>0$, then all eigenvalues are purely imaginary (symmetry not being a factor);

• (b) there are examples of real-valued, even, piecewise constant or piecewise quadratic potentials with two or more “lobes” giving rise to eigenvalues that are not purely imaginary;

• (c) if $V\in L^{1}$ is an odd function, there are no purely imaginary eigenvalues at all.

We shall consider these questions in the semiclassical setting and analytic category, and show that a counterpart of (a) holds for eigenvalues near $\lambda _0=i\mu _0\in i{\mathbb {R}}$ even if one only assumes that V locally has the shape of a single-lobe¹ potential near the “energy level” $\mu _0$. We will also derive precise conditions for eigenvalues when V locally has the shape of a double-lobe potential near the energy level $\mu _0$, and show that when V is symmetric, this leads to an exponentially small splitting of the eigenvalues akin to the well-known splitting phenomenon observed for eigenvalues of the selfadjoint Schrödinger operator with a double-well potential. We prove that when V is even and $h>0$ is sufficiently small, this splitting is vertical from reference points on the imaginary axis; in particular, all eigenvalues are purely imaginary then. (This is in contrast to the examples in (b) which of course do not satisfy the analyticity assumption, and we believe this might help explain the confusion witnessed in the literature prior to the mentioned papers by Klaus and Shaw.) We also show that when V is odd and $h>0$ is sufficiently small, the splitting is horizontal from reference points on the imaginary axis; in particular, in accordance with (c) there can be no purely imaginary eigenvalues in this case. Here we note that for fixed h, (1.1) can be formally interpreted as a non-semiclassical Zakharov–Shabat eigenvalue problem with potential $q(x)=h^{-1}V(x)$ and spectral parameter $\zeta =h^{-1}\lambda$, so it makes sense to compare results between the two settings. In particular, the eigenvalue formation threshold $\int _{-\infty }^\infty |q(x)|\,dx>\pi /2$ established by Klaus and Shaw [22] is always reached as $h\rightarrow 0$. We also wish to mention that some of the examples in (b) together with the corresponding focusing NLS equation have been further analyzed by Desaix, Andersson, Helczynski, and Lisak [5], and Jenkins and McLaughlin [19], among others.

1.1 Statement of results

To be more precise, we shall view P(h) as a densely defined operator on $L^2$ and study the eigenvalue problem (1.1) for spectral parameters $\lambda =i\mu$ close to $\lambda _0=i\mu _0\in i(0,V_0)$, where $V_{0}=\max _{x \in {\mathbb {R}}}|V(x)|$, for which the potential is either a single or double lobe in a sense to be specified below. We assume that the potential satisfies the following assumptions:

$\mathrm {(i)}$:

V(x) is real-valued on ${\mathbb {R}}$ and analytic in a complex domain $D\subset {\mathbb {C}}$ containing an open neighborhood of the real line, and

$\mathrm {(ii)}$:

$\limsup _{x\rightarrow \pm \infty }|V(x)|< \mu _{0}$.

Examples of D are tubular neighborhoods of ${\mathbb {R}}$, or more generally, domains $\{ x \in {\mathbb {C}}: |{\text {Im}}x|< \delta ({\text {Re}}x) \}$ where $\delta :{\mathbb {R}}\rightarrow {\mathbb {R}}_+$ is a positive continuous function which is allowed to decay as $|{\text {Re}}x|\rightarrow \infty$. Note that the spectrum of P(h) is symmetric with respect to reflection in ${\mathbb {R}}$ (as well as with respect to reflections in the imaginary axis), so it is not necessary to treat $\lambda _0\in i(-V_0,0)$ separately. We will also not consider spectral parameters close to the real line. In fact, if (ii) is strengthened to a decay condition of the form

$\mathrm {(ii)}'$:

$|V(x)|\le C |x|^{-1-d}$ for $|x|\gg 1$, where $C,d>0$,

then it is known that the continuous spectrum of P(h) consists of the entire real axis, and that away from the origin there are no real eigenvalues. For potentials of Klaus–Shaw type satisfying $\mathrm {(ii)}'$, a precise description of the reflection coefficients as well as the eigenvalues close to zero has recently been obtained by Fujiié and Kamvissis [9].

Finally, it is not necessary to consider eigenvalues away from ${\mathbb {R}}\bigcup i[-V_0,V_0]$ since the spectrum of P(h) accumulates on this set in the limit as $h\rightarrow 0$. In fact, if $\Omega \Subset \complement ( {\mathbb {R}}\bigcup i[-V_0,V_0])$ then P(h) has no spectrum in $\Omega$ as long as h is sufficiently small, see Dencker [4, Section 2] or Fujiié and Wittsten [12, Proposition 2.1]. After obtaining the necessary properties in Sect. 2 of the exact WKB solutions needed for our analysis, we shall therefore in Sect. 3 study the spectrum of P(h) near $\lambda _0=i\mu _0$ when the potential locally, near the energy level $\mu _0$, corresponds to a single lobe in the following sense.

Definition 1.1

Let $0<\mu _0<V_0$ and assume that the equation $V(x)^2 - \mu ^2_0 = 0$ has exactly two real solutions $\alpha _l(\mu _0)$ and $\alpha _r(\mu _0)$ with $\alpha _l<\alpha _r$ and $V'(\alpha _\bullet ) \ne 0$, $\bullet =l,r$. We then say that V is a single-lobe potential near $\mu _0$.

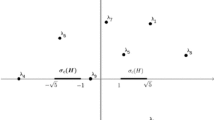
We may without loss of generality assume that the roots of the equation $V(x)^2-\mu ^2=0$ (called turning points) are roots to $V(x)=\mu _0$ (so that $V'(\alpha _l)>0$ and $V'(\alpha _r)<0$) since the case when they are roots to $V(x)=-\mu _0$ can be studied by replacing the potential V with $-V$ and reducing the resulting eigenvalue problem to the original one.² (It is not possible that one turning point is a root to $V(x)=\mu _0$ and the other to $V(x)=-\mu _0$ since this would give four solutions to $V(x)^2-\mu ^2_0=0$ when $V'(\alpha _l),V'(\alpha _r)\ne 0$.) Figure 1 illustrates two stereotypical examples of this situation. Of course, any potential V of Klaus–Shaw type is a single-lobe potential near $\mu _0\in (0,V_0)$. Note also that the turning points depend continuously (even analytically) on $\mu$ as long as the multiplicity is constant. In particular, Definition 1.1 cannot hold at $\mu _0=0$ or $\mu _0=V_0$ (or at any local extreme values of V) because the situation degenerates then, which explains why these values are excluded. It also explains why it makes sense to say that V is a single-lobe potential near $\mu _0$, since there is then an $\varepsilon$-neighborhood $B_\varepsilon (\mu _0)\subset {\mathbb {C}}$ around $\mu _0$ such that if $\mu \in B_\varepsilon (\mu _0)$ then the equation $V(x)^2 - \mu ^2 = 0$ has exactly two solutions $\alpha _l(\mu )$ and $\alpha _r(\mu )$ with ${\text {Re}}\alpha _l<{\text {Re}}\alpha _r$, ${\text {Re}}V^{\prime }(\alpha _l) > 0$ and ${\text {Re}}V^{\prime }(\alpha _r) < 0$. For such $\mu$ we define the action integral

$$\begin{aligned} I(\mu )=\int _{\alpha _l(\mu )}^{\alpha _r(\mu )}(V(t)^2-\mu ^2)^{1/2}\, dt, \end{aligned}$$

(1.3)

where the determination of the square root is chosen so that $I(\mu )$ is real and positive for real $\mu$. In this case, we prove in Sect. 3 that there are constants $\varepsilon ,h_0>0$ such that if $\mu \in B_\varepsilon (\mu _0)$ and $0<h\le h_0$ then $\lambda =i\mu$ is an eigenvalue if and only if the Bohr–Sommerfeld quantization condition

$$\begin{aligned} I(\mu ) = \left( k+\frac{1}{2}\right) \pi h + h^2r(\mu ,h) \end{aligned}$$

(1.4)

is satisfied for some integer k, see Theorem 3.4. Here $r(\mu ,h)$ is a function defined on $B_\varepsilon (\mu _0)\times (0,h_0]$ with $r=O(1)$ as $h\rightarrow 0$. In particular, if $\mu _k^{\mathrm {sl}}(h)$ is the unique root of $I(\mu ) = (k+\frac{1}{2})\pi h$ near $\mu _0$ (where the superscript $\mathrm {sl}$ refers to single lobe), and $\lambda _k^\mathrm {sl}=i\mu _k^{\mathrm {sl}}$, then there is a unique eigenvalue $\lambda _k=i\mu _k$ such that

$$\begin{aligned} |\lambda _k(h)-\lambda _k^\mathrm {sl}(h)|=O(h^2), \end{aligned}$$

see Remark 3.5. We also obtain the following refinement of [9, Theorem 2.2] showing that for single-lobe potentials, the semiclassical eigenvalues are confined to the imaginary axis:

Fig. 1

Two examples of levels $\mu _{0}\in {\mathbb {R}}$ such that the depicted function V is a single-lobe potential near $\mu _0$. The corresponding lobes are shaded blue

Theorem 1.2

If V is a single-lobe potential near $\mu _0=-i\lambda _0$, then there exist positive constants $h_{0}$ and $\varepsilon$ such that the point spectrum of P(h) satisfies

$$\begin{aligned} \sigma _{p}(P(h)) \bigcap \left\{ \lambda \in {\mathbb {C}}: |\lambda -\lambda _{0}|< \varepsilon \right\} \subset i{\mathbb {R}} \end{aligned}$$

when $0 < h \le h_{0}$.

Section 4 studies the eigenvalue problem for potentials assumed to locally have the features of a double lobe.

Definition 1.3

Let $0<\mu _0<V_0$ and assume that the equation $V(x)^2 - \mu ^2_0 = 0$ has exactly four real solutions $\alpha _{l}(\mu _0)$, $\beta _{l}(\mu _0)$, $\beta _{r}(\mu _0)$ and $\alpha _r(\mu _0)$ with $\alpha _{l}< \beta _{l}< \beta _{r}<\alpha _r$ and $V^{\prime }(\alpha _\bullet ),V^{\prime }(\beta _\bullet ) \ne 0$, $\bullet =l,r$. We then say that V is a double-lobe potential near $\mu _0$.

Figure 2 shows two stereotypical examples of double-lobe potentials. In the first example, $V(\beta _l)=V(\beta _r)>0$, whereas $V(\beta _l)=-V(\beta _r)>0$ in the second. As indicated, it suffices to consider these two situations (i.e., peak-peak and peak-valley) since the other two cases can be obtained, as for single-lobe potentials, by replacing the potential V by $-V$ and reducing the corresponding eigenvalue problem to the original one. By continuity there is an $\varepsilon >0$ such that for $\mu \in B_\varepsilon (\mu _0)$, the equation $V(x)^2 - \mu ^2 = 0$ still has exactly four solutions $\alpha _{l}(\mu )$, $\beta _{l}(\mu )$, $\beta _{r}(\mu )$ and $\alpha _r(\mu )$ with ${\text {Re}}\alpha _{l}< {\text {Re}}\beta _{l}< {\text {Re}}\beta _{r}<{\text {Re}}\alpha _r$ and the signs of ${\text {Re}}V'(\alpha _\bullet ),{\text {Re}}V'(\beta _\bullet )$ unaffected. For such $\mu$ we introduce the action integrals

Fig. 2

Two examples of levels $\mu _{0}\in {\mathbb {R}}$ such that the depicted function V is a double-lobe potential near $\mu _0$. The corresponding lobes are shaded blue

$$\begin{aligned} I_l(\mu )=\int _{\alpha _l(\mu )}^{\beta _l(\mu )}\left( V(t)^2-\mu ^2\right) ^{1/2}\, dt,\quad I_r(\mu )=\int _{\beta _r(\mu )}^{\alpha _r(\mu )}\left( V(t)^2-\mu ^2\right) ^{1/2}\, dt, \end{aligned}$$

(1.5)

and

$$\begin{aligned} J(\mu )=\int _{\beta _l(\mu )}^{\beta _r(\mu )}\left( \mu ^2-V(t)^2\right) ^{1/2}\, dt, \end{aligned}$$

(1.6)

where the determinations of the square roots are chosen in such a way that each action integral is real-valued and positive for real $\mu$. We show that there are positive constants $\varepsilon ,h_{0}$ such that if $\mu \in B_\varepsilon (\mu _0)$ and $0<h\le h_0$ then $\lambda = i\mu$ is an eigenvalue in the case when $V(\beta _l) = \pm V(\beta _r)$ if and only if

$$\begin{aligned} \left( e^{iI_l/h}\gamma _l+e^{-iI_l/h}\gamma _l^*\right) \left( e^{iI_r/h}\gamma _r+e^{-iI_r/h}\gamma _r^*\right) \mp e^{-2J/h}\sin (I_l/h)\sin (I_r/h)=0, \end{aligned}$$

(1.7)

see Theorem 4.4. Here $\gamma _\bullet (\mu ,h)$, $\bullet =l,r$, are functions defined on $B_\varepsilon (\mu _0) \times (0,h_{0}]$ with $\gamma _\bullet =1+O(h)$ as $h\rightarrow 0$, and $*$ denotes the operation

$$\begin{aligned} \gamma _l^*(\mu )=\overline{\gamma _l({{\bar{\mu }}})}, \end{aligned}$$

see Sect. 2.5. From the quantization condition (1.7) we see that modulo an exponentially small error the eigenvalues $\lambda = i\mu$ for $\mu \in B_\varepsilon (\mu _{0})$ are given in terms of the roots to the equation

$$\begin{aligned} \left( e^{iI_l/h}\gamma _l+e^{-iI_l/h}\gamma _l^*\right) \left( e^{iI_r/h}\gamma _r+e^{-iI_r/h}\gamma _r^*\right) = 0. \end{aligned}$$

This is equivalent to the two Bohr–Sommerfeld quantization conditions corresponding to each potential lobe, i.e.,

$$\begin{aligned} \frac{ \gamma _l}{ \gamma _l^*} e^{2iI_{l}/h} = -1, \quad \frac{ \gamma _r}{ \gamma _r^*} e^{2iI_{l}/h} = -1. \end{aligned}$$

These may be rewritten in the form

$$\begin{aligned} I_{l}(\mu ) = \left( k + \frac{1}{2} \right) \pi h + h^{2} r_{l}(\mu ,h) , \quad I_{r}(\mu ) = \left( k + \frac{1}{2} \right) \pi h + h^{2} r_{r}(\mu ,h), \end{aligned}$$

where

$$\begin{aligned} r_{l} = \frac{1}{2ih}\log \left( \frac{ \gamma _l}{ \gamma _l^*} \right) , \quad r_{r} = \frac{1}{2ih}\log \left( \frac{ \gamma _r}{ \gamma _r^*}\right) \end{aligned}$$

are both bounded when h tends to 0. Thus we conclude that the set of eigenvalues produced by a double-lobe potential is exponentially close to the union of the sets of eigenvalues produced by each potential lobe (cf. (1.4)). This is a well-known fact for the Schrödinger equation, see [13, 15].

Remark

For readers familiar with the time-independent Schrödinger equation we wish to mention that “inside” the lobe(s) (the projection of the shaded regions in Figs. 1, 2 onto the real axis), solutions to (1.1) are oscillating, while they are exponential in character “outside” the lobe(s). In this sense, the lobes can thus be said to correspond to potential wells (rather than to barriers) in the terminology of quantum mechanics.

Section 5 considers the special case of double-lobe potentials V such that V(x) is either an even or an odd function of $x\in {\mathbb {R}}$. If this assumption holds, the quantization condition (1.7) can be rewritten in the case when $V(x) = \pm V(-x)$ as

$$\begin{aligned} 4\rho ^2 \cos ^2\left( {{\tilde{I}}}/h\right) \mp e^{-2J/h}\sin ^2( I/h)= 0, \end{aligned}$$

(1.8)

see Proposition 5.1. Here, $I= I_l=I_r$, while ${{\tilde{I}}}= I+O(h^2)$ and $\rho =1+ O(h)$ as $h \rightarrow 0$. Thus, modulo an exponentially small error, the eigenvalues produced by each potential lobe satisfy the same Bohr–Sommerfeld quantization condition, namely

$$\begin{aligned} {{\tilde{I}}}(\mu ) = \left( k + \frac{1}{2} \right) \pi h \end{aligned}$$

(1.9)

for some integer $k=k(h)$. If $\mu _k^{\mathrm {dl}}(h)$ is the unique root of (1.9) near $\mu _0$ (where the superscript $\mathrm {dl}$ stands for double lobe), it turns out that $i\mu _k^{\mathrm {dl}}$ is purely imaginary. Now, eigenvalues $\lambda =i\mu$ of the Dirac operator (where $\mu$ satisfies the quantization condition (1.8)) split in pairs symmetrically about the reference points $i\mu _k^{\mathrm {dl}}$.

Theorem 1.4

Suppose that V is a double-lobe potential near $\mu _0$ such that V(x) is either an even or an odd function of $x\in {\mathbb {R}}$, and let $\mu _k^{\mathrm {dl}}(h)$ be the unique root of (1.9) near $\mu _0$. Then $i\mu _k^{\mathrm {dl}}\in i{\mathbb {R}}$ and the two eigenvalues $i\mu _{k}^{+}(h)$, $i\mu _{k}^{-}(h)$ approximated by $i\mu _k^{\mathrm {dl}}(h)$ have the following asymptotic behavior as $h \rightarrow 0$:

(1):

If V(x) is an even function, then

$$\begin{aligned} i\mu _k^\pm (h)-i\mu _k^{\mathrm {dl}}(h) = \pm i e^{-J(\mu _k^{\mathrm {dl}})/h}\left( \frac{h}{2I^{\prime }(\mu _k^{\mathrm {dl}})}+O\left( h^2\right) \right) . \end{aligned}$$

(2):

If V(x) is an odd function, then

$$\begin{aligned} i\mu _k^\pm (h)-i\mu _k^{\mathrm {dl}}(h)= \pm e^{-J(\mu _k^{\mathrm {dl}})/h}\left( \frac{h}{2I^{\prime }(\mu _k^{\mathrm {dl}})}+O\left( h^2\right) \right) . \end{aligned}$$

Moreover, the eigenvalues split precisely vertically in the even case, whereas they split precisely horizontally in the odd case. Thus, for $0<h\le h_0$, all eigenvalues are purely imaginary when V is even, and no eigenvalue is purely imaginary when V is odd.

The proof relies on the explicit exponential error term in (1.8) which we obtain by using a novel method, inspired by recent work due to Mecherout, Boussekkine, Ramond and Sjöstrand [24], to refine the WKB analysis for the Dirac operator by introducing carefully chosen WKB solutions defined “between” the lobes. As already mentioned, the results are reminiscent of the well-known splitting of eigenvalues for the linear Schrödinger operator with a symmetric double-well potential, going back to the work of Landau and Lifshitz [23] and studied mathematically by, among others, Simon [28], Helffer and Sjöstrand [15] and Gérard and Grigis [13]. This type of tunneling effect has recently also been observed for a system of semiclassical Schrödinger operators by Assal and Fujiié [1]. For more on this topic we refer to the mentioned works and the references therein.

In the literature a common focus of study is the appearance and location of purely imaginary eigenvalues as the $L^1$ norm of the potential increases, for example by taking $q(x)=h^{-1}V(x)$ and letting h decrease. Potentials of the form

$$\begin{aligned} q(x)=h^{-1}\left( {\text {sech}}\left( x-x_0\right) +{\text {sech}}\left( x+x_0\right) \right) \end{aligned}$$

consisting of two separated sech-shaped pulses have been numerically investigated by Desaix, Anderson and Lisak [6] for different separations $x_0$. They found that at the first critical amplitude $h^{-1}=1/4$, a purely imaginary eigenvalue $\zeta _1$ appears, and for $h^{-1}<1/4$ there are no eigenvalues (consistent with the threshold of Klaus and Shaw [22]). For small separations, q behaves almost like a single-lobe potential, and the second critical amplitude $h^{-1}=3/4$ also gives rise to a purely imaginary eigenvalue. However, for larger separations such as $x_0=5$, two complex eigenvalues $\zeta _{2,3}=\pm \xi +i\eta$ with nonzero real parts are created already in the vicinity of $h^{-1}=4/10$. As the amplitude $h^{-1}$ increases, the real parts decrease while $\eta$ increases until the two eigenvalues meet and then separate along the imaginary axis (both now purely imaginary, $\zeta _2$ with increasing and $\zeta _3$ with decreasing imaginary part). As $h^{-1}$ reaches the second critical amplitude 3/4, $\zeta _3$ is destroyed and only $\zeta _1$ and $\zeta _2$ remain. Since $\zeta =h^{-1}\lambda$, we should be able to see a similar type of behavior for semiclassical eigenvalues of P(h) as h decreases, which is something we hope to investigate in a future paper. Of course, as h becomes sufficiently small, our results show that for a potential consisting of two separated sech-pulses, all eigenvalues $\lambda =i\mu$ are purely imaginary as long as $\mu \ne 0$ is not close to a local extreme value of V, see Fig. 3. It would also be interesting to see if this property persists as $\mu$ tends to local extreme values of V; the exact WKB method does not work then so other methods are needed.

Fig. 3

An even potential V(x) with a local minimum at $x=0$. Away from the shaded region V is either a single-lobe or a double-lobe potential. For sufficiently small h, any eigenvalue $\lambda$ of P(h) with imaginary part away from the shaded region must therefore be purely imaginary by Theorems 1.2 and 1.4

2 Exact WKB Analysis

2.1 Exact WKB solutions

Here we recall the construction of a solution of the Dirac system in a complex domain as a convergent series, known as an exact WKB solution. Such solutions were first introduced by Ecalle [8] and later used by Gérard and Grigis [13] to study the Schrödinger operator. We shall follow the construction for systems due to Fujiié, Lasser and Nédélec [10].

The system (1.1) can be written in the form

$$\begin{aligned} \frac{h}{i}\frac{du}{dx}=M(x,\lambda )u,\quad M(x,\lambda )=\begin{pmatrix} -\lambda &{} iV(x)\\ -iV(x) &{} \lambda \end{pmatrix}. \end{aligned}$$

(2.1)

Recall (see [10]) that the exact WKB solutions of systems of type (2.1) are of the form

$$\begin{aligned} u^\pm (x,h)=e^{\pm z(x)/h}\begin{pmatrix} 1 &{} 1\\ -1 &{} 1\end{pmatrix}Q(z(x))\begin{pmatrix} 0 &{} 1\\ 1 &{} 0\end{pmatrix}^{(1\pm 1)/2}w^\pm (x,h), \end{aligned}$$

(2.2)

where the function z(x) is the complex change of coordinates

$$\begin{aligned} z(x)=z\left( x;x_0\right) =i\int _{x_0}^x\sqrt{V(t)^2+\lambda ^2}\, dt \end{aligned}$$

for some choice of phase base point $x_0$ in the strip D where V is assumed to be analytic, while Q is the matrix valued function

$$\begin{aligned} Q(z)=\begin{pmatrix} H(z)^{-1} &{} H(z)^{-1}\\ iH(z) &{} -iH(z)\end{pmatrix} \quad \text {with } H(z(x))=\left( \frac{iV(x)+\lambda }{iV(x)-\lambda }\right) ^{1/4}. \end{aligned}$$

(2.3)

Here z(x) and Q(z) are defined on the Riemann surfaces of $(V^2+\lambda ^2)^{1/2}$ and over D, respectively. These Riemann surfaces are defined by introducing branch cuts emanating from the zeros of $x\mapsto \det (M(x,\lambda ))$, i.e., of $iV\pm \lambda$ (the turning points of the system (2.1)), see Sect. 2.4.

The amplitude vectors $w^\pm$ in (2.2) are defined as the (formal) series

$$\begin{aligned} w^\pm (x,h)= \begin{pmatrix} w^\pm _{\mathrm {even}}(x,h)\\ w^\pm _{\mathrm {odd}}(x,h)\end{pmatrix} =\sum _{n=0}^\infty \begin{pmatrix} w^\pm _{2n}(z(x))\\ w^\pm _{2n+1}(z(x))\end{pmatrix}, \end{aligned}$$

(2.4)

where $w^\pm _0(z)\equiv 1$, while $w^\pm _j(z)$ for $j\ge 1$ are the unique solutions to the scalar transport equations

$$\begin{aligned} \left( \frac{d}{dz}\pm \frac{2}{h}\right) w^\pm _{2n+1}(z)= & {} \frac{dH(z)/dz}{H(z)}w^\pm _{2n}(z), \end{aligned}$$

(2.5)

$$\begin{aligned} \frac{d}{dz}w^\pm _{2n+2}(z)= & {} \frac{dH(z)/dz}{H(z)}w^\pm _{2n+1}(z) \end{aligned}$$

(2.6)

with prescribed initial conditions $w_n^\pm ({{\tilde{z}}})=0$ for some choice of amplitude base point ${{\tilde{z}}}=z({{\tilde{x}}})$ where $\tilde{x}$ is not a turning point. When we want to signify the dependence on the base point ${{\tilde{z}}}=z({{\tilde{x}}})$ we write

$$\begin{aligned} w^\pm (x,h;\tilde{x}) =\begin{pmatrix} w^\pm _{\mathrm {even}}(x,h;{{\tilde{x}}})\\ w^\pm _{\mathrm {odd}}(x,h;{{\tilde{x}}})\end{pmatrix} \end{aligned}$$

for the amplitude vectors.

Recall that if $\Omega$ is a simply connected open subset of D which is free from turning points then $z=z(x)$ is conformal from $\Omega$ onto $z(\Omega )$. For fixed $h>0$, the formal series (2.4) converges uniformly in a neighborhood of the amplitude base point ${{\tilde{x}}}$, and $w^\pm _{\mathrm {even}}(x,h)$ and $w^\pm _{\mathrm {odd}}(x,h)$ are analytic functions in $\Omega$, see [10, Lemma 3.2]. As a consequence, the functions $u^\pm$ given by (2.2) are exact solutions of (2.1) and when we wish to indicate the particular choice of amplitude base point ${{\tilde{x}}}\in \Omega$ and phase base point $x_0\in D$ we will write $u^\pm (x;x_0,{{\tilde{x}}})$. We remark that these solutions are defined for example everywhere on ${\mathbb {R}}$, although some of the expressions involved are only defined on Riemann surfaces of $(V^2+\lambda ^2)^{1/2}$ or .

For fixed ${{\tilde{x}}}\in \Omega$, let $\Omega _\pm$ be the set of points x for which there is a path from ${{\tilde{x}}}$ to x along which $t\mapsto \pm {\text {Re}}z(t)$ is strictly increasing. In other words, $x\in \Omega _\pm$ if there is a path which intersects the the level curves of $t\mapsto {\text {Re}}z(t)$ transversally in the appropriate direction. The level curves of $t\mapsto {\text {Re}}z(t)$ are called Stokes lines.

Remark 2.1

For any integers $k,N\in {\mathbb {N}}$

$$\begin{aligned} \partial ^k\left( w^\pm _\mathrm {even}(x,h)-\sum _0^Nw_{2n}^\pm (z(x))\right)= & {} O\left( h^{N+1}\right) ,\\ \partial ^k\left( w^\pm _\mathrm {odd}(x,h)-\sum _0^Nw_{2n+1}^\pm (z(x))\right)= & {} O\left( h^{N+2}\right) , \end{aligned}$$

uniformly on compact subsets of $\Omega _\pm$ as $h\rightarrow 0$, see [10, Proposition 3.3]. In particular,

$$\begin{aligned} w^\pm _\mathrm {even}(x,h)=1+O(h),\quad w^\pm _\mathrm {odd}(x,h)=O(h), \end{aligned}$$

as $h\rightarrow 0$.

2.2 The Wronskian formula

For vector-valued solutions u and v of (2.1), let ${\mathcal {W}}(u,v)$ be the Wronskian defined by

$$\begin{aligned} {\mathcal {W}}(u,v)(x)=\det (u(x)\ v(x)). \end{aligned}$$

Since the trace of the matrix $M(x,\lambda )$ is zero, it follows that ${\mathcal {W}}(u,v)$ is in fact independent of x. If $x_0$ is a phase base point in D and ${{\tilde{x}}},{{\tilde{y}}}$ are different amplitude base points in $\Omega$, a straightforward calculation shows that

$$\begin{aligned}&{\mathcal {W}}\left( u^+\left( x;x_0,{{\tilde{x}}}\right) ,u^-\left( x;x_0,{{\tilde{y}}}\right) \right) \\&\quad =-4i\left( w_\mathrm {odd}^+(x,h;{{\tilde{x}}})w_\mathrm {odd}^-(x,h;{{\tilde{y}}})- w_\mathrm {even}^+(x,h;{{\tilde{x}}})w_\mathrm {even}^-(x,h;{{\tilde{y}}})\right) , \end{aligned}$$

where the solutions $u^\pm$ are given by (2.2). Recalling the initial conditions of the transport equations (2.5)–(2.6) and evaluating at $x={{\tilde{y}}}$ we get

$$\begin{aligned} {\mathcal {W}}\left( u^+\left( x;x_0,{{\tilde{x}}}\right) ,u^-\left( x;x_0,\tilde{y}\right) \right) =4iw_\mathrm {even}^+\left( {{\tilde{y}}},h;\tilde{x}\right) . \end{aligned}$$

(2.7)

We may of course also choose $x={{\tilde{x}}}$, which gives

$$\begin{aligned} {\mathcal {W}}\left( u^+\left( x;x_0,{{\tilde{x}}}\right) ,u^-\left( x;x_0,\tilde{y}\right) \right) =4iw_\mathrm {even}^-\left( {{\tilde{x}}},h;\tilde{y}\right) . \end{aligned}$$

(2.8)

In particular, we see that if there is a path from ${{\tilde{x}}}$ to ${{\tilde{y}}}$ along which the function $t\mapsto {\text {Re}}z(t)$ is strictly increasing, then ${\mathcal {W}}(u^+(x;x_0,{{\tilde{x}}}),u^-(x;x_0,\tilde{y})) =4i+O(h)$ as $h\rightarrow 0$ by Remark 2.1, showing that such a pair of solutions is linearly independent if h is sufficiently small. We also recall the Wronskian formula for pairs of solutions of the same type:

$$\begin{aligned}&{\mathcal {W}}\left( u^\pm \left( x;x_0,{{\tilde{x}}}\right) ,u^\pm \left( x;x_0,{{\tilde{y}}}\right) \right) =-4i(-1)^{(1\pm 1)/2}e^{\pm 2 z\left( x;x_0\right) /h}\\&\quad \times \left( w_\mathrm {even}^\pm (x,h;{{\tilde{x}}}) w_\mathrm {odd}^\pm (x,h;{{\tilde{y}}})- w_\mathrm {even}^\pm (x,h;\tilde{y})w_\mathrm {odd}^\pm (x,h;{{\tilde{x}}})\right) . \end{aligned}$$

Evaluating at $x={{\tilde{x}}}$ gives

$$\begin{aligned} {\mathcal {W}}\left( u^\pm \left( x;x_0,\tilde{x}\right) ,u^\pm \left( x;x_0,{{\tilde{y}}}\right) \right) =-4i(-1)^{(1\pm 1)/2}e^{\pm 2 z\left( {{\tilde{x}}};x_0\right) /h} w_\mathrm {odd}^\pm \left( {{\tilde{x}}},h;{{\tilde{y}}}\right) . \end{aligned}$$

(2.9)

2.3 Stokes geometry

We now describe the configuration of Stokes lines for single-lobe and double-lobe potentials.

2.3.1 Single-lobe potentials

Suppose that V is a single-lobe potential near $\mu _0$ and let $\mu \in B_\varepsilon (\mu _0)$. Fix determinations of H(z(x)) given by (2.3) and of

$$\begin{aligned} z\left( x;\alpha _\bullet \right) =z\left( x;\alpha _\bullet (\mu ),\mu \right) =i\int _{\alpha _\bullet }^x(V(t)^2-\mu ^2)^{1/2}\,dt,\quad \bullet =l,r, \end{aligned}$$

(2.10)

by picking branches so that $H(z(x))>0$ and $(V(x)^2-\mu ^2)^{1/2}>0$ when $\alpha _l<x<\alpha _r$ and $\mu \in {\mathbb {R}}$. Note that this is in accordance with (1.3). The Stokes lines (level curves of $t\mapsto {\text {Re}}z(t;\alpha _\bullet )$) are then found by taking the union of

$$\begin{aligned} \left\{ x \in D :{\text {Im}}\int _{x_0}^{x}\sqrt{V(t)^{2}-\mu ^{2}}\,dt = \mathrm{const.} \right\} \end{aligned}$$

(2.11)

for $x_0=\alpha _l,\alpha _r$. When $\mu$ is real it is known that there are three Stokes lines emanating from $\alpha _l\in {\mathbb {R}}$ having arguments $0, 2\pi /3,4\pi /3$, while the Stokes lines emanating from $\alpha _r\in {\mathbb {R}}$ have arguments $\pi /3, \pi ,5\pi /3$, see Gérard and Grigis [13]. We define the Riemann surfaces of z(x) and H(z(x)) by introducing branch cuts along the Stokes line with argument $2\pi /3$ at $\alpha _l$ and the Stokes line with argument $5\pi /3$ at $\alpha _r$. For real $\mu \in B_\varepsilon (\mu _0)$ there is a bounded Stokes line lying on ${\mathbb {R}}$ starting at $\alpha _l$ and ending at $\alpha _r$. Hence, the Stokes lines separate the complex domain D into four sectors (called Stokes regions). In the top and bottom sectors the function z(x) takes the form (2.10). By continuing the chosen determination of z(x) through rotation clockwise around the turning points (thus avoiding the branch cuts) it is easy to see that

$$\begin{aligned} z\left( x;\alpha _\bullet \right) =\int _{\alpha _\bullet }^{x}\left( \mu ^2-V(t)^2\right) ^{1/2}\,dt \end{aligned}$$

(2.12)

for x belonging to the left and right sector when $\bullet =l$ and $\bullet =r$, respectively. For general $\mu \in B_\varepsilon (\mu _0)$ the picture is slightly perturbed; as $i\mu$ is rotated off the imaginary axis $\alpha _l$ and $\alpha _r$ start migrating in opposite directions along paths in the upper and lower half plane, and the bounded Stokes line connecting $\alpha _l$ and $\alpha _r$ is broken into two unbounded curves, see Fig. 4. (We refer to [11] for a detailed explanation of this phenomenon.) However, for small $\varepsilon$ the arguments of the Stokes lines at the turning points are almost unchanged so for $\mu \in B_\varepsilon (\mu _0)$ we may still place branch cuts as described above. Note that there are now three Stokes regions around the left turning point and three around the right, and (2.12) is still valid if interpreted in this sense. However, we will avoid introducing notation for the different Stokes regions, and simply say (informally) that x is near the lobe if x is not in the Stokes region to the left of $\alpha _l$ or to the right of $\alpha _r$. We also remark that if $x_0(\mu )$ is a turning point satisfying $V(x_0(\mu ))=\mu$, then $x_0(-\mu )$ is also a solution to $V(x)^2-\mu ^2=0$; hence the original Stokes configuration is reached again already when $i\mu$ has traversed half a circuit around the origin, see the left panel of Fig. 6.

Fig. 4

Configuration of Stokes lines in the complex plane for the single-lobe potential $V(x)=\frac{1}{4}{\text {sech}}(x)$ near $\mu _0=0.2$. The left panel describes the situation for $\mu =\mu _0$ and the right panel when $\mu =0.2+0.01i$ has been perturbed to have small positive imaginary part. The panels show the increasing value of ${\text {Re}}z(x;\alpha _r(\mu ))$ as one travels from blue toward red regions. Here $\alpha _r(\mu )$ is the turning point on the right, so as indicated ${\text {Re}}z(x)$ is zero along the Stokes lines emanating from $\alpha _r$. Branch cuts are located along (the curved edges of) the white regions

In Fig. 4 we have also indicated that ${\text {Re}}z(x)$ increases as one travels from top to bottom and left to right, while not passing through a branch cut. This is realized in the following way: For x in the regions between turning points we have by (2.10) and Taylor’s formula that

$$\begin{aligned} z(x;\alpha _\bullet )-z(x_0;\alpha _\bullet )=i(x-x_0)(V(x_0)^2-\mu ^2)^{1/2}(1+g_1(x)), \end{aligned}$$

(2.13)

where $g_1$ is analytic and $g_1(x_0)=0$. Since $V(x_0)>\mu _0$ if $\alpha _l(\mu _0)<x_0<\alpha _r(\mu _0)$ we see by picking $x_0$ real that the square root is approximately real when $\mu \in B_\varepsilon (\mu _0)$, so ${\text {Re}}z(x)$ increases as ${\text {Im}}x$ decreases. On the other hand, for x in the Stokes region left of $\alpha _l$ or right of $\alpha _r$ we have by (2.12) and Taylor’s formula that

$$\begin{aligned} z(x;\alpha _\bullet )-z(x_0;\alpha _\bullet )=(x-x_0)(\mu ^2-V(x_0)^2)^{1/2}(1+g_2(x)), \end{aligned}$$

(2.14)

where $g_2$ is analytic and $g_2(x_0)=0$. By picking $x_0\in D\cap {\mathbb {R}}$ with $|{\text {Re}}x_0|\gg 1$ we have $V(x_0)\approx 0$ showing that ${\text {Re}}z(x)$ increases as ${\text {Re}}x$ increases. This also shows that ${\text {Re}}z(x)$ is constant along lines which are essentially vertical near ${\mathbb {R}}$ when $|{\text {Re}}x|$ is large.

2.3.2 Double-lobe potentials

Suppose now that V is a double-lobe potential near $\mu _0$ and let $\mu \in B_\varepsilon (\mu _0)$. Again, fix determinations of H(z(x)) and z(x) in accordance with (1.5)–(1.6); the obtained configuration of Stokes lines will essentially be two side-by-side copies of the configuration for single-lobe potentials with an appropriate gluing in the region between the two middle turning points $\beta _l$ and $\beta _r$.

Fig. 5

Configuration of Stokes lines in the complex plane for the double-lobe potential $V(x)=\frac{1}{4}({\text {sech}}(x-2)+{\text {sech}}(x+2))$ near $\mu _0=0.2$. The top panel describes the situation for $\mu =\mu _0$ and the bottom panel when $\mu =0.2+0.02i$ has been perturbed to have small positive imaginary part. The panels show the increasing value of ${\text {Re}}z(x;\beta _l(\mu ))$ as one travels from blue toward red regions. Here $\beta _l(\mu )$ is the second turning point from the left, so as indicated ${\text {Re}}z(x)$ is zero along the Stokes lines emanating from $\beta _l$. Branch cuts are located along (the curved edges of) the white regions

Indeed, the Stokes lines are given by the union of (2.11) for $x_0=\alpha _l,\beta _l,\beta _r,\alpha _r$. When $\mu$ is real there are three Stokes lines emanating from $\alpha _l$ and three from $\beta _r$ having arguments $0, 2\pi /3,4\pi /3$, while the Stokes lines emanating from $\beta _l,\alpha _r\in {\mathbb {R}}$ have arguments $\pi /3, \pi ,5\pi /3$, see Gérard and Grigis [13]. As $i\mu$ is rotated off the imaginary axis the turning points start migrating in alternating, opposing directions along paths in the upper and lower half plane, so that $\alpha _l$ moves in the direction opposite from $\beta _l$ but similar to $\beta _r$. We place branch cuts along the Stokes lines which for real $\mu$ have arguments $2\pi /3$ at $\alpha _l,\beta _r$ and the Stokes lines with arguments $5\pi /3$ at $\beta _l,\alpha _r$. Performing the same analysis as above shows that in the sectors to the left of $\alpha _l$ and to the right of $\alpha _r$, and in the intersection of the sectors to the right of $\beta _l$ and to the left of $\beta _r$ (i.e., between $\beta _l$ and $\beta _r$), $z(x;\alpha _\bullet )$ takes the form (2.12). When x is in the other sectors (between $\alpha _l$ and $\beta _l$ or between $\beta _r$ and $\alpha _r$), $z(x;\alpha _\bullet )$ is given by (2.10), and as for single-lobe potentials we shall informally say that x is near the lobes in this case. Using Taylor’s formula as in (2.13)–(2.14) then shows that ${\text {Re}}z(x)$ increases as one travels from top to bottom and left to right, while not passing through a branch cut, see Fig. 5. The right panel of Fig. 6 shows an example of how the turning points of a double-lobe potential migrate as $i\mu$ is rotated off the imaginary axis.

Fig. 6

The migration paths of turning points (solutions to $V(x)^2-\mu ^2=0$) of the potentials in Figs. 4 (left) and 5 (right) as $i\mu$ is rotated $\pi$ radians in the positive direction from the starting value $\mu =0.2$ until $\mu =-0.2$ when the original Stokes geometry is recovered. Black dots and circles mark starting and finishing locations, respectively. Rotation in the opposite direction reverses the direction of migration. Note that since ${\text {sech}}(x+i\pi )=-{\text {sech}}(x)$ the turning points appear periodically in ${\mathbb {C}}$ with complex period $i\pi$ for both potentials. Examples of the domain D (gray) are shown to indicate that only small rotations of $i\mu$ are of interest for the problem under consideration here

2.4 The Riemann surface

Let ${\mathcal {R}}(x_0,\theta )$ denote the operator acting through rotation around $x_0$ by $\theta$ radians, so that, e.g., ${\mathcal {R}}(0,\theta )x=e^{i\theta }x$. Since $V-\mu$ is analytic and $V(\alpha _l)-\mu =0$ it follows that

$$\begin{aligned} V\left( {\mathcal {R}}\left( \alpha _l,2\pi k\right) t\right) -\mu =e^{2i\pi k}(V(t)-\mu ),\quad k\in {\mathbb {Z}}, \end{aligned}$$

i.e., when t is rotated $2\pi k$ radians anticlockwise around $\alpha _l$ then $V(t)-\mu$ is rotated $2\pi k$ radians anticlockwise around the origin. (Negative k results in clockwise rotation by $2\pi |k|$ radians.) We of course have similar behavior near the other turning points of the same type, as well as for $V+\mu$ in the case when e.g. $V(\beta _r)+\mu =0$.

Definition 2.2

Suppose that V is a single-lobe (double-lobe) potential near $\mu _0$ and let y be a point in the upper half plane with ${\text {Re}}\alpha _l<{\text {Re}}y<{\text {Re}}\alpha _r$ (${\text {Re}}\alpha _l<{\text {Re}}y<{\text {Re}}\beta _l$). The point over y that is obtained when rotating y anticlockwise once around $\alpha _l$ will be denoted by ${\hat{y}}$, i.e.,

$$\begin{aligned} {\hat{y}}={\mathcal {R}}\left( {\alpha _l},2\pi \right) y. \end{aligned}$$

More generally, the sheet reached (from the usual sheet) by entering the cut starting at $\alpha _l$ from the right will be referred to as the ${\hat{x}}$-sheet. The point over y that is obtained when rotating y clockwise once around $\alpha _l$ will be denoted by $\check{y}$, i.e.,

$$\begin{aligned} \check{y}={\mathcal {R}}\left( \alpha _l,-2\pi \right) y. \end{aligned}$$

The sheet reached (from the usual sheet) by entering the cut starting at $\alpha _l$ from the left will be referred to as the $\check{x}$-sheet.

Note that this definition is in accordance with [12, Definition 5.2]. When winding this way around a turning point we always assume that the path is appropriately deformed so that it is not obstructed by other branch cuts. Informally, we think of ${\hat{x}}$ as lying in the sheet “above” the usual sheet, and $\check{x}$ as lying in the sheet “below” the usual sheet. It is straightforward to check that the ${\hat{x}}$-sheet is also reached (from the usual sheet) whenever we rotate anticlockwise once around the other zeros of $V-\mu$ (i.e., around $\beta _l$, $\beta _r$ and $\alpha _r$ if $V(\beta _l)=V(\beta _r)$, and around $\beta _l$ if $V(\beta _l)=-V(\beta _r)$). Similarly, the $\check{x}$-sheet is reached (from the usual sheet) by rotating clockwise once around zeros of $V-\mu$. The directions are reversed when rotating around zeros of $V+\mu$, i.e., when rotating around $\beta _r$ and $\alpha _r$ if $V(\beta _l)=-V(\beta _r)$. For a proof of these facts we refer to [12, Lemma 5.3]. We also record the following identities describing how WKB solutions are transformed when switching sheets.

Lemma 2.3

([12, Lemma 5.4]). Let ${\hat{x}}$ and $\check{x}$ be defined as above and in accordance with Definition 2.2. Let $x_0$ be any of the turning points $\alpha _l,\beta _l,\beta _r,\alpha _r$, and let y be an amplitude base point. Then

$$\begin{aligned} u^\pm (x;x_0,y)=-iu^\mp \left( {\hat{x}};x_0,{\hat{y}}\right) =iu^\mp \left( \check{x};x_0,\check{y}\right) . \end{aligned}$$

2.5 Symmetry

For constants $c=c(\lambda )$ depending on the spectral parameter $\lambda$ we shall simply write $c(\mu )$ with the convention that $\mu$ is always defined via $\lambda =i\mu$. We then write $c({{\bar{\mu }}})$ to represent the value of c at the reflection of $\lambda$ in the imaginary axis, i.e., at $i{{\bar{\mu }}}=-{{\bar{\lambda }}}$. We let

$$\begin{aligned} c^*(\mu )=\overline{c\left( {{\bar{\mu }}}\right) }. \end{aligned}$$

Similarly, for functions $f(x)=f(x;\lambda )$ we simply write $f(x;\mu )$, and let $f^*$ denote the function

$$\begin{aligned} f^*(x;\mu )=\overline{f\left( {\bar{x}};{{\bar{\mu }}}\right) }. \end{aligned}$$

For a WKB solution $u(x;x_0(\mu ),y,\mu )$ depending also on phase base point $x_0(\mu )$ and amplitude base point y independent of $\mu$, we thus have

$$\begin{aligned} u^*(x;x_0(\mu ),y,\mu )=\overline{u\left( {\bar{x}};x_0\left( {{\bar{\mu }}}\right) ,y,{{\bar{\mu }}}\right) }. \end{aligned}$$

Recall that we fixed a determination of H(z(x)) so that if $\mu \in {\mathbb {R}}$ then at ${{\tilde{x}}}=(\alpha _l+\beta _l)/2\in {\mathbb {R}}$ we have

$$\begin{aligned} H\left( z\left( {{\tilde{x}}}\right) \right) =\left( \frac{V\left( {{\tilde{x}}}\right) +\mu }{V\left( {{\tilde{x}}}\right) -\mu }\right) ^{1/4}>0. \end{aligned}$$

It is straightforward to check that for $\mu \in {\mathbb {R}}$, this determination implies that

$$\begin{aligned} H(z(x))&\in {\mathbb {R}}_+\quad \text {when }\alpha _l<x<\beta _l, \end{aligned}$$

(2.15)

$$\begin{aligned} H(z(x))&\in e^{i\pi /4}{\mathbb {R}}_+\quad \text {when } x<\alpha _l,\quad \beta _l<x<\beta _r,\quad \alpha _r<x, \end{aligned}$$

(2.16)

while

$$\begin{aligned} H(z(x))\in {\left\{ \begin{array}{ll}{\mathbb {R}}_+&{} \hbox { when}\ V(\beta _l)=V(\beta _r)>0\\ i{\mathbb {R}}_+&{}\hbox { when}\ V(\beta _l)=-V\left( \beta _r\right) >0\end{array}\right. } \quad \text {and }\beta _r<x<\alpha _r. \end{aligned}$$

(2.17)

When $V(\beta _l)=V(\beta _r)>0$ this is in accordance with the fact that

$$\begin{aligned} H(z(-x))=H(z(x))\quad \text {if}\, V(x) = V(-x)\, \text {for}\, x\in {\mathbb {R}}. \end{aligned}$$

(2.18)

When $V(x) = V(-x)$ for $x\in {\mathbb {R}}$, we have

$$\begin{aligned} H(z(-x))=\left( \frac{-(V(x)-\mu )}{-\left( V(x)+\mu \right) }\right) ^{1/4}=c/H(x) \end{aligned}$$

for some constant c. Using the determination above we find that for $\mu \in {\mathbb {R}}$ and $x<\alpha _l$,

$$\begin{aligned} e^{i\pi /4}{\mathbb {R}}_+\ni H(-x)=c/H(x) \in ce^{-i\pi /4}{\mathbb {R}}_+ \end{aligned}$$

which implies that $c=i$. The same conclusion can also be drawn from the observation that if $\mu \in {\mathbb {R}}$ and $\alpha _l<x<\beta _l$ then

$$\begin{aligned} i{\mathbb {R}}_+\ni H(-x)=c/H(x) \in c{\mathbb {R}}_+ \end{aligned}$$

by (2.17), again showing that $c=i$, that is,

$$\begin{aligned} H(z(-x))=i/H(z(x))\quad \text {if}\, V(x) = -V(-x)\,\text { for}\, x\in {\mathbb {R}}. \end{aligned}$$

(2.19)

These observations will be used to prove two symmetry properties: one with respect to reflection of the spectral parameter in the imaginary axis, and one with respect to parity.

Proposition 2.4

Let $\mu \in B_\varepsilon (\mu _0)$ and let $x_0(\mu )\in {\mathbb {C}}$ be a solution to $V(x)^2-\mu ^2=0$. Then $x_0(\mu )=\overline{x_0({{\bar{\mu }}})}$. Let y be an amplitude base point independent of $\mu$. If V is a single-lobe, or a double-lobe with $V(\beta _l)=V(\beta _r)$ then near the lobe(s) we have

$$\begin{aligned} \left( u^\pm \right) ^*\left( x;\alpha _\bullet (\mu ),y,\mu \right) = u^\mp \left( x;\alpha _\bullet (\mu ),{\bar{y}},\mu \right) . \end{aligned}$$

(2.20)

If V is a double-lobe with $V(\beta _l)=-V(\beta _r)$ then (2.20) holds near the left lobe while

$$\begin{aligned} \left( u^\pm \right) ^*\left( x;\alpha _\bullet (\mu ),y,\mu \right) =- u^\mp \left( x;\alpha _\bullet (\mu ),{\bar{y}},\mu \right) \end{aligned}$$

(2.21)

near the right lobe. In the Stokes region to the left of $\alpha _l$ or to the right of $\alpha _r$,

$$\begin{aligned} \left( u^\pm \right) ^*\left( x;\alpha _\bullet (\mu ),y,\mu \right) =iu^\pm \left( x;\alpha _\bullet (\mu ),{\bar{y}},\mu \right) . \end{aligned}$$

Proof

Since V is real-analytic we have $\overline{V({\bar{x}})}=V(x)$, which implies that $V(\overline{\alpha _l(\mu )})-{{\bar{\mu }}}=0$. Since $\alpha _l({{\bar{\mu }}})$ also satisfies this equation it follows that $\overline{\alpha _l(\mu )}=\alpha _l({{\bar{\mu }}})$, for $\alpha _l(\mu _0)\in {\mathbb {R}}$ and the turning points depend continuously on $\mu \in B_\varepsilon (\mu _0)$. Hence $\alpha _l^*(\mu )=\alpha _l(\mu )$. The same arguments show that $x_0^*(\mu )=x_0(\mu )$ when $x_0$ is any of the other three turning points.

Next, if V is a single-lobe and x lies in the domain between the turning points, or if V is a double-lobe and x lies in either the domain between the left pair or in the domain between the right pair of turning points, then $z(x,\mu )=i\int (V^2-\mu ^2)^{1/2}dt$ with real integrand when $x,\mu \in {\mathbb {R}}$. It is then easy to check that $\overline{z({\bar{x}},{{\bar{\mu }}})}=-z(x,\mu )$. (In particular, when x and $\mu$ are real, $z(x,\mu )$ is purely imaginary, as expected.) If V is a single-lobe or a double-lobe with $V(\beta _l)=\pm V(\beta _r)$ then, using (2.15) or (2.17), one checks that $\overline{H(z({\bar{x}},{{\bar{\mu }}}))}=H(z(x,\mu ))$ near the left lobe and $\overline{H(z({\bar{x}},{{\bar{\mu }}}))}=\pm H(z(x,\mu ))$ near the right lobe, which implies that

$$\begin{aligned} \overline{Q\left( z\left( {\bar{x}},{{\bar{\mu }}}\right) \right) }=c\cdot Q(z(x,\mu ))\begin{pmatrix} 0 &{} 1\\ 1&{}0 \end{pmatrix}, \end{aligned}$$

with $c=1$ near the left lobe, and $c=\pm 1$ near the right lobe, with sign determined according to $V(\beta _l)=\pm V(\beta _r)$. Since $\overline{z'({\bar{x}},{{\bar{\mu }}})}=-z'(x,\mu )$, inspection of the governing equations for the amplitude function $w^\pm (x,h;y,\mu )$ shows that

$$\begin{aligned} \overline{w^\pm \left( {\bar{x}},h;y,{{\bar{\mu }}}\right) }= w^\mp \left( x,h;{\bar{y}},\mu \right) \end{aligned}$$

(2.22)

which gives (2.20)–(2.21).

Finally, if x lies in the domain left of $\alpha _l$ or right of $\alpha _r$ then $z(x,\mu )=\int (\mu ^2-V^2)^{1/2}dt$ with real integrand when $x,\mu \in {\mathbb {R}}$, so $\overline{z({\bar{x}},{{\bar{\mu }}})}=z(x,\mu )$. Using (2.16) one checks that $\overline{H(z({\bar{x}},{{\bar{\mu }}}))}=-iH(z(x,\mu ))$ and $\overline{Q(z({\bar{x}},{{\bar{\mu }}}))}=i Q(z(x,\mu ))$. Inspection of the governing equations for the amplitude function $w^\pm (x,h;y,\mu )$ shows that $\overline{w^\pm ({\bar{x}},h;y,{{\bar{\mu }}})}= w^\pm (x,h;{\bar{y}},\mu )$. This proves the last statement of the proposition and the proof is complete. $\quad \square$

Proposition 2.5

Let $\mu \in B_\varepsilon (\mu _0)$ and let $x_0(\mu )\in {\mathbb {C}}$ be a solution to $V(x)^2-\mu ^2=0$. If $V(x) = V(-x)$ for $x \in {\mathbb {R}}$, then

$$\begin{aligned} u^\pm \left( -x;x_0(\mu ),y,\mu \right) =-\begin{pmatrix} 0 &{} 1\\ 1&{}0 \end{pmatrix}u^\mp \left( x;-x_0(\mu ),- y,\mu \right) . \end{aligned}$$

If $V(x) = -V(-x)$ for $x \in {\mathbb {R}}$, then

$$\begin{aligned} u^\pm \left( -x;x_0(\mu ),y,\mu \right) =\pm \begin{pmatrix} 0 &{} -1\\ 1&{}0\end{pmatrix}u^\mp \left( x;-x_0(\mu ),-y,\mu \right) . \end{aligned}$$

Proof

Since we are only concerned with symmetry with respect to $x\mapsto -x$ we will omit $\mu$ from the notation. If $V(x) = V(-x)$ for $x\in {\mathbb {R}}$, a change of variables shows that $z(-x,x_0)=-z(x,-x_0)$. Also $z'(x)=z'(-x)$ and $H(z(- x))=H(z(x))$ by (2.18). The governing equations for the amplitude function $w^\pm (x,h;y)$ imply that

$$\begin{aligned} w^\pm (- x,h;y)= w^\mp (x,h;- y). \end{aligned}$$

Noting that $Q(z(- x))=Q(z(x))$ and

$$\begin{aligned} -\begin{pmatrix} 0 &{} 1\\ 1&{}0 \end{pmatrix}\begin{pmatrix} 1 &{} 1\\ -1&{}1 \end{pmatrix}Q(z(x)) =\begin{pmatrix} 1 &{} 1\\ -1&{}1 \end{pmatrix}Q(z(x))\begin{pmatrix} 0 &{} 1\\ 1&{}0 \end{pmatrix} \end{aligned}$$

and that squaring the right-most matrix gives the identity, we obtain the first formula.

If $V(x)=-V(-x)$ for $x\in {\mathbb {R}}$ then z satisfies the same relations as above while $H(z(- x))=i/H(z(x))$ by (2.19). The governing equations for $w^\pm (x,h;y,\mu )$ now give

$$\begin{aligned} w^\pm (- x,h;y)=\begin{pmatrix}1&{}0\\ 0&{}-1\end{pmatrix} w^\mp (x,h;- y), \end{aligned}$$

while

$$\begin{aligned} Q(z(-x))=\begin{pmatrix}-iH(z(x))&{}-iH(z(x))\\ -1/H(z(x))&{}1/H(z(x))\end{pmatrix}. \end{aligned}$$

Since

$$\begin{aligned} \begin{pmatrix}0&{}1\\ 1&{}0\end{pmatrix}^{(1\pm 1)/2}\begin{pmatrix}1&{}0\\ 0&{}-1\end{pmatrix} =\pm \begin{pmatrix}0&{}-1\\ 1&{}0\end{pmatrix}\begin{pmatrix}0&{}1\\ 1&{}0\end{pmatrix}^{(1\mp 1)/2} \end{aligned}$$

the second formula therefore follows by checking that

$$\begin{aligned} \begin{pmatrix}1&{}1\\ -1&{}1\end{pmatrix}Q(z(-x))\begin{pmatrix}0&{}-1\\ 1&{}0\end{pmatrix} =\begin{pmatrix}0&{}-1\\ 1&{}0\end{pmatrix}\begin{pmatrix}1&{}1\\ -1&{}1\end{pmatrix}Q(z(x)) \end{aligned}$$

with $Q(z(-x))$ described above. This straightforward verification is left to the reader.

$\square$

Proposition 2.6

Let $\mu \in B_\varepsilon (\mu _0)$. Then $I^*=I$, $I^*_\bullet =I_\bullet$ and $J^*=J$. If $V(x)=\pm V(-x)$ then $I_l=I_r$.

Proof

We adapt the arguments in the proof of [16, Lemma IV.2]. Since

$$\begin{aligned} I_l\left( {{\bar{\mu }}}\right) =\int _{\alpha _l({{\bar{\mu }}})}^{\beta _l\left( {{\bar{\mu }}}\right) }\left( V(t)^2-{{\bar{\mu }}}^2\right) ^{1/2}\, dt =\int _{\overline{\alpha _l(\mu )}}^{\overline{\beta _l(\mu )}}\overline{\left( V\left( {\bar{t}}\right) ^2-\mu ^2\right) ^{1/2}}\, dt \end{aligned}$$

by Proposition 2.4, a change of variables gives $I_l({{\bar{\mu }}})=\overline{I_l(\mu )}$, which proves that $I_l^*=I_l$. The same arguments show that $I^*=I$, $I_r^*=I_r$ and $J^*=J$. If $V(x)=\pm V(-x)$ then $\alpha _l=-\alpha _r$ and $\beta _l=-\beta _r$, so the identity $I_l=I_r$ follows by a change of variables. $\quad \square$

We end this section with a result that will be used to determine the location of the reference points $\mu _k^\mathrm {sl}$ and $\mu _k^\mathrm {dl}$ mentioned in the introduction. In the statement, we let for brevity $I(\mu )$ denote either the action integral (1.3), or one of the action integrals $I_l,I_r$ given by (1.5). It will be convenient to allow an error term which can be made exponentially small for any fixed h.

Lemma 2.7

Let ${\mathcal {I}}(\mu ,h)$ satisfy ${\mathcal {I}}={\mathcal {I}}^*$ and suppose that ${\mathcal {I}}(\mu ,h)=I(\mu )+ha(\mu ,h)+O(e^{-A/h})$ for any $A>0$, with $a,\partial a/\partial \mu =O(h)$ as $h\rightarrow 0$, uniformly for $\mu \in B_\varepsilon (\mu _0)$. Then there is an $h_0>0$ such that $\mu \mapsto {\mathcal {I}}(\mu ,h)$ is injective in $B_\varepsilon (\mu _0)$ for all $0<h\le h_0$. In particular, if $0<h\le h_0$ and $\mu _k(h)\in B_\varepsilon (\mu _0)$ is a root of the equation ${\mathcal {I}}(\mu ,h)=y_k(h)$ for some $y_k\in {\mathbb {R}}$, then $\mu _k\in {\mathbb {R}}$.

Proof

Note that

$$\begin{aligned} \partial I_l(\mu )/\partial \mu =-\mu \int _{\alpha _l(\mu )}^{\beta _l(\mu )}(V(t)^2-\mu ^2)^{-1/2}\, dt \end{aligned}$$

since $\alpha _l$ and $\beta _l$ depend analytically on $\mu$ and are roots to $V(x)^2-\mu ^2=0$. At $\mu _0\in {\mathbb {R}}$, this is a real integral with positive integrand. Hence, $I_l'(\mu _0)<0$, where prime denotes differentiation with respect to $\mu$, and we can ensure that $I_l'(\mu )\ne 0$ for $\mu \in B_\varepsilon (\mu _0)$ by choosing $\varepsilon$ sufficiently small. The same arguments show that $I_r'(\mu ), I'(\mu )\ne 0$ for $\mu \in B_\varepsilon (\mu _0)$. Let ${\mathcal {J}}(\mu ,h)= I(\mu )+ha(\mu ,h)$, then ${\mathcal {J}}'(\mu ,h)=I'(\mu )+O(h)$, where now $I'$ is any of the three derivatives just discussed, so ${\mathcal {J}}(\mu ,h)$ is injective in $B_\varepsilon (\mu _0)$ if h is sufficiently small. The same must be true for ${\mathcal {I}}$, for if ${\mathcal {I}}(\mu _1)={\mathcal {I}}(\mu _2)$ for some $\mu _1\ne \mu _2$, then $0={\mathcal {J}}(\mu _1,h)-{\mathcal {J}}(\mu _2,h)+O(e^{-A/h})$. Letting $A\rightarrow \infty$ gives ${\mathcal {J}}(\mu _1,h)={\mathcal {J}}(\mu _2,h)$, a contradiction. By assumption we have ${\mathcal {I}}^*={\mathcal {I}}$, so

$$\begin{aligned} {\mathcal {I}}\left( {{\bar{\mu }}}_k,h\right) =\overline{{\mathcal {I}}\left( \mu _k,h\right) } =\overline{y_k}=y_k={\mathcal {I}}\left( \mu _k,h\right) \end{aligned}$$

since $y_k$ is real. Since ${\mathcal {I}}$ is injective, we conclude that $\mu _k={{\bar{\mu }}}_k$. $\quad \square$

3 Eigenvalues for a Single-Lobe Potential

Here we suppose that V is a single-lobe potential near $\mu _0$, and let $B_\varepsilon (\mu _0)$ be a small neighborhood as described in connection with Definition 1.1. We will consider eigenvalues $\lambda =i\mu$ with $\mu \in B_\varepsilon (\mu _0)$ with the purpose of deriving the quantization condition (1.4) and proving Theorem 1.2. We ask the reader to recall the relevant Stokes geometry described in Sect. 2.3 and Fig. 4.

It is known that there are solutions $u_0=u_0(\mu )\in L^2({\mathbb {R}}_+)$ and $v_0=v_0(\mu )\in L^2({\mathbb {R}}_-)$ of (1.1) (unique modulo constant factors) such that $\lambda = i\mu$ is an eigenvalue of P(h) if and only if $u_0=cv_0$ for some $c=c(\mu ,h)$, thus

$$\begin{aligned} {\mathcal {W}}\left( u_0, v_0\right) = 0. \end{aligned}$$

(3.1)

As in the Schrödinger case, this can be shown by following the program of Olver [25] – see [14] for a detailed presentation in this direction.

Remark 3.1

By modifying $u_0$ and $v_0$ if necessary we may assume that $u_0^*=iu_0$, $v^*_0=iv_0$ and $u_0=cv_0$ with $c=c^*$. Indeed, if $\mu \in B_\varepsilon (\mu _0)$ then ${{\bar{\mu }}}\in B_\varepsilon (\mu _0)$ since $\mu _0\in {\mathbb {R}}$, which implies that $u_0^*(\mu )\in L^2({\mathbb {R}}_+)$ and $v_0^*(\mu )\in L^2({\mathbb {R}}_-)$ for $\mu \in B_\varepsilon (\mu _0)$. Note that $u_0^*$ and $v_0^*$ also solve (1.1). Set ${\widetilde{u}}_0=\frac{1}{2}(u_0-iu_0^*)\in L^2({\mathbb {R}}_+)$ and ${\widetilde{v}}_0=\frac{1}{2}(v_0/c^*-iv_0^*/c)\in L^2({\mathbb {R}}_-)$. By uniqueness follows that $u_0^*$ is a multiple of $u_0$ and $v_0^*$ is a multiple of $v_0$. (If it happens that $u_0^*= iu_0$ then ${\widetilde{u}}_0=u_0$ and ${\widetilde{v}}_0=v_0/c^*$. If it happens that $u_0^*= -iu_0$ we take ${\widetilde{u}}_0=u_0^*$ and ${\widetilde{v}}_0=v_0^*/c$ instead.) It is then easy to see that $\lambda =i\mu$ is an eigenvalue of P(h) if and only if ${\widetilde{u}}_0= cc^*{\widetilde{v}}_0$. Since ${\widetilde{u}}_0^*=i{\widetilde{u}}_0$, ${\widetilde{v}}_0^*=i{\widetilde{v}}_0$ and $(cc^*)^*=cc^*$, the claim follows.

To calculate the Wronskian (3.1), we shall follow [13, §2] and first show that modulo an exponentially small error, $u_0$ and $v_0$ are each multiples of exact WKB solutions. Pick real numbers $x_l,{{\tilde{x}}}_l$ and ${{\tilde{x}}}_r,x_r$ such that $x_l<{{\tilde{x}}}_l < {\text {Re}}\alpha _l$ and ${\text {Re}}\alpha _r<{{\tilde{x}}}_r<x_r$, and pick y in the upper half plane such that ${\text {Re}}\alpha _l<{\text {Re}}y<{\text {Re}}\alpha _r$, see Fig. 7. These may be chosen independent of $\mu \in B_\varepsilon (\mu _0)$ if $\varepsilon$ is small enough. Define two pairs of linearly independent exact WKB solutions $u_{l},{\widetilde{u}}_l$ and $u_{r},{\widetilde{u}}_r$ by setting

$$\begin{aligned} u_l =&u^{+}\left( x;\alpha _l,x_{l}\right) , \quad u_{r} = u^{-}\left( x;\alpha _r,x_{r}\right) , \end{aligned}$$

(3.2)

$$\begin{aligned} {\widetilde{u}}_l =&u^{-}\left( x;\alpha _l,{{\tilde{x}}}_{l}\right) , \quad {\widetilde{u}}_{r} = u^{+}\left( x;\alpha _r,{{\tilde{x}}}_{r}\right) , \end{aligned}$$

(3.3)

with $u^\pm$ given by (2.2). By (a slight modification of) the arguments of Gérard and Grigis [13, §2.2] we obtain the following representation formulas, where we use similar notation to make comparison easier.

Fig. 7

The location of amplitude base points relative the neighboring turning points for generic single-lobe potential V and $\lambda =i\mu \in B_\varepsilon (\lambda _0)$. Branch cuts are indicated by dashed lines

Lemma 3.2

Let $u_\bullet ,{\widetilde{u}}_\bullet$, $\bullet =l,r$, be given by (3.2)–(3.3). Then

$$\begin{aligned} v_0&=m_-(h)u_l+m_+(h){\widetilde{u}}_l, \end{aligned}$$

(3.4)

$$\begin{aligned} u_0&=l_-(h)u_r+l_+(h){\widetilde{u}}_r, \end{aligned}$$

(3.5)

where $l_-(h)l_+(h)$ and $m_-(h)m_+(h)$ are of order O(1) as $h\rightarrow 0$, and $|m_+(h)|\le Ce^{z((x_l+{{\tilde{x}}}_l)/2)/h}$ and $|l_+(h)|\le Ce^{-z((x_r+{{\tilde{x}}}_r)/2)/h}$ are exponentially small as $h\rightarrow 0$.

Note that by Proposition 2.4, $u_r^*(x)=iu_r(x)$ when x belongs to the Stokes domain containing $x_r$, and the same is true for ${\widetilde{u}}_r$. By Remark 3.1 it is also true for $u_0$. In the domain containing $x_l$, the same relation holds for $u_l,{\widetilde{u}}_l,v_0$. A simple calculation then shows that

$$\begin{aligned} l_\pm ^*(\mu ,h)=l_\pm (\mu ,h),\quad m_\pm ^*(\mu ,h)=m_\pm (\mu ,h). \end{aligned}$$

(3.6)

Next, introduce two pairs $u^+_l,u^-_l$ and $u^+_r,u^-_r$ of intermediate exact WKB solutions given as

$$\begin{aligned} u_{\bullet }^{+}=u^{+}(x,h;\alpha _\bullet ,y),\quad u_{\bullet }^{-}=u^{-}(x,h;\alpha _\bullet ,\bar{y}),\quad \bullet =l,r. \end{aligned}$$

(3.7)

Note that

$$\begin{aligned} u_{l}^{\pm } = e^{\pm iI(\mu )/h} u_{r}^{\pm }, \end{aligned}$$

(3.8)

where $I(\mu )$ is the action integral (1.3). Represent $v_0$ and $u_0$ as the linear combinations

$$\begin{aligned} v_{0}=c_{11}u_{l}^{+} + c_{12}u_{l}^{-},\\ u_{0}=c_{21}u_{r}^{+} + c_{22}u_{r}^{-}, \end{aligned}$$

where the coefficients $c_{jk}$ depend on the parameters $\mu$ and h. For x near the lobe we get

$$\begin{aligned} v_0^*(x)=c_{11}^*\left( u_{l}^{+}\right) ^*(x) + c_{12}^*\left( u_{l}^{-}\right) ^*(x)= c_{11}^*u_{l}^{-}(x) + c_{12}^*u_{l}^{+}(x) \end{aligned}$$

(3.9)

by Proposition 2.4. Since $v_0^*=iv_0$ this means that $c_{12}=-ic_{11}^*$. Similarly, one checks that $c_{21}=-ic_{22}^*$. Hence,

$$\begin{aligned} v_{0}&=c_lu_{l}^{+} -i c_l^*u_{l}^{-}, \end{aligned}$$

(3.10)

$$\begin{aligned} u_{0}&=-ic_r^*u_{r}^{+} +c_ru_{r}^{-}, \end{aligned}$$

(3.11)

for some symbols $c_l$ and $c_r$.

Lemma 3.3

Let $\mu \in B_\varepsilon (\mu _0)$. For any $A>0$ we may choose $x_r\gg {{\tilde{x}}}_r$ and $x_l\ll {{\tilde{x}}}_l$ so that the symbols $c_l$ and $c_r$ in (3.10)–(3.11) are given by

$$\begin{aligned} c_l&=m_-\tau _l, \quad \tau _l={{\tilde{\tau }}}_l-R_l, \end{aligned}$$

(3.12)

$$\begin{aligned} c_r&=l_-\tau _r, \quad \tau _r={{\tilde{\tau }}}_r-R_r, \end{aligned}$$

(3.13)

where $\tau _\bullet ,{{\tilde{\tau }}}_\bullet =1+O(h)$ and $R_\bullet =O(he^{-A/h})$ as $h\rightarrow 0$, $\bullet =l,r$.

Proof

Using (3.4)–(3.5) we see that

$$\begin{aligned} c_l=m_-\frac{{\mathcal {W}}\left( u_l,u_l^-\right) }{{\mathcal {W}}\left( u_l^+,u_l^-\right) }+m_+\frac{{\mathcal {W}}\left( {\widetilde{u}}_l,u_l^-\right) }{{\mathcal {W}}\left( u_l^+,u_l^-\right) },\quad c_r=l_-\frac{{\mathcal {W}}\left( u_r^+,u_r\right) }{{\mathcal {W}}\left( u_r^+,u_r^-\right) }+l_+\frac{{\mathcal {W}}\left( u_r^+,{\widetilde{u}}_r\right) }{{\mathcal {W}}\left( u_r^+,u_r^-\right) }. \end{aligned}$$

For ${\mathcal {W}}(u_l, u_l^{-})$, ${\mathcal {W}}(u_l^{+}, u_l^{-})$, ${\mathcal {W}}(u_r^{+}, u_r)$ and ${\mathcal {W}}(u_r^{+}, u_r^-)$, we can directly apply the Wronskian formula (2.7), and obtain

$$\begin{aligned} {\mathcal {W}}(u_l, u_l^{-})&= 4iw_\mathrm {even}^+\left( \bar{y},h;x_l\right) , \quad {\mathcal {W}}\left( u_r^{+}, u_r\right) \quad = 4iw_\mathrm {even}^+\left( x_r,h;y\right) , \\ {\mathcal {W}}(u_l^{+}, u_l^{-})&= 4iw_\mathrm {even}^+(\bar{y},h;y), \quad {\mathcal {W}}\left( u_r^{+}, u_r^{-}\right) \quad = 4iw_\mathrm {even}^+\left( \bar{y},h;y\right) . \end{aligned}$$

In particular, we can easily find curves such that each amplitude function appearing in these expressions has an asymptotic expansion described by Remark 2.1. Indeed, this just requires being able to connect the relevant points (e.g., $x_l$ and ${\bar{y}}$ in $w^+_\mathrm {even}({\bar{y}},h;x_l)$) through curves along which ${\text {Re}}z(x)$ is increasing, which is clearly possible in view of the discussion connected to Fig. 4 (see the figure for comparison). Hence,

$$\begin{aligned} {{\tilde{\tau }}}_l=\frac{{\mathcal {W}}\left( u_l,u_l^-\right) }{{\mathcal {W}}\left( u_l^+,u_l^-\right) }=\frac{w^+_\mathrm {even}\left( {\bar{y}},h;x_l\right) }{w^+_\mathrm {even}\left( {\bar{y}},h;y\right) }, \quad {{\tilde{\tau }}}_r=\frac{{\mathcal {W}}(u_r^+,u_r)}{{\mathcal {W}}\left( u_r^+,u_r^-\right) }=\frac{w^+_\mathrm {even}(x_r,h;y)}{w^+_\mathrm {even}\left( {\bar{y}},h;y\right) } \end{aligned}$$

(3.14)

have the stated asymptotic properties as $h\rightarrow 0$ by Remark 2.1.

To compute ${\mathcal {W}}({\widetilde{u}}_l,u_l^-)$ and ${\mathcal {W}}(u_r^+,{\widetilde{u}}_r)$ we use the Wronskian formula (2.9) for solutions of the same type instead of (2.8). We then obtain

$$\begin{aligned} {\mathcal {W}}\left( {\widetilde{u}}_l,u_l^-\right)&= -4ie^{-2z\left( {{\tilde{x}}}_l;\alpha _l\right) /h}w^-_\mathrm {odd}\left( {{\tilde{x}}}_l,{\bar{y}}\right) ,\\ {\mathcal {W}}\left( u_r^+,{\widetilde{u}}_r\right)&= -4ie^{2z({{\tilde{x}}}_r;\alpha _r)/h}w^+_\mathrm {odd}({{\tilde{x}}}_r, y). \end{aligned}$$

We then obtain (3.12)–(3.13) by setting

$$\begin{aligned} R_l=\frac{m_+}{m_-}e^{-2z({{\tilde{x}}}_l;\alpha _l)/h}\frac{w^-_\mathrm {odd}({{\tilde{x}}}_l,{\bar{y}})}{w_\mathrm {even}^+({\bar{y}},y)},\quad R_r=\frac{l_+}{l_-}e^{2z({{\tilde{x}}}_r;\alpha _r)/h}\frac{w^+_\mathrm {odd}({{\tilde{x}}}_r, y)}{w_\mathrm {even}^+({\bar{y}},y)}. \end{aligned}$$

Since ${\text {Re}}z(x)\rightarrow \pm \infty$ as $x\rightarrow \pm \infty$, the asymptotic properties of $R_\bullet$ follow from Lemma 3.2 and Remark 2.1. $\quad \square$

These intermediate WKB solutions will allow us to prove the following quantization condition.

Theorem 3.4

Suppose that V is a single-lobe potential near $\mu _0$. Then, there exist positive constants $\varepsilon$ and $h_{0}$, and a function $r(\mu , h)$ bounded on $B_\varepsilon (\mu _{0}) \times (0, h_{0}]$ such that $\lambda = i\mu$, $\mu \in B_\varepsilon (\mu _{0})$, is an eigenvalue of P(h) for $h \in (0,h_{0}]$ if and only if

$$\begin{aligned} I(\mu ) = \left( k+\frac{1}{2}\right) \pi h + h^{2}r(\mu ,h) \end{aligned}$$

(3.15)

holds for some integer k. Moreover, $r=r^*$.

Proof

By (3.1), the quantization condition is ${\mathcal {W}}(v_{0}, u_{0}) = 0$. Using the representations (3.10)–(3.11) together with (3.8) we see that ${\mathcal {W}}(v_{0}, u_{0}) = 0$ if and only if

$$\begin{aligned} 0=\left( e^{iI(\mu )/h}c_{l}c_{r} +e^{-iI(\mu )/h}c_{l}^*c_{r}^*\right) {\mathcal {W}}(u_{l}^{+}, u_{l}^{-}). \end{aligned}$$

Since $u_{l}^+$ and $u_{l}^-$ are linearly independent we have ${\mathcal {W}}(u_{l}^{+}, u_{l}^{-}) \ne 0$, so the quantization condition is reduced to

$$\begin{aligned} e^{2iI(\mu )/h}\left( \frac{c_lc_r}{c_l^*c_r^*}\right) = -1, \end{aligned}$$

that is, (3.15) holds with

$$\begin{aligned} r(\mu ,h) = -\frac{1}{2ih}\log \left( \frac{c_{l}c_{r}}{c_{l}^*c_{r}^*}\right) =-\frac{1}{2ih}\log \left( \frac{{{\tilde{\tau }}}_{l}{{\tilde{\tau }}}_{r}}{{{\tilde{\tau }}}_{l}^*{{\tilde{\tau }}}_{r}^*}\right) +O(e^{-A/h}) \end{aligned}$$

(3.16)

where the second identity follows from an easy calculation using (3.6) and Lemma 3.3. By the same lemma we have ${{\tilde{\tau }}}_\bullet (\mu )=1+O(h)$ as $h\rightarrow 0$, and this holds for all $\mu \in B_\varepsilon (\mu _0)$. Since $\mu _0\in {\mathbb {R}}$ we have ${{\bar{\mu }}}\in B_\varepsilon (\mu _0)$, so ${{\tilde{\tau }}}_\bullet ^*(\mu )=\overline{{{\tilde{\tau }}}_\bullet ({{\bar{\mu }}})}=1+O(h)$, and hence $r(\mu ,h)=O(1)$ as $h\rightarrow 0$.

To see that $r^*=r$, we use (3.16) and a logarithmic identity and get

$$\begin{aligned} r(\mu ,h) =\frac{1}{2ih}\log \left( \frac{c_{l} c_{r}}{c_{l}^*c_{r}^*}\right) ^{-1}= \frac{1}{2ih}\log \left( \frac{c_{l}^*c_{r}^*}{c_{l} c_{r}}\right) =r^*(\mu ,h), \end{aligned}$$

which completes the proof. $\quad \square$

Proof of Theorem 1.2

Let r be given by Theorem 3.4, and let ${{\tilde{r}}}$ be defined by the logarithm on the right of (3.16), so that $r={{\tilde{r}}}+O(e^{-A/h})$ for any $A>0$. Note that the amplitude functions $w^+_\mathrm {even}$ are so-called analytic symbols with respect to the spectral parameter $\lambda =i\mu$ and $h>0$. This means that $\partial w^+_\mathrm {even}(\mu )/\partial \mu =O(h)$ uniformly for $\mu \in B_\varepsilon (\mu _0)$, see [13] or [29]. Using the definition of ${{\tilde{r}}}$ together with (3.14) it is then easy to see that $h\partial {{\tilde{r}}}(\mu ,h)/\partial \mu =O(h)$.

Let us define a function ${\mathcal {I}}(\mu ,h)$ as

$$\begin{aligned} {\mathcal {I}}(\mu ,h) = I(\mu ) - h^{2} r(\mu ,h). \end{aligned}$$

Then ${\mathcal {I}}^*={\mathcal {I}}$ so we may apply Lemma 2.7 (with a in the lemma given by $a(\mu ,h)=-h{{\tilde{r}}}(\mu ,h)$) to conclude that if h is sufficiently small then there is precisely one $\mu _k$ which solves ${\mathcal {I}}(\mu ,h)=(k+\frac{1}{2})\pi h$. Moreover, $\mu _k\in {\mathbb {R}}$. By Theorem 3.4 this means that eigenvalues $\lambda = i\mu$ of P(h) are purely imaginary for $\mu$ near $\mu _0$. $\quad \square$

Remark 3.5

By Lemma 2.7 (with $a(\mu ,h)\equiv 0$) there is precisely one solution $\mu _k^{\mathrm {sl}}$ to $I(\mu )=(k+\frac{1}{2})\pi h$, and $\mu _k^{\mathrm {sl}}\in {\mathbb {R}}$. From the previous proof we then infer that $|\mu _k-\mu _k^{\mathrm {sl}}|=O(h^2)$ by the aid of Taylor’s formula, where $\lambda _k=i\mu _k$ is the eigenvalue of P(h) satisfying (3.15). Moreover, similar arguments also show that

$$\begin{aligned} |\mu _j^\mathrm {sl}-\mu _k^{\mathrm {sl}}|\ge \frac{1}{C}|j-k|\pi h, \end{aligned}$$

where C is an upper bound of $\partial I(\mu )/\partial \mu$ for $\mu \in B_\varepsilon (\mu _0)$. Hence, if $\lambda _j=i\mu _j$ is an eigenvalue such that $\mu _j$ solves (3.15) with k replaced by $j\ne k$, then

$$\begin{aligned} |\mu _j-\mu _k^{\mathrm {sl}}|\ge ||\mu _j-\mu _j^\mathrm {sl}|-|\mu _j^\mathrm {sl}-\mu _k^{\mathrm {sl}}||\ge O(h), \end{aligned}$$

showing that there is a unique eigenvalue $O(h^2)$-close to $\mu _k^{\mathrm {sl}}$.

Remark

As shown by Theorem 1.2, eigenvalues of P(h) are purely imaginary for single-lobe potentials. In particular, the Stokes geometry depicted in the right panel of Fig. 4 is never realized in the occasion of an eigenvalue. Heuristically this can be explained by the fact that there would otherwise be a curve transversal to the Stokes lines which connects the Stokes sector to the left of $\alpha _l$ with the sector to the right of $\alpha _r$. Hence, the exact WKB solution $u_l$ above, which can be written as $u_l(x)=e^{z(x)}{{\tilde{u}}}$ for some ${{\tilde{u}}}$, could be continued into this right sector along a curve where ${\text {Re}}z(x)$ is increasing. Letting $x\rightarrow \infty$ along ${\mathbb {R}}$ would yield a contradiction to the fact that $u_l$ is collinear (modulo an exponentially small error) with the function $u_0\in L^2({\mathbb {R}}_+)$.

4 Eigenvalues for a Double-Lobe Potential

In this section we suppose that V is a double-lobe potential near $\mu _0$ and consider eigenvalues $\lambda =i\mu$ with $\mu \in B_\varepsilon (\mu _0)$, where $B_\varepsilon (\mu _0)$ is a small neighborhood as described in connection with Definition 1.3. The goal is to derive a quantization condition for such eigenvalues, which will then be used to prove the eigenvalue splitting occurring for symmetric potentials described in the introduction. For this reason, we will repeatedly include additional statements resulting from imposing the assumption that $V(x)=\pm V(-x)$ for $x\in {\mathbb {R}}$.

The Stokes geometry has been described in Sect. 2.3 and Fig. 5. As in Sect. 3 we choose real numbers $x_l,{{\tilde{x}}}_l$ and ${{\tilde{x}}}_r,x_r$ such that $x_l<{{\tilde{x}}}_l<{\text {Re}}\alpha _l$ and ${\text {Re}}\alpha _r<{{\tilde{x}}}_r<x_r$. We also choose points $y_l$ and $y_r$ in the upper half-plane such that

$$\begin{aligned} {\text {Re}}\alpha _l<{\text {Re}}y_l<{\text {Re}}\beta _l,\quad {\text {Re}}\beta _r<{\text {Re}}y_r<{\text {Re}}\alpha _r, \end{aligned}$$

see Fig. 8. All points are chosen independent of $\mu \in B_\varepsilon (\mu _0)$. In the case when $V(x)=\pm V(-x)$ for $x\in {\mathbb {R}}$ we choose $y_\bullet$ and $x_\bullet ,{{\tilde{x}}}_\bullet$ so that

$$\begin{aligned} y_l=-{\bar{y}}_r,\quad \text {and}\quad x_l=-x_r,\quad {{\tilde{x}}}_l=-{{\tilde{x}}}_r. \end{aligned}$$

Let $u_0\in L^2({\mathbb {R}}_+)$ and $v_0\in L^2({\mathbb {R}}_-)$ be the functions described in Sect. 3 such that $\lambda =i\mu$ is an eigenvalue of P(h) if and only if $u_0=cv_0$ for some constant $c=c(\mu ,h)$. We choose $u_0$ and $v_0$ in accordance with Remark 3.1 so that $v_0^*=iv_0$, $u_0^*=iu_0$ and $c=c^*$. When V is even we can choose $v_0$ as above and define

$$\begin{aligned} u_0(x)=-\begin{pmatrix} 0&{}1\\ 1&{}0\end{pmatrix}v_0(-x). \end{aligned}$$

(4.1)

Then $u_0^*=iu_0$ and, using the fact that $v_0$ solves (1.1), it is easy to check that $u_0$ also solves (1.1). When V is odd we instead define $u_0$ as

$$\begin{aligned} u_0(x)=-\begin{pmatrix}0&{}-1\\ 1&{}0\end{pmatrix}v_0(-x), \end{aligned}$$

(4.2)

compare with Proposition 2.5.

Fig. 8

The location of amplitude base points relative the neighboring turning points for generic double-lobe potential V and $\mu \in B_\varepsilon (\mu _0)$. Branch cuts are indicated by dashed lines

Introduce intermediate exact WKB solutions $u^+_\bullet =u^+(x;\alpha _\bullet ,y_\bullet ,\mu )$ and $u_\bullet ^-=u^-(x;\alpha _\bullet ,{\bar{y}}_\bullet ,\mu )$, $\bullet =l,r$. Note that these are defined as in Sect. 3 except that y has now been replaced by $y_\bullet$, compare with (3.7). The reason for this is of course that we now have two lobes instead of one. Represent $v_0$ and $u_0$ as the linear combinations

$$\begin{aligned} v_{0}=&c_{11}u_{l}^{+} + c_{12}u_{l}^{-},\\ u_{0}=&c_{21}u_{r}^{+} + c_{22}u_{r}^{-}. \end{aligned}$$

As for single-lobes one checks that $c_{12}=-ic_{11}^*$ using Proposition 2.4 near the left lobe, see (3.9). When $V(\beta _l)=\pm V(\beta _r)$ we use Proposition 2.4 near the right lobe and obtain

$$\begin{aligned} u_0^*(x)=c_{21}^*(u_{r}^{+})^*(x) + c_{22}^*(u_{r}^{-})^*(x)= \pm c_{21}^*u_{r}^{-}(x) \pm c_{22}^*u_{r}^{+}(x). \end{aligned}$$

Since $u_0^*=iu_0$ this means that $c_{21}=\mp ic_{22}^*$. Hence,

$$\begin{aligned} v_{0}&=c_lu_{l}^{+} -i c_l^*u_{l}^{-}, \end{aligned}$$

(4.3)

$$\begin{aligned} u_{0}&=\mp ic_r^*u_{r}^{+} +c_ru_{r}^{-}, \end{aligned}$$

(4.4)

for some symbols $c_l$ and $c_r$.

Remark 4.1

In the symmetric case when $V(-x)=\pm V(x)$ we have $c_l=c_r$. Indeed, then $\alpha _l=-\alpha _r$ and by definition we have $y_l=-{\bar{y}}_r$. If V is even then

$$\begin{aligned} u_l^\pm (-x)=-\begin{pmatrix}0&{}1\\ 1&{}0\end{pmatrix} u_r^\mp (x) \end{aligned}$$

by Proposition 2.5. In view of the definition (4.1) of $u_0$ for even V we get

$$\begin{aligned} u_0(x)=-\begin{pmatrix}0&{}1\\ 1&{}0\end{pmatrix}\left( c_lu_l^+(-x)-ic_l^*u_l^-(-x)\right) =c_l u_r^-(x)-ic_l^*u_r^+(x). \end{aligned}$$

Comparing the right-hand side with (4.4) we see that $c_l=c_r$ since $V(\beta _l)=V(\beta _r)$ when V is even. If V is odd then

$$\begin{aligned} u_l^\pm (-x)=\pm \begin{pmatrix}0&{}-1\\ 1&{}0\end{pmatrix} u_r^\mp (x) \end{aligned}$$

by Proposition 2.5. In view of the definition (4.2) of $u_0$ for odd V we get

$$\begin{aligned} u_0(x)=-\begin{pmatrix}0&{}-1\\ 1&{}0\end{pmatrix}\left( c_lu_l^+(-x)-ic_l^*u_l^-(-x)\right) = c_l u_r^-(x)+ ic_l^*u_r^+(x). \end{aligned}$$

We again see that $c_l=c_r$ in view of (4.4) since $V(\beta _l)=-V(\beta _r)$ when V is odd.

Let $u_l,{\widetilde{u}}_l$ and $u_r,{\widetilde{u}}_r$ be given by (3.2)–(3.3). Then Lemma 3.2 holds also for double-lobe potentials, and by replacing y with $y_\bullet$ in the proof of Lemma 3.3 we find that the symbols $c_l,c_r$ in (4.3)–(4.4) can also be written as in (3.12)–(3.13), that is,

$$\begin{aligned} c_l&=m_-\tau _l,\quad \tau _l={{\tilde{\tau }}}_l-R_l, \end{aligned}$$

(4.5)

$$\begin{aligned} c_r&=l_-\tau _r,\quad \tau _r={{\tilde{\tau }}}_r-R_r, \end{aligned}$$

(4.6)

where $\tau _\bullet ,{{\tilde{\tau }}}_\bullet =1+O(h)$ and $R_\bullet =O(he^{-A/h})$ for any $A>0$ as $h\rightarrow 0$, $\bullet =l,r$. When V is symmetric we have $u_l(-x)=u_r(x)$ and ${\widetilde{u}}_l(-x)={\widetilde{u}}_r(x)$, so using the representations (3.4)–(3.5) one checks that $m_-=l_-$ (while $m_+=\pm l_+$ when $V(x)=\pm V(-x)$) as in Remark 4.1. Since $c_l=c_r$ it follows that $\tau _l=\tau _r$.

It will be convenient to introduce WKB solutions $u_1,u_2,u_3,u_4$ defined, when $V(\beta _l)=\pm V(\beta _r)$, by

$$\begin{aligned} u_1(x)&=i\tau _lu^+\left( x;\beta _l,y_l\right) , \quad u_2(x)=-\tau _l^*u^-\left( x;\beta _l,{\bar{y}}_l\right) , \end{aligned}$$

(4.7)

$$\begin{aligned} u_3(x)&=i\tau _r u^-\left( x;\beta _r,{\bar{y}}_r\right) , \quad u_4(x)=\mp \tau _r^*u^+\left( x;\beta _r, y_r\right) . \end{aligned}$$

(4.8)

Note that $u_1^*=iu_2$ and $u_3^*=iu_4$ by Proposition 2.4. A simple calculation shows that

$$\begin{aligned} u_l^+(x)&=e^{iI_l/h}u^+\left( x;\beta _l,y_l\right) ,\quad u_l^-(x)=e^{-iI_l/h}u^-\left( x;\beta _l,{\bar{y}}_l\right) ,\\ u_r^-(x)&=e^{iI_r/h}u^-\left( x;\beta _r,{\bar{y}}_r\right) ,\quad u_r^+(x)=e^{-iI_r/h}u^+\left( x;\beta _r, y_r\right) , \end{aligned}$$

where $I_l$ and $I_r$ are the action integrals given by (1.5). In view of (4.3)–(4.4) we get

$$\begin{aligned} v_0/m_-&=-ie^{i I_l/h}u_1+ie^{-i I_l/h} u_2, \end{aligned}$$

(4.9)

$$\begin{aligned} u_0/l_-&=-ie^{i I_r/h}u_3+ie^{-i I_r/h} u_4. \end{aligned}$$

(4.10)

Inspired by the analysis in [24] we define the central solutions

$$\begin{aligned} v_l=e^{-J/h}\frac{1}{2i}(u_3-u_4),\quad v_r=e^{-J/h}\frac{1}{2i}(u_1-u_2). \end{aligned}$$

(4.11)

Since $J^*=J$ by Proposition 2.6 we have $v_l^*=iv_l$ and $v_r^*=iv_r$.

Lemma 4.2

The central solutions $v_l$ and $v_r$ are linearly independent if h is sufficiently small.

Proof

We prove linear independence by showing that the Wronskian of $v_l$ and $v_r$ is nonzero for small h. By (4.11) we have

$$\begin{aligned} {\mathcal {W}}\left( v_l,v_r\right) =-\frac{e^{-2J/h}}{4} \left( {\mathcal {W}}(u_3,u_1)-{\mathcal {W}}\left( u_4,u_1\right) -{\mathcal {W}}\left( u_3,u_2\right) + {\mathcal {W}}\left( u_4,u_2\right) \right) , \end{aligned}$$

so an application of Corollary A.3 gives

$$\begin{aligned} {\mathcal {W}}\left( v_l,v_r\right)&=-ie^{-J/h}\left( \tau _l\tau _rw_\mathrm {even}^+ \left( {\bar{y}}_r,y_l\right) +\tau _l\tau _r^*w_\mathrm {even}^+\left( \check{y}_l,y_r\right) \right. \\&\quad \left. +\tau _l^*\tau _rw_\mathrm {even}^+({\bar{y}}_r,\hat{\bar{y}}_l)+\tau _l^*\tau _r^*w_\mathrm {even}^+\left( {\bar{y}}_l,y_r\right) \right) , \end{aligned}$$

where the expression in parenthesis is $4+O(h)$ as $h\rightarrow 0$. $\square$

Now write

$$\begin{aligned} v_l&=d_{11}u_1+d_{12}u_2, \end{aligned}$$

(4.12)

$$\begin{aligned} v_r&=d_{21}u_3+d_{22}u_4. \end{aligned}$$

(4.13)

By Lemma 4.2, the relations (4.12)–(4.13) constitute an invertible change of basis, and a straightforward calculation yields

$$\begin{aligned} \begin{pmatrix} u_1\\ u_2\end{pmatrix}= D_l\begin{pmatrix} v_l\\ v_r\end{pmatrix},\quad D_l=\frac{1}{d_{11}+d_{12}}\begin{pmatrix} 1&{} 2i e^{J/h} d_{12} \\ 1&{} -2i e^{J/h} d_{11} \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} \begin{pmatrix} u_3\\ u_4\end{pmatrix}= D_r\begin{pmatrix} v_l\\ v_r\end{pmatrix},\quad D_r=\frac{1}{d_{21}+d_{22}}\begin{pmatrix} 2i e^{J/h} d_{22} &{}1\\ -2i e^{J/h} d_{21} &{}1\end{pmatrix}. \end{aligned}$$

Recall that $\lambda =i\mu$ is an eigenvalue precisely when $\det (v_0\ u_0)=0$. Since $v_l$ and $v_r$ are linearly independent by Lemma 4.2, a straightforward computation using (4.9)–(4.10) shows that $\det (v_0\ u_0)=0$ is equivalent to

$$\begin{aligned} \det \begin{pmatrix} \begin{pmatrix}-ie^{iI_l/h} &{} ie^{-iI_l/h}\end{pmatrix} D_l \\ \begin{pmatrix}-ie^{iI_r/h}&{} ie^{-iI_r/h}\end{pmatrix} D_r\end{pmatrix}=0, \end{aligned}$$

i.e.,

$$\begin{aligned} 0&=\frac{1}{i}\left( e^{iI_l/h}-e^{-iI_l/h}\right) \frac{1}{i}\left( e^{iI_r/h}-e^{-iI_r/h}\right) \\&\quad -4e^{2J/h}\left( e^{iI_l/h}d_{12}+e^{-iI_l/h}d_{11}\right) \left( e^{iI_r/h}d_{22}+e^{-iI_r/h}d_{21}\right) . \end{aligned}$$

We rewrite this as

$$\begin{aligned} 0&=\left( e^{iI_l/h}d_{12}+e^{-iI_l/h}d_{11}\right) \left( e^{iI_r/h}d_{22}+e^{-iI_r/h}d_{21}\right) \nonumber \\&\quad -e^{-2J/h}\sin \left( I_l/h\right) \sin \left( I_r/h\right) . \end{aligned}$$

(4.14)

Lemma 4.3

Let $\mu \in B_\varepsilon (\mu _0)$. In the case when $V(\beta _l)=\pm V(\beta _r)$ we have

$$\begin{aligned} d_{12}&=-\gamma _l, \quad d_{11}= -\gamma _l^*,\\ d_{22}&= \mp \gamma _r, \quad d_{21}= \mp \gamma _r^*, \end{aligned}$$

where $\gamma _\bullet$ are $1+O(h)$ as $h\rightarrow 0$ for $\bullet =l,r$. In addition, if $V(x) = \pm V(-x)$ for $x\in {\mathbb {R}}$ then $\gamma _l=\gamma _r$.

Proof

We first note that since $v_l^*=iv_l$, $u_1^*=iu_2$ we have $d_{11}^*=d_{12}$ in view of (4.12). Similarly, $d_{21}^*=d_{22}$ by (4.13). Using the arguments in Remark 4.1 it is easy to check that in the symmetric case $V(x)=\pm V(-x)$ we have $d_{12}=\pm d_{22}$.

We thus need to calculate $d_{12}$ and $d_{22}$, and begin with $d_{12}$. By (4.11) and (4.12) we have

$$\begin{aligned} d_{12}=\frac{{\mathcal {W}}\left( u_1,v_l\right) }{{\mathcal {W}}\left( u_1,u_2\right) } =\frac{e^{-J/h}}{2i}\frac{{\mathcal {W}}\left( u_1,u_3\right) -{\mathcal {W}}(u_1,u_4)}{{\mathcal {W}}\left( u_1,u_2\right) }. \end{aligned}$$

An application of Corollary A.3 in the appendix therefore gives $d_{12}=-\gamma _l$ where

$$\begin{aligned} \gamma _l=\frac{\tau _rw_\mathrm {even}^+\left( {\bar{y}}_r,y_l\right) +\tau _r^*w_\mathrm {even}^+\left( {\hat{y}}_r,y_l\right) }{2\tau _l^*w_\mathrm {even}^+\left( {\bar{y}}_l,y_l\right) } \end{aligned}$$

so that $\gamma _l=1+O(h)$ as $h\rightarrow 0$ by Remark 2.1 and (4.5)–(4.6).

Next,

$$\begin{aligned} d_{22}=\frac{{\mathcal {W}}\left( u_3,v_r\right) }{{\mathcal {W}}\left( u_3,u_4\right) } =\frac{e^{-J/h}}{2i}\frac{{\mathcal {W}}\left( u_3,u_1\right) -{\mathcal {W}}\left( u_3,u_2\right) }{{\mathcal {W}}\left( u_3,u_4\right) }. \end{aligned}$$

Using Corollary A.3 we then get

$$\begin{aligned} d_{22}=\mp \frac{\tau _lw_\mathrm {even}^+\left( {\bar{y}}_r,y_l\right) + \tau _l^*w_\mathrm {even}^+\left( {\bar{y}}_l,\hat{\bar{y}}_r\right) }{ 2\tau _r^*w_\mathrm {even}^+\left( {\bar{y}}_r,y_r\right) }. \end{aligned}$$

We see that $d_{22}=\mp \gamma _r$ where $\gamma _r=1+O(h)$ as $h\rightarrow 0$. $\quad \square$

Combining (4.14) and Lemma 4.3 we obtain the following Bohr–Sommerfeld quantization condition.

Theorem 4.4

Assume that V is a double-lobe potential near $\mu _0$ and that $V(\beta _l)=\pm V(\beta _r)$. Then then there exist positive constants $\varepsilon ,h_{0}$ and functions $\gamma _\bullet (\mu ,h)$, $\bullet =l,r$, defined on $B_\varepsilon (\mu _0) \times (0,h_{0}]$ with $\gamma _\bullet =1+O(h)$ as $h\rightarrow 0$, such that if $\mu \in B_\varepsilon (\mu _0)$ then $\lambda = i\mu$ is an eigenvalue if and only if

$$\begin{aligned} \left( e^{iI_l/h}\gamma _l+e^{-iI_l/h}\gamma _l^*\right) \left( e^{iI_r/h}\gamma _r+e^{-iI_r/h}\gamma _r^*\right) \mp e^{-2J/h}\sin \left( I_l/h\right) \sin \left( I_r/h\right) =0. \end{aligned}$$

If $V(x)=\pm V(-x)$ for $x\in {\mathbb {R}}$ then $\gamma _l=\gamma _r$.

5 Symmetric Potentials

The purpose of this section is to prove Theorem 1.4. When doing so it will be convenient to use the following alternative form of Theorem 4.4.

Proposition 5.1

Assume that V is a double-lobe potential near $\mu _0$ and that $V(x)=\pm V(-x)$ for $x\in {\mathbb {R}}$. Then there exist positive constants $\varepsilon ,h_{0}$ and functions $\rho _l,\rho _r$ defined on $B_\varepsilon (\mu _0) \times (0,h_{0}]$ such that $\lambda = i\mu$, $\mu \in B_\varepsilon (\mu _0)$, is an eigenvalue of P(h) for $h \in (0, h_0]$ if and only if

$$\begin{aligned} 4\rho _l\rho _r\cos \left( {\widetilde{I}}_l/h\right) \cos \left( {\widetilde{I}}_r/h\right) \mp e^{-2J/h}\sin \left( I_l/h\right) \sin \left( I_r/h\right) =0, \end{aligned}$$

where ${\widetilde{I}}_\bullet =I_\bullet +h\theta _\bullet =I_\bullet +O(h^2)$ and $\rho _\bullet =1+O(h)$ satisfy ${\widetilde{I}}_\bullet ={\widetilde{I}}_\bullet ^*$ and $\rho _\bullet =\rho _\bullet ^*$, $\bullet =l,r$. If $V(x)=\pm V(-x)$ then $I_l=I_r$ and ${\widetilde{I}}_l={\widetilde{I}}_r$.

Proof

We adapt the arguments in [24, pp. 878–879] to our situation. By Theorem 4.4, $\lambda =i\mu$ is an eigenvalue if and only if

$$\begin{aligned} \left( e^{iI_l/h}\gamma _l+e^{-iI_l/h}\gamma _l^*\right) \left( e^{iI_r/h}\gamma _r+e^{-iI_r/h}\gamma _r^*\right) \mp e^{-2J/h}\sin \left( I_l/h\right) \sin \left( I_r/h\right) =0, \end{aligned}$$

where $\gamma _\bullet ,\gamma _\bullet ^*$ are $1+O(h)$ as $h\rightarrow 0$ for $\mu \in B_\varepsilon (\mu _0)$. Write

$$\begin{aligned} \gamma _l&=\left( \gamma _l\gamma _l^*\right) ^{1/2}\left( \gamma _l/\gamma _l^*\right) ^{1/2}=\rho _l e^{i\theta _l},\\ \gamma _l^*&=\left( \gamma _l\gamma _l^*\right) ^{1/2}\left( \gamma _l/\gamma _l^*\right) ^{-1/2}=\rho _l e^{-i\theta _l} \end{aligned}$$

where we choose branches of the square roots and the logarithm in such a way that $\rho _l=1+O(h)$, $\theta _l=O(h)$. Since

$$\begin{aligned} \rho _l^*=\left( \left( \gamma _l\gamma _l^*\right) ^{1/2}\right) ^*=\rho _l, \end{aligned}$$

it follows that

$$\begin{aligned} \rho _le^{-i\theta _l}=\gamma _l^*=\left( \gamma _l\right) ^*=\left( \rho _le^{i\theta _l}\right) ^*=\rho _l^*e^{-i\theta _l^*}=\rho _l e^{-i\theta _l^*} \end{aligned}$$

so $\theta _l=\theta _l^*$. Treating $\gamma _r,\gamma _r^*$ the same way we find that $\lambda =i\mu$ is an eigenvalue if and only if

$$\begin{aligned} \rho _l\rho _r\left( e^{i{\widetilde{I}}_l/h}+e^{-i{\widetilde{I}}_l/h}\right) \left( e^{i{\widetilde{I}}_r/h}+e^{-i{\widetilde{I}}_r/h}\right) \mp e^{-2J/h}\sin \left( I_l/h\right) \sin \left( I_r/h\right) =0, \end{aligned}$$

where ${\widetilde{I}}_\bullet =I_\bullet +h\theta _\bullet =I_\bullet +O(h^2)$ satisfies ${\widetilde{I}}_\bullet ^*={\widetilde{I}}_\bullet$. Moreover, if $V(x)=\pm V(-x)$ then ${\widetilde{I}}_l={\widetilde{I}}_r$ since $\gamma _l=\gamma _r$ then. The result now follows by an application of Euler’s formula. $\quad \square$

Remark 5.2

Note that ${\widetilde{I}}_\bullet$ is injective near $\mu _0$ if h is sufficiently small. Indeed, since the amplitude functions $w^+_\mathrm {even}$ are analytic symbols with respect to the spectral parameter $\lambda =i\mu$ and $h>0$, inspecting their definition we see that $\gamma _\bullet ={{\tilde{\gamma }}}_\bullet +O(he^{-A/h})$ for any $A>0$, where $\partial {{\tilde{\gamma }}}_\bullet (\mu )/\partial \mu =O(h)$ uniformly for $\mu \in B_\varepsilon (\mu _0)$, see the proof of Theorem 1.2. Define ${{\tilde{\theta }}}_\bullet$ via $e^{i{{\tilde{\theta }}}_\bullet }=({{\tilde{\gamma }}}_\bullet /{{\tilde{\gamma }}}_\bullet ^*)^{1/2}$. Then $\theta _\bullet ={{\tilde{\theta }}}_\bullet +O(he^{-A/h})$, and differentiating the identity $e^{i{{\tilde{\theta }}}_\bullet }=({{\tilde{\gamma }}}_\bullet /{{\tilde{\gamma }}}_\bullet ^*)^{1/2}$ gives

$$\begin{aligned} \partial {{\tilde{\theta }}}_\bullet /\partial \mu =O(h),\quad h\rightarrow 0,\quad \bullet =l,r, \end{aligned}$$

since $e^{i{{\tilde{\theta }}}_\bullet }=1+O(h)$ by Taylor’s formula. The claim now follows from Lemma 2.7.

Proof of Theorem 1.4

If V(x) is either an even or an odd function of $x\in {\mathbb {R}}$ then ${\widetilde{I}}_l={\widetilde{I}}_r$ by Proposition 5.1. Omitting the indices l and r, the proposition then implies that

$$\begin{aligned} \cos \left( {{\tilde{I}}}(\mu )/h \right) \pm R(\mu ,h)=0, \end{aligned}$$

(5.1)

where

$$\begin{aligned} R(\mu ,h)={\left\{ \begin{array}{ll} (2 \rho (\mu ))^{-1}e^{-J(\mu )/h}\sin (I(\mu )/h) &{}\text {when }V(x)=V(-x),\\ ( 2i \rho (\mu ))^{-1}e^{-J(\mu )/h}\sin (I(\mu )/h)&{}\text {when }V(x)=-V(-x). \end{array}\right. } \end{aligned}$$

(5.2)

Since $J(\mu _0)>0$ and ${\text {Im}}I_\bullet (\mu _0)=0$ by definition we can choose $\varepsilon >0$ small enough to ensure that, say,

$$\begin{aligned} {\text {Re}}J(\mu )\ge \tfrac{1}{2}J(\mu _0),\quad |{\text {Im}}I_\bullet (\mu )|\le \tfrac{1}{4} J(\mu _0),\quad \mu \in B_\varepsilon (\mu _0). \end{aligned}$$

(5.3)

Using (5.3) it is not difficult to check that $R(\mu ,h)=O(e^{-\frac{1}{4}J(\mu _0)/h})$ for $\mu \in B_\varepsilon (\mu _0)$. By (5.1) we must then have ${{\tilde{I}}}(\mu )/h=x_k(h)+y_k$ where $y_k=(k+\frac{1}{2})\pi$ for some integer k and $x_k(h)={{\tilde{I}}}(\mu )/h-y_k$ is close to zero. Hence,

$$\begin{aligned} \cos \left( {{\tilde{I}}}(\mu )/h \right) = \cos \left( x_k(h)+y_k\right) =(-1)^{k+1}\sin \left( {{\tilde{I}}}(\mu )/h-y_k\right) , \end{aligned}$$

which together with (5.1) implies that

$$\begin{aligned} {{\tilde{I}}}(\mu )=\left( k+\frac{1}{2}\right) \pi h\pm (-1)^{k}h\arcsin \left( R(\mu ,h)\right) \end{aligned}$$

(5.4)

when $\mu$ satisfies (5.1). By Remark 5.2 and Lemma 2.7, ${{\tilde{I}}}=I+h\theta$ is injective near $\mu _0$ for all sufficiently small h, so that the roots $\mu _k^{\mathrm {dl}}$ to ${{\tilde{I}}}(\mu )=(k+\frac{1}{2})\pi h$ are unique and real. Moreover, for such h there are precisely two solutions of (5.4) which are denoted by $\mu _k^\pm$, and since ${{\tilde{I}}}^*={{\tilde{I}}}$ and $R^*=R$ these solutions must satisfy

$$\begin{aligned} \overline{\mu ^\pm _k}=\mu ^\pm _k\quad \text {or}\quad \overline{\mu ^\pm _k}=\mu ^\mp _k. \end{aligned}$$

(5.5)

By Taylor expanding ${{\tilde{I}}}(\mu ^\pm _k)$ near $\mu _k^{\mathrm {dl}}$ and using $R(\mu ^\pm _k,h)=O(e^{-\frac{1}{4}J(\mu _0)/h})$ we obtain the auxiliary estimate $|\mu _k^\pm -\mu _k^{\mathrm {dl}}|=O(he^{-\frac{1}{4}J(\mu _0)/h})$.

We now improve this estimate by noting that $J(\mu ^\pm _k)=J(\mu _k^{\mathrm {dl}})+O(he^{-\frac{1}{4}J(\mu _0)/h})$ by Taylor’s formula, which implies that

$$\begin{aligned} e^{-J\left( \mu ^\pm _k\right) /h}=e^{-J(\mu _k^{\mathrm {dl}})/h}\left( 1+O\left( h^\infty \right) \right) . \end{aligned}$$

Since ${{\tilde{I}}}(\mu ) = I(\mu ) + h\theta =I(\mu )+O(h^2)$, we find by (5.4) that

$$\begin{aligned} \sin \left( I(\mu _k^\pm )/h\right) =\sin \left( {{\tilde{I}}}(\mu _k^\pm )/h-\theta \left( \mu _k^\pm \right) \right) =(-1)^k\left( 1+O\left( h^2\right) \right) . \end{aligned}$$

Hence, by (5.2) we have

$$\begin{aligned} R\left( \mu ^\pm _k,h\right) =c(-1)^ke^{-J(\mu _k^{\mathrm {dl}})/h}\left( 1+O(h)\right) \end{aligned}$$

(5.6)

where $c=\frac{1}{2}$ when V is even and $c=\frac{1}{2i}$ when V is odd. By Taylor expanding ${{\tilde{I}}}(\mu ^\pm _k)$ near $\mu _k^{\mathrm {dl}}$ and using (5.4) and (5.6) we obtain the improved estimate $|\mu _k^\pm -\mu _k^{\mathrm {dl}}|=O(he^{-J(\mu _k^{\mathrm {dl}})/h})$. On the other hand,

$$\begin{aligned} {{\tilde{I}}}\left( \mu _k^\pm \right)&={{\tilde{I}}}(\mu _k^{\mathrm {dl}}) +{{\tilde{I}}}^{\prime }(\mu _k^{\mathrm {dl}})\left( \mu _k^\pm -\mu _k^{\mathrm {dl}}\right) +O\left( h^2e^{-2J(\mu _k^{\mathrm {dl}})/h}\right) \\&={{\tilde{I}}}(\mu _k^{\mathrm {dl}}) + I^{\prime }(\mu _k^{\mathrm {dl}})\left( \mu _k^\pm -\mu _k^{\mathrm {dl}}\right) +O\left( h^2e^{-J(\mu _k^{\mathrm {dl}})/h}\right) \end{aligned}$$

by Remark 5.2, and hence a straightforward computation gives

$$\begin{aligned} \cos \left( {{\tilde{I}}}\left( \mu ^\pm _k\right) /h \right) = (-1)^{k+1} I'(\mu _k^{\mathrm {dl}})\frac{\mu _k^\pm -\mu _k^{\mathrm {dl}}}{h}+O\left( he^{-J(\mu _k^{\mathrm {dl}})/h}\right) . \end{aligned}$$

By combining this identity with (5.1) and (5.6) we obtain the asymptotic formulas (1) and (2) of Theorem 1.4. The final statement of the theorem is then an immediate consequence of taking complex conjugates of these formulas and applying the symmetry relations (5.5). $\quad \square$

Appendix A

1.1 Connection formulas between the left and right lobe

Here we compute Wronskians between WKB solutions defined near the left and right lobes. The proofs of these results could be obtained by inspecting the proofs in [16, Sec. III] and [12, Sec. 5], and are included here for the benefit of the reader. To shorten notation we mostly omit h-dependence from the expressions below. We always assume that $V(\beta _l(\mu _0))>0$ and that $\mu$ belongs to some small neighborhood $B_\varepsilon (\mu _0)$. We shall often refer to the case when $V(\beta _l(\mu ))=V(\beta _r(\mu ))$ as case $1^\circ$ and $V(\beta _l(\mu ))=-V(\beta _r(\mu ))$ as case $2^\circ$, which is in accordance with the terminology used by Fujiié and Wittsten [12].

Lemma A.1

Let $u^+(x;\beta _\bullet ,y_\bullet )$ and $u^-(x;\beta _\bullet ,\bar{y}_\bullet )$, $\bullet =l,r$, be given by (2.2). Then

$$\begin{aligned} {\mathcal {W}}\left( u^+\left( x;\beta _\bullet ,y_\bullet \right) ,u^-\left( x;\beta _\bullet ,{\bar{y}}_\bullet \right) \right) =4iw_\mathrm {even}^+\left( {\bar{y}}_\bullet ;y_\bullet \right) ,\quad \bullet =l,r, \end{aligned}$$

where the amplitude function appearing on the right is $1+O(h)$ as $h\rightarrow 0$ for $\mu \in B_\varepsilon (\mu _0)$ and $\bullet =l,r$.

Proof

According to the behavior of ${\text {Re}}z(x)$, there is a curve from $y_\bullet$ to ${\bar{y}}_\bullet$ along which ${\text {Re}}z(x)$ is strictly increasing. By evaluating the Wronskian at ${\bar{y}}_\bullet$ (see (2.7)) we get

$$\begin{aligned} {\mathcal {W}}\left( u^+\left( x;\beta _\bullet ,y_\bullet \right) ,u^-\left( x;\beta _\bullet ,{\bar{y}}_\bullet \right) \right) =4iw^+_\mathrm {even}\left( {\bar{y}}_\bullet ;y_\bullet \right) ,\quad \bullet =l,r, \end{aligned}$$

where $w^+_\mathrm {even}({\bar{y}}_\bullet ;y_\bullet )=1+O(h)$ by Remark 2.1. $\quad \square$

Lemma A.2

Let $u^+(x;\beta _\bullet ,y_\bullet )$ and $u^-(x;\beta _\bullet ,{\bar{y}}_\bullet )$, $\bullet =l,r$, be given by (2.2). Then in the case when $V(\beta _l)=\pm V(\beta _r)$ we have

$(\mathrm {i})$:

${\mathcal {W}}(u^+(x;\beta _l,y_l),u^-(x;\beta _r,{\bar{y}}_r))=4ie^{J/h}w_\mathrm {even}^+({\bar{y}}_r;y_l)$,

$(\mathrm {ii})$:

${\mathcal {W}}(u^+(x;\beta _l,y_l),u^+(x;\beta _r,y_r))=\pm i\cdot 4ie^{J/h}w_\mathrm {even}^+({\hat{y}}_r;y_l)$,

where the amplitude functions appearing on the right are $1+O(h)$ as $h\rightarrow 0$ for $\mu \in B_\varepsilon (\mu _0)$.

Proof

We start with the proof of (i) and note that the phase base points of $u^+(x;\beta _l,y_l)$ and $u^-(x;\beta _r,{\bar{y}}_r)$ differ. We therefore rewrite $u^+(x;\beta _l,y_l)$ as

$$\begin{aligned} u^+\left( x;\beta _l,y_l\right) =e^{J/h}u^+\left( x;\beta _r,y_l\right) , \end{aligned}$$

(A.1)

where we have used the fact that

$$\begin{aligned} \exp \left( i\int _{\beta _l}^{\beta _r}\sqrt{V(t)^2-\mu ^2}\, dt/h\right) =e^{J/h}. \end{aligned}$$

This identity is straightforward to check; in fact it can be established using the proof of [12, Lemma 5.5] with obvious modifications. Since we can find a curve from $y_l$ to ${\bar{y}}_r$ along which ${\text {Re}}z(x)$ is strictly increasing we can evaluate the Wronskian at ${\bar{y}}_r$ (see (2.8)) which gives (i), with $w^+_\mathrm {even}({\bar{y}}_r;y_l)=1+O(h)$ by Remark 2.1.

We now prove (ii). By Lemma 2.3 we have $u^+(x;\beta _r,y_r)=iu^-(\check{x};\beta _r,\check{y}_r)$ for $\check{x}$ near $\check{y}_r$ in case $1^\circ$ and $u^+(x;\beta _r,y_r)=-iu^-({\hat{x}};\beta _r,{\hat{y}}_r)$ for ${\hat{x}}$ near ${\hat{y}}_r$ in case $2^\circ$. In each case, take the function on the right and continue it through the branch cut starting at $\beta _r$ into the domain in the usual sheet containing $y_l$. Note that at $y_l$ these functions take the values $iu^-(y_l;\beta _r,\check{y}_r)$ and $-iu^-(y_l;\beta _r,{\hat{y}}_r)$, respectively. Using (A.1) and evaluating the Wronskian at ${\hat{y}}_r$ (see (2.7)) gives

$$\begin{aligned} {\mathcal {W}}\left( u^+\left( x;\beta _l,y_l\right) ,u^+\left( x;\beta _r,y_r\right) \right) = 4ie^{J/h}{\left\{ \begin{array}{ll}i w_\mathrm {even}^+\left( \check{y}_r;y_l\right) &{}\hbox { in case}\ 1^\circ ,\\ -iw_\mathrm {even}^+({\hat{y}}_r;y_l)&{}\hbox { in case}\ 2^\circ .\end{array}\right. } \end{aligned}$$

Since $z({\hat{x}})=z(\check{x})$ the two amplitude functions on the right coincide. Also, since ${\text {Re}}z(\check{x})$ (${\text {Re}}z({\hat{x}})$) is a strictly increasing function of ${\text {Im}}\check{x}$ (${\text {Im}}{\hat{x}}$) near $\check{x}=\check{y}_r$ (${\hat{x}}={\hat{y}}_r$), we can find a curve from $y_l$ to $\check{y}_r$ (${\hat{y}}_r$), passing through the branch cut at $\beta _r$, along which $t\mapsto {\text {Re}}z(t)$ is strictly increasing. Hence, $w_\mathrm {even}^+(\check{y}_r;y_l)=1+O(h)$ as by Remark 2.1, which proves (ii). $\quad \square$

Corollary A.3

Let $u_1,u_2,u_3,u_4$ be the WKB solutions defined in (4.7)–(4.8). Then in the case when $V(\beta _l)=\pm V(\beta _r)$ we have

$(\mathrm {i})$:

${\mathcal {W}}(u_1,u_3)=- 4ie^{J/h}\tau _l\tau _rw_\mathrm {even}^+({\bar{y}}_r;y_l)$,

$(\mathrm {ii})$:

${\mathcal {W}}(u_1,u_4)=4ie^{J/h}\tau _l\tau _r^*w_\mathrm {even}^+(\check{y}_l;y_r)$,

$(\mathrm {iii})$:

${\mathcal {W}}(u_3,u_2)=-4ie^{J/h}\tau _l^*\tau _rw_\mathrm {even}^+({\bar{y}}_r;\hat{\bar{y}}_l)$,

$(\mathrm {iv})$:

${\mathcal {W}}(u_4,u_2)=4ie^{J/h}\tau _l^*\tau _r^*w_\mathrm {even}^+({\bar{y}}_l;y_r)$,

$(\mathrm {v})$:

${\mathcal {W}}(u_1,u_2)=-i\cdot 4i\tau _l\tau _l^*w_\mathrm {even}^+({\bar{y}}_l;y_l)$,

$(\mathrm {vi})$:

${\mathcal {W}}(u_3,u_4)=\pm i\cdot 4i\tau _r\tau _r^*w_\mathrm {even}^+({\bar{y}}_r;y_r)$,

where all amplitude functions appearing on the right are $1+O(h)$ as $h\rightarrow 0$ for $\mu \in B_\varepsilon (\mu _0)$.

Proof

$(\mathrm {i})$-$(\mathrm {ii})$ and $(\mathrm {v})$-$(\mathrm {vi})$ are immediate consequences of Lemmas A.1 and A.2 together with the definitions (4.7)–(4.8) of $u_1,u_2,u_3,u_4$.

Now note that ${\mathcal {W}}(u_4,u_2)={\mathcal {W}}(-iu_3^*,-iu_1^*)=({\mathcal {W}}(u_1,u_3))^*$. Let $c=c(\mu )$ be the constant $c(\mu )=w_\mathrm {even}^+({\bar{y}}_r;y_l,\mu )$. Since $y_\bullet$ is independent of $\mu$ by construction (see Sect. 4) we have

$$\begin{aligned} c^*(\mu )=\overline{c\left( {{\bar{\mu }}}\right) }=\overline{w_\mathrm {even}^+\left( {\bar{y}}_r;y_l,{{\bar{\mu }}}\right) }. \end{aligned}$$

By (2.22) we then get

$$\begin{aligned} c^*(\mu )=w_\mathrm {even}^-\left( y_r;{\bar{y}}_l,\mu \right) =w_\mathrm {even}^+\left( {\bar{y}}_l; y_r,\mu \right) , \end{aligned}$$

where the last identity follows by inspecting the Wronskian formulas (2.8)–(2.7). In view of $(\mathrm {i})$ this proves $(\mathrm {iv})$ since $J^*=J$. Since ${\mathcal {W}}(u_3,u_2)=({\mathcal {W}}(u_1,u_4))^*$ and $\bar{{\check{y}}}=\hat{\bar{y}}$, it is easy to check that $(\mathrm {iii})$ follows from $(\mathrm {ii})$ in a similar manner. $\quad \square$