Fuzzy dynamic-prioritization agent-based system for forecasting job cycle time in a wafer fabrication plant

Abstract

A fuzzy dynamic-prioritization agent-based system was developed in this study to improve the forecasting of the cycle time of a job in a wafer fabrication plant (wafer fab). In this system, multiple fuzzy agents forecast the cycle time of a job from various viewpoints, after which the aggregation and evaluation agent aggregates these fuzzy cycle time forecasts using an innovative operator (i.e., the fuzzy weighted intersection) into a single representative value. Subsequently, the optimization agent varies the authority levels of the fuzzy cycle time forecasting agents to optimize the forecasting performance. A practical example was used to evaluate the effectiveness of the fuzzy dynamic-prioritization agent-based system. The experiment results indicated that the fuzzy dynamic-prioritization agent-based system outperformed three rival methods in improving forecasting accuracy. In addition, the forecasting performance could be enhanced by discriminating the authority levels of the fuzzy cycle time forecasting agents.

Introduction

The cycle time, or manufacturing lead time, of a job is the time it takes for the job to go through a factory [25, 59]. Numerous studies have aimed to reduce the average cycle time of all jobs in a factory [12, 25, 27]. Therefore, forecasting the cycle time of a job is important for production planning and control, such as internal due date assignment [14, 24, 54, 55], job sequencing and scheduling [32, 56, 58], and order tracking [38, 50].

Chen [10] classified existing approaches for forecasting the cycle time of a job into six categories: statistical analysis [10, 32, 43, 54], simulation [34, 43], artificial neural networks (ANNs, [6, 7, 33], case-based reasoning (CBR, [5], fuzzy theory [6, 7], and hybrid approaches [6, 19]. Recently, advanced data analysis techniques, such as big-data analysis and deep learning, have also been used for forecasting the cycle time of a job [47, 53,54,55]. However, the cycle time of a job is highly uncertain [49] and unpredictable even with these advanced data analysis techniques. Therefore, forecasting also involves estimating the range of a job’s cycle time. In particular, the spread of a fuzzy cycle time forecast provides information about the range of the cycle time [7]. However, such forecasting is based on the prerequisite that a fuzzy cycle time forecast contains actual values [16]. To ensure this, fuzzy collaborative forecasting methods have been proposed to narrow the range of a cycle time forecast through the collaboration of multiple experts (or agents, [11, 13, 16].

The following problems were observed in previous studies in this field:

• 1. Most studies in this field have employed only a single forecasting method. Combining multiple forecasting methods can improve the forecasting of a job’s cycle time [11, 15].

• 2. Although some studies have employed hybrid methods, each method has been used for a unique purpose, such as clustering and forecasting [8, 10, 55].

• 3. Studies that employ multiple forecasting methods usually assume that the forecasts generated using these methods have equal reference values. However, some forecasting methods are more suitable than others for a specific forecasting task.

Therefore, to overcome these problems, this study proposed a fuzzy dynamic-prioritization agent-based system for forecasting the job cycle time in a wafer fabrication plant (wafer fab). In this proposed system, multiple fuzzy agents construct fuzzy backpropagation networks (FBPNs) or fuzzy deep neural networks (FDNNs) to collaboratively forecast the cycle time of a job. Autonomous and intelligent agents are adopted because they are efficient and can collaborate smoothly [21, 57]. These fuzzy agents for forecasting the cycle time may have unequal levels of authority. Therefore, this system uses the fuzzy weighted intersection (FWI) operator proposed by Chen et al. [18] to aggregate the fuzzy cycle time forecasts made by all agents in a reasonable manner. In addition, this study designed a dynamic-prioritization mechanism for adjusting the authority levels of agents to enhance forecasting performance.

The rest of this paper is organized as follows. The next section presents the literature review followed by which introduces the fuzzy dynamic-prioritization agent-based system, including its system architecture, operational procedure, and major parts. The subsequent section details the application of the system to a practical example where data were collected from a real wafer fab. Before the concluding section, the performance of the system with those of some existing approaches are compared. Finally, main conclusions are concluded and some directions for future research are proposed.

Literature review

Mosinski et al. [34] extended a short-term simulation system of a wafer fab to simulate the long-term operations of the wafer fab. This allowed the cycle time of a future job to be forecast. Various simulation techniques, such as process flow compression, flexible equipment dedication, model warm-up, wafer start generation, and considerations on changes to fab capacity, have been implemented to the forecast of job cycle time.

Pfeiffer et al. [43] forecasted the cycle time of a job using a regression model that fit data retrieved from the manufacturing execution system of a factory. In addition, a factory simulation was conducted to validate the effectiveness of the fitted regression equation. Lingitz et al. [32] compared the accuracy levels achieved by existing regression methods for forecasting the cycle time of a job in a wafer fab. Wang et al. [54] focused on identifying factors critical for forecasting the cycle time of a job. To this end, correlation analyses [16] have been conducted. Subsequently, they fitted an adaptive logistic regression equation to generate a job cycle time forecast. A parallel computing architecture was also established to improve the computational efficiency. However, Nielsen et al. [37] believed that the relationship between the cycle time of an order (composed of many jobs that are simultaneously manufactured) and the order size may not be linear. Therefore, numerous nonlinear forecasting methods, particularly those including ANNs, have been proposed to forecast the cycle time of a job based on its attributes.

Chen and Wu [16] constructed an FBPN to generate a fuzzy cycle time forecast. The FBPN was efficient because only the threshold of the output node was fuzzified. Wang et al. [53] constructed a two-dimensional long short-term memory (LSTM) model with multiple memory units to forecast the cycle time of a job in a wafer fab. An LSTM is a recurrent neural network in which the outputs from some nodes are fed back to earlier nodes. The two layers in their model were used to consider the correlation between layers and the correlation between wafers, respectively, owing to the machine dedication constraint. Wang et al. [54, 55] constructed a density peak-based radial basis function network (RBFN) to forecast the cycle time of a job. They also classified jobs before forecasting the cycle times, which was common in previous studies [10, 14]. The experiment results revealed that the density peak-based RBFN outperformed regression methods. Murphy et al. [35] compared the performances of two types of ANNs [backpropagation network (BPN) and H₂O] and three regression methods (random forest, XGBoost, and Cubist) for estimating the cycle time of a job under various manufacturing environments governed by different job scheduling policies. The experiment results indicated that the ANNs performed better in most cases.

Methodology

The fuzzy dynamic-prioritization agent-based system is a client–server system [2] comprising five major parts Fig. 1: the central control unit, fuzzy cycle time forecasting agents, the aggregation and evaluation agent, the dynamic-prioritization agent, and the system database.

Fig. 1

Architecture of the fuzzy dynamic-prioritization agent-based system

The operational procedure of the fuzzy dynamic-prioritization agent-based system is as follows:

Step 1 The central control unit retrieves the historical data of jobs from the system server and transmits the data to the fuzzy cycle time forecasting agents.

Step 2 Each fuzzy cycle time forecasting agent constructs and trains an FBPN (or FDNN) to forecast the cycle time of a job based on the received data.

Step 3 Each fuzzy cycle time forecasting agent saves the fuzzy cycle time forecast into the system server through the intervention of the central system server.

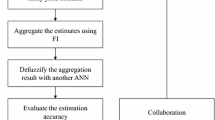
Step 4 The aggregation and evaluation agent retrieves the fuzzy cycle time forecasts by all fuzzy cycle time forecasting agents from the system server, aggregates these fuzzy cycle time forecasts, defuzzifies the aggregation result, and evaluates the forecasting performance.

Step 5 If the forecasting performance is satisfactory, go to Step 8; otherwise, go to Step 6.

Step 6 The optimization agent optimizes the authority levels of the fuzzy cycle time forecasting agents.

Step 7 Return to Step 4.

Step 8 End.

An activity diagram [23] is shown in Fig. 2, illustrating the operational procedure.

Fig. 2

Operational procedure of the fuzzy dynamic-prioritization agent-based system

The parts of the fuzzy dynamic-prioritization agent-based system are introduced in the following sections.

Fuzzy cycle time forecasting agents

In the fuzzy dynamic-prioritization agent-based system, multiple fuzzy cycle time forecasting agents are employed. Each agent constructs an FBPN (or FDNN) to forecast the cycle time of a job according to the values of some production conditions collected when the job is released into a factory [9]. Such production conditions include job size, factory utilization, queue length on the processing route, bottleneck queue length, factory queue length, factory work in process, average lateness, future workload, and forecasting error [8, 16, 42]. In the literature, various techniques for select the relevant production conditions have been employed, such as backward-elimination-based regression analysis [7], backward-elimination-based genetic programming [4], conditional mutual-information-based feature selection [52], and adaptive logistic regression correlation analysis [54, 55]. The relationship between job cycle time and production conditions is nonlinear [13]. An FBPN (or FDNN) is suitable for fitting such a nonlinear relationship [48].

Fuzzy parameters and variables in the proposed method are provided or approximated with triangular fuzzy numbers (TFNs). However, other types of fuzzy numbers are also applicable. In addition, all inputs to (and outputs from) the FBPN (or FDNN) are normalized values [15, 40]:

$$ N(\tilde{v}_{j} ) = \frac{{\tilde{v}_{j} ( - )\mathop {\min }\nolimits_{k} \tilde{v}_{k} }}{{\mathop {\max }\limits_{k} \tilde{v}_{k} ( - )\mathop {\min }\nolimits_{k} \tilde{v}_{k} }}( \times )0.9( + )0.1, $$

(1)

where $\tilde{v}_{j}$ is any input to (or output from) the FBPN (or FDNN); (+), (−), and (×) denote fuzzy addition, subtraction, and multiplication, respectively. To restore the original value,

$$ \tilde{v}_{j} = \mathop {\min }\nolimits_{k} \tilde{v}_{k} ( + )\frac{{(N(\tilde{v}_{j} )( - )0.1)( \times )(\mathop {\max }\nolimits_{k} \tilde{v}_{k} ( - )\mathop {\min }\nolimits_{k} \tilde{v}_{k} )}}{0.9}. $$

(2)

FBPN

The FBPN used by each fuzzy cycle time forecasting agent is configured as follows Fig. 3.

• 1. Number of layers: Three layers exist in the FBPN: the input layer, a single hidden layer, and the output layer [11].

• 2. Inputs: P inputs to the FBPN, which are the values of production conditions for job j and are indicated by $x_{jp}$; p = 1 ~ P.

• 3. Number of nodes in the hidden layer: L. The value of L is chosen from P to 2P [45].

• 4. Transfer (or transformation) function: linear function applied to the input layer, and the log-sigmoid function applied to the other layers.

• 5. Output ($\tilde{o}_{j}$): fuzzy cycle time forecast of job j.

Fig. 3

Architecture of the FBPN

The procedure for training the FBPN is described as follows. First, inputs to the input layer are propagated to the hidden layer, then transformed, and finally output as:

$$ \tilde{h}_{jl} = \frac{1}{{1( + ){\text{e}}^{{ - \tilde{n}_{jl}^{h} }} }}, $$

(3)

where

$$ \tilde{n}_{jl}^{h} = I_{jl}^{h} ( - )\tilde{\theta }_{l}^{h} , $$

(4)

$$ \tilde{I}_{jl}^{h} = \sum\limits_{p = 1}^{P} {{(}\tilde{w}_{pl}^{h} ( \times )x_{jp} {)}} , $$

(5)

$\tilde{h}_{jl}$ is the output from hidden-layer node l, $\tilde{\theta }_{l}^{h}$ is the threshold of the hidden-layer node l, and $\tilde{w}_{pl}^{h}$ is the weight of the connection between input node p and hidden-layer node l. $\tilde{h}_{jl}$ is passed to the output layer in the same manner. The output from the output node is generated as:

$$ \tilde{o}_{j} = \frac{1}{{1( + )e^{{ - \tilde{n}_{j}^{o} }} }}, $$

(6)

where

$$ \tilde{n}_{j}^{o} = \tilde{I}_{j}^{o} ( - )\tilde{\theta }^{o} , $$

(7)

$$ \tilde{I}_{j}^{o} = \sum\limits_{l = 1}^{L} {{(}\tilde{w}_{l}^{o} ( \times )\tilde{h}_{jl} {)}} , $$

(8)

with $\tilde{\theta }^{o}$ being the threshold of the output node and $\tilde{w}_{l}^{o}$ being the weight of the connection between the hidden-layer node l and the output node.

To simplify the network training process, Chen [11] and Chen and Wu [16] only fuzzified the threshold of the output node ($\tilde{\theta }^{o}$) to ensure that the membership of actual value ($a_{j}$) in the network output ($\tilde{o}_{j}$) is higher than a threshold (s,Fig. 4:

$$ (1 - s)o_{j1} + so_{j2} \le a_{j} \le (1 - s)o_{j3} + so_{j2} , $$

(9)

where s ∈ [0, 1]. Through such an approach, the forecasting accuracy is improved before forecasting precision is optimized [17]. By contrast, most existing FBPNs only optimize forecasting accuracy [6, 28, 40].

Fig. 4

Threshold for the membership of actual value in the fuzzy cycle time forecast

Subsequently, the FBPN is treated as a crisp one and trained using any existing algorithm, such as the gradient descent (GD) algorithm, the Levenberg–Marquardt (LM) algorithm, the Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-Newton algorithm, and the resilient backpropagation algorithm, [41, 46, 63], to optimize the cores of all fuzzy parameters. The optimized values of these cores are denoted as $w_{pl2}^{h*}$, $\theta_{l2}^{h*}$, $w_{l2}^{o*}$, and $\theta_{2}^{o*}$, respectively. Under these conditions, the following theorem holds.

Theorem 1.

$$ \theta_{3}^{o} \ge \theta_{2}^{o} + \mathop {\max }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right), $$

(10)

$$ \theta_{1}^{o} \le \theta_{2}^{o} + \mathop {\min }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right). $$

(11)

Proof

According to the arithmetic on TFNs [26],

$$ \begin{gathered} \tilde{n}_{j}^{o} = (n_{j1}^{o} ,\;n_{j2}^{o} ,\;n_{j3}^{o} ) \\ = (I_{j1}^{o} - \theta_{3}^{o} ,\;I_{j2}^{o} - \theta_{2}^{o} ,\;I_{j3}^{o} - \theta_{1}^{o} ) \\ = (I_{j2}^{o} - \theta_{3}^{o} ,\;I_{j2}^{o} - \theta_{2}^{o} ,\;I_{j2}^{o} - \theta_{1}^{o} ) \\ \end{gathered} $$

(12)

Substituting Eq. (12) into Eq. (5) gives

$$ \begin{gathered} \tilde{o}_{j} = (o_{j1} ,\;o_{j2} ,\;o_{j3} ) \\ = \frac{1}{{1 + e^{{ - \tilde{n}_{j}^{o} }} }} \\ = \left( {\frac{1}{{1 + {\text{e}}^{{ - n_{j1}^{o} }} }},\;\frac{1}{{1 + {\text{e}}^{{ - n_{j2}^{o} }} }},\;\frac{1}{{1 + {\text{e}}^{{ - n_{j3}^{o} }} }}} \right) \\ = \left( {\frac{1}{{1 + {\text{e}}^{{ - (I_{j2}^{o} - \theta_{3}^{o} )}} }},\;\frac{1}{{1 + {\text{e}}^{{ - (I_{j2}^{o} - \theta_{2}^{o} )}} }},\;\frac{1}{{1 + {\text{e}}^{{ - (I_{j2}^{o} - \theta_{1}^{o} )}} }}} \right) \\ \end{gathered} $$

(13)

Substituting Eq. (13) into Inequality (9) gives

$$ \frac{(1 - s)}{{1 + {\text{e}}^{{ - (I_{j2}^{o} - \theta_{3}^{o} )}} }} + so_{j2} \le a_{j} \le \frac{(1 - s)}{{1 + {\text{e}}^{{ - (I_{j2}^{o} - \theta_{1}^{o} )}} }} + so_{j2} , $$

(14)

which is equivalent to the following two inequalities:

$$ \frac{(1 - s)}{{1 + {\text{e}}^{{ - (I_{j2}^{o} - \theta_{3}^{o} )}} }} + so_{j2} \le a_{j} , $$

(15)

$$ a_{j} \le \frac{(1 - s)}{{1 + {\text{e}}^{{ - (I_{j2}^{o} - \theta_{1}^{o} )}} }} + so_{j2} . $$

(16)

Subsequently, substituting Eqs. (6) and (7) into Inequality (15) results in

$$ \theta_{3}^{o} \ge \theta_{2}^{o} + \ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right). $$

(17)

To guarantee this,

$$ \theta_{3}^{o} \ge \theta_{2}^{o} + \mathop {\max }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right). $$

(18)

Similarly, substituting Eqs. (6) and (7) into Inequality (16) results in:

$$ \theta_{1}^{o} \le \theta_{2}^{o} + \mathop {\min }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right). $$

(19)

Theorem 1 is proved.

To optimize the forecasting precision in terms of the average range of $\tilde{o}_{j}$, the following theorem can be used [11].

Theorem 2.

$$ \theta_{3}^{o*} = \theta_{2}^{o*} + \mathop {\max }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right), $$

(20)

$$ \theta_{1}^{o*} = \theta_{2}^{o*} + \mathop {\min }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right). $$

(21)

Proof

The proof is trivial.

Finally, the fuzzified network output is derived as follows.

Theorem 3

$$ o_{j3} = \frac{1}{{1 + \left( {\frac{1}{{o_{j2} }} - 1} \right){\text{e}}^{{\mathop {\min }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right)}} ,}} $$

(22)

$$ o_{j1} = \frac{1}{{1 + \left( {\frac{1}{{o_{j2} }} - 1} \right){\text{e}}^{{\mathop {\max }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right)}} }}. $$

(23)

Proof

$$\begin{gathered} o_{j3} = \frac{1}{{1 + {\text{e}}^{{ - (I_{j2}^{o} - \theta_{1}^{o*} )}} }} \\ = \frac{1}{{1 + e^{{ - \left( {I_{j2}^{o} - (\theta_{2}^{o*} + \mathop {\min }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right)} \right)}} }} \\ = \frac{1}{{1 + {\text{e}}^{{ - (I_{j2}^{o} - \theta_{2}^{o*} )}} {\text{e}}^{{\mathop {\min }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right)}} }} \\ = \frac{1}{{1 + \left( {\frac{1}{{o_{j2} }} - 1} \right){\text{e}}^{{\mathop {\min }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right)}} }} \\ \end{gathered}$$

(24)

Similarly,

$$ \begin{gathered} o_{j1} = \frac{1}{{1 + {\text{e}}^{{ - (I_{j2}^{o} - \theta_{3}^{o*} )}} }} \\ = \frac{1}{{1 + {\text{e}}^{{ - \left( {I_{j2}^{o} - (\theta_{2}^{o*} + \mathop {\max }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right)} \right)}} }} \\ = \frac{1}{{1 + {\text{e}}^{{ - (I_{j2}^{o} - \theta_{2}^{o*} )}} {\text{e}}^{{\mathop {\max }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right)}} }} \\ = \frac{1}{{1 + \left( {\frac{1}{{o_{j2} }} - 1} \right){\text{e}}^{{\mathop {\max }\limits_{j} \left( {\ln \left( {\frac{1 - s}{{a_{j} - so_{j2} }} - 1} \right) - \ln \left( {\frac{1}{{o_{j2} }} - 1} \right)} \right)}} }} \\ \end{gathered} $$

(25)

Theorem 3 is proved.

FDNN

This study extended the FBPN to an FDNN by increasing the number of hidden layers, as shown in Fig. 5. An FDNN may have the following advantages over an FBPN:

• 1. The forecasting accuracy achieved using an FDNN may be higher than that achieved using an FBPN [39].

• 2. An FBPN may require a fewer number of nodes than an FDNN to achieve the same forecasting accuracy [29].

• 3. The training process of an FDNN may be much more efficient than that of an FBPN [1].

Fig. 5

Architecture of the FDNN

However, the superiority of an FDNN over an FBPN depends on the nature of the forecasting problem [30].

In the network training phase, inputs to an FDNN are weighted and transmitted to each node of the first hidden layer, on which they are aggregated and then output as:

$$ \tilde{h}_{jl}^{(1)} = \frac{1}{{1 + {\text{e}}^{{ - \tilde{n}_{jl}^{h(1)} }} }}, $$

(26)

where

$$ \tilde{n}_{jl}^{h(1)} = \tilde{I}_{jl}^{h(1)} ( - )\tilde{\theta }_{l}^{h(1)} , $$

(27)

$$ \tilde{I}_{jl}^{h(1)} = \sum\limits_{p = 1}^{P} {\tilde{w}_{pl}^{h(1)} z_{jp} } , $$

(28)

with $\tilde{h}_{jl}^{(1)}$ being the output from node l of the first hidden layer; l = 1 ~ L. $\tilde{\theta }_{l}^{h(1)}$ being the threshold of this node; $\tilde{w}_{kl}^{h(1)}$ being the weight of the connection between input node k and this node; and $\tilde{h}_{jl}^{(1)}$ being passed to the second hidden layer, aggregated, transformed, and finally output in the same manner as

$$ \tilde{h}_{jq}^{(2)} = \frac{1}{{1 + {\text{e}}^{{ - \tilde{n}_{jq}^{h(2)} }} }}. $$

(29)

Specifically,

$$ \tilde{n}_{jq}^{h(2)} = \tilde{I}_{jq}^{h(2)} ( - )\tilde{\theta }_{q}^{h(2)} , $$

(30)

$$ \tilde{I}_{jq}^{h(2)} = \sum\limits_{l = 1}^{L} {\tilde{w}_{lq}^{h(2)} ( \times )\tilde{h}_{jl}^{(1)} } , $$

(31)

where $\tilde{h}_{jq}^{(2)}$ is the output from node q of the second hidden layer; q = 1 ~ Q. $\tilde{\theta }_{q}^{h(2)}$ is the threshold of this node; and $\tilde{w}_{lq}^{h(2)}$ is the weight of the connection between node l of the first hidden layer and this node. In total, there are L∙Q connections between the two hidden layers. After passing $\tilde{h}_{jq}^{(2)}$ to the output layer, the network output $\tilde{o}_{j}$ is generated as

$$ \tilde{o}_{j} = \frac{1}{{1 + {\text{e}}^{{ - \tilde{n}_{j}^{o} }} }}, $$

(32)

where

$$ \tilde{n}_{j}^{o} = \tilde{I}_{j}^{o} ( - )\tilde{\theta }^{o} , $$

(33)

$$ \tilde{I}_{j}^{o} = \sum\limits_{q = 1}^{Q} {\tilde{w}_{q}^{o} ( \times )\tilde{h}_{jq}^{(2)} } , $$

(34)

with $\tilde{\theta }^{o}$ being the threshold of the output node and $\tilde{w}_{q}^{o}$ being the weight of the connection between node q of the second hidden layer and the output node.

The training process of an FDNN is similar to that of an FBPN. Only the threshold of the output node is fuzzified according to Theorems 1–3. The values of the other parameters are derived by training the FDNN as a crisp deep neural network using the commonly used GD or LM algorithm [3, 20].

The fuzzy cycle time forecasts made by different agents using FBPNs or FDNNs are not equal for the following reasons:

• 1. The initial values of network parameters are usually randomized.

• 2. The values of the threshold (s) set by different fuzzy cycle time forecasting agents are not the same.

Therefore, a mechanism to aggregate the agents’ time forecasts of the cycle time is required.

Aggregation and evaluation agent

Assuming the fuzzy cycle time forecast made by fuzzy cycle time forecasting agent m for job j is $\tilde{o}_{j} (m)$ for m = 1 ~ M. In addition, fuzzy cycle time forecasting agents may have unequal authority levels [18, 22, 61]. With $\omega_{m}$ indicating the authority level of a fuzzy cycle time forecasting agent m, the following is obtained:

$$ \sum\limits_{m} {\omega_{m} } = 1, $$

(35)

$$ \omega_{{m_{1} }} \ne \omega_{{m_{2} }} \;{\text{and}}\;\exists m_{1} \ne \;m_{2} . $$

(36)

The FWI operator proposed by Chen et al. [18] is used to aggregate the fuzzy cycle time forecasts made by agents:

$$ \tilde{o}_{j} ({\text{all}}) = \widetilde{{{\text{FWI}}}}(\{ \tilde{o}_{j} (m)\} ), $$

(37)

where

$$ \mu_{{\widetilde{{{\text{FWI}}}}(\{ \tilde{o}_{j} (m)\} )}} (x) = \mathop {\min }\limits_{m} \mu_{{\tilde{o}_{j} (m)}} (x) + \sum\limits_{m} {{(}\omega_{m} - \mathop {\min }\limits_{l} \omega_{l} {)(}\mu_{{\tilde{o}_{j} (m)}} (x) - } \mathop {\min }\limits_{l} \mu_{{\tilde{o}_{j} (l)}} (x)). $$

(38)

An example is given as follows. Assuming the fuzzy cycle time forecasts by three fuzzy cycle time forecasting agents are:

$$ \begin{gathered} o_{j} (1) = \left( {{12}0{5},{ 135}0,{ 162}0} \right), \hfill \\ o_{j} (2) = \left( {{115}0,{ 124}0,{ 1495}} \right), \hfill \\ o_{j} (3) = \left( {{123}0,{ 1415},{ 1735}} \right). \hfill \\ \end{gathered} $$

The levels of authority of fuzzy cycle time forecasting agents are given by the tuple ($\omega_{1}$, $\omega_{2}$, $\omega_{3}$) = (0.35, 0.15, 0.50). The corresponding aggregation result using the FWI operator is shown in Fig. 6. Values that were considered to be highly possible by either all fuzzy cycle time forecasting agents or only the most authoritative fuzzy cycle time forecasting agent had higher membership values in the FWI result.

Fig. 6

FWI result

The forecasting precision can be evaluated based on the aggregation result in terms of the average range [31, 62], and the hit rate, respectively, as follows:

$$ {\text{Average range }} = \frac{{\sum\nolimits_{j = 1}^{n} {(\max \tilde{o}_{j} ({\text{all}})} - \min \tilde{o}_{j} ({\text{all}}))}}{n}, $$

(39)

$$ {\text{Hit rate }} = \frac{{\sum\nolimits_{j = 1}^{n} {z_{j} } }}{n}, $$

(40)

where

$$ z_{j} = \left\{ {\begin{array}{*{20}l} 1 & {{\text{if}}} & {\min \tilde{o}_{j} ({\text{all}}) \le a_{j} \le \max \tilde{o}_{j} ({\text{all}})} \\ 0 & {{\text{otherwise}}} & {} \\ \end{array} } \right.. $$

(41)

Subsequently, the center-of-gravity method [51, 60] is employed to defuzzify the aggregation result to arrive at a crisp/representative value:

$$ o_{j} = {\text{COG}}(\tilde{o}_{j} ({\text{all}})) = \frac{{\int {x\mu_{{\tilde{o}_{j} ({\text{all}})}} (x){\text{d}}x} }}{{\int {\mu_{{\tilde{o}_{j} ({\text{all}})}} (x){\text{d}}x} }}. $$

(42)

Based on the result, the forecasting accuracy can be evaluated in terms of the

$$ {\text{mean absolute error }}\left( {{\text{MAE}}} \right) \, = \frac{{\sum\nolimits_{j = 1}^{n} {|o_{j} - a_{j} |} }}{n}, $$

(43)

$$ {\text{mean absolute percentage error }}\left( {{\text{MAPE}}} \right) = \frac{{\sum\nolimits_{j = 1}^{n} {\frac{{|o_{j} - a_{j} |}}{{a_{j} }}} }}{n} \cdot 100\% , $$

(44)

$$ {\text{root mean squared error }}\left( {{\text{RMSE}}} \right) \, = \sqrt {\frac{{\sum\nolimits_{j = 1}^{n} {(o_{j} - a_{j} )^{2} } }}{n}} . $$

(45)

Dynamic prioritization agent

The authority levels of fuzzy agents for forecasting the cycle time can be dynamically adjusted to improve the forecasting performance. The dynamic-prioritization agent executes the following procedure:

Step 1 Randomize the authority levels of fuzzy cycle time forecasting agents.

Step 2 Aggregate the fuzzy cycle time forecasts by the agents based on their newest authority levels.

Step 3 Evaluate the forecasting performance.

Step 4 If the forecasting performance is good enough, go to Step 8; otherwise, go to Step 5.

Step 5 If sufficient data are collected, retrain the BPN optimizer for estimating the forecasting performance from the authority levels of the agents; otherwise, return to Step 1.

Step 6 Estimate the best setting of the authority levels of these agents.

Step 7 Return to Step 2.

Step 8 Stop.

A flowchart is shown in Fig. 7 that illustrates the procedure. The architecture of the BPN optimizer is shown in Fig. 8. There exist only M − 1 inputs to the BPN optimizer because $\omega_{M} = 1 - \sum\nolimits_{m = 1}^{M - 1} {\omega_{m} }$.

Fig. 7

Operational procedure of the dynamic-prioritization agent

Fig. 8

Architecture of the BPN optimizer

Application

The fuzzy dynamic-prioritization agent-based system was evaluated in a practical case featuring real data collected from a wafer fab located in Hsin Chu Science Park, Taiwan [16]. More than ten products in the wafer fab were competing for the limited fab capacity. Therefore, the cycle time of each product was highly uncertain. The product occupying the majority of the fab capacity was analyzed in this study.

The collected data included the cycle times of 120 jobs and the values of six production conditions when each job was released into the fab (shown in Fig. 9.

Fig. 9

Collected data

Three agents collaborated to fulfill the task of forecasting job cycle time. First, each agent configured an FBPN (or FDNN) to forecast the cycle time of a job. The configurations of these FBPNs and FDNNs are listed in Table 1. The first 3/4 of the collected data were used to train each FBPN (or FDNN), and the remaining data were used as test data for evaluating the forecasting performance. The forecasting results are shown in Fig. 10. The forecasting results obtained by the agents for the test data are presented in Table 2. Clearly, the forecasting performances had room for improvement, indicating the need for these agents to collaborate.

Table 1 Configurations of FBPNs

Fig. 10

Forecasting results

Table 2 Forecasting results obtained by individual agents

Subsequently, the aggregation and evaluation agent applied the FWI operator to aggregate the fuzzy cycle time forecasts of the agents. The authority levels of these agents were first set to 0.49, 0.31, and 0.20. Job #1 was taken as an example, and the aggregation result is shown in Fig. 11. After aggregation, the forecasting performance improved in terms of the MAE, MAPE, RMSE, and hit rate:

Fig. 11

Aggregation result for job #1

MAE = 108.3 (h),

MAPE = 8.2%,

RMSE = 137.9 (h),

Average range = 682.4 (h),

Hit rate = 100%.

The average range was slightly widened.

To enhance the forecasting performance, the optimization agent constructed a BPN to optimize the values of the authority levels of agents, thereby minimizing the MAPE. The optimization results were $\omega_{\text{m}} = \{0.43,\; 0.15,\; 0.42\}$, yielding a minimal MAPE of 7.6%. In addition, the MAE, RMSE, average range, and hit rate were 98.6 h, 120.6 h, 642.4 h, and 100%, respectively. The forecasting performance was considerably improved, as shown in Fig. 12.

Fig. 12

Performances before and after optimization

Comparison

To further verify the effectiveness of the fuzzy dynamic-prioritization agent-based system, three counterpart methods—the BPN method, CBR [5], and the FBPN-fuzzy intersection (FI) approach [16]—were applied to the collected data for comparison. The BPN approach involved a single hidden layer. The number of hidden-layer nodes were chosen from two previous studies [6, 14] to minimize the RMSE. Therefore, the hidden layer had 14 nodes, yielding a minimum RMSE of 113 h for the training data. In addition, four training algorithms—the LM algorithm, the BFGS quasi-Newton algorithm, the GD algorithm with momentum and an adaptive learning rate, and the resilient backpropagation algorithm—were used to train the BPN. The experimental results demonstrated that the BFGS algorithm achieved the highest forecasting accuracy in terms of the RMSE. In the CBR method, the number of cases was varied from 2 to 13 to observe the changes in forecasting performance. The MAPE was minimized at ten cases. In Chen and Wu’s FBPN-FI approach, the threshold of the output node of the FBPN was also fuzzified. However, FI, rather than FWI, was used to aggregate the fuzzy cycle time forecasts of the clouds, which increased the forecasting precision for the training data but also increased the risk of missing an actual value in the test data.

The forecasting performances of the various methods operating on the test data are presented in Table 3.

Table 3 Forecasting performances of various methods

The following conclusion can be drawn from the experimental results:

• 1. The fuzzy dynamic-prioritization agent-based system outperformed three existing methods in optimizing the forecasting accuracy in terms of the MAE, MAPE, and RMSE. The BPN method exhibited the lowest performance in comparison to the proposed method, with its RMSE being 45% higher than that of the proposed method.

• 2. Both the fuzzy dynamic-prioritization agent-based system and Chen and Wu’s FBPN-FI approach had a significantly lower MAPE than the other two methods, which verified the effectiveness of agent (or cloud) collaboration in increasing the performance of forecasting the cycle times of jobs.

• 3. The fuzzy dynamic-prioritization agent-based system also achieved satisfactory forecasting precision in terms of hit rate. Although the CBR method achieved a perfect hit rate, it generated very wide fuzzy cycle time forecasts that provided no useful information.

• 4. If all fuzzy cycle time forecasting agents were of equal authority levels, then the forecasting performance would be

MAE = 114.3 (h),

MAPE = 8.7%,

RMSE = 147.1 (h),

Average range = 408.0 (h),

Hit rate = 76%.

These results are much worse than those for unequal authority levels.

Conclusions and directions for future research

Forecasting the cycle time of each job is critical in a wafer fab. Therefore, this study proposes a fuzzy dynamic-prioritization agent-based system to forecast the cycle time of each job. In this system, multiple fuzzy cycle time forecasting agents collaboratively forecast the cycle time of a job. Then, the aggregation and evaluation agent aggregates these fuzzy cycle time forecasts into a single representative value that is then compared with an actual value to evaluate the forecasting performance, for which the FWI operator, rather than FI, is employed. Through such a process, agents can have unequal authority levels. The optimization agent improves the forecasting performance by varying the authority levels of fuzzy cycle time forecasting agents.

The fuzzy dynamic-prioritization agent-based system was used in a practical example featuring data collected from a real wafer fab. Three existing methods in this field were also evaluated for comparison. After analyzing the experiment results, the following conclusions were drawn:

• 1. This study’s system outperformed three existing methods, especially in forecasting accuracy in terms of the MAE, MAPE, and RMSE.

• 2. The collaboration of agents was again demonstrated to improve the effectiveness of forecasting the cycle time of a job.

• 3. The forecasting performance was considerably improved by discriminating the authority levels of fuzzy cycle time forecasting agents.

In future studies, the fuzzy dynamic-prioritization agent-based system should be employed in various production environments, such as a ramping-up fab, foundry fab, or memory fab, to further examine its effectiveness.