Abstract
A new tuberculosis model consisting of ordinary differential equations and partial differential equations is established in this paper. The model includes latent age (i.e., the time elapsed since the individual became infected but not infectious) and relapse age (i.e., the time between cure and reappearance of symptoms of tuberculosis). We identify the basic reproduction number \(\mathcal {R}_{0}\) for this model, and show that the \(\mathcal {R}_{0}\) determines the global dynamics of the model. If \(\mathcal {R}_{0}<1\), the disease-free equilibrium is globally asymptotically stable, which means that tuberculosis will disappear, and if \(\mathcal {R}_{0}>1\), there exists a unique endemic equilibrium that attracts all solutions that can cause the spread of tuberculosis. Based on the tuberculosis data in China from 2007 to 2018, we use Grey Wolf Optimizer algorithm to find the optimal parameter values and initial values of the model. Furthermore, we perform uncertainty and sensitivity analysis to identify the parameters that have significant impact on the basic reproduction number. Finally, we give an effective measure to reach the goal of WHO of reducing the incidence of tuberculosis by 80% by 2030 compared to 2015.
Similar content being viewed by others
1 Introduction
Tuberculosis (TB), one of the top 10 causes of death worldwide, is an infectious disease caused by the bacillus mycobacterium tuberculosis. The bacillus can attack any part of the body such as the lungs (pulmonary TB), kidney, spine and brain (extra-pulmonary TB). The disease is spread through the air from one person to another, when people who are sick with pulmonary TB expel the bacillus into the air, for example, by coughing, speaking and so on, people nearby may breathe in these bacillus and become infected. The extrapulmonary TB is usually not infectious. About 5–10% of people who infected with the bacillus will develop TB during their lifetime. However, people with weak immune systems have a much higher risk of TB, such as people living with HIV, malnutrition or diabetes, or people who smoke. TB occurs in every part of the world. In 2017, there were an estimated 10 million new cases of TB worldwide, the majority of them were concentrated in the African, South-East Asia and Western Pacific regions. The following eight countries accounted for two thirds of the new TB cases: India, China, Indonesia, the Philippines, Pakistan, Nigeria, Bangladesh and South Africa (WHO 2019; CDC 2019).
Prevention and treatment have always been considered as important means of controlling the spread of TB, they mainly include: treatment of latent TB infection, vaccination of children with the bacille Calmette–Guérin (BCG) vaccine, people with TB take the drugs exactly as prescribed for 6–9 months, and so on. These measures are considered to have made a major contribution to the reduction in TB burden since 2000. TB incidence has fallen 1.5% per year since 2000, for a total reduction of 18% worldwide. However, as the WHO notes, TB kills millions of people worldwide each year, which is unacceptable in an era when you can diagnose and cure nearly every person with TB. At this rate, the WHO 2030 goal (the new TB cases will reduce by 80% by 2030 compared to 2015) will not be achieved. If the world is to end TB, it needs to scale up services and invest in research. Unfortunately, the gap between the funding available and the requirement has widened over the past 2 years, this is not a good sign for TB control. Therefore, increasing investment and developing the most effective control measures are crucial for the current control of TB (WHO 2019; CDC 2019).
Mathematical modeling has always been a very useful and important tool in studying the transmission mechanism of epidemic disease, drinking or other behavior, through mathematical analysis and numerical simulation of the model, effective control measures can be designed and evaluated (Ullah et al. 2019; Wang et al. 2019; Agusto and Khan 2018; Rebaza 2019; Ngeleja et al. 2018; Zhao et al. 2019; Huo et al. 2019b; Xiang et al. 2019; Ma 2019; Shi and Wang 2019; Cai et al. 2018; Du and Feng 2018; Zhang and Xing 2019; Meng et al. 2018; Meng and Wu 2018; Zhang et al. 2018; Bao et al. 2020; Bao and Li 2020; Huang and Tian 2019; Li and Huang 2019; Huo et al. 2019a; Zhang et al. 2019a, b; Huo et al. 2020; Huang 2020). Due to the complexity of the pathogenesis of tuberculosis, there have been many articles to establish different models to study TB and incorporate certain factors, such as treatment, drug resistance, HIV/TB co-infection, relapse, vaccination and so on (Whang et al. 2011; Zhao et al. 2017; Ozcaglar et al. 2012; Liu and Zhang 2011; Ren 2017; Choi et al. 2015). Liu and Zhang (2011) argued that vaccination can only reduce infection, not eliminate it entirely, and treatment can also only reduce the infectivity of treated TB cases (compared to untreated cases). According to this, they investigated the effects of vaccination and treatment on the spread of TB. Agusto and Adekunle (2014) formulated a mathematical model of the transmission of TB-HIV/AIDS co-infection. By using treatment of infected individuals with TB as the system control variable, they investigated optimal strategies for controlling the spread of the disease. Most of the models are qualitative analysis of tuberculosis transmission, and few are quantitative analysis based on actual data. Recently, more and more researchers are beginning to combine data to study the spread of diseases (Jing et al. 2020; Ullah et al. 2019; Zhao et al. 2017; Ghosh et al. 2018; Liu et al. 2020). Ullah et al. (2019) studied a TB model and used the actual data to estimate the model parameters, then they analyzed the effect of various parameters to define the importance of these parameters to disease transmission. Based on tuberculosis data from China, Zhao et al. (2017) evaluated the parameters by the Least Square method. Then, they gave two effective measures to achieve WHO’s goal through numerical simulation.
During the spread of tuberculosis, it is worth noting that after becoming infected, some people develop TB disease soon (within weeks), before their immune system can fight the TB bacteria. Other people may get sick years later, when their immune system becomes weak for some reason. Many people with TB infection never develop TB disease. Iannelli and Milner (2017) argued that age structure is important when modeling a long-lasting disease, because the chance of infected individuals becoming infectious individuals and recovering patients relapsing is variable.
Motivated by these factors, in this paper, we formulate a new age-structured TB model to study the effects of relapse and treatment on transmission dynamics of TB. We not only introduce the treatment individuals as a class but also assume that the treatment class is also infectious. The article is organized as follows. In Sect. 2, we introduce an age-structured TB model and present some basic properties. In Sect. 3, we define the basic reproductive number and prove the local stability of the disease-free equilibrium and the unique endemic equilibrium. In Sect. 4, we present the uniform persistence result and prove the global stability of the disease-free equilibrium and the unique endemic equilibrium. In Sect. 5, we perform data fitting and sensitivity analysis of the basic reproductive number, and assess the feasibility of the WHO End TB Strategy by 2030. In Sect. 6, we give a brief discussion.
2 TB model and basic properties
2.1 Model formulation
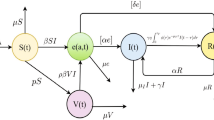
The model divides the total population at time t into five mutually-exclusive subgroups: susceptible class, latent class (those who are infected but not yet infectious), infectious class, treatment and recovered class denoted by S(t), e(t, a), I(t), T(t) and \(r(t,\theta )\), respectively. Here the parameter a denotes the latent age of the infected individuals, \(\theta \) denotes the relapse age of the recovered individuals. We assume that people during treatment may still be re-infected due to contact with TB patients. If some people have been treated successfully, but in the process of treatment, they re-contact with tuberculosis patients, they will enter the latent class, and those who are re-infected in other situations will enter the infectious class. Burman et al. (2009) argued that recurrent TB can develop in some patients after they complete therapy. This shows that people who have recovered may have a relapse. The flow among those subgroups is shown in the following flowchart (Fig. 1).
Base on the above notations and the flowchart (Fig. 1), we formulate the TB model as follows:
with the following boundary conditions
and initial conditions
where \(e_{0}(a), r_{0}(\theta )\in L_{+}^{1}(0,+\infty )\), and \(s_{0}, i_{0}, t_{0}\in \mathbb {R}_{+}.\) The meanings of the parameters in (1) are explained in Table 1.
Throughout this paper, we make the following assumptions and notations.
(A1) : \(\Lambda , \mu , \beta ,\rho _{1},\eta ,\gamma , \rho , \alpha ,\mu _{I},\mu _{t}>0;\)
(A2) : \(\omega (\theta ),\delta (a),\sigma (a)\in L_{+}^{\infty }(0,+\infty ) \) with essential upper bounds \(\bar{ \omega }, \bar{ \delta }, \bar{ \sigma }>0\) , respectively;
For \(a,\theta \ge 0\), we denote
\(\mathscr {Y}=\mathbb {R}_{+}^{3}\times (L_{+}^{1}(0,+\infty ))^{2},\) with norm
2.2 Well-posedness
Base on above assumptions, we can verify the local existence of unique and nonnegative solution of the model (1) with the nonnegative initial conditions (see Webb 1985 and Iannelli (1994)), thus we obtain the following proposition.
Proposition 1
Let \(x_{0}\in \mathscr {Y},\) then there exists \(\epsilon >0\) and neighborhood \(B_{0}\subset \mathscr {Y}\) with \(x_{0}\in B_{0}\) such that there exists a unique continuous function, \(\Phi : [0,\epsilon ]\times B_{0}\rightarrow \mathscr {Y}\), where \(\Phi (t,x_{0})\) is the solution to (1) with \(\Phi (0,x_{0})=x_{0}.\)
For \(t\in [0,\epsilon ],\) \(\parallel \Phi (t,x_{0})\parallel _{\mathscr {Y}}=S(t)+I(t)+T(t) +\int _{0}^{+\infty }e(t,a)da+\int _{0}^{+\infty }r(t,\theta )d\theta ,\) we deduce that \(\parallel \Phi (t,x_{0})\parallel _{\mathscr {Y}}\) satisfies the following inequality:
According to the comparison principle, we have
which yields
Boundedness is a direct consequence of nonnegativity of solution. Then we have the following proposition.
Proposition 2
Let \(x_{0}\in \mathscr {Y},\) then there exists a unique continuous semiflow, \(\Phi : \mathbb {R}_{+}\times \mathscr {Y}\rightarrow \mathscr {Y}\), where \(\Phi (t,x_{0})\) is the solution to (1) with \(\Phi (0,x_{0})=x_{0},\) and (4),(5) are satisfied for \(t\in \mathbb {R}_{+}.\) The following set is positively invariant for system (1)
From Proposition 2 and inequality (4), we obtain the following proposition.
Proposition 3
(i) The solution of (1), \(\Phi (t,\cdot )\), is point dissipative, and \(\Omega \) attracts all points in \(\mathscr {Y}\);
(ii) Let \(B \subset \mathscr {Y}\) be bounded, then \(\Phi (t,B) \) is bounded;
(iii) If \(x_{0}\in \mathscr {Y}\) and \(\parallel x_{0}\parallel _{\mathscr {Y}}\le A\) for some \(A\ge \frac{\Lambda }{\mu },\) then \(S(t),\ I(t), \ T(t), \parallel e(t,\cdot )\parallel _{L_{+}^{1}}, \parallel r(t,\cdot )\parallel _{L_{+}^{1}}\le A.\)
2.3 Asymptotic smoothness
Integrating the equations for \(e(t,a),r(t,\theta )\) in (1) along the characteristic lines, \(t-a\)=const., \(t-\theta \)=cost., respectively, we deduce that
The continuous semiflow \(\{\Phi (t,\cdot )\}_{t\ge 0}\) is said to be asymptotically smooth, if each positively invariant bounded closed set is attracted by a nonempty compact set.
We will use the following two lemmas proposed by Smith and Thieme (2011) to prove the asymptotic smoothness of the semiflow.
Lemma 1
The semiflow \(\Phi : \mathbb {R}_{+}\times \mathscr {Y}\rightarrow \mathscr {Y}\) is asymptotically smooth if there are maps \(U_{1}, U_{2}:\mathbb {R}_{+}\times \mathscr {Y}\rightarrow \mathscr {Y}\) such that \(\Phi (t,x) =U_{1}(t,x) + U_{2}(t,x)\), and the following hold for any bounded closed set \(\mathscr {A}\subset \mathscr {Y}\) that is forward invariant under \(\Phi \):
(i) \(\lim \limits _{t\rightarrow +\infty } diam U_{2}(t,\mathscr {A})=0\);
(ii) there exists \(t_{\mathscr {A}}\ge 0\) such that \(U_{1}(t,\mathscr {A})\) has compact closure for each \(t\ge t_{\mathscr {A}}\) .
Since \(\mathscr {Y}\) is an infinite dimensional space, space \(L_{+}^{1}(0,+\infty )\) is a component of \(\mathscr {Y}\). For infinite dimensional space, we cannot deduce precompactness only from boundedness. Thus, to derive the precompactness of \(\mathscr {Y}\), we apply the following lemma:
Lemma 2
Let \(\mathscr {B}\) be a bounded subset of \(L_{+}^{1}(0,+\infty )\). Then \(\mathscr {B}\) has compact closure if and only if the following conditions hold:
-
(i)
\(\sup \limits _{f\in \mathscr {B}}\int _{0}^{+\infty }\mid f(s)\mid ds<+\infty \);
-
(ii)
\(\lim \limits _{h\rightarrow +\infty }\int _{h}^{+\infty }\mid f(s)\mid ds=0 \) uniformly in \(f\in \mathscr {B}\);
-
(iii)
\(\lim \limits _{h\rightarrow 0^{+}}\int _{0}^{+\infty }\mid f(s+h)-f(s)\mid ds=0\) uniformly in \(f\in \mathscr {B}\);
-
(iv)
\(\lim \limits _{h\rightarrow 0^{+}}\int _{0}^{h}\mid f(s)\mid ds=0 \) uniformly in \(f\in \mathscr {B}\).
We are now ready to prove a result on the semiflow \(\Phi \) generated by system (1) is asymptotically smooth.
Theorem 1
The semiflow \(\Phi \) generated by system (1) is asymptotically smooth.
Proof
We first decompose \(\Phi \) into the following two parts: \(U_{1},U_{2}\) defined respectively by
where
for \(x=(S(0), I(0),T(0),e_{0}(a),r_{0}(\theta )),\) clearly, we have \(\Phi (t,x)=U_{1}(t,x)+U_{2}(t,x).\)
Let \(\mathscr {A}\subset \mathscr {Y}\), r is a constant greater than \(\frac{\Lambda }{\mu }\), for each \( x \in \mathscr {A}\), we set \(\parallel x \parallel _{\mathscr {Y}}\le r.\) So we can derive
Thus, \(\lim \nolimits _{t\rightarrow +\infty } diam \ U_{2}(t,\mathscr {A})=0\). In the following we will show that \(U_{1}(t,\mathscr {A})\) has compact closure for each \(t\ge 0\).
From Proposition 3, we know that S(t), I(t), T(t) remain in the compact set [0, r] for all \(t\ge 0\). Next, we will show that \(\widetilde{e}(t,a) \ and\ \widetilde{r}(t,\theta )\) remain in a precompact subset of \(L^{1}_{+}(0,+\infty )\) which is independent of x. According to
and (2), it is easy to show that
Therefore, the conditions (i),(ii) and (iv) of Lemma 2 are satisfied. Now, we only need to check the condition (iii) of Lemma 2.
where
Notice that \(\mid \dfrac{dI(t)}{dt}\mid \le (\bar{\omega }+\bar{\sigma })r +(1-\eta )\rho _{1}r+(\gamma +\mu +\mu _{I})r\), \( \mid \dfrac{dS(t)}{dt}\mid \le \Lambda +\beta (1+\rho )r^{2}+\mu r\), \( \mid \dfrac{dT(t)}{dt}\mid \le \gamma r+(\mu +\mu _{T}+\alpha +\rho _{1})r\), then
where
Then
Hence,
Thus, the condition (iii) of Lemma 2 holds, then we can get that \(\widetilde{e}(t,a)\) satisfies the conditions of Lemma 2. In a similar way, \(\widetilde{r}(t,\theta ) \) also satisfies the conditions of Lemma 2. Therefore, we obtain \(U_{1}(t,\mathscr {A})\) has compact closure for each \(t\ge 0\), Using Lemma 1, we know semiflow \(\Phi \) is asymptotically smooth. This completes the proof. \(\square \)
Combining Proposition 3 and \(\Phi \) is asymptotically smooth, as well as the existence theory of global attractors, the following result is immediate from Theorem 2.6 in Magal and Zhao (2005) and Theorem 2.4 in D’Agata et al. (2006).
Theorem 2
The semiflow \(\Phi \) has a global attractor \(\mathcal {A}\) in \(\mathscr {Y}\) , which attracts any bounded subset of \(\mathscr {Y}\).
3 Equilibria and their local stability
3.1 Existence of equilibria
System (1) always has a disease free equilibrium \(E_{0} =(\frac{\Lambda }{\mu },0,0,0_{L^{1}(0,+\infty )},0_{L^{1}(0,+\infty )})\). One can obtain the reproduction number from system (1)
\(\mathscr {R}_{0}\) represents the average number of secondary infected individuals produced by a primary infected individual.
Next, we investigate the endemic equilibria of system (1). A endemic equilibrium \((S^{*}, I^{*}, T^{*},e^{*}(a), r^{*}(\theta ))\) of system (1) satisfies the following equations:
From (8) we can easily find that if \(\mathscr {R}_{0}>1,\) system (1) has a endemic equilibrium \(E^{*}=(S^{*}, I^{*}, T^{*},e^{*}(a),r^{*}(\theta )),\) where
Summarizing the discussions above, we have the following theorem.
Theorem 3
System (1) always has the disease free equilibrium \(E_{0}\). Moreover, apart from \(E_{0}\) , if \(\mathscr {R}_{0}>1\), system (1) exists a unique endemic equilibrium \(E^{*}\).
3.2 Local stability of the equilibria
Now we consider the linearized system of (1) at an equilibrium \(\widetilde{E}=(\widetilde{S}, \widetilde{I}, \widetilde{T}, \widetilde{e}(a), \widetilde{r}(\theta )).\) Let \(\overline{S}(t)=S(t)-\widetilde{S},\ \overline{I}(t)=I(t)-\widetilde{I},\ \overline{T}(t)=T(t)-\widetilde{T}, \overline{e}(a,t)=e(a,t)-\widetilde{e}(a), \ \overline{r}(t,\theta )=r(t,\theta )-\widetilde{r}(\theta ),\) then removing the bar, we obtain the following linearized system:
with the following boundary conditions
Let
For (9), let \( S(t)=S^{0}e^{\lambda t},\ I(t)=I^{0}e^{\lambda t},\ T(t)=T^{0}e^{\lambda t}, \ e(t,a)=e^{0}(a)e^{\lambda t}, r(t,\theta )=r^{0}(\theta )e^{\lambda t}\), we have
with initial conditions
We obtain from the system (10) that
Combined with the third equation of system (10), and by simple calculation, we have
We obtain the characteristic equation of system (1) at an equilibrium \(\widetilde{E}\) as follows:
where
Next we will analyze the local stability of the equilibria. Rigorous proof of local stability require more thorough spectral analysis, which be referred to in Liu et al. (2017). Liu et al. (2017) formulated an age-structured model as an abstract non-densely defined Cauchy problem, and Lemma 3.4 in Liu et al. (2017) shows that point spectrum and spectrum are equal. Thus, the growth rate of solutions is given by the point spectrum, so we only need to study the eigenvalues of the characteristic equation of system (1).
Theorem 4
(Local stability) (i) The disease-free equilibrium \(E_{0}\) of system (1) is locally stable if \(\mathscr {R}_{0}<1 \) and is unstable if \(\mathscr {R}_{0}>1 \).
(ii) The endemic equilibrium \(E^{*}\) of system (1) is locally stable if it exists.
Proof
We first consider the local stability of the disease-free equilibrium \(E_{0}\). The characteristic equation corresponding to \(E_{0}\) is
Clearly, we have \(f(0)=\mathscr {R}_{0}\), \(f'(\lambda )<0\) and \(\lim \limits _{\lambda \rightarrow \infty } f(\lambda ) = 0\). Hence, if \(\mathscr {R}_{0}> 1\), then \(f(\lambda ) = 1\) has a unique positive real root. That is, if \(\mathscr {R}_{0}>1\), the disease-free equilibrium \(E_{0}\) is unstable.
If \(\mathscr {R}_{0}<1\), the disease-free equilibrium \(E_{0}\) is locally stable. Otherwise, \(f(\lambda _{0})=1\) has at least one root \(\lambda _{0}=a_{1}+ib_{1}\) satisfying \(a_{1}\ge 0.\) But
Hence, if \(\mathscr {R}_{0}<1\), all roots of \(f(\lambda ) = 1\) have negative real parts, then the disease-free equilibrium \(E_{0}\) is locally stable if \(\mathscr {R}_{0}<1\).
Next, we consider the local stability of the endemic equilibrium \(E^{*}\). The characteristic equation corresponding to \(E^{*}\) is
If \(\mathscr {R}_{0}>1\), the endemic equilibrium \(E^{*}\) is locally stable. Otherwise, \(f(\lambda ^{*})=1\) has at least one root \(\lambda ^{*}=a_{2}+ib_{2}\) satisfying \(a_{2}\ge 0.\) We notice that
and
Hence, if \(\mathscr {R}_{0}>1\), all roots of \(f(\lambda ) = 1\) have negative real parts, then the endemic equilibrium \(E^{*}\) is locally stable if \(\mathscr {R}_{0}> 1 \). This completes the proof. \(\square \)
4 Uniform persistence and global stability
4.1 Uniform persistence
In this subsection, our purpose is to show that system (1) is uniformly persistent when \(\mathscr {R}_{0}>1\). Define
let \(\partial M_{0}=\mathscr {Y}{\setminus } M_{0}\). Then, we have \(\mathscr {Y}=M_{0}\cup \partial M_{0}.\)
Theorem 5
The sets \(M_{0}\) and \(\partial M_{0}\) are forward invariant under the semiflow \(\Phi (t,\cdot )\). Also, the disease-free equilibrium \(E_{0}\) of system (1) is globally asymptotically stable for the semiflow \(\Phi (t,\cdot )\) restricted to \(\partial M_{0}\).
Proof
First we prove \(M_{0}\) is forward invariant under the semiflow \(\Phi (t,\cdot )\). Let \(\Phi (0,x_{0})\in M_{0}\), \(U(t)=I(t)+T(t)+\int _{0}^{+\infty }e(t,a)da+\int _{0}^{+\infty }r(t,\theta )d\theta ,\)
This implies the fact that \(\Phi (t,M_{0})\subset M_{0},\) i.e. \(M_{0}\) is forward invariant under the semiflow \(\Phi (t,\cdot )\).
Next, we will prove \(\partial M_{0}\) is forward invariant under the semiflow \(\Phi (t,\cdot )\). Let \(\Phi (0,x_{0})\in \partial M_{0},\) we consider the following system
Since \(S(t)\le \Delta _{1}\), where \(\Delta _{1}=max\{\dfrac{\Lambda }{\mu },\parallel x_{0}\parallel _{\mathscr {Y}}\}\), it follows that
where
By the formulation (6), we have
Substituting (15) into the first two equations of (14) yield
where
Since
due to \(\Phi (0,x_{0})\in \partial M_{0},\) then \(F(t)\equiv 0\) for \(t\ge 0\).
The system (16) can be written
Thus, (16) has a unique solution \( \hat{I}(t)\equiv 0,\hat{T}(t)\equiv 0\) for \( t\ge 0.\)
From (14), (15), we know that \(\hat{e}(t,s)=0, \hat{r}(t,s)=0\) for \( 0\le s\le t,\) thus,
Similarly, we have \(\parallel \hat{r}(t,\theta )\parallel _{L_{+}^{1}}=0.\)
By using (13) we can obtain that \(I(t)=0,\ T(t)=0, \parallel e(t,a)\parallel _{L_{+}^{1}}=0, \parallel r(t,\theta )\parallel _{L_{+}^{1}}=0\) for \( t\ge 0\). Thus, \(\partial M_{0}\) is forward invariant under the semiflow \(\Phi (t,\cdot )\).
Finally, we prove the disease-free equilibrium \(E_{0}\) of system (1) is globally asymptotically stable for the semiflow \(\Phi (t,\cdot )\) restricted to \(\partial M_{0}\). In \(\partial M_{0}\), system (1) can be written as follows
Obviously, \(\lim \limits _{t\rightarrow +\infty }S(t)=\frac{\Lambda }{\mu }.\) Hence, the equilibrium \(E_{0} \) is globally asymptotically stable restricted to \(\partial M_{0}\). The proof of Theorem 5 is complete. \(\square \)
Theorem 6
If \(\mathscr {R}_{0}>1,\) then semiflow \(\{\Phi (t,\cdot )\}_{t\ge 0}\) generated by system (1) is uniformly persistent with respect to the decomposition \((M_{0},\ \partial M_{0})\). Moreover, there is a compact subset \(\mathcal {A}_{0}\subset M_{0}\), which is a global attractor for \(\{\Phi (t,\cdot )\}_{t\ge 0}\) in \(M_{0}\).
Proof
Since the disease-free equilibrium \(E_{0}\) is globally asymptotically stable restricted to \(\partial M_{0}\), applying Theorem 4.2 in Hale and Waltman (1989), we only need to prove
where \(W_{s}(E_{0})=\{x\in \mathscr {Y}\ :\lim \limits _{t\rightarrow +\infty }\Phi (t,x)=E_{0}\}.\) By way of contradiction, we assume that there exists a \(x_{0}\in M_{0}\) such that \(x_{0}\in W_{s}(E_{0}).\) Then we can find a list of \(\{x_{n}\}\subset M_{0}\) such that
Denote \(\Phi (t,x_{n})=(S_{n}(t),I_{n}(t),T_{n}(t),e_{n}(t,\cdot ),r_{n}(t,\cdot )).\) Then for all \(t\ge 0\), we have
and \(\Phi (t,x_{n}) \subset M_{0}.\) From the system (1), we know that there exists \(t_{0}\ge 0\) such that \( I(t)>0\) for \(t\ge t_{0}\) or \( T(t)>0\) for \(t\ge t_{0}\), so without loss of generality, we can take \( t_{0}=0\) and \(I(0)>0\). Since \(\mathcal {R}_{0}>1,\) we can choose sufficiently large n such that \(\frac{\Lambda }{\mu }>\frac{1}{n}\) and
Now we construct the following system
Using similar analysis as in Sect. 2, we can get existence, uniqueness and nonnegative of solution to system (18). By the comparison principle, we know
By use of Volterra formulation (6), we have
Substituting (20) into the first two equations of (18) yield
We can claim that at least one of \(\hat{I}(t),\hat{T}(t)\) is unbounded. Otherwise, we can use Laplace transform in the first two inequations of (21) yield
where
After a simple calculation, we obtain
\( \mathcal {L}[u_{i}](\lambda )\rightarrow \mathcal {L}[u_{i}](0), (i=1,2,3,4), \mathcal {L}[\omega ](\lambda )\rightarrow \mathcal {L}[\omega ](0)\) as \(\lambda \rightarrow 0\) by the Dominated Convergence Theorem.
Since
then there exists \(\varepsilon >0\) such that
for all \( \lambda \in [0,\varepsilon )\). According to (23), we have \(\mathcal {L}[\hat{I}](\lambda )<0\) for all \( \lambda \in (0,\varepsilon )\). But this contradicts the nonnegative of \(\hat{I}(t)(t\ge 0)\). Hence, at least one of \(\hat{I}(t),\hat{T}(t)\) is unbounded. Since \(I(t)\ge \hat{I}(t),\ \ T(t)\ge \hat{T}(t)\), we get that at least one of I(t), T(t) is unbounded. This contradicts the Proposition 3. Therefore, \(W_{s}(E_{0})\cap M_{0}=\emptyset \). By Theorem 4.2 in Hale and Waltman (1989) , we get that semiflow \(\{\Phi (t,\cdot )\}_{t\ge 0}\) generated by system (1) is uniformly persistent. By Theorem 3.7 in Magal and Zhao (2005), we get that there exists a compact subset \(\mathcal {A}_{0}\subset M_{0}\) which is a global attractor for \(\{\Phi (t,\cdot )\}_{t\ge 0}\) in \(M_{0}\). \(\square \)
4.2 Global stablility
Theorem 7
The disease-free equilibrium \(E_{0}\) of system (1) is globally asymptotically stable if \(\mathcal {R}_{0}<1\).
Proof
Let \(g(x)=x-\ln x-1\), note that g(x) is non-negative and continuous in \((0,+\infty )\) with a unique root at \(x=1\). Using similar arguments to the proof of Lemma 4.2 in Browne and Pilyugin (2013), we can get that any solution in \(\mathcal {A}\) satisfies that \(S(t)>0\) for \(t\in \mathbb {R}\) (In Theorem 2, we have proved that \(\mathcal {A}\) exists). Next, we construct the following Lyapunov function \(L=L_{0}+L_{1}+L_{2}+L_{3}+L_{4}\) on the global attractor \(\mathcal {A}\), by the compactness of \(\mathcal {A}\), we can easily deduce L is bounded on \(\mathcal {A}\), where
Calculating the derivative of \(L_{0}\),\(L_{1}\), \(L_{2}\), \(L_{3}\), \(L_{4}\) along solutions of system (1), respectively. We can deduce
Therefore,
Notice that if \(\mathcal {R}_{0}<1\), then \(\frac{dL}{dt}\le 0\) holds. According to the proof of the Theorem 4.3 in Guo et al. (2019), we can easily obtain that \(\mathcal {A}=\{E_{0}\}\). This proves that \(E_{0}\) is globally asymptotically stable. The proof is complete. \(\square \)
If \(\mathcal {R}_{0}>1\), we have know that the system (1) is uniformly persistent and has a global attractor \(\mathcal {A}_{0}\) in \(M_{0}\). Let \(x \in \mathcal {A}_{0}\), we can find a complete orbit \(\{\Phi (t,\cdot )\}_{t\in \mathbb {R}}\) through x in \(\mathcal {A}_{0}\). By similar analytical method used in [ Browne and Pilyugin (2013), subsection 3.2], system (1) can be written as
In order to study the global stability of \(E^{*}\), we first prove the following lemma.
Lemma 3
There exist \(\epsilon , M>0\) such that all solutions in \(\mathcal {A}_{0}\) for \(t\in \mathbb {R}\), the following inequalities are satisfied
Proof
Let \((S(t), I(t), T(t), e(t,a), r(t,\theta ))\in \mathcal {A}_{0}\). First we prove that \(S(t)>0\) for \(t\in \mathbb {R}\). We assume that there exists \(t_{1}\in \mathbb {R}\) such that \(S(t_{1})=0\). From (24) we have \(\dfrac{dS(t_{1})}{dt}\ge \Lambda >0\), then \(\exists \ \eta _{1}>0\) such that \(S(t_{1}-\eta _{1})<0\). This contradicts the \(\mathcal {A}_{0} \subset M_{0}\). Thus \( S(t)>0\) for \(t\in \mathbb {R}\).
Next we prove that \(I(t)>0,\ T(t)>0\) for \(t\in \mathbb {R}\). First we assume that there exists \(t_{0}\in \mathbb {R}\) such that \(I(t_{0})=0\) and \(T(t_{0})=0\), then according to \(I(t),\ T(t)\) equations in (24), we can deduce that \(I(t)=0,\ T(t)=0\) for \(t\le t_{0}.\) Next, form (24) we know \(\int _{0}^{+\infty }e(t,a)da=0,\ \int _{0}^{+\infty }r(t,\theta )d\theta =0\) for all \(t\le t_{0}\). This contradicts the \(\mathcal {A}_{0} \subset M_{0}\).
On the other hand, we assume that there exists \(t_{0}\in \mathbb {R}\) such that one of \(I(t_{0}),\ T(t_{0})\) is positive, so without loss of generality we assume that \(I(t_{0})=0,\ T(t_{0})>0\). From (24) we have \(\dfrac{dI(t_{0})}{dt}\ge (1-\eta )\rho _{1} T(t_{0})>0\), then \(\exists \ \eta _{2}>0\) such that \(I(t_{0}-\eta _{2})<0\). This contradicts the \(\mathcal {A}_{0} \subset M_{0}\). Hence, \(I(t)>0,\ T(t)>0 \) for all \(t\in \mathbb {R}\). In addition, from (24), we deduce that \(e(t,a)>0, r(t, \theta )>0\) for \(t\in \mathbb {R}, a,\theta \in \mathbb {R}_{+}\).
According to the compactness of \(\mathcal {A}_{0}\), we know there exist \(\epsilon , M>0\) such that
The proof is complete. \(\square \)
Theorem 8
If \(\mathcal {R}_{0}>1\), then endemic equilibrium \(E^{*}\) of system (1) is globally asymptotically stable in \(M_{0}\).
Proof
We define the following Lyapunov function \(V=V_{1}+V_{2}+V_{3}+V_{4}+V_{5}\) on the global attractor \(\mathcal {A}_{0}\) (In Theorem 6, we have proved that \(\mathcal {A}_{0}\) exists), using Lemma 3, we can easily deduce V is bounded on \(\mathcal {A}_{0}\), where
and
Calculating the derivative of V along a solution in \(\mathcal {A}_{0}\) . When calculate the time derivative of \(V_{1}\), we notice that \(\Lambda =\beta S^{*}(I^{*}+\rho T^{*})+\mu S^{*}\).
By using
we have
When calculate the time derivative of \(V_{3}\), we notice that
Notice that \(\mu +\mu _{T}+\alpha +\rho _{1}=\dfrac{I^{*}}{T^{*}}\gamma \), we can get
By using
we have
Thus, \( \dfrac{d\sum \limits _{i=1}^{5}V_{i}}{dt} =H_{1}+H_{2}+H_{3}+H_{4}+H_{5}+H_{6}+H_{7},\)
where
It follows from the non-negativity of g, we know that \(\dfrac{dV}{dt}\le 0\), and according to the proof of the Theorem 4.3 in Guo et al. (2019), we can easily obtain that \(\mathcal {A}_{0}=\{E^{*}\}\). This proves that \(E^{*}\) is globally asymptotically stable. The proof is complete. \(\square \)
5 Study on TB control strategy in China
5.1 Data fitting
In this section, we firstly use the system (1) to simulate the annual new TB cases data of China from 2007 to 2018, then we predict whether current tuberculosis control measures in China will be able to achieve the WHO End TB Strategy in 2030. To do so, we need to estimate the parameters of system (1). Some of the parameters in our model are distributed, which is different from ODE models, and we believe that the parameter values may be different due to different research groups and different time units. According to the WHO (2019) report in 2018, the TB incidence rate is falling, and the treatment success rate is also falling. Through the analysis of these data, it can be found that the parameter values in system (1) are related to the time of the study. Thus, some of parameters are fitted. According to the data from the National Bureau of Statistics of China (2019), the average birth population and the average natural mortality rate between 2007 and 2018 are \(\Lambda =16{,}439{,}333 \, \text {persons year}^{-1}\) and \(\mu =1/74.83 \, \text {yea}r^{-1}\), respectively, and the number of the initial susceptible population \(S(0)=1{,}314{,}480{,}000\, \text {person} \). The number of new TB cases (Table 2) come from the Chinacdc (2019).
Next, we estimate the unknown parameters and initial values
of system (1), where we assume \(\delta (a)=\delta _{1}e^{-\delta _{2} a}\), \(\sigma (a)=\sigma _{1}e^{-\sigma _{2} a}\), \(\omega (a)=\omega _{1}e^{-\omega _{2} a}\), \(e_{0}(a)=e(0)\delta _{2}e^{-\delta _{2} a}\), \(r_{0}(\theta )=r(0)\omega _{2}e^{-\omega _{2} \theta }\).
Let \(P(t,\hat{\theta })\) be the number of new TB cases from model (1) at the \(t^{th}\) year, then \(P(t,\hat{\theta })\) can be written as
where X(t) represents the cumulative number of people infected with TB by the \(t^{th}\) year, and satisfies the following equation
Thus, we use \(P(t,\hat{\theta })\) to simulate the new TB cases per year. We are attracted by the advantages of algorithms mentioned in Seyedali Mirjalili (2014) when reading it, and we find that the convergence was good and the error was small after combining with the model (1) (the mean absolute percentage error of TB cases is 0.75%). By Grey Wolf Optimizer (GWO) algorithm, we estimate the optimal parameters and initial values for model (1) (Table 3).
The comparison between the new TB cases in China from 2007 to 2018 and the simulation of \(P(t,\hat{\theta })\) from model (1) is given in Fig. 2. Moreover, we also find the basic reproduction numbers \(\mathcal {R}_{0}=1.0608.\)
Fitting for the annual new TB cases in China for model (1)
Remark 1
By comparison with Moualeu et al. (2015), it can be found that the transmission rate of the Moualeu et al. (2015) is \(\beta _{3}=6.33563\times 10^{-6}\), while that of this paper is \(\beta =1.1479\times 10^{-10}\). Analysis shows that the Moualeu et al. (2015) studies the transmission of TB in Cameroon from 1994 to 2010, and the new cases of TB in Cameroon increased rapidly during this period. In this paper, we used new TB cases in China from 2007 to 2018, during which the number of new TB cases in China decreased gradually. Therefore, the transmission rate of this paper is much lower than that of Moualeu et al. (2015). This is also why some parameters in this paper need to be estimated. Parameter estimation is very important for studying the transmission of TB. Arregui et al. (2018) and Dowdy et al. (2013) also provide some methods to analyze the parameters in tuberculosis models.
Remark 2
The GWO algorithm mimics the leadership hierarchy and hunting mechanism of grey wolves in nature. Four types of grey wolves such as alpha, beta, delta, and omega are employed for simulating the leadership hierarchy. In addition, the three main steps of hunting, searching for prey, encircling prey, and attacking prey, are implemented. Twenty nine test functions were employed in order to benchmark the performance of the proposed algorithm in terms of exploration, exploitation, local optima avoidance, and convergence. The goal of this paper is to minimize the target function
where r(t) represents the actual number of new TB cases at the \(t^{th}\) year.
5.2 Uncertainty and sensitivity analysis of \(\mathcal {R}_{0}\)
The outputs of system (1) is governed by the system input parameters and the initial values, but some of these parameters and initial values are obtained by data fitting, which may exhibit some uncertainty in their selection. The purpose of uncertainty analysis (UA) (Samsuzzoha et al. 2013; Ghosh et al. 2018; Marino et al. 2008) is to determine the reliability of parameter estimates. To ensure the reliability of the estimates of \(\beta ,\rho _{1},\gamma ,\mu _{I},\mu _{t},\alpha ,\rho ,\eta \) obtained through the GWO, we employ Markov Chain Monte Carlo (MCMC) method with Delayed Rejection and Adaptive Metropolis (DRAM) algorithm (DRAM is an algorithm combining DR and AM in MCMC method, and the efficiency of the combination is demonstrated with various examples in Haario et al. (2006)). The convergence of the chain is confirmed by using the Geweke’s Z-scores (According to the MCMC program (MCMC 2019), the closer the Geweke’s Z-score is to 1, the better the convergence of Markov Chain) . The mean, standard deviation and 95\(\%\) confidence interval of the estimated parameters are shown in Table 4, and the fitting result can be seen in Fig. 3.
Sensitivity analysis (SA) is to identify critical parameters that have significant impact on the basic reproduction numbers \(\mathcal {R}_{0}\) and to quantify how parameters uncertainty impact \(\mathcal {R}_{0}\). Now, a global sensitivity analysis is usually implemented by using sampling-based methods. We will use partial rank correlation coefficient (PRCC) method to study SA. For the parameters in Table 3, we fix \( \sigma _{1}, \sigma _{2}, \delta _{1}, \delta _{2}, \omega _{1}, \omega _{2}, e(0), I(0), T(0), r(0), \) other parameters are considered to obey normal distribution, their mean and standard deviation are shown in Table 4. The sampling method is Latin hypercube sampling(LHS). We draw 1000 samples and obtain distribution histogram of the basic reproduction number \(\mathcal {R}_{0}\) (see Fig. 4). From Fig. 4, we know that the distribution of the basic reproduction number in the range [0.6838, 1.5672], and the average is 1.0660. Combined with the analysis in Sect. 4, we can conclude that under current control measures, the possibility of extinction of TB is small. We calculate the PRCC between the parameters and the basic reproduction number \(\mathcal {R}_{0}\) (see Fig. 5).
From the PRCC values, we can know that \(\beta ,\ \mu _{t},\ \rho \) have the most important impact on \(\mathcal {R}_{0}\), \(\beta \) represents the transmission rate coefficient of TB, and \(\beta \) is in direct proportion to bc, b represents the number of times an infected person has contact with other person per unit time, c represents the probability of infection per contact. \(\rho \) represents reduce the rate of transmission due to treatment. \(\mu _{t}\) represents the death rate due to treatment.
The major software packages we used for our analysis were GWO, LHS, PRCC and MCMC, all of which can be found on the websites GWO (2019), LHS (2019), MCMC (2019).
Remark 3
We explain the specific steps of the LHS-PRCC scheme by studying the relationship between parameters parameters \(x_{1}, x_{2}, x_{3}\) and output \(y=f(x_{1},x_{2},x_{3})\).
Step 1 Take uniform distribution as an example, the parameter distributions are divided into N equal probability intervals, which are then sampled. N represents the sample size (see Fig. 6).
Step 2 We set up the LHS matrix by assembling the samples from each probability density functions. Each row of the LHS matrix represents a unique combination of parameter values sampled.
Step 3 Next, X and Y are rank transformed to \(X_{R}\) and \(Y_{R}\) in order from small to large.
Step 4 We calculate the residuals \(X_{1}=X_{R1}-\hat{X}_{R1}\) and \(Y_{1}=Y_{R}-\hat{Y}_{R}\), where \(\hat{X}_{R1}\) and \(\hat{Y}_{R}\) are the following linear regression models:
Then
is the PRCC between \(x_{1}\) and y. In the same way, we can calculate the PRCC between \(x_{2}\) and y, and the PRCC between \(x_{1}\) and y.
5.3 Feasible measures of reaching WHO End TB strategy
Over the past few decades, China has made great efforts to control the spread of TB, such as vaccination of newborns with BCG and active treatment of tuberculosis patients and so on. However, based on the above theoretical analysis and numerical simulation results, by using the current TB control measures, China may not reach the WHO’s goal by 2030. To do so, China should give more feasible control measures. In the above analysis, we know that \(\beta ,\ \mu _{t},\ \rho \) are the most important factors for TB control. Next, we adjust \(\beta ,\ \rho \) to predict whether an optimal control measure can be given to achieve the WHO’s goal by 2030.
We use the parameter values in Table 2 as the baseline to compare the following control effects. First, we only consider changing the value of parameter \(\beta \) (see Fig. 7), we can find that the value of \(\beta \) needs to be reduced by 90% to reach the WHO 2030 target. Next, we only consider changing the value of parameter \(\rho \) (see Fig. 8), we can find the value of \(\rho \) needs to be reduced by 95% to reach the WHO 2030 target. Finally, we consider changing both parameter \(\beta \) and parameter \(\rho \) (see Fig. 9), we can find that if we can reduce parameter \(\beta \) by 70%, and reduce parameter \(\rho \) by 70%, then we will reach the WHO 2030 target. Parameters \(\beta \) and \(\rho \) represent the TB transmission coefficient and the reduction of infectiousness of treated individuals infected with TB, respectively. Some researchers mentioned that media coverage and public education campaigns can reduce the transmission coefficient \(\beta \) of disease (Barbara et al. 2020). Barbara et al. (2020) suggests that the following measure can accelerate progress toward TB elimination: maintaining awareness of both the incidence of TB disease for the public through news releases and posting of information online. Take the COVID-19 pandemic as an example, media coverage and public education campaigns play very important role in the process of controlling the pandemic. People know more about the COVID-19 and enhance their self-protecting awareness by the media report about the COVID-19, and will change their behaviours and take correct precautions such as frequent hand-washing, wearing masks, reducing the party, keeping social distances, and even quarantining themselves at home to avoid contacting with others (CDC 2021). Therefore, if the media strengthen the publicity of tuberculosis and COVID-19, it will certainly have a good effect (Saunders and Evans 2020; The Lancet Infectious Diseases 2021). Reducing the contact between treated patients and susceptible individuals can reduce the parameter \(\rho \).
Currently, the treatment of TB patients in China includes hospitalization and home treatment, and they are not forced to be hospitalized, so these people may still infect susceptible individuals. Based on the above analysis, China should strengthen the publicity of tuberculosis knowledge so that susceptible people can know how to avoid being infected. Also, patients who are treated with TB should be given longer hospital stays to reduce their chances of contact with susceptible people. By using these control measures, China may reach the WHO End TB Strategy in 2030.
6 Discussion
In this study, we used an age-structured mathematical model with treatment and relapse to study the transmission dynamics of TB. Sufficient conditions were derived for the global asymptotic stability of TB-free equilibrium and the endemic equilibrium. We estimated model parameters by fitting the annual new TB cases data of China, and concluded that, by using current tuberculosis control measures, China may not reach the WHO’s goal by 2030. In order to achieve the WHO’s goal, China needs to develop more practical control measures. PRCC values of the basic reproduction number, \(\mathcal {R}_{0}\), with respect to some important model parameters demonstrate that the control measures for the spread of TB include reduction of the TB transmission coefficient \(\beta \) and reduction of the TB transmission coefficient \(\beta \rho \) of treated individuals infected with TB. These can be achieved through media coverage, public education campaigns and increased hospital stays for TB patients.
TB is prevalent in many countries including China (Creswell et al. 2014). The transmission mechanism of TB in different countries is the same, so the TB model in this paper can be used in the research of TB in other countries, and some feasible measures to control the transmission of TB can also be put forward by using local data of TB and some population data such as birth rate and death rate.
References
Agusto FB, Adekunle AI (2014) Optimal control of a two-strain tuberculosis-HIV/AIDS co-infection model. Biosystems 119:20–44
Agusto FB, Khan MA (2018) Optimal control strategies for dengue transmission in Pakistan. Math Biosci 305:102–121
Arregui S, Iglesias MJ, Samper S, Marinova D, Martin C, Sanz J, Moreno Y (2018) Data-driven model for the assessment of mycobacterium tuberculosis transmission in evolving demographic structures. Proc Natl Acad Sci USA 115(14):E3238–E3245
Bao X, Li WT (2020) Propagation phenomena for partially degenerate nonlocal dispersal models in time and space periodic habitats. Nonlinear Anal Real World Appl. https://doi.org/10.1016/j.nonrwa.2019.102975
Bao X, Li WT, Wang ZC (2020) Uniqueness and stability of time-periodic pyramidal fronts for a periodic competition-diffusion system. Commun Pure Appl Anal 19:253–277
Barbara C, Diana MN, Lorna W et al (2020) Essential components of a public health tuberculosis prevention, control, and elimination program: recommendations of the advisory council for the elimination of tuberculosis and the national tuberculosis controllers association. MMWR Recomm Rep 69(7):1–27
Browne CJ, Pilyugin SS (2013) Global analysis of age-structured within-host virus model. Discret Contin Dyn Syst B 18(8):1999–2017
Burman WJ, Bliven EE, Cowan L, Bozeman L, Nahid P, Diem L, Vernon A (2009) Relapse associated with active disease caused by Beijing strain of mycobacterium tuberculosis. Emerg Infect Dis 15(7):1061–7
Cai YL, Jiao J, Gui Z, Liu Y, Wang WM (2018) Environmental variability in a stochastic epidemic model. Appl Math Comput 329:210–226
CDC (2019) https://www.cdc.gov/tb/
CDC (2021) https://www.cdc.gov/coronavirus/2019-ncov
Chinacdc (2019) http://www.chinacdc.cn/
Choi S, Jung E, Lee SM (2015) Optimal intervention strategy for prevention tuberculosis using a smoking-tuberculosis model. J Theor Biol 380(2):256–270
Creswell J, Sahu S, Sachdeva KS, Ditiu L, Barreira D, Mariandyshev A, Mingting C, Pillay Y (2014) Tuberculosis in BRICS: challenges and opportunities for leadership within the post-2015 agenda. Bull World Health Organ 92(6):459–460
D’Agata EMC, Magal P, Ruan S, Webb G (2006) Asymptotic behavior in nosocomial epidemic models with antibiotic resistance. Differ Integr Equ 19(5):573–600
Dowdy DW, Dye C, Cohen T (2013) Data needs for evidence-based decisions: a tuberculosis modeler’s “wish list.”. Int J Tuberc Lung Dis 17(7):866–877
Du Z, Feng Z (2018) Existence and asymptotic behaviors of traveling waves of a modified vector-disease model. Commun Pure Appl Anal 17:1899–1920
Ghosh I, Tiwari PK, Samanta S, Elmojtaba IM, Al-Salti N, Chattopadhyay J (2018) A simple SI-type model for HIV/AIDS with media and self-imposed psychological fear. Math Biosci 306:160–169
Guo ZK, Huo HF, Xiang H (2019) Global dynamics of an age-structured malaria model with prevention. Math Biosci Eng 16:1625–1653
GWO (2019) http://www.alimirjalili.com/GWO.html
Haario H, Laine M, Mira A, Saksman E (2006) Dram: efficient adaptive MCMC. Stat Comput 16:339–354
Hale JK, Waltman P (1989) Persistence in infinite-dimensional systems. SIAM J Math Anal 20(2):388–395
Huang S (2020) Quasilinear elliptic equations with exponential nonlinearity and measure data. Math Method Appl Sci. https://doi.org/10.1002/mma.6088
Huang S, Tian Q (2019) Marcinkiewicz estimates for solution to fractional elliptic Laplacian equation. Comput Math Appl 78:1732–1738
Huo HF, Jing SL, Wang XY, Xiang H (2019a) Modelling and analysis of an alcoholism model with treatment and effect of twitter. Math Biosci Eng 16(5):3595–3622
Huo HF, Yang P, Xiang H (2019b) Dynamics for an SIRS epidemic model with infection age and relapse on a scale-free network. J Frankl Inst 356:7411–7443
Huo HF, Yang Q, Xiang H (2020) Dynamics of an edge-based SEIR model for sexually transmitted diseases. Math Biosci Eng 17(1):669–699
Iannelli M (1994) Mathematical theory of age-structured population dynamics. Giadini Editori e Stampatori, Pisa
Iannelli M, Milner F (2017) The Basic Approach to Age-Structured Population dynamics. Springer, Dordrecht
Jing SL, Huo HF, Xiang H (2020) Modeling the effects of meteorological factors and unreported cases on seasonal influenza out breaks in Gansu province, China. Bull Math Biol 82:73
Li X, Huang S (2019) Stability and bifurcation for a single-species model with delay weak kernel and constant rate harvesting. Complexity 2019:17
Liu J, Zhang T (2011) Global stability for a tuberculosis model. Math Comput Model 54(1):836–845
Liu Z, Magal P, Ruan S (2017) Oscillations in age-structured models of consumer-resource mutualisms. Discret Contin Dyn Syst B 21(2):537–555
Liu Z, Magal P, Seydi O, Webb G (2020) Predicting the cumulative number of cases for the COVID-19 epidemic in China from early data. Math Biosci Eng 17(4):3040–3051
Ma ZP (2019) Spatiotemporal dynamics of a diffusive Leslie–Gower prey–predator model with strong Alee effect. Nonlinear Anal Real World Appl 50:651–674
Magal P, Zhao XQ (2005) Global attractors and steady states for uniformly persistent dynamical systems. SIAM J Math Anal 37(1):251–275
Marino S, Hogue IB, Ray CJ, Kirschner DE (2008) A methodology for performing global uncertainty and sensitivity analysis in systems biology. J Theor Biol 254(1):178–196
MCMC (2019) https://mjlaine.github.io/mcmcstat/index.html
Meng XY, Wu YQ (2018) Bifurcation and control in a singular phytoplankton-zooplankton-fish model with nonlinear fish harvesting and taxation. Int J Bifurc Chaos 28(3):24
Meng XY, Qin NN, Huo HF (2018) Dynamics analysis of a predator–prey system with harvesting prey and disease in prey species. J Biol Dyn 12(1):342–374
Moualeu DP, Rblitz S, Ehrig R, Deuflhard P (2015) Parameter identification for a tuberculosis model in Cameroon. PloS One 10(4):e0120607
National Bureau of Statistics of China (2019) http://www.stats.gov.cn/
Ngeleja RC, Luboobi LS, Nkansah-Gyekye Y (2018) Plague disease model with weather seasonality. Math Biosci 302:80–99
Ozcaglar C, Shabbeer A, Vandenberg SL, Yener B, Bennett KP (2012) Epidemiological models of mycobacterium tuberculosis complex infections. Math Biosci 236(2):77–96
Rebaza J (2019) Global stability of a multipatch disease epidemics model. Chaos Solitons Fractals 120:56–61
Ren S (2017) Global stability in a tuberculosis model of imperfect treatment with age-dependent latency and relapse. Math Biosci Eng 14(5/6):1337–1360
Samsuzzoha M, Singh M, Lucy D (2013) Uncertainty and sensitivity analysis of the basic reproduction number of a vaccinated epidemic model of influenza. Appl Math Model 37(3):903–915
Saunders MJ, Evans CA (2020) Covid-19, tuberculosis and poverty: preventing a perfect storm. Eur Respir J. https://doi.org/10.1183/13993003.01348-2020
Seyedali Mirjalili AL, Mohammad Mirjalili Seyed (2014) Grey wolf optimizer. Adv Eng Softw 69:46–61
Shi Q, Wang S (2019) Klein–Gordon–Zakharov system in energy space: blow-up profile and subsonic limit. Math Methods Appl Sci 42:3211–3221
Smith HL, Thieme HR (2011) Dynamical systems and population persistence. American Mathematical Society, Providence
The Lancet Infectious Diseases (2021) Tuberculosis and malaria in the age of covid-19. Lancet Infect Dis 21(1):1
Ullah S, Khan MA, Farooq M, Gul T (2019) Modeling and analysis of Tuberculosis (TB) in Khyber Pakhtunkhwa, Pakistan. Math Comput Simul 165:181–199
Wang X, Shen M, Xiao Y, Rong L (2019) Optimal control and cost-effectiveness analysis of a Zika virus infection model with comprehensive interventions. Appl Math Comput 359:165–185
Webb G (1985) Theory of nonlinear age-dependent population dynamics. Marcel Dekker, New York, NY
Whang S, Choi S, Jung E (2011) A dynamic model for tuberculosis transmission and optimal treatment strategies in South Korea. J Theor Biol 279(1):120–131
WHO (2019) Global tuberculosis report 2018. https://www.who.int/tb/en/
Xiang H, Zou MX, Huo HF (2019) Modeling the effects of health education and early therapy on tuberculosis transmission dynamics. Int J Nonlinear Sci Numer Simul 20:243–255
Zhang L, Xing YF (2019) Extremal solutions for nonlinear first-order impulsive integro-differential dynamic equations. Math Notes 105:124–132
Zhang XB, Shi QH, Ma SH, Huo HF, Li DG (2018) Dynamic behavior of a stochastic SIQS epidemic model with Levy jumps. Nonlinear Dyn 93:1481–1493
Zhang XB, Chang SQ, Huo HF (2019a) Dynamic behavior of a stochastic SIR epidemic model with vertical transmission. Electron J Differ Equ 125:1–20
Zhang YD, Huo HF, Xiang H (2019b) Dynamics of tuberculosis with fast and slow progression and media coverage. Math Biosci Eng 16(3):1150–1170
Zhao Y, Li M, Yuan S (2017) Analysis of transmission and control of tuberculosis in Mainland China, 2005–2016, based on the age-structure mathematical model. Int J Environ Res Public Health 14(10):1192
Zhao L, Zhang L, Huo HF (2019) Traveling wave solutions of a diffusive SEIR epidemic model with nonlinear incidence rate. Taiwan J Math 23(4):951–980
Acknowledgements
This work is supported by the National Natural Science Foundation of China (NSFC, 11861044 and 11661050), the HongLiu first-class disciplines Development Program of Lanzhou University of Technology, the Youth Science Fund of Lanzhou Jiaotong University (1200060930), and the Scientific Research Foundation of Lanzhou Jiaotong University (1520020410)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Guo, ZK., Xiang, H. & Huo, HF. Analysis of an age-structured tuberculosis model with treatment and relapse. J. Math. Biol. 82, 45 (2021). https://doi.org/10.1007/s00285-021-01595-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00285-021-01595-1