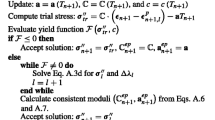A Nonlinear Solver with Phase Boundary Detection for Compositional Reservoir Simulation

Abstract

Compositional simulation is typically used to study subsurface displacement processes that involve complex physics. Such processes are highly nonlinear and they occur at the interplay of phase thermodynamics (phase stability and split) and rock/fluid interaction (relative permeability). To better characterize the convergence failures of compositional nonlinear solvers, we study the analytical and discrete forms of the component flux functions for the transport problem. We focus on isothermal, two-hydrocarbon phase models in the presence of viscous forces. Our analysis shows that the component flux function exhibits both kinks and inflection points, as described in the literature. We study the kinks due to the crossing of phase boundaries and we show their impact on residual terms. We, then, investigate the location, direction, and evolution of the inflection loci inside the two-phase region. Our findings suggest that these inflection loci may exhibit complex features, as a result of which an a priori determination of such loci is computationally prohibitive. We propose a nonlinear solver that detects phase boundaries and guides the Newton update to avoid crossing these boundaries. Our numerical results show that this phase change detection solver has superior performance in comparison with standard Newton solvers for a wide range of cases.

Article Highlights

• We study the nonlinearities of compositional flow and transport.

• Our analysis of the component flux function shows that it exhibits both kinks and inflection loci that have significant impact on the nonlinear convergence of the Newton solver.

• A new nonlinear solver that detects phase boundaries and adjusts the Newton update was developed. This led to considerable improvement of the nonlinear solution process.

1 Introduction

Compositional simulation deals with the modeling of flow of hydrocarbon phases in porous medium. Depending on the pressure, temperature and fluid composition, a complex set of interactions takes place between the flowing phases. Lighter components from the liquid phase vaporize into the gas phase, while heavier components from the gas phase condense into the liquid phase (Orr 2007). If miscibility is achieved, the interface separating the two phases disappears leading to a single hydrocarbon phase flow. The interactions between the hydrocarbon phases take place at the interplay of phase behavior, flow, and transport. In mathematical terms, these interactions are represented as a complex nonlinear system of equations. This system is, commonly, discretized and solved using the finite volume method. Both explicit and implicit treatments of the time discretization are used (Aziz and Settari 1979). An explicit discretization limits the maximum allowed time step size as defined by the Courant–Friedrichs–Lewy (CFL) constraint. This has made the implicit formulation very popular for reservoir simulation, since the implicit formulation is unconditionally stable.

As discussed in the literature, for an isothermal compositional model consisting of $n_c$ components and two hydrocarbon phases, $2n_c+4$ equations can be formulated (Aziz and Settari 1979). The unknowns consist of primary and secondary variables. The primary variables represent the set of independent variables that are solved simultaneously for a fully implicit method (FIM). Secondary variables can be calculated explicitly as a function of the primary variables. Equations for conservation of mass are usually used as primary equations; this is mainly due to the tight coupling of flow and transport and the exchange of mass among different grid cells. The remaining equations (thermodynamic relations, saturation/composition constraints, and capillary pressure relations) are local in nature, where each equation is limited to a single grid cell. These equations are usually used as secondary equations. While the choice of primary equations is straightforward, the choice of the primary variables is not, giving rise to different formulations in the literature (Cao 2002). There are two main classes of formulations in the literature: (1) molar variables formulation (Acs et al. 1985), and (2) natural variables formulation (Coats 1980). Since saturations are primary variables for natural variables formulation, a major consideration appears when an existing phase disappears or a new one appears in a grid cell during a Newton iteration. In this case, a variable substitution procedure is required leading to different primary variables in different grid cells, which complicates the implementation of this formulation. Stability and flash calculations are also required during each Newton iteration for the molar formulation (Cao 2002). These two formulations have been extensively studied and compared in the literature (Voskov and Tchelepi 2012; Alpak and Vink 2018).

The system of mass balance equations is solved using an iterative Newton process. The solution path starts from an initial guess and converges through an iterative scheme. Despite its quadratic rate of convergence, standard Newton solver can suffer from convergence issues due to poor initial guess or large time step size (Jiang and Wen 2020), and many strategies have been proposed to improve its nonlinear convergence. Alternative approaches have focused on improving the nonlinearities of the underlying equations by proposing better relative permeability models (Khebzegga et al. 2020; Alzayer et al. 2017; Yuan and Pope 2012; Neshat and Pope 2017; Khorsandi et al. 2017). These models are compositionally consistent and depend on temperature, pressure, and composition.

Various authors have proposed techniques that take advantage of the underlying physics of the flow and transport in porous media to guide the nonlinear solver. Younis et al. (2010) developed a Newton solver that can converge for any time step size using a continuation-based approach. A reordering of the equations to reduce the nonlinear system was also introduced (Kwok and Tchelepi 2007; Natvig and Lie 2008; Lie 2014). Lastly, trust region solvers were introduced for black-oil models (Wang and Tchelepi 2013; Li and Tchelepi 2015), and they were extended to compositional simulation (Voskov and Tchelepi 2011). Recently, Møyner (2017) developed a trust region solver for three-phase system that can handle non-smooth flux functions. This model was further developed using an adaptive approach to detect oscillations in the Newton update (Klemetsdal et al. 2019). Mansour and Voskov (2020) developed a trust region solver for compositional simulation using the operator-based-linearization (OBL) framework. They showed improvement in nonlinear performance for single grid cell models. Jiang and Wen (2020) developed a smooth formulation for compositional simulation. Their work focused on smoothening the transition between the single and two-phase regions. Removing discontinuities introduced by phase jump led to improvements in nonlinear performance. It also introduced additional smoothening to saturation and composition fronts.

The residual of the mass balance equation is composed of three terms: the accumulation term, the flux term, and the source/sink term. For black-oil models, the shape of the phase flux term dictates most of the nonlinear behavior of the transport problem. If the source/sink term is ignored, Jenny et al. (2009) showed that the Newton solver may fail to converge when it oscillates around the inflection point of the phase flux term. For black-oil simulations, this flux term plays a key role in the mass balance equation because the accumulation term is a linear function of saturation and its second-order derivative is null. However, for compositional simulation, the second-order derivatives of the accumulation term exist in the general case. These derivatives vanish only if the compositional path is along a tie-line. Nevertheless, the nonlinearities related to component flux functions play a central role in the convergence of the Newton solver.

The nonlinear system of compositional equations is solved using two families of implicit methods: (1) the fully implicit method (FIM), and (2) the sequential implicit method (SI) (Cao 2002). The fully implicit method solves the flow and transport equations together, whereas the sequential implicit method separates the elliptic (flow) subsystem from the hyperbolic (transport) subsystem and solves them sequentially. This separation allows for better implementation of advanced strategies to improve the nonlinear convergence of the transport problem. In this work, we use the implementation of the sequential molar formulation developed by Møyner (2017). The primary variables for the transport problem are the overall compositions z and the total saturation $S_{\mathrm{t}}$. $S_{\mathrm{t}}$ plays the role of a volume balance error resulting from the solution of the flow equation. The compositional model is described in “Appendix 1.”

In this paper, we study the continuous and discrete forms of the component flux function for compositional models. We show the shapes and locations of inflection loci and their impact on the residual terms. We look into the impact of the phase change discontinuities on the convergence of the Newton solver and we design a nonlinear solver that avoids such discontinuities. In Sect. 2, we discuss the nonlinearities that lead to the failure of the nonlinear solver. In Sect. 3, we study the analytical and discrete forms of flux function, and we present a new phase change detection solver in Sect. 4. The results for the new nonlinear solver will be presented in Sect. 5. Finally, Sect. 6 will contain the conclusions of this research.

2 Component Flux Function

The mass balance equation expressed in terms of total velocity is given in Eq. 6.6. In this equation, the expression $h_c= x_c \rho _{\mathrm{o}} f_{\mathrm{o}} + y_c \rho _{\mathrm{g}} f_{\mathrm{g}}$ is the total flux (molar or mass) of component c by a unit of volume. This flux function defines most of the nonlinear behavior of the mass balance equation. Two major characteristics of the flux term lead to nonlinear convergence difficulties for the Newton solver:

• Appearance of kinks Kinks appear when the first-order derivatives of a function are discontinuous. They correspond to an abrupt change to the flux function curvature and they are a major cause of Newton oscillations. This happens for multiple reasons. The most important one is the crossing of phase boundaries (Voskov and Tchelepi 2011; Abadpour and Panfilov 2009). Phase boundaries are the bubble and dew curves, and crossing of these boundaries happens when a composition that was initially single-phase becomes two-phase or vice versa. Kinks also appear when the flow direction changes due to gravitational or capillary forces. Oil and gas phases that were initially flowing in the same direction (co-current), switch to flowing on opposite directions (counter-current), or vice versa (Li and Tchelepi 2015). Lastly, kinks can be caused by the non-smoothness of the relative permeability model, which is the case for tabulated relative permeability values.

• Existence of inflection locus A single variable function f(x) has an inflection point at a coordinate $x^*$ if the second-order derivative of f, $f^{\prime \prime }$, changes sign at $x^*$. The function f is S-shaped in the vicinity of the point $x^*$, and the first-order derivative $f^\prime$ has a local optimum at $x^*$. Figure 1 shows a simple S-shaped function and its first- and second-order derivatives. The inflection point is the red cross in the center. It has been shown that Newton solver may fail to converge if the residual is S-shaped and the initial guess is far from the solution (Ortega and Rheinboldt 1970). The general form of the inflection point in the case of a two-variable function can be represented by an inflection line (locus). This line can be straight or curved depending on the underlying physics. Furthermore, the inflection points become direction-dependent if the function depends on two or more variables.

Fig. 1

S-shaped function and its first- and second-order derivatives. The inflection locus is located at $x^*=0.5$ (red cross)

Fig. 2

Single cell setup. Boundary conditions are fixed (fixed total velocity ${\mathbf {u}}_{\mathrm{T}}$) and the flow is from left to right. $F_{c_iL}$ is a fixed total flux and $p_R$ is a fixed pressure

It is important to recall that the Newton solver does not operate directly on the flux term; instead, it minimizes the residual term. While the component flux term contributes to the residual equation (Eq. 6.1), there is also the accumulation term that may impact the shape and magnitude of the residual function. So, we need to clarify how the discontinuities and inflections we observed on the flux term translate into the residual term. For this purpose, we use the single cell setup of Fig. 2. The flux is from left to right, we inject pure $\hbox {C}_{2}$ at reservoir conditions of $p=30$ bar and $T=350$ K into pure $\hbox {nC}_{10}$. The properties of all the hydrocarbon components used in this work are presented in “Appendix 2.” The relative permeabilities are $k_{\mathrm{ro}}=S_{\mathrm{o}}^2$ and $k_{\mathrm{rg}}= (1-S_{\mathrm{o}})^2$. To be more realistic, we used a ratio of 20 between the oil and gas densities and viscosities. The transition from the initial to the injection composition happens along a single tie-line. The residual terms as well as their first-order derivatives for both $\hbox {C}_{2}$ and $\hbox {nC}_{10}$ are plotted versus the component fraction of $\hbox {C}_{2}$ represented by $z_1$ (Fig. 3). Different time steps were used, they are expressed in terms of total throughput $c=\Delta t/\Delta x$, with t in days and x in meters. To express the residuals in terms of molar errors, we multiply the residuals by $\Delta t/(M \cdot \hbox {PV})$, where $\Delta t$ is the time step size, M is the component molar mass, and PV represents the pore volume.

First, we observe that the first derivative of the residual is discontinuous at the boundary between the oil phase and the two-phase region. Another discontinuity exists at the interface between the two-phase region and the gas phase region at $z_1=0.99$. The second-order derivatives do not exist at these phase transitions. The magnitude of the discontinuity for the first-order derivative increases with c, this is expected since $\Delta t$ is a multiplier of the flux terms in the residual equation. The kinks of the flux term have translated into kinks of the residual term.

Second, as c increases, the magnitude of the first-order derivative increases especially at the inflection locus which, in this case, is close to the phase change interface at around $z_1=0.31$. The inflection locus is shifted toward the phase change interface because of the ratio between the oil and gas densities and viscosities. It is now clear that kinks and inflections of the component flux terms lead to similar features in the residual equation. Previous works showed that kinks and inflection locus in the residual term can create oscillation for the Newton solver and increase the computation time (Voskov and Tchelepi 2011; Li and Tchelepi 2015; Wang and Tchelepi 2013; Hamon et al. 2016). For the remaining part of this paper, we will only focus on the study of the component flux terms while taking into consideration that the nonlinearities observed on these flux terms will result in nonlinearities of the residuals.

Fig. 3

Residuals and their derivatives for a binary system of $\hbox {C}_{2}$ and $\hbox {nC}_{10}$ at $p=30$ bar and $T=350$ K. Different time steps are used, expressed in the form of total throughput c

3 Analysis of Inflection Loci

In this section, we investigate the appearance of inflection loci inside the two-phase region of the compositional space. First, we study the analytical form of the flux functions with fixed densities and viscosities. Second, we generalize the study using numerical modeling.

3.1 Analytical Flux Function

Since we are mainly interested in the transport problem, the pressure is taken to be constant. Furthermore, we assume that the phase behavior is represented using constant K-values, with $K_c=y_c/x_c$. Viscosity and density for each phase are taken constant, so $\rho _{\mathrm{o}}$, $\rho _{\mathrm{g}}$, $\mu _{\mathrm{o}}$ and $\mu _{\mathrm{g}}$ are expressed as function of pressure only (p is constant). Quadratic Corey-type relative permeabilities are used for both hydrocarbon phases.

The two-phase region can be parameterized using tie-lines and the oil phase saturation $S_{\mathrm{o}}$. For the tie-lines, we can use any parameter that can identify each tie-line uniquely. In the case of a constant K-values system, we will use the composition of the first component in the oil phase $x_1$.

Since the boundaries of the two-phase region are straight lines, the molar oil fraction of the second and third components can be expressed as,

$$\begin{aligned} x_2&=\alpha x_1+\beta \end{aligned}$$

(3.1)

$$\begin{aligned} x_3&=1- x_1-x_2. \end{aligned}$$

(3.2)

Here $\alpha$ and $\beta$ are constant values.

Equations (3.3–3.8) give the first derivatives of the component flux functions $h_c$, for $c\in \{1,2,3\}$, as a function of $S_{\mathrm{o}}$ and $x_1$.

$$\begin{aligned} \frac{\partial h_1}{\partial S_{\mathrm{o}}}&= x_1(\rho _{\mathrm{o}}-K_1\rho _{\mathrm{g}})\frac{\partial f_{\mathrm{o}}}{\partial S_{\mathrm{o}}} \end{aligned}$$

(3.3)

$$\begin{aligned} \frac{\partial h_1}{\partial x_1}&= \rho _{\mathrm{o}} f_{\mathrm{o}}+K_1\rho _{\mathrm{g}}(1-f_{\mathrm{o}}) \end{aligned}$$

(3.4)

$$\begin{aligned} \frac{\partial h_2}{\partial S_{\mathrm{o}}}&= (\alpha x_1 + \beta )(\rho _{\mathrm{o}}-K_2\rho _{\mathrm{g}})\frac{\partial f_{\mathrm{o}}}{\partial S_{\mathrm{o}}} \end{aligned}$$

(3.5)

$$\begin{aligned} \frac{\partial h_2}{\partial x_1}&= \alpha (\rho _{\mathrm{o}} f_{\mathrm{o}}+K_2\rho _{\mathrm{g}}(1-f_{\mathrm{o}})) \end{aligned}$$

(3.6)

$$\begin{aligned} \frac{\partial h_3}{\partial S_{\mathrm{o}}}&= (1-x_1-\alpha x_1 - \beta )(\rho _{\mathrm{o}}-K_3\rho _{\mathrm{g}})\frac{\partial f_{\mathrm{o}}}{\partial S_{\mathrm{o}}} \end{aligned}$$

(3.7)

$$\begin{aligned} \frac{\partial h_3}{\partial x_1}&= -(1+\alpha )(\rho _{\mathrm{o}} f_{\mathrm{o}}+K_3\rho _{\mathrm{g}}(1-f_{\mathrm{o}})). \end{aligned}$$

(3.8)

Along tie-lines, $S_{\mathrm{o}}$ changes while $x_1$ is fixed. The inflection points of the component flux functions are identical to the inflection point of the phase flux function. For an arbitrary tie-line identified with the parameter $x_1^*$, the inflection point is at the locus $S_{\mathrm{o}}^*$ defined by:

$$\begin{aligned} \frac{\partial ^2h_c}{\partial S_{\mathrm{o}}^2}(x_1^*, S_{\mathrm{o}}^*)= C \frac{\partial ^2 f_{\mathrm{o}}}{\partial S_{\mathrm{o}}^2}(x_1^*, S_{\mathrm{o}}^*)=0. \end{aligned}$$

(3.9)

Here C is a function of phase densities and K-values. C is constant along a given tie-line.

Considering the assumptions mentioned above, the variation of the component flux function along the non-tie-line axis, when $S_{\mathrm{o}}$ is fixed and $x_1$ varies, is linear. The first derivatives $\partial h_c/\partial x_1$ are independent of $x_1$, and the second derivatives $\partial ^2 h_c/\partial x_1^2$ are zero.

We can conclude that for the case of constant density, viscosity and K-values, inflection points of the component flux functions are encountered along the tie-lines only.

3.2 Directional Derivatives

In the previous section, we limited the search for inflection loci to the main axis of the variables space (along $S_{\mathrm{o}}$ and $x_1$). In this section, we will specify the conditions for the appearance of an inflection point at a particular composition along an arbitrary direction. For this purpose, we analyze the directional derivatives of the component flux functions $h_c=x_c\rho _{\mathrm{o}}f_o + y_c\rho _{\mathrm{g}}f_g$ inside the compositional space. Without loss of generality, we can assume constant K-values, so:

$$\begin{aligned} y_c&=K_c x_c\\ x_2&=\alpha x_1+\beta \\ x_3&=1-x_1-x_2.\end{aligned}$$

With the assumption of viscous forces only, the flux function for phase j is $f_j=u_j/u_{\mathrm{t}}=\lambda _j/\lambda _{\mathrm{t}}$, where $\lambda _{\mathrm{t}}=\lambda _{\mathrm{o}}+\lambda _{\mathrm{g}}$.

The Hessian matrix for component $\hbox {C}_{1}$ is given as,

$$\begin{aligned} \mathbf {H}_{{\mathbf {C1}}}=\begin{pmatrix} \frac{\partial ^2 h_1}{\partial S_{\mathrm{o}}^2}&{}\quad \frac{\partial ^2 h_1}{\partial x_1 \partial S_{\mathrm{o}}}\\ \frac{\partial ^2 h_1}{\partial S_{\mathrm{o}} \partial x_1}&{}\quad \frac{\partial ^2h_1}{\partial x_1^2} \end{pmatrix} \end{aligned}$$

(3.10)

we define $\mathbf {A}_{\mathbf {c}}(S_{\mathrm{o}}, x_1|{\mathbf {u}})=\mathbf {u}^{\mathbf {T}}\mathbf {H}_{\mathbf {c}}(S_{\mathrm{o}},x_1) {\mathbf {u}}$, where ${\mathbf {u}}=\langle u, v \rangle$ is a unitary vector representing the direction for which we want to calculate the directional derivatives and c refers to a component. For component $c=\hbox {C}_{1}$, it is given as,

$$\begin{aligned} \mathbf {A}_{\hbox {C}_{1}}(S_{\mathrm{o}}, x_1|{\mathbf {u}})=\mathbf {u}^{\mathbf {T}}\mathbf {H}_{\hbox {C}_{1}}(S_{\mathrm{o}},x_1) {\mathbf {u}} =\frac{\partial ^2 h_1}{\partial S_{\mathrm{o}}^2} u^2 +2\frac{\partial ^2 h_1}{\partial x_1 \partial S_{\mathrm{o}}} uv +\frac{\partial ^2 h_1}{\partial x_1^2} v^2. \end{aligned}$$

(3.11)

The problem of searching for inflection locus can be expressed as following:

Given an overall composition in the two-phase state and known pressure and temperature conditions, find $S_{\mathrm{o}}^*$, $x_1^*$ and a unitary vector ${\mathbf {u}}^* = \langle u^*,v^*\rangle$ inside the $S_{\mathrm{o}},~ x_1$ space such that:

$$\begin{aligned}&\mathbf {A}_{\mathbf {c}}(S_{\mathrm{o}}^*, x_1^*|{\mathbf {u}}^*)=0 \, \text {, and } \mathbf {A}_{\mathbf {c}} \text { changes sign at }S_{\mathrm{o}}^*, x_1^*\text { along } {\mathbf {u}}^* .\end{aligned}$$

(3.12)

To illustrate this for the case of constant densities and viscosities of Sect. 3.1, Fig. 4 shows the variation of $\hbox {sign}(\mathbf {A}_{\mathbf {c}})$ as a function of the natural variables $S_{\mathrm{o}}$ and $x_1$ for different directions of the unitary vector ${\mathbf {u}}$, which is parametrized using the angle $\theta$. For this three-component system, $\theta$ is defined as the angle between vector ${\mathbf {u}}$ and the $S_{\mathrm{o}}$ axis. Viscosity ratio is assumed to be 3. Green and red are used to show the positive and negative values of $\mathbf {A}_{\mathbf {c}}$, respectively. The transition line from negative to positive represents the inflection locus of the second-order directional derivative $\mathbf {A}_{\mathbf {c}}$. For $\theta =0^{\circ }$ (along tie-lines), the inflection loci is the same for all components (recall K-values are assumed to be constant). As $\theta$ increases, the inflection loci becomes different from one component to another. It disappears when $\theta =90^{\circ }$, since variations are along iso-saturations, and they appear again when $\theta >90^{\circ }$.

Fig. 4

Sign of the second-order directional derivatives $\mathbf {A}_{\mathbf {c}}$ for different components and along different angles. Phase densities and viscosities are constant

Using directional derivatives to identify inflection loci along arbitrary directions inside the compositional space is motivated by the direction of the Newton update. During a Newton update, the change of composition from $z^k$ to $z^{k+1}$ can follow any possible direction. So, in order to verify if other types of inflection loci exist along non-tie-line paths, we need to study the component flux functions along all possible directions. It is true that the theory of the Method of Characteristics (MoC) (Orr 2007) can determine the compositional path formed by the successive compositional states taken by a grid cell to transition from the initial composition to the injection composition. This path is composed of tie-line segments connected by non-tie-line paths. The transitions from the single to the two-phase regions happen along the injection and production tie-lines. In practice, however, factors like numerical dispersion, opening and closing of wells, or changes of the injected composition can alter this path significantly (Orr 2007; Dindoruk 1992). Numerical dispersion for instance moves this path closer to the dilution line. This effect increases as the grid cells are coarsened. To illustrate this, Fig. 5 shows two compositional paths for 1D cases composed, respectively, of 10 and 1000 grid cells. The length of the domain is identical between the two cases, and they have the same reservoir and injection conditions; the only difference is the refinement of the domain. It is noted that the path is different for both cases. For the 1000 grid cells, the path enters and exits the two-phase region along tie-lines. By knowing these tie-lines, we can predict in advance the shape of the component fluxes along this path. But for the case with 10 grid cells, this path neither enters nor exits the two-phase region along the tie-lines. Furthermore, the non-tie-line path is closer here to the dilution line. This simple comparison shows that in the general case we should expect any possible direction between Newton iterations k and $k+1$.

Fig. 5

Assessment of the impact of the numerical dispersion on the non-tie-line portion of the compositional path

Next, in Sect. 3.3 we investigate the appearance of inflection loci inside the compositional space, for the general case, by applying Eq. 3.12 to the discrete form of the component flux function.

3.3 Numerical Flux Functions

The assumption of constant density and viscosity is very restrictive. Figure 6 shows the density and viscosity curves along an arbitrary line (non-tie-line) inside the two-phase region of a ternary system composed of $\hbox {C}_{1}$, $\hbox {CO}_{2}$ and $\hbox {nC}_{10}$ at $p=50$ bar and $T=400$ K. Density and viscosity are calculated using Peng–Robinson EoS model (Peng and Robinson 1976) and Lohrenz–Bray–Clark (LBC) (Lohrenz et al. 1964) viscosity model, respectively. We see that the two functions are variable along this line. Moreover, they are nonlinear and the viscosity is non-monotonic.

Fig. 6

Analysis of oil density and viscosity over a non-tie-line in a ternary compositional space composed of $\hbox {C}_{1}$, $\hbox {CO}_{2}$ and $\hbox {nC}_{10}$ at $p=50\,$bar and $T=400$ K

To analyze the variations of component flux functions over the two-phase region in the case of variable density and viscosity, we use the setup of two grid cells shown in Fig. 7. A small $\Delta p$ is fixed across the domain; the permeability of the two grid cells is $K_x=200$ mD. The flow is from left to right, the composition of the right grid cell is fixed, and we vary the composition of the left grid cell. We analyze the component fluxes over the interface separating the two grid cells. Only viscous forces are considered here. The goal of this analysis is to find the inflection loci inside the two-phase space. First, we will show the impact of pressure variation on the inflection loci. Then, we present the dependence of inflection loci on the angle $\theta$. We also added a simple case of transport along a single tie-line in “Appendix 3.” That case validates the findings of Sect. 3.1

Fig. 7

The simulation setup used to calculate the discrete form of the component flux term $F_{c,i}$

3.3.1 Dependence of the Inflection Loci on Pressure

In this section, we analyze variation of the directional derivatives of the flux function $\mathbf {A}_{\mathbf {c}}$, $c \in \{1,\ldots , n_c\}$ (Eq. 3.11), inside the two-phase region of the compositional space. Figure 8 shows the sign of $\mathbf {A}_{\mathbf {c}}$ along the angle $\theta = 50^\circ$ at different pressures. The system is composed of $\hbox {C}_{1}$, $\hbox {FC}_{6}$ and $\hbox {nC}_{10}$. We plot the inflection loci for different values of pressure $p\in \{30,80, 180\}$ bar. First, for the constant K-values case of $p=30$ bar (Fig. 8a), all the components have two inflection loci. Also, the location of the inflection locus near the bubble curve is identical for all the components. The inflection locus near the dew curve is very different from one component to another. As pressure increases from $p=30$ bar to $p=180$ bar, the two-phase region shrinks, and the inflection locus near the bubble point curve for component $\hbox {FC}_{6}$ starts to differ from the other two components. For $p=180$ bar, the inflection loci near the dew curve for both $\hbox {C}_{1}$ and $\hbox {nC}_{10}$ disappear completely, while it continues to exist for component $\hbox {FC}_{6}$.

Fig. 8

Directional derivatives for $\theta = 50^\circ$ at different pressures. The blue line represents the boundaries between regions of different phase labels

3.3.2 Dependence of the Inflection Loci on the Angle $\theta$

In this section, we identify the inflection loci inside the two-phase region for different values of the angle $\theta$. The setup of Fig. 9 is used. For a particular composition inside the two-phase region and a particular direction defined by the angle $\theta$, we would like to check if the second-order directional derivative changes sign at the target composition. The target composition is shown in orange. Along the direction defined by $\theta$, we sample four additional compositions located at $-2\varepsilon , ~-\varepsilon ,~+\varepsilon ,~+2\varepsilon$, where $\varepsilon$ represents a small value. We use the component flux functions at these compositions to evaluate the directional second-order derivatives (Eq. 3.11) both before ($\mathbf {A}_{\mathbf {c}}^-({\mathbf {z}}-\varepsilon {\mathbf {u}})$) and after the target composition ($\mathbf {A}_{\mathbf {c}}^+({\mathbf {z}}+\varepsilon {\mathbf {u}})$). Here, ${\mathbf {z}}$ is the composition vector and ${\mathbf {u}}$ represents a unitary vector along the direction defined by $\theta$. In their discrete form, these two functions are defined as:

$$\begin{aligned}&\mathbf {A}^-_{\mathbf {c}}=\frac{h_{c,0}-2 h_{c,-\varepsilon } +h_{c,-2\varepsilon }}{\varepsilon ^2} \end{aligned}$$

(3.13)

$$\begin{aligned}&\mathbf {A}^+_{\mathbf {c}}=\frac{h_{c,+2\varepsilon }-2 h_{c,+\varepsilon } +h_{c,0}}{\varepsilon ^2}. \end{aligned}$$

(3.14)

The flux function for component c has an inflection point if $\mathbf {A}^-_{\mathbf {c}}$ and $\mathbf {A}^+_{\mathbf {c}}$ have different signs. Figure 11 shows the results for the system of $\hbox {C}_{1}$, $\hbox {FC}_{6}$ and $\hbox {nC}_{10}$ at $p=180$ bar and $T=470$ K. Figure 10 shows the target compositions inside the two-phase region. Figure 11a, b shows the inflection loci for the component fluxes of $\hbox {C}_{1}$ and $\hbox {FC}_{6}$ along the angles $\pi /4$, $\pi /2$ and $3\pi /4$. We observe that the inflection loci change from one component to another, and that these inflection loci change as a function of the angle $\theta$.

Fig. 9

Discretization scheme for evaluation of the second-order directional derivatives before and after the target composition. The target composition is shown in orange

Fig. 10

Set of composition points (red circles) we use to search for inflection loci along different angles. The dark blue, green, and yellow regions refer to the gas, oil, and two-phase regions, respectively

Fig. 11

Inflection locus variation as a function of $\theta$ for a ternary system of $\hbox {C}_{1}$, $\hbox {FC}_{6}$ and $\hbox {nC}_{10}$ at $p=180$ bar and $T=470$ K. The dark blue, green and yellow regions refer to the gas, oil and two-phase regions, respectively

3.4 Discussion

In Sect. 3, we analyzed the kinks and inflections of the component flux functions. While identifying the kinks caused by phase changes is possible since they are localized at phase boundaries, identifying the inflection loci for a compositional system is challenging since it requires information of the second-order directional derivatives in the vicinity of a given target composition. This requires either the calculation and storage of the Hessian matrix, which is expensive, or on the fly calculation of an approximation to the second-order directional derivatives. Both approaches can result in ill-defined second-order derivatives, for example at phase boundaries, where the first-order directional derivatives are discontinuous or when the relative permeability model is non-smooth (e.g., piecewise linear models). Even when the second-order derivatives are well defined, calculating them on the fly would require additional flash calculations.

Previously, Voskov and Tchelepi (2011) proposed a trust region solver that detects the discontinuities and inflection loci of the flux function in the case of an MoC type of displacement. In that scenario, the entry/exit of the two-phase region occurs along a limited number of key tie-lines, so knowing the location of inflection points and discontinuities along these key tie-lines is possible. In our work, we do not assume a priori knowledge about such key tie-lines. In the next section, we will present a Newton solver that specializes in detecting phase change discontinuities and guides the Newton path to avoid oscillations caused by these discontinuities.

4 Nonlinear Solver for Compositional Transport Problem

4.1 Background

Chopping strategies have been developed to limit the Newton update $\Delta {\mathbf {Z}}_i$, where ${\mathbf {Z}}_i$, in our case, is the vector of the transport variables of grid cell i composed of the total saturation $S_{\mathrm{t}}$ and the compositions $z_c$ (Eq. 4.1).

$$\begin{aligned} {\mathbf {Z}}_i=[S_{\mathrm{t}}, z_1,\ldots , z_{n_c-1}]^{\mathsf {T}}_i .\end{aligned}$$

(4.1)

Chopping can be suitable if the update is large, or if it crosses kinks and inflection loci. The most widely used chopping strategy is the Appleyard chop (Geoquest 2008). It limits either the saturation update, the composition update, or both to some fixed value (e.g., 0.2). Two categories of the chopping strategy are used in practice: (1) local chopping and (2) global chopping. A local chopping strategy uses different $\omega _i$ for different grid cells, where $\omega _i$ is the chopping ratio used to limit the variable update:

$$\begin{aligned} {\mathbf {Z}}^{k+1}_i = {\mathbf {Z}}^k_i + \omega _i \Delta {\mathbf {Z}}_i,\quad \omega _i \in [0,1] .\end{aligned}$$

(4.2)

The benefit of using a local chopping ratio is that it separates the updates of the different grid cells; the ones that cross kinks or inflections will be adjusted, while the ones that do not cross any discontinuities will keep their standard update. This is the least conservative approach. The shortcoming of this approach is that it alters the direction of the update.

A global chopping strategy uses a global chopping ratio $\omega$ for all the grid cells. This ratio is, commonly, calculated as the minimum of the chopping ratios of all the grid cells (n grid cells)

$$\begin{aligned} \omega= \,& {} \underset{i\le n}{\min }(\omega _i)\quad \end{aligned}$$

(4.3)

$$\begin{aligned} {\mathbf {Z}}^{k+1}_i= \,& {} {\mathbf {Z}}^k_i + \omega \Delta {\mathbf {Z}}_i,\quad \omega \in [0,1]. \end{aligned}$$

(4.4)

In this case, we are sure that the update will follow the original direction of the Newton’s path. Unfortunately, this approach is very conservative since it is limited by the smallest $\omega _i$ of the entire grid.

Other approaches exploit the locality of the hyperbolic nature of the transport equations, where only few cells are interdependent during a time step. So, the grid can be divided into independent regions, where we can define a chopping ratio per region. This approach has been used for black-oil models (Natvig and Lie 2008; Møyner 2017).

4.2 Phase Change Detection Solver

In this section, we present a Newton solver that detects phase boundaries and applies a damping strategy to the transport update $\Delta {\mathbf {Z}}$. The main idea behind this solver is to prevent the Newton solver from oscillating between the single and two-phase regions. It works by chopping the Newton update if it crosses the phase boundary so that the new update is at the boundary. Algorithm 1 implements this strategy.

In this work, we use two global approaches: (1) standard global approach, where $\omega =\underset{i\le n}{\min }(\omega _i)$, and (2) median global approach, where $\omega =\underset{i\le n}{\text {median}}(\omega _i)$. Approach (2) allows us to avoid half of the discontinuities encountered during a Newton iteration.

4.3 Algorithm Steps

The algorithm is a modified bisection that calculates the optimal $\omega$ recursively. Various aspects of this algorithm are discussed in the following:

• 1. Enforce physical updates

  
  

  This is a prerequisite part of the algorithm. The solution at iteration $k+1$ should remain within the physical boundaries of the compositional space. In our case, ${\mathbf {Z}}^{k+1}$ is composed of two parts, $S_{\mathrm{t}}$ and ${\mathbf {z}}=[z_1, \ldots z_{n_c-1}]^{\mathsf {T}}$. The physical constraints of these two parts are different. While every $z_c$ should remain within the range [0, 1] and the sum of all the components equal to unity $\mathop{\sum }\nolimits_{c\le n_c}z_c=1$, $S_{\mathrm{t}}$ is unbounded; it can be less than zero or greater than one. The physical constraints will only be applied to the compositions, and the adjusted update $\Delta {\mathbf {Z}}^{k+1}$ will be further chopped using our algorithm.

• 2. Identify target cells

  
  

  Phase detection solver subroutine is triggered for target cells only. A target cell is a grid cell for which the update $\Delta {\mathbf {Z}}_i$ crosses the phase boundaries. It must also have an update $\Delta {\mathbf {Z}}_i$ that is greater than or equal to a predefined threshold $\epsilon$. This prevents the algorithm from chopping very small updates.

• 3. Recursive loop

  
  

  For each target cell, we search along the segment connecting ${\mathbf {Z}}_i^k$ to ${\mathbf {Z}}_i^{k+1}$ for a point with a different phase state from ${\mathbf {Z}}_i^k$. We use a recursive bisection algorithm with depth m. The higher the value of m the closer we can get to the phase boundary. Next, we calculate $\omega _i$ for the grid cell.

• 4. Calculate global $\omega$

  We calculate the global value of $\omega$ that will be applied to all grid cells, using one of the formulations (min or median).

• 5. Calculate the update ${\mathbf {Z}}^{k+1}$

  The new variables ${\mathbf {Z}}^{k+1}$ are calculated using the global $\omega$ (Eq. 4.4)

5 Numerical Examples

We validate our algorithm for a variety of fluid compositions and reservoir models. While the solver can be used for 3D models, we limit our analysis in this work to 1D and 2D cases. The first case is a 2D case with gravity and viscosity effects. The second case is a 1D homogeneous model with viscous forces only. Our last case is a 2D horizontal case with multiple wells. These tests are split into two categories: (1) single time step run and (2) full simulation run. We compare four nonlinear solution strategies:

• STD Standard Newton solver without any relaxation.

• APL Newton solver with Appleyard chop strategy for overall composition z. The maximum value allowed for update of z, $\Delta z$, is 0.2.

• PCD min Phase change detection solver (Algorithm 1) with the use of $\omega =\underset{i\le n}{\min }(\omega _i)$ as a global relaxation factor.

• PCD median Phase change detection solver (Algorithm 1) with the use of $\omega =\underset{i\le n}{\mathrm {median}}(\omega _i)$ as a global relaxation factor.

The nonlinear convergence criterion for the transport problem is: $|(R_c)_i|\le 10^{-4}$. Here, $(R_c)_i$ is the discrete residual of component c in grid cell i. PCD solvers were implemented using Matlab Reservoir Simulation Toolbox (MRST) (Lie 2019).

5.1 Single Time Step Run

For the following case, we run a single time step of different lengths, and we compare the performance of the different solvers. This is a standard approach to test the behavior of nonlinear solvers for a single time step using various initial conditions. For the first case, we use six different analytical relative permeability models:

• 1. Quadratic and cubic standard Corey models (Eq. 5.1), with $n=\{2,3\}$, respectively.

  $$\begin{aligned} k_{\mathrm{rgo}}(S_{\mathrm{g}})=S_{\mathrm{g}}^n, \quad k_{\mathrm{rog}}(S_{\mathrm{g}})=(1-S_{\mathrm{g}})^n .\end{aligned}$$

  (5.1)

• 2. Brooks–Corey models (Brooks and Corey 1964). We assume oil is the wetting phase and gas is the non-wetting phase (Eq. 5.2). We tested the cases with $\beta \in \{1,2,3,4\}$

  $$\begin{aligned} k_{\mathrm{rgo}}(S_{\mathrm{g}})=S_{\mathrm{g}}^2\Big (1-(1-S_{\mathrm{g}})^\frac{\beta +2}{\beta } \Big ),\quad k_{\mathrm{rog}}(S_{\mathrm{g}})=(1-S_{\mathrm{g}})^{\frac{3\beta +2}{\beta }}. \end{aligned}$$

  (5.2)

To simplify the analysis, we chose to neglect the endpoint relative permeability values and the residual saturations. The relative permeability models are shown in Fig. 12.

Fig. 12

Gas and oil relative permeability models. The quadratic and cubic models are based on the standard Corey model with $n\in \{2,3\}$, respectively. The remaining models are based on the Brooks–Corey model with $\beta \in \{1,2,3,4\}$

5.1.1 Case 1: 2D Flow with Gravity

The main flow mechanisms, for this case, are a combination of the gravitational and viscous forces. The gravity number value is $N_{\mathrm{g}}=2.74$ (Eq. 5.3). The viscous forces are created by the pressure gradient in the domain due to the opening of the wells (total velocity $u_{\mathrm{T}}\ge 0$).

$$\begin{aligned} N_{\mathrm{g}}=\frac{k(\rho _{\mathrm{o}}-\rho _{\mathrm{g}})g\nabla d}{\mu _{\mathrm{g}} u_{\mathrm{T}}}. \end{aligned}$$

(5.3)

The number of grid cells in the (x, y, z) directions are $(x,y,z)=(220, 1, 10)$ and the dimensions are $(220\,\hbox {m}\times 1\,\hbox {m})$, resulting in a very thin model where gravity is enhanced. The permeability is homogeneous in each direction $(K_x,K_y,K_z)=(1000,1000,100)$ mD, while the porosity $\phi$ is extracted from layer 83 of SPE-10 dataset (Christie and Blunt 2001). The y axis in the SPE-10 grid is used in the vertical direction in our grid (Fig. 13). The reservoir fluid is composed of $\hbox {C}_{2}$, $\hbox {iC}_{5}$ and $\hbox {nC}_{10}$. The initial composition is $(\hbox {C}_{2}, {\hbox {iC}_{5}}, \hbox {nC}_{10})=(0.01, 0.5, 0.49)$. The reservoir pressure and temperature are, respectively, $p=70$ bar and $T=390$ K. The model has two vertical wells, perforated along the entire thickness of the grid. An injector well is located in the first column, and it injects a gas with composition of $(\hbox {C}_{2}, \hbox {iC}_{5}, \hbox {nC}_{10})=(0.9, 0.09, 0.01)$. The injection rate is tuned to inject one pore volume of gas during a time step of $\Delta t=1$ day. The producer is at the last column, operating at BHP $=50$ bar. These pressure conditions are far from the small $\Delta p$ assumption used in the MoC approach. As before, we compare the nonlinear performance of various solvers.

Fig. 13

Case 1: $\phi$ and $K_x$ maps. ($\phi ,~K_x$):(channelized, homogeneous)

Fig. 14

Case 1: Transport Newton iterations count for the case of channelized $\phi$ and homogeneous $K_x$. White color indicates that the solver has failed to converge after more than 100 Newton iterations

Figure 14 shows the number of Newton iterations for different scenarios. In this figure, dark blue represents fast convergence (1–3 iterations), while yellow shows slow convergence (90–100 iterations); the white region indicates that the solver has failed to converge after more than 100 Newton iterations. For this case, the STD solver performs very poorly in comparison with the other solvers. For small time step sizes of $\Delta t \le 0.25$ day, both PCD solvers have fewer Newton iterations than APL and STD. Also, both PCD solvers have only failed to converge for a single configuration, while APL has four failures and STD has many. For medium to large time step sizes of $\Delta t \ge 0.5$ day, APL’s overall performance is better than both PCD solvers. These results show that the damping strategy has a significant impact on the Newton solver. In fact, our PCD solvers allowed the convergence of many configurations that failed to converge using either STD or APL.

5.2 Time-Stepping Simulation Cases

For cases 2 and 3, instead of running the simulation for a single time step, we run the simulation for a long period of time using multiple time steps. While this is a more realistic simulation scenario, it is less straightforward to analyze, since the solution trajectories for the different solvers change at each new time step. A quadratic relative permeability model is used for these cases, and we use a simple time-stepping strategy. If the Newton solver converges, we double the time step size attempted and if it fails we divide the subsequent time step size by 2. The maximum allowed number of time step cuts is 10. To assess the difficulty of the different scenarios, we will be comparing their standard saturation-based CFL numbers (Coats 2003). Two values of CFL will be calculated: (1) maximum CFL over the entire simulation run (2) the maximum CFL averaged over each time step.

5.2.1 Case 2: 1D Homogeneous

This is a 1D ternary case of $\hbox {C}_{1}$, $\hbox {nC}_{4}$ and $\hbox {nC}_{10}$. The domain is discretized using 500 grid cells, with a homogeneous permeability and porosity of $K=1000$ mD and $\phi =0.2$. We inject a gas mixture of composition $(\hbox {C}_{1},\hbox {nC}_{4},\hbox {nC}_{10})=(1, 0, 0)$ into a composition of $(\hbox {C}_{1},\hbox {nC}_{4},\hbox {nC}_{10})=(0.01, 0.5, 0.49)$. The reservoir pressure and temperature conditions are $p=70$ and $T=370$ K. We inject one pore volume during the simulation time of $t=500$ days, so the injection rate is very low. We compare STD, APL, PCD min and PCD median for five different scenarios of maximum time step size $\Delta t_{\max }=\{1, 10, 50, 100, 150\}$ days. Figure 15 shows a comparison of the number of Newton iterations for the transport problem.

Fig. 15

Case 2: cumulative Newton iterations for the transport problem. We compare the different Newton solvers for a range of maximum time steps $\Delta t_{\max }=\{1, 10, 50, 100, 150\}$ days

For all solvers, increasing the maximum time step size will lead to a sharp reduction of the number of Newton iterations. The decline in Newton iterations of PCD solvers is sharper; for instance at $\Delta t_{\max }=150$ days, the STD solver takes two times more Newton iterations than PCD median. The APL solver still performs better than STD except for the cases of $\Delta t_{\max }\in \{10,150\}$ days. Comparing the two PCD solvers, we note that the minimum of Newton iterations count for PCD min is reached when $\Delta t_{\max }=100$ days. For $\Delta t_{\max }> 100$ days, PCD min requires additional Newton iterations to converge. On the other hand, the Newton iterations count of PCD median continues to decline reaching its minimum value at $\Delta t_{\max }=150$ days. This suggests that PCD min is slightly conservative for this time step. Table 1 shows the maximum CFL for the different models at different time steps. We see that the CFL numbers are very similar between the different models and that higher values of $\Delta t_{\max }$ lead to more difficult convergence of the nonlinear solver.

Table 1 Case 2: the absolute maximum CFL as well as the maximum averaged CFLs by time step (in parentheses)

Figure 16 shows the oil saturation and the composition profiles at the last time step for $\Delta t_{\max } \in \{1, 150\}$ days. For $\Delta t_{\max }=1$ day, the models are identical in terms of composition profiles. We can clearly see the saturation shocks connected by rarefactions. For $\Delta t_{\max }=150$ days, the shocks are smoothened. The appearance of shocks is very different between the models. STD captures the leading and trailing shocks very well. Both PCD models are very smooth and they only capture the trailing shock. We think that STD and APL models perform better in capturing compositional shocks because they cut time steps, resulting in a better evolution of the saturation and composition fronts. Since PCD models allow larger time steps to converge, these models will inevitably lead to smoother solution profiles.

This case clearly shows improvement of nonlinear performance due to better handling of phase jump discontinuities.

Fig. 16

Case 2: comparison of oil saturation and compositions profiles for the four Newton solvers at the last time step. a $\Delta t_{\max }=1$ and b $\Delta t_{\max }=150$

5.2.2 Case 3: Multiple Wells Case

This is a 2D horizontal plan with multiple wells. The grid is $60 \times 60$. The permeability and porosity are extracted from layer 85 of SPE-10 as shown in Fig. 17. The wells are configured in a five spot pattern, with a producer in the center of the grid, operating at a BHP $=45$ bar, and four injectors, located at the corners of the domain, injecting a gas composition of $(\hbox {C}_{2}, \hbox {nC}_{5}, \hbox {nC}_{10})=(0.8, 0.2, 0)$ at a BHP $=55$ bar. This case will test the performance of various nonlinear solvers in the presence of multiple composition fronts. The initial composition is $(\hbox {C}_{2}, \hbox {nC}_{5}, \hbox {nC}_{10})=(0, 0.3, 0.7)$ at pressure and temperature conditions of $p=50$ bar and $T=400$ K. The simulation is run for 400 days. The pressure conditions are below the minimum miscibility pressure (MMP), resulting in a complex displacement combining shocks and rarefactions.

Fig. 17

Case 3: porosity $\phi$ and Permeability $K_x$ maps are extracted from layer 85 of SPE-10

Figure 18 shows the cumulative number of Newton iterations for the transport problem. As the maximum time step size increases, the Newton count for PCD models decline steadily. For $\Delta t_{\max }=100$ days case, Newton count for PCD min represents almost half the number of Newton iterations taken by the STD model, while PCD median reaches the third of this value. The superior performance of the PCD models in this case can be attributed to the presence of multiple composition fronts. As time advances, additional grid cells switch from single-phase oil to two-phase hydrocarbon when the leading saturation shock reaches them. A second transition, from two-phase to single-phase gas, occurs at the trailing shock. Figure 19 shows the gas saturation $S_{\mathrm{g}}$ at breakthrough time of 160 days for the case of $\Delta t_{\max }=10$ days. The figure also shows $\Delta S_{\mathrm{g}}=|S_{\mathrm{g}}^m-S_{\mathrm{g}}^{\mathrm{std}}|$, for APL, PCD min, PCD median calculated as the absolute value of the difference between the gas saturation of solver m and the gas saturation of STD solver. We chose STD as reference here since its number of Newton iterations is much higher than the remaining models. We observe that the maximum value of $\Delta S_{\mathrm{g}}$ is comparable between the different solvers (APL, PCD min, and PCD median), in the range [0.35, 0.4]. Most of these differences in saturation are localized at the shocks. This result is similar to Case 2, where the shocks represented the main difference between the models. Since APL, PCD min and PCD median typically take larger time steps, their saturation fronts appear to be smoother.

Fig. 18

Case 3: cumulative count of Newton iterations for transport problem using different maximum time steps $\Delta t_{\max } \in \{1,10,50,100\}$

Table 2 shows the maximum CFL for different runs. We observe that the values are comparable between the different solvers and they increase sharply as $\Delta t_{\max }$ increases.

Table 2 Case 3: the absolute maximum CFL as well as the maximum of averaged CFLs for each time step (in parentheses)

Fig. 19

Case 3: comparison of gas saturation maps for the case of $\Delta t_{\max }=10$ at gas breakthrough time of $t=160$ days (1st row). The second row shows the delta of gas saturation between each model and the STD case

The cumulative oil and gas production for the different cases is shown in Fig. 20. For oil production, PCD min and APL have the highest and lowest values of cumulative oil production, respectively. The difference between the cumulative oil productions of these two cases represents $0.4\%$ of their average cumulative oil production. For gas production, STD has the highest value of cumulative gas production, while PCD min has the lowest value. The difference between these two values is much higher compared to the difference in oil production, reaching $15\%$ of the average cumulative gas production. We observe also that gas breakthrough is the determining factor of the cumulative gas production. STD and PCD median cases that have a gas breakthrough around the same time of 130 days, have higher cumulative gas production, while APL and PCD min simulation cases that have a gas breakthrough around 150 days, have lower cumulative gas productions. Owing to the reservoir heterogeneity, it is not straightforward to derive any relationship between the solution strategy and the gas breakthrough time.

Fig. 20

Case 3: oil and gas cumulative production over 400 days. The four solvers are compared for the case of $\Delta t_{\max }=10$

6 Conclusions

In this paper, we studied the nonlinearities of isothermal compositional simulation. Our goal was to better understand the underlying physics of compositional simulation. We focused our work on the nonlinearities of the coupled flow and transport. Our approach was to identify the nonlinearities that cause the Newton solver to fail, and to develop robust, fit-for-purpose, nonlinear strategies.

Nonlinearities associated with compositional flow and transport are captured in the component flux function. Our nonlinear analysis of this function showed the appearance of both kinks and inflection loci. We first focused on kinks that appear due to the crossing of phase boundaries. We, then, showed how these kinks in the flux term translate into the residual term, which leads to convergence difficulties for the Newton solver. Analysis of the inflection loci along the main axis of the primary variables $S_{\mathrm{o}}$ and $z_1$, for the case of constant densities, viscosities and K-values showed that the inflection locus is unique and coincides with the inflection locus of the phase flux. Since the inflection loci are direction-dependent, we introduced the usage of second-order directional derivatives to track and characterize these inflection loci. For the case of constant densities and viscosities, we found that there is a single inflection locus inside the two-phase region whose position and curvature change depending on the direction. To further study the inflection loci for variable densities and viscosities, we used numerical simulation. For the three-component case, our results showed that the inflection loci at least depends on pressure, composition, and direction of Newton update. We also found that the shape of the inflection locus changes from one component to another. Inflection locus is also function of pressure and temperature. Designing a trust region solver that detects all the inflection loci during a simulation run is challenging because of the considerable variation of the inflection loci inside the two-phase region. Not only this would require calculation of the second-order derivatives of the component flux functions, but it will also lead to additional flash calculations. We then discussed the design of a nonlinear solver that detects phase boundaries. The algorithm works by searching for the phase change point along the segment $\Delta {\mathbf {Z}}^{k+1}$ connecting the current Newton iteration variable ${\mathbf {Z}}^k$ to the next one ${\mathbf {Z}}^{k+1}$. The search is recursive and once the boundary is detected, we adjust the variable update $\Delta {\mathbf {Z}}^{k+1}$ so that the solution at the next Newton iteration ${\mathbf {Z}}^{k+1}$ will land at the boundary. We tested the algorithm for a variety of reservoirs and fluid models. Our numerical experiments show that avoiding phase discontinuities prevents the Newton solver from oscillating and improves convergence behavior.

Appendices

Appendix 1: Compositional Model

Our compositional model represents an isothermal two-phase gas–oil compressible system. The conservation equations expressed in one dimension, x, are given as,

$$\begin{aligned} \frac{\partial }{\partial t }[\phi (x_c\rho _{\mathrm{o}} S_{\mathrm{o}} + y_c\rho _{\mathrm{g}} S_{\mathrm{g}})] + \frac{\partial }{\partial x}(x_c \rho _{\mathrm{o}} u_{\mathrm{o}} + y_c \rho _{\mathrm{g}} u_{\mathrm{g}})- q_c=0 \end{aligned}$$

(6.1)

where $\phi$ is porosity, $x_c$ and $y_c$ are the component mole fractions in the oil and gas phases, respectively. c refers to the component index $c \in \{1,\ldots ,n_c\}$, $\rho _{\mathrm{o}}$ and $\rho _{\mathrm{g}}$ are the oil and gas molar densities, $S_{\mathrm{o}}$ and $S_{\mathrm{g}}$ are the phase saturations, and $q_c$ is the source/sink flow rate of each component.

The general Darcy’s law is used to express the oil and gas phase velocities, $u_{\mathrm{o}}$ and $u_{\mathrm{g}}$, as a function of the gradient in phase potentials,

$$\begin{aligned} u_j=-K_x\lambda _j\left( \frac{\partial p_j}{\partial x}- \gamma _j \frac{\partial D}{\partial x}\right). \end{aligned}$$

(6.2)

The subscript j here refers to the phase $j \in \{o,g\}$, $p_j$ is the phase pressure, $K_x$ is the permeability in the x direction and $\lambda _j$ is the phase mobility, which is given as the ratio of relative permeability $k_{rj}$ to viscosity $\mu _j$, $\lambda _j=k_{rj}/\mu _j$. $\gamma _j=\rho _j g$, with g the gravity and D the vertical displacement. In the absence of gravitational and capillary forces, Eq. 6.2 simplifies to:

$$\begin{aligned} u_j=-K_x\lambda _j \frac{\partial p}{\partial x}. \end{aligned}$$

(6.3)

In this work, we study the transport problem, so it is helpful to express the phase velocities $u_j$ as a function of the total velocity $u_{\mathrm{T}}= \sum _k u_k$.

$$\begin{aligned} u_j= \frac{\lambda _j}{\sum _k \lambda _k} u_{\mathrm{T}}. \end{aligned}$$

(6.4)

We can now define the phase flux functions $f_j$ as,

$$\begin{aligned} f_j=\frac{u_j}{u_{\mathrm{T}}}= \frac{\lambda _j}{\sum _k \lambda _k}. \end{aligned}$$

(6.5)

Replacing Eq. 6.5 into Eq. 6.1 and assuming incompressible rock system (constant $\phi$), we get:

$$\begin{aligned} \phi \frac{\partial }{\partial t} (x_c\rho _{\mathrm{o}} S_{\mathrm{o}} + y_c\rho _{\mathrm{g}} S_{\mathrm{g}}) + \frac{\partial }{\partial x} \big [ u_{\mathrm{T}} (x_c \rho _{\mathrm{o}} f_{\mathrm{o}} + y_c \rho _{\mathrm{g}} f_{\mathrm{g}})\big ]- q_c=0. \end{aligned}$$

(6.6)

To close the nonlinear system of equations, we add the thermodynamic equations that characterize the repartition of components between phases:

$$\begin{aligned} f_{c,o}(p,x)= f_{c,g}(p,y). \end{aligned}$$

(6.7)

Here $f_{c,j}~j\in \{o,g\}$ is the fugacity of component c in phase j. We need also to add the composition and saturation constraints:

$$\begin{aligned}&\sum _c x_c -1 =0 \end{aligned}$$

(6.8)

$$\begin{aligned}&\sum _c y_c -1 =0 \end{aligned}$$

(6.9)

$$\begin{aligned}&\sum _j S_j -1 =0. \end{aligned}$$

(6.10)

With Eqs. (6.7–6.10), the system is complete; we have $2n_c+3$ equations and variables for an isothermal compositional model without gravity and capillarity. To fully describe the intensive state of a system, Gibbs phase rule requires $I_{\mathrm{thermo}}=n_c+2-n_j$ degrees of freedom. The number of phases is $n_j$. An additional $n_j-2$ equations are required to describe the extensive state for the isothermal case. Altogether, we need to solve $I_{\mathrm{primary}}= n_c+2-n_j+(n_j-2)= n_c$ equations, they represent the number of primary variables. The remaining variables represent the secondary variables, which can be calculated explicitly as a function of the primary variables (Cao 2002). Specifying the set of primary variables is what defines a formulation.

Appendix 2: Hydrocarbon Components Properties

The properties of the hydrocarbon components used in our work are obtained from WinProp user manual (2014). We provide below a non-exhaustive list of the components we used in our work and their properties (Table 3):

Table 3 Properties of the hydrocarbon components

Appendix 3: Variations of Component Flux Function Along a Tie-Line

This is a ternary system composed of $\hbox {C}_{1}$, $\hbox {CO}_{2}$ and $\hbox {nC}_{10}$. The reservoir conditions are $p=50$ bars and $T=400$ K. Figure 21 shows a tie-line. We analyze the shape of the component flux functions along this tie-line. For this purpose, we define the coordinates L-axis along this tie-line. L is zero on the dew curve, and it reaches the tie-line length value at the bubble curve. The composition of the left grid cell (in a two-cell setup) will be selected along this tie-line. Figure 22 shows the discrete component fluxes $F_i$ for $i \in \{\hbox {C}_{1},\hbox {CO}_{2}, \hbox {nC}_{10}\}$ and their directional derivatives as a function of the L coordinate. The fluxes for all the three components have inflection points along the tie-line where the first-order derivatives reach a local optimum. The location of all the inflection points is the same for all the components. This observation is in accordance with the results of Sect. 3.1.

Fig. 21

Tie-line inside the two-phase region of compositional space

Fig. 22

Component fluxes and their derivatives over a single tie-line of Fig. 21