Analysis on multi-mode nonlinear resonance and jump behavior of an asymmetric rolling bearing rotor

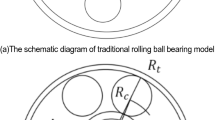
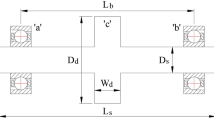
Abstract

This paper takes an asymmetric support ball bearing-rotor system subjected by unbalanced force and parametric excitation (varying compliance) as the research object. Multi-modes of resonance such as natural frequency resonance region of each order, VC (varying compliance) frequency resonance region, the 1/2 sub-harmonic VC frequency resonance region, and quasi-periodic regions, and the nonlinear characteristics in these regions are analyzed. Besides, the effect of the number of balls of the ball bearing is also considered and the result shows that the parity of this parameter matters a lot. By introducing a definition of the absolute quasi-periodic frequency, the law of the occurrence of the quasi-periodic motion is demonstrated and the possible cause is given to some extent. The work provides a theoretical basis for clarifying the nonlinear characteristics of the bearing-rotor system and suppressing the nonlinear behavior of the system.

Appendix

Expanded form of Eq. (1)

$$\begin{aligned} \left\{ \begin{array}{l} m\ddot{x}+c_{1}(\dot{x}-\dot{x}_{1})-c_{2}(\dot{\theta }_{y}-\dot{\theta } _{y1})+k_{rr}(x-x_{1})-k_{r\varphi }(\theta _{y}-\theta _{y1})=m\delta \Omega ^{2}\cos \Omega t\\ m\ddot{y}+c_{1}(\dot{y}-\dot{y}_{1})+c_{2}(\dot{\theta }_{x}-\dot{\theta } _{x1})+k_{rr}(y-y_{1})+k_{r\varphi }(\theta _{x}-\theta _{x1})=m\delta \Omega ^{2}\sin \Omega t-mg\\ J_{d}\ddot{\theta }_{x}+J_{p}\Omega \dot{\theta }_{y}+c_{3}(\dot{y}-\dot{y} _{1})+c_{4}(\dot{\theta }_{x}-\dot{\theta }_{x1})+k_{\varphi r}(y-y_{1} )+k_{\varphi \varphi }(\theta _{x}-\theta _{x1})=0\\ J_{d}\ddot{\theta }_{y}-J_{p}\Omega \dot{\theta }_{x}-c_{3}(\dot{x}-\dot{x} _{1})+c_{4}(\dot{\theta }_{y}-\dot{\theta }_{y1})-k_{\varphi r}(x-x_{1} )+k_{\varphi \varphi }(\theta _{y}-\theta _{y1})=0\\ m_{a}\ddot{x}_{a}-\gamma _{2}c_{1}(\dot{x}-\dot{x}_{1})+\gamma _{2}c_{2} (\dot{\theta }_{y}-\dot{\theta }_{y1})-\gamma _{2}k_{rr}(x-x_{1})+\gamma _{2}k_{r\varphi }(\theta _{y}-\theta _{y1})+F_{bx1}=0\\ m_{a}\ddot{y}_{a}-\gamma _{2}c_{1}(\dot{y}-\dot{y}_{1})-\gamma _{2}c_{2} (\dot{\theta }_{x}-\dot{\theta }_{x1})-\gamma _{2}k_{rr}(y-y_{1})-\gamma _{2}k_{r\varphi }(\theta _{x}-\theta _{x1})+F_{by1}=-m_{a}g\\ m_{b}\ddot{x}_{b}-\gamma _{1}c_{1}(\dot{x}-\dot{x}_{1})+\gamma _{1}c_{2} (\dot{\theta }_{y}-\dot{\theta }_{y1})-\gamma _{1}k_{rr}(x-x_{1})+\gamma _{1}k_{r\varphi }(\theta _{y}-\theta _{y1})+F_{bx2}=0\\ m_{b}\ddot{y}_{b}-\gamma _{1}c_{1}(\dot{y}-\dot{y}_{1})-\gamma _{1}c_{2} (\dot{\theta }_{x}-\dot{\theta }_{x1})-\gamma _{1}k_{rr}(y-y_{1})-\gamma _{1}k_{r\varphi }(\theta _{x}-\theta _{x1})+F_{by2}=-m_{b}g\\ m_{o}\ddot{x}_{o}+k_{a}x_{o}-F_{bx2}=0\\ m_{o}\ddot{y}_{o}+k_{a}y_{o}-F_{by2}=-m_{o}g \end{array} \right. \end{aligned}$$

where $x_{1}=\gamma _{2}x_{a}+\gamma _{1}x_{b}$, $y_{1}=\gamma _{2} y_{a}+\gamma _{1}y_{b}$, $\theta _{x1}=(y_{b}-y_{a})/l$ and $\theta _{y1} =(x_{a}-x_{b})/l$ represent the disk center’s rigid body displacements and rotation angles, respectively; $l=l_{1}+l_{2}$ is the total length of the rotating shaft; $l_{1}$ is the length of left part of the shaft, while $l_{2}$ is the right; m, $m_{a}$, $m_{b}$ and $m_{o}$ represent the equivalent mass of the hub, the left and right journals and the outer ring of the bearing, respectively; $k_{rr}$, $k_{r\varphi }$, $k_{\varphi r}$ and $k_{\varphi \varphi }$ represent the equivalent stiffness of the shaft in different directions, respectively; $J_{d}$ and $J_{p}$ represent the moment of inertia and pole moment of inertia of the wheel equator, respectively; $c_{1}-c_{4}$ represent the equivalent damping coefficients of the rotating shaft; $\gamma _{1}$ and $\gamma _{2}$ are the length proportional coefficients, respectively, in which $\gamma _{1}=l_{1}/l\$and $\gamma _{2}=l_{2}/l$; $\delta$ represents the eccentricity of the unbalanced mass; $F_{bx1}$ and $F_{by1}$ are the horizontal and vertical bearing forces at the left end, respectively; $F_{bx2}$ and $F_{by2}$ are the horizontal and vertical bearing force at the right end, respectively; g is the gravitational acceleration.

Expanded form of Eq. (5)

$$\begin{aligned}&\left\{ \begin{array}{l} q_{1}^{^{\prime \prime }}+\zeta _{1}q_{1}^{^{\prime }}-\zeta _{2}q_{4}^{^{\prime } }-(\zeta _{2}+\zeta _{1}\gamma _{2})q_{5}^{^{\prime }}+(\zeta _{2}-\gamma _{1} \zeta _{1})q_{7}^{^{\prime }}+\kappa _{1}q_{1}-\kappa _{2}q_{4}\\ -(\kappa _{2}+\kappa _{1}\gamma _{2})q_{5}+(\kappa _{2}-\gamma _{1}\kappa _{1} )q_{7}=U_{1}\cos \tau \\ q_{2}^{^{\prime \prime }}+\zeta _{1}q_{2}^{^{\prime }}-\zeta _{2}q_{3}^{^{\prime } }-(\zeta _{2}+\zeta _{1}\gamma _{2})q_{6}^{^{\prime }}+(\zeta _{2}-\gamma _{1} \zeta _{1})q_{8}^{^{\prime }}+\kappa _{1}q_{2}-\kappa _{2}q_{3}\\ -(\kappa _{2}+\kappa _{1}\gamma _{2})q_{6}+(\kappa _{2}-\gamma _{1}\kappa _{1} )q_{8}=U_{1}\sin \tau -W\\ \alpha _{0}q_{3}^{^{\prime \prime }}+\alpha _{0}\eta q_{4}^{^{\prime }}+\zeta _{3}q_{2}^{^{\prime }}+\zeta _{4}q_{3}^{^{\prime }}-(\zeta _{4}+\zeta _{3} \gamma _{2})q_{6}^{^{\prime }}+(\zeta _{4}-\gamma _{1}\zeta _{3})q_{8}^{^{\prime } }+\kappa _{3}q_{2}+\kappa _{4}q_{3}\\ -(\kappa _{4}+\kappa _{3}\gamma _{2})q_{6}+(\kappa _{4}-\gamma _{1}\kappa _{3} )q_{8}=0\\ \alpha _{0}q_{4}^{^{\prime \prime }}-\alpha _{0}\eta q_{3}^{^{\prime }}-\zeta _{3}q_{1}^{^{\prime }}+\zeta _{4}q_{4}^{^{\prime }}+(\zeta _{4}+\zeta _{3} \gamma _{2})q_{5}^{^{\prime }}-(\zeta _{4}-\gamma _{1}\zeta _{3})q_{7}^{^{\prime } }-\kappa _{3}q_{1}+\kappa _{4}q_{4}\\ +(\kappa _{4}+\kappa _{3}\gamma _{2})q_{5}-(\kappa _{4}-\gamma _{1}\kappa _{3} )q_{7}=0 \end{array} \right. \\&\left\{ \begin{array}{l} \alpha _{1}q_{5}^{^{\prime \prime }}-\gamma _{2}\zeta _{1}q_{1}^{^{\prime }} +\gamma _{2}\zeta _{2}q_{4}^{^{\prime }}+\gamma _{2}(\zeta _{2}+\gamma _{2}\zeta _{1})q_{5}^{^{\prime }}-\gamma _{2}(\zeta _{2}-\gamma _{1}\zeta _{1})q_{7} ^{^{\prime }}-\gamma _{2}\kappa _{1}q_{1}+\gamma _{2}\kappa _{2}q_{4}\\ +\gamma _{2}(\kappa _{2}+\gamma _{2}\kappa _{1})q_{5}-\gamma _{2}(\kappa _{2} -\gamma _{1}\kappa _{1})q_{7}+\bar{C}_{b}\bar{F}_{bx1}=0\\ \alpha _{1}q_{6}^{^{\prime \prime }}-\gamma _{2}\zeta _{1}q_{2}^{^{\prime }} -\gamma _{2}\zeta _{2}q_{3}^{^{\prime }}+\gamma _{2}(\zeta _{2}+\gamma _{2}\zeta _{1})q_{6}^{^{\prime }}-\gamma _{2}(\zeta _{2}-\gamma _{1}\zeta _{1})q_{8} ^{^{\prime }}-\gamma _{2}\kappa _{1}q_{2}-\gamma _{2}\kappa _{2}q_{3}\\ +\gamma _{2}(\kappa _{2}+\gamma _{2}\kappa _{1})q_{6}-\gamma _{2}(\kappa _{2} -\gamma _{1}\kappa _{1})q_{8}+\bar{C}_{b}\bar{F}_{by1}=-\alpha _{1}W \end{array} \right. \\&\left\{ \begin{array}{l} \alpha _{2}q_{7}^{^{\prime \prime }}-\gamma _{1}\zeta _{1}q_{1}^{^{\prime }} +\gamma _{1}\zeta _{2}q_{4}^{^{\prime }}+\gamma _{1}(\zeta _{2}+\gamma _{2}\zeta _{1})q_{5}^{^{\prime }}-\gamma _{1}(\zeta _{2}-\gamma _{1}\zeta _{1})q_{7} ^{^{\prime }}-\gamma _{1}\kappa _{1}q_{1}+\gamma _{1}\kappa _{2}q_{4}\\ +\gamma _{1}(\kappa _{2}+\gamma _{2}\kappa _{1})q_{5}-\gamma _{1}(\kappa _{2} -\gamma _{1}\kappa _{1})q_{7}+\bar{C}_{b}\bar{F}_{bx2}=0\\ \alpha _{2}q_{8}^{^{\prime \prime }}-\gamma _{1}\zeta _{1}q_{2}^{^{\prime }} -\gamma _{1}\zeta _{2}q_{3}^{^{\prime }}+\gamma _{1}(\zeta _{2}+\gamma _{2}\zeta _{1})q_{6}^{^{\prime }}-\gamma _{1}(\zeta _{2}-\gamma _{1}\zeta _{1})q_{8} ^{^{\prime }}-\gamma _{1}\kappa _{1}q_{2}-\gamma _{1}\kappa _{2}q_{3}\\ +\gamma _{1}(\kappa _{2}+\gamma _{2}\kappa _{1})q_{6}-\gamma _{1}(\kappa _{2} -\gamma _{1}\kappa _{1})q_{8}+\bar{C}_{b}\bar{F}_{by2}=-\alpha _{2}W \end{array} \right. \\&\left\{ \begin{array}{l} \alpha _{3}q_{9}^{^{\prime \prime }}+\kappa _{5}q_{9}-\bar{C}_{b}\bar{F}_{bx1}=0\\ \alpha _{3}q_{10}^{^{\prime \prime }}+\kappa _{5}q_{10}-\bar{C}_{b}\bar{F} _{by1}=-\alpha _{2}W \end{array} \right. \end{aligned}$$

where $q_{1}=x/c$, $q_{2}=y/c$, $q_{3}=\theta _{x}l/c$, $q_{4}=\theta _{y}l/c$, $q_{5}=x_{a}/c$, $q6=y_{a}/c$, $q_{7}=x_{b}/c$ , $q_{8}=y_{b}/c$, $q_{9}=x_{o}/c$ and $q_{10}=y_{o}/c$ are dimensionless displacements of the disk center, the left and right journals, and the outer ring. The dimensionless forces $\bar{F}_{bx1}$, $\bar{F}_{bx2}$, $\bar{F}_{by1}$, and $\bar{F}_{by2}$ have same expressions as shown in Eqs. (3) and (4), respectively, just with the replacement of the corresponding dimensionless parameters.

All other dimensionless parameters are listed as $\alpha _{0}=J_{d}/ml^{2}$, $\alpha _{1}=m_{a}/m$, $\alpha _{2}=m_{b}/m$, $\alpha _{3}=m_{o}/m$, $\kappa _{1}=k_{rr}/m\Omega ^{2}$, $\kappa _{2}=k_{r\varphi }/ml\Omega ^{2}$, $\kappa _{3}=k_{\varphi r}/ml\Omega ^{2}$, $\kappa _{4}=k_{\varphi \varphi }/ml^{2} \Omega ^{2}$, $\kappa _{5}=k_{a}/m\Omega ^{2}$, $\zeta _{1}=c_{1}/m\Omega$, $\zeta _{2}=c_{2}/ml\Omega$, $\zeta _{3}=c_{3}/ml\Omega$, $\zeta _{4} =c_{4}/ml^{2}\Omega$, $\eta =J_{p}/J_{d}$, $U_{1}=\delta _{1}/c$, $\bar{C} _{b}=C_{b}c^{0.5}/m\Omega ^{2}$, and $W=g/c\Omega ^{2}$ , in which $c=mg/k$.