1 Introduction

Linear static response structural optimization is highly efficient and is therefore embedded in a considerable number of applications commonly used during the design process in industry. Many commercial codes are available in this area, enabling sizing, shape, and topology optimization in an acceptable amount of time. The time saving can especially be attributed to the availability of (semi-) analytical sensitivity analysis enabling the application of very efficient gradient-based optimizers. In contrast to the well-established optimization based on linear analysis, the real challenge in optimization is the optimization of highly nonlinear dynamic systems. A prime example is the optimization of crash-related problems in automotive industry which is also the main objective of this paper. Furthermore, we restrict ourselves to the use of commercial crash solvers for the nonlinear dynamic analysis to ensure that the proposed DiESL (difference-based equivalent static load) method can be applied to real automotive crash problems. Worldwide, only explicit solvers are used in automotive crash analysis. Here, the most dominating part of the nonlinearities does not result from material or geometric nonlinearities but from contact forces. They may not only change in magnitude but especially in location from time step to time step. As a consequence, it is very difficult to apply sensitivity analysis which may be the reason that no commercial code in this area is able to compute sensitivities enabling gradient-based optimization for crash. Instead, metamodel-based methods are often used. Examples for such metamodels are polynomials, radial basis functions (Powell 1992; Schaback and Wendland 2001; Schaback 2002), neural networks (Hornik et al. 1990, 1992; Waszczyszyn 1999), and kriging models (Matheron 1963; Cressie 1988, 1989, 1990). The drawback of the metamodel-based optimization is that the number of design variables is limited and applications with extremely high number of design variables such as topology optimization are impossible due to the large number of required designs that need to be evaluated in order to fit the metamodels.

A promising approach to circumvent the missing-sensitivity-problem of commercial crash solvers is to define linear auxiliary load cases enabling linear static response optimization. This means that the nonlinear dynamic optimization problem is solved by solving a sequence of linear static response optimization subproblems. The equivalent static load method (ESLM) provides a procedure to compute such auxiliary load cases. These auxiliary load cases are created by applying equivalent static loads (ESLs) to linear statics.

The ESLM has been successfully applied to various kinds of optimization like sizing, shape, free sizing, and topology optimization (Choi and Park 2002; Park et al. 2005; Lee et al. 2013b; Shin et al. 2007; Lee et al. 2007, 2013a; Jeong et al. 2008; Jang et al. 2012; Hong et al. 2010; Kim and Park 2010; Park 2011; Lee and Park 2015; Karev et al. 2018; Choi et al. 2018; Karev et al. 2019). Nevertheless, the ESLM has some limitations and disadvantages which are discussed in this paper. The main issues result from the fact that the ESLs are always calculated based on the undeformed initial geometry. The idea presented in this paper tries to overcome these issues by using a difference-based approach for calculating the ESLs. The focus is on solving nonlinear dynamic response optimization problems which require usage of explicit solvers.

This paper is structured in the following way: In Section 2, the ESLM approach is presented. In Section 3, a difference-based extension for calculating the ESLs called the DiESL method is introduced in detail. In that process, a general approach for handling structural responses is given. Furthermore, the implementation of the DiESL method is explained. Afterwards, the DiESL approach is tested and compared to the ESLM for two different examples in Section 4. Finally, a conclusion and an outlook are worked out.

2 The ESLM (equivalent static load method)

The ESLM has been introduced by Choi and Park (Choi and Park 2002). It provides a well-defined procedure to create linear auxiliary load cases for nonlinear dynamic response optimization problems which are used in optimization based on linear static analysis. The objective function and the constraints used in the linear static response optimization and in the nonlinear dynamic response optimization are identical. The only difference is that the nonlinear dynamic responses are approximated by linear static responses. For dynamic responses such as section forces, velocities, and accelerations, which are not defined in linear statics, it is necessary to find proper approximations. For velocity and acceleration, for instance, simple finite forward (Jeong et al. 2010) or central (Karev et al. 2018; Karev et al. 2019) differences between adjacent load cases (corresponding to adjacent time steps) can be used. The advantage of ESLM is that well-developed commercial software systems such as MSC NASTRAN, Altair OptiStruct, or VRAND GENESIS can be used for analysis and optimization and no development of own sensitivity analysis and optimization algorithm is necessary. In this sense, ESLM is not an optimization algorithm but a method to transform an optimization problem involving nonlinear and/or dynamic responses into one using responses from a set of linear static subcases.

The procedure for computing the ESLs of the auxiliary load cases is now the following: In the first step, the user defines a set of nT time steps ti, i = 1, …, nT, to capture the behavior of the nonlinear problem with sufficient accuracy. The basic idea is now to calculate loads \( {\mathbf{f}}_{\mathrm{ESL}}^i \) which yield the same displacement vector ui in linear statics as those obtained for the selected time steps ti in the nonlinear dynamic analysis uNL(ti) (Park 2011). Thus, the loads received are equivalent in the sense that they lead to same displacement fields.

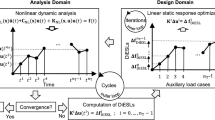
In Fig. 1, the process of the ESLM is illustrated for a nonlinear dynamic problem. The process starts in the analysis domain with a nonlinear dynamic analysis from which the displacement vectors uNL(ti) for nT user-selected time steps ti are obtained. The equivalent static loads \( {\mathbf{f}}_{\mathrm{ESL}}^i \) are then calculated by multiplying the stiffness matrix K(x) by the displacements fields

$$ \mathbf{K}\left(\mathbf{x}\right){\mathbf{u}}^{\mathrm{NL}}\left({t}^i\right)={\mathbf{f}}_{\mathrm{ESL}}^i;i=1,\dots, {n}_{\mathrm{T}}. $$
(1)
Fig. 1
figure 1

Optimization process of ESLM and DiESL methods for a nonlinear dynamic problem (note that equations and symbols refer to ESLM and are different for DiESL)

Full size image

This leads to a set of ESLs and a corresponding linear auxiliary load case for each time step ti. Based on these nT load cases, linear static response optimization is performed in the design domain afterwards. All load cases are based on the same FE model (i.e., with the same initial geometry) and thus have the same stiffness matrix K(x). Hence, the optimization can be performed with a single optimization deck containing nT subcases. After the optimization step (inner loop), nonlinear analysis has to be applied again with the updated design variables. In the following, the outer loop iterations are called cycles to distinguish them from the iterations of the inner loop in the linear static response subproblem.

Note that the displacement fields of the nonlinear and the linear analysis are identical only at the beginning of the optimization in the inner loop. At the end of the inner loop, the linear and the nonlinear dynamic responses no longer match perfectly because the linear auxiliary load cases are only an approximation of the nonlinear behavior of the system. If the difference is too high, the process is iterated (outer loop) until the difference is small enough and additional termination criteria (Shin et al. 2007; Jeong et al. 2010; Kim and Park 2010; Park 2011) are fulfilled. Furthermore, it can be expected that the difference between the linear and nonlinear dynamic responses increases with the length of the inner loop optimization path. If this difference is too high, the update in the outer loop may result in huge changes in the search directions and convergence is slowed down or even not guaranteed anymore. For this reason, commercial ESLM codes, such as VRAND ESLDYNA, limit the number of iterations and offer the application of move limits to restrict the length of the inner loop optimization path in each cycle.

ESLM has been successfully applied to different types of optimization and analyses (Park 2011) such as

  • linear dynamic response optimization

    $$ \mathbf{M}\left(\mathbf{x}\right)\ddot{\mathbf{u}}+\mathbf{C}\dot{\mathbf{u}}+\mathbf{K}\left(\mathbf{x}\right)\mathbf{u}=\mathbf{f}(t) $$
    (2)

  • structural optimization for multi-body dynamic systems

  • structural optimization for flexible multi-body dynamic systems

  • nonlinear static response optimization

    $$ {\mathbf{K}}^{\mathrm{NL}}\left(\mathbf{x},{\mathbf{u}}^{\mathrm{NL}}\right){\mathbf{u}}^{\mathrm{NL}}=\mathbf{f} $$
    (3)

  • nonlinear dynamic response optimization

    $$ \mathbf{M}\left(\mathbf{x}\right){\ddot{\mathbf{u}}}^{\mathrm{NL}}+\mathbf{C}\left(\mathbf{x}\right){\dot{\mathbf{u}}}^{\mathrm{NL}}+{\mathbf{K}}^{\mathrm{NL}}\left(\mathbf{x},\mathbf{u}\right){\mathbf{u}}^{\mathrm{NL}}=\mathbf{f}(t) $$
    (4)

The most challenging application is the optimization of crash problems in the field of nonlinear dynamic response optimization, which is the focus of this publication. The original crash optimization problem can be stated as

$$ \min f\left(\mathbf{x},{\mathbf{u}}^{\mathrm{NL}}\left(\mathbf{x},t\right)\right) $$
(5a)
$$ \mathrm{s}.\mathrm{t}.{g}_j\left(\mathbf{x},{\mathbf{u}}^{\mathrm{NL}}\left(\mathbf{x},t\right)\right)\le 0;j=1,\dots, m $$
(5b)
$$ {\mathbf{x}}^{\mathrm{L}}\le \mathbf{x}\le {\mathbf{x}}^{\mathrm{U}};\mathbf{x}\in {\mathbb{R}}^n $$
(5c)

Here, f(x) is the objective function, m the number of constraints gj, and xL and xU are the lower and upper bounds of the design variable x, respectively. The displacement vector uNL is the solution of

$$ \mathbf{M}\left(\mathbf{x}\right){\ddot{\mathbf{u}}}^{\mathrm{NL}}(t)+\mathbf{C}\left(\mathbf{x}\right){\dot{\mathbf{u}}}^{\mathrm{NL}}(t)+{\mathbf{K}}^{\mathrm{NL}}\left(\mathbf{x},{\mathbf{u}}^{\mathrm{NL}}(t)\right){\mathbf{u}}^{\mathrm{NL}}(t)=\mathbf{f} $$
(5d)

For crash problems, the external forces f are typically zero (except for gravity) but the internal forces fint =  − KNLuNL may change in magnitude and location very fast from time step to time step due to contact. Commercial codes are available for crash analysis such as LSTC LS-DYNA, ESI Pam-Crash, or Altair RADIOSS. They use an explicit time integration scheme and a penalty formulation for contacts. This means that the contacts are modeled by springs and a very time-consuming task in a crash code is the computation of contact areas and resulting contact forces. It results in an adding and removing of contact spring elements for closing or opening contacts, respectively. Of course, such codes can handle complicated nonlinear material models and geometric nonlinearities as well. Nevertheless, the most important or dominating nonlinearities result from the contacts.

The ESLM solves the following optimization problem:

$$ \min f\left(\mathbf{x},\mathbf{u}\left(\mathbf{x}\right)\right) $$
(6a)
$$ \mathrm{s}.\mathrm{t}.{g}_j\left(\mathbf{x},\mathbf{u}\left(\mathbf{x}\right)\right)\le 0;j=1,\dots, m $$
(6b)
$$ {\mathbf{x}}^{\mathrm{L}}\le \mathbf{x}\le {\mathbf{x}}^{\mathrm{U}};\mathbf{x}\in {\mathbb{R}}^n $$
(6c)

where u is the solution of

$$ \mathbf{K}\left(\mathbf{x}\right){\mathbf{u}}^i={\mathbf{f}}_{\mathrm{ESL}}^i;i=1,\dots, {n}_{\mathrm{T}}, $$
(6d)

the equivalent static loads \( {\mathbf{f}}_{\mathrm{ESL}}^i \) for load case i are computed as

$$ {\mathbf{f}}_{\mathrm{ESL}}^i=\mathbf{K}\left(\mathbf{x}\right){\mathbf{u}}^{\mathrm{NL}}\left({t}^i\right);i=1,\dots, {n}_{\mathrm{T}} $$
(6e)

and uNL(ti) is the solution of

$$ \mathbf{M}\left(\mathbf{x}\right){\ddot{\mathbf{u}}}^{\mathrm{NL}}(t)+\mathbf{C}\left(\mathbf{x}\right){\dot{\mathbf{u}}}^{\mathrm{NL}}(t)+{\mathbf{K}}^{\mathrm{NL}}\left(\mathbf{x},{\mathbf{u}}^{\mathrm{NL}}(t)\right){\mathbf{u}}^{\mathrm{NL}}(t)=\mathbf{f}(t) $$
(6f)

for the selected time steps ti.

It was stated in Park and Kang 2003 that the Karush-Kuhn-Tucker (KKT) conditions of the linear static subproblem and the original dynamic problem are identical if the ESLM satisfies specific termination criteria. Stolpe 2014 showed that the proof is incomplete and not correct. According to Stolpe, the most critical point is that the displacement sensitivities of the original problem and the subproblem are not necessarily identical. Therefore, Stolpe supposes an alternative algorithm where these sensitivities are identical by definition. However, the supposed algorithm requires the computation of sensitivities of the original dynamic problem and is therefore not applicable to optimization of crash problems. Furthermore, Stolpe et al. 2018 presented an example illustrating that ESLM may fail to find the optimal design of the dynamic response optimization problem. Nevertheless, the topic is still under discussion because Park and Lee claimed in their latest publication (Park and Lee 2019) that Stolpe’s correction had now been taken into account and that the ESLM solution is a KKT point if additional mathematical aspects are added. This discussion history demonstrates how difficult it is sometimes to prove convergence and optimality criteria for methods based on an engineering approach such as ESLM. The same holds for the DiESL approach presented in the next chapter and future will show if it is possible to prove if this method really guarantees to find the optimum of the original dynamic problem.

3 The DiESL (difference-based equivalent static loads) method

As mentioned above, ESLM is not really an optimization algorithm but a method to compute linear static auxiliary load cases to approximate nonlinear dynamic responses. The intention of DiESL is to improve this approximation quality as well as the resulting approximation quality of the sensitivities. It can be expected that the better the approximation quality, the higher the convergence speed of the optimization. It is intended to improve the ESLM by improving the approximation of the sensitivities.

To explain the idea of DiESL, we assume that a nonlinear dynamic FE analysis has been carried out. We now study the nonlinear spatial path of an arbitrary FEM node where its location at time t = 0 corresponds to the initial undeformed structure and the coordinate at t = ti to the deformed structure at this time step (see Fig. 2, left). The main drawback of ESLM is that it always starts from the initial undeformed structure. This means that we always obtain a linear “path” from the location at t = 0 to the location at t = ti if we want to compute the ESLs for displacement uNL(ti) in linear static path (Fig. 2, middle). This “path” is in general completely different from the nonlinear path, causing the following issues:

  • The ESLs in the linear static subproblem are completely different to the nodal forces in the original nonlinear dynamic problem. Typically, the ESLs are significantly higher.

  • The strains in the linear static subproblem and the nonlinear dynamic problem are completely different.

  • The stresses in the linear static subproblem and the nonlinear dynamic problem are completely different.

  • The sensitivities in the linear static subproblem and the nonlinear dynamic problem may be completely different and may not even match in sign.

Fig. 2
figure 2

Displacement path of an arbitrary node during the deformation of a structure (left) and the corresponding displacement uNL(ti) (middle) and ΔuNL(ti) (right) used for the computation of the ESLs and DiESLs at time step ti, respectively

Full size image

The idea of the difference-based equivalent static loads (DiESL) is now to improve the approximation quality of the subproblem by following the nonlinear displacement path. Here, the displacements of each node j at time step ti used for computing the ESLs are not referring to the initial coordinates rj(t = 0), but to the coordinates of the deformed geometry rj(ti − 1) at the previous time step ti − 1 (Fig. 2, right). As a consequence, the DiESL approach requires nT FE models, one for each time step ti, i = 0, …, nT − 1 (note: t0 corresponds to the first FE model with undeformed geometry at t = 0). In the following, we call each of these FE models at time step ti the “ith linear submodel” (LSMi). An additional consequence is that the approximation of a nonlinear displacement at time ti is no longer given by the displacement of load case i but as a sum of incremental displacements of different LSMis. Each LSMi is created by modifying the coordinates of each node without changing the topology of the FE mesh.

The node coordinates of an LSMi are collected in the vector

$$ {\mathbf{r}}^T\left({\mathrm{t}}^i\right)=\left({\mathbf{r}}_1^T\left({t}^i\right),{\mathbf{r}}_2^T\left({t}^i\right),\dots, {\mathbf{r}}_{n_{\mathrm{N}}}^T\left({t}^i\right)\right) $$
(7)

which contains the coordinates rj(ti) of all nN nodes. Accordingly, r(t0) describes the coordinates of all nodes of the undeformed model. Furthermore, the vector

$$ {\mathbf{u}}^{\mathrm{N}\mathrm{L}}{(t)}^T=\left({\mathbf{u}}_1^{\mathrm{N}\mathrm{L}}{(t)}^T,{\mathbf{u}}_2^{\mathrm{N}\mathrm{L}}{(t)}^T,\dots, {\mathbf{u}}_{n_{\mathrm{N}}}^{\mathrm{N}\mathrm{L}}{(t)}^T\right) $$
(8)

contains the nonlinear displacements of all nN nodes at the time t. The coordinates of a linear submodel LSMi describing the deformed geometry at time ti can therefore be calculated by

$$ \mathbf{r}\left({t}^i\right)=\mathbf{r}\left({t}^0\right)+{\mathbf{u}}^{\mathrm{NL}}\left({t}^i\right). $$
(9)

Note that we used the ESLM displacement “path” to compute the coordinates of the deformed geometry in (9). Generally, this can also be done by summing up the incremental displacements ΔuNL(ti) (see Fig. 2, right) but this is more complicated and leads to the same result.

To determine the incremental equivalent static loads \( {\Delta \mathbf{f}}_{\mathrm{DiESL}}^i \) in the linear submodel LSMi, the corresponding stiffness matrix Ki = K(x, r(ti)), which depends on the design variables x and the nodal coordinates r(ti) of LSMi, has to be multiplied by the vector of the incremental nonlinear displacements ΔuNL(ti)

$$ {\mathbf{K}}^i\Delta {\mathbf{u}}^{\mathrm{NL}}\left({t}^i\right)=\Delta {\mathbf{f}}_{\mathrm{DiESL}}^i. $$
(10)

The incremental nonlinear displacements leading from r(ti) to r(ti + 1) are calculated by

$$ \Delta {\mathbf{u}}^{\mathrm{NL}}\left({t}^i\right)={\mathbf{u}}^{\mathrm{NL}}\left({t}^{i+1}\right)-{\mathbf{u}}^{\mathrm{NL}}\left({t}^i\right) $$
(11)

which is illustrated in Fig. 3 for an arbitrary node. Using the incremental equivalent static loads \( \Delta {\mathbf{f}}_{\mathrm{DiESL}}^i \), gradient-based linear static response optimization can now be performed similar as described before for the ESLM as illustrated in Fig. 1. But in contrast to the ESLM, which requires only a single FE model representing the undeformed structure of the underlying initial model, now nT FE models have to be considered in one optimization run. Consequently, multi-model optimization (MMO) has to be applied where more than one FE model can be taken into account simultaneously in one linear static response optimization run. Here, the FE equation of linear statics

$$ {\mathbf{K}}^i\Delta {\mathbf{u}}^i=\Delta {\mathbf{f}}_{\mathrm{DiESL}}^i $$
(12)

is solved for each LSMi, which yields the incremental linear displacements \( \Delta {{\mathbf{u}}^i}^T=\left(\Delta {{\mathbf{u}}_1^i}^T,\Delta {{\mathbf{u}}_2^{\mathrm{i}}}^T,\dots, \Delta {{\mathbf{u}}_{n_{\mathrm{N}}}^i}^T\right) \).

Fig. 3
figure 3

Relationship between absolute and incremental displacements

Full size image

Figure 4 illustrates the benefits of the DiESL approach based on the example of a three-point bending load case. ELSM can only capture the bending behavior of the beam but not the tensile stress that occurs in the deformed states. The reason is that ESLM always starts from the undeformed structure; hence, the stiffness matrix K is assembled from only bending contributions for all beam elements. There are no tensile stiffness contributions which appear only after deformation. In contrast, DiESL captures the tensile stiffness contributions because it is based on deformed structures as illustrated on the right side of Fig. 4. Here, the dotted and the solid lines show the deformed shape at t = ti − 1 and t = ti, respectively. The displacements ΔuNL(ti − 1) describe the gap between the dotted and the solid line, and it is obvious that the smaller ΔuNL(ti − 1), the more accurately the nonlinearities should be captured. Furthermore, it is expected that the nonlinear strains can be determined by linear theory with sufficient accuracy if one chooses the difference between time step ti and ti − 1 adequately small. Note that the linear strains of each LSM can be considered as “true strains” because they are based on deformed geometries. In addition, the DiESL approach can also capture the dependencies of the stiffness matrix on the displacements, because each stiffness matrix Ki is now based on the deformed structure at time step ti.

Fig. 4
figure 4

Different states of deformation in three-point bending illustrating the benefits of the DiESL approach

Full size image

Summarizing, the DiESL approach solves the following optimization problem:

$$ \min f\left(\mathbf{x},\Delta {\mathbf{u}}^0\left(\mathbf{x}\right),\dots, \Delta {\mathbf{u}}^{n_T-1}\left(\mathbf{x}\right)\right) $$
(13a)
$$ \mathrm{s}.\mathrm{t}.{g}_j\left(\mathbf{x},\Delta {\mathbf{u}}^0\left(\mathbf{x}\right),\dots, \Delta {\mathbf{u}}^{n_T-1}\left(\mathbf{x}\right)\right)\le 0;j=1,\dots, m $$
(13b)
$$ {\mathbf{x}}^{\mathrm{L}}\le \mathbf{x}\le {\mathbf{x}}^{\mathrm{U}};\mathbf{x}\in {\mathbb{R}}^n $$
(13c)

where Δui is the solution of

$$ {\mathbf{K}}^i\left(\mathbf{x}\right)\Delta {\mathbf{u}}^i={\Delta \mathbf{f}}_{\mathrm{DiESL}}^i;i=0,\dots, {n}_{\mathrm{T}}-1 $$
(13d)

in LSMi, the equivalent static loads \( \Delta {\mathbf{f}}_{ESL}^i \) are computed as

$$ {\Delta \mathbf{f}}_{\mathrm{DiESL}}^i={\mathbf{K}}^i\left(\mathbf{x}\right)\left({\mathbf{u}}^{\mathrm{NL}}\left({t}^{i+1}\right)-{\mathbf{u}}^{\mathrm{NL}}\left({t}^i\right)\right);i=0,\dots, {n}_T-1 $$
(13e)

and uNL(ti) is the solution of

$$ \mathbf{M}\left(\mathbf{x}\right){\ddot{\mathbf{u}}}^{\mathrm{NL}}(t)+\mathbf{C}\ \left(\mathbf{x}\right){\dot{\mathbf{u}}}^{\mathrm{NL}}(t)+{\mathbf{K}}^{\mathrm{NL}}\left(\mathbf{x},{\mathbf{u}}^{\mathrm{NL}}(t)\right){\mathbf{u}}^{\mathrm{NL}}(t)=\mathbf{f}(t) $$
(13f)

for the selected time steps ti.

In the following, it is described in more detail how different kinds of structural responses are handled in the DiESL approach.

3.1 Computation of displacements

During optimization of all LSMs using MMO, each LSM analysis yields incremental displacements. The total linear displacement of a node at time ti is used as an approximation of the respective nonlinear displacement ui ≈ uNL(ti). It can be computed recursively as

$$ {\mathbf{u}}^i={\mathbf{u}}^{i-1}+\Delta {\mathbf{u}}^{i-1} $$
(14)

where Δui − 1 is the solution of (12) for LSMi − 1. Accordingly, the accumulated displacements can be calculated as

$$ {\mathbf{u}}^i={\mathbf{u}}^0+{\sum}_{j=0}^{i-1}\Delta {\mathbf{u}}^j. $$
(15)

In general, u0 = 0 applies. This accumulation is processed by the MMO, which handles all LSMs and accumulates their solutions Δui.

3.2 Computation of strains and stresses

Strains and stresses can be accumulated in a similar way as the displacements. The procedure is shown in the following for strains. A strain component εi in LSMi is calculated as

$$ {\varepsilon}^i={\varepsilon}^{i-1}+{\alpha}^{i-1}\Delta {\varepsilon}^{i-1}.\kern0.5em $$
(16)

Here, the scaling factor α is introduced to obtain a better description of nonlinearities such as geometric nonlinearity and plastic material behavior. The factor is calculated as

$$ {\alpha}^{i-1}=\frac{\varepsilon^{\mathrm{NL}}\left({t}^i\right)-{\varepsilon}^{\mathrm{NL}}\left({t}^{i-1}\right)}{\Delta {\hat{\varepsilon}}^{i-1}} $$
(17)

where \( \Delta {\hat{\varepsilon}}^{i-1} \) in (17) is the linear static strain value in LSMi − 1 computed at the beginning of the linear static optimization (i.e., iteration 0) in each cycle. The nonlinear true strains εNL(ti) and εNL(ti − 1) are obtained from the nonlinear analysis. The accumulated strain can be calculated as

$$ {\varepsilon}^i={\varepsilon}^0+{\sum}_{j=0}^{i-1}{\alpha}^j\Delta {\varepsilon}^j $$
(18)

where in general ε0 = 0 applies. Note that the linear static strain εi is also a true strain, at least in good approximation, because it is computed based on the respective deformed geometries in each LSM. Hence, the correction factor α for strains is not necessary if the time difference between adjacent LSMs is small enough. This is not necessarily true for stresses in the plastic area because the effective plastic yield stress tangent modulus differs strongly from the linear Young’s modulus.

3.3 Computation of velocities and accelerations

Generally, velocities and accelerations can be computed in good approximation as finite differences of displacements between adjacent time steps if the time step in between is sufficiently small. In DiESL, this is simplified because the solution Δui of LSMi is already a difference. Consequently, the velocity \( {\dot{\mathbf{u}}}^i \) at time step ti can simply be computed as forward difference by

$$ {\dot{\mathbf{u}}}^i=\frac{\Delta {\mathbf{u}}^i}{\Delta {t}^i} $$
(19)

where Δti is the time difference between LSMi and LSMi + 1. Hence, the acceleration can be calculated as

$$ {\ddot{\mathbf{u}}}^i=\frac{{\dot{\mathbf{u}}}^i-{\dot{\mathbf{u}}}^{\boldsymbol{i}-\mathbf{1}}}{\Delta {\overline{t}}^{i,i-1}};\kern35pt \Delta {\overline{t}}^{i,i-1}=\frac{\Delta {t}^i+\Delta {t}^{i-1}}{2}. $$
(20)

3.4 Implementation

In a first step, a Python code of the ESLM (Spohner 2018; Triller 2019) had been developed. In a second step, this code was extended to handle both ESL and DiESL methods. It uses the commercial solver LSTC LS-DYNA (LSTC 2015) for nonlinear dynamic analysis and OptiStruct (HyperWorks A 2012) for the computation of the ESLs and for the linear static response optimization. Furthermore, the same termination criteria were used for both methods ESLM and DiESL. The first criterion is that the design has to be feasible. Since the linear static subproblem only provides estimations for the actual problem, the convergence check has to be performed after the nonlinear dynamic analysis. However, the responses of the linear static analysis often differ from those of the nonlinear dynamic analysis. In some cases, to avoid unnecessary cycles with little changing design variables, a small constraint violation may be tolerated. Hence, the implemented first convergence criterion is that the maximum normalized constraint violation gmax has to be smaller than a specified limit δ:

$$ {g}_{\mathrm{max}}\le \delta $$
(21)

The second criterion is that the relative change of the objective function between two subsequent cycles k − 1 and k has to be smaller than a given value ϵ:

$$ \frac{\left|f\left({\mathbf{x}}^{(k)}\right)-f\left({\mathbf{x}}^{\left(k-1\right)}\right)\right|}{\left|f\left({\mathbf{x}}^{(k)}\right)\right|}\le \epsilon $$
(22)

The values δ = 0.01 and ϵ = 0.01 have been used for both test problems.

For the limitation of the length of the optimization path in the inner loop, in the current implementation of the ESL and DiESL method, the same strategy is used as in the commercial code ESLDYNA (VRAND 2012) based on two parameter sets. The first set controls the move limits of the current cycle k:

$$ {\displaystyle \begin{array}{c}{\hat{x}}_i^{\mathrm{U},(k)}=\min \left({x}_i^{\mathrm{U}},{x}_i^{\left(k-1\right)}+D\left|{x}_i^{\left(k-1\right)}\right|\right)\\ {}{\hat{x}}_i^{\mathrm{L},(k)}=\max \left({x}_i^{\mathrm{L}},{x}_i^{\left(k-1\right)}-D\left|{x}_i^{\left(k-1\right)}\right|\right);D\in \left[0,1\right]\end{array}} $$
(23)

Parameter D controls the size of the current move limits in cycle k by means of two parameters Dini and βred. The parameter Dini corresponds to the initial value of D in (23). The reduction factor βred ∈ (0, 1] is used to control how D changes from cycle to cycle (outer loop)

$$ {\displaystyle \begin{array}{c}D(1)={D}_{\mathrm{ini}};k=1\\ {}D(k)=D(1){\beta}_{\mathrm{red}}^{k-1};k>1.\end{array}} $$
(24)

In this publication, the parameter set Dini = 0.2 and βred = 0.9 has been used in all test problems. The other parameter set controls the number of iterations (inner loop) by the parameters \( ma{x}_{\mathrm{ite}{\mathrm{r}}_{\mathrm{ini}}} \) and maxiter defining the maximum number of iterations per cycle in the first and in subsequent cycles (outer loop), respectively. For all examples shown below, the parameter set \( ma{x}_{\mathrm{ite}{\mathrm{r}}_{\mathrm{ini}}}= ma{x}_{\mathrm{ite}\mathrm{r}}=2 \) has been used. This means that each cycle contains 2 iterations.

Very often, the FE mesh topologies in the nonlinear dynamic and the linear model are not identical. In such a case, all the coordinates and responses are mapped from the nonlinear dynamic to the linear static mesh before applying the formulas described above. In the test problems below, this was not necessary because the mesh topologies in the LS-DYNA and the OptiStruct model were identical.

Due to the fact that DiESL does not start from a single undeformed initial model but from deformed structures related to the different LSMs, it may happen that the linear static response optimization terminates with an error during the calculation of the ESLs due to excessively deformed elements and thus poor element quality. In order to realize a robust application of DiESL, an automatic repair mechanism for the mesh of the affected LSMs has been developed by deleting the failed elements. Note that such failed elements typically do not appear in all but only in a few LSMs at very early cycles only. For this reason, the deleted elements of the previous cycle are added back at the beginning of each cycle and it is checked again if there are failed elements. Furthermore, it should be noted that in all applications in this paper, failed elements appeared only in the early cycles at 3 of the 20 DOE (Design of Experiments) points described in chapter 4.2. Here, some initial thicknesses were very low leading to huge deformations and thus distorted elements.

The overall flow scheme explained before is implemented as follows:

  1. Step 1:

    Set initial design variables and parameters (k = 0, x(k = 0), δ, ϵ, Dini, \( {\beta}_{\mathrm{r}\mathrm{ed}},\kern0.5em ma{x}_{\mathrm{ite}{\mathrm{r}}_{\mathrm{ini}}} \), maxiter)

  2. Step 2:

    Perform nonlinear dynamic analysis with xk

  3. Step 3:

    If k > 0, check criteria of convergence for ti: if (21) and (22) are satisfied then terminate the process.

  4. Step 4:

    If the mesh of the model used for nonlinear dynamic analysis and linear static response optimization is not identical, map nonlinear displacements to linear static mesh.

  5. Step 5:

    Calculate the incremental displacements ΔuNL(ti) and the node coordinates rT(ti) of all LSMs for all selected time steps ti

  6. Step 6:

    Check the element quality of each LSM FE mesh. If check was not successful, delete failed elements in respective LSM and repeat Step 6 for the remaining mesh.

  7. Step 7:

    Calculate the incremental equivalent static loads \( \Delta {\mathbf{f}}_{\mathrm{DiESL}}^i \)

  8. Step 8:

    Update the move limits D according to (24)

  9. Step 9:

    Solve the linear static response optimization problem with the incremental equivalent static loads \( \Delta {\mathbf{f}}_{\mathrm{DiESL}}^i \)

  10. Step 10:

    Update the design variables in the nonlinear model, set k = k + 1, and go to Step 2

Note that the scheme of the ESL algorithm is similar: \( \Delta {\mathbf{f}}_{\mathrm{DiESL}}^i \) is replaced by \( {\mathbf{f}}_{\mathrm{ESL}}^i \) above, and Steps 5 and 6 can be omitted.

4 Test problems

Two test problems for comparison of the two methods ESLM and DiESL are presented in this chapter. The first test problem is a simple 1-dimensional academic example with only one design variable for which the optimum can be determined graphically or by applying bisection. It has the advantage that the optimal solution can be computed easily in advance and that there are no local minima. Therefore, it is an ideal test example to compare the convergence speed of ESLM and DiESL without distorting influences such as becoming trapped in a local minimum. Furthermore, it is well suited for the approximation capability of structural responses such as strains. The second test problem is a more practical example because a simplified model for a crash side impact problem with 7 design variables is used. Both test problems represent sizing optimization problems in which the mass of the structure is to be minimized, while the intrusion of an impactor is constrained. A contact formulation for the contact between impactor and structure is used in the LS-DYNA and the OptiStruct model for both test problems. Consequently, the displacement of the impactor is used as response for the constraint in each example. For both test problems the averaged run times per cycle are given in tables 3 and 4 in the appendix

For the second test problem, we compare both ESLM and DiESL results with the result of the commercial code LSTC LS-OPT (LSTC 2015). LS-OPT uses the Successive Response Surface Method (SRSM) (Roux et al. 1998; Stander and Craig 2002) which is a metamodel-based approach. It starts with a DOE in the current subdomain, which is the whole design space at the beginning of the optimization. After computing all responses of interest at the sample points, the metamodels are created in the current subdomain for both objective function and constraints, and then, the optimization problem based on the metamodels is solved. The optimized point becomes the center of the new subdomain (panning). Additionally, the size of the subdomain is reduced (zooming) during the iterations. This procedure is repeated until termination criteria are fulfilled. We used the recommended default settings in LS-OPT, which are DOE creation with 50% oversampling and D-optimal samples (Roux et al. 1998) and a linear regression as metamodel.

4.1 Three-point bending test

As shown in Fig. 5, a rigid cylindrical impactor with diameter = 100 mm, massimpactor = 1.256 kg and initial speed vz =  − 7.5 m/s strikes a rectangular sheet metal plate (length = 300 mm, width = 25.47 mm, thickness = x1, Youngs’s modulus E = 210 GPa, density ρ = 7850 kg/m3, LS-DYNA element type = fully integrated shells) which has fixed translational degrees of freedom in x- and z-direction on both ends. Bilinear plastic material (tangent modulus = 0.6 GPa, yield stress = 0.25 GPa) is assigned to the sheet metal. The impactor is constrained to motion in z-direction only. Both impactor and plate are subjected to gravitation g = 9.81 m/s2.

Fig. 5
figure 5

Three-point bending test setup

Full size image

The FE model used for modeling is shown in Fig. 6. In order to reduce the computational costs of the model, only a quarter of the whole model is used by applying symmetry conditions. Both linear and nonlinear dynamic analyses are based on the same mesh, and contact between impactor and plate is defined in both models. The plate’s elements are colored by the value of the normal strains in global x-direction as obtained from the nonlinear dynamic simulation at time t = 12.5 ms for the initial configuration. The majority of the plate shows a relatively homogeneous tensile strain distribution and the superimposed bending strains on the left where the plate wraps around the rigid impactor. Three elements near the longitudinal symmetry line were chosen as representative elements for detailed strain analysis: (1) plate center near the impactor, (3) near the clamping (but not too close), and (2) in between.

Fig. 6
figure 6

Quarter FE model (bottom view in z-direction) of the three-point bending test used for linear and nonlinear analysis and three representative elements 1, 2, and 3

Full size image

The objective of the optimization problem is to minimize the mass of the sheet metal while the intrusion d of the impactor must not exceed 45 mm. The thickness of the sheet metal x1 ∈ [0.85 mm, 2 mm] is the only design variable. Consequently, the optimization problem reads as

$$ \mathrm{suchthat}{\displaystyle \begin{array}{c}\min\ mass\left({x}_1\right)\\ {}d\left({x}_1\right)\le 45\ \mathrm{mm}\\ {}0.85\ \mathrm{mm}\le {x}_1\le 2\ \mathrm{mm}\end{array}} $$

For the selection of ESL times, the following consideration had been made: For the initial value \( {x}_1^{(0)}=0.85\ \mathrm{mm} \), the maximum intrusion \( d\left({x}_1^{(0)}\right)\approx 60\ \mathrm{mm} \), as illustrated in Fig. 7, occurs at time t ≈ 12.5 ms. Hence, the design is infeasible. This means that the optimizer will increase the stiffness to become feasible. Increasing stiffness will cause the maximum deflection to move to smaller times. Therefore, the last ESL time can be set to 12.5 ms to ensure that the maximal intrusions are captured. In order to resolve the maximum intrusion and to capture the nonlinear displacement path (Fig. 2, left) properly, ten uniformly distributed ESL time steps from 1.25 to 12.5 ms have been used for ESLM and DiESL. This results in ten auxiliary load cases in ESLM and ten LSMs with one load case each in DiESL.

Fig. 7
figure 7

Intrusion d(x1) over time for the initial design and optimal design

Full size image

The optimization histories of the ESL and DiESL method are shown in Figs. 8 and 9, respectively. The objective function and the normalized maximum constraint violation are plotted in the left diagrams as a function of cumulated iterations. For example, this means for the selected values of \( ma{x}_{\mathrm{ite}{\mathrm{r}}_{\mathrm{ini}}}= ma{x}_{\mathrm{ite}\mathrm{r}}=2 \) that the cumulated iteration 4 is the second iteration in the linear static response optimization in cycle 2 and the cumulated iteration 5 is the first iteration in the linear static response optimization in cycle 3. Blue circles show the values of each linear static response optimization iteration whereas red circles mark values obtained from nonlinear analyses of each cycle. The constraint violation decreases during optimization iterations until the allowed level of constraint violation is reached (1% in this example). Typically, the approximation error in the linear model can be seen at the beginning of each cycle (after every 2 iterations in our example, i.e., after iteration 2, 4, 6, …) after recalculation of the responses by the nonlinear solver. The approximation error results in an increase of the maximum constraint violation at all even iteration numbers in the history diagram. In this case, there is no jump in the objective function, because mass can be calculated exactly in the subproblem for sizing optimization. The right diagrams plot the relative change of objective function and maximum constraint violation in the design domain over cycles together with the respective termination criteria ϵ and δ. We used cycles here and not cumulated iterations because these criteria are only tested once per cycle. It turns out that both methods find the optimum, but it can be seen that DiESL satisfies the termination criteria within fewer cycles than ESLM.

Fig. 8
figure 8

Objective function and maximum relative constraint violation over cumulated iterations (left) and convergence criteria over cycles (right) using ESL

Full size image
Fig. 9
figure 9

Objective function and maximum relative constraint violation over cumulated iterations (left) and convergence criteria over cycles (right) using DiESL

Full size image

Figures 10 and 11 examine the normal strains in the x-direction in the three representative elements (see Fig. 6). In Fig. 10, each subfigure shows the strains from the nonlinear dynamic analysis as well as from the DiESL and ESL approach at the beginning of the linear static response optimization. The order of legend entries reflects the chronological order of execution: first, the nonlinear dynamic analysis is executed. Then, the linear static analysis at the beginning of the optimization takes place (after having computed the ESLs). This means, the linear models merely reproduce the nonlinear results because no optimization has taken place yet. The first subplot shows the strains for the central element 1. Both ESLM and DiESL give excellent agreement with the nonlinear dynamic analysis. However, for elements 2 and 3, the ESLM strains no longer match with those from the nonlinear dynamic analysis, whereas the DiESL approach still provides a reasonable approximation. Note that the DiESL strains are not scaled according to Section 3.1 (i.e., αj in (18) is set to a constant value 1) because scaled strains have to match exactly those of the nonlinear dynamic analysis by definition (i.e., at the beginning of the linear static response optimization). It is evident from Fig. 10 that for elements 2 and 3 the ESLM entirely fails to approximate the correct strains, in most cases, even the sign is reversed. The DiESL method is not highly accurate, either, but it approximates the strains much better than ESLM.

Fig. 10
figure 10

Normal strains in the x-direction of three representative elements over time (α = 1, x1 = 0.85 mm) for the lower element surface before the linear static optimization

Full size image
Fig. 11
figure 11

Normal strains in the x-direction based on the DiESL approach of three representative elements over time ( x1 = 0.103 mm) for the lower element surface after linear static optimization (2 iterations)

Full size image

Figure 11 examines the strains at the end of a linear static response optimization (i.e., after maxiter = 2 iterations). The nonlinear dynamic results are computed with the updated design. Again, the order of legend entries reflects the chronological order of execution. Similar to the previous findings, the strains of the DiESL method provide a good approximation for those of the nonlinear dynamic analysis. The scaling approach improves the accuracy, so that the strains of elements 2 and 3 still match well with those from the nonlinear dynamic analysis. However, this is not the case for element 1. The reason may be that the poor displacement field approximation in iteration 2 (as seen from maximum constraint violation in iteration 2 in Fig. 9 left diagram) does affect the strains of element 1 primarily due to its position in the impact zone of the impactor. In fact, the intrusion of the impactor is underestimated and therefore the strains are as well.

4.2 Pole impact

Figure 12 shows a rigid pole with initial speed vy =  − 8 m/s colliding with a frame structure. The translational degrees of freedom of the pole in x- and z-direction as well as all its rotations are locked. The structure is clamped along the distant edge in all 6 degrees of freedom using single-point constraints (SPC). The frame structure is made of steel (Youngs’s modulus E = 210 GPa, density ρ = 7850 kg/mm3, LS-DYNA element type = Belytschko-Lin-Tsay shell elements, number of nodes = 12,813), and bilinear plastic material behavior is applied (tangent modulus = 0.6 GPa, yield stress = 0.25 GPa). The simulation end time is 100 ms. This captures the pole’s maximum intrusion and part of its rebound. Consequently, the last ESL time step is selected as 100 ms.

Fig. 12
figure 12

FE model of the pole impact and labeling of design variables (left). Deformed FE model at state of maximum intrusion for initial thickness \( {x}_i^{(0)}=0.8\ \mathrm{mm} \) (right)

Full size image

As shown in Fig. 12, the design of the FE model is specified by seven different design variables each corresponding to a single sheet metal thickness (except x1 representing all 12 facets of both crossbars and x7 representing both end caps of rocker profile). As before, the same mesh is used for both linear and nonlinear analysis to avoid result mapping and a contact is defined between the frame structure and the pole. The objective is to minimize the mass of the frame structure while constraining the maximum intrusion of the pole in y-direction d(x). Mathematically, the problem is given as

$$ \mathrm{such}\ \mathrm{that}\ {\displaystyle \begin{array}{c}\min\ mass\left(\mathbf{x}\right)\\ {}d\left(\mathbf{x}\right)\le 200\ \mathrm{mm}\\ {}0.5\ \mathrm{mm}\le {x}_i\le 3\ \mathrm{mm};i=1,\dots, 7\end{array}} $$

In order to capture the maximum intrusion of the pole properly, 20 uniformly distributed ESL time steps from 5 to 100 ms have been used for both methods. The time increment ∆t = 5 ms is considered to be adequately small to neglect the error due to the time shift of the maximum intrusion d(x). This results in 20 auxiliary load cases in ESL and 20 LSMs in DiESL.

In Figs. 13 and 14, the optimization history for an initial thickness of \( {x}_i^{(0)}=0.8\ \mathrm{mm} \); i = 1, …, 7 is shown. As before, DiESL satisfies the termination criteria within fewer cycles than ESLM. In Table 1, the resulting design variables are presented as well as the corresponding mass(x∗) and the number of nonlinear dynamic analyses required. Additionally, the optimization result obtained by LS-OPT is given. It is remarkable that the best point for ESLM did not occur at the end of iterations. This means that ESLM converged to a point which is obviously not the nonlinear optimum. Obviously, the best point is found by accident and the convergence behavior is forced by the continuous reduction of the move limits only. In order to confirm whether the solution found by ESLM is an optimum of the nonlinear problem, an LS-OPT optimization run was executed using the ESLM solution as an initial design. It turned out that LS-OPT converged to a very different optimum. This shows that ESLM in this case was not capable of finding the actual optimum of the nonlinear problem. In contrast, DiESL and LS-OPT yield a similar design, which is significantly lighter than the one obtained from ESLM (note that due to their equal size and relative position with respect to the impactor, panels 4 and 5 have a similar effect on both mass and intrusion). This confirms that DiESL really found a nonlinear optimum in a good approximation. But it is also obvious that there is a big difference in the number of nonlinear dynamic analyses for DiESL and LS-OPT because the number of nonlinear dynamic analyses required by LS-OPT is more than 10 times as high as that required for DiESL. Note that the number of nonlinear analyses in LS-OPT scales with the number of design variables in each iteration due to the DOE. In contrast, only one nonlinear analysis per cycle is required in DiESL.

Fig. 13
figure 13

Objective function and maximum relative constraint violation over cumulated iterations (left) and convergence criteria over cycles (right) using ESLM. Note that the best design (green circle) is not obtained at the end of iterations

Full size image
Fig. 14
figure 14

Objective function and maximum relative constraint violation over cumulated iterations (left) and convergence criteria over cycles (right) using DiESL

Full size image
Table 1 Optimization results using ESLM, DiESL, and LS-OPT (metamodel based approach)
Full size table

It is remarkable that five of seven design variables are at their bounds in the DiESL optimum, which is not the case for ESLM. In particular, the design variables \( {x}_4^{\ast } \) and \( {x}_6^{\ast } \) differ considerably. ESLM produces a more bending resistant design by increasing \( {x}_6^{\ast } \), the thickness of the panel in contact with the pole. This can be attributed to the fact that every ESLM auxiliary load case refers to the undeformed initial structure and therefore is loaded with pure bending. No tensile loading occurs in panel 6 in any ESLM subcase. ESLM therefore increases the panel’s thickness to compensate the missing tensile contribution. In contrast, the DiESL auxiliary load cases take the tensile contributions into account because the stiffness matrix is assembled using the deformed geometry. Consequently, DiESL leads to a similar result as LS-Opt.

The results shown so far indicate that DiESL leads to better results with less computational effort compared to ESLM because the optimized mass \( mas{s}_{\mathrm{DiESL}}^{\ast }=15.50\ \mathrm{kg} \) is significantly smaller than \( mas{s}_{\mathrm{ESL}}^{\ast }=18.75\ \mathrm{kg} \). However, it is well known that the optimization’s course varies depending on the selected initial values of the design variables. In order to evaluate DiESL independently from the selected initial values, a multi-start optimization study was conducted: A DOE was created to generate 20 configurations of uniformly distributed design variables (space-filling design) used as initial values. The DOE was created as a Strength Two Orthogonal Array. These 20 configurations are optimized using ESLM, DiESL, and LS-OPT. Table 2 shows the average results over all configurations for both methods. The average results confirm the previous findings: the DiESL method performs significantly better than the ESLM both in terms of number of nonlinear dynamic analyses and in terms of the objective improvement.

Table 2 Multi-start results averaged for ESLM, DiESL, and LS-OPT (metamodel-based approach)
Full size table

5 Conclusions and outlook

In this paper, a difference-based extension of the ESLM is presented, which is called DiESL. Both methods are compared on the basis of two representative sizing optimization examples by minimizing mass with a displacement constraint on an impactor.

As expected, both methods produce the same optimal design for the three-point bending example. For DiESL, the results show a faster convergence to the optimum as well as a significant increase of the approximation quality for the true strains. This enables implementing a strain-based criterion of material failure in nonlinear dynamic response optimization for crash load cases.

The second example is a pole with an initial velocity impacting a frame structure. The thicknesses of seven different parts are optimized. Here, DiESL reduces the number of nonlinear dynamic analyses required for convergence significantly. At the same time, DiESL leads to a considerably lighter design than the ESLM. The ESLM results in a more bending resistant design whereas DiESL produces a more tensile resistant one. To rule out that this result depends on the initial values of the design variables, a DOE-based multi-start optimization was executed in which the initial values of the design variables were varied. The results reconfirmed the previously determined observations. Additionally, the optimal design obtained with the DiESL method was confirmed to be an optimum of the nonlinear dynamic problem by solving the optimization using LS-OPT utilizing a metamodel-based approach. Furthermore, it was shown that the solution determined with ESLM is not an optimum of the nonlinear dynamic problem. However, the number of nonlinear dynamic analyses required when using the metamodel is about 10 times as high as that required for DiESL.

A critical point in DiESL is that due to excessively deformed elements and thus poor element quality in intermediate linear FE models, the linear solver was terminated with an error during the calculation of the ESL forces. In order to realize a robust application of DiESL, a solution has to be developed to automatically repair the mesh of the LSMs if such poor element quality occurs. This could, for example, be realized by deleting failed elements, splitting warped quad-elements into tria-elements, or by remeshing critical areas. The deletion approach has been successfully implemented and applied.

Summarizing, the test examples confirm the expectation that DiESL enables a significant increase in approximation quality of displacements and strains from nonlinear dynamic problems while simultaneously providing faster convergence. An extension of the methodology to other structural responses such as stresses and forces seems promising and would open up the way for other types of constraints. Additionally, the adaption of Young’s modulus in the LSMs on element level addressing local plasticity should lead to a better stiffness representation and thus more realistic stresses. Furthermore, for optimization problems like those considered in this paper—where the maximum of a response is needed—the implementation of an automatic and adaptive selection of the ESL times at the beginning of each inner loop can help to make sure that the constrained response is well captured. The upper value of the ESL-time range can then be chosen as the time of the maximum of the response of interest plus a defined fraction (e.g., 10%). If there is more than one response needed then the maximum value of all is chosen. The optimal ESL time increments can be computed by minimizing the difference between the polygonal line of the DiESL approximation and the real response curve.

When using the ESLM, the optimization’s convergence depends significantly on the chosen move limits. If the move limits are too big, the convergence is not guaranteed anymore. In case of DiESL, the approximation quality seems to be sufficiently accurate to justify larger move limits and therefore a reconsideration of the chosen move limit strategy.

Compared to a metamodel-based approach, the number of nonlinear dynamic analyses required is remarkably lower to optimize such nonlinear dynamic problems. Furthermore, the number of nonlinear dynamic analyses required for DiESL is not directly dependent on the number of design variables. Therefore, DiESL may enable topology optimization for nonlinear dynamic problems such as crash tests.