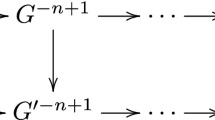Derived categories of NDG categories

Abstract

In this paper we study N-differential graded categories and their derived categories. First, we introduce modules over an N-differential graded category. Then we show that they form a Frobenius category and that its homotopy category is triangulated. Second, we study the properties of its derived category and give triangle equivalences of Morita type between derived categories of N-differential graded categories. Finally, we show that this derived category is triangle equivalent to the derived category of some ordinary differential graded category.

5 Appendix

In this section, we give the following results concerning Frobenius categories and triangulated categories. Let $\mathcal {C}$ be an exact category with a collection $\mathcal {E}$ of exact sequences in the sense of Quillen [16]. An exact sequence $0 \rightarrow X \xrightarrow {f} Y \xrightarrow {g} Z \rightarrow 0$ in $\mathcal {E}$ is called a conflation, and f and g are called an inflation and a deflation, respectively. An additive functor $F: \mathcal {C} \rightarrow \mathcal {C}'$ is called exact if it sends conflations in $\mathcal {C}$ to conflations in $\mathcal {C}'$. An exact category $\mathcal {C}$ is called a Frobenius category provided that it has enough projectives and enough injectives, and that any object of $\mathcal {C}$ is projective if and only if it is injective. In this case, the stable category $\underline{\mathcal {C}}$ of $\mathcal {C}$ by projective objects is a triangulated category (see [5]). This stable category is called an algebraic triangulated category.

Proposition 4.3

([7] Proposition 7.3) Let $(\mathcal {C}, \mathcal {E}_{\mathcal {C}}), (\mathcal {C}, \mathcal {E}_{\mathcal {C}'})$ be Frobenius categories, $F: \mathcal {C} \rightarrow \mathcal {C}'$ an exact functor. If F sends projective objects of $\mathcal {C}$ to projective objects of $\mathcal {C}'$, then it induces the triangle functor ${\underline{F}} : \underline{\mathcal {C}} \rightarrow \underline{\mathcal {C}}'$.

Let $\mathcal {D}$ be a triangulated category with arbitrary coproducts. An object U in $\mathcal {D}$ is compact if the canonical morphism $\coprod _{i}{\text {Hom}}_{\mathcal {D}}(U, X_i)\rightarrow {\text {Hom}}_{\mathcal {D}}(U, \coprod _{i }X_i)$ is an isomorphism for any set $\{X_i \}$ of objects in $\mathcal {D}$. A triangulated category $\mathcal {D}$ is called compactly generated if there is a set ${\mathsf {U}}$ of compact objects such that ${\text {Hom}}_{\mathcal {D}}({\mathsf {U}}, X) = 0$ implies $X=0$ in $\mathcal {D}$.

Theorem 4.5

Let $\mathcal {D}$ be a compactly generated triangulated category with a set ${\mathsf {U}}$ of compact generators for $\mathcal {D}$. Let $F: \mathcal {D} \rightarrow \mathcal {D}'$ be a triangle functor between triangle categories such that F preserves coproducts. Then the following are equivalent.

• (1) F is a triangle equivalence.

• (2)

  • 1. $F({\mathsf {U}})$ is a set of compact generators for $\mathcal {D}'$.

  • 2. ${\text {Hom}}_{\mathcal {D}}(U, V) \rightarrow {\text {Hom}}_{\mathcal {D}'}(FU,FV)$ is an isomorphism for any $U, V \in {\mathsf {U}}$.

Proof

(1) $\Rightarrow$ (2) Trivial.

(2) $\Rightarrow$ (1) We may assume that ${\mathsf {U}}=\Sigma {\mathsf {U}}$. Let $\mathcal {U}$ be the full subcategory of coproducts of objects U in ${\mathsf {U}}$. Let $<\mathcal {U}>_0:=\mathcal {U}$. For $n \ge 1$ let $<\mathcal {U}>_n$ be the full subcategory of $\mathcal {D}$ consisting of objects X such that there is a triangle $U \rightarrow V \rightarrow X \rightarrow \Sigma U$ with $U \in <\mathcal {U}>_0$, $V \in <\mathcal {U}>_{n-1}$. Given $U \in {\mathsf {U}}$, for any $U_i \in {\mathsf {U}}$ $(i \in I)$, we have a commutative diagram

such that all vertical arrows are isomorphisms. Therefore, for any $V \in \mathcal {U}$ we have the canonical morphism ${\text {Hom}}_{\mathcal {D}}(U, V) {\mathop {\rightarrow }\limits ^{\sim }}{\text {Hom}}_{\mathcal {D}'}(FU, FV)$ is an isomorphism. For any $W\in <\mathcal {U}>_n$ we have a triangle $U' \rightarrow V \rightarrow W \rightarrow \Sigma U$ with $U' \in <\mathcal {U}>_0$, $V \in <\mathcal {U}>_{n-1}$. Applying ${\text {Hom}}_{\mathcal {D}}(U, -)$ to this triangle, by the induction the five lemma implies that the canonical morphism ${\text {Hom}}_{\mathcal {D}}(U, W) {\mathop {\rightarrow }\limits ^{\sim }}{\text {Hom}}_{\mathcal {D}'}(FU, FW)$ is an isomorphism. According to Brown’s representability theorem (e.g. [15]), for any $Y \in \mathcal {D}$, there is a sequence $Y_0 \rightarrow Y_1 \rightarrow \cdots$ with $Y_i \in <\mathcal {U}>_i$ which has a triangle

$$\begin{aligned} \coprod _{i}Y_i \xrightarrow {1-\text {shift}} \coprod _{i}Y_i \rightarrow Y \rightarrow \Sigma \coprod _{i}Y_i \end{aligned}$$

Applying ${\text {Hom}}_{\mathcal {D}}(U, -)$ to this triangle, the five lemma implies that the canonical morphism ${\text {Hom}}_{\mathcal {D}}(U, Y) {\mathop {\rightarrow }\limits ^{\sim }}{\text {Hom}}_{\mathcal {D}'}(FU, FY)$ is an isomorphism. Similarly, by the induction on n for any $W \in <\mathcal {U}>_n$, any $Y \in \mathcal {D}$ the canonical morphism ${\text {Hom}}_{\mathcal {D}}(W, Y) {\mathop {\rightarrow }\limits ^{\sim }}{\text {Hom}}_{\mathcal {D}'}(FW, FY)$ is an isomorphism. Brown’s representability theorem implies that the canonical morphism ${\text {Hom}}_{\mathcal {D}}(X, Y) {\mathop {\rightarrow }\limits ^{\sim }}{\text {Hom}}_{\mathcal {D}'}(FX, FY)$ is an isomorphism for any $X. Y \in \mathcal {D}$. Then F is fully faithful. Therefore we have $<F(\mathcal {U})>_i= F(<\mathcal {U}>_i)$ for any i. Since $F({\mathsf {U}})$ is a set of compact generator for $\mathcal {D}'$, for any $Z \in \mathcal {D}'$, there is a sequence $Z_0 \xrightarrow {\beta _0} Z_1 \xrightarrow {\beta _1} \cdots$ with $Z_i \in <F(\mathcal {U})>_i$ which has a triangle

$$\begin{aligned} \coprod _{i}Z_i \xrightarrow {1-\text {shift}} \coprod _{i}Z_i \rightarrow Z \rightarrow \Sigma \coprod _{i}Z_i \end{aligned}$$

Then there is a morphism $\alpha _i:X_i \rightarrow X_{i+1}$ such that $F\alpha _i=\beta _i$ for any i. Let X be the homotopy colimit of the sequence $X_0 \xrightarrow {\alpha _0} X_1 \xrightarrow {\alpha _1} \cdots$, then we have a commutative diagram

where the first, second, fourth vertical arrows are isomorphisms. Then the third vertical arrow is an isomorphism. Therefore F is dense, and hence a triangle equivalence. $\square$