1 Introduction

Underwater acoustic channels are considered as one of the most challenging communication channels, generally characterized by low propagation speed of sound in water (nominally 1500 m/s), limited bandwidth, and complex multipath propagation which results in frequency-selective fading [1,2,3,4,5]. Multipath propagation and limited bandwidth place significant constraints on the achievable throughput of underwater acoustic communication (UAC) systems. The bandwidth efficiency is an important system indicator [6,7,8], to increase the bandwidth efficiency of UAC systems, adaptive modulation (AM) schemes, which have the ability to adjust modulation modes according to channel conditions, can be employed.

The investigation on the application of AM to underwater acoustic communications has been limited in comparison to the extensive investigations for terrestrial radio communication. In [9], an AM scheme based on channel prediction is proposed, in which the channel state information (CSI) of future time is predicted with the estimated CSI of a previous time and then used to adjust the modulation mode. An adaptive modulation approach based on the signal-to-noise ratio (SNR) is proposed in [10], in the approach, the SNR is obtained after channel estimation and then used as the working mode indicator to select the appropriate modulation mode. In [11, 12], the future BER is predicted based on the CSI and SNR using the decision tree approach. In [13,14,15], the machine learning algorithms are used to select the modulation mode. However, these schemes in [9,10,11,12,13,14,15] assume that the CSI can be well estimated and non-blind equalization approach is adopted. For practical underwater acoustic communication, due to the complexity and variability of the underwater acoustic environment, the CSI is actually difficult to obtain. Moreover, to obtain a better estimation for the channel, sufficient pilot sequence length is required by non-blind equalization, and thus the transmission efficiency of the underwater acoustic channel with limited bandwidth is significantly reduced.

In this paper, we propose an adaptive modulation scheme based on steady-state mean square error (SMSE) for the underwater acoustic communication system. In the proposed scheme, the channel state information does not need to be assumed to be known, the adjustment of modulation mode is realized based on the output SMSE of blind equalization detector (BED). To achieve better performance, an adjustable tap-length BED (ATL-BED) is also adopted. Compared with the fixed tap-length BED (FTL-BED), better SMSE can be obtained under the same conditions. In addition, for BED, a priori knowledge of transmitted signal statistics is used to recover transmitted signals, no training sequence is required. Therefore, the transmission efficiency of the system can be improved.

2 System model

For communication over underwater acoustic channels, OFDM is an efficient scheme. However, its performance will suffer from high peak-to-average power ratio (PAPR) value, and inter-carrier interference (ICI) caused by uneven Doppler frequency shift [16]. Compared with OFDM, Single-carrier (SC) technology has a better PAPR and is less sensitive to frequency offset. To avoid being affected by these problems, the SC is also a promising alternative approach [17]. Therefore, in the system model, the SC is adopted.

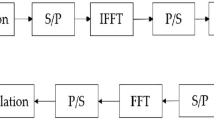
In the adaptive modulation, BPSK, 4QAM, 8QAM, and 16QAM are provided at the transmitter. For each transmission, the modulation mode may be adjusted to maximize the throughput. The channel is modeled by statistical underwater acoustic channel model [18, 19]. At the receiver, demodulation is performed using a blind equalization detector. The discrete model of the system is depicted in Fig. 1.

Fig. 1
figure 1

Discrete model of the system

Full size image

All the signals are sampled at the symbol rate, where the index n represents the signal sample at time nTs, where Ts is the symbol period. The received signals can be expressed as

$$r(n) = s(n) * h(n) + v(n)$$
(1)

where * denotes convolution, s(n) represents the transmitted signal after the modulation, h(n) denotes the discrete underwater acoustic channel impulse responses, v(n) represents samples of additive white Gaussian noise with zero mean and variance σ2.

The adaptive modulation procedure is described below. First, a transmitter node will initiate a request-to-send (RTS) message, and the receiver node will reply with a clear-to-send (CTS) message after receiving RTS. The CTS will report the steady-state mean square error (SMSE) of blind equalization, upon which the transmitter node will estimate the SNR and chose a suitable modulation scheme, and transmit a data burst to the receiver node.

3 Method: the proposed adaptive modulation scheme based on steady-state mean square error

One critical component of an AM system is to find an appropriate performance metric, based on which the transmitter can switch to a suitable transmission mode. The existing schemes assume that the CSI can be well estimated. However, due to the variability of the underwater acoustic channel, the CSI is difficult to obtain. Considering the realization of the actual AM system, the output SMSE of BED can be used as the performance metric to select the appropriate modulation mode. The proposed scheme does not need to know the CSI, thus, it is more suitable for practical underwater acoustic AM systems.

3.1 Acquisition of steady-state mean square error

The SMSE is an important parameter in the detection performance of BED. The smaller the value is, the better performance the detector can achieve. In contrast, a larger value of SMSE may induce worse performance. Therefore, the SMSE can be used as the metric to adjust the modulation mode. Compared with constant modulus algorithm-(CMA) based blind equalization, the multi-modulus algorithm-(MMA) based blind equalization can implement carrier phase recovery at the same time, and thus the rotator does not require to be added in steady-state operation. For MMA, the cost function is defined as [20]

$$J_{M} (k) = J_{R} (k) + J_{I} (k)$$
(2)

where Ji(k) is the cost function, \(i \in \left\{ {R,I} \right\}\), and can be given by

$$J_{i} (k) = E\left\{ {\left[ {\hat{y}_{i}^{2} (k) - G_{2,i} } \right]^{2} } \right\}$$
(3)

where \(i \in \left\{ {R,I} \right\}\), R denotes the real part of a complex variable, I represents the imaginary part, \(\hat{y}_{i} (k)\) denotes the output of blind equalization, \(G_{2,i}\) can be calculated with \(G_{2,i} = E\left\{ {d_{i}^{4} (k)} \right\}/E\left\{ {d_{i}^{2} (k)} \right\}\), \(i \in \left\{ {R,I} \right\}\), \(d_{R} (k)\) represents the real part of \(d(k)\), and \(d_{I} (k)\) is the imaginary part of \(d(k)\). \(d(k)\) denotes the equiprobable and statistical independent quadrature phase shift keying (QPSK) data stream sent by the transmitter. The total error is resolved by the difference between the BED output and the signal statistics of the transmitted signal, and can be expressed as

$$e(k) = e_{R} (k) + je_{I} (k)$$
(4)

where \(e_{i} (k) = \hat{y}_{i} (k)(\hat{y}_{i}^{2} (k) - G_{2,i} )\), \(i \in \left\{ {R,I} \right\}\), \(e_{R} (k)\) represents the real part of error signal \(e(k)\) and \(e_{I} (k)\) is the imaginary part of \(e(k)\). Here, we will adopt the adaptive normalized MMA proposed in [21] to dynamically adjust the tap coefficient vector according to the error \(e(k)\). In most formulations of the BED, the tap-length of the BED is assumed fixed [20, 22,23,24]. However, in different times and different underwater environments, the channel profile is different, and the optimal tap-length of BED is related to the specific channel profile. Therefore, optimal tap-length is difficult to be obtained in advance. The tap-length is an important parameter affecting the SMSE performance of blind equalization. To achieve better SMSE performance, the detector should have the ability to dynamically adjust the tap-length according to the specific underwater acoustic channel. The SMSE performance of BED can be measured with the mean square error of \(e(k)\)

$${\text{MSE}}(k) = E\left[ {\left| {e(k)} \right|^{2} } \right] = \frac{{\sum\nolimits_{j = 1}^{k} {e(j)e^{*} (j)} }}{k}$$
(5)

The normalized least mean square algorithm can be used to update the tap coefficient vector of BED. To reduce the computational complexity, in the process of tap-length adjustment, the accumulated squared error (ASE) is adopted as the measure criterion [25]

$${\text{ASE}}(k) = \sum\nolimits_{j = 1}^{k} {e(j)e^{*} (j)}$$
(6)

where the repetitive computation of division is avoided. Ideally, the out ASE will decrease with the increase of tap-length

$${\text{ASE}}_{L} (k) < {\text{ASE}}_{L - 1} (k)$$
(7)

where

$${\text{ASE}}_{m} (k) = \sum\nolimits_{i = 1}^{k} {\zeta^{k - i} \left| {y_{R,mi} (k)\left( {y_{R,mi}^{2} (k) - G_{2,R} } \right) + jy_{I,mi} (k)\left( {y_{I,mi}^{2} (k) - G_{2,I} } \right)} \right|}$$
(8)

where \(m \in \{ L,L - 1\}\), \(\zeta\) is a forgetting factor used to weight the relative importance of preceding and recent samples, \(\zeta \le 1\), the input sequence is equally divided into several segments, \(y_{mi} (k)\) denotes the ith output of the BED for the mth segment input sequence, \(y_{R,mi} (k)\) represents the real part of equalization out \(y_{mi} (k)\), \(y_{I,mi} (k)\) is the imaginary part of \(y_{mi} (k)\) and \({\text{ASE}}_{m} (k)\) denotes the ASE corresponding to the mth segment input sequence.

By comparing the sizes of \({\text{ASE}}_{L} (k)\) and \({\text{ASE}}_{L - 1} (k)\), the adjustment of tap-length can be determined [25]. If \({\text{ASE}}_{L} (k) \le \beta_{u} {\text{ASE}}_{L} (k)\), the tap-length increases \(q\) taps, and vice versa, if \({\text{ASE}}_{L} (k) \ge \beta_{d} {\text{ASE}}_{L} (k)\), the tap-length decreases \(q\) taps, where \(\beta_{d}\) needs to meet \(\beta_{d} \le 1\), \(\beta_{u}\) and \(\beta_{d}\) should satisfy \(\beta_{u} \le \beta_{d}\). The function of \(\beta_{u}\) and \(\beta_{d}\) is to determine the sum of adjustments to increase or decrease the tap-length of BED according to the improvement or deterioration of ASE. The closer the values of \(\beta_{u}\) and \(\beta_{d}\) are, the more frequently the tap-length will be adjusted by the detector. In addition, it is worth noting that when the tap-length of ATL-BED and fixed tap-length (FTL) BED is the same, the incremental complexity caused by the adjustment of tap-length is finite. This is because, for ATL-BED, the adjustments of tap-length only require multiplication, subtraction, and addition operations.

After the convergence of BED, the steady-state mean square error can be obtained by

$${\text{SMSE}} = \frac{{\sum\nolimits_{{j = N_{c} }}^{k} {e(j)e^{*} (j)} }}{{k - N_{c} + 1}}$$
(9)

where Nc denotes the minimum number that can make the algorithm converge.

For the underwater environment, the channel dynamics tend to change rapidly in local so that the statistic of channel gains is highly nonstationary [26]. If the data packet is too long, the channel may have changed during the transmission of the packet. Therefore, a short data packet is adopted for the UAC system. The channel is assumed to be stationary in the transmission process for the short data packet. To ensure the convergence of the algorithms, each packet is repeated to use until the algorithms converge to steady-state. For the reuse of each packet, the tap coefficient vector is initialized by the last update in the previous training using the same packet.

3.2 Fitting between estimated SNR and actual SNR

The output SNR \(\gamma_{o}\) of BED can be calculated by [27]

$$\gamma_{o} = \frac{{1 - {\text{SMSE}}}}{{{\text{SMSE}}}}$$
(10)

Due to the influence of noise and ISI, the ideal blind equalization performance cannot be obtained. To make the estimated SNR approximate to the actual SNR \(\gamma_{a}\), polynomial fitting is used to correct the estimated SNR \(\gamma_{o}\). Suppose N data \(\gamma_{o,n}\) have been obtained, \(n = 0,1, \ldots ,N - 1\) and we have a function that describes the relationship between \(\gamma_{o,n}\) and \(\gamma_{a,n}\)

$$\gamma_{a,n} = f(\gamma_{o,n} ) + \varepsilon_{n} ,\quad n = 0,1, \ldots ,N - 1$$
(11)

where \(\varepsilon_{n}\) is the error at \(\gamma_{o,n}\). Our goal is to determine \(\gamma_{a,n}\) from the estimated data \(\gamma_{o,n}\), \(n = 0,1, \ldots ,N - 1\). Therefore, a fitting function \(F(\gamma_{o,n} ) = F(\gamma_{o,n} ;c_{0} , \ldots ,c_{k - 1} )\) should be selected, where \(F(\gamma_{o,n} )\) is an approximation to \(f(\gamma_{o,n} )\), \(c_{0} , \ldots ,c_{k - 1}\) denote the parameters of the fitting function. To the function \(f(\gamma_{o,n} )\), the equation of polynomial fitting can be written as follows

$$F(\gamma_{o,n} ) = c_{0} + c_{1} \gamma_{o,n} + c_{2} \gamma_{o,n}^{2} + \cdots + c_{k - 1} \gamma_{o,n}^{k - 1}$$
(12)

Next, we should determine the values for the parameter \(c_{0} , \ldots ,c_{k - 1}\) that make \(F(\gamma_{o,n} )\) a good approximation. To solve the problem, we use the approach of least-squares fitting [28], which minimizes the following error function

$$E(c_{0} , \ldots ,c_{k - 1} ) = \sum\limits_{n = 0}^{N - 1} {\left[ {\gamma_{a,n} - F(\gamma_{o,n} ;c_{0} , \ldots ,c_{k - 1} )} \right]^{2} }$$
(13)

In order to obtain the parameter value \(c_{i}\), a necessary condition for \(E( \cdot )\) to be a minimum is that

$$\frac{\partial E}{{\partial c_{i} }} = 0,\quad i = 0,1, \ldots ,k - 1$$
(14)

After the differential calculation for Eq. (13), we obtain

$$\begin{aligned} \frac{\partial E}{{\partial c_{i} }} & = \sum\limits_{n = 0}^{N - 1} {\frac{\partial }{{\partial c_{i} }}\left[ {\gamma_{a,n} - F(\gamma_{o,n} ;c_{0} , \ldots ,c_{k - 1} )} \right]^{2} } \\ & = - 2\sum\limits_{n = 0}^{N - 1} {\left[ {\gamma_{a,n} - F(\gamma_{o,n} ;c_{0} , \ldots ,c_{k - 1} )} \right]} \frac{\partial }{{\partial c_{i} }}F(\gamma_{o,n} ;c_{0} , \ldots ,c_{k - 1} ) \\ \end{aligned}$$
(15)

Because function \(F( \cdot )\) has the form of (12), we get

$$\frac{\partial }{{\partial c_{i} }}F(\gamma_{o,n} ;c_{0} , \ldots ,c_{k - 1} ) = \gamma_{o,n}^{i}$$
(16)

Therefore, applying (16) to (15), we have

$$\sum\limits_{n = 0}^{N - 1} {\left[ {\gamma_{a,n} - F(\gamma_{o,n} ;c_{0} , \ldots ,c_{k - 1} )} \right]} \gamma_{o,n}^{i} = 0,\quad i = 0,1, \ldots ,k - 1$$
(17)

Equation (17) forms a system of k equations in k unknown parameters \(c_{i}\)

$$\begin{aligned} & \sum\limits_{n = 0}^{N - 1} {\left[ {c_{0} + c_{1} \gamma_{o,n} + c_{2} \gamma_{o,n}^{2} + \cdots + c_{k - 1} \gamma_{o,n}^{k - 1} } \right]} \gamma_{o,n}^{i} = \sum\limits_{n = 0}^{N - 1} {\gamma_{a,n} } \gamma_{o,n}^{i} , \\ & \quad \quad i = 0,1, \ldots ,k - 1 \\ \end{aligned}$$
(18)

By solving formula (18), the estimation \(\hat{c}_{i}\) for parameters \(c_{i}\) can be obtained. Then, we substitute \(\hat{c}_{i}\) into (12), the correction estimation value for \(\gamma_{a,n}\) can be given by

$$\hat{\gamma }_{a,n} = F(\gamma_{o,n} ) = \hat{c}_{0} + \hat{c}_{1} \gamma_{o,n} + \hat{c}_{2} \gamma_{o,n}^{2} + \cdots + \hat{c}_{k - 1} \gamma_{o,n}^{k - 1}$$
(19)

\(\gamma_{o,n}\) can be calculated with (10)

$$\gamma_{o,n} = \frac{{1 - {\text{SMSE}}_{n} }}{{{\text{SMSE}}_{n} }}$$
(20)

Substitute (20) into (19), the relationship between SMSE, SMSEn and estimation SNR \(\widehat{\gamma }_{a,n}\) can be given by

$$\hat{\gamma }_{a,n} = \hat{c}_{0} + \hat{c}_{1} \frac{{1 - {\text{SMSE}}_{n} }}{{{\text{SMSE}}_{n} }} + \hat{c}_{2} \left( {\frac{{1 - {\text{SMSE}}_{n} }}{{{\text{SMSE}}_{n} }}} \right)^{2} + \cdots + \hat{c}_{k - 1} \left( {\frac{{1 - {\text{SMSE}}_{n} }}{{{\text{SMSE}}_{n} }}} \right)^{k - 1}$$
(21)

3.3 Adaptive modulation based on steady-state mean square error

After obtaining the SMSE, the fitted SNR \(\hat{\gamma }_{a,n}\) can be calculated with (21), and then be used to adjust the modulation levels.

To maintain the BER below the target threshold, we propose the following optimization criterion:

$$\begin{aligned} &{\text{maximize}}\,\Gamma (\gamma ) \\ &{\text{subject}}\,P_{e} \le P_{{{\text{th}}}} \hfill \\ \end{aligned}$$
(22)

where \(P_{e}\) expresses the BER of system, Pth is the expected BER, \(\Gamma (\gamma )\) denotes the throughput of modulation scheme, and can be expressed as [29]

$$\Gamma (\gamma ) = (1 - {\text{BER}}(\gamma ))R$$
(23)

where R denotes the transmitted number of information bits per second. The probability of bit error for the corresponding modulation approach is approximated by [9]

$${\text{BER}}(\gamma ) = 0.2e^{{ - \frac{{m(M_{k} )}}{{2(M_{k} - 1)}}\gamma }}$$
(24)

where coefficients \(m(M_{k} )\) are determined numerically for each modulation alphabet, as accurately as desired for the BER approximation and take values 2.2, 3.3, 3.5, 3.6 for \(M_{k} = 2,4,8,16\), respectively [9].

To realize the optimization criterion (22), for a given target BER, the thresholds for the available modulation levels can be obtained by the following method.

The throughput curve of N modulation modes would produce N-1 intersection points, which divide the SNR into N segment intervals. The switching threshold of modulation mode can be obtained by finding the corresponding SNR for the N-1 intersection points. Let the throughput of two adjacent modulation modes equal, the intersection point can be solved

$$\begin{array}{*{20}c} {\Gamma_{i} (\gamma ) = \Gamma_{i + 1} (\gamma )} & {i = 1,2,...,N - 1} \\ \end{array}$$
(25)

where \(\Gamma_{i} (\gamma )\) denotes the throughput of ith modulation mode. By Eq. (25), the obtained threshold set can be expressed as \({\varvec{\gamma}}_{\Gamma } = \{ \gamma_{\Gamma ,1} ,\gamma_{\Gamma ,2} ,...,\gamma_{\Gamma ,N - 1} \}\).

The obtained threshold set \({\varvec{\gamma}}_{\Gamma }\) divides the whole SNR interval into N parts. Under different SNRs \(\gamma_{a}\), the corresponding modulation mode can be selected according to the interval where the estimated SNR \(\hat{\gamma }_{a}\) is located. The AM algorithm based on the SMSE can be summarized as follows.

figure a

4 Simulation results and discussion

In this section, we present simulation results to validate the feasibility, and prove the advantages of the proposed scheme. The programs are developed in Python. We assume perfect synchronization and also assume that the underwater acoustic channel is quasi-static, which means that in the process of data packet transmission, the channel is unchanged, but for the next packet, the channel will change. In the simulation, the statistical underwater acoustic channel model is used. In the model, the carrier frequency is 12KHz, the band is limited to 1 kHz, the depth is set as 60 m, the speed of sound in water is set to 1500 m/s, the range between transmitter and receiver is set as 200 m, both transmitter and receiver are located at a depth of 20 m, wave height is set as 0.2 m. We assume that the information bits frame length is 200. For FTL-BED, the tap-length is set as 5. For the ATL-BED, the initial length of the tap coefficient vector is set as 1, the segment length is 10 bits, and the parameter q of each tap-length adjustment is set as 2.

4.1 Effect of tap-length on SMSE

In this section, the simulation is based on a given UAC envelope, which is generated with the statistical underwater acoustic channel model. The influences of tap-length on steady-state MSE (SMSE) of BED are showed in Fig. 2. Each point on the curve is acquired through averaging the SMSE on every data packet. The output SMSE of BED can be calculated with (9) after the BED achieves convergence. As shown in Fig. 2, the tap-length can severely affect the SMSE performance of BED. Taking into account computational complexity, the optimum tap-length is defined according to the minimum requirement, which means that the required minimum tap-length for achieving optimal SMSE performance is adopted. From Fig. 2, it can be observed that when tap-length is probably set between 13 and 20, the BED achieves extremely similar SMSE performance, which approximates to the optimal SMSE performance. Based on the definition of the optimum tap-length, from Fig. 2, we can obtain the optimum tap-length, which is about 13.

Fig. 2
figure 2

SMSE performance under different tap-length

Full size image

The evolving curve of tap-length is obtained with the approach of averaging all the evolving curves, which are acquired with different data packets. Figure 3 shows the adaptive adjustment process of tap-length of ATL-BED. In the simulation, for (18), \(\zeta\) is set to 0.999. \(\beta_{u}\) is set as 0.98, and \(\beta_{d}\) is set to 0.989. In Fig. 3, the same underwater acoustic channel used in Fig. 2 is adopted. It can be seen from Fig. 3 that after ATL-BED has adjusted the tap-length, the tap-length can finally converge to the optimal tap-length as shown in Fig. 2. Based on the above results, for the ATL-BED, it can adjust the tap length according to the difference of channel, so as to obtain close to the optimal SMSE performance.

Fig. 3
figure 3

Tap-length evolution curve

Full size image

4.2 Validation of the relationship between SMSE and SNR

In this section, we verify the effectiveness of SNR estimation based on SMSE. The SNR estimation is calculated based on the SMSE with (10). All calculated SMSE were obtained by averaging the MSE with (9) after the convergence of BED.

In Fig. 4, we compare the estimated SNR \(\gamma_{o}\) with (10) and actual SNR \(\gamma_{a}\). It is observed that the calculation with (10) for SNR is not very accurate, which deviates from the actual SNR. However, it is noted that the estimated SNR remains the same trend as the actual SNR. To better realize adaptive modulation, the polynomial fitting is adopted to approximate the actual SNR, the fitting formulas for BPSK, 4QAM, 8QAM and 16QAM are \(\hat{\gamma }_{{a,{\text{BPSK}}}} = - 19.16 + 2.434\left( {\frac{{1 - {\text{SMSE}}_{{{\text{BPSK}}}} }}{{{\text{SMSE}}_{{{\text{BPSK}}}} }}} \right) - 0.05237\left( {\frac{{1 - {\text{SMSE}}_{{{\text{BPSK}}}} }}{{{\text{SMSE}}_{{{\text{BPSK}}}} }}} \right)^{2} + 0.0005736\left( {\frac{{1 - {\text{SMSE}}_{{{\text{BPSK}}}} }}{{{\text{SMSE}}_{{{\text{BPSK}}}} }}} \right)^{3}\), \(\hat{\gamma }_{{a,4{\text{QAM}}}} = - 9.167 + 1.128\left( {\frac{{1 - {\text{SMSE}}_{{4{\text{QAM}}}} }}{{{\text{SMSE}}_{{4{\text{QAM}}}} }}} \right) - 0.01011\left( {\frac{{1 - {\text{SMSE}}_{{4{\text{QAM}}}} }}{{{\text{SMSE}}_{{4{\text{QAM}}}} }}} \right)^{2} + 0.0001968\left( {\frac{{1 - {\text{SMSE}}_{{4{\text{QAM}}}} }}{{{\text{SMSE}}_{{4{\text{QAM}}}} }}} \right)^{3}\),\(\hat{\gamma }_{{a,8{\text{QAM}}}} = - \,4.956 + 0.07977\left( {\frac{{1 - {\text{SMSE}}_{{8{\text{QAM}}}} }}{{{\text{SMSE}}_{{8{\text{QAM}}}} }}} \right) + 0.04093\left( {\frac{{1 - {\text{SMSE}}_{{8{\text{QAM}}}} }}{{{\text{SMSE}}_{{8{\text{QAM}}}} }}} \right)^{2} - 0.000524\left( {\frac{{1 - {\text{SMSE}}_{{8{\text{QAM}}}} }}{{{\text{SMSE}}_{{8{\text{QAM}}}} }}} \right)^{3}\), \(\hat{\gamma }_{{a,16{\text{QAM}}}} = - 10.68 + 0.8887\left( {\frac{{1 - {\text{SMSE}}_{{16{\text{QAM}}}} }}{{{\text{SMSE}}_{{16{\text{QAM}}}} }}} \right) + 0.006173\left( {\frac{{1 - {\text{SMSE}}_{{16{\text{QAM}}}} }}{{{\text{SMSE}}_{{16{\text{QAM}}}} }}} \right)^{2} - 0.0001217\left( {\frac{{1 - {\text{SMSE}}_{{16{\text{QAM}}}} }}{{{\text{SMSE}}_{{16{\text{QAM}}}} }}} \right)^{3}\), respectively, where \(\hat{\gamma }_{a,j}\) denotes the fitting SNR for modulation mode j, SMSEj expresses the steady-state mean square error corresponding to the modulation mode j, \(j \in \left\{ {{\text{BPSK}},4{\text{QAM}},8{\text{QAM}},16{\text{QAM}}} \right\}\). It is seen from Fig. 4 that the fitting SNR is very close to the actual SNR for the four modulation modes. According to the simulation results, it is proved that the fitting approach is feasible, we can use the estimated SNR based on SMSE as the measurement to adjust the modulation mode.

Fig. 4
figure 4

Estimated SNR versus actual SNR. a Comparison under BPSK modulation, b comparison under 4QAM modulation, c comparison under 8QAM modulation, d comparison under 16QAM modulation

Full size image

4.3 Comparison of throughput performance

In this section, we will compare the throughput performance of the proposed method based on SMSE and existing approaches. In the simulation, we assume that the target of BER performance is 10–2. Figure 5 shows the throughput performance comparison for different modulation modes. It can be seen from the Fig. 5 that the intersection point of the throughput curve for adjacent modulation mode using adaptive modulation based on FTL-BED is greater than that using adaptive modulation based on ATL-BED. This is because adaptive modulation based on ATL-BED can achieve better SMSE performance than that based on FTL-BED, and thus achieve better BER performance under the same SNR. As a result, throughout performance can also be improved according to (23).

Fig. 5
figure 5

Throughput performance comparison under different modulation modes. a Comparison for adaptive modulation based on SNR with FTL-BED, b comparison for adaptive modulation based on SNR with ATL-BED, c comparison for adaptive modulation based on SMSE with FTL-BED, d comparison for adaptive modulation based on SMSE with ATL-BED

Full size image

The threshold set of adjustments for modulation mode can be obtained according to (25). The SNR is divided into several intervals by the threshold set. By determining which interval the estimated SNR is located, based on the maximum throughput criterion (22), the corresponding modulation mode can be selected. Figure 6 shows the throughput performance comparison for the proposed and existing schemes. It is observed that the throughput performance of the proposed adaptive modulation scheme based on SMSE is close to that of the adaptive modulation scheme based on SNR. This is because, after the fitting process, the estimated SNR based on SMSE approximates the actual SNR. In addition, it is also seen that the proposed adaptive modulation scheme based on ATL-BED achieves better throughput performance than that based on FTL-BED. This is because that the tap-length is an important parameter affecting BER performance, the ATL-BED can achieve better BER performance than the FTL-BED, and thus obtain better throughput performance under the same SNR.

Fig. 6
figure 6

Throughput performance comparison for different schemes

Full size image

5 Conclusion

In this paper, an adaptive modulation scheme based on SMSE is proposed for the underwater acoustic communication system. The effect of underwater channel complexity on adaptive modulation is taken into account, the proposed scheme does not need to assume that the CSI is known, or well estimated. The adjustment of modulation mode is implemented based on the SMSE of BED. To achieve better equalization performance, an ATL-BED is adopted. The polynomial fitting is adopted to correct the estimated SNR based on the SMSE of BED. Simulation results validate the feasibility of polynomial fitting. Simulation results also demonstrate that the proposed adaptive modulation scheme can achieve approximated throughput performance as the scheme based on SNR, the throughput performance of AM based on ATL-BED significantly outperforms that based on FTL-BED.