1 Introduction

The development of high-entropy alloys (HEAs)[1,2,3,4] has received broad attention in the materials research community due to their exceptional engineering properties, including high mechanical strength,[5,6] good corrosion and wear resistance,[7,8] and improved radiation resistance.[9,10,11] In HEAs, various high-concentration elemental species are originally assumed to be randomly arranged in a simple lattice, resulting in maximized chemical disorder and configuration entropy that is believed to stabilize the structure. Derived from the concept of HEA, multi-principal elemental alloys (MPEAs) have aroused increasing interest from the perspective of alloy design.

The properties of MPEAs are strongly dependent on the underlying compositionally disordered state due to the random arrangement of different elemental species, especially their mechanical properties and irradiation resistance.[1,12] At high temperatures, the mixing of different elements is driven mainly by configurational entropy, leading to uniform elemental distributions. With decreasing temperature, however, the entropy contribution is lowered, and the mixing enthalpy starts to play a dominant role. As a result, local ordering may develop in MPEAs depending on temperatures, as verified by different experiments and simulations.[13,14,15,16,17] Experimentally, Zhang et al.[14] measured the local structure of CoCrNi using the x-ray and neutron total scattering and extended x-ray absorption fine structure (EXAFS) techniques. The results indicate that the Cr atoms are predominantly bonded with Ni and Co, suggesting favorable bonding between Ni-Co and Ni-Cr. Ordering behavior is also found in Al1.3CoCrCuFeNi HEAs.[15,16] Based on the Monte Carlo method combined with density-functional theory (DFT), Tamm et al.[17] reported the short-range ordering (SRO) in CoCrNi and CoCrFeNi MPEAs. Specifically, negative SRO parameters between Ni–Cr and positive SRO between Cr–Cr pairs in CoCrNi were found. In CoCrFeNi, negative SRO parameters for Ni–Cr and Ni–Fe pairs and positive ones for Cr–Cr and Fe–Fe pairs were revealed. Therefore, Cr is not preferred to be the first nearest neighbors (1nn) of other Cr atoms, probably due to magnetic interactions.[18]

Besides the above-mentioned Face-Centered Cubic (FCC) HEAs, SRO is also found in Body-Centered Cubic (BCC) HEAs even if all of the constituent elements are BCC metals. For instance, Widom et al. found considerable short-range ordering in the Mo-Nb-Ta-W system with the hybrid Monte Carlo and molecular dynamics (MD) method based on DFT.[19] Cluster expansion (CE) Hamiltonian from DFT energetics was also built to study SRO in MoNbTaVW and its sub-quaternary systems by Fernandez-Caballero et al.[20] In this system, the strongest SRO is found for the 1nn Mo-Ta pairs, which was interpreted by the high mixing enthalpy of their B2 structures in the binary system. In addition, negative SRO parameters were also predicted for the V–W pairs. In the Cr-Ta-V-W HEA, El-Atwani et al.[21] revealed negative SRO parameters for V–Cr pairs at low temperatures by combining CE and DFT. The strong segregation tendency of Cr and V is consistent with their experimental observations.

The prediction of SRO in MPEAs based on DFT is computationally expensive since it requires frequent total energy calculations. Thus, CE Hamiltonians are usually constructed to evaluate the energy of configurations with different atomic arrangements.[20,21] In these methods, the obtained energies are based on the rigid lattice approximation in which local lattice distortion is neglected. For BCC MPEAs, it is well established that they usually exhibit more considerable local lattice distortion than FCC ones.[22] Such lattice distortion may have a great impact on the total energy and stability of BCC MPEAs. Unlike the first-principles methods mentioned above, a phenomenological treatment of SRO would enable fast prediction of possible short-range ordering in MPEAs, which significantly promotes the understanding of experimental observations pertinent to local structures.

In the present work, we combine MC and DFT energetics to exploit the elemental distribution in typical ternary MPEAs, including CrFeV, HfNbZr, TaVW, NbTaV, and TaTiV. These MPEAs are chosen because they are fundamental units of other complexed HEAs with more than three constituent elements.[23] To the best of our knowledge, there are no existing reports on the local ordering tendency in the considered MPEAs. Previous studies on local ordering for BCC MPEAs were performed for the Mo-Nb-Ta-W quaternary system,[19] MoNbTaVW and its quaternary systems,[20] and Cr-Ta-Ti-V-W and its quaternary systems.[24] In these studies, either a small supercell (16 atoms) was used, or the Cluster Expansion Hamiltonian was built to perform MC steps. In contrast, in this work, we employed a large supercell size (128 atoms) and direct DFT relaxation to perform MC, in which the atomic relaxation is included between successive MC steps. Thus, our MC+DFT method properly considers the local lattice distortion in these MPEAs. We further utilize a modified quasi-chemical model to predict the SRO values in the considered MPEAs. Our results suggest that all these MPEAs may exhibit short-range ordering at a temperature of 500 K. We further show that the presence of SRO has significant influences on their structural properties, specifically, the local lattice distortion. In addition, SRO also affects the electronic and elastic properties of MPEAs.

2 Method

We combine canonical MC with DFT calculations to explore the tendency of elemental distribution in BCC MPEAs. Though we mainly studied ternary MPEAs in this study, the calculation method can be easily extended to new alloy systems, including multi-component (> 3) HEAs, by randomly choosing different species for an atomic exchange. Specifically, we started with a special quasi-random structure (SQS) with zero SRO parameters that was constructed by simulated annealing.[25] The total energy was calculated by DFT calculations. We then started to swap different atomic species with an acceptance probability p based on the Metropolis-Hastings sampling technique.[26] Suppose the energy change induced by the atom swap is ΔE, then

$$ p = \exp \left( { - \frac{\Delta E}{{k_{{\text{B}}} T}}} \right), $$
(1)

where kB and T are the Boltzmann constant and temperature, respectively. After each swap event, DFT calculations were carried out to relax the system, taking the lattice distortion into consideration. The relaxed system then acted as the new structure to initiate the swap process again. Our calculations were initiated with one SQS structure with optimized zero short-range order parameters. The SQS structure is representative of the MPEA with a random state. After MC steps, we have found a decrease in energy and the development of local ordering. Although comparing results from different initial structures may be helpful, we believe that the development of local ordering is universal for these MPEAs due to the lowering of energy compared to the structures with zero short-range order.

The DFT calculations between MC steps were performed using the Vienna ab initio simulation package.[27,28] The projector augmented wave (PAW) pseudopotentials[29] were used to describe the ion-electron interactions. The exchange-correlation interactions were modeled by the generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE) form.[30] The Methfessel–Paxton smearing[31] with a smearing width of 0.2 eV was employed. The cutoff energy of plane waves was 300 eV. A 4 × 4 × 4 supercell of the BCC structure containing 128 atoms was used. As the MC scheme requires lots of energy calculations, we adopted a single k-point during relaxation. The error induced by this k-point sampling scheme is around 5 meV per atom. The convergence criteria for the total energy and atomic force were 10−4 eV and 0.03 eV/Å, respectively. After the MC/DFT process, we calculated the density of states (DOS) and elastic properties of the final structures with 3 × 3 × 3 k-points.

In this study, a relatively low temperature of 500 K was used to highlight the short-range ordering tendency. It is well established that with decreasing temperature, a disorder-to-order transition happens for MPEAs.[24] At a low temperature as 500 K considered here, it is highly likely that the transition has already been completed. Therefore, the local ordering tendency can be identified at this temperature. The temperature effects are not included in static DFT relaxations; the temperature we considered is used for the MC process. A more practical relaxation method may be molecular dynamics based on DFT. By combining such ab initio molecular dynamics (AIMD) with MC, one can simulate the finite temperature response of the system, taking into account both the vibrational and configurational contributions. However, such a simulation scheme would be computationally costly. In this work, the temperature effects are considered as temperature-dependent configurational entropy only.

As discussed previously,[17, 19] the steps required to arrive at thermodynamic equilibrium in MC simulations are typically around 104. However, for MC combined with DFT calculations, only a limited number of steps is possible. In this study, around 500–3000 steps were simulated for different MPEAs. This number is in the same order as previous studies.[17] Although the results may not be well converged, the trend of SROs observed can still reflect the tendency of elemental distribution in the considered MPEAs. With the MC process explained above, the total energy of the system decreases, suggesting a more stable state is being found.

The short-range ordering is described by the Warren-Cowley short-range order (SRO) parameter defined as:[32]

$$ \alpha_{k}^{ij} = 1 - \frac{{p_{k}^{ij} }}{{c_{i} }}, $$
(2)

where \(p_{k}^{ij}\) is the conditional probability to find a i atom around the j atom at its kth nearest-neighbor shell, and ci is the concentration of species i. In random alloys, \(\alpha_{k}^{ij}\) is 0, since the probability to find i and j atoms corresponds to their concentrations, ci and cj. \(\alpha_{k}^{ij} > 0\) suggests a tendency of clustering or segregation of i–i and j–j pairs (these bonds predominant), while \(\alpha_{k}^{ij} < 0\) indicates there is a tendency of ordering-type correlations (i–j bonds predominant). In BCC structures, the distances between 1 and 2 nn pairs are close, so a weighted SRO parameter combining the 1 and 2 nn shell was introduced to describe the overall local ordering:[20]

$$ \alpha_{12}^{ij} = \frac{{8\alpha_{1}^{ij} + 6\alpha_{2}^{ij} }}{14}, $$
(3)

where 8 and 6 are the number of 1 and 2 nn neighbors, respectively.

3 MC/DFT Results of SRO in MPEAs

3.1 CrFeV

The MPEAs comprised of Cr, Fe, and V are promising candidates for nuclear applications due to the low-activation nature of constituent elements.[33,34] The irradiation performance of Fe-Cr-V-Si (-Mo) HEAs has been characterized experimentally,[33,35] and promising irradiation resistance has been observed. For BCC CrFeV alloys, our calculations indicate that the ground state of this MPEA is magnetic, which is different from other nonmagnetic refractory MPEAs.[22] We have checked the energy-volume relations for CrFeV in nonmagnetic and ferromagnetic states. It is found that the ferromagnetic states exhibit much lower energy (~ 0.05 eV/atom) than the nonmagnetic states. For this reason, spin-polarization is considered in DFT calculations.

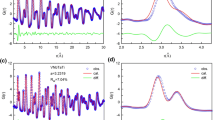
The evolution of total energy and SRO parameters for CrFeV is provided in Fig. 1. The total energy decreases steadily with increasing MC steps. After 400 MC steps, the energy starts to saturate, indicating that the equilibrium state has been found. Along with the decrease in energy, we find considerable SRO values for different atomic pairs. Therefore, SRO tendency is predicted for this MPEA at 500 K. After 500 MC steps, Fe-Cr and V-V exhibit relatively high SRO values, ~ 0.6 at 1 nn. This positive number dictates that these two atomic pairs are unfavorable. On the other hand, Fe-Fe, Fe-V, and Cr-V pairs have the most negative SRO parameters, suggesting high probabilities of having these pairs in the 1 nn shell. The favorable bonding between Fe-V and Cr-V is consistent with their negative enthalpy of mixing in the binary BCC structures.[13] On the other hand, Fe-Cr exhibits positive mixing enthalpy in random binary alloys for most compositions,[36,37] in agreement with the current prediction of positive SROs for Fe-Cr pairs.

Fig. 1
figure 1

Structural properties of CrFeV. (a) shows the evolution of total energy with MC steps, (b) the atomic configuration after equilibrium, (c) shows the pair correlation functions g(r) in the equilibrated structure, (d), (e), and (f) show the SRO parameters at 1nn shell, 2nn shell, and the averaged SRO from both 1 and 2 nn shells, respectively

Full size image

In FCC MPEAs, it is shown that Cr is not preferred to be 1 nn to other Cr atoms, as evidenced by its positive SRO value in previous studies.[17] However, in BCC MPEAs considered here, we found Cr tends to segregate, as suggested by their negative SRO parameters. Such clustering of Cr is also found in Fe-Cr alloys, in which Cr may develop a Cr-riched phase when its concentration is higher than 9%.[37] The origin of the observation is believed due to the peculiarities of the enthalpy of mixing in the Fe-Cr mixtures, which is negative below a critical concentration and becomes positive above it.

During the calculations, we have considered the effects of local lattice distortion. The obtained equilibrium structure can be used to analyze the structural properties. Figure 1(c) provides the partial pair correlation functions g(r) for each atomic pair, which show the spatial distribution between different atomic pairs as a function of distance. The calculated g(r) is normalized by their atomic densities. In the BCC structure, the position of the first peak is located at 1 nn distance, \(\sqrt 3 a_{0} /2\), while the second peak occurs at 2 nn distance, a0, where a0 is the equilibrium lattice constant (2.87 Å for CrFeV in this study). These two positions are indicated by dotted lines in Fig. 1c. A comparison between the SRO results and the g(r) distribution suggests that dominant nearest-neighbor correlations are those atomic pairs with negative SROs (Fe-V, Fe-Fe, and Cr-Cr), which is reasonable since they are predominant in the equilibrium structure.

3.2 HfNbZr

For nonmagnetic HfNbZr, spin-polarization is not considered. The evolution of total energy and SRO parameters are provided in Fig. 2. The total energy saturates starting from 600 MC steps. At equilibrium states, slightly positive SRO parameters are obtained for Hf-Hf pairs. In general, all the SRO values are small in this system, ranging from − 0.2 to 0.2. This observation may be understood from the values of mixing enthalpy among the three atom species. In particular, experiments show zero mixing enthalpy of Zr-Hf pairs and slightly positive mixing enthalpy for Nb-Zr and Nb-Hf pairs.[38] Therefore, the low values of SRO in this system are expected. Furthermore, our results are consistent with the experimental characterization of this MPEA, where no specific Zr, Hf, or Nb-contained phases are found during in-situ TEM observation of the thermally formed crystalline phases.[39] The Hf-Nb-Zr phase is stable even after electron irradiation.[39]

Fig. 2
figure 2

Structural properties of HfNbZr. (a) shows the evolution of total energy with MC steps, (b) the atomic configuration after equilibrium, (c) shows the pair correlation functions g(r) in the equilibrated structure, (d), (e), and (f) show the SRO parameters at 1 nn shell, 2 nn shell, and the averaged SRO from both 1 and 2 nn shells, respectively

Full size image

In the equilibrium structure of Hf-Nb-Zr, the 1 and 2 nn peaks are indistinguishable due to severe local lattice distortions. Such a phenomenon has been observed in other BCC HEAs.[22] Notably, the first peak of Nb-Nb exhibits the most substantiate deviation toward shorter bonding lengths, whereas Zr-Zr pairs deviate most toward the longer bonding length. The distortion may arise from the atomic size mismatch. Indeed, the atomic size of Nb (1.47 Å) is much smaller than that of Zr (1.60 Å) and Hf (1.58 Å) (All the atomic radius values in this study are from Ref 40).

3.3 TaVW

The evolution of total energy and SRO parameters for nonmagnetic TaVW are provided in Fig. 3. The total energy saturates starting from 300 MC steps. At equilibrium states, substantially negative SRO parameters at 1 nn are found for the V-Ta and Ta-W pairs, while positive SRO parameters are found for Ta-Ta pairs. The trend of SRO at 2nn is different from that in 1nn. Particularly, SRO for Ta-Ta becomes negative while SRO of V-Ta is positive. Combining SROs at 1 and 2 nn, we find positive SROs for W-W and negative SRO for V-W and V-Ta. Considering the mixing enthalpy, the values for V-Ta, V-W, and Ta-W are all negative, suggesting preferable bonding among these three elements.

Fig. 3
figure 3

Structural properties of TaWV. (a) shows the evolution of total energy with MC steps, (b) the atomic configuration after equilibrium, (c) shows the pair correlation functions g(r) in the equilibrated structure, (d), (e), and (f) show the SRO parameters at 1 nn shell, 2 nn shell, and the averaged SRO from both 1 and 2 nn shells, respectively

Full size image

The lattice constant of TaVW is calculated to be 3.17 Å. The g(r) function provided in Fig. 3(c) shows well-separated 1nn and 2nn peaks, signifying limited local lattice distortion in this MPEA. At 1nn, the contributions of V-Ta and Ta-W pairs are dominant, consistent with their negative SROs. The largest deviation is found in V-V pairs, which can be attributed to the smallest atomic size of V among these three elements.

3.4 NbTaV

NbTaV is one of the subsystems of NbTaV(Ti, W, Mo) system, which demonstrates great high-temperature strength and ductility.[41,42] These alloys also exhibit promising irradiation resistance under irradiation.[43] The evolution of total energy and SRO parameters for nonmagnetic VNbTa are provided in Fig. 4. The total energy saturates starting from 800 MC steps. At equilibrium states, we find a strong SRO tendency at 1 nn for Ta-V pairs (negative), as well as V-V and Ta-Ta pairs (positive). At 2 nn, the aforementioned SRO trend is reversed, i.e., positive SRO for Ta-V and negative V-V and Ta-Ta pairs. Combining 1 and 2 nn, the averaged SROs show negative values for Nb-Nb and Ta-V, while Nb-Ta and Ta-Ta pairs are positive. It is found from DFT that the enthalpies of mixing for BCC Nb-V alloys are positive in the whole composition range, suggesting weak attractive interactions.[20] For Ta-V, their mixing enthalpies are negative,[13] agreeing with the negative SROs averaged from 1 to 2 nn.

Fig. 4
figure 4

Structural properties of NbTaV. (a) shows the evolution of total energy with MC steps, (b) the atomic configuration after equilibrium, (c) shows the pair correlation functions g(r) in the equilibrated structure, (d), (e), and (f) show the SRO parameters at 1 nn shell, 2 nn shell, and the averaged SRO from both 1 and 2 nn shells, respectively

Full size image

The calculated lattice constant for VNbTa is 3.02 Å. The g(r) function in Fig. 4 shows separated 1 and 2 nn peaks. At 1 nn, the contribution of Ta-V and Nb-Nb pairs is dominant, consistent with their negative SROs. The largest deviation from the ideal distance is found in V-V pairs, in line with the smallest atomic radius of V compared to Ta and Nb.

3.5 TaTiV

TaTiV is the composition unit of complexed TaTiVZr, TaTiVCr, TaTiVNb, and TaTiV(Zr,Hf) HEAs. These HEAs exhibit good mechanical strength and irradiation tolerance.[43,44] The evolution of total energy and SRO parameters for nonmagnetic TaTiV are provided in Fig. 5. The total energy saturates starting from 500 MC steps. At equilibrium states, we find strong SRO tendencies at 1 nn for Ta-V, Ti-Ti, and Ta-Ta pairs (negative), as well as Ti-Ta and V-V pairs (positive). At 2 nn, positive SRO for Ta-V and Ta-Ti, and negative SRO for V-V and Ti-Ti pairs are found. Based on the averaged SRO at 1 and 2 nn, Ti-Ti and Ta-Ta exhibit strong negative SROs, whereas Ti-Ta shows strong positive SROs.

Fig. 5
figure 5

Structural properties of TaTiV. (a) shows the evolution of total energy with MC steps, (b) the atomic configuration after equilibrium, (c) shows the pair correlation functions g(r) in the equilibrated structure, (d), (e), and (f) show the SRO parameters at 1 nn shell, 2 nn shell, and the averaged SRO from both 1 and 2 nn shells, respectively

Full size image

The lattice constant is 3.20 Å for TaTiV. The g(r) function in Fig. 5 shows mixed peaks for 1nn and 2nn, suggesting severe local lattice distortion. The first peak of V-V occurs at the shortest distance due to the smallest atomic radius of V compared to Ti and Ta. This observation is consistent with TaVW and NbTaV MPEAs shown in Figs. 3 and 4.

Experiments show that the equiatomic Ta-Ti-V MPEA has high thermal stability without secondary phases after long-time annealing.[45] On the contrary, non-equiatomic Ta-Ti-V MPEAs, including Ta27Ti40V33 and Ta35Ti45V20, exhibit second α′′ phases. The high-angle annular dark-field (HAADF) images with EDS-mappings demonstrate that the secondary phase is Ti-rich and V/Ta-depleted. Our prediction suggests Ti-Ti pairs possess the most negative SROs while Ta-Ti pairs have the most positive SROs, which is in line with the experimental observation.

4 Summary of SROs in Considered MPEAs

The SRO parameters for all the considered MPEAs are summarized in Fig. 6. The SRO parameters are relatively small in HfNbZr and TaTiV. On the other hand, NbTaV and TaVW exhibit large SRO values at both 1 and 2 nn shells. Nevertheless, their averaged SRO values from 1 to 2 nn are low. The averaged SRO values may be much smaller if the SRO values at 1 and 2 nn have opposite signs. For example, the averaged SROs are close to 0 in NbTaV for all pairs. However, the individual SRO value at 1 and 2 nn is rather high.

Fig. 6
figure 6

Summary of the SRO results for the considered MPEAs. For each alloy, the SRO parameters at 1nn, 2nn, and the averaged values from 1 to 2 nn shells are provided

Full size image

The same atomic pairs may exhibit different SRO features in different MPEAs. For example, Ta-Ta pairs in the 1 nn shell show positive SRO values in TaVW and NbTaV, but negative SRO values in TaTiV. For atom pairs composed of different atomic species, we find consistent SRO trends in different MPEAs, such as Ta-V, which exhibits negative SRO at 1 nn and positive SRO at 2 nn. The negative SRO for Ta-V pairs is attributed to the negative enthalpy of mixing for Ta–V mixtures, which can be confirmed from previous DFT results.[13] In previous work, the SRO parameter of V-Ta in MoNbTaVW is determined to be positive arising from the calculated positive mixing enthalpies in the whole composition range for the BCC phase.[20]

5 Mechanistic Understanding of SRO

The above results indicate that the enthalpy of mixing of different atomic pairs has a dominant role in influencing the SRO tendency in MPEAs. Specifically, a positive enthalpy of mixing suggests the tendency towards atomic segregation, while a negative enthalpy of mixing indicates a tendency to form intermetallic phases (SRO). Such a correlation has been found in current calculations as well as previous results. For example, in the Cr-Ta-Ti-V-W system and its derivative alloys, the most negative SRO values are observed for the Ta-W and Cr-V pairs, which is in accordance with the low enthalpies of mixing of these two atomic pairs.[24] Our results in TaVW agree with the negative enthalpy of mixing of Ta-W pairs. Such a tendency is also consistent with microstructure characterization after melt-casting and homogenization for TaTiVZrW,[46] where Ta-W atomic-pair clustering is found.

To further elucidate the correlation between SRO values and the enthalpy of mixing of atomic pairs, we modify the quasi-chemical model[47,48] for solutions to build the thermodynamic quantities for the considered MPEAs. We only consider the interactions between nearest-neighbor pairs. For the formation of an A–B pair, the enthalpy of mixing is

$$ H_{{{\text{mix}}}} = e_{AB} - \left( {e_{AA} + e_{BB} } \right)/2, $$
(4)

where eij represents the interaction energy of an i–j nearest neighbor pair. The enthalpy change of the total system with three components is thus

$$ \Delta H = \frac{{N_{AB} }}{2}H_{AB} + \frac{{N_{AC} }}{2}H_{AC} + \frac{{N_{BC} }}{2}H_{BC} . $$
(5)

Here Nij is the number of i–j pairs, and Hij is mixing enthalpy per atom (resulting in a factor of 2) for atomic species with different atomic types. The configurational entropy of mixing considering local ordering is:[48]

$$ \begin{aligned} \Delta S & = - N_{{{\text{tot}}}} k_{B} \left( {c_{A} \ln c_{A} + c_{B} \ln c_{B} + c_{C} \ln c_{C} } \right) - N_{{{\text{tot}}}} k_{B} \left( \frac{Z}{2} \right) \\ & \quad \left[ {p_{AA} \ln \left( {\frac{{p_{AA} }}{{c_{A}^{2} }}} \right) + p_{BB} \ln \left( {\frac{{p_{BB} }}{{c_{B}^{2} }}} \right) + p_{CC} \ln \left( {\frac{{p_{CC} }}{{c_{C}^{2} }}} \right) + p_{AB} \ln \left( {\frac{{p_{AB} }}{{2c_{A} c_{B} }}} \right) + p_{AC} \ln \left( {\frac{{p_{AC} }}{{2c_{A} c_{C} }}} \right) + p_{BC} \ln \left( {\frac{{p_{BC} }}{{2c_{B} c_{C} }}} \right)} \right], \\ \end{aligned} $$
(6)

where \(p_{ij} = \frac{{N_{ij} }}{{N_{tot} }}\) and ci is the atomic concentration of the i component. Note that for random mixture, the entropy reduces to the ideal mixing case. The free energy of the system is then given by \(\Delta G = \Delta H - T\Delta S\). By minimizing the free energy with respect to Nij (i ≠ j), the following equations can be obtained:

$$ \frac{{p_{AB}^{2} }}{{p_{AA} p_{BB} }} = 4\exp \left( { - \frac{{2H_{AB} }}{{Zk_{B} T}}} \right), $$
(7)
$$ \frac{{p_{AC}^{2} }}{{p_{AA} p_{CC} }} = 4\exp \left( { - \frac{{2H_{AC} }}{{Zk_{B} T}}} \right), $$
(8)
$$ \frac{{p_{BC}^{2} }}{{p_{BB} p_{CC} }} = 4\exp \left( { - \frac{{2H_{BC} }}{{Zk_{B} T}}} \right). $$
(9)

The constraints of the number of atomic pairs for N atoms give:

$$ 2N_{AA} + N_{AB} + N_{AC} = ZN_{A} = Zc_{A} N, $$
(10)
$$ 2N_{BB} + N_{AB} + N_{BC} = ZN_{B} = Zc_{B} N, $$
(11)
$$ 2N_{CC} + N_{AC} + N_{BC} = ZN_{C} = Zc_{C} N. $$
(12)

From Eq 7-12, the number of atomic pairs Nij can be solved numerically. The SRO parameters can then be calculated based on the obtained Nij for each atomic pair using Eq 2. Apparently, the number of atomic pairs depends on the enthalpy of mixing for each unlike atomic pair Hij. In the previous derivation of the quasi-chemical model, it is assumed that the mixing enthalpy is independent of compositions and temperature. In solving the above equations, we, therefore, take the values of Hij from the enthalpy matrix in Ref 13 that is calculated based on the lowest energy structures of binary compounds relative to pure elements. With T = 500 K, \(c_{A} = c_{B} = c_{C} = \frac{1}{3}\), and Z = 14 by combining 1 and 2 nn in BCC MPEAs, we obtain the trend of SRO in Fig. 7(a) with respect to the mixing enthalpy and compare the model results with our MC/DFT calculation in Fig. 7(b).

Fig. 7
figure 7

SRO values predicted from the model. (a) shows the SRO trend calculated by varying HAB while setting HAC = HBC = 0, (b) compares the model SRO values with the calculated SRO

Full size image

The SRO trend in Fig. 7(a) is calculated by varying HAB while setting HAC = HBC = 0. It demonstrates that the SRO values for A–B pairs increase with increasing HAB, which is consistent with the favorable (unfavorable) binding of A–B pairs for negative (positive) HAB. The preference of A–B pairs, on the other hand, can affect the number of A–A and B–B pairs, as manifested by the reverse trend of SROs for these two pairs compared to that of A–B pairs. Though HAC = HBC = 0, these atomic pairs also exhibit low values of SRO due to the varying number of A–B pairs. Note that the trend of SRO is asymmetric with increasing mixing enthalpy.

The model results in Fig. 7(a) are in line with general observations. Based on the model, we calculate the SRO values for the five considered MPEAs and compare them with values from Fig. 6. Generally, we find a good agreement between the values of calculated SRO and model SRO. There are, however, some points deviating from the identity line y = x. Those points are mainly from CrFeV, which may be attributed to the large differences in the mixing enthalpy of Fe-Cr pairs. Specifically, the lowest Hmix for Fe-Cr is − 8 meV/atom based on Ref [13]. However, other reports show positive values in the majority of the compositional space.37 Therefore, the knowledge of accurate enthalpy of mixing between elements is the key in quantitively explain the SRO trend in MPEAs using the model.

6 Influences of SRO on the Properties of MPEAs

To highlight the SRO tendency, we have employed a low temperature of 500 K in the MC procedure. With increasing temperature, it is expected that all the SRO parameters approach zero due to the increasing contribution of configurational entropy, corresponding to an ideal solid solution with randomly distributed elements.[24] The presence of SRO at low or intermediate temperatures in MPEAs can strongly affect their properties. For instance, in FCC HEAs, Tamm et al.[17] showed that the electronic structure of CoCrNi and CoCrFeNi alloys exhibits differences near the Fermi energy owing to SRO.

To reveal the influences of SRO on the properties of BCC MPEAs, we show in Fig. 8 the pair correlation functions for all the atomic pairs in the initial random structures and the equilibrium structure with SRO. For the five MPEAs, it is seen that the presence of SRO has significant impacts on the local lattice distortion, especially for HfNbZr and TaTiV, manifesting by the shift of peaks in g(r) functions. The changes in the intensities of g(r) peaks are also noticeable, which is induced by the changes of nearest atomic pair numbers due to SRO.

Fig. 8
figure 8

Pair distribution function of MPEAs in the random states (black dotted) and SRO states (red)

Full size image

For the two MPEAs with the largest local structural changes (HfNbZr and TaTiV), we have further studied the effects of SRO on their electronic and elastic properties. The density of states (DOS) is provided in Fig. 9, in which the total DOS (TDOS) and projected DOS (PDOS) of d states are shown. There is a pseudogap below the Fermi level, separating the DOS into the bonding and antibonding states. For both MPEAs, the presence of SRO decreases the TDOS at the Fermi level, consistent with the lowering of the total energy. Comparison between these two MPEAs suggests that the change of TDOS is more pronounced in HfNbZr, which also exhibits greater local distortion than TaTiV (Fig. 8). The difference mainly arises from the negative SRO of Hf-Nb and Hf-Zr pairs and positive SRO of Hf-Hf and Nb-Nb pairs. The presence of SRO leads to a shoulder near the first peak in the g(r) curves, as seen in Fig. 8(b). This shoulder is mainly contributed by Zr-Zr, Zr-Hf and Hf-Hf bonds, as indicated in Fig. 2(c). Consequently, the d states of Zr and Hf experience the most significant changes from the PDOS plot. In TaTiV, the d states of Ti decrease the most, which is in line with the negative SRO of Ti-Ti.

Fig. 9
figure 9

Total density of states (TDOS) and projected density of states (PDOS) of d states for HfNbZr (left column) and TaTiV (right column) in the random and SRO states. The Fermi level at 0 eV is denoted by the dotted line

Full size image

We further study the effects of SRO on the elastic constants of HfNbZr and TaTiV. The results are summarized in Table 1. Consistent with g(r) and DOS showed above, the presence of SRO has larger effects on elastic constants for HfNbZr than for TaTiV. A common feature in these two MPEAs is that the SRO tends to increase the values of C44. As indicated by the DOS, the development of SRO tends to lower the energy of the system, rendering them more stable by forming stronger atomic bonds. Therefore, the appearance of SRO may enhance the mechanical strength of MPEAs.

Table 1 Elastic constants (in GPa) calculated in HfNbZr and TaTiV in random and SRO structures
Full size table

7 Conclusion

Combining MC and DFT calculations, we have studied the tendency of atomic arrangement in five typical BCC MPEAs. Our results indicate that all the considered MPEAs may develop a certain degree of short-range ordering at a temperature of 500 K. By considering the mixing enthalpy of different atomic pairs, we have formulated the SRO values in different MPEAs based on a quasi-chemical model. The good agreement between the model and calculation results suggests that SRO in MPEAs can be predicted accurately as long as the mixing enthalpy between unlike atomic pairs is known. The appearance of SRO affects the structural, electronic, and mechanical properties of MEPAs. Specifically, SRO tends to make the system more stable and may enhance the shear modulus of the alloy. Our method, i.e., DFT+MC and the quasi-chemical model, can be easily extended to new alloy systems, including multi-component (> 3) HEAs, probably at a higher computational cost.