Abstract
In a previous paper (Lipovetsky and Dyn in Comput Aided Geom Des 48:36–48, 2016), we introduced a weighted binary average of two 2D point-normal pairs, termed circle average, and investigated subdivision schemes based on it. These schemes refine point-normal pairs in 2D and converge to limit curves and limit normals. Such a scheme has the disadvantage that the limit normals are not the normals of the limit curve. In this paper, we address this problem by proposing a new averaging method and obtaining a new family of algorithms based on it. We demonstrate their new editing capabilities and apply this subdivision technique to smooth a precomputed feasible polygonal point robot path.











Similar content being viewed by others
References
Aihua, M., Jie, L., Jun, C., Guiqing, L.: A new fast normal-based interpolating subdivision scheme by cubic Bézier curves. Vis. Comput. 32(9), 1085–1095 (2016)
Chalmovianský, P., Jüttler, B.: A non-linear circle-preserving subdivision scheme. Adv. Comput. Math. 27, 375–400 (2007)
Connors, J., Elkaim, G.: Analysis of a spline based, obstacle avoiding path planning algorithm (2007)
Conti, C., Dyn, N.: Analysis of subdivision schemes for nets of functions by proximity and controllability. J. Comput. Appl. Math. 236, 461–475 (2011)
de Berg, M., Cheong, O., van Kreveld, M., Overmars, M.: Computational Geometry: Algorithms and Applications, 3rd edn. Springer, Berlin (2008)
Dokken, T., Dæhlen, M., Lyche, T., Mørken, K.: Good approximation of circles by curvature-continuous Bézier curves. Comput. Aided Geom. Des. 7, 33–41 (1991)
Dyn, N., Farkhi, E.: Spline subdivision schemes for compact sets-a survey. Serdica Math. J. 28(4), 349–360 (2002)
Dyn, N., Levin, D.: Subdivision schemes in geometric modelling. Acta Numerica 11, 73–144 (2002)
Dyn, N., Sharon, N.: Manifold-valued subdivision schemes based on geodesic inductive averaging. J. Comput. Appl. Math. 311, 54–67 (2017)
Ewald, T., Reif, U., Sabin, M.: Hölder regularity of geometric subdivision schemes. Constr. Approx. 42, 425–458 (2015)
Gloderer, M., Hertle, A.: Spline-based trajectory optimization for autonomous vehicles with Ackerman drive (2010)
Lipovetsky, E., Dyn, N.: A weighted binary average for subdivision schemes of point-normal pairs. Comput. Aided Geom. Des. 48, 36–48 (2016)
Lipovetsky, E., Dyn, N.: \({C}^1\) analysis of some \({2D}\) subdivision schemes refining point-normal pairs with the circle average. Comput. Aided Geom. Des. 69, 45–54 (2019)
Micchelli, C., Sauer, T.: On vector subdivision. Math. Z. 229, 641–674 (1998)
Prautzsch, H., Boehm, W., Paluszny, M.: Bézier and B-Spline Techniques, 1st edn. Springer, Berlin, Heidelberg (2002)
Rahman, I.U., Drori, I., Stodden, V.C., Donoho, D.L., Schröder, P.: Multiscale representations for manifold-valued data. Multiscale Model. Simul. 4(4), 1201–1232 (2005)
Thompson, S., Kagami, S.: Continuous curvature trajectory generation with obstacle avoidance for car-like robots (2006)
Wallner, J., Dyn, N.: Convergence and \({C}^1\) analysis of subdivision schemes on manifolds by proximity. Comput. Aided Geom. Des. 22(7), 593–622 (2005)
Zhang, A., Zhang, C.: Tangent direction controlled subdivision scheme for curve. In: The 2nd Conference on Environmental Science and Information Application Technology, p. 4 (2010)
Acknowledgements
The author thanks Prof. Nira Dyn for fruitful discussions and useful comments that contributed to the quality of this paper, and especially for shaping the proof of Lemma 15. The author thanks the referees for their valuable comments and proposed directions for future work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The contribution of Evgeny Lipovetsky is part of his Ph.D. research conducted at Tel-Aviv University.
Appendices
A Convergence analysis of \(\hbox {MLR}_1\)
In this section, we prove the convergence of \(\hbox {MLR}_1\) and show that it generates limit normals that are the normals of the limit curve. We do this for a certain type of inputs. The proof is organized in several steps. We first split the set of all possible inputs and define a “good” configuration of two PNPs. We study more properties of \(\hbox {BQA}_\frac{1}{2}\) in regard to this type of input. Next, we use these properties to prove the convergence of \(\hbox {MLR}_1\) under the assumption that each two consecutive PNPs in the input form a good configuration. As part of the proof, we show that the generated normals tend to the perpendiculars of the generated segments.
1.1 A.1 Properties of \(BQA_{\frac{1}{2}}\)
First, we define what is a good configuration of two PNPs.
Definition 10
For two points \(p_0\) and \(p_1\), we define their corridor by the two lines, perpendicular to \([p_0, p_1]\) and passing through \(p_0, p_1\).
Definition 11
For two PNPs \(P_0, P_1\), consider the corridor of \(p_0\) and \(p_1\). We say that the pairs \(P_0, P_1\) form a good configuration if the following two conditions hold:
-
C1:
both \(c_1\) and \(c_2\) are inside the corridor.
-
C2:
The polygon \(p_0p_1c_2, c_1\) is strictly convex.
See Fig. 12 for a good (a) and bad (b–d) examples. In this figure: case (b) lacks C1, case (c) lacks C2, and (d) demonstrates the case when both conditions do not hold.
We introduce more notation for further investigations. We denote \(P_2 = (p_2, n_2) = BQA_{\frac{1}{2}}(P_0, P_1)\). We define local coordinate system with \(p_0 = (0,0), p_1 = (e,0)\). Consider the line that connects the midpoints of the tangents \(d_0\) and \(d_1\). We denote by \(\gamma \) the angle between this line and the x-axis. By construction of a cubic Bezier curve, \(n_2\) is perpendicular to this line. Let \(L^\prime \) be the line passing through \(p_2\) which is perpendicular to \(n_2\). Let \(p^\prime \) be the intersection point of \(L^\prime \) and the x-axis. See Fig. 13 for an example.
We study the following angles:  ,
,  ,
,  ,
,  . W.l.o.g. we assume that \(\alpha _L < \alpha _R\).
. W.l.o.g. we assume that \(\alpha _L < \alpha _R\).
In the next proofs, we often compare some quantity, computed for \(P_0, P_1\) with a similar one computed for \(P_0, P_2\) (left), and \(P_2,P_1\) (right). We use the superscripts \(next\_left\) or \(next\_right\) to denote these quantities. For example, consider the three angles \(\theta , \theta ^{next\_left}, \theta ^{next\_right}\) between the pairs of normals \((n_0, n_1), (n_0, n_2), (n_2, n_1)\), respectively. Armed with this notation, we are ready to dive into the coming proofs.
First, we show that a good configuration of \(P_0, P_1\) leads to two good configurations.
Examples of \([p_0,c_1^{next\_left}]\) (blue) and \([c_2^{next\_left},p_2]\) (red) in the proof of Lemma 12
Lemma 12
Let two PNPs \(P_0, P_1\) be such that both C1 and C2 hold. Then, C1 and C2 also hold for \(P_0, P_2\), and for \(P_2, P_1\).
Proof
We prove conditions C1 and C2 for the left pair \(P_0,P_2\). The reasoning for the right pair is similar.
Let \(q'\) be the intersection point between \(L'\) and \([p_0,c_1]\), and let \(p_0c_1^{next\_left}c_2^{next\_left}p_2\) be the control polygon of the auxiliary Bezier curve of \(BQA_{\frac{1}{2}}(P_0, P_2)\). By Theorem 2, the segments \([p_0,c_1^{next\_left}]\) and \([c_2^{next\_left},p_2]\) do not intersect. So, \(c_1^{next\_left} \in [p_0q']\) and \(c_2^{next\_left} \in [q'p_2]\). See Fig. 14 for an example.
This implies that
-
1.
the angles
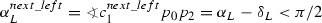 , and
, and 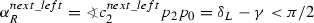 . Namely, condition C1 holds for \(P_0, P_2\).
. Namely, condition C1 holds for \(P_0, P_2\). -
2.
The polygon \(p_0 c_1^{next\_left}c_2^{next\_left} p_2\) is convex, i.e., condition C2 holds too.
\(\square \)
Next, we show
Lemma 13
Let two PNPs \(P_0, P_1\) be such that both C1 and C2 hold. Then, \(|p_0p_2|< \mu |p_0p_1|, |p_2p_1| < \mu |p_0p_1|\), \(\mu = \frac{\sqrt{13}}{4} < 1\).
Proof
The outline of the proof is as follows. We compute the coordinates of \(p_2 = (p^x_2, p^y_2)\), then compute \(|p_0p_2|\), and show that \(|p_0p_2| < \mu e\), where \(\mu < 1\).
The coordinates of the control points are: \(p_0 = (0,0)\), \(c_1 = (\ell \cos \alpha _L, \ell \sin \alpha _L)\), \(c_2 = (e-\ell \cos \alpha _R\), \( \ell \sin \alpha _R)\), \(p_1 = (e, 0)\). We compute a point of a cubic Bezier curve at parameter \(\frac{1}{2}\) (see, e.g., [15]) and get,
We use (1) and get
Then
Since \(\theta < \pi \), we bound \(\cos ^2\frac{\theta }{4} > \frac{1}{2}\) and get
Since both conditions C1 and C2 hold, \(0 \le \cos \alpha _R \le 1\). Thus, we obtain
Similar reasoning can be applied to obtain \(|p_2p_1| \le \frac{e\sqrt{5}}{4}\). So, the claim of the lemma holds with \(\mu = \max \Big \{ \frac{\sqrt{5}}{4}\),\( \frac{\sqrt{13}}{4} \Big \}\) \( = \frac{\sqrt{13}}{4}\). \(\square \)
Next, we show
Lemma 14
Let two PNPs \(P_0, P_1\) be such that both C1 and C2 hold. If \(0 < \theta \), then \(0< \theta ^{next\_left}, \theta ^{next\_right} < \theta \).
Proof
It is easy to see that \(\theta = \alpha _L + \alpha _R\). Also, since \(p_2\) is in the convex hull of \(p_0, c_1, c_2, p_1\), and by condition C2, \(0< \delta _L < \alpha _L\) and \(0< \delta _R < \alpha _R\). Furthermore, it holds that \(\gamma< \delta _L < \alpha _L\), since \(\delta _L\) is an external angle of \(\vartriangle p_2p'p_0\). We have for the left pair of PNPs, \(P_0\) and \(P_2\), by the proof of Lemma 12 (see Fig. 13),

Thus, we obtain
In a similar way, we have for the right pair of PNPs, \(P_2\) and \(P_1\),
It is easy to see from (24) and (25) that \(0 < \theta ^{next\_left}\) and \(0 < \theta ^{next\_right}\). Thus, the statement of the lemma holds. \(\square \)
For the next discussion, we define
and show
Lemma 15
Let two PNPs \(P_0, P_1\) be such that both C1 and C2 hold. Then, for \(\theta \) small enough, \(\frac{\theta ^{next}}{\theta } < \frac{3}{4}\).
Proof
We begin with study of \(\tan \gamma \). We get
If \(\theta \rightarrow 0\), then also \(\alpha _L\rightarrow 0\), \(\alpha _R\rightarrow 0\), \(\gamma \rightarrow 0\), since \(\gamma< \alpha _L < \alpha _R\) and \(0<\alpha _L+\alpha _R = \theta \). Recall that for x small enough, \(\sin x \approx x\), \(\tan x \approx x\), \(\cos x \approx 1\). We use this in (27) and get
Next, we define the angle \(\gamma '\) to be the angle between the line passing through \([c_1,c_2]\) and the x-axis. See Fig. 15 for an example. We have
For \(\theta < \epsilon \), it holds \(\alpha _L< \alpha _R< \theta < \epsilon \). Also, \(\gamma ' < \alpha _L\), due to the convexity of \(p_0c_1c_2p_1\). Thus
We use (28) and get \(\gamma ' \approx 4\gamma \), when \(\theta \) is small enough. So,
or, equivalently,
By the proof of Lemma 14,
\(\square \)

1.2 A.2 Convergence analysis of \(\hbox {MLR}_1\)
In this section, we use the properties proven in A.1 to show the convergence of \(\hbox {MLR}_1\), when each two consecutive PNPs of the input data form a good configuration. We first recall the definition of the algorithm. While it can be stated as a special case of Algorithm 1, we put it in a less formal way for the reader’s convenience. See Algorithm 3.
In the notation of Algorithm 3, we define
where \(P^{j}_i = (p^{j}_i, n^{j}_i)\), and \(\theta (u,v)\) is the angle between the vectors u and v.
We prove the convergence of \(\hbox {MLR}_1\) in accordance with Definition 3. First, we prove the convergence of the points and then the convergence of the normals. Both proofs are based on the following result, given in its variant for points:
Result A ( [9], Theorem 3.6) A subdivision scheme refining points converges for any initial data, if any sequence of control polygons \(\big \{ {\mathcal {P}}^j=\{p^j_i:i\in {\mathbb {Z}}\}\big \}_{j\in {\mathbb {N}}_0}\) generated by this scheme satisfies for \(j> J^* > 0\)
-
\(e^{j+1} \le \mu e^j\), \(\mu \in (0,1)\), where \(e^j\) is defined as in (35) (contractivity with factor \(\mu \)).
-
\(|p^{j+1}_{2i} - p^j_i| \le ce^j\), with \(c > 0\) (safe displacement).
As defined in Algorithm 3, \(\hbox {MLR}_1\) is an interpolatory scheme. By definition, any interpolatory subdivision scheme is displacement safe. Thus, it remains to prove the contractivity of the points and the normals in \(\hbox {MLR}_1\), in order to show its convergence by Result A. The convergence of points is provided by Lemma 13, where the contractivity factor \(\mu =\sqrt{13}/4\) is shown. Therefore, the final piece of the puzzle is the contractivity of the normals.
We regard the normals as points on the unit circle and the distance between two normals is the angle between them. Thus it remains to show, that \(\frac{\theta ^{j+1}}{\theta ^j} \le \eta < 1\) for j large enough.
By Lemma 14, \(\theta ^{j+1} < \theta ^j\), whenever \(\theta ^j > 0\). Therefore \(\lim _{j \rightarrow \infty }\theta ^j = 0\). Lemma 15 shows that for j large enough
which implies the convergence of the normals with contractivity factor 7/8, for j large enough.
Another conclusion from the fact that \(\theta ^j \rightarrow 0\), when \(j \rightarrow \infty \), and from the last equality in (24), is
Corollary 16
The angles between \(n_i^j\) and the segments \([p_{i-1}^j, p_{i}^j]\) and \([p_{i}^j, p_{i+1}^j]\) tend to \(\pi /2\).
Lemma 15 and Corollary 16 lead to the main result of this appendix.
Theorem 17
If every two consecutive initial PNPs form a good configuration, then \(\hbox {MLR}_1\) converges and the limit normals are the normals of the limit curve.
B Numerical experiments
In this section, we provide results of several numerical experiments done for the input data shown in Fig. 4, in the bottom row. The input data consist of \(\{P_i^0\}_{i = 0,\ldots ,4}\), i.e., five PNPs. The superscript indicates the index of iteration, and zero is for initial data.
First, we check Conjecture 5. We apply several iterations of \(\hbox {MLR}_m, m=2, 3, 4\) and M4Pt to the input data mentioned above. We study three values for every refined polygon on each iteration:
Tables 1, 2 and 3 show values of \(e^j\), \({\mathbb {A}}^j\), \({\mathbb {A}}^j_{\perp }\) correspondingly. As expected, the edge lengths and the angles between two successive edges become smaller as the subdivision progresses, which indicates convergence. Also, the angle between an edge and its corresponding normal goes to \(90^\circ \). This supports the claim of the conjecture.
In Sect. 4.1 and Fig. 4b, we mention that the curve generated with \(\hbox {MLR}_3\) seems to interpolate the initial points though it is not expected to do so. In Table 4, we show
where \(\varDelta _i^j\) is the distance between an initial point \(p_i^0\) and a polygon refined by j iterations of \(\hbox {MLR}_m\), \(m = 2,\ldots ,7\), \(j = 1,\ldots ,6\). We conclude two properties with this data. First, the \(\hbox {MLR}_m\) scheme is not an interpolatory scheme, for any \(m \ge 2\). Second, the refined polygon becomes closer to the initial polygon as the subdivision progresses.
Rights and permissions
About this article
Cite this article
Lipovetsky, E. Subdivision of point-normal pairs with application to smoothing feasible robot path. Vis Comput 38, 2271–2284 (2022). https://doi.org/10.1007/s00371-021-02110-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00371-021-02110-9








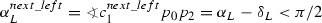 , and
, and 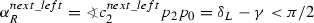 . Namely, condition C1 holds for
. Namely, condition C1 holds for 