A general phase-field model for fatigue failure in brittle and ductile solids

Abstract

In this work, the phase-field approach to fracture is extended to model fatigue failure in high- and low-cycle regime. The fracture energy degradation due to the repeated externally applied loads is introduced as a function of a local energy accumulation variable, which takes the structural loading history into account. To this end, a novel definition of the energy accumulation variable is proposed, allowing the fracture analysis at monotonic loading without the interference of the fatigue extension, thus making the framework generalised. Moreover, this definition includes the mean load influence of implicitly. The elastoplastic material model with the combined nonlinear isotropic and nonlinear kinematic hardening is introduced to account for cyclic plasticity. The ability of the proposed phenomenological approach to naturally recover main features of fatigue, including Paris law and Wöhler curve under different load ratios is presented through numerical examples and compared with experimental data from the author’s previous work. Physical interpretation of additional fatigue material parameter is explored through the parametric study.

1 Introduction

Material fatigue is a weakening phenomenon caused by cyclic loading whose failure state is far below the material strength of monotonic loading [1, 2]. This can result in a progressive structural damage and crack growth. Although fatigue has traditionally been associated with metal components, most materials seem to experience some sort of fatigue-related failure. Once initiated, fatigue crack will steadily grow until it reaches a critical size producing rapid crack propagation and following a complete structural failure [3]. This can be schematically shown by the crack growth rate curve usually obtained in standardized fatigue fracture experiments in Fig. 1a. Such curve is regularly approximated by the fracture mechanics motivated Paris’ law [4], or one of its more complex extensions—NASGRO equation [5]. Furthermore, fatigue phenomena is generally divided into low- and high-cyclic fatigue regimes [6], as presented by the strain-life $\varepsilon - N$ curve in Fig. 1b. Such strain-life approach is suitable for the low-cyclic fatigue regime which is generally driven by a combination of material damage and plastic strains. It is often further accompanied by complex cyclic material behaviour as cyclic hardening or softening, ratcheting or stress relaxation. On the other hand, the stress-life portrayed by the Wöhler curve is usually reserved for high-cyclic fatigue regime where the underlaying material behaviour is elastic. Such regime is governed by material degradation leading to a brittle fracture.

Fig. 1

a Crack growth curve approximated by Paris law where C and m are material parameters, b strain–life curve where Δε is load amplitude and N_f is the number of cycles to failure

Fatigue failure in engineering practice is often a direct cause of a loss of products, services or in more extreme cases, life. Its prediction and prevention as well as increasing component lifetime are then undoubtedly still a major concern, and as such, an area of great interest to many engineers and researchers.

Aside from the experimental fatigue analyses, fatigue phenomenon is generally quantified by (semi-)empirical methods, fracture mechanics-based approaches or constitutive material models with included fatigue effects. The first often require calibration of problem-dependent parameters based on extensive experimental data [7, 8] and rarely allow for generalizations. The approaches based on classical fracture mechanics, heavily relying on Paris’ law and its extensions [5, 9], are not able to describe crack initiation without an initial notch or final rapid failure stage. Therefore, ad hoc criteria are often introduced to determine the crack evolution. On the other hand, several approaches exist in the literature for the inclusion of fatigue effects into constitutive material models, which provide a much more flexible framework. See for example [10,11,12,13,14,15,16,17,18] and the citations therein. Specifically, the continuum phase-field model for high and low cyclic fatigue life prediction is employed within the presented contribution.

In this regard, phase-field approach to fracture has proven successful in solving crack nucleation in absence of stress singularity as well as crack propagation, merging, kinking or branching without introducing any ad hoc criteria. It originates from the variational approach to brittle fracture [19], as an extension of the Griffith’s energy-based fracture theory [20] recast as the energy minimization problem. Later regularization [21], enabled the efficient numerical implementation by reformulating it as a partial differential equations system completely determining the crack evolution. Its smooth approximation of the crack topology on a fixed finite element mesh circumvents the complex crack-surface tracking problem. This, in turn, significantly simplifies finite element implementation, especially in 3D settings. Certain challenges in the computational treatment of the phase-field fracture method within the finite element framework still exist and have recently become a subject of intensive research, providing some great insights and innovative solutions. In recent years, a considerable number of brittle [22,23,24,25,26,27,28,29,30,31,32] and ductile [33,34,35,36,37,38,39,40,41,42] phase-field fracture formulations have been proposed. These studies range from the modelling of 2D/3D small and large strain deformations, various variational formulations, multi-scale/physics problems, mathematical analysis, different decompositions and discretization techniques with many applications in science and engineering, showing the great potential of this method.

The phase-field fracture framework has been very recently extended to the fatigue crack propagation problems. Unlike the fatigue models using empirical data or parameters with no clear physical interpretation [43,44,45], the extended phase-field fracture method is able to reproduce the main features of fatigue failure with fracture-based input parameters. Boldrini et al. [46] presented a phase-field model coupling the fracture behaviour with thermal and fatigue problem, where fatigue behaviour is introduced via additional scalar parameter. On the other hand, Caputo and Fabrizio [47], as well as Amendola et al. [48] adopted the phase-field fracture model with Ginzburg–Landau formalism, where the material degradation under cyclic loadings is introduced by incorporating a fatigue potential. In this direction, Schreiber et al. [49] proposed an additional energy density contribution to account for the sum of additional driving forces associated with the mechanism of cyclic mechanical fatigue. A more intuitive approach has been very recently proposed by Alessi et al. [50], Carrara et al. [51], Seiler et al. [52] and Aldakheel et al. [53] where not only the stiffness is being degraded due to phase-field evolution, but also the fracture energy on the account of strain or stress history. The models are developed under the assumption of elastic material behaviour, which corresponds to the so-called high-cyclic fatigue regime. Recently, a phase-field fatigue model with elastoplastic material behaviour for low-cyclic regime was proposed in [54].

In this work, a full range phenomenological fatigue fracture model able to reproduce the main features of low- and high-cycle fatigue is presented. It fits into a general framework also capable of recovering monotonic fracture without the influence of the fatigue extension. The proposed formulation is schematically shown in Fig. 2. Hereby, the contour-plot in Fig. 2a represents the number of cycles for both low and high cyclic fatigue cases. Furthermore, it fits into a general framework capable of recovering monotonic fracture without the influence of the fatigue extension, as plotted in Fig. 2a for both brittle and ductile failure. This model is based on the phase-field staggered scheme with a residual control-based stopping criterion [55]. The material model incorporates elastoplastic material behaviour based on the von Mises plasticity criterion with combined nonlinear isotropic and kinematic hardening to account for the cyclic plasticity phenomena. Furthermore, a new energy accumulation variable is introduced to account for the cyclic loading history while simultaneously not influencing the monotonic fracture analysis. Special attention is given to the verification of fatigue fracture examples through the parametric study. Main features of fatigue, including Wöhler and Paris law curves in low- and high-cycle regimes, are easily recovered without any additional criteria. The two-part cycle skipping technique is implemented to allow for the calculation of a very high number of cycles on moderate size examples.

Fig. 2

Schematic representation of material response obtainable with the proposed generalized phase-field fracture model for a monotonic (proportional) loading, b cyclic loading

The paper is structured as follows. The general concepts of the proposed generalized phase-field fracture model are provided in Sect. 2. The basic relations extending the brittle fracture model to ductile and fatigue fracture problems are explained. Section 3 deals with the numerical implementation of the proposed model. Hereby, a two-part cycle skipping technique to reduce computational costs is explained. Numerical examples including the cyclically loaded round bar and compact tension specimens are presented in Sect. 4. The results are compared to the experimentally obtained data from previous works of some of the authors [56] (Croatian group). Moreover, the parametric study is conducted showing the influence of load ratio, fatigue and fracture parameters on material behaviour modelling. Finally, concluding remarks are drawn in Sect. 5.

2 Phase-field formulation

This section outlines a theoretical background for the variational phase-field fracture model of solid deformable bodies. The model is considered isothermal and is derived under the assumptions of small-strain settings. The energy dissipation due to heat and sound release at the onset of fracture is neglected.

The general phase-field framework for monotonic fracture is derived first. The material behaviour is described by the elastoplastic material model based on the von Mises plasticity criterion with combined nonlinear isotropic and kinematic hardening. Lastly, the extension to cyclic fracture, i.e., fatigue is introduced.

2.1 Governing functional

An n-dimensional body $\Omega \subset {\mathbb{R}}^{n}$, $n \in \left[ {1,2,3} \right]$ with its surface ${\text{d}}\Omega \subset {\mathbb{R}}^{n - 1}$, evolving crack surface Γ(t) and displacement u is considered. Following the variational approach to fracture [19], the entire fracture process is governed by the minimization of the internal energy functional $\Psi$ consisting of the body’s stored energy and the fracture induced dissipated energy, as follows

$$ \Psi = \int_{\Omega /\Gamma } {\psi \left( {{\varvec{\upvarepsilon}}} \right){\text{d}}\Omega } + \int_{\Gamma } {G_{c} {\text{d}}\Gamma } . $$

(1)

According to the Griffith’s theory of fracture, the materials fail upon reaching the critical value of fracture energy density G_c, which is a material property.

2.1.1 Fracture surface regularization

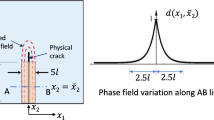
Explicit tracking of fracture surface Γ(t) can be numerically costly and complicated when the interactions between multiple cracks are considered, especially in 3D settings. Therefore, the basic idea of the phase-field models is to approximate this discrete surface Γ(t) by a crack density function $\gamma \left( {\phi ,\nabla \phi } \right),$ using a phase-field order parameter $\phi \in \left[ {0,1} \right]$ and length scale parameter l to control the width of the approximation zone. Parameter $\phi$ describes the scalar damage field ranging smoothly between the broken $\left( {\phi = 1} \right)$ and the intact $\left( {\phi = 0} \right)$ material states, as proposed by Bourdin et al. [21]. That way the fracture surface energy $\Psi^{{\text{f}}}$ can be calculated as a domain integral. Following the work of Miehe et al. [57] and model termed “Strain criterion with threshold model”, the crack density function is chosen as $\gamma \left( {\phi ,\nabla \phi } \right) = \tfrac{3}{8\sqrt 2 }\left[ {\tfrac{1}{l}2\phi + l\left| {\nabla \phi } \right|^{2} } \right]$. Such model shows great resemblance to AT-1 model [58]. The local part of the crack density function γ is represented by a linear term responsible for recovering the linear elastic stage before the onset of fracture, which is not the case for the now-standard phase-field model with quadratic local term. The fracture induced dissipated energy can now be written as

$$ \Psi^{{\text{f}}} = \int_{\Omega } {\psi_{{\text{c}}} \left[ {2\phi + l^{2} \left| {\nabla \phi } \right|^{2} } \right]{\text{d}}\Omega } , $$

(2)

where $\psi_{{\text{c}}} = \tfrac{3}{8\sqrt 2 }\tfrac{{G_{{\text{c}}} }}{l}$ is a constant specific fracture energy serving as an energetic threshold. Schematic representation of the sharp crack topology approximation by the phase-field parameter ϕ and the influence of length scale parameter l on the width of transition zone is clearly displayed in Fig. 3.

Fig. 3

Sharp crack topology Γ approximation represented with the parameter ϕ and the influence of length scale parameter “l” on the width of transition zone

2.1.2 Bulk energy regularization

Correspondingly, the bulk energy term in (1) is regularized by the introduction of a monotonically decreasing degradation function $g\left( \phi \right)$ to account for the subsequent loss of stiffness caused by the fracture initiation and propagation. The standard quadratic form $g\left( \phi \right) = \left( {1 - \phi } \right)^{2}$ is chosen. For the detailed argumentation on the degradation function properties see Pham et al. [58] and Kuhn et al. [59]. The bulk energy term can now be written as

$$ \Psi^{{\text{b}}} = \int_{\Omega /\Gamma } {\psi \left( {{\varvec{\upvarepsilon}}} \right){\text{d}}\Omega } = \int_{\Omega }^{{}} {g\left( \phi \right) \cdot \psi \left( {{\varvec{\upvarepsilon}}} \right)} {\text{d}}\Omega . $$

(3)

2.1.3 Governing equations

The energy functional for the isotropic crack topology is written as

$$ \Pi = \Psi - W^{{{\text{ext}}}} $$

(4)

where $W^{{{\text{ext}}}}$ is the external energy potential formulated as

$$ W^{{{\text{ext}}}} = \int_{\Omega } {{\overline{\mathbf{b}}}} \, \cdot {\mathbf{u}}\,{\text{d}}\Omega + \int_{\partial \Omega } {{\overline{\mathbf{t}}}} \cdot \,{\mathbf{u}}\,{\text{d}}\partial \Omega \,, $$

(5)

with ${\overline{\mathbf{b}}}$ and ${\overline{\mathbf{t}}}$ being the prescribed volume and surface force vectors, respectively. The regularized internal energy potential for monotonic fracture can now be written as follows

$$ \Psi \left( {{{\varvec{\upvarepsilon}}},\phi } \right) = \int_{\Omega } {g\left( \phi \right)\psi \left( {{\varvec{\upvarepsilon}}} \right){\text{d}}\Omega } + \psi_{{\text{c}}} \int_{\Omega } {\left[ {2\phi + l^{2} \left| {\nabla \phi } \right|^{2} } \right]{\text{d}}\Omega } . $$

(6)

The variation of the internal energy potential (6) yields

$$ {\updelta }\Psi = \tfrac{\partial \Psi }{{\partial {{\varvec{\upvarepsilon}}}}}\delta {{\varvec{\upvarepsilon}}} + \tfrac{\partial \Psi }{{\partial \phi }}\delta \phi = \int_{\Omega } {{{\varvec{\upsigma}}}\,{\updelta }{{\varvec{\upvarepsilon}}}\,} {\text{d}}\Omega + \int_{\Omega } {\left[ { - 2\left( {1 - \phi } \right)\psi \left( {{\varvec{\upvarepsilon}}} \right) + \tfrac{8\sqrt 2 }{3}\psi_{{\text{c}}} l\tfrac{{\partial \gamma \left( {\phi ,\nabla \phi } \right)}}{\partial \phi }} \right]} {\updelta }\phi \,{\text{d}}\Omega \,, $$

(7)

where the Cauchy stress σ is obtained as

$$ {{\varvec{\upsigma}}} = g\left( \phi \right)\frac{{\partial \psi \left( {{\varvec{\upvarepsilon}}} \right)}}{{\partial {{\varvec{\upvarepsilon}}}}} $$

(8)

Accordingly, the variation of the external energy potential is formulated as

$$ {\updelta }W^{{{\text{ext}}}} = \int_{\Omega } {{\overline{\mathbf{b}}}} \,{\updelta }{\mathbf{u}}\,{\text{d}}\Omega + \int_{\partial \Omega } {{\overline{\mathbf{t}}}} \,{\updelta }{\mathbf{u}}\,{\text{d}}\partial \Omega \,. $$

(9)

Implementing the small strain settings as ${{\varvec{\upvarepsilon}}} = \tfrac{1}{2}\left[ {\nabla {\mathbf{u}} + \nabla^{T} {\mathbf{u}}} \right]$ and the divergence theorem yields the variation of internal energy potential as

$$ \begin{aligned} \delta \Psi & = - \int_{\Omega } {\nabla \cdot {{\varvec{\upsigma}}}\delta {\mathbf{u}}} {\text{d}}\Omega + \int_{\Omega } {\left\{ {\tfrac{{{\text{d}}g\left( \phi \right)}}{{{\text{d}}\phi }}\psi \left( {{\varvec{\upvarepsilon}}} \right) + 2\psi_{{\text{c}}} \left[ {1 - l^{2} \Delta \phi } \right]} \right\}\delta \phi } {\text{d}}\Omega \\ & \quad + \,\int_{\partial \Omega } {{{\varvec{\upsigma}}} \cdot {\mathbf{n}}\delta {\mathbf{u}}} {\text{d}}\partial \Omega + 2\psi_{{\text{c}}} \int_{\partial \Omega } {l^{2} \nabla \phi \cdot {\mathbf{n}}\delta \phi } {\text{d}}\partial \Omega , \\ \end{aligned} $$

(10)

where n is the outward-pointing normal vector on the boundary ∂Ω. Corresponding strong form equations related to the minimization problem of the energy functional (4) can be now written as follows

$$ \nabla \cdot {{\varvec{\upsigma}}} + {\overline{\mathbf{b}}} = 0{\text{ in }}\Omega \,, $$

(11)

$$ {{\varvec{\upsigma}}} \cdot {\mathbf{n}} = {\overline{\mathbf{t}}}{\text{ on }}\partial \Omega_{{{\overline{\mathbf{t}}}}} \,, $$

(12)

$$ {\mathbf{u}} = {\overline{\mathbf{u}}}{\text{ on }}\partial \Omega_{{{\overline{\mathbf{u}}}}} \,, $$

(13)

$$ - l^{2} \Delta \phi + \left[ {1 + \tilde{D}} \right]\phi = \tilde{D}{\text{ in }}\Omega \,, $$

(14)

$$ \nabla \phi \cdot {\mathbf{n}} = 0{\text{ on }}\partial \Omega \,, $$

(15)

with ${\overline{\mathbf{u}}}$ as the prescribed displacement vector. The Helmholtz type equation (14) representing the evolution of the phase-field parameter ϕ is derived in terms of the crack driving state function D̃ [57], which takes the form

$$ \tilde{D} = \frac{{\psi \left( {{\varvec{\upvarepsilon}}} \right)}}{{\psi_{{\text{c}}} }} - 1. $$

(16)

It is then clear that the fracture evolution in the phase-field monotonic fracture model is governed by the deformation energy term $\psi \left( {{\varvec{\upvarepsilon}}} \right)$. Note that $\tilde{D}$ can be negative, leading to the unphysical solution $\phi < 0$. Such behaviour is typical of models with linear local term in the crack density function $\gamma$. A penalty function is introduced in [58]. On the other hand, the addition of Macaulay brackets also resolves the issue, as presented in [60, 61]

$$ \tilde{D} = \left\langle {\frac{{\psi \left( {{\varvec{\upvarepsilon}}} \right)}}{{\psi_{{\text{c}}} }} - 1} \right\rangle_{ + } . $$

(17)

2.1.4 Fracture irreversibility

The rate of dissipative fracture energy $\dot{\Psi }^{{\text{f}}}$ has to be non-negative, $\dot{\Psi }^{{\text{f}}} \ge 0$. Physically, it means preventing the crack healing after the load is removed. The basic idea is to somehow enforce the monotonicity of the phase-field parameter $\phi$, i.e., $\dot{\phi } \ge 0$. There are a few different approaches to irreversibility within the phase-field community, e.g., [32, 62]. In this work, the so-called implicit enforcement of the constraint is used. It is based on the previous observation of $\tilde{D}\left( \psi \right)$ driving the fracture evolution (14). The irreversibility condition can be then imposed by introducing the history field parameter ${\mathcal{H}}\left( t \right)$ [22] as

$$ {\mathcal{H}}\left( t \right): = \max_{{\tau = \left[ {0,t} \right]}} \tilde{D}\left( {\psi \left( \tau \right)} \right){,} $$

(18)

thus rewriting the evolution equation (14) as

$$ - l^{2} \Delta \phi + \left[ {1 + {\mathcal{H}}} \right]\phi = {\mathcal{H}}{\text{ in }}\Omega \,. $$

(19)

As the crack driving force is now not allowed to decrease upon unloading, i.e., when $\psi \left( {{\varvec{\upvarepsilon}}} \right)$ decreases, the constraint $\dot{\phi } \ge 0$ is enforced. Furthermore, the introduction of history field parameter ${\mathcal{H}}\left( t \right)$ enables an elegant decoupling of the governing equation system characteristic to the staggered solution scheme.

2.2 Elastoplastic material model

The material behaviour is defined by the energy potential $\psi \left( {{\varvec{\upvarepsilon}}} \right)$. In this work, the material is assumed to be elastoplastic to account for the ductile fracture phenomena characterized by an extensive plastic deformation prior to the onset of fracture. The energy potential $\psi \left( {{\varvec{\upvarepsilon}}} \right)$ can then be written as

$$ \psi \left( {{\varvec{\upvarepsilon}}} \right) = \psi_{{\text{e}}} \left( {{{\varvec{\upvarepsilon}}}^{{\text{e}}} } \right) + \psi_{{\text{p}}} \left( {{{\varvec{\upvarepsilon}}}^{{\text{p}}} } \right), $$

(20)

where ${{\varvec{\upvarepsilon}}}^{{\text{e}}}$ and ${{\varvec{\upvarepsilon}}}^{{\text{p}}}$ represent elastic and plastic strain tensors additively contributing to the total strain ${{\varvec{\upvarepsilon}}} = {{\varvec{\upvarepsilon}}}^{{\text{e}}} + {{\varvec{\upvarepsilon}}}^{{\text{p}}}$. Such additive decomposition implies that the elastic response is not affected by plastic flow. Equation (3) now directly follows the phase-field ductile fracture model proposed in Miehe et al. [33], where the coupling between the accumulated plastic energy and fracture is achieved by the degradation of both elastic and plastic bulk energy.

Elastic energy density can be written as $\psi_{{\text{e}}} \left( {{{\varvec{\upvarepsilon}}}^{{\text{e}}} } \right) = \tfrac{1}{2}\lambda {\text{tr}}^{2} \left( {{{\varvec{\upvarepsilon}}}^{{\text{e}}} } \right) + \mu {\text{tr}}\left( {{{\varvec{\upvarepsilon}}}^{{\text{e}}} } \right)^{2}$ with Lamé constants λ and μ. The plastic energy potential $\psi_{{\text{p}}} \left( {{{\varvec{\upvarepsilon}}}^{{\text{p}}} } \right)$ can be represented by a large variety of plasticity models.¹ In this work, the von Mises yield criterion is used with the combined nonlinear isotropic and nonlinear kinematic hardening to account for cyclic plasticity. The plastic energy dissipation potential can then be written as

$$ \psi^{{\text{p}}} \left( {{{\varvec{\upvarepsilon}}}_{{}}^{{\text{p}}} } \right) = \int_{0}^{t} {\left( {{{\varvec{\upsigma}}}^{ * } - {{\varvec{\upalpha}}}} \right):{\dot{\mathbf{\varepsilon }}}_{{}}^{{\text{p}}} {\text{d}}t} , $$

(21)

where ${{\varvec{\upsigma}}}^{ * }$ is the effective (non-degraded) Cauchy stress tensor and ${{\varvec{\upalpha}}}$ is the backstress tensor accounting for the shift of the yield surface. Note that the equations are derived in the effective stress space, meaning that the plastic material behaviour is decoupled from the previously shown fracture part of the model. The effective plastic energy dissipation potential $\psi^{{\text{p}}}$ is convex and positive satisfying $\psi^{{\text{p}}} \left( 0 \right) = 0$. The von Mises pressure-independent yield function states

$$ F = \left\| {{\text{dev}}\left[ {{{\varvec{\upsigma}}}^{ * } } \right] - {{\varvec{\upalpha}}}} \right\| - \sqrt {\tfrac{2}{3}} \sigma_{{\text{y}}} \left( {\varepsilon_{{{\text{eqv}}}}^{{\text{p}}} } \right) \le 0, $$

(22)

where $\left\| {\mathbf{x}} \right\| = \sqrt {{\mathbf{x}} \cdot {\mathbf{x}}}$ is an Euclidean norm. In the cyclic plasticity model with combined nonlinear kinematic hardening, the associated plastic flow is assumed as

$$ {\dot{\mathbf{\varepsilon }}}^{{\text{p}}} = \lambda \frac{\partial F}{{\partial {{\varvec{\upsigma}}}^{ * } }}, $$

(23)

where $\lambda$ is the plastic multiplier. The assumption of associated plastic flow is acceptable for metals subjected to cyclic loading if microscopic details are not of interest. In Eq. (20), $\dot{\varepsilon }_{{{\text{eqv}}}}^{{\text{p}}}$ is the equivalent plastic strain rate whose evolution is defined as

$$ \dot{\varepsilon }_{{{\text{eqv}}}}^{{\text{p}}} = \sqrt {\tfrac{2}{3}{\dot{\mathbf{\varepsilon }}}^{{\text{p}}} :{\dot{\mathbf{\varepsilon }}}^{{\text{p}}} } . $$

(24)

The saturation type isotropic hardening $\sigma_{y} \left( {\varepsilon_{{{\text{eqv}}}}^{{\text{p}}} } \right) = \sigma_{y}^{0} + Q_{\infty } \left( {1 - \exp \left[ { - b\varepsilon_{{{\text{eqv}}}}^{{\text{p}}} } \right]} \right)$ controls the size of the yield surface, where $\sigma_{y}^{0}$ is the elasticity limit, $Q_{\infty }$ and $b$ are material parameters defining the maximum increase in yield stress due to hardening at saturation (when $\varepsilon_{{{\text{eqv}}}}^{{\text{p}}} \to \infty$), and the rate of saturation, respectively.

Kinematic hardening evolution law is defined according to Chaboche [63] multicomponent model as

$$ {\dot{\mathbf{\alpha }}}_{k} = C_{k}^{{}} \frac{1}{{\sigma_{y} \left( {\varepsilon_{{{\text{eqv}}}}^{{\text{p}}} } \right)}}\left( {{{\varvec{\upsigma}}}^{ * } - {{\varvec{\upalpha}}}} \right)\dot{\varepsilon }_{{{\text{eqv}}}}^{{\text{p}}} - \gamma_{k}^{{}} {{\varvec{\upalpha}}}_{k} \dot{\varepsilon }_{{{\text{eqv}}}}^{{\text{p}}} . $$

(25)

Each backstress component ${{\varvec{\upalpha}}}_{k}$ is defined by the material parameters $C_{k}$ and $\gamma_{k}$ determining the initial kinematic hardening modulus and the rate of its decrease with increasing plastic deformation, respectively. The addition of the nonlinear term thus limits the translation of the yield surface in principal stress space. The total backstress tensor is then obtained as

$$ {{\varvec{\upalpha}}} = \sum\limits_{k} {{{\varvec{\upalpha}}}_{k} } . $$

(26)

When kinematic material parameters $C_{k}$ and $\gamma_{k}$ are set to zero, the model reduces to an isotropic hardening model. Moreover, when only $\gamma_{k}$ is set to zero, the linear Ziegler hardening law is recovered, removing the limiting surface. The isotropic and kinematic hardening phenomena are schematically represented in Fig. 4 in the deviatoric stress space.

Fig. 4

Schematic representation of a nonlinear isotropic and b nonlinear kinematic hardening

The combined isotropic-kinematic model features allow modelling of inelastic deformation in metals subjected to the cyclic loads and resulting in low-cycle fatigue failure. Such models are able to reproduce the characteristic cyclic phenomena as Bauschinger effect causing a reduced yield stress upon load reversal; plastic shakedown characteristic of symmetric stress- or strain-controlled experiments where soft or annealed metals tend to harden toward a stable limit, and initially hardened metals tend to soften; progressive “ratcheting” or “creep” in the direction of the mean stress related to the unsymmetrical stress cycles between prescribed limits; or the relaxation of the mean stress observed in an unsymmetrical strain-controlled experiment.

2.2.1 Modification for fracture in tension

To prevent the unphysical crack propagation in the compressive state, the bulk energy term can now be rewritten as

$$ \Psi^{b} = \int_{\Omega }^{{}} {\left\{ {g\left( \phi \right) \cdot \psi^{ + } \left( {{\varvec{\upvarepsilon}}} \right) + \psi^{ - } \left( {{\varvec{\upvarepsilon}}} \right)} \right\}} {\text{d}}\Omega , $$

(27)

by introducing an additive decomposition of the deformation energy where $\psi^{ + } \left( {{\varvec{\upvarepsilon}}} \right) = \psi_{{\text{e}}}^{ + } \left( {{{\varvec{\upvarepsilon}}}^{{\text{e}}} } \right) + \psi_{{\text{p}}} \left( {{{\varvec{\upvarepsilon}}}^{{\text{p}}} } \right)$ and $\psi^{ - } \left( {{\varvec{\upvarepsilon}}} \right) = \psi_{{\text{e}}}^{ - } \left( {{{\varvec{\upvarepsilon}}}^{{\text{e}}} } \right)$. The volumetric-deviatoric decomposition proposed by Amor [64] is used as

$$ \begin{gathered} \psi_{{\text{e}}}^{ + } : = \tfrac{1}{2}\left( {\lambda + \tfrac{2\mu }{n}} \right)\left\langle {{\text{tr}}\left( {{\varvec{\upvarepsilon}}} \right)} \right\rangle_{ + }^{2} + \mu \left( {{{\varvec{\upvarepsilon}}}_{{{\text{dev}}}} :{{\varvec{\upvarepsilon}}}_{{{\text{dev}}}} } \right), \hfill \\ \psi_{{\text{e}}}^{ - } : = \tfrac{1}{2}\left( {\lambda + \tfrac{2\mu }{n}} \right)\left\langle {{\text{tr}}\left( {{\varvec{\upvarepsilon}}} \right)} \right\rangle_{ - }^{2} , \hfill \\ \end{gathered} $$

(28)

in terms of Macaulay brackets $\left\langle x \right\rangle_{ \pm } = \tfrac{x \pm \left| x \right|}{2}$. n represents the dimension number and ${{\varvec{\upvarepsilon}}}_{{{\text{dev}}}} : = \left( {{{\varvec{\upvarepsilon}}} - \tfrac{1}{3}{\text{tr}}\left( {{\varvec{\upvarepsilon}}} \right){\mathbf{I}}} \right)$ stands for the deviatoric part of the strain tensor. Since the plastic energy potential is derived in the deviatoric stress plane following the von Mises yield criterion, only the elastic deformation energy contributes to $\psi^{ - } \left( {{\varvec{\upvarepsilon}}} \right)$. Correspondingly, Eq. (8) for stress ${{\varvec{\upsigma}}}$ is now rewritten as.

$${{\varvec{\upsigma}}} = g\left( \phi \right)\frac{{\partial \psi^{ + } \left( {{\varvec{\upvarepsilon}}} \right)}}{{\partial {{\varvec{\upvarepsilon}}}}} + \frac{{\partial \psi^{ - } \left( {{\varvec{\upvarepsilon}}} \right)}}{{\partial {{\varvec{\upvarepsilon}}}}}$$

(29)

while the crack driving state function now includes only the positive energy part as

$$ \tilde{D} = \left\langle {\frac{{\psi_{{\text{e}}}^{ + } }}{{\psi_{{\text{c}}} }} + \frac{{\psi_{{\text{p}}} }}{{\psi_{{\text{c}}} }} - 1} \right\rangle_{ + } . $$

(30)

2.3 Fatigue extension

The current model is actually capable of producing some features of the low-cyclic fatigue regime. The plastic potential (21) is monotonic and irreversible, by definition, causing the crack driving state function (30) to increase during the loading cycles, eventually leading to the onset of fracture. On the other hand, it is not able to reproduce the crack initiation, nor the crack growth, when the applied cyclic loads are below the plasticity limit in ductile materials, or the fracture limit in brittle materials, corresponding to the high-cyclic fatigue regime.

In this subsection, the phase-field model for brittle and ductile fracture is extended to account for the fatigue phenomena. The presented extension contains only one additional material parameter ($\overline{\psi }_{\infty }$, explained later), enabling it to reproduce the main material fatigue features. The goal is then to produce a generalized phase-field framework which can, depending on the type of loading, recover brittle/ductile fracture in monotonic as well as low- and high-cycle fatigue regime, including the transition. The general idea is to introduce the fracture energy degradation due to the repeated externally applied loads. Physically, it would mean the degradation of material fracture properties during the cyclic loading, which eventually causes the crack initiation and propagation occurrence at lower loads. In a way, material “mileage” would be introduced. To that end, a local energy accumulation variable $\overline{\psi }\left( t \right)$ is introduced accounting for the changes in deformation energy $\psi \left( {{\varvec{\upvarepsilon}}} \right)$ during the loading cycles, thus taking the structural loading history into account. A fatigue degradation function $\hat{F}\left( {\overline{\psi }} \right)$ is introduced only affecting the fracture energy term as discussed. The generalised internal energy potential can be now written as

$$ \begin{aligned} \Psi \left( {{{\varvec{\upvarepsilon}}}^{{\text{e}}} ,{{\varvec{\upvarepsilon}}}^{{\text{p}}} ,\phi ,\overline{\psi }} \right) &= \int_{\Omega } {\left\{ {g\left( \phi \right)\left[ {\psi_{{\text{e}}}^{ + } \left( {{{\varvec{\upvarepsilon}}}^{{\text{e}}} } \right) + \psi_{{\text{p}}} \left( {{{\varvec{\upvarepsilon}}}^{{\text{p}}} } \right)} \right] + \psi_{{\text{e}}}^{ - } \left( {{{\varvec{\upvarepsilon}}}^{{\text{e}}} } \right)} \right\}{\text{d}}\Omega } \\ &\quad +\, \int_{\Omega } {\hat{F}\left( {\overline{\psi }} \right)\psi_{{\text{c}}} \left[ {2\phi + l\left| {\nabla \phi } \right|^{2} } \right]{\text{d}}\Omega } \end{aligned} . $$

(31)

This model is in line with the phase-field fatigue fracture formulation for the brittle materials, proposed in Carrara et al. [51] and Alessi et al. [50]. In line with previous Sections, the modified crack driving state function D̃ is now defined as

$$ \tilde{D} = \left\langle {\frac{{\psi_{{\text{e}}}^{ + } }}{{\hat{F}\left( {\overline{\psi }} \right)\psi_{{\text{c}}} }} + \frac{{\psi_{{\text{p}}} }}{{\hat{F}\left( {\overline{\psi }} \right)\psi_{{\text{c}}} }} - 1} \right\rangle_{ + } . $$

(32)

2.3.1 Local energy accumulation variable $\overline{\psi }\left( t \right)$

This variable is conceived as a local measure of repeated deformation energy changes during the loading history. It is a major feature of the novel generalized phase-field fatigue formulation. To fully fit into this framework, it should not affect the proportional (monotonic) loading case. To satisfy this condition, in this work, the variable is introduced as the sum of negative differences of the total deformation energy during the cyclic loading. That way, the variable value increases only during the unloading part of the cycle, consequently degrading the fracture material properties. Note that the plastic deformation energy $\psi_{{\text{p}}} \left( t \right)$ is dissipative, and therefore never decreasing. The degradation of fracture properties due to fatigue is then, in fact, only influenced by the repetitive changes in elastic deformation energy $\psi_{{\text{e}}} \left( {{{\varvec{\upvarepsilon}}}^{{\text{e}}} } \right).$

The basic idea is explained schematically on the example of 1D bar subjected to the sinusoidal displacement with load ratio $R = 0$, defined as the ratio of the minimum and maximum loads during the cyclic loading, and three different amplitudes A1 < A2 < A3. Unlike the amplitudes A2 and A3, the loading amplitude A1 is below the material plastic limit, characteristic to the high-cycle fatigue regime. The evolution of total energy $\left( {\psi_{{\text{e}}} + \psi_{{\text{p}}} } \right)$ and energy accumulation variable $\overline{\psi }\left( t \right)$ is shown in Fig. 5.

Fig. 5

a Total deformation energy and b energy accumulation variable of 1D bar subjected to sinusoidal displacement-controlled loading

The maximum deformation energy value of curve corresponding to the amplitude A1 does not increase through the course of cycles. On the other hand, the increase of the maximum total deformation energy due to the increase of plastic dissipation $\psi_{{\text{p}}} \left( t \right)$ over the cycles can be clearly seen for curves corresponding to amplitudes A2 and A3. Furthermore, a clear peak shift to the left caused by the kinematic hardening plasticity is observed.

The only difference distinguishing between the high- and low-cycle fatigue regime is the influence of increasing plastic energy $\psi_{{\text{p}}} \left( t \right)$ on the crack driving state function D̃ in the low-cycle fatigue regime. The competition is thus introduced between the total deformation energy $\left( {\psi_{{\text{e}}} + \psi_{{\text{p}}} } \right)$ (whose maximal value is constant for the case of high-cyclic fatigue regime, and increasing in low-cyclic for the case of constant load amplitudes), and the fracture resistance decrease due to the repetitive change in elastic energy, i.e., fatigue.

The local energy accumulation function can be then formulated in the integral form as

$$ \overline{\psi }\left( t \right) = \int_{0}^{t} {\psi_{{\text{e}}} \left( t \right)H\left( { - \dot{\psi }_{{\text{e}}} } \right)} {\text{d}}t, $$

(33)

where $H\left( { - \dot{\psi }_{{\text{e}}} } \right)$ is the Heaviside function taking the value of 1 when $\dot{\psi }_{{\text{e}}} < 0$ and the value of 0 when $\dot{\psi }_{{\text{e}}} \le 0$. The incremental form can be written as

$$ \overline{\psi }_{N} = \overline{\psi }_{N - 1} - \left\langle {\psi_{N} - \psi_{N - 1} } \right\rangle_{ - } , $$

(34)

where N is the cycle number.

The energy accumulation variable increases only during the unloading, thus not affecting the proportional loading cases, as clearly seen in Fig. 5b.

2.3.2 Mean load effect

The energy accumulation variable description implicitly includes the mean load effect often expressed by a load ratio $R$. For the shown case of strain-control loaded bar, the load ratio can be expressed as $R = \tfrac{{\varepsilon_{\min } }}{{\varepsilon_{\max } }},$ with $\varepsilon_{{\text{M}}} = \tfrac{{\varepsilon_{\max } + \varepsilon_{\min } }}{2}$ being the mean strain imposed to the bar. The deformation energy amplitude can then be written as $\Delta \psi_{{\text{e}}} = \tfrac{1}{2}E\left( {\varepsilon_{\max }^{2} - \varepsilon_{\min }^{2} } \right) = 2E\varepsilon_{{\text{M}}}^{2} \tfrac{{1 + R^{2} }}{{\left( {1 + R} \right)^{2} }},$ for the case where maximum load value does not reach the plastic yield limit, and $R \ge 0$. This clearly proves the mean load, and the load ratio influence is implicitly considered in this energy accumulation variable description. It is further explained on the example of 1D bar loaded with sinusoidal displacements B1 and B2 of same amplitudes, but different mean values, as presented in Fig. 6.

Fig. 6

a Prescribed load, b resulting elastic deformation energy and c energy accumulation variable of 1D bar subjected to sinusoidal displacement-controlled loading with different mean values

Loads of the same displacement amplitudes, or strain therefore, with different mean values, produce much different deformation energy values. Consequently, the accumulated energy variable obtained by the higher mean load case (B2 in Fig. 6) increases much faster than in the lower mean load case (B1), as predicted.

2.3.3 Fatigue degradation function $\hat{F}\left( {\overline{\psi }} \right)$

Following the proper definition of the energy accumulation variable $\overline{\psi }\left( t \right)$, the degradation of the fracture energy has to be defined. Herein, the fatigue degradation function $\hat{F}\left( {\overline{\psi }} \right) \in \left[ {0,1} \right]$ is introduced. It should be continuous and piecewise differentiable with the following properties

$$ \begin{gathered} \hat{F}\left( {\overline{\psi } = 0} \right) = 1, \, \\ \hat{F}\left( {\overline{\psi } \to \infty } \right) = 0, \, \\ \frac{{{\text{d}}\hat{F}}}{{{\text{d}}t}}\left( {0 < \overline{\psi } < \infty } \right) \le 0. \\ \end{gathered} $$

(35)

Similar degradation function properties have been used in [50, 51]. In this work, three functions are presented fitting the description

$$ \begin{gathered} \hat{F}_{1} = \left( {1 - \frac{{\overline{\psi }}}{{\overline{\psi } + \overline{\psi }_{\infty } }}} \right)^{2} {\text{ for }}\overline{\psi } \in \left[ {0, + \infty } \right], \hfill \\ \hat{F}_{2} = \left( {1 - \frac{{\overline{\psi }}}{{\overline{\psi }_{\infty } }}} \right)^{2} {\text{ for }}\overline{\psi } \in \left[ {0,\overline{\psi }_{\infty } } \right], \hfill \\ \hat{F}_{3} = \left( {\xi \log \frac{{\overline{\psi }_{\infty } }}{{\overline{\psi }}}} \right)^{2} {\text{ for }}\overline{\psi } \in \left[ {\overline{\psi }_{\infty } ,10^{{\frac{1}{\xi }}} \cdot \overline{\psi }_{\infty } } \right]. \hfill \\ \end{gathered} $$

(36)

Their respective semi-logarithmic graphs are shown in Fig. 7. In Eq. (36), $\overline{\psi }_{\infty }^{{}}$ is the newly introduced parameter used to bound the functions between 0 and 1, and is therefore included in every function. It can be seen as a fatigue material parameter whose physical interpretation will be provided through the next simple examples, as well as the numerical examples in Sect. 4. The parameter $\xi$ embedded into $\hat{F}_{3}$ is introduced to allow for better fine-tuning.

Fig. 7

Influence of parameter $\overline{\psi }_{\infty }$ for three different fatigue degradation functions a $\hat{F}_{1}$, b $\hat{F}_{2}$, c $\hat{F}_{3}$

The following figures present the proposed fatigue degradation functions in terms of number of cycles N, for the cyclically loaded 1D bar. Pure elastic material behaviour is assumed leading to a constant change of the elastic deformation energy $\Delta \psi$ between each cycle. A clear link between the number of cycles N, and energy accumulation variable $\overline{\psi }$, can be then constructed as $\overline{\psi } = \Delta \psi \cdot N.$ Figure 7 shows the influence of the parameter $\overline{\psi }_{\infty }^{{}}$ in each function expressed as the multiples of elastic deformation energy increment at each cycle $\Delta \psi$.

The parameter $\overline{\psi }_{\infty }$ obviously affects the number of cycles at which the fatigue degradation takes off, with all other parameters being equal. The physical interpretation of this parameter will be explored through the parametric study conducted in Sect. 4. On the other hand, the increase in the loading amplitude would cause earlier onset of fatigue degradation. Lastly, the influence of the tuning parameter $\xi$ is observed in Fig. 8.

Fig. 8

Influence of parameter $\xi$ in the fatigue degradation function $\hat{F}_{3}$

3 Finite element implementation

3.1 Discretization

The domain $\Omega$ is discretized with finite elements containing the displacement ${\mathbf{v}}_{i}^{{\text{T}}} = \left[ {\begin{array}{*{20}c} {u_{i} } & {v_{i} } \\ \end{array} } \right]$ and phase-field $\phi_{i}$ degrees of freedom (DOFs). The subscript "i" represents the node number while u and v represent the displacements in x and y directions, respectively, for the considered 2D element. For the case of 1D truss element, only axial displacement is considered. The same shape functions ${\text{N}}_{i}$ interpolate both the displacement and the phase-field variable

$$ \begin{gathered} {\mathbf{u}} = \sum\nolimits_{i}^{{\text{n}}} {{\mathbf{N}}_{i}^{{\mathbf{v}}} {\mathbf{v}}_{i} } , \quad {{\varvec{\upvarepsilon}}} = \sum\nolimits_{i}^{{\text{n}}} {{\mathbf{B}}_{i}^{{\mathbf{v}}} {\mathbf{v}}}_{i} , \\ \phi = \sum\nolimits_{i}^{{\text{n}}} {{\text{N}}_{i}^{{}} \phi_{i} } , \quad \nabla \phi = \sum\nolimits_{i}^{{\text{n}}} {{\mathbf{B}}_{i}^{\phi } \phi_{i} } , \\ \end{gathered} $$

(37)

where n is the total number of nodes in the element, while N and B are shape function and spatial derivative matrices, respectively.

3.2 Virtual work principle

After the substitution of the corresponding history field (18), the variation of internal energy can be written as

$$ \delta \Psi = \tfrac{\partial \Psi }{{\partial {{\varvec{\upvarepsilon}}}}}\delta {{\varvec{\upvarepsilon}}} + \tfrac{\partial \Psi }{{\partial \phi }}\delta \phi = \int_{\Omega } {{{\varvec{\upsigma}}}\delta {{\varvec{\upvarepsilon}}}{\text{d}}\Omega } + \int_{\Omega } {\left\{ {\left[ {\left( {1 + {\mathcal{H}}} \right)\phi - {\mathcal{H}}} \right]\delta \phi + l^{2} \nabla \phi \delta \nabla \phi } \right\}} {\text{d}}\Omega = \delta W^{{\text{int}}} , $$

(38)

representing the weak form of the generalized phase-field fracture model. The history field ${\mathcal{H}}$ includes all the important features for resolving brittle/ductile fracture in monotonic loading and fatigue fracture in cyclic loading (32). The virtual work principle $\delta W^{{{\text{ext}}}} - \delta W^{{{\text{int}}}} = 0$ can be then discretized as

$$ \left( {{\mathbf{F}}_{{{\text{ext}}}}^{{\mathbf{v}}} - {\mathbf{F}}_{{\text{int}}}^{{\mathbf{v}}} } \right)\delta {\mathbf{v}} + \left( {{\mathbf{F}}_{{{\text{ext}}}}^{\phi } - {\mathbf{F}}_{{\text{int}}}^{\phi } } \right)\delta \phi = 0, $$

(39)

where

$$ \begin{aligned} {\mathbf{F}}_{{{\text{ext}}}}^{{\mathbf{v}}} & = \int_{\Omega } {{\mathbf{N}}_{{}}^{{\mathbf{v}}} {\overline{\mathbf{b}}}{\text{d}}\Omega } + \int_{\partial \Omega } {{\mathbf{N}}_{{}}^{{\mathbf{v}}} \overline{{\mathbf{t}}} } \,{\text{d}}\partial \Omega , \\ {\mathbf{F}}_{{{\text{ext}}}}^{\phi } & = 0, \\ \end{aligned} $$

(40)

are the external force vectors. ${\mathbf{F}}_{{\text{int}}}^{{\mathbf{v}}}$ and ${\mathbf{F}}_{{\text{int}}}^{\phi }$ correspond to the internal displacement and phase-field force vectors, respectively, as follows

$$ \begin{aligned} {\mathbf{F}}_{{\text{int}}}^{{\mathbf{v}}} & = \int_{\Omega } {{\mathbf{B}}_{{}}^{{{\mathbf{v}}^{{\text{T}}} }} {{\varvec{\upsigma}}}{\text{d}}\Omega } , \\ {\mathbf{F}}_{{\text{int}}}^{\phi } & = \int_{\Omega } {\left\{ {l^{2} {\mathbf{B}}_{{}}^{{\phi^{{\text{T}}} }} {\mathbf{B}}_{{}}^{{\phi^{{}} }} {{\varvec{\upphi}}} + \left( {\left[ {1 + {\mathcal{H}}} \right]{\mathbf{N}}^{\phi } {{\varvec{\upphi}}} - {\mathcal{H}}} \right){\mathbf{N}}^{\phi } } \right\}{\text{d}}\Omega } , \\ \end{aligned} $$

(41)

where ${{\varvec{\upphi}}}$ is the vector containing phase-field DOFs $\phi_{i}$.

3.3 Residual vectors and stiffness matrices

Residual vectors can be now obtained as ${\mathbf{R}} = {\mathbf{F}}_{{{\text{ext}}}} - {\mathbf{F}}_{{\text{int}}}$ leading to

$$ \begin{aligned} {\mathbf{R}}_{{}}^{{\mathbf{v}}} & = \int_{\Omega } {{\mathbf{N}}_{{}}^{{\mathbf{v}}} {\overline{\mathbf{b}}}{\text{d}}\Omega } + \int_{\partial \Omega } {{\mathbf{N}}_{{}}^{{\mathbf{v}}} \overline{{\mathbf{t}}} } \,\,{\text{d}}\partial \Omega - \int_{\Omega } {{\mathbf{B}}_{{}}^{{{\mathbf{v}}^{{\text{T}}} }} {{\varvec{\upsigma}}}{\text{d}}\Omega } , \\ {\mathbf{R}}^{\phi } & = - \int_{\Omega } {\left\{ {l^{2} {\mathbf{B}}_{{}}^{{\phi^{{\text{T}}} }} {\mathbf{B}}_{{}}^{{\phi^{{}} }} {{\varvec{\upphi}}} + \left( {\left[ {1 + {\mathcal{H}}} \right]{\mathbf{N}}^{\phi } {{\varvec{\upphi}}} - {\mathcal{H}}} \right){\mathbf{N}}^{\phi } } \right\}{\text{d}}\Omega } . \\ \end{aligned} $$

(42)

Correspondingly, the stiffness matrices are obtained as

$$ \begin{aligned} {\mathbf{K}}_{{}}^{{{\mathbf{vv}}}} & = - \tfrac{{\partial {\mathbf{R}}_{{}}^{{\mathbf{v}}} }}{{\partial {\mathbf{v}}}} = \int_{\Omega } {{\mathbf{B}}_{{}}^{{{\mathbf{v}}^{{\text{T}}} }} {\mathbf{CB}}_{{}}^{{\mathbf{v}}} {\text{d}}\Omega } , \\ {\mathbf{K}}^{\phi \phi } & = - \tfrac{{\partial {\mathbf{R}}^{\phi } }}{{\partial {{\varvec{\upphi}}}}} = \int_{\Omega } {\left\{ {l^{2} {\mathbf{B}}_{{}}^{{\phi^{{\text{T}}} }} {\mathbf{B}}_{{}}^{{\phi^{{}} }} + \left[ {1 + {\mathcal{H}}} \right]{\mathbf{N}}^{\phi } {\mathbf{N}}^{\phi } } \right\}{\text{d}}\Omega } , \\ \end{aligned} $$

(43)

where C is the degraded tangent material matrix.

3.4 Staggered solution scheme

The finite element model can be then written in terms of a decoupled equation system as follows

$$ \left[ {\begin{array}{*{20}c} {\mathbf{v}} \\ {{\varvec{\upphi}}} \\ \end{array} } \right]_{n} = \left[ {\begin{array}{*{20}c} {\mathbf{v}} \\ {{\varvec{\upphi}}} \\ \end{array} } \right]_{n - 1} + \left[ {\begin{array}{*{20}c} {{\mathbf{K}}^{{{\mathbf{vv}}}} } & 0 \\ 0 & {{\mathbf{K}}^{\phi \phi } } \\ \end{array} } \right]^{ - 1} \cdot \left[ {\begin{array}{*{20}c} {{\mathbf{R}}^{{\mathbf{v}}} } \\ {{\mathbf{R}}^{\phi } } \\ \end{array} } \right]. $$

(44)

which corresponds to the staggered algorithmic approach, also known as alternative minimization approach. It is generally more robust than standard monolithic approaches [65]. However, the efficiency and convergence rate of such staggered systems depend on the stopping criterion [26], which usually differs between the implementations. Herein, the residual norm-based stopping criterion [55] is briefly presented. It governs the iterative process by controlling the residuals corresponding to the fields ${\mathbf{v}}$ and ${{\varvec{\upphi}}}$, as presented in Box 1. where “tol” is a required user-defined tolerance. The choice of which field to solve first is usually arbitrary. Herein, the $\phi^{kk}$ is solved first as it more closely fits with the developed ABAQUS implementation framework. For a more detailed explanation see [66], where the presented algorithm source code is provided.

Box 1. Residual control (RCTRL) staggered solution scheme [55, 66]

3.5 Cycle skipping option for high-cyclic fatigue analysis

The presented extension to fatigue within the phase-field fracture model is based on the time evolving properties. To properly calculate the fracture nucleation, stabilised propagation and final rapid growth, one should precisely compute every cycle in the analysis. However, such approach is exceedingly time-consuming for the analysis of high-cycle fatigue regime even for medium size problems.

In this work, a two-part cycle skipping technique is implemented and is used throughout this work, where applicable. Note first that the underlying phase-field model recovers linear elastic material behaviour stage before the onset of damage. For the case of high-cyclic fatigue regime analysis $\left( {\psi_{{\text{p}}} = 0} \right)$ with constant loading amplitude, the total deformation energy amplitude per cycle $\Delta \psi$ is constant. The energy accumulation variable $\overline{\psi }$ then grows linearly as $\overline{\psi } = N \cdot \Delta \psi$ until fatigue degradation function $\hat{F}\left( {\overline{\psi }} \right)$ reaches the point where $\hat{F}\left( {\overline{\psi }} \right) \cdot \psi_{{\text{c}}} < \psi$, thus triggering the onset of damage ${\mathcal{H}} > 0$. The first part of the two-part cycle skipping technique refers to this linear part. It can be easily achieved by calculating the cycle at which the onset of damage will happen for each proposed fatigue function as

$$ \begin{aligned} N_{i}^{{\hat{F}_{1} }} & = \tfrac{{\overline{\psi }_{\infty } }}{\Delta \psi }\left( {\sqrt {\tfrac{{\psi_{{\text{c}}} }}{\psi }} - 1} \right); \\ N_{i}^{{\hat{F}_{2} }} & = \tfrac{{\overline{\psi }_{\infty } }}{\Delta \psi }\left( {1 - \sqrt {\tfrac{\psi }{{\psi_{{\text{c}}} }}} } \right); \\ N_{i}^{{\hat{F}_{3} }} & = \tfrac{{\overline{\psi }_{\infty } }}{\Delta \psi } \cdot 10^{{ - \tfrac{1}{\xi }\sqrt {\tfrac{\psi }{{\psi_{{\text{c}}} }}} }} . \\ \end{aligned} $$

(45)

After we know the cycle number N_i at which $\hat{F}\left( {\overline{\psi }} \right) \cdot \psi_{{\text{c}}} < \psi$ happens, we can jump the simulation to a few cycles before this event, set the energy accumulation variable to the corresponding value $\overline{\psi } = N \cdot \Delta \psi$, set the cycle number counter to the corresponding value N and thus ultimately skip this linear part in high-cyclic fatigue regime.

The subsequent non-linear part of the analysis can be further accelerated by including the cycle skipping technique based on the idea proposed in [67] for structures with time-evolving properties. A schematic representation of such procedure is shown in Fig. 9.

Fig. 9

Schematic representation cycle skipping technique

It is based on the extrapolation of the selected time-evolving solution variable, in this case the accumulation energy variable $\overline{\psi }$. Herein, the time duration of the cycle is assumed constant. The idea is to first perform a complete FE analysis for a set of cycles to establish a trend line of the energy accumulation variable time(cycle)-evolution, as presented in Fig. 10.

Fig. 10

Establishing the trend line for the energy accumulation variable $\overline{\psi }$

At least three consecutive cycle data values have to be defined by points ${\text{P}}_{1} \left( {N_{1} ,\overline{\psi }\left( {N_{1} } \right)} \right)$,${\text{P}}_{2} \left( {N_{2} ,\overline{\psi }\left( {N_{2} } \right)} \right)$ and ${\text{P}}_{3} \left( {N_{3} ,\overline{\psi }\left( {N_{3} } \right)} \right)$. The maximum allowed number of cycles to skip $\Delta N_{{{\text{jump}}}}^{ip}$ is determined at each integration point ip through a control function based on the user-input allowed relative error $q_{{\text{y}}}$ as

$$ \frac{{\left| {\Delta \overline{\psi }\left( {N_{1} + \Delta N_{{{\text{jump}}}}^{ip} } \right) - \Delta \overline{\psi }\left( {N_{1} } \right)} \right|}}{{\left| {\Delta \overline{\psi }\left( {N_{1} } \right)} \right|}} \le q_{{\text{y}}} , $$

(46)

where $\Delta \overline{\psi }\left( {N_{1} + \Delta N_{{{\text{jump}}}}^{ip} } \right)$ is the predicted, linearly extrapolated difference in the accumulated energy moment after the jump. It can be obtained as

$$ \Delta \overline{\psi }\left( {N_{1} + \Delta N_{{{\text{jump}}}}^{ip} } \right) = \Delta \overline{\psi }\left( {N_{1} } \right) + \left[ {\Delta \overline{\psi }\left( {N_{1} } \right) - \Delta \overline{\psi }\left( {N_{2} } \right)} \right]\Delta N_{{{\text{jump}}}}^{ip} . $$

(47)

The allowed jump value for each variable is then computed as

$$ \Delta N_{{{\text{jump}}}}^{ip} = q_{{\text{y}}} \frac{{\left| {\Delta \overline{\psi }\left( {N_{1} } \right)} \right|}}{{\left| {\Delta \overline{\psi }\left( {N_{1} } \right) - \Delta \overline{\psi }\left( {N_{2} } \right)} \right|}}, $$

(48)

while the final cycle jump is computed as the minimum allowed jump $\Delta N_{{{\text{jump}}}} = \min \left\{ {\Delta N_{{{\text{jump}}}}^{ip} } \right\}$. Finally, the extrapolated value $\overline{\psi }\left( {N_{1} + \Delta N_{{{\text{jump}}}} } \right)$ after the jump is calculated in each integral point as

$$ \overline{\psi }\left( {N_{1} + \Delta N_{{{\text{jump}}}} } \right) = \overline{\psi }\left( {N_{1} } \right) + \Delta \overline{\psi }\left( {N_{1} } \right)\Delta N_{{{\text{jump}}}} + \tfrac{1}{2}\left[ {\Delta \overline{\psi }\left( {N_{1} } \right) - \Delta \overline{\psi }\left( {N_{2} } \right)} \right]\left( {\Delta N_{{{\text{jump}}}} } \right)^{2} $$

(49)

Such extrapolation method is usually most suited for quasi-linearly evolving systems. However, the employment of control function enables it to accurately solve the highly non-linear time evolving behaviour by automatically calculating lower number of cycles to skip or no cycle skip at all.

4 Numerical examples

The performance of the proposed generalised phase-field model for brittle/ductile and fatigue fracture modelling, according to the underlaying material behaviour and loading conditions is demonstrated by means of representative boundary value problems. In this regard, the proposed model is implemented into the commercial FE software ABAQUS. Furthermore, it is made freely available at https://data.mendeley.com/datasets/p77tsyrbx2/4 [66], thus further promoting the phase-field methodology with other engineers, researchers and students.

4.1 Single edge notched specimen

The proposed generalized phase-field fracture model is first tested on the most common benchmark test used in the verification of the phase-field fracture models to show that the presented fatigue extension does not influence the monotonic analysis. The specimen geometry and boundary conditions, shown in Fig. 11, together with the material properties, $E = 210 \, {{{\text{kN}}} \mathord{\left/ {\vphantom {{{\text{kN}}} {{\text{mm}}^{{2}} }}} \right. \kern-\nulldelimiterspace} {{\text{mm}}^{{2}} }},$ $\nu = 0.3$ and $G_{{\text{c}}} = 2.7 \times 10^{ - 3} {{{\text{kN}}} \mathord{\left/ {\vphantom {{{\text{kN}}} {{\text{mm}}}}} \right. \kern-\nulldelimiterspace} {{\text{mm}}}}$ are adopted from Miehe et al. [22]. The length scale parameter is set to $l = 0.0377{\text{ mm}}{.}$ The specimen domain is discretized with 18,868 finite elements with refinement in the region of the expected crack path evolution. Two cases are analysed: one with the phase-field model for monotonic fracture modelling only, and the other with the proposed model with three different $\overline{\psi }_{\infty }$ values. Herein, the results are shown with the fatigue degradation function $\hat{F}_{3}$. However, the same results are obtained with every proposed function as the presented property is governed by the novel description of the accumulated energy variable $\overline{\psi }$.

Fig. 11

Single edge notched specimen geometry and boundary conditions

The force–displacement curves in Fig. 12 clearly show there is no influence of the presented fatigue extension in the monotonic loading, unlike the fatigue extensions presented in [51].

Fig. 12

Influence of the fatigue extension on monotonic fracture analysis force–displacement curves

Furthermore, energy accumulation variable $\overline{\psi }$ and total energy $\psi \left( {{\varvec{\upvarepsilon}}} \right)$ are shown in Figs. 13 and 14 at two consecutive increments before and after the complete fracture.

Fig. 13

Total deformation energy in MPa a before and b after the formation of crack

Fig. 14

Energy accumulation variable in MPa a before and b after the formation of crack

The energy accumulation variable $\overline{\psi }$ obviously increases at the locations where total energy, i.e., elastic energy decreases. The increase is negligible compared to the value of total energy at the corresponding points. Moreover, the locations with high total energy, corresponding to the localization of damage, do not exhibit the energy accumulation variable increase. Therefore, it proves that the proposed model can handle monotonic loading case without the interference of the extension.

4.2 Cyclically loaded homogeneous round bar

This example is used to assess the ability of the model to recover the full scope of fatigue domain, ranging from low- to high-cyclic regime. It follows the example of cyclically loaded round bar specimen experimentally tested in author’s previous work [56, 68]. The specimen is discretized by a truss element. The geometry and boundary conditions are illustrated in Fig. 15. Strain-controlled loading is used with load ratio $R = 0.$

Fig. 15

Cyclically loaded round bar specimen. Geometry and boundary conditions

The material properties of nodular cast iron with nonlinear isotropic and kinematic hardening are taken from [68] for the so-called flotret casting technique. The elastoplastic material properties are set as follows: $E = 140{\text{ GPa,}}$ $\nu = 0.3,$ $\sigma_{y}^{0} = 123{\text{ MPa,}}$ $Q_{\infty } = 95{\text{ MPa,}}$ $b = 18,$ $C_{1} = 22,734{\text{ MPa,}}$$\gamma_{1} = 261.8,$ $C_{2} = 136,029\;{\text{MPa,}}$ $\gamma_{2} = 2,113.5.$ The fracture toughness is set to $G_{{\text{c}}} = {74 }{{\text{N}} \mathord{\left/ {\vphantom {{\text{N}} {{\text{mm}}}}} \right. \kern-\nulldelimiterspace} {{\text{mm}}}}$ following the J-integral measurements taken in [56, 68]. Length scale parameter is chosen to be $l = 0.25{\text{ mm,}}$ while the fatigue material parameter is set to $\overline{\psi }_{\infty } = 5000{\text{ MPa}}{.}$ First, the elastoplastic material model is tested and compared with the experimental results for loading amplitude $\varepsilon_{{\text{a}}} = 0.8\% \pm 0.8\% .$ The stress–strain diagram in Fig. 16a shows the comparison with experimental measurements from [56], until the onset of fracture. The time evolution of stress, energetic values and phase-field parameter is shown in Fig. 16b.

Fig. 16

Cyclically loaded round bar specimen. a Stress–strain hysteresis loop experimental comparison, b time evolution of stress, energy variables and phase-field parameter

The results obtained with the proposed model match the experimental measurements well. Slight discrepancy can be observed in the first cycle, as expected, because the material properties were calibrated for the stabilized hysteresis loop. It can be clearly seen how the dissipated plastic energy $\psi_{{\text{p}}}$ and accumulated deformation energy $\overline{\psi }$ grow with each cycle. Their respective slopes are influenced by the magnitude of load amplitude, i.e., the influence of $\psi_{{\text{p}}}$ diminishes and eventually vanishes with lower amplitudes, making the transition between low- and high-cyclic fatigue regime.

Next, 35 different strain amplitudes are subjected to the specimen to assess the model behaviour in different fatigue regimes. The simulations are stopped at cycle $N_{{\text{f}}}$ when phase-field parameter reaches $\phi = 0.99,$ thus assuming a total failure. Figure 17 presents the $\varepsilon - N$ curve for the three different fatigue functions with $\overline{\psi }_{\infty } = 5000{\text{ MPa,}}$ as well as the case without the fatigue degradation named “noF”. Note that each marker in Fig. 17 represents one full simulation obtained with a different load amplitude.

Fig. 17

Cyclically loaded round bar specimen. ε–N curve

The obtained results show great resemblance to the theoretical $\varepsilon - N$ curve (Fig. 1b). Clear difference can be seen in the results obtained with $\hat{F}_{1}$ compared to the results obtained with $\hat{F}_{2}$ and $\hat{F}_{3}$ due to their obvious mathematical difference. Moreover, it is obvious that the fracture can be obtained with high loading amplitude values even with the model without fatigue degradation, up until the point where plastic energy in system becomes negligible, shown as “noF limit”. On the other hand, the present model does not exhibit an endurance limit usually found in steel like materials. Such limit could be easily introduced by modifying the fatigue degradation function with inclusion of additional stress-like or strain-like parameters, as presented in [50]. It can be thus concluded that the proposed generalized phase-field fracture model is capable of reproducing the low- and high-cycle regime and the transition in-between. Moreover, the strain amplitude and cycle number values $N_{{\text{f}}}$ correspond to the values normally observed in literature thus giving even more credibility to these results.

4.3 Compact tension (CT) specimen test—low cyclic regime

To further assess the proposed model’s capability in reproducing fatigue crack evolution, the compact tension (CT) specimen subjected to cyclic loading is simulated. The geometry is presented in Fig. 18, corresponding to the experimental setup made in in some of the authors’ previous work [56].

Fig. 18

Cyclically loaded CT specimen. Geometry with thickness B = 0.5 W

Loading pins boundary conditions are simulated by kinematically constraining nodes at the hole edge constituting 60° angle with the reference point at the pin centreline. The reference point corresponding to the bottom pin is fixed, while the load is imposed to the top pin reference point. Even though force-control is imposed, standard Newton–Raphson solver can be efficiently used in this example until the complete failure point at which Newton–Raphson solver is unable to converge.

The elastoplastic material properties are taken for the nodular cast iron, as presented in the previous example. On the other hand, the length scale parameter has been set to l = 0.05 mm, and the fracture parameter to $G_{{\text{c}}} = 0.74\,{\text{kN/mm}}$ accordingly. The fatigue parameter is set to $\overline{\psi }_{\infty } = 5000\,{\text{MPa}}.$ Following [68], the load amplitude is set to $F = 6\,{\text{kN}}$ with load ratio R = 0.1. The obtained crack path after various number of cycles is presented in Fig. 19, while the energy accumulation variable $\overline{\psi }$ is shown in Fig. 20.

Fig. 19

Cyclically loaded CT specimen. Crack path after a 2000 cycles, b 7000 cycles, c 10,000 cycles, d 13,000 cycles

Fig. 20

Cyclically loaded CT specimen. Energy Accumulation variable $\overline{\psi }$ in MPa after a 2000 cycles, b 7000 cycles, c 10,000 cycles, d 13,000 cycles

The comparison with experimentally observed crack propagation is now presented in Fig. 21.

Fig. 21

Cyclically loaded CT specimen. Crack length vs cycle number

It can be seen there are some discrepancies between the experimentally observed and the numerically obtained results. Although better results could be obtained by carefully calibrating the fracture and fatigue material parameters, the corresponding a–N trend shows great potential in predicting fatigue fracture.

The change in stress intensity factor can be now calculated as

$$ \Delta K_{i} = \frac{\Delta F}{{B\sqrt W }}f\left( {\frac{{a_{i} }}{W}} \right) $$

(50)

according to ASTM standard [69], where $\Delta F$ is the difference between minimal and maximal load magnitude, $a_{i}$ is the current crack length, while B and W are geometric quantities of the specimen, shown in Fig. 18. Geometric function $f\left( {\frac{{a_{i} }}{W}} \right)$ is calculated as

$$ f\left( {\frac{{a_{i} }}{W}} \right) = \frac{{\left( {2 + {{a_{i} } \mathord{\left/ {\vphantom {{a_{i} } W}} \right. \kern-\nulldelimiterspace} W}} \right) \cdot \left[ {0.886 + 4.64 \cdot \left( {{{a_{i} } \mathord{\left/ {\vphantom {{a_{i} } W}} \right. \kern-\nulldelimiterspace} W}} \right) - 13.32 \cdot \left( {{{a_{i} } \mathord{\left/ {\vphantom {{a_{i} } W}} \right. \kern-\nulldelimiterspace} W}} \right)^{2} + 14.72 \cdot \left( {{{a_{i} } \mathord{\left/ {\vphantom {{a_{i} } W}} \right. \kern-\nulldelimiterspace} W}} \right)^{3} - 5.6 \cdot \left( {{{a_{i} } \mathord{\left/ {\vphantom {{a_{i} } W}} \right. \kern-\nulldelimiterspace} W}} \right)^{4} } \right]}}{{\sqrt[{}]{{\left( {1 - {{a_{i} } \mathord{\left/ {\vphantom {{a_{i} } W}} \right. \kern-\nulldelimiterspace} W}} \right)^{3} }}}}. $$

(51)

The crack growth rate ${{{\text{d}}a} \mathord{\left/ {\vphantom {{{\text{d}}a} {{\text{d}}N}}} \right. \kern-\nulldelimiterspace} {{\text{d}}N}}$ versus the change in stress intensity factor $\Delta K$ can now be constructed and is shown in Fig. 22 in comparison with experimental data and NASGRO curve calculated in [68].

Fig. 22

Cyclically loaded CT specimen. Crack rate growth versus stress intensity factor change

It can be observed that there is a great overlap between the experimentally obtained curve, NASGRO equation and numerically obtained curves for lower values of stress intensity factor $\Delta K.$ However, there seems to be a discrepancy for the higher values of $\Delta K.$ Results obtained by fatigue function $\hat{F}_{2}$ with the chosen material parameters show the best match in comparison with experimental results. As already mentioned, careful calibration of fracture and fatigue material parameters could lead to even better match. Nevertheless, the results show the great potential of the phase-field fracture method in dealing with fatigue problems and capturing fundamental features of material fatigue. Again, it has to be noted that no ad-hoc criteria are added in this expansion of phase-field fracture model to fatigue, while only one additional parameter, $\overline{\psi }_{\infty } ,$ is introduced in the expansion. However, the choice of degradation function $\hat{F}$ remains an open question and will be considered in future works.

4.4 Compact tension (CT) specimen test—high cyclic regime

The same specimen geometry is used to assess the influence of different input material parameters. However, in this example a different academic linear elastic material is chosen with the following unchanging material properties: $E = 210\,{\text{GPa,}}$ $\nu = 0.3$ and $l = 0.5\,{\text{mm}}{.}$ The influence of load ratio $R = \tfrac{{F_{\min } }}{{F_{\max } }}$, fatigue parameter $\overline{\psi }_{\infty }$ and fracture toughness $G_{{\text{c}}} ,$ is observed in terms of Paris law and Wöhler curves. First, the influence of loading amplitude on crack growth rate ${{{\text{d}}a} \mathord{\left/ {\vphantom {{{\text{d}}a} {{\text{d}}N}}} \right. \kern-\nulldelimiterspace} {{\text{d}}N}}$ versus stress intensity factor change $\Delta K$ is shown in Fig. 23 for constant $R = 0,$ $G_{{\text{c}}} = 5\,{\text{kN/mm}}$ and $\overline{\psi }_{\infty } = 50\,{\text{MPa}}{.}$

Fig. 23

Crack rate growth versus stress intensity factor change loading amplitude influence for fatigue degradation function a $\hat{F}_{1}$ b $\hat{F}_{2}$ and c $\hat{F}_{3}$

The curves in Fig. 23 follow well-known empirical trend, recovering a major fatigue fracture feature. The steady linear propagation stage usually described by a Paris law follows the same slope for every amplitude. Moreover, the fracture initiation and final unstable growth can be clearly observed as described in Fig. 1a.

4.4.1 The influence of the load ratio R

Load ratio influence is tested on $R = 0,$ $R = \tfrac{1}{3},$ $R = \tfrac{1}{2},$ and $R = \tfrac{2}{3},$ while fracture toughness and fatigue parameter are held constant at $G_{{\text{c}}} = 5\,{\text{ kN/mm}}$ and $\overline{\psi }_{\infty } = 50\,{\text{MPa}}{.}$ The load ratio influence results are presented in Figs. 24 and 25 in terms of fatigue life, i.e., Wöhler curves where instead of stress, the loading amplitude is set on vertical axis, and ${{{\text{d}}a} \mathord{\left/ {\vphantom {{{\text{d}}a} {{\text{d}}N}}} \right. \kern-\nulldelimiterspace} {{\text{d}}N}}$ versus $\Delta K$, respectively.

Fig. 24

Load ratio influence on fatigue life for fatigue degradation function a $\hat{F}_{1}$ b $\hat{F}_{2}$ and c $\hat{F}_{3}$

Fig. 25

Load ratio influence on crack rate growth versus stress intensity factor change for fatigue degradation function a $\hat{F}_{1}$ b $\hat{F}_{2}$ and c $\hat{F}_{3}$

Obvious load ratio influence is observed in accordance with known empirical trends. Note that no additional terms have been set to recover the load ratio influence. The results prove the validity of the energy accumulation variable $\overline{\psi }$ choice where the mean load influence is implicitly included, as explained in Sect. 2.

4.4.2 The influence of the fatigue parameter $\overline{\psi }_{\infty }$

The influence of the fatigue parameter $\overline{\psi }_{\infty }$ is tested on $R = 0$ with the fracture toughness again held constant at $G_{{\text{c}}} = 5\,{\text{kN/mm}}{.}$ Three different values of fatigue parameter $\overline{\psi }_{\infty }$ are tested; $\overline{\psi }_{\infty } = 20\,{\text{MPa,}}$ $\overline{\psi }_{\infty } = 50\,{\text{MPa}}$ and $\overline{\psi }_{\infty } = 100\,{\text{MPa}}{.}$ The results are shown in Figs. 26 and 27 in terms of Wöhler curves and ${{{\text{d}}a} \mathord{\left/ {\vphantom {{{\text{d}}a} {{\text{d}}N}}} \right. \kern-\nulldelimiterspace} {{\text{d}}N}}$ versus $\Delta K$, respectively.

Fig. 26

Fatigue parameter $\overline{\psi }_{\infty }$ influence on fatigue life for fatigue degradation function a $\hat{F}_{1}$ b $\hat{F}_{2}$ and c $\hat{F}_{3}$

Fig. 27

Fatigue parameter $\overline{\psi }_{\infty }$ influence on crack rate growth versus stress intensity factor change for fatigue degradation function a $\hat{F}_{1}$ b $\hat{F}_{2}$ and c $\hat{F}_{3}$

An increase in fatigue parameter $\overline{\psi }_{\infty }$ clearly shifts the Wöhler curves to the right by postponing the fatigue crack initiation and propagation. Furthermore, it shifts the crack growth rate $\tfrac{{{\text{d}}a}}{{{\text{d}}N}}$ down. Such observation leads to the conclusion that the fatigue parameter $\overline{\psi }_{\infty }$ could be undoubtedly associated to the fatigue material parameter C used in Paris law $\tfrac{{{\text{d}}a}}{{{\text{d}}N}} = C\left( {\Delta K} \right)^{m}$, as presented in Fig. 1a. This adds on to the validity of the proposed model as the parameter $\overline{\psi }_{\infty }$ is the only material parameter extending the phase-field fracture model to fatigue problem.

4.4.3 The influence of the fracture toughness G_c

Following the Paris law empirical equation $\tfrac{{{\text{d}}a}}{{{\text{d}}N}} = C\left( {\Delta K} \right)^{m}$ where the parameter C is now linked to the parameter $\overline{\psi }_{\infty } ,$ the slope controlled by parameter m remains unexplored. It seems the slope in the proposed model is implicitly obtained by already existing fracture material properties, $G_{{\text{c}}}$ and l. Therefore, to examine the fracture material properties influence on the slope, fracture toughness is changed to $G_{{\text{c}}} = 1\,{\text{kN/mm}}$ and $G_{{\text{c}}} = 25\,{\text{kN/mm}},$ while keeping the $\overline{\psi }_{\infty } = 50\,{\text{MPa}}$ constant. It has to be noted that such parametric study of fracture properties influence is purely numerical and hardly achievable experimentally. However, it certainly serves the purpose of better understanding the proposed model.

The results show clear fracture properties influence on the slope of the Paris law curve, more pronounced in fatigue degradation functions $\hat{F}_{2}$ and $\hat{F}_{3} .$ Moreover, Fig. 28a shows the influence of the fracture toughness on the vertical shift, i.e., the start of the fatigue propagation, which is not observed in functions $\hat{F}_{2}$ and $\hat{F}_{3}$. This could be due to the underlying difference in the fatigue degradation functions which further emphasises the remaining open questions on the choice of such function. Nevertheless, it can be concluded that the parameter m in the empirical Paris law equation can be directly linked to the fracture material parameters already contained in the proposed phase-field model for monotonic fracture.

Fig. 28

Fracture toughness G_c influence on crack rate growth versus stress intensity factor change for fatigue degradation function a $\hat{F}_{1}$ b $\hat{F}_{2}$ and c $\hat{F}_{3}$

The Paris law slope can also be fine-tuned using the parameter $\xi$ in $\hat{F}_{3}$ (36). For this example, only function $\hat{F}_{3}$ is used with constant $\overline{\psi }_{\infty } = 50\,{\text{MPa,}}$ $G_{{\text{c}}} = 5\,{\text{kN/mm}}$ and $R = 0.$ The change in Paris law slope is presented in Fig. 29. Similar parameter can be introduced in other function as well, thus having the complete control on fatigue material behaviour described with Paris law curve.

Fig. 29

The influence of the ξ parameter on crack rate growth versus stress intensity factor change for fatigue degradation function $\hat{F}_{3}$

5 Conclusion

In this work, the extension of the phase-field fracture approach to fatigue was presented, recovering its main features like $\varepsilon - N$ and Paris law curves in low- and high-cycle regimes without any additional criteria. Two-part cycle skipping technique was included for better computational efficiency. The elastoplastic material model with the combined nonlinear isotropic and kinematic hardening was included to account for cyclic plasticity. A fatigue degradation function was developed for the degradation of fracture energy. Hereby, three different fatigue degradation functions are proposed. These functions include the structural loading history information by introducing the local energy accumulation variable and an additional fatigue material parameter.

The novel description of the energy accumulation variable was discussed in detail. It implicitly includes the influence of mean load, which was first shown theoretically and schematically, and then proven through parametric study of cyclically loaded CT specimen. Such definition of the accumulation variable prevents the interference of the fatigue extension in the monotonically loaded cases. This was proven on the example of single edge notched specimen subjected to monotonic loading.

The proposed model recovers the full scope of fatigue domain, ranging from low- to high-cyclic regime, as presented on the example of cyclically loaded round bar. Moreover, the numerical results are compared with experimental data on nodular cast iron CT specimen from the author’s previous work and show great match in terms of fatigue crack growth and Paris law curves in low-cycle fatigue regime. However, further experimental validation is needed for better understanding of the underlying phase-field fatigue model. The numerical experiments are concluded with the parametric study of cyclically loaded CT specimen in high-cyclic regime where the influence of different fatigue functions, load ratios, and fracture and fatigue material parameters was observed. The additional fatigue material parameter is thus clearly linked to the well-known empirical parameters.