Abstract
Discrete ill-posed inverse problems arise in various areas of science and engineering. The presence of noise in the data often makes it difficult to compute an accurate approximate solution. To reduce the sensitivity of the computed solution to the noise, one replaces the original problem by a nearby well-posed minimization problem, whose solution is less sensitive to the noise in the data than the solution of the original problem. This replacement is known as regularization. We consider the situation when the minimization problem consists of a fidelity term, that is defined in terms of a p-norm, and a regularization term, that is defined in terms of a q-norm. We allow 0 < p,q ≤ 2. The relative importance of the fidelity and regularization terms is determined by a regularization parameter. This paper develops an automatic strategy for determining the regularization parameter for these minimization problems. The proposed approach is based on a new application of generalized cross validation. Computed examples illustrate the performance of the method proposed.
Similar content being viewed by others
1 Introduction
In many areas of science and engineering one is faced with the problem of having to compute a meaningful approximate solution, defined in an appropriate way, of linear systems of equations of the form
where \(A\in {\mathbb R}^{m\times n}\) is a given matrix, \(\mathbf {x}\in {\mathbb R}^{n}\) is the desired solution, and \(\mathbf {b}\in {\mathbb R}^{m}\) is a data vector. The symbol ≈ indicates that we would like to determine a vector x such that Ax approximates b in a suitable way. We consider the case when the singular values of A decrease to zero quickly without a significant gap. Then the matrix A is severely ill-conditioned and, moreover, it is not meaningful to define the rank of A. Approximation problems (1) with a matrix of this kind are commonly referred to as discrete ill-posed problems; see, e.g., [17, 26, 27] for discussions.
In applications of interest to us, the data vector b is not available; instead a measured vector \(\mathbf {b}^{\delta }\in {\mathbb R}^{m}\), which is contaminated by noise \(\boldsymbol {\eta }\in {\mathbb R}^{m}\), is known, i.e.,
replaces the vector b in (1). Here and throughout this paper the superscript T denotes transposition. We assume that η is made up of white Gaussian noise, impulse noise and/or salt and pepper noise. Impulse noise modifies only some entries of b and leaves the other entries unchanged. In detail, we have for 1 ≤ i ≤ m,
where the di are realizations of a random variable with uniform distribution in the interval \([d_{\min \limits },d_{\max \limits }]\), which is the dynamic range of bi. If \(d_{i}\in \{d_{\min \limits },d_{\max \limits }\}\), i.e., if the di only attain their maximal or minimal achievable values, then impulse noise is commonly referred to as salt-and-pepper noise. Impulse noise simulates the effect of broken sensors on a measuring device such as a CCD camera.
Since A is ill-conditioned and bδ is contaminated by noise, the least-squares solution A‡bδ of minimal norm of (1) with b replaced by bδ is meaningless due to propagation and severe amplification of the error η in bδ into the solution; here A‡ denotes the Moore-Penrose pseudo-inverse of A. To reduce the propagated error in the computed solution, one typically modifies the problem to be solved. This modification is commonly referred to as regularization.
A regularization method that recently has received considerable attention is the ℓp-ℓq minimization method; see [14, 18, 30, 35]. This method solves the minimization problem
where \(L\in \mathbb {R}^{r\times n}\) is a regularization matrix, μ > 0 a regularization parameter, and \(\| \mathbf {z} \|_{p}^{p}={\sum }_{i=1}^{k}|z_{i}|^{p}\) for \(\mathbf {z}=[z_{1},z_{2},\ldots ,z_{k}]^{T}\in {\mathbb R}^{k}\) for k ∈{m,n}. We are interested in parameters p and q in the interval (0,2]. Observe that z↦∥z∥p is a norm only if p ≥ 1; however, for notational convenience, we will refer to the quantity ∥z∥p as an ℓp-norm also for 0 < p < 1.
The regularization parameter μ > 0 determines the trade-off between the first and second terms in (2), and decides how sensitive the solution of (2) is to the error η in bδ. Moreover, the choice of μ affects how close the solution is to the desired vector xtrue = A‡b. An imprudent choice of μ may result in that the solution of (2) is a poor approximation of xtrue. It therefore is important to develop methods that are able to determine a suitable value of μ. This value will depend on the matrices A and L, the vectors bδ and η, as well as the parameters p and q. If p = q = 2, then the problem (2) reduces to Tikhonov regularization in general form; see, e.g., [17, 22, 27, 38] for discussions on Tikhonov regularization.
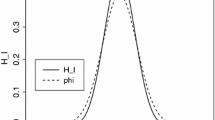
We now briefly discuss different choices for p and q, and first comment on the choice of q, which affects the second term in (2). This terms is commonly referred to as the regularization term. In many situations the desired solution xtrue of (1) is sparse after some transformation. For instance, if we represent xtrue in terms of framelets or wavelets, then xtrue typically has a sparse representation, i.e., many coefficients in this representation vanish. Moreover, when L is a discretized gradient operator, the vector Lxtrue generally has many vanishing entries. To promote sparsity of the computed solution of (2), we may consider letting L = I and q = 0. Then the regularization term measures the size of the computed solution by the ℓ0-norm. This “norm” counts the number of nonzero entries in the vector x in (2). Note that this norm is not convex. Similarly, to promote sparsity in the vector Lx, we may consider letting q = 0 in (2). However, the minimization problems so obtained are extremely difficult to solve. Therefore, it is common to approximate the ℓ0-norm by the ℓ1-norm. This approximation has the advantage that the ℓ1-norm is convex, which makes it easier to solve (2) than when using the ℓ0-norm. However, ℓq-norms with 0 < q < 1 are better approximations of the ℓ0-norm than the ℓ1-norm. In particular, smaller values of q > 0 yield better approximations of the ℓ0-norm than larger values; see Fig. 1 for an illustration. For 0 < q < 1 the resulting minimization problem (2) is not convex and its solution may be difficult to determine; see Lanza et al. [36] for a recent discussion on the choice of q in the context of image restoration.
The choice of p affects the first term in (2), known as the fidelity term, and should depend on the type of noise η in the data vector bδ. If the noise η is white Gaussian, then p = 2 is appropriate and a method for determining μ for this kind of noise, based on the discrepancy principle, is described in [7]. This method requires that a fairly accurate estimate of the norm of η be available and allows 0 < q < 1. However, for impulse noise, choosing p = 2 usually produces computed solutions of poor quality. It has been shown, see, e.g., [8, 30, 35], that the choice 0 < p < 1 leads to accurate restorations in the case of salt-and-pepper noise. In [8], the authors developed two strategies based on cross-validation for determining a suitable value of μ for any 0 < p ≤ 2 without any knowledge of the noise. This method is further commented on below.
Let \(\mathcal {N}(M)\) denote the null space of the matrix M. We will assume that the matrices A and L are such that
Then the matrix ATA + μLTL is nonsingular for any μ > 0, and the minimization problem (2) for p = q = 2 has the unique solution
We remark that both the selection of L and μ are important for the quality of the computed solution and have been widely discussed; see, e.g., [15, 19, 31,32,33, 37].
Generalized cross validation (GCV) introduced by Golub et al. [23] is a popular approach to choosing the regularization parameter for Tikhonov regularization; more recent discussions on this method can be found in [19, 20, 24, 29]. The GCV method is statistically based and chooses a regularization parameter that minimizes the GCV functional
Denote the minimizer of G(μ) by μGCV. In rare events, when the minimizer is not unique, we choose the largest one.
The minimization of G(μ) requires the computation, or at least estimation, of the trace of the matrix I − A(ATA + μLTL)− 1AT that is not explicitly known. This can make the computation of G(μ) expensive when the matrices A and L are large. Different ways to speed up the computations by application of a global block Lanczos method or Golub-Kahan bidiagonalization are described in [19, 20]. However, these works are limited to the situation when L = I.
In this paper, we combine ideas in [19] with the techniques described in [30] to derive an algorithm for computing the GCV parameter for (2) for general values of 0 < p,q ≤ 2. Specifically, we consider the AMM-GKS algorithm in [30] for the solution of (2) (see Section 3.1 for more details), and modify it so that at each iteration the regularization parameter is chosen adaptively by minimizing a reduced version of the function (5). The computation of the GCV parameter is fully automatic in the sense that no information about the noise η is required. The GCV method for determining the regularization parameter is a so-called heuristic method, see Kindermann [32], and therefore may fail for certain data vectors b. In our experience, failure is extremely rare. The GCV method is related to cross validation (CV), another heuristic method for determining a suitable regularization parameter; see [8, 39]. We will illustrate in Section 4 that GCV typically gives about the same value of the regularization parameter as CV for a much lower computational effort.
This paper is organized as follows: Section 2 reviews how the GCV parameter for Tikhonov regularization in general form can be computed fairly inexpensively by projection into a Krylov subspace, and in Section 3 we discuss how to determine the GCV parameter for large-scale minimization problems (2). A smoothed variant of GCV that can give better regularization parameter values also is presented. Section 4 contains numerical examples that illustrate the performance of the proposed approach. Finally, Section 5 contains some concluding remarks.
2 GCV for Tikhonov regularization in general form
This section discusses the computation of the GCV parameter for Tikhonov regularization in general form, i.e., when solving the minimization problem (2) with p = q = 2. We first describe an approach that requires the generalized singular value decomposition (GSVD) of the matrix pair {A,L}. This approach is computationally feasible only for small to medium-sized problems since the computation of the GSVD for a large matrix pair is very expensive. We then discuss how the computational burden for large-scale problems can be reduced by projecting the matrix pair {A,L} into a Krylov subspace of fairly small dimension.
2.1 GCV computation by using the GSVD
This subsection reviews material in [27], where further details can be found. Consider the Tikhonov regularization problem in general form with μ > 0,
and introduce the GSVD of the matrix pair {A,L},
where ΣA and ΣL are diagonal, possibly rectangular, matrices, the matrices U and V are orthogonal, and the matrix Y is square and non-singular. Further details of these matrices, including their sizes, can be found, e.g., in [16, 25, 27]. The evaluation of the GCV function G(μ), defined by (5), requires the computation of the quantities
for several values of μ > 0, where the vector xμ is given by (4). These quantities can be evaluated inexpensively when the factorizations (7) are available as follows. For notational simplicity, the formulas below assume that all matrices are square. This restriction easily can be removed; see, e.g., [16, 25, 27] for details.
The quantity rμ can be expressed as
where (a) is obtained by using the definition (4) of xμ, and (b) is derived using the factorizations (7) with \(\tilde {\mathbf {b}}^{\delta }=U^{T}\mathbf {b}^{\delta }\). Analogously,
where we have used the factorizations (7) and the fact that trace is invariant under similarity transformation. We have
where we in rare cases of nonunicity let μGCV be the largest of the minimizers.
It is clear from the above expressions for rμ and tμ that the main computational cost for evaluating (5) is the computation of the GSVD (7) of the matrix pair {A,L}. Observe that, to determine μGCV we typically have to evaluate G(μ) for many values of μ. However, it suffices to compute the factorizations (7) only once, since they are independent of μ.
2.2 GCV computation in a Krylov subspace
When the matrices A and L are large, the computation of the GSVD (7) is unattractive due to its high cost; for instance, Paige’s algorithm generally requires at least 35.3n3 arithmetic floating point operations when \(A,L\in {\mathbb R}^{n\times n}\); see [1, Table 5.1] for details. We therefore now describe a more computational attractive approach that is based on projecting the problem into a Krylov subspace of fairly small dimension. Our projection method extends the method used in [19] by allowing the matrix L to be different from the identity.
Let \(A\in {\mathbb R}^{m\times n}\) and \(L\in {\mathbb R}^{r\times n}\) and let the columns of V ∈ Rn×d form an orthonormal basis for the Krylov subspace \(\mathcal {V}\) of dimension \(1\leq d\ll \min \limits \{m,n,r\}\),
We assume here that d is small enough so that \(\dim (\mathcal {K}_{d}\left (A^{T}A,A^{T}\mathbf {b}^{\delta } \right ))=d\). This is the generic situation. It is convenient to compute the columns of V by applying d steps of Golub-Kahan bidiagonalization to A with initial vector bδ. This gives the decomposition
where the matrices [U,ud+ 1] ∈ Rm×(d+ 1) and V ∈ Rn×d have orthonormal columns and \(B^{(A)}\in {\mathbb R}^{(d+1)\times d}\) is lower bidiagonal; see, e.g., [25]. We assume that d is small enough so that this decomposition exists.
We would like to compute an approximate solution of the Tikhonov minimization problem (6) in \(\mathcal {V}\). The restriction of the approximate solution to the subspace \(\mathcal {V}\) of low dimension d reduces the computational cost of significantly. Thus, we would like to solve
Substituting x = V y for some \(\mathbf {y}\in {\mathbb R}^{d}\) into the above equation gives
Substitute the QR factorization
where the matrix \(Q^{(L)}\in {\mathbb R}^{r\times d}\) has orthonormal columns and \(R^{(L)}\in {\mathbb R}^{d\times d}\) is upper triangular, and the decomposition (8) into (9) gives
with e1 = [1,0,…,0]T denoting the first axis vector. The projected problem (10) is of quite inexpensive to compute and of fairly small dimension. In particular, it is feasible to compute the GSVD of the matrix pair {B(A),R(L)} and use it to calculate an approximation of the GCV function G(μ).
3 GCV for ℓ p-ℓ q regularization
We describe how to combine the computations discussed in Section 2 for determining the regularization parameter by the GCV method with the algorithms presented in [30] for minimizing the expression (2).
3.1 Solution of the ℓ p-ℓ q minimization problem for fixed μ > 0
For convenience of the reader, we outline the AMM-GKS method for solving (2) proposed in [30]. Introduce a smoothed version of the q-norm \(\| \mathbf {x} \|_{q}^{q}\) for 0 < q ≤ 1 as follows. Let \({\varPhi }_{q}:{\mathbb R}\rightarrow {\mathbb R}\) be defined by
and observe that, if 0 < q ≤ 1, then t↦Φq(t) is not differentiable at t = 0. We approximate Φq by the differentiable function
where ε > 0 is a (small) constant. Similarly, we define for \(\mathbf {x}=[x_{1},x_{2},\ldots ,x_{n}]^{T}\in {\mathbb R}^{n}\) the smoothed version of \(\| \mathbf {x} \|_{q}^{q}\) as
Finally, introduce the smoothed version of the functional that is minimized in (2),
This gives us the smoothed version
of the minimization problem (2).
The AMM-GKS method described in [30] is a majorization-minimization method for computing a stationary point of the functional (12). This method determines a sequence of iterates x(k), k = 1,2,…, that converge to a stationary point of (12). Each iterate is computed in by two steps: first the functional (12) is majorized by a quadratic tangent majorant \(\mathbf {x}\rightarrow \mathcal {Q}(\mathbf {x},\mathbf {x}^{(k)})\) for \(\mathcal {J}_{\varepsilon }\) at x(k). Then the unique minimizer of \(\mathbf {x}\rightarrow \mathcal {Q}(\mathbf {x},\mathbf {x}^{(k)})\) is calculated. This minimizer is the next iterate x(k+ 1). We outline this method in the remainder of this subsection.
Definition 1 (30)
Consider the differentiable functional \(\mathcal {J}_{\varepsilon }(\mathbf {x}):{\mathbb R}^{n}\rightarrow {\mathbb R}\). We say that the functional \(\mathbf {x}\mapsto \mathcal {Q}(\mathbf {x},\mathbf {y}):{\mathbb R}^{n}\rightarrow {\mathbb R}\) is a quadratic tangent majorant for \(\mathcal {J}_{\varepsilon }(\mathbf {x})\) at \(\mathbf {y}\in {\mathbb R}^{n}\) if the following conditions are satisfied:
-
\(\mathcal {Q}(\mathbf {x},\mathbf {y})\) is quadratic,
-
\(\mathcal {Q}(\mathbf {x},\mathbf {y})\geq \mathcal {J}(\mathbf {x})\) for all \(\mathbf {x}\in {\mathbb R}^{n}\),
-
\(\mathcal {Q}(\mathbf {y},\mathbf {y})=\mathcal {J}(\mathbf {y})\) and \(\nabla _{\mathbf {x}}\mathcal {Q}(\mathbf {y},\mathbf {y})=\nabla _{\mathbf {x}}\mathcal {J}(\mathbf {y})\),
where ∇x denotes the gradient with respect to the first argument of Q.
- Majorization step.:
-
The quadratic tangent majorant at the point x(k) constructed by the AMM-GKS method is determined as follows. Let
$$ \begin{array}{ll} \mathbf{v}^{(k)}&:=A\mathbf{x}^{(k)}-\mathbf{b}^{\delta},\\ \mathbf{u}^{(k)}&:=L\mathbf{x}^{(k)}, \end{array} $$and compute the vectors
$$ \begin{array}{ll} \boldsymbol{\omega}_{\text{fid}}^{(k)}&:=((\mathbf{v}^{(k)})^{2}+\varepsilon^{2})^{p/2-1},\\ \boldsymbol{\omega}^{(k)}_{\text{reg}}&:=((\mathbf{u}^{(k)})^{2}+\varepsilon^{2})^{q/2-1}, \end{array} $$where all the operations, including squaring, are meant element-wise. Define the diagonal matrices
$$ W^{(k)}_{\text{fid}}=\text{diag}(\boldsymbol{\omega}_{\text{fid}}^{(k)}),\quad W^{(k)}_{\text{reg}}=\text{diag}(\boldsymbol{\omega}_{\text{reg}}^{(k)}). $$It is shown in [30] that the functional
$$ \mathcal{Q}(\mathbf{x},\mathbf{x}^{(k)})=\frac{1}{2}\| (W^{(k)}_{\text{fid}})^{1/2}(A\mathbf{x}-\mathbf{b}^{\delta}) \|_{2}^{2}+ \frac{\mu}{2}\| (W^{(k)}_{\text{reg}})^{1/2}L\mathbf{x} \|_{2}^{2}+c, $$(13)with c a suitable constant that is independent of x, is a quadratic tangent majorant for \(\mathcal {J}_{\varepsilon }\) at x(k); see [30] for details on the derivation of \(\boldsymbol {\omega }^{(k)}_{\text {fid}}\), \(\boldsymbol {\omega }^{(k)}_{\text {reg}}\), and c.
- Minimization step.:
-
We describe the computation of the minimizer x(k+ 1) of (13). Since \(\mathcal {Q}\) is quadratic, x(k+ 1) can be determined as the zero of the gradient, i.e., by solving
$$ (A^{T}W^{(k)}_{\text{fid}}A+\mu L^{T}W^{(k)}_{\text{reg}}L)\mathbf{x}=A^{T}W^{(k)}_{\text{fid}}\mathbf{b}^{\delta}. $$(14)The system matrix is nonsingular and positive definite for all μ > 0 if and only if
$$ \mathcal{N}(A^{T}W^{(k)}_{\text{fid}}A)\cap\mathcal{N}(L^{T}W^{(k)}_{\text{reg}}L)=\{\mathbf{0}\}. $$This condition typically is satisfied. Then the solution x(k+ 1) of (14) is the unique minimizer of \(\mathbf {x}\to \mathcal {Q}(\mathbf {x},\mathbf {x}^{(k)})\).
The computation of the solution of (14) can be demanding when the matrices A and L are large. An approximate solution can be computed efficiently by projecting the problem into a low-dimensional subspace \(\mathcal {V}_{d}\) of dimension \(1\leq d\ll \min \limits \{m,n,r\}\). Let the columns of the matrix \(V_{d}\in {\mathbb R}^{n\times d}\) form an orthonormal basis for \(\mathcal {V}_{d}\) and calculate the skinny QR factorizations
where the matrices QA and QL have orthonormal columns and the matrices RA and RL are upper triangular. Using these factorizations, we obtain the reduced analogue of (14),
The solution y(k+ 1) of this equation gives, with a slight abuse of notation, the approximate solution
of (14). Substituting this expression into (14) gives the residual vector
Observe that this vector in general is nonvanishing, since we are solving (14) in the subspace \(\mathcal {V}_{d}\) of \({\mathbb R}^{n}\). We enlarge at each step the solution subspace by adding the scaled residual vector \(\mathbf {v}_{\text {new}}=\mathbf {r}^{(k+1)}/\|\mathbf {r}^{(k+1)}\|\) to the solution subspace. This vector is orthogonal to the columns of the matrix Vd. Define the matrix \(V_{d+1}=[V_{d},\mathbf {v}_{\text {new}}]\in {\mathbb R}^{n\times (d+1)}\). Its columns form an orthonormal basis for the new solution subspace \(\mathcal {V}_{d+1}\). The so determined solution subspace is referred to as a Generalized Krylov subspace (GKS); see, e.g., [34] for another application of this kind of subspaces. The computations are initialized by choosing a d0-dimensional solution subspace of \({\mathbb R}^{n}\) and letting the columns of the matrix \(V_{d_{0}}\) form an orthonormal basis for this subspace. Typically, setting d0 = 1 and \(V_{0}=A^{T}\mathbf {b}^{\delta }/\| A^{T}\mathbf {b}^{\delta } \|_{2}\) is appropriate. An algorithm that describes these computations and determines the regularization parameter μ by the GCV method is described in the following subsection.
3.2 GCV and MM-GKS
In the computations outlined in the previous subsection, the regularization parameter is kept fixed. We now describe how a value μk of the regularization parameter can be determined in a fairly simple manner before computing the next approximate solution x(k+ 1) of (2).
Equation (15) is the normal equation associated with the minimization problem
This minimization problem is analogous to (10). Since it stems from projecting a large problem into a generalized Krylov subspace of modest dimension d, the matrices RA and RL are small enough to allow the computation of the GSVD of the matrix pair {RA,RL} at moderate expense. We therefore can use the technique described in Section 2.1 to determine a suitable value of the regularization parameter by GCV. In detail, let the GSVD of the matrix pair {RA,RL} be given by
Similarly as in Section 2.1, we define, for any μ > 0, the quantities
This derivation uses that both matrices RA and RL are square. We compute the GCV parameter μ(k) as the solution of
If the minimum is not unique, then we choose the largest one. Typically, the minimum is unique. This is assumed in Algorithm 1, which describes the computations. The parameter μ(k) is updated in each iteration.

Algorithm 1 requires the computation of the GSVD of the matrix pair {RA,RL} in each iteration. Since the matrices RA and RL are not very large, this is not very expensive.
3.3 Smoothed GCV for impulse noise
We describe a modified version of the GCV that, as we will see in Section 4, is well suited for impulse noise. The Euclidean norm of impulse noise is infinite. Therefore, the numerator in G(μ), see (5), may be infinite. It therefore may be difficult to compute the minimum of G(μ). In computations in finite precision arithmetic, the Euclidean norm of impulse noise is extremely large and this leads to that it may be difficult to determine the minimum of G(μ). To remedy this issue, we smooth the data vector bδ by convolving it with a Gaussian filter with small variance. Let \(\mathbf {k}_{\nu ^{2}}\in {\mathbb R}^{m}\) represent a sampling of a Gaussian function with mean zero and variance ν2, and define the smoothed vector
where ∗ denotes the convolution operator. It is well known that if we assume periodic boundary conditions, then convolution can be carried out easily with the aid of the Fourier transform \(\mathfrak {F}\). We have
where ⊙ denotes element-wise multiplication. Moreover, if bδ represents the vectorization of a multi-dimensional array, e.g., an image, it is beneficial to let \(\mathbf {k}_{\nu ^{2}}\) be the vectorization of a discretized multi-dimensional Gaussian function.
Using \(\mathbf {b}^{\delta }_{\text {smooth}}\) we can define the smoothed version of the GCV functional by
This functional is the standard GCV functional (5) with the data vector bδ replaced by the smoothed data vector \(\mathbf {b}^{\delta }_{\text {smooth}}\). The MM-GKS-GCV-Smooth algorithm is obtained by minimizing Gsmooth at each iteration in Algorithm 1 instead of G.
4 Numerical examples
This section shows some numerical examples that illustrate the performance of the proposed methods. The examples are concerned with the restoration of images that have been contaminated by noise and space-invariant blur, as well as with computerized tomography; see [28] for details on image restoration and [9] for a description of computerized tomography.
We set q = 0.1 in all examples, while the value of p depends on the type of noise the data vector bδ is corrupted by. For white Gaussian noise, we set p = 2; for other kinds of noise, we let p = 0.8.
We would like to compute a sparse solution in the framelet domain and therefore use a two-level framelet analysis operator as regularization operator L. Framelets are extensions of wavelets. They are defined as follows:
Definition 2
Let \(\mathcal {W}\in {\mathbb R}^{r\times n}\) with n ≤ r. The set of the rows of \(\mathcal {W}\) is a framelet system for \(\mathbb {R}^{n}\) if \(\forall \mathbf {x}\in {\mathbb R}^{n}\) it holds
where \(\mathbf {y}_{j}\in \mathbb {R}^{n}\) is the j th row of \(\mathcal {W}\) (written as a column vector), i.e., \(\mathcal {W}=\left [\mathbf {y}_{1},\ldots ,\mathbf {y}_{r}\right ]^{T}\). The matrix \(\mathcal {W}\) is referred to as an analysis operator and \(\mathcal {W}^{T}\) as a synthesis operator. The matrix \(\mathcal {W}\) defines a tight frame if and only if \(\mathcal {W}^{T}\mathcal {W}=I\).
We remark that in general \(\mathcal {W}\mathcal {W}^{T}\ne I\), unless r = n and the framelets are orthonormal. Note that \({\mathcal N}({\mathcal W})=\{\mathbf {0}\}\). Therefore, property (3) holds. Tight frames have been used in many image restoration applications including inpainting and deblurring; see, e.g., [2,3,4,5,6, 10,11,12,13].
We use framelets determined by linear B-splines. In one space-dimension they are made up of a low-pass filter W0 and two high-pass filters W1 and W2, whose masks are
respectively. We can derive the synthesis operator \(\mathcal {W}\) starting from these masks by imposing reflexive boundary conditions. These boundary conditions secure that \(\mathcal {W}^{T}\mathcal {W}= I\). Defining
and
The synthesis operator is obtained by stacking the three matrices above
We can extend the operator above to two space-dimension by means of tensor products
This yields the analysis operator
The matrix W00 is a low-pass filter. All the other matrices Wij contain at least one high-pass filter in some direction. In our examples, we set \(L=\mathcal {W}\).
We compare generalized cross validation with two other approaches to selecting the regularization parameter in (2), including cross validation as described in [8] and the discrepancy principle as discussed in [7]. We also compare the quality of the computed solutions determined by these method with the solution obtained with the optimal choice of the regularization parameter. The latter choice of the regularization parameter is not practical, because it requires that the desired solution xtrue be known; the regularization parameter is then determined to yield a computed solution that minimizes the restoration error
where xtrue denotes the desired solution.
The method described in [7] determines a sequence of regularization parameters, in a similar fashion as in this work, by requiring that the computed approximate solution in each iteration satisfies the discrepancy principle (DP). To perform well, this method requires that a fairly accurate estimate of the norm of the error ∥η∥2 in the data vector bδ be known. This norm is not meaningful for impulse noise. Therefore, the discrepancy principle cannot be used when bδ is contaminated by impulse noise.
Two methods for determining the regularization parameter by cross-validation are described in [8]. The first method determines the regularization parameter so that missing data is well predicted. This classical approach of carrying out cross-validation is referred to as CV in the tables. The other method, which we refer to as modified cross-validation (MCV), seeks to determine the regularization parameter so that missing entries of the computed solution are well predicted. The MCV method typically gives approximations of the desired solution xtrue of somewhat higher quality than the CV method; see [8] for illustrations. This paper compares different parameter choice rules for the minimization problem (2). A comparison with other methods for solving the minimization problem (2), that require the regularization parameter to be hand-tuned, can be found in [30, 35].
The restoration error (17) and the structural and similarity index (SSIM) are compared in our tests. The definition of the latter is somewhat involved; here we just note that the SSIM measures how well the overall structure of an image is recovered, and that the larger the index the better the reconstruction. In particular, the highest value achievable is 1; see [40] for details.
For all examples we set ε = 1 in (11); see [7] for a discussion on the choice of ε. We terminate the iterations either after 100 iterations or when
Finally, for the computations of \(\mathbf {b}^{\delta }_{\text {smooth}}\), we set ν2 = 1 in all examples.
All the computations were performed using Matlab R2018b running on a Windows 10 laptop computer with a i7-8750H @2.20 GHz CPU and 16 GB of RAM.
Tomography
The first example considers a tomography problem. The example is constructed with the aid of the IR Tools Matlab package [21]. The phantom has 256 × 256 pixels, and we consider 90 equispaced angles in the interval [0,π(, and 362 rays per angle. This results in a matrix \(A\in {\mathbb R}^{32580\times 65536}\). We added 1% of white Gaussian noise to the sinogram, i.e., ∥η∥2 = 0.01∥b∥2. Since the noise is Gaussian, we set p = 2 and, like in all considered examples, q = 0.1. We show the true phantom and the sinogram in Fig. 2.
Table 1 reports the RRE and SSIM for the computed solutions determined by all the parameter choice rules considered in Table 1. All the rules can be seen to perform very similarly. Obviously, the optimal parameter provides the best reconstruction in terms of RRE. This parameter choice rule requires knowledge of the exact solution xtrue and therefore cannot be used in real application. The DP provides the second best approximation of xtrue, however, it demands knowledge of the norm of the noise η. The CV, MCV, and GCV methods do not require any knowledge of the noise. We can observe, that although the MCV method slightly outperforms the GCV method in terms of the RRE (but not in terms of the SSIM), the GCV method demands much less CPU time than the CV and MCV methods. This is due to the fact that both the CV and MCV methods require several runs of the MM-GKS algorithm, while the GCV method only carries out a single run. Finally, we note that the GCV-Smooth method does not perform well. This is due to the fact that the noise in the data bδ is purely Gaussian. The smoothing of bδ leads to an underestimation of the amount of noise in bδ, which results in a too small value of the regularization parameter; the computed solution is under-regularized. These considerations are confirmed by the visual comparison of the reconstructions shown in Fig. 3.
Peppers
Our second example considers an image deblurring problem. We blur the image in Fig. 4a with the PSF shown in Fig. 4b, and add 25% of impulse noise. This yields the blurred and noisy image displayed in Fig. 4c. When we construct this example, we cut the boundaries of the blurred image to simulate realistic data; see [28] for more details. Since the image is generic, we impose reflexive boundary conditions. Moreover, since the blurred image is corrupted by impulse noise, we set p = 0.8.
We report the results obtained in Table 1. Since the noise is not Gaussian, we cannot apply the discrepancy principle to determine the regularization parameter. However, the CV, MCV, and GCV methods can be applied. We also report the RRE and SSIM for the optimal choice of the regularization parameter. We can see that the GCV and GCV-Smooth methods provide the best reconstructions. In particular, the reconstruction obtained with GCV is slightly better than the optimal one, and the one obtained with GCV-Smooth is significantly better. While this may appear strange, it is due to the construction of the generalized Krylov subspace. In particular, since the solution subspace depends on the approximate solutions generated during the computations, the solution subspaces determined by the various methods differ, and this may lead to different results. We remark that, while we for stationary methods (with μ fixed) can show converge of the computed iterates, we have no such result for the iterates determined by the CV and GCV methods. Finally, we observe that the use of the smoothed GCV function yields a very accurate reconstruction which, in particular, is more accurate than the one obtained with the standard GCV method. These observations are confirmed by visual inspection of the reconstructions displayed in Fig. 5.
Cameraman
The last example describes another image deblurring problem. We consider the exact image in Fig. 6a and blur it with the PSF in Fig. 6b. Adding 20% of salt-and-pepper noise produces the blurred and noisy image in Fig. 6c. As in the previous example, we cut the boundary of the blurred image to simulate realistic data. In view of that the image is generic, we impose reflexive boundary conditions. Since the PSF is quadrantically symmetric, the matrix A obtained can be diagonalized by the discrete cosine transform. Because LTL = I, we therefore could avoid the application of generalized Krylov subspaces in the MM-GKS method. However, for consistency we use the same approach as in the previous examples. Since the noise is not Gaussian, we set p = 0.8, similarly as in the example above.
Table 1 shows the RRE and SSIM values obtained with the different parameter choice rules. We observe that the GCV and GCV-smooth methods provide more accurate approximations of xtrue in terms of RRE, than both the CV and MCV, for a much lower computational cost. Moreover, the RRE obtained with the GCV method is close to the optimal one, and the RRE for the restoration determined by the GCV-Smooth method is significantly smaller. Figure 7 displays the obtained reconstructions. Visual inspection shows that the reconstruction obtained with the GCV-Smooth method is very detailed, but “grayish”. The latter is due to the presence of some pixels, whose values are significantly larger than 255 (which is the value corresponding to white, the value 0 corresponds to black), which causes a rescaling before plotting. Projecting the reconstruction orthogonally into the cube [0,255]n gives the image in Fig. 8. We can observe that the gray-scale level is now correct and the reconstruction is very close to the original image.
5 Conclusions
We propose the GCV method for choosing the regularization parameter for the ℓp-ℓq regularization method. This method is easy to implement and computationally fairly inexpensive thanks to that the original minimization problem (2) is projected into a generalized Krylov subspace of small to moderate size. A comparison with some other available methods shows that the proposed approach is competitive and provides accurate approximations of the desired solution. Moreover, the proposed approach is completely automatic and does not need hand-tuning of any parameter. Thus, it can be considered for real world applications.
References
Bai, Z.: The CSD, GSVD, their applications and computation 958 (1992)
Bianchi, D., Buccini, A.: Generalized structure preserving preconditioners for frame-based image deblurring. Mathematics 8(4), 468 (2020)
Bianchi, D., Buccini, A., Donatelli, M.: Structure preserving preconditioning for frame-based image deblurring. In: Donatelli, M., Serra-Capizzano, S. (eds.) Computational Methods for Inverse Problems in Imaging, pp 33–49. Springer, Cham (2019)
Buccini, A., Donatelli, M.: A multigrid frame based method for image deblurring. Electron. Trans. Numer. Anal. 53, 283–312 (2020)
Buccini, A., Park, Y., Reichel, L.: Numerical aspects of the nonstationary modified linearized Bregman algorithm. Appl. Math. Comput. 337, 386–398 (2018)
Buccini, A., Pasha, M., Reichel, L.: Linearized Krylov subspace Bregman iteration with nonnegativity constraint. Numer. Algorithms, in press (2020)
Buccini, A., Reichel, L.: An ℓ2-ℓq regularization method for large discrete ill-posed problems. J. Sci. Comput. 78(3), 1526–1549 (2019)
Buccini, A., Reichel, L.: An ℓp-ℓq minimization method with cross-validation for the restoration of impulse noise contaminated images. J. Comput. Appl. Math. 375, Art. 112824 (2020)
Buzug, T.M.: Computed tomography. In: Kramme, R., Hoffmann, K.P., Pozos, R.S. (eds.) Springer Handbook of Medical Technology, pp 311–342. Springer, Berlin (2011)
Cai, J.F., Chan, R.H., Shen, L., Shen, Z.: Simultaneously inpainting in image and transformed domains. Numer. Math. 112(4), 509–533 (2009)
Cai, J.F., Chan, R.H., Shen, Z.: A framelet-based image inpainting algorithm. Appl. Comput. Harmon. Anal. 24(2), 131–149 (2008)
Cai, J.F., Osher, S., Shen, Z.: Linearized Bregman iterations for frame-based image deblurring. SIAM J. Imaging Sci. 2(1), 226–252 (2009)
Cai, Y., Donatelli, M., Bianchi, D., Huang, T.Z.: Regularization preconditioners for frame-based image deblurring with reduced boundary artifacts. SIAM J. Sci. Comput. 38(1), B164–B189 (2016)
Chan, R.H., Liang, H.X.: Half-Quadratic algorithm for ℓp-ℓq problems with applications to TV-ℓ1 image restoration and compressive sensing. In: Efficient Algorithms for Global Optimization Methods in Computer Vision, Lecture Notes in Comput. Sci. #8293, Springer, Berlin, pp. 78--103 (2014)
Donatelli, M., Neuman, A., Reichel, L.: Square regularization matrices for large linear discrete ill-posed problems. Numer. Linear Algebra Appl. 19(6), 896–913 (2012)
Dykes, L., Noschese, S., Reichel, L.: Rescaling the GSVD with application to ill-posed problems. Numer. Algorithms 68, 531–545 (2015)
Engl, H.W., Hanke, M., Neubauer, A.: Regularization of Inverse Problems. Kluwer, Doordrecht (1996)
Estatico, C., Gratton, S., Lenti, F., Titley-Peloquin, D.: A conjugate gradient like method for p-norm minimization in functional spaces. Numer. Math. 137(4), 895–922 (2017)
Fenu, C., Reichel, L., Rodriguez, G.: GCV For Tikhonov regularization via global Golub-Kahan decomposition. Numer. Linear Algebra Appl. 23 (3), 467–484 (2016)
Fenu, C., Reichel, L., Rodriguez, G., Sadok, H.: GCV For Tikhonov regularization by partial SVD. BIT Numer. Math. 57, 1019–1039 (2017)
Gazzola, S., Hansen, P.C., Nagy, J.G.: IR Tools: a MATLAB package of iterative regularization methods and large-scale test problems. Numer. Algorithms 81(3), 773–811 (2019)
Gazzola, S., Novati, P., Russo, M.R.: On Krylov projection methods and Tikhonov regularization. Electron. Trans. Numer. Anal. 44, 83–123 (2015)
Golub, G.H., Heath, M., Wahba, G.: Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 21(2), 215–223 (1979)
Golub, G.H., von Matt, U.: Generalized cross-validation for large-scale problems. J. Comput. Graph. Stat. 6, 1–34 (1997)
Golub, G.H., Van Loan, C.F.: Matrix Computations, 4th edn. Johns Hopkins University Press, Baltimore (2013)
Hanke, M., Hansen, P.C.: Regularization methods for large-scale problems. Surv. Math. Ind. 3(4), 253–315 (1993)
Hansen, P.C.: Rank Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion. SIAM, Philadelphia (1998)
Hansen, P.C., Nagy, J.G., O’Leary, D.P.: Deblurring Images: Matrices, Spectra, and Filtering. SIAM, Philadelphia (2006)
Hansen, P.C., Nagy, J.G., Tigkos, K.: Rotational image deblurring with sparse matrices. BIT Numer. Math. 54, 649–671 (2014)
Huang, G., Lanza, A., Morigi, S., Reichel, L., Sgallari, F.: Majorization-minimization generalized Krylov subspace methods for ℓp-ℓq optimization applied to image. BIT Numer. Math. 57, 351–378 (2017)
Huang, G., Reichel, L., Yin, F.: On the choice of solution subspace for nonstationary iterated Tikhonov regularization. Numer. Algorithms 81, 33–55 (2019)
Kindermann, S.: Convergence analysis of minimization-based noise level-free parameter choice rules for linear ill-posed problems. Electron. Trans. Numer. Anal. 38, 233–257 (2011)
Kindermann, S., Raik, K.: A simplified L-curve as error estimator. Electron. Trans. Numer. Anal. 53, 213–238 (2020)
Lampe, J., Reichel, L., Voss, H.: Large-scale Tikhonov regularization via reduction by orthogonal projection. Linear Algebra Appl. 436, 2845–2865 (2012)
Lanza, A., Morigi, S., Reichel, L., Sgallari, F.: A generalized Krylov subspace method for ℓp-ℓq minimization. SIAM J. Sci. Comput. 37(5), S30–S50 (2015)
Lanza, A., Morigi, S., Sgallari, F.: Constrained TVp−ℓ2 model for image restoration. J. Sci. Comput. 68(1), 64–91 (2016)
Reichel, L., Rodriguez, G.: Old and new parameter choice rules for discrete ill-posed problems. Numer. Algorithms 63(1), 65–87 (2013)
Reichel, L., Yu, X.: Matrix decompositions for Tikhonov regularization. Electron. Trans. Numer. Anal. 43, 223–243 (2015)
Stone, M.: Cross-validatory choice and assessment of statistical prediction. J. R Stat. Soc. Series B 36, 111–147 (1977)
Wang, Z., Bovik, A.C., Sheikh, H.R., Simoncelli, E.P.: Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 13(4), 600–612 (2004)
Acknowledgements
We would like to thank Marco Donatelli and Caterina Fenu for the precious discussions that inspired and greatly improved this work.
Funding
Open access funding provided by Università degli Studi di Cagliari within the CRUI-CARE Agreement. A.B. is a member of the GNCS-INdAM group that partially supported this work with the Young Researchers Project (Progetto Giovani Ricercatori) “Variational methods for the approximation of sparse data”. Moreover, his research is partially supported by the Regione Autonoma della Sardegna research project “Algorithms and Models for Imaging Science [AMIS]” (RASSR57257, intervento finanziato con risorse FSC 2014-2020 - Patto per lo Sviluppo della Regione Sardegna). The work of L.R is supported in part by NSF grants DMS-1720259 and DMS-1729509.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Buccini, A., Reichel, L. Generalized cross validation for ℓp-ℓq minimization. Numer Algor 88, 1595–1616 (2021). https://doi.org/10.1007/s11075-021-01087-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-021-01087-9
Keywords
- ℓ p-ℓ q minimization
- Regularization parameter
- Generalized cross validation
- Inverse problem
- Iterative method