Generalizing 0-1 conflict hypergraphs and mixed conflict graphs: mixed conflict hypergraphs in discrete optimization

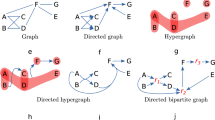
Abstract

This work starts a new level of research in the area of conflict graphs and hypergraphs. We introduce a new term “mixed conflict hypergraphs”, which comes from merging and generalizing 0-1 conflict hypergraphs and mixed conflict graphs. Two structured mixed integer problems (referred to as convexification of posynomial and signomial functions, CoPF and CoSF, respectively) are solved efficiently with applying new strong cutting planes, outperforming modern commercial software.

Appendices

Appendix A. Derivation of MIP1 constraints

This “Appendix” provides the details of refining and adjusting the initial inequalities with “big-M’s” and “small m’s” to constraints of set S (initially constraints (1)-(9)). Our approach offers 4 variants for constraints (13), (14), (16), and (17) in the form of $\bar{\tilde{q}}+ binary$, $\tilde{q}+ binary$, $\bar{\tilde{q}}+ \overline{binary}$, and $\tilde{q}+ \overline{binary}$. Inequalities marked as $(\surd )$ have the structure suitable for MVP (positive coefficients, addition only, $\le$, etc.).

Constraint (1) ${y_{ij}} \le t_{j} ~ ~ \forall i,j$ is also ${y_{ij}} + \bar{t}_{j} \le 1 ~ (\surd )$

Constraint (11) $\sum _{j = 1}^{n} {s_{ij}} \le 1 ~ ~\forall i$ is $\sum _{j \in J^{+}_{i}} {s_{ij}} \le 1 ~ (\surd )$

Constraint (12) $\sum _{j = 1}^n a_{ij}q_{ij} + \tilde{m_i}\sum _{j = 1}^n s_{ij}\ge \tilde{m_i} + 1~ ~\forall i ~$

$\Longrightarrow \sum _{j \in J^{+}_{i}} a_{ij}q_{ij} + \sum _{j \in J^{-}_{i}} a_{ij} + \tilde{m_i}\sum _{j \in J^{+}_{i}}s_{ij} \ge \tilde{m_i} + 1~ \Longrightarrow \tilde{m_i} + 1 = -u \sum _{j \in J^{+}_{i}} a_{ij} + \sum _{j \in J^{-}_{i}} a_{ij}$

$\Longrightarrow \sum _{j \in J^{+}_{i}} a_{ij}q_{ij} + u \sum _{j \in J^{+}_{i}} a_{ij} + (\sum _{j \in J^{-}_{i}} a_{ij} - u \sum _{j \in J^{+}_{i}} a_{ij} -1) \sum _{j \in J^{+}_{i}}s_{ij} \ge 0$.

So, $-\sum _{j \in J^{+}_{i}} a_{ij}\tilde{q}_{ij} +(-\sum _{j \in J^{-}_{i}} a_{ij} + u \sum _{j \in J^{+}_{i}} a_{ij} +1) \sum _{j \in J^{+}_{i}}s_{ij} \le 0$,

or $\sum _{j \in J^{+}_{i}} a_{ij}\bar{\tilde{q}}_{ij} +(-\sum _{j \in J^{-}_{i}} a_{ij} + u \sum _{j \in J^{+}_{i}} a_{ij} +1) \sum _{j \in J^{+}_{i}}s_{ij} \le 2u \sum _{j \in J^{+}_{i}} a_{ij}~ (\surd )$.

We assume here that $-\sum _{j \in J^{-}_{i}} a_{ij} + u \sum _{j \in J^{+}_{i}} a_{ij} +1 \le 2u \sum _{j \in J^{+}_{i}} a_{ij}$, i.e. $u \sum _{j \in J^{+}_{i}} a_{ij} \ge 1 - \sum _{j \in J^{-}_{i}} a_{ij}$. Otherwise, power p does not exist for term i ($\sum _{j \in J^{+}_{i}} s_{ij}=0$) and we have to accept only negative transformations. Thus, we can see an alternative way in choosing u depending on $a_{ij}$: $u_{i}=\frac{1-\sum _{j \in J^{-}_{i}} a_{ij}}{\sum _{j \in J^{+}_{i}} a_{ij}}$ for each posynomial term i or for all i $\hat{u}=\max _i(\frac{1-\sum _{j \in J^{-}_{i}} a_{ij}}{\sum _{j \in J^{+}_{i}} a_{ij}})$ with the requirement of $u > 1$. For practical purposes, we can choose u as the ceiling of $max(u^{*}, \hat{u})$ or admit for some terms negative transformations only to avoid u becoming large.

Constraint (13) $q_{ij} + m_1s_{ij} \ge m_1 +1 ~ ~\forall i, j ~ s.t. ~ a_{ij} > 0$

$m_1 = -u-1 ~ \Longrightarrow q_{ij} \ge (u+1)s_{ij} -u ~\forall i, j \in J^{+}_{i}$

So, $\bar{\tilde{q}}_{ij} + (u+1)s_{ij} \le 2u ~ (\surd )$,

or $-\tilde{q}_{ij} + (u+1)s_{ij} \le 0$,

or $\bar{\tilde{q}}_{ij} + (u+1)(1-\bar{s}_{ij}) \le 2u$,

or $-\tilde{q}_{ij} + (u+1)(1-\bar{s}_{ij}) \le 0$

Constraint (14) $q_{ij} \le \varepsilon (s_{ij}-1) -m_2 s_{ij}~ ~\forall i, j ~ s.t. ~ a_{ij} > 0$

$m_2 = -u ~ \Longrightarrow q_{ij} \le \frac{1}{u}(s_{ij}-1) + us_{ij} ~ \Longrightarrow q_{ij} \le (u+\frac{1}{u})s_{ij} - \frac{1}{u} ~\forall i, j \in J^{+}_{i}$

So, $-\bar{\tilde{q}}_{ij} - (u+\frac{1}{u})s_{ij} \le -(u+\frac{1}{u})$,

or $\tilde{q}_{ij} - (u+\frac{1}{u})s_{ij} \le u - \frac{1}{u}$,

or $-\bar{\tilde{q}}_{ij} + (u+\frac{1}{u})\bar{s}_{ij} \le 0$,

or $\tilde{q}_{ij} + (u+\frac{1}{u})\bar{s}_{ij} \le 2u ~ (\surd )$

Constraint (15) $y_{ij} + s_{ij} \ge 1~ ~\forall i, j ~ s.t. ~ a_{ij} > 0$ is also $\bar{y}_{ij} + \bar{s}_{ij} \le 1 ~\forall i, j \in J^{+}_{i}$

Constraint (16) $q_{ij} - 1 \ge m_1y_{ij}~ ~\forall i, j ~ s.t. ~ a_{ij} > 0$

$m_1 = -u-1 ~ \Longrightarrow q_{ij} + (u+1)y_{ij} \ge 1 ~\forall i, j \in J^{+}_{i}$

So, $\bar{\tilde{q}}_{ij} - (u+1)y_{ij} \le u - 1$,

or $-\tilde{q}_{ij} - (u+1)y_{ij} \le -(u+1)$,

or $\bar{\tilde{q}}_{ij} + (u+1)\bar{y}_{ij} \le 2u ~ (\surd )$,

or $-\tilde{q}_{ij} + (u+1)\bar{y}_{ij} \le 0$

Constraint (17) $q_{ij} - 1 \le M_1y_{ij}~ ~\forall i, j ~ s.t. ~ a_{ij} > 0$

$M_1 = u-1 ~ \Longrightarrow q_{ij} \le (u-1)y_{ij} + 1 ~\forall i, j \in J^{+}_{i}$

So, $-\bar{\tilde{q}}_{ij} - (u-1)y_{ij} \le -(u-1)$,

or $\tilde{q}_{ij} - (u-1)y_{ij} \le u+1$,

or $-\bar{\tilde{q}}_{ij} + (u-1)\bar{y}_{ij} \le 0$,

or $\tilde{q}_{ij} + (u-1)\bar{y}_{ij} \le 2u ~ (\surd )$

Constraint (18) $y_{ij} \le (1- \varepsilon ) q_{ij} + M(1- s_{ij})~ ~\forall i, j ~ s.t. ~ a_{ij} > 0$

$\Longrightarrow y_{ij} \le (1- \frac{1}{u})q_{ij} + u(1-s_{ij}) \Longrightarrow \frac{1-u}{u}q_{ij} + y_{ij} + us_{ij} \le u ~\forall i, j \in J^{+}_{i}$

So, $\frac{u-1}{u}\bar{\tilde{q}}_{ij} + y_{ij} + us_{ij} \le 2u - 1 \Longrightarrow \bar{\tilde{q}}_{ij} + \frac{u}{u-1}y_{ij} + \frac{u^2}{u-1}s_{ij} \le 2u + \frac{u}{u-1} ~ (\surd )$,

or $-\tilde{q}_{ij} + \frac{u}{u-1}y_{ij} + \frac{u^2}{u-1}s_{ij} \le \frac{u}{u-1}$

Appendix B. Separation problem details for MIP1

Consider a maximal cut violation as a separation problem for MIP1.

1. The weighted complementary inequalities (after weakening) can be written as:

$a_{ij}(u-1)(1-y_{ij})+ (1-\sum _{\gamma \in J^{-}_{i}}a_{i\gamma } +u\sum _{\gamma \in J^{+}_{i}-\{j\}}a_{i\gamma }+\frac{1}{u}a_{ij})\sum _{l \in J^{+}_{i}-\{j\}}s_{il} + (1-\sum _{\gamma \in J^{-}_{i}}a_{i\gamma } +u\sum _{\gamma \in J^{+}_{i}-\{j\}}a_{i\gamma }-ua_{ij})s_{ij}-\sum _{l \in J^{+}_{i}-\{j\}} a_{il}\tilde{q}_{il} \le 0$

For brevity, we drop the index i and denote $\varPsi = 1-\sum _{\gamma \in J^{-}}a_{\gamma }+ u\sum _{\gamma \in J^{+}}a_{\gamma }$ (different for each i) the coefficient presented in the formulation of the problem, see constraint (12).

Introducing the characteristic vector z for the yet-to-be-determined partition (j, all other $l \ne j$) in the same manner as in the covering problems (where z is the unit vector for the indicating variable j), we can show that the separation problem for weighted complementary inequalities is polynomial time solvable. Indeed, the y-term becomes $(u-1)\sum _{\gamma }a_{\gamma }z_{\gamma }(1-y^*_{\gamma })$; the $\tilde{q}$-term is $\sum _{\gamma }a_{\gamma }\tilde{q}^*_{\gamma }(z_{\gamma }-1)$; the $s_j$-term is $\sum _{\gamma }s^*_{\gamma }(\varPsi -2ua_{\gamma })z_{\gamma }$; the $s_l$-term can be viewed initially as quadratic with respect to z: $(\varPsi -\sum _{\gamma }(u-\frac{1}{u})a_{\gamma }z_{\gamma })\sum _{\gamma }s^*_{\gamma }(1-z_{\gamma })$, but it can be simplified into a linear one combining with $s_j$-term, and using the facts that $z_{\gamma _1}z_{\gamma _2}=0$ and $z^2_\gamma =z_\gamma$ in the following way:

$$\begin{aligned}&\left( \varPsi -{\sum }_{\gamma }\left( u-\frac{1}{u}\right) a_{\gamma }z_{\gamma }\right) {\sum }_{\gamma }s^*_{\gamma }(1-z_{\gamma })+ {\sum }_{\gamma }s^*_{\gamma }\left( \varPsi -2ua_{\gamma }\right) z_{\gamma } \\&\quad = \varPsi {\sum }_{\gamma }s^*_{\gamma }-\varPsi {\sum }_{\gamma }s^*_{\gamma }z_{\gamma } - {\sum }_{\gamma }\left( u-\frac{1}{u}\right) a_{\gamma }z_{\gamma }{\sum }_{\gamma }s^*_{\gamma } \\&\quad + {\sum }_{\gamma }\left( u-\frac{1}{u}\right) a_{\gamma }z_{\gamma }\\&\quad {\sum }_{\gamma }s^*_{\gamma }z_{\gamma } + \varPsi {\sum }_{\gamma }s^*_{\gamma }z_{\gamma }- {\sum }_{\gamma }2ua_{\gamma }s^*_{\gamma }z_{\gamma } \\&\quad = \varPsi {\sum }_{\gamma }s^*_{\gamma }- {\sum }_{\gamma }\left( u-\frac{1}{u}\right) a_{\gamma }z_{\gamma }{\sum }_{\gamma }s^*_{\gamma }+ {\sum }_{\gamma }\left( u-\frac{1}{u}\right) a_{\gamma }s^*_{\gamma }z_{\gamma }\\&\quad - {\sum }_{\gamma }2ua_{\gamma }s^*_{\gamma }z_{\gamma }\\&\quad =\left( {\sum }_{\gamma }s^*_{\gamma }\right) \left( \varPsi -\left( u-\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }\right) \\&\quad -\left( u+\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }s^*_{\gamma }. \end{aligned}$$

The separation objective function (subject to the unit vector z) becomes

$max_z (\sum _{\gamma }s^*_{\gamma })(\varPsi -(u-\frac{1}{u})\sum _{\gamma }a_{\gamma }z_{\gamma })-(u+\frac{1}{u})\sum _{\gamma }a_{\gamma }z_{\gamma }s^*_{\gamma } +(u-1)\sum _{\gamma }a_{\gamma }z_{\gamma }(1-y^*_{\gamma })+\sum _{\gamma }a_{\gamma }\tilde{q}^*_{\gamma }(z_{\gamma }-1)$. The z-coefficient with the maximal value gives j in the partition with the condition that an optimal objective value is positive. So, we are looking for index $j^*$, if any, which is related to the maximal value ($j^* = argmax_{j}$) among $-(u+\frac{1}{u})a_js^*_j+(u-1)a_j(1-y^*_j)+ a_j\tilde{q}^*_j -(u-\frac{1}{u})a_j\sum _{\gamma }s^*_{\gamma }$ with the condition that this value $> \sum _{\gamma }(a_{\gamma }\tilde{q}^*_{\gamma }-\varPsi s^*_{\gamma })$.

The weakening in this type of inequalities may happen if some $a_{ij}$ bigger than all other entries in the magnitude of the same row in matrix A. Indeed, $u - \frac{1}{u} + \frac{W_{ij}-ua_{ij}}{\sum _{\gamma \in J^{+}_{i}-\{j\}}a_{i\gamma }} <0$ means $a_{ij} > {\sum _{\gamma \in J^{+}_{i}-\{j\}}a_{i\gamma }} +\frac{1}{u}(1-{\sum _{\gamma \in J^{-}_{i}-\{j\}}a_{i\gamma }})$. At most one such element can be in the row. Moreover, it can be controlled by choosing the parameter u.

2. In a similar manner, consider the mixed star-clique inequalities. Note that we can omit the plus sign in the y-related expressions $(u - \frac{1}{u} + \frac{1}{a_{ij}}(W_{il}-a_{il}))^{+}$. They are always positive with our assumption that no binary variable is fixed a priori (i.e. $W_{il} \le a_{il} ~\forall l \in J^{+}_{i}$) and necessity to satisfy the “cover” (12) with one value $\tilde{q}$ fixed at $u+1$ and all other $q \in [0, u- \frac{1}{u}]$. Indeed, (12) requires $\sum _{j \in J^{+}_{i}} a_{ij}\tilde{q}_{ij} \ge 1 -\sum _{j \in J^{-}_{i}} a_{ij} + u \sum _{j \in J^{+}_{i}} a_{ij}$. Suppose that $\tilde{q}_{il_1}=u+1, ~ \tilde{q}_{il_2}=0$ (for a future contradiction), and the best choice for all other $\tilde{q}=u- \frac{1}{u}$. We have $(u- \frac{1}{u})\sum _{j \in J^{+}_{i}-\{l_1,~l_2\}} a_{ij} + (u+1) a_{il_1} \ge 1 - \sum _{j \in J^{-}_{i}} a_{ij} + u \sum _{j \in J^{+}_{i}} a_{ij}$. So, $a_{il_1} \ge 1 -\sum _{j \in J^{-}_{i}} a_{ij} + u a_{il_2} + \frac{1}{u}\sum _{j \in J^{+}_{i}-\{l_1,~l_2\}} a_{ij} \ge 1 -\sum _{j \in J^{-}_{i}} a_{ij} + u W_{il_2} + \frac{1}{u}\sum _{j \in J^{+}_{i}-\{l_1,~l_2\}} a_{ij} = 1 -\sum _{j \in J^{-}_{i}} a_{ij} + u (1 -\sum _{j \in J^{-}_{i}} a_{ij}) + u \sum _{j \in J^{+}_{i}-\{l_2\}} a_{ij} +\frac{1}{u}\sum _{j \in J^{+}_{i}-\{l_1,~l_2\}} a_{ij}$. Thus, $(1-u)a_{il_1} \ge (u+1)(1 -\sum _{j \in J^{-}_{i}} a_{ij})+ (u+\frac{1}{u})\sum _{j \in J^{+}_{i}-\{l_1,~l_2\}} a_{ij}$ with a contradiction because $u>1$ and the left hand side is negative, but the right hand side is positive.

After weakening, the mixed star-clique inequalities can be written in the form:

$$\begin{aligned}&max\left( \frac{u^2}{u-1}, ~u+\frac{W_{ij}}{a_{ij}}\right) s_{ij} + min\left( -\frac{1}{u-1}, ~1-\frac{W_{ij}}{a_{ij}}\right) (1-y_{ij}) \\&\quad + \sum _{l \in J^{+}_{i}-\{j\}} \left( \left( u - \frac{1}{u} + \frac{1}{a_{ij}}(W_{il}-ua_{il})\right) s_{il} + (u -1) \frac{a_{il}}{a_{ij}} (1-y_{il})\right) - \tilde{q}_{ij} \le 0 \end{aligned}$$

After multiplying each term by $a_{ij}$ and dropping for brevity the index i, denote (different for each i) $\varPhi = 1-\sum _{\gamma \in J^{-}}a_{\gamma }+ \frac{1}{u}\sum _{\gamma \in J^{+}}a_{\gamma }$. This number is connected with the previous notations as follows: $\varPhi = \varPsi -(u-\frac{1}{u})\sum _{\gamma \in J^{+}}a_{\gamma }$ and $\varPhi = W_{\gamma }+ \frac{1}{u}a_{\gamma }$. The $y_l$-term becomes $(u-1)\sum _{\gamma }a_{\gamma }(1-z_{\gamma })(1-y^*_{\gamma })$; the $y_j$-term is $\sum _{\gamma }min(\frac{-a_{\gamma }}{u-1},\frac{u+1}{u}a_{\gamma }-\varPhi )z_{\gamma }(1-y^*_{\gamma })$; the $s_j$-term is $\sum _{\gamma }s^*_{\gamma }z_{\gamma }max(\frac{u^2}{u-1}a_{\gamma },(u-\frac{1}{u})a_{\gamma }+\varPhi )$; the $s_l$-term can be viewed initially as quadratic with respect to z: $(\varPhi +\sum _{\gamma }(u-\frac{1}{u})a_{\gamma }z_{\gamma })\sum _{\gamma }s^*_{\gamma }(1-z_{\gamma })+ (u+\frac{1}{u})\sum _{\gamma }a_{\gamma }s^*_{\gamma }(z_{\gamma }-1)$, but it can be simplified into a linear one combining with $s_j$-term and using the facts that $z_{\gamma _1}z_{\gamma _2}=0$ and $z^2_\gamma =z_\gamma$ in the following way:

$$\begin{aligned}&\left( \varPhi +{\sum }_{\gamma }\left( u-\frac{1}{u}\right) a_{\gamma }z_{\gamma }\right) {\sum }_{\gamma }s^*_{\gamma }(1-z_{\gamma })+ \left( u+\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }s^*_{\gamma }(z_{\gamma }-1) \\&\quad + {\sum }_{\gamma }s^*_{\gamma }z_{\gamma }max\left( \frac{u^2}{u-1}a_{\gamma }, \left( u-\frac{1}{u}\right) a_{\gamma }+\varPhi \right) =\varPhi {\sum }_{\gamma }s^*_{\gamma } - \varPhi {\sum }_{\gamma }s^*_{\gamma }z_{\gamma }\\&\quad +{\sum }_{\gamma }\left( u-\frac{1}{u}\right) a_{\gamma }z_{\gamma }{\sum }_{\gamma }s^*_{\gamma } - {\sum }_{\gamma }\left( u-\frac{1}{u}\right) a_{\gamma }z_{\gamma }{\sum }_{\gamma }s^*_{\gamma }z_{\gamma }+ \left( u+\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }s^*_{\gamma }z_{\gamma }\\&\quad -\left( u+\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }s^*_{\gamma }+ {\sum }_{\gamma }s^*_{\gamma }z_{\gamma }max \left( \frac{u^2}{u-1}a_{\gamma },\left( u-\frac{1}{u}\right) a_{\gamma }+\varPhi \right) \\&\quad = \varPhi {\sum }_{\gamma }s^*_{\gamma } - \varPhi {\sum }_{\gamma }s^*_{\gamma }z_{\gamma }+{\sum }_{\gamma } \left( u-\frac{1}{u}\right) a_{\gamma }z_{\gamma }{\sum }_{\gamma }s^*_{\gamma }\\&\quad - {\sum }_{\gamma } \left( u-\frac{1}{u}\right) a_{\gamma }s^*_{\gamma }z_{\gamma }+ \left( u+\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }s^*_{\gamma }z_{\gamma }\\&\quad -\left( u+\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }s^*_{\gamma }+ {\sum }_{\gamma }s^*_{\gamma }z_{\gamma }max\left( \frac{u^2}{u-1}a_{\gamma },(u-\frac{1}{u})a_{\gamma }+\varPhi \right) = \varPhi {\sum }_{\gamma }s^*_{\gamma } \\&\quad - \varPhi {\sum }_{\gamma }s^*_{\gamma }z_{\gamma }+{\sum }_{\gamma }\left( u-\frac{1}{u}\right) a_{\gamma }z_{\gamma } {\sum }_{\gamma }s^*_{\gamma }\\&\quad + \frac{2}{u}{\sum }_{\gamma }a_{\gamma }s^*_{\gamma }z_{\gamma } -\left( u+\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }s^*_{\gamma }\\&\quad + {\sum }_{\gamma }s^*_{\gamma }z_{\gamma }max\left( \frac{u^2}{u-1}a_{\gamma }, \left( u-\frac{1}{u}\right) a_{\gamma }+\varPhi \right) \\&\quad = \left( {\sum }_{\gamma }s^*_{\gamma }\right) \left( \varPhi +\left( u-\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }\right) \\&\quad + {\sum }_{\gamma }s^*_{\gamma }z_{\gamma }\left( -\varPhi +\frac{2}{u}a_{\gamma }+ max\left( \frac{u^2}{u-1}a_{\gamma },\left( u-\frac{1}{u}\right) a_{\gamma }+\varPhi \right) \right) - \left( u+\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }s^*_{\gamma }\\&\quad = \left( {\sum }_{\gamma }s^*_{\gamma }\right) \left( \varPhi +\left( u-\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }\right) + {\sum }_{\gamma }s^*_{\gamma }z_{\gamma } max\left( a_{\gamma }\left( \frac{u^2}{u-1}\right. \right. \\&\quad \left. \left. +\frac{2}{u}\right) -\varPhi , \left( u+\frac{1}{u}\right) a_{\gamma }\right) - \left( u+\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }s^*_{\gamma }. \end{aligned}$$

The separation objective function (subject to the unit vector z) becomes

$max_z (\sum _{\gamma }s^*_{\gamma }) (\varPhi +(u-\frac{1}{u})\sum _{\gamma }a_{\gamma }z_{\gamma })+ \sum _{\gamma }s^*_{\gamma }z_{\gamma } max(a_{\gamma }(\frac{u^2}{u-1}+\frac{2}{u})-\varPhi , (u+\frac{1}{u})a_{\gamma })- (u+\frac{1}{u})\sum _{\gamma }a_{\gamma }s^*_{\gamma }+ (u-1)\sum _{\gamma }a_{\gamma }(1-z_{\gamma })(1-y^*_{\gamma })+ \sum _{\gamma }min(\frac{-a_{\gamma }}{u-1},\frac{u+1}{u}a_{\gamma }-\varPhi )z_{\gamma }(1-y^*_{\gamma })- \sum _{\gamma }a_{\gamma }\tilde{q}^*_{\gamma }z_{\gamma }$. The z-coefficient with the maximal value gives j in the partition with the condition that an optimal objective value is positive. So, we are looking for index $j^*$, if any, which is related to the maximal value ($j^* = argmax_{j}$) among $s^*_jmax(a_{j}(\frac{u^2}{u-1}+\frac{2}{u})-\varPhi , (u+\frac{1}{u})a_{j})+(1-y^*_j)(-(u-1)a_j+ min(\frac{-a_j}{u-1},\frac{u+1}{u}a_{j}-\varPhi ))- a_j\tilde{q}^*_j +(u-\frac{1}{u})a_j\sum _{\gamma }s^*_{\gamma }$ with the condition that this value $> \sum _{\gamma }((a_{\gamma }(u+\frac{1}{u})-\varPhi ) s^*_{\gamma }-(u-1)a_{\gamma }(1-y^*_{\gamma }))$.

Appendix C. Separation problem for MIP2

We apply the same separation scheme for MIP2 as that for MIP1.

1. Consider a maximal cut violation as a separation problem for the weighted complementary inequalities. Taking into account that $C_{ij}= \frac{1}{u}-B_{ij}(J-1)$ and after multiplying all terms by $\sum _{\gamma \in J^{+}_{i}-\{j\}}a_{i\gamma }$, they can be written in the form:

$$\begin{aligned}&(1-y_{ij})\left( a_{ij}-\tilde{W}_{ij}+\left( 1-\frac{2}{u}\right) \sum _{\gamma \in J^{+}_{i}-\{j\}}a_{i\gamma }\right) \\&\quad + \left( \sum _{l \in J^{+}_{i}-\{j\}}y_{il}-J+1\right) \left( -\frac{1}{u}a_{ij}+\tilde{W}_{ij} -\left( 1-\frac{2}{u}\right) \right. \\&\quad \left. \sum _{\gamma \in J^{+}_{i}-\{j\}}a_{i\gamma }\right) +\sum _{l \in J^{+}_{i}-\{j\}} a_{il}\tilde{q}_{il} \le \left( u+1-\frac{1}{u}\right) \sum _{\gamma \in J^{+}_{i}-\{j\}}a_{i\gamma } \end{aligned}$$

Dropping for brevity index i, denote (different for each i) $\tilde{\varPsi } = 1-(1-\frac{1}{u})\sum _{\gamma \in J^{+}}a_{\gamma }$. Introducing the characteristic vector z (the unit vector for indicating variable j) for yet to be determined partition (j, all other $l \ne j$), we show that the separation problem for weighted complementary inequalities is polynomial time solvable. Indeed, having an LP solution with $(y^*,\tilde{q}^*)$, the $y_j$-term $(1-y_{j})(\frac{1}{u}a_{j}-\tilde{\varPsi })$ becomes $\sum _{\gamma }(1-y^*_{\gamma })(\frac{1}{u}a_{\gamma }-\tilde{\varPsi })z_{\gamma }$; the $\tilde{q}$-term is $\sum _{\gamma }a_{\gamma }\tilde{q}^*_{\gamma }(1-z_{\gamma })$; the right hand side is $(u+1-\frac{1}{u})\sum _{\gamma }a_{\gamma }(1-z_{\gamma })$; the $y_l$-term $(\sum y_{l}-J+1)(\tilde{\varPsi }+(1-\frac{2}{u})a_{j})$ can be viewed initially as quadratic with respect to z: $(\sum _{\gamma }y^*_{\gamma }(1-z_{\gamma })-J+1)(\tilde{\varPsi }+(1-\frac{2}{u})\sum _{\gamma }a_{\gamma }z_{\gamma })$, but it can be simplified into a linear one combining with $y_j$-term and using the facts that $z_{\gamma _1}z_{\gamma _2}=0$, $\sum _{\gamma }z_\gamma =1$, and $z^2_\gamma =z_\gamma$ in the following way:

$$\begin{aligned}&\left( \tilde{\varPsi }+\left( 1-\frac{2}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }\right) \left( {\sum }_{\gamma }y^*_{\gamma }(1-z_{\gamma })-J+1\right) + {\sum }_{\gamma }(1-y^*_{\gamma })\left( \frac{1}{u}a_{\gamma }-\tilde{\varPsi }\right) z_{\gamma }\\&\qquad =\tilde{\varPsi }{\sum }_{\gamma }y^*_{\gamma }- \tilde{\varPsi }{\sum }_{\gamma }y^*_{\gamma }z_\gamma + \tilde{\varPsi }(1-J)\\&\qquad + \left( 1-\frac{2}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }{\sum }_{\gamma }y^*_{\gamma }- \left( 1-\frac{2}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }{\sum }_{\gamma }y^*_{\gamma }z_{\gamma } \\&\qquad + \left( 1-\frac{2}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }(1-J)+ \frac{1}{u}{\sum }_{\gamma }a_{\gamma }z_{\gamma }-\tilde{\varPsi }{\sum }_{\gamma }z_{\gamma }- \frac{1}{u}{\sum }_{\gamma }y^*_{\gamma }a_{\gamma }z_{\gamma }\\&\qquad + \tilde{\varPsi }{\sum }_{\gamma }y^*_{\gamma }z_\gamma = \left( \tilde{\varPsi }+\left( 1-\frac{2}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }\right) {\sum }_{\gamma }y^*_{\gamma }-\tilde{\varPsi }J- \left( 1-\frac{2}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }y^*_{\gamma }\\&\qquad + \left( 1-\frac{2}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }(1-J)+ \frac{1}{u}{\sum }_{\gamma }a_{\gamma }z_{\gamma }- \frac{1}{u}{\sum }_{\gamma }y^*_{\gamma }a_{\gamma }z_{\gamma }\\&\qquad = \left( \tilde{\varPsi }+\left( 1-\frac{2}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }\right) \\&\qquad {\sum }_{\gamma }y^*_{\gamma }-\tilde{\varPsi }J- \left( 1-\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }y^*_{\gamma }+ \left( 1-\frac{1}{u}+\left( \frac{2}{u}-1\right) J\right) \\&\qquad {\sum }_{\gamma }a_{\gamma }z_{\gamma }. \end{aligned}$$

The separation objective function (subject to the unit vector z) becomes

$max_z (\sum _{\gamma }y^*_{\gamma })(\tilde{\varPsi }+(1-\frac{2}{u})\sum _{\gamma }a_{\gamma }z_{\gamma })-\tilde{\varPsi }J- (1-\frac{1}{u})\sum _{\gamma }a_{\gamma }z_{\gamma }y^*_{\gamma }+ (1-\frac{1}{u}+(\frac{2}{u}-1)J)\sum _{\gamma }a_{\gamma }z_{\gamma }+ \sum _{\gamma }a_{\gamma }\tilde{q}^*_{\gamma }(1-z_{\gamma })- (u+1-\frac{1}{u})\sum _{\gamma }a_{\gamma }(1-z_{\gamma })$. The z-coefficient with the maximal value gives j in the partition with the condition that an optimal objective value is positive. So, we are looking for index $j^*$, if any, which is related to the maximal value ($j^* = argmax_{j}$) among $a_j(\sum _{\gamma }y^*_{\gamma }(1-\frac{2}{u})-(1-\frac{1}{u})y^*_j- \tilde{q}^*_j+ (\frac{2}{u}-1)(J-1)+u+1)$ with the condition that this value $> \sum _{\gamma }(a_{\gamma }(u+1-\frac{1}{u}-\tilde{q}^*_{\gamma })-\tilde{\varPsi } y^*_{\gamma })+ \tilde{\varPsi }J$.

2. Similarly, the mixed star-clique inequalities and incomplete linking inequalities are polynomial time separable. After weakening, multiplying each term by $a_{ij}$ and dropping for brevity index i, denote (different for each i) $\tilde{\varPhi } = 1- \frac{1}{u}\sum _{\gamma \in J^{+}}a_{\gamma }$. This number is connected with the previous notation as follows: $\tilde{\varPhi } = W_{\gamma }- \frac{1}{u}a_{\gamma }$.

2a. The mixed star-clique inequalities can be written in the form:

$$\begin{aligned} \frac{1}{u}a_{j}y_{j}+ \sum _{l \ne j}\left( \left( 1-\frac{2}{u}\right) a_j - \tilde{\varPhi } + \left( 1-\frac{1}{u}\right) a_l\right) (1-y_l) + a_j\tilde{q}_{j} \le (u+1)a_j \end{aligned}$$

After introducing the characteristic vector z, the $y_j$-term becomes $\frac{1}{u}\sum _{\gamma }a_{\gamma }y^*_{\gamma }z_{\gamma }$; the $\tilde{q}$-term is $\sum _{\gamma }a_{\gamma }\tilde{q}^*_{\gamma }z_{\gamma }$; the right hand side is $(u+1)\sum _{\gamma }a_{\gamma }z_{\gamma }$; the $y_l$-term can be viewed initially as quadratic with respect to z: $(-\tilde{\varPhi }+(1-\frac{2}{u})\sum _{\gamma }a_{\gamma }z_{\gamma })\sum _{\gamma }(1-y^*_{\gamma })(1-z_{\gamma })+ (1-\frac{1}{u})\sum _{\gamma }a_{\gamma }(1-y^*_{\gamma })(1-z_{\gamma })$, but it can be simplified into a linear one combining with $y_j$-term and using the facts that $z_{\gamma _1}z_{\gamma _2}=0$, $\sum _{\gamma }z_\gamma =1$, and $z^2_\gamma =z_\gamma$ in the following way:

$$\begin{aligned}&\left( -\tilde{\varPhi }+\left( 1-\frac{2}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }\right) {\sum }_{\gamma }\left( 1-y^*_{\gamma }\right) + \tilde{\varPhi }{\sum }_{\gamma }(1-y^*_{\gamma })z_{\gamma }\\&\qquad - \left( 1-\frac{2}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }{\sum }_{\gamma }(1-y^*_{\gamma })z_{\gamma }+ \left( 1-\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }\left( 1-y^*_{\gamma }\right) \\&\qquad - \left( 1-\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }(1-y^*_{\gamma })z_{\gamma }+ \frac{1}{u}{\sum }_{\gamma }a_{\gamma }y^*_{\gamma }z_{\gamma }= \left( -\tilde{\varPhi }+\left( 1-\frac{2}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }\right) \\&\qquad {\sum }_{\gamma }\left( 1-y^*_{\gamma }\right) + \tilde{\varPhi }{\sum }_{\gamma }z_{\gamma }- \tilde{\varPhi }{\sum }_{\gamma }y^*_{\gamma }z_{\gamma }\\&\qquad - \left( 1-\frac{2}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }\left( 1-y^*_{\gamma }\right) + \left( 1-\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }\left( 1-y^*_{\gamma }\right) \\&\qquad - \left( 1-\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }\left( 1-y^*_{\gamma }\right) z_{\gamma }+ \frac{1}{u}{\sum }_{\gamma }a_{\gamma }y^*_{\gamma }z_{\gamma }\\&\qquad = \left( -\tilde{\varPhi }+\left( 1-\frac{2}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }\right) {\sum }_{\gamma }\left( 1-y^*_{\gamma }\right) \\&\qquad + \tilde{\varPhi }- \tilde{\varPhi }{\sum }_{\gamma }y^*_{\gamma }z_{\gamma }- \left( 2-\frac{3}{u}\right) {\sum }_{\gamma }a_{\gamma }z_{\gamma }\\&\qquad + \left( 2-\frac{3}{u}\right) {\sum }_{\gamma }a_{\gamma }y^*_{\gamma }z_{\gamma }+ \left( 1-\frac{1}{u}\right) {\sum }_{\gamma }a_{\gamma }(1-y^*_{\gamma })\\&\qquad + \frac{1}{u}{\sum }_{\gamma }a_{\gamma }y^*_{\gamma }z_{\gamma }. \end{aligned}$$

The separation objective function (subject to the unit vector z) becomes

$max_z (-\tilde{\varPhi } + (1-\frac{2}{u}) \sum _{\gamma }a_{\gamma }z_{\gamma }) \sum _{\gamma }(1-y^*_{\gamma })+ \tilde{\varPhi }- \tilde{\varPhi }\sum _{\gamma }y^*_{\gamma }z_{\gamma }- (3+u-\frac{3}{u})\sum _{\gamma }a_{\gamma }z_{\gamma }+ 2(1-\frac{1}{u})\sum _{\gamma }a_{\gamma }y^*_{\gamma }z_{\gamma }+ (1-\frac{1}{u})\sum _{\gamma }a_{\gamma }(1-y^*_{\gamma })+ \sum _{\gamma }a_{\gamma }\tilde{q}^*_{\gamma }z_{\gamma }$. The z-coefficient with the maximal value gives j in the partition with the condition that an optimal objective value is positive. So, we are looking for index $j^*$, if any, which is related to the maximal value ($j^* = argmax_{j}$) among $a_j(1-\frac{2}{u})\sum _{\gamma }(1-y^*_{\gamma })-\tilde{\varPhi }y^*_j- (3+u-\frac{3}{u})a_j+ 2(1-\frac{1}{u})a_{j}y^*_{j} +a_j\tilde{q}^*_j$ with the condition that this value $> \tilde{\varPhi }\sum _{\gamma }(1-y^*_{\gamma })- \tilde{\varPhi }- (1-\frac{1}{u})\sum _{\gamma }a_{\gamma }(1-y^*_{\gamma })$.

2b. The incomplete linking inequalities can be written in the form:

$$\begin{aligned} \left( \left( 1-\frac{1}{u}\right) a_{j}-\tilde{\varPhi }\right) y_{j}+ \left( 1-\frac{1}{u}\right) \sum _{l \ne j}a_l(1-y_l) + a_j\tilde{q}_{j} \le (u+1)a_j \end{aligned}$$

After introducing the characteristic vector z, the $y_j$-term becomes $\sum _{\gamma }z_{\gamma }((1-\frac{1}{u})a_{\gamma }-\tilde{\varPhi })y^*_{\gamma }$; the $\tilde{q}$-term is $\sum _{\gamma }a_{\gamma }\tilde{q}^*_{\gamma }z_{\gamma }$; the right hand side is $(u+1)\sum _{\gamma }a_{\gamma }z_{\gamma }$; the $y_l$-term becomes $(1-\frac{1}{u})\sum _{\gamma }a_{\gamma }(1-y^*_{\gamma }) (1-z_{\gamma })$.

Combining all terms together for the separation objective function (subject to the unit vector z), we have $\sum _{\gamma }z_{\gamma }((1-\frac{1}{u})a_{\gamma }-\tilde{\varPhi })y^*_{\gamma }+ (1-\frac{1}{u})\sum _{\gamma }a_{\gamma }(1-y^*_{\gamma }) (1-z_{\gamma })+ \sum _{\gamma }a_{\gamma }\tilde{q}^*_{\gamma }z_{\gamma }-(u+1)\sum _{\gamma }a_{\gamma }z_{\gamma }= \sum _{\gamma }z_{\gamma }((1-\frac{1}{u})a_{\gamma }-\tilde{\varPhi })y^*_{\gamma }+ (1-\frac{1}{u})\sum _{\gamma }a_{\gamma }- (1-\frac{1}{u})\sum _{\gamma }a_{\gamma }z_{\gamma }- (1-\frac{1}{u})\sum _{\gamma }a_{\gamma }y^*_{\gamma }+ (1-\frac{1}{u})\sum _{\gamma }a_{\gamma }y^*_{\gamma }z_{\gamma }+ \sum _{\gamma }a_{\gamma }\tilde{q}^*_{\gamma }z_{\gamma }- (u+1)\sum _{\gamma }a_{\gamma }z_{\gamma }= \sum _{\gamma }z_{\gamma }(2(1-\frac{1}{u})a_{\gamma }-\tilde{\varPhi })y^*_{\gamma }+ (1-\frac{1}{u})\sum _{\gamma }a_{\gamma }- (u+2-\frac{1}{u})\sum _{\gamma }a_{\gamma }z_{\gamma }- (1-\frac{1}{u})\sum _{\gamma }a_{\gamma }y^*_{\gamma }+ \sum _{\gamma }a_{\gamma }\tilde{q}^*_{\gamma }z_{\gamma }$. The z-coefficient with the maximal value gives j in the partition with the condition that an optimal objective value is positive. So, we are looking for index $j^*$, if any, which is related to the maximal value ($j^* = argmax_{j}$) among $(2(1-\frac{1}{u})a_{j}-\tilde{\varPhi })y^*_{j}- (u+2-\frac{1}{u})a_{j}+ a_{j}\tilde{q}^*_{j}$ with the condition that this value $> -(1-\frac{1}{u})\sum _{\gamma }a_{\gamma }+ (1-\frac{1}{u})\sum _{\gamma }a_{\gamma }y^*_{\gamma }$.

It is known that finding a maximal or minimal element in an array of J variables requires $J-1$ comparisons, and for finding two largest or smallest entries it is sufficient to take $J + \lceil log_2J \rceil - 2$ comparisons (see, for example, Chapter 9 in Cormen et al. [3]).

Replication of results

We provide all numerical data and parameters ($a_{ij}$, u, $I_{+}$, $I_{-}$, and J) in the computational section explicitly. So, the results of all examples can easily be reproduced.