Introduction

In recent years, with the development of hydraulic fracturing technologies, multistage hydraulic fracturing has gradually become the key technology for tight gas reservoir development. After hydraulic fracturing, large fracture networks are generated by connection of the induced high conductivity fractures with the existing natural fractures. The hydraulic fractured tight gas reservoir not only has high preliminary production, but also is more favorable for long-term stable production (Gale et al. 2007; Zeng et al. 2013; Pang et al. 2016; Yang et al. 2017; Ren et al. 2018). The flow in formation involves the coupling of fracture, horizontal well, and reservoir. Due to the complexity of fractures in tight gas reservoir, it is difficult to accurately describe the fractured horizontal well and reservoir flow mechanism (Ozkan 2011; Xu et al. 2015; Paul et al. 2016; He et al. 2017).

Medeiros et al. (2008) discussed the performance and productivity of fractured horizontal wells in heterogeneous, tight gas formations. They found that if hydraulic fracturing affected stress distribution to create or rejuvenate natural fractures around the well, the productivity of the system would be significantly increased. Based on the fluid properties, Wang et al. (2014) established the formation characteristics and development measures of Chang 8 formation tight oil reservoir in Ordos Basin through the methods of reservoir engineering and numerical simulation. Hyeonseog and Seil (2015) carried out various rate transient analysis techniques (flowing material balance, type curve matching, square root time plot, and analytical model analysis) to estimate ultimate recovery (EUR), stimulated reservoir volume (SRV) and relevant information. Egberts and peters (2015) developed a simulation tool to calculate the production performance of a radial well, which provided an efficient way to assess the production potential of a stimulated well for many different well designs. Jimenez et al. (2017) proposed a method based on the gas production analysis technique in conjunction with pressure transient analysis for diagnostics specialized of linear flow, which improves the confidence in reserve estimations, specifically in early time production. Qin et al. (2018) allowed each hydraulic fracture of multi-fractured horizontal well consists of two individual segments with their own properties and presented a novel approach to evaluate effective fracture properties.

To date, there is few analytical or semi-analytical models to calculate the production of fractured horizontal well in tight gas reservoir, and the coupling model of conventional gas reservoir and fractured horizontal well is not suitable for tight gas reservoir (Larsen and Hegre 1994; Lian et al. 2010; Zhao et al. 2014; Ma et al. 2015; Jia et al. 2016; Wang et al. 2017; Tang et al. 2018). Therefore, it is necessary to further study the coupled flow of tight gas reservoir and fractured horizontal well to clarify the flow characteristics near the fracture and wellbore. In this paper, by using the Green function and Newman product principle, the coupling model of the anisotropy tight gas reservoir and fractured horizontal well is established, and a solving method is also given. Taking a tight gas reservoir data as an example, the sensitivity parameters of the model are analyzed.

Flow model of fractured horizontal well

Assumptions

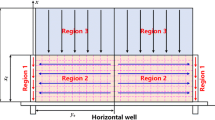
The schematic diagram of tight gas model is shown in Fig. 1, and the main assumptions are as follows:

Fig. 1
figure 1

Horizontal well model in tight gas reservoir with non-flow boundaries

Full size image

(1) There is a tight gas reservoir, with no-flow boundaries in all directions. The length, width, and height of the drainage volume are a, b, and h, respectively.

(2) The permeability of the matrix is so low that it can be ignored. The permeability of natural fractures in x, y, and z directions is expressed as Kx, Ky, and Kz. The equivalent porosity of natural fractures and matrix is φ.

(3) A horizontal well placed in the tight gas reservoir with radius rw and length L. The well is placed from (x0, y1, z0) to (x0, y2, z0) and is parallel to the y-axis.

(4) The horizontal segment has a number of Nf segments of hydraulic fractures. The fractures are perpendicular to the wellbore, equidistant distribution and pass through the thickness of the whole gas reservoir, the fractures have a length xf, and width yd.

(5) Initially, at time t = 0, the pressure is uniform throughout the reservoir and is equal to p0.

Single fracture flow model

Defining the pseudo-pressure function as follows (Li et al. 2009):

$$\psi = \int \rho dp + C$$
(1)

By using instantaneous point sink function (Green function) and Neumann product principle (Gringarten and Ramey 1973), the pressure drops at any location (\(0 \le x \le a,\;0 \le y \le b,\;0 \le z \le h\)) of a single fracture vertical to wellbore at any time (t > 0) can be expressed as follows:

$$\psi_{0} - \psi (x,y,z,t) = \frac{{\tilde{q}}}{{abh\phi C_{t} }}\int\limits_{0}^{t} {(S_{x} \cdot S_{y} \cdot S_{z} )} d\tau$$
(2)
$$S_{x} (x,x_{0} ,\tau ) = \frac{{x_{f} }}{a}\left[ {1 + \frac{4a}{{\pi x_{f} }}\sum\limits_{n = 1}^{ + \infty } \frac{1}{n} \exp ( - \frac{{n^{2} \pi^{2} \eta_{x} t}}{{a^{2} }})\sin \frac{{n\pi x_{f} }}{2a}\cos \frac{{n\pi x_{0} }}{a}\cos \frac{n\pi x}{a}} \right]$$
(3)
$$S_{y} (y,y_{0} ,\tau ) = \frac{{y_{d} }}{b}\left[ {1 + \frac{4b}{{\pi y_{d} }}\sum\limits_{n = 1}^{ + \infty } \frac{1}{n} \exp ( - \frac{{n^{2} \pi^{2} \eta_{y} t}}{{b^{2} }})\sin \frac{{n\pi y_{d} }}{2b}\cos \frac{{n\pi y_{0} }}{b}\cos \frac{n\pi y}{b}} \right]$$
(4)
$$S_{z} (z,z_{0} ,\tau ) = 1 + \frac{4}{\pi }\sum\limits_{n = 1}^{ + \infty } \frac{1}{n} \exp ( - \frac{{n^{2} \pi^{2} \eta_{z} t}}{{h^{2} }})\sin \frac{n\pi }{2}\cos \frac{{n\pi z_{0} }}{h}\cos \frac{n\pi z}{h}$$
(5)

where \(\eta_{x} = \frac{{K_{x} }}{{\phi \mu C_{t} }},\eta_{x} = \frac{{K_{y} }}{{\phi \mu C_{t} }},\eta_{x} = \frac{{K_{z} }}{{\phi \mu C_{t} }}\) are transmissibility factors in x, y, and z directions, respectively; \(\tilde{q}\) is the mass flow rate under pseudo-pressure; S1, S2 and S3 are instantaneous point sink functions located at (x0, y0, z0).

According to equations of state of the actual gas, the mass flow rate of the fractured horizontal well is transformed into volumetric flow rate under the standard condition. It can be written as:

$$\psi_{0} - \psi = \frac{{\rho_{sc} }}{{2p_{sc} }}\frac{{T_{sc} Z_{sc} }}{TZ}\left( {p_{0}^{2} - p_{{}}^{2} } \right)$$
(6)

According to Eq. (1) and (5), the following equation is obtained:

$$p_{0}^{2} - p^{2} = \frac{{2qp_{sc} ZT}}{{\phi C_{t} Z_{sc} T_{sc} }}\int\limits_{0}^{t} {(S_{x} \cdot S_{y} \cdot S_{z} )} d\tau$$
(7)

where q is the volumetric flow rate under the standard condition, m3/s; psc is the pressure under the standard condition; T is the reservoir temperature, K; Tsc is the temperature under the standard condition, K.

In Eq. (7), after integration to instantaneous point sink functions, time t is the only unknown variable, so the total pressure drop from the fracture is given by (Penmatcha and Aziz 1998):

$$\Delta p^{2} = (p_{0}^{2} - p^{2} ) = q \cdot F(t)$$
(8)

Coupling model of fractured horizontal well and tight gas reservoir

In order to establish the fractured horizontal well and tight gas coupling model, we firstly divide the horizontal well into Nf segments, in which segment 1 is assumed to lie closest to the heel of the well, while segment Nf lies closest to the toe of the well. There is a fracture in the middle of each segment, and the fractures are uniformly distributed. There is no fluid inflow in the horizontal section, so the total production of horizontal well is equal to the flow rates all of fractures.

As shown in Fig. 2, there are 6·Nf unknown variables in the model, respectively:

  1. (1)

    Tight gas reservoir nodal pressure: \(p_{1} ,p_{2} ,...,p_{{N_{f} }}\);

  2. (2)

    Right nodal pressure hydraulic fracture: \(p_{{R_{f} ,1}} ,p_{{R_{f} ,2}} ,...,p_{{R_{f} ,N_{f} }}\);

  3. (3)

    Left node pressure of hydraulic fracture: \(p_{{L_{f} ,1}} ,p_{{L_{f} ,2}} ,...,p_{{L_{f} ,N_{f} }}\);

  4. (4)

    Central nodal pressure of hydraulic fracture: \(p_{f,1} ,p_{f,2} ,...,p_{{f,N_{f} }}\);

  5. (5)

    Flow rate from the tight gas reservoir node: \(q_{1} ,q_{2} ,...,q_{{N_{f} }}\);

  6. (6)

    Flow rate between hydraulic fractures: \(q_{f,1} ,q_{f,2} ,...,q_{{f,N_{f} }}\).

Fig. 2
figure 2

Fractured horizontal well and tight gas coupling model

Full size image

Mass conservation equations

According to mass conservation principles, the wellbore nodal flow rate equals to the tight gas flow rate from the reservoir and fractures. For simplicity, we assume that the tight gas density is constant, and we can get Nf equations:

$$q_{f,j} = \sum\limits_{i = j}^{{N_{f} }} {q_{i} } \quad j = 1,2,...,N_{f}$$
(9)

Relationship between nodal pressures of hydraulic fracture

Because of gas flow from fracture to wellbore, the pressure at the right side of the fracture is not equal to the pressure at the left side. Therefore, we adopt the average pressure of two sides of fracture as the central nodal pressure of the hydraulic fracture (Lian et al. 2011):

$$p_{f,i} = \frac{{p_{{L_{f} ,i}} + p_{{R_{f} ,i}} }}{2}\quad i = 1,2,...,N_{f}$$
(10)

Pressure drop in hydraulic fracture

Assume the ith central fracture nodal coordinate is \((x_{0} ,y_{i} ,z_{0} )\), the tight gas reservoir nodal coordinate is (\(\overline{{x_{i} }} ,\overline{{y_{i} }} ,\overline{{z_{i} }}\) ), if the fracture is anisotropic, the following equations can be used to transform the fracture into isotropic:

$$\theta = a\tan \left( {\sqrt {\frac{{3.0\sqrt {K_{z} } + \sqrt {K_{x} } }}{{3.0\sqrt {K_{x} } + \sqrt {K_{z} } }}} } \right)$$
(11)

The flow of tight gas into the wellbore presents an elliptical flow, the major axis is a = xf, and minor axis is b = h. In order to facilitate the simulation, the elliptic flow is transformed into a circular flow with equal radius, as shown in Fig. 3. The seepage radius can be calculated:

$$\pi r_{f}^{2} = \frac{1}{4}\pi ab = \frac{1}{4}\pi x_{f} h$$
(12)
$$r_{f} = \frac{1}{2}\sqrt {x_{f} h}$$
(13)
Fig. 3
figure 3

Radial flow conversion in fracture

Full size image

Because the cross-sectional area of fractures is larger than that of wellbore, the flow from the edge of the fractures to the wellbore can be considered as radial flow ignoring gravity. The area has thickness yd, permeability K0, well skin factor S, flow radius rf, and boundary pressure pi.

In the nth time step, the flow equation can be written as follows:

$$p_{i}^{2} (n\Delta t) - p_{f,i}^{2} (n\Delta t) = \frac{{P_{sc} ZT}}{{Z_{sc} T_{sc} }}\frac{{q_{i} (n\Delta t)\mu }}{{\pi dK_{0} }}\ln \left[ {\frac{{r_{f} }}{{2r_{w} }} + S} \right]\quad i = 1,2,...,N_{f}$$
(14)

Continuity equations

The time step is assumed as \(\Delta t\), and \(t=n\Delta t\), the spatial and temporal superposition of pressure drop caused by all Nf fracture production is calculated, and we can get the continuity equation of the ith fracture at the nth time step:

$$p_{0}^{2} - p_{i}^{2} (n\Delta t) = \sum\limits_{j = 1}^{s} {\left( {q_{j} (\Delta t)F_{ij} (n\Delta t) + \sum\limits_{k = 2}^{n} {(q_{j} (k\Delta t) - q_{j} ((k - 1)\Delta t))F_{ij} ((n - k + 1)\Delta t)} } \right)} \quad i = 1,2,...,N_{f}$$
(15)

where Fij is the effect of fracture j on fracture i.

Constraint equations

If the flow rate constraint is used, the equation would be:

$$\sum\limits_{i = 1}^{{N_{s} }} {q_{i} } - Q_{\max } = 0$$
(16)

where Qmax is the maximum flow rate.

If the bottom-hole pressure constraint is used, the equation would be:

$$P_{w,1} - P_{\min ,wf} = 0$$
(17)

where pmin,wf is the minimum bottom-hole pressure.

Pipe flow model in horizontal well

Figure 4 shows skeleton diagram of the gas flow model in fracture and horizontal well. In the horizontal well section between two fractures, there is no gas flow from reservoir to wellbore, and the frictional pressure drop mainly exists in the pipe. Because of gas flow from fracture to wellbore, there is acceleration of pressure drop.

Fig. 4
figure 4

Flow model in a horizontal wellbore

Full size image

Wellbore friction pressure drop

The frictional pressure drop of horizontal well section between two fractures could be written as follows:

$$P_{{Rf,j - 1}}^{2} - P_{{Lf,j}}^{2} = 1.0\times10^{{ - 6}} f_{j} \frac{{M_{{air}} \gamma _{g} }}{R}\frac{{16p_{{sc}}^{2} q_{{f,j}}^{2} TZ}}{{\Pi ^{2} D^{5} T_{{sc}}^{2} }}\Delta l_{j} \quad j = 2,3,...,N_{f}$$
(18)

where Mair is molecular mass of air, g/mol; γg is the relative density of gas, dimensionless; \(\Delta l_{j}\) is the length of the jth section; \(f_{j}\) is the friction factor of the jth section; R is ideal gas constant, 8.314 J⋅mol−1⋅K−1; D is the diameter of wellbore, m.

The friction factor f is different in laminar and turbulent flow. The key parameter to distinguish turbulent flow and laminar flow is Reynolds number, which is expressed as follows:

$$P_{Rf,j - 1}^{2} - P_{Lf,j}^{2} = 1.0\times10^{ - 6} f_{j} \frac{{M_{air} \gamma_{g} }}{R}\frac{{16p_{sc}^{2} q_{f,j}^{2} TZ}}{{\pi^{2} D^{5} T_{sc}^{2} }}\Delta l_{j} \quad j = 2,3,...,N_{f}$$
(19)

According to the classification criteria, the state of fluid is laminar flow when the Reynolds number is less than 2100, the state of fluid is turbulent flow when the Reynolds number is greater than 2100. The Reynolds number is related to the seepage velocity, and the flow velocity depends on the flow rate.

According to the study of Ouyang et al. (1996), the formulas for calculating friction factor in laminar and turbulent flow are as follows:

$$f = \frac{64}{{N_{{\text{Re}}} }}\quad N_{{\text{Re}}} \le 2100$$
(20)
$$\frac{1}{\sqrt f } = 1.14 - 2\lg \left( {\frac{\tau }{D} + \frac{21.25}{{N_{{\text{Re}}}^{0.9} }}} \right)\quad N_{Re} \ge 2100$$
(21)

Acceleration pressure drop

As shown in Fig. 4, it is assumed that the flow velocity at the right and left sides of the fracture i is v1,i and v2,i, respectively:

$$v_{1,j} = \frac{{p_{sc} q_{f,i + 1} TZ}}{{p\pi r_{w}^{2} T_{sc} }}$$
(22)
$$v_{2,j} = \frac{{p_{sc} q_{f,j} TZ}}{{p\pi r_{w}^{2} T_{sc} }}$$
(23)

The acceleration pressure drop is:

$$\Delta p_{acc} = 1.0\times10^{ - 6} \left( {\rho_{2,i} v_{2,i}^{2} - \rho_{1,i} v_{1,i}^{2} } \right)$$
(24)

Substituting (23) and (24) into (25), the following equation can be obtained:

$$p_{Lf,i}^{2} - p_{Rf,i}^{2} = 1.0 \times 10^{ - 6} \left[ {\frac{{M_{air} \gamma_{g} }}{R}\frac{{32p_{sc}^{2} TZ}}{{\pi^{2} D^{4} T_{sc}^{2} }}\left( {2q_{i} q_{f,i + 1} + q_{f,i + 1}^{2} } \right)} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,...,N_{f}$$
(25)

Solving method

For the established model above, there are 6·Nf unknown variables and 6·Nf equations (Eqs.9, 10, 14, 15, 16 or 17, 18, 25), the model can be solved. In order to simplify the solution process, the flow from the tight gas reservoir node and central nodal pressure of hydraulic fracture is eliminated by using Eqs. 9 and 10.

After simplification, there are 4·Nf unknown quantities, which are shown, respectively, as follows:

(1) Tight gas reservoir nodal pressure: \(p_{1} ,p_{2} ,...,p_{{N_{f} }}\);

(2) Right nodal pressure hydraulic fracture: \(p_{{R_{f} ,1}} ,p_{{R_{f} ,2}} ,...,p_{{R_{f} ,N_{f} }}\);

(3) Left node pressure of hydraulic fracture: \(p_{{L_{f} ,1}} ,p_{{L_{f} ,2}} ,...,p_{{L_{f} ,N_{f} }}\);

(4) Flow rate between hydraulic fractures: \(q_{f,1} ,q_{f,2} ,...,q_{{f,N_{f} }}\)。

According to eqs. (14), (15), (18), (25) plus constraint equation (Eq. (16) or (17)) to form the following equation group:

$$\left\{ \begin{gathered} p_{i}^{2} (n\Delta t) - p_{f,i}^{2} (n\Delta t) = \frac{{P_{sc} ZT}}{{Z_{sc} T_{sc} }}\frac{{q_{i} (n\Delta t)\mu }}{{\pi dK_{0} }}\ln \left[ {\frac{r_{f}}{{2r_{w} }} + S} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,...,N_{f} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ p_{0}^{2} - p_{i}^{2} (n\Delta t) = \sum\limits_{j = 1}^{s} {\left( \begin{gathered} q_{j} (\Delta t)F_{ij} (n\Delta t) + \sum\limits_{k = 2}^{n} {(q_{j} (k\Delta t)} \hfill \\ - q_{j} ((k - 1)\Delta t))F_{ij} ((n - k + 1)\Delta t) \hfill \\ \end{gathered} \right)} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,...,N_{f} \hfill \\ p_{Rf,j - 1}^{2} - p_{Lf,j}^{2} = 1.0 \times 10^{ - 6} \left( {f_{j} \frac{{M_{air} \gamma_{g} }}{R}\frac{{16p_{sc}^{2} q_{f,j + 1}^{2} TZ}}{{\pi^{2} D^{5} T_{sc}^{2} }}\Delta l_{j} } \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} j = 2,...,N_{f} \hfill \\ p_{Lf,i}^{2} - p_{Rf,i}^{2} = 1.0 \times 10^{ - 6} \left[ {\frac{{M_{air} \gamma_{g} }}{R}\frac{{32p_{sc}^{2} TZ}}{{\pi^{2} D^{4} T_{sc}^{2} }}\left( {2q_{i} q_{f,i + 1} + q_{f,i + 1}^{2} } \right)} \right]{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2,...,N_{f} \hfill \\ \sum\limits_{i = 1}^{{n_{s} }} {q_{i} } - Q_{\max } = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} or{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} p_{w,1} - p_{\min ,wf} = 0 \hfill \\ \end{gathered} \right.$$
(26)

The equation group (26) has nonlinear characteristics, so the Newton iterative method is used to solve them. At the right hand, only flow rates are unknown variables, we can build Jacobi matrix by calculating the coefficients. The initial values of a set of solutions are given firstly, and then, cyclic iteration is performed. When the error between certain iteration and the next iteration is less than 10–4, the iteration is stopped and the results are adopted. We use VC ++ to compile the procedure, and the calculation flow diagram is shown in Fig. 5. By adjusting the input parameters and convergence criteria, the calculation process can be converged.

Fig. 5
figure 5

Calculation flow diagram

Full size image

Calculation examples and sensitive parameter analysis

Taking the tight gas reservoir data as an example, the sensitive parameters of the model are analyzed by using the proposed model. The parameters of tight gas reservoir and fractured horizontal well are shown in Table 1.

Table 1 Parameters of tight gas reservoir and horizontal well
Full size table

Production analysis of fractured horizontal well

Figure 6 shows the relationship between horizontal well production rate and time with different number of hydraulic fractures. The minimum bottom-hole pressure is set as 5 MPa. Because of the low permeability of tight gas reservoir, when the fractured horizontal well begins to produce, only the reservoir near the fracture flows. At this time, there is no interference between the fractures, and the flow state is the early unsteady state. In Fig. 6, it can be seen that the production of fractured horizontal wells is proportional to the number of fractures. As time increases, the pressure wave gradually propagates outward. When the pressure waves of adjacent fractures overlap, interference occurs between the fractures, and the production of each fracture begins to decrease. The more fractures there is, the stronger is the interference, and the larger is the decline of single fracture production.

Fig. 6
figure 6

Flow rate of fractured horizontal well vs. time

Full size image

When the pressure wave propagates to the outer boundary, the flow enters pseudo-steady state, and the flow rate is gradually stabilized. Because tight gas reservoirs are mostly in the pseudo-steady state during the development process, there is an optimized number of fractures. In this example, when the number of fractures is larger than 10, the production of the pseudo-steady state changes little, so it is enough to use 10 fractures.

Figures 7 and 8 show the relationship between the total flow rate and the length of the fractured horizontal well at 0.01 and 10 days, respectively. It can be seen that in the unsteady state, with the increasing wellbore length, the total flow rate of horizontal well decreases. Because there is no interference between the fractures in the unsteady state, when the fracture parameters are the same, the total flow is affected by the wellbore friction. With the increase in the horizontal well length, the friction pressure drops of the wellbore increases, leading to the lower production of the toe and heel fractures, which results in the decrease of the total flow rate. This is obviously different from the pseudo-steady state. In the pseudo-steady state, with the increase of the horizontal well length, the interference between fractures decreases, and the horizontal well production increases gradually.

Fig.7
figure 7

Relationship between horizontal well length and flow rate in the unsteady state

Full size image
Fig.8
figure 8

Relationship between horizontal well length and flow rate in the pseudo-steady state

Full size image

Flow rate and pressure distribution along the fractured horizontal well

Figure 9 shows the distribution of fracture flow rate in unsteady state (0.01 days) and pseudo-steady state (10 days). The number of hydraulic fractures is 10, and the maximum flow rate of fractured horizontal wells is 100000 m3/d. It can be seen from Fig. 9 that in the unsteady stage, the flow rate of the heel fracture is obviously larger than that of the other position, and the closer the toe is, the smaller the flow rate of the fracture is. Because of the existence of wellbore pressure drop, the pressure drop of the heel is greater than that of the toe, resulting in uneven distribution of flow. In the pseudo-steady state, the pressure in the wellbore is balanced, and the flow distribution becomes relatively balanced.

Fig.9
figure 9

Flow rate comparison between non-steady state and pseudo-steady state of fractures

Full size image

Figure 10 shows the pressure drop of the heel of the horizontal well variation with time, considering the impact of the friction and acceleration. The impact of the friction on pressure drop is small, but the influence of the acceleration on pressure drop is even smaller. Only when the length of the horizontal well is very short and the flow rate is very high, the effect of acceleration would be great. Figure 10 also shows that the unsteady flow phase lasts about 7 days, and then the pseudo-steady state begins, and the pressure difference between infinite conductivity model and finite conductivity model in the pseudo-steady state is about 35 kPa. According to the research results of this study, it is concluded that the impact of friction on low permeability oil and gas reservoirs is much smaller than that of high permeability reservoirs.

Fig.10
figure 10

Effect of wellbore frictional and fracture acceleration pressure drops

Full size image

Figure 11 shows the pressure distribution along the wellbore of fractured horizontal wells with 10 fractures at 10 days. The pressure drops at the heel and toe are 1,044 kPa and 997 kPa, respectively. Therefore, the pressure drop in the wellbore is about 46 kPa. Under this pressure drop, the fluid in the wellbore can flow from the toe to the heel. In the wellbore, the flow rate at the heel is larger than that at the toe, and the friction and acceleration pressure drop are larger too.

Fig.11
figure 11

Pressure along the well at 10 days in pseudo-steady state

Full size image

Influence of anisotropy on tight gas reservoir

Figure 12 shows the influence of the changing Kx, Ky and Kz on wellbore flow distribution. Due to the thin thickness of tight gas reservoir, and the fracture runs through the thickness of the gas reservoir, the fluid is mainly from X and Y directions, and Kx and Ky have great influence on well flow rate distribution. X direction is parallel to the fracture, with the increase of Kx, the interference between the fractures decreases and the flow rate distribution is more balanced. Y direction is perpendicular to the fracture. When Ky is small, the energy is mainly obtained from X direction, and the distribution of flow rate is relatively balanced. When Ky becomes large, the interference between fractures is stronger, more gas flows into the wellbore from fractures at both ends, and the “U” shape distribution of the wellbore flow is more significant.

Fig.12
figure 12

Effect of permeability anisotropy on the distribution of flow rate

Full size image

Conclusions

The flow mechanics of fractured horizontal well in anisotropic tight gas reservoir is studied in detail. The flow characteristics under both unsteady state and pseudo-steady state are also analyzed. The distribution of pressure and flow rate along the wellbore are compared. The main conclusions are as follows.

(1) The flow pattern of the horizontal well is unstable during the early stage of production, and the decline rate of production is large. But after a short time, the decline rate will become stable, and the flow enters the pseudo-steady state. In the early stage of unsteady flow, the flow rate is proportional to the number of the fractures. In the pseudo-steady state, the fractures are interfered and the flow rate of each fracture is reduced.

(2) When the number of fractures is constant, the total flow rate of horizontal well decreases slightly with the increasing wellbore length in the unsteady stage, while the total flow rate of horizontal well increases slightly with the increasing wellbore length in the pseudo-steady stage.

(3) The influence of anisotropy on tight gas reservoir is studied, with the increasing Kx, the interference between the fractures decreases, and the flow distribution is more balanced. When Ky becomes larger, the interference between fractures are stronger, and the “U” shape distribution of the wellbore flow is more significant.