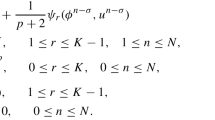Abstract
We consider a family of variational time discretizations that are generalizations of discontinuous Galerkin (dG) and continuous Galerkin–Petrov (cGP) methods. The family is characterized by two parameters. One describes the polynomial ansatz order while the other one is associated with the global smoothness that is ensured by higher order collocation conditions at both ends of the subintervals. Applied to Dahlquist’s stability problem, the presented methods provide the same stability properties as dG or cGP methods. Provided that suitable quadrature rules of Hermite type are used to evaluate the integrals in the variational conditions, the variational time discretization methods are connected to special collocation methods. For this case, we present error estimates, numerical experiments, and a computationally cheap postprocessing that allows to increase both the accuracy and the global smoothness by one order.
Similar content being viewed by others
1 Introduction
This paper deals with a family of variational time discretizations that generalizes discontinuous Galerkin (dG) and continuous Galerkin–Petrov (cGP) methods. For its definition, in addition to variational equations, collocation conditions are used. The considered family is characterized by two parameters: the first one is the local polynomial ansatz order and the second parameter is related to the global smoothness of the numerical solution that is ensured by higher order collocation conditions at both ends of the subintervals. Note that a related approach, which also combines variational conditions and a certain number of other conditions, was considered in [12]. Since the test space for each family member is allowed to be discontinuous with respect to the time mesh, the discrete problem can be solved in a time-marching process, i.e., by a sequence of local problems on the subintervals.
With respect to their behavior when applied to Dahlquist’s stability problem, the family of variational time discretizations can be divided into two groups. While the first group shares its stability properties with the cGP method, the second group behaves like the dG method. These observations, presented in [10], imply that the considered methods are at least A-stable. This suggests that the whole family of methods is appropriate to handle stiff problems such as those arising, for example, from semi-discretizations of parabolic partial differential equations in space.
Various aspects of dG and cGP time discretization methods have already been studied in the literature. The a priori and a posteriori analysis of dG methods is well understood, see e.g. [15, 28, Chap. 12], and references therein. Moreover, dG methods are known to be strongly A-stable. Under certain conditions, dG schemes can preserve various versions of dissipativity, see [17] for details. For the cGP method a rigorous a priori and a posteriori error analysis in the context of ordinary differential equations is presented in [16]. Optimal error estimates and superconvergence results for the fully discretized heat equation, based on a finite element method in space and a cGP method in time, are given in [7]. For further investigations of the cGP method we refer to [27]. Therein, using energy arguments, also the A-stability of cGP methods of arbitrary order is shown. In addition, cGP methods provide an energy decreasing property for the gradient flow equation of an energy functional, see [27]. As shown in [18], the cGP schemes are also able to preserve certain energy properties such as Lyapunov functionals.
Postprocessing techniques for dG and cGP methods applied to systems of ordinary differential equations have been given in [24]. They allow to obtain an improved convergence by one order in integral-based norms. Furthermore, the postprocessed dG solution is continuous while the postprocessing of cGP solutions leads to continuously differentiable trajectories. This paper transfers and generalizes the postprocessing ideas to the whole family of variational time discretizations. The postprocessing technique applied to a numerical solution increases the global smoothness by one differentiation order and the local polynomial degree by one. This results in improved accuracy in integral-based norms, see [1, 3, 4, 6, 8, 14, 24]. Note that the postprocessing comes with almost no computational costs since just jumps of derivatives of the discrete solution are needed. Beside the improvements of accuracy and global smoothness, the postprocessing can be used to drive an efficient adaptive time step control, see [2].
As mentioned above, the variational time discretizations analyzed in this paper use collocation conditions at the end points of the time subintervals. We describe connections between pure collocation methods and numerically integrated variational time discretizations provided a suitable quadrature rule of Hermite type is applied. Based on these connections the existence and uniqueness of discrete solutions are shown. Moreover, optimal error estimates follow. The connection between collocation methods and postprocessed numerically integrated discontinuous Galerkin methods using the right-sided Gauss–Radau quadrature formulas was considered in [29]. Moreover, connections between collocation methods and the numerically integrated continuous Galerkin–Petrov methods (using interpolatory quadrature formulas with as many quadrature points as number of independent variational conditions) were shown in [21, 22].
For affine linear systems of ordinary differential equations with time-independent coefficients, an interpolation cascade is presented that allows multiple postprocessing steps leading to very accurate solutions with low computational costs. Moreover, temporal derivatives of discrete solutions to affine linear systems with time-independent coefficients form also solutions of variational time discretization schemes. This relation was used to prove optimal error estimates of stabilized finite element methods for linear first-order partial differential equations [14] and for parabolic wave equations [6, 8].
The paper is organized as follows. In Sect. 2 some notation and the family of variational time discretizations are introduced. The general postprocessing technique is considered in Sect. 3. The connection between collocation methods and numerically integrated variational time discretizations is given in Sect. 4. This connection is exploited to provide results on the existence of unique solutions and to obtain error estimates. Section 5 is devoted to affine linear ODE systems for which an interpolation cascade that enables multiple postprocessing steps is presented. Moreover, properties of derivatives of solutions to variational time discretization methods are discussed. Numerical experiments supporting the theoretical results are presented in Sect. 6.
2 Notation and formulation of the methods
We consider the initial value problem
where \(M \in {\mathbb {R}}^{d\times d}\) is a regular matrix and F, sufficiently smooth, satisfies a Lipschitz-condition with respect to the second variable. Furthermore, let \(I=(t_0,t_0+T]\) be an arbitrary but fixed time interval with positive length T. The value \(u_0\) at \(t=t_0\) is called the initial value in the following.
If the ODE system (2.1) originates from a finite element semi-discretization in space of a parabolic partial differential equation then M is the mass matrix. Since in this context the computation of \(M^{-1}\) is costly, usually a linear system with M is solved instead. By the explicit occurrence of M we can investigate where this is necessary.
To describe the vector-valued case (\(d>1\)) in an easy way, let \((\cdot ,\cdot )\) be the standard inner product and \(\Vert \cdot \Vert \) the Euclidean norm on \({\mathbb {R}}^d\), \(d\in {\mathbb {N}}\). Also, let \(e_j\) be the jth standard unit vector in \({\mathbb {R}}^d\), \(1 \le j \le d\).
For an arbitrary interval J and \(q\in {\mathbb {N}}\), the spaces of continuous and p times continuously differentiable \({\mathbb {R}}^q\)-valued functions on J are written as \(C(J,{\mathbb {R}}^q)\) and \(C^p(J,{\mathbb {R}}^q)\), respectively. Furthermore, the space of square-integrable \({\mathbb {R}}^q\)-valued functions is denoted by \(L^2(J,{\mathbb {R}}^q)\) or, for convenience, sometimes also by \(C^{-1}(J,{\mathbb {R}}^q)\). For \(s \in {\mathbb {N}}_0\) we write \(P_s(J, {\mathbb {R}}^q)\) for the space of \({\mathbb {R}}^q\)-valued polynomials on J of degree less than or equal to s. Further notation is introduced later at the beginning of the sections where it is needed.
In order to describe the methods, we need a time mesh. Therefore, the interval I is decomposed by
into N disjoint subintervals \(I_n := (t_{n-1},t_n]\), \(n = 1,\ldots , N\). Furthermore, we set
For any piecewise continuous function v we define by
the one-sided limits and the jump of v at \(t_n\). Moreover, standard notation for the floor function is used, i.e., for any real number x let \(\left\lfloor x \right\rfloor \) be the greatest integer less than or equal to x.
In this paper C denotes a generic constant independent of the time mesh parameter \(\tau \).
2.1 Local formulation
Let \(r, k \in {\mathbb {N}}_0\) with \(0 \le k \le r\). In order to numerically solve the initial value problem (2.1), we introduce the family of variational time discretization methods \({\mathbf {VTD}_{k}^{r}}\) with parameters r and k.
Using a standard time-marching strategy, the discrete solution is successively determined on \(I_n\), \(n=1,\ldots ,N\), by local problems of the form
Find \(U\in P_r(I_n,{\mathbb {R}}^d)\) such that
and
where \(U(t_0^-) = u_0\) and \(\delta _{i,j}\) denotes the Kronecker delta. Moreover, the integrator \({\mathscr {I}}_n\) represents either the integral over \(I_n\) or the application of a quadrature formula for approximate integration over \(I_n\). Details will be described later.
Note that the formulation can easily be extended to the case \(k = r+1\). Then the variational condition (2.2d) must formally hold for all \(\varphi \in P_{-1}(I_n,{\mathbb {R}}^d)\). This should be interpreted as “there is no variational condition”. Hence, only conditions at both ends of the interval \(I_n\) are used.
The method \({\mathbf {VTD}_{k}^{r}}\) can shortly be described by

The notation \(\mathrm {ODE}^{(i)}\) means that the discrete solution fulfills the ith derivative of the system of ordinary differential equations. Obviously, the reduction of the test space for \(k \ge 1\) is compensated by other conditions. For a somewhat related approach see [12, (3.3)].
Counting the number of conditions leads for \(k\ge 1\) to
while we have \(\dim P_{r} = r+1\) conditions if \(k = 0\). The number of degrees of freedom equals for all k to \(\dim P_r = r+1\). Hence, in any case the number of conditions coincides with the number of degrees of freedom.
Remark 2.1
The \({\mathbf {VTD}_{k}^{r}}\) framework generalizes two well-known types of variational time discretization methods. The method \({\mathbf {VTD}_{0}^{r}}\) is the discontinuous Galerkin method \(\mathrm {dG}(r)\) whereas the method \({\mathbf {VTD}_{1}^{r}}\) equates to the continuous Galerkin–Petrov method \(\mathrm {cGP}(r)\).
On closer considerations we see that methods \({\mathbf {VTD}_{k}^{r}}\) with even k are \(\mathrm {dG}\)-like since there are point conditions on the \(\left\lfloor \frac{k}{2} \right\rfloor \)th derivative of the discrete solution but this derivative might be discontinuous. The methods \({\mathbf {VTD}_{k}^{r}}\) with odd k are \(\mathrm {cGP}\)-like since there are point conditions up to the \(\left\lfloor \frac{k}{2} \right\rfloor \)th derivative of the discrete solution and this derivative is continuous. We have in detail
where we use and generalize the definitions and notation of [24]. Note that there is also another reason to name the methods this way. All methods with odd k share their A-stability with the cGP method while methods with even k are strongly A-stable as the dG method, for more details see Remark 5.3.
In order to obtain a fully computable discrete problem usually a quadrature formula \(Q_n\) is chosen as integrator, i.e., \({\mathscr {I}}_n= Q_n\). To indicate this choice, we simply write \(Q_n\)-\({\mathbf {VTD}_{k}^{r}}\). Moreover, we agree that integration over \(I_n\) is used if no quadrature rule is specified. We mostly use quadrature rules that are exact for polynomials of degree up to \(2r-k\). This ensures in the case of an affine linear right-hand side \(F(t,u) = f(t)-Au\) with time-independent A that all u depending terms in (2.2d) are integrated exactly.
The special structure of the method (2.2) motivates to use an associated interpolation operator that conserves derivatives at the end points of the interval up to a certain order. In detail, we define on the reference interval \([-1,1]\) the interpolation operator \({\widehat{{\mathcal {I}}}_{k}^{r}} : C^{\left\lfloor \frac{k}{2} \right\rfloor }([-1,1]) \rightarrow P_r([-1,1])\) that uses the interpolation points
Note that there is no point evaluation at the left end for \(k=0\). In any case, the number of interpolation conditions is
and, thus, coincides with the dimension of \(P_r\). The interpolation operator \({\widehat{{\mathcal {I}}}_{k}^{r}}\) is of Hermite-type and provides the standard error estimates for Hermite interpolation.
In addition, we define by
a quadrature rule on \([-1,1]\) that is in a natural way assigned to the method \({\mathbf {VTD}_{k}^{r}}\). The quadrature rules \({{\widehat{Q}}_{k}^{r}}\) are known in the literature as generalized Gauss–Radau and Gauss–Lobatto formulas, respectively, see e.g. [19, 23]. The weights of the quadrature rule \({{\widehat{Q}}_{k}^{r}}\) can be calculated by integrating the appropriate Hermite basis functions on \([-1,1]\). Finally, we obtain
The quadrature rule \({{\widehat{Q}}_{k}^{r}}\) is exact for polynomials up to degree \(2r-k\). It can be shown that all quadrature weights are different from zero, see [23]. More precisely, we have
so even the sign of the weights is known. Note that for \(k \ge 2\) not all weights are positive. Semi-explicit and recursive formulas for the weights of these methods can be found in [26].
Transferring the quadrature rule \({{\widehat{Q}}_{k}^{r}}\) and the interpolation operator \({\widehat{{\mathcal {I}}}_{k}^{r}}\) from \([-1,1]\) to the interval \(I_n\), we obtain \({Q_{k}^{r}}\) and \({{\mathcal {I}}_{k}^{r}}\) where we skip the interval \(I_n\) in the notation because this will be clear from the context. Hence, we have
where \(t_{n,i} = \frac{1}{2}\left( t_{n-1}+t_n+\tau _n {\hat{t}}_i\right) \in I_n\), \(i =1,\ldots ,r-k\). The factors \(\left( \tfrac{\tau _n}{2}\right) ^{\!i}\) originate from the chain rule.
Remark 2.2
The quadrature rule \({Q_{0}^{r}}\) is the well-known right-sided Gauss–Radau quadrature formula with \(r+1\) points that is typically used for the discontinuous Galerkin method \(\mathrm {dG}(r)\). \({Q_{1}^{r}}\) is the Gauss–Lobatto quadrature rule with \(r+1\) points that is often used together with the continuous Galerkin–Petrov method \(\mathrm {cGP}(r)\).
Remark 2.3
For \(1 \le k \le r\) the \({\mathbf {VTD}_{k}^{r}}\) method with exact integration could be analyzed also in a generalization of the unified framework of [5] as we shall show below, see (2.5). Note that the dG method (\(k=0\)) has already been fitted in this framework, cf. [5].
We define for \(k\ge 1\) a projection operator \({\mathcal {P}}_n : C^{\left\lfloor \frac{k}{2} \right\rfloor -1}({\overline{I}}_n,{\mathbb {R}}^d) \rightarrow P_{r-1}({\overline{I}}_n,{\mathbb {R}}^d)\) by
and
Then an equivalent formulation of (2.2) with \(1 \le k \le r\) and exact integration reads
Find \(U\in P_r(I_n,{\mathbb {R}}^d)\) with given \(U(t_{n-1})\in {\mathbb {R}}^d\) such that
where \(U(t_0) = u_0\).
Indeed, if U solves (2.2) then \(M U' \in P_{r-1}(I_n,{\mathbb {R}}^d)\) obviously satisfies all conditions of (2.3) with \(v= F\big (\cdot ,U(\cdot )\big )\). Since \({\mathcal {P}}_n v\) is uniquely defined we directly get (2.5).
Otherwise let U solve (2.5). Since there are polynomials on both sides, we can differentiate the equation by any order. With (2.4a) and (2.4b) we have
for \({\tilde{t}}=t_n^-\) and all \(i = 0, \ldots , \left\lfloor \frac{k}{2}\right\rfloor -1\) if \(k\ge 2\), as well as for \({\tilde{t}}=t_{n-1}^+\) and all \(i = 0, \ldots , \left\lfloor \frac{k-1}{2}\right\rfloor -1\) if \(k\ge 3\), respectively. Hence, the conditions (2.2b) and (2.2c) hold. Taking the inner product of (2.5) with an arbitrary \(\varphi \in P_{r-k}(I_n,{\mathbb {R}}^d)\) and integrating over \(I_n\) yield together with (2.4c)
which is (2.2d) with exact integration.
Note that certain numerically integrated versions of \({\mathbf {VTD}_{k}^{r}}\) can also be written in the form (2.5) if appropriate projections are applied.
2.2 Global formulation
For \(s \in {\mathbb {N}}_0\) we define the space \(Y_{s}\) of vector-valued piecewise polynomials of maximal degree s by
Studying the conditions (2.2a), (2.2b), and (2.2c) we see that the solution U of \({\mathscr {I}}_n\)-\({\mathbf {VTD}_{k}^{r}}\) is \(\left\lfloor \frac{k-1}{2} \right\rfloor \) times continuously differentiable on I if F is sufficiently smooth. Furthermore, the condition (2.2b) for \(U \in C^{\left\lfloor \frac{k-1}{2} \right\rfloor }(I)\) already implies (2.2c) for \(n \ge 2\). Consequently, the method could be reformulated as follows
Find \(U \in Y_{r} \cap C^{\left\lfloor \frac{k-1}{2} \right\rfloor }(I,{\mathbb {R}}^d)\) such that
for all \(n = 1, \ldots , N\), and
where \(U^{(i)}(t_0^-) = u^{(i)}(t_0)\), \(0 \le i \le \left\lfloor \frac{k}{2} \right\rfloor \), which includes the initial value \(u_0\) in the problem formulation. We agree on defining \(u^{(j)}(t_0)\) recursively using the differential equation, i.e.,
The term \(\frac{\mathrm {d}^{j-1}}{\mathrm {d}t^{j-1}} F\big (t,u(t)\big ) \big |_{t=t_0}\) depends only on \(u(t_0), \ldots , u^{(j-1)}(t_0)\) and can be calculated using some generalization of Faà di Bruno’s formula, see e.g. [13, 25]. If F is affine linear in u, i.e., \(F(t,u(t)) = f(t)-A(t)u(t)\), then we simply have
for \(j \ge 1\), by Leibniz’ rule for the \((j-1)\)th derivative.
Note that since the test space \(Y_{r-k}\) in (2.6c) allows discontinuities at the boundaries of subintervals, the problem can be decoupled by choosing test functions \(\varphi \) supported on a single time interval \(I_n\) only. Moreover, exploiting for \(k\ge 1\) that \(U \in C^{\left\lfloor \frac{k-1}{2} \right\rfloor }\) as well as (2.6a) and (2.6b), we also obtain (2.2a) and (2.2c). Therefore, the global problem (2.6) can be converted back into a sequence of local problems (2.2) in time on the different subintervals \(I_n\), \(n=1,\dots , N\).
3 Postprocessing
We present in this section a simple postprocessing that makes considerable use of the properties of the quadrature rule \({Q_{k}^{r}}\) associated to \({\mathbf {VTD}_{k}^{r}}\).
Theorem 3.1
(Postprocessing \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\) \(\leadsto \) \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\)) Let \(r, k \in {\mathbb {N}}_0\) with \(0 \le k \le r\) and suppose that \(U \in Y_{r}\) solves \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\). For every \(n = 1, \ldots , N\) set
where \(\vartheta _n\) vanishes in all \((r+1)\) quadrature points of \({Q_{k}^{r}}\) and satisfies \(\vartheta _n^{\left( \left\lfloor \frac{k}{2} \right\rfloor +1\right) }(t_n^-) = 1\) while the vector \(a_n \in {\mathbb {R}}^d\) is defined by
Moreover, let \({\widetilde{U}}(t_0^-) = U(t_0^-)\). Then \({\widetilde{U}} \in Y_{r+1}\) solves \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\).
Proof
We have to verify that \({\widetilde{U}}\) satisfies all conditions for \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\) where \({Q_{k}^{r}}\) is the quadrature rule associated to \({\mathbf {VTD}_{k}^{r}}\) which is exact for polynomials up to degree \(2r-k\).
First of all we show an identity needed later. The special form of \(\vartheta _n\), the exactness of \({Q_{k}^{r}}\), and integration by parts yield
Precisely, we used that both \(\vartheta _n' \varphi \) and \(\vartheta _n \varphi '\) are polynomials of maximal degree \(2r-k\) and that \(\vartheta _n\) vanishes in all quadrature points, especially in \(t_n^-\) and for \(k\ge 1\) also in \(t_{n-1}^+\).
For \(k \ge 1\) we have \(\vartheta _n(t_{n-1}^+) = \vartheta _n(t_n^-) = 0\). Therefore, the initial condition holds due to \({\widetilde{U}}(t_{n-1}^+) = U(t_{n-1}^+) = U(t_{n-1}^-) = {\widetilde{U}}(t_{n-1}^-)\). For \(k=0\) it is somewhat more complicated to prove \({\widetilde{U}}(t_{n-1}^+) = {\widetilde{U}}(t_{n-1}^-)\), for details see (iii) below. The remaining conditions can be verified as follows. \(\square \)
-
(i)
\({\hbox {Conditions at }t_n^-\hbox { for } 0 \le i \le \left\lfloor \tfrac{k+2}{2}\right\rfloor -2 = \left\lfloor \tfrac{k}{2}\right\rfloor -1:}\)
From the definitions of \(\widetilde{U}\) and U we obtain
$$\begin{aligned} M {\widetilde{U}}^{(i+1)}(t_n^-)= & {} M U^{(i+1)}(t_n^-) + M a_n \underbrace{\vartheta _n^{(i+1)}(t_n^-)}_{=0}\\= & {} \frac{\mathrm {d}^i}{\mathrm {d}t^i} F\big (t,U(t)\big ) \Big |_{t=t_n^-} = \frac{\mathrm {d}^i}{\mathrm {d}t^i} F\big (t,{\widetilde{U}}(t)\big ) \Big |_{t=t_n^-} \end{aligned}$$since the derivatives of U and \({\widetilde{U}}\) in \(t_n^-\) coincide up to order \(\left\lfloor \tfrac{k}{2} \right\rfloor \) due to the definition of \(\vartheta _n\).
-
(ii)
\({\hbox {Condition at }t_n^-\hbox { for }i = \left\lfloor \tfrac{k+2}{2}\right\rfloor -1 = \left\lfloor \tfrac{k}{2}\right\rfloor :}\)
Just like above we get, additionally using the definition of \(a_n\),
$$\begin{aligned}&M {\widetilde{U}}^{\left( \left\lfloor \frac{k}{2} \right\rfloor +1\right) }(t_n^-)= M U^{\left( \left\lfloor \frac{k}{2} \right\rfloor +1\right) }(t_n^-) + M a_n \underbrace{\vartheta _n^{\left( \left\lfloor \frac{k}{2} \right\rfloor +1\right) }(t_n^-)}_{=1} \\&\quad = M U^{\left( \left\lfloor \frac{k}{2} \right\rfloor +1\right) }(t_n^-) + \frac{\mathrm {d}^{\left\lfloor \frac{k}{2} \right\rfloor }}{\mathrm {d}t^{\left\lfloor \frac{k}{2} \right\rfloor }} F\big (t,U(t)\big ) \Big |_{t=t_n^-} - M U^{\left( \left\lfloor \frac{k}{2} \right\rfloor +1\right) }(t_n^-) \\&\quad = \frac{\mathrm {d}^{\left\lfloor \frac{k}{2} \right\rfloor }}{\mathrm {d}t^{\left\lfloor \frac{k}{2} \right\rfloor }} F\big (t,U(t)\big ) \Big |_{t=t_n^-} = \frac{\mathrm {d}^{\left\lfloor \frac{k}{2} \right\rfloor }}{\mathrm {d}t^{\left\lfloor \frac{k}{2} \right\rfloor }} F\big (t,{\widetilde{U}}(t)\big ) \Big |_{t=t_n^-}.\end{aligned}$$ -
(iii)
Variational condition:
We have to prove that \({Q_{k}^{r}}\big [(M {\widetilde{U}}',\varphi )\big ] = {Q_{k}^{r}}\big [(F(\cdot ,{\widetilde{U}}(\cdot )),\varphi )\big ]\) for all \(\varphi \in P_{(r+1)-(k+2)}(I_n,{\mathbb {R}}^d)\). Actually, we can even test with functions \(\varphi \in P_{r-k}(I_n,{\mathbb {R}}^d)\). We first study the case \(k \ge 1\). By the definitions of \({\widetilde{U}}\) and U, the identity (3.2), and the fact that U and \({\widetilde{U}}\) coincide at all quadrature points we have
$$\begin{aligned} {Q_{k}^{r}}\Big [\big (M {\widetilde{U}}',\varphi \big )\Big ]= & {} {Q_{k}^{r}}\Big [\big (M U',\varphi \big )\Big ] + {Q_{k}^{r}}\Big [\big (M a_n \vartheta _n',\varphi \big )\Big ] \\= & {} {Q_{k}^{r}}\Big [\big (F(\cdot ,U(\cdot )),\varphi \big )\Big ] + \underbrace{{Q_{k}^{r}}\Big [\vartheta _n' \big (M a_n,\varphi \big )\Big ]}_{ \begin{array}{c} =0, \text { since} \\ (M a_n,\varphi ) \in P_{r-k}(I_n,{\mathbb {R}}) \end{array}} \\= & {} {Q_{k}^{r}}\Big [\big (F(\cdot ,{\widetilde{U}}(\cdot )),\varphi \big )\Big ] \qquad \qquad \forall \varphi \in P_{r-k}(I_n,{\mathbb {R}}^d). \end{aligned}$$Now let \(k=0\). The same arguments as for \(k \ge 1\) yield for all \(\varphi \in P_{r}(I_n,{\mathbb {R}}^d)\)
$$\begin{aligned} {Q_{0}^{r}}\Big [\big (M {\widetilde{U}}',\varphi \big )\Big ]= & {} {Q_{0}^{r}}\Big [\big (F(\cdot ,{\widetilde{U}}(\cdot )),\varphi \big )\Big ] - \big (M \big [U\big ]_{n-1}, \varphi (t_{n-1}^+)\big )\\&- \vartheta _n(t_{n-1}^+) \big (M a_n,\varphi (t_{n-1}^+)\big ). \end{aligned}$$We study the last two terms. Using the definitions of the jump \(\big [U\big ]_{n-1}\) and of \({\widetilde{U}}\), we find
$$\begin{aligned} \big [U\big ]_{n-1} + a_n \vartheta _n(t_{n-1}^+) = {\widetilde{U}}(t_{n-1}^+) - U(t_{n-1}^-) = \big [{\widetilde{U}}\big ]_{n-1} \end{aligned}$$(3.3)where we also exploited that \(\vartheta _{n-1}(t_{n-1}^-)=0\). Hence, we have
$$\begin{aligned} {Q_{0}^{r}}\Big [\big (M {\widetilde{U}}',\varphi \big )\Big ] + \big (M \big [{\widetilde{U}}\big ]_{n-1}, \varphi (t_{n-1}^+)\big ) = {Q_{0}^{r}}\Big [\big (F(\cdot ,{\widetilde{U}}(\cdot )),\varphi \big )\Big ] \qquad \forall \varphi \in P_{r}(I_n,{\mathbb {R}}^d).\nonumber \\ \end{aligned}$$(3.4)Choosing the special test functions \(\varphi _j \in P_{r}(I_n,{\mathbb {R}}^d)\), \(j=1,\dots ,d\), that vanish in the r inner quadrature points of \({Q_{0}^{r}}\) and satisfy \(\varphi _j(t_{n-1}^+) = e_j\) as well as having in mind (ii), we find \(\big [{\widetilde{U}}\big ]_{n-1} = 0\) component by component. Thereby, at once we have proven the initial condition and verified the needed variational condition since now also the jump term in (3.4) can be dropped.
-
(iv)
\({\hbox {Conditions at }t_{n-1}^+\hbox { for } 0 \le i \le \left\lfloor \tfrac{k+2-1}{2}\right\rfloor -2 = \left\lfloor \tfrac{k-1}{2}\right\rfloor -1}\):
With an argumentation similar to that in (i) we gain
$$\begin{aligned} M {\widetilde{U}}^{(i+1)}(t_{n-1}^+)= & {} M U^{(i+1)}(t_{n-1}^+) + M a_n \underbrace{\vartheta _n^{(i+1)}(t_{n-1}^+)}_{=0} \\= & {} \frac{\mathrm {d}^i}{\mathrm {d}t^i} F\big (t,U(t)\big ) \Big |_{t=t_{n-1}^+} = \frac{\mathrm {d}^i}{\mathrm {d}t^i} F\big (t,{\widetilde{U}}(t)\big ) \Big |_{t=t_{n-1}^+}\!. \end{aligned}$$ -
(v)
\({\hbox {Condition at }t_{n-1}^+\hbox { for }i = \left\lfloor \tfrac{k+2-1}{2}\right\rfloor -1 = \left\lfloor \tfrac{k-1}{2}\right\rfloor \hbox { if }k \ge 1:}\)
It remains to prove that
$$\begin{aligned} M{\widetilde{U}}^{\left( \left\lfloor \frac{k-1}{2}\right\rfloor +1\right) }(t_{n-1}^+) = \frac{\mathrm {d}^{\left\lfloor \frac{k-1}{2} \right\rfloor }}{\mathrm {d}t^{\left\lfloor \frac{k-1}{2} \right\rfloor }} F\big (t,{\widetilde{U}}(t)\big ) \Big |_{t=t_{n-1}^+}. \end{aligned}$$We use the variational condition for \({\widetilde{U}}\) with specially chosen test functions \(\varphi _j \in P_{r-k}(I_n,{\mathbb {R}}^d)\), \(j=1,\dots ,d\), that vanish at all inner quadrature points of \({Q_{k}^{r}}\), i.e.,
$$\begin{aligned} \varphi _j(t_{n,i}) = 0,\quad i = 1,\ldots ,r-k, \qquad \qquad \text {and satisfy} \qquad \qquad \varphi _j(t_{n-1}^+) = e_j. \end{aligned}$$As shown in (iii) we have
$$\begin{aligned} {Q_{k}^{r}}\Big [\big (M {\widetilde{U}}',\varphi _j\big )\Big ] = {Q_{k}^{r}}\Big [\big (F(\cdot ,{\widetilde{U}}(\cdot )),\varphi _j\big )\Big ], \qquad j=1,\dots ,d, \end{aligned}$$since \(k\ge 1\). The special choices of \(\varphi _j\), the definition of the quadrature rule, and the already known identities from (i), (ii), and (iv) yield after a short calculation using Leibniz’ rule for the ith derivative that
$$\begin{aligned}&{Q_{k}^{r}}\Big [\big (M {\widetilde{U}}',\varphi _j\big )\Big ] = {Q_{k}^{r}}\Big [\big (F(\cdot ,{\widetilde{U}}(\cdot )),\varphi _j\big )\Big ], \quad j=1,\dots ,d, \\&\quad \Leftrightarrow w_{\left\lfloor \frac{k-1}{2}\right\rfloor }^L M {\widetilde{U}}^{\left( \left\lfloor \frac{k-1}{2}\right\rfloor +1\right) } (t_{n-1}^+) \cdot \underbrace{\varphi _j(t_{n-1}^+)}_{=e_j}\\&\qquad =w_{\left\lfloor \frac{k-1}{2}\right\rfloor }^L \frac{\mathrm {d}^{\left\lfloor \frac{k-1}{2} \right\rfloor }}{\mathrm {d}t^{\left\lfloor \frac{k-1}{2} \right\rfloor }} F\big (t,{\widetilde{U}}(t)\big ) \Big |_{t=t_{n-1}^+} \!\!\!\cdot \underbrace{\varphi _j(t_{n-1}^+)}_{=e_j}, \quad j=1,\dots ,d,\\&\quad \Leftrightarrow M {\widetilde{U}}^{\left( \left\lfloor \frac{k-1}{2}\right\rfloor +1\right) }(t_{n-1}^+) =\frac{\mathrm {d}^{\left\lfloor \frac{k-1}{2} \right\rfloor }}{\mathrm {d}t^{\left\lfloor \frac{k-1}{2} \right\rfloor }} F\big (t,{\widetilde{U}}(t)\big ) \Big |_{t=t_{n-1}^+}. \end{aligned}$$Note that we also used that \(w_{\left\lfloor \frac{k-1}{2}\right\rfloor }^L \ne 0\).
Collecting the above arguments, we see that \({\widetilde{U}}\) solves \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\). \(\square \)
From the definition (3.1), it seems that a linear system with the mass matrix M has to be solved in every time step in order to obtain the correction vector \(a_n\). However, the computational costs for calculating \(a_n\) can be reduced significantly as we show now.
Proposition 3.2
The correction vectors \(a_n \in {\mathbb {R}}^d\) defined in (3.1) for the postprocessing presented in Theorem 3.1 can alternatively be calculated by
and
where \(u^{\left( \left\lfloor \frac{k-1}{2} \right\rfloor +1\right) }(t_0)\) is defined in (2.7).
Proof
For \(k=0\), we get from (3.3) combined with \(\big [{\widetilde{U}}\big ]_{n-1}=0\), which was shown just below (3.4), that \(a_n = \frac{-1}{\vartheta _n(t_{n-1}^+)} \big [U\big ]_{n-1} = \frac{-1}{\vartheta _n(t_{n-1}^+)} \big (U(t_{n-1}^+)-{\widetilde{U}}(t_{n-1}^-)\big )\). Taking \({\widetilde{U}}(t_0^-) = U(t_0^-) = u(t_0) = u_0\) into account, we are done in this case.
Otherwise, for \(k \ge 1\), using the definition of the postprocessing and (v) of the proof of Theorem 3.1, we obtain that
Furthermore, we have \(\vartheta _n^{(i)}(t_{n-1}^+) = 0\) for \(i = 0, \ldots , \left\lfloor \frac{k-1}{2} \right\rfloor \) and therefore
Since F is sufficiently smooth and U is \(\left\lfloor \frac{k-1}{2} \right\rfloor \) times continuously differentiable we get for \(n > 1\)
where also \(\vartheta _{n-1}^{(i)}(t_{n-1}^-) = 0\) for \(i = 0, \ldots , \left\lfloor \frac{k}{2} \right\rfloor \) and (i) or (ii) of the proof of Theorem 3.1 were used. Altogether exploiting that M is regular an easy manipulation of the identities yields
A similar formula can also be established for \(n=1\). Since U satisfies (2.2c) and \(U(t_0) := u_0\), we obviously obtain, recalling the definition (2.7) of \(u^{(i)}(t_0)\), that
Therefore, we have in (3.5) for \(n=1\)
This results in
Hence, the alternative calculation provides the same correction vector. \(\square \)
Note that \(a_n\) can be calculated in this way without solving a system of linear equations. From the structure of \(a_n\) we see that the postprocessing can be interpreted as a correction of the jump in the lowest order derivative of the discrete solution that is not continuous by construction.
Since the division by \(\vartheta _n^{\left( \left\lfloor \frac{k-1}{2} \right\rfloor +1\right) }(t_{n-1}^+)\) changes the normalization of \(\vartheta _n\) only, we conclude the following.
Corollary 3.3
(Alternative postprocessing \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\) \(\leadsto \) \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\)) Let \(r, k \in {\mathbb {N}}_0\) with \(0 \le k \le r\) and suppose that \(U \in Y_{r}\) solves \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\). For every \(n = 1, \ldots , N\) set
where \({\tilde{\vartheta }}_n(t) = \vartheta _n(t)/\vartheta _n^{\left( \left\lfloor \frac{k-1}{2}\right\rfloor +1\right) }(t_{n-1}^+)\) with \(\vartheta _n\) from Theorem 3.1, i.e., \({\tilde{\vartheta }}_n\) vanishes in all \((r+1)\) quadrature points of \({Q_{k}^{r}}\) and satisfies \({\tilde{\vartheta }}_n^{\left( \left\lfloor \frac{k-1}{2} \right\rfloor +1\right) }(t_{n-1}^+) = 1\). The vector \({\tilde{a}}_n \in {\mathbb {R}}^d\) is defined by
where \(u^{\left( \left\lfloor \frac{k-1}{2} \right\rfloor +1\right) }(t_0)\) is given by (2.7). Moreover, let \({\widetilde{U}}(t_0^-) = U(t_0^-)\). Then \({\widetilde{U}} \in Y_{r+1}\) solves \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\).
A direct proof for the alternative postprocessing is given in [9, App. A].
4 Connections between numerically integrated variational time discretization methods and collocation methods
In this section we prove that the (local) solution of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{l}^{r+1}}\) with \(1 \le l \le k+2\) (which obviously includes \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\)) can be characterized as the solution of the (local) collocation problem with respect to the quadrature points of \({Q_{k}^{r}}\), i.e.,
Find \({\widetilde{U}} \in P_{r+1}(I_n,{\mathbb {R}}^d)\) with given \({\widetilde{U}}(t_{n-1}) \in {\mathbb {R}}^d\) such that
where \({\widetilde{U}}(t_0) = u_0\). Here, \(t_{n,i}\) are the zeros of the \((r-k)\)th Jacobi-polynomial with respect to the weight \((1+{\hat{t}})^{\left\lfloor \frac{k-1}{2}\right\rfloor +1} (1-{\hat{t}})^{\left\lfloor \frac{k}{2}\right\rfloor +1}\) transformed to the interval \([t_{n-1},t_n]\), see also (2.3).
Methods similar to (4.1) are known as collocation methods with multiple nodes, see e.g. [20, p. 275]. Unfortunately, existing results in the literature often neglect to study the unique solvability or conditions on F are not explicitly given. However, the connections mentioned above directly imply that all these methods are equivalent as we prove now.
Theorem 4.1
(Equivalence to collocation methods) Let \(r, k, l \in {\mathbb {N}}_0\), \(0 \le k \le r\), and \(1 \le l \le k+2\). Then \({\widetilde{U}} \in P_{r+1}(I_n,{\mathbb {R}}^d)\) solves \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{l}^{r+1}}\) if and only if \({\widetilde{U}}\) solves the collocation method (4.1) with respect to the quadrature points of \({Q_{k}^{r}}\).
Proof
For clarity and convenience, we recall the conditions of the \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{l}^{r+1}}\) method with \(0 \le k \le r\) and \(1 \le l \le k+2\).
Given \({\widetilde{U}}(t_{n-1}^-)\), find \({\widetilde{U}} \in P_{r+1}(I_n,{\mathbb {R}}^d)\) such that
First of all, assume that \({\widetilde{U}}\) solves (4.1). Then because of (4.1a) and (4.1b) obviously \({\widetilde{U}}\) satisfies the conditions (4.2a) and (4.2b) since \(l\le k+2\). In order to gain a better understanding of the numerically integrated variational condition, we have a look at its detailed definition. For \(\varphi \in C^{\left\lfloor \frac{k}{2} \right\rfloor }({\overline{I}}_n,{\mathbb {R}}^d)\) we have by definition of the quadrature rule
Applying Leibniz’ rule for the ith derivative, the right-hand side above can be rewritten as
Using the collocation conditions (4.1b), (4.1c), and (4.1a), we see that all three sums equal to 0. Hence, we obtain
which immediately gives (4.2c).
Now, we study the other direction and assume that \({\widetilde{U}}\) solves (4.2). In order to verify (4.1a), for example, we need to prove that (4.2a) also holds for \(i = \left\lfloor \tfrac{l}{2} \right\rfloor , \ldots , \left\lfloor \tfrac{k}{2} \right\rfloor \). For this purpose (in the case that \(\left\lfloor \tfrac{l}{2} \right\rfloor \le \left\lfloor \tfrac{k}{2} \right\rfloor \)) we use the special test function
with an arbitrary vector \(c \in {\mathbb {R}}^d\) where \(t_{n,i}\), \(i=1,\ldots , r-k\), denote the inner quadrature points of \({Q_{k}^{r}}\). Then (4.2c), the special construction of \(\psi \), (4.2a), and (4.2b) yield
Furthermore, we have that \(\psi ^{(i)}(t_{n-1}^+) = 0\) for \(i=0,\ldots , \left\lfloor \tfrac{k-1}{2} \right\rfloor - \left\lfloor \tfrac{l-1}{2}\right\rfloor \) and \(\psi ^{(i)}(t_{n}^-) = 0\) for \(i=0,\ldots , \left\lfloor \tfrac{k}{2} \right\rfloor - \left\lfloor \tfrac{l}{2} \right\rfloor - 1\). Thus, the above identity simplifies to
with \(i= \left\lfloor \frac{k}{2} \right\rfloor \) and \(j = \left\lfloor \frac{l}{2} \right\rfloor \). Since \(w_i^R \ne 0\), \(\psi ^{\left( \left\lfloor \frac{k}{2} \right\rfloor -\left\lfloor \frac{l}{2} \right\rfloor \right) }(t_{n}^-) \ne 0\), and the vector \(c \in {\mathbb {R}}^d\) can be chosen arbitrarily, it follows
Using the test functions
with an arbitrary vector \(c \in {\mathbb {R}}^d\) and \(j = 1, \ldots , \left\lfloor \tfrac{k}{2} \right\rfloor - \left\lfloor \tfrac{l}{2} \right\rfloor \) we iteratively also prove
A similar argument can also be used for the missing point conditions at \(t_{n-1}^+\). For the above implications we needed that the weights of \({Q_{k}^{r}}\) do not vanish which is known from [23].
It remains to verify (4.1c). Since we already know that \({\widetilde{U}}\) satisfies the collocation conditions (4.1a) and (4.1b), the variational condition (4.2c) reduces to
Recalling that \(w_j^I > 0\) for all \(1 \le j \le r-k\) and choosing in (4.4) test functions of the form
with an arbitrary vector \(c \in {\mathbb {R}}^d\), we get the collocation condition (4.1c) in \(t_{n,j}\).
Hence, the stated equivalence has been proven. \(\square \)
Summarizing, we have shown that a solution of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\) also solves \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{l}^{r+1}}\) with \(1 \le l \le k+2\) as well as a collocation with respect to the quadrature points of \({Q_{k}^{r}}\) and vice versa. Shortly, we have
Remark 4.2
Independent of the above findings, the connection between collocation methods and (postprocessed) numerically integrated discontinuous Galerkin methods (using the right-sided Gauss–Radau quadrature), i.e., Theorem 4.1 for \(k = 0 \le r\) and \(l=2\), was already observed in [29]. Moreover, connections between collocation methods and the numerically integrated continuous Galerkin–Petrov methods (using interpolatory quadrature formulas with as many quadrature points as number of independent variational conditions) were shown in [21, 22].
4.1 Error estimates for collocation methods
The method defined in (4.1) is a collocation method with multiple nodes as considered for example in [20, p. 275]. Thus, the usual error analysis for collocation methods also applies here, provided that F and u are sufficiently smooth. According to [20, p. 276], we have the following error estimate.
Proposition 4.3
The collocation method (4.1) possesses the same order \(2r-k+1\) as the underlying quadrature formula \({Q_{k}^{r}}\). Hence, it holds
where \({\widetilde{U}}\) and u denote the solutions of the collocation method (4.1) and the initial value problem (2.1), respectively.
Moreover, global error estimates can be shown by adapting techniques presented in [21, Theorem 2]. Together with [20, p. 276, pp. 212–214], we obtain the following.
Proposition 4.4
Let \({\widetilde{U}}\) denote the solution of the collocation method (4.1) and u the exact solution of (2.1). Then we have
and
where the derivatives are understood in an interval-wise sense.
The term \(2r-k+1\) inside the minimum is due to the fact that the convergence order of these collocation methods is limited by the accuracy of the underlying quadrature formula \({Q_{k}^{r}}\) that is exactly \(2r-k+1\). Note that the limitation is active for \(r=k\) only.
4.2 Reversed postprocessing
In Sect. 3 we studied a postprocessing for \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\). We have seen that starting from a solution U of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\) we can easily construct a solution \({\widetilde{U}}\) of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\). This already implies uniqueness of U provided that solutions of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\) or (4.1) are unique. Indeed, if \(U^1\) and \(U^2\) solve \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\) and their postprocessed solutions are identical, then by construction of the postprocessing \(U^1\) and \(U^2\) coincide in the \((r+1)\) quadrature points of \({Q_{k}^{r}}\). Thus, since both are polynomials of degree r, it follows \(U^1 \equiv U^2\).
We now ask whether or not this postprocessing step can be reversed for \(0 \le k \le r\). Then the solvability of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\) follows provided that \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\) or (4.1) has a solution.
Proposition 4.5
(Reversed postprocessing) Let \(r, k \in {\mathbb {N}}_0\), \(0 \le k \le r\), and suppose that \({\widetilde{U}} \in Y_{r+1}\) solves \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\). Then \({{\mathcal {I}}_{k}^{r}} {\widetilde{U}} \in Y_{r}\) solves \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\).
Proof
Let \({\widetilde{U}} \in P_{r+1}(I_n,{\mathbb {R}}^d)\) solve \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\). We shall prove that then \({{\mathcal {I}}_{k}^{r}} {\widetilde{U}} \in P_{r}(I_n,{\mathbb {R}}^d)\) is a solution of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\). Since \({{\mathcal {I}}_{k}^{r}}\) conserves the derivatives up to order \(\left\lfloor \frac{k}{2} \right\rfloor \) at \(t_{n}^-\) and up to order \(\left\lfloor \frac{k-1}{2} \right\rfloor \) at \(t_{n-1}^+\), respectively, we have
and analogously
These are in fact (2.2b) and (2.2c).
It remains to prove that \({{\mathcal {I}}_{k}^{r}} {\widetilde{U}}\) also satisfies the variational condition (2.2d) with \({\mathscr {I}}_n= {Q_{k}^{r}}\). According to (4.3) we have for \({\widetilde{U}}\) that
Note that originally from the definition of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\) the variational condition is postulated for \(\varphi \in P_{r-k-1}(I_n,{\mathbb {R}}^d)\) only. Since \({{\mathcal {I}}_{k}^{r}} {\widetilde{U}} - {\widetilde{U}} \in P_{r+1}(I_n,{\mathbb {R}}^d)\) vanishes in the quadrature points of \({Q_{k}^{r}}\) it holds
and \({\tilde{\vartheta }}_n \in P_{r+1}(I_n,{\mathbb {R}})\) as defined in Corollary 3.3. Hence, using (3.2) we conclude
which, because of
for \(k=0\), completes the argument. \(\square \)
4.3 Consequences for existence, uniqueness, and error estimates
The connections between numerically integrated variational time discretization methods and collocation methods with multiple nodes observed in the previous subsections can now be used to obtain results on the existence and uniqueness of solutions of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\) as well as give rise to global error estimates and superconvergence estimates in the time mesh points.
Corollary 4.6
(Existence and uniqueness) If there is a solution \({\widetilde{U}} \in P_{r+1}(I_n,{\mathbb {R}}^d)\) of the collocation method with multiple nodes defined by (4.1) then \(U = {{\mathcal {I}}_{k}^{r}} {\widetilde{U}} \in P_{r}(I_n,{\mathbb {R}}^d)\) solves \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\). Furthermore, if \({\widetilde{U}}\) is uniquely defined as solution of (4.1) then so is U as solution of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\).
Corollary 4.7
(Global error estimates) Let the error estimates of Proposition 4.4 hold for the solution \({\widetilde{U}}\) of (4.1) and the exact solution u of (2.1). Then we have for the solution U of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\) that
and
where the derivatives are understood in an interval-wise sense.
Proof
Since \(U = {{\mathcal {I}}_{k}^{r}} {\widetilde{U}}\), Proposition 4.4 and standard error estimates yield
In order to estimate \(\sup _{t \in I} \Vert {\widetilde{U}}^{(r+1)}(t)\Vert \) we again use Proposition 4.4 as follows
Because of \(0 \le k \le r\) this completes the proof of the first statement. The second estimate can be proven similarly. \(\square \)
Corollary 4.8
(Superconvergence in time mesh points) Let the error estimates of Proposition 4.3 hold for the solution \({\widetilde{U}}\) of (4.1) and the exact solution u of (2.1). Then we have
for the solution U of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\).
Proof
Recall that \(U = {{\mathcal {I}}_{k}^{r}} {\widetilde{U}}\) and that \({{\mathcal {I}}_{k}^{r}}\) especially preserves the function value in \(t_n^-\). Hence, \(U(t_n^-) = {{\mathcal {I}}_{k}^{r}} {\widetilde{U}}(t_n^-) = {\widetilde{U}}(t_n^-)\) and the estimate follows immediately from Proposition 4.3. \(\square \)
Remark 4.9
(Superconvergence in quadrature points) We obtain under the assumptions of Corollary 4.7 also a (lower order) superconvergence estimate for the solution U of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\) in the quadrature points of \({Q_{k}^{r}}\) if \(0 \le k < r\). In fact, let \(t_{n,i}\), \(i = 1,\ldots ,r-k\), denote the local quadrature points of \({Q_{k}^{r}}\) in the interior of \(I_n\). Then, we have
In addition, we obtain
and
provided \(k\ge 1\).
These superconvergence estimates especially imply
which compared to
gives an extra order of convergence.
Remark 4.10
(Superconconvergence of derivative(s) in time mesh points) From the point conditions (2.2b) and the bound of Corollary 4.8 we also gain superconvergence estimates up to the \(\left\lfloor \frac{k}{2} \right\rfloor \)th derivative of the solution U of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\) in \(t_n^-\), provided that F satisfies certain Lipschitz-conditions. Indeed, supposing that
holds for all \(0 \le i \le \left\lfloor \frac{k}{2}\right\rfloor -1\), we obtain
by iteration over \(i=0,\ldots ,\left\lfloor \frac{k}{2}\right\rfloor -1\).
Remark 4.11
In order to assess the considered methods, we look at their costs, measured in the size of the local systems to be solved, and their benefit in terms of reachable convergence orders. From the \(r+1\) vector coefficients needed to describe the local solution \(U|_{I_n}\) of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\), already \(\left\lfloor \frac{k-1}{2} \right\rfloor +1= \left\lfloor \frac{k+1}{2} \right\rfloor \) coefficients are fixed by the initial conditions or data inherited from the previous subinterval \(I_{n-1}\) since \(U \in C^{\left\lfloor \frac{k-1}{2} \right\rfloor }\). Hence, the local system size is \(r- \left\lfloor \frac{k-1}{2} \right\rfloor \). The extreme case \(k=r\) leads to a system size of \(\left\lfloor \frac{r}{2} \right\rfloor +1\) that is roughly half of the size \(r+1\) obtained for \(k=0\).
Although the system size decreases with increasing k, the global supremum error converges always with order \(r+1\), see Corollary 4.7. This suggests to choose large values for k, also cf. [10]. However, the larger k the more derivatives of the function F have to be provided. Depending on F, this may result in more complex systems on \(I_n\) that might be more difficult to solve. The suggestion how to choose k changes if one is interested in the value at the time mesh points only. Given a required superconvergence order, the size of the local systems is independent of k. Thus, small values for k are preferable since no derivatives of F are needed then.
5 Special features for affine linear problems
This section is restricted to the study of affine linear problems of the form
Find \(u : {\overline{I}} \rightarrow {\mathbb {R}}^d\) such that
where \(M, A \in {\mathbb {R}}^{d \times d}\) are time-independent matrices and M is regular, i.e., in the general setting we have \(F(t,u) = f(t)-Au\).
5.1 A slight modification of the method
Let \(0\le k\le r\). In order to solve (5.1) numerically, we define the \({\mathscr {I}}_n\)-\({\mathbf {VTD}_{k}^{r}}\big (g\big )\) problem by
Given \(U(t_{n-1}^-)\), find \(U\in P_r(I_n,{\mathbb {R}}^d)\) such that
and
where \(U(t_0^-) = u_0\) and g will be chosen later depending on f. As before \({\mathscr {I}}_n\) denotes an integrator, typically the integral over \(I_n\) or a quadrature formula.
In a first step, we consider \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\big ({{\mathcal {I}}_{k+2}^{r+1}} f\big )\) for \(0 \le k \le r-1\). Here, the case \({r=k}\) is excluded since otherwise \({{\mathcal {I}}_{k+2}^{r+1}} f\) would not be well defined, cf. (2.3). In view of the postprocessing of Sect. 3 this modified method has some interesting properties.
Theorem 5.1
Let \(r, k \in {\mathbb {N}}_0\), \(0 \le k \le r-1\). Suppose that \(U \in Y_{r}\) solves \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\big ({{\mathcal {I}}_{k+2}^{r+1}}f\big )\). Determine \({\widetilde{U}} \in Y_{r+1}\) by the postprocessing of Theorem 3.1 or Corollary 3.3, respectively. Then \({\widetilde{U}}\) solves \({Q_{k+2}^{r+1}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\big (f\big )\).
Proof
First of all, note that \({{\mathcal {I}}_{k+2}^{r+1}}f\) could be used instead of f in the definition of the correction vector \(a_n \in {\mathbb {R}}^d\), see (3.1), since \({{\mathcal {I}}_{k+2}^{r+1}}\) preserves all occurring point values. Hence, postprocessing U as in Sect. 3 gives a function \({\widetilde{U}} \in Y_{r+1}\) that solves \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\big ({{\mathcal {I}}_{k+2}^{r+1}}f\big )\).
Since the interpolation operator \({{\mathcal {I}}_{k+2}^{r+1}}\) preserves all point values occurring in the collocation conditions of the method \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\big ({{\mathcal {I}}_{k+2}^{r+1}}f\big )\), it could be dropped there. Moreover, only polynomials of maximal degree \(2r-k\) appear in the variational condition of this method. Since both quadrature rules \({Q_{k}^{r}}\) and \({Q_{k+2}^{r+1}}\) are exact in this case and since \({{\mathcal {I}}_{k+2}^{r+1}}\) uses the quadrature points of \({Q_{k+2}^{r+1}}\), we obtain that \({\widetilde{U}}\) also solves \({Q_{k+2}^{r+1}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\big (f\big )\). \(\square \)
Remark 5.2
Within the above argument we proved that the method \({Q_{k+2}^{r+1}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\big (f\big )\) and the method \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\big ({{\mathcal {I}}_{k+2}^{r+1}} f\big )\) are equivalent for \(0 \le k \le r-1\). Similarly, one can show that \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\big (f\big )\) and \({Q_{k+2}^{r+1}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}\big ({{\mathcal {I}}_{k}^{r}} f\big )\) are equivalent for \(0 \le k \le r-1\). Note that also \({{\mathcal {I}}_{k}^{r}}\) preserves all derivatives that appear in the point conditions at both ends of the interval.
5.2 Interpolation cascade
Having a closer look at the result of Theorem 5.1, we see that the postprocessed solution of the modified discrete problem also solves a numerically integrated variational time discretization method but with the “right” associated quadrature rule. This enables one further postprocessing step.
For \(1 \le \ell \le r-k\), using an interpolation cascade we even could enable up to \(\ell + 1\) additional postprocessing steps. More concretely we have
where \(\leadsto \) denotes the postprocessing steps. Note that f itself can be used in each postprocessing step to calculate the correction vector \(a_n \in {\mathbb {R}}^d\) (cf. Theorem 3.1) since in each step the occurring derivative of f at \(t_n^-\) is preserved by the respective interpolation cascade.
Remark 5.3
For Dahlquist’s stability equation, i.e., \(d=1\), \(M = 1\), \(A = -\lambda \), and \(f = 0\) in (5.1), we easily see that
for all \(\ell = 0,\ldots ,\left\lfloor \frac{k}{2} \right\rfloor \). Thus, \(\ell \) postprocessing steps can be applied for this equation. Since the postprocessing does not change the function value in the end points of the intervals, the stability function does not change either. Therefore, \({\mathbf {VTD}_{k}^{r}}\) as well as \({Q_{k}^{r}}\text {-}{\mathbf {VTD}_{k}^{r}}\) provide the same stability function as \({\mathbf {VTD}_{k-2\ell }^{r-\ell }}\). With the special choice \(\ell = \left\lfloor \frac{k}{2} \right\rfloor \), we immediately find that \({\mathbf {VTD}_{k}^{r}}\) shares its stability properties with
Hence, all methods with even k share their strong A-stability with the dG method while methods with odd k are A-stable as the cGP method, cf. Remark 2.1 and [6].
Remark 5.4
Analogously to Theorem 3.1 also a postprocessing from \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}(g)\) to \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k+2}^{r+1}}(g)\) can be proven when instead of (3.1) the correction vector is determined by
However, when g and its derivatives are not globally continuous up to a sufficiently high order, then usually the discrete solution of \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}(g)\) is not \(\left\lfloor \frac{k-1}{2} \right\rfloor \)-times continuously differentiable. Therefore, in general the postprocessing by jumps and the postprocessing by (modified) residuals do not provide the same correction anymore, also cf. Tables 6 and 7.
5.3 Derivatives of solutions
Since the quadrature formula \({Q_{k}^{r}}\) is exact for polynomials up to degree \(2r-k\) and the associated interpolation operator \({{\mathcal {I}}_{k}^{r}}\) yields polynomials of degree r, we easily find that
for all \(r,k \in {\mathbb {N}}_0\), \(0 \le k \le r\). Therefore, \({\mathbf {VTD}_{k}^{r}}\big (f\big )\) and \({Q_{k}^{r}}\)-\({\mathbf {VTD}_{k}^{r}}\big (f\big )\) can nicely be written as one method of the form \({\mathbf {VTD}_{r}^{k}}\big ({\mathcal {I}}f\big )\) with \({\mathcal {I}}= \mathrm {Id}\) and \({\mathcal {I}}= {{\mathcal {I}}_{k}^{r}}\), respectively.
Theorem 5.5
Let \(r, k \in {\mathbb {N}}_0\), \(0 \le k \le r\), and suppose that \(U \in Y_{r}\) solves \({\mathbf {VTD}_{r}^{k}}\big ({\mathcal {I}}f\big )\) with \({\mathcal {I}}\in \{\mathrm {Id},{{\mathcal {I}}_{k}^{r}}\}\). Then it holds
for all \(0 \le j \le \left\lfloor \frac{k}{2} \right\rfloor \) and all \(\varphi \in P_{r-k+j}(I_n,{\mathbb {R}}^d)\). Note that the integrals can be replaced for \({\mathcal {I}}= {{\mathcal {I}}_{k}^{r}}\) by any quadrature rule which is exact for polynomials of degree less than or equal to \(2r-k\), for example by \({Q_{k-2j}^{r-j}}\).
Proof
Let us start with the case \(0 \le j \le \left\lfloor \frac{k-1}{2} \right\rfloor \). Integrating by parts several times and using (5.2) with \(g = {\mathcal {I}}f\), we gain for any \(\varphi \in P_{r-k+j}(I_n,{\mathbb {R}}^d)\)
which is the desired statement. So, for odd k we are done due to \(\left\lfloor \frac{k-1}{2}\right\rfloor = \left\lfloor \frac{k}{2}\right\rfloor \) in this case.
Hence, it only remains to study the case \(j=\left\lfloor \frac{k}{2} \right\rfloor \) for even \(k\ge 2\). Similar as above we conclude from (5.2) with \(g = {\mathcal {I}}f\) for any \(\varphi \in P_{r-k+j}(I_n,{\mathbb {R}}^d)\) that
Since point values of \({\mathcal {I}}f\) and f only appear at \(t_n^-\) and \(t_{n-1}^+\) up to the \(\left( \left\lfloor \frac{k}{2} \right\rfloor -1\right) \)th derivative which are preserved by the operator \({\mathcal {I}}\in \{\mathrm {Id},{{\mathcal {I}}_{k}^{r}}\}\), we obtain, for \(n \ge 2\)
where the continuity of \(f^{(j-1)}\) and (5.2b) with \(g = {\mathcal {I}}f\) is used. Since also \(U^{(j-1)}\) is continuous, we get
with \(\big [U^{(j)}\big ]_{n-1} = U^{(j)}(t_{n-1}^+)-U^{(j)}(t_{n-1}^-)\). Thus, for \(n \ge 2\) the wanted identity is proven. Moreover, recalling the definitions of \(U^{(j)}(t_0^-)\) and \(u^{(j)}(t_0)\), we find
which yields the wanted statement also for \(n=1\). So, the proof is completed. \(\square \)
Using the appropriate initial condition, derivatives of \(\mathbf {VTD}\) solutions are themselves solutions of \(\mathbf {VTD}\) methods.
Corollary 5.6
Let \(r, k \in {\mathbb {N}}_0\), \(0 \le k \le r\), and suppose that \(U \in Y_{r}\) solves \({\mathbf {VTD}_{k}^{r}}\big ({\mathcal {I}}f\big )\) where \({\mathcal {I}}\in \{\mathrm {Id}, {{\mathcal {I}}_{k}^{r}}\}\). Then \(U^{(j)} \in Y_{r-j}\), \(0 \le j \le \left\lfloor \frac{k}{2} \right\rfloor \), solves \({\mathbf {VTD}_{k-2j}^{r-j}}\big (({\mathcal {I}}f)^{(j)}\big )\) if \(u^{(j)}(t_0)\) is used as initial condition.
Proof
Because of Theorem 5.5 it only remains to prove the needed conditions at \(t_{n-1}^+\) and \(t_n^-\). Since by construction U is \(\left\lfloor \frac{k-1}{2} \right\rfloor \)-times continuously differentiable, the desired identities follow easily from (5.2a), (5.2b), and (5.2c) with \(g = {\mathcal {I}}f\). \(\square \)
6 Numerical experiments
In this section we present some numerical tests supporting the theoretical results. All calculations were carried out using the software Julia [11] using the floating point data type BigFloat with 512 bits.
Example 6.1
We consider for \(t\in (0,15)\) the initial value problem
with the initial condition
Its solution is
where \(\theta \) is for any given t the unique solution of
The problem is taken from [16, Example 4.4].
The appearing nonlinear systems within each time step were solved by Newton’s method where we applied a Taylor expansion of the inherited data from the previous time interval to calculate an initial guess for all unknowns on the current interval. If higher order derivatives were needed at initial time \(t=0\), the ODE system and its temporal derivatives were used, see (2.7). The postprocessing used the jumps of the derivatives, as given in Corollary 3.3.
We denote by
the error of the solution U and the error of the postprocessed solution \({\widetilde{U}}\), respectively. Errors were measured in the norms
where \(\Vert \cdot \Vert \) denotes the Euclidean norm in \({\mathbb {R}}^d\).
Table 1 presents the results for \({Q_{0}^{6}}\)-\({\mathbf {VTD}_{0}^{6}}\) which is just \(\mathrm {dG}(6)\) with numerical quadrature by the right-sided Gauss–Radau formula with 7 points. We show norms of the error between the solution u and the discrete solution U as well as the error between the solution u and the postprocessed discrete solution \({\widetilde{U}}\) in different norms. Using the results for \(N=4096\) and \(N=8192\), the experimental order of convergence (eoc) is calculated. In addition, the theoretically predicted convergence orders (theo) are given. We see clearly from Table 1 that the experimental orders of convergence coincide with the theoretical predictions. This holds for the function itself and its time derivative. Moreover, the order of convergence increases by 1 if one postprocessing step is applied. It is noteworthy that the error norm \(\Vert {\tilde{e}}'\Vert _{\ell ^{\infty }}\) shows the same high order superconvergence order as \(\Vert e\Vert _{\ell ^{\infty }}\). This behavior is due to the collocation conditions satisfied by the postprocessed solution \({\widetilde{U}}\).
The results of our calculations using the variational time discretization \({Q_{5}^{6}}\)-\({\mathbf {VTD}_{5}^{6}}\) are collected in Table 2. Again we present the results in different norms for both the error itself and the error obtained after postprocessing the discrete solution. Also for this temporal discretization, all theoretically predicted orders of convergence are met by our numerical experiments. Compared to the results of \({Q_{0}^{6}}\)-\({\mathbf {VTD}_{0}^{6}}\) the superconvergence order measured in \(\Vert \cdot \Vert _{\ell ^{\infty }}\) is much smaller which is in agreement with our theory. In addition, the order of convergence of \(\Vert {\tilde{e}}'\Vert _{\ell ^{\infty }}\) is the same as the order of convergence of \(\Vert e'\Vert _{\ell ^{\infty }}\) since collocation conditions are fulfilled already by the discrete solution U. Hence, an improvement of this quantity by applying the postprocessing is not possible.
Table 3 shows the results for calculations using \({Q_{6}^{6}}\)-\({\mathbf {VTD}_{6}^{6}}\) as discretization in time. The presented error norms indicate that the experimental order of convergence are in agreement with our theory. Note that the postprocessing does not lead to an improvement of the error itself. However, there is an improvement if we look at the \(L^2\) norm of the time derivative. We clearly see that the order of convergence is increased from 6 to 7 which is in agreement with Proposition 4.4. Moreover, there is no superconvergence at the discrete time points, as predicted by our theory.
Example 6.2
We consider the affine linear initial value problem
where the initial condition is given by
This results in
as the solution components. This problem is a slight modification of [15, Example 7.3]. In particular, a non-trivial mass matrix was introduced. Moreover, in order to see effects caused by the interpolation cascade, we added a non-vanishing right-hand side function \(f = \left( -10 e^{-10t}, 0\right) ^T\).
Table 4 presents the results for \({Q_{0}^{9}}\)-\({\mathbf {VTD}_{0}^{9}}\) where the cascadic interpolation has been applied to the function f on the right-hand side, see Sect. 5. Let \(\mathrm {PP}_{\!s}U\) denote the discrete solution obtained after applying s postprocessing steps starting from U. We show norms of the error after s postprocessing steps using 2048 time steps. The given experimental orders of convergence were calculated from the results with 1024 and 2048 time steps. Looking at the convergence orders in the \(L^2\)-like norms, we clearly see that each postprocessing step increases the experimental order of convergence by 1 if at most 9 postprocessing steps are applied. The postprocessing step 10 leads to an improvement of the convergence order only for the temporal derivative since the function itself already converges with the optimal order 19. The postprocessing has no influence to the \(\ell _{\infty }\) norm of the error itself while the very first postprocessing step improves the results for the derivative of the error in the \(\ell _{\infty }\) norm. This is caused by the fact that the postprocessed solution fulfills a collocation condition at the discrete time points.
Table 5 presents the experimental orders of convergence of \(\Vert (u-\mathrm {PP}_{\!s}U)'\Vert _{L^2}\) for \({Q_{k}^{9}}\)-\({\mathbf {VTD}_{k}^{9}}\), \(k=0,\dots ,9\), after s postprocessing steps where at most \(r+1-k = 10-k\) steps have been applied. The cascadic interpolation of the right-hand function f is used for all considered methods. It can clearly be seen that each additional postprocessing step increases the convergence by one order. Using the same number of postprocessing steps, the obtained convergence orders do not depend on the particular methods. Since each postprocessing step is covered by our theory and postprocessing by jumps and postprocessing by residual are equivalent for every single step, both types of postprocessing lead to identical results if the cascadic interpolation of the right-hand side function f is used.
The behavior changes substantially if just f and not its cascadic interpolation is used. Table 6 shows for the methods \({Q_{k}^{9}}\)-\({\mathbf {VTD}_{k}^{9}}\), \(k=0,\dots ,9\), the experimental convergence order of the error \(\Vert (u-\mathrm {PP}_{\!s}U)'\Vert _{L^2}\) after s postprocessing steps based on jumps where at most \(r+1-k= 10-k\) steps have been carried out. The column \(s=1\) shows, as predicted by our theory, that the convergence order increases by 1 for all methods. The behavior after using at least two postprocessing steps depends strongly on the parameter k of the variational time discretizations. For dG-like methods (characterized by even k), an additional improvement by one order is obtained independent of the number of postprocessing steps. The situation is completely different for cGP-like method (corresponding to odd k). For \(k\equiv 3\pmod 4\), the second postprocessing step does not lead to an improvement of the convergence order compared to a single postprocessing step. If \(k\equiv 1\pmod 4\) then the second postprocessing step provides an increased convergence order. However, for all cGP-like methods, the obtained convergence rates start to decrease with increasing numbers of postprocessing steps. This is in complete contrast to dG-like methods. Calculations for the methods \({Q_{k}^{10}}\)-\({\mathbf {VTD}_{k}^{10}}\), \(k=0,\dots ,10\), show for dG-like methods the same behavior as in the case \(r=9\). However, the roles of \(k\equiv 1\pmod 4\) and \(k\equiv 3\pmod 4\) for cGP-like methods are switched compared to the case \(r=9\).
Our theory provides that postprocessing based on jumps and postprocessing based on residuals are equivalent if a single postprocessing step is applied. The situation changes if at least two postprocessing steps are used, also cf. Remark 5.4. Table 7 shows the experimental orders of convergence of \(\Vert (u-\mathrm {PP}_{\!s}U)'\Vert _{L^2}\) after s postprocessing steps based on residuals for the methods \({Q_{k}^{9}}\)-\({\mathbf {VTD}_{k}^{9}}\), \(k=0,\dots ,9\), that are the same ones as used for obtaining the results in Table 6. Independent of k, the application of at least two postprocessing steps leads always to an improvement of the convergence order by two compared to the results without postprocessing. Moreover, the orders of convergence do not decrease even if more than two postprocessing steps based on residuals are applied. The same behavior is observed for the methods \({Q_{k}^{10}}\)-\({\mathbf {VTD}_{k}^{10}}\), \(k=0,\dots ,10\).
Example 6.3
We consider the one-dimensional heat equation \(u_t(t,x)-u_{xx}(t,x)=f(t,x)\) for \((t,x)\in (0,2)\times (0,1)\) with homogeneous Dirichlet boundary conditions. The initial condition at \(t=0\) and the right-hand side function f are chosen such that the solution is given by
For semi-discretization in space we use a finite element method with continuous, piecewise cubic elements on an equidistant decomposition of the spatial interval (0, 1) into 10 subintervals. This results in an ODE system of dimension 29 due to the homogeneous Dirichlet boundary conditions at \(x=0\) and \(x=1\). Note that by the proper choice of the trial space for the semi-discretization in space the spatial error is negligible.
On the basis of Example 6.3 we want to take another view on the interpolation cascade. To this end, the results for \({Q_{0}^{6}}\)-\({\mathbf {VTD}_{0}^{6}}\) which is just \(\mathrm {dG}(6)\) are presented in Table 8. The errors in the \(L^2\) norm and the \(\ell ^\infty \) norm are compared for the standard method and the method with cascadic interpolation. While measured in \(\Vert \cdot \Vert _{L^2}\) the error is almost equal for both methods and the expected order of convergence is clearly reached, there are significant differences with regard to the error in the time mesh points. For the standard method without cascade the expected superconvergence order (which is 13) clearly is not obtained, even for quite small time steps. This is probably due to the well-known order reduction phenomenon. In contrast, the wanted superconvergence behavior is achieved already for large time steps when the interpolation cascade is used. Moreover, the \(\ell ^\infty \) norm error is also considerably smaller. This suggests that the cascadic interpolation could be quite advantageous in some cases.
References
Ahmed, N., Becher, S., Matthies, G.: Higher-order discontinuous Galerkin time stepping and local projection stabilization techniques for the transient Stokes problem. Comput. Methods Appl. Mech. Eng. 313(1), 28–52 (2017)
Ahmed, N., John, V.: Adaptive time step control for higher order variational time discretizations applied to convection–diffusion–reaction equations. Comput. Methods Appl. Mech. Eng. 285, 83–101 (2015)
Ahmed, N., Matthies, G.: Higher order continuous Galerkin–Petrov time stepping schemes for transient convection–diffusion–reaction equations. ESAIM: M2AN 49(5), 1429–1450 (2015)
Ahmed, N., Matthies, G.: Numerical study of SUPG and LPS methods combined with higher order variational time discretization schemes applied to time-dependent linear convection–diffusion–reaction equations. J. Sci. Comput. 67(1), 988–1018 (2016)
Akrivis, G., Makridakis, C., Nochetto, R.H.: Galerkin and Runge–Kutta methods: unified formulation, a posteriori error estimates and nodal superconvergence. Numer. Math. 118, 429–456 (2011)
Anselmann, M., Bause, M., Becher, S., Matthies, G.: Galerkin-collocation approximation in time for the wave equation and its post-processing. ESAIM: M2AN 54(6), 2099–2123 (2020)
Aziz, A.K., Monk, P.: Continuous finite elements in space and time for the heat equation. Math. Comput. 52(186), 255–274 (1989)
Bause, M., Köcher, U., Radu, F.A., Schieweck, F.: Post-processed Galerkin approximation of improved order for wave equations. Math. Comput. 89(322), 595–627 (2020)
Becher, S., Matthies, G.: Variational time discretizations of higher order and higher regularity. Preprint. arXiv: 2003.04056
Becher, S., Matthies, G., Wenzel, D.: Variational methods for stable time discretization of first-order differential equations. In: Georgiev, K., Todorov, M.I.G. (eds.) Advanced Computing in Industrial Mathematics: BGSIAM 2017, Studies in Computational Intelligence, vol. 793, pp. 63–75. Springer International Publishing, Cham (2019)
Bezanson, J., Edelman, A., Karpinski, S., Shah, V.B.: Julia: a fresh approach to numerical computing. SIAM Rev. 59(1), 65–98 (2017)
Delfour, M.C., Dubeau, F.: Discontinuous polynomial approximations in the theory of one-step, hybrid and multistep methods for nonlinear ordinary differential equations. Math. Comput. 47(175), 169–189 (1986)
Encinas, L.H., Masqué, J.M.: A short proof of the generalized Faà di Bruno’s formula. Appl. Math. Lett. 16, 975–979 (2003)
Ern, A., Schieweck, F.: Discontinuous Galerkin method in time combined with a stabilized finite element method in space for linear first-order PDEs. Math. Comput. 85(301), 2099–2129 (2016)
Estep, D.: A posteriori error bounds and global error control for approximation of ordinary differential equations. SIAM J. Numer. Anal. 32(1), 1–48 (1995)
Estep, D.., French, D..: Global error control for the continuous Galerkin finite element method for ordinary differential equations. ESAIM: M2AN 28(7), 815–852 (1994)
Estep, D., Stuart, A.: The dynamical behavior of the discontinuous Galerkin method and related difference schemes. Math. Comput. 71(239), 1075–1103 (2002)
French, D., Schaeffer, J.W.: Continuous finite element methods which preserve energy properties for nonlinear problems. Appl. Math. Comput. 39(3), 271–295 (1990)
Gautschi, W.: Orthogonal Polynomials: Computation and Approximation. Numerical Mathematics and Scientific Computation. Oxford University Press, Oxford (2004)
Hairer, E., Nørsett, S.P., Wanner, G.: Solving Ordinary Differential Equations I, 2nd edn. Springer-Verlag (1993). Corrected 3rd printing (2008)
Hulme, B.L.: Discrete Galerkin and related one-step methods for ordinary differential equations. Math. Comput. 26(120), 881–891 (1972)
Hulme, B.L.: One-step piecewise polynomial Galerkin methods for initial value problems. Math. Comput. 26(118), 415–426 (1972)
Joulak, H., Beckermann, B.: On Gautschi’s conjecture for generalized Gauss–Radau and Gauss–Lobatto formulae. J. Comput. Appl. Math. 233(3), 768–774 (2009)
Matthies, G., Schieweck, F.: Higher order variational time discretizations for nonlinear systems of ordinary differential equations. Preprint 23/2011, Fakultät für Mathematik, Otto-von-Guericke-Universität Magdeburg (2011)
Mishkov, R.L.: Generalization of the formula of Faà di Bruno for a composite function with a vector argument. Int. J. Math. Math. Sci. 24(7), 481–491 (2000)
Petrova, G.: Generalized Gauss–Radau and Gauss–Lobatto formulas with Jacobi weight functions. BIT Numer. Math. 57(1), 191–206 (2017)
Schieweck, F.: A-stable discontinuous Galerkin–Petrov time discretization of higher order. J. Numer. Math. 18(1), 25–57 (2010)
Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems, 2nd edn. Springer, Berlin (2006)
Vlasák, M., Roskovec, F.: On Runge–Kutta, collocation and discontinuous Galerkin methods: mutual connections and resulting consequences to the analysis. In: Programs and Algorithms of Numerical Mathematics 17, pp. 231–236. Institute of Mathematics AS CR, Prague (2015)
Acknowledgements
We would like to thank the anonymous referees for their useful comments.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Communicated by Rolf Stenberg.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Becher, S., Matthies, G. Variational time discretizations of higher order and higher regularity. Bit Numer Math 61, 721–755 (2021). https://doi.org/10.1007/s10543-021-00851-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10543-021-00851-6
Keywords
- Discontinuous Galerkin
- Continuous Galerkin–Petrov
- Stability
- Collocation method
- Postprocessing
- Superconvergence