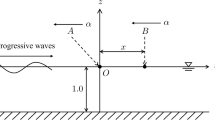
Appendix A: Shift of multipoles among different spherical coordinate systems
Separating the real and imaginary parts of Eq. (36), we obtain
$$\begin{aligned} & r_{p}^{ - n - 1} P_{n}^{m} (\cos \theta_{p} )\cos (m\beta_{p} ) \\ & \quad = \sum\limits_{{m^{\prime} = 0}}^{\infty } {\sum\limits_{{n^{\prime} = m^{\prime}}}^{\infty } {r_{q}^{{n^{\prime}}} P_{{n^{\prime}}}^{{m^{\prime}}} (\cos \theta_{q} )\left[ {W_{1} (n,m,n^{\prime},m^{\prime},p,q)\cos (m^{\prime}\beta_{q} ) + W_{2} (n,m,n^{\prime},m^{\prime},p,q)\sin (m^{\prime}\beta_{q} )} \right]} },\end{aligned}$$
(A1)
$$\begin{aligned} & r_{p}^{ - n - 1} P_{n}^{m} (\cos \theta_{p} )\sin (m\beta_{p} ) \\ & \quad = \sum\limits_{{m^{\prime} = 0}}^{\infty } {\sum\limits_{{n^{\prime} = m^{\prime}}}^{\infty } {r_{q}^{{n^{\prime}}} P_{{n^{\prime}}}^{{m^{\prime}}} (\cos \theta_{q} )\left[ {W_{3} (n,m,n^{\prime},m^{\prime},p,q)\cos (m^{\prime}\beta_{q} ) + W_{4} (n,m,n^{\prime},m^{\prime},p,q)\sin (m^{\prime}\beta_{q} )} \right]} },\end{aligned} $$
(A2)
where
$$ W_{1} (n,m,n^{\prime},m^{\prime},p,q) = \frac{{\varepsilon_{{m^{\prime}}} ( - 1)^{{n^{\prime}}} r_{pq}^{{ - n - n^{\prime} - 1}} }}{{2(n - m)!(n^{\prime} + m^{\prime})!}}\left[ \begin{gathered} (n + n^{\prime} - m - m^{\prime})!P_{{n + n^{\prime}}}^{{m + m^{\prime}}} (\cos \theta_{pq} )\cos ((m + m^{\prime})\beta_{pq} ) \hfill \\ + ( - 1)^{{m^{\prime}}} (n + n^{\prime} - m + m^{\prime})!P_{{n + n^{\prime}}}^{{m - m^{\prime}}} (\cos \theta_{pq} )\cos ((m - m^{\prime})\beta_{pq} ) \hfill \\ \end{gathered} \right], $$
(A3)
$$ W_{2} (n,m,n^{\prime},m^{\prime},p,q) = \frac{{\varepsilon_{{m^{\prime}}} ( - 1)^{{n^{\prime}}} r_{pq}^{{ - n - n^{\prime} - 1}} }}{{2(n - m)!(n^{\prime} + m^{\prime})!}}\left[ \begin{gathered} (n + n^{\prime} - m - m^{\prime})!P_{{n + n^{\prime}}}^{{m + m^{\prime}}} (\cos \theta_{pq} )\sin ((m + m^{\prime})\beta_{pq} ) \hfill \\ - ( - 1)^{{m^{\prime}}} (n + n^{\prime} - m + m^{\prime})!P_{{n + n^{\prime}}}^{{m - m^{\prime}}} (\cos \theta_{pq} )\sin ((m - m^{\prime})\beta_{pq} ) \hfill \\ \end{gathered} \right], $$
(A4)
$$ W_{3} (n,m,n^{\prime},m^{\prime},p,q) = \frac{{\varepsilon_{{m^{\prime}}} ( - 1)^{{n^{\prime}}} r_{pq}^{{ - n - n^{\prime} - 1}} }}{{2(n - m)!(n^{\prime} + m^{\prime})!}}\left[ \begin{gathered} (n + n^{\prime} - m - m^{\prime})!P_{{n + n^{\prime}}}^{{m + m^{\prime}}} (\cos \theta_{pq} )\sin ((m + m^{\prime})\beta_{pq} ) \hfill \\ + ( - 1)^{{m^{\prime}}} (n + n^{\prime} - m + m^{\prime})!P_{{n + n^{\prime}}}^{{m - m^{\prime}}} (\cos \theta_{pq} )\sin ((m - m^{\prime})\beta_{pq} ) \hfill \\ \end{gathered} \right], $$
(A5)
$$ W_{4} (n,m,n^{\prime},m^{\prime},p,q) = \frac{{\varepsilon_{{m^{\prime}}} ( - 1)^{{n^{\prime}}} r_{pq}^{{ - n - n^{\prime} - 1}} }}{{2(n - m)!(n^{\prime} + m^{\prime})!}}\left[ \begin{gathered} - (n + n^{\prime} - m - m^{\prime})!P_{{n + n^{\prime}}}^{{m + m^{\prime}}} (\cos \theta_{pq} )\cos ((m + m^{\prime})\beta_{pq} ) \hfill \\ + ( - 1)^{{m^{\prime}}} (n + n^{\prime} - m + m^{\prime})!P_{{n + n^{\prime}}}^{{m - m^{\prime}}} (\cos \theta_{pq} )\cos ((m - m^{\prime})\beta_{pq} ) \hfill \\ \end{gathered} \right]. $$
(A6)
By applying Eq. (31), the multipoles in Eqs. (15)–(18) are finally rewritten as
$$ \begin{aligned} \varphi_{nm}^{p,1} & = \sum\limits_{{m^{\prime} = 0}}^{\infty } {\sum\limits_{{n^{\prime} = m^{\prime}}}^{\infty } {r_{q}^{{2n^{\prime}}} P_{{2n^{\prime}}}^{{2m^{\prime}}} (\cos \theta_{q} )\left[ \begin{gathered} Q_{1} (2n,2m,2n^{\prime},2m^{\prime},p,q)\cos (2m^{\prime}\beta_{q} ) \hfill \\ + Q_{2} (2n,2m,2n^{\prime},2m^{\prime},p,q)\sin (2m^{\prime}\beta_{q} ) \hfill \\ \end{gathered} \right]} } \hfill \\ &\quad + \sum\limits_{{m^{\prime} = 0}}^{\infty } {\sum\limits_{{n^{\prime} = m^{\prime}}}^{\infty } {r_{q}^{{2n^{\prime} + 1}} P_{{2n^{\prime} + 1}}^{{2m^{\prime} + 1}} (\cos \theta_{q} )\left[ \begin{gathered} Q_{1} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q)\cos ((2m^{\prime} + 1)\beta_{q} ) \hfill \\ + Q_{2} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q)\sin ((2m^{\prime} + 1)\beta_{q} ) \hfill \\ \end{gathered} \right]} }, \hfill \\ \end{aligned} $$
(A7)
$$ \begin{aligned} \varphi_{nm}^{p,2} & = \sum\limits_{{m^{\prime} = 0}}^{\infty } {\sum\limits_{{n^{\prime} = m^{\prime}}}^{\infty } {r_{q}^{{2n^{\prime}}} P_{{2n^{\prime}}}^{{2m^{\prime}}} (\cos \theta_{q} )\left[ \begin{gathered} Q_{3} (2n,2m,2n^{\prime},2m^{\prime},p,q)\cos (2m^{\prime}\beta_{q} ) \hfill \\ + Q_{4} (2n,2m,2n^{\prime},2m^{\prime},p,q)\sin (2m^{\prime}\beta_{q} ) \hfill \\ \end{gathered} \right]} } \hfill \\ &\quad + \sum\limits_{{m^{\prime} = 0}}^{\infty } {\sum\limits_{{n^{\prime} = m^{\prime}}}^{\infty } {r_{q}^{{2n^{\prime} + 1}} P_{{2n^{\prime} + 1}}^{{2m^{\prime} + 1}} (\cos \theta_{q} )\left[ \begin{gathered} Q_{3} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q)\cos ((2m^{\prime} + 1)\beta_{q} ) \hfill \\ + Q_{4} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q)\sin ((2m^{\prime} + 1)\beta_{q} ) \hfill \\ \end{gathered} \right]} }, \hfill \\ \end{aligned} $$
(A8)
$$ \begin{aligned} \varphi_{nm}^{p,3} & = \sum\limits_{{m^{\prime} = 0}}^{\infty } {\sum\limits_{{n^{\prime} = m^{\prime}}}^{\infty } {r_{q}^{{2n^{\prime}}} P_{{2n^{\prime}}}^{{2m^{\prime}}} (\cos \theta_{q} )\left[ \begin{gathered} Q_{1} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q)\cos (2m^{\prime}\beta_{q} ) \hfill \\ + Q_{2} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q)\sin (2m^{\prime}\beta_{q} ) \hfill \\ \end{gathered} \right]} } \hfill \\&\quad + \sum\limits_{{m^{\prime} = 0}}^{\infty } {\sum\limits_{{n^{\prime} = m^{\prime}}}^{\infty } {r_{q}^{{2n^{\prime} + 1}} P_{{2n^{\prime} + 1}}^{{2m^{\prime} + 1}} (\cos \theta_{q} )\left[ \begin{gathered} Q_{1} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q)\cos ((2m^{\prime} + 1)\beta_{q} ) \hfill \\ + Q_{2} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q)\sin ((2m^{\prime} + 1)\beta_{q} ) \hfill \\ \end{gathered} \right]} }, \hfill \\ \end{aligned} $$
(A9)
$$ \begin{aligned} \varphi_{nm}^{p,4}&= \sum\limits_{{m^{\prime} = 0}}^{\infty } {\sum\limits_{{n^{\prime} = m^{\prime}}}^{\infty } {r_{q}^{{2n^{\prime}}} P_{{2n^{\prime}}}^{{2m^{\prime}}} (\cos \theta_{q} )\left[ \begin{gathered} Q_{3} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q)\cos (2m^{\prime}\beta_{q} ) \hfill \\ + Q_{4} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q)\sin (2m^{\prime}\beta_{q} ) \hfill \\ \end{gathered} \right]} } \hfill \\ & \quad + \sum\limits_{{m^{\prime} = 0}}^{\infty } {\sum\limits_{{n^{\prime} = m^{\prime}}}^{\infty } {r_{q}^{{2n^{\prime} + 1}} P_{{2n^{\prime} + 1}}^{{2m^{\prime} + 1}} (\cos \theta_{q} )\left[ \begin{gathered} Q_{3} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q)\cos ((2m^{\prime} + 1)\beta_{q} ) \hfill \\ + Q_{4} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q)\sin ((2m^{\prime} + 1)\beta_{q} ) \hfill \\ \end{gathered} \right]} }, \hfill \\ \end{aligned} $$
(A10)
where
$$ Q_{s} (n,m,n^{\prime},m^{\prime},p,q) = W_{s} (n,m,n^{\prime},m^{\prime},p,q) + U_{s} (n,m,n^{\prime},m^{\prime},p,q), \quad s = 1,2,3,4, $$
(A11)
$$ U_{1} (n,m,n^{\prime},m^{\prime},p,q) = \frac{{\varepsilon_{{m^{\prime}}} ( - 1)^{{m^{\prime}}} {\text{i}}^{{m + m^{\prime}}} }}{{2\pi (n - m)!(n^{\prime} + m^{\prime})!}}\int_{L}^{{}} {\int_{ - \pi }^{\pi } {{\hbar} (\mu )\mu^{{n + n^{\prime}}} \cos (m\gamma )\cos (m^{\prime}\gamma ){\text{e}}^{{{\text{i}} \mu (x_{q} - x_{p} )\cos \gamma + {\text{i}} \mu (y_{q} - y_{p} )\sin \gamma }} {\text{d}} \gamma\; {\text{d}} \mu } }, $$
(A12)
$$ U_{2} (n,m,n^{\prime},m^{\prime},p,q) = \frac{{\varepsilon_{{m^{\prime}}} ( - 1)^{{m^{\prime}}} {\text{i}}^{{m + m^{\prime}}} }}{{2\pi (n - m)!(n^{\prime} + m^{\prime})!}}\int_{L}^{{}} {\int_{ - \pi }^{\pi } {{\hbar} (\mu )\mu^{{n + n^{\prime}}} \cos (m\gamma )\sin (m^{\prime}\gamma ){\text{e}}^{{{\text{i}} \mu (x_{q} - x_{p} )\cos \gamma + {\text{i}} \mu (y_{q} - y_{p} )\sin \gamma }} {\text{d}} \gamma\; {\text{d}} \mu,} } $$
(A13)
$$ U_{3} (n,m,n^{\prime},m^{\prime},p,q) = \frac{{\varepsilon_{{m^{\prime}}} ( - 1)^{{m^{\prime}}} {\text{i}}^{{m + m^{\prime}}} }}{{2\pi (n - m)!(n^{\prime} + m^{\prime})!}}\int_{L}^{{}} {\int_{ - \pi }^{\pi } {{\hbar} (\mu )\mu^{{n + n^{\prime}}} \sin (m\gamma )\cos (m^{\prime}\gamma ){\text{e}}^{{{\text{i}} \mu (x_{q} - x_{p} )\cos \gamma + {\text{i}} \mu (y_{q} - y_{p} )\sin \gamma }} {\text{d}} \gamma\; {\text{d}} \mu,} } $$
(A14)
$$ U_{4} (n,m,n^{\prime},m^{\prime},p,q) = \frac{{\varepsilon_{{m^{\prime}}} ( - 1)^{{m^{\prime}}} {\text{i}}^{{m + m^{\prime}}} }}{{2\pi (n - m)!(n^{\prime} + m^{\prime})!}}\int_{L}^{{}} {\int_{ - \pi }^{\pi } {{\hbar} (\mu )\mu^{{n + n^{\prime}}} \sin (m\gamma )\sin (m^{\prime}\gamma ){\text{e}}^{{{\text{i}} \mu (x_{q} - x_{p} )\cos \gamma + {\text{i}} \mu (y_{q} - y_{p} )\sin \gamma }} {\text{d}} \gamma\; {\text{d}} \mu,} } $$
(A15)
Applying the definition in Eq. (37) and the relations in Eqs. (22) and (23), Eqs. (A12)–(A15) are further written as
$$ U_{1} (n,m,n^{\prime},m^{\prime},p,q) = \frac{{\varepsilon_{{m^{\prime}}} ( - 1)^{{m^{\prime} + m}} }}{{2(n - m)!(n^{\prime} + m^{\prime})!}}\int_{L}^{{}} {{\hbar} (\mu )\mu^{{n + n^{\prime}}} \left[ \begin{gathered} ( - 1)^{{m^{\prime}}} \cos ((m + m^{\prime})\beta_{pq} ){\text{J}}_{{m + m^{\prime}}} (\mu R_{pq} ) \hfill \\ + \cos ((m - m^{\prime})\beta_{pq} ){\text{J}}_{{m - m^{\prime}}} (\mu R_{pq} ) \hfill \\ \end{gathered} \right]{\text{d}} \mu,} $$
(A16)
$$ U_{2} (n,m,n^{\prime},m^{\prime},p,q) = \frac{{\varepsilon_{{m^{\prime}}} ( - 1)^{{m^{\prime} + m}} }}{{2(n - m)!(n^{\prime} + m^{\prime})!}}\int_{L}^{{}} {{\hbar} (\mu )\mu^{{n + n^{\prime}}} \left[ \begin{gathered} ( - 1)^{{m^{\prime}}} \sin ((m + m^{\prime})\beta_{pq} ){\text{J}}_{{m + m^{\prime}}} (\mu R_{pq} ) \hfill \\ - \sin ((m - m^{\prime})\beta_{pq} ){\text{J}}_{{m - m^{\prime}}} (\mu R_{pq} ) \hfill \\ \end{gathered} \right]{\text{d}} \mu,} $$
(A17)
$$ U_{3} (n,m,n^{\prime},m^{\prime},p,q) = \frac{{\varepsilon_{{m^{\prime}}} ( - 1)^{{m^{\prime} + m}} }}{{2(n - m)!(n^{\prime} + m^{\prime})!}}\int_{L}^{{}} {{\hbar} (\mu )\mu^{{n + n^{\prime}}} \left[ \begin{gathered} ( - 1)^{{m^{\prime}}} \sin ((m + m^{\prime})\beta_{pq} ){\text{J}}_{{m + m^{\prime}}} (\mu R_{pq} ) \hfill \\ + \sin ((m - m^{\prime})\beta_{pq} ){\text{J}}_{{m - m^{\prime}}} (\mu R_{pq} ) \hfill \\ \end{gathered} \right]{\text{d}} \mu,} $$
(A18)
$$ U_{4} (n,m,n^{\prime},m^{\prime},p,q) = \frac{{\varepsilon_{{m^{\prime}}} ( - 1)^{{m^{\prime} + m}} }}{{2(n - m)!(n^{\prime} + m^{\prime})!}}\int_{L}^{{}} {{\hbar} (\mu )\mu^{{n + n^{\prime}}} \left[ \begin{gathered} - ( - 1)^{{m^{\prime}}} \cos ((m + m^{\prime})\beta_{pq} ){\text{J}}_{{m + m^{\prime}}} (\mu R_{pq} ) \hfill \\ + \cos ((m - m^{\prime})\beta_{pq} ){\text{J}}_{{m - m^{\prime}}} (\mu R_{pq} ) \hfill \\ \end{gathered} \right]{\text{d}} \mu }. $$
(A19)
Appendix B: Derivation of the linear system for perforated reef balls
Substituting velocity potentials into the first equals sign of Eq. (13), multiplying both sides of the resulting equation by
$$P_{{2n^{\prime}}}^{{2m^{\prime}}} (\cos \theta_{q} )\sin \theta_{q} \left\{ \begin{gathered} \cos (2m^{\prime}\beta_{q} ) \hfill \\ \sin (2m^{\prime}\beta_{q} ) \hfill \\ \end{gathered} \right.\;\text{or}\;P_{{2n^{\prime} + 1}}^{{2m^{\prime} + 1}} (\cos \theta_{q} )\sin \theta_{q} \left\{ \begin{gathered} \cos((2m^{\prime} + 1)\beta_{q} ), \hfill \\ \sin ((2m^{\prime} + 1)\beta_{q} ), \hfill \\ \end{gathered} \right.$$
, then integrating with respect to βq and θq from 0 to 2π and 0 to π/2, respectively, and applying the orthogonality of trigonometric function and associated Legendre function
$$ \int_{0}^{\pi /2} {P_{n}^{m} (\cos \theta_{q} )P_{s}^{m} (\cos \theta_{q} )\sin \theta_{q} {\text{d}} \theta_{q} } = \frac{{\delta_{ns} (n + m)!}}{(2n + 1)(n - m)!}, $$
(B1)
where the values of n + m and s + m are even, δns = 1 for n = s and δns = 0 for n ≠ s, we obtain for q = 1, 2, …, S:
$$ \begin{aligned} & \sum\limits_{p = 1,p \ne q}^{S} {\sum\limits_{m = 0}^{\infty } {\sum\limits_{n = m}^{\infty } {2n^{\prime}\left[ \begin{gathered} A_{nm}^{(p)} Q_{1} (2n,2m,2n^{\prime},2m^{\prime},p,q) + B_{nm}^{(p)} Q_{3} (2n,2m,2n^{\prime},2m^{\prime},p,q) \hfill \\ + C_{nm}^{(p)} Q_{1} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q) + D_{nm}^{(p)} Q_{3} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q) \hfill \\ \end{gathered} \right]} } } \hfill \\& \quad - (2n^{\prime} + 1)a_{q}^{{ - 4n^{\prime} - 1}} A_{{n^{\prime}m^{\prime}}}^{(q)} + \sum\limits_{{n = m^{\prime}}}^{\infty } {A_{{nm^{\prime}}}^{(q)} (2n^{\prime})K(2n,2m^{\prime},2n^{\prime})} - 2n^{\prime}E_{{n^{\prime}m^{\prime}}}^{(q)} = - 2n^{\prime}f(2n^{\prime},2m^{\prime},q)\cos (2m^{\prime}\alpha ), \hfill \\ &\quad m^{\prime} = 0,1,2,\ldots, n^{\prime} = m^{\prime},m^{\prime} + 1,... \hfill \\ \end{aligned} $$
(B2)
$$ \begin{aligned} & \sum\limits_{p = 1,p \ne q}^{S} {\sum\limits_{m = 0}^{\infty } {\sum\limits_{n = m}^{\infty } {2n^{\prime}\left[ \begin{gathered} A_{nm}^{(p)} Q_{2} (2n,2m,2n^{\prime},2m^{\prime},p,q) + B_{nm}^{(p)} Q_{4} (2n,2m,2n^{\prime},2m^{\prime},p,q) \hfill \\ + C_{nm}^{(p)} Q_{2} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q) + D_{nm}^{(p)} Q_{4} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q) \hfill \\ \end{gathered} \right]} } } \hfill \\ & \quad - (2n^{\prime} + 1)a_{q}^{{ - 4n^{\prime} - 1}} B_{{n^{\prime}m^{\prime}}}^{(q)} + \sum\limits_{{n = m^{\prime}}}^{\infty } {B_{{nm^{\prime}}}^{(q)} (2n^{\prime})K(2n,2m^{\prime},2n^{\prime})} - 2n^{\prime}F_{{n^{\prime}m^{\prime}}}^{(q)} = - 2n^{\prime}f(2n^{\prime},2m^{\prime},q)\sin (2m^{\prime}\alpha ), \hfill \\ \end{aligned} $$
(B3)
$$ \begin{aligned} & \sum\limits_{p = 1,p \ne q}^{S} {\sum\limits_{m = 0}^{\infty } {\sum\limits_{n = m}^{\infty } {\left[ \begin{gathered} A_{nm}^{(p)} Q_{1} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q) + B_{nm}^{(p)} Q_{3} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q) \hfill \\ + C_{nm}^{(p)} Q_{1} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q) + D_{nm}^{(p)} Q_{3} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q) \hfill \\ \end{gathered} \right]} } } \hfill \\ & \quad - \frac{{2n^{\prime} + 2}}{{2n^{\prime} + 1}}a_{q}^{{ - 4n^{\prime} - 3}} C_{{n^{\prime}m^{\prime}}}^{(q)} + \sum\limits_{{n = m^{\prime}}}^{\infty } {C_{{nm^{\prime}}}^{(q)} K(2n + 1,2m^{\prime} + 1,2n^{\prime} + 1)} - G_{{n^{\prime}m^{\prime}}}^{(q)} = - f(2n^{\prime} + 1,2m^{\prime} + 1,q)\cos ((2m^{\prime} + 1)\alpha ), \hfill \\ \end{aligned} $$
(B4)
$$ \begin{aligned} & \sum\limits_{p = 1,p \ne q}^{S} {\sum\limits_{m = 0}^{\infty } {\sum\limits_{n = m}^{\infty } {\left[ \begin{gathered} A_{nm}^{(p)} Q_{2} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q) + B_{nm}^{(p)} Q_{4} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q) \hfill \\ + C_{nm}^{(p)} Q_{2} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q) + D_{nm}^{(p)} Q_{4} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q) \hfill \\ \end{gathered} \right]} } } \hfill \\ & \quad - \frac{{2n^{\prime} + 2}}{{2n^{\prime} + 1}}a_{q}^{{ - 4n^{\prime} - 3}} D_{{n^{\prime}m^{\prime}}}^{(q)} + \sum\limits_{{n = m^{\prime}}}^{\infty } {D_{{nm^{\prime}}}^{(q)} K(2n + 1,2m^{\prime} + 1,2n^{\prime} + 1)} - H_{{n^{\prime}m^{\prime}}}^{(q)} = - f(2n^{\prime} + 1,2m^{\prime} + 1,q)\sin ((2m^{\prime} + 1)\alpha ), \hfill \\ \end{aligned} $$
(B5)
where the value of Qs (s = 1, 2, 3, 4) is calculated by Eq. (A11).
Substituting velocity potentials into the second equals sign of Eq. (13), and conducting similar algebraic operation as above, we obtain:
$$ \begin{aligned}& \sum\limits_{p = 1,p \ne q}^{S} {\sum\limits_{m = 0}^{\infty } {\sum\limits_{n = m}^{\infty } {\left[ \begin{gathered} A_{nm}^{(p)} Q_{1} (2n,2m,2n^{\prime},2m^{\prime},p,q) + B_{nm}^{(p)} Q_{3} (2n,2m,2n^{\prime},2m^{\prime},p,q) \hfill \\ + C_{nm}^{(p)} Q_{1} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q) + D_{nm}^{(p)} Q_{3} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q) \hfill \\ \end{gathered} \right]} } } \\ & \quad + a_{q}^{{ - 4n^{\prime} - 1}} A_{{n^{\prime}m^{\prime}}}^{(q)} + \sum\limits_{{n = m^{\prime}}}^{\infty } {A_{{nm^{\prime}}}^{(q)} K(2n,2m^{\prime},2n^{\prime})} - \left( {1 - \frac{{2n^{\prime}}}{{{\text{i}} kG_{q} a_{q} }}} \right)E_{{n^{\prime}m^{\prime}}}^{(q)} = - f(2n^{\prime},2m^{\prime},q)\cos (2m^{\prime}\alpha ), \hfill \\ \end{aligned} $$
(B6)
$$ \begin{aligned} & \sum\limits_{p = 1,p \ne q}^{S} {\sum\limits_{m = 0}^{\infty } {\sum\limits_{n = m}^{\infty } {\left[ \begin{gathered} A_{nm}^{(p)} Q_{2} (2n,2m,2n^{\prime},2m^{\prime},p,q) + B_{nm}^{(p)} Q_{4} (2n,2m,2n^{\prime},2m^{\prime},p,q) \hfill \\ + C_{nm}^{(p)} Q_{2} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q) + D_{nm}^{(p)} Q_{4} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q) \hfill \\ \end{gathered} \right]} } } \hfill \\ & \quad + a_{q}^{{ - 4n^{\prime} - 1}} B_{{n^{\prime}m^{\prime}}}^{(q)} + \sum\limits_{{n = m^{\prime}}}^{\infty } {B_{{nm^{\prime}}}^{(q)} K(2n,2m^{\prime},2n^{\prime})} - \left( {1 - \frac{{2n^{\prime}}}{{{\text{i}} kG_{q} a_{q} }}} \right)F_{{n^{\prime}m^{\prime}}}^{(q)} = - f(2n^{\prime},2m^{\prime},q)\sin (2m^{\prime}\alpha ), \hfill \\ \end{aligned} $$
(B7)
$$ \begin{aligned} &\sum\limits_{p = 1,p \ne q}^{S} {\sum\limits_{m = 0}^{\infty } {\sum\limits_{n = m}^{\infty } {\left[ \begin{gathered} A_{nm}^{(p)} Q_{1} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q) + B_{nm}^{(p)} Q_{3} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q) \hfill \\ + C_{nm}^{(p)} Q_{1} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q) + D_{nm}^{(p)} Q_{3} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q) \hfill \\ \end{gathered} \right]} } } \hfill \\ &\quad + a_{q}^{{ - 4n^{\prime} - 3}} C_{{n^{\prime}m^{\prime}}}^{(q)} + \sum\limits_{{n = m^{\prime}}}^{\infty } {C_{{nm^{\prime}}}^{(q)} K(2n + 1,2m^{\prime} + 1,2n^{\prime} + 1)} - \left( {1 - \frac{{2n^{\prime} + 1}}{{{\text{i}} kG_{q} a_{q} }}} \right)G_{{n^{\prime}m^{\prime}}}^{(q)} = - f(2n^{\prime} + 1,2m^{\prime} + 1,q)\cos ((2m^{\prime} + 1)\alpha ), \hfill \\ \end{aligned} $$
(B8)
$$ \begin{aligned} & \sum\limits_{p = 1,p \ne q}^{S} {\sum\limits_{m = 0}^{\infty } {\sum\limits_{n = m}^{\infty } {\left[ \begin{gathered} A_{nm}^{(p)} Q_{2} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q) + B_{nm}^{(p)} Q_{4} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q) \hfill \\ + C_{nm}^{(p)} Q_{2} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q) + D_{nm}^{(p)} Q_{4} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q) \hfill \\ \end{gathered} \right]} } } \hfill \\& \quad + a_{q}^{{ - 4n^{\prime} - 3}} D_{{n^{\prime}m^{\prime}}}^{(q)} + \sum\limits_{{n = m^{\prime}}}^{\infty } {D_{{nm^{\prime}}}^{(q)} K(2n + 1,2m^{\prime} + 1,2n^{\prime} + 1)} - \left( {1 - \frac{{2n^{\prime} + 1}}{{{\text{i}} kG_{q} a_{q} }}} \right)H_{{n^{\prime}m^{\prime}}}^{(q)} = - f(2n^{\prime} + 1,2m^{\prime} + 1,q)\sin ((2m^{\prime} + 1)\alpha ). \hfill \\ \end{aligned} $$
(B9)
A system of linear equations formulated by Eqs. (B2)–(B9), having the size of [8(M + 1)(N + 1)S] × [8(M + 1)(N + 1)S], is obtained by truncating m and m′ after M terms, and n and n′ after m (m′) + N terms according to the desired accuracy. Solving this linear system gives all the unknown coefficients in the velocity potentials.
Appendix C: Linear system for the special case of impermeable reef balls
Substituting the velocity potentials into Eq. (43) and conducting a similar process as that leading to Eqs. (B2)–(B5), we obtain
$$ \begin{aligned} & \sum\limits_{p = 1,p \ne q}^{S} {\sum\limits_{m = 0}^{\infty } {\sum\limits_{n = m}^{\infty } {2n^{\prime}\left[ \begin{gathered} A_{nm}^{(p)} Q_{1} (2n,2m,2n^{\prime},2m^{\prime},p,q) + B_{nm}^{(p)} Q_{3} (2n,2m,2n^{\prime},2m^{\prime},p,q) \hfill \\ + C_{nm}^{(p)} Q_{1} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q) + D_{nm}^{(p)} Q_{3} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q) \hfill \\ \end{gathered} \right]} } } \hfill \\ & \quad - (2n^{\prime} + 1)a_{q}^{{ - 4n^{\prime} - 1}} A_{{n^{\prime}m^{\prime}}}^{(q)} + \sum\limits_{{n = m^{\prime}}}^{\infty } {A_{{nm^{\prime}}}^{(q)} (2n^{\prime})K(2n,2m^{\prime},2n^{\prime})} = - 2n^{\prime}f(2n^{\prime},2m^{\prime},q)\cos (2m^{\prime}\alpha ), \hfill \\ \end{aligned} $$
(C1)
$$ \begin{aligned} & \sum\limits_{p = 1,p \ne q}^{S} {\sum\limits_{m = 0}^{\infty } {\sum\limits_{n = m}^{\infty } {2n^{\prime}\left[ \begin{gathered} A_{nm}^{(p)} Q_{2} (2n,2m,2n^{\prime},2m^{\prime},p,q) + B_{nm}^{(p)} Q_{4} (2n,2m,2n^{\prime},2m^{\prime},p,q) \hfill \\ + C_{nm}^{(p)} Q_{2} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q) + D_{nm}^{(p)} Q_{4} (2n + 1,2m + 1,2n^{\prime},2m^{\prime},p,q) \hfill \\ \end{gathered} \right]} } } \hfill \\ &\quad - (2n^{\prime} + 1)a_{q}^{{ - 4n^{\prime} - 1}} B_{{n^{\prime}m^{\prime}}}^{(q)} + \sum\limits_{{n = m^{\prime}}}^{\infty } {B_{{nm^{\prime}}}^{(q)} (2n^{\prime})K(2n,2m^{\prime},2n^{\prime})} = - 2n^{\prime}f(2n^{\prime},2m^{\prime},q)\sin (2m^{\prime}\alpha ), \hfill \\ \end{aligned} $$
(C2)
$$ \begin{aligned} & \sum\limits_{p = 1,p \ne q}^{S} {\sum\limits_{m = 0}^{\infty } {\sum\limits_{n = m}^{\infty } {\left[ \begin{gathered} A_{nm}^{(p)} Q_{1} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q) + B_{nm}^{(p)} Q_{3} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q) \hfill \\ + C_{nm}^{(p)} Q_{1} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q) + D_{nm}^{(p)} Q_{3} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q) \hfill \\ \end{gathered} \right]} } } \hfill \\ &\quad - \frac{{2n^{\prime} + 2}}{{2n^{\prime} + 1}}a_{q}^{{ - 4n^{\prime} - 3}} C_{{n^{\prime}m^{\prime}}}^{(q)} + \sum\limits_{{n = m^{\prime}}}^{\infty } {C_{{nm^{\prime}}}^{(q)} K(2n + 1,2m^{\prime} + 1,2n^{\prime} + 1)} = - f(2n^{\prime} + 1,2m^{\prime} + 1,q)\cos ((2m^{\prime} + 1)\alpha ), \hfill \\ \end{aligned} $$
(C3)
$$ \begin{aligned}& \sum\limits_{p = 1,p \ne q}^{S} {\sum\limits_{m = 0}^{\infty } {\sum\limits_{n = m}^{\infty } {\left[ \begin{gathered} A_{nm}^{(p)} Q_{2} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q) + B_{nm}^{(p)} Q_{4} (2n,2m,2n^{\prime} + 1,2m^{\prime} + 1,p,q) \hfill \\ + C_{nm}^{(p)} Q_{2} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q) + D_{nm}^{(p)} Q_{4} (2n + 1,2m + 1,2n^{\prime} + 1,2m^{\prime} + 1,p,q) \hfill \\ \end{gathered} \right]} } } \hfill \\ &\quad - \frac{{2n^{\prime} + 2}}{{2n^{\prime} + 1}}a_{q}^{{ - 4n^{\prime} - 3}} D_{{n^{\prime}m^{\prime}}}^{(q)} + \sum\limits_{{n = m^{\prime}}}^{\infty } {D_{{nm^{\prime}}}^{(q)} K(2n + 1,2m^{\prime} + 1,2n^{\prime} + 1)} = - f(2n^{\prime} + 1,2m^{\prime} + 1,q)\sin ((2m^{\prime} + 1)\alpha ). \hfill \\ \end{aligned} $$
(C4)