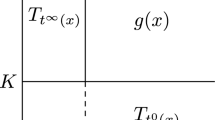Description of Shapiro steps on the potential energy surface of a Frenkel–Kontorova model, Part II: free boundaries of the chain

Abstract

We explain Shapiro steps in a Frenkel–Kontorova (FK) model for a 1D chain of particles with free boundaries. The action of an external alternating force for the oscillating structure of the chain is important here. The different ’floors’ of the potential energy surface (PES) of this model play an important role. They are regions of kinks, double kinks, and so on. We will find out that the preferable movements are the sliding of kinks or antikinks through the chain. The more kinks / antikinks are included the higher is the ’floor’ through the PES. We find the Shapiro steps moving and oscillating anywhere between the floors. They start with a single jump over the highest SP in the global valley through the PES, like in part I of this series. They finish with complicated oscillations in the PES, for excitations directly over the critical depinning force. We use an FK model with free boundary conditions. In contrast to other results in the past, for this model, we obtain Shapiro steps in an unexpected, inverse sequence. We demonstrate Shapiro steps for a case with soft ’springs’ between an 8-particle FK chain.

Graphic abstract

1 Introduction

Shapiro steps are reported in many experiments, see part I of this series for references [1]. We concentrate here on such steps in calculations of a Langevin equation with the FK model [2], which many workers saw for a good model of real Shapiro steps. Shapiro steps emerge for a combination of direct and alternating external forces where the frequency of the oscillation of the FK-chain is locked, and its sliding velocity is constant, though the direct force is increased. This paper is devoted to the aim to understand what happens under a Shapiro step inside the FK chain? How does the chain in the PES mountains moves if it slides downhill the effective PES? Average velocities of the chain are studied up to date. To look inside the FK chain we use, in a new treatment, the potential energy surface (PES) of the chain [3,4,5,6], as well as the tool of the highest Lyapunov exponent [1, 7].

The FK model describes the situation of a chain of particles with harmonic spring forces in between, where we additionally assume free boundaries of the chain here, in contrast to part I of this series [1]. We search the form of the movement of a 1D FK chain through a site-up potential. In every step, the chain changes. That is the reason why the boundary conditions should be free. A very surprising result of this part II is a reversed sequence of the Shapiro steps.

We specialize in the spring force to a soft value, in comparison to the site-up potential, and in contrast to our former references [3,4,5,6]. The chain is really of finite length. The ’winding number’ is the relation, the ’misfit’, between the original spring distance, $a_o$, and the periodicity, $a_s$, of the site-up potential. We discuss an example with winding number 1/2.

Overall, we treat here the PES for N particles of the chain and search for global valleys through the ’mountains’ of the N-dimensional PES for a sliding of the chain. Beside the use of a Langevin equation [2], an important part of the theory is the use of Newton trajectories (NT) for the description of the ’running’ stationary points of the PES under an external force. The NTs are curves in the configuration space of the chain. The NT theory was discussed recently in Refs.  [8,9,10,11], to name just a few. They are curves where at every point the gradient of the PES points into the same direction, called the search direction, or even the direction of the external force. If we compress or pull the chain, some or all coordinates of the particles change. Some examples of a changed chain are drawn in the paper. Because we can draw all N particles of a chain we can illustrate here N changing dimensions, like in chemistry for a molecule with N atoms. Such events are described in depth by the NTs. Every point of an NT is a configuration of the chain. To a given external driving force, the search direction, on any number of chain particles, we get the ’static’ curve of the NT on the PES of the movements of the chain. For practical reasons, we divide every NT into M nodes. The number of nodes used depends on the step length of the predictor of the NT program [8]. It holds analogously for the Langevin equation treated here as well.

We find that the chain does not move as an inelastic, solid body, or with a fixed, collective sliding along the site-up potential with translational symmetry of the chain. The chain of particles will be picked up by the external force (see Eq. (4) below). If the force is high enough then the chain forms a kink or an antikink, or pairs of them, or higher combinations [12] which usually break the symmetry of the initial chain. The FK model predicts the formation of such topological solitons [13]. A kink is a stretched structure of a part of the chain where an antikink is its compressed counterpart. These are quasiparticles which can move like a wave through the chain along a more or less flat valley of the PES, named a floor, and they so affect the current movement. The motion of the chain goes on by steps of the periodicity $a_s$ by antikinks, and/or kinks. The form of the existence of a movement under an excitation energy is the forward sliding of antikinks, akin to the biomechanical motion of an earthworm or a caterpillar, or the backward sliding of kinks.

Note that here the emergence of kinks or antikinks anywhere in the chain forbids the treatment of a ’unit cell’ of the chain, as it is assumed in Ref.  [14].

In Sect. 2, we introduce the FK model used in this paper and in Sect. 3, we explain the use of NTs. In Sect. 4, the case of the spring potential with N=8 chain length [2, 15] and $k/v=1/4$ soft springs is discussed. Using the tool of NTs we explore the many ’floors’ of the PES of the 8-chain. The aim is to be able to sort the different Shapiro steps into the PES later. In the main Sect. 5 we calculate and discuss a Langevin equation where the Shapiro steps emerge as solutions with locked frequency. To detect all possible such steps, we use the highest Lyapunov exponent which is explained in Sect. 5.2. Finally, we give a discussion and some conclusions.

2 The FK model

$\mathbf{x}=(x_1,...,x_N)$ represents the position of N discrete particles of a chain. We treat a finite chain. The positions $x_i$ are on a linear axis. It holds $x_i < x_{i+1}$ for the ordered chain. A boundary condition like $x_N=x_1$ [16] is not correct. The free end points of the chain determine the current average distance ${\tilde{a}}_o=(x_N-x_1)/(N-1)$. The harmonic spring potential is the sum of all particles and it results in the harmonic energy of a nearest neighbor potential

$$\begin{aligned} S(\mathbf{x})= \frac{k}{2} \sum _{i=1}^{N-1} (x_{i+1} - x_i - a_o)^2 \ . \end{aligned}$$

(1)

$a_o$ is the equilibrium distance of the chain without the site-up potential, and without the external force. We use another scaling of the particles than in Ref.  [1] to facilitate the connection to our former refs.  [3,4,5]. We emphasize that we do not use the so-called ’periodic boundary conditions’ [2]. The spring potential (1) belongs to the standard FK model. The PES for the variable changes of the $x_i$ is the Frenkel–Kontorova model

$$\begin{aligned} V(\mathbf{x}) = P(\mathbf{x}) + S(\mathbf{x}), \end{aligned}$$

(2)

where the site-up P is the potential

$$\begin{aligned} P(\mathbf{x}) = v \sum _{i=1}^N (1 - Cos(2\pi \,x_i/a_s)) \ . \end{aligned}$$

(3)

In numerical tests, we scale the $a_s$-constant of the P-potential to $2\pi$ for computational simplicity. We fix the potential constants $v=1$ and $k=1/4$ and use a short chain with $N=8$ particles [2, 15]. We treat a simple special case of the FK model with $a_s=2\,a_o$ with misfit 1/2 between the two potentials.

Because $v>0$, the on-site potential will modulate the chain if an external further force is applied. We use a linear force. We name the resulting PES an effective PES

$$\begin{aligned} V_{eff}(\mathbf{x})= V(\mathbf{x}) - F \ (l_1,..,l_N)^T \cdot \mathbf{x} \ . \end{aligned}$$

(4)

The multiplication point between the N-dimensional normalized force direction vector $(l_1,..,l_N)^T$ and the N-variable x means the scalar product. F is the factor for the amount of the external force. The new term is often named dc driving [17, 18] (for direct current) if F is fixed. If the amount of the force alternates in time then one names it ac driving [19] (for alternate current) with

$$\begin{aligned} F=F_{dc}+F_{ac}\,sin(2\pi \,\nu _o\,t) \end{aligned}$$

(5)

with a frequency $\nu _o$, and a ’time’ variable, t, which will also be used for the step length below in a Langevin equation. The force tilts the former on-site potential for particle $x_i$ with the incline $F\, l_i, \ i=1,...,N$. The extremal points of the effective PES, $V_{eff}$, minimums and SPs, move if F increases or decreases. A corresponding curve is described by NTs [8,9,10,11].

3 Brief summary on the theory of Newton trajectories

The stationary points on the effective potential with the general force vector $\mathbf{f}=F\,(l_1,..,l_N)^T$ satisfy the condition $\nabla _\mathbf{x}\ V_{eff}(\mathbf{x})=\mathbf{0}$. Its minimums and SPs satisfy the vector equation

$$\begin{aligned} \nabla _\mathbf{x}\ V_{eff} (\mathbf{x}) = \mathbf{g}(\mathbf{x}) - \mathbf{f} =\mathbf{0}. \end{aligned}$$

(6)

It meets a point where the gradient of the original PES, $\mathbf{g}(\mathbf{x})$, has to be equal to the force, f. The ansatz (6) is named Newton trajectory [20, 21] to the force direction, f. The gradient of $V(\mathbf{x})$ is the inner force of the chain, x, against changes of its structure. This force has to be equal to the external force, f. Then the chain is again in an equilibrium. We are at a stationary point of $V_{eff}(\mathbf{x})$. The NT describes a curve of force-displaced stationary points (FDSPs) of the tilted PES under a different load, F [8, 20,21,22,23,24,25]. Usually, the energy of minimums is increased, but the energy of SPs is lowered. This means that the barriers become lower. Any NT describes a connection between stationary points of an index difference of one [26]. Following numerically an NT is a method to search a next SP if a minimum is given, or vice versa.

Equation (6) can be written in a projector form [20, 21]

$$\begin{aligned} \left( \mathbf{U}-\mathbf{l}\,\mathbf{l}^T\right) \mathbf{g}(\mathbf{x})=\mathbf{0}, \end{aligned}$$

(7)

where $\mathbf{U}$ is the $N\times N$-unit matrix and the $\mathbf{l}$-unit vector is the normalized direction of $\mathbf{f}$. Equation (7) means nothing else than that g and l are parallel. If we differentiate the projector Eq. (7) with respect to the parameter that characterizes the FDSPs curve, s in a curve $\mathbf{x}(s)$, we obtain with the Hessian, H, in a tangent equation [21, 24]

$$\begin{aligned} \left( \mathbf{U}-\mathbf{l}\,\mathbf{l}^{T}\right) \mathbf{H}(\mathbf{x})\frac{d\mathbf{x}}{ds}=\mathbf{0}. \end{aligned}$$

(8)

For a calculation, the continuous NT is approximated by L node points. Here we have the Hessian of the FK model [3]. Then Eq. (8) is a way to generate the NT of a successive tilting. We use a predictor–corrector method for the calculations. For the predictor we use the tangent of the NT with Eq. (8).

The NT to any search direction describes the curve of FDSPs which emerges on the family of effective PES under this tilting direction. The NT connects the minimum and the SP of the process of interest because these two points belong to the $F=0$ effective surface, thus the original PES. Under increasing F value, diverse stationary points move on the NT, and at a critical $F_c$ they coalesce in a shoulder.

The extremal points of the effective PES, $V_{eff}$, move if F increases. Along the NT, F increases to a maximum at the barrier breakdown point (BBP) [10], where $F_c=|\mathbf{g}|_{max}$ is the critical force, and it decreases again to zero at the next SP. The situation is depicted in a schematic Fig. 1.

Fig. 1

The upper curve may be the profile over an NT through a PES, from a minimum to an SP of index one. The lower, red curve is the corresponding value of the gradient norm of the profile. At the maximum of the gradient norm one finds the BBP of the profile. It is at the zero of the curvature of the profile

Of course, to a given amount of F one can directly solve Eq. (6). It is an optimization task. However, it only works for $F \le F_c$ because for $F > F_c$ Eq. (6) has no solution, at least not in the neighborhood of the BBP of the current NT. There is no gradient of the PES with such a length. This insight will become important below in the paper.

Fig. 2

The MEP over consecutive SPs of index one (red) through the PES of an 8-FK chain. The SP structures are shown in Fig. 3, but the minimums in Fig. 4. ’Left’ BBPs are depicted by a cross, x

Fig. 3

Antikink SPs of index 1. $E = 5.2093, 5.3984, 5.4475, 5.8067$. One particle each climbs over its next top of the site-up potential. Note that the particles are artificially lifted on the potential to guide the eye. The real chain is on a straight line. Only the distances can change. The spring potential is not shown in the scheme

Fig. 4

Two different global and three antikink intermediate minimums. The energy is 4.37948, 4.78203, 4.80332, 4.87559, and 4.38004 correspondingly

For $N>2$, we cannot draw the PES of the chain, however, we can draw the energy profile of an NT over its coordinates. This is a one-dimensional curve of the N-dimensional configuration space. To any N, we can draw the structure of the chain at certain points of the NT. In this case, we will imagine the course of diverse NTs of interest hereinafter.

4 The PES of FK chain $N=8, v=1, k=1/4$

4.1 A low-energy path (LEP) for antikink SPs and intermediate minimums

There are some SP$_1$ of antikink character of the chain, being compressed structures, see Figs. 2 and 3. They can be obtained if one pushes the chain with a force from the left-hand side. SP$_1$ means a saddle point on the PES of index one, with one valley-direction along an eigenvector of the Hessian of the PES, but $N-1$ directions pointing uphill. It has one particle on the consecutive tops of the side potential. Further particles are sorted in their former wells. So, the chain is moved by one consecutively moving particle. We report a combined energy profile over four NTs in Fig. 2. Each one goes over one SP of index one, and all are joined together. Note that every part of the combined pathway curves through another dimension of the eight-dimensional configuration space. In sum, it describes a low-energy path through the PES. The four different search directions are taken so that we have an eye on the next SP$_1$ starting at the consecutive minimum left of the SP. At the first SP$_1$ is the second particle on the top of the potential; thus, we use $l_2=1$ and all other $l_i=0$ in Eq. (4). The second SP$_1$ has particle 4 on the top of the potential; thus, we use $l_4=1$ and all other $l_i=0$, and so on.

The corresponding ’moving’ SPs are shown in Fig. 3. Note that the two central SPs are not the vice versa mirror forms. In Fig. 4, we still present one global minimum at the top panel on the left-hand side, and the intermediate minima between the SPs of index one of Fig. 3, as well as a second global minimum down on the right-hand side. The two global minimums are no vice versa mirror forms either, though they themselves have mirror structure against their mean point.

The BBPs are depicted by crosses ’x’ in Fig.2, the corresponding critical forces $F_c$ are 0.523, 0.436, 0.459, and 0.632, correspondingly. If the first antikink is created, at the first, left SP$_1$ in Fig. 2, then there starts the first ’floor’ through the PES mountains. The barriers along this floor are named Peierls–Nabarro barriers [27]. Note that the floor here in this example is not really periodic, for $k=1/4$.

The ’width’ of the antikink is only 3 particles, in contrast to examples with stronger k parameter [6]. The length of the left, upper global minimum structure is $6.3\,\pi$, but the length of the right, lower global minimum structure is $7.7\,\pi$. Thus the one ${\tilde{a}}_o=2.829<a_o=\pi$ and the other ${\tilde{a}}_o=3.456>a_o=\pi$.

4.2 An LEP for kink SPs and intermediate minimums

If one pulls the FK chain at the right-hand side, there emerges further SP$_1$ of kink character, being stretched structures. Such an SP$_1$ has again one particle on the consecutive tops of the side potential. Another particle is ’alone’ in its well. So, the chain is moved to the right-hand side by one consecutive moving gap sliding to the left-hand side.

Fig. 5

The next low-energy pathway over consecutive SPs of index one through the PES of an 8-FK chain connecting kink stationary structures. The SP structures are shown in Fig. 6, but the minimums in Fig. 7

Fig. 6

Kink SPs of index 1. $E=5.208921, 5.39838, 5.44775$, and 5.81173 units

Fig. 7

Two different global and three kink intermediate minimums. The energy is 4.38004, 4.7822419, 4.8046913, 4.88193, and 4.37948 correspondingly

We report the energy profile over four NTs, every one over one SP of index one joined together, which describes the next low-energy path through the PES, in Fig. 5. Again the left BBPs on the NTs are depicted by crosses ’x’, the corresponding critical forces $F_c$ are 0.543, 0.46, 0.461, and 0.605, correspondingly. The corresponding SPs are shown in Fig. 6. In Fig. 7, we still present the kink minimums.

If one compiles the pathways of Fig. 2 and Fig. 5 together, one gets the movement of the chain by $2\,\pi =a_s$, the period of the side potential. Thus, one needs to overcome at least the SPs of index one near 5.8 units of energy to realize a continuous movement of the FK chain along the side potential, a sliding. Under the external force, one only needs the amount for the steepest BBP.

Kinks and antikinks have already been studies elsewhere [12, 28,29,30] for the simplest excited states which connect two neighboring ground states. ’Trains’ of equidistant antikinks are reported as well [27, 30]. We obtain here the shape of a kink/antikink by a numerical calculation, see Figs. 3, 4, 6 and 7.

It is worth noting that the kink, as well as the antikink form a spontaneous symmetry break of the given chain [31] since the global minimum is a symmetric structure which is the case here. The symmetry break for both LEPs is outside of an assumption of a ’symmetry operation’ in an FK chain in references [2, 14, 16, 32], see also Sect. 5.

Fig. 8

Energy profile of an NT for the FK 8-chain with $v=1$ and $k=1/4$. 25 stationary points are crossed here. The NT consequently connects SPs of an index difference of one. Peaks without color bullets are TPs of the NT. The first three SP$_1$ on the left-hand side are the same as in Fig. 2

Fig. 9

Diverse SPs with consecutive increase of the index from 1 to 4. Energies: SP$_1$ 5.80671, SP$_2$ 6.63568, SP$_3$ 7.42578, and SP$_4$ 8.0 units

4.3 A ’global’ NT to unit direction f=1/$\sqrt{N}$ (1,...,1)

In Ref.  [15], and many other references, the unspecific washboard force direction l=1/$\sqrt{N}$ (1,1,...,1) for the external force is used throughout. Thus, the force acts on all particles to the same amount. It is the ansatz which we test for the chain of interest, in contrast to the former subsections. The profile of the corresponding NT is presented in Fig. 8. The calculation leads in one run from the global antikink minimum of the chain up to the ’global’ SP of index four with four particles on the tops of the side potential, and four particles down in the wells, thus the energy is 4 times the pure side potential, thus 8 units, compare the lowermost right panel in Fig. 9.

The special NT fortunately reveals the four ’floors’ in the PES mountains of the 8-chain. Every floor is characterized by the number of kinks and/or antikinks on it [3,4,5]. All floors combined represent the ’global’ valley through which the chain has to move if it slides along the site-up potential. Together with Sects. 4.1 and 4.2, we conclude that we need a minimal transition energy of approximately 5.8 units, to move through an LEP, thus an energy difference of approx 1.4 units to the minimum. If one uses an energy difference of $(8-4.4)=3.6$ units, then one should ’fly’ more or less straight forward through the ’global’ valley.

The consecutive gallery of SPs of Fig. 8 might be a bit misleading here. The axis of the nodes only represents the development of the calculation of the NT, not the ’geographic’ position of the floors to each other. On the PES, the floors form parallel pathways through the mountains [3,4,5].

Note that an NT is not a dynamical description of the behavior of the chain under the force. It is a ’static’ artificial curve that fulfills only one condition: always on the curve, the gradient of the PES points into the search direction. Additionally, the trick with projector equations (6) and (7) allows us to follow the NT without using the corresponding amount, F, of the external force. The NT describes the movement of the stationary points on the corresponding effective PESs.

The first four minimums and the first three SP$_1$ on the pathway of the NT in Fig. 8 are the same as in Fig. 2. Here only some additional turning points (TP) of the profile emerge. The SP$_4$ in Fig. 9 has a higher symmetry than the two global minimums.

A real chain of particles will start to slide after the first BBP under force, and will then decrease after the last SP in any floor to the next minimum. As long as the force continues to act, the chain can again start to slide and so jump as a whole along the side potential. An ascend from the ith floor to the $i+1$st floor is a specialty of our NT. If the chain is pushed, or pulled by the external force into any SP region, it will follow another, a dynamical trajectory down to the next minimum, compare Sect. 5.

One can assume that generally the solution of an NT is different from the solution of the overdamped Langevin equation. Note that the full NT of Fig. 8 goes along a pathway with g$_{eff}$(x)=0 throughout. One can ascend from a global minimum to the ’global’ SP of index 4 with appropriate F values where at every point of the NT the ’Langevin’ Eq. (12), see below, does not make a micro step!

5 The overdamped Langevin equation

In Eq. (6), we already treated the derivation of the tilted potential Eq. (4). The components of the gradient of the effective PES are

$$\begin{aligned}&g_{eff\,1}= k\,( x_1-x_2 -a_o) + v\,sin(x_1) -F\,l_1\nonumber \\&\quad \mathrm{for }\, i=1, \end{aligned}$$

(9)

$$\begin{aligned}&g_{eff\,i}= k\,( 2\ x_{i} - x_{i+1} - x_{i-1}) +v\, sin(x_{i}) -F\,l_i \nonumber \\&\quad \mathrm{for }\, i=2,...,N-1, \end{aligned}$$

(10)

$$\begin{aligned}&g_{eff\,N}= k\, ( x_{N-1}-x_{N} -a_o) + v\,sin(x_{N})-F\,l_N\nonumber \\&\quad \mathrm{for }\, i=N \ . \end{aligned}$$

(11)

Note that here, under the free boundaries of the chain, two extra components emerge, in contrast to the case of the so-called ’periodic boundary conditions’ [1, 2]. If we put the gradient components to zero, we get the ansatz of the NT theory described in the former section. In contrast, one may use them on the right-hand side of an overdamped Langevin equation [2, 15]

$$\begin{aligned} \eta \ \dot{\mathbf{x}}= - \mathbf{g}_{eff}(\mathbf{x},t) \ . \end{aligned}$$

(12)

A ’time’, t, comes into the effective gradient by the external ac-force, Eq. (5). We use the damping factor $\eta =100$ throughout. Because of the damping, the ’velocity’ $\dot{\mathbf{x}}$ in Eq. (12) describes the steepest descent along $\mathbf{g}_{eff}$ in small steps. It is a mathematical tool for the description of an abstract sliding along the tilted site-up potential. Nevertheless, the abstract velocity also originates the Shapiro steps being the yield of many former references [2, 14, 16, 17, 33], to mention but a few.

Usually in former works the unspecific washboard force [34] $l_i=1/\sqrt{N}$ for all i is used. Note that the two boundary conditions for $x_1$, Eq. (9), and $x_N$, Eq. (11), are often missing. It also means that the constant $a_o$ is not directly present in the Langevin ansatz.

At a beginning, at $F=0$ and in a minimum, the gradient components are zero. All particles $x_i$ are in their equilibrium. What happens for small amounts of the external force, F? We can move the chain structure along the NT to direction $(l_1,...,l_N)$ using the tangent equation (8) as predictor and some corrector steps, as described before. The chain moves along the pathway of the NT, where all effective gradient components (9)-(11) stay on zero, step by step.

The Langevin Eq. (12) also leads to a solution with $\mathbf{g}_{eff}(\mathbf{x})=0$ using a pure $F_{dc}$-force. One can assume to find any point on the NT to the given amount F. After the BBP with the critical force, $F=F_c$, the NT goes on to the next SP$_1$, however, with an again decreasing force value F. If one assumes, in contrast, to choose $F>F_c$ in the Langevin equation then really an amount emerges for the velocity of a change of the chain. Thus one can understand the first increase of the ladder of Shapiro steps in Figures of Ref.  [15], see Sect. 5.2 below. By a stronger tilting of the force, F, stronger than $F_c$, the chain will be depinned and slides downhill the effective PES.

If $F>F_c$ then the NT has no solution, it becomes $|g_{eff}| >0$ and $\dot{\mathbf{x}}$ increases along the Langevin-ansatz. Such steps must move the chain over the BBP being a shoulder on the corresponding effective PES. On the other side of the shoulder the steepest descent of the Langevin ansatz then leads in direction to the next minimum of the effective PES, an intermediate, or, if the force, F, is higher than the corresponding $F_c$ of the next increase of the profile the move also continues in the direction to a global minimum. Here the process starts again. Thus, the chain moves without any stop.

5.1 Description of a usual dc- and a $(dc+ac)$-excitation of an 8-chain

We use the case N=8, $a_0=a_s/2=\pi$, $v=1$ and $k=1/4$. For the numerics, we tested that a step length of the steepest descent of 0.01 units is exact enough for our treatments. We approach $F_c=0.451$ where the sliding of the chain begins to start. (In comparison to Sects. 4.1 and 4.2, we have here a full external force acting on all particles at the same time but not only on one particle. So, the BBPs, the value of $F_{c}$, is not directly comparable.) Using $F_{dc}= 0.47$ and $F_{ac}=0$ we get Figs. 10 and 11. The profile of the effective energy, $V_{eff}$, is given in Fig. 10. If one increases the external force, $F_{dc}$, then the global slope in every Figure like Fig. 10 increases. Thus, the sliding becomes quicker. It is a quasi-trivial fact which one expects [2]. A higher excitation makes a higher sliding velocity.

To imagine the behavior of the chain, we reduce for Fig. 11 (and most of the next figures as well) the representation to the part of the original PES without the external potential. Note that the region of the PES where the chain slides is now far over the first floor of the PES mountains. Thus, the steepest descent, Eq. (12), does not go along the valley ground downhill which was depicted in Figs. 2 and 5. It does not cross the lower SPs of index one. It criss-crosses along any mountain flanks. The chain is not rigid. Every particle moves in its own dimension. It is only weakly held together by the weak spring constant, $k=1/4$. If one particle overcomes the top of the site-up potential, then other particles can stay in their wells. Thus, the pathway of the chain in the eight dimensions of the problem will be very curvilinear. The steepest descent does not immediately follow the sharp curves of the valley ground. It trots after along the side slopes of the mountains.

Principally, it is possible that a steepest descent can cross a ridge on its path downhill a PES. This was demonstrated by a 2D toy surface [26, 35].

Fig. 10

Effective energy profile of a Langevin solution for the FK 8-chain with $v=1$ and $k=1/4$. The energy decreases continuously because of $F_{dc}>F_{c}$ but with a different slope

Fig. 11

Energy profile (PES only) of the same Langevin solution like in Fig. 10. The remaining energy globally oscillates quasi-periodically in a complicated kind. The special start here at the SP$_4$ [2] does not play a deeper role after 5000 steps settling for the damped descent

If one adds the alternating force, the shape of the sliding profile becomes a little wilder. We use $F_{dc}= 0.4585$, $F_{ac}=0.85$, and $\nu _o=0.2$ in Fig. 12. It is a typical result of the Langevin Eq. (12). The nodes of the calculation play the role of the time, t, which is included in the ac-vibration, Eq.(5).

Fig. 12

Energy profile (PES only) of a Langevin solution with an additional ac-force. A quasi-oscillation over a large interval like in Fig. 11 is overlayed by a small oscillation caused by the external ac-force. (Start is at a global minimum.)

5.2 Lyapunov exponents

To understand the global behavior of the solutions of the Langevin equation, one studies the action of the phase flow on certain partial sets of the phase space R$^N$ [1]. The vector field, $\mathbf{g}_{eff}$, of Eq. (12) is the velocity field of the phase flow. The divergence, $div \,\mathbf{g}_{eff}$, then determines the velocity by which the value of an infinitesimal volume element changes at x(t), under the action of the flow.

The Lyapunov exponent $\lambda$ was introduced and discussed in Ref.  [1], part I of this series. If $\lambda <0$ then one can expect some sort of order for different trajectories. The more negative $\lambda <0$ the more regular movement can be expected. Usually the rate depends on the initial points. However, here we have a dissipative system where the start only determines some transient steps.

Fig. 13

The first Lyapunov exponent, $\lambda$, for increasing external force, $F_{dc}$, with $F_{ac} =0.285$ and $\nu _o=0.2$ fixed. The biggest spike at $F_{dc}=0.9$ depict the first, the main Shapiro step. Further steps go backwards in $F_{dc}$. The inlay below left is the extended left part at the beginning at $F_c$. One may guess more than 10 consecutive Shapiro steps

We fix $F_{ac}=0.285$, and $\nu _o=0.2$. For a step length of 0.01 in t and 100 000 steps for the equation system (12) we calculate the Lyapunov exponent for a series of $F_{dc}$ values in the range from $F_c$ to 1.0, with steps of $\varDelta F_{dc}=0.001$. We represent the first Lyapunov exponent, $\lambda$, in Fig. 13. Note the increasing spikes up to $F_{dc}=0.9$. The sequence of the spikes is found in inverse order to former results [2] for the FK ’in a box model’. An experimental result for a linear chain of Josephson junctions [36] has a similar sequence, like in Fig. 13. However, the model which belongs to the experiment has different parameters to ours, but one should note that the used boundary conditions are free ends.

We will treat the regions of the spikes of Fig. 13: they all ’house’ one Shapiro step of the FK model. The deeper the value of $\lambda$, the more ’stable’ is the oscillation of the chain on its way downhill the tilted site-up potential. Note: all interesting aspects concern the sliding region of the external force.

Fig. 14

Energy profile (PES only) of a Langevin trajectory with dc-force in the range of the first Shapiro step, with special $F_{dc}=0.9$, $F_{ac}=0.285$ and $\nu _o=0.2$. After a short transient process on the lhs, one has a perfect oscillation in unison with the ac-excitation. Every loop indicates the movement of the chain by the period, 2$\pi$, over the site-up potential, compare Figs. 15 and 16

Fig. 15

Enlarged energy profiles (PES only) of a cycle of Langevin trajectories at the Shapiro step 1 of Fig. 14. The colors are: (1) $F_{dc}=0.868$ light blue, (2) $F_{dc}=0.88$ blue, (3) $F_{dc}=0.90$ green, (4) $F_{dc}=0.92$ red, and (5) $F_{dc}=0.933$ black. The four turning points of the green profile of one cycle of the Langevin trajectory are depicted by $M_i$ for maximal TPs, or by $m_i$ for minimal TPs. One cycle of 1000 nodes of the profile corresponds to a double step of the chain by one period over the site-up potential, see Fig. 16

Fig. 16

Structures of the chain for the four turning points of the green profile of the Langevin trajectory of Fig. 15. They form the corner stones of a full cycle of the moving chain with a 2$\pi$ step along the site-up potential. Note that the upper TPs are near the two different structures of the SP$_4$

5.3 The first Shapiro step for the periodic movements of 2$\pi$ along the site-up potential

In the range of $F_{dc} \in [0.868,\,0.932]$ one meets the first Shapiro step, compare Ref.  [2] where the first step starts contrarily at the lowest side of $F_{dc}$. We use the fixed ac-force $F_{ac}=0.285$ and $\nu _o=0.2$. A global view of the profile of the PES only, over a trajectory is shown in Fig. 14 for the case $F_{dc}=0.9$. The profile shows periodic, regular, and short oscillations of a stable kind. Compare also an animation in the Supplementary data.

For the cases of $F_{dc}$ in the full range $[0.868,\,0.932]$ we find the same frequency of the profile: it is locked. First, we show the profile over the trajectory for 25 000 nodes, being the time steps, in Fig. 14, and second, we emphasize a cycle of 1000 time steps of the profile, before step 50 000, and we show the section in a larger form. It is done in Fig. 15 by the central green profile for $F_{dc}=0.9$, by the light blue profile for the smaller $F_{dc}=0.868$, by the blue profile for $F_{dc}=0.88$, and by the red profile for the larger $F_{dc}=0.92$, and by the black profile for $F_{dc}=0.932$. The turning points (TP) of the green profile are depicted by $M_i$ for the upper ones, and by $m_i$ for the lower ones. One full cycle over 4 TPs makes a movement of the chain by one site-up well further, a step of $2\pi$ along the site-up potential, see Fig. 16. Two full cycles of the ac-force are used here. A trajectory in the region of the first Shapiro step explores the PES of the chain in an impressive way: the upper TPs on the PES are slightly over the ’global’ SP$_4$ where half of the particles turn at the same time over their next tops of the site-up potential. The two upper SP$_4$ are mirror pictures, vice versa, thus they are equal in energy. The lower TPs are slightly over the two global minimums of the chain. The two global minimums, on the other hand, are of the same energy, but they are not mirror pictures, vice versa. The oscillation fits into the ’global’ valley over the two SP$_4$ structures. One can imagine the step from $m_1$ to $M_2$ near the SP$_4$ by forming a fourfold antikink, a fourfold compression of the chain, but the next step from $m_2$ to $M_1$ near the next SP$_4$ by forming of a fourfold kink, a fourfold stretching. The corresponding times for an increase, or a decrease of the pathways on the PES are perfectly synchronized with the ac-oscillation.

On the frequency itself: We have the t-step length of 1/$\eta$=0.01 in the program, and $\nu _o=0.2$, thus a cycle of 500 t-steps is one period of the ac-force. 1000 steps correspond to a double-cycle in the ac-force (5) of $sin(4 \pi )$ in Fig. 15. 500 Steps of the ac excitation make the cycle from $M_1$ to $m_1$, but the next 500 steps finish the cycle over $M_2$ to $m_2$. Then the next double-cycle starts. The maxima of the profile correspond to the maxima of the ac-force, and the minima of the profile correspond to the minima of the ac-force. The Shapiro step needs such a lockstep of the sliding and the ac-force (5).

We try to understand how the period of the sliding acts, and how it can be locked along the region of the Shapiro step. We are in the region of $0.9=F_{dc}>>F_c=0.451$ of a strong sliding. The negative part of the ac-force, of $F_{ac}\ sin(2\pi \nu _o t)$, cannot cause that the sum of both parts become smaller than $F_c$. We guess that under the positive part of the ac-force the chain ascends to an upper TP, M$_i$; however, then the negative part of the ac-force fits to a downhill pathway near to a global minimum. Then, if the chain structure is near the bottom of the PES well, just in time, the next ascend starts, and so on. Here it is still quite similar to the ’box’-case of the chain described in part I [1].

Fig. 17

Energy profile (PES only) of a Langevin trajectory with the final dc-force of the first Shapiro step, at $F_{dc}=0.933$. After a short transient process, we find a time-interval of approximately 25,000 steps with a quite good periodic oscillation. But then it degenerates, and so on

Fig. 18

Effective energy profile of the Langevin trajectory for $F_{dc}=0.7$ + the ac-force. The energy alternates

Fig. 19

Energy profile (PES only) of a Langevin trajectory with dc-force in the range of the second Shapiro step, with $F_{dc}=0.7$, $F_{ac}=0.285$ and $\nu _o=0.2$. After a transient process, one has again an oscillation in unison with the ac-excitation

If $F_{dc}$ varies in the region of the first Shapiro step, then the former remarks apply in an analogous kind, for every $F_{dc}$ in the region of the Shapiro step. Any small change of $F_{dc}$ does not make a quicker frequency. It will now change the exact crossing of a ridge of the PES; however, this does not determine another periodicity. The oscillation may slightly change its course on the PES, its frequency is fixed. One may imagine that the oscillation revolves in the PES mountains. The finding is in contrast to the box-case, where a larger $F_{dc}$ is balanced by an internal back-vibration of the chain, but where the pathway of the oscillation holds the high symmetric ridge over the SP$_4$ but does not revolve [1].

So, one can ask how the large interval of $F_{dc}$ values of the main Shapiro step will come to its end? A profile is shown for the upper border of the interval, at $F_{dc}=0.933$ in Fig. 17. After a short transient process, we find a time interval of approximately 25,000 steps with a nice periodic oscillation. One can imagine the pathway of the chain over the PES where in every vibration it turns from one vibration to the next a little, only a very small piece. But over 25,000 vibrations, this accumulates to a degeneration. So the region of the PES which it uses by the oscillation will slowly change, and then the vibration degenerates for some steps. Just to start again a time interval of approximately 25,000 steps for a stable oscillation, and so on. Note that also in the regions of the ’degeneracy’ of the oscillation, near steps 33,000 and 70,000, the chain slides continuously further downhill. The behavior is different for the box-case model. There at the ’end’ of Shapiro step one in part I, Ref.  [1], Fig. 6 holds, nevertheless, the non-periodic sliding downhill the ridge symmetry over the SP$_4$, throughout.

5.4 Second Shapiro step

This step includes the interval $F_{dc}\in [0.695,\,0.717]$. We use a fixed ac-force $F_{ac}=0.285$ and $\nu _o=0.2$. Now there emerges a difference to the first step: it has parts with $F < F_c =0.451$; thus, pinned regions exist for a part of the external force. The energy profile of the full, effective PES demonstrates such a different action of the external force by the existence of minima, see Fig. 18.

A global view of the profile of the PES only, over a trajectory is shown in Fig. 19 for the case $F_{dc}=0.7$. The profile shows periodic, and regular oscillations of a stable kind for large enough nodes. For the cases of $F_{dc}$ in the range [0.695, 0.717], we find the same frequency of the profile: it is locked. First, we show the profile over the trajectory for 25 000 nodes, in Fig. 19, and second, we emphasize a cycle over 1500 time steps of the profile, and we show the section in a larger form. It is done in Fig. 20 by the blue profile for $F_{dc}=0.6975$, by the green profile for $F_{dc}=0.7$, and for $F_{dc}=0.715$ in red. Compare also an animation in the Supplementary data.

Fig. 20

Enlarged energy profiles (PES only) of a cycle of 1500 t-steps of Langevin trajectories at the Shapiro step 2 of Fig. 19. The colors are (1) $F_{dc}=0.6975$ blue, (2) $F_{dc}=0.7$ green, (3) $F_{dc}=0.715$ red. One cycle of the profile corresponds to a step of the chain by one period over the site-up potential, see Fig. 21. The curves are postponed by a cycle of the ac-force because of different settlings for initial nodes

Fig. 21

The six turning points of the green profile of a Langevin trajectory of Fig. 20 form a full cycle of the moving chain with 2$\pi$ along the site-up potential

Note the equal frequencies of all curves in Fig. 20. The turning points of the green profile are depicted with $M_i$ for upper, and $m_i$ for lower ones. Note that no stationary points are crossed. The turning point M$_1$ of the profile is over an SP$_3$, but this of M$_2$ is below an SP$_3$, compare the structures in Fig. 21.

One full cycle over 6 turning points makes a movement of the chain by one site-up well further, a step of $2\pi$ along the site-up potential. By the structures in Fig. 21, it is not to visible that some parts of the chain do a back-step in their site-up wells if the ac part of the force is in a pinned region. Though a half-loop of the Langevin trajectory is in the pinned region of the energy, it does not converge to a fixpoint because the trajectory escapes for the next $F>F_c$ from the pinned region and slides into the next well. This means that no ’steady state’ emerges, as it is claimed [14]. If any, one could speak about a steady flow. Accidentally, at this Shapiro step, the PES has the shape to allow such a periodic movement for an interval of $F_{dc}$ values. Correspondingly inverse parts of the ac-force will cause a sliding of the chain after the next ridge.

Note that other site-up potentials, or another choice of the external forces do not destroy the pattern of Shapiro steps [2, 16, 17, 33]. If there is any appropriate PES then the periodic ac-force will find a region in the mountains of the PES where the lock-down of a Shapiro step can happen.

First, we try to understand how the period of the sliding comes into play. A cycle of 500 time steps is one period of the ac-force. In Fig. 20 1500 steps correspond to 3 cycles in the ac-force (5) of $sin(6 \pi )$. In contrast to Shapiro step one, where one finds two times a jump of the chain over the two global SP$_4$, we find here that the chain jumps through the regions of three different SP$_3$, for one cycle.

If $F_{dc}$ varies in the region of the Shapiro step, then the former remarks apply in an analogous kind. A larger $F_{dc}$ does not make a quicker frequency. The exact crossing of a ridge of the PES at a step t does not determine the periodicity. A larger $F_{dc}$ needs larger negative ac-parts for the pinning, but the period of $sin(2\pi \nu _o t)$ is the same. But this period determines the average velocity of the sliding oscillations being locked here [2].

5.5 Third Shapiro step

The next Shapiro step of the movement of 2$\pi$ along the site-up potential is in the range of $F_{dc} \in [0.61, 0.62]$. We again use the fixed ac-force $F_{ac}=0.285$ and frequency $\nu _o=0.2$. A global view of the energy profile of a Langevin trajectory is shown in Fig. 22 for the case $F_{dc}=0.6175$. The profile shows periodic, regular, and short oscillations of a stable kind. For all cases of $F_{dc}$ in the range [0.61, 0.62], we find the same frequency of the profile: it is again locked. We depict the profile over the trajectory in Fig. 22, and then we emphasize 2000 nodes, so to say one period, and show the section of the profile in a larger form. It is done in Fig. 23 by the green profile, as well as for other profiles for some other dc values.

Fig. 22

Energy profile (PES only) of a Langevin trajectory with dc-force in the range of Shapiro step 3, with $F_{dc}=0.6175$, $F_{ac}=0.285$, and $\nu _o=0.2$. One has only a local oscillation in lockstep with the ac-excitation which indicates the movement of the chain by a period of the site-up potential

Fig. 23

Enlarged energy profiles (PES only) of a double-cycle of 2000 t-steps of Langevin trajectories at the Shapiro step 3 of Fig. 22. The colors are $F_{dc}=0.6125$ red, $F_{dc}=0.6150$ blue, $F_{dc}=0.6175$ green and $F_{dc}=0.6200$ black. The crosses, x, depict energy levels of stationary points, nearby on the PES. One double cycle of the profile corresponds to a step of the chain by one period over the site-up potential, see Fig. 24

Fig. 24

The eight turning points of the (green) profile of a Langevin curve of Fig. 22 form a full cycle of the moving chain along the site-up potential. The upper TPs M$_1$ and M$_3$ seem to be near to an SP$_3$; however, the M$_2$ and M$_4$ seem to be nearer to an SP$_2$

Fig. 25

Intermediate minimums and SPs near the turning points of Fig. 24

Note the equal frequencies of all curves in Fig. 23, but the different amplitudes. Now the constant $F_{dc}$ is smaller than for the second Shapiro step. Again the resulting force, F, is not throughout over $F_c$, and we have some pieces where the trajectory turns back to potential minima. However, now the PES fits exactly the doubling of such steps of the trajectory, and again the period of the ac-force determines the period of the sliding: the same for all $F_{dc}$ values in the Shapiro interval. The turning points of the profiles are again depicted with $M_i$ for upper, and $m_i$ for lower ones. For the green profile, the points are depicted by brown bullets. Note that no stationary points are crossed. By colored crosses we indicate stationary points of the PES nearby the points $M_i$ or $m_i$. It means here red x: SP1, green x: SP$_2$, and blue x: SP$_3$. Corresponding structures of the chain for the points $M_i$ or $m_i$, and the neighboring stationary points are shown in Figs. 24 and 25.

A full cycle over 8 turning points causes a movement of the chain by one site-up well further. But such a cycle consists of two nearly equal subcycles. It is like for the MEP over the SPs of index one, in Sect. 4.1, that at least 8 stationary points form this oscillation. However, here we are anywhere high in the mountains of the PES. The highest upper turning point of the profile is in a region over an SP$_3$.

The spread of the profiles starts with the smallest $F_{dc}$ and ends with the largest $F_{dc}$. A cycle of 2000 steps in Fig. 23 corresponds to four cycles in the ac-force (5) of $sin(2 \pi )$.

5.6 Shapiro step 4

At $F_{dc} =0.565$ is a small region of a periodic oscillation with 10 TPs, over a time interval of 2500 time steps. We represent one profile in Fig. 26.

Fig. 26

Energy profiles (PES only) of a cycle of 2500 t-steps of the Langevin trajectory at Shapiro step 4

5.7 Shapiro step 5

In the range of $F_{dc} \in [0.530, 0.538]$ one meets a next Shapiro step for the fixed ac-force $F_{ac}=0.285$ and $\nu _o=0.2$. The profile again shows periodic and regular oscillations of a stable kind. Now a cycle of the oscillation takes 3000 time steps and includes 12 TPs. For the cases of $F_{dc}$ in the range [0.530, 0.538] we find the same frequency of the profile: it is locked. We emphasize a cycle of the profile, and we show the section in a larger form. It is done in Fig. 27 by the black profile for $F_{dc}=0.535$, as well as for other $F_{dc}$ values. Note the equal frequencies of all curves in Fig. 27, but the different amplitudes. No stationary points are crossed.

Fig. 27

Energy profiles (PES only) of a cycle of 3000 t-steps of the Langevin trajectories at Shapiro step 5. The colors are: (1) $F_{dc}=0.531$ red, (2) $F_{dc}=0.5325$ blue, (3) $F_{dc}=0.535$ black, and (4) $F_{dc}=0.5375$ green. One cycle of the profile corresponds to a step of the chain by one period over the site-up potential, see Fig. 28. The curves are somehow postponed because of different settlings for initial nodes

The upper TPs of the profile often go over an SP$_3$, but sometimes also below an SP$_3$. Corresponding structures of the chain for the points $M_i$ or $m_i$ are shown in Fig. 28. One full cycle over 12 turning points makes a movement of the chain by one site-up well further, a step of $2\pi$ along the site-up potential.

Some parts of the chain sometimes make a back-step in their site-up wells if the ac part of the force is in a pinned region. It is interesting that the spread of the profiles starts with the smallest $F_{dc}$ and ends with the largest $F_{dc}$. The smallest $F_{dc}$ makes the largest amplitude between the turning points. This is connected with the ac-force. For the lower end of the $F_{dc}$-force interval, at 0.53, we find for 42.6$\%$ of t-steps the external force lower than $F_c$, but for the upper end, at 0.538, there are only 41.6$\% \ t$-steps of the external force lower than $F_c$. Below a larger part of the ac-force makes a pinning, but for the other end, for a higher dc-force, a smaller part of the ac-force pins the chain. So, a downhill backwards search of the Langevin equation is the longer, the larger the influence of the negative part of the ac-force is. Then the next increase to the ridge of the PES has also to be longer, up to the point where a new sliding starts. The alternating change of these antipode movements is not dictated by the PES, however, by the period of the ac-force. Accidentally at this Shapiro step the PES has the shape to allow such a complicated periodic movement for an interval of $F_{dc}$ values. Correspondingly inverse parts of the ac-force will cause a sliding of the chain after the next ridge.

Fig. 28

The 12 turning points of the black profile of a Langevin trajectory of Fig. 27 form a full cycle of the moving chain with 2$\pi$ along the site-up potential

A cycle of 500 steps is one period of the ac-force. In Fig. 27 1500 steps correspond to 3 cycles in the ac-force (5). Observe in Fig. 27 that again the node-axis does not exactly describe the direction of the movement of single particles of the chain. The global direction of the movement of the chain goes along the site-up potential; however, single particles can back-oscillate if Langevin steps search in a pinned region of the chain.

5.8 Shapiro step 6

At $F_{dc} =0.515$ is a small region of a periodic oscillation with 14 TPs, over a time interval of 3500 time steps. We represent one profile in Fig. 29.

5.9 Shapiro step 7

At $F_{dc} =0.5037$ is a small region of a periodic oscillation with 16 TPs, over a time interval of 4000 time steps. We represent one profile in Fig. 30.

5.10 Shapiro step 8

Step 8 seems to be not assignable.

5.11 Shapiro step 9

There is a small Shapiro step for the used parameters, ac-force $F_{ac}=0.285$ and $\nu _o=0.2$, in the range of $F_{dc} \in [0.4895, 0.4905]$. The profile shows periodic and regular oscillations. For all cases of $F_{dc}$ in the range [0.61, 0.62] we find the same frequency of the profile: it is again locked. We emphasize 5000 nodes, one period of the chains movement, and show the section of the profile. This is done in Fig. 31.

Fig. 29

Energy profiles (PES only) of a cycle of 3500 t-steps of the Langevin trajectory at Shapiro step 6

Fig. 30

Energy profiles (PES only) of a cycle of 4000 t-steps of the Langevin trajectory at Shapiro step 7. It seems that a period of 2000 t-steps is one period; however, one needs a doubling for a full cycle

Fig. 31

Energy profile (PES only) of a double-cycle of 5000 t-steps of a Langevin trajectory at the Shapiro step 9. It is $F_{dc}=0.49$. Shown is one cycle of the oscillation

There are 20 turning points of the profile on 5000 t-steps. No stationary points are crossed. A full cycle over 20 turning points makes a movement of the chain by one site-up well further. Such a cycle consists of two subcycles.

5.12 Shapiro steps 10 to 12

These steps again seem to be not assignable.

5.13 Shapiro step 13

The assignment of this step is a little tricky. At $F_{dc} =0.477$ is we have an external excitation of a periodic oscillation with 28 TPs, over a time interval of 7000 time steps. We represent one profile in Fig. 32.

Fig. 32

Energy profile (PES only) of a cycle of 7000 t-steps of a Langevin trajectory at Shapiro step 13 with $F_{dc}=0.477$

The numbering of the Shapiro steps was adapted for steps 9 and 13 to the regularity of Table 1, compare Fig. 13.

Table 1 Turning points and oscillation frequency of Shapiro steps. Note one ac-period is 500 t-steps

5.14 Fractional steps

We treat the external excitation with $F_{dc}=0.779$ between the first and the second Shapiro steps, compare Fig. 13. It was named in former treatments Shapiro step with number 3/2. It results in a periodic oscillation with one cycle over 2500 t-steps, and an oscillation number of 14 TPs at all. It causes a movement of the chain over 4$\pi$ along the site-up potential. In Fig. 33, we show the energy profile of one cycle.

Fig. 33

Energy profile (PES only) of a cycle 2500 t-steps of a Langevin trajectory at Shapiro step 3/2 with $F_{dc}=0.779$. One cycle moves the chain by 4$\pi$

For the external excitation $F_{dc}=0.753$ between the 3/2 and the second Shapiro step, compare Fig. 13, we find a further regular oscillation. One can name it Shapiro step with number 7/4. It results in a periodic oscillation with one cycle over 4000 t-steps, and an oscillation number of 12 TPs at all. It causes a movement of the chain over 6$\pi$ along the site-up potential. In Fig. 34, we show the energy profile of one cycle.

Fig. 34

Energy profile (PES only) of a cycle 4000 t-steps of a Langevin trajectory at Shapiro step 7/4 with $F_{dc}=0.753$. Note that the similar peaks of two half cycles represent different structures of the chain, though the two half-cycles look similar. One cycle moves the chain by 6$\pi$

We assume that further fractional steps could be observed up to diverse Farey steps [32, 37].

6 Discussion

Shapiro steps concern the average velocity of the trajectory of the Langevin equation. This velocity is locked on a step. Note that there is no such construct like a ’steady state’ as it is often pretended in former papers [14, 33].

Every periodic curve with period 2$\pi$ can be characterized by a relation of the kind

$$\begin{aligned} \mathbf{x}(t+s)=\mathbf{x}(t)+2\pi \end{aligned}$$

(13)

for the chain, $\mathbf{x}(t)$, with an appropriate value of t-steps, s. The periodic loops of the Langevin trajectories of the Shapiro step fulfill such a relation. Here we find the rule

$$\begin{aligned} s=(r+1)*1000 \end{aligned}$$

(14)

if the damping factor $\eta =100$ and the $F_{ac}$ frequency $\nu _o=0.2$ are used and where r is the number of the Shapiro step, compare Table 1.

However, the quasi-periodic long-loops of pure dc-tilted chains, like those in Fig. 11, or $dc+ac$ driven like in Fig. 12, also fulfill a periodicity, with a larger s value, and may be with a further factor by the period, 2$\pi$. So, such a relation may be not the criterion for the existence of the Shapiro steps, as it is pretended in former papers [2, 14, 16, 17, 33], to name but a few.

7 Conclusion

In both cases of the FK model, in parts I and II of this series, we have Shapiro steps for a Langevin equation. However, with a very different character. We find out that for an FK chain with free boundaries the results of the FK model with the periodic boundary conditions [1] are not transferable. We find that the sequence of the Shapiro steps is of an inverse order. Of course, our FK model with free boundaries is quite more flexible, in comparison to the variable box frame caused by the PBC used in former papers [1, 2]. This inversion of the sequence of the Shapiro steps is a strange result of this part II of the series.

In the box model of the FK chain, the oscillations of all Shapiro steps go over the barriers of the consecutive SP$_4$ versions. It may be induced by the full symmetry of the ’washboard’-force used. Let us remind at this point that for the FK chain with free ends we find another kind of oscillations. They criss-cross along the flanks of the PES mountains and find lower pathways using the barriers of SP$_3$ and SP$_2$ of the PES. The break of the symmetry of the exciting force, f, is possible by the very lower rigidity of the chain with free ends. The locked frequency of the Shapiro steps, on the other hand, may be enforced by a corresponding revolving of the chain’s oscillation across the PES. The shutdown of such a revolving is illustrated in Fig. 17.

Both parts I and II of this series help the unpaired socks to reunite with their soul mates.