Analytical treatment of the transient motion of inertial beams attached to coupling inertial resonators

Abstract

This paper presents, for the first time, an analytical formulation to determine the transient response of an elastic beam possessing distributed inertia and connected to a coupling inertial resonator, represented by a gyroscopic spinner. The latter couples the transverse displacement components of the beam in the two perpendicular directions, thus producing roto-flexural vibrations. A detailed parametric study is presented that illustrates the effects of the beam’s distributed inertia and of the resonator’s characteristics. The limit case of massless beam is examined and it is shown that in some situations the distributed inertia in the beam should not be neglected. Analytical results are also validated by finite element computations. An illustration is also presented that demonstrates the effectiveness of using the considered inertial devices to mitigate hazardous vibrations in structural systems. It is envisaged that this paper may be useful in the analysis of flexural waveguides and metamaterials consisting of inertial elastic beam elements.

1 Introduction

In recent years, there has been an increasing interest in the study of engineering elements that produce inertial coupling effects. This has been partially motivated by the need to better characterise the tools embedded in pre-existing technologies, for instance, rotor systems used in aircraft and drive shafts employed in a variety of land and sea vehicles. Rotating elements also play a crucial role in the stabilisation of light, flexible and large spacecraft, and this has motivated research in this direction concerning mechanical elements with embedded gyroscopic effects in the last 40 years. More recently, this research has been reinvigorated through the development of devices used to design structured systems or metamaterials possessing rotating inertial elements for the purposes of controlling wave motion. Here, we study an example of such a device, which is formed from connecting a gyroscopic spinner to a beam, and demonstrate its performance in controlling the vibration of structures exposed to hazardous environmental conditions.

Gyroscopic systems are widely used not only in the flight control of aircrafts and spacecrafts, but also in gas turbines and in the construction of robotic manipulators [1]. In a recent work [2], it has been proposed to employ beams with gyroscopic properties to reduce the low-frequency vibrations, produced by seismic sources, in a bridge. This novel device has potential applications in the earthquake protection of civil engineering structures and represents an efficient alternative to other approaches [3]. In elastic lattices, the introduction of gyroscopic spinners has been exploited to alter the dispersive properties of the system [4, 5], to create waveforms localised in a single line passing through any point of the medium [6] and to generate one-way interfacial and edge waves [7,8,9,10]. A novel asymptotic model has been developed in [11] to determine the transient responses of gyro-elastic lattices capable of exhibiting cloaking properties and creating unidirectional waveforms. In [12], it has been proposed to use gyroscopic spinners for the stabilisation of slender monopole towers that are very sensitive to wind and earthquakes.

The mechanical action of gyroscopic spinners induces chiral effects into a system. Chiral structures have gathered increasing interest in the scientific community due to their unique properties and numerous potential applications. A structure or an object is “chiral” if it cannot be mapped onto its mirror image by rotations and translations [13]. In the literature, most of the elastic and mechanical chiral systems are geometrically chiral [14,15,16,17,18,19,20,21,22].

Systems of elastic beams connected to gyroscopic spinners have been considered in [23,24,25]. The spinners are used to tune the natural frequencies and vibration modes of the structure for stabilisation purposes. The models presented in [23, 24] represent physical interpretations of the so-called “gyrobeams”, which are theoretical structural elements consisting of elastic beams with a continuous distribution of angular momentum. The analytical formulation of gyrobeams and gyro-elastic continua has been developed in [26,27,28,29,30]. In elastic plates, gyroscopic spinners attached at the tips of elastic beams have been introduced to create one-way interfacial flexural waves [31, 32].

In previous works, the study of a system of elastic beams connected to gyroscopic spinners has been carried out in the frequency domain. In some cases, in order to obtain a closed-form analytical solution, it has been assumed that the distributed inertia in the beam is negligible when compared to the concentrated mass of the spinner. In this paper, we present an analytical formulation that provides a method to determine the response of an inertial beam in the transient regime. It will be shown that taking into account the distributed inertia of the beam leads to a response of the system with significantly different features with respect to the case of a massless beam. In the present paper, the beam is connected to a “gyro-hinge”, which is a special constraint represented by a hinge attached to a gyroscopic spinner, as described in Sect. 2. Motivated by applications to turbo-machinery and rotor systems, in [33] the natural frequencies and mode shapes of a flexible system composed of a spinning disk and a shaft have been obtained by using the finite element method.

The proposed formulation corresponds to a linearised model, following from the coupling of Euler’s equations for the spinner and the equations of the Euler–Bernoulli beam, resulting from the assumption that the nutation angle of the spinner is small. This is in accordance with Euler–Bernoulli theory, which is constructed under the premise that the displacements and rotations in the beam are small. Accordingly, stability problems are not considered in this paper (the interested reader can refer to other works, for example [34]). Perturbation methods used in the analysis of the stability of multi-parameter gyroscopic systems in the presence of non-conservative forces have been discussed in [35, 36]. Vibrations of a rotating beam connected to a point mass have been studied in [37], in conjunction with the dynamic stability of the rectilinear shape of the beam by employing the Lyapunov direct method. Stability problems in a nanobeam have been investigated in [38] using a higher-order non-local strain gradient theory.

The use of gyroscopic spinners in civil structures is not common as in other fields, such as aerospace and mechanical engineering. Nonetheless, it is important to emphasise that gyroscopic spinners are different from rotors that have a prescribed spin and are employed in several applications dealing with vibration problems of rotating machines. In fact, a gyroscopic spinner not only spins around its axis, as a common rotor, but it also nutates and precesses. This motion is governed by a separate set of differential equations, the Euler equations. Moreover, the sum of precession and spin rates of a gyroscope remains constant throughout the motion, while the individual rates may change in time. This brings additional physical features that are not present when classical rotors are considered. Here, we show that the main effect of a gyroscopic spinner attached to a single elastic beam is to couple the two transverse displacement components of the beam that would be independent in the absence of the spinner; we also demonstrate that this effect significantly modifies the dynamic behaviour of the beam.

The growth of interest in flexural systems with uncommon properties (“flexural metamaterials”) has led to the design of innovative structures consisting of beams and rods. Dispersion degeneracies and localisation phenomena in lattices of Rayleigh beams have been studied in [39,40,41]. Applications in soft robotics and structural folding of beams undergoing large deformations have been considered in [42,43,44]. The effect of configurational forces on periodic systems of elastic beams with sliding sleeves has been investigated in [45]. A passive technique to suppress localised vibrations in periodic structures made of small beams has been proposed in [46]. Analytical and experimental approaches have been developed in [47] to extract torsional and flexural bandgaps in phononic crystal beams. Near-resonance phenomena, total reflection and trapping of flexural waves in elastic plates connected to spring-mass oscillators have been investigated in [48] for both plates in vacuo and those floating on the surface of water. Wave propagation and bandgap optimisation in quasi-crystalline structures made of rods have been analysed in [49, 50]. Problems of dynamic failure propagation in periodic flexural systems have been presented and solved in [51,52,53]. Characterisation of waves in periodic micro-structured flexural systems incorporating rotational inertia has been carried out in [54].

The present paper is organised as follows. In Sect. 2, we present the analytical formulation to determine the transient response of an elastic beam with distributed inertia connected to a gyro-hinge. In Sect. 3, we consider the limit case of a massless beam, for which a simplified approach can be employed. We also compare the analytical results obtained in Sect. 3 with those based on the general formulation developed in Sect. 2 in the case when the beam’s density is assumed to be small, showing that there is a very good agreement. In Sect. 4, we analyse the transient motion of the flexural system for different values of the beam’s density and for various properties of the gyroscopic spinners. In Sect. 5, we provide concluding remarks. Further, in Appendices A and B, we present some important results used in deriving the solution to the considered problem. In Appendix C, we compare the analytical results yielded by the procedure described in Sect. 2 with the numerical outcomes provided by an independent finite element model built in a commercial software, which is used to validate the analytical procedure. Finally, in the Supplementary Material accompanying this paper, we present the results of a physical application demonstrating how gyro-hinges can be implemented in a structural frame to reduce the vibrations due to external loading.

2 Transient motion of a beam with distributed inertia and gyroscopic boundary conditions

We study the flexural vibrations of an Euler–Bernoulli beam, clamped at one end and connected to a gyro-hinge at the other end, as shown in Fig. 1. The gyro-hinge is a special constraint, introduced for the first time in [23], consisting of a hinge attached to a gyroscopic spinner. Physically, this configuration for the connection between the beam and the gyroscopic spinner can be realised by drilling a hole at the tip of the beam and nesting the base of the gyroscopic spinner inside that hole. This allows the gyroscope to spin and, at the same time, prevents the transmission of the twisting motion to the beam. Furthermore, this type of connection ensures the continuity of rotation between the beam and the spinner. Namely, the flexural rotations of the beam at its tip and the tilting of the gyroscope at its base are equal at any instant of time. The reader is also referred to [24] for a more detailed description of the connection.

The beam has length L, mass density $\rho$, Young’s modulus E and square cross-section of area A and second moment of area J. We are interested in the beam’s transverse motion, characterised by the displacements u and v in the x- and y-direction, respectively. The system is subjected to an initial disturbance, whose specific form is described in what follows. The presence of external loads, which are not considered in this formulation for the sake of simplicity, can be taken into account following standard procedures based on Duhamel’s principle; in particular, the effect of time-dependent bending moments applied at the boundary $z = L$ can be incorporated using a similar method to that described in [55].

Since Euler–Bernoulli beam theory is based on the assumption of small displacements and small rotations, the equations of motion of the gyroscopic spinner (namely, Euler’s equations) are linearised, in particular assuming that the angle of nutation is small. As discussed in detail in [23], this linearised formulation leads to the derivation of coupled boundary conditions for the gyro-hinge, which relate the curvatures in the beam with the time derivatives of the beam’s rotations at the junction (see (2d)).

Fig. 1

Euler–Bernoulli beam, with a clamped end at $z = 0$ and a gyro-hinge at $z = L$

2.1 Formulation of the problem

The governing equations for the flexural vibrations of an Euler–Bernoulli beam are given by

$$\begin{aligned} EJ u''''(z,t) + \rho A \ddot{u}(z,t) = 0 \, , \quad EJ v''''(z,t) + \rho A \ddot{v}(z,t) = 0 \, , \end{aligned}$$

(1)

where the primes and the dots denote derivatives with respect to the longitudinal coordinate z and to time t, respectively. We point out that the equation of motion for the displacement component w along the z-axis is decoupled from Eqs. (1), and hence axial vibrations will not be considered in the present paper.

At the end $z = 0$ the transverse displacements and flexural rotations are zero, while at the end $z = L$ the gyro-hinge boundary conditions are imposed (see [23]). Therefore, the boundary conditions for the beam in Fig. 1 have the form

$$\begin{aligned} u(0,t)&= 0 \, , \qquad v(0,t) = 0 \, , \end{aligned}$$

(2a)

$$\begin{aligned} u'(0,t)&= 0 \, , \qquad v'(0,t) = 0 \, , \end{aligned}$$

(2b)

$$\begin{aligned} u(L,t)&= 0 \, , \qquad v(L,t) = 0 \, , \end{aligned}$$

(2c)

and

$$\begin{aligned}&EJ u''(L,t) + I_0 \ddot{u}'(L,t) + I_1 \varOmega \dot{v}'(L,t) = 0 \, , \nonumber \\&EJ v''(L,t) + I_0 \ddot{v}'(L,t) - I_1 \varOmega \dot{u}'(L,t) = 0 \, , \end{aligned}$$

(2d)

for $t > 0$. The gyro-hinge boundary conditions are given by (2c) and (2d), where the latter correspond to the balance of angular momentum for the spinner. Eqs. (2d) are obtained assuming that the rotations of the gyroscopic spinner and of the beam at their connection remain the same at every instant of time. Further, the connection is designed such that the spinning motion of the spinner is not transmitted to the beam; this can be realised by drilling a cylindrical hole inside the beam, make it frictionless and nest the end of the spinner inside the hole. In (2d), $I_0$ and $I_1$ indicate the moments of inertia of the spinner. Assuming that the latter is a solid of revolution, $I_1$ is the moment of inertia about the axis of revolution, while $I_0$ is the moment of inertia about the transverse principal axes passing through the spinner’s base. The parameter $\varOmega$ is referred to as gyricity and represents the sum of the initial precession and spin rates of the gyroscopic spinner, which remains constant throughout the motion when the nutation angle of the spinner is small, as proved in [23]. We point out that the gyricity is an independent parameter, which can be varied by changing the precession and spin rates at $t = 0$. We also note that the precession and spin rates can vary during time, but their sum $\varOmega$ is constant. When $I_0 = I_1 = 0$, the gyro-hinge reduces to a classical hinge, characterised by zero displacements and moments. When $I_0 \ne 0$ and $I_1 = 0$ or $\varOmega = 0$, the gyroscopic spinner behaves as a mass with non-zero rotational inertia.

The initial conditions are expressed by

$$\begin{aligned} u(z,0)= & {} u_0(z) \, , \qquad v(z,0) = v_0(z) \, , \end{aligned}$$

(3a)

$$\begin{aligned} \dot{u}(z,0)= & {} \dot{u}_0(z) \, , \qquad \dot{v}(z,0) = \dot{v}_0(z) , \end{aligned}$$

(3b)

where $u_0(z)$, $v_0(z)$, $\dot{u}_0(z)$ and $\dot{v}_0(z)$ are given functions.

2.2 Normalisation of governing equations

Now, we formulate the problem in normalised form in order to study the effect of non-dimensional parameters on the behaviour of the system. To this aim, we use the following normalisations:

$$\begin{aligned}&z = \hat{z} L \, , \; t = \sqrt{\frac{I_0 L}{EJ}} \hat{t}, \, \; u(z,t) = \hat{u}(\hat{z},\hat{t}) L \, , \; v(z,t) = \hat{v}(\hat{z},\hat{t}) L \, , \nonumber \\&u_0(z) = \hat{u}_0(\hat{z}) L \, , \; v_0(z) = \hat{v}_0(\hat{z}) L \, , \; \dot{u}_0(z) = \sqrt{\frac{EJ}{I_0 L}} \dot{\hat{u}}_0(\hat{z}) \, , \; \dot{v}_0(z) = \sqrt{\frac{EJ}{I_0 L}} \dot{\hat{v}}_0(\hat{z}). \end{aligned}$$

(4)

In addition, we introduce the non-dimensional quantities

$$\begin{aligned} \mu = \frac{\rho A L^3}{I_0} \quad \text {and} \quad \varOmega ^{*} = \varOmega \sqrt{\frac{L I_1^2}{EJ I_0}} , \end{aligned}$$

(5)

that play the role of the effective mass of the beam and the effective gyricity of the spinner, respectively.

In going forward, we use the above normalisation and we drop the symbol “$^{\wedge }$” for ease of notation. Accordingly, the governing equations (1) become

$$\begin{aligned} u''''(z,t) + \mu \ddot{u}(z,t) = 0 \, , \quad v''''(z,t) + \mu \ddot{v}(z,t) = 0 \, , \qquad 0< z < 1 \, , \; t > 0 \, , \end{aligned}$$

(6)

with the boundary conditions at the base

$$\begin{aligned} u(0,t) = v(0,t) = 0 \, , \; u'(0,t) = v'(0,t) = 0 \, , \end{aligned}$$

(7)

the gyro-hinge conditions at the tip

$$\begin{aligned}&u(1,t) = v(1,t) = 0 \, , \end{aligned}$$

(8a)

$$\begin{aligned}&u''(1,t) + \ddot{u}'(1,t) + \varOmega ^{*} \dot{v}'(1,t) = 0 \, , \; v''(1,t) + \ddot{v}'(1,t) - \varOmega ^{*} \dot{u}'(1,t) = 0 \, , \end{aligned}$$

(8b)

and the initial conditions

$$\begin{aligned} u(z,0)= & {} u_0(z) \, , \quad v(z,0) = v_0(z) \, , \end{aligned}$$

(9a)

$$\begin{aligned} \dot{u}(z,0)= & {} \dot{u}_0(z) \, , \quad \dot{v}(z,0) = \dot{v}_0(z) \, . \end{aligned}$$

(9b)

2.3 Eigenfunction expansions for the displacement functions

The displacements satisfying (6)–(9) can both be expressed in the form of a series as follows:

$$\begin{aligned} u(z,t) = \sum _{k=1}^{\infty } F_1^{(k)}(t) G_1^{(k)}(z) \, , \qquad v(z,t) = \sum _{k=1}^{\infty } F_2^{(k)}(t) G_2^{(k)}(z) \, . \end{aligned}$$

(10)

Here, $F^{(k)}_j(t)$ and $G^{(k)}_j(z)$, for $k\ge 1$ and $j=1,2,$ govern the temporal and spatial variation of the response of the system, respectively, for $t>0$. Upon substitution of these representations into (6)–(9), using a standard procedure outlined in Appendix A, one can decouple the functions $F_j^{(k)}(t)$ and $G^{(k)}_j(z)$, for $k\ge 1$ and $j=1,2$, and then solve the problems satisfied by these functions separately. It follows that the time-dependent functions are

$$\begin{aligned} \begin{pmatrix} F_1^{(k)}(t) \\ F_2^{(k)}(t) \end{pmatrix} = d_1^{(k)} \begin{pmatrix} 1 \\ 1 \end{pmatrix} \mathrm {e}^{\mathrm {i} \omega _k t} + d_2^{(k)} \begin{pmatrix} 1 \\ -1 \end{pmatrix} \mathrm {e}^{-\mathrm {i} \omega _k t} \, , \end{aligned}$$

(11)

where $d_1^{(k)}$ and $d_2^{(k)}$ are unknown constants that are determined from the initial conditions (9). Here, the quantity $\omega _k$ will be interpreted as the dimensionless frequency of vibration for mode k. Additionally, the spatially dependent functions are retrieved in the form

$$\begin{aligned} G_j^{(k)}(z) = B_j \left\{ -\gamma _k \left[ \cos (\beta _k z) - \cosh (\beta _k z) \right] + \sin (\beta _k z) - \sinh (\beta _k z) \right\} \, , \end{aligned}$$

(12)

where

$$\begin{aligned} \gamma _k = \frac{\sinh (\beta _k) - \sin (\beta _k)}{\cosh (\beta _k) - \cos (\beta _k)} \, . \end{aligned}$$

(13)

The quantity $\beta _k = (\mu \omega _k^2)^{1/4}$ in (12) and (13) represents a dimensionless spectral parameter.

2.3.1 Orthogonality conditions for the eigenfunctions

Let

$$\begin{aligned} \varvec{G}^{(k)}(z) = \begin{pmatrix} {G}_1^{(k)}(z) \\ {G}_2^{(k)}(z) \end{pmatrix} \quad \hbox {and} \quad \tilde{\varvec{G}}^{(k)}(z) = \begin{pmatrix} {G}_1^{(k)}(z) \\ -{G}_2^{(k)}(z) \end{pmatrix} \, . \end{aligned}$$

(14)

Using the above conditions on $G_j^{(k)}$, $k\ge 1$ and $j=1,2$, and applying integration by parts, one can show that the vector functions $\varvec{G}^{(j)}(z)$ and $\varvec{G}^{(m)}(z)$, $j \ne m$, satisfy the orthogonality conditions

$$\begin{aligned} 0=&\mu \int _{0}^1 \varvec{G}^{(j)}(z) \cdot \varvec{G}^{(m)}(z) \mathrm {d}z + \left. \left( \varvec{G}^{(j)}(z)\right) '\right| _{z=1} \cdot \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} \nonumber \\&+\frac{\mathrm {i} \varOmega ^{*}}{\omega _j - \omega _m} \left. \left( \varvec{G}^{(j)}(z)\right) '\right| _{z=1} \cdot \varvec{R} \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} \quad (j \ne m) \, , \end{aligned}$$

(15)

with

$$\begin{aligned} \varvec{R} = \begin{pmatrix} 0 &{} 1 \\ -1 &{} 0 \end{pmatrix} \, , \end{aligned}$$

(16)

where (15) will be referred to as orthogonality condition 1, and

$$\begin{aligned} 0=&\mu \int _{0}^1 \varvec{G}^{(j)}(z) \cdot \tilde{\varvec{G}}^{(m)}(z) \mathrm {d}z + \left. \left( \varvec{G}^{(j)}(z)\right) '\right| _{z=1} \cdot \left. \left( \tilde{\varvec{G}}^{(m)}(z)\right) '\right| _{z=1} \nonumber \\&+ \frac{\mathrm {i} \varOmega ^{*}}{\omega _j + \omega _m} \left. \left( \varvec{G}^{(j)}(z)\right) '\right| _{z=1} \cdot \varvec{R} \left. \left( \tilde{\varvec{G}}^{(m)}(z)\right) '\right| _{z=1} \quad (j \ne m) , \end{aligned}$$

(17)

that we call orthogonality condition 2. The proofs of the orthogonality conditions 1 and 2 are given in Appendix B.

2.3.2 Eigenfrequency equation

Substituting the expression (12) for $G_j^{(k)}(z)$ ($j=1,2$) into the gyro-hinge boundary conditions, we derive the following homogeneous system:

$$\begin{aligned} \begin{pmatrix} \nu _k &{}\mathrm{i} \eta _k \\ -\mathrm{i}\eta _k &{} \nu _k \end{pmatrix} \begin{pmatrix} B_1 \\ B_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \, , \end{aligned}$$

(18)

where

$$\begin{aligned} \nu _k =&\left\{ \gamma _k \left[ \cos {(\beta _k)} + \cosh {(\beta _k)} \right] - \sin {(\beta _k)} - \sinh {(\beta _k)} \right\} \nonumber \\&- \frac{\beta _k^3}{\mu } \left\{ \gamma _k \left[ \sin {(\beta _k)} + \sinh {(\beta _k)} \right] + \cos {(\beta _k)} - \cosh {(\beta _k)} \right\} \, \end{aligned}$$

(19a)

$$\begin{aligned} \eta _k =&\frac{\beta _k \varOmega ^{*}}{\sqrt{\mu }} \left\{ \gamma _k \left[ \sin {(\beta _k)} + \sinh {(\beta _k)} \right] + \cos {(\beta _k)} - \cosh {(\beta _k)} \right\} . \end{aligned}$$

(19b)

Looking for non-trivial solutions of (18), we determine the equations which provide the eigenfrequencies of the system:

$$\begin{aligned} \nu _k + \eta _k = 0 \, , \quad \nu _k - \eta _k = 0 . \end{aligned}$$

(20)

We note that when the effective gyricity $\varOmega ^{*} = 0$ we have that $\eta _k = 0$, and (20) yields the double eigenfrequencies of a beam, clamped at one end and with a hinge at the other end that connects the beam’s tip to a rotational mass. Furthermore, we observe that the system (18) allows to determine $B_1$ as a function of $B_2$ (or vice versa), providing the complete representation of the eigenfunctions of the system. In this case, one of the components of the eigenfunction is purely imaginary if the other one is chosen as real in determining the eigenmode.

Additionally, if $\beta _k\rightarrow \infty$, (13), (19) and (20) imply that the eigenfrequencies for the system are determined from the equation

$$\begin{aligned} \left[ 1-\cos (\beta _k)\cosh (\beta _k)\right] ^2=0 , \end{aligned}$$

(21)

which provides the double eigenfrequencies of a beam whose ends are clamped. This observation also follows from the governing equations of the system in Appendix A (see (A.23)–(A.26)).

2.3.3 Expressions of transverse displacements as series representations

The transverse displacements u and v of the beam are thus given by

$$\begin{aligned} \begin{pmatrix} u(z,t) \\ v(z,t) \end{pmatrix} =&\sum _{k=1}^{\infty } \begin{pmatrix} F_1^{(k)}(t) G_1^{(k)}(z) \\ F_2^{(k)}(t) G_2^{(k)}(z) \end{pmatrix} \nonumber \\ =&\sum _{k=1}^{\infty } \left\{ d_1^{(k)} \varvec{G}^{(k)}(z) \mathrm {e}^{\mathrm {i} \omega _k t} + d_2^{(k)} \tilde{\varvec{G}}^{(k)}(z) \mathrm {e}^{-\mathrm {i} \omega _k t} \right\} \, , \end{aligned}$$

(22)

where (10) and (11) were used.

2.4 Initial conditions

Using the initial conditions (9), we calculate the coefficients $d_1^{(k)}$ and $d_2^{(k)}$ in order to fully determine the transverse displacements u and v (see Eq. (22)).

2.4.1 Initial displacement vector

Evaluating the displacement vector in (22) at the initial time $t=0$ using (9a), taking the dot product with $\varvec{G}^{(m)}(z)$ and integrating, we obtain

$$\begin{aligned} \int _{0}^1 \varvec{U_0}(z) \cdot \varvec{G}^{(m)}(z) \mathrm {d}z= \sum _{k=1}^{\infty } \left\{ d_1^{(k)} \int _{0}^1 \varvec{G}^{(k)}(z) \cdot \varvec{G}^{(m)}(z) \mathrm {d}z + d_2^{(k)} \int _{0}^1 \tilde{\varvec{G}}^{(k)}(z) \cdot \varvec{G}^{(m)}(z) \mathrm {d}z \right\} , \end{aligned}$$

(23)

where $\varvec{U_0}(z) = \left( u_0(z), v_0(z) \right) ^{\mathrm {T}}$. Next, by using (22) to compute the initial rotation at the beam’s tip at $z=1$, in a similar way we obtain

$$\begin{aligned} \varvec{U_0}'(1) \cdot \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} =&\sum _{k=1}^{\infty } \left\{ d_1^{(k)} \left. \left( \varvec{G}^{(k)}(z)\right) '\right| _{z=1} \cdot \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} \right. \nonumber \\&\left. + d_2^{(k)} \left. \left( \tilde{\varvec{G}}^{(k)}(z)\right) '\right| _{z=1} \cdot \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} \right\} \, . \end{aligned}$$

(24)

We combine (23) with (24) and employ the orthogonality conditions 1 and 2, given by Eqs. (15) and (17), respectively, to retrieve the following infinite algebraic system for the coefficients $d_j^{(k)}$ ($j=1,2$):

$$\begin{aligned} U^{(m)}&= d_1^{(m)} \alpha ^{(m)} + d_2^{(m)} \tilde{\alpha }^{(m)}+ \sum _{\begin{array}{c} k=1\\ k \ne m \end{array}}^{\infty } \left\{ d_1^{(k)} \frac{\mathrm {i} \varOmega ^{*}}{\omega _m - \omega _k} \left. \left( \varvec{G}^{(k)}(z)\right) '\right| _{z=1} \cdot \varvec{R} \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} \right. \nonumber \\&\quad \left. +d_2^{(k)} \frac{\mathrm {i} \varOmega ^{*}}{\omega _m + \omega _k} \left. \left( \tilde{\varvec{G}}^{(k)}(z)\right) '\right| _{z=1} \cdot \varvec{R} \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} \right\} \, , \end{aligned}$$

(25)

where $U^{(m)}$ on the left-hand side is

$$\begin{aligned} U^{(m)} = \mu \int _{0}^1 \varvec{U_0}(z) \cdot \varvec{G}^{(m)}(z) \mathrm {d}z + \varvec{U_0}'(1) \cdot \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} \, \end{aligned}$$

(26a)

that is found from combining (23) and (24) according to the orthogonality conditions. Additionally, in the right-hand side of (25) we have

$$\begin{aligned} \alpha ^{(m)}= & {} \mu \int _{0}^1 \varvec{G}^{(m)}(z) \cdot \varvec{G}^{(m)}(z) \mathrm {d}z + \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} \cdot \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} \, , \end{aligned}$$

(26b)

$$\begin{aligned} \tilde{\alpha }^{(m)}= & {} \mu \int _{0}^1 \tilde{\varvec{G}}^{(m)}(z) \cdot \varvec{G}^{(m)}(z) \mathrm {d}z + \left. \left( \tilde{\varvec{G}}^{(m)}(z)\right) '\right| _{z=1} \cdot \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} \, . \end{aligned}$$

(26c)

In the calculations, we consider a finite number of M terms in the series of (25), with M taken sufficiently large (note that when $\varOmega ^{*} = 0$ there is no need to employ such an approach). Accordingly, we can write (25) as

$$\begin{aligned} \varvec{U} = \varvec{\varSigma }^{(1)} \varvec{D}^{(1)} + \varvec{\varSigma }^{(2)} \varvec{D}^{(2)} , \end{aligned}$$

(27)

where

$$\begin{aligned} \varvec{U} = \left\{ U^{(m)} \right\} _{m=1}^{M} \, , \quad \varvec{D}^{(j)} = \left\{ d_j^{(m)} \right\} _{m=1}^{M},\quad \varvec{\varSigma }^{(j)} = \left[ \varSigma _{pq}^{(j)} \right] _{p,q=1}^{M} \quad (j=1,2) \end{aligned}$$

(28)

with

$$\begin{aligned} \varSigma _{pq}^{(1)} = {\left\{ \begin{array}{ll} \alpha _p &{} \text {if } p = q,\\ \frac{\mathrm {i} \varOmega ^{*}}{\omega _p - \omega _q} \left. \left( \varvec{G}^{(q)}(z)\right) '\right| _{z=1} \cdot \varvec{R} \left. \left( \varvec{G}^{(p)}(z)\right) '\right| _{z=1} &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(29a)

and

$$\begin{aligned} \varSigma _{pq}^{(2)} = {\left\{ \begin{array}{ll} \tilde{\alpha }_p &{} \text {if } p = q,\\ \frac{\mathrm {i} \varOmega ^{*}}{\omega _p + \omega _q} \left. \left( \tilde{\varvec{G}}^{(q)}(z)\right) '\right| _{z=1} \cdot \varvec{R} \left. \left( \varvec{G}^{(p)}(z)\right) '\right| _{z=1} &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(29b)

Note that the components of the eigenfunctions $\varvec{G}^{(p)}(z)$ are related by a purely imaginary factor (see Sect. 2.3.2). Hence the corresponding scalar products in the off-diagonal components $\varvec{\varSigma }^{(j)}$, $j=1,2$, will be real.

2.4.2 Initial velocity vector

Following a similar procedure to that presented in Sect. 2.4.1, we use the initial condition (9b) to obtain

$$\begin{aligned} \varvec{V} = \mathrm {i} \varvec{S}^{(1)} \varvec{D}^{(1)} - \mathrm {i} \varvec{S}^{(2)} \varvec{D}^{(2)} . \end{aligned}$$

(30)

In the above,

$$\begin{aligned} \varvec{V} = \left\{ V^{(m)} \right\} _{m=1}^{M}, \quad \varvec{S}^{(j)} = \varvec{\varSigma }^{(j)}\varvec{P} \quad (j=1,2), \end{aligned}$$

(31)

with

$$\begin{aligned} \varvec{P}={\text {diag}}_{1\le k\le M}\{\omega _k\} \end{aligned}$$

(32)

and

$$\begin{aligned} V^{(m)} = \mu \int _{0}^1 {\dot{\varvec{U}}_0}(z) \cdot \varvec{G}^{(m)}(z) \mathrm {d}z + {\dot{\varvec{U}}_0}'(1) \cdot \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} \, , \end{aligned}$$

(33)

where ${\dot{\varvec{U}}_0}(z) = \left( \dot{u}_0(z), \dot{v}_0(z) \right) ^{\mathrm {T}}$.

2.4.3 Determination of coefficients $d_j^{(m)}$

From (27) and (30), we derive the vectors $\varvec{D}^{(1)}$ and $\varvec{D}^{(2)}$, corresponding to approximate solutions of the infinite system, which are given by

$$\begin{aligned} \varvec{D}^{(1)} = - \mathrm {i} \left( \varvec{S}^{(1)} \right) ^{-1} \left[ \varvec{V} + \mathrm {i} \varvec{S}^{(2)} \varvec{D}^{(2)} \right] \end{aligned}$$

(34a)

and

$$\begin{aligned} \varvec{D}^{(2)} = \left[ \varvec{\varSigma }^{(2)} + \varvec{\varSigma }^{(1)} \left( \varvec{S}^{(1)} \right) ^{-1} \varvec{S}^{(2)} \right] ^{-1} \left[ \varvec{U} + \mathrm {i} \varvec{\varSigma }^{(1)} \left( \varvec{S}^{(1)} \right) ^{-1} \varvec{V} \right] \, , \end{aligned}$$

(34b)

respectively. By construction, the matrices involved in the above expressions contain real entries (see Sect. 2.4.1 and 2.4.2). Nonetheless, if both the initial displacement and velocity vectors are non-zero, the resulting coefficients $d_1^{(k)}$ and $d_2^{(k)}$ of the vectors $\varvec{D}^{(1)}$ and $\varvec{D}^{(2)}$ are generally complex.

Substituting the coefficients of the vectors $\varvec{D}^{(1)}$ and $\varvec{D}^{(2)}$ into the approximate expressions for the transverse displacements u and v along the beam’s axis during time, we obtain

$$\begin{aligned} \begin{pmatrix} u(z,t) \\ v(z,t) \end{pmatrix} = {\left[ \sum _{k=1}^{M} \left\{ d_1^{(k)} \varvec{G}^{(k)}(z) \mathrm {e}^{\mathrm {i} \omega _k t} + d_2^{(k)} \tilde{\varvec{G}}^{(k)}(z) \mathrm {e}^{-\mathrm {i} \omega _k t} \right\} \right] }+ R_{M}(z,t)\, , \end{aligned}$$

(35)

where $R_{M}(z,t)$ is the remainder term resulting from the truncation of the infinite system (25). In the subsequent calculations, we use the first term in the right-hand side of (35). Since the coefficients $d_1^{(k)}$ and $d_2^{(k)}$ are generally complex, the displacement components u(z, t) and v(z, t) are given by the real part of the right-hand side of (35).

The method proposed above has also been validated with an independent finite element simulation performed in Comsol Multiphysics (version 5.3). The comparison between analytical and numerical results is presented in Appendix C.

3 Limit case: non-inertial beam

In this section, we study the limit case when the density of the beam is negligibly small in comparison with the inertia of the gyroscopic spinner.

3.1 Problem formulation for a massless beam

The governing equations for the flexural motion of a massless beam are given by (6) with $\mu = 0$. Consequently, the transverse displacements are cubic functions of the spatial coordinate z. In this case, we write the boundary conditions as follows:

$$\begin{aligned} u(0,t)&= 0 \, , \qquad v(0,t) = 0 \, , \end{aligned}$$

(36a)

$$\begin{aligned} u'(0,t)&= 0 \, , \qquad v'(0,t) = 0 \, ,\end{aligned}$$

(36b)

$$\begin{aligned} u(1,t)&= 0 \, , \qquad v(1,t) = 0 \, ,\end{aligned}$$

(36c)

$$\begin{aligned} u'(1,t)&= \theta _y(t) \, , \qquad v'(1,t) = -\theta _x(t) , \end{aligned}$$

(36d)

where $\theta _y(t)$ and $\theta _x(t)$ are the unknown rotations around the x- and y-axis, respectively. Therefore, the expressions for the transverse displacements in the beam are given by

$$\begin{aligned} u(z,t) = \theta _y(t) \left( z^3 - z^2 \right) \, , \qquad v(z,t) = -\theta _x(t) \left( z^3 - z^2 \right) \, . \end{aligned}$$

(37)

Using the gyro-hinge boundary conditions (8b), we obtain the following system of ordinary differential equations for the rotations:

$$\begin{aligned} \ddot{\theta _y}(t) - \varOmega ^{*} \dot{\theta _x}(t) + 4 \theta _y(t) = 0,\quad \ddot{\theta _x}(t) + \varOmega ^{*} \dot{\theta _y}(t) + 4 \theta _x(t) = 0 . \end{aligned}$$

(38)

The initial conditions (9) lead to

$$\begin{aligned}&\theta _y(0) \left( z^3 - z^2 \right) = u_0(z) \, , \qquad \theta _x(0) \left( z^3 - z^2 \right) = -v_0(z) \, , \end{aligned}$$

(39a)

$$\begin{aligned}&\dot{\theta _y}(0) \left( z^3 - z^2 \right) = \dot{u}_0(z) \, , \qquad \dot{\theta _x}(0) \left( z^3 - z^2 \right) = -\dot{v}_0(z) \, , \end{aligned}$$

(39b)

where $u_0(z)$, $v_0(z)$, $\dot{u}_0(z)$ and $\dot{v}_0(z)$ are given functions that have to be consistent with the boundary conditions.

3.2 Example and comparison with the analytical formulation based on the series representations

We assume that $u_0(z) = \bar{u}_0(z^3-z^2)$, $\dot{u}_0(z) = 0$, $v_0(z) = 0$ and $\dot{v}_0(z) = 0$. Hence, the initial conditions for the rotations are given by

$$\begin{aligned} \theta _y(0) = \bar{u}_0 \, , \qquad \theta _x(0) = 0 \, , \qquad \dot{\theta _y}(0) = 0 \, , \qquad \dot{\theta _x}(0) = 0 \, . \end{aligned}$$

(40)

We solve the system of differential equations (38) complemented with the initial conditions (40) using the solver ODE45 in Matlab. In particular, we calculate the time-histories of the transverse displacements in the middle point of the beam’s axis, located at $z = 1/2$. The trajectory of this point is shown in Fig. 2 by a solid black line.

In the same figure, the dashed grey line represents the trajectory obtained with the method developed in Sect. 2 when the effective density $\mu$ is very small. The total number of modes considered in the present simulation is $M = 8$. This value has been chosen after checking the convergence of results for increasing values of M (see Sect. 4.2). Figure 2 shows that the agreement between the formulations presented in Sects. 2 and 3.1 is excellent, as the two curves are almost indistinguishable. We emphasise that additional studies have been performed for this linearised system (whose results are not reported here for brevity) where different initial conditions have been considered; also for those cases, the approaches developed in Sects. 2 and 3.1 yield almost indiscernible outcomes, as expected.

The results of Fig. 2 also highlight the coupling introduced into the system by the gyro-hinge between the two transverse displacements u and v. Although the initial disturbance is produced by a displacement in the x-direction, the beam also vibrates in the y-direction. The motion of each point of the beam’s axis is not circular, but small oscillations are generated by the contributions of different harmonics.

Fig. 2

Trajectory of the point of the beam’s axis positioned at $z = 1/2$, determined for a massless beam using the formulation in Sect. 3.1 (solid black line) and the analytical approach in Sect. 2 (dashed grey line) when $\mu = 0.001$, $\varOmega ^{*} = 25$ rad/s and $\bar{u}_0 = 0.1$. The trajectories are shown up to $t = 9.845$

4 Dynamic regimes in the elastic gyroscopic system: parametric study

In this section, we explore the dynamic behaviour of the elastic beam due to the gyroscopic effect induced by the gyro-hinge. In particular, we investigate how the transient response of the elastic system varies if either the effective density of the beam or the effective gyricity of the spinner is changed.

In the numerical examples, the initial conditions (9) are taken as $u_0(z) = \bar{u}_0(z^3-z^2)$, $\dot{u}_0(z) = 0$, $v_0(z) = 0$ and $\dot{v}_0(z) = 0$, with $\bar{u}_0 = 0.1$. We note that the initial disturbance is applied in the x-direction only; however, the coupling terms in the gyro-hinge boundary conditions will also produce displacements in the y-direction.

4.1 Case of zero effective gyricity

First, we discuss the special case when the effective gyricity is zero, which will be used as a reference for the investigations performed in Sects. 4.2 and 4.3.

When $\varOmega ^{*} = 0$, because of the symmetry of the problem in the x- and y-directions (see in particular how the gyro-hinge boundary conditions (8b) are modified in this case), the system is characterised by double eigenvalues, since the vibrations in the x- and y-directions are identical. The values of $\beta _k$ for $k = 1,\ldots ,10$ are reported in Fig. 3 for a unitary effective density. The shapes of the modes corresponding to these spectral parameters are also illustrated in the insets.

In particular, we are interested in the slopes at the end $z = 1$, where the gyroscopic spinners are connected. We notice that these slopes, associated with the first derivatives of the displacements, are large in the lowest two modes, while they are negligibly small in all the higher modes. Hence, the effective gyricity will affect mainly the lowest two modes, as shown in the following sections.

Fig. 3

Spectral parameters $\beta _k$ versus k for $\varOmega ^{*} = 0$ and $\mu = 1$. The mode shapes associated with the double values of $\beta _k$ are also plotted in the figure. In these insets, the solids at $z = 1$ represent masses with rotational inertia that do not spin ($\varOmega ^{*} = 0$)

4.2 Effect of the beam’s effective density

We set $\varOmega ^{*} = 25$ and consider different values of the beam’s effective density, i.e. $\mu = 0.1, 1, 10$. We determine the transient response of the system employing the analytical approach developed in Sect. 2. In the series we take $M = 8$ terms that ensure convergence of results up to the eight decimal digit. An illustrative example is shown in Fig. 4, where the values of the displacement components u and v calculated at the middle point of the beam and at a specific time are plotted for increasing values of M.

Fig. 4

Dependence of the displacement components a u and b v, computed at $z=1/2$ and $t=1$, on the number of terms M in the series of (35). Here, $\varOmega ^{*} = 25$ and $\mu = 1$. The values of the two displacement components for the different values of M are detailed in the figures

In Fig. 5 we show the trajectory of the middle point of the beam’s axis when the effective density is $\mu = 0.1$ (part a), $\mu = 1$ (part b) and $\mu = 10$ (part c). It can be noticed that the transverse displacement of the beam changes dramatically if the effective density is varied; in particular, the contributions of higher-order terms, which are responsible for the generation of smaller oscillations, are more significant when the effective density is increased. This implies that the effect of inertia cannot be neglected when the aim of the analysis is to predict accurately the transient response of the system.

Fig. 5

Trajectory of the point of the beam’s axis located at $z = 1/2$, calculated for an inertial beam with a $\mu = 0.1$, b $\mu = 1$ and c $\mu = 10$. The time required to complete a closed loop is a $t = 39.568$, b $t = 39.590$ and c $t = 39.799$

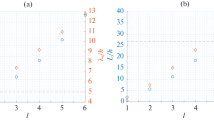
Figure 6a contains the lowest ten values of the spectral parameter $\beta _k$, corresponding to the three values of the beam’s effective density used in this section. The dots with a surrounding circle indicate the positions of two values of the spectral parameter, which are too close to each other to be discriminated. The values of $\beta _k$ ($k = 1,\ldots ,10$) are detailed in Table 1. From the figure and the table, it is apparent that the lowest frequency slightly increases with the effective density $\mu$ (see the lowest dashed line); consequently, the beam can be approximated as massless only if the initial configuration of the beam induces a dynamic behaviour of the flexural system resembling the lowest vibration mode. The second frequency for $\mu = 0.1$ increases more rapidly as the effective density is increased, as shown by the other dashed line, which indicates it can move through the spectrum positioning itself between higher frequency modes. Conversely, the positions of the couples of two close values of $\beta _k$ are not affected significantly by a change in $\mu$. We note that unlike these pairs of values of $\beta _k$ that are very close, the lowest two eigenfrequencies for $\mu = 0.1$ appear to be isolated and easily distinguishable from other members of the spectrum. This is due to the separation induced by the effective gyricity, which only affects the lowest two modes in a significant way, as discussed in Sect. 4.1. Additionally, as mentioned in Sect. 2.3.2, when the spectral parameter is large, the system begins to behave like a beam with clamped ends, having double eigenfrequencies. This behaviour is reflected in Fig. 6a in the high frequency range.

Figure 6b shows the values of $\beta _k$ for $k=1,\ldots ,10$ and for $\mu = 0.1$ (circles), $\mu = 1$ (stars) and $\mu = 10$ (squares). The insets present the mode shapes associated with the isolated values of $\beta _k$ (the modes corresponding to the double values of $\beta _k$ are very similar to those illustrated in Fig. 3, and hence they are not reported here). From the insets in Fig. 6b it can be noticed how the deformed shape of the beam changes as the effective density is increased.

Fig. 6

a Spectral parameters $\beta _k$ ($k = 1,\ldots ,10$) for the three values of the beam’s effective density considered in Fig. 5. The horizontal axis is in logarithmic scale. The dots inside circles represent two distinct values of $\beta _k$, which are too close to be distinguished in the diagram. The single dots indicate isolated frequencies, and they are linked by dashed lines which show their evolutions with $\mu$. b Spectral parameters $\beta _k$ versus k. Some illustrative mode shapes are also included

Table 1 Values of the spectral parameter $\beta _k$ ($k = 1,\ldots ,10$) for three values of the beam’s effective density $\mu$

4.3 Effect of the spinner’s effective gyricity

Here, we consider a beam with effective density $\mu = 1$, connected to a gyro-hinge where the spinner is assigned three different values of effective gyricity, namely $\varOmega ^{*} = 1/2, 5, 50$. As in Sect. 4.2, the proposed series solution (see (35)) converges when the number of terms in the series is $M = 8$ for the parameters and initial conditions considered.

Figure 7 illustrates how the middle point of the beam’s axis moves when the effective gyricity is $\varOmega ^{*} = 1$ (part a), $\varOmega ^{*} = 10$ (part b) and $\varOmega ^{*} = 100$ (part c). For smaller effective gyricities, the central point of the beam’s axis undergoes more complex trajectories. All trajectories shown are contained within an annulus whose inner and outer radii approach each other with increase of the effective gyricity. The trajectory becomes “more circular” as the effective gyricity is increased, since for larger values of $\varOmega ^{*}$ the oscillations are smaller. The patterns presented in Fig. 7 could not be obtained if the simulations were performed in the frequency regime, where the trajectory associated with each mode of vibration would be circular. In fact, as discussed in [24], typically circular trajectories for the flexural system are associated with scenarios where individual eigenmodes can be initiated with a specific choice of the initial conditions.

Fig. 7

Trajectory of the point of the beam’s axis positioned at $z = 1/2$, obtained for different values of the spinner’s effective gyricity: a $\varOmega ^{*} = 1/2$; b $\varOmega ^{*} = 5$; c $\varOmega ^{*} = 50$. All the trajectories are shown up to $t = 80$

Figure 8a shows how $\beta _k$ ($k = 1,\ldots ,10$) depend on the effective gyricity of the spinner. As in Fig. 6, the dots surrounded by a circle represent two close frequencies. From Fig. 8, it can be seen that the first (second) frequency for $\varOmega ^{*} = 1$ decreases (increases) as the effective gyricity is increased; the dashed lines are plotted to show these trends more clearly, where the second frequency for $\varOmega ^{*} = 1$ can migrate upward within the spectrum with increase of effective gyricity. On the other hand, the pairs of values of $\beta _k$, which are practically indistinguishable in Fig. 8, change very slightly with effective gyricity. This can also be noticed by looking at Table 2, containing the values of $\beta _k$ ($k = 1,\ldots ,10$). These results are in agreement with the observations made in Sect. 4.1, concerning the effect of the effective gyricity on the modes of the system. In Fig. 8b, the values of the spectral parameter are given in an increasing sequence of the integer k. Some mode shapes are also plotted in the figure to show how they are affected by the effective gyricity. We emphasise that only the two lowest modes are influenced by $\varOmega ^{*}$, because the slopes at the right end of the beam for the higher modes are close to zero. Being the slopes associated with the first derivatives of the displacements, from the gyro-hinge boundary conditions (8b) it is clear that the effect of effective gyricity on the higher modes is negligible.

Fig. 8

a Spectral parameters $\beta _k$ ($k = 1,\ldots ,10$) corresponding to the systems characterised by the three values of the effective gyricity used in Fig. 7. The horizontal axis is plotted in logarithmic scale. The dots inside circles represent two distinct values of $\beta _k$, which are too close to be distinguished in the diagram. The single dots indicate isolated frequencies, and they are joined by dashed lines to show how they evolve with $\varOmega ^{*}$. b Spectral parameters $\beta _k$ versus k. Examples of some mode shapes are also shown in the figure

Table 2 Values of the spectral parameter $\beta _k$ ($k = 1,\ldots ,10$) for three values of the spinner’s effective gyricity $\varOmega ^{*}$

5 Conclusions

In this paper, we have presented an approach for analysing the transient response of an inertial beam, clamped at one end and attached to a gyro-hinge at the other end. The method developed here relies on an eigenfunction expansion of the transverse displacements of the beam. This expansion embeds two infinite collections of eigenfunctions: one governing the beam’s response in time and the other providing information about the spatial variation in the beam’s profile. The individual elements of these collections are attributed to different harmonics of the system and the gyro-hinge induces a coupling between the functions associated with each harmonic. Due to the nature of the orthogonality conditions for the spatial eigenfunctions and the gyricity possessed by the spinner, the coefficients of the expansions of the transverse displacements of the inertial beam are determined as solutions of a truncated algebraic system.

The eigenfunction expansion for the inertial beam has been shown to reduce to the case of the massless beam if the beam’s inertia is assumed to be sufficiently small. An additional verification of the proposed expansion has been implemented using an independent method based on finite element calculations.

A parametric study of the system has been carried out and the examples considered have revealed:

• The beam undergoes transverse displacements contained inside annuli whose thickness and size are sensitive to the choice of the beam’s density and the spinner’s gyricity.

• The system possesses a spectrum composed of closely situated pairs of eigenfrequencies, in addition to isolated eigenfrequencies that for small density and gyricity are situated in the low-frequency regime.

• The beam’s density has a significant role in promoting the influence of high-frequency harmonic motion of the system. Increasing the density allows some isolated eigenfrequencies to migrate to higher frequencies within the system’s spectrum.

• The gyricity can dramatically affect the response of the beam, producing a variety of complex motions if the gyricity is sufficiently low. In contrast to the effect attributed to beam’s density, increasing the gyricity of the spinner forces isolated eigenfrequencies to diverge from each other moving to either a higher frequency range or a lower frequency regime.

The numerical example in the Supplementary Material has also illustrated that gyro-hinges can be introduced into a structural frame to mitigate significant vibrations caused by an external load.

We believe that the results presented here will be important in the design of new resonator systems, with applications in controlling vibration processes in structured and continuous systems having potential technological benefits in civil engineering.

Appendices

Appendix A: Derivation of the governing equations of the functions composing the eigenfunction expansions

Here, we show how to determine the governing equations of the functions $G^{(k)}_j(z)$ and $F^{(k)}_j(t)$, $j=1,2$ and $k\ge 1$. First, we introduce the transverse displacements in the form:

$$\begin{aligned} u(z, t)=G_1(z, \omega )F_1(t, \omega )\;, \qquad v(z, t)=G_2(z, \omega )F_2(t, \omega )\;, \end{aligned}$$

(A.1)

where $\omega$ represents the radian frequency.

Governing equations for $F_j$ and $G_j$, $j=1,2$. By direct substitution of the above into (6), we immediately obtain via standard arguments that

$$\begin{aligned} \frac{1}{\mu } \frac{G_j^{\prime \prime \prime \prime }(z, \omega )}{G_j(z, \omega )} = - \frac{\ddot{F}_j(t, \omega )}{F_j(t, \omega )} = \omega ^2 = \hbox {Const} \end{aligned}$$

(A.2)

or, equivalently,

$$\begin{aligned} {G_j^{\prime \prime \prime \prime }(z, \omega )} -\beta (\omega )^4G_j(z, \omega )=0\;, \qquad {\ddot{F}_j(t, \omega )}+\omega ^2{F_j(t, \omega )} =0\;, \end{aligned}$$

(A.3)

with $\beta (\omega )=(\mu \omega ^2)^{1/4}$ being the spectral parameter.

Boundary conditions for $G_j$ and the determination of $F_j$, $j=1,2$. In a similar way, using (7) and (8a) one can determine a subset of the boundary conditions for $G_j$, $j=1,2$, as

$$\begin{aligned} G_j(0, \omega )=G_j^\prime (0, \omega )=0\;, \quad G_j(1, \omega )=0\;, \text { for } j=1,2\;. \end{aligned}$$

(A.4)

It remains to obtain the conditions representing the spinner’s effect through the gyro-hinge, which couples both $G_j$, $j=1,2,$ in addition to the functions $F_j$, $j=1,2$. From substituting (A.1) into the boundary conditions (8b) we obtain

$$\begin{aligned}&F_1(t, \omega ) G_1^{\prime \prime }(1, \omega ) + \ddot{F}_1(t, \omega ) G_1^{\prime }(1, \omega ) + \varOmega ^{*} \dot{F}_2(t, \omega ) G_2^{\prime }(1, \omega ) = 0 \, , \nonumber \\&F_2(t, \omega ) G_2^{\prime \prime }(1, \omega ) + \ddot{F}_2(t, \omega ) G_2^{\prime }(1, \omega ) - \varOmega ^{*} \dot{F}_1(t, \omega ) G_1^{\prime }(1, \omega ) = 0 \, . \end{aligned}$$

(A.5)

Using (A.3), (A.5) also takes the matrix form:

$$\begin{aligned} \begin{pmatrix} \dot{F}_1(t, \omega ) \\ \dot{F}_2(t, \omega ) \end{pmatrix} = \begin{pmatrix} 0 &{} \xi (\omega )\\ \zeta (\omega ) &{} 0 \end{pmatrix} \begin{pmatrix} F_1(t, \omega ) \\ F_2(t, \omega ) \end{pmatrix} , \end{aligned}$$

(A.6)

with

$$\begin{aligned} \xi (\omega )= & {} \frac{G_2^{\prime \prime }(1, \omega ) - \omega ^2 G_2^{\prime }(1, \omega )}{\varOmega ^{*} G_1^{\prime }(1, \omega )}\;, \end{aligned}$$

(A.7)

$$\begin{aligned} \zeta (\omega )= & {} -\frac{G_1^{\prime \prime }(1, \omega ) - \omega ^2 G_1^{\prime }(1, \omega )}{\varOmega ^{*} G_2^{\prime }(1, \omega )}\;. \end{aligned}$$

(A.8)

Next, we identify the forms of $\xi (\omega )$ and $\zeta (\omega )$ that allow us to fully prescribe the problems for $G_j$, $j=1,2.$ Based on (A.6), we introduce the time-dependent functions in the form

$$\begin{aligned} \begin{pmatrix} F_1(t, \omega ) \\ F_2(t, \omega ) \end{pmatrix} = \begin{pmatrix} c_1 \\ c_2 \end{pmatrix} \mathrm {e}^{\lambda (\omega ) t}, \end{aligned}$$

(A.9)

which upon substitution into (A.6) produces the homogenous system

$$\begin{aligned} \begin{pmatrix} -\lambda (\omega ) &{}\,\,\, \xi (\omega ) \\ \,\,\,\zeta (\omega ) &{} -\lambda (\omega ) \end{pmatrix} \begin{pmatrix} c_1 \\ c_2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \, . \end{aligned}$$

(A.10)

Seeking a non-trivial solution to the above system yields

$$\begin{aligned} (\lambda (\omega ))^2 - \xi (\omega ) \zeta (\omega ) = 0 \, . \end{aligned}$$

(A.11)

Note that by combining (A.3) and (A.6), we can also write

$$\begin{aligned} \ddot{F}_1(t, \omega ) = \xi (\omega ) \dot{F}_2(t, \omega ) = \xi (\omega ) \zeta (\omega ) F_1(t, \omega ) = -\omega ^2 F_1(t, \omega ) \, , \end{aligned}$$

(A.12)

which implies that

$$\begin{aligned} \xi ( \omega ) \zeta (\omega ) = -\omega ^2 \, . \end{aligned}$$

(A.13)

Thus, it follows from (A.11) and (A.13) that

$$\begin{aligned} \lambda (\omega )= \pm \mathrm {i} \omega \, . \end{aligned}$$

(A.14)

Using (A.14) in the homogeneous system (A.10), we have that if $\lambda = \mathrm {i} \omega$, then

$$\begin{aligned} -\mathrm{i}\omega c_1+\xi (\omega ) c_2= & {} 0, \end{aligned}$$

(A.15)

$$\begin{aligned} \zeta (\omega ) c_1-\mathrm{i}\omega c_2= & {} 0, \end{aligned}$$

(A.16)

whereas if $\lambda = -\mathrm {i} \omega$, then

$$\begin{aligned} \mathrm{i}\omega c_1+\xi (\omega ) c_2= & {} 0,\end{aligned}$$

(A.17)

$$\begin{aligned} \zeta (\omega ) c_1+\mathrm{i}\omega c_2= & {} 0. \end{aligned}$$

(A.18)

Here, (A.15) and (A.16) coincide if $\xi (\omega )$ and $\zeta (\omega )$ both coincide with either $\mathrm{i}\omega$ or $-\mathrm{i}\omega$. The same is also true for (A.17) and (A.18). Hence, we can choose

$$\begin{aligned} \xi (\omega )=\zeta (\omega )= \mathrm{i}\omega \;. \end{aligned}$$

(A.19)

With regard to the case when the above right-hand side has the opposite sign, we note that this yields the same solution (22) (see also the remark below).

Now (A.15), (A.16) and (A.19) imply that $c_1=c_2$ if $\lambda =\mathrm{i}\omega$, whereas (A.17), (A.18) and (A.19) show that $c_1=-c_2$ if $\lambda =-\mathrm{i}\omega$. Thus, according to (A.9) and (A.14), the time-dependent functions take the form

$$\begin{aligned} \begin{pmatrix} F_1(t, \omega ) \\ F_2(t, \omega ) \end{pmatrix} = d_1 \begin{pmatrix} 1 \\ 1 \end{pmatrix} \mathrm {e}^{\mathrm {i} \omega t} + d_2 \begin{pmatrix} 1 \\ -1 \end{pmatrix} \mathrm {e}^{-\mathrm {i} \omega t} . \end{aligned}$$

(A.20)

From (A.7) and (A.8), we also derive the conditions

$$\begin{aligned}&{G_2^{\prime \prime }(1, \omega ) - \omega ^2 G_2^{\prime }(1, \omega )}-\mathrm{i}\omega {\varOmega ^{*} G_1^{\prime }(1, \omega )}=0, \end{aligned}$$

(A.21)

$$\begin{aligned}&{G_1^{\prime \prime }(1, \omega ) - \omega ^2 G_1^{\prime }(1, \omega )}+\mathrm{i}\omega {\varOmega ^{*} G_2^{\prime }(1, \omega )}=0\;. \end{aligned}$$

(A.22)

The problem satisfied by $G_j^{(k)}$. Therefore, we have identified the complete set of conditions, found in (A.3), (A.4), (A.21) and (A.22), enabling us to determine the functions $G_j$, $j=1,2$. The solutions of the associated homogeneous problem can exist when the radian frequency $\omega =\omega _k$, where $\omega _k$ ($k\ge 1$) are the roots of (20) and form a monotonically increasing sequence. As a result, we can define the collection of eigenfunctions $G^{(k)}_j(z)=G_j(z, \omega _k)$ for $k\ge 1$ and $j=1,2$, that we have shown satisfy

$$\begin{aligned} (G_j^{(k)})^{\prime \prime \prime \prime }(z)- \beta _k^4 G_j^{(k)}(z) = 0 \, ,\quad j=1,2\,, \qquad 0< z < 1 , \end{aligned}$$

(A.23)

together with the clamping conditions at the beam’s base

$$\begin{aligned} G_j^{(k)}(0) =(G_j^{(k)})^{\prime }(0) = 0 \, , \quad j=1,2, \end{aligned}$$

(A.24)

and the constraints representing influence of the gyro-hinge at the other end, given by

$$\begin{aligned} G_j^{(k)}(1) = 0 \quad j=1,2, \end{aligned}$$

(A.25)

and

$$\begin{aligned}&(G_1^{(k)})^{\prime \prime }(1) - \omega _k^2 (G_1^{(k)})^\prime (1) + \mathrm {i} \omega _k \varOmega ^{*} (G_2^{(k)})^\prime (1) = 0 , \nonumber \\&(G_2^{(k)})^{\prime \prime }(1) - \omega _k^2 (G_2^{(k)})^\prime (1) - \mathrm {i} \omega _k \varOmega ^{*} (G_1^{(k)})^\prime (1) = 0 . \end{aligned}$$

(A.26)

The problem for $F_j^{(k)}$. Additionally, if we define $F^{(k)}_j(t)=F_j(t, \omega _k)$, from (A.3), (A.6) and (A.20) we have that these time-dependent functions satisfy

$$\begin{aligned} \ddot{F}_j^{(k)}(t) + \omega _k^2 F_j^{(k)}(t) = 0 . \end{aligned}$$

(A.27)

They are coupled via the constraint

$$\begin{aligned} \begin{pmatrix} \dot{F}_1^{(k)}(t) \\ \dot{F}_2^{(k)}(t) \end{pmatrix} = \begin{pmatrix} 0 &{} \mathrm{i}\omega _k \\ \mathrm{i}\omega _k &{} 0 \end{pmatrix} \begin{pmatrix} F_1^{(k)}(t) \\ F_2^{(k)}(t) \end{pmatrix}, \end{aligned}$$

(A.28)

and take the form (A.20).

Finally, due to the linearity of the considered problem, we construct the general solutions for the transverse displacements as in (10).

Remark

With regard to the choice taken in (A.19), we note that if the right-hand side is replaced with $-\mathrm{i}\omega$ then the associated results can be obtained by replacing $F_2(t, \omega )$ and $G_2(t, \omega )$ by $-F_2(t, \omega )$ and $-G_2(t, \omega )$, respectively, in the above procedure, which does not influence the form of the solution in (A.1).

Appendix B: Derivation of orthogonality conditions

Owing to (A.23)–(A.26), the vector $\varvec{G}^{(k)}(z)$ defined in (14) is governed by the differential equation

$$\begin{aligned} \left( \varvec{G}^{(k)}(z)\right) '''' - \beta _k^4 \varvec{G}^{(k)}(z) = \mathbf{0} \end{aligned}$$

(B.1)

and is subjected to the boundary conditions

$$\begin{aligned}&\varvec{G}^{(k)}(0) = \mathbf{0} \, , \end{aligned}$$

(B.2a)

$$\begin{aligned}&\left. \left( \varvec{G}^{(k)}(z)\right) '\right| _{z=0} = \mathbf{0} \, ,\end{aligned}$$

(B.2b)

$$\begin{aligned}&\varvec{G}^{(k)}(1) = \mathbf{0} \, ,\end{aligned}$$

(B.2c)

$$\begin{aligned}&\left. \left[ \left( \varvec{G}^{(k)}(z)\right) '' - \omega _k^2 \left( \varvec{G}^{(k)}(z)\right) ' + \mathrm {i} \omega _k \varOmega ^{*} \varvec{R} \left( \varvec{G}^{(k)}(z)\right) ' \right] \right| _{z=1} = \mathbf{0} \, , \end{aligned}$$

(B.2d)

where $\varvec{R}$ is defined in (16).

Fig. 9

Comparison between the analytical results based on (35) (black solid lines) and the numerical findings (grey dashed lines), showing the time-histories of the transverse displacements a in the x-direction and b in the y-direction, calculated at $z = 1/2$. The magnifications in the insets clearly show that there are two distinct curves, which are very close to each other

Fig. 10

Differences between the peaks of the curves determined numerically from the finite element model in Comsol Multiphysics and those obtained from the analytical approach developed in this paper, relative to the displacement in the a x- and b y-direction, plotted by dots at the average times $(t_{\mathrm{peaks}}^{\mathrm{num}} + t_{\mathrm{peaks}}^{\mathrm{anal}})/2$ where the peaks are detected

The vector $\tilde{\varvec{G}}^{(k)}(z)$, also found in (14), is determined from the same governing equations and boundary conditions, provided that in (B.2d) the matrix $\varvec{R}$ of (16) is replaced with $-\varvec{R}$.

Next, consider the following expression:

$$\begin{aligned}&\left( \beta _j^4 - \beta _m^4 \right) \int _{0}^1 \varvec{G}^{(j)}(z) \cdot \varvec{G}^{(m)}(z) \mathrm {d}z \nonumber \\&\quad = \int _{0}^1 \left[ \left( \varvec{G}^{(j)}(z)\right) '''' \cdot \varvec{G}^{(m)}(z) - \varvec{G}^{(j)}(z) \cdot \left( \varvec{G}^{(m)}(z)\right) '''' \right] \mathrm {d}z \, , \end{aligned}$$

(B.3)

where $j \ne m$ and (B.1) was used. By successive application of integration by parts twice we obtain

$$\begin{aligned}&\left( \beta _j^4 - \beta _m^4 \right) \int _{0}^1 \varvec{G}^{(j)}(z) \cdot \varvec{G}^{(m)}(z) \mathrm {d}z \nonumber \\&\quad = \left[ \left( \varvec{G}^{(j)}(z)\right) ''' \cdot \varvec{G}^{(m)}(z) - \varvec{G}^{(j)}(z) \cdot \left( \varvec{G}^{(m)}(z)\right) ''' \right] _{0}^{1} \nonumber \\&\qquad - \left[ \left( \varvec{G}^{(j)}(z)\right) '' \cdot \left( \varvec{G}^{(m)}(z)\right) ' - \left( \varvec{G}^{(j)}(z)\right) ' \cdot \left( \varvec{G}^{(m)}(z)\right) '' \right] _{0}^{1} \, . \end{aligned}$$

(B.4)

Making use of the boundary conditions (B.2), we find

$$\begin{aligned}&\left( \beta _j^4 - \beta _m^4 \right) \int _{0}^1 \varvec{G}^{(j)}(z) \cdot \varvec{G}^{(m)}(z) \mathrm {d}z \nonumber \\&\quad =- \left( \omega _j^2 - \omega _m^2 \right) \left. \left( \varvec{G}^{(j)}(z)\right) '\right| _{z=1} \cdot \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} \nonumber \\&\qquad - \mathrm {i} \varOmega ^{*} \left( \omega _j + \omega _m \right) \left. \left( \varvec{G}^{(j)}(z)\right) '\right| _{z=1} \cdot \varvec{R} \left. \left( \varvec{G}^{(m)}(z)\right) '\right| _{z=1} \, . \end{aligned}$$

(B.5)

Recalling that $\beta _k^4 = \mu \omega _k^2$, we arrive at (15). In a similar way we can also derive (17).

Appendix C: Independent numerical simulation

Here, we validate the analytical method based on the series representations by comparing the analytical results with the outcomes of a finite element simulation carried out in Comsol Multiphysics.

In this example, we assume that the beam has effective mass $\mu = 1$ and the gyroscopic spinner has effective gyricity $\varOmega ^{*} = 25$. The initial conditions are given by

$$\begin{aligned} u(z,0)= & {} 16 \bar{u}_0 z^2 \left( z-1\right) ^2 \, , \qquad v(z,0) = 0 \, , \end{aligned}$$

(C.1a)

$$\begin{aligned} \dot{u}(z,0)= & {} 16 \bar{\dot{u}}_0 z^2 \left( z-1\right) ^2 \, , \qquad \dot{v}(z,0) = 0 \, , \end{aligned}$$

(C.1b)

where $\bar{u}_0 = 0.1$ and $\bar{\dot{u}}_0 = -2$. We point out that the initial displacement and velocity vectors are parallel to the x-axis.

The analytical approach provides the following values for the spectral parameter $\beta _k$ corresponding to the first ten modes (see Sect. 2.3.2): $\beta _1 = 0.398722$, $\beta _2 = 4.667555$, $\beta _3 = 4.734515$, $\beta _4 = 5.073915$, $\beta _5 = 7.854675$, $\beta _6 = 7.856682$, $\beta _7 = 10.996231$, $\beta _8 = 10.996557$, $\beta _9 = 14.137480$ and $\beta _{10} = 14.137570$. We highlight that with $M=8$ modes the convergence of solutions is attained.

The model in Comsol Multiphysics consists of an Euler–Bernoulli beam with unit length and flexural stiffness, and having zero displacements and rotations at the base where $z = 0$ and the gyro-hinge boundary conditions (8) at $z = 1$. The beam is divided into 1000 finite elements and the normalised time step is $10^{-3}$.

Figure 9 shows the transverse displacements u (part a) and v (part b), determined at the middle point of the beam’s axis and calculated in the normalised time interval $0 \le t \le 2$. The solid black curves are obtained with the analytical approach presented in Sect. 2, while the dashed grey curves are produced by the numerical code. It is apparent that the agreement between the analytical and numerical methods is very good. This confirms the validity of the analytical approach developed in this paper.

From Fig. 9 it is apparent that the curves obtained numerically and analytically exhibit a slight time shift that increases with time due to the numerical scheme employed in the finite element model. Consequently, the local maxima and minima of the curves are attained at different times. In Fig. 10a (Fig. 10b) we show the differences between the peaks relative to the u (v) displacement component, denoted as $u_{\mathrm{peaks}}^{\mathrm{num}} - u_{\mathrm{peaks}}^{\mathrm{anal}}$ ($v_{\mathrm{peaks}}^{\mathrm{num}} - v_{\mathrm{peaks}}^{\mathrm{anal}}$), plotted at the average times $(t_{\mathrm{peaks}}^{\mathrm{num}} + t_{\mathrm{peaks}}^{\mathrm{anal}})/2$. It is clear that these differences become larger as the computational time increases.