The emergence of social ties between individuals is fundamental for understanding the evolution of sociality in human and other animals. As pointed out in the classic work by Alexander (1974), social animals are relatively rare in nature because there are no automatic and universal benefits of group living, and the opposite effects such as social conflict and disease transmission seem to be common. Consequently, sociality must evolve under ecological conditions that can generate significant fitness and benefits for individuals such that the detrimental effects of sociality can be overcome; and gaining access to and defending critical resource is one of the fundamental reasons that animal form social groups (Shen et al., 2017).

As for humans, it has been suggested that the early stage of human history is characterized by the expansion of humans across the globe (Boyd et al., 2011). During the process humans constantly encountered new and changing environments, and new skills were often required for humans to learn in order to survive (Boyd et al., 2011). Mastering all skills or knowledge by one individual is a very time consuming process, and the energy required might be of high cost that lowers this individual’s fitness (Kaplan et al., 2009; Dyble et al., 2016). A more plausible way in which one might survive under these circumstances is to develop some sorts of dependency on others who have already mastered skills that this individual is not familiar with (Kaplan et al., 2009; Dyble et al., 2016). Thus, it has been suggested that humans is a highly cultural species where the diversification of skills or knowledge drive the social dependence between individuals (Boyd et al., 2011; Hill et al., 2011).

Intuition suggests that some skills can be associated with the sense that if one excels in one and he might also excel in another. For example, “fishing” and “sailing” are two skills to be mastered if one wishes to catch fish in the ocean. Another example is that an individual who excels in “mathematics” might also excel in “computer programming” as he might need to write computer programs to solve mathematical problems. Thus, it is not farfetched to envisage various skills or knowledge being connected in a network manner where one skill or a piece of knowledge is more closely linked to some but less so with others (Arthur, 2009; Yeh et al., 2019; Phoa et al., 2020). The diversification of skills or knowledge can be regarded as changes in their network structure; and how those changes might serve as ecological conditions that favor social dependency on other individuals remains elusive, and this serves as the motivation behind our study here.

In this paper, we ask whether the diversification of skills or knowledge can favor some sorts of sociality among individuals. Specifically, we model a network of resource-containing patches where each patch represents a skill or a particular piece of knowledge. Similar skills or knowledge are connected by links; thus, a densely connected patch network implies little difference between skills or knowledge, whereas a sparsely connected network implies diversification. We then construct an agent-based model to simulate resource competition between individuals of two different behavior types on a given resource-containing patch network, and see which behavior type becomes the dominant one after several generations. The first behavior type consists of solitary individuals who move between patches and acquire resources; and the second is the social type where individuals behave like the solitary type, but with some probability, they can also use their social ties (hence social networks) to acquire resources. To be more specific, a social-type individual uses his social ties to ask his friends or acquaintances to explore their neighboring patches for resources. In other words, a friend or acquaintance with a particular skill or knowledge can easily adopt or learn related skills or knowledge in order to help the social-type actor acquiring resources. Owing to one’s capacity for learning might be limited, we have to emphasize that we do not intend to model the use of social ties for learning; instead, social ties develop such that one can ask for help from his friend and acquaintances to acquire resources. We assume in our model that resources are commodities that can increases one’s prestige, and the amount accumulated throughout one’s life time can be a proxy to how successful he is. In the end of one generation, the level of “success” associated with one particular behavior type can be totaled from individuals bearing such a behavior; and this then dictates the proportion of individuals adopting such a behavior type in the next generation (i.e., following the intuition that successful behaviors tend to be adopted more frequently than less successful ones (Kendal et al., 2015)). In a nutshell, with our simulation model, we ask how the extent of diversification of skills and knowledge, as modeled by patch networks of various structures, can favor the emergence of the social-type behavior. Note that we model skills or knowledge in the form of a resource-containing patch network where resources are being depleted by individuals. Resources within a patch can also be regarded as credits given to those pioneering individuals who were the first to exploit the patch (either directly occupying the patch or exploit the resource via social ties). The depletion of resources here resembles the loss of novelty if late comers visit patches already being exploited by pioneers.

A real-life example that is of relevance to the context of our model is from academic research. Here, a subject or research field is a patch, and resources within a patch are credits given to those pioneering individuals who publish papers on the corresponding subject. We assume credits are given to those pioneering individuals such that their prestige increases and their work get frequently cited by others. When a subject or research field is being explored by many individuals, many problems get solved; therefore the novelty or interest in this particular research field starts to wear out, and this is portrayed by the depletion of resources within a patch in our model. Subjects or research fields form a network where similar ones are being linked together. The solitary-type actors are those individuals who navigate on their own and write papers on similar subjects. In contrast, modern academic research has emphasized the importance of interdisciplinary collaboration in advancing science where people from different disciplines are brought together to work on new research topics other than their original fields of interests (Katz and Martin, 1997); and this is similar to social-type actors using their social ties to acquire resources. For instance, a field ecologist is well trained in conducting surveying experiments to quantify the observed species richness in the wild. However, with little knowledge on statistics, he is unlikely to take one step further in predicting or inferring the real number of species. If the knowledge required to solve the ecologist’s problem is closely related to his current knowledge, then he can easily learn it by himself (i.e., by exploiting patches neighboring his current patch). However, if the knowledge required is beyond the ecologist’s reach, then he might spend more effort to learn it (i.e., by navigating through the patch network to exploit distant patches). The field ecologist can certainly devote time to learn statistics, but due to reasons such as shortage of time or limits in his learning capacity, he might be better off to seek helps from elsewhere. If he has a friend who is a statistician, then he can ask for help from such a friend. This statistician friend may apply his current knowledge to help the ecologist (i.e., exploiting the statistician’s current patch), or uses his current knowledge to develop new methodology to solve the ecologist’s research problem (i.e., exploring the patches neighboring the statistician’s current patch).

We note that there exist a huge amount of theoretical works on how sociality might arise and the majority of this can be found in behavior ecology under the broad framework of social foraging theory (Giraldeau and Caraco, 2000). Generally, evolutionary game theory approach is employed to investigate how sociality emerges while individuals of different strategies compete for resources in order to sustain their physiological need for survival. The theory covers topics such as the condition favoring group foraging (Clark and Mangel, 1986), the outcome of producer-scrounger game (Vickery et al., 1991; Ohtsuka and Toquenaga, 2009; Afshar and Giraldeau, 2014), behavior in resource-patch exploitation (Pyke, 1984), and social learning (Rendell et al., 2011; Nakahashi et al., 2012; Hoppitt and Laland, 2013). Many of those theoretical works investigate how different strategies can be beneficial under different assumptions about the underlying ecological processes; these include how resources are shared or partitioned between individuals, how resources are distributed among patches, accessibility to resource patches, different ways of patch exploitation for resource and environmental heterogeneities. Our model here conceptually is similar to models of produce-scrounger games and social learning as we assume social-type individuals use information from some others to acquire resources; but it differs from them in that such information is limited by the range of one’s social network. Furthermore, existing works rarely consider the relationship between resource patches; and here we model resource patches as a network explicitly and investigate how different network structure can affect the outcome of two competing strategies. In other words, our modeling framework simulates two learning processes, one solitary and one social, on a network of skills or knowledge; and investigate which one is favored under different level of skill or knowledge diversification. We next present our simple simulation model.

Methods

Simulation model

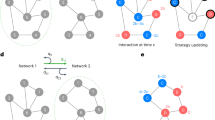
Our simulation model assumes that there are M patches that each contains Q resources and that there are N actors. X is a square matrix of dimension M by M, which represents the network of patches in the model. In this matrix, elements xij and xji equal one if patches i and j are connected. Y is a square matrix of dimension N by N, and it represents the social network of actors in the model. Elements yij and yji equal one if actors i and j are connected. Here, we assume there are two types of actors. First is the solitary type (Fig. 1); an actor of this type looks for resources by moving from his current patch to one of the neighboring patches chosen at random. The second is the social type (Fig. 2), and an actor of this type normally behaves like the solitary type, but there is a probability p that this actor will seek new resources by making and utilizing social ties.

Fig. 1: A schematic diagram showing the behavior of a solitary-type actor in the resource patch network.
figure 1

The nodes and links represent the resource patch network. Filled circles are patches with resources whereas open circles are patches with no resources. Here the actor (shown as red) travels freely in the resource patch network and takes resources when he encounters them.

Full size image
Fig. 2: A schematic diagram showing the behavior of a social-type actor.
figure 2

The resource patch network is represented by the black nodes and solid black lines. Filled black circles are patches with resources and open circles are empty patches. Red, yellow, blue and green nodes are individual actors and the dashed lines represent their social ties. Here, the red actor is allowed to use his social ties for collecting resources, and by chance he uses the tie connected to the green actor. The red actor then randomly picks a patch near the green actor (one of the nodes circled in red) and takes away a resource if it exists. Note that an actor immediately takes away a resource once he occupies a patch; therefore in the figure, the patches occupied by red, yellow, blue, and green actors have no resources left.

Full size image

A single simulation experiment of the model consists of several consecutive generations, each of which has a generation time of T time steps; and a simulation experiment is then terminated if the entire population consists of actors of the same behavior type (i.e., either solitary type or social type). At the start of each simulation experiment—more precisely, at the beginning of first generation—we assume that the probability of an actor belonging to the social type is qinitial = 0.1. Specifically, for each of the N actors, we draw a random number between 0 and 1; if it is smaller than qinitial, then this actor is of the social type, otherwise he belongs to the solitary type. Thus on average, 90% of the actors are of the solitary type and 10% are of the social type. For each generation, the model specifies the following procedures.

  1. 1.

    Construct the patch network with link density D (see Patch network section for more detail), and place Q resources in each patch.

  2. 2.

    Construct the actors’ social network without any social ties (i.e., an empty graph).

  3. 3.

    Set time t = 0.

  4. 4.

    For each time step t, select an actor uniformly at random. If the selected actor is of the solitary type, then carry out procedure 4.1; otherwise, carry out procedure 4.2 (meaning this actor is of the social type).

    • 4.1 If the selected actor is not assigned to any patch, then one patch is chosen uniformly at random; let this be his starting patch. If the selected actor is already at one patch, then he chooses uniformly at random one of patches from his neighborhood and moves to there. In our model, an actor’s neighborhood consists of his current patch and those patches connected to it. After the actor has moved to the chosen patch, he takes away one resource from this patch if there are still resources available; if so, then the number of resources in this patch is decreased by one. Next, go to procedure 5.

    • 4.2 Draw a random number between 0 and 1. If it is smaller than p, then carry out the procedure outlined in this sub-section (i.e., acting like a social actor); otherwise, go to sub-section 4.1 (i.e., acting like a solitary actor). Here, the actor i chooses another actor j randomly with a weight inversely proportional to their distance in the social network:

    $$\Pr \left( j \right) = \frac{{1/d\left( {i,j} \right)}}{{\mathop {\sum}\nolimits_{k = 1,i < > k}^N {1/d\left( {i,k} \right)} }}$$
    (1)

    where d is the length of the shortest path between two actors in social network Y. If no such shortest path exists (i.e., i and j are not reachable from one another), then we assume that they are separated by the theoretical maximum path length of a network with N nodes and then add one to this length (i.e., N − 1 + 1 = N). Once a target actor j is chosen by actor i, a link is added between actors i and j if no such link existed before (i.e., setting yij = yji = 1). Next, actor j then picks randomly one patch from his neighborhood and peeks into it. If there are resources available in the chosen patch, then actor i is allowed to take one resource and share it with actor j; and the number of resources in the chosen patch is decreased by one. This is akin to actor j learning a new skill or knowledge similar to his current one in order to help actor i to acquire a resource. Furthermore, we assume actor i shares the acquired resource with actor j as follows: a proportion S of the acquired resource goes to actor i, and the remaining proportion 1 − S goes to actor j. Next, go to procedure 5.

  5. 5.

    Set time t = t + 1 (i.e., next time step) and repeat procedures 4 and 5 until t = generation time T.

  6. 6.

    At the end of each generation, we count how many resources each actor has accumulated. We then sum up the number of resources from actors of the solitary type and let it be rsolitary, and do the same for actors of the social type and let this number be rsocial. The proportion q = rsocial /(rsolitary + rsocial) is then calculated and it is the probability of one actor belonging to the social type in the next generation. All actors are then removed from the system, and a new set of N actors enters the system as actors for the next generation. For each of these new actors, a random number between 0 and 1 is drawn. If it is lower than q, then he is of the social type; otherwise, he is of the solitary type. If the number of resources associated with a particular behavior type is regarded as a measure of its success, then this is equivalent to the notion that an actor is more likely to adopt the more successful behavior.

Procedures 1 to 6 are repeated until all actors belong to the same behavior type (i.e., either solitary type or social type). Furthermore, if q = 1 at the end of one simulation experiment, then all actors in the system are of the social type; we define this as the “fixation of the social-type strategy”. In other words, the social-type strategy outcompetes the solitary-type strategy. However, if q = 0 at the end of one simulation experiment, then all actors in the system are of the solitary type; thus, the solitary-type strategy outcompetes the social-type strategy. Note that throughout one simulation experiment, the structure of the patch network does not change, whereas the structure of the actors’ social network can change from time to time (i.e., in fact it is a random network). The patch network and the actors’ social network are only related in the sense that the former servers as a road map for actors to navigate, otherwise those two networks are formed independent of each other. Program codes written in Delphi (or Pascal) for simulating the model are provided as supplementary information, in a file named CodesForModelSimulation.txt.

In this study, we are interested in how parameters p, T, and D can affect the outcome of the simulation model. Thus, for each combination of parameter values of p, T, and D, we perform the simulation experiment E times. From those simulation experiments, we then count how many of those resulting in the “fixation of the social-type strategy” and let this number be s.

Patch network

One important aspect of this study is to investigate how the relationship between various resources (via the patch network) can affect the emergence of social ties. If a patch network has a ring structure, then it implies that a resource in a particular patch is more closely related to those in nearby patches but less so to those in more distant patches. A real-life analogy of this is again from academic research, where a patch can represent a specific subject, such as “linear algebra” or “social capital”, and a resource within a patch can represent a “credit” given to an individual who publishes a paper on that corresponding academic subject. The deleting naturel of resources resembles the loss of novelty when many papers have being published on the same subject. Our intuition suggests that scientific subjects should more or less have a local network structure; for instance, the subject “gene expression” should relate more to the subject “DNA sequencing” than to subjects such as “social economics”. Therefore, an actor, or an academic researcher in this case, tends to know more about closely related subjects than unrelated subjects due to the local structure of the knowledge domain network. On the contrary, if a patch network is highly connected, as in a complete graph, then it will result in each resource being related to many other resources. Returning to the real-life analogy of academic research, the knowledge network for one specific discipline such as “ecology” might be highly connected. For instance, topics such as “food webs” tend to be studied in conjunction with topics such as “predator–prey interaction” and “exploitive competition”. Thus, an ecologist who works on “predator–prey interaction” should share some interest in “food webs” with another ecologist who works on “exploitive competition”; this will potentially spark some sort of competition between those ecologists if they are to be the first to write a novel paper on “food webs”. In a nutshell, a ring has a localized network structure and resources embedded in such a network structure are in general dissimilar from each other, whereas a complete graph would imply all resources are similar with each other. In other words, a ring-like network structure implies high diversification among the resource patches, and a complete graph implies low diversification. Furthermore, our model allows for the random movement of actors within the patch network. Therefore, a ring structure implies a less competitive setting where actors are unlikely to encounter each other, whereas a complete graph implies a more competitive setting where actors are more likely to visit patches that others have visited before.

Here, we describe in detail how a patch network with a link density D is constructed. D is the value obtained when one divides the observed number of links by the maximum number of links in the network, (LM/2)/((M2 − M)/2), where L is the number of links each patch has. We should start by using a patch network with a ring structure, where each patch has exactly two links, each of which connects to one of its closest neighbors. We then progressively increase D such that each patch now gets exactly the same number of extra links. To keep a ring-like network structure while progressively diminishing the structure at the local level, for each patch we then connect each of its extra links to one of its closest unconnected neighbors. The maximum value D can take is 1, implying that the patch network is now a complete graph and that all resources are now connected with each other. Figure 3 summarizes the effect of changing D on the structure of the patch network. Note that we use the terms “resource network” and “patch network” interchangeably. Also note that for each simulation experiment, the structure of the underling patch network remains the same for all generations (i.e., the same value of D for all generations).

Fig. 3: The effect of changing parameter D on the resource patch network.
figure 3

The simplest resource patch network assumed in the mode is a ring. As D increases, a patch is then connected to the next closest neighboring patches that were not connected before. With D = 1, the resource patch network is a complete graph where all patches are connected with each other.

Full size image

Testing the statistical significance of the model results

To ascertain that the result of the simulation model is truly due to what is assumed in the model, not just by random chance, we also need to construct a null model for comparison purposes (i.e., like hypothesis testing in statistics). A null model here is exactly the same as the simulation model, except the actors of the social type now adopt the same behavior as their solitary counterparts (or simply set p = 0). For simplicity and convenience, we add a superscript “Null” to each of the abovementioned statistics to distinguish the null model from our simulation model. As with the simulation model, we can also perform the simulation experiment with the null model E times, count how many of them end up with the “fixation of the social-type strategy”, and determine sNull accordingly. If we repeat the entire process F times, then there will be F-values of sNull forming a null distribution. In fact, sNull follows a binomial distribution, with the number of trials and the probability of a successful trial equal to E and qinitial, respectively (i.e., the fixation of the social-type strategy is the outcome of a successful trial). From this null distribution, we can then calculate α, the probability of observing an sNull that is greater than s under the null model, and define this as the p-value to test whether the social-type strategy does indeed outperform its solitary counterpart with any statistical significance. Here, a cutoff value of 0.05 is chosen, just as one would do in hypothesis testing. Furthermore, in the cases where the social-type strategy does not outperform the solitary-type strategy, it is of interest to know whether the former is being significantly outperformed by the latter. To this end, we also need to test, for the same model parameter combination, whether the solitary-type strategy outperforms the social-type strategy with any statistical significance or not. Similarly, we can calculate the quantity β, the probability of observing an sNull that is smaller than s under the null model; this probability can then be considered the p-value for testing whether the solitary-type strategy significantly outperforms the social-type strategy. Again, a cutoff value of 0.05 is used here.

Results

We explore the behavior of the simulation model in the T-p parameter space for various values of D in two ways. First, for one particular parameter combination, we test whether the social-type strategy can outcompete the solitary-type strategy with any statistical significance. Second, with the same parameter combination, we also test whether the solitary-type strategy can outperform the social-type strategy with any statistical significance. These two pieces of information are complementary to each other, as this allows us to see if one strategy does not outperform the other, whether this is because the latter outperforms the former or not. We summarize these results in Figs. 4 and 5. Each sub-figure in Fig. 4 is an array of squares, with each square representing a specific combination of parameter values. A square with a brighter color scheme indicates the social-type strategy is more likely to outcompete the solitary-type strategy under this parameter combination; a black square implies that the social-type strategy does not outcompete the solitary-type strategy with any statistical significance. As D increases, or when the patch network (or resource network) shifts from a more localized structure to a complete graph, the social-type strategy becomes less likely to outcompete its solitary counterpart. Intuitively, we would expect actors who acquire resources using their social ties tend to have a greater advantage in all circumstances because they can access resources located in different parts of the patch network. However, our results do not verify this expectation when the patch network is densely connected. This is because in a densely connected patch network actors with a solitary-type strategy can move to patches that they have not visited before relatively quicker than they would in a more localized patch network. Consequently, such actors will also accumulate resources relatively quickly. In contrast, actors with a social-type strategy waste time making social contacts while resources are quickly taken up by their solitary counterparts.

Fig. 4: The outcome of competition between the solitary-type strategy and the social-type strategy in the T-p parameter space for various values of D.
figure 4

The non-black squares indicate that social-type strategy outcompetes the solitary-type strategy more frequently than what is expected by random chance (i.e., when the simulation model is compared with the null model), with the brightness indicating the statistical significance of the result. A black square indicates that the frequency of the social-type strategy outcompeting the solitary-type strategy is not significantly different from what is expected by random chance at the 5% significance level. Values for other parameters are: M = 1000, N = 20, Q = 1, S = 1, E = 5000.

Full size image
Fig. 5: The outcome of competition between the solitary-type strategy and the social-type strategy in the T-p parameter space for various values of D.
figure 5

The non-black squares indicate that solitary-type strategy outcompetes the social-type strategy more frequently than what is expected by random chance (i.e., when the simulation model is compared with the null model), with the brightness indicating the statistical significance of the result. A black square indicates that the frequency of the solitary-type strategy outcompeting the social-type strategy is not significantly different from what is expected by random chance at the 5% significance level. Values for other parameters are: M = 1000, N = 20, Q = 1, S = 1, E = 5000.

Full size image

What is even worse is that the social-type strategy seems to be detrimental to its bearers when the patch network is densely connected. We can observe this effect in Fig. 5, where each brightly colored square now indicates the solitary-type strategy is more likely to outcompete the social-type strategy. As the density of patch network increases, the number of brightly colored squares also increases in the T-p parameter space. Even with a highly localized patch network, the social-type strategy is not always the winning strategy. In fact, social-type strategies with large values of p (ranging from 1 to 0.7) are detrimental to their bearers; this can be observed by the lack of bright squares in the bottom part of each sub-figure in Fig. 4 and the presence of bright squares in the bottom part of the sub-figures in Fig. 5. This finding suggests that actors who rely solely on social ties to acquire resources are competitively inferior to solitary actors.

One last notable result from the simulation model is that the social-type strategy seems to be more successful than the solitary ones only when the generation time T is long. This can be observed by noting the presence of bright squares on the right portion of top sub-figures in Fig. 4. Furthermore, when generation time T is short, the social-type strategy even becomes more detrimental to its bearers; this can be observed in all sub-figures of Fig. 5, where bright squares occupy the bottom-left part of each sub-figure. Thus, the solitary-type strategy tends to be more advantageous and, therefore, prevalent strategy for actors in future generations when competition for limiting resources occurs in a very short timeframe.

We also investigated the effect of system size, namely the number of patches and the number of actors, on the behavior of our simulation model. Social behavior is favored in the expanse of solitary behavior when the number of patches increases from as few as 100 to a larger number of 1000 (Figs. 6 and 7). In a large resource patch network, an actor is not likely to visit places that have being visited before by others, but he still can visit patches exploited by him previously. An actor of the social type not only can acquire resources from places he has visited just like all others have done, but he also gains resources from other actors by utilizing his social ties. Therefore, a social type actor can acquire resources via his social ties before exhausting resources from near-by patches. This in effect renders an actor of the social type an advantage over an actor of the solitary type. In contrast, increasing the number of actors in the system has the opposite effect as solitary behavior is now more advantageous than social behavior (Figs. 8 and 9). This is because increasing the number of actors results in a more crowded system where competition for resources is severe, and many patches being exploited for resources. An actor of the social type not only has difficulties in acquiring resources via his social tie, he also risks his near-by patches being exhausted of resource by other actors. Therefore, social-type strategy might not be as effective as its solitary counterpart in terms of acquiring resources in those circumstances.

Fig. 6: The effect of the number of patches M on model behavior.
figure 6

Explanation of the figure is exactly the same as in Fig. 4. In general, more non-black squares appear as M increases, implying social behavior is favored. Values for other parameters are: D = 0.002, N = 20, Q = 1, S = 1, E = 5000.

Full size image
Fig. 7: The effect of the number of patches M on model behavior.
figure 7

Explanation of the figure is exactly the same as in Fig. 5. In general, more non-black squares appear as M decreases, implying solitary behavior is favored. Values for other parameters are: D = 0.002, N = 20, Q = 1, S = 1, E = 5000.

Full size image
Fig. 8: The effect of the number of actor N on model behavior.
figure 8

Explanation of the figure is exactly the same as in Fig. 4. In general, more non-black squares appear as N decreases, implying social behavior is favored. Values for other parameters are: D = 0.002, M = 1000, Q = 1, S = 1, E = 5000.

Full size image
Fig. 9: The effect of the number of actors N on model behavior.
figure 9

Explanation of the figure is exactly the same as in Fig. 5. In general, more non-black squares appear as N increases, implying solitary behavior is favored. Values for other parameters are: D = 0.002, M = 1000, Q = 1, S = 1, E = 5000.

Full size image

Furthermore, we investigated the effect of Q, the number of resources within a patch, on the behavior of our model (Figs. 10 and 11). Solitary behavior is favored in the expanse of social behavior when Q increases. In other words, social behavior is only advantageous when resources are not abundant. This is because when resources are scarce, one might exhaust his neighborhood of resources; and using social ties to acquire resources can be advantageous here as such individual can have access to resources in other parts of the patch network. We also investigated the effect of S, the proportion of a shared resource that goes to the actor who utilizes his social tie for resource acquisition, on the behavior of our model. Our result shows that as S decreases from one, social behavior becomes more disadvantageous (Figs. 12 and 13). This suggests that social behavior is only viable if the actor who utilizes social ties has a majority share of the acquired resource. Moreover, we also investigated the effect of initial condition, namely qinitial, on the outcome of our simulation model; and it appears that our model result is robust against different values of qinitial used (Figs. 14 and 15).

Fig. 10: The effect of the number of resources Q within a patch on model behavior.
figure 10

Explanation of the figure is exactly the same as in Fig. 4. In general, more non-black squares appear as Q decreases, implying social behavior is favored. Values for other parameters are: D = 0.002, M = 1000, Q = 1, S = 1, E = 5000.

Full size image
Fig. 11: The effect of the number of resources Q within a patch on model behavior.
figure 11

Explanation of the figure is exactly the same as in Fig. 5. In general, more non-black squares appear as Q increases, implying solitary behavior is favored. Values for other parameters are: D = 0.002, M = 1000, Q = 1, S = 1, E = 5000.

Full size image
Fig. 12: The effect of the sharing parameter S on model behavior.
figure 12

Explanation of the figure is exactly the same as in Fig. 4. In general, more non-black squares appear as S decreases, implying social behavior is favored. Values for other parameters are: D = 0.002, M = 1000, Q = 1, S = 1, E = 5000.

Full size image
Fig. 13: The effect of the sharing parameter S on model behavior.
figure 13

Explanation of the figure is exactly the same as in Fig. 5. In general, more non-black squares appear as S increases, implying solitary behavior is favored. Values for other parameters are: D = 0.002, M = 1000, Q = 1, S = 1, E = 5000.

Full size image
Fig. 14: The effect of different initial conditions, qinitial, on model behavior.
figure 14

Explanation of the figure is exactly the same as in Fig. 4. Values for other parameters are: D = 0.002, M = 1000, N = 20, Q = 1, S = 1, E = 5000.

Full size image
Fig. 15: The effect of different initial conditions, qinitial, on model behavior.
figure 15

Explanation of the figure is exactly the same as in Fig. 5. Values for other parameters are: D = 0.002, M = 1000, N = 20, Q = 1, S = 1, E = 5000.

Full size image

Finally, we also investigated how the social network changes when we vary the structure of the patch network. For various values of D, we simulated the models to determine the best value of p such that the social-type strategy can outperform the solitary-type strategy; we then simulated the model with this particular value of p several times, and determined the average number of social ties an actor has, the number of social groups, and the size of the largest social group in the end of each simulation. Note that a social group here refers to a group of actors where group members can reach each other via direct or indirect social ties. Figure 16 shows that as the structure of the patch network becomes more localized (i.e., D decreases), the average number of social ties an actor has also increases, but this reaches a stable limit. When the patch network is a complete graph or has a non-localized structure (i.e., a large D), the number of social groups equals to the number of actors in the simulation (i.e., all actors are isolated individuals). As the structure of the patch network becomes more localized, the number of social groups also decreases; and it doesn’t take long until a single large social network emerges connecting all actors. As for the size of the largest social group, we can see form Fig. 16 that its transition is the same as that for the number of social groups: at first, for large values of D, the social network consists of isolate actors, thus the size of the largest social group is one; but as D decreases, it then starts to increases and very quickly attains the maximum possible value (i.e., the number of actors in the simulation). To summarize, the transition of average number of social ties an actor has occurs in a wider range of D; whereas the transition for the number of social groups and the size of the largest social group occurs for a narrower range of D.

Fig. 16: Box plots showing changes in the actors’ social network for various values of D.
figure 16

Values for other parameters are: N = 50, M = 4000, G = 100, E = 1000, T = 2000. For each combination of parameter values, the model was simulated 100 times.

Full size image

Discussion and conclusion

Human is a highly cultural species (Boyd et al., 2011; Hill et al., 2011), and in this paper we ask whether the diversification of human skills or knowledge can be a potential process that drives the emergence of social relation between individuals. Social relation is a very general term and here we focus on social ties as channels through which an individual can acquire resources from his acquaintances. One clear pattern has emerged from the analysis and simulation of our simple model. Social ties are only feasible and viable when resources are distributed in a highly localized patch network (i.e., a situation where human skills or knowledge are highly diversified). When a resource patch network becomes highly connected (i.e., a less diversified set of human skills or knowledge), it then tends to favor solitary behavior. Furthermore, once social behavior is selected for in the expense of solitary behavior, social ties start to emerge and connect actors forming a social network. Slightly unexpected, although social behavior tend to be favored in highly localized patch network, our simulation model shows that actors who rely solely on social ties to acquire resources are in fact competitively inferior to those who adopt solitary behavior.

Our simple model conceptually shares some similarity with producer-scrounger models. In those models, scroungers take advantage of producers’ searching effort and acquire resources found by producers. A social-type actor in our model in a sense behaves like a scrounger as he uses social ties to acquire resources from the vicinity of others. In general, producer-scrounger models predict that large variation in resource quality among patches (Afshar and Giraldeau, 2014) and aggregation of resources (Vickery et al., 1991; Ohtsuka and Toquenaga, 2009) should favor the frequency of scroungers. This implies that heterogeneities in resource distribution or resource accessibility should favor scrounger behavior. As for our simple model, it predicts that social-type actors are favored when the resource patch network is sparsely connected. The consequence of a sparsely connected network is that actors cannot move freely to most patches in the network; and social-type actors have an advantage over solitary ones in that the former can utilize social ties (or social network to be more precise) to reach resources that are unlikely to be encountered by random search. Thus, this also translates to a setting of how changes in resource accessibility can promotes social behavior.

Our simple model also has concepts similar to social learning models. Past literature distinguishes two types of learning behavior (Boyd and Richerson, 1985; Laland et al., 1993; Henrich, 2016). One is individual learning where individuals spend time and effort to learn or acquire resources in a trial-and-error manner. The other is social learning where individuals benefit from information gathered from others such that they learn more efficiently or collect better resources. In general, social learning is likely to evolve under non-fluctuating environment or low resource turnover rate (Feldman et al., 1996; Wakano and Aoki, 2006; Smolla et al., 2015) and when competition for resources is weak (Smolla et al., 2015; Lee et al., 2016). Our simple model also demonstrates similar outcomes. First, our simulation model assumes that after each generation the resource patch network is reset and all individuals are removed from the system before the addition of the new generation. A long generation time T in a sense implies a low turnover rate of the resource patch network and a more stable environment, and our result shows this condition favors the social-type actor. Second, our simulation model shows that social-type actors are favored when the resource patch network is not well connected. The consequence of a highly connected resource patch network is that individuals are free to move within the network and, therefore, they are more likely to visit patches that have already been visited by others. In a sense, a highly connected resource patch network implies a stronger competitive setting than a localized network does. Thus, our simulation model shows that social-type actors are favored when competition for resources is weak.

Our work here also has some relevance to the social brain hypothesis. One characteristic that makes humans and primates so different from other species is their large brain size to body size ratio (Jerison, 1973; Dunbar, 1998). Neuron materials required for brain development are believed to be costly (Aiello and Wheeler, 1995; Kaufman, 2003), and a variety of studies have suggested reasons for why humans and primates evolve to have such high costs (Clutton-Brock and Harvey, 1980; Gibson, 1986; Brothers, 1990; Dunbar, 1998; Reader and Laland, 2002; Lefebvre et al., 2004; Dunbar, 2011). One of those, the social brain hypothesis, suggests that the large brains of primates and humans enable them to become aware, track, or understand the complex social relationships surrounding them (Brothers, 1990; Dunbar, 1998; Dunbar, 2011); and it argues that the emergence of complex cognitive ability requires some processes or ecological conditions that favor the emergence of complex social behaviors. Here, in our work, we have shown that the emergence of social ties and social groups is related to the diversification of skills or knowledge; and we speculate this could be a potential ecological condition for the emergence of complex social behavior as required in social brain hypothesis. One prediction from social brain hypothesis is the positive relationship between brain size and the size of the social circle of a species (Dunbar, 1992, 2014); and extrapolating data from primates has shown that a person should have around 150 acquaintances. Our model demonstrates the number of one’s social ties (i.e., the size of his social circle) and the emergence of large social groups also relate positively with the diversification of skills and knowledge. Thus, one potential direction of research using our simulation model is to predict the size of social circle for various primate species as well as human’s. However, parameterizing our model, especially how to represent skills and knowledge in a network form for various species, is not an easy issue and, therefore, warrants further research.

Our work here is also relevant to theories from sociology. In a broad sense, social exchange theory hypothesizes that relationship is likely to form between two individuals if they each has goods (tangible or intangible) that the other person values (Homans, 1958; Emerson, 1976). This implies a case of dissimilarity in resources possessed by two individuals, and social interaction in the form of exchange between them is likely to occur. Our simulation model also exhibits similar outcomes in that social ties, as instrumental tools for acquiring resources, is more likely to emerge if resources are dissimilar. Moreover, in a setting where a society is highly (or hieratically) structured, social resource theory (Lin, 2001) and weak tie hypothesis (Granovetter, 1973) have emphasized the benefit of using social ties when an individual attempts to reach out to acquire valuable resources or information that are embedded in different locations of a society. This echoes our finding that social behavior tends to be more advantageous than solitary behavior in a more localized resource patch network.

Although our model is formulated to investigate theoretically how diversification of skills and knowledge can affect the emergence of social ties, it may correspond loosely to other contexts. One real-life example is from industrial sector where a particular technology or invention resembles a patch, and the associated patent is the resource. Here, different technologies or inventions form a network, and a link exists between two if one piece of technology or invention build on from the other. A solitary-type actor is a company or inventor who relies on his own ability to produce similar technologies or inventions; whereas a social-type actor seeks for collaboration from others such that he can produce products of various types. Another example is from a setting where business companies competing for customers. Here, companies and customers can respectively be actors and patches in our model. In this setting, customers form a network, and a link exists between two customers if they are related in some way (i.e., as family members, friends, or members of the same demographic group). A company with solitary-type strategy tends to exploit and sell products to similar customers; whereas a company with social-type strategy can form alliance with other companies and reach out to customers in different parts of a society.

Finally, we would like to conclude with some remarks on the limitation of our work and possible future directions in extending our model. Firstly, our model assumes that when a social-type actor utilizes his social ties to acquire resources, none of his friends or acquaintances can acquire those resources. This assumption might be appropriate in academic research as it is often the one who initiates or conceives the research ideas (and hence collaboration) get to be the first author, and therefore taking the credit of publishing a paper. However, this is not always the case. Thus, one possible extension of our model is to allow more than one resources in each patch, and devise some rule that partitions those resources between a social-type actor and his friends. Secondly, the social networks constructed in our model are in fact random networks. A fruitful research direction is to include the features of real social networks such as closed triads in the construction of social networks in our model. Third, in our model, skills and knowledge are modeled as patch networks with very simple structure. One challenge here will be to construct from real data the evolution of human skills and knowledge, and incorporate those into our model. Lastly, our model assumes that an actor is either of the solitary type or the social-type, and remains the same throughout his life time. In reality, people change behavior by gauging information from others. Thus, one important direction in extending our model is to allow mutation in actors’ behavior, and investigate how this affects the evolution of social ties.