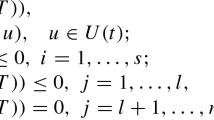1 Introduction

Convergence analysis of optimal control algorithms typically aims to demonstrate that accumulation points of sequences of control functions, generated by the algorithm under consideration, satisfy necessary conditions of optimality. The nature of the necessary conditions is not fixed, but depends on the algorithm and on the analytical techniques employed in the convergence analysis.

In a series of papers [6, 9], Mayne and Polak, building on earlier work by Jacobson and Mayne [3], proposed algorithms (with accompanying convergence analysis) for solving optimal control problems with endpoint inequality constraints, based on strong variations. In consequence of the strong variations employed in the algorithms, one might expect that the necessary conditions featuring in the convergence analysis would be the minimum principle. (This is on account of fact that the minimum principle can be proved by consideration of strong variations to the control.) But, in fact, another condition was used in this earlier literature, a necessary condition of optimality that we, in this paper, shall call the first-order minimax condition. Necessary conditions similar to an integral version of the first-order minimax condition, but applicable to optimal control problems with pathwise state constraints (we shall refer to them as ‘state constraint problems’), are implicit in the convergence analysis of feasible directions algorithms due to Pytlak and Vinter [11].

The first-order minimax condition (for state constraint-free problems) originates in a systematic approach to algorithm construction in nonlinear programming and optimal control, due to Polak [8]; the idea, in the case of optimal control problems, is to find, for a given control \(u'\), an ‘optimality function’ \(u \rightarrow \theta (u,u')\) with the property that arg min\(\{u \rightarrow \theta (u,u')\}\) provides, in the event that \(\min _u\theta (u,u')< 0\) , search directions for the reduction of cost and endpoint constraint violations. The convergence analysis involves showing that accumulation points \({{\bar{u}}}\) satisfy \(\min _u \theta (u, {\bar{u}}) =0\). For the optimal control problems treated by Mayne and Polak in [6, 9], ‘\(\min _u \theta (u, {\bar{u}}) =0\)’ can be interpreted as our first-order minimax condition.

Investigating the strength of a necessary condition based on particular computational scheme gives insights into pathological situations when the necessary condition is satisfied at some non-minimizing process and hence into circumstances when the scheme might fail to yield a minimizer. This is the reason why, in this paper, we investigate the strength of two necessary conditions previously encountered in algorithm analysis, by comparing them with the known minimum principle.

We provide a rather complete picture of the relations between the following necessary conditions of optimality, both for problems with and without pathwise state constraints: the first-order minimax condition (on which the algorithms in [6, 9] are based), the integrated first-order minimax condition (implicit in the algorithm convergence analysis of [11]), and the minimum principle. For problems without state constraints, our investigations reveal that the minimum principle is a stronger necessary condition than the first-order minimax condition and that the integrated first-order minimax condition and the minimum principle are equivalent. An example is provided demonstrating that the minimum principle is strictly stronger than the first-order minimax condition.

When we pass to problems with pathwise state constraints, we find, once again, that the integrated first-order minimax condition and the minimum principle are equivalent. But we discover that the first-order minimax condition is neither stronger nor weaker than the minimum principle. Thus, the first-order minimax condition is revealed to be an optimality condition that is distinct from the minimum principle. An example illustrates how it can be used to show that a certain admissible process is not a minimizer, when the minimum principle fails to do so.

It is well known that first necessary conditions for free right endpoint problem can be simply derived, by consideration of needle variations and performance of elementary gradient calculations. When general endpoint constraints are present, the derivation of necessary conditions akin to the minimum principle necessitates the use of a more sophisticated analysis (based on separation of approximating cones of the reachable set [2], or non-smooth perturbation methods [7]). We observe, however, that when the endpoint constraints take the form of inequality constraints, the derivation of necessary conditions based on simple gradient calculations becomes once again possible. (The ‘necessary conditions’ referred to here are ‘first-order minimax conditions.’) There is a parallel here with the derivation of Fritz John-type first-order necessary conditions in nonlinear programming where, as is well known, the analysis is greatly simplified, if the constraints are inequality constraints [5], not mixed inequality and equality constraints. A secondary purpose of this paper is to make explicit these simplifications, also in an optimal control context.

2 Problem Formulation

Consider the optimal control problem with endpoint inequality constraints:

$$\begin{aligned} (P) \left\{ \ \begin{array}{l} \text{ Minimize } g_0(x(1) ) \\ \text{ over } \text{ absolutely } \text{ continuous } \text{ functions } x \text{ and } \text{ meas. } \text{ functions } u \text{ such } \text{ that } \\ \dot{x}(t) =f(x(t),u(t)), \; \text{ a.e. } t \in [0,1], \\ u(t)\in \varOmega , \; \text{ a.e. } t \in [0,1], \\ x(0)=x_0 \text{ and } g_j(x(1)) \le 0, \text{ for } j =1,2., \ldots , r\,. \end{array} \right. \end{aligned}$$

The data comprise functions \(g_j:R^n \rightarrow R\), \(j=0,\ldots ,r\) and \(f:R^n \times R^m \rightarrow R^n\) and a closed set \(\varOmega \subset R^m\).

A pair of functions (x, u) is called a process if x is absolutely continuous, u is Lebesgue measurable, \(\dot{x}(t) =f(x(t,u(t))\) a.e., \(u(t) \in \varOmega \) a.e. and \(x(0)=x_0\). If x also satisfies the right endpoint constraints in (P), we say that (x, u) is an admissible process. The first component x of a process (x, u) is called a state trajectory. The second component is called a control function.

We shall also consider a generalization that includes state constraints

$$\begin{aligned} h_k (x(t)) \le 0,\; \text{ for } \text{ all } t \in [0,1] \text{ and } k=1,\dots N_s\,, \end{aligned}$$

for given functions \(h_k :R^n \rightarrow R\), \(k =1,\ldots ,N_s\).

$$\begin{aligned} (S) \left\{ \ \begin{array}{l} \text{ Minimize } g_0(x(1) ) \\ \text{ over } \text{ absolutely } \text{ continuous } \text{ functions } x \text{ and } \text{ meas. } \text{ functions } u \text{ such } \text{ that } \\ \dot{x}(t) =f(x(t),u(t)), \; \text{ a.e. } t \in [0,1], \\ h_k(x(t)) \le 0, \text{ for } \text{ all } \text{ index } \text{ values } j\in \{1,\ldots ,N_s\} \text{ and } t \in [0,1], \\ u(t)\in \varOmega , \; \text{ a.e. } t \in [0,1], \\ x(0)=x_0 \text{ and } g_j(x(1)) \le 0, \text{ for } j =1,2., \ldots , r\,. \end{array} \right. \end{aligned}$$

‘Admissible processes for (S)’ are understood in the obvious sense. The following hypotheses will be invoked:

  1. (H1):

    The set \(\varOmega \) is compact, and the functions \(g_j\), \(j=0,\ldots N\) and \(h_k\), \(k =1,\ldots , N_s\) are continuously differentiable,

  2. (H2):

    f(., u) is continuously differentiable for each \(u \in \varOmega \), f, \(\nabla _x f\) is continuous, and there exists \(c >0\) such that

    $$\begin{aligned} |f(x,u)| \le c(1+ |x|)\, \text{ for } \text{ all } (x,u) \in R^n \times \varOmega \,. \end{aligned}$$

Notation: In Euclidean space, the Euclidean length of a vector x is denoted by |x| and the closed unit ball in Euclidean space is written B. Given numbers a and b, we write \(a \vee b := \max \{a,b\} \) and \(a \wedge b := \min \{a,b\} \).

Given \(x \in L^\infty ([0,1];R^n)\), we write the \(L^\infty \) norm of x as \(||x||_{L^{\infty }}\). \(NBV^+ \) \(([0,1];R^{N_s})\) denotes the space of \(N_s\)-tuples of (normalized) increasing functions \(\nu = \{\nu _k\}\) on [0, 1] such that each \(\nu _k\) is right continuous on (0, 1). For each k, \(d\nu _k\) is the Stieltjes measure associated with \(\nu _k\). \(R^+\) denotes \([0, \infty )\).

For a given nominal admissible process \(({\bar{x}}, {\bar{u}})\), S(t, s) is the transition matrix for the linear system

$$\begin{aligned} \dot{y}(t) =\nabla _x f({\bar{x}} (t), {\bar{u}}(t))y(t), \text{ a.e. } t \in [0,1], \end{aligned}$$
(1)

i.e., for each \(s \in [0,1]\), \(t \rightarrow S(t,s)\) is the unique solution on [0, 1] of the matrix differential equation

$$\begin{aligned} \left\{ \begin{array}{l} dS/dt (t,s) =\nabla _x f ({\bar{x}} (t), {\bar{u}}(t))S(t,s), \text{ a.e. } t \in [0,1]\,, \\ S(s,s)= I_{n \times n} \, \quad (I_{n \times n} \text{ denotes } \text{ the } n \times n \text{ unit } \text{ matrix) } , \end{array} \right. \end{aligned}$$

\({{{\mathcal {U}}}}:= \{ \text{ meas. } \text{ functions } u \text{ s.t. } u(t)\in \varOmega \) a.e.},

\(\varDelta f(t,u) := f({\bar{x}}(t),u) -f({\bar{x}} (t) , {\bar{u}}(t)), \text{ for } t \in [0,1] \text{ and } u \in \varOmega , \)

\(\varLambda ^N := \{(\lambda _0,\ldots , \lambda _N) \in R^{N+1}\,:\, \lambda _j \ge 0 \text{ for } \text{ all } j \text{ and } \sum _j \lambda _j =1\}\),

\(I({\bar{x}}):= \{0\} \cup \{j\in \{1,\ldots ,r\}\,:\, g_j({\bar{x}} (1))=0 \}\).

3 Analytical Tools

1. Relaxation. The following optimal control problem is known as the relaxation of (P).

$$\begin{aligned} (RP) \left\{ \ \begin{array}{l} \text{ Minimize } g_0(x(1) ) \\ \text{ over } \text{ abs. } \text{ continuous } \text{ functions } x, \text{ meas. } \text{ functions } \mu :[0,1] \rightarrow \varLambda ^{n} \\ \qquad \quad \text{ and } \text{ meas. } \text{ functions } \{u_k:[0,1] \rightarrow \varOmega \}_{k=0}^n \text{ such } \text{ that } \\ \dot{x}(t) =\sum _{k=0}^n \mu _k (t)f(x(t),u_k(t)), \; \text{ a.e. } t \in [0,1], \\ x(0)=x_0 \text{ and } g_j(x(1)) \le 0, \text{ for } j =1,2., \ldots , r \end{array} \right. \end{aligned}$$

A process \((x, \{(u_k, \mu _k)\}_{k=0}^n)\) for (R) is called a relaxed process for (P). If x satisfies the endpoint constraints, the relaxed process is called a relaxed admissible process. A function x (associated with some relaxed process) is called a relaxed state trajectory, and the \((n+1)\)-tuple or pairs \(\{(\mu _i, u_i))\}\) (likewise associated) are called a relaxed control function. If, say, \(\mu _k= 0\) for \(k =2,\dots , r\), we write \(\{(\mu _k, u_k))\}\) simply as \(((\mu _0, u_0), (\mu _1,u_1))\).

The relaxation theorem [1] tells us that a given relaxed state trajectory can be uniformly approximated by a state trajectory.

Theorem 3.1

(The Relaxation Theorem) Take \((x,\{(\mu _k ,u_k ,)\}_{k=0}^n)\) to be any relaxed process for (P) and any \(\delta >0\). Then, there exists a process \((x',u')\) for (P) such that

$$\begin{aligned} || x- x'||_{L^{\infty }} \le \delta \,. \end{aligned}$$

2. A Minimax Theorem. Minimax theorems originate in the game theory literature. We shall make use of their important role also in variational analysis.

Theorem 3.2

(Von Neumann Minimax Theorem) Consider a function \(F:X \times Y \rightarrow R\) in which X and Y are subsets of topological linear spaces. Assume that

  1. (i)

    X and Y are convex, compact sets,

  2. (ii)

    F(., y) is convex and continuous for every \(y \in Y\),

  3. (x,.)

    F(x, .) is concave and continuous for every \(x \in X\).

Then, there exists \((x^{*},y^{*}) \in X \times Y\) which is a saddlepoint for F, i.e.,

$$\begin{aligned} \sup _{y \in Y}F(x^{*}, y) = F(x^{*},y^{*}) = \inf _{x \in X} F(x,y^{*}) \end{aligned}$$
(2)

and

$$\begin{aligned} \inf _{x \in X} \sup _{y \in Y} F(x,y) = \sup _{y \in Y} \inf _{x \in X} F(x,y). \end{aligned}$$

For a proof, see, e.g., [10, Thm. 3.4.6].

3. First-Order Local Approximations

The following proposition gives error bounds for needle variations associated with a given nominal process \(({\bar{x}}, {\bar{u}})\).

Proposition 3.1

Take a process \(({\bar{x}}, {\bar{u}})\) for (P). Assume hypotheses (H1)-(H2) are satisfied. Fix \(t \in [0,1)\) and \(u \in \varOmega \). Define, for each \(\sigma \in (0, 1-t]\), the control function

$$\begin{aligned} u_\sigma (s):= \left\{ \begin{array}{ll} u&{} \text{ if } t \le s \le t+ \sigma \\ {\bar{u}} (s) &{} \text{ otherwise } \,. \end{array} \right. \end{aligned}$$
(3)

Let \(x_\sigma \) be the corresponding state trajectory on [0, 1] such that \(x_\sigma (0)=x_0\). Then, there exist a number K (that does not depend on \(\sigma \)) and a continuity modulus \(\theta \) (i.e., a function \(\theta : (0,\infty ) \rightarrow (0, \infty )\) such that \(\lim _{s \downarrow 0}\, \,\theta (s) =0\)) with the following properties.

  1. (a):

    \(||x_\sigma - {\bar{x}}||_{L^{\infty }} \le K\sigma \),

  2. (b):

    for any index value \(j \in \{0,\ldots ,r\}\) and process (x, u),

    $$\begin{aligned} g_j (x_\sigma (1)) - g_j ({\bar{x}} (1)) \le \int _t^{t+ \sigma }\varDelta f(s,u(s)) \cdot S^T(1,s)\nabla g_j ({\bar{x}}(1)) ds + \sigma \times \theta (\sigma ) \,' \end{aligned}$$
  3. (c):

    for any index value \(k=1,\ldots , N_s\), \( t' \in (t,1]\) and \(\sigma ' : = \sigma \wedge (t' - t))\)

    $$\begin{aligned}&h_k (x_\sigma (t')) - h_k ({\bar{x}} (t')) \\&\quad \le \int _t^{t + \sigma '} \varDelta f(s,u(s))\cdot S^T(t',s)\nabla h_k ({\bar{x}}(t'))ds + \sigma ' \times \theta (\sigma '). \end{aligned}$$

Proof

Choose constants \(K_1\), \(R>0\) and k with the following properties:

$$\begin{aligned}&K_1> e^c |x_0| + (e^c -1),\, R> \max \{ |f(x,u)| \, :\, |x| \le K_1 , u \in \varOmega \} \text{ and } \\&\quad k >\max \{ |\nabla _x f (x,u)| \, : \, |x| \le K_1, u \in \varOmega \} \,. \end{aligned}$$

We deduce from hypothesis (H2) and Gronwall’s inequality that, for any process \((x',u')\) such that \(x'(0)=x_0\),

$$\begin{aligned} |x'(t)|< K_1 \text{ for } \text{ all } t \in [0,1] \text{ and } |f(x'(t), u('t))|< R \text{ a.e. } t \in [0,1]\,. \end{aligned}$$

Furthermore, \(x \rightarrow f(x,v)\) is Lipschitz continuous on \(K_1 B\), with Lipschitz constant k, for all \( v \in \varOmega \).

Using the facts that \(x_\sigma \) and \({\bar{x}}\) are state trajectories with the same initial state, we can show that

$$\begin{aligned} |x_\sigma (t) -{\bar{x}} (t)|&\,=\, |\int _0 ^t f(x_\sigma ((s), u_\sigma ((s)) -f({\bar{x}} (s), {\bar{u}} (s)) | ds \\&\quad \le \int _0^t k|x_\sigma (s)- {\bar{x}} (s)|ds + \int _{[t , t + \sigma ] \cap [0,t]} |\varDelta f(s, u)|ds \end{aligned}$$

for each \(t \in [0,1]\). But then, by Gronwall’s inequality,

$$\begin{aligned} ||x_\sigma - {\bar{x}}||_{L^{\infty }} \le K \times \sigma , \end{aligned}$$
(4)

in which \(K:= 2 e^k R\,\) . We have confirmed property (a).

To complete the proof, it is required only to establish property (c). (The proof of property (b) follows from (c), when we substitute \(g_j\) in place of \(h_k\) in the analysis and select \(t' =1\).) Take any index value k and \(t' \ge t\). We have

$$\begin{aligned}&h_k(x_\sigma (t')) - h_k({\bar{x}} (t')) = h_k(x_\sigma (t'))- h_k({\bar{x}} (t'))\,+\, \\&\;\int _0^{t'}(\dot{x}_\sigma (s)-\dot{{\bar{x}}}(s)- [f(x_\sigma (s),u_\sigma (s)) -f({\bar{x}} (s), {\bar{u}} (s))])\cdot S^T(1,s) \nabla h_k ({\bar{x}} (1))ds\,. \end{aligned}$$

The second term on the right can be written

$$\begin{aligned}&+ \int _0^{t'}(\dot{x}_\sigma (s)-\dot{{\bar{x}}}(s)- [f(x_\sigma (s),{\bar{u}}(s)) -f({\bar{x}} (s), {\bar{u}} (s))])\cdot S^T (1,s) \nabla h_k({\bar{x}} (1))ds \\&\quad + \int _{t}^{ t + \sigma '}\Big (\varDelta f(s, u) + [f(x_\sigma (s), u)-f({\bar{x}} (s),u)]\Big )\cdot S^T (1,s) \nabla h_k({\bar{x}} (1))ds\,. \end{aligned}$$

Furthermore, since \((d/dt)S^{T} (1,t) = - f^T_x ({\bar{x}}(t), {\bar{u}} (t))S^T (1,t)\),

$$\begin{aligned}&\int _0^{t'}(\dot{x}_\sigma (s)-\dot{{\bar{x}}}(s)\cdot S^T (1,s) \nabla h_k ({\bar{x}} (t'))ds = (x_\sigma (t')- {\bar{x}} (t')) \cdot \\&\quad \nabla h_k ({\bar{x}} (t')) - \int _0^{t'} [\nabla _x f({\bar{x}}(s), {\bar{u}} (s)) (x_{\sigma } (s) -{\bar{x}} (s))]\cdot S^T (1,s) \nabla h_k ({\bar{x}} (t'))ds \, \end{aligned}$$

(‘integration by parts’). We know, however, that, under the differentiability hypotheses on the \(g_j\)’s and \(x \rightarrow f(x,u)\), there exists a modulus of continuity \(\theta _1\) (that does not depend on k or \(t'\)) such that

$$\begin{aligned}&|h_k(x_\sigma (t')) -h_k ({\bar{x}} (t'))-\nabla h_k({\bar{x}} (t'))\cdot (x_\sigma (t')- {\bar{x}} (t'))| \\&\quad \le |x_\sigma (t')- {\bar{x}} (t')| \times \theta _1( |x_\sigma (t')- {\bar{x}} (t')|) \,, \text{ for } \text{ each } k \in \{1, \ldots , N_s\} \end{aligned}$$

and

$$\begin{aligned}&|f(x_\sigma (s), u ) -f({\bar{x}} (s), u) - \nabla _x f({\bar{x}} (s), u)\cdot (x_\sigma (s)- {\bar{x}} (s))| \\&\quad \le |x_\sigma (s)- {\bar{x}} (s)| \times \theta _1( |x_\sigma (t)- {\bar{x}} (t)|) \,, \end{aligned}$$

for each \(s \in [t, t+ \sigma ]\). Combining these relations and noting property (a), we find that, for some \(M >0\) that does not depend on i,

$$\begin{aligned}&h_k (x_\sigma (t')) - h_k ({\bar{x}} (t')) \, \\&\le \, \int _{t}^{t+ \sigma '} \varDelta f(s,u)\cdot S^T (1,s)\nabla h_k ({\bar{x}} (s))ds + M\times \sigma ' \times \Big ( \theta _1 ( E \times \sigma ' )+ \sigma ' \Big )\,. \nonumber \end{aligned}$$
(5)

Here, as before, \(\sigma ' = \sigma \wedge (t' - t))\). We have confirmed property (c) with modulus of continuity \(\theta (s):= M \times \Big ( \theta _1 ( E \times s )+ s \Big ) \). \(\square \)

The preceding proposition provides estimates on solutions to the controlled differential equation \(\dot{x} =f(x,u)\) induced by needle variations. Similar analysis yields estimates on solutions, induced by another kind of ‘local’ variation:

Proposition 3.2

Take a process \(({\bar{x}}, {\bar{u}})\). Take any control function \(u \in {{\mathcal {U}}}\). For each \(\sigma \in [0,1] \), define \(x_\sigma \) to be the solution of the differential equation

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_\sigma (t)= \sigma \Big ( f(x_\sigma (t),u(t))- f(x_\sigma (t),{\bar{u}}(t)\Big ) + f(x_\sigma (t),{\bar{u}}(t), \\ x_\sigma (0) = x_0 \,. \end{array} \right. \end{aligned}$$

(Notice that \(x_\sigma \) is the relaxed state trajectory corresponding to the relaxed control \((\mu _0=(1- \sigma ), {\bar{u}}), (\mu _1 = \sigma , u))\).)

Then, there exists a \(K >0\) (independent of \(\sigma \)) and a continuity modulus \(\theta \) (i.e., a function \(\theta : (0,\infty ) \rightarrow (0, \infty )\), such that \(\lim _{s \downarrow 0}\, \,\theta (s) =0\)), and

  1. (a):

    \(||x_\sigma - {\bar{x}}||_{L^{\infty }} \le K\sigma \),

  2. (b):

    for any index value \(j \in \{0,\ldots ,r\}\) and process (x, u),

    $$\begin{aligned} \sigma ^{-1}( g_j (x_\sigma (1)) - g_j ({\bar{x}} (1))) \, \le \,\int _0^{1} \varDelta f(s,u(s)) \cdot S^T(1,s)\nabla g_j ({\bar{x}}(1)) ds + \theta (\sigma ) \, \end{aligned}$$
  3. (c):

    for any index value \(k=1,\ldots , N_s\), \( t' \in [t,1]\)

    $$\begin{aligned}&\sigma ^{-1}\Big ( h_k (x_\sigma (t')) - h_k ({\bar{x}} (t')) \Big ) \\&\quad \,\le \, \int _0^{t'} \varDelta f(s,u(s))\cdot S^T(t',s)\nabla h_k ({\bar{x}}(t'))ds + \theta (\sigma ). \end{aligned}$$

4 Necessary Conditions of Optimality (No State Constraints)

This section provides three sets of necessary conditions for an admissible process \(({\bar{x}}, {\bar{u}})\) to be a minimizer for (P).

Theorem 4.1

(The First-Order Minimax Condition)

Let \(({\bar{x}}, {\bar{u}})\) be a minimizer for (P). Assume (H1)-(H2) are satisfied. Then, for a.e. \(t \in [0,1]\)

$$\begin{aligned} {\max }_{j \in I({\bar{x}})} \left\{ \varDelta f(t,u)\cdot S^T (1,t)\ \nabla g_j({\bar{x}}(1))\Big )\right\} \ge 0 ,\; \text{ for } \text{ all } u \in \varOmega \,. \end{aligned}$$

Proof

We can always arrange, by adding a constant to \(g_0\) if necessary, that

$$\begin{aligned} g_0({\bar{x}} (1))=0\,. \end{aligned}$$

Since \(({\bar{x}}, {\bar{u}})\) is a minimizer, we must have

$$\begin{aligned}&g_0(x(1)) \vee \ldots \vee g_r(x(1)) \, \ge \, 0 \end{aligned}$$
(6)

for all processes (x, u) for (P). (Otherwise, there would exist a process for which the cost is reduced and all the endpoint constraints are satisfied, a contradiction.)

Let \({{\mathcal {T}}}\) be the subset of points \(t \in (0,1)\) such that t is a Lebesgue point of \(s \rightarrow f({\bar{x}}(s), {\bar{u}} (s))\), \(\dot{x}(t)\) exists, \(\dot{x} (t) =f({\bar{x}}(t),{\bar{u}}(t))\) and \({\bar{u}}(t) \in \varOmega \).

Assume that the assertions of the theorem are false. Since \({{\mathcal {T}}}\) is a set of full measure, there exist a time \(t \in {{\mathcal {T}}} \), \(u \in \varOmega \) and a number \(\gamma >0\) such that

$$\begin{aligned} \varDelta f({\bar{t}},u)\cdot S^T (1,{\bar{t}})\nabla g_j({\bar{x}}(1)) \le - \gamma \end{aligned}$$
(7)

for all \(j\in I({\bar{x}})\). Take \(\sigma _i \downarrow 0\) and, for each i, let \(u_i \in {{\mathcal {U}}}\) to be

$$\begin{aligned} \left\{ \begin{array}{ll} u_i(s) = u &{}\text{ if } s \in [{\bar{t}}, {\bar{t}} + \sigma _i] \\ u_i(s) = {\bar{u}}(s) &{}\text{ otherwise. } \end{array} \right. \end{aligned}$$

Recalling that \(g_0({\bar{x}} (1))=0 \) and that \(g_j ({\bar{x}} (1))\le 0\) for \(j >0\), we deduce from Proposition 3.1 that there exists a modulus of continuity \(\theta (.)\) such that, for each \(j \in \{0,\ldots ,r\}\) and \(i=1,2,\dots \),

$$\begin{aligned} \sigma _i^{-1} g_j (x_i (1))&\,\le \sigma _i^{-1} (g_j (x_i (1)) -g_j ({\bar{x}} (1))) \\&\quad \le \, \sigma _i^{-1} \int _{ t}^{ t+ \sigma _i} \varDelta f(s,u)\cdot S^T (1,s)\nabla g_j ({\bar{x}} (1))ds +\theta (\sigma _i) \,. \nonumber \end{aligned}$$
(8)

By properties of Lebesgue points, there exists a modulus of continuity \(\psi :(0,\infty ) \rightarrow (0, \infty ) \) (that does not depend on j) such that, for all i,

$$\begin{aligned}&\sigma _i^{-1} \int _{ t}^{ t+ \sigma _i} \varDelta f(s,u)\cdot S^T (1,s)\nabla g_j ({\bar{x}} (1))ds \\&\quad \le \varDelta f( t,u)\cdot S^T (1, t)\nabla g_j ({\bar{x}} (1)) + \psi (\sigma _i) \,. \nonumber \end{aligned}$$
(9)

It follows from (7), (8) and (9) that, for all i sufficiently large,

$$\begin{aligned} \sigma _i^{-1} g_j (x_i (1)) \le -\gamma /2 \text{ for } \text{ all } j \in I({\bar{x}})\,. \end{aligned}$$
(10)

Note, on the other hand, that for each \(j \notin I({\bar{x}})\), \(g_j ({\bar{x}} (1)) <0\). So there exists \(\gamma _1 >0\) such that

$$\begin{aligned} g_j ({\bar{x}}(1)) \le -\gamma _1 \text{ for } \text{ each } j \notin I(x)\,. \end{aligned}$$

It follows that, for all i sufficiently large,

$$\begin{aligned} g_j ( x_i (1)) \le -(\sigma _i \gamma \wedge \gamma _1 ) /2 \text{ for } \text{ all } j \in \{0,\ldots , r\}\,. \end{aligned}$$
(11)

This contradicts (6) when \(x =x_i\). The proof is concluded. \(\square \)

Theorem 4.2

(The Integral First-Order Minimax Condition)

Let \(({\bar{x}}, {\bar{u}})\) be a minimizer for (P). Assume (H1)-(H2) are satisfied. Then,

$$\begin{aligned} \max _{j \in I({\bar{x}})} \left\{ \int _0^1 \varDelta f(t,u(t))\cdot S^T (1,t)\ \nabla g_j({\bar{x}}(1))\Big )dt\right\} \ge 0 \;, \end{aligned}$$

for all control functions \(u \in {{\mathcal {U}}}\).

Proof

Assume again, without loss of generality, that \(g_0 ({\bar{x}} (1))=0\). Take any \(u \in {{\mathcal {U}}}\) and \(\sigma \in [0,1]\). Let \(x_\sigma \) be the relaxed state trajectory of Proposition 3.2. We claim that

$$\begin{aligned} g_0(x_\sigma (1)) \vee \ldots \vee g_r(x_\sigma (1)) \, \ge 0, \end{aligned}$$
(12)

This follows from the fact that \((x_\sigma , \{(\mu _0=(1-\sigma ), \mu _1= \sigma ), (u_0={\bar{u}}, u_1 = u)\})\) is a relaxed process. Indeed if, to the contrary, there exists \(\bar{r} > 0\) such that

$$\begin{aligned} g_0(x_\sigma (1)) \vee \ldots \vee g_r(x_\sigma (1)) \, < \, -{\bar{r}}, \end{aligned}$$

then, according to the relaxation theorem and in view of the continuity of the \(g_k\)’s, we would be able to find an (unrelaxed) state trajectory \(x'\) and such that \(g_0(x'(1)) \vee \ldots \vee g^{'}_r(x(1)) \, < \, -{\bar{r}} /2 \), in contradiction of the optimality of \(({\bar{x}}, {\bar{u}})\). The claim is therefore correct.

Suppose that the assertions of the theorem are false. In view of the foregoing observations, we are justified in reproducing the analysis in the proof of the earlier theorem, but now based on the perturbation estimates provided by Proposition 3.2 in place of Proposition 3.1, to obtain a contradiction of (12), for \(\sigma >0\) sufficiently small. The assertions of the theorem must therefore be true. \(\square \)

Finally, we state a special case of the minimum principle, in a form that emphasizes its connection with the preceding two sets of necessary conditions.

Theorem 4.3

(The Minimum Principle)

Let \(({\bar{x}}, {\bar{u}})\) be a minimizer for (P). Assume (H1)-(H2) are satisfied. Then, there exists \(\lambda =(\lambda _0,\ldots , \lambda _r) \in \varLambda ^r\) such that \(\lambda _j =0 \), for \(j \notin I({\bar{x}})\) and

$$\begin{aligned} \varDelta f(t,u)\cdot S^T (1,t)\Big (\sum _{j \in I({\bar{x}})} \lambda _j \nabla g_j({\bar{x}}(1))\Big )\ge 0 \end{aligned}$$
(13)

for all \(u \in \varOmega \), a.e. \(t \in [0,1]\).

We shall give an independent proof of this well-known optimality condition, as a by-product of our investigations into the relationships between the first-order minimax condition, the integral first-order minimax condition and the minimum principle.

Comments.

  1. 1.

    The first-order minimax condition, originating in earlier algorithm convergence of Mayne and Polak [6, 9] , has the alternative expression:

    $$\begin{aligned} \max _{j \in I({\bar{x}})} \left\{ \varDelta f(t,u)\cdot p_j(t) \right\} \ge 0\; \text{ for } \text{ all } u \in \varOmega , \text{ a.e. } t \in [0,1], \end{aligned}$$

    in which, for each j, \(p_j(t):= S^T (1,t)\nabla g_j ({\bar{x}} (1)) \); it can be interpreted as the solution to the costate equation:

    $$\begin{aligned} \left\{ \begin{array}{l} -\dot{p}_j(t) =f^T_x ({\bar{x}} (t), {\bar{u}} (t)) p_j(t) \; \text{ a.e. } t \in [0,1], \\ p_j(1)= \nabla g_j ({\bar{x}} (1)) \,. \end{array} \right. \end{aligned}$$
  2. 2.

    The optimality condition of Theorem 4.3 can be equivalently written in terms of a single costate arc \(p(t) :=S^T (1,t)( \sum _j \lambda _j \nabla g_j ({\bar{x}} (1))\), thus:

    $$\begin{aligned} \varDelta f(t,u)\cdot p(t)\ge 0 \text{ for } \text{ all } u \in \varOmega , \text{ a.e. } t \in [0,1]. \end{aligned}$$

    By the properties of the transition matrix S(t, s), the costate arc p satisfies

    $$\begin{aligned} \left\{ \begin{array}{l} -\dot{p}(t) =f^T_x ({\bar{x}} (t), {\bar{u}} (t)) p(t) \; \text{ a.e. } t \in [0,1], \\ p(1)= \sum _j \lambda _j \nabla g_j ({\bar{x}} (1)) \,. \end{array} \right. \end{aligned}$$

    In this form, it will be recognized as the special case of the minimum principle, applied to problems with endpoint inequality constraints. (Note the Lagrange multipliers satisfy the non-triviality condition \(\lambda \not = 0\), since \(\lambda \in \varLambda ^{r}\), and \(\lambda _j =0\) if \(h_j({\bar{x}}(1))< 0\).)

5 Relations Between the Necessary Conditions

The following theorem relates the necessary conditions of Sect. 4.

Theorem 5.1

Assume the data for problem (P) satisfy hypotheses (H1)-(H2), for some arbitrary admissible process \(({\bar{x}}, {\bar{u}})\). We have:

  1. (i):

    An admissible process \(({\bar{x}}, {\bar{u}})\) satisfies the first-order minimax condition if it satisfies the integral first-order minimax condition, i.e., the integral first-order minimax condition is stronger than the first-order minimax condition.

  2. (ii):

    An admissible process \(({\bar{x}}, {\bar{u}})\) satisfies the integral first-order minimax condition if and only if it satisfies the minimum principle.

  3. (iii):

    The minimum principle (and therefore also the integral first-order minimax condition) is a strictly stronger necessary condition than the first-order minimax condition, in the sense that data can be chosen for problem (P) such that the integrated first-order minimax condition can be used to exclude a non-minimizer, but the first-order minimax condition fails to do so.

Proof

  1. (i):

    Suppose the minimax condition is not satisfied. Then, there exists \( u \in \varOmega \) and \(t \in (0,1)\) such that t is a Lebesgue point of \(s \rightarrow f({\bar{x}} (s), {\bar{u}}(s))\), \(\dot{{\bar{x}}}(t)\) exists, \({\bar{u}}(t) \in \varOmega \), \(\dot{{\bar{x}}}(t) \in f({\bar{x}} (t) , {\bar{u}} (t) )\) and

    $$\begin{aligned} \varDelta f(t, u)\cdot S^T (1,t ) \nabla g_j( {\bar{x}} (1) ) < 0\, \text{ for } \text{ all } j \in I({\bar{x}})\,. \end{aligned}$$

    For arbitrary \(\sigma \in (0,1-t)\), define the ‘needle variation’ \(u_\sigma \in {{\mathcal {U}}}\) according to (3). From the Lebesgue point property, we have that, for all \(j \in I({\bar{x}})\),

    $$\begin{aligned}&\sigma ^{-1} \int _0^1 \varDelta f(s, u_\sigma (s) )\cdot S^T (1,s ) \nabla g_j( {\bar{x}} (1) )ds \\&\quad = \sigma ^{-1} \int _t^{t+\sigma } \varDelta f(s, u)\cdot S^T (1,s ) \nabla g_j( {\bar{x}} (1) )ds < 0\,, \end{aligned}$$

    for \(\sigma \) sufficiently small. We have shown that the integrated first-order minimax condition is not satisfied. The proof is complete.

  2. (ii):

    Take any \(u \in {{\mathcal {U}}}\). Suppose the minimum principle is satisfied (with Lagrange multipliers \(\lambda = (\lambda _0 , \ldots , \lambda _r ) \in \varLambda ^r \text{ such } \text{ that } \lambda _j = 0\) if \(j \notin I({\bar{x}}) \)). Then, for any \(u \in {{\mathcal {U}}}\),

    $$\begin{aligned} \int _0^1\varDelta f(t,u(t))\cdot S^T (1,t)\Big (\sum _{j \in I({\bar{x}})} \lambda _j \nabla g_j({\bar{x}}(1))\Big )dt \ge 0 \,. \end{aligned}$$

    This implies the existence of \({\bar{j}} \in I({\bar{x}})\) such that

    $$\begin{aligned} \int _0^1\varDelta f(t,u(t))\cdot S^T (1,t) \nabla g_{{\bar{j}}}({\bar{x}}(1))dt \ge 0 \,. \end{aligned}$$

    Hence,

    $$\begin{aligned} \max _{j \in I({\bar{x}})}. \left\{ \int _0^1\varDelta f(t,u(t))\cdot S^T (1,t) \nabla g_{ j}({\bar{x}}(1))dt\right\} \ge 0 \,. \end{aligned}$$

    We have shown that the conditions of the minimum principle imply the conditions of the integral first-order minimax theorem.

Now, suppose that the conditions of the integral first-order minimax theorem are satisfied. It is convenient to introduce, at this stage, the notation:

$$\begin{aligned} E :=\{e \in L^1 (0,1)\,:\, e(t) \in \varDelta f(t,\varOmega ) \text{ a.e. } t \in [0,1] \} . \end{aligned}$$

Write \({{\tilde{\varLambda }}}^r := \{\lambda \in \varLambda ^r\,:\, \lambda _j =0 \text{ if } j \notin I({\bar{x}}) \}\). Define \(J: L^1 \times {{\tilde{\varLambda }}}_r \rightarrow R\):

$$\begin{aligned} J(e,\lambda ) := \int _0^1 e(t) \cdot S^T (1,t) \Big (\sum _{j \in I({\bar{x}})} \lambda _j \nabla g_j({\bar{x}}(1))\Big )dt\,. \end{aligned}$$

Notice that the integral first-order minimax condition can be expressed as

$$\begin{aligned} \max _{j \in I({\bar{x}})} \int _0^1 e(t) \cdot S^T (1,t)\nabla g_j ({\bar{x}} (1)) dt \ge 0, \text{ for } \text{ all } e \in E\,. \end{aligned}$$
(14)

Making use of the following representation of the convex hull of E:

$$\begin{aligned}&\text {co}\, E :=\{e \in L^1 (0,1)\,:\, e(t) = \sum _{i=0}^{N} \nu _i \varDelta f(t,u_i(t)) \text { for an integer } N, \\&\qquad \quad \text {control functions} \{u_0,\ldots , u_N\} \text { and } \nu \in \varLambda ^N, \text { a.e. } t \in [0,1]\} , \end{aligned}$$

and noting that \(e \rightarrow J(e, \lambda )\) is continuous w.r.t. the weak \(L^1\) topology, we can replace (14) by the strengthened condition

$$\begin{aligned} \max _{j \in I({\bar{x}})} \int _0^1 e(t) \cdot S^T (1,t)\nabla g_j ({\bar{x}} (1)) dt \ge 0, \text{ for } \text{ all } e \in \overline{\text{ co }}\,E\,, \end{aligned}$$
(15)

in which \(\overline{\text{ co }}\) denotes ‘convex closure’ w.r.t. the \(L^1\) norm. Note the following properties of J and its domain (which take to be \(\overline{\text{ co }}\, E \times {\tilde{\varLambda }}^r\)):

  1. (A):

    co\(\,E\) and \({\tilde{\varLambda }}^r \) are convex sets, and they are compact w.r.t. the weak \(L^1\) topology and the Euclidean topology, respectively. (The weak \(L^1\) compactness of E can be deduced from the hypotheses (H1) and (H2), with the help of Ascoli’s theorem),

  2. (B):

    \(J(e,\lambda )\) is continuous in e, for fixed \(\lambda \in {\tilde{\varLambda }}^r\), and continuous in \(\lambda \), for fixed \(e \in \text{ co }\, E\), w.r.t. the above topologies.

  3. (C):

    \(J(e,\lambda )\) is convex in e for fixed \(\lambda \) and convex in \(\lambda \) for fixed e.

We have checked the hypotheses are satisfied for the application of Von Neumann’s Minimax theorem. (See [10, Thm. 3.4.6] ). This tells us that J has a saddlepoint \((e^*, \lambda ^*) \in \text{ co }\,E \times {\tilde{\varLambda }}^r\), i.e.,

$$\begin{aligned} J(e^*, \lambda ) \le J(e^*, \lambda ^*) \le J(e, \lambda ^*) \, \text{ for } \text{ all } e \in E \text{ and } \lambda \in {\tilde{\varLambda }}^r. \end{aligned}$$

Now, notice that (15) implies that, for any \(e' \in E\) (and in particular \(e' =e^*\))

$$\begin{aligned} 0 \le \max _\lambda J(e', \lambda )\,. \end{aligned}$$

But then, by the saddlepoint condition,

$$\begin{aligned} 0 \le \max _\lambda J(e^*, \lambda ) =J(e^*, \lambda ^*) \le J(e,\lambda ^*)\,, \end{aligned}$$

for any \(e \in E\). This inequality tells us that

$$\begin{aligned} \int _0^1 \varDelta f(t,u(t))\cdot S^T (1,t)\Big (\sum _{j=0}^{r} \lambda ^*_j \nabla g_j({\bar{x}}(1))\Big )dt \ge 0 \,, \end{aligned}$$
(16)

for any control function \(u \in {{\mathcal {U}}}\). A standard ‘needle variation’ argument permits us to conclude from this last relation that

$$\begin{aligned} \varDelta f(t,u)\cdot S^T (1,t)\Big ( \sum _{ j \in I({\bar{x}})} \lambda ^*_j \nabla g_j({\bar{x}}(1))\Big ) \ge 0 \text{ for } \text{ all } u \in \varOmega , \text{ a.e. } t \in [0,1]. \end{aligned}$$

This is the minimum principal condition, in which the endpoint constraint Lagrange multiplier vector is \(\lambda ^*\).

(iii): This assertion is confirmed by the example of Sect. 6. \(\square \)

6 Example One

Consider the following example of (P), in which the state and control dimensions are both 2 and there is one endpoint constraint.

$$\begin{aligned} (P) \left\{ \ \begin{array}{l} \text{ Minimize } [0.5,-1] \,x(1) \\ \text{ subject } \text{ to } \\ \dot{x}(t) =u , \; \text{ a.e. } t \in [0,1], \\ u(t)\in \varOmega := \left\{ [0, 0]^T, [1, 0]^T , [0, 1]^T \right\} , \; \text{ a.e. } t \in [0,1], \\ x(0)=0 \text{ and } [-1,0.5 ]\, x(1) \le 0 \end{array} \right. \end{aligned}$$

Take \(({\bar{x}}, {\bar{u}})\equiv (0,0) \) . (H1) and (H2) are satisfied.

Proposition 6.1

  1. (a):

    The admissible process \(({\bar{x}}, {\bar{u}})\) is not a minimizer,

  2. (b):

    the first-order minimax condition is satisfied at \(({\bar{x}}, {\bar{u}})\),

  3. (c):

    the integral minimax condition (and therefore also the minimum principle condition) is not satisfied at \(({\bar{x}}, {\bar{u}})\) .

Proof

Consider the process (u, x) such that \( u(t)=[1,0]^T\) on [0, 1/2] and \({{\tilde{u}}}(t)=[0,1]^T\) on (1/2, 1]. Then, \(x(1)= [1/2,1/2]^T\). We see that the values of the cost and endpoint constraint functional are, respectively,

$$\begin{aligned} {[}0.5,-1]\, x(1) = - 1/2 \text{ and } [-1,0.5]\, x(1) = - 1/2, \end{aligned}$$

i.e., (u, x) is admissible and has strictly negative cost. It follows that \((x\equiv [0,0]^T\), \(u \equiv [0,0]^T)\) cannot therefore be a minimizer.

(b): Using our generic notation, we have

$$\begin{aligned}&S(s,t) \equiv I_{2\times 2} \text { for all values of } s \text { and } t, \\&\{ \varDelta f(t,u)\,:\, u \in \varOmega \}= \{[0,0]^T, [1,0 ] , [0,1]^T\} , \\&\nabla g_0({\bar{x}}(1))= [0.5,-1]^T \text { and } \nabla g_1({\bar{x}}(1))= [-1,5]^T \end{aligned}$$

Then, for any time \(t \in [0,1]\),

$$\begin{aligned}&\max \nolimits _{j \in \{ 0,\ldots ,r\}} \varDelta f(t,u)\cdot S(t,1)\ \nabla g_j({\bar{x}}(1))\Big ) = \\&\quad \left\{ \begin{array}{ll} \max \left\{ [0,0] [0.5, -1]^T, [0,0] [-1, 0.5]^T \right\} = 0 &{} \qquad \text{ if } u= [1,0]^T \\ \max \left\{ [1,0] [0.5, -1]^T, [1,0] [-1, 0.5]^T \right\} = 0.5 &{} \qquad \text{ if } u= [1,0]^T \\ \max \left\{ [0,1] [0.5 ,-1]^T, [0,1] [-1, 0.5]^T \right\} = 0.5 &{} \qquad \text{ if } u= [0,1]^T\,. \end{array} \right. \end{aligned}$$

It follows that the first-order minimax condition is satisfied at \(({\bar{u}}, {\bar{x}})\).

(c): For \(u \in {{\mathcal {U}}}\) as in part (a), we calculate

$$\begin{aligned}&\max _{j}\,\int _0^1 \varDelta f(t, u(t))\cdot S^T(1,t)\ \nabla g_j({\bar{x}}(1))dt\, = \\&\quad \max \left\{ [1/2,1/2] [0.5\, -1]^T , [1/2,1/2] [-1, 0.5]^T \right\} = -1/2\, <\, 0. \end{aligned}$$

We have shown that the integrated first-order minimax condition is violated. \(\square \)

7 State Constraints

Consider the state constrained problem formulated in the introduction

$$\begin{aligned} (S) \left\{ \ \begin{array}{l} \text{ Minimize } g_0(x(1) ) \\ \text{ over } \text{ absolutely } \text{ continuous } \text{ functions } x \text{ and } \text{ meas. } \text{ functions } u \text{ such } \text{ that } \\ \dot{x}(t) =f(x(t),u(t)), \; \text{ a.e. } t \in [0,1], \\ h_k(x(t)) \le 0, \text{ for } \text{ all } \text{ index } \text{ values } k\in \{1,\ldots ,N_s\} \text{ and } t \in [0,1], \\ u(t)\in \varOmega , \; \text{ a.e. } t \in [0,1], \\ x(0)=x_0 \text{ and } g_j(x(1)) \le 0, \text{ for } j =1,2., \ldots , r \,. \end{array} \right. \end{aligned}$$

For \(k=1,\ldots ,N_s\), \(A_k({\bar{x}})\) will denote the set of times at which the k’th state constraint is active, for the nominal process \(({\bar{x}}, {\bar{u}})\), that is

$$\begin{aligned} A_k({\bar{x}}) \,:=\, \{t \in [0,1] \,:\, h_k ({\bar{x}} (t)) =0\}, \text{ for } k=0,\ldots ,r\,. \end{aligned}$$

We derive similar necessary conditions of optimality to those of Sect. 4, but now allowing for state constraints.

Theorem 7.1

The First-Order Minimax Condition (State Constraints)

Let \(({\bar{x}}, {\bar{u}})\) be a minimizer for (S). Assume (H1)-(H2) are satisfied. Then, for a.e. \(t \in [0,1]\),

$$\begin{aligned}&\max _{j \in I({\bar{x}})} \left\{ (\varDelta f(t,u) \cdot S^T (1,t)\ \nabla g_j({\bar{x}}(1)) \right\} \\&\vee \; \max _{k \in \{1,\ldots N_s \}} \Big ( \max _{t' \in A_k ({\bar{x}})\cap [t, 1] } \left\{ \varDelta f(t',u) \cdot S^T(t',t)\ \nabla h_k({\bar{x}}(t'))\right\} \Big ) \, \ge \, 0 \,, \end{aligned}$$

for all \(u \in \varOmega \).

Proof

We may assume that \(g_0\) satisfies \( g_0({\bar{x}} (1))=0\,. \) Since \(({\bar{x}}, {\bar{u}})\) is a minimizer, we must have

$$\begin{aligned}&g_0(x(1)) \vee \ldots \vee g_r(x(1)) \vee \max _{t \in [0,1]} h_j (x(t)) \vee \ldots \vee \max _{t \in [0,1]} h_{N_s} (x(t))\, \ge \, 0\,, \end{aligned}$$
(17)

for all processes (x, u) for (S).

Let \({{\mathcal {T}}}\) be the subset of points \(t \in [0,1]\) with the following properties: t is a Lebesgue point of \(s \rightarrow f({\bar{x}}(s), {\bar{u}} (s))\), \(\dot{x}(t)\) exists, \(\dot{x} (t) =f({\bar{x}}(t),{\bar{u}}(t))\) and \({\bar{u}}(t) \in \varOmega \). Define, for arbitrary \(\epsilon >0\) and \( k \in \{1,\ldots , N_s\}\),

$$\begin{aligned} A_k^\epsilon ({\bar{x}}):= \{ t\in [0,1]\,:\, h_k ({\bar{x}}_k(t)) \ge - \epsilon \} \,. \end{aligned}$$
(18)

We claim it suffices to prove a modified version of the theorem, in which we require, for arbitrary \(t \in {{\mathcal {T}}}\) and \(\epsilon >0\),

$$\begin{aligned}&\max _{j \in I({\bar{x}})} \left\{ (\varDelta f(t,u(t)) \cdot S^T(1,t)\ \nabla g_j({\bar{x}}(1)) \right\} \\&\quad \vee \; \max _{k \in \{0,\ldots N_s \}} \Big (\max _{t' \in A^{\epsilon }_k ({\bar{x}})\cap [t, 1] } \left\{ \varDelta f(t',u) \cdot S^T(t',t)\ \nabla h_k({\bar{x}}(t))\right\} \Big ) \, \ge \, 0 \, \end{aligned}$$

for all \(u \in \varOmega \) and \(t' \ge t\).

Indeed, if this modified condition was true for arbitrary \(\epsilon >0\), then it would be valid for each \(\epsilon = \epsilon _i\), \(i =1,2,\dots \), where \(\epsilon _i \downarrow 0\). This means that, for each \(t \in {{\mathcal {T}}}\) and \(u \in \varOmega \) and every i, either there exists \(j(i) \in I({\bar{x}})\) such that

$$\begin{aligned} \varDelta f(t,u(t)) \cdot S^T(1,t)\ \nabla g_{j(i)}({\bar{x}}(1)) \ge 0 \end{aligned}$$

or there exist \(k(i) \in \{1, \ldots , N_s\}\) and \(t^{'}(i) \in A^{\epsilon _{i} }_{k(i)} \cap [t,1]\) such that

$$\begin{aligned} \varDelta f(t'(i),u) \cdot S^T(t'(i),t)\ \nabla h_k({\bar{x}}(t)) \ge 0\,. \end{aligned}$$

By extracting subsequences, we can arrange the \(i(j)= \bar{i} \in I({\bar{x}})\), \(k(i)= \bar{k}\) for all i and \(t^{'}_i \rightarrow \bar{t}'\) as \(i \rightarrow \infty \), for some \(\bar{i} \in I({\bar{x}})\), \(\bar{k} \in \{1,\ldots , N_s\} \) and \(\bar{t}^{'} \in A_{\bar{k}} \cap [t,1]\). Since, for each k,

$$\begin{aligned} A_k ({\bar{x}}) \cap [t,1]= \{\lim _i t_i\,:\, t_i \in A^{\epsilon _i}_k ({\bar{x}}) \cap [t,1] \text{ for } \text{ each } i \}\,, \end{aligned}$$

we can deduce that either there exists \({\bar{j}} \in I({\bar{x}})\) such that

$$\begin{aligned} \varDelta f(t,u(t)) \cdot S(t,1)\ \nabla g_{{\bar{j}}}({\bar{x}}(1)) \ge 0 \end{aligned}$$

or there exist \({\bar{k}} \in \{ 1,\ldots , N_s \} \) and \(\bar{t}^{'} \in A_{{\bar{k}}} ({\bar{x}})\) such

$$\begin{aligned} \varDelta f({\bar{t}}',u) \cdot S({\bar{t}}',t)\ \nabla h_{{\bar{k}}}({\bar{x}}(t)) \ge 0\,. \end{aligned}$$

These relations combine to yield the required (stronger) necessary condition of the theorem statement.

Assume, for some \(\epsilon >0\), the modified condition above is false; we show that this leads to a contradiction. Then, for some \(t \in {{\mathcal {T}}}\), \(u \in \varOmega \) and \(\gamma >0\),

$$\begin{aligned} \varDelta f(t,u)\cdot S^T (1, t)\nabla g_j({\bar{x}}(1)) \le - \gamma , \text{ for } \text{ all } j\in I({\bar{x}}) \end{aligned}$$
(19)

and

$$\begin{aligned}&\varDelta f( t,u)\cdot S^T (t', t)\nabla h_k ({\bar{x}}(t')) \\&\quad \le - \gamma , \text{ for } \text{ all } k \in \{1, N_s\}, t' \in A^{\epsilon }_k({\bar{x}}) \cap [ t,1] \,. \nonumber \end{aligned}$$
(20)

Take \(\sigma _i \downarrow 0\) and, for each i, let \(u_i \in {{\mathcal {U}}}\) to be control function

$$\begin{aligned} \left\{ \begin{array}{ll} u_i(s) = u &{}\text{ if } s \in [{\bar{t}}, {\bar{t}} + \sigma _i] \\ u_i(s) = {\bar{u}}(s) &{}\text{ otherwise }\,. \end{array} \right. \end{aligned}$$

Since \(g_j ({\bar{x}} (1))\le 0\) for all \(j\in \{0,\dots ,r\}\) and \(h_k({\bar{x}} (t)) \le 0\) for all \(t \in [0,1]\) and \(k \in \{ 0,\ldots , N_s\}\), we deduce from Proposition 3.1 that there exists a modulus of continuity \(\theta (.)\) such that, for each \(j \in \{0,\ldots ,r\}\) and \(j=1,2,\dots \),

$$\begin{aligned} \sigma _i^{-1} g_j (x_i (1))&\,\le \sigma _i^{-1} (g_j (x_i (1)) -g_j ({\bar{x}} (1))) \\&\quad \le \, \sigma _i^{-1} \int _{t}^{ t+ \sigma _i} \varDelta f(s,u)\cdot S^T (1,s)\nabla g_j ({\bar{x}} (1))ds +\theta (\sigma _i) \,. \nonumber \end{aligned}$$
(21)

and, for each \(k \in \{1,\ldots , N_s \}\) and \(\sigma ^{'}_i := \sigma _i\wedge (t' -t)\),

$$\begin{aligned}&h_k (x_{i} (t')) \le h_k (x_{i} (t')) - h_k ({\bar{x}} (t')) \\&\quad \le \, \int _{t}^{ t + \sigma ^{'}_i} (\varDelta f(s,u)\cdot S^T(t',s)\nabla h_k ({\bar{x}}(t'))ds + \sigma ^{'}_i \times \theta (\sigma ^{'}_i)\,. \nonumber \end{aligned}$$
(22)

Since t is a Lebesgue point, there exists a further modulus of continuity \(\psi :(0,\infty ) \rightarrow (0, \infty ) \) (that does not depend on j, k or \(t'(\ge {\bar{t}})\)) such that

$$\begin{aligned}&\sigma _i^{-1} \int _{t}^{t+ \sigma _i} \varDelta f(s,u)\cdot S^T (1,s)\nabla g_j ({\bar{x}} (1))ds \\&\quad \le \varDelta f(t,u)\cdot S^T (1,t)\nabla g_j ({\bar{x}} (1)) + \psi (\sigma _i) \,. \nonumber \end{aligned}$$
(23)

and

$$\begin{aligned}&\int _{t}^{t+ \sigma ^{'}_i} \varDelta f(s,u)\cdot S^T (t',s)\nabla h_k ({\bar{x}} (t'))ds \\&\quad \le \sigma ^{'}_{i} \varDelta f(t,u)\cdot S^T (1,t)\nabla h_k ({\bar{x}} (1)) + \sigma ^{'}_i\psi (\sigma ^{'}_i) \,. \nonumber \end{aligned}$$
(24)

Since \(g_j({\bar{x}} (1)) \le 0\) for each j, it follows from (19), (21), (22), (23) and (24) that, for all i sufficiently large,

$$\begin{aligned} \sigma _i^{-1} g_j (x_i (1)) \le -\gamma /2 \text{ for } \text{ all } j \in I({\bar{x}})\,. \end{aligned}$$
(25)

Note, on the other hand, that for each \(j \notin I({\bar{x}})\), \(g_j ({\bar{x}} (1)) <0\). So there exists \(\gamma _1 >0\) such that

$$\begin{aligned} g_j ({\bar{x}}(1)) \le -\gamma _1 \text{ for } \text{ each } j \notin I(x)\,. \end{aligned}$$
(26)

It follows from Proposition 3.1(a) that, for all i sufficiently large,

$$\begin{aligned} g_j ( x_i (1)) \le -\gamma _1 /2 \text{ for } \text{ all } j \notin I({\bar{x}})\,. \end{aligned}$$
(27)

Now take any \(k \in \{ 1,\ldots , N_s\}\). Since \(h_k({\bar{x}} (t)) \le 0\) for all \(t \in [0,1]\), we can deduce from (20) (22) and (24) that, for all i sufficiently large,

$$\begin{aligned} (\sigma _1 \vee (t' -t))^{-1} h_k (x_i (t')) \le -\gamma /2 \text{ for } t' \in A^\epsilon _k ({\bar{x}}) \cap (t,1] \,. \end{aligned}$$
(28)

Since \(x_i\) coincides with \({\bar{x}}\) on [0, t] and \(h_k ({\bar{x}} (t)) \le 0\), we know also that

$$\begin{aligned} h_k (x_i (t')) \le 0 \text{ for } \text{ all } t' \in [0,t] \,. \end{aligned}$$
(29)

Since \(h_k ({\bar{x}} (t)) < -\epsilon \) for all \(t'\in [0,1]\) such that \(t' \notin A^\epsilon _k ({\bar{x}})\), we deduce from Proposition 3.1 (a) that, for i sufficiently large,

$$\begin{aligned} h_k (x_i (t')) \le - \epsilon /2 \text{ for } \text{ all } t' \in [[0,t] \text{ such } \text{ that } t \notin A^{\epsilon }_k \,. \end{aligned}$$
(30)

Relations (25), (27) ,(28), (29) and (30) combine to tell us that, for i sufficiently large, condition (17) is violated by the admissible state trajectory \(x_i\). The validity of the assertions of the theorem follow from this contradiction. \(\square \)

Theorem 7.2

(The State Constrained Integral First-Order Minimax Condition)

Let \(({\bar{x}}, {\bar{u}})\) be a minimizer for (S). Assume (H1)-(H2) are satisfied. Then

$$\begin{aligned}&\max _{j \in I({\bar{x}})} \left\{ \int _0^1 \varDelta f(t,u(t)) \cdot S^T(t,1)\ \nabla g_j({\bar{x}}(1)) dt \right\} \\&\quad \vee \; \max _{k \in \{1,\ldots N_s \}} \Big (\max _{t' \in A_k ({\bar{x}})} \left\{ \int _0^{t'} \varDelta f(t,u(t)) \cdot S^T (t',t)\ \nabla h_k({\bar{x}}(t'))dt \right\} \Big ) \, \ge \, 0 \,, \end{aligned}$$

for all \(u \in {{\mathcal {U}}}\).

(We interpret \(\max _{t' \in A_j ({\bar{x}})} \{\dots \}:= -\infty \), if \( A_j ({\bar{x}})= \emptyset \).)

Proof

We may assume, without loss of generality, that \(g_0 ({\bar{x}} (1))=0\). We claim it suffices to prove a weaker form of the theorem, in which the inequality is replaced, for arbitrary \(\epsilon >0\), by the weaker condition

$$\begin{aligned}&\max _{j \in I({\bar{x}})} \left\{ \int _0^1 (\varDelta f(t,u(t)) \cdot S(t,1)\ \nabla g_j({\bar{x}}(1))dt \right\} \\&\quad \vee \; \max _{k \in \{1,\ldots N_s \}} \Big ( \max _{t' \in A^{\epsilon }_k ({\bar{x}})} \left\{ \int _0^{t'}\varDelta f(t',u(t)) \cdot S(t',t)\ \nabla h_k({\bar{x}}(t))\right\} dt \Big ) \, \ge \, 0 \, , \end{aligned}$$

for all \(u \in {{\mathcal {U}}}\). (Here, the set \(A^{\epsilon }_k ({\bar{x}})\) is as defined by (18 ).) Indeed if this weaker condition were true for arbitrary \(\epsilon >0\) then it would be valid for \(\epsilon = \epsilon _i\), \(i =1,2,\dots \), where \(\epsilon _i \downarrow 0\). This means that, for any \(u \in {{\mathcal {U}}}\) , either there exists \(j(i) \in I({\bar{x}})\) such that

$$\begin{aligned} \int _0^1 \varDelta f(t,u(t)) \cdot S(t,1)\ \nabla g_{j(i)}({\bar{x}}(1)) dt \ge 0,\; \text{ for } \text{ all } i, \end{aligned}$$

or there exists \(k(i) \in \{1, \ldots , N_s\}\) and \(t^{'}(i) \in A^{\epsilon _{i} }_{k(i)} \) such that

$$\begin{aligned} \int _0^{t'(i)} \varDelta f(t'(i),u(t)) \cdot S(t'(i),t)\ \nabla h_k({\bar{x}}(t')) dt \ge 0,\; \text{ for } \text{ all } i\,. \end{aligned}$$

By extracting subsequences, we can arrange that there exist \(\bar{j} \in I({\bar{x}})\), \({\bar{k}} \in \{1,\ldots , N_s \}\) and \({\bar{t}}^{'} \in A_{\bar{k}} ({\bar{x}})\) such that \(j(i)= {\bar{j}}\), \(k(i) ={\bar{k}}\), for all i; furthermore \(t^{'}_i \rightarrow {\bar{t}}' \).

We deduce in the limit that either

$$\begin{aligned} \int _0^1 \varDelta f(t,u(t)) \cdot S(t,1)\ \nabla g_{{\bar{j}}}({\bar{x}}(1))dt \ge 0 \end{aligned}$$

or

$$\begin{aligned} \int _0^{{\bar{t}}'} \varDelta f({\bar{t}}',u) \cdot S({\bar{t}}',t)\ \nabla h_{{\bar{k}}}({\bar{x}}(t))dt \ge 0\,, \end{aligned}$$

in which, we recall, \(\bar{j} \in I({\bar{x}})\), \({\bar{k}} \in \{1,\ldots , N_s \}\) and \({\bar{t}}^{'} \in A_{\bar{k}} ({\bar{x}})\). These relations combine to yield the required (stronger) necessary condition of the theorem.

So assume that the assertions of this weaker version of the theorem, in which \(A_k^\epsilon ({\bar{x}})\) replaces \(A_k({\bar{x}})\) for some arbitrary \(\epsilon >0\), are false; we shall show that this leads to a contradiction. Take any \(u \in {{\mathcal {U}}}\). Under the contraposition hypothesis, there exists \(\gamma >0\) such that, for all \(\sigma \in (0,1)\),

$$\begin{aligned}&\max _{j \in I({\bar{x}})} \left\{ \int _0^1 \varDelta f(t,u(t)) \cdot S(t,1)\ \nabla g_j({\bar{x}}(1))dt \right\} \\&\quad \vee \; \max _{k \in \{1,\ldots N_s \}} \Big (\max _{t' \in A^{\epsilon }_k ({\bar{x}}) } \left\{ \int _0^{t'} \varDelta f(t,u(t)) \cdot S(t',t)\ \nabla h_k({\bar{x}}(t))dt \right\} \Big ) \, < \, -\gamma \,. \nonumber \end{aligned}$$
(31)

Take \(\sigma _i \downarrow 0\). For each i, let \(x_i\) be the relaxed state trajectory corresponding to the relaxed control \(((\sigma _i,{\bar{u}}), (1- \sigma _i), u) )\). We can deduce from the relaxation theorem and the optimality of \(({\bar{x}} , {\bar{u}})\) that, for each i,

$$\begin{aligned} g_0(x_i (1)) \vee \ldots \vee g_r(x_i (1)) \vee \max _{t \in [0,1]} h_1 (x_i (t)) \vee \ldots&\vee \max _{t \in [0,1]} h_{N_s} (x_i(t)) \nonumber \\&\quad \ge \, 0\,. \end{aligned}$$
(32)

Since \(g_j ({\bar{x}} (1))\le 0\) for all \(j\in \{0,\dots ,r\}\) and \(h_k({\bar{x}} (t)) \le 0\) for all \(t \in [0,1]\) and \(k \in \{ 0,\ldots , N_s\}\), we deduce from Proposition 3.2 that there exists a modulus of continuity \(\theta (.)\) with the following properties: for any i,

$$\begin{aligned} \sigma _i^{-1} g_j (x_i (1)) \, \le \,\int _0^{1} \varDelta f(s,u(s)) \cdot S^T(1,s)\nabla g_j ({\bar{x}}(1)) ds + \theta (\sigma _i), \end{aligned}$$

for \(j=0,\ldots , r\) and

$$\begin{aligned} \sigma _i^{-1} h_k (x_i (t')) \,\le \, \int _0^{t'} \varDelta f(s,u(s))\cdot S^T(t',s)\nabla h_k ({\bar{x}}(t'))ds + \theta (\sigma _i), \end{aligned}$$

for all \(t' \in A_k^\epsilon ({\bar{x}}),\, k=1,\dots ,N_s\).

We conclude from (31) that, for all i sufficiently large,

$$\begin{aligned} \sigma _i^{-1} g_j (x_i (1)) \le -\gamma /2 \text{ for } \text{ all } j \in I({\bar{x}})\, \end{aligned}$$

and

$$\begin{aligned} \sigma _i^{-1} h_k (x_i (t')) \le -\gamma /2, \text{ for } k \in {1,\ldots , N_s} \text{ and } t' \in A_k^{\epsilon }({\bar{x}})\,. \end{aligned}$$

Note, on the other hand, that for each \(j \notin I({\bar{x}})\), \(g_j ({\bar{x}} (1)) <0\). It follows that there exists \(\gamma _1 >0\) such that

$$\begin{aligned} g_j ({\bar{x}}(1)) \le -\gamma _1 \text{ for } \text{ each } j \notin I(x)\,. \end{aligned}$$
(33)

Proposition 3.1 now tells us that, for all i sufficiently large,

$$\begin{aligned} g_j ({\bar{x}}_i (1)) \le -\gamma _1/2 \text{ for } \text{ each } j \notin I(x)\,. \end{aligned}$$
(34)

By the definition of \(A_k^{\epsilon } ({\bar{x}})\),

$$\begin{aligned} h_k ({\bar{x}}(1)) \le -\epsilon \text{ for } \text{ each } k \in \{1,\ldots , N_s \} \text{ and } t \notin A_k^{\epsilon } ({\bar{x}})\,, \end{aligned}$$
(35)

and consequently,

$$\begin{aligned} h_k (x_i(1)) \le -\epsilon /2 \text{ for } \text{ each } k \in \{1,\ldots , N_s \} \text{ and } t \notin A_k^{\epsilon } ({\bar{x}})\,. \end{aligned}$$
(36)

We conclude from the preceding four relations that

$$\begin{aligned}&g_0(x_i (1)) \vee \ldots \vee g_r(x_i (1)) \vee \max _{t \in [0,1]} h_1 (x_i (t)) \vee \ldots \vee \max _{t \in [0,1]} h_{N_s} (x_i(t))\\&\quad \le \, - \min \{ \epsilon , \sigma _i \times \gamma , \gamma _1\}/2 \,, \end{aligned}$$

for i sufficiently large. This contradicts (32). The proof is concluded. \(\square \)

The following necessary condition is a version of the minimum principle for the state constrained problem (S), which makes its relation with the preceding first-order minimax theorem explicit.

Theorem 7.3

(The State Constrained Minimum Principle)

Let \(({\bar{x}}, {\bar{u}})\) be a minimizer for (S). Assume (H1)-(H2) are satisfied. Then, there exist \(\lambda = \{ \lambda _j \} \in ( R^+ )^{r+1}\) and non-decreasing functions of bounded variation \(\nu _k \in BV(0,1)\), \(k =1,\ldots , N_s\), with the following properties:

  1. (a):

    \(\lambda _j =0\) if \(j \notin I({\bar{x}})\), supp\(\, \{\nu _k\} \subset A_k ({\bar{x}})\) for \(k =1,\ldots , N_s\),

  2. (b)

    \((\lambda , \{\nu _k\}) \not = (0,0)\) and

  3. (c):

    for a.e. \(t \in [0,1]\),

    $$\begin{aligned}&\quad \varDelta f(t,u) \cdot S^T(t,1)\sum _{j \in I({\bar{x}})}\lambda _j \nabla g_j({\bar{x}}(1)) \\&\quad + \varDelta f(t,u) \cdot \sum _{k=1}^{N_s} \Big ( \int _t^1 S^T(t',t)\ \nabla h_k({\bar{x}}(t')) d\nu _k (t') \Big ) \,\ge \,0\, ,\, \text{ for } \text{ all } u \in \varOmega . \end{aligned}$$

Comments.

  1. 1.

    The necessary condition of Theorem 7.1 (the state constrained first-order minimax condition) can also be expressed: for a.e. \(t \in [0,1]\),

    $$\begin{aligned}&\max _{j \in I({\bar{x}})} \left\{ (\varDelta f(t,u(t)) \cdot p_j (t) \right\} \\&\vee \; \max _{k \in \{1,\ldots N_s \}} \Big (\max _{t' \in A_k ({\bar{x}})\cap [t, 1] } \left\{ \varDelta f(t',u) \cdot p_k (t' ,t)\right\} \Big ) \, \ge \, 0 \text{ for } \text{ all } u \in \varOmega . \nonumber \end{aligned}$$
    (37)

    Here, \(p_j (t):= S^T (1,t)\nabla g_j ({\bar{x}} (1)) \), for each \(j \in I({\bar{x}})\) and \(p_k (t',t):= S^T (t',t) \) \(\nabla h_k ({\bar{x}} (t')) \), for each \(k \in \{1,\ldots N_s \}\). For each \(j \in I({\bar{x}})\), \(p_j\) (the ‘costate function corresponding to \(g_j\)’) satisfies

    $$\begin{aligned} \left\{ \begin{array}{l} -\dot{p}_j(t) =f^T_x ({\bar{x}} (t), {\bar{u}} (t)) p_j(t) \; \text{ a.e. } t \in [0,1], \\ p_j(1)= \nabla g_j ({\bar{x}} (1)) \,. \end{array} \right. \end{aligned}$$

    For each \(k \in \{1,\ldots , N_s\}\) and \(t' \in [0,1]\), \(p_k (t', .)\) (the ‘costate corresponding to \(h_k\) at time \(t'\)’) is the solution to the differential equation

    $$\begin{aligned} \left\{ \begin{array}{l} -\dot{p}_k(t' ,t) =f^T_x ({\bar{x}} (t), {\bar{u}} (t)) p_k(t' ,t) \; \text{ a.e. } t \in [0,t'], \\ p_k(t' ,t')= \nabla h_k ({\bar{x}} (t')) \,. \end{array} \right. \end{aligned}$$
  2. 2.

    The necessary condition provided by Theorem 7.2 is implicit in convergence analysis of [11]. It can be expressed as

    $$\begin{aligned}&\max _{j \in I({\bar{x}})} \left\{ \int _0^1 \varDelta f(t,u(t)) \cdot p_j(t))dt \right\} \\&\vee \; \max _{k \in \{1,\ldots N_s \}} \Big (\max _{t' \in A_k ({\bar{x}}) } \left\{ \int _0^{t'} \varDelta f(t',u(t)) \cdot p_k(t',t)\right\} \Big ) \, \ge \, 0, \text{ for } \text{ all } u \in {{\mathcal {U}}}\,. \end{aligned}$$

    Here, \(p_j (t)\) and \(p_k (t,s)\) are as defined in the preceding comment.

  3. 3.

    An equivalent version of the necessary condition of Theorem 7.3 is: There exist \(\lambda = \{\lambda _j\} \in (R^+)^{r+1}\) and non-decreasing functions of bounded variation \(\nu _k \in BV(0,1)\), \(k =1,\ldots , N_s\), such that \(\lambda _j =0\) if \(j \notin I({\bar{x}})\), supp\(\, \{\nu _k\} \subset A_k ({\bar{x}})\) for \(k =1,\ldots , N_s\), \((\lambda , \{\nu _k\}) \not = (0,0)\) and

    $$\begin{aligned} \varDelta f(t,u)\cdot p(t)\ge 0 \text{ for } \text{ all } u \in \varOmega , \text{ a.e. } t \in [0,1]\,, \end{aligned}$$

    Here, p satisfies the ‘measure driven’ differential equation

    $$\begin{aligned} \left\{ \begin{array}{l} - dp(t) =f^T_x ({\bar{x}} (t), {\bar{u}} (t)) p(t)dt + \sum _{k=1}^{N_s} \nabla h_k ({\bar{x}} (t)) d\nu _k (t) \; \text{ a.e. } t \in [0,1], \\ p(T )= \sum _k \lambda _k \nabla g_k ({\bar{x}} (1)) \,. \end{array} \right. \end{aligned}$$

    In this form, it will be recognized as a special case of the standard state constrained minimum principle ( [10, Thm. 9.3.1]).

The following theorem relates the necessary conditions of Theorem 7.1 (the state constrained first-order minimax condition), Theorem 7.2 (the state constrained integral first-order minimax condition) and Theorem 7.3 (the state constrained minimum principle).

Theorem 7.4

Assume the data for problem (S) satisfy hypotheses (H1)-(H2), for some arbitrary admissible process \(({\bar{x}}, {\bar{u}})\). We have:

  1. (i):

    An admissible process \(({\bar{x}}, {\bar{u}})\)) satisfies the state constrained integral first-order minimax condition if and only if it satisfies the (state constrained) minimum principle.

  2. (ii):

    Data can be chosen for problem (S) and an admissible process \(({\bar{x}}, {\bar{u}})\) such that the first-order minimax condition confirms that \(({\bar{x}}, {\bar{u}})\) is not a minimizer, but the minimum principle fails to do so. The converse is also true: Data can be chosen for problem (S) and an admissible process \(({\bar{x}}, {\bar{u}})\) such that the minimum principle confirms that \(({\bar{x}}, {\bar{u}})\) is not a minimizer, but the first-order minimax condition fails to do so.

Comment:

  • The assertions of Theorem 7.4 remain true even if we replace the classical state constrained minimum principle by Arutyunov and Aseev’s strengthened ‘non-degenerate’ state minimum principle [4]. This is because in Example Two, establishing that, for some (non-optimal) admissible process \(({\bar{x}} , {\bar{u}})\), the first-order minimax condition is not satisfied, while the minimum principle is satisfied, both endpoints of \({\bar{x}}\) are interior to the state constraint set. For such problems, the controllability hypotheses of [4] are automatically satisfied because there are no nonzero normal vectors to the state constraint set at \({\bar{x}}(0)\) or \({\bar{x}} (1)\) and the assertions of both the original minimum principle and its non-degenerate form are the same.

Proof

  1. (i):

    The first assertion in (i) is already confirmed by Example One of Sect. 6, in the special case of problem (P) in which none of the state constraints are active. The second assertion is confirmed by Example Two in Sect. 8.

  2. (ii)

    First, suppose that necessary condition of Theorem 7.3 (the minimum principle) is satisfied. Take any \(u \in {{\mathcal {U}}}\). Inserting \(u =u(t)\) into the inequality in part (b) of the theorem statement, integrating w.r.t. t and changing the order of integration give

    $$\begin{aligned}&\int _0^1 \varDelta f(t,u(t)) \cdot S^T(1,t)\sum _{j \in I({\bar{x}})}\lambda _j \nabla g_j({\bar{x}}(1)) dt \nonumber \\&+ \; \sum _{j=1}^{N_s} \int _0^1 \Big ( \int _0^{t'} \varDelta f(t,u(t)) \cdot S^T(t',t) \nabla h_j({\bar{x}}(t'))dt \Big ) d\nu _k (t') \,\ge \,0\, . \end{aligned}$$
    (38)

If the necessary condition of Theorem 7.2 is violated, we know that \(u \in {{\mathcal {U}}}\) can be chosen such that, for some \(\gamma >0\),

$$\begin{aligned}&\max _{j \in I({\bar{x}})} \left\{ \int _0^1 \varDelta f(t,u(t)) \cdot S^T(t,1)\ \nabla g_j({\bar{x}}(1)) dt \right\} \\&\quad \vee \; \max _{k \in \{1,\ldots N_s \}} \Big (\max _{t' \in A_k ({\bar{x}})} \left\{ \int _0^{t'} \varDelta f(t,u(t)) \cdot S^T (t',t)\ \nabla h_k({\bar{x}}(t'))dt \right\} \Big ) \, \le \, -\gamma \,. \end{aligned}$$

We deduce from the non-triviality of the Lagrange multipliers, together with the facts that the elements \(\{\lambda _j\}\) have support in \(I({\bar{x}})\) and the measures \(d\mu _k\) have support in \(A_k ({\bar{x}})\) for each k, that there exists \(\rho >0\) such that

$$\begin{aligned} \sum _{j \in I({\bar{x}}) } \lambda _j + \sum _{\{k \,:\, A_k ({\bar{x}}) \not = \emptyset \} } \int _{A_k ({\bar{x}})} d\mu _k (t) = \rho \,. \end{aligned}$$
(39)

It follows from (39) and (39) that

$$\begin{aligned}&\int _0^1 \varDelta f(t,u(t)) \cdot S^T(1,t)\sum _{j \in I({\bar{x}})}\lambda _j \nabla g_j({\bar{x}}(1)) dt \\&+ \sum _{j=1}^{N_s} \int _0^1 \Big ( \int _0^{t'} \varDelta f(t,u(t)) \cdot S^T(t',t) \nabla h_j({\bar{x}}(t'))dt \Big ) d\nu _k (t') \\&\le -\gamma \times ( \sum _{j \in I({\bar{x}}) } + \sum _{\{k \,: \, A_k ({\bar{x}}) \not = \emptyset \} }\,\int _{A_k ({\bar{x}})} d\nu _k (t) ) ) = \gamma \times \rho <0\,. \end{aligned}$$

This contradicts (38). We have shown that the integral first-order minimax condition is satisfied.

Now, suppose that the conditions of the integral first-order minimax theorem are satisfied. Define:

$$\begin{aligned}&E :=\{e \in L^1 (0,1)\,:\, e(t) \in \varDelta f(t,\varOmega )) \text{ a.e. } t \in [0,1] \} \text{ and } \text{ write } \\&D:= \{(\lambda , \nu ) \in (R^+ )^{(r+1)}\times NBV^+ ([0,1]; R^{N_s}) \,:\, \\&\quad \lambda _j =0 \text{ if } j \notin I({\bar{x}}), \text{ supp }\, \{\nu _k\} \in A_k({\bar{x}})\} \text{ and } \sum _{j } \lambda _j + \sum _k \int _{A_k({\bar{x}})} d\nu _k=1\}\,. \end{aligned}$$

Define also the function \(J: L^1 \times D \rightarrow R\) to be

$$\begin{aligned} J(e,(\lambda ,\nu ))&:= \int _0^1 e(t) \cdot \Big ( S^T (1,t) ( \sum _{j \in I({\bar{x}})} \lambda _j \nabla g_j({\bar{x}}(1))) \\&\quad + \;\sum _{j=1}^{N_s} ( \int _t^1 S^T(t',t)\ \nabla h_j({\bar{x}}(t')) d\nu _k (t')) \Big ) dt \,. \end{aligned}$$

The integral first-order minimax condition can be expressed as

$$\begin{aligned} \max _{(\lambda ,\nu ) \in D}J(e,(\lambda ,\nu )) \,\ge \, 0 \text{ for } \text{ all } e \in E\,. \end{aligned}$$

Now, equip \( \overline{\text{ co }}\,E\) with its relative weak \(L^1\) topology. We also take the topology on D to be the relative topology induced on this set by the product topology \(E^r \times {{\mathcal {D}}}\), where \(E^r\) is the Euclidean topology and \({{\mathcal {D}}}\) is the weak\(^*\) topology on \(C^* ([0,1];R^{N_s})\). Since (with respect to these topologies) \(e \rightarrow J(e, (\lambda ,\nu ))\) is continuous and linear for fixed \((\lambda ,\nu )\), we can deduce from the preceding relation that

$$\begin{aligned} \max _{(\lambda ,\nu ) \in D}J(e,(\lambda ,\nu )) \,\ge \, 0 \text{ for } \text{ all } e \in \overline{\text{ co }}\,E\,. \end{aligned}$$
(40)

Now, apply the Von Neumann Minimax theorem, taking the pay-off function to be J with domain \(\overline{\text{ co }}\,E \times D\) and identifying the topologies as above. We thereby obtain an element \((e^*, (\lambda ^*, \nu ^*)) \in \overline{\text{ co }} \, E \times D\) such that

$$\begin{aligned} J(e^*, (\lambda ,\nu )) \le J(e^*, (\lambda ^*,\nu ^*)) \le J(e, (\lambda ^*,\nu ^*)) \, \text{ for } \text{ all } (e, (\lambda , \nu )) \in \overline{\text{ co }} \, E \times D. \end{aligned}$$

It follows from (40) that \( 0 \le \max _{(\lambda ,\nu ) \in D} J(e^*, (\lambda ,\nu ))\,. \) From the saddlepoint condition then

$$\begin{aligned} 0 \le \max _{(\lambda , \nu ) \in D} J(e^*, (\lambda ,\nu )) =J(e^*, (\lambda ^*, \nu ^*)) \le J(e,(\lambda ^*, \nu ^*)) \text{ for } \text{ all } e \in E\,. \end{aligned}$$

We conclude that, for all \(u \in {{\mathcal {U}}}\),

$$\begin{aligned} \int _0^1 \varDelta f(t, u(t))&\cdot \Big ( S^T (1,t) ( \sum _{j \in I({\bar{x}})} \lambda _j \nabla g_j({\bar{x}}(1))) \\&\quad + \sum _{j=1}^{N_s} ( \int _t^1 S^T(t',t)\ \nabla h_j({\bar{x}}(t')) d\nu _k (t')) \Big ) dt \,\ge 0\,. \end{aligned}$$

This relation will be recognized as the state constrained minimum principle condition. The proof is complete. \(\square \)

8 Example Two

Consider the following example of Problem (S), the data which satisfy hypotheses (H1) and (H2):

$$\begin{aligned} \left\{ \begin{array}{l} \text{ Minimize } x_1(1) \text{ subject } \text{ to } \\ (\dot{x}_1 (t), \dot{x}_2(t) = (x_2(t), u(t))\,, \text{ a.e. } t \in [0,1], \\ u \in [-1,+1] \,, \text{ a.e. } t \in [0,1], \\ x_1(t) \le 0 \,, \text{ for } \text{ all } t \in [0,1], \\ x_1(0)= - \frac{1}{8} \text{ and } x_2 (0) = \frac{1}{2}. \end{array} \right. \end{aligned}$$

Take as nominal admissible process \(({\bar{x}}, {\bar{u}})\), in which \( {\bar{u}} (t) = \left\{ \begin{array}{ll} -1 &{} \text{ if } 0 \le t \le \frac{1}{2} \\ - \frac{1}{2} &{} \text{ if } \frac{1}{2} < t \le 1 \end{array} \right. \text{ and } \)

$$\begin{aligned} ({\bar{x}}_1(t), {\bar{x}}_2 (t)) = \left\{ \begin{array}{ll} (- \frac{1}{8} + \frac{1}{2} t - \frac{1}{2} t^2 , \frac{1}{2} -t ) &{} \text{ if } 0 \le t \le \frac{1}{2} \\ ( -\frac{1}{4} \times (t-\frac{1}{2})^2 , - \frac{1}{2} (t-\frac{1}{2} ) &{} \text{ if } \frac{1}{2} < t \le 1 \end{array} \right. \,. \end{aligned}$$

Proposition 8.1

  1. (a):

    \(({\bar{x}}, {\bar{u}})\) is not a minimizer for (S),

  2. (b):

    the first-order minimax condition is not satisfied at \(({\bar{x}}, {\bar{u}})\),

  3. (c):

    the minimum principle condition is satisfied at \(({\bar{x}}, {\bar{u}})\) .

Proof

  1. (a):

    \(({\bar{x}}, {\bar{u}})\) is an admissible process and has cost \(- \frac{1}{16}\). Since the cost of the admissible process \((x' , u')\) in which

    $$\begin{aligned} u'(t) = 1 \text{ and } (x^{'}_1(t), x^{'}_2 (t)) = (- \frac{1}{8} + \frac{1}{2} t - \frac{1}{2} t^2 , \frac{1}{2} -t) \text{ for } t \in [0,1] \end{aligned}$$

    has cost \(- \frac{1}{8}\), the nominal process \(({\bar{x}}, {\bar{u}})\) is not a minimizer.

  2. (b):

    For any \(t \in (\frac{1}{2} ,1)\), the left side of the first-order minimax condition at time t, for control value \(u= -1\), is

    $$\begin{aligned} \varDelta f(t,u) \cdot S^T (1,t) \nabla g({\bar{x}}(1)) = (-1 + \frac{1}{2})\times (1-t) = -\frac{1}{2}\times (1-t) < 0\,. \end{aligned}$$

    (Notice that \(A_1 ({\bar{x}})) \cap [t,1]\) is empty, so the state constraint makes no contribution to the relation.) We see that the first-order minimax condition is violated, confirming that \(({\bar{x}}, {\bar{u}})\) is not a minimizer.

  3. (c):

    The minimum principle (in the traditional form described in Comment 2 after the statement of Theorem 7.3) is satisfied for \(({\bar{x}}, {\bar{u}})\), when we choose

    $$\begin{aligned} \lambda _0 =0,\; d\nu (t) = \frac{1}{2} \times \delta (t- \frac{1}{2} )\, dt \end{aligned}$$

    (\(\delta (t- \frac{1}{2})\) denotes the Dirac delta function concentrated at time \(t =\frac{1}{2}\)) and

    $$\begin{aligned} (p_1 (t), p_2(t)) = \left\{ \begin{array}{ll} (1, \frac{1}{2}-t ) &{} \text{ for } 0 \le t \le \frac{1}{2} \\ (0,0)&{} \text{ for } \frac{1}{2} < t \le 1\,. \end{array} \right. \end{aligned}$$

\(\square \)

Comment: To clarify the ideas behind Example Two, we note that it is an optimal control problem in which the velocity function f(x, u) is linear in x and u, the state constraint function h(x) and right endpoint cost function g(x) are linear in x, and there is no right endpoint state constraint. For such problems, the minimum principle is not satisfied at an admissible nominal process \(({\bar{x}} , {\bar{u}})\) if and only if there is exists an admissible process (x, u) such that

$$\begin{aligned} g(x(1))< g({\bar{x}}(1)) \text{ and } \max _{s \in [0,1]} \,h(x(s)) <0\,. \end{aligned}$$

For the problem of Example Two, we have

$$\begin{aligned} \max _{t \in [0,1]} \,h(x(t)) =0 \text{ for } \text{ all } \text{ admissible } \text{ processes } (x,u) \,. \end{aligned}$$

So the minimum principle is satisfied at all admissible processes. On the other hand, it is easy to check that the first-order minimax condition is not satisfied at the specified admissible process \(({\bar{x}},{\bar{u}})\) if there exists an admissible process \((x',u')\) and \(t \in (0,1)\) such that

$$\begin{aligned} g(x'(1))< g({\bar{x}}'(1)) \text{ and } \max _{s \in [t,1]} \,h(x(s)) <0\,. \end{aligned}$$

Since, in Example Two, we exhibit such a process \((x', u')\), the first-order minimax condition is not satisfied at \(({\bar{x}}, {\bar{u}})\).

9 Conclusions

It is important to investigate the strength of the optimality condition associated with a particular optimal control algorithm, because this gives insights into anomalous situations where the algorithm fails to generate minimizing processes. We have investigated two optimality conditions that have arisen in earlier convergence analysis, the first-order minimax conditions and the integrated first-order minimax conditions, and have compared them with the minimum principle. For problems without pathwise state constraints, we find that the minimum principle is strictly stronger than the first-order minimax and the minimum principle and the integrated first-order minimax condition are equivalent. For problems with state constraints, we have found once again that the minimum principle and the integrated first-order minimax condition are equivalent, but the (non-integrated) first-order minimax condition is neither strictly stronger nor strictly weaker than the minimum principle. We provide an example in which the first-order minimax condition can be used to exclude a non-minimizer, but the minimum principle fails to do so. This example establishes that the first-order minimax condition for state constrained problems is an independent necessary condition that can, in certain circumstances, supply more information than the minimum principle.