1 Introduction

As we know, nonlinear systems are widespread in practice, especially with the advancement of science and technology, there are more and more nonlinear phenomena in actual control systems. Therefore, the control problem of nonlinear systems has naturally become a hot topic. In the past few decades, a series of nonlinear system control methods have been developed, such as backstepping control, sliding mode control, robust control, and adaptive control, which greatly enriched the nonlinear system control theory. Besides, many scholars have successfully dealt with a lot of complex control problems by combining multiple control technologies [1,2,3,4,5,6] or fusing some intelligent control methods (fuzzy control [7,8,9] and neural network control [10, 11]). For example, a robust adaptive control strategy for the nonlinear system with actuator failures is given in [5]. By means of the approximation abilities of the fuzzy logic system (FLS) and neural network (NN), two adaptive control strategies for switched nonlinear systems are proposed in [8] and [10], respectively. It should be noted that a common feature of literature [7,8,9,10,11] is that the controlled systems are all in the form of the lower triangle structure, so the final controllers can be calculated according to the idea of backstepping recursion. However, this method is not suitable for the more general nonstrict-feedback nonlinear system, in which the unknown i-th subsystem function contains all state variables. A variable separation method based on the structural characteristics and monotonically increasing nature of the boundary function is adopted to solve this problem in [12]. Moreover, the authors of [13] and [14] successfully overcome this difficulty by using the properties of FLS and NN.

On the other hand, due to the limitations of physical components, actual control systems often have many nonlinear characteristics such as saturation [15, 16], dead zone [17, 18], and hysteresis [19,20,21] that can adversely affect system performance. In order to make the control method of nonlinear systems more effective in practical engineering, it is necessary to fully understand these nonlinear characteristics. Different from the time delay in the usual sense, the hysteresis phenomenon is often a dynamic process and has the characteristics of nonsmooth, multi-mapping, and memory. In recent years, the sensing and driving technology with smart materials as the core has been widely used in many fields due to its strong adaptability to environmental changes and excellent performance, such as aerospace, micro-robots, and bioengineering. However, the hysteresis characteristics existing in many smart materials can not only cause system oscillations, reduce the control accuracy of the system, and even cause the system to fail to operate normally. Therefore, the research on the control problems of nonlinear systems with hysteresis input is beneficial to realize the high requirements on the system performance. In view of the rich practical application background of nonlinear systems with hysteresis, the related research has always been favored by scholars [22,23,24,25,26,27]. Huang et al. [24] and Yu et al. [26] consider the output feedback control problems for switched and stochastic nonlinear systems with unknown hysteresis input, respectively. For the nonlinear multi-agent system with unknown actuator hysteresis, an adaptive event-triggered control scheme is given in [27].

However, in practical applications, the system cannot maintain a long or even infinite operating cycle, especially for some systems that require relatively high time performance. Therefore, it is necessary to study how to obtain the ideal tracking performance in a finite time. Finite-time control is usually regarded as a time-optimal control strategy and has a good robust performance. Since the finite-time Lyapunov stability theory is proposed, finite-time control has been developed rapidly and widely used, and a large number of excellent results have been reported [28,29,30,31,32]. Based on the above discussions, the tracking control problem of nonstrict-feedback nonlinear systems with unknown backlash-like hysteresis is taken into account in this study. With the help of FLS and finite-time Lyapunov stability theory, a finite-time adaptive fuzzy control algorithm is developed to resolve this problem, the characteristics of which compared with the existing results are listed as follows:

  1. (1)

    Different from [22], since the system considered in this study is a nonstrict-feedback form, it is more general and has greater model versatility for the actual system. Moreover, the effect caused by the unknown hysteresis input is compensated by approximating an intermediate variable, and this method can avoid the singularity problem, which is different from [23].

  2. (2)

    Based on finite-time stability theory, the proposed control scheme in this study could guarantee that the tracking error converges to near the origin in a finite time. Meanwhile, a higher tracking accuracy can be realized.

2 System Description and Preliminaries

Consider the following nonstrict-feedback nonlinear system with unknown hysteresis input

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{\zeta }_i\,=\zeta _{i+1}+f_i(\zeta )+d_i(t), &{} \\ ~~~~~~~~~~1\le i\le n-1 &{} \\ \dot{\zeta }_n=u(\nu )+f_n(\zeta )+d_n(t), &{} \\ ~~y=\zeta _1, &{} \end{array} \right. \end{aligned}$$
(1)

where \(\zeta _i\) is the system state with \(\zeta =[\zeta _1,\ldots ,\zeta _n]^T\), \(y\in R\) is the system output, \(f_i(\zeta )\) is the unknown smooth nonlinear function, \(d_i(t)\) is the unknown time-varying disturbance, \(u\in R\) is the output of the unknown backlash-like hysteresis described by

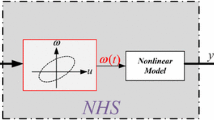
$$\begin{aligned} \frac{d u}{d t}=k\left| \frac{d \nu }{d t}\right| (\varsigma \nu -u) +c\frac{d \nu }{d t}, \end{aligned}$$
(2)

where \(\nu\) is the input of the backlash-like hysteresis; k, \(\varsigma\) and c are unknown constants, \(\varsigma >0\) is the slope of the lines and satisfies \(\varsigma >c\). Figure 1 shows the backlash-like hysteresis curves generated by the model (2), where \(k=1\), \(\varsigma =3.1635\), \(b=0.345\), the input signals are \(\nu (t)=\kappa \sin (2.3t)\) with \(\kappa =4.5\) and \(\kappa =6.5\), and the initial values are \(\nu (0)=0\) and \(u(0)=0\).

Fig. 1
figure 1

Backlash-like hysteresis curves

Full size image

As stated in [19], (2) can be expressed as

$$\begin{aligned}&u(\nu )=\varsigma \nu (t)+d(\nu ),\\&d(\nu )=[u_0-\varsigma \nu _0]e^{-k(\nu -\nu _0)sgn (\dot{\nu })}\\&~~~~~~~~~~~+e^{-k\nu sgn (\dot{\nu })}\int _{\nu _0}^{\nu }[c-\varsigma ] e^{k\eta sgn (\dot{\nu })}d \eta , \end{aligned}$$

where \(\nu _0=\nu (0)\), \(u_0=u(0)\), \(d(\nu )\) satisfies \(|d(\nu )|\le D\) with the unknown constant D. Therefore, the system (1) is rewritten as

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{\zeta }_i=\zeta _{i+1}+f_i(\zeta )+d_i(t), &{} \\ ~~~~~~1\le i\le n-1 &{} \\ \dot{\zeta }_n=\varsigma \nu (t)+d(\nu )+f_n(\zeta )+d_n(t), &{} \\ ~~y=\zeta _1, &{} \end{array} \right. \end{aligned}$$
(3)

The control objective of this study is to construct an adaptive fuzzy controller for the system (1) such that the system output y can track the reference signal \(y_r\) in a finite time, and all signals in the closed-loop system are bounded. To this end, we need to introduce the following assumptions and knowledge.

Assumption 1

The reference signal \(y_r\) and its time derivative up to the nth order \(y^{(n)}_{r}\) are continuous and bounded.

Assumption 2

There exists the unknown constant \(\bar{d}_i\) such that \(|d_i(t)|\le \bar{d}_i\), \(i=1,\dots ,n\).

Definition 1

[33] Consider the nonlinear system \(\dot{\zeta }=f(\zeta (t))\), the equilibrium \(\zeta =0\) is practical finite-time stable, if for any \(\zeta (0)\in \zeta _0\), there exist a constant \(\varepsilon >0\) and the settling time \(T(\varepsilon ,\zeta _0)<\infty\) such that

$$\begin{aligned} \Vert \zeta (t)\Vert <\varepsilon ,~\forall t>T. \end{aligned}$$

Lemma 1

[34] For positive constants \(\alpha\), \(\beta\), \(0<p<1\) and \(0<\Gamma <\infty\), if there is a positive-definite function \(V(\zeta )\) satisfying

$$\begin{aligned} \dot{V}(\zeta )\le -\alpha V^p(\zeta )-\beta V(\zeta )+\Gamma , \end{aligned}$$

then the trajectory of \(\dot{\zeta }=f(\zeta (t))\) is practical finite-time stable, and \(V(\zeta )\) satisfies

$$\begin{aligned} V^p(\zeta )\le \frac{\Gamma }{(1-\omega )\alpha },~\forall t\ge T \end{aligned}$$

with \(0<\omega <1\) and \(T=\frac{1}{\beta (1-p)}\ln \frac{\beta V^{1-p}(\zeta _0)+\omega \alpha }{\omega \alpha }\).

Lemma 2

[35] For real variables \(\mu , \varpi\) and constant \(\pi _i>0~(i=1,2,3)\), one has

$$\begin{aligned} |\mu |^{\pi _1}|\varpi |^{\pi _2}\le \frac{\pi _1}{\pi _1+\pi _2}\pi _3|\mu |^{\pi _1+\pi _2} +\frac{\pi _2}{\pi _1+\pi _2}\pi _3^{-\frac{\pi _1}{\pi _2}}|\varpi |^{\pi _1+\pi _2}. \end{aligned}$$

Lemma 3

[36]: For any \(\zeta _i\in R\), \(i=1,\ldots ,n\), \(0<p\le 1\), one has

$$\begin{aligned} \left( \sum ^n_{i=1}|\zeta _i|\right) ^p\le \sum ^n_{i=1}|\zeta _i|^p. \end{aligned}$$

In the subsequent control design, FLS would be utilized to estimate the unknown nonlinear function.

IF-THEN Rules: \({\mathcal{R}}^i\): If \(\zeta _1\) is \({\mathcal{F}}^i_1\) and ...and \(\zeta _n\) is \({\mathcal{F}}^i_n\), then y is \({\mathcal{G}}^i\), \(i=1,\ldots ,N\).

The FLS could be formulated as

$$\begin{aligned} y(\zeta )=\frac{\sum ^N_{i=1}h_i\prod ^n_{j=1}\mu _{{\mathcal{F}}^i_j}(\zeta _j)}{\sum ^N_{i=1}\left[ \prod ^n_{j=1}\mu _{{\mathcal{F}}^i_j}(\zeta _j)\right] }. \end{aligned}$$

Denote \(\phi _i(\zeta )=\frac{\prod ^n_{j=1}\mu _{{\mathcal{F}}^i_j}(\zeta _j)}{\sum ^N_{i=1}\left[ \prod ^n_{j=1}\mu _{{\mathcal{F}}^i_j}(\zeta _j)\right] }\), \(\Phi (\zeta )=[\phi _1(\zeta ),\ldots ,\phi _N(\zeta )]^T\), \({\mathcal{H}}=[h_1,\ldots ,h_N]^T\), then one has

$$\begin{aligned} y(\zeta )={\mathcal{H}}^T\Phi (\zeta ). \end{aligned}$$

Lemma 4

[28]: For any continuous function \(h(\zeta )\) defined on the compact set U, there is a FLS \({\mathcal{H}}^T\Phi (\zeta )\) satisfying

$$\begin{aligned} \sup \limits _{\zeta \in U}|h(\zeta )-{\mathcal{H}}^T\Phi (\zeta )|\le \epsilon \end{aligned}$$

with \(\epsilon >0\) being an arbitrary constant.

3 Adaptive Fuzzy Control Design

The control design begins with the following coordinate transformations

$$\begin{aligned}&s_1=\zeta _1-y_r, \end{aligned}$$
(4)
$$\begin{aligned}&\quad s_i=\zeta _i-\alpha _{i-1},~i=2,\dots ,n, \end{aligned}$$
(5)

where \(\alpha _{i-1}\) is the virtual control law. Next, we denote \(\theta =\max {\{\Vert {\mathcal{H}}_i\Vert ^2, i=1,\dots ,n\}}\) and \(\rho =\frac{1}{\varsigma }\), \({\hat{\theta }}\) and \({\hat{\rho }}\) are estimates of \(\theta\) and \(\rho\), respectively. In accordance with the backstepping technique, the virtual and actual controllers are designed as

$$\begin{aligned}&\alpha _1=-c_1s_1-\frac{{\hat{\theta }} s_1}{2a^2_1\Phi ^T_1(Z_1)\Phi _1(Z_1)}, \end{aligned}$$
(6)
$$\begin{aligned}&\,\alpha _i=-c_is_i-s_{i-1}-\frac{{\hat{\theta }} s_i}{2a^2_i\Phi ^T_i(Z_i)\Phi _i(Z_i)},~i=2,\dots ,n, \end{aligned}$$
(7)
$$\begin{aligned}&~~\nu ={\hat{\rho }}\alpha _n \end{aligned}$$
(8)

with the constant \(c_i, a_i>0\) \((i=1,\dots ,n)\). Meanwhile, the corresponding adaptive laws are

$$\begin{aligned}&\dot{{\hat{\rho }}}=-\gamma s_n\alpha _n-\sigma {\hat{\rho }}, \end{aligned}$$
(9)
$$\begin{aligned}&\dot{{\hat{\theta }}}=\lambda \tau _n-r{\hat{\theta }}, \end{aligned}$$
(10)

where \(\sigma ,r>0\) are known constants, and \(\tau _n\) will be defined later.

Step 1: Based on (3), (4), and (5), the derivative of \(s_1\) is calculated as

$$\begin{aligned}&\dot{s}_1=\dot{\zeta }_1-\dot{y}_r \\&=s_2+\alpha _1+f_1(\zeta )+d_1(t)-\dot{y}_r. \end{aligned}$$
(11)

Define

$$\begin{aligned} V_1=\frac{1}{2}s^2_1 +\frac{1}{2\lambda }\tilde{\theta }^2 \end{aligned}$$
(12)

with \(\tilde{\theta }=\theta -{\hat{\theta }}\). Then, it is deduced that

$$\begin{aligned}&\dot{V}_1=s_1\Big (s_2+\alpha _1+f_1(\zeta )+d_1(t)-\dot{y}_r\Big ) -\frac{1}{\lambda }\tilde{\theta }\dot{{\hat{\theta }}} \\&~~~~\,=s_1\Big (-k_1s^{2p-1}_1-s_1+s_2+\alpha _1+\bar{f}_1(X_1)+d_1(t)\Big ) -\frac{1}{\lambda }\tilde{\theta }\dot{{\hat{\theta }}}, \end{aligned}$$
(13)

where \(p=\frac{\check{m}}{\check{n}}<1\) with positive odd integers \(\check{m}\), \(\check{n}\), \(\bar{f}_1(X_1)=f_1(\zeta )-\dot{y}_r+k_1s^{2p-1}_1+s_1\) and \(X_1=[\zeta ,y_r,\dot{y}_r]^T\). According to Lemma 4, the FLS \({\mathcal{H}}^T_1\Phi _1(X_1)\) could be employed to approximate the unknown term \(\bar{f}_1(X_1)\), i.e.,

$$\begin{aligned}&\bar{f}_1(X_1)={\mathcal{H}}^T_1\Phi _1(X_1)+\Delta _1(X_1),\\&|\Delta _1(X_1)|\le \epsilon _1 \end{aligned}$$

with an approximation error \(\Delta _1(X_1)\) and \(\epsilon _1>0\). Based on Young’s inequality and the property of FLS \(0<\Phi ^T_1(\cdot )\Phi _1(\cdot )\le 1\), one has

$$\begin{aligned}&s_1\bar{f}_1(X_1)=s_1{\mathcal{H}}^T_1\Phi _1+s_1\Delta _1(X_1) \\&~~~~~~~~~~~~\le \frac{\theta s^2_1\Phi ^T_1(X_1)\Phi _1(X_1)}{2a^2_1} +\frac{1}{2}a^2_1 +\frac{1}{2}s^2_1 +\frac{1}{2}\epsilon ^2_1 \\&~~~~~~~~~~~~\le \frac{\theta s^2_1}{2a^2_1\Phi ^T_1(Z_1)\Phi _1(Z_1)} +\frac{1}{2}a^2_1 +\frac{1}{2}s^2_1 +\frac{1}{2}\epsilon ^2_1, \end{aligned}$$
(14)
$$\begin{aligned}&~~~s_1d_1(t)\le \frac{1}{2}s^2_1+\frac{1}{2}\bar{d}^2_1, \end{aligned}$$
(15)

where \(Z_1=[\zeta _1,y_r,\dot{y}_r]^T\). Substituting (14) and (15) into (13) produces

$$\begin{aligned} \dot{V}_1\le & {} s_1\left( -k_1s^{2p-1}_1+\alpha _1 +\frac{{\hat{\theta }} s_1}{2a^2_1\Phi ^T_1(Z_1)\Phi _1(Z_1)}\right) \\&+s_1s_2 +\frac{1}{2}(\bar{d}^2_1+a^2_1+\epsilon ^2_1) \\&+\tilde{\theta }\left( \frac{s^2_1}{2a^2_1\Phi ^T_1(Z_1)\Phi _1(Z_1)}-\frac{1}{\lambda }\dot{{\hat{\theta }}}\right) . \end{aligned}$$
(16)

Furthermore, by substituting the first virtual controller (6) into (16), we have

$$\begin{aligned} \dot{V}_1\le -k_1s^{2p}_1 -c_1s^2_1 +s_1s_2 +\tilde{\theta }\left( \tau _1-\frac{1}{\lambda }\dot{{\hat{\theta }}}\right) +\iota _1 \end{aligned}$$
(17)

with \(\tau _1=\frac{s^2_1}{2a^2_1\Phi ^T_1(Z_1)\Phi _1(Z_1)}\) and \(\iota _1=\frac{1}{2}(\bar{d}^2_1+a^2_1+\epsilon ^2_1)\).

Step \(i~(i=2,\dots ,n-1)\): It follows from (3) and (5) that

$$\begin{aligned}&\dot{s}_i=\dot{\zeta }_i-\dot{\alpha }_{i-1} \\&~~~=s_{i+1}+\alpha _i+f_i(\zeta )+d_i(t)-\dot{\alpha }_{i-1}. \end{aligned}$$
(18)

When the following Lyapunov function candidate is considered

$$\begin{aligned} V_i=V_{i-1}+\frac{1}{2}s^2_i, \end{aligned}$$
(19)

then one has

$$\begin{aligned}&\dot{V}_i=\dot{V}_{i-1} +s_i\Big (s_{i+1}+\alpha _i+f_i(\zeta )+d_i(t)-\dot{\alpha }_{i-1}\Big ) \\&~~~\le -\sum ^{i-1}_{j=1}k_js^{2p}_j-\sum ^{i-1}_{j=1}c_js^2_j+s_is_{i+1} +\tilde{\theta }(\tau _{i-1}-\frac{1}{\lambda }\dot{{\hat{\theta }}}) +\iota _{i-1} \\&~~~~~~\, +s_i\Big (-k_is^{2p-1}_i-s_i+s_{i-1}+\alpha _i+\bar{f}_i(X_i)+d_i(t)\Big ), \end{aligned}$$
(20)

where \(\bar{f}_i(X_i)=f_i(\zeta )-\sum ^{i-1}_{j=1}\frac{\partial \alpha _{i-1}}{\partial \zeta _j}(\zeta _{j+1}+f_j(\zeta )+d_j(t)) -\sum ^{i-1}_{j=0}\frac{\partial \alpha _{i-1}}{\partial y^{(j)}_r}y^{(j+1)}_r -\frac{\partial \alpha _{i-1}}{\partial {\hat{\theta }}}\dot{{\hat{\theta }}}+k_is^{2p-1}_i+s_i\) and \(X_i=[\zeta ,y_r,\dots ,y^{(i)}_r,{\hat{\theta }}]^T\). Based on Lemma 4, there exists a FLS \({\mathcal{H}}^T_i\Phi _i(X_i)\) that can estimate the unknown term \(\bar{f}_i(X_i)\). For any \(\epsilon _i>0\),

$$\begin{aligned} \bar{f}_i(X_i)={\mathcal{H}}^T_i\Phi _i(X_i)+\Delta _i(X_i), \end{aligned}$$

where \(|\Delta _i(X_i)|\le \epsilon _i\) is an approximation error. As the same case of (14) and (15), the following inequalities hold

$$\begin{aligned}&s_i\bar{f}_i(X_i)=s_i{\mathcal{H}}^T_i\Phi _i(X_i)+s_i\Delta _i(X_i) \\&~~~~~~~~~~\,\le \frac{\theta s^2_i\Phi ^T_i(X_i)\Phi _i(X_i)}{2a^2_i} +\frac{1}{2}a^2_i +\frac{1}{2}s^2_i +\frac{1}{2}\epsilon ^2_i \\&~~~~~~~~~~\,\le \frac{\theta s^2_i}{2a^2_i\Phi ^T_i(Z_i)\Phi _i(Z_i)} +\frac{1}{2}a^2_i +\frac{1}{2}s^2_i +\frac{1}{2}\epsilon ^2_i, \end{aligned}$$
(21)
$$\begin{aligned}&~~\,s_id_i(t)\le \frac{1}{2}s^2_i +\frac{1}{2}\bar{d}^2_i, \end{aligned}$$
(22)

where \(Z_i=[\zeta _1,\dots ,\zeta _i,y_r,\dots ,y^{(i)}_r,{\hat{\theta }}]^T\). Substituting them into (20), we have

$$\begin{aligned} \dot{V}_i\le & {} -\sum ^{i-1}_{j=1}k_js^{2p}_j -\sum ^{i-1}_{j=1}c_js^2_j +s_is_{i+1} \\&+s_i\left( -k_is^{2p-1}_i+s_{i-1}+\alpha _i +\frac{{\hat{\theta }}s_i}{2a^2_i\Phi ^T_i(Z_i)\Phi _i(Z_i)}\right) \\&+\tilde{\theta }\left( \tau _{i-1} +\frac{s^2_i}{2a^2_i\Phi ^T_i(Z_i)\Phi _i(Z_i)} -\frac{1}{\lambda }\dot{{\hat{\theta }}}\right) \\&+\iota _{i-1} +\frac{1}{2}(\bar{d}^2_i+a^2_i+\epsilon ^2_i). \end{aligned}$$
(23)

Then, substituting (7) into (23) yields

$$\begin{aligned}&\dot{V}_i\le -\sum ^{i}_{j=1}k_js^{2p}_j -\sum ^{i}_{j=1}c_js^2_j +s_is_{i+1} +\tilde{\theta }\left( \tau _i -\frac{1}{\lambda }\dot{{\hat{\theta }}}\right) +\iota _i \end{aligned}$$
(24)

with \(\tau _i=\tau _{i-1}+\frac{s^2_i}{2a^2_i\Phi ^T_i(Z_i)\Phi _i(Z_i)}\) and \(\iota _i=\iota _{i-1}+\frac{1}{2}(\bar{d}^2_i+a^2_i+\epsilon ^2_i)\).

Step n : From (3) and (5), we have

$$\begin{aligned}&\dot{z}_n=\dot{\zeta }_n-\dot{\alpha }_{n-1} \\&~~~=\varsigma \nu +d(\nu )+f_n(\zeta )+d_n(t)-\dot{\alpha }_{n-1}. \end{aligned}$$
(25)

Choose

$$\begin{aligned} V_n=V_{n-1}+\frac{1}{2}s^2_n+\frac{\varsigma }{2\gamma }\tilde{\rho }^2 \end{aligned}$$
(26)

with \(\tilde{\rho }=\rho -{\hat{\rho }}\). Then, it could be obtained that

$$\begin{aligned}&\dot{V}_n=\dot{V}_{n-1} +s_n\Big (\varsigma \nu +d(\nu )+f_n(\zeta )+d_n(t)-\dot{\alpha }_{n-1}\Big ) -\frac{\varsigma }{\gamma }\tilde{\rho }\dot{{\hat{\rho }}} \\&\le -\sum ^{n-1}_{j=1}k_js^{2p}_j -\sum ^{n-1}_{j=1}c_js^2_j +\tilde{\theta }\left( \tau _{n-1} -\frac{1}{\lambda }\dot{{\hat{\theta }}}\right) +\iota _{n-1} \\&+s_n\Big (-k_ns^{2p-1}_n-s_n+s_{n-1}+\varsigma \nu +d(\nu )+\bar{f}_n(X_n)+d_n(t)\Big ) -\frac{\varsigma }{\gamma }\tilde{\rho }\dot{{\hat{\rho }}} \end{aligned}$$
(27)

with \(\bar{f}_n(X_n)=f_n(\zeta )-\sum ^{n-1}_{j=1}\frac{\partial \alpha _{n-1}}{\partial \zeta _j}(\zeta _{j+1}+f_j(\zeta )+d_j(t)) -\sum ^{n-1}_{j=0}\frac{\partial \alpha _{n-1}}{\partial y^{(j)}_r}y^{(j+1)}_r -\frac{\partial \alpha _{n-1}}{\partial {\hat{\theta }}}\dot{{\hat{\theta }}}+k_ns^{2p-1}_n+s_n\) and \(X_n=[\zeta ,y_r,\dots ,y^{(n)}_r,{\hat{\theta }}]^T\). According to Lemma 4, for the arbitrary constant \(\epsilon _n>0\), one has

$$\begin{aligned} \bar{f}_n(X_n)={\mathcal{H}}^T_n\Phi _n(X_n)+\Delta _n(X_n), \end{aligned}$$

where the approximation error \(\Delta _n(X_n)\) satisfies \(|\Delta _n(X_n)|\le \epsilon _n\). Similar to (14) and (15), the following inequalities hold

$$\begin{aligned}&s_n\bar{f}_n(X_n)=s_n{\mathcal{H}}^T_n\Phi _n(X_n)+s_n\Delta _n(X_n) \\&~~~~~~~~~~~~\,\le \frac{\theta s^2_n\Phi ^T_n(X_n)\Phi _n(X_n)}{2a^2_n} +\frac{1}{2}a^2_n +\frac{1}{2}s^2_n +\frac{1}{2}\epsilon ^2_n \\&\,\le \frac{\theta s^2_n}{2a^2_n\Phi ^T_n(Z_n)\Phi _n(Z_n)} +\frac{1}{2}a^2_n +\frac{1}{2}s^2_n +\frac{1}{2}\epsilon ^2_n, \end{aligned}$$
(28)
$$\begin{aligned}&~~~s_n(d(\nu )+d_n(t))\le \frac{1}{2}s^2_n +\frac{1}{2}(D+\bar{d}_n)^2, \end{aligned}$$
(29)

where \(Z_n=X_n\). Substituting them into (27) leads to

$$\begin{aligned} \dot{V}_n\le & {} -\sum ^{n-1}_{j=1}k_js^{2p}_j -\sum ^{n-1}_{j=1}c_js^2_j +s_n \\&\left( -k_ns^{2p-1}_n+s_{n-1} +\varsigma \nu +\frac{{\hat{\theta }}s_n}{2a^2_n\Phi ^T_n(Z_n)\Phi _n(Z_n)}\right) \\&\, +\tilde{\theta }\left( \tau _n -\frac{1}{\lambda }\dot{{\hat{\theta }}}\right) -\frac{\varsigma }{\gamma }\tilde{\rho }\dot{{\hat{\rho }}} +\iota _n, \end{aligned}$$
(30)

where \(\tau _n=\tau _{n-1}+\frac{s^2_n}{2a^2_n\Phi ^T_n(Z_n)\Phi _n(Z_n)}\) and \(\iota _n=\iota _{n-1}+\frac{1}{2}\Big ((D+\bar{d}_n)^2+a^2_n+\epsilon ^2_n\Big )\). By combining (8)–(10), it could be deduced that

$$\begin{aligned} \dot{V}_n\le & {} -\sum ^{n-1}_{j=1}k_js^{2p}_j -\sum ^{n-1}_{j=1}c_js^2_j +s_n\varsigma {\hat{\rho }}\alpha _n +s_n \\&\left( -k_ns^{2p-1}_n +s_{n-1} +\frac{{\hat{\theta }}s_n}{2a^2_n\Phi ^T_n(Z_n)\Phi _n(Z_n)}\right) \\&+\frac{r}{\lambda }\tilde{\theta }{\hat{\theta }} +s_n\varsigma \tilde{\rho }\alpha _n +\frac{\sigma \varsigma }{\gamma }\tilde{\rho }{\hat{\rho }} +\iota _n \\&= -\sum ^{n-1}_{j=1}k_js^{2p}_j -\sum ^{n-1}_{j=1}c_js^2_j +s_n\alpha _n +s_n \\&\left( -k_ns^{2p-1}_n +s_{n-1} +\frac{{\hat{\theta }}s_n}{2a^2_n\Phi ^T_n(Z_n)\Phi _n(Z_n)}\right) \\&+\frac{r}{\lambda }\tilde{\theta }{\hat{\theta }} +\frac{\sigma \varsigma }{\gamma }\tilde{\rho }{\hat{\rho }} +\iota _n \\&= -\sum ^{n}_{j=1}k_js^{2p}_j -\sum ^{n}_{j=1}c_js^2_j +\frac{r}{\lambda }\tilde{\theta }{\hat{\theta }} +\frac{\sigma \varsigma }{\gamma }\tilde{\rho }{\hat{\rho }} +\iota _n. \end{aligned}$$
(31)

4 Main Results

Theorem 1

For the nonlinear system (1) with unknown hysteresis input (2), under Assumption 1 and 2, applying the proposed control scheme (6)–(10), the following conclusions hold:

  1. (1)

    the tracking error could converge to near the origin in a finite time;

  2. (2)

    all signals in the closed-loop system are bounded.

Proof Recalling the definitions of \(\theta\) and \(\rho\), one has

$$\begin{aligned}&~\,\frac{r}{\lambda }\tilde{\theta }{\hat{\theta }} \le -\frac{r}{2\lambda }\tilde{\theta }^2 +\frac{r}{2\lambda }\theta ^2,\\&\frac{\sigma \varsigma }{\gamma }\tilde{\rho }{\hat{\rho }} \le -\frac{\sigma \varsigma }{2\gamma }\tilde{\rho }^2 +\frac{\sigma \varsigma }{2\gamma }\rho ^2. \end{aligned}$$

By substituting them into (31), we could get

$$\begin{aligned}&\dot{V}_n\le -\sum ^{n}_{j=1}k_js^{2p}_j -\sum ^{n}_{j=1}c_js^2_j -\frac{r}{2\lambda }\tilde{\theta }^2 +\frac{r}{2\lambda }\theta ^2 -\frac{\sigma \varsigma }{2\gamma }\tilde{\rho }^2 +\frac{\sigma \varsigma }{2\gamma }\rho ^2 \\&~~~~~~\, -r(\frac{\tilde{\theta }^2}{2\lambda })^p +r(\frac{\tilde{\theta }^2}{2\lambda })^p -\sigma (\frac{\varsigma }{2\gamma }\tilde{\rho }^2)^p +\sigma (\frac{\varsigma }{2\gamma }\tilde{\rho }^2)^p +\iota _n. \end{aligned}$$
(32)

Based on Lemma 2, one has

$$\begin{aligned}&r(\frac{\tilde{\theta }^2}{2\lambda })^p \le p\frac{r}{2\lambda }{\tilde{\theta }}^2 +r(1-p), \end{aligned}$$
(33)
$$\begin{aligned}&\sigma (\frac{\varsigma }{2\gamma }\tilde{\rho }^2)^p \le p\frac{\sigma \varsigma }{2\gamma }{\tilde{\rho }}^2 +\sigma (1-p). \end{aligned}$$
(34)

Substituting (33) and (34) into (32) and combining Lemma 3, we could further derived that

$$\begin{aligned} \dot{V}_n\le & {} -\sum ^{n}_{j=1}k_js^{2p}_j -r(\frac{\tilde{\theta }^2}{2\lambda })^p -\sigma (\frac{\varsigma }{2\gamma }\tilde{\rho }^2)^p \\&-\sum ^{n}_{j=1}c_js^2_j -(1-p)\frac{r}{2\lambda }\tilde{\theta }^2 -(1-p)\frac{\sigma \varsigma }{2\gamma }\tilde{\rho }^2 \\&\, +\iota _n +\frac{r}{2\lambda }\theta ^2 +\frac{\sigma \varsigma }{2\gamma }\rho ^2 +(r+\sigma )(1-p) \\&\,\le -\alpha V^p_n-\beta V_n+\Gamma \end{aligned}$$
(35)

with \(\alpha =\min \{2^pk_j,r,\sigma \}\), \(\beta =\min \{2c_j,(1-p)r,(1-p)\sigma \}\) and \(\Gamma =\iota _n +\frac{r}{2\lambda }\theta ^2 +\frac{\sigma \varsigma }{2\gamma }\rho ^2 +(r+\sigma )(1-p).\)

It follows from (35) and Lemma 1 that

$$\begin{aligned} V^p_n(t)\le \frac{\Gamma }{(1-\omega )\alpha },~\forall t\ge T, \end{aligned}$$

and \(T=\frac{1}{\beta (1-p)}\ln \frac{\beta V^{1-p}_n(\zeta _0)+\omega \alpha }{\omega \alpha }\).

Then combining with the definition \(V_n\), it is not difficult to deduce that

$$\begin{aligned} |s_1|\le \sqrt{2\left( \frac{\Gamma }{(1-\omega )\alpha }\right) ^{\frac{1}{p}}},~\forall t\ge T, \end{aligned}$$

that is, the tracking error could converge to near the origin in the limited time by choosing the suitable parameters.

On the other hand, from (35), we have \(\dot{V}_n(t)\le -\beta V_n(t)+\Gamma\) and \(V_n(t)\le \left( V_n(0)-\frac{\Gamma }{\beta }\right) e^{-\beta t}+\frac{\Gamma }{\beta }\), which means that \(s_i\), \(\tilde{\theta }\), \({\hat{\theta }}\), \(\tilde{\rho }\) and \({\hat{\rho }}\) are bounded. It follows from (6) to (8) that \(\alpha _i\) \((i=1,\dots ,n)\) and \(\nu\) are bounded because of the boundedness of the included variables. Moreover, combining (4) and (5), we could obtained that \(\zeta _i\) \((i=1,\dots ,n)\) is bounded. Consequently, all signals in the closed-loop system remain bounded. This completes the proof.

Remark 1 The challenges of this study mainly include two aspects: on the one hand, the controlled system in this study is a nonstrict-feedback form, which makes the standard backstepping technology not directly applicable to the control design of such systems. To this end, we have solved this problem with the help of the property of the fuzzy logic system \(0<\Phi ^T_i(\cdot )\Phi _i(\cdot )\le 1\) (Details can be seen in formulas (14), (21), and (28)). On the other hand, how to deal with the problems caused by the unknown hysteresis input also needs to be considered in control design. Inspired by Reference [23], we introduced a new intermediate variable \(\rho =\frac{1}{\varsigma }\). Furthermore, the effect caused by the unknown hysteresis input can be compensated by approximating the new variable \(\rho\). It should be pointed out that, compared with the method in Reference [23], the proposed method does not discuss whether the parameter \({\hat{\rho }}\) will be equal to 0, because \({\hat{\rho }}\) will not appear in the denominator.

5 Simulation Example

This section aims to further intuitively verify the proposed control algorithm through simulation results.

Consider the following nonlinear system with unknown actuator hysteresis

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{\zeta }_1=\zeta _2+f_1(\zeta )+d_1(t), &{} \\ \dot{\zeta }_2=u(\nu )+f_2(\zeta )+d_2(t), &{} \\ ~\,y=\zeta _1, &{} \end{array} \right. \end{aligned}$$
(36)

where \(f_1(\zeta )=0.05\zeta _2\cos (\zeta _1)\), \(f_2(\zeta )=0.1\zeta _1\sin (\zeta _2)\), \(d_1(t)=0.1\cos t\), \(d_2(t)=0.5\sin t\); u is the output of the backlash-like hysteresis described by (2) with \(k=1\), \(\varsigma =3.1635\) and \(c=0.345\). The reference trajectory is \(y_r=\sin t\).

In this simulation, the following membership functions are selected

$$\begin{aligned} \mu _{{\mathcal{F}}^{i}_{j}}=e^{-\frac{1}{2}(\zeta _j+\chi _i)^{2}} \end{aligned}$$

with \(\chi _i=9,7,5,3,1,0,-1,-3,-5,-7,-9\), \(j=1,2\) and \(i=1,\dots ,11\). To fulfill the control objective, the controllers are designed in accordance with the aforementioned design procedures

$$\begin{aligned}&\alpha _1=-c_1s_1-\frac{{\hat{\theta }} s_1}{2a^2_1\Phi ^T_1(Z_1)\Phi _1(Z_1)},\\&\quad \,\alpha _2=-c_2s_2-s_1-\frac{{\hat{\theta }} s_2}{2a^2_2\Phi ^T_2(Z_2)\Phi _2(Z_2)},\\&\quad \nu ={\hat{\rho }}\alpha _2, \end{aligned}$$

and adaptive laws can be calculated as

$$\begin{aligned}&\dot{{\hat{\rho }}}=-\gamma s_2\alpha _2-\sigma {\hat{\rho }},\\&\dot{{\hat{\theta }}}=\lambda \tau _2-r{\hat{\theta }} \end{aligned}$$

with \(\tau _2=\frac{s^2_1}{2a^2_1\Phi ^T_1(Z_1)\Phi _1(Z_1)} +\frac{s^2_2}{2a^2_2\Phi ^T_2(Z_2)\Phi _2(Z_2)}\).

Fig. 2
figure 2

The system output y and the reference signal \(y_r\)

Full size image
Fig. 3
figure 3

The tracking error \(s_1\)

Full size image
Fig. 4
figure 4

States \(\zeta _1\) and \(\zeta _2\)

Full size image
Fig. 5
figure 5

Control signals u and \(\nu\)

Full size image
Fig. 6
figure 6

Adaptive parameters \({\hat{\theta }}\) and \({\hat{\rho }}\)

Full size image

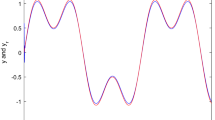
The initial conditions are \(\zeta _1(0)=-0.2\), \(\zeta _2(0)=0\), \({\hat{\theta }}(0)={\hat{\rho }}(0)=1\). The parameters to be designed are \(c_1=16\), \(c_2=10\), \(a_1=a_2=1\), \(\lambda =1\), \(r=0.1\), \(\gamma =6\), \(\sigma =0.1\). The simulation results are exhibited in Figs. 2, 3, 4, 5, and 6. The system output y and the reference signal \(y_r\) are plotted in Fig. 2. Figure 3 presents the curve of the tracking error \(s_1\). As shown in Fig. 2, the maximum tracking error is less than 0.05 after 2 second. Thus, it can be seen from these two figures the system output y could track the reference trajectory \(y_r\). The trajectories of system states \(\zeta _1\) and \(\zeta _2\) are displayed in Fig. 4. The control signals are exhibited in Fig. 5. Then combined with Fig. 2, we could get that the proposed control scheme can still achieve tracking control performance in the presence of unknown hysteresis input. Figure 6 gives the trajectories of adaptive parameters \({\hat{\theta }}\) and \({\hat{\rho }}\). As these figures show, all signals in the closed-loop system are bounded. Consequently, the proposed scheme could achieve the control objective.

6 Conclusions

In this study, a finite-time tracking control strategy is proposed for the nonstrict-feedback nonlinear system with unknown actuator hysteresis. Based on the property of FLS, the design difficulties caused by the nonstrict-feedback structure are successfully resolved. In the presence of unknown nonlinear input, better tracking performance could be obtained in a finite time by combining FLS and adaptive backstepping technology. In the future, how to address the fixed-time tracking control problem for the nonlinear system with unknown nonlinear input is very meaningful and challenging work.