1 Introduction

Base support vibrations can lead to dangerous relative displacements in structures, as occurs in buildings [5], or to misalignment and focusing problems in vibration sensitive devices, such as exist in research centres with scientific equipment, precision manufacturing industries or space applications, in which more than one device can be involved in the same task [6, 17, 19, 23]. The use of an isolator between a base and a platform with the aim to reduce the vibration transmission between them is known as vibration isolation. The force that the isolator applies to the platform is usually called control force. Depending on the way in which the force has been generated, it is possible to distinguish three techniques: (1) passive vibration isolation (PVI); (2) semi-active vibration isolation (SAVI); (3) active vibration isolation (AVI). In PVI systems, the control force is generated by the isolator as a reaction to the relative displacement between the platform and the support structure [26] due to platform inertia. This technique presents some disadvantages, such as the fact that attenuation of platform response occurs only for frequencies greater than \(\sqrt{2}\) times the natural frequency of the isolator, the inability to achieve zero static deflection or the impossibility to adapt the control force to changes in the conditions of the vibration isolation task. Due to the poor performance of PVI systems at low frequencies, non-linear techniques have been developed [5, 10, 12, 13, 21, 31], thus increasing the isolation frequency bandwidth.

Unpredictable forces which may not have been considered in the design process or changes in work conditions and desire for improved low frequency performance have motivated the use of more sophisticated techniques, such as semi-active or active techniques [4, 9, 15, 20]. SAVI techniques provide the ability to change the dynamic parameters (stiffness and damping) of the isolator in real time, achieving a degree of adaptability to changing conditions.

The demanding requirements of some modern vibration sensitive applications require a level of performance over and above that achievable with PVI and SAVI techniques. Active isolators offer some important advantages, such as the possibility to change the position, to provide zero static deflection or the capability to introduce adaptive control techniques [27]. The control force in AVI systems is not only generated as a reaction of the relative movement between base and platform but an actuator is located between them, allowing application of an additional control force by the use of feedback or feedforward control techniques. This makes AVI systems the most suitable for many applications [2, 16, 18, 25]. However, it is necessary to deal with some additional challenges of AVI, such as instability of the control system, real-time signal processing, the inherent isolator dynamics and the influence of the control force on the support structure.

The hypothesis that the isolator does not interact with the base structure is usually assumed in many applications, when the effect of the isolator in the base structure response is negligible [14, 22, 28, 29]. There are other applications where the displacement of a flexible base structure must be considered as part of the isolation problem, as occurs in some marine applications [7]. Hence, the performance of the isolation problem, which can be defined as the ratio between the displacement of the isolated platform and the base, may depend on the interaction of both systems [1, 11, 32].

This paper proposes a different conceptual framework from the classical vibration isolation approach. The case studied here considers a flexible base supported by rigid ground. This base structure is not a part of the vibration isolation system, as in floating raft systems [30]. It represents a general base structure on which an isolator is situated. The perturbation input, which is applied on the base structure, may arise from different sources, whose nature depends on the application type. The isolation system, composed of a single isolator in this work, is oriented to reduce the vibration transmitted from that base structure to the platform, where the mass to be isolated is situated.The two techniques individually used for that purpose are PVI and AVI.

The objective of this work is to study and to illustrate the influence that the vibration isolation task has in the base structure, which has been considered as a single degree of freedom system. It is motivated by the interaction phenomenon, which may produce undesired base movements even though the vibration isolation objective is achieved. In particular, the effect that the AVI strategy has in the base structure is studied and compared with the effect of the PVI strategy. With this aim, the same isolation performance has been achieved for different isolator damping ratios. The effect it has on the base response is analysed in depth for a range of base structures, by varying the mass and the natural frequency. Interesting experimental results have been obtained on a full-scale laboratory structure, demonstrating the developed theory.

The remainder of the paper is as follows. The next section presents the general framework of the active isolation problem. In Sect.  3, the influence on the base structure response of including an AVI strategy is formulated, also showing the effect, in simulations, for the particular case of a direct velocity feedback (DVF). To validate the simulation carried out, laboratory experimental measurements are conducted and presented in Sect.  4. Finally, conclusions are presented in Sect.  5.

2 General vibration isolation framework

The objective of this section is to formulate a general framework to consider the influence of the isolation platform on the base structure (i.e. structure on which the isolation platform is placed). First of all, Fig.  1 shows an AVI system, where the variables \(k_p\), \(c_p\) and \(m_p\) denote the stiffness, viscous damping coefficient and mass of the isolator placed on the platform, respectively.

Fig. 1
figure 1

Dynamic isolation system model with a rigid base structure

Full size image

The force imparted by the isolation platform (\(m_p\ddot{x}_p(t)\)) on the base structure is calculated as follows:

$$\begin{aligned} f_a(t)-c_p(\dot{x}_p(t)-\dot{x}_b(t))-k_p(x_p(t)-x_b(t))=m_p\ddot{x}_p(t), \end{aligned}$$
(1)

where \(f_a(t)\) is the active force, which depends on the acceleration measured on top of the isolation platform \(\ddot{x}_p(t)\) and the impulse response of the AVI control law \(c_f(t)\). Thus, Eq. (1) can be rewritten as:

$$c_f(t)*\ddot{x}_p(t)-c_p(\dot{x}_p(t)-\dot{x}_b(t))-k_p(x_p(t)-x_b(t))=m_p\ddot{x}_p(t),$$
(2)

where \(*\) is the convolution operator. Then, the transfer function (TF) between the accelerations of the isolation platform and base structure \(\left( G_i(s)=s^2X_p(s)/s^2X_b(s) \right)\) is as follows:

$$\begin{aligned} G_i(s)=\frac{2\zeta _p\omega _ps+\omega ^2_p}{s^2+2\zeta _p\omega _ps+\omega ^2_p-\frac{1}{m_p}C_f(s)s^2}, \end{aligned}$$
(3)

where s is the Laplace operator and capital letters indicate the Laplace transforms of the variables. The parameters \(\zeta _p\) and \(\omega _p\) are the damping ratio and natural frequency, respectively, which can be obtained from these relationships \(c_p/m_p=2\zeta _p\omega _p\) and \(k_p/m_p=\omega _p^2\).

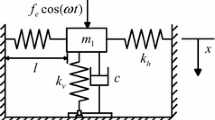
If the base is considered as a single degree of freedom system, the model now is the one shown in Fig.  2.

Fig. 2
figure 2

Dynamic isolation system model with a flexible base structure

Full size image

The equation of motion of the base structure is as follows:

$$\begin{aligned} f_d(t)-m_p\ddot{x}_p(t)-c_b\dot{x}_b(t)-k_bx_b(t) = m_b\ddot{x}_b(t) \end{aligned}$$
(4)

where \(f_d(t)\) is defined as an external perturbation force and \(k_b\), \(c_b\) and \(m_b\) denote the stiffness, viscous damping coefficient and mass of the base structure, respectively. Thus, the base structure can be modelled as a two-input (\(f_d(t)\) and \(m_p\ddot{x}_p(t)\)) one-output (\(\ddot{x}_b(t)\)) system. The base acceleration is then:

$$\begin{aligned} s^2X_b(s)=\frac{s^2/m_b}{s^2+2\zeta _b\omega _bs+\omega ^2_b}(F_d(s)-m_ps^2X_p(s)), \end{aligned}$$
(5)

where the variables \(\zeta _b\) and \(\omega _b\) are the damping ratio and the natural frequency of the base structure, respectively, obtained from the expressions \(c_b/m_b=2\zeta _b\omega _b\) and \(k_b/m_b=\omega _b^2\).

It can derived from Eq. (5) that the TF from any disturbance force to the base structure acceleration is:

$$\begin{aligned} G_b(s)=\frac{s^2/m_b}{s^2+2\zeta _b\omega _bs+\omega ^2_b}. \end{aligned}$$
(6)

The general vibration isolation framework, considering the interaction between the isolator and the base structure, can be described by taking into account the TFs of Eqs. 3, 5 and 6 and the system of Fig. 2. It is shown conceptually in the block diagram in Fig. 3, where the TFs T(s) and \(G_a(s)\) are defined as:

$$\begin{aligned} T(s)= & {} \frac{2\zeta _p\omega _ps + \omega _p^2}{s^2 + 2\zeta _p\omega _ps + \omega _p^2} \end{aligned}$$
(7)
$$\begin{aligned} G_a(s)= & {} \frac{1}{m_p}\frac{s^2}{s^2 + 2\zeta _p\omega _ps + \omega _p^2} . \end{aligned}$$
(8)
Fig. 3
figure 3

General scheme of the vibration isolation problem

Full size image

T(s) is the TF from the base structure movement to the the platform movement in passive mode. This is the well-known transmissibility for passive vibration isolation problems. \(G_a(s)\) is the TF from the active force \(f_a(t)\) to the platform acceleration \(\ddot{x}_p(t)\). The force received by the platform, and therefore by the base structure, is the control force, which is denoted by \(f_c(t)\) in Fig.  3. Its value can be calculated by \(m_p\ddot{x}_p(t)\).

The vibration isolation performance depends on the dynamic parameters of the isolator (\(\zeta _p, \omega _p\)) and the chosen controller \(C_f(s)\). This means that, for the general vibration isolation problem shown in Fig.  2, the dynamics of the base structure \(G_b(s)\) do not affect \(G_i(s)\), as proved in Eq. (3). Therefore, \(G_i(s)\) is only a function of the isolator dynamics and the controller. However, although this TF does not depend on the dynamics of the base structure, the platform acceleration value (\(\ddot{x}_p(t)\)) is affected by the interaction problem. This is because one of the two inputs of the base structure \((f_d(t), \ddot{x}_p(t))\) is the platform acceleration. Therefore, the perturbation input of the isolator \((\ddot{x}_b(t))\) changes as the platform movement does. The base structure TFs, considering the isolator dynamics, are as follows:

$$\begin{aligned} G_b^{PVI}(s)= & {} \frac{G_b(s)}{1+m_pG_bs(s)T(s)}, \end{aligned}$$
(9)
$$\begin{aligned} G_b^{AVI}(s)= & {} \frac{G_b(s)}{1+m_pG_b(s)G_i(s)}, \end{aligned}$$
(10)

where \(G_b^{PVI}(s)\) and \(G_b^{AVI}(s)\) are the TFs from the perturbation force \(F_d(s)\) to the base acceleration \(s^2X_b(s)\), when the isolation force is generated passively (PVI) and actively (AVI), respectively.

The effect on the base response of using an AVI control system compared with PVI control can be studied using the following variable:

$$\begin{aligned} \gamma = \frac{\Vert G_b^{AVI}(s)\Vert _{\infty }}{\Vert G_b^{PVI}(s)\Vert _{\infty }}, \end{aligned}$$
(11)

in which \(\gamma\) is the ratio between H-infinity norm of the frequency response functions (FRFs) of the TFs \(G_b^{AVI}(s)\) and \(G_b^{PVI}(s)\). On one hand, if the value of \(\gamma\) is greater than one, the maximum value of the FRF of \(G_b^{AVI}(s)\) is higher than that of those obtained for the FRF of the TF \(G_b^{PVI}(s)\), which means that the vibration level of the base structure due to a disturbance force is higher when AVI is used. On the other hand, if the value of \(\gamma\) is less than one, the vibration level is reduced when AVI is applied. If the value of \(\gamma\) is approximately one, it means that there is not a significant difference in response of \(G_b(s)\) when an PVI or AVI are used.

In order to generalise the studies derived from this framework, the following ratios can be defined: mass ratio \(r_m = m_p / m_b\) and frequency ratio \(r_\omega = \omega _p / \omega _b\). They allow to set a dynamic relation between the isolator and the base structure.

The influence of the isolation system on the response of the base structure also depends on the damping ratios \(\zeta _p\) and \(\zeta _b\). The value of \(\zeta _p\) is one of the main reasons of including AVI. Note that the objective of including an AVI strategy is to obtain a \(G_i(s)\) with no resonance peak and a rejected band similar to a PVI with low damping ratio (\(\zeta _p\)). Thus, if \(\zeta _p\) is increased, an attenuation of -40 dB/dec cannot be obtained because the zero placed at \(-\omega _p/\zeta _p\) is close to the poles \(-\zeta _p\omega _p\pm \omega _p\sqrt{1-2\zeta _p}\), which means that only a -20 dB/dec can be achieved. Therefore, a set of values of \(\zeta _p\) must be considered to show that significant differences exist in the base response for values \(0 \le \zeta _p \le 1\). Finally, small changes in the damping values of \(G_b^{PVI}(s)\) and \(G_b^{AVI}(s)\), which are due to \(G_i(s)\), are more significant when \(\zeta _b\) is smaller. Thus, a low damped base structures is of particular interest for this study.

3 Influence of PVI and AVI technique on the base structure

This section studies the isolator-structure interaction with PVI and AVI. Firstly, the design criterion of the used AVI, which is a direct velocity feedback system (DVF), is explained. In addition, the range of values for the numerical comparison are defined and justified. Secondly, the interaction of PVI and AVI is studied by analysing the value of \(\gamma\). Finally, some illustrative examples of PVI and AVI are included in order to show how the base structure is damped by including different vibration isolation techniques.

3.1 Proposed controller design and simulation setup

The system defined by \(m_pG_i(s)\) (see the general closed-loop system of Fig. 3) influences in the resulting damping of the base structure. Thus, the value of \(\Vert G_b^{AVI}(s)\Vert _{\infty }\) depends on \(m_pG_i(s)\). This subsection studies the influence of using DVF as the AVI control strategy on the response of the base structure. This influence is illustrated for different values of \(r_m\), \(r_{\omega }\) and \(\zeta _p\).

Ideal DVF has the form \(C_f(s) = K_{v}/s\), which introduces a pure integrator to the system. This DVF damps the system \(G_i(s)\) by increasing the parameter \(K_v\), being the damping ratio of the AVI \(K_v/(2\sqrt{k_pm_p})\) (see Eq. (3)). In the literature, it is said that this DVF is equivalent to a virtual sky-hook damper [24], introducing a damping force that does not depend on its relative movement with respect to the base in the bandwidth of interest.

However, this pure integrator has an infinite magnitude response at zero frequency, making this controller very sensitive to low-frequency noise. Therefore, it is not suitable for being used in practice because it may saturate the actuator used for imparting the force due to offsets in the acceleration signal [8]. Thus, the following lossy integrator is considered in this case study:

$$\begin{aligned} C_{f}(s) = \frac{K_{v}}{s/\omega _c + 1}, \end{aligned}$$
(12)

in which \(\omega _c\) represents the low frequency cut-off frequency of the lossy-integrator and \(K_v\) is the control gain. If the value of \(\omega _c\) is defined as \(0.1\omega _p\), the ideal and real DVF has a similar behaviour in the bandwidth of interest.

As was mentioned at the beginning of this subsection, the PVI (T(s)) and AVI (\(G_i(s)\)) can impart damping to the base structure, hence reducing the value of \(\Vert G_b^{PVI}(s)\Vert _{\infty }\) and \(\Vert G_b^{AVI}(s)\Vert _{\infty }\). The influence of including an AVI respect to a PVI can be better illustrated for small values of \(\zeta _b\). This arises from small changes in the closed-loop value of \(\zeta _b\) implies large changes in \(\Vert G_b^{AVI}(s)\Vert _{\infty }\) respect to \(\Vert G_b^{PVI}(s)\Vert _{\infty }\). The value of \(\zeta _b\) considered in this theoretical analysis is equal to 0.005, which is similar to the experimental validation of the following section. The rest of parameters considered are defined in Table 1. Note that the parameters \(r_m\) and \(r_{\omega }\) are closed intervals, where 10 intermediate values have been considered for each order of magnitude.

Table 1 Mass, frequency and damping ratio values of \(r_m\), \(r_{\omega }\) and \(\zeta _p\)
Full size table

The numerical results are organised into two subsections. The first one shows a comparison between the FRFs of T(s) and \(G_i(s)\), and the value of \(\gamma\) as a function of \(r_m\) and \(r_{\omega }\). The controller gain \(K_v\) is adapted so that the TF \(G_i(s)\) reaches -3 dB at the damped frequency of the isolator, defined by \(\omega _{p_d} = \omega _p \sqrt{1 - \zeta _p^2}\). The second subsection shows some illustrative examples where the frequency responses of \(G_b(s)\), \(G_b^{PVI}(s)\) and \(G_b^{AVI}(s)\) are compared. Three examples are proposed to show when AVI reduces or increases the vibration level of the base structure.

3.2 Isolation performance and influence of AVI on the base structure response

Figure 4 shows the comparison between T(s) and \(G_i(s)\) (top) and the value of \(\gamma\) (bottom) for \(\zeta _p\) equal to 0.001 and 0.1. For these values of \(\zeta _p\), the platform response (\(\ddot{x}_p(t)\)) in PVI mode would exhibit high amplitude response, which is reduced using the active force \(f_a(t)\). In addition, the rejected band is the same for the AVI even though the damping is increased. This is the case when the beneficial effect of including AVI is better justified from an isolation point of view. If the influence into the base structure is analysed (i.e. the value of \(\gamma\)), AVI affects \(G_b(s)\) positively when \(\zeta _p=0.001\) and high values of \(r_m\) are considered. In other words, AVI introducing damping to the base structure more than PVI. For remaining values of \(r_m\) and \(r_{\omega }\), the differences between AVI and PVI are not significant. However, when \(\zeta _p=0.1\) the response of the base structure for AVI can be up to three times higher than the response with PVI. The critical region is observed for similar frequency values (\(r_{\omega } \rightarrow 1\)) and mass ratios between [\(10^{-4}\), 0.20], approximately. The base response is reduced for AVI control for the region \([r_m>10^{-3}, r_{\omega } > 1]\), compared with the PVI control.

Fig. 4
figure 4

FRFs of T(s) and \(G_i(s)\) (top row) and influence ratio \(\gamma\) (bottom row) for \(\zeta _p = 0.001\) and \(\zeta _p = 0.1\)

Full size image

Figure 5 is similar to Fig.  4 but for values of \(\zeta _p\) equal to 0.3 and 0.5. The use of AVI always lead to better results from the isolation perspective. However, it should be noted that this improvement is not so significant as compared with low values \(\zeta _p\) (Fig.  4). In addition, an increment of almost two times the base response with AVI control is observed compared with that with PVI control. In case of \(\zeta _p = 0.3\), the region for which the base response is critically increased is observed for base frequency values slightly higher than the isolator frequency (\(r_{\omega } \rightarrow 0.9\) and \(0.9< r_m < 10^{-4}\)). However, for high frequency and mass ratios, the use of AVI control provides a huge reduction in the base response compared with PVI control. The same behaviour is presented in the case of \(\zeta _p = 0.5\), but this region is softer and the critical region is situated at lower frequency ratios.

Fig. 5
figure 5

FRFs of T(s) and \(G_i(s)\) (top row) and influence ratio \(\gamma\) (bottom row) for \(\zeta _p = 0.3\) and \(\zeta _p = 0.5\)

Full size image

Finally, in Fig. 6, the isolation performance is quite similar when PVI and AVI are compared. In addition, the rejected band is \(-\,20\) dB/dec since the poles and zeros are quite close. In these cases an AVI to increase the damping value is not well justified. Moreover, for \(\zeta _p = 1/ \sqrt{2}\), \(\gamma\) reaches its maximum value when the frequency of the base structures tends to be the double the isolator frequency, \(r_{\omega } \rightarrow 0.5\) (approximately two times). In terms of mass ratio, its influence is important for high frequency ratios, for which the base response is reduced. However, if the damping of the isolator is almost critical \(\zeta _p = 0.9\), the response is only slightly different. The maximum values of \(\gamma\) are located in a lower frequency ratio region than for the rest of the cases. Also, the value increases respect to the case of \(\zeta _p = 1 / \sqrt{2}\). Therefore, for high mass ratios and high values of \(\zeta _p\), the use of AVI depends on the ratio between the natural frequencies of the base and the isolator (\(r_{\omega }\)).

Fig. 6
figure 6

FRFs of T(s) and \(G_i(s)\) (top row) and influence ratio \(\gamma\) (bottom row) for \(\zeta _p = 1/\sqrt{2}\) and \(\zeta _p = 0.9\)

Full size image

3.3 Influence of PVI and AVI on the base structure

To show the effect that PVI and AVI have on the base response, three different cases of \(r_m\) and \(r_{\omega }\) are studied for damping values \(\zeta _p = \lbrace 0.1, 0.5, 0.9 \rbrace\). This phenomenon is not shown in the above figures, since \(G_b(s)\) was not plotted and the parameter \(\gamma\) considers only the difference between PVI and AVI. It is important to note that these cases are extracted from the data shown above, so the same isolation performance is achieved in all the cases studied here. The figures show the effect of the use of both techniques PVI and AVI on the base structure. The FRFs are normalised with respect the peak base response when no isolator device is situated on it, which can be expressed as \(\Vert G_b(s)\Vert _{\infty }\).

3.3.1 Case \(r_m=0.0889\) and \(r_{\omega }=0.8\)

This case shows an example for which the collocation of the isolator implies a reduction of the base response, but the use of AVI control in the isolator increases the response in the base structure compared with the passive mode. Figure 7 shows that the maximum reduction in PVI mode is achieved for \(\zeta _p = 0.5\). When the AVI control is activated in the isolator, there is an increase in the base response for all three cases compared with the PVI case. Also, the resonance frequency of base structure is moved sightly.

In this scenario, the accomplishment of the vibration isolation requirement affects negatively the dynamic response of the base structure and there exists a possibility that its vibration serviceability will be compromised.

Fig. 7
figure 7

Case \(r_m = 0.0889\) and \(r_{\omega }. = 0.8\). Normalised FRFs of the base with no isolator situated on the structure (dashed line), with an isolator collocated but no control activated (black line), with the isolator collocated and DVF working (grey line).

Full size image

3.3.2 Case \(r_m = 0.048\) and \(r_{\omega } = 1.6\)

In this scenario, the use of AVI control induces a reduction in the base response compared with PVI control. Fig.8 shows that the use of PVI implies basically the same base response for \(\zeta _p = 0.1\). However, the damping imparted by the AVI control is greater (\(\gamma\) is increased). This effect, although less significant in terms of \(\gamma\) reduction, can be seen for \(\zeta _p\) equal to 0.5 and 0.9. For this combination of dynamic parameters, the use of AVI does not compromise the base structure response. However, it is important to note that only a single degree of freedom system is considered for the base, and only one isolator is studied. This effect may be different when multiple modes and multiple isolators are considered.

Fig. 8
figure 8

Case \(r_m = 0.048\) and \(r_{\omega } = 1.6\). Normalised FRFs of the base with no isolator situated on the structure (dashed line), with an isolator collocated but no control activated (black line), with the isolator collocated and DVF working (grey line).

Full size image

3.3.3 Case \(r_m = 0.0794\) and \(r_{\omega } = 1.3\)

This case presents a scenario in which the damping ratio of the isolator determines if the base response for AVI control increases or not with respect to PVI control. The following mass and frequency ratio values considered here are \(r_m = 0.0794\) and \(r_{\omega } = 1.3\) (Fig.9). If AVI control is used, \(\Vert G_b^{AVI}(s)\Vert _{\infty } > \Vert G_b^{PVI}(s)\Vert _{\infty }\) for \(\zeta _p = 0.1\). A different phenomenon occurs for \(\zeta _p = 0.5\), for which \(\Vert G_b^{AVI}(s)\Vert _{\infty } \approx \Vert G_b^{PVI}(s)\Vert _{\infty }\). If the damping of the isolator is 0.9, \(\Vert G_b^{AVI}(s)\Vert _{\infty } < \Vert G_b^{PVI}(s)\Vert _{\infty }\). This shows the importance of the isolator damping in terms of its influence in the base. According to this fact, different control strategies must be considered to accomplish possible base acceleration requirements.

Fig. 9
figure 9

Case \(r_m = 0.0794\) and \(r_{\omega } = 1.3\). Normalised FRFs of the base with no isolator situated on the structure (dashed line), with an isolator collocated but no control activated (black line), with the isolator collocated and DVF working (grey line)

Full size image

4 Experimental test

This section presents the experimental validation of the theoretical framework proposed above. The experimental set-up used is shown in Figs.  4 and 10. The base structure is a simply supported beam (knife edge supports at both ends) of length 5.0 m. The device used for isolation is an APS Dynamics Model 400 electrodynamic actuator. This isolator device has mass 82 kg when \(m_p\) is unattached and the total mass of the isolation platform \(m_p\) is equal to 31 kg. The mass of the beam without the isolator is approximately 126 kg. The perturbation force \(f_d(t)\) is generated by an exciter situated on the ground and linked to the base structure by a stinger. The exciter is also an APS Dynamics Model 400 electrodynamic actuator. This actuator is configured as a force actuator, being this force independent of the response of the base and isolator (Fig. 11).

Fig. 10
figure 10

Illustration of the experimental set-up

Full size image
Fig. 11
figure 11

General view of the experimental setup (Structures Laboratory. ETS Ingenieros de Caminos, Canales y Puertos, Universidad Politécnica de Madrid. Madrid. Spain)

Full size image

It is important to note that this experiment emulates the problem of an isolator placed on a flexible base. The objective is to show how the transmissibility of the isolator can influence on the base response, as it was illustrated in the previous section. The scenario presented here shows a case in which the use of AVI control implies the improvement of both the vibration isolation performance and the response of the base structure.

4.1 Experimental identification of the system dynamics

The theoretical framework presented in this work only needs the identification of the subsystems \(G_b(s)\), T(s) and \(G_a(s)\). The instrumentation used is:

  1. (i)

    An accelerometer is attached to the platform to measure \(\ddot{x}_p(t)\) and another one to the beam, close to the isolator, to measure the acceleration of the base \(\ddot{x}_b(t)\)

  2. (ii)

    A data acquisition device National Instruments compactRIO 9066 equipped with an IEPE acquisition module for accelerometers and an output module to generate both the excitation signals and the control law for the AVI

The FRF of the TF of the beam \(G_b(s)\) from the perturbation force \(f_d(t)\) to the acceleration of the base \(\ddot{x}_b(t)\) is shown in Fig. 12. It shows only the first flexural mode of the beam, which is used to analyse the results. To obtain this FRF, the isolator device is collocated on the beam without the moving mass \(m_p\). Thus, the weight of the device is included in the identification but not the effect of the force \(f_c(t)\) due to platform movement. According to the form of Eq. (6), the natural frequency of the first mode of the beam is therefore identified at \(\omega _b = 27.64\) \(\hbox {rads}^{-1}\) (4.4 Hz). The damping ratio, extracted by the half power bandwidth method [3] is \(\zeta _b = 0.0046\). The value of the identified mass is 120.2 kg. Thus, the identified \(G_b(s)\) is as follows:

$$\begin{aligned} G_b(s) = \frac{0.0078s^2}{s^2 + 0.25s + 738.46} \end{aligned}$$
(13)
Fig. 12
figure 12

TF of the beam \(G_b(s)\)

Full size image

The isolator is placed on a rigid ground and is excited by a random perturbation in order to obtain the FRF of T(s), which is shown in Fig.14-left-top. Analogous to \(G_b(s)\), the identified natural frequency and damping ratio are \(\omega _p =\) 8.79 \(\hbox {rads}^{-1}\) (1.4 Hz) and \(\zeta _p = 0.075\), respectively (Eq. (7)). The identified T(s) is as follows:

$$\begin{aligned} T(s) = \frac{1.32s + 77.37}{s^2 + 1.32s + 77.37}, \end{aligned}$$
(14)

Using the identified parameters \(\omega _p\) and \(\zeta _p\) and the value of \(m_p=31\) kg, it is possible to obtain the TF from the force applied in \(m_p\) to the mass acceleration \(\ddot{x}_p(t)\) (Equation (8)), which is:

$$\begin{aligned} G_a(s) = \frac{0.032s^2}{s^2 + 1.32s + 77.37}. \end{aligned}$$
(15)

4.2 Vibration isolation effect on the base structure

The control strategy chosen for this experiment is DVF as defined in Eq. (12). According to that, and using the natural frequency of the isolator (1.4 Hz), the following controller, for unitary static gain, results:

$$\begin{aligned} C_f(s) = \frac{0.8796}{s + 0.8796}. \end{aligned}$$
(16)

It should be highlighted that the imparted damping by using \(C_f(s)\) would be improved theoretically if only the TF \(G_a(s)\) is considered (i.e. the mechanical dynamic part of the isolator). But there are further dynamics (e.g. the amplifier driving the shaker, the accelerometers, the signal conditioning electronics) that have not been considered in Eq. (15). Therefore, the isolation reduction around the resonant frequency is worse in practice since these non-considered dynamics tend to make the AVI unstable at high gains. However, it should also be highlighted that the damping achieved with the active force is enough to demonstrate the influence that AVI has in the base structure compared with PVI.

Fig. 13
figure 13

Influence map for the isolator used in the experimental test on different base structures

Full size image

The influence that an isolator with various dynamic properties has on different structures is shown in Fig.13. As can be observed, the surface shape is very similar to those showed in Fig.  4 for \(\zeta _p =0.1\). According to Eq. (6), the equivalent mass of the first mode of the base structure \(m_b\) can be extracted from the identified TF of the beam (Fig.12). Thus, if the beam is simplified to a single degree of freedom system, the equivalent mass is 128.2 kg. The resulting mass and frequency ratios are \(r_m = 0.24\) and \(r_{\omega } = 0.31\), respectively. The value of \(\gamma\) for the numerical simulations is 0.80. This implies that the use of an AVI system provides an improvement with respect to the PVI system.

Fig. 14
figure 14

Experimental and theoretical results for the transmissibility functions (top row) and the beam TFs (bottom row) for PVI and AVI.

Full size image

The identified transmissibility for both PVI and AVI systems and their influence on the beam TFs are shown in Fig.14. At the top, the passive (black line) and active (grey line) FRFs of the transmissibility functions (T(s), \(G_i(s)\)) are shown for both experimental (left) and numerical (right) cases. The response of the base for both strategies is shown at the bottom of the figure. For AVI control, the response in the base is reduced with respect to PVI control. This implies that, for these dynamic parameters, the use of AVI provides improvement in terms of vibration isolation and also reduces the base acceleration. If numerical and experimental results are compared, the following conclusions can be derived: the first one is that the frequency responses of T(s) are quite similar, which shows that the isolator without base interaction is well identified. The second one is that there is a non-significant difference between experimental and numerical frequency responses of \(G_i(s)\), which show the influence of the electrical part of the APS Dynamics Model 400. Note that this additional dynamics was the main restriction to design the DVF of Eq. (16). The third one is the similar value of \(\gamma\), which is 0.78 for the experimental, whereas for the numerical simulation it is 0.80. These results validate the experimental validation proposed in this section.

5 Conclusions

The problem of vibration isolation has been studied extensively in the past without considering its effect on the base structure. When it has been considered, the previous studies have only dealt with the effect in the vibration isolation performance. In this work, a theoretical development of the complete interaction problem has been developed.

The transmitted vibration from the isolator to light-weight, and usually lively, base structures might not always be negligible and should be carefully considered in some cases. This study has provided understanding of how the vibration isolation system might affect the base response for an active controller. This perspective grants to the problem the possibility to analyse the effect of an isolator for a range of different base structures. The controller used for this study is direct velocity feedback (DVF). Its implementation on a generic isolator has been studied, and its influence on different base structures has been illustrated using influence contour plots. Different particular cases have been analysed to show the effect in the base structure. Thus, the parameter \(\gamma\), that shows how the base response changes with active vibration isolation (AVI) control with respect to passive vibration isolation (PVI) control, has been chosen to determine whether the base response improves or worsens for AVI respect the PVI and by how much. The formulation has been validated against an experimental test, which was developed on a full-scale structure with appropriate sensor, controller and actuator hardware.

Future works will be carried out to study the effect of multiple isolators situated on the same base structure and also to propose controllers to achieve a dual objective of platform vibration isolation and whilst keeping the base acceleration inside an acceptable range.