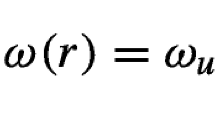Abstract
Estimates from above and below by the same positive prototype function for suitably modified Green functions in bounded smooth domains under Dirichlet boundary conditions for elliptic operators L of higher order \(2m\ge 4\) have been shown so far only when the principal part of L is the polyharmonic operator \((-\Delta )^m\). In the present note, it is shown that such kind of result still holds when the Laplacian is replaced by any second order uniformly elliptic operator in divergence form with smooth variable coefficients. For general higher order elliptic operators, whose principal part cannot be written as a power of second order operators, it was recently proved that such kind of result becomes false in general.
Similar content being viewed by others
1 Introduction
In a series of works [3, 4, 6, 7, 9, 13], Dall’Acqua, Meister, Pulst, Robert, Sweers, and the present author have studied the question whether (suitably modified) Green functions in bounded smooth domains \(\Omega \subset {\mathbb {R}}^n\) under Dirichlet boundary conditions for elliptic operators L of higher order \(2m\ge 4\) may be estimated from above and below by the same positive prototype function. Such kind of result may be considered as a kind of substitute or relaxation of the maximum principle which in its strong form is true only for second order operators. Employing perturbative and blow-up arguments, all these works are based on Boggio’s explicit formula for the polyharmonic Green function under Dirichlet boundary conditions in balls (see [2, p. 126] and also [5, Lemma 2.27]) and similarly in half spaces (see [5, Remark 2.28]). This does not only show its positivity in these special domains but does also allow for precise estimates from above and below, see [5, Theorem 4.6] and Remark 2(a) below.
In order to keep this note short and as simple as possible, I shall consider only the (simplest) generic case
The “small” dimensions \(n=2,\ldots ,2m\) require more effort, but related results will also hold there. The most general class of operators, which could be treated so far, was considered by Pulst [13]. He could show that in general bounded smooth domains the estimate (2) below holds for operators of the form
where the coefficients obey symmetry, smoothness, and coercivity conditions.
The goal here is to show that the same estimates can be proved for a principal part with variable coefficients, as long as this stays in the class of powers of second order elliptic operators.
Theorem 1
For \(n,m\in \mathbb {N}\) with
let \(\Omega \subset {\mathbb {R}}^n\) be a bounded \(C^{\infty }\)-smooth domain and L be a uniformly elliptic symmetric operator of the form
For the coefficients, we assume that
and that there exist numbers
Let \(G_{\Omega ,L}\) denote the Green function in \(\Omega \) for the following Dirichlet problem
Then there exist constants \(c_1\ge 0\), \(c_2 >0\), depending on the domain \(\Omega \) and the elliptic operator L, such that we have the following Green function estimate:
for all \( x,y\in \Omega \), where
and
Remark 2
-
(a)
If \(L=(-\Delta )^m\) and \(\Omega \) is a ball or a half space in \({\mathbb {R}}^n\), (2) holds true with \(c_1=0\). This follows from Boggio’s formula as already mentioned at the beginning of the introduction. Since \(n>2m\), one has a unique Green function even in the whole space and this is given by the positive fundamental solution \(G_{(-\Delta )^m,{\mathbb {R}}^n}(x,y)=c_{m,n}|x-y|^{2m-n}\) with a suitable positive normalisation constant \(c_{m,n}>0\).
-
(b)
The existence of a Green function is in the case of a principal part with nonconstant coefficients by no means obvious and is due to Krasovskiĭ [11, Theorem 3.3]. Thanks to the symmetry of the operator L, this is symmetric, i.e. \( G_{\Omega ,L} (x,y)= G_{\Omega ,L} (y,x)\).
-
(c)
Krasovskiĭ’s work requires high regularity of the coefficients of L and of the domain. To keep the exposition as simple as possible, I just assume everything to be \(C^\infty \)-smooth.
-
(d)
The estimate from above follows from [4, 10, 11], see also [6], so that only the estimate from below has to be proved here.
-
(e)
With the techniques used here and developed in the mentioned works, one may admit also lower order terms as long as symmetry and coercivity assumptions are obeyed.
-
(f)
As it was investigated in [8], the situation becomes completely different when L is a general uniformly elliptic operator (even with constant coefficients), which cannot be written as a composition of second order operators, and when the dimension is large, i.e. \(n\ge 2m+2\). Here, in general, even the fundamental solution is sign changing near its singularity. This means that close to its singularity the negative part of any corresponding Green function becomes unbounded of the same order of magnitude as the positive part.
-
(g)
For implications of two-sided estimates as in Theorem 1, one may see [14,15,16].
An interesting consequence of Theorem 1 is a uniform local positivity result, which was shown in the mentioned works before for the more special class of operators.
Theorem 3
Let the assumptions of Theorem 1 be satisfied. Then there exist a constant \(r_{\Omega ,L}>0\) such that
2 Local estimates from below
Lemma 4
Suppose that the assumptions of Theorem 1 are satisfied. Then for each \(x_0\in \overline{\Omega }\), there exists a radius \(r=r_{x_0}>0\) and a constant \(C=C_{x_0}>0\) such that for all \(x,y\in \Omega _{x_0,r}:={\Omega }\cap B_r(x_0)\), \(x\not =y\), one has
where \(H_\Omega \) is defined in (3).
Proof
We assume by contradiction that no such positive numbers exist such that (5) is satisfied. This means that we may find sequences \((x_k)_{k\in \mathbb {N}},\ (y_k)_{k\in \mathbb {N}}\subset \Omega \) with
and
We shall rescale the domain and the Green function such that \(|x_k-y_k|\) becomes the new length unit. In the scaling limit, we shall end up with a Green function for a constant coefficient elliptic operator in the half space or in the whole space which is known to enjoy an estimate like (5) so that we end up with a contradiction. This key argument relies on knowing the Green functions in these prototype situations explicitly, see Remark 2(a) above.
To this end, we need to distinguish the cases whether the \(x_k,y_k\) are as close together as to the boundary or much closer.
First case: The sequence \(d_\Omega (x_k)/|x_k-y_k|\) remains bounded.
This means that there exists a constant \(c_3>0\) such that
Thanks to the triangle inequality \(d_\Omega (y_k)\le d_\Omega (x_k)+|x_k-y_k|\), we also have
This yields in view of (6) that
and due to our assumption (7) that
Without loss of generality, we may assume that \(x_0=0\) and that the first unit vector \(\mathbf {e}_1\) is the exterior unit normal to \(\partial \Omega \) at \(x_0\).
For k large enough, we may define \(\tilde{x}_k\in \partial \Omega \) as the closest boundary point to \(x_k\). We introduce the rescaled Green functions
for
These belong to the elliptic operators
with
in \(\Omega _k\). This can be seen as follows. For smooth \(v:\overline{\Omega _k}\rightarrow {\mathbb {R}}\), we define
and find
Since \(\tilde{x}_k\rightarrow x_0= 0\), the exterior unit normal at \(\partial \Omega \) converges to the first unit vector and so we conclude that
In order to understand the limit of the \(G_k\), we observe first that Krasovskiĭ’s estimates [11, Theorem 3.3] yield uniformly in k that
Employing local elliptic estimates [1], we find a limit
in \(L^1_{loc}\) and locally uniformly in \(\overline{\mathcal {H}}\times \overline{\mathcal {H}}\setminus \{(\xi ,\xi ):\xi \in \overline{\mathcal {H}}\}\). This is symmetric, i.e. \(\overline{G}(\xi ,\eta ) = \overline{G} (\eta ,\xi )\), obeys homogeneous Dirichlet boundary conditions on \(\partial {\mathcal {H}}\), and satisfies
We introduce the limit operator
with the constant coefficients
One should observe that this operator can easily be transformed by means of a linear transformation into the polyharmonic \((-\Delta )^m\). To be more precise, let \(C_1\in SO(n)\) diagonalise \(\left( a^{\infty }_{ij} \right) _{i,j=1,\ldots ,n}\). We then introduce a diagonal dilation matrix \(C_2\) with positive diagonal entries such that \(\left( C_1 \cdot C_2 \right) ^T \cdot \left( a^{\infty }_{ij} \right) _{i,j=1,\ldots ,n} \cdot \left( C_1 \cdot C_2 \right) \) becomes the n-dimensional identity matrix. Finally we introduce a further “rotation” \(C_3\in SO(n)\) such that \(C:=C_1 \cdot C_2 \cdot C_3:{\mathcal {H}} \rightarrow {\mathcal {H}} \) maps again the half space onto itself. Using this transformation, we find that
The latter is given by Boggio’s formula
where \(k_{m,n}> 0\) is a suitable constant and \(\xi ^*=(-\xi _1,\xi _2,\ldots ,\xi _n)\). So we conclude from [5, Theorem 4.6] that
with a strictly positive constant \(c_4\). \(H_{\mathcal {H}}\) is as in (3) with \(d_{\mathcal {H}}(\xi )=|\xi _1|\). Since Boggio’s formula has the same form in \({\mathcal {H}}\) as in the ball, (13) is deduced in \({\mathcal {H}}\) in the same way as in the ball. Moreover, as explained in [6, 7], \(G_{{\mathcal {H}},L_\infty }\) is unique under the assumption
In order to conclude that \(\overline{G}=G_{{\mathcal {H}},L_\infty }\), we only need to show that
in the distributional sense. To this end, we consider any function \(\psi \in C^\infty _0 ({\mathcal {H}})\) and find from the fact that \(G_k\) is the Green function for \(L_k\) that one has for any \(\xi \in {\mathcal {H}}\) and k large enough,
The smoothness assumptions on the coefficients yield that \(a_{ij}^{(k)} \rightarrow a_{ij}^{\infty } \) in \(C^{2m-1}_{loc}({\mathcal {H}})\) and hence
uniformly in \(C^0_0 ({\mathcal {H}})\). We come up with
This shows that \(\overline{G}\) is a Green function for \(L_\infty \) in \({\mathcal {H}}\), which in view of its uniqueness explained above yields that
Defining
on the one hand, the assumption gives via (10) that
On the other hand, we have
After passing to a further subsequence, we find \(\xi ,\eta \in \overline{\mathcal {H}}\) with \(\xi =\lim _{k\rightarrow \infty }\xi _k \), \(\eta =\lim _{k\rightarrow \infty }\eta _k\). In view of the local smooth convergence of \(G_k\) to the Green function \(G_{{\mathcal {H}},L_\infty }\), we see from (13) that there exists a positive constant \(c_5>0\) such that for k large enough,
This contradicts (15) and the proof of the lemma is complete in the first case.
Second case: The sequence \(d_\Omega (x_k)/|x_k-y_k|\) becomes unbounded.
The reasoning here is similar to the first case and I outline only the main steps. After passing to a subsequence, we may assume that
This also implies that
We obtain from the assumption (7) that in this case
We rescale again such that \(|x_k-y_k|\) becomes the new length unit; however, here it is the \(x_k\) which become the new origins.
for
These belong to the elliptic operators
with
in \(\Omega _k\). In view of the assumptions in this case, we conclude that
For the sequence \(G_k\), we find a limit in \(L^1_{loc}\) and locally uniformly in \({\mathbb {R}}^n\times {\mathbb {R}}^n\setminus \{(\xi ,\xi ):\xi \in {\mathbb {R}}^n\}\), which is symmetric and decays like \((\xi ,\eta )\mapsto |\xi -\eta |^{2m-n}\) at infinity. Thanks to the uniqueness of such kind of Green function, we conclude that in the sense just described we have
where the constant coefficient operator \(L_\infty \) is obtained precisely as in the first part. I emphasise that here the assumption \(n>2m\) simplifies the proof a lot because the uniqueness conclusion follows directly from Liouville’s theorem for polyharmonic operators, cf. e.g. [12, p. 19]. Observe that a linear transformation changes \(L_\infty \) into the polyharmonic operator.
Defining
our assumption gives via (16) that
Thanks to \(| \eta _k |=1\), we may pass to a subsequence and find \(\eta _k\rightarrow \eta _\infty \) with \(|\eta _\infty |=1\) and
We proceed now precisely as explained in some detail above in the first case. After applying a linear transformation, we may change \(L_\infty \) into \((-\Delta )^m\) whose Green function in \({\mathbb {R}}^n\) is given by the fundamental solution with zero boundary conditions at infinity, i.e. a positive multiple of \((\xi ,\eta )\mapsto |\xi -\eta |^{2m-n}\). We conclude that \(G_{{\mathbb {R}}^n,L_\infty }(0,\eta _\infty )>0\) and achieve a contradiction. So the proof of the lemma is complete also in this case. \(\square \)
3 Proof of the main results: a compactness argument
3.1 Proof of Theorem 1
Applying a compactness argument to
we see that there exist positive numbers \(r>0\), \(c_6>0\), such that \(|x-y|\le r\) implies that \(G_{\Omega ,L} (x,y) \ge c_6 H_\Omega (x,y)\). If \(|x-y|\ge r\), we take from [4, 11], cf. also [5], that \( G_{\Omega ,L} (x,y) \ge -c_7 H_\Omega (x,y) \) so that
Since \(H_\Omega (x,y)\le |x-y|^{-n}d_\Omega (x)^m d_\Omega (y)^m\le r^{-n}d_\Omega (x)^m d_\Omega (y)^m\), we end up with
and positive constants \(c_7,c_8>0\). The proof of Theorem 1 is complete. \(\square \)
3.2 Proof of Theorem 3
This theorem was proved for \(L=\Delta ^2\) in [6] when \(n\ge 3\) and in [5, Theorem 6.15] when \(n =2\). See also [7, Theorem 2] for a unified and simpler proof, which I shall adapt to the present situation.
Case I: \(d_\Omega (x)d_\Omega (y)\le \left| x-y\right| ^2\). For this situation, we have
Then there is \(c>0\) such that we find \(c_2^{-1} H_{\Omega }(x,y)\ge 2 c_1 d_\Omega (x)^md_\Omega (y)^m\) for \(\left| x-y\right| <c\).
Case II: \(d_\Omega (x)d_\Omega (y) > \left| x-y\right| ^2\). Now we have
Since \(n>2m\) by assumption and since \(d_\Omega (x)d_\Omega (y)\) is bounded on \(\Omega \), one finds a constant \(c>0\) such that \(c_2^{-1} H_{\Omega }(x,y)\ge 2 c_1 d_\Omega (x)^m d_\Omega (y)^m\) for \(\left| x-y\right| <c\). The proof of Theorem 3 is complete. \(\square \)
References
Agmon, S., Douglis, A., Nirenberg, L.: Estimates near the boundary for solutions of elliptic partial differential equations satisfying general boundary conditions. I. Comm. Pure Appl. Math. 12, 623–727 (1959)
Boggio, T.: Sulle funzioni di Green d’ordine \(m\). Rend. Circ. Mat. Palermo 20, 97–135 (1905)
Dall’Acqua, A., Meister, Ch., Sweers, G.: Separating positivity and regularity for fourth order Dirichlet problems in 2d-domains. Analysis (Munich) 25, 205–261 (2005)
Dall’Acqua, A., Sweers, G.: Estimates for Green function and Poisson kernels of higher order Dirichlet boundary value problems. J. Differ. Equ. 205, 466–487 (2004)
Gazzola, F., Grunau, H.-C., Sweers, G.: Polyharmonic Boundary Value Problems. Positivity Preserving and Nonlinear Higher Order Elliptic Equations in Bounded Domains. Springer Lecture Notes in Mathematics, vol. 1991. Springer, Berlin (2010)
Grunau, H.-C., Robert, F.: Positivity and almost positivity of biharmonic Green’s functions under Dirichlet boundary conditions. Arch. Ration. Mech. Anal. 195, 865–898 (2010)
Grunau, H.-C., Robert, F., Sweers, G.: Optimal estimates from below for biharmonic Green functions. Proc. Amer. Math. Soc. 139, 2151–2161 (2011)
Grunau, H.-C., Romani, G., Sweers, G.: Differences between fundamental solutions of general higher order elliptic operators and of products of second order operators. Math. Ann. (2020). https://doi.org/10.1007/s00208-020-02015-3
Grunau, H.-C., Sweers, G.: Positivity for perturbations of polyharmonic operators with Dirichlet boundary conditions in two dimensions. Math. Nachr. 179, 89–102 (1996)
Krasovskiĭ, J.P.: Investigation of potentials connected with boundary value problems for elliptic equations (Russian). Izv. Akad. Nauk SSSR Ser. Mat. 31, 587–640 (1967). (English translation in: Math. USSR Izv. 1, 569–622 (1967))
Krasovskiĭ, J.P.: Isolation of singularities in Green’s function (Russian). Izv. Akad. Nauk SSSR Ser. Mat. 31, 977–1010 (1967). (English translation in: Math. USSR Izv. 1, 935–966 (1967))
Nicolesco, M.: Les Fonctions Polyharmoniques. Hermann, Paris (1936)
Pulst, L.: Dominance of positivity of the Green’s function associated to a perturbed polyharmonic Dirichlet boundary value problem by pointwise estimates. PhD thesis, Otto-von-Guericke-Universität Magdeburg (2014)
Schnieders, I., Sweers, G.: A biharmonic converse to Krein–Rutman: a maximum principle near a positive eigenfunction. Positivity 24, 677–710 (2020)
Schnieders, I., Sweers, G.: Note on a sign-dependent regularity for the polyharmonic Dirichlet problem. J. Differential Equations 279, 1–9 (2021)
Schnieders, I., Sweers, G.: Classical solutions up to the boundary to some higher order semilinear Dirichlet problems. Nonlinear Anal. 207, 112265 (2021)
Acknowledgements
The author is grateful to Guido Sweers for valuable discussions and to the anonymous referee for valuable suggestions how to better explain the key argument and to improve the presentation.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grunau, HC. Optimal estimates from below for Green functions of higher order elliptic operators with variable leading coefficients. Arch. Math. 117, 95–104 (2021). https://doi.org/10.1007/s00013-021-01597-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00013-021-01597-x