Performance measurement and joint production of intended and unintended outputs

Abstract

The generation of unintended residuals when producing intended outputs is the key factor behind our serious problems with pollution. The way this joint production is modelled is therefore of crucial importance for our understanding and empirical efforts to change economic activities in order to reduce harmful residuals. Estimation of efficiency and productivity when producing both intended and unintended outputs has emerged as an important research strand. The most popular models in the field are based on weak disposability of the two types of outputs together and null-jointness introduced by Shephard. The purpose of the paper is to show that these model types are built on some questionable assumptions. An alternative model based on the production theory of Frisch introduces technical jointness for the case when the unintended output is unavoidable. The materials balance based on physical laws tells us that when material inputs are used unintended outputs are unavoidable. The modelling of joint production must therefore reflect this. The production of the two types of outputs occurs simultaneously. It is the maximisation of intended outputs for given inputs that engineers are striving at to achieve. The production functions for intended and unintended outputs are linked through common use of inputs. However, separate functions for the two types of output can be estimated because the intended outputs are independent of the unintended ones and vice versa, facilitating calculating separate efficiency and productivity measures using non-parametric DEA methods.

1 Introduction

A crucial building block in environmental economics is the phenomenon of joint generation of intended outputs and unintended ones¹ in production and consumption activities. The discharge of unintended outputs causes the ubiquitous environmental problems facing humankind today. Estimation of efficiency and productivity when producing both intended and unintended outputs has emerged as an important research strand. However, mainstream environmental economics has hardly considered inefficiency issues. The literature spawned by the Porter hypothesis (Porter (1991); Porter and van den Linde 1995) is an exception (empirical studies and critique of the hypothesis are extensively reviewed in Brännlund and Lundgren (2009); Lanoie et al. (2011); Ambec et al. 2013).

Based within the inefficiency research strand Färe et al. (1986); (1989) pioneered the issue of measuring inefficiency empirically when producers generate both desirable and undesirable outputs. The measurement was based on theoretical schemes presented in Shephard (1970), that introduced jointly weak disposability of intended and unintended outputs, and null jointness.² Färe and Grosskopf (1983) developed the theoretical ideas into explicit efficiency measures³ using single-equations distance functions presented in Shephard (1970). Up to now, single-equation models have completely dominated the literature on efficiency when producing simultaneously intended and unintended outputs.

The introduction of a directional distance function in Chung et al. (1997) lead to the widespread adoption of this approach in the literature, and replaced the hyperbolic efficiency measure used in Färe et al. (1989). The output-oriented radial distance function of Shephard (1970) was generalised using a distance function that adds to the desirable output of an inefficient observation and subtracts from the observed inefficient level of the undesirable output in order for a projection of the observation to be on the frontier. The calculation of the added/subtracted values where done using the same scalar factor multiplied with the observed values of both types of outputs, using as the direction of scaling the observed output values.

The rise of the Shephard single-equation models of joint production of intended and unintended outputs in journals has been rather spectacular, with Färe et al. (1989) having 903 citations and Chung et al. (1997) having 1001 citations in Web of Science per 20.07.2020. However, critical journal papers offering other approaches are coming (see Førsund (2009); Murty et al. (2012); Murty and Russell (2018) and extensive surveys in Murty and Russell (2017); Dakpo and Ang 2019).

A crucial feature of the technology specification is the unavoidability of generation of residuals. I am only interested in the residuals that cause environmental damage, identified as having positive willingness to pay to reduce the damage.⁴ Residuals are then called pollutants. The materials balance, introduced in environmental economics in Ayres and Kneese (1969), expresses the essential insight that the material content of inputs cannot disappear, but must be part of the intended outputs or become residuals discharged to the natural environment.⁵ The materials balance reflects the two thermodynamic laws of conservation of matter and energy. Due to entropy, there is a minimum of energy and materials that will not be contained in the intended output. The pervasiveness of residuals generation then follows.

The seminal papers Färe et al. (1989); Chung et al. (1997) answered the question of how to calculate efficiency measures when both intended and unintended outputs are produced. This achievement was impressive. However, the single-equation Shephard distance function they used are not without flaws, and were first criticized in Førsund (1998); (2009) and more forcefully in Murty and Russell (2002); Murty et al. (2012). The main purpose of the paper is to expose the problems of Shephard-inspired measures, and to present an approach based on a specific form of joint production based on Frisch (1965), developed further in Førsund (2009); (2018a). The alternative approaches both in Førsund (2009) and Murty et al. (2012) are based on a separation of the technology into two types of production functions; one for intended outputs and another for unintended outputs.⁶ However, the two types of outputs are not produced in separate activities, but generated simultaneously. Murty et al. (2012) provided solid mathematical arguments for the necessity of operating with multi equations rather than with a single equation that was used employing distance functions.

My critique is not based so much on technical or mathematical insights as to an understanding of how to model the production relationships for an intended output when the creation of unavoidable unintended products causing negative externalities are also produced simultaneously. For the analysis, I will use mostly production functions with continuous partial derivatives of first and second order, and assuming that the requisite assumptions of the implicit function theorem hold. Of course, these are stricter assumptions than necessary. Starting out with some reasonable assumptions or axioms about production sets and then deriving their properties will yield richer results as to the generality of the analysis, and may be required for disentangling disposal properties of multiple equations (Murty et al. (2012); Murty and Russell (2017); 2018). However, it is not necessary for my purpose to go for maximal generality.

The plan of the paper is to discuss the materials balance in Section 2, and to present the seminal approaches of Shephard (1970) and Baumol and Oates (1988) in Section 3. The nature of joint production and my alternative to the Shephard-inspired models are presented and discussed in Section 4 together with short reviews of alternative multi-equation models. The key model development in the paper is based on the factorially determined multi- output production functions of Frisch (1965). Section 5 is summing up the critique of Shephard-inspired models. Section 6 discusses the efficiency concept and points to a simple way to estimate efficiency and productivity measures in the case of both intended and unintended outputs using a radial non-parametric DEA model. Section 7 concludes.

2 The materials balance

The mass of material inputs appears in the materials balance relation, and it is therefore convenient to operate with two classes of inputs. Ayres and Kneese (1969, p. 289) named them tangible raw materials and services; I will call them material inputs, x_M, and service inputs, x_S, being non-material. These latter inputs are not “used up” or transformed in the production process. The materials balance tells us that mass contained in material inputs cannot disappear, but must be contained in the products y or end up as residuals z. The residuals are discharged to the natural environment. The variables in the materials balance relation must be expressed in the same unit of measurement. Weight of mass is a natural unit of measurement. The weight of the different inputs containing a specific substance k can then be summed over the number of material inputs j = 1,…, n_M. Part of this substances are contained in intended outputs i = 1,…, m if they are of the material kind. The difference between the mass of substance k in the material inputs and the mass of substance k contained in the m types of outputs is the amount of substance k discharged to Nature, measured in the same weight unit as the substance in material inputs and in intended outputs. However, the residual may be discharged to Nature in different forms, e.g. CO₂, CO, tar, ash, etc., that can be classified as different types r = 1,…, R. For example, coal used in producing electricity contains carbon, but in the combustion process, oxygen is picked up and CO₂ is emitted to air. A coefficient c_rk measures the amount of the substance k contained in residual of type r per unit of total discharged residual z_k. The weights a_jk, b_ik, c_rk convert the unit of measurements commonly used for the variables (piece, length, area, volume, etc.) into weight. The general materials balance can then be written:

$$\begin{array}{l}\mathop {\sum}\nolimits_{j = 1}^{n_M} {a_{jk}x_{Mj}} \equiv \mathop {\sum}\nolimits_{i = 1}^m {b_{ik}y_i} + \mathop {\sum}\nolimits_{r = 1}^R {c_{rk}z_k\left( {k = 1,...,K} \right),} \\ \mathop {\sum}\nolimits_{k = 1}^K {\mathop {\sum}\nolimits_{j = 1}^{n_M} {a_{jk}x_{Mj}} } \equiv \mathop {\sum}\nolimits_{k = 1}^K {\mathop {\sum}\nolimits_{i = 1}^m {b_{ik}y_i} } + \mathop {\sum}\nolimits_{k = 1}^K {\mathop {\sum}\nolimits_{r = 1}^R {c_{rk}z_k.} } \end{array}$$

(1)

The coefficient a_jk in front of material inputs x_Mj tells us the mass of substance k in a unit of x_Mj, the coefficient b_ik in front of intended output y_i is the mass of substance k contained in a unit of the output y_i, and the coefficient c_rk in front of the residual z_k contains the mass of substance k in type r of the emitted residual. If it is the type of residual r that is used as the definition of the residual, then the carbon in coal must be converted to units of CO₂, etc.⁷

The first line in Eq. (1) shows the mass balance for one type of substance k (see Baumgärtner and de Swaan Arons 2003, footnote 5, p. 121). However, the balance is here extended to cover the different types of residuals r containing the substance k. The second line shows the total mass balance for a production unit. In the case k is only appearing in a single type of residual, i.e., r = 1, then c_rk = c_k. However, the distribution on different types r for substance k may change, as when a combustion process transforms the material inputs, and temperature, pressure, supply of oxygen, etc., vary. Variable mix of types of emissions all containing a common substance implies inefficiency in some of the operations.

The creation of residuals during the production process also contain materials provided free by nature: oxygen for combustion processes and oxygen decomposing organic waste discharged to water (biological- and chemical oxygen demand, BOD and COD, respectively), nitrogen oxides created during combustion processes, and water for pulp and paper that adds to the weight of residuals discharged to the environment. Such substances must either be added to the left-hand side as material inputs - and then contained in the residuals z - or we can focus on the actual materials in inputs and redefine z accordingly, like calculating the carbon content in weight for all three types of variables and not measure residuals as CO₂ or CO, etc. This is what we have done in Eq. (1).

For each production unit we have an accounting identity for the use of materials contained in the input x_Mj. The relation holds as an identity, meaning that it must hold for any accurately measured observation, being efficient or inefficient. The relation should not be regarded as a production function, but serves as a restriction on specifications of these.⁸

The importance of the materials balance is the insight that generation of unintended residuals cannot be avoided. However, measuring all the factors involved in the materials balance accurately may not be so easy, especially on the more aggregated level that is commonly used in efficiency analyses. If we accept that residuals are measured accurately, we know that all observations of production units, efficient as well as inefficient units, must obey the materials balance as an identity. If we do not have observations, but data that are theoretical it may not be feasible to assign the materials balance accurately to hypothetical observations based on observed ones.

3 Early models for production of intended and unintended outputs

3.1 The Shephard model

The theoretical model in Shephard (1970) for producing simultaneously intended and unintended outputs⁹ based on assuming weak disposability has up to now completely dominated the empirical literature on efficiency for that case. The general point of departure in the literature is to represent the technology by formulating the general production possibility set T:

$$T = \left\{ {\left( {y,z,x} \right)\left| {y \ge 0\,{\mathrm{and}}\,z \ge 0\,{\mathrm{can}}\,{\mathrm{be}}\,{\mathrm{produced}}\,{\mathrm{by}}\,x\, \ge \,0} \right.} \right\}$$

(2)

The variables are regarded as vectors. Here y is the intended output vector, z is the unintended output vector and x is the vector of inputs. The production possibility set is conventionally defined as containing all known possible ways of producing given outputs. Assumptions about specific properties, presumably based on a combination of how the real world functions, and the practical and analytical needs for simplifications, are stated so many times in the literature that this is skipped here. Main properties are that the set is assumed to be convex, closed, and allowing no free lunch. (See Coelli et al. (2005) for an elementary introduction and Cooper et al. (2007) for a more advanced treatment.) It is rather obvious that if no material inputs are consumed, no material residuals will be generated.¹⁰

The technology set Eq. (2) can equivalently be represented by the output set P(x) or input set L(y, z):

$$\begin{array}{l}P\left( x \right) = \left\{ {\left( {y,z} \right)\left| {\left( {y,z} \right)\,{\mathrm{can}}\,{\mathrm{be}}\,{\mathrm{produced}}\,{\mathrm{by}}\,x} \right.,\left( {y,z,x} \right) \in T} \right\},\\ L\left( {y,z} \right) = \left\{ {x\left| {{\mathrm{at}}\,{\mathrm{least}}\,x\,{\mathrm{is}}\,{\mathrm{required}}\,{\mathrm{to}}\,{\mathrm{produce}}\,\left( {y,z} \right)} \right.,\left( {y,z,x} \right) \in T} \right\}.\end{array}$$

(3)

Usual assumptions on the sets are that the output and input sets are closed sets and that the output set is bounded. The boundary of the sets represents efficient operations. If the efficient operations could be formulated by a function this function would represent the frontier production function, and the output- and input isoquants would belong to this frontier function. Points in the interior of the production possibility sets are inefficient per definition.

It is obvious that the general characterisations of the production possibility set T and output- and input sets are not meant to tell us about the nature of the joint production involved. However, output- or input distance functions are introduced as representation of technology. Since the formulations of technology using distance functions do not exclude assorted production, restrictions must be introduced ruling out such a form of joint production, as will be explained below.

3.2 The weak disposability assumption and null-jointness

A way out of the assorted production problem was introduced in Shephard (1970) formulating weak disposability between the intended and unintended outputs in Eq. (4a):

$${\mathrm{If}}\,\left( {y,z} \right) \in P\left( x \right),\,{\mathrm{then}}\,\left( {\theta y,\theta z} \right) \in P\left( x \right)\,{\mathrm{for}}\,0 \le \theta \le 1$$

(4a)

and Eq. (4b) is null-jointness of outputs (Shephard and Färe 1974):

$${\mathrm{If}}\,\left( {y,z} \right) \in P\left( x \right)\,{\mathrm{and}}\,z = 0\,{\mathrm{then}}\,y = 0$$

(4b)

These two conditions are adopted in the subsequent literature. However, although there is an extensive discussion of joint production also involving undesirable outputs in Shephard (1970, Section 9.5), assorted production is not mentioned or recognised as a problem; the concern is about disposability properties of the two types of outputs. The condition Eq. (4a) says that if realisations of the two types are reduced proportionally, then the new points will belong to the production possibility set P(x).¹¹ The consequence of assumptions Eqs. (4a, b) is illustrated by the original Figure 32(a) in Shephard (1970, p. 188), here Fig. 1. The solidly drawn frontier segments are efficient parts of the output sets, according to Shephard (1970), and the thin lines starting from the origin show that the intended output (here u₂) and the unintended one (u₁) have what in Shephard and Färe (1974) is called null-jointness. We see that any point on the efficient parts of the thick lines satisfies the conditions Eq. (4a, b), due to convexity of the sets and no free lunch, in the case of two outputs and one input. On the thin lines from (or to) the origin proportionality holds.¹²

Fig. 1

Output sets P(x) obeying weak disposability for outputs u₁ (undesirable) and u₂ (desirable) for given levels of inputs x. Source: Shephard (1970, p. 188)

The point $\overline u$ and the line to the origin of the set $\overline P \left( x \right)$ represents the case of a constant relationship between the intended and unintended outputs and thus conforms to extreme jointness that will be defined in Subsection 4.1.

Shephard was “concerned with technologies which yield several different joint products for a given input vector of the factors of production.” Furthermore, he “refer[s] to the technical relationship between the inputs and outputs as a production correspondence” (Chapter 9.1, p. 179), and defines the efficient subset E_P(x) of an output set P(x) and the efficient subset E_L(y) of an input set L(y) (p. 180) that may not contain all points on isoquants.

Shephard did not expand on how to measure efficiency. However, his concept of distance functions¹³ correspond to Farrell (1957) radial efficiency measures. As mentioned in Section 1 the empirical use of the theoretical model of Shephard was first implemented empirically in Färe et al. (1986); (1989). Distance functions are used in estimating efficiency scores within the strand of Shephard-inspired modelling.

3.3 Types of distance functions

The radial output-oriented distance function is defined as

$$\begin{array}{l}D_o\left( {x,y,z} \right) = \min _\theta \left\{ {\theta :\left( {y/\theta ,\,z/\theta } \right) \in P\left( x \right)} \right\},\\ \qquad\quad\ 0 \le D_o\left( {x,y/\theta ,z/\theta } \right) \le 1\end{array}$$

(5a)

It is obvious that maximising also the unintended output does not make much sense measuring efficiency relative to a boundary of the production possibility set. Färe et al. (1989) introduced the hyperbolic distance function to overcome this problem:

$$\begin{array}{l}D_o^H\left( {x,y,z} \right) = \min _\theta \left\{ {\theta :\left( {y/\theta ,\,\theta z} \right) \in P\left( x \right)} \right\},\\ \qquad\qquad\!\! 0 \le D_o\left( {x,y/\theta ,\theta z} \right) \le 1\end{array}$$

(5b)

The projection to the frontier of an inefficient unit is weighting unintended output z with the inverse of the weighting of the intended output y.

The output oriented directional distance function $\overrightarrow D _o$ has been the preferred model after being introduced in Chung et al. (1997):

$$\begin{array}{l}\overrightarrow D _o\left( {x,y,z;g_y, - g_z} \right) = \max _\beta \left\{ {\beta :\left( {y + \beta g_y,z - \beta g_z} \right) \in P\left( x \right)} \right\},\\ \qquad\quad\,\,\,\overrightarrow D _o\left( {x,y,z;g_y, - g_z} \right) \ge 0\end{array}$$

(5c)

Instead of a radial direction of projections to the frontier of inefficient points, a projection point is found by adding to the observed intended output following a chosen direction g_y and a subtracting from the observed unintended output following the direction g_z. In Eq. (5c) it is most common to set the directional vector g = (g_y,-g_z) to (y,-z) or (1,−1). However, the projection to the frontier is crucially dependent on the existence of an isoquant between intended and unintended outputs. Assuming differentiability, as is often done (Färe et al. 2013, p. 111), then $\left( {\partial \overrightarrow D _o\left( {x,y,z;g_y, - g_b} \right)/\partial z} \right)/\left( {\partial \overrightarrow D _o\left( {x,y,z;g_y, - g_b} \right)/\partial y} \right)$ is the rate of transformation between the good and the bad for given inputs. This ratio is used for estimating shadow price of the residual (Färe et al. 2013, Eq. (12), p.111), and the isoquant curve is illustrated there and in numerous papers by Färe et al. and other authors of similar models. All distance functions above are single equations.

3.4 The externality model of Baumol and Oates

In Baumol and Oates (1988) (first edition 1975) that has been an influential book on environmental economics, both desirable and undesirable outputs were introduced in the context of an environmental externality model. Although inefficiency aspects and efficiency measures were not discussed, their externality model is interesting because it led to a discussion later whether unintended outputs are inputs instead. A production possibility set was specified by using a single transformation function relation $F\left( {y,z,x} \right) \le 0$ extended with residuals vector z where y is the intended output vector, and x the input vector.¹⁴ The relation $F\left( {y,z,x} \right) = 0$ defines the boundary of the set and is called the transformation relation. This is an implicit representation of efficient combinations of variables that we call the frontier.¹⁵ Inefficient points yield function values$F\left( {y,z,x} \right) \ < \ 0$.¹⁶ However, Baumol and Oates (1988) do not study inefficiency, but are only interested in the frontier. In economics, it is commonly assumed that the transformation function is differentiable and have continuous partial derivatives of first and second order. This is also the case in Baumol and Oates (1988). In addition, it is also common to assume that the requisite assumptions of the implicit function theorem hold. A standard convention is that increasing an output at a frontier point will increase the function value, and increasing an input from a frontier point will decrease the function value. We then have $F_y^\prime \ > \ 0,F_x^\prime \ < \ 0$¹⁷. This signing conforms to regarding y and x as being freely disposable. The question is how to sign the partial derivative of the residual. Differentiating the transformation function w.r.t. y, z and x, assuming for simplicity single variables of each type, yields:

$$\begin{array}{l}F_y^\prime \left( {y,z,x} \right)dy + F_x^\prime \left( {y,z,x} \right)dx = 0 \Rightarrow {{dy}}/{{dx}} = - {{F_x^\prime}}/{{F_y^\prime}}> \ 0\\ F_z^\prime \left( {y,z,x} \right)dz + F_x^\prime\left( {y,z,x} \right)dx = 0 \Rightarrow {{dz}}/{{dx}} = - {{F_x^\prime}}/{{F_z^\prime}}\\ F_y^\prime \left( {y,z,x} \right)dy + F_z^\prime \left({y,z,x} \right)dz=0\Rightarrow {{dy}}/{{dz}} =-{{F_z^\prime}}/{{F_y^\prime }}\end{array}$$

(6)

The first relation defines the standard positive marginal productivity of the input x. If $F_z^\prime \ > \ 0$ for the unintended output in the second line an increase in the input x will also give an increase in the unintended output. Thus, having $F_z^\prime \ > \ 0$ is not a property our model should have, given that the unintended output is an environmental pollutant. Assuming assorted production, this problem is solved reallocating all resources to producing the intended output y and zero unintended output (Førsund 2009). However, it clearly goes against the main problem with joint production of intended and unintended outputs that generation of the unintended outputs is unavoidable.

Assuming that the partial derivative of F(.) with respect to the unintended output is negative, i.e. as if z is an input, we see in the second line that this implies that there is a substitution between the input x and the variable z; increasing x reduces z. However, if x is a material input z cannot be reduced if x increases. This goes against the materials balance that tells us that z increases if material input increases.

Furthermore, adopting the positive sign of the unintended output the third relation shows a trade-off between the intended and the unintended outputs; if one of them increases, the other has to decrease. But this is what happens when assuming assorted production and then optimality implies that z is set to zero, and this is impossible given that z is unintended.

The residual z is not only unintended, but also unavoidable. The firm has no choice but to produce the pollutant. The negative trade-off appearing when both partial derivatives of y and z are positive cannot be realised except in the case of assorted production. If this is the case, then reallocating resources can reduce the residual z in order to producing more of the intended output y. But this is per definition the type of joint production that is not possible in the case of unintended outputs; the joint production cannot be assorted production when an output is unintended, but must either be the type technical jointness or extreme jointness.

However, Baumol and Oates (1988) do not discuss the implication of the type of jointness. They “solve” the dilemma - without informing the reader - simply by assuming that the partial derivative of the residual is negative; $\partial F/\partial z \ < \ 0$ (see Table 4.1, in Baumol and Oates (1988, p. 39), as if the residual is an input. Then we have $- F_z^\prime /F_y^\prime \ > \ 0$. An increase (decrease) in z now increases (decreases) y. To reduce the residual generation z at a frontier point is costly in terms of reduced intended output y. However, the residual is definitely an output and not an input. What is missing here is the fact that there is no direct substitution between the two types of outputs when we have technical jointness. The generation of both types of outputs occurs simultaneously by use of a given set of inputs. There is no interaction possible between the two types of outputs for fixed inputs. Assuming that our three variables are all single, then we have the classical definition of efficient production that for given input x output y is maximised. To treat the residual just as a normal output does not make sense, because the production cannot be efficient if the pollutant is to be maximised. The opposite is the case; efficient production implies that the residual has to be as small as the technology allows for given resources in order to maximise intended output. Regarding z as an input does not work because substitution between x and z as inputs for given intended output is impossible according to the materials balance.

There is a confusion here in the literature. A standard mistake is to disregard the micro setting of production and thinking at a more aggregated level implying the resources can be used to abate pollution and thus take resources away from production of intended output. However, at the micro level, a firm’s use of resources must be explicitly specified, and this is not the case in literature claiming the unintended output is an input (see Førsund (2009) for a critique of the assumption that the unintended output can be treated as an input).

4 Production functions satisfying technical jointness

The type of joint production is crucial to construct a model generating both intended and unintended outputs. Although there is a Chapter 9.5 devoted to joint production in Shephard (1970), the nature of joint production when dealing with unintended outputs is not discussed there or in many of the subsequent papers following the Shephard (1970) approach of introducing weak disposability and null-jointness. The lack of clarification of the nature of joint production when desirable and undesirable outputs are produced, may be a key reason for the Shephard-inspired approaches developing unsatisfactory modelling of efficiency for intended and unintended outputs. A short exposition of joint production therefore seems to be warranted.

4.1 Joint production

Frisch (1965, Chapter 14a-d, pp. 269–281) devoted a chapter to multi-output production and started with defining joint production.¹⁸ He stated (p. 269) that “… the production law cannot be studied separately for each separate product, but must be considered simultaneously for all connected products.” He introduced a system of relations:¹⁹

$$F^i\left( {y_1,...,y_m,x_1,...,x_n} \right) = 0,\,i = i,...,\mu$$

(7)

The µ relations are assumed to be independent of each other. He introduced three types of joint production. The types are:

• (a) Assorted production: Inputs can be applied alternatively to produce different products; agricultural land can be used for different crops, a wood cutting machine can be used to making different objects. An assortment of outputs is produced during a production period. The inputs are then output-specific. The technical connection between outputs making it joint production is that the same types of inputs are used to produce the outputs.²⁰

• (b) Technical jointness: Standard classical examples are given by agricultural production; sheep yield mutton and wool, hens yield eggs and poultry, growing wheat also yields straw, and coke and gas is gotten from coal as input, to name a few classical examples. The connections between outputs are also based on common inputs as for assorted production. The main difference to assortment is that the inputs are not product specific; it is not possible to reallocate inputs to different outputs. However, the mix of outputs can change if the mix of inputs changes; examples in Frisch (1965) are change of feed to hens changing the mix of eggs and poultry meat, and changing types of sheep from a type of high share of wool compared with meat to the opposite.

• (c) Extreme jointness: Fixed proportions between outputs independent of inputs as in distillates of crude oil, and pure factor bands, i.e., relations between factors independent of outputs. The former case is called complete [product] coupling in Frisch (1965, p. 273). If we assume fixed input-output coefficients as in the Leontief input – output case this case belongs to the category of extreme jointness.

However, unintended outputs are not mentioned in Frisch (1965). Examples from today’s industrial activities using material inputs generating residuals are ubiquitous, e.g., pulp and paper industry, steel production industry, cement, oil refineries, fossil fuel-based electricity generation to mention just a few.²¹

The classical writers²² introduced three types of outputs; intended outputs that have positive prices in a market, by-products that also have positive prices, but contribute rather less to the revenue, and waste that has no economic value. The examples above do not connect waste to intended products. However, Jevons (1883, p.144)²³ remarks

“The waste products of a chemical works, for instance, will sometimes have a low value; at other times it will be difficult to get rid of them without fouling the rivers and injuring the neighbouring estates; in this case they are discommodities and take the negative sign”

He included many forms of industrial production as examples of all three types of outputs.

In the case of assorted production, resources can be reallocated among outputs. If this reallocation is without limits unintended outputs will, of course, be set to zero by an efficient producer (Førsund 2009). We must have the case of technical jointness (including extreme jointness) in order to generate unintended outputs. The consequence of generating an unintended output is thus that a firm operating a technology efficiently, will by definition generate as little as possible of the unintended output; the minimum dictated by the technology used given the input quantities. The material inputs are used to produce intended outputs, and materials contained in the residual come at the expense of producing them. To be efficient in producing an intended output for given inputs there is a minimum of an unintended output that is unavoidable according to the second law of thermodynamics. The materials balance (Eq. (1)) shows the split of material inputs on intended and unintended outputs.²⁴ It is meaningless to split non-material inputs on intended and unintended outputs because the generation of intended and unintended outputs take place simultaneously; technically, there is only a single common process. Unintended residuals cannot be generated in physically separate processes from intended outputs or in separate stages. When formulating production relations this must be taken seriously. When engineers construct a best practice technology for producing the intended outputs, then unavoidable unintended output is also generated, but at a minimum level given the inputs generating the intended output.

4.2 Factorially determined multi-output production functions

When joint production was discussed in Frisch (1965, pp. 270–276), he introduced just a type of technical jointness that fits our case. He named the type as factorially determined multi-output production. This type of production function is formulated by separation of outputs introducing a production function for each output i, all having the same n inputs:

$$y_i = f^i\left( {x_1,...,x_n} \right),\,\,\left( {i = 1,...,m} \right)$$

(8a)

Frisch considered only intended outputs with positive demand and specified traditional production functions for them. He did not introduce unintended outputs. However, I find that his scheme can also be applied to unintended outputs and have separate functions (given another function symbol g for ease of recognition):²⁵

$$z_k = g^k\left( {x_1,...,x_n} \right),\,\,\left( {k = 1,...,u} \right)$$

(8b)

where u is the number of unintended outputs. There is a separation of both intended and unintended outputs making it possible to estimate separate functions. However, the outputs are unavoidably joint because the input bundle is identical for all m + u production functions.

The unintended outputs are of a different nature than the classical example of technical jointness of wool and mutton where both outputs are desirable and have a positive market demand. The residual in that example may be the sheep excrements.²⁶ Another classical example of joint production is that a cow gives milk and also meat and hide; all three marketable goods,²⁷ but the emission of methane gas during digestion is a pollutant with climate-change effects. This output is unintended and unavoidable.

The importance of the factorially determined multi-output system is twofold; the common use of inputs for the production of all outputs make the functions the type of technical jointness, and the separation of outputs facilitates the estimation of each production function. This is in contrast to the single equations of distance functions in Eq. (5) and the single Baumol and Oates (1988) transformation relation in Subsection 3.2.

In order to illustrate the model in the simplest way I specify only two outputs, y and z, and two inputs, x_M and x_S (the number of intended and unintended outputs and factors of production can easily be extended as shown above in Eqs. (8a, b)). However, the arguments in the functions Eqs. (8a, b) consists of two types, the material outputs x_M and the service outputs x_S. The functions fⁱ(.) have normal substitution between the two types of inputs in the substitution region. However, the functions g^k(.) is only influenced by the material input x_M due to the materials balance; the materials in z can only come from the material inputs.²⁸ The system of equations then reads:²⁹

$$\begin{array}{l}y = f\left( {x_M,x_S} \right),f_{x_M}^\prime ,f_{x_S}^\prime \ > \ 0,\,f_{x_M}^{\prime \prime} ,f_{x_S}^{\prime \prime}\ < \ 0\\ z = g\left( {x_M} \right),\,\,g_{s_M}^\prime \ > \ 0, \ g_{xM}^{\prime \prime} > \ 0\end{array}$$

(9)

In the factorially determined multi output scheme each output has typically a unique set of isoquants in factor space. Joint production means simultaneous determination of common input levels generating the outputs. The intended output function has the usual property of positive but decreasing marginal productivities within the substitution region. The unintended output function does not have substitution as in the normal case of the intended output due to only x_M being the input.

Shephard (1970, p. vii) has the following statement about production functions:

“… the central topic [of production functions]³⁰ being an understanding of the possibilities of substitution between factors of production to achieve a given output.”

Accordingly, I will focus on the isoquants in the factor space for production functions. The marginal rates of substitution for the production of the intended- and unintended output in Eq. (10) are:

$$\begin{array}{l} - dx_S/dx_M = {{f_{x_M} \left( {x_M,x_S} \right)}}/{{f_{x_S} \left( {x_M,x_S} \right)}} \ > \ {\mathrm{0}}\,\, \Rightarrow \, \\ dx_M = - ({{f_{x_S} \left( {x_M,x_S} \right)}}/{{f_{x_M} \left( {x_M,x_S} \right)}})dx_S \ < \ {\mathrm{0}}\end{array}$$

(10)

In Eq. (10) we have the standard situation of a positive rate of substitution with an increase in x_S generating a negative change in x_M along an isoquant. The unintended output z is generated only by the materials input. If we can call it an isoquant in a two-input case it has to be vertical, as will be shown in Fig. 2.³¹

Fig. 2

Isoquants for the production of y and z, and max-min values of z

The production functions for intended outputs are assumed to have the standard properties of a neoclassical production function with positive (but decreasing) marginal productivities of inputs implying substitution possibilities. The two functions in Eq. (9) are frontier functions. When considering substitution along an isoquant of f(.) in factor space there is a relation between the inputs keeping the value of the f(.) function constant. Regarding e.g. cost minimisation as economic adaptation of the firm implies that the choice of input levels for given intended outputs depends on the price ratio between the inputs (assuming no external regulation of z). The choice of a factor point (x_M, x_S) for the production of the chosen level of y then also determines the level of residual z.

Since the two production function types represent frontier functions the intended output y is maximal for given inputs, and the unintended output is minimal. The materials balance in Eq. (1) shows the distribution of mass in material inputs on intended and unintended outputs³². There are the usual possibilities of substitution of service for material inputs when producing intended outputs.

Introducing inefficiency, we have the two inequalities for a unit i belonging to N homogenous units in an industry having the same common frontier functions f(.) and g(.) for all units:

$$\begin{array}{l}y_i \le f\left( {x_{Mi},x_{Si}} \right),\\ \overline z _i \ge z_i \ge g\left( {x_{Mi}} \right),\,i = 1,...,N.\end{array}$$

(11)

Here $\overline z _i$ is the total material contained in x_Mi. If we consider only one type of substance for convenience, we have from the materials balance Eq. (1) that $\overline z _i = ax_{Mi}$. Obviously, the maximal amount of residual cannot be greater than this amount, but will be less if the intended output contains materials. Inefficient use of resources producing the intended output results in less intended output than realised on the frontier f(.). At the same time more of the unintended output is produced than what will be produced on the efficient frontier g(.). Efficient use of resources implies that both intended output and unintended output are at efficient levels simultaneously.

Regarding disposability properties of the frontier functions the intended output and the two inputs in the f(.) function are freely disposable, but this is not the case for the unintended output and material input in the g(.) function; z can only be reduced by reducing x_M. This is costly because y is then also reduced.³³ Without abatement, another option is to reduce the unintended output reducing x_M by substitution with x_S keeping the intended output constant, but then input cost is increasing and thus profit decreasing.

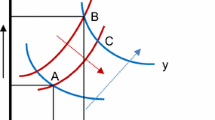
As pointed out by Shephard (1970, p. vii) substitution properties are important. On pp. 193–194 he illustrates for single valued production function with weak and strong disposal, respectively, of outputs, isoquants in input space. However, the linear segments have almost the same shape with non-positive slopes. Few other efficiency papers exhibit substitution possibilities in input space. The substitution possibilities for the production functions in Eq. (9) and consequence of choice of a common input point are shown in Fig. 2. There are two isoquants for the intended output, AB and CD. As exhibited in Fig. 2, I draw only the part of isoquants within the substitution region for the intended output. The blue curved lines are traditional textbook isoquants for the intended good y with typical text-book curvature.³⁴ The level of the intended output increases in the northeast direction. The start of the substitution region is at the origin. The substitution will be narrow at the beginning and getting wider the more inputs employed. However, the substitution region will typically be rather narrow in general. Increasing the service input on the frontier function isoquant keeping the output constant will reduce the use of the material input. Increasing a service input like labour results in more efficient use of raw materials thus needing less of them.³⁵

The input levels of x_M are common both for intended and unintended outputs, but x_S only common for intended outputs. To choose one point in factor space both outputs are determined, as in the intersection point I on the intended isoquant AB and a dotted vertical line representing the z value. If the objective of the production unit is cost minimisation for a given a level of the intended output, and prices of both types of inputs are positive, then a point in the substitution region of the intended output will be chosen. This situation is illustrated in Fig. 2 by point I. It is only the level of x_M that determines the level of unintended output z. This is also the case for the by-production model presented in the next Subsection 4.3.

Obviously, dealing with material inputs there must be limitations on the substitution possibilities. It follows from the materials balance that the possibility for substitution between the material inputs x_M and the service inputs x_S as shown in Eq. (10) must be limited for a given level of the intended output. This means that the length of the isoquants may be rather short compared with textbook illustrations, where isoquants often cover the entire first quadrant. I have tried to capture this by setting limits for intended output isoquants by the levels z^min and z^max for the unintended output.³⁶ By definition, if we consider points B and C in Fig. 2, the intended output isoquants must be vertical at these points; the partial derivative of the service input is then zero: $f_{x_S}^\prime = 0$. It is not possible to produce more intended output by increasing the service input. At the other end of the isoquants the partial derivatives of the material input is zero, $f_{x_M}^\prime = 0$ and the isoquants are horizontal at these points like at A and D. It is not possible to produce more intended output by increasing the material input. The “min” and “max” values of the unintended output delimits the substitution region of the isoquants of the intended output as indicated by the straight lines.³⁷ The limits are not dictated by the intended or unintended outputs as such; the outputs y and z are independent of each other, but both are determined by the input levels that are chosen. I have assumed in Fig. 2 that the length of isoquants increases with the amount of material inputs. This seems to be reasonable given the signing of derivatives, but is not essential for my story.

Using the notation z^min should not be misunderstood to mean that this is the minimum of the unintended output for all realisations of the amount of the intended output. The amounts z^min and z^max give the individual range of the unintended output for each isoquant for the intended output. Remember that it is assumed that we are at the frontier function of both types of outputs; any z-value at a point on a y isoquant is the minimum value for the chosen amounts of inputs. It is not of economic interest to consider points outside the substitution region. Without any regulation of the generation of residuals, profit maximisation or cost minimisation are solely based on determining the optimal levels of the intended output and the two inputs (in the cost minimisation case only the level of inputs needs to be determined).

Let us start at point A with $f_{x_M}^\prime = 0$ in Fig. 2. The efficient amount of the unintended output (i.e. the minimum of z for the level of inputs at A) is given by the z^max level at this point. Moving to point B along the intended output isoquant utilising the substitution possibilities, the use of material input decreases from A’ to the smallest possible level at B’ with $f_{x_S}^\prime = 0$ at B. The service input has increased considerably more to realise the minimal generation of the unintended output while keeping the level of the intended output constant (see the two arrows indicating the changes along the axes). Point B has the minimal amount of the unintended output for the given level of the intended output. All levels of the unintended output along the isoquant for the intended output are minimal for the varying mix of inputs.

Point D (with $f_{x_M}^\prime = 0$) exhibits a larger z^max than point A and a higher level of the service input x_S (it seems reasonable when the intended output increases to increase both inputs). The isoquant ends at point C (with $f_{x_S}^\prime = 0$) that has a larger z^min than at point B.

The material input is essential in the production functions in Eq. (9); zero material input implies zero production both of the intended output and the unintended one. In the case of only two inputs in Eq. (9) it is also the case that x_S is essential and outputs are zero if x_S is zero and x_M positive:

$$\begin{array}{l}f\left( {x_M,x_S} \right) = \,\,g\left( {x_M,x_S} \right) = 0\,\,{\mathrm{for}}\,\,x_M = 0\,\,{\mathrm{and}}\,\,x_S \ > \ 0,\\ {\mathrm{and}}\,\,{\mathrm{for}}\,\,x_S = 0\,\,{\mathrm{and}}\,\,x_M \ > \ 0\end{array}$$

(12)

Frisch (1965, Fig. (14b.2), p. 272) points out that if the isoquants are separable then it is possible to choose producing more of one output and less of the other by changing the input mix. The situation in the output space can be illustrated in Fig. 3 using the points exhibited in the factor space in Fig. 2. All five points have different levels and mix of inputs. As can also be seen in Fig. 2 points A, B and I have the same level of intended output y, and C and D have the same higher level of the intended output. As to the levels of the unintended output z all points have different levels, starting with the lowest level at B and then successively increasing levels at I, C, A and D. The consequence of having technical jointness as the type of joint production implies that there are just output points in the output space. To make connection lines between the output points in the form of isoquants or trade-off curves for given inputs is not possible. According to the special variant of technical jointness, inputs have to change to generate different levels of outputs. Technical jointness blocks the possibility of isoquants in the output space because inputs cannot be kept constant along an isoquant in output space.

Fig. 3

Points in output space corresponding to the points in Fig. 2

4.3 The by-production model

Starting out with a single transformation relation similar to the Baumol and Oates (1988) model in Subsection 3.2, using the implicit function theorem, it is stated in Murty et al. (2012, p.120) ³⁸ that there seems to be some inconsistencies concerning the relationship between z and y, and between z and x_M. This correspond to the discussion of Baumol and Oates (1988) in Subsection 3.2, Eq. (6).

Murty et al. (2012) then introduced a model with separate production possibility sets for intended outputs and unintended outputs and called it the by-production approach. In the most simple case for the intended output they operate with one transformation relation involving two inputs; the non-material input x_S and the material input x_M (using my notation), and two outputs; the intended (traded) output y and an intended abatement output y^a for internal use.³⁹ The second relation is for the generation of the net pollutant z using two inputs; the material input x_M and the abatement output y^a from the first process.⁴⁰ The functional representation of the frontier functions is:⁴¹

$$\begin{array}{l}f\left( {x_S,x_M,y,y^a} \right) = 0,\,\,\,f_i\left( {x_S,x_M,y,y^a} \right) \le 0,\,\,i = x_S,\,x_M\\ f_y\left( {x_S,x_M,y,y^a} \right) \ge \,0,\,\,\,f_a\left( {x_S,x_M,y,y^a} \right) \ge 0\\ z = g\left( {x_M,y^a} \right),\,\,\,\,g_{x_M}\left( {x_M,y^a} \right) > 0,\,\,\,g_a\left( {x_M,y^a} \right) \, < \, 0\end{array}$$

(13)

We notice that the value of the f(.) function is independent of the level of z, and th at the g(.) function is independent of the level of y. In Murty and Russell (2018), the same type of model is used (abatement output y^a is now called a, I keep the notation y^a here).

The type of the first transformation relation f(.) = 0 in Eq. (13) may be a case of assorted production; the resources can be reallocated to the two types of intended outputs; output for sale and abatement output for internal use.⁴² Assuming a single raw material used for both the two intended outputs the residual generation is the same. (However, it may be more realistic that the two outputs are using different raw materials. Then we may also have two different types of unintended outputs.) When this is the case, it should be stated if the generation of residuals is the same per unit of the two outputs or different. The production function in the third line of Eq. (13) for the residual z is influenced only by material input x_M and abatement output, now in the role as input. In the transformation function for the intended outputs there is a substitution possibility for inputs due to the assumption about derivatives in the first line of Eq. (13).

In the empirical part of Murty et al. (2012, Subsection 6.2, p. 130) an output oriented non-radial efficiency index named Färe–Grosskopf–Lovell (FGL) index (Färe et al. 1985) is used. This index is formulated separately for the intended and unintended output in Eq. 6.1 and 6.2, respectively. The efficiency score for the total by-production technology is calculated as the average of the two scores for each of the two technologies. Annual data for 92 coal-fired electric power plants from 1985 to 1995 are used.⁴³ Mean efficiency indices under the technology weak disposability of the type hyperbolic and FGL, are compared with the same indices with by-production technology for all years.

In Section 7 of Murty et al. (2012), a DEA version with producing abatement output y^a is shown for the by-production technology and for the two separate technologies. An artificial dataset for the variables x, y^a, y, z for eight units is used when calculating efficiency scores. It is pointed out that the technology for (y^a, z) (here y^a is an input) is independent of y and the technology for (y^a, y) is independent of z, with y^a as an output.

Dakpo et al. (2016); Dakpo and Ang (2019); Murty and Russell (2017) have extensive reviews of the by-production approach. The approach is implemented empirically in Murty et al. (2012); Dakpo et al. (2017); (2018); Arjomandi et al. (2018); Aparicio et al. (2020) (however, abatement is not used). Murty and Nagpal (2019) also present a comprehensive review of the by-production model, and apply this model to an empirical study of Indian electricity coal-fired electricity producers. They have key critical remarks about Shephard-inspired technologies.

The by-production model is quite close to the factorially determined multi-output model in Subsection 4.2 regarding the splitting into two types of production functions. However, the two model types are based on different arguments. The factorially determined multi-output model was introduced by Frisch (1965) as a variant of his general multi-output model Eq. (7) for technically connected outputs. Production functions are specified for each output, thus separating outputs. Technical jointness is maintained by having the same bundle of inputs in all functions. Only intended outputs were considered, but an extension to include unintended outputs as done in Subsection 4.2 seems obvious (but need a modification as to the role of service inputs as seen in Eq. (9)).

The fundamental reason for having two types of production functions in the by-production model according to Murty et al. (2012) is based on the different disposabilities of production of intended and unintended outputs.⁴⁴ As expressed in Murty et al. (2012, p. 119):

“… the by-production technology, which is an intersection of the intended-production technology and nature’s residual-generating technology, violates standard disposability with respect to goods that cause (or affect) pollution generation and exhibits costly disposability with respect to pollution.”

The by-production papers Murty et al. (2012); Murty (2015); Murty and Russell (2017); (2018) have rigorous mathematical treatment of assumptions or axioms, and in the last three papers prove theorems about necessary and sufficient requirements for an emission-generating technology to be of the by-production type (see also Dakpo and Ang 2019). Thus, these analyses give more general results and insights than the specification in Subsection 4.2.

4.4 The network representation of pollution-generating technologies

Production of goods may involve several activities producing intermediate products serving the final outputs within a firm using a proper time period. It may be of interest to study the efficiency of such intermediate stages. Such models were termed network models in the seminal paper by Färe and Grosskopf (1996). In order to go from the criticised single equation model to a multi-equation one, Bostian et al. (2018) present a network model for a multi-equation model for intended and unintended outputs. However, the danger is that a network model is closely associated with production in stages. The general insight of technical joint production is that all outputs—intended as well as unintended—are produced simultaneously and not in stages in different periods.

4.5 Abatement

There are two main possibilities for how to abate, the first one being internal technical changes not regarded as major changes, as discussed in Porter and van den Linde (1995). Some measures are short-run measures like improved process control, small-scale re-engineering, introducing more internal recycling of waste, etc. All such measures lead to improved efficiency of utilising material inputs and thereby reducing pollutants (Førsund (2018a, b, c). The second possibility is to introduce end-of-pipe technologies most popular in environmental economics (see e.g. Førsund (2009, pp. 28–30); (2018a, pp. 80–82); (2018b, pp. 58–61); (2018c, pp. 299–300)).⁴⁵ Although the first possibility may be the most used one in practice, it is usually very difficult to get data for internal abatement activities of the types mentioned. Short-run changes in technology may be mistaken for more long-run changes, and allocation of inputs such as labour on activities may not be recorded or even not be possible to distinguish. On the other hand, there are better possibilities to get data for end-of-pipe abatement due to the distinct separation of activities. However, end-of-pipe is not necessarily a unit separated from the main production equipment. I regard e.g. scrubbers and electrostatic filters on smokestacks as end-of-pipe because primary pollutants are inputs in these processes, and capital equipment and inputs like lime or chemicals do not interfere with the production of intended outputs, or play any role in that production. End-of-pipe abatement transforms primary pollutants into usually harmless residuals and sometimes to by-products that have market value (Porter and van den Linde 1995).

Polluting firms often have capital equipment with embodied technologies. When reducing environmental pollution became a policy priority in the early 70s adding end-of-pipe equipment was seen as a more realistic and economic alternative for existing firms than requiring development of new technology reducing waste. However, in the long run technology changes focussing on reducing generation of pollutants (i.e. prevention) would often be the most effective and the most economic measure.

Internal measures typically change technology. However, a popular measure due to regulation imposed by policy makers not changing the technology is to substitute cleaner inputs for more polluting ones, like using lighter oil for heating purposes, and using natural gas instead of coal in electricity generation.

The nature of the abatement is rather hidden in Murty et al. (2012); Murty and Russell (2018). What I have called internal abatement (called prevention in the literature) is not mentioned, but the role of y^a in Eq. (13) appears as prevention. As far as I know the internal type of abatement in the by-production model has not been implemented empirically in the literature. The papers mentioned above have relevant examples of end-of-pipe abatement, but it is not so easy to see that the formulation in (11) of two types of production functions can be turned into three separate equations as required introducing end-of-pipe abatement proper (Førsund 2018a, b, c).

In the environmental economics literature substitution between inputs as mentioned previously and end-of-pipe are the typical abatement options modelled. The latter option distinguishes between primary and secondary pollutants (or uncontrolled and controlled pollutants as used by EPA, or gross and net used in Murty and Russell 2018). In end-of-pipe abatement, primary pollutants are used as inputs. This feature seems to be absent in the abatement specification in Murty et al. (2012); Murty and Russell (2017); (2018).

5 The critique of the Shephard-inspired literature

I use the Shephard Fig. 1 with two outputs and one input as the departure for my critique. Two restrictions are put on the technology; weak disposability and null jointness. The latter restriction drives the shape of the isoquant curves in the figure. The isoquants curves must start at the origin, thus giving the positive slopes of the efficient output isoquant segments in Fig. 1. However, these isoquants are the boundary of the output sets and by definition efficient (in the case of two outputs and one input), and efficiency is based on producing maximal quantity of the intended output. The shape of the isoquants is in direct conflict both with the efficiency requirement and with the materials balance. Taking Fig. 1 at face value goes against the materials balance assuming that the single input is material; input is constant along each output isoquant in Fig. 1. It is not possible to reduce both intended and unintended output keeping inputs constant, containing a certain fixed amount of materials. This is obvious if the inputs are fully used in the production of the two outputs producing less of both for a given amount of inputs, moving from the right to the left along the isoquant curves.

The property of null-jointness between outputs in Shephard and Färe (1974, p. 80) is introduced as a definition, and it is difficult to see the basis in a real-life joint production. To claim null- jointness between the intended and unintended outputs does not reflect the basic relationships of technical jointness; the point is that each output will be zero simultaneously if the material inputs are zero, as stated in Eq. (12). Furthermore, null jointness between y and z as portrayed by the output isoquants in Fig. 1 definitely breaks with the materials balance having positive input at the origin; it does not make sense to have y = z = 0 with x > 0.

It does not help to assume that part of the inputs are used to abate the unintended output.⁴⁶ This proposal cannot be taken seriously when there is no abatement activity modelled. You cannot draw curves assuming a given level of input along the curve and then say that the input is actually reduced when moving along the isoquant curve. This is not in accordance with the basic definition of an isoquant. The abatement process must be explicitly modelled. If inputs are reallocated to abatement, then the input cannot be constant along the output isoquants of the production possibility sets. If it is the case that some of the inputs are actually reallocated this does not show up in Fig. 1. In order to satisfy the definition of isoquants as based on keeping the input level constant, a part of input cannot be removed at the same time.

Weak disposability does not appear as a technical restriction in an engineering sense concerning the shape of the boundary of the output sets. It just tells us that reducing the quantities of an output point on the boundaries or in the interior of the set proportionally with a factor in the interval [0, 1], then the new point also belongs to the output set. We are only interested in the efficient points on the boundary, and it is clear from Fig. 1 that going from the right to the left along the boundary the change is not proportional, as stated in several papers, except for the last segments ending at the origin. The ratio between the outputs change continuously along the other frontier segments in Fig. 1.

Although joint production functions are discussed in mathematical detail in Shephard (1970, Chapter 9.5, pp. 212–220) neither the concept of assorted production nor the concept of technical jointness are used. Introducing weak disposability as in Eq. (4a) takes care of the problem with assorted production, but this is done without commenting on the existence of this form of joint production. It seems to be the disposability properties that are in focus.

As stressed in Subsection 4.2 the generation of intended and unintended outputs takes place simultaneously. There is only a single common process. Unintended residuals cannot be generated in physically separate processes from intended outputs per definition. As illustrated in Figs. 2 and 3 in Subsection 4.2 the very nature of unintended production implies that efficient utilisation of inputs to produce given levels of intended outputs will unavoidably generate positive minima of unintended outputs when having frontier functions.⁴⁷

Figure 1 presenting the figure in Shephard (1970, p. 188) has been reproduced in one form or another in almost all papers using the Shephard-inspired model. This type of figure postulates a positively sloped connecting curve, or an isoquant curve, between the intended and the unintended outputs in the case of one of each for given inputs. As demonstrated in Subsection 4.2, this is impossible taking technical jointness seriously.

By the nature of technical jointness and the thermodynamic laws there will be a positive minimum of residuals generated on the frontier for given inputs and given the applied production technology. There is no such minimum formulated in Shephard-inspired literature as far as I know. The Shephard-inspired literature on intended and unintended outputs all use an isoquant between the two types of outputs for given inputs. However, this is not possible given that the joint production is of the type technical jointness.

The use of directional distance functions (Chung et al. 1997) is also based on an isoquant between intended and unintended outputs. Therefore, this approach has all the weaknesses of the Shephard-inspired models. In addition, the assumption that the frontier point is found by adding/subtracting values using the same scalar factor multiplied with the observed values of both types of outputs, constrains the calculation of efficiency and productivity in a way that is difficult to accept as giving valid measures. In the single equation approach, using distance functions the argument for this special treatment is based on giving ‘credit’ for intended outputs and ‘penalise’ unintended output.⁴⁸ Lastly, the choice of direction influences the results, and this seems rather arbitrary, especially when using efficiency scores for productivity measures like the Malmquist productivity index with varying choice of directions for each period (Chung et al. 1997).

The Shephard-inspired models using the distance function being a single equation seem to have imposed a restriction on the estimation of efficiency and productivity in the literature. In the case of output oriented efficiency scores that are of interest here, intended and unintended outputs are forced to have inverse inefficiencies with the unintended score being lowest.

In Murty and Russell (2017, Section 10.4, p. 12) it is stated:

“…a single functional relation is not sufficient to capture all the complex trade-off among inputs and outputs involved in the production of economic outputs and the generation of emissions.”

However, the problems with null jointness and weak disposability used in the Shephard-inspired single-equation models all disappear when introducing two types of production functions, one for each type of output, as shown in Section 4.

6 Measuring inefficiency in a nonparametric multi-equation model

6.1 Defining inefficiency

The efficiency literature is in general focussed on measuring efficiency. However, the causes of inefficiency are rarely researched (see e.g. Førsund (2010) for a review of reasons for inefficiency).

Inefficiency arises in general when the potential engineering or blueprint technology, the frontier for short, is not achieved when transforming inputs into outputs, assuming that this is feasible.⁴⁹ For given desirable outputs too many resources of raw materials and service inputs are used. For a given amount of inputs containing physical mass, it means that at the frontier more outputs could have been produced. In terms of the materials balance Eq. (1) the implication is that the amount of residuals z for constant inputs x_M at inefficient operation will be reduced if the frontier is achieved. Inefficiency in the use of service inputs means that with better organisation of the activities more output could be produced if the frontier is realised for constant x_S.

The materials balance also holds for inefficient observations (as pointed out in Section 2). It is the amount of residuals and outputs that have potentials for change given the inputs, while the a, b, c coefficients in Eq. (1) remain the same. The combustion process may be run less efficiently in converting the raw material into heat, and a different mix of combustion substances may be produced than at efficient operation. In thermal electricity production based on coal, the mix of substances such as CO₂, CO, particles, NO_x and ash may differ between inefficient and efficient operations. Another source of inefficiency is the occurrence of rejects of intended outputs and unnecessary waste of raw materials, e.g., producing tables of wood, residuals consist of pieces of wood of different sizes from rejects and down to chips and sawdust. The ways of improving the use of raw materials and thereby reducing the amount of residuals are more or less of the same nature as factors explaining substitution possibilities between material and service inputs in Subsection 4.2. However, inefficient use of service inputs (labour and capital) should not be confused with substitution between labour and raw materials on a frontier isoquant for intended output as shown in Fig. 2.

There is another type of problem within the efficiency strand of research not often mentioned concerning the behaviour of (or the management of) firms. It is difficult to assume, as in standard production theory using frontier functions only, that inefficient firms can optimise in the usual sense of obtaining maximal profit or minimising costs. It is very seldom that production functions are formulated for inefficient firms in non-parametric analyses. Introducing behaviour in non-parametric DEA models for a unit it is necessary to assume that frontier technology is used if there are no known obstacles for being efficient. If firms do know the frontier, why do they end up being inefficient? To appeal to randomness only is not so satisfying.

However, in the real world all firms, also inefficient ones, have production functions and react to e.g. environmental regulation. When efficiency is estimated, the observations are usually taken as given and no behavioural action on the part of the units is assumed to take place. It is the analyst that creates an optimisation problem when calculating efficiency measures. This may be a reason for the lack of pursuing policy instruments in the literature addressing efficiency when both desirable and undesirable outputs are produced. In the environmental economics literature not addressing efficiency issues, the design of policy instruments, playing on giving firms incentives to change behaviour as to emitting pollutants, is of paramount interest. However, the assumptions in the inefficiency literature based on Shephard (1970) in Subsection 3.1 are made for measuring efficiency, and may not be suitable for developing policy instruments applied to all units in an industry. We saw this in Färe et al. (1986) making introduction of regulation of emissions change the form of the production possibility set for all units, and not addressing the reactions of each individual unit to the regulation. If economic behaviour is applied in the efficiency literature, then the unit in question typically operates on the frontier.

6.2 Efficiency and productivity measures

6.2.1 Efficiency measures

The technical jointness characteristic of producing simultaneously intended and unintended outputs has been satisfied by splitting the production function into two separate frontier functions as in Eq. (9). It should then be straightforward to estimate standard radial Farrell output-oriented efficiency measures for each technology as formulated in Murty et al. (2012, p.130) for the FGL efficiency index for each technology. On p. 133 in Murty et al. (2012), DEA versions are given for each technology. The data for inputs will be identical for the estimation of frontiers for the intended- and unintended outputs for the factorially determined multi output model Eq. (9). This takes care of technical jointness.

It is standard to estimate the boundary of the intended output set and find the projection points for inefficient units, calculating an output-oriented efficiency measure. The Farrell radial efficiency measures for the intended- and unintended output for a unit i are:

$$\begin{array}{l}E_{yi} = \left( {y_i^{obs}/y_i ^{\ast} } \right) \in \left( {0,1} \right]\\ E_{zi} = \left( {z_i ^{\ast}/z_i^{obs}} \right) \in \left( {0,1} \right]\,,i = 1,...,N\end{array}$$

(14)

The super index “obs” indicates the observation of the observed output, and the variables marked with “*” are estimated frontier values using a standard DEA model.⁵⁰ I will call the efficiency measure for the unintended output for residual efficiency (and not environmental efficiency⁵¹). A unit is overall efficient if both measures are equal to one. In the case of the frontier function being equal for all units it should be the case that an efficient unit is efficient on both measures. However, since the frontiers estimated with the non-parametric DEA model is piecewise linear there is a question about the validity of the projections to the frontier of output values of inefficient units regarding the materials balance (see Førsund (2018a) for further discussion).

6.3 Productivity measures

It is not only of interest to estimate efficiency measures for the two types of outputs, but also to measure the productivity change of them. Suppressing the unit index for convenience the efficiency measures can straightforwardly be converted to separate standard Malmquist productivity change indexes for each output using discrete time periods t:

$$\begin{array}{l}M_y^{t,t + 1} = {{E_y^{CRS,t + 1}}}/{{E_y^{CRS,t}}},\,{\mathrm{greater}}\,{\mathrm{than}}\,{\mathrm{1}}\,{\mathrm{is}}\,{\mathrm{progress,}}\,{\mathrm{less}}\,{\mathrm{than}}\,{\mathrm{1}}\,{\mathrm{decline}}\\ M_z^{t + 1,t} = {{E_z^{CRS,t}}}/{{E_z^{CRS,t + 1}}}{\mathrm{,}}\,{\mathrm{greater}}\,{\mathrm{than}}\,{\mathrm{1}}\,{\mathrm{is}}\,{\mathrm{progress,}}\,{\mathrm{less}}\,{\mathrm{than}}\,{\mathrm{1}}\,{\mathrm{decline}}\end{array}$$

(15)

With a standard Malmquist productivity index, I mean that the efficiency scores are calculated relative to a benchmark frontier based on an intertemporal frontier (Tulkens and van den Eeckhaut 1995) using all yearly data for estimation, and assuming constant returns to scale (marked with super index “CRS”), making output orientation equal to input orientation of efficiency scores (see Førsund 2016). Calculating the productivity change index for the unintended output z the time period indices for the efficiency scores are simply switched. A decrease in the unintended output is regarded as productivity progress. Regarding policy use of efficiency and productivity results separate measures for intended and unintended outputs seem to yield the most interesting information.

7 Conclusions

Models that we make for calculating efficiency measures for production activities are quite aggregated compared to the engineering level of real life. In a study of efficiency in metal machining industry, Kurz and Manne (1963) identify 129 separate production functions for basic activities. It is of paramount importance that the much simpler models we make capture essential features of production activities we analyse (Frisch 2010). However, the Shephard-inspired efficiency models involving intended and unintended outputs are too restrictive, based on a single equation in the form of a distance function as a function of all output and input variables. In the literature based on the Shephard approach of a single function using DEA to calculate efficiency measures, both using the hyperbolic measure and using the directional distance function, the measure of technical efficiency and a measure termed environmental performance are linked together through a common parameter. A problem is that the importance of the type of joint production faced by having intended outputs produced at the same time as generating unintended ones, is not sufficiently taken into account. It is demonstrated that introducing weak disposability and null-jointness are not the solution. The type of joint production must be such that unintended outputs are impossible to avoid producing. The Frisch (1965) categories of technical jointness and extreme jointness of outputs imply that both types of outputs are generated by the same inputs simultaneously in one activity. In this paper, the technical jointness is assumed (less strict than extreme jointness including the Leontief type of models), opening up for change in the input mix and levels to generate different mix of the type of outputs. However, in output space, this implies that there is no isoquant between intended and unintended output for given inputs; there are just points in the output space generated by a different mix and different levels of inputs.

An important assumption is that one or more of the inputs must be material. The materials balance (Ayres and Kneese 1969) tells us that matter contained in inputs cannot disappear, but will be contained in the intended outputs or discharged to the environment as waste or residuals. These residuals are pollutants if causing environmental problems and that there is a willingness to pay to reduce the amounts. The two thermodynamic laws ensure that intended outputs cannot utilise all mass; some positive amount of unintended waste will always occur. If we assume that intended and unintended outputs compete for the material inputs, then efficient production based on frontier functions of the intended outputs imply that there is a minimum of mass ending up in the unintended outputs. Furthermore, this minimum amount implies that there cannot be, with inputs given, any trade-off isoquant between intended and unintended outputs when production of the intended output is efficient. The null-jointness assumption of the intended output and the unintended one results in positive slopes of output isoquants for given inputs. However, this goes against the material balance.

Shephard-inspired models have been very popular judged by the citations. However, the type of model I have developed in Subsection 4.2 takes explicitly the type of joint production into consideration, and has no problem obeying theoretically the materials balance. The model used in Subsection 4.2 has been the simplest one with two types of outputs and two types of inputs. Introducing several variables of both types should be explored in empirical studies. Extending the model in Eq. (9) by entering more single equations for both types following the scheme of factorially determined multi-output functions is one possibility. The by-production model can extend the list of output and input variables within the two types of technologies for intendent- and unintended outputs. Another development may be a combination of factorially determined multi-output functions satisfying technical jointness and assorted production.