Abstract
We lay the foundations of Fatou theory in one and several complex variables. We describe the main contributions contained in E. M. Stein’s book Boundary Behavior of Holomorphic Functions, published in 1972 and still a source of inspiration. We also give an account of his contributions to the study of the boundary behavior of harmonic functions. The point of this paper is not simply to exposit well-known ideas. Rather, we completely reorganize the subject in order to bring out the profound contributions of E. M. Stein to the study of the boundary behavior both of holomorphic and harmonic functions in one and several variables. In an appendix, we provide a self-contained proof of a new result which is relevant to the differentiation of integrals, a topic which, as witnessed in Stein’s work, and especially by the aforementioned book, has deep connections with the boundary behavior of harmonic and holomorphic functions.
Similar content being viewed by others
1 Introduction
The difference between the boundary behavior of holomorphic functions (defined on a certain class of bounded domain in \(\mathbb {C}^n\)) and that of harmonic functions (defined on the same domains, seen as subdomains of \(\mathbb {R}^{2n}\)) becomes much more significant if \(n>1\), due to a subtler interplay between potential theory and complex analysis. This is one of the many places where the insight of Elias Menachem Stein has reached new depths.
Stein also contributed a profound understanding of the boundary behavior of harmonic functions per se—a subject that grew out of the Dirichlet problem.
When Stein started his work in this second area, classical potential theory had already reached a high degree of development: It had been axiomatized, or was being axiomatized, by the French school (H. Cartan, M. Brelot, G. Choquet), with deep contributions from the German one (H. Bauer and his pupils), from the Prague Harmonic Group (J. Král and his pupils), as well as from the Romanian school (S. Stoilow and his pupils) [8, 9, 11, 17,18,19,20, 28,29,30, 33, 66, 67, 69, 95, 130, 170, 178]. In the hands of Kakutani and Doob, the subject had produced a spectacular result—such as Theorem 8.7 below—on the boundary behavior of harmonic functions for any bounded domain in \(\mathbb {R}^n\) [52, 84, 85]. However, the geometric meaning of this result is not easy to grasp, since its statement does not immediately yield a geometric insight about the boundary approach which ensures the existence of boundary values.
At that time, some precise and geometrically crafted results on boundary behavior did exist, but most of them, with perhaps the only exceptions given by the work of Privalov and Kouznetzoff (1939) for Lyapunov domains in \(\mathbb {R}^n\), Tsuji (1939) for the unit ball in \(\mathbb {R}^n\), Tsuji (1944) for Lyapunov domains in \(\mathbb {R}^n\), and Calderón (1950) for the upper half-space, were confined to planar domains and to holomorphic function and thus heavily depended on conformal mappings, which transfer the problem to the unit disc [24, 25, 144, 176, 177].
It is then useful, in order to put things in perspective and be able to appreciate Stein’s contributions, to give an overview of the state of the art at that time and to see exactly what those precise and geometrically crafted results on boundary behavior (mainly of holomorphic functions and, to a lesser extent, harmonic functions) were, and what was the motivation that led to them.
Hence we start with the unit disc and follow the development of a certain stream of ideas, which motivated Stein’s contributions, even at the cost of sacrificing completeness, and, with few exceptions, omitting proofs. Before we plunge into the field, we introduce some notation that will make the treatment run smoothly, and say a few words on the notion of “boundary property” occurring in these matters.
2 Pointwise Boundary Behavior
The collection of all functions which have a set D as domain and a set C as codomain is denoted \(C^{D}\). If \( \mathbf {Y} \) is a topological space, \( C( \mathbf {Y} ) {\mathop {=}\limits ^{\mathrm{def}}} \left\{ u\in \mathbb {C}^{ \mathbf {Y} }: u\text { is continuous on } \mathbf{Y} \right\} \). If \(\Omega \subset \mathbb {R}^n\) is open, \( h(\Omega ) \) denotes the vector space \( \left\{ u\in \mathbb {C}^\Omega : u\text { is harmonic on } \Omega \right\} \). If \(\Omega \subset \mathbb {C}^n\) is open, \(\mathcal {O}(\Omega )\) denotes the space \( \left\{ u\in C(\Omega ) : u\text { is holomorphic on } \Omega \right\} \). A domain in a topological space is an open and connected subset.
The generic expression boundary behavior of a function \(u\in \mathcal {O}(\Omega )\) or \(u\in h(\Omega ) \) that appears in the so-called Fatou-type theorems, hinges on any property or datum which only depends on the values of the function near the boundary of \(\partial \Omega \). This general concept assumes manifold shapes.
2.1 The General Setting for Pointwise Boundary Behavior
The boundary behavior is called pointwise if it refers to any property of \(u\) or datum defined from \(u\) which lies unaffected by changes of the values of \(u\) at points away from a given point in the boundary of the domain of \(u\). A more precise definition will be given momentarily.
If \( \mathbf {W} \) is a topological space (seen as the ambient space) and \(\Omega \subset \mathbf {W} \), the boundary of \( \Omega \) in \( \mathbf {W} \) is the set:
where \(\overline{ \Omega }\) is the closure of \( \Omega \) in \( \mathbf {W} \) and \( { \Omega }^{\circ } \) its interior. If no ambiguity is likely, we write \(\partial { \Omega }\) for \(\partial _{ \mathbf {W} }{ \Omega }\).
The notion of pointwise boundary behavior is of interest not only when the domain of \(u\) is an open subset of \(\mathbb {R}^n\) or \(\mathbb {C}^n\), but also if the ambient space is infinite-dimensional (in some sense). Hence we set our notation in order to account for the more general case, and we make the following assumptions.
- (P 1):
-
A function \(u: \Omega \rightarrow \mathbb {C}\) is defined on a given open subset \( \Omega \) of a topological space \( \mathbf {W} \).
- (P 2):
-
A point \(q\) in \(\partial \Omega \) is given.
- (P 3):
-
A filter \( \Phi \) of subsets of \( \Omega \) which ends at \(q\) is given (roughly speaking, the elements of \( \Phi \) play the role of neighborhoods, although they are not actually neighborhoods; see below for the details).
The property
(which the function \(u\) may or may not have) describes the pointwise boundary behavior of \(u\) with respect to the given filter at the given point. If a theorem gives sufficient conditions which entail (2.1), it is called a pointwise Fatou-type theorem.
The limiting value in (2.1) is called the boundary value of \(u\) at \(q\) along \( \Phi \), and it is the datum associated to this boundary behavior: It is denoted by \(u_{ \Phi }(q)\). The notion of filter, coupled with an explanation of the meaning of (2.1), the appropriate motivation, and the most relevant examples, will be given momentarily.
Following Doob [52], a boundary set for \(\Omega \) is a (possibly proper) subset of the boundary of \(\Omega \), and a boundary function for \(\Omega \) is a function defined on a (possibly proper) subset of the boundary of \(\Omega \).
Other variants of the notion of pointwise boundary behavior, which are central to the field, are the qualitative and the quantitative boundary behavior of functions (see below).
2.2 Unrestricted Boundary Values
The property that the limiting value
exists is a pointwise boundary property, which \(u\) may or may not have. The boundary value \(u_{ \Omega }(q)\) is then called the unrestricted boundary value of \(u\) at \(q\) in \( \Omega \) and it is the datum associated to this boundary property. It would be misleading to denote the limiting value in (2.2) by \(u(q)\), since \(u\) is only defined on \( \Omega \) (and, thus, \(u(q)\) is not defined). The existence of the unrestricted boundary value is a strong condition, and it is important on theoretical grounds (as for example in the set-up that leads to the notion of harmonic measure). In general, its actual occurrence is more an exception than a rule. However, there are always examples where it occurs: The restriction to the domain of a function which is continuous on the whole ambient space has unrestricted boundary value at any boundary point.
2.3 Approach Regions
The collection of all subsets [nonempty subsets] of a set \( {X} \) is denoted by \(\varvec{\mathcal {P}}( {X} ) \) [\( \varvec{\mathcal {P}}_{\bullet }( {X} ) \), resp.].
If \( \mathbf {Y} \) is a topological space and \(q\in \mathbf {Y} \), a neighborhood of \(q\) in \( \mathbf {Y} \) is a subset of \( \mathbf {Y} \) which contains an open set containing \(q\). Denote by
the set of all neighborhoods of \(q\) in \( \mathbf {Y} \). The notion of approach region is a general geometrical device that enables us to describe a whole class of concrete instances of pointwise boundary behavior of a function \(u: \Omega \rightarrow \mathbb {C}\). This notion plays a distinguished role in Stein’s work in this area.
An approach region in \( \Omega \subset \mathbf {W} \) ending at \(q\in \partial _{ \mathbf {W} }{(\Omega )}\) is a subset \(V\subset \mathbf {W} \) such that
We indicate the fact that \(V\) is an approach region in \(\Omega \subset \mathbf {W} \) ending at \(q\) by writing \( \mathbf {W} \supset \Omega \supset V\rightarrow q \). If \(V\) is an approach region in \(\Omega \) ending at \(q\), we say that the boundary value of \(u\) at \(q\) through \(V\) exists and is equal to \(\xi \in \mathbb {C}\), and write
if for each \(O\in {\mathcal {N}}_{\xi }(\mathbb {C}) \), there exists \(U\in {\mathcal {N}}_{q}( \mathbf {W} ) \) such that \(\{u(z):z\in V\cap {}U\}\subset {}O\). If \(\xi =\infty \) in the Riemann sphere, or if \(u\) is real valued and \(\xi =+\infty \) or \(\xi =-\infty \), this definition is modified in the familiar way. This statement is a pointwise boundary property of \(u\), and \(u_{V}(q)\) is the associated datum.
The uncluttered notation adopted in (2.5) responds to the fact that boundary values through various approach regions will be studied. It would be misleading to denote the limiting value in (2.5) by \(u(q)\), since the function \(u\) is only defined on \( \Omega \), and therefore, \(u(q)\) is not defined; moreover, the notation \(u(q)\) does not express the fact that the value in (2.5) depends on \(V\).
If \(V= \Omega \), then we recapture the notion of unrestricted boundary value of \(u\) at \(q\), which is a very stringent condition. Less stringent conditions arise by choosing smaller approach regions ending at \(q\), such as, for example, a sequence of points in \( \Omega \) converging to \(q\). Then the approach region is called sequential, and the limiting value \(u_{V}(q)\) is called a sequential boundary value. If \(V\) is a half-open Jordan arc in \( \Omega \) ending at \(q\), i.e., the image of a continuous, injective function \(\varvec{c}:[0,1)\rightarrow \Omega \) such that \({\lim _{s\rightarrow 1}\varvec{c}(s)=1}\), then, following a consolidated terminology, the approach region is called asymptotic, and the limiting value \(u_{V}(q)\) is called an asymptotic boundary value [36, 126, 132]. For example, if \( \Omega \) is the unit disc \(\mathbb {D}{\mathop {=}\limits ^{\mathrm{def}}} \left\{ z\in \mathbb {C}: \left| z\right| <1 \right\} \), \( \mathbf {W} =\mathbb {C}\), and \(R{\mathop {=}\limits ^{\mathrm{def}}} \left\{ sq: 0\le {}s<1 \right\} \) is the radius in \(\mathbb {D}\) ending at \(q= e^{i\theta }\), then \( {u}_{R}(q) \) is called radial boundary value of \(u\) at \(q\) (if it exists).
Another variant of this notion arises from the choice of a collection \({ {\varvec{\Lambda }}} \subset \varvec{\mathcal {P}}_{\bullet }(\Omega ) \) of approach regions in \(\Omega \) ending at \(q\). The property
is a pointwise boundary property of \(u\) (which \(u\) may or may not have). The associated datum is the limiting value \(u_{V}(q)\) (which, by assumption, does not depend on \(V\)), called the boundary value of \(u\) at \(q\) through \({ {\varvec{\Lambda }}} \) and denoted by \(u_{{ {\varvec{\Lambda }}} }(q)\). Hence \( \displaystyle { u_{{ {\varvec{\Lambda }}} }(q) {\mathop {=}\limits ^{\mathrm{def}}} \lim _{V\ni z\rightarrow q}u(z) , \, \text { for all } V\in { {\varvec{\Lambda }}} }\).
2.4 Angular Boundary Values in the Unit Disc. The Fatou Set and the Plessner Sets
In the unit disc \(\mathbb {D}\), if \(q=e^{i\theta }\in \partial \mathbb {D}\), consider the following sets of approach regions: (1) the set (denoted by \( \mathsf {Stolz}_{q} \)) of all open Euclidean triangles contained in \(\mathbb {D}\) and having \(q\) as a vertex; (2) the set (denoted by \( \mathsf {Stolz}_{q}^{s} \)) of all such triangles which are symmetric with respect to the radius ending at \(q\); (3) the set of all sets \(\Gamma _{j}(q)\), where \({j}\ge {}1\), defined as follows
The sets in (1) are called Stolz triangles at \(q\); those in (2) are called symmetric Stolz triangles at \(q\); those in (3) are called nontangential approach regions in \(\mathbb {D}\) at \(q\). These sets yield the same notion of boundary value, denoted by
and called angular boundary value of \(u\) at \(q\): We will see that this fact can be understood by observing that these sets determine the same filter (see below). Indeed, when studying the mere existence of boundary values, the relevant datum in an approach region, or in a set of approach regions, is the filter associated to it (see below). The existence of the angular boundary value \( {u}_{\flat }(q)\) is a more stringent condition than the existence of the radial boundary value, but it is weaker than the existence of unrestricted boundary values. The subscript in \(u_\flat \) is reminiscent of an angle. Indeed, if \( {u}_{\flat }(q)\) exists, given a half-open Jordan arc \(\varvec{c}:[0,1)\rightarrow \mathbb {D}\) such that \(\lim _{r\uparrow {}1}\varvec{c}(r)=q\), if the visual angle between 0 and \(\varvec{c}(r)\) as seen from \(q\) is bounded away from \(\pi /2\), then \(\lim _{r\uparrow {}1}u(\varvec{c}(r)) = {u}_{\flat }(q)\). On the other hand, in 1927, John Edensor Littlewood [113] proved the following result.
Lemma 2.1
If \(u:\mathbb {D}\rightarrow \mathbb {C}\) is a function for which \( {u}_{\flat }(q)\) exists, for a certain \(q\in \partial \mathbb {D}\), then it is possible to select a certain half-open Jordan arc \(\varvec{c}:[0,1)\rightarrow \mathbb {D}\) ending at \(q\) such that
- (a):
-
For each \(\textsc {t}\in \mathsf {Stolz}_{q} \), there exists \(s_{\textsc {t}}\in [0,1)\) such that \(\varvec{c}(s)\not \in \textsc {t}\) for each \(s\in (s_{\textsc {t}},1)\).
- (b):
-
\(\lim _{s\uparrow {}1}u(\varvec{c}(s))= {u}_{\flat }(q)\).
The condition in (a) says that the curve \(\varvec{c}\), whose existence is established in Lemma 2.1 is eventually disjoint from any given Stolz triangle in \(\mathbb {D}\) ending at \(q\) (see below). This condition is a set-theoretical expression of the notion that the curve may be chosen to be tangential to \(\partial \mathbb {D}\) at \(q\): Here, set theoretical means that this notion does not rest on any smoothness assumption on \(\varvec{c}\).
The Fatou set of \(u\in \mathbb {C}^{\mathbb {D}}\) is the following boundary set for \(\mathbb {D}\):
Let \(\widehat{\mathbb {C}}\) be the one-point compactification of \(\mathbb {C}\). The Plessner set of \(u\in \mathbb {C}^{\mathbb {D}}\) is antithetical to its Fatou set:
If \(u\) is real valued, then the real Plessner set of \(u\) is slightly different in its definition but similar in spirit:
2.5 Filters
The examples we have seen so far of pointwise boundary behavior can be subsumed under a unique general construction, resting on the notion of filter, due to H. Cartan, which we now introduce [27]. Recall from (2.3) that if \( \mathbf {Y} \) is a topological space and \(q\in \mathbf {Y} \), the set of all neighborhoods of \(q\) in \( \mathbf {Y} \) is denoted by \( {\mathcal {N}}_{q}( \mathbf {Y} ) \). The key observations that lead to the notion of filter and show its relevance in issues of limiting values, are the following. First, the set \( {\mathcal {N}}_{q}( \mathbf {Y} ) \), seen as subset of \(\varvec{\mathcal {P}}( \mathbf {Y} ) \), has the following essential properties:
- (F 1):
-
It is closed under finite intersections.
- (F 2):
-
It contains every superset of each of its elements.
Second, the familiar \(\epsilon \)-\(\delta \) description of the existence of a limiting value \({\lim _{z\rightarrow {}q}{u(z)}}\) of \(u\in \mathbb {C}^{ \mathbf {Y} }\) shows that this notion only depends on the set \( {\mathcal {N}}_{q}( \mathbf {Y} ) \) and on the values of \(u\) on (set theoretically) small sets in \( {\mathcal {N}}_{q}( \mathbf {Y} ) \). This model case sheds light on the following definition.
If \( {Y} \) is a nonempty set, a filter on \( {Y} \) (or filter of subsets of \( {Y} \)) is a nonempty collection of nonempty subsets of \( {Y} \) with the properties (F 1) and (F 2) (hence with this definition, the empty set is not a filter). The set \( {Y} \) is called the total space of the filter. Hence, if \( \Phi \) is a filter on \( {Y} \), then \( \Phi \subset \varvec{\mathcal {P}}_{\bullet }( {Y} ) \) and \(\emptyset \not \in \Phi \). The collection of all filters in \( {Y} \) is denoted by \(\varvec{ \mathsf {Filters}( {Y} ) }\). A filtered space \(( {Y} , \Phi )\) is a nonempty set \( {Y} \) endowed with a filter \( \Phi \).
If \( \mathbf {Y} \) is a topological space and \(q\in \mathbf {Y} \), \( {\mathcal {N}}_{q}( \mathbf {Y} ) \) is a filter on \( \mathbf {Y} \), called neighborhood filter on \( \mathbf {Y} \) at \(q\).
Observe that the set \( \mathsf {Filters}( {Y} ) \), being a subset of \( \varvec{\mathcal {P}}_{\bullet }( \varvec{\mathcal {P}}_{\bullet }( {Y} ) ) \), is a partially ordered set under inclusion, and the assignment \( {Y} \mapsto \mathsf {Filters}( {Y} ) \) is the object function of a functor from the category of sets to the category of partially ordered sets. The associated arrow function assigns to each function \(f: {Y} \rightarrow {Y} ^\prime \) the order-preserving function \(f_*: \mathsf {Filters}( {Y} ) \rightarrow \mathsf {Filters}( {Y} ^\prime ) \) which associates to each filter \( \Phi \in \mathsf {Filters}( {Y} ) \) the filter:
Filtered spaces form a category, where a morphism \(f:( {Y} , \Phi )\rightarrow ( {Y} ^\prime , \Phi ^\prime )\) is a function \(f: {Y} \rightarrow {Y} ^\prime \) such that \( \Phi ^\prime \subset {}f_*( \Phi )\). For background, see [118].
Lemma 2.2
Given any family of filters on a nonempty set, its intersection is not empty and is a filter.
2.5.1 Small Sets, Large Sets, Filter Bases, and Localization of Filters
The information conveyed by a filter \( \Phi \) is given by the “small” sets in \( \Phi \), because of (F 2). Loosely speaking, if \( \Phi _1, \Phi _2\in \mathsf {Filters}( {Y} ) \), then \( \Phi _1\subset \Phi _2\) if \( \Phi _2\) contains sets which are “smaller” than those of \( \Phi _1\), and \( \Phi _1\subsetneq \Phi _2\) if \( \Phi _2\) contains sets which are “too small” compared to those of \( \Phi _1\). Hence some authors write that \(R\) is \( \Phi \) large instead of \(R\in \Phi \), meaning that \(R\) is “large enough” to contain sets in \( \Phi \). For example, a set belongs to the neighborhood filter \( {\mathcal {N}}_{q}( \mathbf {Y} ) \) (where \( \mathbf {Y} \) is a topological space) if and only if it contains some open set which contains a point \(q\).
The vague notion of “small” sets in \( \Phi \) leads to the notion of a filter base of \( \Phi \) on \( {Y} \), defined as a collection \(\Psi \subset \Phi \) such that a set belongs to \( \Phi \) if and only if it contains some set in \(\Psi \); we then say that \( \Phi \) is generated by \(\Psi \) on \( {Y} \) and write \( \Phi ={\langle \Psi \rangle }_{ {Y} }\). For example, the subsets of \(\mathbb {N}\) of the form \( \left\{ k\in \mathbb {N}: k\ge j \right\} \), called tails, generate the so-called cofinite filter on \(\mathbb {N}\), and the open sets which contain \(q\) generate the neighborhood filter \( {\mathcal {N}}_{q}( \mathbf {Y} ) \).
A nonempty collection \(\Psi \subset \varvec{\mathcal {P}}_{\bullet }( {Y} ) \) is a filter base of some filter on \( {Y} \) if and only if the intersection of any two sets in \(\Psi \) contains some set in \(\Psi \). For example, if \(\Omega \subsetneq W\) and \( \Phi \in \mathsf {Filters}(\Omega ) \) then \( \Phi \notin \mathsf {Filters}(W) \) but \( \Phi \) is a filter base of the filter \({\langle \Phi \rangle }_{ \mathbf {W} }\), i.e., the filter of subsets of \(W\) generated by \( \Phi \). Observe that \({\langle \Phi \rangle }_{ \mathbf {W} }=\imath _*( \Phi )\), as in (2.12), where \(\imath :\Omega \rightarrow W\) is the standard injection. Hence
If \( \mathbf {Y} \) is a topological space and \(q\in \mathbf {Y} \), then the neighborhood filter \( {\mathcal {N}}_{q}( \mathbf {Y} ) \) is “localized” in the sense that the intersection of all its member is nonempty. This property is not shared by all filters: For example, the cofinite filter on \(\mathbb {N}\) does not have this property. However, filters are “localized” in two ways: First, a filter cannot contain as elements two disjoint sets. Second, if \(\Omega \) and \(W\) are sets, and \(\Omega \subset W\), then \( \mathsf {Filters}(\Omega ) \cap \mathsf {Filters}(W) \not =\emptyset \) if and only if \(\Omega =W\). However, if \(\Omega \subsetneq W\), (2.13) yields a useful injective map \(\imath _*: \mathsf {Filters}(\Omega ) \rightarrow \mathsf {Filters}(W) \), obtained by (2.12) where \(\imath :\Omega \rightarrow W\) is the natural injection.
2.5.2 Limiting Values Along a Filter
If \(( {Y} , \Phi )\) is a filtered space and \(u\in \mathbb {C}^{ {Y} }\), we say that the limiting value of \(u\) along \( \Phi \) exists and is equal to \(\xi \in \mathbb {C}\), and write
if for each \(O\in {\mathcal {N}}_{\xi }(\mathbb {C}) \), there exists \(R\in \Phi \) such that \(\{u(z):z\in R\}\subset {}O\). If \(\xi =\infty \) in the Riemann sphere, or if \(u\) is real valued and \(\xi =+\infty \) or \(\xi =-\infty \), this definition is modified in the familiar way. In (2.14), \( {Y} \) (the domain of \(u\)) is not required to be a topological space, but only the total space of a filter, i.e., a set endowed with the filter \( \Phi \). If \(u: {Y} \rightarrow \mathbf {S} \), where \( \mathbf {S} \) is a topological space, the existence of \({\lim _{ \Phi }u=\xi \in \mathbf {S} }\) is defined in a similar way: Each open set in \( \mathbf {S} \) containing \(\xi \) also contains the \(u\) image of a set in \( \Phi \).
The definition (2.14) recaptures the topological one: If \( \mathbf {Y} \) is a topological space, and \(q\in \mathbf {Y} \), then
where, in the left-hand side of (2.15), the limiting value is understood in the usual topological sense. The definition (2.14) recaptures the familiar notion of convergence for sequences as well: A sequence \(u:\mathbb {N}\rightarrow \mathbb {C}\) converges to \(\xi \in \mathbb {C}\) in the usual sense if and only if the limiting value of \(u\) along the cofinite filter on \(\mathbb {N}\) exists and is equal to \(\xi \).
2.5.3 Compatibility of a Filter with the Topology at a Point
If \( \mathbf {Y} \) is a topological space, \(q\in \mathbf {Y} \), and \( \Phi \in \mathsf {Filters}( \mathbf {Y} ) \), we say that \( \Phi \) converges to \(q\) in \( \mathbf {Y} \) if the following compatibility condition between the topology at \(q\) and the filter holds: For each topological space \( \mathbf {S} \) and each function \(u: \mathbf {Y} \rightarrow \mathbf {S} \),
For example, the filter \( \Phi \in \mathsf {Filters}(\mathbb {R}) \) generated by the collection of intervals \((j,+\infty )\) does not converge to 0, since the existence of \({\lim _{\mathbb {R}\ni {}z\rightarrow {}0}u(z)}\) and the existence of \({\lim _{ \Phi }u}\) (which amounts to the existence of \({\lim _{z\rightarrow +\infty }u(z)}\)) are independent of each other. The filter \( \Phi \in \mathsf {Filters}(\mathbb {R}) \) generated by the collection of intervals \((-\frac{1}{j},0)\), \(j\in \mathbb {N}\), converges to 0, since if \({\lim _{\mathbb {R}\ni z\rightarrow 0}u(z)=\xi }\), then \({\lim _{ \Phi }u}\) exists and is equal to \(\xi \).
Lemma 2.3
A filter \( \Phi \) of subsets of a topological space \( \mathbf {Y} \) converges to \(q\) in \( \mathbf {Y} \) if and only if \( {\mathcal {N}}_{q}( \mathbf {Y} ) \subset \Phi \).
If a topological space is Hausdorff, a filter cannot converge to two distinct points.
2.5.4 The Notion of Filter on a Domain Ending at a Boundary Point
If \(\Omega \) is a proper subset of a topological space \( \mathbf {W} \), \( \Phi \in \mathsf {Filters}(\Omega ) \), and \(q\in \partial \Omega \), then we say that \( \Phi \) ends at \(q\) if the following condition holds: For each topological space \( \mathbf {S} \) and each function \(u: \mathbf {W} \rightarrow \mathbf {S} \),
where \(u|_{\Omega } \) is the restriction of \(u\) to \(\Omega \). Observe that in this setting, \( \Phi \) does not converge to \(q\) in \( \mathbf {W} \) (since \( \Phi \) is not a filter of subsets of \( \mathbf {W} \)), and \( \Phi \) does not converge to \(q\) in \(\Omega \) (since \(q\notin \Omega \)). For a similar reason, \( \Phi \) does not converge to \(q\) in the topology of \(\overline{ \Omega }\).
Lemma 2.4
If \( \mathbf {W} \) is a topological space, \(\Omega \subsetneq \mathbf {W} \), \(q\in \partial \Omega \), and \( \Phi \in \mathsf {Filters}(\Omega ) \), then \( \Phi \) ends at \(q\) if and only if the filter of subsets of \( \mathbf {W} \) generated by \( \Phi \) converges to \(q\) in \( \mathbf {W} \).
Recall that the filter of subsets of \( \mathbf {W} \) generated by \( \Phi \) is defined in (2.13).
Observe that (2.17) is of interest only if \(q\in \partial \Omega \). Indeed, if \(q\not \in \overline{ \Omega }\), then no filter \( \Phi \in \mathsf {Filters}(\Omega ) \) satisfies (2.17); if \(q\in {\Omega }^{\circ } \), then Lemma 2.3 implies that (2.17) is equivalent to \( {\mathcal {N}}_{q}(\Omega ) \subset \Phi \).
We now show that to every approach region \(V\) in \(\Omega \subset \mathbf {W} \) ending at \(q\in \partial \Omega \), it is possible to associate a filter of subsets of \(\Omega \) which ends at \(q\).
2.5.5 The Filter Associated to an Approach Region
We have seen that the notion of limiting value along a filter is general enough to recapture the familiar topological notion of convergence for functions and sequences. We now show that it is also able to recapture the notion of convergence through approach regions (or through collections of approach regions).
Let \(V\) be an approach region in \(\Omega \subset \mathbf {W} \) ending at \(q\in \partial \Omega \). The relevant data that determine the existence of the boundary value of \(u\) at \(q\) through \(V\) defined in (2.5) are the values of \(u\) on the so-called tails of \(V\) at \(q\): A tail of \(V\) at \(q\) is the intersection of \(V\) with some neighborhood of \(q\) in \( \mathbf {W} \). Indeed, a subset \(V\subset \Omega \) is an approach region in \( \Omega \) ending at \(q\) if and only if the collection of all its tails at \(q\) is a filter base of a filter on \(\Omega \). For example, the filter on \( \Omega \) associated to \( \Omega \) at \(q\) (where we see \(\Omega \) as an approach region in \( \Omega \) ending at \(q\)) is called the unrestricted filter at \(q\). A filter base for this filter is the collection \({ \left\{ O\cap \Omega : O\in {\mathcal {N}}_{q}( \mathbf {W} ) \right\} }\). Another example is given by the radial filter ending at \(q\in \partial \mathbb {D}\), which is associated to the radius in \(\mathbb {D}\) ending at \(q\).
The filter on \( \Omega \) associated to \(V\) at \(q\), denoted by
is the filter on \( \Omega \) generated by the collection of all tails of \(V\) at \(q\). Hence \( {[V]}_q \in \mathsf {Filters}(\Omega ) \).
Lemma 2.5
If \( \mathbf {W} \) is a topological space, \(\Omega \subset \mathbf {W} \), \(q\in \partial \Omega \), and \(V\) is an approach region in \(\Omega \) ending at \(q\), then the associated filter \( {[V]}_q \) ends at \(q\). Moreover,
Hence the notion of limiting value along a filter, given in (2.14), recaptures that of limiting value through an approach region, given in (2.5). In view of (2.19), the filter \( {[V]}_q \) associated to \(V\) at \(q\) is called the essential shape of the approach region \(V\) at \(q\).
Filters associated to approach regions or to collections of approach regions (see below) are called geometric filters. We will mostly be concerned with geometric filters.
2.5.6 The Filter Associated to a Collection of Approach Regions. The Angular Filter
A filter is called geometric if it is associated to a collection of approach regions, as described below. The filter \( {[{ {\varvec{\Lambda }}} ]}_q \) associated to a collection \({ {\varvec{\Lambda }}} \) of approach regions in \(\Omega \subset \mathbf {W} \) ending at \(q\in \partial \Omega \) is the intersection of the filters associated to the various approach regions in \({ {\varvec{\Lambda }}} \). Hence \({ {[{ {\varvec{\Lambda }}} ]}_q =\bigcap _{V\in { {\varvec{\Lambda }}} } {[V]}_q }\). A filter base of \( {[{ {\varvec{\Lambda }}} ]}_q \) may be described using the notion of selector. A selector of \({ {\varvec{\Lambda }}} \) is a function \(s:{ {\varvec{\Lambda }}} \rightarrow \varvec{\mathcal {P}}_{\bullet }(\Omega ) \) which assigns to each \(V\in { {\varvec{\Lambda }}} \) a tail \(s(V)\) of \(V\) at \(q\). For each selector s of \({ {\varvec{\Lambda }}} \), denote by \(\widetilde{s}\) the set \({\widetilde{s} {\mathop {=}\limits ^{\mathrm{def}}}\bigcup _{V\in { {\varvec{\Lambda }}} }s(V)}\) and call it a tail of \({ {\varvec{\Lambda }}} \). The collection of all tails of \({ {\varvec{\Lambda }}} \) is a filter base of \( {[{ {\varvec{\Lambda }}} ]}_q \). The filter \( {[{ {\varvec{\Lambda }}} ]}_q \) ends at \(q\), and, for each \(u\in \mathbb {C}^{\Omega }\):
Hence the concept of boundary value through a collection of approach region is subsumed under the notion of convergence along a filter. In view of (2.20), the filter \( {[{ {\varvec{\Lambda }}} ]}_q \) associated to \({ {\varvec{\Lambda }}} \) is called the essential shape of \({ {\varvec{\Lambda }}} \) at \(q\).
The angular filter on \(\mathbb {D}\) ending at \(q\) is the filter on \(\mathbb {D}\) ending at \(q\in \partial \mathbb {D}\), associated to the collection \( \mathsf {Stolz}_{q} \) (defined in Sect. 2.4).
2.5.7 Equivalent (Collections of) Approach Regions
The pointwise boundary behavior of a function through an approach region is dictated by its behavior along the associated filter. Hence the comparison between approach regions, from the viewpoint of pointwise boundary behavior, depends on the comparison of the associated filters, which we now introduce. Stein understood that, from the viewpoint of quantitative Fatou-type theorems, where families of approach regions are the relevant object of study, the comparison between [families of] approach regions is given on different grounds, as we will see.
In the following discussion, \(V_1\) and \(V_2\) denote approach regions in \(\Omega \subset \mathbf {W} \) ending at \(q\), and \(u\) is a function \(\Omega \rightarrow \mathbb {C}\). We say that the approach regions \(V_1\) and \(V_2\) are equivalent at \(q\), and write \( V_1\sim _{q}\,V_2 \), if they have the same essential shape at \(q\), i.e., if \( {[V_1]}_q = {[V_2]}_q \).
Lemma 2.6
The approach regions \(V_1\) and \(V_2\) are equivalent at \(q\) if and only if
If \( V_1\sim _{q}\,V_2 \), then \(u_{V_1}(q)\) exists \(\Leftrightarrow \) \(u_{V_2}(q)\) exists, and the two boundary values are equal.
If \({ {\varvec{\Lambda }}} _1,{ {\varvec{\Lambda }}} _2\) are two collections of approach regions in \(\Omega \subset \mathbf {W} \) ending at \(q\in \partial \Omega \), we say that \({ {\varvec{\Lambda }}} _1\) and \({ {\varvec{\Lambda }}} _2\) are equivalent at \(q\), and write \( { {\varvec{\Lambda }}} _1\sim _{q}\,{ {\varvec{\Lambda }}} _2 \), if they have the same essential shape at \(q\), i.e., if \( {[{ {\varvec{\Lambda }}} _1]}_q = {[{ {\varvec{\Lambda }}} _2]}_q \).
Lemma 2.7
The collections of approach regions \({ {\varvec{\Lambda }}} _1\) and \({ {\varvec{\Lambda }}} _2\) are equivalent at \(q\) if and only if
If \( { {\varvec{\Lambda }}} _1\sim _{q}\,{ {\varvec{\Lambda }}} _2 \), then \(u_{{ {\varvec{\Lambda }}} _1}(q)\) exists \(\Leftrightarrow \) \(u_{{ {\varvec{\Lambda }}} _2}(q)\) exists, and the two boundary values are equal. For example, the collections \( \mathsf {Stolz}_{q} \), \( \mathsf {Stolz}_{q}^{s} \), and \({\{\Gamma _{j}(q)\}}_{{j}}\) are equivalent at \(q\), since they are associated to the same filter, i.e., the angular filter on \(\mathbb {D}\) ending at \(q\).
2.5.8 Comparison of Filters
We have seen that the comparison of approach regions is subordinate to the comparison of the associated filters. Our terminology is motivated by the application to the comparison of approach regions, where we will also be able to appreciate the meaning of the following notions. Let \( \Phi _1, \Phi _2\in \mathsf {Filters}( {Y} ) \).
We already observed that the set \( \mathsf {Filters}( {Y} ) \), being a subset of \( \varvec{\mathcal {P}}_{\bullet }( \varvec{\mathcal {P}}_{\bullet }( {Y} ) ) \), is a partially ordered set under inclusion. Moreover, \( \mathsf {Filters}( {Y} ) \) is a complete semi-lattice, since the following properties hold.
- (inf):
-
The infimum (greatest lower bound) \(\bigwedge _{\alpha \in {I} } \Phi _{\alpha }\) of any family \({\{ \Phi _{\alpha }\}}_{\alpha \in {I} }\) of filters exists in \( \mathsf {Filters}( {Y} ) \). It is the intersection \(\bigcap _{\alpha \in {I} } \Phi _{\alpha }\) of all the filters in the family (see Lemma 2.2).
- (sup):
-
The supremum (least upper bound) \( \Phi _1\vee \Phi _2\) of two filters does not necessarily exist.
Since \( \Phi _1\cap \Phi _2\not =\emptyset \), for any two filters \( \Phi _1, \Phi _2\in \mathsf {Filters}( {Y} ) \), and the supremum \( \Phi _1\vee \Phi _2\) exists only in certain cases, only the following possibilities may occur:
-
(E–D) \( \Phi _1\vee \Phi _2\) does not exist: We say that \( \Phi _1\) and \( \Phi _2\) are eventually disjoint.
-
(C) The filters \( \Phi _1\) and \( \Phi _2\) are comparable if either \( \Phi _2\subset \Phi _1\) or \( \Phi _1\subset \Phi _2\). In this case, \( \Phi _1\vee \Phi _2\) exists and is equal to \( \Phi _1\) or to \( \Phi _2\).
-
(C 1) If \( \Phi _1\vee \Phi _2= \Phi _1\) (i.e., \( \Phi _2\subset \Phi _1\)), we say that \( \Phi _2\) is broader than \( \Phi _1\), and write \({ \Phi _2\succeq \Phi _1}\). We say that \( \Phi _2\) is strictly broader than \( \Phi _1\), and write \( \Phi _2 \succeq \Phi _1\), if \( \Phi _2\subsetneq \Phi _1\).
-
(C 2) If \( \Phi _1\vee \Phi _2= \Phi _2\), the roles are reversed.
-
-
(F–D) The filters \( \Phi _1\) and \( \Phi _2\) are not comparable, but \( \Phi _1\vee \Phi _2\) exists. Hence \( \Phi _1\vee \Phi _2\) is neither \( \Phi _1\) nor \( \Phi _2\). Then we say that \( \Phi _1\) and \( \Phi _2\) are frequently disjoint.
The filters \( \Phi _1\) and \( \Phi _2\) are disjoint if \( \Phi _1\setminus \Phi _2\not =\emptyset \) and \( \Phi _2\setminus \Phi _1\not =\emptyset \). Disjoint filters are either eventually disjoint or frequently disjoint. If two filters are not disjoint, then they are comparable.
It is convenient at times to say that \( \Phi _1\) is eventually (frequently) disjoint from \( \Phi _2\) to mean that \( \Phi _1\) and \( \Phi _2\) are eventually (frequently) disjoint.
Lemma 2.8
The filters \( \Phi _1\) and \( \Phi _2\) are eventually disjoint if and only if
Lemma 2.9
The filters \( \Phi _1\) and \( \Phi _2\) are frequently disjoint if and only if
A broader filter casts a more stringent condition on the existence of limiting values, in a precise sense.
Lemma 2.10
The filter \( \Phi _1\) is broader than the filter \( \Phi _2\) if and only if for each topological space \( \mathbf {S} \) and each function \(u: {Y} \rightarrow \mathbf {S} \), if \(\lim _{ \Phi _1}u\) exists and is equal to \(\xi \in \mathbf {S} \), then \(\lim _{ \Phi _2}u\) exists and is equal to \(\xi \).
In the study of limiting values, a relevant situation is the case where \( \Phi _1\) is not broader than \( \Phi _2\), i.e., when it is not true that \( \Phi _1\subset \Phi _2\). We say that \( \Phi _2\) lies frequently outside of \( \Phi _1\) if
This situation encompasses three different cases:
- (1):
-
\( \Phi _2\) is strictly broader than \( \Phi _1\).
- (2):
-
\( \Phi _1\) and \( \Phi _2\) are eventually disjoint.
- (3):
-
\( \Phi _1\) and \( \Phi _2\) are frequently disjoint.
The relevance of these three different conditions in the study of limiting values is this: If \( \Phi _2\) lies frequently outside of \( \Phi _1\), then the existence of \(\lim _{ \Phi _2}u\) does not follow a priori from the existence of \(\lim _{ \Phi _1}u\). The following results shed light on the meaning of this condition. Recall that \( \Phi _1\wedge \Phi _2\) is the intersection of \( \Phi _1\) with \( \Phi _2\), i.e., the collection \(\{R:R\in \Phi _1 \text { and }R\in \Phi _2\}\).
Lemma 2.11
The filter \( \Phi _2\) lies frequently outside of \( \Phi _1\) if and only if \( \Phi _1\wedge \Phi _2\text { is strictly broader than } \Phi _1\).
Lemma 2.12
If \(\lim _{ \Phi _1}u=\xi \) and \(\lim _{ \Phi _2}u=\xi \), then \(\lim _{ \Phi _1\wedge \Phi _2}u=\xi \).
2.5.9 Comparison of Approach Regions
We say that the approach regions \(V_1\) and \(V_2\) are eventually disjoint at \(q\) if the essential shape of \(V_1\) at \(q\) and the essential shape of \(V_2\) at \(q\) are eventually disjoint.
Lemma 2.13
The approach regions \(V_1\) and \(V_2\) are eventually disjoint if and only if
The approach region \(E_j\) defined in (2.24) and \(\Gamma _{k}(1)\) are eventually disjoint at 1 (for \(j=1,2\) and \(k\ge 1\)).
We say that the approach regions \(V_1\) and \(V_2\) are frequently disjoint at \(q\) if the essential shape of \(V_1\) at \(q\) and the essential shape of \(V_2\) at \(q\) are frequently disjoint.
Lemma 2.14
The approach regions \(V_1\) and \(V_2\) are frequently disjoint at 1 at \(q\) if and only if
The approach region \(E_3\) defined in (2.25) and \(\Gamma _{j}(1)\) are frequently (but not eventually) disjoint at 1 (\(j\ge 1\)).
It is convenient at times to say that \(V_1\) is eventually (frequently) disjoint from \(V_2\) to mean that \(V_1\) and \(V_2\) are eventually (frequently) disjoint.
The effect of inclusion on the associated filters is contravariant: Indeed, if \(V_2\subset V_1\), then \( {[V_1]}_q \subset {[V_2]}_q \), and the existence of \(u_{V_2}(q)\) is a weaker property than the existence of \(u_{V_1}(q)\). Indeed, if \(u_{V_1}(q)\) exists, then \(u_{V_2}(q)\) also exists and is equal to \(u_{V_1}(q)\). In view of Lemmas 2.10 and 2.5, we say that the approach region \(V_1\) is broader at \(q\) than the approach region \(V_2\), and write \(V_1\succeq V_2\), if the essential shape of \(V_1\) at \(q\) is broader than the essential shape of \(V_2\) at \(q\), i.e., if \( {[V_1]}_q \subset {[V_2]}_q \). This condition does not exclude the possibility that \(V_1\) and \(V_2\) are equivalent at \(q\).
Lemma 2.15
The approach region \(V_1\) is broader than \(V_2\) at \(q\) if and only if
It is possible that \(V_1\) is broader than \(V_2\) and yet that neither \(V_1\supset V_2\) nor \(V_2\supset V_1\) holds, as can be see from the following example, where \( \mathbf {W} =\mathbb {C}\), \(\Omega =\mathbb {D}\), \(q=1\).
We say that the approach region \(V_1\) is strictly broader at \(q\) than \(V_2\), and write \(V_1\succeq V_2\), if the essential shape of \(V_1\) at \(q\) is strictly broader than the essential shape of \(V_2\) at \(q\), i.e., if \( {[V_{1}]}_q \subsetneq {[V_{2}]}_q \).
Lemma 2.16
The approach region \(V_1\) is strictly broader than \(V_2\) at \(q\) if and only if
For example, \(\Gamma _{j+1}(q)\subset \mathbb {D}\) is strictly broader than \(\Gamma _{j}(q)\) at \(q\).
Lemma 2.17
If \(V_1\) and \(V_2\) are approach regions in \(\Omega \subset \mathbf {W} \) ending at \(q\), then \(V_1\cup V_2\) is an approach region ending at \(q\) and \( {[V_1\cup V_2]}_q = {[V_1]}_q \wedge {[V_2]}_q \).
In the study of limiting values, a relevant situation is the case where \(V_1\) is not broader than \(V_2\). We then say that \(V_2\) lies frequently outside of \(V_1\). This situation encompasses three different cases: (1) \(V_2\) is strictly broader than \(V_1\); (2) \(V_1\) and \(V_2\) are eventually disjoint; and (3) \(V_1\) and \(V_2\) are frequently disjoint. The relevance of these three different conditions in the study of limiting values is this: If \(V_2\) lies frequently outside of \(V_1\), then the existence of \(u_{V_2}(q)\) does not follow a priori from the existence of \(u_{V_1}(q)\).
Lemma 2.18
If \(V_1\) and \(V_2\) are approach regions in \(\Omega \subset \mathbf {W} \) ending at \(q\), then the following conditions are equivalent:
- (1):
-
\(V_2\) lies frequently outside of \(V_1\)
- (2):
-
For each \(O\in {\mathcal {N}}_{q}( \mathbf {W} ) \), \((O\cap V_2)\setminus V_1\ne \emptyset \).
- (3):
-
The approach region \(V_1\cup V_2\) is strictly broader than \(V_1\) at \(q\).
If \(V_2\) and \(V_1\) are eventually disjoint, then \(V_2\) lies eventually outside of \(V_1\). The approach region \(E_3\) defined in (2.25) lies frequently outside of \(\Gamma _{j}(1)\), but \(E_3\) and \(\Gamma _{j}(1)\) are not eventually disjoint.
Observe that \(\Gamma _{{j}+1}(q)\) is strictly broader than \(\Gamma _{j}(q)\) and hence it lies frequently outside of \(\Gamma _{j}(q)\), but \(\Gamma _{{j}+1}(q)\) and \(\Gamma _{{j}}(q)\) are not eventually disjoint.
If \(E\) is an approach region in \(\Omega \subset \mathbf {W} \) ending at \(q\in \partial \Omega \), and \({ {\varvec{\Lambda }}} \) is a collection of approach regions in \(\Omega \subset \mathbf {W} \) ending at \(q\in \partial \Omega \), we say that \(E\) lies frequently outside of \({ {\varvec{\Lambda }}} \) if, for each \(V\in { {\varvec{\Lambda }}} \), \(E\) lies frequently outside of \(V\). If \({ {\varvec{\Lambda }}} = \mathsf {Stolz}_{q} \), then \(E\) is said to lie frequently outside of the angular filter on \(\mathbb {D}\) ending at \(q\). We say that \(E\) and \({ {\varvec{\Lambda }}} \) are eventually disjoint if for each \(V\in { {\varvec{\Lambda }}} \), \(E\) and \(V\) are eventually disjoint. Of special interest is the case where \({ {\varvec{\Lambda }}} = \mathsf {Stolz}_{q} \): We then say that \(E\) and the angular filter on \(\mathbb {D}\) ending at \(q\) are eventually disjoint. For example, the approach region \(E\) defined in (2.25) lies frequently outside of the angular filter on \(\mathbb {D}\) ending at 1, but \(E\) and the angular filter are not eventually disjoint.
These notions are set theoretical and only depend on the particular “shape” of the two approach regions (more precisely, on the associated filters). We will soon describe another way approach regions may be “essentially larger” than one another: It depends on the notion of family of approach regions and is one of the spectacular contributions that Stein has given to the subject.
3 Pointwise Results for Holomorphic Functions in the Unit Disc
We are now ready to resume our discussion and plunge into the unit disc, which is a special domain, for a number of intertwined reasons. A group of symmetries acts on this space and makes it possible to derive the relevant objects from first principles—this is the point of view that enabled Hua Luogeng to derive the reproducing kernels in other contexts, which are also endowed with a rich group of symmetries. In this specific case, the Poisson kernel had already been explicitly determined long before, because of its link to the Abel summability of power series. The more concrete reason that makes the unit disc so special, is that it is the natural home of complex analysis,
that favored ally of one-dimensional Fourier analysis [166]
as Stein put it, and the fact that the latter—the study of Fourier series—lives precisely on its boundary. Indeed, many early results on Fourier series were obtained by the Moscow school of mathematics by first treating a trigonomeric series as the real part of a power series, and then, in Antoni Zygmund’s words, by
entering the interior of the unit disc [191].
Here, powerful methods of complex analysis are applicable. This is the so-called “complex method,” whose final step was to go back to the boundary by taking boundary values of holomorphic functions. For example, using the complex method, Privalov extended to integrable functions the theorem (previously proved by Lusin for \(L^2\) functions) about the existence of a fundamental singular integral (the Hilbert transform). This method of course required knowledge about the boundary behavior of holomorphic function in the unit disc, and indeed, the Moscow school (centered around Lusin and his outstanding students Privalov, Menshov, Kolmogorov, among others) contributed to this topic with seminal work, which was part of the background on which Stein operated, as we will see.
3.1 A Pointwise Theorem of Fatou Type for Radial Boundary Values in the Unit Disc
In 1826, Niels Henrik Abel proved a result that appears to be the first example of a pointwise Fatou-type theorem associated to radial boundary values. According to Konrad Knopp,
The theorem had already been stated and used by Gauss [...] The proof given by Gauss [...] is however incorrect, as he interchanged the two limiting processes which come under consideration for this theorem, without at all testing whether he was justified in so doing. [90, p. 177]
Theorem 3.1
([1]) If a power series
has radius of convergence equal to 1 and it converges for \(z=e^{i\theta }\) to a finite limit \(\xi \), then the radial boundary value of \(u\) at \(e^{i\theta }\) exists and is equal to \(\xi \).
In the special case \(\theta =0\), to which the general one may be reduced, Abel’s theorem says that
3.2 Abel’s Heuristic Principle
In retrospect, we can read in Abel’s theorem the elements of a principle that reappears over and over again in different guises. The partial sums \({\{{f}_{j}\}}_{{j}}\) in the hypothesis may be seen as a “boundary datum.” The conclusion concerns the behavior of the function \(u\), defined inside the unit disc by (3.1) in terms of the boundary datum. Abel’s heuristic principle says that there is a direct correspondence between a “regular” behavior of the boundary datum and a “good” boundary behavior of \(u\). Abel’s heuristic principle also governs the correspondence between functions harmonic in a domain and their boundary values:
The behavior of harmonic functions (in particular Poisson integrals) near the boundary is closely related to the differentiability properties of the boundary functions [168].
Stein’s work reached the roots of this correspondence.
3.3 Frobenius’ Rendition of Abel’s Principle
In 1880, Ferdinand Georg Frobenius proved the following result, whish is another instance of Abel’s principle: Indeed, it is an improvement of Abel’s theorem, since the same conclusion is obtained from a weaker assumption, which still concerns the “regularity” of the boundary data.
Theorem 3.2
([64]) If the power series in (3.1) has radius of convergence equal to 1 and if the averages of the partial sums defined in (3.2)
have a finite limit \(\xi \), then the radial boundary value of \(u\) at 1 exists and is equal to \(\xi \).
Frobenius was inspired by some ideas of Leibniz (1713), who had been questioned about the series \(1-1+1-1+1-\ldots \), whose sum, according to Grandi (1703), was 1/2 [68]. Leibniz observed that the partial sums \(\mathrm{f}_n\) are 0 or 1 with equal frequency and thus the value of \(1-1+1-1+1-\ldots \) had to be the average between 0 and 1, since
in going from the finite to the infinite the two values [0 and 1] merge in their mean-value [107]
In hindsight, Leibniz’s intuition can be interpreted as an anticipation of four related topics, where mean-values, or averages, play a prominent role: (i) the work of Henri Léon Lebesgue on a differentiation theorem (in the notion of Lebesgue point); (ii) martingale convergence theorems; (iii) ergodic theorems; (iv) the work of Godfrey Harold Hardy and John Edensor Littlewood on the maximal function, inspired by
[any] game in which a player compiles a series of scores of which an average is recorded [73]
Harmonic (and subharmonic) functions enter in this picture precisely because of their well-known properties related to averages. Stein’s curiosity led him to develop a keen interest in the link between these apparently unrelated topics, to which he contributed with deep conceptual results, also offering an impressive showcase of unsurpassed mastery of techniques where averages are central. Indeed, the “differentiability properties of the boundary functions” (which is “closely related to the behavior of harmonic functions near the boundary”) are expressed in terms of mean values, as in the differentiation of integrals (see below) [168].
3.4 Tauberian Results
If the \(\lim _{r\uparrow 1}\sum _{k=0}^{+\infty }a_kr^k\) exists and is finite, then the sequence \(f_n{\mathop {=}\limits ^{\mathrm{def}}}\sum _{k=0}^{n-1}a_k\) does not have to converge, unless we also assume some additional condition on the coefficients \({\{{a}_{j}\}}_{{j}}\). In other words, a “good” boundary behavior of \(u\) does not necessarily imply a “regular” behavior of the boundary datum, unless additional conditions are assumed. Alfred Tauber was perhaps the first to determine an additional condition of this kind. His result may thus be seen as an instance of Abel’s principle, in the converse direction: Under an additional hypothesis (now called Tauberian), from the boundary behavior of \(u\), we may deduce that the boundary datum behaves in some “good” way. In 1897, Tauber proved the following result.
Theorem 3.3
([175]) If \(a_k=o({1}/{k})\), then
Thus, this result says that, under an additional condition, if the radial boundary value at 1 of the holomorphic function in (3.1) exists and is finite, then the partial sums in (3.2) converge to the same limit. The following improvements of Tauber’s result, proved by Littlewood in 1911, are another instance of Abel’s principle in the converse direction.
Theorem 3.4
([112]) If \(a_k=O(1/k)\), then (3.4) holds.
These results have been completed by Hardy and Littlewood in 1924 as follows.
Theorem 3.5
([72]) If \(a_k=O(1/k)\) and \(u(z)=\sum _{k=0}^{+\infty }a_k{z}^k\) has the asymptotic boundary value \(\xi \) along some half-open Jordan arc ending at 1, then \(\sum _{k=0}^{n-1}a_k\) converges to \(\xi \).
Theorem 3.6
([72]) If
then the necessary and sufficient condition for the following to hold:
is that
for some half-open Jordan arc \(\varvec{c}\) in \(\mathbb {D}\) ending at 1. The hypothesis (3.5) is sharp: It cannot be relaxed to \(a_k=O(\phi _k/k)\) where the sequence \( { \{ {\phi }_{j} \} }_{j\ge 1} \) diverges to \(\infty \), because, in this case, (3.7) ceases to be either a necessary or a sufficient condition for (3.6).
Results of Tauberian type are also valid for the boundary behavior of harmonic functions (in much the same way as results of Abel type are also valid for harmonic functions): A result of this form is then called a converse of Fatou’s theorem.
3.5 Pointwise Theorems of Fatou Type for Angular Boundary Values
The following result, proved by Otto Stolz in 1875, is also an improvement of Abel’s theorem. Indeed, from the same assumptions, we obtain a stronger conclusion, since the existence of an angular boundary value is stronger than the existence of a radial boundary value.
Theorem 3.7
([171]) If a power series
has radius of convergence equal to 1 and it converges for \(z=e^{i\theta }\) to a finite limit \(\xi \), then the angular boundary value of \(u\) at \(e^{i\theta }\) exists and is equal to \(\xi \).
This result by Stolz has been improved by Alfred Pringsheim in 1901 in the following result, where only the existence of the limiting value of the averages in (3.3) is required, rather than the convergence of \(\sum _{k}a_k\).
Theorem 3.8
([140]) If the power series in (3.1) has radius of convergence equal to 1 and the averages in (3.3) have a finite limit \(\xi \), then the angular boundary value of \(u\) at 1 exists and is equal to \(\xi \).
3.6 Littlewood’s Sharpness Problem and Littlewood’s Principle
We now present a question that belongs to a general circle of ideas, which was dear to Hardy and Littlewood, centered on the task of finding “sharp” or “best possible” results.
Assumption 3.1
Assume that, in the setting of Sect. 2.1, a pointwise Fatou-type theorem holds, which asserts (for a given function \(u\) or class of functions) the existence of a filter \( \Phi \in \mathsf {Filters}( \Omega ) \) such that
- (1):
-
The filter \( \Phi \) ends at \(q\in \partial \Omega \).
- (2):
-
For each function \(u\) in the given class, the limiting value \({\lim _{ \Phi }u}\) exists.
The filter \( \Phi \) is called the convergence filter (for the given pointwise Fatou-type theorem). We say that the convergence filter \( \Phi \) is sharp, for the given pointwise Fatou-type theorem, if the following statement is not true:
Lemmas 2.10, 2.11, and 2.12 imply that (3.8) holds if and only if the following holds:
Question 3.1
In the context of a given pointwise Fatou-type theorem, as in Assumption 3.1, Littlewood’s Sharpness Problem is to determine whether the convergence filter in the theorem is sharp.
Recall that, if \({\Psi }\) is strictly broader than \( \Phi \), then the existence of \(\lim _{{\Psi }}u\) is a more stringent condition than the existence of \(\lim _{ \Phi }u\). Hence, if the given convergence filter is not sharp, it is then possible to obtain a stronger result. For example, in Abel’s theorem, the convergence filter is the radial filter. Stolz’s theorem shows that convergence holds along the angular filter, which is strictly broader then the radial filter. Hence the radial filter in Abel’s theorem is not sharp, and Stolz’s theorem is an improvement of Abel’s theorem. Littlewood’s sharpness problem can be posed for Stolz’s theorem as well, where the convergence filter is the angular filter. Observe that if C is any circle interior to and osculating the unit circle at 1, the associated filter \( {[C]}_1 \) is eventually disjoint from (and lies frequently outside of) the angular filter.
Theorem 3.9
([70]) There exists a convergent series \(\sum _ka_k\) such that, given any circle C interior to and osculating the unit circle at 1, the limiting value of the function \(u(z){\mathop {=}\limits ^{\mathrm{def}}}\sum _{k=0}^{+\infty }a_k{z}^k\) along \( {[C]}_1 \) does not exist.
Theorem 3.9 is important because it established for the first time “Littlewood’s principle,” which was accepted for several decades as unconditionally valid:
it is not possible to obtain boundary values through “tangential” approach regions.
The opposition between “angular” and “tangential” approach turned out to be a key to understand the boundary behavior of holomorphic (or merely harmonic) functions, but it also exhibited unexpected, surprising results. Indeed, Stein showed that the limitations of Littlewood’s Principle lie in the difference (which had remained overlooked for a long time) between approach regions which are eventually disjoint from the angular filter (which are actually tangential) and those lying frequently outside of it.
4 Qualitative Boundary Behavior (I)
The term collection is a synonym for set, but family is not: Following Samuel [152], if \(E\) is a set, a family of elements of \(E\) based on \( {I} \) is a function \(\alpha : {I} \rightarrow {}E\), where \( {I} \) is a “set of indexes.” If \( {I} \) is the boundary of a topological space, we may omit the explicit reference to it, as, e.g., in family of filters.
4.1 Notation in Measure Theory
The term measure (on a set \( {X} \)) denotes a positive and complete measure, defined on a \(\sigma \)-algebra \(\varvec{\mathcal {S}}\) of subsets of \( {X} \), where complete means that each subset of a set in \(\varvec{\mathcal {S}}\) which has measure zero also belongs to \(\varvec{\mathcal {S}}\). The term Borel measure on a topological space \( {X} \) denotes a measure defined on a \(\sigma \)-algebra \(\varvec{\mathcal {S}}\) of subsets of \( {X} \) which contains the \(\sigma \)-algebra \( \varvec{\mathcal {B}}( {X} )\) of Borel sets of \( {X} \).
Following common usage, harmonic measure on the boundary \( {X} \) of a bounded domain in \(\mathbb {R}^n\) (with respect to a given pole) is denoted by \(\omega \). If \( {X} \) is the boundary of the unit disc, harmonic measure with pole at the origin is normalized arc-length \(\mathrm{d}\theta /2\pi \). If \( {X} =\mathbb {R}^n\), Lebesgue measure is denoted by \(\mathrm{d}\,\omega \) or \(dq\). If no ambiguity is possible, we may omit explicit mention of \(\omega \), and, following Stein [163], denote the \(\omega \)-measure of a set \(\{\ldots \}\) by \(|\{\ldots \}|\) instead of \(\omega (\{\ldots \})\).
The symbol \(\varvec{\omega }\) (in bold-face) denotes the average operator associated to \(\omega \) (see below).
In order to simplify the statements of many results in the subject, it is handy to introduce the following binary relations “
 ” and “
\(\varvec{\subset _{\omega }}\)” between subsets of a measure space, which are obtained from the ordinary relations “
\(=\)” and “
\(\subset \)” by replacing the empty set with a null set. A null set in a measure space
\(( {X} ,\varvec{\mathcal {S}}, \omega )\) is a subset
\(Q\in \varvec{\mathcal {S}}\) with
\(\omega (Q)=0\). If
\(Q,R\subset {X} \), we say that
\(Q\) is a.e. contained in
\(R\), and write
” and “
\(\varvec{\subset _{\omega }}\)” between subsets of a measure space, which are obtained from the ordinary relations “
\(=\)” and “
\(\subset \)” by replacing the empty set with a null set. A null set in a measure space
\(( {X} ,\varvec{\mathcal {S}}, \omega )\) is a subset
\(Q\in \varvec{\mathcal {S}}\) with
\(\omega (Q)=0\). If
\(Q,R\subset {X} \), we say that
\(Q\) is a.e. contained in
\(R\), and write
if the difference \(Q\setminus R\) is a null set: This means that almost all of \(Q\) is a subset of \(R\). We say that the sets \(Q,R\) are almost everywhere equal, and write

if
Observe that
 if and only if the symmetric difference
\(Q\triangle R{\mathop {=}\limits ^{\mathrm{def}}}(Q\setminus R)\cup (R\setminus Q)\) is a null set. We say that
\(R\) is a.e. disjoint from
\(Q\) if
if and only if the symmetric difference
\(Q\triangle R{\mathop {=}\limits ^{\mathrm{def}}}(Q\setminus R)\cup (R\setminus Q)\) is a null set. We say that
\(R\) is a.e. disjoint from
\(Q\) if
 , i.e., if
\(Q\cap R\) is a null set.
, i.e., if
\(Q\cap R\) is a null set.
A set
\(Q\subset {X} \) has full measure if
 , i.e., if
\( {X} \setminus Q\) is a null set. A property is said to hold a.e. if the set of points in
\( {X} \) for which it holds has full measure. A set
\(Q\subset R\) has full measure in
\(R\) if
, i.e., if
\( {X} \setminus Q\) is a null set. A property is said to hold a.e. if the set of points in
\( {X} \) for which it holds has full measure. A set
\(Q\subset R\) has full measure in
\(R\) if
 .
.
If \( {X} \equiv ( {X} ,\varvec{\mathcal {S}}, \omega )\) is a measure space (where \(\varvec{\mathcal {S}}\subset \varvec{\mathcal {P}}( {X} ) \) a \(\sigma \)-algebra, and \(\omega :\varvec{\mathcal {S}}\rightarrow [0,+\infty ]\) a measure), the vector space of measurable complex-valued functions defined a.e. on \( {X} \), whose p th power is integrable, is denoted by \(\mathcal {L}^p( {X} )\) ( \(p>0\)). The space \( L^{p}( {X} ) \) is the quotient of \(\mathcal {L}^p( {X} )\) modulo a.e. equivalence. Elements of \(L^p( {X} )\) are denoted in normal font. Hence the class of functions which contains \(f\in \mathcal {L}^p( {X} )\) is denoted by \(\mathrm{f}\in L^p( {X} )\).
The mean value of \(f\in \mathcal {L}^1( {X} )\) over \(Q\in \varvec{\mathcal {S}}\) is defined, provided \(0<\omega (Q)<+\infty \), as follows:

In (4.4), the the vertical bar notation, which is well established in probability theory to denote conditional expectation, of which (4.4) is a particular case (see below), has been modified to a vertical dashed line in order to reduce notational clutter when absolute values are involved.
The sets \(Q\in \varvec{\mathcal {S}}\) for which \(0<\omega (Q)<+\infty \) are called amenable:
Since mean values do not depend on the representative of \(\mathrm{f}\in L^1( {X} )\), the mean value pairing \(\varvec{\omega }\), associated to the measure space \(( {X} ,\varvec{\mathcal {S}},\omega )\), may be defined with \(L^1( {X} )\) in place of \(\mathcal {L}^1( {X} )\), as follows:

4.2 A General Setting for Qualitative Boundary Behavior
In qualitative Fatou-type theorems, the main concern is the a.e. existence of boundary values (as opposed to pointwise results, which only concern the boundary behavior at individual points).
4.2.1 Imbeddings in the Boundary
We say that \(\imath : {X} \rightarrow \mathbf {W} \) is an imbedding of \( {X} \) into \( \mathbf {W} \), and write \(\imath : {X} \hookrightarrow \mathbf {W} \), if the following holds:
- (I 1):
-
\( {X} \) and \( \mathbf {W} \) are topological spaces.
- (I 2):
-
\(\imath : {X} \rightarrow \mathbf {W} \) is a homeomorphism of \( {X} \) with \(\{\imath (q):q\in {X} \}\), where the set \(\{\imath (q):q\in {X} \}\) is endowed with the subspace topology inherited by the ambient space \( \mathbf {W} \).
Observe that, unless the set \(\imath [ {X} ]{\mathop {=}\limits ^{\mathrm{def}}}\{\imath (q):q\in {X} \}\) is isolated in \( \mathbf {W} \), in a neighborhood of \(q\) in \( {X} \), there are only points of \( {X} \), but in a neighborhood of \(\imath (q)\) in \( \mathbf {W} \), there are also points of the ambient space \( \mathbf {W} \) other than \(\imath [ {X} ]\). Since an imbedding \(\imath : {X} \hookrightarrow \mathbf {W} \) preserves the topology of \( {X} \), we may identify \(q\) with \(\imath (q)\).
Now assume that the following additional condition holds:
-
(I 3) \(D\) is a subset of \( \mathbf {W} \) and \(\imath [ {X} ]\subset \partial _{ \mathbf {W} }{D}\).
It follows that the function \(\imath : {X} \rightarrow \partial _{ \mathbf {W} }{D}\) (obtained by restriction of \(\imath : {X} \rightarrow \mathbf {W} \)) is also an imbedding of \( {X} \) into \(\partial _{ \mathbf {W} }{D}\). We then say that \( {X} \) is imbeddable in the boundary of \(D\) in \( \mathbf {W} \), and write
The case where \( {X} \) is (a subset of) the topological boundary \(\partial \Omega \) of a bounded domain \(\Omega \) in \(\mathbb {R}^n\) fits within this general setting: Here, \( \Omega \) plays the role of \(D\), and the imbedding is the identity. The reader may keep this standard setting in mind, before we see examples of the more general setting described above, which arise in the area of the differentiation of integrals (see below). Having this standard setting in mind, functions \(f: {X} \rightarrow \mathbb {C}\) will be called boundary functions, and subsets of \( {X} \) boundary sets; cf. Sect. 2.1.
4.2.2 Families of Boundary Filters and Families of Approach Regions
If \(\imath : {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \) is an imbedding of \( {X} \) in the boundary of \(D\) in \( \mathbf {W} \), and \( S\subseteq {X} \), a family of boundary filters on \(D\) (based on \( S\)) is a function \( \varvec{{\Phi : S\rightarrow \mathsf {Filters}(D) }}\) such that for each \(q\in S\),
A family of approach regions in \(D\) based on \( S\) is a function \(\varvec{\varphi : S\rightarrow \varvec{\mathcal {P}}_{\bullet }(D) }\) such that, for each \(q\in S\),
In other words, \(\varphi (q)\) is an approach region in \(D\) ending at \(\imath (q)\).
As in (2.18), if \(\varphi : S\rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) is a family of approach regions in \(D\) based on \( S\), the associated family of boundary filters on \(D\) based on \( S\) is denoted by
The value of \( [\varphi ] \) at \(q\in S\) is the essential shape of the approach region \(\varphi (q)\) at \(q\): In order to reduce notational clutter, we denote it by \( [\varphi (q)] \) rather than \( {[\varphi (q)]}_q \).
4.2.3 The Relative Fatou set and the Associated Boundary Function
If \(\imath : {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \) is an imbedding of \( {X} \) in the boundary of \(D\) in \( \mathbf {W} \), and \(\Phi : S\rightarrow \mathsf {Filters}(D) \) is a family of boundary filters on \(D\) based on \( S\subseteq {X} \), the Fatou set of \(u\in \mathbb {C}^{D}\) relative to \(\Phi \) is defined as follows:
Observe that the relative Fatou set \( \mathsf {Fatou}(u;\varphi )\) may be empty. The boundary-values function of \(u\) along \(\Phi \) is the boundary function
defined as \( { (\lim _{\Phi }u)(q){\mathop {=}\limits ^{\mathrm{def}}}\lim _{\Phi (q)}u}\).
If \(\varphi \) is a family of approach regions in \(D\) based on \( S\), the relative Fatou set \(\varvec{ \mathsf {Fatou}(u;\varphi )}\) and the associated boundary-values function \(\varvec{{\lim _{\varphi }u}}\) are well defined, since to every family of approach regions, we may associate a family of boundary filters, as in (4.10).
4.2.4 The Radial Approach and the Angular Approach in the Unit Disc
The angular approach to the boundary of \(\mathbb {D}\) is the family of boundary filters \(\partial \mathbb {D}\rightarrow \mathsf {Filters}(\mathbb {D}) \) which assigns to every \(q\in \partial \mathbb {D}\) the angular filter on \(\mathbb {D}\) ending at \(q\), as defined in Sect. 2.5.6. The associated boundary function \( {u}_{\flat }: \mathsf {Fatou}{(u)} \rightarrow \mathbb {C}\), defined in (2.8), encodes the angular boundary values of \(u\).
The radial approach to the boundary of \(\mathbb {D}\) is the family of boundary filters associated to the family of radial approach regions:
where \(\rho (q){\mathop {=}\limits ^{\mathrm{def}}}\{sq:0\le {}s<1\}\). The associated boundary function \(u_{\rho }: \mathsf {Fatou}(u;\rho )\rightarrow \mathbb {C}\) yields the radial boundary values of \(u\).
4.2.5 A General Setting for Qualitative Boundary Behavior
A setting where we may study the a.e. existence of boundary values, as well as results which arise in the area of differentiation of integrals, will now be given. Hence this setting will provide a formal unification of two topics which, as Stein observed many times, are closely related: The “behavior of harmonic functions [\(u\)] near the boundary” and the “differentiability properties of the boundary functions [\(f\)]” [168]. The typical example of this close relation is this:
(see below for a definition of the notion of Lebesgue point). The close relation between the two topic has already been touched upon in Sect. 3.2, and it appears prominently in Fatou’s work as well as in Stein’s work and elsewhere [32, 59, 163, 165].
The study of the “differentiability properties of [boundary] functions” is known in the literature as “differentiation of integrals.” Results on differentiation of integrals are usually based on subtle “covering theorems” [97, 99]. In the appendix, we will present a new result (the existence of “amenable nets”) which capitalizes on an idea due to de la Vallee Poussin, which was precisely meant to avoid the Vitali covering theorem employed by Lebesgue in his differentiation theorem (see below) [39, 40, 104]. Here is the setup.
- (Q 1):
-
An imbedding \(\imath : {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\) of \( {X} \) in the boundary of \(D\) in \( \mathbf {W} \) is given.
- (Q 2):
-
A complex-valued function \(u:D\rightarrow \mathbb {C}\) is given.
- (Q 3):
-
A measure \(\omega \) is given on \( {X} \).
- (Q 4):
-
A subset \( S\subseteq {X} \) of positive measure is given.
- (Q 5):
-
A family \(\Phi : S\rightarrow \mathsf {Filters}(D) \) of boundary filters on \(D\) based on \( S\) is given.
The property
(which the function \(u\) may or may not have) describes the qualitative boundary behavior of \(u\) with respect to the given family of boundary filters \(\Phi \). If a theorem gives sufficient conditions which entail (4.15), it is called a qualitative Fatou-type theorem.
Contrary to what one may think at first, as we will see, it is not true that a qualitative Fatou-type theorem necessarily arises from the “superposition” of many pointwise results (and in this case, a result of this kind is not considered to be genuinely qualitative). We use the term qualitative because, as Stein observed several times, the mere existence of a limit is
of an elusive nature and thus difficult to pin down analytically [160].
Another variant of the notion of boundary behavior, which is central to the field, is the quantitative boundary behavior (see below). We will see that most qualitative results arise from quantitative ones.
4.3 A Pseudo-Qualitative Fatou-Type Theorem for Unrestricted Convergence
Theorem 4.1
If \(\Omega \subset \mathbb {R}^n\) is bounded and open and \(u:\Omega \rightarrow \mathbb {C}\) is uniformly continuous, then \(u_{\Omega }(q)\) exists for each \(q\in \partial \Omega \).
Theorem 4.1 is not a genuine example of a qualitative Fatou-type theorem, since ultimately it arises from the superposition of pointwise results [15, p. 157]. It is associated to unrestricted convergence (where the filter \(\Phi (q)\) is the unrestricted filter at \(q\)).
4.4 A Qualitative Theorem of Fatou Type for Arbitrary Functions: A Bootstrap Result
An important example of a qualitative Fatou-type result, which is not obtained as the superposition of many pointwise Fatou-type theorems, is Theorem 4.2, based on the family of approach regions in \(\mathbb {D}\):
defined in (2.7) for \({j}\ge {}1\). Define \(\Gamma _0(e^{i\theta }){\mathop {=}\limits ^{\mathrm{def}}}\{re^{i\theta }:0\le {}r<1\}\). Observe that \(\Gamma _{j}\) is a family of approach regions in \(\mathbb {D}\), for each integer \({j}\ge 0\); For each \(q\in \partial \mathbb {D}\), the set \(\Gamma _{{j}}(q)\) increases monotonically to \(\mathbb {D}\) as \({j}\rightarrow {}+\infty \); \(\Gamma _{{j}}(e^{i\theta })\) equals \(\Gamma _{{j}}(1)\) rotated through an angle \(\theta \) around \(z=0\), i.e., \(\Gamma _{{j}}(e^{i\theta }) = \{ z{}e^{i\theta }: z\in \Gamma _{{j}}(1) \} \). The measure on \(\partial \mathbb {D}\) is normalized arc-length.
Theorem 4.2
If \(u\in \mathbb {C}^{\mathbb {D}}\) and \(Q\in \varvec{\mathcal {A}}({\partial \mathbb {D}}) \), then
Observe that Theorem 4.2 holds for any function \(u:\mathbb {D}\rightarrow \mathbb {C}\). Recall from (4.1) that \( Q\subset _{\omega } \mathsf {Fatou}{(u)} \) means that \(Q\setminus \mathsf {Fatou}{(u)} \) is a null set.
Theorem 4.2 is a qualitative Fatou-type theorem, since at any individual point \(q\in \partial \mathbb {D}\), it is not true that the existence of a limiting value through \(\Gamma _{1}(q)\) implies the existence of the angular boundary value. Theorem 4.2 exhibits a “bootstrap” phenomenon which holds for any function: The existence of finite boundary values through \(\Gamma _{1}(q)\) at each \(q\in S\), implies, at points \(q\) which form a set of full measure in \( S\), the existence of boundary values through \(\Gamma _{j}(q)\) for each \({j}\). This conclusion is a definite improvement of the original assumption. Hence the statement of Theorem 4.2 is not pointwise and cannot be obtained as the superposition of many pointwise Fatou-type theorems. If we replaced \(\Gamma _1\) with \(\Gamma _0\) in (4.16), the conclusion would be false.
4.5 A Qualitative Theorem of Fatou Type for Bounded Holomorphic Functions
Theorem 4.3 is perhaps the first occurrence of a qualitative Fatou-type theorem. It is due to Fatou in 1906, in a seminal work to which the origin of the “complex method” may be traced. Indeed, Fatou was interested in the problem of reconstructing a Lebesgue integrable function (modulo a null set) from its Fourier coefficients. Significantly, he was also interested in the study of a generalized version of the Dirichlet problem for the open unit disc, where the boundary datum is assumed to be merely Lebesgue integrable—rather than continuous, as in the classical Dirichlet problem (see below). Both problems are inversion problems, i.e., they may be formulated in the following general terms: Given an injective map
one wants to recapture \(\mathrm{f}\) from a knowledge of \(R(\mathrm{f})\). In the first problem, \(R\) is the Fourier transform of periodic functions; in the second one, \(R\) is the Poisson operator, which maps an integrable function on \(\mathbb {D}\) to its “harmonic extension” (see below). The link between the two inversion problems is given by “the complex method,” coupled with the fact that harmonic functions in \(\mathbb {D}\) are real parts of holomorphic functions. Indeed, in this setting, real-variable theory (including potential theory), complex analysis, and Fourier analysis form a threefold unity, as Stein would put it.
Theorem 4.3
([59]) If \(u\in \mathcal {O}(\mathbb {D})\) and
then \( \mathsf {Fatou}{(u)} \) has full measure in \(\partial \mathbb {D}\).
Recall that in \( \mathsf {Fatou}{(u)} \), defined in (2.9), the limiting value is the angular one. An important class of qualitative Fatou-type theorems, which will shed light on Theorem 4.3, is given by results on differentiation of integrals (see below).
4.6 The Inversion Problem for Functional Representations
Let \(( {X} ,\varvec{\mathcal {S}}, \omega )\) be a measure space, and let \(D\) be a set. A linear and injective operator
defined on \( L^{p}( {X} ) \), is called a functional representation of \( L^{p}( {X} ) \) on \(D\), because an element \(\mathrm{f}\in L^{p}( {X} ) \) is not a function but an equivalence class of functions, while \(R(\mathrm{f}) \in {\mathbb {C}}^{D}\) is a genuine function. If \(R\) is only defined on a subspace \( \mathcal {H}\) of \( L^{p}( {X} ) \), we say that \(R\) is a functional representation of \( \mathcal {H}\).
A left inverse of \(R\) exists, since \(R\) is injective: It is an operator \(\widetilde{R}:{\mathbb {C}}^{D}\rightarrow {} L^{p}( {X} ) \) such that
In other words, a left inverse of \(R\) enables us to reconstruct \(\mathrm{f}\) in terms of \(R{\mathrm{f}}\). The inversion problem for a functional representation \(R\) is the task of finding an explicit description of a left-inverse \(\widetilde{R}\) of \(R\). For example, the task of reconstructing a periodic function from its Fourier coefficients, known as the Fourier inversion problem, is the inversion problem for the functional representation \( L^{p}(\partial \mathbb {D}) \rightarrow \mathbb {C}^{\mathbb {Z}}\) which maps a periodic function to the sequence of its Fourier coefficients.
4.7 The Inversion Problem for Geometrizable Functional Representations
A functional representation (4.18) is said to be geometrizable if \( {X} \) is imbeddable in the boundary of \(D\) in an appropriate ambient space \( \mathbf {W} \).
If the functional representation \(R\) in (4.18) is geometrizable, a solution of the inversion problem for \(R\) may be given by a family \(\Phi : {X} \rightarrow \mathsf {Filters}(D) \) of boundary filters on \(D\) based on \( {X} \), as follows: We say that \(\Phi \) solves the inversion problem for \(R\) if
Observe that (4.19) implies, in particular, which \( \mathsf {Fatou}(R(\mathrm{f}) ;\Phi )\) has full measure in \( {X} \). Here, the same family of boundary filters is used for all functions in \( L^{p}( {X} ) \).
Similarly, a solution of the inversion problem for \(R\) may be given by a family of approach regions \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) in \(D\) based on \( {X} \), and we say that \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) solves the inversion problem for \(R\) if (4.19) holds with \(\Phi \) replaced by \( [\varphi ] \).
4.8 The Poisson Integral
The Poisson integral \( Pf \) of \(f\in \mathcal {L}^1( {X} )\) is the function \( Pf :\mathbb {D}\rightarrow \mathbb {C}\) defined by
Since (4.20) does not change if we alter \(f\) on null sets, we obtain the operator \(P: L^{1}(\partial \mathbb {D}) \rightarrow \mathbb {C}^{\mathbb {D}}\), called the Poisson operator, which is a functional representation of \( L^{1}(\partial \mathbb {D}) \) on \(\mathbb {D}\). The Poisson operator was first met in the study of summability methods of series: If \(\mathrm{f}\in L^{1}(\partial \mathbb {D}) \) and
is its Fourier series, then the Abel means of (4.21) are the Poisson integral of \(\mathrm{f}\)
The Poisson operator
solves the classical Dirichlet problem for \(\mathbb {D}\) (see below) and is geometrizable, since \(\partial \mathbb {D}\) is the boundary of \(\mathbb {D}\) in \(\mathbb {C}\). In 1906, Fatou showed that the angular approach solves the inversion problem for (4.22).
Theorem 4.4
([59]) If \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\), then the Fatou set of \(\, Pf \) has full measure in \(\partial \mathbb {D}\), and the boundary function \( {( Pf )}_{\flat }: \mathsf {Fatou}{( Pf )} \rightarrow \mathbb {C}\) is equal almost everywhere to \(f\).
Recall that in \( \mathsf {Fatou}{( Pf )} \), the limiting value is the angular one; see (2.9). This result should be compared to the following:
Theorem 4.5
There exists a function \(\mathrm{f}\in L^{1}(\partial \mathbb {D}) \) such that the unrestricted boundary value \({( P\mathrm{f} )}_{\mathbb {D}}(q)\) exists for no \(q\in \partial \mathbb {D}\).
Another qualitative theorem of Fatou type, motivated by its applications to the study of Fourier series, is due to Privalov (1919) and is based on Theorem 4.3. Given a real-valued function \(f\in \mathcal {L}^1(\partial \mathbb {D})\), we denote by \( Q{}f \in h(\mathbb {D}) \) the harmonic function conjugate to \( Pf \), normalized so as to vanish at 0.
Theorem 4.6
([141]) If \(f\in \mathcal {L}^1(\partial \mathbb {D})\), then \( \mathsf {Fatou}{( Q{}f )} \subset \partial \mathbb {D}\) has full measure.
Hence the function \(\widetilde{f} (q){\mathop {=}\limits ^{\mathrm{def}}}{( Q{}\mathrm{f} )}_{\flat }(q)\) is defined a.e. on \(\partial \mathbb {D}\). It is called the function conjugate to \(f\), and it can be expressed as a singular integral. The function \(\widetilde{f} \) does not necessarily belong to \(\mathcal {L}^1(\partial \mathbb {D})\), and there are functions \(f\in \mathcal {L}^1(\partial \mathbb {D})\) such that \(\widetilde{f} \) does not belong to \(\mathcal {L}^1(I)\) on any interval I. However, in 1925, Andrej Nikolaevič Kolmogorov proved the following substitute result, called weak-type (1,1) inequality, motivated by its applications to the study of Fourier series:
Theorem 4.7
([91]) There exists \( \varvec{c} >0\) such that for each \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\) and each \(r>0\)
In (4.23), we use the uncluttered notation \({\{g\,{>}r\}}\) to denote the set \({\{q{\in }\,\partial \mathbb {D}:g(q)\,{>}r\}}\). Theorem 4.7 yields an inequality involving the so-called distribution function of the angular boundary values of the harmonic conjugate of the Poisson integral of \(\mathrm{f}\), where the inequality is uniform w.r.t. functions of a certain class, since the same constant \( \varvec{c} \) applies to all functions in \(\mathcal {L}^1(\partial \mathbb {D})\): It is a weak-type (1, 1) inequality, and it belongs to the so-called quantitative theorems of Fatou type (see below).
In order to understand which points in \(\partial \mathbb {D}\) belong to \( \mathsf {Fatou}{( Pf )} \), the notion of Lebesgue point of \(f\), which is a key to the answer, leads us to the problem of the differentiation of integrals, which has a deep role in the subject. In the appendix, we present a new result, on the existence of amenable nets, which is deeply connected to differentiation of integrals, thanks to a technique due to de la Vallée Poussin [39, 40].
5 Differentiation of Integrals
The mean-value pairing \(\varvec{\omega }:L^1( {X} )\times \varvec{\mathcal {A}}({ {X} }) \rightarrow \mathbb {C}\) in (4.6) is linear in the first variable, and we may, by the familiar device of fixing the first variable first, represent it as a linear and injective operator as follows:
where (with slight but innocuous abuse of language)  . The function
. The function
encodes all the averages of \(\mathrm{f}\in L^1( {X} )\), and (5.1) is called the mean-value operator for \( {X} \).
The problem of recapturing a function from its mean values may be described as follows. If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a \(\sigma \)-finite measure space and a measure \(\nu \) on \(\varvec{\mathcal {S}}\) is absolutely continuous with respect to \(\omega \), then there is a measurable function \(f\) on \( {X} \) (which is unique modulo alterations on null sets) such that
The function \(f\) is called the Radon–Nykodim derivative of \(\nu \) with respect to \(\omega \), and the task of recapturing \(f\) from \(\nu \) and \(\omega \) is equivalent to the task of recapturing \(\mathrm{f}\in L^{1}( {X} ) \) from the knowledge of all its averages. Now, observe that the latter is the inversion problem for the functional representation \(\varvec{\omega }\) in (5.1). This problem is known in the literature as the problem of the differentiation of integrals.
The problem of expressing a left inverse of \(\varvec{\omega }\) may also be posed for its restriction to certain subcollections \( \varvec{\mathcal {A}}'({ {X} }) \subset \varvec{\mathcal {A}}({ {X} }) \), in the following terms: Determine conditions on \( \varvec{\mathcal {A}}'({ {X} }) \) which ensure that the map \(\varvec{\omega }^{\prime }: L^{1}( {X} ) \rightarrow {\mathbb {C}}^{ \varvec{\mathcal {A}}'({ {X} }) }\), obtained by restriction, is injective, and find an explicit expression for its left-inverse.
We will present some solutions (in various degrees of generality) to the inversion problem for the functional representation in (5.1).
5.1 Martingales and the Dyadic Decomposition of \(\varvec{\partial \mathbb {D}}\)
The function  is linear in \(\mathrm{f}\), and it has the following mean-value property in \(Q\): If \(Q\) is the disjoint union of \(Q_1\) and
\(Q_2\), then
is linear in \(\mathrm{f}\), and it has the following mean-value property in \(Q\): If \(Q\) is the disjoint union of \(Q_1\) and
\(Q_2\), then
 is the mean value of
is the mean value of
 and
and
 , where the average is taken with respect to the relative measures
\(p_{k}{\mathop {=}\limits ^{\mathrm{def}}}\frac{\omega (Q_k)}{\omega (Q)}\) of
\(Q_1\) and
\(Q_2\) in
\(Q\), so that
, where the average is taken with respect to the relative measures
\(p_{k}{\mathop {=}\limits ^{\mathrm{def}}}\frac{\omega (Q_k)}{\omega (Q)}\) of
\(Q_1\) and
\(Q_2\) in
\(Q\), so that

There is indeed a strong analogy between (4.22) and (5.1), i.e., between \( Pf \) and \( \varvec{\omega }(\mathrm{f}) \); cf. [52]. The mean-value property (5.3) leads to a martingale, a structure which has strong ties to the notion of net (defined below). de la Vallée Poussin, motivated by the need to avoid the Vitali covering theorem arising in the differentiation of integrals, introduced the notion of a net in 1915 (under the name of reseau) [39, 40]. The existence of a net is a premise for the applicability of de la Vallée Poussin’s ideas, which may be established quite explicitly on Euclidean spaces: In the appendix, we show that amenable nets do exist in great generality, and therefore provide the necessary premise for the differentiability of integrals à la de la Vallée Poussin. This result has the potential of producing new results in applications to the behavior of holomorphic functions of several complex variables, as well as in applications to that part of probability theory connected with martingales. We plan to return to these matters in the near future.
Martingales reappeared implicitly in analysis (although not with this name) in the work of Paley in 1932 [135], in the context of the Walsh–Kaczmarz functions (now called Walsh–Paley functions). In the same year, they peeped into probability theory in the work of Serge Bernstein and, a few years later, hidden in a technical condition, in the work of Paul Levy (1935) but still at the level of the unconscious. The notion of a martingale was later brought to full light by Jean André Ville and it blossomed in the hands of J. L. Doob (see Sect. 12).
The Walsh–Paley functions, as well as the dyadic decomposition of the interval [0, 1], are intimately related to each other. Indeed, Stein used the latter in his recasting of the Littlewood-Paley theory in general terms, which has been seminal in the subject [164]. A decomposition of dyadic type is a sequence of nested partitions that appears prominently in the stopping-time argument used in the Calderón-Zygmund decomposition: The prototype example is the collection of dyadic arcs, i.e., intervals of the form:
where \(m=0,1,2,\ldots \), k is an integer, and \(0\le {}k\le {}2^{m}-1\). The open arc in (5.4) is a dyadic arc of generation m. The dyadic arcs are obtained by consecutive bisections from the arc \(\{e^{i\theta }:0<\theta <2\pi \}\). Hence the collection of all dyadic arcs has the inclusion–exclusion property: Two dyadic arcs are either disjoint, or one of them is contained in the other. We will soon show the relevance of these structures.
5.2 Differentiation of Integrals in a Metric Measure Space
A metric measure space is a set \( {X} \) endowed with a metric \(\delta \) and a positive Borel measure \(\omega \). An open (closed) ball of center \(q\in {X} \) and radius \(r>0\) in a metric space \( {X} \equiv ( {X} ,\delta )\) is defined as follows. The closed ball is the set \(\varvec{{B}[q,r]{\mathop {=}\limits ^{\mathrm{def}}} \left\{ q^{\prime }\in {X} : \delta (q^{\prime },q)\le r \right\} }\). The open ball is the set \({B}(q,r){\mathop {=}\limits ^{\mathrm{def}}} \left\{ q^{\prime }\in {X} : \delta (q^{\prime },q)<{}r \right\} \). If any ambiguity is likely, instead of \({B}({q},{r})\), we may write \( {B}_{ {X} ,\delta } \left( q,r\right) \), or \( {B}_{ {X} } \left( q,r\right) \), or \( {B}_{\delta } \left( q,r\right) \), according to which ambiguity must be avoided. The collection of all open (closed) balls in \( {X} \) is denoted by \( \mathbf {B}( {X} ) \) ( \( \mathbf {B}[{ {X} }] \), resp.). The topology generated by \( \mathbf {B}( {X} ) \) is denoted by \( \varvec{\mathcal {G}}( {X} ,\delta )\) or by \( \varvec{\mathcal {G}}( {X} )\) if there is no ambiguity about the metric. Generic elements of \( \mathbf {B}( {X} ) \) are denoted by I, since they play the role of intervals.
An extended pseudometric on a set Z is a function \(\delta :Z\times {}Z\rightarrow [0,+\infty ]\) which differs from a metric in two ways: First, it may happen that \(\delta (z_{1},z_{2})=0\) and \(z_{1}\ne z_{2}\). Second, \(\delta \) may assume the value \(+\infty \). A basis for the topology induced by an extended pseudometric is also given, as in the case of a metric space, by the open balls (defined in the same way). The topology induced by an extended pseudometric is usually not \(T_0\).
5.2.1 The Mean-Value Operator is Geometrizable
If we wish to solve the inversion problem for the mean-value operator \(\varvec{\omega }: L^{1}( {X} ) \rightarrow {\mathbb {C}}^{ \varvec{\mathcal {A}}({ {X} }) }\) within the setting of Sect. 4.7, we first need to know that \( {X} \) is imbeddable in the boundary of \( \varvec{\mathcal {A}}({ {X} }) \) in an appropriate ambient space \( \mathbf {W} \). In other words, we need to show that the mean-value operator \( L^{1}( {X} ) \rightarrow {\mathbb {C}}^{ \varvec{\mathcal {A}}({ {X} }) }\) is geometrizable. A natural candidate for \( \mathbf {W} \) is the collection \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \) of nonempty subsets of \( {X} \), topologized by the Hausdorff extended pseudometric \(\varvec{\delta _H: \varvec{\mathcal {P}}_{\bullet }( {X} ) \times \varvec{\mathcal {P}}_{\bullet }( {X} ) \rightarrow [0,+\infty ]}\) defined as follows: If \( {Q_{1}} , {Q_{2}} \in \varvec{\mathcal {P}}_{\bullet }( {X} ) \), then \(\delta _H( {Q_{1}} , {Q_{2}} )\) is the infimum of the set of all \(r>0\) such that
where \(\delta _H( {Q_{1}} , {Q_{2}} )=+\infty \) if there is no such r. The topology on \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \) induced by \(\delta _H\) is called the Hausdorff topology.
A hyperspace on \( {X} \) is a subset of \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \), endowed with the Hausdorff topology inherited from \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \). Some hyperspaces on \( {X} \) which are met in practice are given in Table 1. The Hausdorff topology on \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \) is not \(T_0\), but it has useful properties if restricted to certain subsets of \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \). For example, \(\delta _H\) is a metric if restricted to the collection of nonempty closed and bounded subsets of \( {X} \). Hausdorff (1914) proved that this collection is compact if \( {X} \) is compact.
The natural injection
is the injective function defined by \(\imath (q){\mathop {=}\limits ^{\mathrm{def}}}\{q\}\). Observe that if \(Q\in \varvec{\mathcal {P}}_{\bullet }( {X} ) \) and \(q\in {X} \), then
It follows that, if \(( {X} ,\delta )\) is a metric space, then the natural injection (5.5) is an isometry:
Hence \( \imath : {X} \hookrightarrow {} \varvec{\mathcal {P}}_{\bullet }( {X} ) \) is an imbedding of \( {X} \) into \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \). Thus we may geometrically identify a point \(q\in {X} \) with the singleton \(\imath (q)=\{q\}\in \varvec{\mathcal {P}}( {X} ) \), and we may look at \( {X} \) as being inside the hyperspace \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \). In particular, since (5.6) implies that \(\delta _H(q, {B}(q,1/n))\le {}1/n\), it follows that \(q\) belongs to the closure of \( \mathbf {B}( {X} ) \) in \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \).
Lemma 5.1
If \(( {X} ,\delta )\) is a metric space and no point in \( {X} \) is open, then \( {X} \) is imbeddable in the boundary of \( \mathbf {B}( {X} ) \) in \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \). The imbedding is the natural injection (5.5).
Proposition 5.2
If \(( {X} ,\delta , \omega )\) is a metric measure space, \(\omega (\{x\})=0\) for each \(x\in {X} \), and \( \mathbf {B}( {X} ) \subset \varvec{\mathcal {A}}({ {X} }) \), then
- (1):
-
The natural injection (5.5) yields an imbedding of \( {X} \) in the boundary of \( \mathbf {B}( {X} ) \) in \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \).
- (2):
-
The natural injection (5.5) yields an imbedding of \( {X} \) in the boundary of \( \varvec{\mathcal {A}}({ {X} }) \) in \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \).
Observe that the hypotheses of Proposition 5.2 imply that no point of \( {X} \) is open.
5.2.2 Differentiation Bases
In this section, we assume, without further notice that the hypotheses of Proposition 5.2 are met. Hence the functional representation (5.1) is geometrizable, and we may be able to solve the inversion problem for \(\varvec{\omega }: L^{1}( {X} ) \rightarrow {\mathbb {C}}^{ \varvec{\mathcal {A}}({ {X} }) }\) using the approach indicated in Sect. 4.7. A family of approach regions in \( \varvec{\mathcal {A}}({ {X} }) \) based on \( {X} \) is called a differentiation basis for \( {X} \). Hence a differentiation basis for \( {X} \) is a function
such that for each \(q\in {X} \),
just as in (2.4). From the viewpoint of boundary values, the relevant object associated to \(\varphi \) is the family
of boundary filters on \( \varvec{\mathcal {A}}({ {X} }) \) based on \( {X} \), which is associated to (5.7), as in Sect. 2.5.5. Hence the value of \( [\varphi ] \) on \(q\in {X} \) is the filter \( [\varphi (q)] \in \mathsf {Filters}( \varvec{\mathcal {A}}({ {X} }) ) \) generated by the tails of \(\varphi (q)\) at \(\imath (q)\) (in the topology of the ambient space \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \)). The filter \( [\varphi (q)] \) ends at \(\imath (q)\), as in (4.8).
A differentiation basis (5.7) is called a Lebesgue differentiation basis if it solves the inversion problem for the mean-value operator \(\varvec{\omega }: L^{1}( {X} ) \rightarrow {\mathbb {C}}^{ \varvec{\mathcal {A}}({ {X} }) }\), as described in Sect. 4.7. This means that, for each \(f\in \mathcal {L}^1( {X} )\), the set \( \mathsf {Fatou}( \varvec{\omega }(f) ;\varphi )\) has full measure in \( {X} \), and the boundary function
is equal a.e. to \(f\). This means that for each \(f\in \mathcal {L}^{1}( {X} )\),
Recall from (2.14) that \( { \lim _{ [ \varphi ( q) ] } \varvec{\omega }(f) } \) is defined as  and that the meaning of “\(Q\rightarrow q\)” is that \(\delta _H(Q,q)\rightarrow 0\), i.e., \(Q\) converges to \(\{q\}\) in the Hausdorff topology of \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \).
and that the meaning of “\(Q\rightarrow q\)” is that \(\delta _H(Q,q)\rightarrow 0\), i.e., \(Q\) converges to \(\{q\}\) in the Hausdorff topology of \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \).
If \(\varphi (q)\equiv \varvec{\mathcal {A}}({ {X} }) \), then (5.9) holds if \(f\) is continuous, but not for each \(f\in \mathcal {L}^{1}( {X} )\). This example corresponds to unrestricted convergence.
If \(\textsf {v}: {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }( \varvec{\mathcal {A}}({ {X} }) ) \) is defined by \({ \textsf {v}(q){\mathop {=}\limits ^{\mathrm{def}}}\{Q\in \varvec{\mathcal {A}}({ {X} }) :q\in Q\}}\), then the approach regions in \(\textsf {v}\) are also too large (see below) and \(\textsf {v}\) is not a Lebesgue differentiation basis.
5.2.3 The Radial Differentiation Basis
If the hypotheses of Proposition 5.2 are met, then the functional representation
(obtained by restriction) is also geometrizable, and we may approach the corresponding inversion problem along the lines of Sects. 4.7 and 5.2.2. Observe that the analogy of
with
is formalized by the fact that both cases fall within the framework of (4.7) in Sect. 4.2.1. In order to obtain the analog of (2.7), observe that \(\delta _H\) plays in \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \) the role of the Euclidean distance \( \varvec{ {d} } \) in \(\mathbb {C}\), and that the expression \(1-|z|\) which appears in (2.7) is precisely the distance from \(z\) to the boundary of \(\mathbb {D}\) in \(\mathbb {C}\). Hence in \(\mathbb {D}\), \(z\in \Gamma _{j}(q)\) if and only if
and \(z\in \Gamma _{0}(q)\) if and only if \({ \frac{ \varvec{ {d} } (z,\partial \mathbb {D}) }{ \varvec{ {d} } (z,q) } =1 }\). Thus, in (5.12), a special role is played, for \(z\in \mathbb {D}\), by the distance to the boundary \( \varvec{ {d} } (z,\partial \mathbb {D})\), defined by
In (5.11), a similar role is played, for \(I\in \mathbf {B}( {X} ) \), by the quantity
which is called the intrinsic radius of I. Observe that, if \(Q\subset {X} \), then
For example, if \( {X} =\mathbb {R}^n\) and \(Q\) is a ball, then \(r_{\delta }(Q)\) is the radius of \(Q\). We are thus led to define
If \( {X} =\mathbb {R}^n\), then \(G_0(q)\subset \mathbf {B}( {X} ) \) is the collection of all balls in \(\mathbb {R}^n\) centered at \(q\). The family of approach regions \(G_0\) is called the radial differentiation basis, since it plays the role of \(\Gamma _0\) in \(\mathbb {D}\), and \(\Gamma _0(q)\) is the radius in \(\mathbb {D}\) ending at \(q\).
Lebesgue proved that if \( {X} =\mathbb {R}^n\), then \(G_0\) solves the inversion problem for (5.10).
Theorem 5.3
If \(f\in \mathcal {L}^{1}(\mathbb {R}^n)\), then

This result holds in particular for \( {X} =\partial \mathbb {D}\), where we denote by \(I(q,r)\subset \partial \mathbb {D}\) the open ball (i.e., the open interval) of center \(q\in \partial \mathbb {D}\) and radius \(r>0\). It is useful to restate it as a separate result.
Theorem 5.4
If \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\), then

5.2.4 The Centered Hardy–Littlewood Maximal Function
The proof of the qualitative result in Theorem 5.4 is based on the centered Hardy–Littlewood maximal function, which, following [169], we denote as follows:

defined for \(f\in \mathcal {L}^1( {X} )\) on any metric measure space \(( {X} ,\delta ,\omega )\). If, in particular, \( {X} =\mathbb {D}\), the following weak-type (1,1) inequality, established in 1930 by Hardy and Littlewood, plays a central role.
Theorem 5.5
([73]) There exists \( \varvec{c} >0\) such that for each \(r>0\) and \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\)
In (5.17), \(\{m_{f}>r\}\) denotes \({\{q\in \partial \mathbb {D}:m_{f}(q)>r\}}\), similar to (4.23). An analogous result holds in \(\mathbb {R}^n\):
Theorem 5.6
There exists \( \varvec{c} >0\) such that for each \(f\in \mathcal {L}^1(\mathbb {R}^n)\) and \(r>0\)
5.2.5 The Standard Method
In order to derive Theorem 5.4 (which is a qualitative theorem) from Theorem 5.5 (a quantitative theorem), it suffices to use the fact that functions \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\) may be globally approximated in the \(L^1\)-norm by continuous functions. Given \(j>0\) and \(\epsilon >0\), write \(f=\xi +g\), where \(\xi \in C(\partial \mathbb {D}) \) and g has a \(L^1\) norm smaller then \(\epsilon \). The set \(Q_j\) of those points \(q\in \partial \mathbb {D}\) such that  is contained in the union of three sets: (1) The set of points \(q\) where
is contained in the union of three sets: (1) The set of points \(q\) where  ; (2) the set where \({1/3j<\left| g\right| }\); (3) the set of points \(q\) where
; (2) the set where \({1/3j<\left| g\right| }\); (3) the set of points \(q\) where  . The first set is empty, since \(\xi \) is continuous. The measure of the second is bounded by \(3j\epsilon \). The measure of the third set is bounded by \(c_n3j\epsilon \), by (5.17). Hence \( |{Q_j}| =0\), and therefore, (5.15) holds a.e.
. The first set is empty, since \(\xi \) is continuous. The measure of the second is bounded by \(3j\epsilon \). The measure of the third set is bounded by \(c_n3j\epsilon \), by (5.17). Hence \( |{Q_j}| =0\), and therefore, (5.15) holds a.e.
The reasoning which leads from (5.17) to (5.15) is used very often: It is called “the standard method.” Theorem 5.3 follows from Theorem 5.6 in the same way.
5.2.6 Stein’s Theorem on Limits of Sequences of Operators
According to Zygmund, in 1909, Jerosch and Weyl first came up with the idea of replacing a lim, as in (5.15) with a sup, as in (5.16), but
“unfortunately, that paper does not sufficiently exploit the brilliance of this idea” [190].
In 1930, Hardy and Littlewood [73] were the first to “exploit the brilliance of this idea,” and Zygmund immediately foresaw that the idea of replacing a “lim” with a “sup” would turn out to be the key tool in the project of developing “real-analysis” methods that could be extended to higher-dimensional situations, where complex analysis plays no role, as we will see. Stein raised this intuition to a powerful technique with far-reaching results, as R. Fefferman observed [60]:
Although Hardy and Littlewood invented the idea, it is only fair to give Zygmund and his students such as Calderón and Stein much credit for realizing its pervasive role in analysis.
Recall Theorem 4.7, where Kolmogorov proved that, from Theorem 4.6, due to Privalov, on the “existence” of the conjugate function \(\widetilde{\mathrm{f}} \), for \(\mathrm{f}\in \mathcal {L}^1(\partial \mathbb {D})\) (which is a result on the existence of angular boundary values), there follows a weak-type estimate for the operator \(\mathrm{f}\mapsto \widetilde{\mathrm{f}} \). In his proof, Kolmogorov proceded by contraposition: from the assumption that the weak-type inequality was false, he constructed a function in \(\mathcal {L}^1(\partial \mathbb {D})\) for which the conjugate function diverged, against Privalov’s result.
In the 1950s, Calderón proved a result similar in spirit but of a conditional nature, about the convergence of the Fourier series of \(L^2\) functions. He showed that, assuming the convergence a.e. of the Fourier series \({\{s_n(\mathrm{f})\}}\) of square-integrable functions, one could deduce that the operator
is of weak type (2,2) [191, II, p. 165]
Stein was intrigued by the similarities between these two results and saw that a general principle was hidden behind them. In 1961, he proved that, under fairly general conditions of rotational invariance, a weak-type estimate (for the maximal function associated to a sequence of operators) is a necessary condition for the existence, on a set of full measure, of pointwise limits for the sequence of operators. The version given below is not the more general one given in [161], but it contains its main elements.
Theorem 5.7
([161]) If \({\{T_n\}}_n\) is a sequence of bounded linear operators on \( L^{1}(\partial \mathbb {D}) \) which commute with the rotations, and for every \(\mathrm{f}\in L^{1}(\partial \mathbb {D}) \), the limiting value \(\lim _{n\rightarrow +\infty } T_n\mathrm{f}(q)\) exists for a set of full measure in \(\partial \mathbb {D}\), then the operator \(\mathrm{f}\mapsto \sup \{|T_n\mathrm{f}(q)|:n\in \mathbb {N}\}\) is of weak-type (1, 1).
Theorem 5.7 says, roughly speaking, that the link between qualitative results and quantitative ones, which is met in practice, is not incidental but essential. However, when we apply Theorem 5.7 to the setting of qualitative boundary behavior, the hypothesis that the operators \(T_n\) commute with rotations means that the family of approach regions is rotationally invariant. The differentiation basis \(G_0\) in (5.13), when specialized to the unit disc, is rotationally invariant. The following result shows that we cannot dispose of this hypothesis. In order to state it, we need to define the \(\tau \)-Hardy–Littlewood maximal function of \(f\) at \(q\in \partial \mathbb {D}\) associated to a given family \(\tau \) of approach regions in \( \mathbf {B}(\partial \mathbb {D}) \) based on \(\partial \mathbb {D}\). If \(\tau :\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }( \mathbf {B}(\partial \mathbb {D}) ) \) is such a family of approach regions, we define

Theorem 5.8
There exists a family of approach regions \(\tau :\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }( \mathbf {B}(\partial \mathbb {D}) ) \) such that
- (a):
-
The family \(\tau \) is a Lebesgue Differentiation Basis: For each \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\)
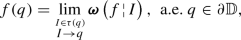 (5.20)
(5.20)where \(I\rightarrow {}q\) means that \(\delta _H(q,I)\rightarrow {}0\).
- (b):
-
It is not true that there exists \( \varvec{c} >0\) such that for each \(f\in \mathcal {L}^1(\partial \mathbb {D})\) and all \(r>0\)
$$\begin{aligned} | \{ M_{f,\tau } >r\} | \le \frac{ \varvec{c} }{r}\int _{\partial \mathbb {D}}|f|\,\mathrm{d}~\omega . \end{aligned}$$(5.21)
5.2.7 Maximal Functions Associated to Special Differentiation Bases
In order to understand why Theorem 5.5 holds, and having in mind that from a weak-type inequality for the maximal function we may derive an a.e. result, we are led to the following general definition. The maximal function associated to a subset \(\varvec{\mathcal {Z}}\subset \varvec{\mathcal {A}}({ {X} }) \) is the function, defined for \(f\in \mathcal {L}^1( {X} )\) and \(q\in {X} \), given by

where \( \mathcal {M}_{\varvec{\mathcal {Z}}} {f} (q) =0\) if the set in (5.22) is empty.
Lemma 5.9
If \(\varvec{\mathcal {Z}}\subset \varvec{\mathcal {A}}({ {X} }) \) is countable, then \( \mathcal {M}_{\varvec{\mathcal {Z}}} {f} \) is measurable for each \(f\in \mathcal {L}^{1}( {X} )\).
A collection \(\varvec{\mathcal {Z}}\subset \varvec{\mathcal {A}}({ {X} }) \) has the inclusion–exclusion property if
Lemma 5.10
If \(\varvec{\mathcal {Z}}\subset \varvec{\mathcal {A}}({ {X} }) \) is countable and (5.23) holds, then for each \(r>0\) and \(f\in \mathcal {L}^{1}( {X} )\)
5.2.8 The Dyadic Maximal Function
The collection \(\varvec{\mathcal {Z}}_2\subset \varvec{\mathcal {A}}({\partial \mathbb {D}}) \) of dyadic intervals, defined in (5.4), has the inclusion–exclusion property, since these intervals are obtained by consecutive bisections from the interval \((0,2\pi )\). The open arc in (5.4) is a dyadic arc of generation m. Lemma 5.10 applied to \(\varvec{\mathcal {Z}}_2\) yields the following result.
Proposition 5.11
For each \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\) and \(r>0\)
The maximal function \( \mathcal {M}_{\varvec{\mathcal {Z}}_2} {f} \) is called the dyadic maximal function, and Proposition 5.11 says that it is of weak type (1, 1). If there was a number \( \varvec{c} >0\) such that
for each \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\) and each \(q\in \partial \mathbb {D}\), then Theorem (5.5) (the Hardy–Littlewood weak-type estimate for the centered maximal operator) would follow at once from Proposition (5.11). Now, the symbol \((**)\) in (5.25) is used to alert the reader that its statement is false, but the following result holds.
Proposition 5.12
For each \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\) and each \(r>0\)
The inequality (5.26) is not a pointwise inequality, but a distribution function inequality, i.e., an inequality between the measures of the super-level sets of the two maximal operators. The Hardy–Littlewood weak-type estimate for the centered maximal operator follows at once from Proposition 5.11 and Proposition 5.12.
Theorem 5.6 may be proved along similar lines, using the collection of dyadic cubes in \(\mathbb {R}^n\), which is used prominently in the Calderón–Zygmund decomposition.
The dyadic intervals are the prime example of an amenable net. In the appendix, we show that amenable nets exist in great generality.
5.2.9 Conjugate Nets (after de la Vallée Poussin)
Although (5.25) is false, there is indeed a way to obtain a pointwise inequality where the centered Hardy–Littlewood maximal function is bounded in terms of the maximal functions associated to countable subsets of \( \varvec{\mathcal {A}}({\partial \mathbb {D}}) \). But, in order to do so, we need two countable subsets \(\varvec{\mathcal {Z}}_{3}\) and \(\varvec{\mathcal {Z}}_{3}^{\prime }\) of \( \varvec{\mathcal {A}}({\partial \mathbb {D}}) \), which are conjugate to each other, in the sense that the endpoints of the intervals of generation m of \(\varvec{\mathcal {Z}}_3\) are the midpoints of the endpoints of intervals of \(\varvec{\mathcal {Z}}_3\) of the same generation, and conversely. The notion of conjugate nets was introduced by C. de la Vallée Poussin in 1916. He was motivated by the wish to avoid the use the Vitali covering theorem, used by Lebesgue in 1910 [40, p. 64, footnote 2]. Let \(\varvec{\mathcal {Z}}_3\) be the collection of intervals \(\varvec{\{ e^{i\theta }: k2\pi {}3^{-m}\le \theta <(k+1)2\pi {}3^{-m}\}}\) where \(m\ge 0\) and \(k\ge 0\) are integers, and let \(\varvec{\mathcal {Z}}_{3}^{\prime }\) be the collection of intervals of the form \(\varvec{\{e^{i\theta }: (k+{1}/{2})2\pi {}3^{-m}\le \theta <(k+{3}/{2})2\pi {}3^{-m}\}}\).
Theorem 5.13
If \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\) then, for each \(q\in \partial \mathbb {D}\),
Hence (5.27) is the correct way of expressing the initial hope behind (5.25). Theorem 5.13 leads to another proof of Theorem 5.5, since both \( \mathcal {M}_{\varvec{\mathcal {Z}}_{3}} \) and \( \mathcal {M}_{\varvec{\mathcal {Z}}_{3}^{\prime }} \) are of weak type (1, 1), by Lemma 5.10. Theorem 5.6 may also be proved along similar lines.
5.2.10 The Uncentered Hardy–Littlewood Maximal Function
We have seen that Lebesgue proved that if \( {X} =\mathbb {R}^n\), then the radial differentiation basis \(G_0\), defined in (5.13), solves the inversion problem for (5.10). Recall that, in \(\mathbb {R}^n\), \(G_0(q)\) is the collection of balls in \( {X} \) concentric with \(q\), and that \(\varvec{G_{1}(q)= \{I\in \mathbf {B}( {X} ) :q\in {}I\}}\). Lebesgue also proved that, if \( {X} =\mathbb {R}^n\), then \(G_{1}\) solves the inversion problem for (5.1).
Theorem 5.14
If \(f\in \mathcal {L}^{1}(\mathbb {R}^n)\), then \( { f(q) = \lim _{ [G_1(q)] } \varvec{\omega }(f) \quad \text { for a.e. } q\in \mathbb {R}^n } \).
Recall from (2.14) that \({ \lim _{ [ G_1(q)] } \varvec{\omega }(f) }\) denotes  , where the meaning of “\(I\rightarrow q\)” is that \(I\in \mathbf {B}( {X} ) \) converges to \(q\) in the Hausdorff topology of \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \). That is, that \(\delta _H(q,I)\rightarrow 0\), and observe that, if \(q\in {}I\), the condition \(\delta _H(q,I)\rightarrow 0\) is equivalent to \(\text {diam}(I)\rightarrow 0\), since \(q\in {}I\) implies that
, where the meaning of “\(I\rightarrow q\)” is that \(I\in \mathbf {B}( {X} ) \) converges to \(q\) in the Hausdorff topology of \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \). That is, that \(\delta _H(q,I)\rightarrow 0\), and observe that, if \(q\in {}I\), the condition \(\delta _H(q,I)\rightarrow 0\) is equivalent to \(\text {diam}(I)\rightarrow 0\), since \(q\in {}I\) implies that
Hence Theorem 5.14 says that

where I ranges over balls in \(\mathbb {R}^n\), and it is in this form that it appears in the literature.
If in (5.28), one tries to employ the collection of rectangles, then deep problems arise. The subtlety has been hinted in Stein’s rendition of the turn of events that led Zygmund to
[...] turn his attention from the one-dimensional situation to problems in higher dimensions. At first, this represented merely an incidental interest, but then later he followed it with increasing dedication, and eventually it was to become the main focus of his scientific work. [...] In higher dimensions it is natural to ask whether [(5.28)] holds when the intervals are replaced by appropriate generalizations in \(\mathbb {R}^n\). The fact that this is the case when the Is are replaced by balls (or more general sets with “bounded eccentricity”) was well known at the time. What must have piqued Zygmund’s interest in the subject was his realization (in 1927) that a paradoxical set constructed by Nikodym showed that the answer is irretrievably false when the Is are taken to be rectangles (each containing the point in question) but with arbitrary orientation. To this must be added the counterexample found by Saks several years later, which showed that the desired analogue [of (5.28)] still failed even if we now restricted the rectangles to have a fixed orientation (e.g., with sides parallel to the axes) as long as one allowed \(f\) to be a general function in \(\mathcal {L}^1\). [167]
Theorem 5.14 is proved on the basis of the uncentered Hardy–Littlewood maximal function

and the associated weak-type (1, 1) inequality, which can be derived from (5.18) once we observe that there is a constant \( \varvec{c} >0\) such that for each \(f\in \mathcal {L}^1(\mathbb {R}^n)\) and \(q\in \mathbb {R}^n\),
The inequality (5.30) follows from a property which relates the measure \(\omega \) to the metric \(\delta \). This property, called the doubling property, is valid in \(\mathbb {R}^n\), as well as in many other cases.
5.2.11 Spaces of Homogeneous Type
A metric measure space \(( {X} ,\omega ,\delta )\) is called a space of homogeneous type if
- (1):
-
The measure \(\omega \) is a complete Radon measure.
- (2):
-
There is a constant \( \varvec{c} >0\) such that \(\omega ({B}(q,2r))\le {} \varvec{c} \omega ({B}(q,2r))\) for each \(q\in {X} \) and each \(r>0\).
- (3):
-
\( \mathbf {B}( {X} ) \subset \varvec{\mathcal {A}}({ {X} }) \).
In this definition, the condition that \(\delta \) is a metric may be relaxed: It suffices to ask that \(\delta \) be a quasi-metric, where instead of the triangular inequality, one has \(\delta (x,y)\le {} \varvec{c} ^{\prime }(\delta (x,z)+\delta (z,y))\) for a constant \( \varvec{c} ^\prime >0\) which does not depend on x, y, z. Some variants of this notion that can be found in the literature require an “engulfing property,” but in our definition, this condition is not necessary since it follows from the triangle inequality.
Recall that \(m_{f}\) is the centered maximal function for \( {X} \), as in (5.16), and \( \mathcal {M}_{\varvec{\mathcal {Z}}} {f} \) is the maximal operator associated to a subset \(\varvec{\mathcal {Z}}\subset \varvec{\mathcal {A}}({ {X} }) \), as in (5.22). In 1990, Michael Christ proved the following result.
Theorem 5.15
([34]) If \(( {X} ,\omega ,\delta )\) is a space of homogeneous type, then there is a countable collection \(\varvec{\mathcal {Z}}\subset \varvec{\mathcal {A}}({ {X} }) \) of bounded open sets which has the inclusion–exclusion property, and such that there are positive constants \( \varvec{c} >0\) and \( \varvec{c} ^{\prime }>0\) such that for each \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\) and each \(r>0\)
Corollary 5.16
In a space of homogeneous type \(( {X} ,\omega ,\delta )\), both the centered Hardy–Littlewood maximal operator \(m_{f}\) and the uncentered Hardy–Littlewood maximal operator \(M_{f}\) are of weak-type (1, 1).
5.2.12 Lebesgue Points
Corollary 5.16 implies the following result, which recaptures Theorems 5.3 and 5.4.
Theorem 5.17
If \(( {X} ,\omega , \delta )\) is a space of homogeneous type and \(f\in \mathcal {L}^{1}( {X} )\) then

A Lebesgue point of \(f\in \mathcal {L}^{1}( {X} )\) is a point \(q\in {X} \) which satisfies a condition stronger than (5.31):

Formula (5.32) is a form of “continuity” of \(f\) at \(q\). The collection of all Lebesgue points of \(f\) is denoted by \( \mathsf {Lebesgue}[f]\). The following improvement of (5.31) follows from the standard method.
Theorem 5.18
If \( {X} \) is a space of homogeneous type and \(f\in \mathcal {L}^{1}( {X} )\), then \( \mathsf {Lebesgue}[f]\) has full measure.
5.3 Differentiation of Integrals in a Topological Measure Space
A topological measure space \(( {X} ,\varvec{\mathcal {S}},\omega , \varvec{\mathcal {G}})\) is a set \( {X} \) endowed with a topology \( \varvec{\mathcal {G}}\) and a complete, positive Borel measure \(\omega \) defined on a \(\sigma \)-algebra \(\varvec{\mathcal {S}}\) which contains the Borel \(\sigma \)-algebra. If \( {X} \equiv ( {X} ,\varvec{\mathcal {S}},\omega , \varvec{\mathcal {G}})\) is a topological measure space, then the mean-value operator (5.1) is well defined. The associated inversion problem may be treated as in Sect. 4.2, provided we endow \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \) with an appropriate topology which makes the natural injection \(\imath : {X} \rightarrow {} \varvec{\mathcal {P}}_{\bullet }( {X} ) \), defined in (5.5), an imbedding.
5.3.1 The Natural Topology on \(\varvec{ \varvec{\mathcal {P}}_{\bullet }( {X} ) }\)
If \( {X} \equiv ( {X} , \varvec{\mathcal {G}})\) is a topological space, \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \) is endowed with the natural topology, defined as the coarsest topology in \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \) which contains the following subsets of \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \)
and
where \(C\in \varvec{\mathcal {F}}( {X} ) \), \(U,V\in \varvec{\mathcal {G}}_{\bullet }( {X} )\), and \( {Q}^{\circ } \) denotes the interior of \(Q\) (see Table 1, p. 26).
Lemma 5.19
If \( {X} \) is a topological space, then the natural injection \(\imath : {X} \rightarrow {} \varvec{\mathcal {P}}_{\bullet }( {X} ) \), defined in (5.5), is an imbedding, where \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \) is endowed with the natural topology.
Lemma 5.20
If \( {X} \) is a topological space, \(q\in {X} \), \( \Phi \subset \varvec{\mathcal {P}}_{\bullet }( {X} ) \), and \( \Phi \) is a filter on \( {X} \), then \( \Phi \) converges to \(q\) if and only if \(\{q\}\) belongs to the closure of \( \Phi \) in the natural topology of \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \).
Lemma 5.21
If \( {X} \) is metrizable and \(q\in {X} \), then the neighborhood filter of \(\{q\}\in \varvec{\mathcal {P}}_{\bullet }( {X} ) \) in the Hausdorff topology is equal to the neighborhood filter of \(\{q\}\in \varvec{\mathcal {P}}_{\bullet }( {X} ) \) in the natural topology of \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \).
Observe that if the topological measure space \( {X} \) has finite measure and if the natural injection (5.5) yields an imbedding of \( {X} \) in the boundary of \( \varvec{\mathcal {A}}({ {X} }) \) in \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \), then
Lemma 5.22
Let \( {X} \) be a topological measure space. If (5.35) holds, the measure is Radon, and no nonempty open set of \( {X} \) is a null set, then the natural injection (5.5) is an imbedding of \( {X} \) in the boundary of \( \varvec{\mathcal {A}}({ {X} }) \) in \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \).
5.3.2 Differentiation Bases for a Topological Measure Space
If \( {X} \) is a topological measure space and the natural injection (5.5) is an imbedding of \( {X} \) in the boundary of \( \varvec{\mathcal {A}}({ {X} }) \) in \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \), then a family of approach regions in \( \varvec{\mathcal {A}}({ {X} }) \) based on \( {X} \) is called a differentiation basis for \( {X} \). Hence a differentiation basis is a function \({ \varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }( \varvec{\mathcal {A}}({ {X} }) ) }\) such that, for each \(q\in {X} \),
It is useful to compare (5.36) to (2.4), (4.8), (4.9), and (5.8). From the viewpoint of boundary values, the relevant object associated to \(\varphi \) is the family
of boundary filters on \( \varvec{\mathcal {A}}({ {X} }) \) based on \( {X} \) which is associated to (5.7). See also Sect. 2.5.5.
A differentiation basis \({ \varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }( \varvec{\mathcal {A}}({ {X} }) ) }\) is called a Lebesgue differentiation basis if it solves the inversion problem for the mean-value operator \(\varvec{\omega }: L^{1}( {X} ) \rightarrow {\mathbb {C}}^{ \varvec{\mathcal {A}}({ {X} }) }\). This means that, for each \(f\in \mathcal {L}^{1}( {X} )\), the set \( \mathsf {Fatou}( \varvec{\omega }(f) ;\varphi )\) has full measure in \( {X} \) and that the boundary function
is equal a.e. to \(f\). In other words, for each \(f\in \mathcal {L}^{1}( {X} )\),
Observe that \( { \lim _{ [ \varphi ( q) ] } \varvec{\omega }(f) } \) is defined as  and that the meaning of “\(Q\rightarrow q\)” is that \(Q\) converges to \(\{q\}\) in the natural topology of \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \).
and that the meaning of “\(Q\rightarrow q\)” is that \(Q\) converges to \(\{q\}\) in the natural topology of \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \).
Nets provide differentiation bases when there is no metric. The first appearance of this notion in the Euclidean setting is due to de la Vallée Poussin (1916), under the name of reseau [40]. In the appendix, we prove that amenable nets exist in great generality.
5.3.3 Partitions and Amenable Nets
A partition of a nonempty set \( {X} \) is a nonempty collection \(\mathsf {C}\subset \varvec{\mathcal {P}}_{\bullet }( {X} ) \) such that each point \(q\in {X} \) belongs to one and only one set in \(\mathsf {C}\). The sets in \(\mathsf {C}\) are called tiles of the partition \(\mathsf {C}\). A partition \(\mathsf {C}\) is finite if it has a finite number of tiles. The tile of \(\mathsf {C}\) which contains \(q\in {X} \) is denoted by \(\mathsf {C}[q]\). The collection of all finite partitions of \( {X} \) is denoted by \(\Pi ( {X} )\). The set \(\Pi ( {X} )\) is endowed with a partial order which makes it a directed set: The partition \(\mathsf {C}_2\) is nested in the partition \(\mathsf {C}_1\) if each tile of \(\mathsf {C}_2\) is contained in a tile of \(\mathsf {C}_1\). We then write \(\mathsf {C}_1{\preceq }\mathsf {C}_2\) and say that \(\mathsf {C}_2\) is finer than \(\mathsf {C}_1\), and that \(\mathsf {C}_1\) is coarser than \(\mathsf {C}_2\). A net in \( {X} \) is a sequence \(\mathsf {C}_1, \mathsf {C}_2,\ldots , \mathsf {C}_k,\ldots \) of nested and finite partitions, i.e.,
The partitions \(\mathsf {C}_{j}\) are called the partitions of the net. If \({{\mathbf {\mathsf{{c}}}}}={\{\mathsf {C}_{j}\}}_{j\in \mathbb {N}}\) is a net in \( {X} \), then the sets \(\mathsf {C}_{j}[q]\), for \(j\in \mathbb {N}\) and \(q\in {X} \), are called tiles of the net. The collection of all the tiles of \({{\mathbf {\mathsf{{c}}}}}\) is denoted by \( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}\). Hence
The collection \( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}\) has the inclusion–exclusion property. The coarsest topology which contains \( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}\) is called the topology generated by the net and is denoted by \( \varvec{\mathcal {G}}_{{{\mathbf {\mathsf{{c}}}}}}\). A net \({{\mathbf {\mathsf{{c}}}}}\) in a topological space \( {X} \equiv ( {X} , \varvec{\mathcal {G}})\) is called compatible with the topology of \( {X} \) if \( \varvec{\mathcal {G}}\subset \varvec{\mathcal {G}}_{{{\mathbf {\mathsf{{c}}}}}}\), i.e., if
If \( {X} \equiv ( {X} ,\varvec{\mathcal {S}},\omega )\) is a measure space, then a partition \(\mathsf {C}\) of \( {X} \) is measurable (amenable) if all its tiles belong to \(\varvec{\mathcal {S}}\) (\( \varvec{\mathcal {A}}({ {X} }) \), resp.). A net in \(( {X} ,\varvec{\mathcal {S}},\omega )\) is measurable (amenable) if all its partitions are measurable (amenable, resp.). Observe that the existence of an amenable net in a measure space \(( {X} ,\varvec{\mathcal {S}},\omega )\) implies that \( {X} \) has finite measure (these notions may be adapted to measure spaces of infinite measure). Hence we may assume, after normalization, which \(\omega ( {X} )=1\), i.e., \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a probability space. An amenable net \({{\mathbf {\mathsf{{c}}}}}={\{\mathsf {C}_{j}\}}_{j\in \mathbb {N}}\) in \(( {X} ,\varvec{\mathcal {S}},\omega )\) determines a function:
The function \(\varphi _{{{\mathbf {\mathsf{{c}}}}}}\) is called the standard sequence of tiles in the net.
Lemma 5.23
If \( {X} \equiv ( {X} ,\varvec{\mathcal {S}},\omega , \varvec{\mathcal {G}})\) be a topological measure space of finite measure for which (5.35) holds, then the following conditions, for a given amenable net \({{\mathbf {\mathsf{{c}}}}}={\{\mathsf {C}_{j}\}}_{j\in \mathbb {N}}\) in \( {X} \), are equivalent.
- (1):
-
\({{\mathbf {\mathsf{{c}}}}}\) is compatible with the topology of \( {X} \).
- (2):
-
For each \(q\in {X} \), the closure of \(\varphi _{{{\mathbf {\mathsf{{c}}}}}}(q)\) in \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \) (in the natural topology) contains \(\{q\}\).
Moreover, any of the conditions \(\varvec{(1)}\), \(\varvec{(2)}\) implies the following:
- (a):
-
The natural injection (5.5) is an imbedding of \( {X} \) in the boundary of \( \varvec{\mathcal {A}}({ {X} }) \) in \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \).
- (b):
-
The function \(\varphi _{{{\mathbf {\mathsf{{c}}}}}}\) defined in (5.38) is a differentiation basis in \( {X} \).
In the following result, no doubling condition is required: Its proof only relies on the standard method of Sect. 5.2.5 and on the maximal function inequality established in Lemma 5.10.
Theorem 5.24
Let \( {X} \) be a topological measure space such that (5.35) holds. Assume that an amenable net \({{\mathbf {\mathsf{{c}}}}}={\{\mathsf {C}_{j}\}}_{j\in \mathbb {N}}\) in \( {X} \) is given, and that the following conditions hold:
- (1):
-
The net is compatible with the topology of \( {X} \).
- (2):
-
\( C( {X} ) \) is dense in \( L^{1}( {X} ) \).
Then the standard sequence \(\varphi _{{{\mathbf {\mathsf{{c}}}}}}\) of tiles in the net in (5.38) forms a Lebesgue differentiation basis for \( {X} \).
Two observations are in order: First, (5.37) with \(\varphi =\varphi _{{{\mathbf {\mathsf{{c}}}}}}\) is equivalent to the following condition:

Second, if \(\mathsf {C}\) is an amenable and finite partition of \(( {X} ,\varvec{\mathcal {S}},\omega )\), and \(\mathsf {C}^*\) denotes the \(\sigma \)-algebra generated by \(\mathsf {C}\), then for each \(f\in \mathcal {L}^1( {X} )\), the conditional expectation of \(f\) with respect to the \(\sigma \)-algebra \(\mathsf {C}^*\) generated by \(\mathsf {C}\) is the unique element of \(\mathcal {L}^1( {X} )\) which is \(\mathsf {C}^*\) measurable (i.e., constant on each tile of \(\mathsf {C}\)) and which, on all sets in \(\mathsf {C}^*\), has the same averages as \(f\). The conditional expectation of \(f\) with respect to \(\mathsf {C}^*\) is denoted by  . In the notation of (5.2),
. In the notation of (5.2),

The conditional expectation  has the following simple explicit expression:
has the following simple explicit expression:

where \(1_{Q}\) is the indicator function of \(Q\). Hence

Thus, in the right-hand side of (5.39), the conditional expectation of \(f\) relative to \(\mathsf {C}_{j}^*\) appears. Since conditional expectations are uniformly integrable, Vitali’s theorem implies that  converges to \(f\) not only a. e. but also in \(L^1\) (see Sect. 11).
converges to \(f\) not only a. e. but also in \(L^1\) (see Sect. 11).
One of the attractions of Theorem 5.24 is that the underlying measure is not assumed to be doubling. The price to be paid is that we have to rely on the existence of an amenable net. In the following section, we will see that amenable nets exist under appropriate countability hypothesis on the measure space.
5.4 Differentiation of Integrals in a Measure Space
In 1936, one year before filters appeared in the literature, René de Possel observed that only some of the main properties of Lebesgue measure admit d’une manière évidente (in evident ways) an extension to the case of an arbitrary measure space, but others semblent perdre toute signification dès que l’espace n’est plus métrique (appear to lose their meaning as soon as the space is not metric) [27, 41]. Among the latter, he listed the properties related to differentiation of integrals. Indeed, in our set-up, if \(( {X} ,\omega )\) is a measure space, with no further structure, it does not seem possible to define, in this degree of generality, a topology on \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \) which would make the natural injection \( {X} \hookrightarrow \varvec{\mathcal {P}}_{\bullet }( {X} ) \) an imbedding. de Possel proposed to adopt an axiomatic approach, which, with the benefit of hindsight, we think may be usefully rephrased in terms of filters. We leave this full task to a future occasion and now limit ourselves to revise the general setting of Sect. 4.2 as follows: We seek a function
such that for each \(f\in \mathcal {L}^{1}( {X} )\)
A concrete solution to this general problem is given by the following result, proved in the appendix. The existence of an amenable net is a necessary premise for the applicability of the differentiation of integrals à la de la Vallée Poussin, which has the advantage of avoiding covering theorems [21].
Theorem 5.25
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a measure space of finite measure and at least one of the following holds:
- (1):
-
The \(\sigma \)-algebra \(\varvec{\mathcal {S}}\) is countably generated.
- (2):
-
\( L^{1}( {X} ) \) is separable as a metric space.
Then there exists an amenable net \({{\mathbf {\mathsf{{c}}}}}={\{{\mathsf {C}}_{j}\}}_{{j}}\) in \( {X} \) such that for each \(f\in \mathcal {L}^{1}( {X} )\), the sequence of conditional expectations  converges to \(f\) a.e. and in \(L^1\).
converges to \(f\) a.e. and in \(L^1\).
The following result may be considered to be implicit in the work of de la Vallée Poussin (1916).
Theorem 5.26
([40]) If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a measure space of finite measure, and \({{\mathbf {\mathsf{{c}}}}}={\{{\mathsf {C}}_{j}\}}_{{j}}\) is an amenable net on \( {X} \) such that the \(\sigma \)-algebra generated by the tiles of \({{\mathbf {\mathsf{{c}}}}}\) is equal to \(\varvec{\mathcal {S}}\), then, for each \(f\in \mathcal {L}^{1}( {X} )\), the conditional expectations  converge to \(f\) a.e. and in \(L^1\).
converge to \(f\) a.e. and in \(L^1\).
In Sect. 11, we show that Theorems 5.25 and 5.26 may be proved by only relying on the quantitative results associated to the maximal operator in Lemma 5.10, thus, avoiding more complex techniques.
In order to see more precisely how Theorems 5.25 and 5.26 fit within the general framework of (5.43) and (5.44), observe that, if \({{\mathbf {\mathsf{{c}}}}}= { \{ {\mathsf {C}}_{j} \} }_{j\ge 1} \) is an amenable net, then for each \(q\in {X} \), the collection \({\{\mathsf {C}_{j}[q]\}}_{j}\) is a filter base, and, if we denote by \(\Phi (q)\) the filter on \( \varvec{\mathcal {A}}({ {X} }) \) generated by \({\{\mathsf {C}_{j}[q]\}}_{j}\), then (5.44) is equivalent to the following statement:

6 Qualitative Boundary Behavior (II)
The set-up of Sect. 5.2.1 shows that results on differentiation of integrals fit within the general study of boundary behavior. Moreover, in the previous section, we have illustrated in various cases the general principle that a qualitative Fatou-type theorem (i.e., an almost everywhere convergence result) may be derived from a quantitative information (i.e., from a weak-type inequality on the boundary). For example, we have seen that quantitative estimates based on maximal operators (such as, for example, Theorem 5.5) can be used to obtain results on differentiation of integrals (such as, for example, Theorem 5.4). A general expression of these facts can be given in terms of the intrinsic maximal function (which does not depend on a functional representation). We briefly delve into this matter now, in order to prepare the ground for the more detailed treatment of the quantitative Fatou-type theorems of Sect. 7.
6.1 The Intrinsic Maximal Function
If \(\imath : {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \) is an imbedding of a topological measure space \( {X} =( {X} ,\varvec{\mathcal {S}},\omega , \varvec{\mathcal {G}})\) in the boundary of \(D\) (a subset of \( \mathbf {W} \)), and \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }( {X} ) \) is a family of approach regions in \(D\) based on \( {X} \), then the intrinsic maximal operator (called “complex max” in [115]):
associated to \(\varphi \) is defined (for \(u\in \mathbb {C}^{D}\) and \(q\in {X} \)) as follows:
Observe that \({ \displaystyle {\sup _{\varphi }} \,{u} (q) }\) may be infinite for any given \(q\). The boundary function defined in (6.2)
is called the \(\varvec{\varphi }\)-maximal function of \(u\) (or maximal function of \(u\) over a family \(\varphi \) of approach regions). This construction is implicit in the definition of the (un)centered Hardy–Littlewood maximal function. Indeed, \(m_{\mathrm{f}}({q})\), defined in (5.16), may be written in the form (6.2), if we make the following choices:
- (1):
-
\(u{\mathop {=}\limits ^{\mathrm{def}}} \varvec{\omega }(|f|) \).
- (2):
-
The imbedding \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \) is given by \(D= \mathbf {B}( {X} ) \) and \( \mathbf {W} = \varvec{\mathcal {P}}_{\bullet }( {X} ) \).
- (3):
-
The family of approach regions \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }( \mathbf {B}( {X} ) ) \), is defined as \({ \varphi (q){\mathop {=}\limits ^{\mathrm{def}}}\{{B}(q,r):r>0\}}\).
The uncentered Hardy–Littlewood maximal function \(M_{\mathrm{f}}\), defined in (5.29), may be similarly written in the form (6.2), if the family of approach region is chosen as \({ \varphi (q){\mathop {=}\limits ^{\mathrm{def}}}\{I\in \mathbf {B}( {X} ) :q\in {}I\}}\).
The \(\varphi \)-maximal function of \(u\) is able to detect, in a quantitative manner, the change in the “shape” of \({\varphi }(q)\), as \(q\) varies within \( {X} \). More precisely, the function which detects the change in the “shape” of \({\varphi }(q)\), as \(q\) varies within \( {X} \), is the distribution function of \({ \displaystyle {\sup _{\varphi }} \,{|u|} }\).
6.2 The Distribution Function of the Intrinsic Maximal Function
In Sect. 4.8 and in Sect. 5.2.4, we have already seen some important examples of quantitative theorems of Fatou type, such as Theorems 4.7 and 5.5. These give a uniform control of the relative size of certain boundary functions, as in (4.23) and in (5.17), where uniform means that the constant which appears in the inequality only depends on the class of functions being considered, not on the particular function in the class. In inequalities of this sort, which are weak-type inequalities, one has to control the measure of boundary sets of the form:
Here, \(g\) is a given boundary function, and it is sometimes necessary to deal with an “unpleasant point in the argument,” as Stein puts it, namely, the fact that the set in (6.3) is not necessarily measurable. One could get around this difficulty by making a certain assumption, and it is sometimes necessary to do so, but that assumption would be “an artificial one in the general context of our problems,” as Stein wrote in a different, but related, case [163, p. 251]. Indeed, the device used by Stein in that case is also useful in our context: He considered the outer measure induced by \(\omega \), denoted by \(\omega ^{*}\) and defined by
Then, \(\omega ^{*}\) is the outer measure induced by \(\omega \), as defined in [63, p. 30]. Now, the point is that, in order to obtain a.e. convergence results, it is indeed enough to control the outer measure of the set in (6.3). Hence if \(g: {X} \rightarrow \mathbb {C}\) is a boundary function, the distribution function of \(g\) is the function:
(we borrow the handy notation from [163, p. 4]). One of the key observations made by Stein [61] is that the distribution function of the \(\varphi \)-maximal function of \(u\in \mathbb {C}^{D}\) (where \(\varphi \) is a family of approach regions) may be expressed as follows:
where, in the same spirit as in (4.23), we use the short-hand notation \(\{|u|>r\}{\mathop {=}\limits ^{\mathrm{def}}}\{z\in D:|u(z)|>r\}\). The quantity in (6.4) is denoted by  . Hence
. Hence

The observation in (6.4) is an example of Stein’s ability to see deep results hidden in simple things, and it is at the basis of his simplification of a crucial step which involves the so-called Carleson’s tent condition (see below). We will see that it is precisely the distribution function of the intrinsic maximal function over a family of approach regions, in (6.4) that encodes the way in which the various approach regions change their “shape” from point to point, and that enables us to control, on the quantitative side, the boundary behavior through a given family of approach regions. Results which entail a uniform control of the distribution function of \( \displaystyle {\sup _{\varphi }} \,{|u|} \) (i.e., uniform over a certain class of function) belong to the quantitative results on the boundary behavior of functions.
6.3 The Lebesgue Differentiation Theorem in the Unit Disc
The Lebesgue differentiation theorem describes the boundary behavior of the mean-value operator and is the prototype example of qualitative Fatou-type theorems: Indeed, Theorems 4.2 and 4.3 are both based upon it, as well as the other qualitative Fatou-type theorems, as we will see. In \(\partial \mathbb {D}\), the Lebesgue differentiation theorem is the following result, proved in 1904 by Lebesgue. It is a special case of Theorem 5.18. Here, we denote by \(I[q,r]\) the closed interval in \(\partial \mathbb {D}\) of center \(q\) and radius r.
Theorem 6.1
([102]) If \(f\in \mathcal {L}^1(\partial \mathbb {D})\), then \( \mathsf {Lebesgue}[f]\) has full measure in \(\partial \mathbb {D}\).
Fatou obtained Theorem 4.4 as a corollary of Theorem 6.1 (which is a qualitative theorem of Fatou type) coupled with the following result (which is a pointwise theorem of Fatou type).
Theorem 6.2
If \(f\in \mathcal {L}^1(\partial \mathbb {D})\), then \( \mathsf {Lebesgue}[f]\subset \mathsf {Fatou}{( Pf )} \). Indeed, if \(q\in \mathsf {Lebesgue}[f]\), then \( {( Pf )}_{\flat }(q)=f(q)\).
Theorem 6.2 is an instance of Abel’s heuristic principle, a general principle that Stein never ceased to emphasize: The link between the boundary behavior of \( Pf \) at \(q\) and the “regularity” properties of \(f\) at \(q\), which is expressed in terms of the differentiability property of the boundary function. Indeed, stronger notions of “regularity” of \(f\) at \(q\) imply that the boundary value of \( Pf \) at \(q\) through \(V\) exists, where \(V\) is eventually disjoint from the angular approach at \(q\) [12, 176]. Differentiation of integrals is important in itself, but also because of the aforementioned link: See Sect. 11.
6.3.1 The Geometric Form of the Lebesgue Differentiation Theorem in the Unit Disc
We have seen how, in general, the Lebesgue Differentiation Theorem may be framed as a Fatou-type theorem. In order to see this fact in the concrete setting of \(\partial \mathbb {D}\), we first express the mean-value operator \( \varvec{\omega }(f) \) in (5.2) as a function on \(\mathbb {D}\) rather than as a function on \( \varvec{\mathcal {A}}({\partial \mathbb {D}}) \). The Hausdorff pseudometric is indeed a genuine metric if restricted to the collection (denoted by \(\varvec{\mathcal {I}}\subset \varvec{\mathcal {A}}({\partial \mathbb {D}}) \)) of all closed intervals in \(\partial \mathbb {D}\), and \(\varvec{\mathcal {I}}\) turns out to be homeomorphic to the unit disc itself under the standard identification mapping (which imbeds \(\mathbb {D}\) inside \( \varvec{\mathcal {A}}({\partial \mathbb {D}}) \)):
where \(\mu (z)\) is the closed arc in \(\partial \mathbb {D}\) of center \(\frac{z}{\left| z\right| }\) and arc-length equal to \(\frac{2\pi }{1-\left| z\right| }\), with \(\mu (0){\mathop {=}\limits ^{\mathrm{def}}}\partial \mathbb {D}\).
The Lebesgue transform
is the functional representation of \( L^{1}(\partial \mathbb {D}) \) over \(\mathbb {D}\) defined by \( L{}{\mathrm{f}} = ( \varvec{\omega }(\mathrm{f}) )\circ \mu \). Hence if \(z\in \mathbb {D}\), then

Proposition 6.3
The following statements are logically equivalent.
- (I):
-
The Lebesgue differentiation theorem (Theorem 6.1)
- (II):
-
If \(f\in \mathcal {L}^1(\partial \mathbb {D})\), the radial boundary values of \( L{}{f} \) exist and are equal to \(f\) a. e.
- (III):
-
If \(f\in \mathcal {L}^1(\partial \mathbb {D})\),
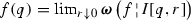 a. e.
a. e.
Observe that (II) and (III) are two equivalent ways of expressing the same statement, the difference being that (II) is more directly geometric than (III). If we apply the general technique of reducing a qualitative statement to a quantitative one, in order to prove (II), it would suffices to show that there exists \( \varvec{c} >0\) such that for each \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\) and each \(r>0\)
where \(\rho \) is the radial family of approach regions. Now, as we observed in Sect. 6.1, \({ \displaystyle {\sup _{\rho }} \,{ L{}{|\mathrm{f}|} } }\) is the centered Hardy–Littlewood maximal function, and hence the conclusion follows from Theorem 5.5. On the other hand, (III) is identical to Theorem 5.4. Apparently, (I) is a stronger statement than (II), but it really is equivalent to (II), as can be seen by a density argument.
6.4 The Nagel–Stein Differentiation Theorem
We now present a deep and surprising contribution of Stein, obtained in collaboration with Alexander Nagel, where a conjecture made by Walter Rudin on the differentiation of integrals is disproved. It is perhaps better to present this result in terms of the boundary behavior of the Lebesgue transform \( L{}{\mathrm{f}} \), defined in (6.7). In order to have a better appreciation of this specific result, it is useful to observe that the Lebesgue differentiation theorem can be bootstrapped so as to yield the following qualitative Fatou-type theorem.
Theorem 6.4
(The angular differentiation theorem) If \(f\in \mathcal {L}^1(\partial \mathbb {D})\), then for almost every \(q\in \partial \mathbb {D}\), the angular boundary value of \( L{}{f} \) exists at \(q\) and equals \(f(q)\).
This result is called the angular differentiation theorem and is an improvement of the Lebesgue differentiation theorem, since the latter result is equivalent to the statement that the radial boundary values of the Lebesgue transform \( L{}{f} \), defined in (6.7), exist and are equal to \(f\) a. e. It is useful to express its content in different terms.
Recall that \(I[q,r]\) is the closed interval in \(\partial \mathbb {D}\) of center \(q\) and radius r. Observe that the Hausdorff distance \(\delta _H(q,J)\) between \(q\) (identified with \(\{q\}\in \varvec{\mathcal {P}}_{\bullet }(\partial \mathbb {D}) \)) and \(J\subset \partial \mathbb {D}\) is equal to the radius of the smallest closed interval centered at \(q\) which contains J, i.e., \(\delta _H(q,J)=\sup \left\{ \left| q-z\right| : z\in {}J \right\} \). The smallest closed interval centered at \(q\) which contains J will be denoted by the uncluttered notation \(I[q,J]\), instead of \(I[q,\delta _H(q,J)]\).
We now need to recall a notion due to Lebesgue. We say that a sequence \( { \{ {J}_{j} \} }_{j\ge 1} \) of intervals of \(\partial \mathbb {D}\) converges angularly to \(q\), and write \(J_n\xrightarrow [nt]{}q\), if there exists \(k>0\) such that
- (a 1):
-
as \(n\rightarrow \infty \), \(\delta _H(q,J_n)\) converges to zero;
- (a 2):
-
\(\left| J_n\right| \ge k \left| I[q,J_n]\right| \) for each \(n\ge 1\).
The angular differentiation theorems is equivalent to saying that, for almost every \(q\in \partial \mathbb {D}\),
for any sequence \( { \{ {J}_{j} \} }_{j\ge 1} \) of intervals in \(\partial \mathbb {D}\) which converges angularly to \(q\). In order to see this equivalence, it suffices to observe that, in the correspondence between closed intervals in \(\partial \mathbb {D}\) and points of \(\mathbb {D}\) given by the standard identification map (6.6), the condition that a sequence of points converges to \(q\equiv {}e^{i\theta }\) staying within some \(\textsc {t}\in \mathsf {Stolz}_{q} \), is equivalent to conditions (a 1) and (a 2).
The condition that \(J_n\xrightarrow [nt]{}q\) does not require that \(q\in {}J_n\) but it does not allow that \(J_n\) occupies a very small portion of \(I[q,J_n]\): This happens precisely when the point which corresponds to \(J_n\), under the standard identification map, converges to \(q\) tangentially.
In 1979, Rudin posed the following question.
Question 6.1
([150]) Is there a sequence \( { \{ {J}_{j} \} }_{j\ge 1} \) of intervals in \(\partial \mathbb {D}\) with the following properties?
- (1):
-
\(\delta _H(1,J_n)\) converges to 0 as \(n\rightarrow \infty \).
- (2):
-
\(\frac{\left| J_n\right| }{\left| I[1,J_n]\right| }\) converges to 0 as \(n\rightarrow \infty \).
- (3):
-
If we set \(qJ_n= \left\{ qq': q'\in {}J_n \right\} \), then \( {f(q)= \lim _{n\rightarrow \infty } \frac{1}{\left| qJ_n\right| } \int _{qJ_n}\mathrm{f}(e^{i\theta })\,\mathrm{d}\theta }\) for each \(f\in \mathcal {L}^1{\partial \mathbb {D}}\) and almost every \(q\in \partial \mathbb {D}\).
Rudin’s conjecture was that the answer was negative. A glimpse of the depth of Stein’s vision is given by the following result, obtained in 1984 in his collaboration with Nagel.
Theorem 6.5
([127]) The answer to Rudin’s question is affirmative.
That is to say, Nagel and Stein prove a Fatou theorem with approach regions that are not nontangential. This runs counter to the expectations of Littlewood and Rudin.
Theorem 6.5 was rather unexpected. It shows the subtlety of the subject and it is only a part of a contribution of larger scope (see below).
6.5 The Local Fatou Theorem of Privalov
One of the results obtained by the Moscow school of mathematics is a stronger version of Theorem 4.3, due to Ivan Ivanovich Privalov in 1923. It is “stronger” because it implies Theorem 4.3. It is called “local” because the action takes place around a subset of the boundary rather than on the whole boundary.
Theorem 6.6
([142, 143]) Let \(u\in \mathcal {O}(\mathbb {D})\). If \(Q\in \varvec{\mathcal {A}}({\partial \mathbb {D}}) \) and, for each \(q\in Q\) there exists \(\textsc {t}\in \mathsf {Stolz}_{q} \) such that \(\sup _{z\in {}\textsc {t}}\left| u(z)\right| <+\infty \), then \( Q\subset _{\omega } \mathsf {Fatou}{(u)} \).
Theorem 6.6 is a qualitative Fatou-type theorem, since at any individual point \(q\), it is not true that boundedness over some \(\textsc {t}\in \mathsf {Stolz}_{q} \) implies the existence of limiting value through \(\textsc {t}\). Recall that the conclusion of Theorem 6.6 says that \(Q\setminus \mathsf {Fatou}{(u)} \) is a null set. Observe the lack of uniformity: The various triangles are not assumed to be congruent to each other, and the bound \(\sup _{z\in {}\textsc {t}}\left| u(z)\right| \) depends on \(q\).
In his proof, Privalov considered (for appropriate values of \({j}\) and \(0<h<1\), where \(R\subset \partial \mathbb {D}\) is a certain closed set) the sawtooth region:
which has rectifiable boundary and then applied a conformal transformation of this region to the unit disc, where Theorem 4.3 is available. Privalov also extended his result to holomorphic functions on planar domains with rectifiable boundary.
6.6 A Prelude to Hardy Spaces
A function \(u\in \mathcal {O}(\mathbb {D})\) is said to belong to \( H^{1}({\mathbb {D}}) \) if
A function \(u\in \mathcal {O}(\mathbb {D})\) is said to be representable by the Cauchy integral if
- (1):
-
The radial limit \( {u}_{\rho }(q) \) exists almost everywhere and is integrable.
- (2):
-
For each \(z\in \mathbb {D}\), \( { u(z) = \frac{1}{2\pi {}i}\int _{\partial \mathbb {D}}\frac{ {u}_{\rho }(\zeta ) }{ \zeta -z} {\,} d\zeta } \).
In 1916, Frigyes Riesz and Marcel Riesz proved the following result.
Theorem 6.7
([149]) If \(u\in \mathcal {O}(\mathbb {D})\), then the following conditions are equivalent:
- (1):
-
\(u\) is representable by the Cauchy integral.
- (2):
-
\(u\in H^{1}({\mathbb {D}}) \).
- (3):
-
The radial limit \( {u}_{\rho }(q) \) exists for almost every \(q\) and \(u= P{u}_{\rho } \).
6.7 Angular Boundary Values for Hardy and Nevanlinna Spaces in the Unit Disc
In 1923, F. Riesz obtained a result stronger than Theorem 4.3, for he proved that the same conclusion of Theorem 4.3 holds under a weaker hypothesis, as follows.
Theorem 6.8
([148]) Let \(0<p<\infty \). If \(u\in \mathcal {O}(\mathbb {D})\) and
then the set \( \mathsf {Fatou}{(u)} \) has full measure and, moreover, \( {u}_{\flat } \in {} \mathcal {L}^{p}(\partial \mathbb {D})\) and
The set of functions in \(\mathcal {O}(\mathbb {D})\) that satisfy (6.9) is denoted by \( H^{p}({\mathbb {D}}) \). The function spaces \( H^{p}({\mathbb {D}}) \) are the Hardy spaces of holomorphic functions in \(\mathbb {D}\). The conclusion that \( \mathsf {Fatou}{(u)} \) has full measure also holds for functions \(u\in \mathcal {O}(\mathbb {D})\) which satisfy the Nevanlinna condition (where \(\ln ^{+}(x){\mathop {=}\limits ^{\mathrm{def}}}\max \{0,\ln (x)\}\))
In 1932, Paley and Zygmund proved that the Nevanlinna condition cannot be weakened:
Theorem 6.9
([136]) If \(\psi \) is a non-negative and measurable and locally bounded function defined on \([0,+\infty )\) and such that \(\psi (s)=o(s)\) as \(s\rightarrow +\infty \), then there exists a function \(u\in \mathcal {O}(\mathbb {D})\) such that
although for almost every \(q\in \partial \mathbb {D}\), the function \(u\) has no radial limit at \(q\).
6.8 A Zero-One Law for Holomorphic Functions: Plessner’s Theorem
In 1927, Abraham Plessner proved that, almost everywhere, the angular boundary behavior of holomorphic functions on \(\mathbb {D}\) is either “good” or “bad.”
Theorem 6.10
([138]) If \(u\in \mathcal {O}(\mathbb {D})\), then \( \mathsf {Fatou}{(u)} \cup \mathsf {Plessner}(u)\) has full measure.
Plessner’s result implies Fatou’s theorem, since \(\mathsf {Plessner}(u)\) is empty if \(u\) is bounded. Plessner proved that the conclusion of Theorem 6.10 also holds for functions that are merely meromorphic on \(\mathbb {D}\).
Table 2 contains an outline of some of the results that we have presented so far on the boundary behavior of holomorphic functions on the unit disc (possibly subject to certain growth conditions of Hardy-type), with an indication of the boundedness conditions (if any) under which the results hold.
6.9 The Area Integral: Qualitative and Quantitative Results
In 1930, in his study of trigonometric series, Nikolaj Nikolaevič Lusin defined the so-called (Lusin’s) area function of \(u\in \mathcal {O}(\mathbb {D})\) (with parameter \(j\ge 1\)) as follows [117]:
The \(\varvec{j}\)-Lusin set of \(u\in C(\mathbb {D}) \), denoted by \(\mathsf {Lusin}_{j}(u)\), is the collection of all points \(q\in \partial \mathbb {D}\) such that
and define the Lusin set of \(u\) as \(\varvec{\mathsf {Lusin}(u)} {\mathop {=}\limits ^{\mathrm{def}}}\bigcup _{j\ge 1}\mathsf {Lusin}_{j}(u)\). Lusin proved two results, one of a qualitative nature, the other quantitative.
Theorem 6.11
([117]) If \(u\in H^{2}({\mathbb {D}}) \) then, for each \(j\ge 1\), \(\mathsf {Lusin}_{j}(u)\) has full measure in \(\partial \mathbb {D}\), and, for each \(j\ge 1\), there exists \( \varvec{c} _{j}>0\) such that, for each \(u\in H^{2}({\mathbb {D}}) \)
In 1938, Jósef Marcinkiewicz and Antoni Zygmund proved the following qualitative result: The finiteness of the area function is related to the existence of nontangential boundary values.
Theorem 6.12
([124]) If \(u\in \mathcal {O}(\mathbb {D})\) and \(Q\in \varvec{\mathcal {A}}({\partial \mathbb {D}}) \), then
The proof of Theorem 6.12 is based on a conformal map applied to the sawtooth region (6.8). Marcinkiewicz and Zygmund also proved the following quantitative results, inspired by Theorem 6.11.
Theorem 6.13
([124]) If \(p>0\) and \(j\ge 1\), there exists \( \varvec{c} _{(p,j)}>0\) such that for each \(u\in H^{p}({\mathbb {D}}) \)
If \(p>1\) and \(j\ge 1\), then there is a constant \( \varvec{c} _{p,j}>0\) such that if \(u\in H^{p}({\mathbb {D}}) \) and \(u(0)=0\), then
In (6.15), it is necessary to assume \(u(0)=0\), since \(S_{j}\) annihilates constants.
In 1943, Donald Clayton Spencer proved the following result, of a qualitative nature. It is a sort of converse of Theorem 6.12, reminiscent of Theorem 6.6.
Theorem 6.14
([157]) If \(u\in \mathcal {O}(\mathbb {D})\) and \(Q\in \varvec{\mathcal {A}}({\partial \mathbb {D}}) \) then
Lusin’s Area Function belongs to the class of square functions:
A deep concept in mathematics is usually not an idea in its pure form, but rather takes various shapes depending on the uses it is put to. The same is true of square functions. These appear in a variety of forms, and while in spirit they are all the same, in actual practice they can be quite different. Thus the metamorphosis of square functions is all important. [166]
Stein contributed more than any other to the “metamorphosis” of square functions, establishing both qualitative and quantitative results for the Area Function in higher dimensions, as we will see.
The (qualitative) Area & Local Fatou Theorem is a corollary of Theorems 6.6, 6.12, and 6.14. In order to state it in a simple form, given \(u\in \mathcal {O}(\mathbb {D})\), we define the Privalov set of \(u\) as follows (recall (6.2)):
Theorem 6.15
If \(u\in \mathcal {O}(\mathbb {D})\) then

Indeed, if \(Q\in \varvec{\mathcal {A}}({\partial \mathbb {D}}) \), then the following three conditions are equivalent:
-
1.
For almost every \(q\in Q\), \(q\in \mathsf {Fatou}{(u)} \).
-
2.
For almost every \(q\in Q\), there exists \({j}\ge 1\) such that \( S_{{j}}u(q)<\infty \).
-
3.
For almost every \(q\in Q\), there exists \(j\ge 1\) such that \(\sup \{\left| u(z)\right| :z\in \Gamma _{j}(q)\}<+\infty \).
Theorem 6.15 is a qualitative Fatou-type theorem, since at any individual point \(q\in \partial \mathbb {D}\), the three conditions in its statement are independent, except that of course, if \(q\) is a Fatou point of \(u\), then \(u\) is bounded in each \(\textsc {t}\in \mathsf {Stolz}_{q} \).
6.10 The Nagel–Stein Theorem for Bounded Holomorphic Functions in the Unit Disc
Assume that, in the setting of Sect. 4.2.5, a qualitative Fatou-type theorem holds, which asserts, for a given class of functions, the existence of a family of boundary filters \( \Phi : {X} \rightarrow \mathsf {Filters}(D) \) based on \( {X} \), such that, for every function \(u\) in the given class, the Fatou set of \(u\) relative to \( \Phi \)
has full measure (see 4.12). In Sects. 4, 5, and 6 so far we have seen various results of this form. The family of boundary filters \( \Phi \) is called the convergence family of filters for the given qualitative Fatou-type theorem. We say that the convergence family of filters \( \Phi \) is sharp, for the given pointwise Fatou-type theorem, if the following statement is not true:
there is a family of boundary filters \({\Psi }: {X} \rightarrow \mathsf {Filters}(D) \) such that
- (1):
For every \(q\in {X} \), the filter \({\Psi }(q)\) is strictly broader than \( \Phi (q)\).
- (2):
For each function \(u\) in the given class, \({\lim _{{\Psi }(q)}u}\) exists for a.e. \(q\in {X} \) and is equal to \({\lim _{ \Phi (q)}u}\).
Observe that, as in Sect. 3.6, if we substitute for the condition (1) the alternative condition
- (\(\varvec{1^\prime }\)):
For every \(q\in {X} \), \({\Psi }(q)\) lies frequently outside of \( \Phi (q)\).
We obtain an equivalent notion of sharpness. Hence we are led to the following question, that first appeared (in a different guise) in Littlewood’s work, and which is akin to the question raised in Sect. 3.6.
Question 6.2
In the context of a given qualitative Fatou-type theorem, Littlewood’s Sharpness Problem is to determine whether the convergence family of filters in the theorem is sharp.
In particular, if the convergence family of filters in the given theorem is not sharp, then it is possible to obtain a stronger result. In 1927, Littlewood proved the following seminal result.
Theorem 6.16
([113]) There does not exist a family \(\tau :\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }(\mathbb {D}) \) of approach regions with the following properties:
- (asymptotic):
-
For each \(q\in \partial \mathbb {D}\), \(\tau (q)\) is the image of a half-open Jordan arc in \(\mathbb {D}\) ending at \(q\).
- (eventually disjoint) :
-
For each \(q\in \partial \mathbb {D}\), the approach region \(\tau (q)\) and the angular filter on \(\mathbb {D}\) ending at \(q\) are eventually disjoint.
- (Fatou):
-
For each \(u\in H^{\infty }({\mathbb {D}}) \), \( \mathsf {Fatou}(u;\tau )\) has full measure and \({\lim _{\tau (q)}u= {u}_{\flat }(q)}\) almost everywhere.
- (rotational invariance) :
-
If \(z\in \tau (q)\), then \(e^{i\theta }z\in \tau (e^{i\theta }q)\) for each \(e^{i\theta }\in \partial \mathbb {D}\).
Indeed, if a family \(\tau :\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }(\mathbb {D}) \) of approach regions has the four properties described above, then there exists \(u\in H^{\infty }({\mathbb {D}}) \) such that, for almost every \(q\in \mathbb {D}\), the limiting value \({\lim _{\tau (q)}u}\) does not exist.
In his proof, Littlewood used a nontrivial measure-theoretic result on Diophantine approximation due to Khintchine (one of Lusin’s pupils). In their book on number theory, Hardy and Wright refer to Khinchin’s result as a “difficult” theorem.
Littlewood’s result is called a negative theorem, since it bars certain families of approach regions, which lie eventually outside the Stolz approach regions, to be allowing almost everywhere convergence for functions in \( H^{\infty }({\mathbb {D}}) \). Observe that, in Littlewood’s theorem, the order of tangency of \(\tau (q)\) to the boundary, is fixed and independent of \(q\). In 1957, Littlewood’s result was improved by Arthur John Lohwater and George Piranian.
Theorem 6.17
([116]) Under the same hypothesis as in Theorem 6.16, there exists \(u\in H^{\infty }({\mathbb {D}}) \) such that for each \(q\in \mathbb {D}\), the limiting value \({ \lim _{\tau (q)}u}\) does not exist.
In 1979, Rudin constructed a highly oscillating inner function in \(\mathbb {D}\) that led to a result which was surprising at that time.
Theorem 6.18
([150]) There exists a family \(\tau :\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }(\mathbb {D}) \) of approach regions such that
- (asymptotic):
-
(same as in Theorem 6.16)
- (frequently outside the angular filter):
-
For each \(q\in \partial \mathbb {D}\), \(\tau (q)\) lies frequently outside of the angular filter ending at \(q\).
- (Fatou):
-
(same as in Theorem 6.16)
- (not rotationally invariant):
-
\(\tau \) is not rotationally invariant.
At that time, the condition that \(\tau \) is not rotationally invariant must have been considered essential for the validity of Theorem 6.18, as we can gather from the fact that Rudin asked Question 6.1, which amounts, in effect, to the following question:
Question 6.3
Is there a family \(\tau \) of approach regions in \(\mathbb {D}\) based on \(\partial \mathbb {D}\) with the following properties?
(with the same terminology as in Theorem 6.16).
In 1984, Nagel and Stein proved the following result, which came unexpectedly.
Theorem 6.19
([127]) The answer to Question 6.3 is affirmative.
The approach regions \(\tau (q)\) in Theorem 6.19 are sequential. However, Nagel and Stein also proved the following result.
Theorem 6.20
([127]) There exists a family \(\tau \) of approach regions in \(\mathbb {D}\) with the following properties:
Theorem 6.20 shows that the absence of rotational invariance is not at the heart of Theorem 6.18. The picture of this subject has perhaps been completed by the following results. The first one is a theorem of Littlewood type.
Theorem 6.21
([47]) There is no family \(\tau :\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }(\mathbb {D}) \) of approach regions for which the following hold:
- (a*):
-
For each \(q\in \partial \mathbb {D}\), the set \(\{q\}\cup \tau (q)\) is connected
- (eventually disjoint from the angular filter):
-
(same as in Theorem 6.16)
- (Fatou):
-
(same as in Theorem 6.16)
- (a regularity condition):
-
$$\begin{aligned} \text {For each open set } O\subset \mathbb {D},\text { the set } \left\{ q\in \partial \mathbb {D}: O\cap \tau (q)\ne \emptyset \right\} \text { is a measurable subset of } \partial \mathbb {D}. \end{aligned}$$(6.19)
Indeed, if a family \(\tau \) of approach regions in \(\mathbb {D}\) based on \(\partial \mathbb {D}\) has the four properties described above, then there exists \(u\in H^{\infty }({\mathbb {D}}) \) such that, for almost every \(q\in \mathbb {D}\), the limiting value \({\lim _{\tau (q)}u}\) does not exist.
Condition (a*) is strictly weaker than (asymptotic) and it identifies the property of curves that is relevant for a theorem of Littlewood type.
A regularity condition, in the statement of a theorem, is a hypothesis that is not a priori needed in order for the conclusion of the theorem to make sense. For example, (6.19) is a regularity condition in Theorem 6.21. Inspiration for this regularity condition (6.19) comes from a circle of ideas due to Stein (cf. 6.4), which originates in Calderon’s extension to harmonic functions of Privalov’s Local Fatou Theorem, presented in Sect. 8.2.5.
The results presented so far are concerned with geometric filters, i.e., with filters associated to (collections of) approach regions. The following result is due to Joseph Leo Doob in 1973.
Theorem 6.22
([51]) If \(\Phi :\partial \mathbb {D}\rightarrow \mathsf {Filters}(\mathbb {D}) \) is a rotationally invariant family of boundary filters such that, for each \(u\in H^{\infty }({\mathbb {D}}) \), \( \mathsf {Fatou}(u;\Phi )\) has full measure and \({\lim _{\Phi (q)}u= {u}_{\flat }(q)}\) almost everywhere, then there exists a rotationally invariant family of boundary filters \({\Psi }:\partial \mathbb {D}\rightarrow \mathsf {Filters}(\mathbb {D}) \) such that
- (1):
-
For every \(q\in {X} \), the filter \({\Psi }(q)\) is strictly broader than \( \Phi (q)\).
- (2):
-
For each function \(u\in H^{\infty }({\mathbb {D}}) \), \({\lim _{{\Psi }(q)}u}\) exists for almost every \(q\in {X} \) and is equal to \({\lim _{ \Phi (q)}u}\).
6.11 Epilogue in the Unit Disc
Consider the following
Littlewood-Type Statement. There is no family \(\tau :\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }(\mathbb {D}) \) of approach regions with the following properties:
The question of the truth value of the Littlewood-Type Statement is another rendition of Question 6.2, which has inspired the results we have seen in this section. The answer is outflanking.
Theorem 6.23
([47]) It is neither possible to prove the Littlewood-Type Statement nor to disprove it.
Theorem 6.23 says that the Littlewood-Type Statement is independent of ZFC (acronym for Zermelo, Fraenkel and the Axiom of Choice). The proof of Theorem 6.23 is based on a combination of methods of modern logic and harmonic analysis, based on an insight about the location of the link that makes the combination possible.
7 Quantitative Boundary Behavior
In quantitative Fatou-type theorems, in the setting of Sect. 6.1 and Sect. 6.2, the objects of study are families of approach regions rather than families of boundary filters. If \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) is a family of approach regions in \(D\) based on \( {X} \) and \( \displaystyle {\sup _{\varphi }} \,{|u|} \) is the \(\varphi \)-maximal function of \(u\in \mathbb {C}^{D}\), then the distribution function of \( \displaystyle {\sup _{\varphi }} \,{|u|} \), defined in (6.5), is able to detect, in a quantitative manner, the change in the “shape” of \(\varphi (q)\), as \(q\) varies within \(\partial \mathbb {D}\). The function  in (6.5) is called the \(\varvec{\varphi }\) -gauge of \(u\). Theorem 7.1 below, based on the notion of subordination, attests to the relevance of the notion of \(\varphi \)-gauge, associated to a family of approach regions.
in (6.5) is called the \(\varvec{\varphi }\) -gauge of \(u\). Theorem 7.1 below, based on the notion of subordination, attests to the relevance of the notion of \(\varphi \)-gauge, associated to a family of approach regions.
7.1 Subordination
Given two families of approach regions on \(D\) based on \( {X} \), say \(\tau : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) and \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \), we say that \(\tau \) is subordinate to \(\varphi \) if there exists \( \varvec{c} >0\) such that

for each \(u\in \mathbb {C}^{D}\) and each \(r>0\). Observe that the condition of being subordinate does not hinge on the pointwise shape of \(\tau (q)\) and \(\varphi (q)\) but is a global condition.
7.2 A Bootstrap Result
At the heart of Theorem 4.2, there lies the following result, Theorem 7.1, which is a special case of a more general result, Theorem 7.7 that will be presented after we have introduced the appropriate language. Thus for the time being, we present the result in the unit disc. Recall that \(\Gamma _{k}:\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }(\mathbb {D}) \) is the family of approach regions defined in (2.7).
Theorem 7.1
Let \(\tau :\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }(\mathbb {D}) \) be a family of approach regions in \(\mathbb {D}\) which is subordinate to \(\Gamma _{j_0}\) for some given \({j}_0\ge 1\). If \(u\in \mathbb {C}^{\mathbb {D}}\) and \(Q\in \varvec{\mathcal {A}}({\partial \mathbb {D}}) \), then
and, moreover, for almost every \(q\in Q\), \(\lim _{\tau (q)}u=\lim _{\Gamma _{k_0}}u\).
Theorem 7.1 is important for a number of reasons: (1) It exhibits a bootstrap phenomenon; (2) It derives a qualitative result from the quantitative inequality in (7.1); (3) It contains a good part of the explanation of the “magic” of Theorem 4.2 and of the Nagel–Stein results; (4) It provides the basis for a proper understanding of Stein’s insight into the boundary behavior of holomorphic functions of several variables.
We are now ready to explain in part the “magic” of Theorem 4.2 and of the Nagel–Stein results, on the basis of the following facts: (i) The condition that \(\tau \) is subordinate to \(\Gamma _{{j}_0}\) is compatible with the condition that, for each \(q\), \(\tau (q)\) lies frequently outside \(\Gamma _{{j}}(q)\) for each \({j}\ge {}1\), or even that it is eventually disjoint from \(\Gamma _{{j}}(q)\) for each \({j}\ge {}1\); (ii) For each \({j}\ge {}1\) and each \(k\ge {}1\), \(\Gamma _{{j}}\) is subordinate to \(\Gamma _{k}\).
Observe that it is essential to assume that the value of \(j_0\) in the statement of Theorem 7.1 is strictly greater than 0. Indeed, the statement of Theorem 7.1 with \(j_0=0\) is false. Hence there is something “special” about the family of approach region \(\Gamma _{{j}}\) for \({j}\ge {}1\), which will be explained momentarily.
We postpone these tasks for a while, since we would now like to point out another application of these ideas, which is based on the existence of a pointwise inequality.
7.3 Quantitative Estimates vs. Qualitative Results
The Hardy–Littlewood maximal operator \(M_{f}({q})\) was defined in (5.29). Consider the following statements:
- (1):
-
If \({j}\ge 0\), there exists \(c_j>0\) such that for each \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\) and \(q\in \partial \mathbb {D}\)
$$\begin{aligned} \displaystyle {\sup _{ \Gamma _{j} }} { | Pf | }\,( q) \le c_{j} M_{f}({q}). \end{aligned}$$(7.2) - (2):
-
For each \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\), \( \mathsf {Lebesgue}[f]\subset \mathsf {Fatou}{( Pf )} \) and if \(q\in \mathsf {Lebesgue}[f]\), then \( {( Pf )}_{\flat }(q)=f(q)\).
- (3):
-
If \({j}\ge 0\), then there exists \(c_{j}>0\) such that, for each \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\) and each \(r>0\),
$$\begin{aligned} |{ \{ \displaystyle {\sup _{ \Gamma _{j} }} \,{ | Pf | } >r\} }| \le \frac{c_{j}}{r} \int _{\partial \mathbb {D}} |f|\mathrm{d}~\omega . \end{aligned}$$(7.3) - (4):
-
For each \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\) the set \( \mathsf {Fatou}{( Pf )} \) has full measure.
The following observations are meant to illustrate the power of quantitative estimates.
-
(1) implies (2), by a variant of the standard method: Write \(f\) as the sum of a local part (localized at a given Lebesgue point) and a remainder which vanishes around the given point.
-
(1) implies (3), since the Hardy–Littlewood maximal operator is of weak-type (1,1).
-
(3) implies (4), by the standard method.
7.4 The Hardy–Littlewood Pointwise Maximal Inequality
The form of the Poisson kernel enabled Hardy and Littlewood to prove the following pointwise inequality.
Theorem 7.2
([73]) If \(j\ge 0\), then there exists \(c_{j}>0\) such that (7.2) holds for each \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\) and \(q\in \partial \mathbb {D}\).
7.5 The Hardy–Littlewood \(\varvec{L^p}\) Inequality
The following result, based on Theorem 7.2, is the crowning achievement among the quantitative results on the boundary behavior of holomorphic functions in the unit disc. The subtleties exhibited in the setting of several complex variables, uncovered by Stein, arise precisely in its extension to that setting. This subtle result is based on the work of Hardy and Littlewood, who “contrary to spelling, in this context a single name” [190]. It is called the Hardy–Littlewood \(\varvec{L^{p}}\) Inequality.
Recall that \({u}_{\rho }\) denotes the boundary function which encodes the radial boundary values of \(u\).
Theorem 7.3
([73]) For each \({j}\ge 0\) and \(p>0\), there exists \( \varvec{c} = \varvec{c} _{p,{j}}>0\) such that for each \(u\in {} H^{p}({\mathbb {D}}) \):
The power of the Hardy–Littlewood maximal function revealed itself in the following result as well. It was obtained in 1971 by Donald Lyman Burkholder, Richard Floyd Gundy, and Martin Louis Silverstein, with a proof based on Brownian motion. Shortly thereafter, in 1972, Stein gave a far-reaching version of this result, in collaboration with Charles Fefferman [62].
Theorem 7.4
([22]) If \(0<p<\infty \), \({j}\ge 1\), \(u\in h(\mathbb {D}) \) is real valued, and \( \displaystyle {\sup _{\Gamma _{j}}} \,{u} \in \mathcal {L}^{p}(\mathbb {D})\), then \(u\) is the real-part of a function in \( H^{p}({\mathbb {D}}) \).
Another instance of the general principle according to which a quantitative result implies a qualitative one can be seen in the following result, obtained from Theorem 7.3 by the standard method.
Proposition 7.5
The Hardy–Littlewood \({L^{p}}\) Inequality (7.4) implies that, if \(0<p\le {}+\infty \), then for each \(u\in {} H^{p}({\mathbb {D}}) \), the set \( \mathsf {Fatou}{(u)} \) has full measure.
Hence Theorem 7.3 enables us to recapture the qualitative result on the almost everywhere existence of angular values, provided we know that radial boundary values exist almost everywhere.
The importance of Theorem 7.3 is clarified by the following result as well. It can also be proved using the standard method.
Theorem 7.6
If \(\varphi :\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }(\mathbb {D}) \) is a family of approach regions such that, for each \(u\in C(\mathbb {D}) \), the function \(\sup _{\varphi }|u|\) is measurable on \(\partial \mathbb {D}\), and for each \(p>0\), there exists \( \varvec{c} = \varvec{c} _{p}>0\) such that for each \(u\in {} H^{p}({\mathbb {D}}) \)
then for each \(0<p\le +\infty \) and each \(u\in H^{p}({\mathbb {D}}) \), \(\lim _{\varphi (q)} u\) exists and is equal to \( {u}_{\flat }(q)\) for a.e. \(q\in \partial \mathbb {D}\).
7.6 Imbeddings as General Setting for Quantitative Boundary Behavior
A good understanding of Theorem 7.1 may be achieved in the following general setting, which also serves as a framework that contains all the applications we have in mind.
If \( {X} =( {X} ,\omega ,\delta )\) is a space of homogeneous type, \( \mathbf {W} =( \mathbf {W} , \varvec{ {d} } )\) is a pseudometric space, and \(D\subset \mathbf {W} \), then an imbedding \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \) is called admissible if it has the following property, where we identify as usual points of \( {X} \) with their images in \( \mathbf {W} \) via the imbedding \( {X} \hookrightarrow \mathbf {W} \).
- (AI):
-
If \({\{q_n\}}_{n}\) and \({\{p_n\}}_{n}\) are sequences in \( {X} \), then \({\lim _{n\rightarrow +\infty }\delta (q_n,p_n)=0}\Leftrightarrow {\lim _{n\rightarrow +\infty } \varvec{ {d} } (q_n,p_n)=0}\).
An example, which we have already met, is the following: Any space of homogeneous type \( {X} \) is admissibly imbeddable in the boundary of \( \mathbf {B}( {X} ) \) in \( \varvec{\mathcal {P}}_{\bullet }( {X} ) \).
In many cases, if \(\Omega \subset \mathbb {R}^n\) is a domain in \(\mathbb {R}^n\), then it is possible to endow \(\partial \Omega \) with an appropriate measure and metric for which the natural imbedding \(\partial \Omega \hookrightarrow \mathbb {R}^n\) is admissible (see below).
7.7 The Intrinsic Maximal Function in the Setting of an Admissible Imbedding
We assume that
-
\(\imath : {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \) is an admissible imbedding of \( {X} \) in the boundary of \(D\subset \mathbf {W} \).
-
\(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) is a family of approach regions in \(D\) based on \( {X} \).
-
\(R: L^{p}( {X} ) \rightarrow \mathbb {C}^{D}\) is a functional representation of \( L^{p}( {X} ) \) on \(D\).
The \(\varphi \)-maximal operator of \(|u|\) is defined as in \(\mathbb {D}\) without substantial changes:
where \( \displaystyle {\sup _{\varphi }} \,{|u|} (q) {\mathop {=}\limits ^{\mathrm{def}}}\sup \left\{ \left| u(z)\right| : z\in {}{\varphi }(q) \right\} \), for \(u\in \mathbb {C}^{D}\) and \(q\in {X} \). The intrinsic \(\varvec{\varphi }\)-maximal operator associated to a functional representation \(\varvec{R}\) is defined as follows: For \(\mathrm{f}\in L^{p}( {X} )\) and \(q\in {X} \)
Hence the property “a weak-type/strong-type inequality holds for the operator \(R_{\varphi }\)” (which the operator \(R_{\varphi }\) may or may not have) describes the quantitative boundary behavior of the functional representation \(R\) with respect to the family of approach regions \(\varphi \). A theorem, which gives sufficient conditions entailing the validity of a weak type or of a strong-type inequality for \({\sup _{\varphi }|R|}\), is called a quantitative Fatou-type theorem. Observe that a quantitative Fatou-type theorem relies on the actual choice of a certain family of approach regions, rather than on the specification of a family of boundary filters.
7.8 Regular Families of Approach Regions
We say that \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) is regular if one of the following equivalent conditions holds:
- (R 1):
-
For each \(u\in C(D) \), the function \( \displaystyle {\sup _{\varphi }} \,{|u|} \) is measurable.
- (R 2):
-
For each open set \(O\subset D\), the set \( \left\{ q\in {X} : O\cap {}{\varphi }(q)\ne \emptyset \right\} \) is a measurable subset of \( {X} \).
The set which appears in (R 2) also appears in the regularity condition of Theorem 6.21.
The function
defined by
is called the inverse of \({\varphi }\). The family of approach regions \({\varphi }\) is uniquely determined by its inverse. Observe that a family of approach regions \( {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) may be identified with a subset of \( {X} \times D\). A subset of \( {X} \times D\) is called a relation of \( {X} \) with \(D\) [87, p. 6]. Then, \( {\varphi }^*\) is the “inverse relation” [87, p. 7].
The set \( {\varphi }^*(z) \) is called the shadow projected by \(z\) along \({\varphi }\). The shadow along \({\varphi }\) determine the sets which appear in the notion of regularity, since
The set \( \left\{ q\in {X} : O\cap {}{\varphi }(q)\ne \emptyset \right\} \) is called the shadow projected by O along \({\varphi }\) and is denoted by \( {\varphi }^*[O]\). Hence, with slight abuse of notation, the function
is defined by \( {\varphi }^*[O]{\mathop {=}\limits ^{\mathrm{def}}} \left\{ q\in {X} : O\cap {}{\varphi }(q)\ne \emptyset \right\} \).
7.8.1 Lower Semicontinuity
A condition stronger than regularity is the following one: The family of approach regions \({\varphi }\) is called lower semicontinuous if one of the following equivalent conditions is satisfied:
-
(LS.1) For any function \(u:D\rightarrow \mathbb {C}\), the maximal function \({ \displaystyle {\sup _{\varphi }} \,{|u|} }\) is lower semicontinuous on \( {X} \).
-
(LS.2) For each \(z\in D\), \( {\varphi }^*(z) \) (the shadow projected by \(z\) along \(\varphi \)) is open in \( {X} \).
For example, the family of approach regions \(\Gamma _{j}\) is lower semicontinuous if \(j\ge {}1\), while \(\Gamma _0\) is regular but not lower semicontinuous.
7.9 Adapted Families of Approach Regions
In order to see what are the properties of the family of nontangential approach region \(\Gamma _{j}\), for \({j}\ge 1\), which are behind the validity of Theorem 7.1 we introduce, in the setting of Sect. 7.6, the following notions. The family of approach regions \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) is said to be adapted to the admissible imbedding \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \) if (roughly speaking) the shadow of \(z\in D\) is an open set in \( {X} \) of small diameter, close to \(z\), and uniformly comparable to a ball. More precisely, \(\varphi \) is adapted to the admissible imbedding \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \) if it has the following properties:
-
(1) The family of approach regions \(\varphi \) is lower semicontinuous.
-
(2) There are constants \( \varvec{c} _1, \varvec{c} _2\in (0,+\infty )\) such that, for each \(z\in D\), there exist \( q(z) \in {X} \) and \( r(z) >0\) such that
$$\begin{aligned} {B}_{ {X} ,\delta } \left( q(z) , \varvec{c} _1\cdot r(z) \right) \subset {\varphi }^*(z) \subset {B}_{ {X} ,\delta } \left( q(z) , \varvec{c} _2\cdot r(z) \right) . \end{aligned}$$(7.11) -
(3) For each \(q\in {X} \) and each sequence \({\{z_{j}\}}_{j}\) of points in \(D\) converging to \(q\) in \(( \mathbf {W} , \varvec{ {d} } )\), the following properties hold:
-
(3.a) \({ \lim _{ j\rightarrow +\infty } \text {diam}_{\delta }\left[ {\varphi }^*(z_{j}) \right] = 0 } \), where \( \text {diam}_{\delta }\left[ Q\right] \) is the diameter of \(Q\) in the metric \(\delta \).
-
(3.b) \({ \lim _{j\rightarrow +\infty } \sup \{ \varvec{ {d} } (z_{j},p): p\in {\varphi }^*(z_{j}) \}=0. } \)
-
For example, if \({j}\ge 1\) then \(\Gamma _{j}:\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }(\mathbb {D}) \) is adapted to the admissible imbedding of \(\partial \mathbb {D}\) in \(\mathbb {C}\). Observe that \(\Gamma _0\) is not adapted to this imbedding.
7.9.1 A General Bootstrap Result
Theorems 7.1 and 4.2 are special cases of the following result.
Theorem 7.7
Let \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) be a family of approach regions that is adapted to the admissible imbedding \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \), and let \(\tau : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) be a family of approach regions that is subordinate to \(\varphi \). If \(Q\in \varvec{\mathcal {A}}({ {X} }) \) and \(u\in \mathbb {C}^{D}\), then
and, moreover, for almost every \(q\in Q\), \({\lim _{[\tau (q)]}u=\lim _{[\varphi (q)]}u}\).
7.10 An Intrinsic Condition for Subordination
In order to give an intrinsic condition that identifies a family of approach regions as being subordinate to a given family of approach regions (which, in turn, is adapted to an admissible imbedding), we introduce the following notions. In what follows, \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) is a family of approach regions.
7.10.1 The Lebesgue Transform
The family of approach regions \({\varphi }\) is called amenable if \( \overline{\varphi }(z) \in \varvec{\mathcal {A}}({ {X} }) \) for all \(z\in D\). The \(\varphi \)-Lebesgue transform associated to an amenable family of approach regions \(\varphi \) is the functional representation
defined by \( {L}^{\varphi } {\mathrm{f}} {\mathop {=}\limits ^{\mathrm{def}}} \varvec{\omega }(\mathrm{f}) \,\circ \, {\varphi }^*\), i.e.,  , for \(z\in D\).
, for \(z\in D\).
7.10.2 Tents
Stein had a crucial role in unearthing the role played by the notion of tent associated to a family of approach regions. The notion of tent is used to give an intrinsic characterization of those families of approach regions which are subordinate to a family of approach regions which is adapted to an admissible imbedding. The \({\varphi }\)-tent above a subset \(Q\subset {X} \) is the set:
Hence \( \Delta ^{\varphi } :\varvec{\mathcal {P}}( {X} ) \rightarrow \varvec{\mathcal {P}}(D) \). The term “tent” draws its origin from the case where \(\varphi =\Gamma _{j}\): In this case, we denote \( \Delta ^{\varphi }Q \) by \( \Delta ^{{j}}B \).
7.10.3 The Bootstrap of a Family of Approach Regions
The bootstrap of \({\varphi }\) is the function \( {\varphi }^{\sharp } :D\rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) where
If \(\tau \) is another family of approach regions, the \(\varphi \)-bootstrap of \(\tau \) is the family of approach regions \(\tau ^{\varphi }\)
7.10.4 The Action on Outer Measures
Denote by \(\textsf {Outer}[{S}]\) the collection of all outer measures defined on a set S (nonnegative, monotonic, subadditive set functions vanishing on the empty set; see [63, p. 28]), and define
as follows: if \(m\in \textsf {Outer}[{ {X} }]\) and \(Z\subset D\), we let \(( {\varphi }^{\circ } {m}{\,} )(Z){\mathop {=}\limits ^{\mathrm{def}}}{}m( {\varphi }^*(Z) )\).
7.10.5 A Synthetic Diagram
We summarize the various operators introduced so far in the following diagrams.

In this notation, a subscript indicates that the end result lives in \( {X} \), a superscript that it lives in \(D\).
7.10.6 An Intrinsic Condition for Subordination in the General Setting
Theorem 7.8
Let \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) be a family of approach regions that is adapted to the admissible imbedding \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \), and let \(\tau : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) be a family of approach regions. Then, the following conditions are equivalent:
- (1):
-
\(\tau \) is subordinate to \(\varphi \), i.e., there exists \( \varvec{c} >0\) such that, for all \(u\in {[0,+\infty )}^{D}\) and each \(r>0\),
$$\begin{aligned} \omega ^{*} \{ \displaystyle {\sup _{\tau }} \,{u}>r\} \le \varvec{c} \omega { \{ \displaystyle {\sup _{\varphi }} \,{u} >r\}. } \end{aligned}$$(7.12) - (2):
-
There is a constant \( \varvec{c} >0\) such that for each open ball \({B}\in \mathbf {B}( {X} ) \),
$$\begin{aligned} \omega ^{*}( { \tau }^*[ \Delta ^{\varphi }{B} ] ) \le {} \varvec{c} {} \omega {({B})}. \end{aligned}$$(7.13) - (3):
-
There is a constant \( \varvec{c} >0\) such that for all \(\mathrm{f}\in L^{1}( {X} ) \) and each \(r>0\),
$$\begin{aligned} \displaystyle { \omega ^{*} \{ \displaystyle {\sup _{\tau }} \,{\, {L}^{\varphi } {|\mathrm{f}|} }> r\} \le {} \varvec{c} {} \, \omega { \{ \displaystyle {\sup _{\varphi }} \,{\, {L}^{\varphi } {|\mathrm{f}|} } > r\}. } } \end{aligned}$$ - (4):
-
There is a constant \( \varvec{c} >0\) such that for all \(\mathrm{f}\in L^{1}( {X} ) \) and each \(r>0\),
$$\begin{aligned} \omega ^{*} \{ \displaystyle {\sup _{\tau }} \,{ {L}^{\varphi } {|\mathrm{f}|} } > r\} \le \frac{ \varvec{c} }{r} \int _{ {X} }|\mathrm{f}|\,\mathrm{d}~\omega . \end{aligned}$$ - (5):
-
The \(\varphi \)-bootstrap of \(\tau \) is subordinate to \(\varphi \).
The condition in (7.13) is the tent condition for \(\tau \) relative to \(\varphi \). It is intrinsic, since it is stated purely in terms of \(\tau \).
7.11 An Explanation of the Nagel–Stein Phenomenon
An application of the tent condition shows that
even though, for each \(q\in \partial \mathbb {D}\), \(\Gamma _{{j}+1}(q)\) is strictly broader than \(\Gamma _{j}(q)\). The Nagel–Stein phenomenon says that there is a family of approach regions \(\tau \) with the properties (a) and \(\mathbf (b) \) described below:
- (a):
-
\(\tau \) is subordinate to \(\Gamma _1\) (and therefore to \(\Gamma _{j}\), for all \({j}\), in view of (7.14)).
- (b):
-
For each \(q\in \partial \mathbb {D}\), \(\tau (q)\) is eventually disjoint from the angular filter ending at \(q\).
Now, (a) implies
- (a 1):
-
Functions in \( H^{p}({\mathbb {D}}) \) have a.e. boundary values through \(\tau \) (by Theorem 7.1).
- (a 2):
-
For each \(p>0\), there exists \( \varvec{c} _p>0\) such that
$$\begin{aligned} \int _{\partial \mathbb {D}} {(\textstyle {\sup _{\tau }|u|})}^p \,\mathrm{d}~\omega \le \varvec{c} \int _{\partial \mathbb {D}} {|{u}_{\rho }|}^p\,\mathrm{d}~\omega \quad \text { for each } u\in {} H^{p}({\mathbb {D}}) \end{aligned}$$
Observe that (b) says that the qualitative Fatou theorem in (a 1) is more stringent than Theorem 6.9. Hence the point is to establish the compatibility of (b) with (a), i.e., with the tent condition (7.13) where, say, \(\varphi =\Gamma _1\). This possibility arises if \(\tau (q)\) is sequential and “lacunary,” i.e., fast convergent, so that the shadow projected by the tent which lies above an interval will have many “holes,” and therefore, its measure will be bounded in terms of the measure of the interval, uniformly over the interval. Hence the magic of Theorem 6.19 is revealed. A similar reasoning explains Theorem 6.20, where now the approach regions \(\tau (q)\) consist of curves.
7.11.1 The Cross-Section Condition
A family of approach regions \(\varphi :\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }(\mathbb {D}) \) is rotationally invariant if it has the following property:
This notion plays an important role in Littlewood’s Theorem 6.16. A family of approach regions \(\varphi :\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }(\mathbb {D}) \) satisfies the cross-section condition if there is a constant \( \varvec{c} >0\) such that, for each \(q\in \partial \mathbb {D}\) and each \(r\in (1/2,1)\),
Observe that the family of approach regions \(\Gamma _{j}\) defined in (2.7) satisfies the cross-section condition. The relevance of this condition was discovered by Nagel and Stein [35, 99, 127, 172,173,174].
Lemma 7.9
If \(\varphi :\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }(\mathbb {D}) \) is a rotationally invariant family of approach regions, then the tent condition (7.13) holds for \(\varphi \) if and only if the cross-section condition (7.16) holds.
The following result says that if \(\varphi \) is not group invariant, then \(\varphi \) may satisfy the cross-section condition but not the tent condition: Hence \(\varphi \) is not subordinate to \(\Gamma _{j}\).
Lemma 7.10
([42]) There is a family of approach regions \(\varphi :\partial \mathbb {D}\rightarrow \varvec{\mathcal {P}}_{\bullet }(\mathbb {D}) \) with the following properties:
- (1):
-
\(\varphi \) is not rotationally invariant.
- (2):
-
The cross-section condition (7.16) holds.
- (3):
-
The tent condition (7.13) does not hold, and hence \(\varphi \) is not subordinate to \(\Gamma _1\).
We are thus led to the following notion.
7.12 Distributionally Broader Families of Approach Regions
We say that a family \(\tau : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) of approach regions in \(D\) is distributionally broader than a given family of approach regions \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) if \(\tau \) is not subordinate to \(\varphi \). This notion plays a distinguished role in Stein’s contributions on the boundary behavior of holomorphic functions in \(\mathbb {C}^n\).
7.13 Sequences of Families of Approach Regions
If \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \) is an admissible imbedding, a sequence of families of approach regions is a sequence \( { \{ {\varphi }_{j} \} }_{j\ge 1} \) where each \(\varphi _j\) is a family of approach regions in \(D\) based on \( {X} \).
We say that the sequence of families of approach regions \( { \{ {\varphi }_{j} \} }_{j\ge 1} \) is adapted to the admissible imbedding \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\) if
- (1):
-
For each \(j\in \mathbb {N}\), \(\varphi _{j}\) is adapted to the admissible imbedding \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \).
- (2):
-
For each \(q\in {X} \) and each \(j\in \mathbb {N}\), \(\varphi _{j}(q)\subset \varphi _{j+1}(q)\).
- (3):
-
For each \(j\in \mathbb {N}\), there exist \(c_{j}, c^{\prime }_{j}\in (0,+\infty )\) such that, for each \(z\in D\), there exist \( q(z) \in {X} \) and \( r(z) >0\) such that
$$\begin{aligned} {B}_{ {X} ,\delta } \left( q(z) ,c_{j}\, r(z) \right) \subset {(\varphi ^{*}_{j})}{(z)} \subset {B}_{ {X} ,\delta } \left( q(z) ,c^\prime _{j} r(z) \right) . \end{aligned}$$(7.17)
Theorem 7.11
If the sequence of families of approach regions \( { \{ {\varphi }_{j} \} }_{j\ge 1} \) is adapted to the admissible imbedding \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \), then for each \(j_1\) and \(j_2\in \mathbb {N}\), \(\varphi _{j_1}\) is subordinate to \(\varphi _{j_2}\).
Observe that the conclusion of Theorem 7.11 holds for \(j_1< j_2\) as well as for \(j_2 < j_1\). The case \(j_2 < j_1\) is the nontrivial one. Indeed, under the hypothesis in the theorem, \(\varphi _{j_1}\) is subordinate to \(\varphi _{j_2}\) even if it is strictly broader than \(\varphi _{j_2}\).
Corollary 7.12
If the sequence of families of approach regions \( { \{ {\varphi }_{j} \} }_{j\ge 1} \) is adapted to the admissible imbedding \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \), and \(u\in \mathbb {C}^{D}\), then for each \(j_1\) and \(j_2\in \mathbb {N}\), if \(u\) has boundary values through \(\varphi _{j_1}(q)\) for a.e. \(q\), then it has the same boundary values through \(\varphi _{j_2}(q)\) for a.e. \(q\).
The conclusion of Corollary 7.12 says that, from the viewpoint of a.e. convergence, if \(j_1\not =j_2\), then the families of approach regions \(\varphi _{j_1}\) and \(\varphi _{j_2}\) yield the same results. Hence Theorem 4.2 follows from Theorem 7.1 and from Corollary 7.12.
7.13.1 Applications to Lebesgue Differentiation Bases
Recall that \( {L}^{\varphi } {\mathrm{f}}\) is the Lebesgue transform of \(\mathrm{f}\), defined in Sect. 7.10.1.
Theorem 7.13
If \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \) is an admissible imbedding and \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) is an amenable family of approach regions which is adapted to it, then for each \(\mathrm{f}\in C( {X} ) \) and each \(q\in {X} \), the unrestricted boundary value of \( {L}^{\varphi } {\mathrm{f}}\) exists at \(q\) and is equal to \(\mathrm{f}(q)\).
Recall that \(M_{\mathrm{f}}\) is the Hardy–Littlewood maximal operator of \(\mathrm{f}\in L^{1}( {X} ) \) defined in Sect. 5.2.11.
Theorem 7.14
If \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \) is an admissible imbedding and \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) is an amenable family of approach regions which is adapted to it, then there exists a constant \( \varvec{c} >0\) such that for each \(\mathrm{f}\in L^{1}( {X} ) \), the following pointwise inequality holds for each \(q\in {X} \):
Corollary 7.15
If \( {X} \hookrightarrow \partial _{ \mathbf {W} }{D}\subset \mathbf {W} \) is an admissible imbedding, \(\varphi : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) is an amenable family of approach regions which is adapted to it, and \(\tau : {X} \rightarrow \varvec{\mathcal {P}}_{\bullet }(D) \) is a family of approach regions subordinate to \(\varphi \), then for each \(f\in \mathcal {L}^{1}( {X} )\), the boundary value of \( {L}^{\varphi } {f} \) through \(\tau (q)\) exists for a.e. \(q\in {X} \) and is equal to \(f(q)\).
8 Harmonic Functions
Having given an outline of the results about the boundary behavior of holomorphic functions that were relevant to “the complex method,” we are now almost ready to look at history with the benefit of hindsight. The first attempts to find an extension of the results of Fatou can be found in the work of the Moscow school of mathematics. Here, the term “extension” refers both to extension to functions holomorphic on domains in the plane other than the unit disc, as well as to extension to functions defined on general domains in Euclidean spaces and harmonic therein. For example, the first definition of the Hardy space of holomorphic functions over a domain \(\Omega \) in the plane, other than the unit disc, is due to the Moscow school. Indeed, Lusin himself was aware of the fact that the results on Fourier series obtained by the complex method belonged to real analysis and imagined that in order to prove his conjecture about the a.e. convergence of Fourier series of \(L^2\) functions, one had to recast the subject again but without relying on the complex method. For example, in the specific instance of the Hilbert transform, he felt the need for a purely real-variable proof of a purely real-variables statement. The first progress in this direction was achieved by Besicovitch in 1923 and 1926. Zygmund and his school carried on with the project of developing new “real-variable” methods aimed at understanding the higher dimensional case, where complex analysis plays no role. Stein referred to this project as Zygmund’s vision and wrote that
[...] only with techniques coming from real-variable theory could one hope to come to grips with many interesting n-dimensional analogues of the one dimensional theory.
Concerning the period from 1950 to 1964, Stein wrote that
The mathematician animating this development was Antoni Zygmund. In many ways he set the broad outlines of the effort, he mastered by his work some of the crucial difficulties, and was throughout the source of inspiration for his students and collaborators.
As a matter of fact, Stein himself played a leading role. We hope that the brief outline we have given so far will make it easier to understand why the study of the boundary behavior of holomorphic or harmonic functions has remained dear to his heart, even in contexts where no group of symmetries is acting on the space. Before we continue our presentation of his achievements in this area, we have to give a sample of the large body of results that grew out of the Dirichlet problem. This will be done in the following section.
8.1 The Dirichlet Problem
We now present an essential account of the Dirichlet problem, where the roots for the study of the boundary behavior of harmonic (and holomorphic) functions are contained [5]. As a prelude to the statement of the Dirichlet problem of classical potential theory, observe that if \(\Omega \) is a bounded domain in \(\mathbb {R}^n\) and the unrestricted boundary value \(u_\Omega (q)\) at \(q\in \partial \Omega \) of a continuous function \(u:\Omega \rightarrow \mathbb {C}\) exists for each \(q\in \partial \Omega \), then the boundary function \(u_\Omega :\partial \Omega \rightarrow \mathbb {C}\) is continuous on \(\partial \Omega \). Loosely speaking, the Dirichlet problem is this: Given a function \(f:\partial \Omega \rightarrow \mathbb {C}\), one has to find (if it exists, or, otherwise, one has to understand under which conditions it exists) a function \(u_{f}\in h(\Omega ) \) such that
As can be seen from this formulation, the Dirichlet problem actually yields a whole class of problem, depending on the precise meaning that we assign to the notion of “boundary values” that appears in (8.1). The associated inversion problem, as in Sect. 4.6, i.e., the problem of describing a way to recapture \(f\) starting from \(u_{f}\in h(\Omega ) \), and, more generally, the problem of understanding the “boundary behavior” of \(u_{f}\in h(\Omega ) \), leads to the Fatou-type theorems, of which we have already met different versions, classified as pointwise, qualitative, and quantitative. As in the classical Dirichlet problem, in (8.1), we consider the unrestricted boundary values. Our initial observation shows that in the classical Dirichlet problem there is no loss of generality in assuming that \(f\in C(\partial \Omega ) \). If a solution \(u_{f}\in h(D) \) exists, it is called the solution of the classical Dirichlet problem with boundary datum \(f\): It is unique and it is bounded on \(\Omega \), i.e., it belongs to the Hardy space \( h^{\infty }({\Omega }) \) of complex-valued functions that are harmonic on \(\Omega \) and bounded therein:
It follows that, if the classical Dirichlet problem can be solved in \(\Omega \), then there exists an operator
which maps the datum \(f\in C(\partial \Omega ) \) to the corresponding solution \(u_{f}\in h^{\infty }({\Omega }) \). We denote by \( C_r(\partial \Omega ) \) the subset of \( C(\partial \Omega ) \) consisting of all functions \(f\in C(\partial \Omega ) \) such that the solution of the classical Dirichlet problem with boundary datum \(f\) exists. Hence
Domains \(\Omega \) for which \( C_r(\partial \Omega ) = C(\partial \Omega ) \) are called regular domains for the classical Dirichlet problem. Functions in \( C_r(\partial \Omega ) \) are called regular for the Dirichlet problem. Since the restriction to \(\partial \Omega \) of any harmonic polynomial is regular, \( C_r(\partial \Omega ) \not =\emptyset \). The subset \( C_r(\partial \Omega ) \) is a closed subspace of \( C(\partial \Omega ) \). The following result is implicit, albeit in a cryptic form, in Riemann’s Inauguraldissertation (1851) [147]:
Lemma 8.1
If \(\Omega \) is a bounded domain, the following conditions are equivalent:
-
\(\Omega \) is regular for the Dirichlet problem;
-
\( C_r(\partial \Omega ) \) is dense in \( C(\partial \Omega ) \) in the uniform norm;
-
\(f,g\in C_r(\partial \Omega ) \) implies that \(f\cdot g\in C_r(\partial \Omega ) \).
Hence a domain \(\Omega \) is regular for the Dirichlet problem if and only if \( C_r(\partial \Omega ) \) is a subalgebra of \( C(\partial \Omega ) \). If \(f\in C_r(\partial \Omega ) \), then we denote by \(Vf\in h^{\infty }({\Omega }) \) the unique solution of the Dirichlet problem with boundary datum \(f\). The map \(f\mapsto Vf\) defines a linear and positive operator:
called the Dirichlet solution operator. Domains that are not regular for the classical Dirichlet problem were discovered by Stanisław Zaremba in 1909 and by Lebesgue in 1913 [105, 187, 188]. See also [76, 184].
8.1.1 The Poisson–Keldych operator
The following result is remarkable.
Theorem 8.2
There is one and only one positive and linear operator:
such that the following diagram is commutative:

The uniqueness result in Theorem 8.2, due to Keldych in 1941 [86], is rather subtle and has been forgotten by the more recent literature. The existence result does not readily follow from the Hahn–Banach theorem or from the maximum principle, as it is sometimes claimed. The operator \(K\) in Theorem 8.2 is called the Poisson–Keldych operator. It is plausible that an extension of \(V\) to \( C(\partial \Omega ) \) may exist, but it would have no special meaning if it was not unique: The uniqueness shows that it has intrinsic meaning. Indeed, the following result, due to Kellogg (1928) and Evans (1933), shows that the Poisson–Keldych operator is relevant to the Dirichlet problem, even if the domain is not regular.
Theorem 8.3
([55, 88]) The set of points \(q\in \partial \Omega \) such that it is not true that
has capacity zero.
A point \(q\in \partial \Omega \) is said to be regular for the classical Dirichlet problem if (8.4) holds.
8.1.2 Kakutani’s Construction of the Poisson–Keldych Operator
In Theorem 8.2, the existence is independently due to Perron (1923), Remak (1924), and Wiener (1924), with different methods [86, 137, 146, 186]. Another construction of the Keldych operator, due to Kakutani, is based on the operator:
defined as follows. If \(z\in \Omega \), let \(B_z\) be the Euclidean ball of center \(z\) and radius equal to \(r(z)/2\), where \(r(z)\) is the Euclidean distance from \(z\) to \(\partial \Omega \), and denote by \(\sigma _{z}\) the normalized Hausdorff measure of dimension \(n-1\) on the boundary of \(B_{z}\). We are now ready to define \(\mathbb {K}\). If \(u\in C( \overline{ \Omega }) \) and \(z\in \Omega \), let
If j is a positive integer, denote by \(\mathbb {K}^j\) the composition of \(\mathbb {K}\) with itself j times.
Theorem 8.4
If \(f\in C(\partial \Omega ) \) and \(u\in C( \overline{ \Omega }) \) is any continuous extension of \(f\) to \(\overline{\Omega }\), then
exists in the topology of uniform convergence in \( C( \overline{ \Omega }) \), belongs to \( h(\Omega ) \), and does not depend on the particular extension \(\varphi \). The operator \(f\mapsto \overline{\mathbb {K}}f\) is a linear and positive extension of \(V\).
The operator \(\mathbb {K}\) is associated to a Markov process which is a discrete version of Brownian motion in \(\Omega \) killed at the hitting time of \(\partial \Omega \) [85].
8.1.3 Harmonic Measure
We assume, without loss of generality that the origin \(0\in \mathbb {R}^n\) belongs to \(\Omega \). There is a unique positive complete Borel measure \({\omega }\) on \(\partial \Omega \) such that
This measure \(\omega \) is called the \(\Omega \)-harmonic measure with pole at \(0\in \Omega \). Similarly, the \(\Omega \)-harmonic measure with pole at \(z\in \Omega \) is the unique complete Borel measure \(\omega _{z}\) on \(\partial \Omega \) such that
If there is no ambiguity about \(\Omega \), \(\omega _{z}\) is called harmonic measure rather than \(\Omega \)-harmonic measure. Observe that \(\omega _{z}(\partial \Omega )=1\). Recall that \( \varvec{\mathcal {B}}(\partial \Omega )\) is the \(\sigma \)-algebra of Borel subsets of \(\partial \Omega \). The measure-theoretic completion of \( \varvec{\mathcal {B}}(\partial \Omega )\) under \(\omega _{z}\), denoted by \( {\widehat{\varvec{\mathcal {B}}}}_{\omega } \), does not depend on \(z\in \Omega \), since for a Borel subset \(E\subset \partial \Omega \), the conditions \(\omega _{z}(E)=0\) and \(\omega (E)=0\) are equivalent. Hence all harmonic measures \(\omega _{z}\) are defined on the same \(\sigma \)-algebra \( {\widehat{\varvec{\mathcal {B}}}}_{\omega } \), and \((\partial \Omega , {\widehat{\varvec{\mathcal {B}}}}_{\omega } ,\omega _{z})\) is a complete measure space for each \(z\in \Omega \). The sets in \( {\widehat{\varvec{\mathcal {B}}}}_{\omega } \) are precisely those for which harmonic measure is defined, and they are called \(\omega \) measurable.
The following notion turns out to be very relevant in measurability issues: A subset of \(\mathbb {R}^n\) is called analytic if it is the continuous image of a Borel subset of a Polish space [14]. Analytic sets exist in nature: For example, denote by \(\partial _{a}\Omega \subset \partial \Omega \), the set of all boundary points, for which there exists a half-closed Jordan arc contained in \(\Omega \) and ending at \(q\).
Theorem 8.5
([52]) Every analytic subset of \(\partial \Omega \) is \(\omega \) measurable. For each \(z\in \Omega \), \(\omega _{z}(\partial _{a}\Omega )=1\).
Theorem 8.6
([45]) In \(\mathbb {R}^n\) with \(n\ge 3\), the set \(\partial _{a}\Omega \subset \partial \Omega \) is not necessarily Borel but it is analytic.
8.1.4 The Poisson Operator
For each \(z_1,z_2\in \Omega \), an \(\omega \)-measurable function \(f:\partial \Omega \rightarrow \mathbb {C}\) is integrable with respect to \(\omega _{z_{1}}\) if and only if it is integrable with respect to \(\omega _{z_2}\). We denote by \( L^{1}(\partial \Omega ,\omega ) {\mathop {=}\limits ^{\mathrm{def}}} L^{1}(\partial \Omega , {\widehat{\varvec{\mathcal {B}}}}_{\omega } ,\omega ) \) the quotient (modulo a.e. equivalence) of the space of all \(\omega \)-measurable and \(\omega \)-integrable functions. The Poisson operator
is defined, for \(\mathrm{f}\in L^{1}(\partial \Omega ,\omega ) \) and \(z\in \Omega \), as follows:
Harmonic measures with different poles are mutually absolutely continuous with respect to each other. For \(z\in \Omega \), the Radon–Nikodym derivative of \(\omega _{z}\) with respect to \(\omega \) is a positive function \(\texttt {p}_z:\partial \Omega \rightarrow (0,+\infty )\). The Poisson kernel \(\texttt {P}:\Omega \times \partial \Omega \rightarrow (0,+\infty )\) is defined as \(\texttt {P}(z,q)=\texttt {p}_z(q)\). The Poisson operator in (8.6) has the representation (for \(\mathrm{f}\in L^{1}(\partial \Omega ,\omega ) \) and \(z\in \Omega \))
8.1.5 The Poisson Operator on Complex Measures
The Banach space of all complex measures on the measure space \((\partial \Omega , {\widehat{\varvec{\mathcal {B}}}}_{\omega } )\) is denoted by
Then the Poisson operator \(P: L^{1}(\partial \Omega ,\omega ) \rightarrow h(\partial \Omega ) \) may be extended to an operator on \({\mathcal {M}}(\partial \Omega ,\omega )\). It will be also denoted by \(P\), by setting, for \({m}\in {\mathcal {M}}(\partial \Omega ,\omega )\) and \(z\in \Omega \),
We then have the following commutative diagram, where the natural map from \( C(\partial \Omega ) \) to \( L^{1}(\partial \Omega ,\omega ) \) is not necessarily injective.

8.1.6 The Poisson Operator and the Dirichlet Problem
We denote the Poisson–Keldych operator \(K\) and the Poisson operator \(P\) with different names, and different symbols, not only because—as operators—they have different domains and different codomains, but because the boundary behavior of \(K\mathrm{f}\), where \(\mathrm{f}\in C(\partial \Omega ) \), is different from that of \( P\mathrm{f} \), where \(\mathrm{f}\in L^{1}(\partial \Omega ,\omega ) \), as can be seen from Theorem 4.5. Observe that, if \(\Omega =\mathbb {D}\), then \( {\widehat{\varvec{\mathcal {B}}}}_{\omega } \) is the \(\sigma \)-algebra of Lebesgue measurable subsets of \(\partial \mathbb {D}\) and \(\omega \) is normalized arc length. Hence it is definitely not possible to recapture \(\mathrm{f}\) from \( P\mathrm{f} \) by taking its unrestricted boundary values, not even if we restrict our attention to a “large” subset of \(\partial \Omega \) and not even in the case of the simplest regular domain such as the unit disc. Thus, some other method has to be devised in order to recapture \(u\) from \( P\mathrm{f} \). In the unit disc, angular boundary values will do, as we have seen. Since Theorem 4.5 holds in the unit disc—perhaps the simplest regular domain—we see that the notion of unrestricted boundary values can be used to solve the inversion problem only if applied to the boundary behavior of \(Kf\) where \(f\in C(\partial \Omega ) \).
8.1.7 A Probabilistic Fatou Type Theorem
If the inversion problem for the Poisson transform \(P: L^{1}(\partial \Omega ,\omega ) \rightarrow h(\partial \Omega ) \) can be solved using a stochastic process, the result is a probabilistic Fatou-type theorem. An example is given in Theorem 8.7, which shows that \(\mathrm{f}\in L^{1}(\partial \Omega ,\omega ) \) can be recaptured by the boundary values of \( P\mathrm{f} \) along Brownian paths. This result is a qualitative theorem of Fatou type and lives in “the magical world of Brownian motion”, as Stein put it [166].
Theorem 8.7
([52]) Assume that \(0\in \Omega \) and that \(f:\partial \Omega \rightarrow \mathbb {C}\) is \(\omega \) integrable. Then,
- 1.:
-
with probability 1,
$$\begin{aligned} \lim _{t\uparrow \tau }( Pf )(w(t))=f(\widehat{w}) \end{aligned}$$where \(w=w(t)\), \(0\le t<\tau \), is Brownian motion in \(\Omega \) starting from 0 killed at the hitting time of \(\partial \Omega \), \(\tau \) is this hitting time, and \(\widehat{w}\in \partial \Omega \) is the hitting point;
- 2.:
-
If \(E\subset \partial \Omega \) is \(\omega \) measurable, then \(\omega (E)\) is equal to the probability that \(\widehat{w}\) belongs to E.
The interest of this statement lies in part in the fact that it holds for any bounded domain, not necessarily regular ones, and indeed, it also holds for unbounded domains when suitably modified.
In order to understand for which domains \(\Omega \subset \mathbb {R}^n\), it is possible to recapture \(\mathrm{f}\in L^{1}(\partial \Omega ,\omega ) \) along angular boundary values, one has to develop “real-variable” methods aimed at understanding the higher-dimensional case, where complex analysis plays no role. We will return to this question momentarily. For the time being, we observe that the notion of angular boundary value does not make sense for every domain, not even in the plane, since, for example, if \(\Omega \) is the von Koch snowflake, then a.e. point in its boundary, with respect to harmonic measure, is not sectorially accessible, i.e., it is not the vertex of an open triangle contained in \(\Omega \) [46, 139, 183]. However, we will see that this is not the crucial difficulty.
8.2 Harmonic Functions in The Unit Disc
The process of developing “real-variable” methods aimed at understanding the higher-dimensional case, where complex analysis play no role was a long one and, in a certain sense, is not yet complete. We will now review the main results obtained in this endeavour, of which Zygmund and his school have been the main actors. The first step was of course that of extending to harmonic functions in the unit disc those results which had therein been obtained for holomorphic functions. The difference between harmonic functions and holomorphic functions is much more dramatic in \(\mathbb {C}^{n}\), where \(n\ge 2\), than in \(\mathbb {C}\), due to the fact that, in one variable, harmonic and holomorphic functions are strongly linked to each other by the Cauchy–Riemann equations. As a consequence, we have already met some of the results, originally obtained for holomorphic functions in the unit disc, which also hold for harmonic functions in the unit disc. Hence we now limit ourselves to present some of the other results which did not fit in the previous sections. The first one is known as the localization principle.
Theorem 8.8
If \(f\in \mathcal {L}^1(\partial \mathbb {D})\), \(Q\subset \partial \mathbb {D}\) is open and \(f\) vanishes at all points of \(Q\), then the unrestricted boundary value of \(Pf\) exists and vanishes at all points of \(Q\).
The existence of the unrestricted limit of \( Pf \) at \(q\) only depends on the asymptotic boundary behavior of \(f\) at \(q\), excluding the value at \(q\). Indeed, if we define
(and similarly for \(\limsup \)), then we obtain the following result.
Theorem 8.9
If \(f\in \mathcal {L}^1(\partial \mathbb {D})\) and \(q\in \partial \mathbb {D}\), then
If a discontinuity of the first kind is given at \(q\), then a precise quantitative result can be given.
Theorem 8.10
([145]) If \(\mathrm{f}\in \mathcal {L}^{1}(\partial \mathbb {D})\), \(q\in \partial \mathbb {D}\), and \(\mathrm{f}\) has a discontinuity of the first kind at \(q\):
then, if we let \(d=\mathrm{f}(q+)-\mathrm{f}(q-)\), for each \(\alpha \in (0,2\pi )\)
If \(\tau =\tau (s)\) is a half-open Jordan arc in \(\mathbb {D}\) ending at \(q\) as \(s\rightarrow 1\) and tangent to \(\partial \mathbb {D}\) at \(q\), then
depending on the side from which \(\tau \) approaches \(q\).
The relation between the existence of the unrestricted limit at \(q\) and the continuity of \(f\) at \(q\) is another instance of Abel’s Principle, which says that the regularity of \(f\) at \(q\) affects the boundary behavior of \(P(f)\) at \(q\). We now present a quantitative version of this principle. It is a bound of \( Pf (z)\) depending both on the “size” of \(f\) near \(q\), and on the way, the point is located with respect to the boundary. The quantity which measures the size of \(f\) at \(q\) is the centered Hardy–Littlewood maximal function of \(f\) at \(q\), defined in (5.16). The bound can be given in two forms. The first one is achieved using methods which make the generalization to higher dimensions difficult, while the second can be generalized directly. In most applications, either of the two forms can be used.
Theorem 8.11
If \(f\in \mathcal {L}^1(\partial \mathbb {D})\) and \(q\in \partial \mathbb {D}\), then, for each \(z\in \mathbb {D}\),
and
This result can be applied (using the method of splitting a function into the local part and the part that lives far away from the point) to prove Theorem 6.2.
Another quantitative version of Abel’s principle is the following one.
Theorem 8.12
If \(f\in \mathcal {L}^1(\partial \mathbb {D})\), \(q\in \partial \mathbb {D}\), and \(z\in \mathbb {D}\), then
As a corollary, we obtain the following result, another rendition of Abel’s Principle.
Theorem 8.13
([59]) If \(f\in \mathcal {L}^1(\partial \mathbb {D})\), \(q\in \partial \mathbb {D}\), and
exists and is finite, then the function \(\frac{d}{d\theta } Pf \) has angular boundary value at \(q\) equal to \(f^\prime (q)\).
Corollary 8.14
If \(f\in \mathcal {L}^1(\partial \mathbb {D})\), \(q\in \partial \mathbb {D}\), and
then \( Pf \) has angular boundary value at \(q\) equal to \(q\).
In 1931, Littlewood proved the following result.
Theorem 8.15
([114]) There exists a real-valued \(u\in h(\mathbb {D}) \) which, for every \(p\in (0,1)\) satisfies
and has the property that for a.e. \(q\in \partial \mathbb {D}\), the radial limiting value of \(u\) at \(q\) does not exist.
The collection of real-valued functions in \( h(\mathbb {D}) \) which satisfy (8.8) is denoted by \( h^{p}({\mathbb {D}}) \).
If \(1\le {}p\le \infty \), then the following qualitative result holds for functions in \( h^{p}({\mathbb {D}}) \).
Theorem 8.16
If \(1\le {}p\le +\infty \), then each \(u\in h^{p}({\mathbb {D}}) \) has angular boundary values a.e.
8.2.1 Littlewood-Type Theorems for Harmonic Functions
Recall that, in Theorem 6.16, Littlewood showed that functions in \( H^{\infty }({\mathbb {D}}) \) do not admit a.e. boundary values along any rotationally invariant family of approach regions, with shape given by a half-open Jordan arc which is tangential to the boundary. In 1949, Zygmund gave two different proofs of Theorem 6.16. The first uses complex analysis methods. The second is entirely within the realm of real analysis and is the most enlightening. In retrospect, one can read in it the elements of three later developments: The link between a.e. pointwise convergence and weak-type estimates for the associated maximal operators, i.e., Stein’s theorem on the limit of sequences of operators (Theorem 5.7); The tent condition (7.13); The quasi-dyadic decomposition of a space of homogeneous type (a result due to M. Christ, of which Theorem 5.15 is a consequence).
Theorem 8.17
([189]) If \(\tau \) is a family of approach regions which satisfies the hypothesis of Theorem 6.16, then there is a function \(\mathrm{f}\in L^{\infty }(\partial \mathbb {D})\) such that for a.e. \(q\in \partial \mathbb {D}\), \({\lim _{[\tau (q)]}P\mathrm{f}}\) does not not exist.
This result has been improved by Hiroaki Aikawa in 1990.
Theorem 8.18
([2]) If C is a tangential curve in \(\mathbb {D}\) which ends at 1 and \(C_{q}{\mathop {=}\limits ^{\mathrm{def}}}q{}C\) is its rotated copy, then there exists \(u\in h^{\infty }({\mathbb {D}}) \) such that, for each \(q\in \partial \mathbb {D}\), \({\lim _{[C_{q}]}u}\) does not exist.
8.2.2 The Nagel–Stein Theorem for Harmonic Functions
The results of Nagel and Stein are valid for harmonic functions as well.
Theorem 8.19
([127]) There exists a family \(\tau \) of approach regions in \(\mathbb {D}\) with the following properties:
- (eventually disjoint):
-
For each \(q\in \partial \mathbb {D}\), \(\tau (q)\) is eventually disjoint from the angular filter at \(q\).
- (Fatou):
-
If \(p>1\), each \(u\in h^{p}({\mathbb {D}}) \) converges through \(\tau \) a.e. to its angular boundary values \(u_{\flat }\).
- (rotational invariance):
-
\( \text {If } z\in \tau (q) \,\, \text { then } \,\, e^{i\theta }z\in \tau (e^{i\theta }q) \,\, \text { for each } \,\, e^{i\theta }\in \partial \mathbb {D}\)
The approach regions \(\tau (q)\) in Theorem 8.19 are sequential, but more can be done.
Theorem 8.20
([127]) There exists a family \(\tau \) of approach regions in \(\mathbb {D}\) with the following properties:
- (asymptotic):
-
\(\tau (q)\) is (the image of) of a half-open Jordan arc in \(\mathbb {D}\) ending at \(q\) for each \(q\in \partial \mathbb {D}\).
- (frequently outside):
-
For each \(q\in \partial \mathbb {D}\), \(\tau (q)\) lies frequently outside of the angular filter ending at \(q\).
- (Fatou):
-
Each \(u\in h^{p}({\mathbb {D}}) \), \(p>1\), converges through \(\tau \) a.e. to its angular boundary values \(u_{\flat }\).
- (rotational invariance):
-
\( \text {If } z\in \tau (q) \,\, \text { then } \,\, e^{i\theta }z\in \tau (e^{i\theta }q) \,\, \text { for each } \,\, e^{i\theta }\in \partial \mathbb {D}\).
8.2.3 Characterization of Poisson Integrals
There is a nonvanishing function \(u\in h(\mathbb {D}) \) such that its unrestricted boundary values are equal to 0 at all points except one. For example: \(\frac{1-{|z|}^2}{{|1-z|}^2}\). It is thus impossible, in general, to reconstruct a harmonic function from its a.e. boundary values, and we say that a function \(u\in h(\mathbb {D}) \) is representable by its Poisson integral if
- (1):
-
The radial limit \( {u}_{\rho }(q) \) exists for a.e. \(q\in \partial \mathbb {D}\) and belongs to \(\mathcal {L}^{1}(\partial \mathbb {D})\).
- (2):
-
\(u=P({u}_{\rho })\).
Theorem 8.21
([56,57,58]) If \(u\in h(\mathbb {D}) \) then the following conditions are equivalent:
- (1):
-
\(u\) is representable by its Poisson integral.
- (2):
-
There is a function \(f\in \mathcal {L}^{1}(\partial \mathbb {D})\) such that \(u=P[f]\).
- (3):
-
For each \(\epsilon >0\), there is \(j>0\) such that \(Q\subset \partial \mathbb {D}\) and \( |{Q}| <\frac{1}{j}\) imply \( { \int _{Q}|u(rq)|\mathrm{d}~\omega (q)<\epsilon }\) for all \(r\in (0,1)\).
Theorem 8.22
If \(1<p\le +\infty \) and \(u\in h(\mathbb {D}) \), then the following conditions are equivalent:
- (1):
-
There is an \(f\in \mathcal {L}^{p}(\partial \mathbb {D})\) such that \(u= Pf \).
- (2):
-
\(u\in h^{p}({\mathbb {D}}) \).
If \(u\in h(\mathbb {D}) \) is real valued, then the following conditions are equivalent:
- (1):
-
\(u\in h^{1}({\mathbb {D}}) \)
- (2):
-
\(u\) is the difference of two positive harmonic functions.
- (3):
-
\(u\) is the Poisson integral of a finite signed Borel measure.
8.2.4 The Hardy–Littlewood \(\varvec{{L^p}}\) Inequality for Harmonic Functions
The following result follows from (7.2).
Theorem 8.23
([73, 115]) If \(p>1\) and \({j}\ge 0\), then there exists \(c=c_{p,{j}}\) such that, for all \(f\in \mathcal {L}^{p}(\partial \mathbb {D})\),
8.2.5 The Local Fatou Theorem for Harmonic Functions
In 1950, Alberto Pedro Calderón extended to harmonic functions in \(\mathbb {D}\) the local Fatou theorem of Privalov.
Theorem 8.24
([24]) If \(Q\in \varvec{\mathcal {A}}({\partial \mathbb {D}}) \) and \(u\in h(\mathbb {D}) \), then the following are equivalent:
-
for a.e. \(q\in Q\), the angular boundary value \( {u}_{\flat }(q) \) exists and is finite;
-
for a.e. \(q\in Q\), there exists \(\textsc {t}\in \mathsf {Stolz}_{q} \) such that \(u\) is bounded in \(\textsc {t}\).
The result is false if we merely ask for radial boundedness. Observe the lack of uniformity with respect to \(q\) in the hypothesis of this theorem. We will return to this result momentarily.
8.2.6 A Zero-One Law for Harmonic Functions
The following result follows from Calderón’s local Fatou theorem, paying some attention to certain measurability issues. It plays the role of a Plessner-type theorem for real-valued harmonic functions.
Theorem 8.25
If \(u\in h(\mathbb {D}) \) is real valued, then \( \mathsf {Fatou}{(u)} \cup \mathsf {realPlessner}[u]\) has full measure in \(\mathbb {D}\).
8.3 Harmonic Functions in Upper Half-Spaces
Theorem 8.24 was part of Calderón’s dissertation, written under Zygmund’s direction. It was a breakthrough in the project of developing new “real-variable” methods aimed at understanding the higher-dimensional case, where complex analysis plays no role. Indeed, Calderón’s proof is “independent of conformal mappings and can be applied to more general situations when conformal mapping is not available,” as Zygmund, with his usual bit of understatement, put it. The “more general situation,” where Calderón proved his result, is the \((n+1)\)-dimensional upper half-space \( \mathbb {E}\), defined as \(\mathbb {R}^n\times (0,+\infty )\). Observe that \( \mathbb {E}\) is an open subset of \(\mathbb {R}^{n+1}\) and that \(\mathbb {R}^n\) can be imbedded in \(\mathbb {R}^{n+1}\) as follows:
\(\mathbb {R}^n\) is a space of homogeneous type with respect to Lebesgue measure, denoted by \(\omega \), and the Euclidean metric, denoted by \(\delta \). We denote by \( \varvec{ {d} } \) the Euclidean metric in \(\mathbb {R}^{n+1}\). Hence \(\mathbb {R}^n\) is admissibly imbedded in the boundary of \( \mathbb {E}\) in \(\mathbb {R}^{n+1}\) by (8.9). The family of approach regions in \( \mathbb {E}\) based on \(\mathbb {R}^n\) defined by \( { \Gamma _{1}(q) {\mathop {=}\limits ^{\mathrm{def}}}\{ z\in \mathbb {E}: 2 \varvec{ {d} } (z,\partial { \mathbb {E}}) > \varvec{ {d} } (z,q) \} } \) is adapted to the admissible imbedding (8.9). If \({j}>0\) is an integer, we similarly define
and define \({ \Gamma _{0}(q){\mathop {=}\limits ^{\mathrm{def}}}\{ z\in \mathbb {E}: \varvec{ {d} } (z,\partial { \mathbb {E}}) = \varvec{ {d} } (z,q)\}}\) as the “radius” ending at \(q\). The one-parameter family of approach regions \( { \{ {\Gamma }_{j} \} }_{j\ge 1} \) defined in (8.10) is adapted to the admissible imbedding (8.9). The approach regions in (8.10) are called cones, or nontangential approach regions. At each point \(q\in \mathbb {R}^n\), the collection \({\{\Gamma _{j}(q)\}}_{j}\) determines the nontangential filter on \( \mathbb {E}\) at \(q\). The boundary value of \(u\in \mathbb {C}^{ \mathbb {E}}\) along this filter is denoted (if it exists) by \( {u}_{\flat }(q)\). The notions of Fatou point and Fatou set are accordingly defined.
8.3.1 Qualitative and Quantitative Theorems of Fatou Type
The Poisson integral for the upper half-space \(P: L^{p}(\mathbb {R}^n) \rightarrow h( \mathbb {E}) \) defined by
where \(\texttt {P}: \mathbb {E}\times \mathbb {R}^n\rightarrow (0,+\infty )\), defined by
is the Poisson kernel for the upper half-space \( \mathbb {E}\), \(c_n\) is a normalizing constant, \(z\in \mathbb {E}\subset \mathbb {R}^{n+1}\), and \(q\) is also identified with a point of \(\mathbb {R}^{n+1}\) via (8.9). The expression \( \varvec{ {d} } (z,\partial { \mathbb {E}})\) is defined as \(\inf \{ \varvec{ {d} } (z,x):x\in \partial { \mathbb {E}}\}\), as usual. Observe that if \(z=(q,y)\), with \(q\in \mathbb {R}^n\) and \(y>0\), then \( \varvec{ {d} } (z,\partial { \mathbb {E}})=y\).
The Poisson integral in (8.11) is associated to the Dirichlet problem in \( \mathbb {E}\). The inversion problem for the functional representation \(P: L^{p}(\mathbb {R}^n) \rightarrow h( \mathbb {E}) \) can be solved by taking a.e. angular boundary values, for \(1\le {}p\le \infty \). The main tools are the Hardy–Littlewood maximal function for \(\mathbb {R}^n\), defined for \(\mathrm{f}\in L^{p}(\mathbb {R}^n) \) and \(q\in \mathbb {R}^n\) by

and the pointwise estimate, valid for each \(q\in \mathbb {R}^n\)
which follows from three facts.
(1) The integral \(\int _{\mathbb {R}^n}\texttt {P}(z,q)\,\mathrm{d}q\) is constant on \( \mathbb {E}\). Indeed, it is constant on \(\Gamma _{0}(w)\) for each \(w\in \mathbb {R}^n\) (since, under the dilation \(q\mapsto {}cq\), Lebesgue measure in \(\mathbb {R}^n\) rescales by \(c^n\)), and it is invariant under horizontal translations, since \(\texttt {P}\) is invariant under horizontal translation. The normalizing constant in (8.12) is chosen to make it equal to one.
(2) If \(p:[0,+\infty )\rightarrow (0,\infty )\) is continuous, decreasing, and \(\int _{\mathbb {R}^n} p(|q|)\,\mathrm{d}q=1\), then
as may be seen with the following “telescoping trick”: Given \(\epsilon >0\), choose \({B}_k{\mathop {=}\limits ^{\mathrm{def}}}{B}(0,r_k)\subset \mathbb {R}^n\) so that \( |{{B}_1}| =\epsilon \) and \( |{{B}_{k+1}\setminus {B}_{k}}| = |{{B}_1}| \) for each \(k\ge 1\). Let \(B_0=\emptyset \) and define \(g{\mathop {=}\limits ^{\mathrm{def}}}\sum _{k=0}^\infty {}p(|k\epsilon |)1_{{B}_{k+1}\setminus {B}_k}\). Then \(p\le {}g\). Write \(g=\sum _{k=1}^{\infty }i_{k}1_{{B}_{k}}\) for appropriate \({i}_k>0\). Then
and
Now, if we let \(\epsilon \rightarrow 0\), (8.14) follows at once.
(3) If \(z\in \Gamma _{{j}}(q)\), then \(\texttt {P}(z,q)\le {}c_{{j}}\texttt {P}(z^{\prime },q)\) for all \(q\in \mathbb {R}^n\), where \(z^{\prime }\in \Gamma _{0}(q)\) and \( \varvec{ {d} } (z,\partial { \mathbb {E}})= \varvec{ {d} } (z^{\prime },\partial { \mathbb {E}})\). Hence (8.13) implies that the Hardy–Littlewood \(L^p\)-inequality holds for \(p>1\):
Once again, the power of Hardy–Littlewood’s maximal function reveals itself in the way it opens the path to results in higher dimensions. In particular, the standard method, coupled with (8.13), (8.15), and Theorem 5.6, implies a whole series of qualitative theorems of Fatou type, similar to those obtained in \(\mathbb {D}\) [169, Chapter 2]. For example, if \(f\in \mathcal {L}^p(\mathbb {R}^n)\), \(1\le {}p\le \infty \), then \( {( Pf )}_{\flat }(q)=f(q)\) for a.e. \(q\in \mathbb {R}^n\).
8.3.2 The Local Fatou-Theorem and a Theorem of Plessner Type
Calderón’s proof of Theorem 8.24 is entirely based on real-variables techniques and leads, in “the more general situation” of \( \mathbb {E}\), to the following result.
Theorem 8.26
([24]) If \(Q\in \varvec{\mathcal {A}}({\mathbb {R}^n}) \) and \(u\in h( \mathbb {E}) \), then the following conditions are equivalent:
-
For a.e. \(q\in Q\), the angular boundary value \( {u}_{\flat }(q) \) exists and is finite.
-
For a.e. \(q\in Q\), there exists \({j}>1\) and there exists a tail of \(\Gamma _{j}(q)\) on which \(u\) is bounded.
The definition of the Privalov set of \(u\in h( \mathbb {E}) \) undergoes the appropriate modification, which is left to the reader. In particular, Theorem 8.26 says that

One of the main points in Calderón’s industrious proof of this theorem, which had already appeared in Zygmund’s proof of Theorem 8.17, is this: For each \(j\ge 1\), there exists \(c_{j}>0\) such that for each Euclidean ball \({B}\subset \mathbb {R}^n\):
where \(1_{{B}}\) is the indicator function of \({B}\), \(P(1_{{B}}): \mathbb {E}\rightarrow (0,\infty )\) is its Poisson integral, and \( \Delta ^{{j}}{B} \) is the \(\Gamma _{{j}}\) tent above \({B}\), defined as \(\{z\in \mathbb {E}: \overline{{{\Gamma _{{j}}}}}(z) \subset {B}\}\), as in Sect. 7.10.6. A result that is stronger than Theorem 8.26, along the lines of a local Fatou theorem, has been obtained by Lennart Axel Edvard Carleson in 1962.
Theorem 8.27
([26]) If \(u\in h( \mathbb {E}) \) is real valued, then the following conditions are equivalent:
-
For a.e. \(q\in \mathbb {R}^n\), the angular boundary value \( {u}_{\flat }(q) \) exists and is finite.
-
For a.e. \(q\in \mathbb {R}^n\), there exists \({j}\ge 1\) and a tail of \(\Gamma _{j}(q)\) on which \(u\) is bounded from below.
In the upper half-space \( \mathbb {E}\), Theorem 8.26 yields the following result, which plays the role of a Plessner-type theorem for harmonic functions.
Theorem 8.28
If \(u\in h( \mathbb {E}) \) is real valued, then the set \( \mathsf {Fatou}{(u)} \cup \mathsf {realPlessner}[u]\) has full measure.
8.3.3 The Generalized Area Integral: Qualitative and Quantitative Results
For \(u\in h( \mathbb {E}) \), \(q\in \mathbb {E}\), \(h>0\), and \({j}\ge 1\), the generalized area integral is defined as follows:
where \(\Gamma _{{j}}^{h}(q){\mathop {=}\limits ^{\mathrm{def}}} \left\{ z\in \Gamma _{j}(q): \varvec{ {d} } (z,\partial { \mathbb {E}})<h \right\} \) is the truncated cone at \(q\) with height h. If \(n=1\), (8.16) specializes to (6.10). In his constant drive to develop real-analysis methods, Zygmund was particularly fascinated by the problem of extending to the upper half-spaces the area theorem (Theorem 6.15), and this task turned out to be much more challenging, because the boundary of the analog of the sawtooth region (6.8) is more difficult to tackle, and because there is no conformal map in this context.
The first result in this direction is one of the “pioneering results” of Calderón, obtained in 1950.
Theorem 8.29
([25]) If \(u\in h( \mathbb {E}) \), \(Q\in \varvec{\mathcal {A}}({\mathbb {R}^n}) \), and for each \(q\in Q\), the function \(u\) is bounded in some truncated cone at \(q\), then, for each \(j\ge {}1\) and each \(h>0\), \( S_{j,h}u(q)<\infty \) for a.e. \(q\in Q\).
It took some time for these results to be completed. Here are Stein’s recollections of a crucial stage.
I remember quite vividly the excitement surrounding the events at the time of this work. It was March 1959, and I had returned to the University of Chicago the fall before. Frequently I met with my friends Guido Weiss and Mary Weiss, and together we often found ourselves in Zygmund’s office (Eckhart 309, two doors from mine). With our teacher our conversations ranged over a wide variety of topics (not all mathematical) and more than once the subject of square functions arose. When this happened the mood would change, if only slightly, as if in deference to their special status, and the enigma that surrounded them. I had an idea which seemed promising. But before we could see where it might lead came the spring break. Further work would have to be held in abeyance since we were each going our own ways: Zygmund travelled to Boston to visit Calderón; Guido and Mary Weiss, having borrowed my Chevrolet, drove to Virginia for a vacation trip; and I went to New York to be married. [166]
The “idea which seemed promising” worked out very well, and Stein proved the following results, of a qualitative and quantitative type.
Theorem 8.30
([158,159,160]) If \(1<p<\infty \), \(j\ge 1\), \(f\in \mathcal {L}^p(\mathbb {R}^n)\), \(u\in h( \mathbb {E}) \), and \(Q\in \varvec{\mathcal {A}}({ \mathbb {E}}) \), then
- (1):
-
There exists a constant \( \varvec{c} _{p,j}\) which only depends on p and \(j\) such that
$$\begin{aligned} \int _{\mathbb {R}^n} {| S_{j,1}( Pf )|}^p \mathrm{d}~\omega \le \varvec{c} _{p,j} \int _{\mathbb {R}^n} {|f|}^p \mathrm{d}~\omega . \end{aligned}$$(8.17) - (2):
-
If \(f\in \mathcal {L}^1(\mathbb {R}^n)\), then
$$\begin{aligned} |{ \{ S_{j,1} Pf >r\} }| \le \frac{ \varvec{c} _{j}}{r} \int _{\mathbb {R}^n}|f|\,\mathrm{d}~\omega . \end{aligned}$$(8.18) - (3):
-
If \(u(q,r)\rightarrow 0\) as \(r\uparrow +\infty \) uniformly in \(q\in \mathbb {R}^n\), and \( S_{j}u\in \mathcal {L}^p(\mathbb {R}^n)\), then there exists \(f\in \mathcal {L}^p(\mathbb {R}^n)\) such that \(u= Pf \) and
$$\begin{aligned} \int _{\mathbb {R}^n}{|f|}^p\,\mathrm{d}~\omega \le \varvec{c} _{p,j} \int _{\mathbb {R}^n}{| S_{j,1} Pf |}^p\,\mathrm{d}~\omega . \end{aligned}$$ - (4):
-
If for each \(q\in Q\), there exist \(j\ge 1\) and \(h>0\) such that \( S_{j,h}u(q)<\infty \), then \( Q\subset _{\omega } \mathsf {Fatou}{(u)} \).
As a corollary, we obtain the Area & Local Fatou Theorem for upper half-spaces.
Theorem 8.31
Let \(u\in h( \mathbb {E}) \) and \(Q\in \varvec{\mathcal {A}}({\mathbb {R}^n}) \). Then the following three conditions are equivalent
-
1.
For a.e. \(q\in Q\), \(q\in \mathsf {Fatou}{(u)} \).
-
2.
For a.e. \(q\in Q\), there exists \(j\ge 1\) and \(h>0\) such that \( S_{j,h}u(q)<\infty \).
-
3.
For a.e. \(q\in Q\), there exists \({j}\ge 1\) and \(h>0\) such that \(\sup \{\left| u(z)\right| :z\in \Gamma _{j}^{h}(q)\}<+\infty \).
The definition of the Lusin set of \(u\in h( \mathbb {E}) \) undergoes the appropriate modification, which is left to the reader. In particular, Theorem 8.31 implies that

Theorem 8.31 is qualitative, since at any individual point, the three conditions are independent, except that of course if \(q\) is a Fatou point of \(u\), then \(u\) is bounded in each truncated cone at \(q\).
In 1972, Stein surpassed himself and, in collaboration with C. Fefferman, proved the following result, whose proof is based on a careful analysis of the quantitative content of the qualitative statements contained in Theorem 8.31.
Theorem 8.32
([62]) If \(u\in h( \mathbb {E}) \) and \(0<p<\infty \), then the following conditions are equivalent:
- (1):
-
\( \displaystyle {\sup _{\Gamma _{j}}} \,{u} \in \mathcal {L}^p(\mathbb {R}^n)\)
- (2):
-
\(u(q,r)\rightarrow 0\) as \(r\rightarrow +\infty \) uniformly in \(q\in \mathbb {R}^n\), and \( S_{j}u\in \mathcal {L}^p(\mathbb {R}^n)\).
If any of the conditions stated above holds, then the \(L^p\) norms of \( \displaystyle {\sup _{\Gamma _{j}}} \,{u} \) and \( S_{j}u\) are equivalent.
8.3.4 Littlewood-Type Theorems
Zygmund’s real-variable proof of Littlewood’s Theorem 6.16 yields Theorem 8.17. An immediate extension of Zygmund’s technique yields the following result.
Theorem 8.33
If \(\tau :\mathbb {R}^{n}\rightarrow \varvec{\mathcal {P}}_{\bullet }( \mathbb {E}) \) is a translation-invariant family of approach regions in \( \mathbb {E}\) based on \(\mathbb {R}^n\) such that \(\tau (q)\) is an n-dimensional hypersurface in \( \mathbb {E}\) which is eventually disjoint from the nontangential filter at \(q\), then there exists \(f\in \mathcal {L}^{\infty }{\mathbb {R}^n}\) such that for a.e. \(q\in \mathbb {R}^n\), the boundary value of \( Pf \) through \(\tau (q)\) does not exist.
Observe that this result does not exclude the possibility that a translation-invariant family of approach regions may exist, such that \(\tau (q)\) is a curve in \( \mathbb {E}\) tangential to the boundary at \(q\). This possibly has been excluded by Aikawa.
Theorem 8.34
([3]) If \(\tau :\mathbb {R}^{n}\rightarrow \varvec{\mathcal {P}}_{\bullet }( \mathbb {E}) \) is a translation-invariant family of approach regions in \( \mathbb {E}\) based on \(\mathbb {R}^n\) such that \(\tau (q)\) is a curve in \( \mathbb {E}\) ending at \(q\) and eventually disjoint from nontangential filter at \(q\), then there exists \(f\in \mathcal {L}^{\infty }(\mathbb {R}^n)\) such that for a.e. \(q\in \mathbb {R}^n\), the boundary value of \( Pf \) through \(\tau (q)\) does not exist.
Aikawa also proved a result of greater scope, where he allows families of approach regions that are not invariant under translation but have, in a precise sense, the same order of tangency to the boundary.
8.3.5 The Nagel–Stein Phenomenon
The Nagel–Stein phenomenon holds in upper half-spaces as well.
Theorem 8.35
([127]) There exists a sequential, translation-invariant family of approach regions \(\tau \) on \( \mathbb {E}\) based on \(\mathbb {R}^n\) such that \(\tau (q)\) is eventually disjoint from the nontangential filter ending at \(q\), and for each \(f\in \mathcal {L}^{p}{(\mathbb {R}^n)}\), \(1\le {}p\le \infty \), \( \mathsf {Fatou}( Pf ;\tau )\) has full measure in \(\mathbb {R}^n\) and \(\lim _{[\tau (q)]} Pf = {( Pf )}_{\flat }(q)\) almost everywhere.
Theorem 8.36
([127]) There exists an asymptotic and translation-invariant family of approach regions \(\tau \) on \( \mathbb {E}\) based on \(\mathbb {R}^n\) such that \(\tau (q)\) lies frequently outside the nontangential filter at \(q\), and for each \(f\in \mathcal {L}^{p}{(\mathbb {R}^n)}\), \(1\le {}p\le \infty \), \( \mathsf {Fatou}( Pf ;\tau )\) has full measure in \(\mathbb {R}^n\) and \(\lim _{[\tau (q)]} Pf = {( Pf )}_{\flat }(q)\) almost everywhere.
Recall that \(\tau \) is asymptotic if \(\tau (q)\) is the image of a half-open Jordan arc ending at the point.
8.4 When is Nontangential Behavior Meaningful?
In 1939, Masatsugu Tsuji extended to the unit ball \(D{\mathop {=}\limits ^{\mathrm{def}}}\{x\in \mathbb {R}^{n+1}:\sum _{j=1}^{n+1}{x_{j}}^2<1\}\subset \mathbb {R}^{n+1}\) the basic results of qualitative and quantitative type which we have seen in the unit disc for harmonic functions [176]. The boundary of \(D\) is the unit sphere \( {X} =\{x\in \mathbb {R}^{n+1}:\sum _{j=1}^{n+1}{x_{j}}^2=1\}\), endowed with harmonic measure \(\omega \) with pole at 0 (which is the normalized n-dimensional Hausdorff measure). We denote by \( \varvec{ {d} } \) the Euclidean metric in the ambient space \(\mathbb {R}^{n+1}\) and by \(\delta \) its restriction to \( {X} \). If \(q\in {X} \), the nontangential filter on \(D\) ending at \(q\) is the one associated to the following approach regions were \({j}\ge 1\):
We define \(\Gamma _{0}(q)\) as \(\{sq:0\le {}s<1\}\). The nontangential filter at \(q\in {X} \) is also associated to the collection of open cones of revolution with vertex \(q\), axis of rotation the inner normal to the boundary of \(D\) at \(q\), and half-angle less than \(\pi /2\). The sequence of families of approach regions \( { \{ {\Gamma }_{j} \} }_{j\ge 1} \) is adapted to these data, in the sense of Sect. 7.9. The Poisson kernel for the Dirichlet problem on \(D\) is given by
where \(c_n\) is uniquely determined by the condition that \(\int _{ {X} }P(0,q)\mathrm{d}{}\omega (q)=1\). If \(\mathrm{f}\in L^{p}( {X} ,\)) , \(1\le {}p\le \infty \), its Poisson integral is \({ P\mathrm{f} (z)=\int _{ {X} }\texttt {P}(z,q)\mathrm{f}(q)\,\mathrm{d}~\omega (q)}\). If \(u\in h(D) \), then \(u\) is the Poisson integral of a function in \( L^{p}( {X} ,\)) with \(1<p\le \infty \) iff \({\sup _{0<r<1}\int _{ {X} }{|u(rq)|}^{p}\mathrm{d}~\omega (q)<\infty }\); \(u\) is the Poisson integral of a finite measure on \( {X} \) iff \({\sup _{0<r<1}\int _{ {X} }{|u(rq)|}\mathrm{d}~\omega (q)<\infty }\); \(u\) is the Poisson integral of a finite positive measure on \( {X} \) iff \(u>0\).
In 1961, Stein posed the following problem:
It would be desirable to extend these results by considering non-tangential behavior for sets lying on more general hyper-surfaces. Presumably this could be done without too much difficulty if the bounding hyper-surface were smooth enough. It would be of definite interest, however, to allow the most general bounding hyper-surface for which non-tangential behavior is meaningful. Hence extension of these results to the case when the bounding surfaces are, for example, of class \(C^1\) would have genuine merit. Whether this can be done is an open problem.
At that time, thanks to the work of Privalov and Kouznetzoff in 1939, and Tsuji in 1944, some preliminary results were already known for Lyapunov domains, of which “bounding hypersurface,” roughly speaking, has smoothness lying between \(C^1\) and \(C^2\). Moreover, in the setting of Lyapunov domains in \(\mathbb {R}^{n+1}\), in 1963, Kjell–Ove Widman proved some qualitative results on the boundary behavior of harmonic functions [144, 177, 185].
The first breakthrough below \(C^1\) boundary was achieved in 1968 and 1970 by Richard Allen Hunt and Richard Lee Wheeden, who obtained results of qualitative and quantitative type for starlike Lipschitz domains, where the nontangential approach regions are meaningful, since, in this case, there are indeed cones in the domain ending at boundary points [78, 79]. These results were stated in terms of harmonic measure on the boundary. In 1977, Björn Dahlberg proved that harmonic measure on the boundary of a Lipschitz domain in \(\mathbb {R}^{n+1}\), \(n\ge 1\), is mutually absolutely continuous with respect to n-dimensional Hausdorff measure [37].
The class of Lipschitz domains does not contain domains such as the interior of the von Koch snowflake \(D\) since the collection of points in the boundary of \(D\) which are sectorially accessible has harmonic measure zero. Indeed, almost every point \(q\) in \(\partial D\), with respect to harmonic measure, is a twist point, i.e., it has the following property: If \(\varvec{c}:[0,1)\rightarrow D\) is continuous and \(\lim _{r\uparrow 1}\varvec{c}(r)=q\), then
where \(\arg \) is a continuous determination of the angle. Observe that (8.22) is reminiscent of a Plessner-type theorem for real-valued harmonic functions [4, 46, 139, 183].
A second breakthrough, which pushed the study below the case where the “bounding hyper-surface” is Lipschitz, was achieved in 1982 by David Jerison and Carlos Kenig [23, 81, 83]. They introduced a class of domains in \(\mathbb {R}^{n+1}\), called non-tangentially accessible domains, or “NTA domains” for short, that is strictly larger than the class of starlike Lipschitz domain, and indeed large enough to include the von Koch snowflake. Indeed, the boundary of an NTA domain may be nonrectifiable and may admit no tangent plane at any point. For an NTA domain \(D\), the nontangential approach regions are defined as in (8.20), but they could not possibly look like a cone at those boundary points which are twist points.
The boundary of an NTA domain is a space of homogeneous type with respect to harmonic measure and the Euclidean metric, and the sequence of families of nontangential approach regions defined in (8.20) for an NTA domain is adapted to the metric and to harmonic measure, in the sense of Sect. 7.13. The area integral for an NTA domain is defined as in (8.16). Jerison and Kenig proved both qualitative and quantitative results for harmonic functions in NTA domains, along the lines of those that we have seen so far, including the local Fatou theorem and the area theorem, in its local (qualitative) version as well as in its global (quantitative) version.
This brief treament of these developments attest to the long range of Zygmund’s vision as well as the extraordinary power of Stein’s interpretation of that vision.
9 Holomorphic Functions of Several Variables
The boundary behavior of functions \(u\in \mathcal {O}( \mathbb {B} )\), where \(\textstyle { \mathbb {B} {\mathop {=}\limits ^{\mathrm{def}}}\{z\in \mathbb {C}^n: \sum _{j=1}^{n}{|z_{j}|}^2<1\}}\) is the unit ball in \(\mathbb {C}^n\), produced unexpected results. We denote by \(\omega \) the normalized surface measure on the boundary \(\partial { \mathbb {B} }{\mathop {=}\limits ^{\mathrm{def}}}\partial _{\mathbb {C}^n}{ \mathbb {B} }\) of \( \mathbb {B} \) in \(\mathbb {C}^n\). If \(0<p<\infty \), functions \(u\in \mathcal {O}( \mathbb {B} )\) such that
form the Hardy spaces \( H^{p}({ \mathbb {B} }) \) of holomorphic functions, where \( H^{\infty }({ \mathbb {B} }) \) is the set of all functions \(u\in \mathcal {O}( \mathbb {B} )\) such that \(\sup \{|u(z)|:z\in \mathbb {B} \}<\infty \). The Fatou-type theorems which are valid for harmonic functions in \( \mathbb {B} \) (considered as a smoothly bounded domain of \(\mathbb {R}^{2n}\)) are also valid for holomorphic functions in \( \mathbb {B} \), since holomorphic functions are harmonic. For example, functions in \( H^{\infty }({ \mathbb {B} }) \) have radial boundary values and nontangential boundary values \(\omega \) almost everywhere on \(\partial { \mathbb {B} }\). Alongside the restriction to \(\partial { \mathbb {B} }\) of the standard, isotropic Euclidean metric \( \varvec{ {d} } \) in \(\mathbb {C}^n\), \(\partial { \mathbb {B} }\) is endowed with a second, anisotropic metric, under which \((\partial { \mathbb {B} },\omega ,\delta )\) is a space of homogeneous type. The metric \(\delta \) is called the Hörmander–Korányi–Stein metric, and it is defined as \(\delta (q,w){\mathop {=}\limits ^{\mathrm{def}}}\sqrt{|1- q\cdot w|}\), where \(q\cdot w\) is the standard Hermitian inner product in \(\mathbb {C}^n\). The natural imbedding of \(\partial { \mathbb {B} }\) in \((\mathbb {C}^n, \varvec{ {d} } )\) is admissible, in the sense of Sect. 7.6. The Korányi (family of ) approach regions \({\mathcal K}_{j}(q):\partial { \mathbb {B} }\rightarrow \varvec{\mathcal {P}}_{\bullet }( \mathbb {B} ) \) is the sequence of families of approach regions in \( \mathbb {B} \) based on \(\partial { \mathbb {B} }\) defined, for \(q\in \partial { \mathbb {B} }\) and \(j\ge 1\), as follows:
where \({\mathcal {T}}_{q}(\partial { \mathbb {B} })\) is the maximal complex subspace of the tangent space at \(\partial { \mathbb {B} }\) at \(q\) (formed by the so-called complex-tangent vectors). This sequence of families of approach regions is adapted to the admissible imbedding of \((\partial { \mathbb {B} },\omega ,\delta )\) in \((\mathbb {C}^n, \varvec{ {d} } )\), in the sense of Sect. 7.13.
One way to understand the form of \({\mathcal K}_{j}(q)\) is to look at its intersection with real two-dimensional planes. Observe that the intersection of \( \mathbb {B} \) with \(E{\mathop {=}\limits ^{\mathrm{def}}}\{xq+y(iq):(x,y)\in \mathbb {R}^2\}\subset \mathbb {C}^n\) is given by the condition \(x^2+y^2<1\) (and therefore describes in a natural way a unit disc inside \( \mathbb {B} \)) and that if \(z\in \mathbb {B} \cap {}E\), then
(The vector \(iq\) is called a complex-normal direction). It follows that \({\mathcal K}_{j}(q)\cap {}E\) can be described, in the coordinates (x, y), by the condition (2.7) where \(z=(x,y)\) and \(q=(1,0)\). Hence the filter associated to \({\mathcal K}_{j}(q)\) along the plane E is the angular filter. On the other hand, if we consider a plane \(E^\prime {\mathop {=}\limits ^{\mathrm{def}}}\{xq+yv:(x,y)\in \mathbb {R}^2\}\), where \(v\in {\mathcal {T}}_{q}(\partial { \mathbb {B} })\) has unit length, we see that \({\mathcal K}_{j}(q)\) has the same degree of contact with \(\partial { \mathbb {B} }\) of the line at \(q\) along v. In particular, it is tangential to the boundary to quadratic order in the complex tangential directions. In 1969, Adam Korányi proved the following result.
Theorem 9.1
If \(1\le {}p\le \infty \) and \(u\in H^{p}({ \mathbb {B} }) \), then \( \mathsf {Fatou}(u;{\mathcal K}_{j})\) has full measure in \(\partial { \mathbb {B} }\).
Korányi also proved a local Fatou theorem for functions in \(\mathcal {O}( \mathbb {B} )\) with respect to \({\mathcal K}_{j}\). His result is of historical significance and lasting importance, because it allows for limiting values along approach regions which have a certain degree of tangency along the complex-tangent directions. In other words, he showed that the approach regions in the unit ball are subject to the usual restriction along the complex-normal direction, but it allows a certain degree of contact in the complex-tangent directions. The original proof of Theorem 9.1 is based on explicit computations of the Poisson–Szegö kernel for \( \mathbb {B} \).
In his 1972 monograph, Stein adapted the definition of the Korányi approach regions to any smoothly bounded domain in \(\mathbb {C}^n\) and completed the results obtained by Korányi. Indeed, he defined the notion of the Nevanlinna class of holomorphic functions in this generality and proved a qualitative Fatou-type theorem in this class (thus, including the case \(p>0\) in Theorem 9.1). Moreover, he defined the notion of the area function and proved the local and area theorem with respect to \({\mathcal K}_{j}\). In his proofs, he could not rely on the explicit expression of reproducing kernels which is available in the unit ball, and proceeded on purely geometrical grounds, with maximal functions as the main tool [165]. Stein never ceased to emphasize the deep link that differentiation of integrals has with Fatou-type theorems, and indeed, this book contains an impressive array of maximal functions that are witness to this link. In an appendix, we provide a self-contained proof of a new result which is relevant to the differentiation of integrals. A few years later, in order to obtain results of quantitative-type, he gave his second main achievement in the subject. Indeed, he surpassed himself and defined, for a class of pseudoconvex domains (finite type) which properly includes the class of strictly pseudoconvex domains, a second sequence of families \({\{{\mathcal A}_{j}\}}_{j\in \mathbb {N}}\) of approach regions such that
- \((\varvec{a}^{\varvec{\prime }})\):
-
For each \(j\in \mathbb {N}\), \({\mathcal A}_{j}\) is distributionally broader than \({\mathcal K}_j\) (this notion is defined in Sect. 7.12).
- \((\varvec{b}^{\varvec{\prime }})\):
-
For each \(u\in H^{p}({\Omega }) \), \({\lim _{[{\mathcal A}_{j}(q)]}u}\) exists and is equal to \({\lim _{[{\mathcal K}_{j}(q)]}u}\) for a.e. \(q\in \partial \Omega \), for each \(j\in \mathbb {N}\).
- \((\varvec{c}^{\varvec{\prime }})\):
-
For almost every \(q\in \partial \Omega \), the filter on \(\Omega \) ending at \(q\) associated to the collection \({\{{\mathcal A}_j(q)\}}_{j\in \mathbb {N}}\) is equal to the filter on \(\Omega \) ending at \(q\) associated to \({\{{\mathcal K}_j(q)\}}_{j\in \mathbb {N}}\)
- \((\varvec{d}^{\varvec{\prime }})\):
-
For each \(p>0\) and \({j}\in \mathbb {N}\), there is a constant \( \varvec{c} _{p,j}>0\) such that, for each \(u\in {} H^{p}({\Omega }) \),
$$\begin{aligned} \int _{\partial \Omega } {( \textstyle {\sup _{{\mathcal A}_{j}}{|u|}} )}^p \, \mathrm{d}~\omega \le {} \varvec{c} _{p,j} \int _{\partial \Omega } {|{u}_{\rho }|}^p \, \mathrm{d}~\omega , \end{aligned}$$(9.2)where \({u}_{\rho }\) is the radial boundary function.
In view of \(\varvec{(c^\prime )}\), Property \(\varvec{(b^\prime )}\) follows at once from the qualitative result which holds for \({\mathcal K}_j\). In particular, \(\varvec{(b^\prime )}\) is not an improvement with respect to the qualitative result which is known to hold for \({\mathcal K}_j\). The improvement lies in the quantitative result \(\varvec{(d^\prime )}\), which holds even though \(\varvec{(a^\prime )}\) holds [128, 129]. See [44, 97].
10 Final Remarks
Our account of Stein’s contributions to the subject is not complete. We have chosen to concentrate on certain main ideas that remained dear to his heart, in an attempt to show the unity and depth of his vision, driven by insatiable, unabated curiosity, and a constant drive to reach, during several decades of scientific activity, the inner core of things.
The study of the boundary behavior of harmonic and holomorphic functions has been a hallowed part of modern analysis for nearly 120 years. Contributors to the subject area have ranged from P. Fatou to A. P. Calderón to A. Zygmund to L. Lempert to A. Koranyi to F. Di Biase to S. G. Krantz and especially to E. M. Stein.
One of the more modern developments that is especially attributable to Stein, is the major differences between the one variable theory and the several variable theory. In one complex variable, harmonic functions and holomorphic functions are very closely related. In several variables, they are not. As a result, real-variable methods play a major role in the several-variable theory; in the one-variable theory, they do not. The methods of proof in the two subject areas are completely different, and the end results even more different.
The study of boundary limits has an impact on complex geometry, differential equations, harmonic analysis, and many other parts of mathematics. It continues to develop and to grow. These two authors have benefitted immensely from its study.
References
Abel, N.H.: Untersuchungen über di Reihe. J. Reine Angew. Math. 1, 311–339 (1826)
Aikawa, H.: Harmonic functions having no tangential limits. Proc. Am. Math. Soc. 108, 457–464 (1990)
Aikawa, H.: Harmonic functions and Green potentials having no tangential limits. J. Lond. Math. Soc. 2(43), 125–136 (1991)
Arcozzi, N., Casadio Tarabusi, E., Di Biase, F., Picardello, M.A.: Twist points of planar domains. Trans. Am. Math. Soc. 358, 2781–2798 (2006)
Armitage, D.H., Gardiner, S.J.: Classical Potential Theory. Springer, London (2001)
Barbu, V., Marinoschi, G., Tomescu, I. (eds.): Pagini din Istoria Matematicii Româneşti. Editura Academiei Române, Bucureşti (2018)
Barker, S.R.: Two theorems on boundary values of holomorphic functions. Proc. Am. Math. Soc. 68, 54–58 (1978)
Bauer, H.: Axiomatische Behandlung das Dirichletschen Problems für elliptische und parabolische Differentialgleichungen. Math. Ann. 146, 1–59 (1962)
Bauer, H.: Harmonische Räume und ihre Potentialtheorie. Lecture Notes in Mathematics, vol. 22. Springer, Berlin (1966)
Bienvenu, L., Shafer, G., Shen, A.: On the history of martingales in the study of randomness. Electron. J. Hist. Probab. Stat. 5(1), 1–40 (2009)
Boboc, N., Constantinescu, C., Cornes, A.: Axiomatic theory of harmonic functions–non-negative superharmonic functions. Ann. Inst. Fourier 15, 283–312 (1965)
Boehme, T.K., Weiss, M.L.: Extensions of Fatou’s theorem of tangential asymptotic values. Proc. Am. Math. Soc. 27, 289–298 (1971)
Bourbaki, N.: Intégration, Chaps. I–IV. Hermann, Paris (1952)
Bourbaki, N.: General Topology, Part 2. Hermann/Addison-Wesley, Paris/Reading MA (1966)
Bourbaki, N.: Topologie Générale, Chapitres 1 à 4. Diffusion C.C.L.S, Paris (1971)
Bourbaki, N.: Integration I, Chaps. 1–6. Hermann, Paris (2004)
Brelot, M.: La théorie moderne du potentiel. Ann. Inst. Fourier 4, 113–140 (1952)
Brelot, M.: Lectures on Potential Theory. Tata Institute of Fundamental Research, Bombay (1960)
Brelot, M.: Axiomatique des fonctions harmoniques. Les presses de l’Université de Montreal, Montreal (1966)
Brelot, M., Choquet, G.: Espaces et lignes de Green. Ann. Inst. Fourier 3, 199–263 (1951)
Bruckner, A.M.: Differentiation of integrals. Am. Math. Mon. 78(9), (1971). Part 2: Differentiation of Integrals, pp. i–iii\(+\)1–51
Burholder, D.L., Gundy, R.F., Silverstein, M.: A maximal function characterization of the class \(H^p\). Trans. Am. Math. Soc. 157, 137–153 (1971)
Caffarelli, L., Fabes, E., Mortola, S., Salsa, S.: Boundary behavior of nonnegative solutions of elliptic operators in divergence form. Indiana Univ. Math. J. 30(4), 621–640 (1981)
Calderón, A.P.: On the behaviour of harmonic functions at the boundary. Trans. Am. Math. Soc. 68, 47–54 (1950)
Calderón, A.P.: On a theorem of Marcinkiewicz and Zygmund. Trans. Am. Math. Soc. 68, 55–61 (1950)
Carleson, L.: On the existence of boundary values of harmonic functions of several variables. Ark. Math. 4, 339–343 (1962)
Cartan, H.: Theorie des filtres. C. R. Acad. Sci. Paris 595–598, 777–779 (1937)
Cartan, H.: Sur les fondements de la théorie du potentiel. Bull. Soc. Math. Fr. 69, 71–96 (1941)
Cartan, H.: Théorie du potentiel newtonien: énergie, capacité, suites de potentiels. Bull. Soc. Math. Fr. 73, 74–106 (1945)
Cartan, H.: Théorie générale du balayage en potentiel newtonien. Ann. Univ. Grenoble 22, 221–280 (1946)
Casanova, G.: Mémoires de J. Casanova de Seingalt. Tome Troisième. Garnier Freres, Libraires-Editeurs, París (1880). https://gallica.bnf.fr
Chirka, E.: The theorems of Lindelöf and Fatou in \(\mathbb{C}^n\). Mat. Sb. 92, 622–644 (1973)
Choquet, G.: Theory of capacities. Ann. Inst. Fourier 5, 131–295 (1954)
Christ, M.: A \(T(b)\) theorem with remarks on analytic capacity and the Cauchy integral. Colloq. Math. 60–61, 601–628 (1990)
Cifuentes, P., Dorronsoro, J.R., Sueiro, J.: Boundary tangential convergence on spaces of homogeneous type. Trans. Am. Math. Soc. 332, 331–350 (1992)
Collingwood, E.F., Lohwater, A.J.: The Theory of Cluster Sets. Cambridge University Press, Cambridge (1966)
Dahlberg, B.E.J.: Estimates of harmonic measure. Arch. Ration. Mech. Anal. 65(3), 275–288 (1977)
De Guzman, M.: Differentiation of Integrals in \(\mathbb{R}^n\). Springer, Berlin (1975)
De La Vallée Poussi, C.: Sur l’intégrale de Lebesgue. Trans. Am. Math. Soc. 16, 435–501 (1915)
De La Vallée Poussin, C.: Intégrale de Lebesgue, fonctions d’ensemble, classes de Baire. Gauthier-Villars, Paris (1916)
De Possel, R.: Sur la dérivation abstraite des fonctions d’ensemble. J. Math Pure Appl. 16, 391–409 (1936)
Di Biase, F.: Fatou Type Theorems. Maximal Functions and Approach Regions. Birkhäuser, Boston (1998)
Di Biase, F.: True or false? A case in the study of harmonic functions. Topoi 28, 143–160 (2009)
Di Biase, F., Fischer, B.: Boundary behaviour of \(H^p\) functions on convex domains of finite type in \(\mathbb{C}^n\). Pac. J. Math. 183, 25–38 (1998)
Di Biase, F., Weiss, T.: Accessible points, harmonic measure, and the Riemann mapping. In: Coen, S. (ed.) Seminari di Geometria 2005–2009. Università degli Studi di Bologna, Bologna (2010)
Di Biase, F., Fischer, B., Urbanke, R.L.: Twist points of the von Koch snowflake. Proc. Am. Math. Soc. 126, 1487–1490 (1998)
Di Biase, F., Stokolos, A., Svensson, O., Weiss, T.: On the sharpness of the Stolz approach. Ann. Acad. Sci. Fenn. Mat. 31, 47–59 (2006)
Doob, J.L.: Book review: Étude Critique de la Notion de Collectif. Bull. Am. Math. Soc. 45, 824 (1939)
Doob, J.L.: Regularity properties of certain families of chance variables. Trans. Am. Math. Soc. 47, 455–486 (1940)
Doob, J.L.: Stochastic Processes. Wiley, New York (1953)
Doob, J.L.: Boundary approach filters for analytic functions. Ann. Inst. Fourier 23(3), 187–213 (1973)
Doob, J.L.: Classical Potential Theory and Its Probabilistic Counterpart. Springer, Berlin (2001)
Drake, F.R.: Set Theory. North Holland, Amsterdam (1974)
Durrett, R.: Brownian Motion and Martingales in Analysis. Wadsworth Advanced Books & Software, Belmont (1984)
Evans, G.C.: Application of Poincaré’s sweeping out process. Proc. Natl Aci. Sci. U.S.A. 19, 457–461 (1933)
Evans, G.C., Bray, H.E.: Sur l’intègrale de Poisson gènèralisèe. C. R. Acad. Sci. Paris Sér. I Math. 176, 1042–1044 (1923)
Evans, G.C., Bray, H.E.: La formule de Poisson et le problème de Dirichlet. C. R. Acad. Sci. Paris Sér. I Math. 176, 1368–1371 (1923)
Evans, G.C., Bray, H.E.: Sur l’intègrale de Poisson. C. R. Acad. Sci. Paris Sér. I Math. 177, 241–242 (1923)
Fatou, P.: Series trigonometriques et series de Taylor. Acta Math. 30, 335–400 (1906)
Fefferman, R.: Foreword. In: Zygmund, A. (ed.) Trigonometric Series, 3rd edn. Cambridge University Press, Cambridge (2002)
Fefferman, C., Stein, E.M.: Some maximal inequalities. Am. J. Math. 93(1), 107–115 (1971)
Fefferman, C., Stein, E.M.: \(H^p\) spaces of several variables. Acta Math. 129, 137–193 (1972)
Folland, G.: Real Analysis. Wiley, New York (1984)
Frobenius, F.G.: Ueber die Leibnitzsche Reihe. J. Reine Angew. Math. 89, 262–264 (1880)
Gilbert, J.E.: Nikišin–Stein theory and factorization with applications. In: Harmonic Analysis in Euclidean Spaces, Proc. Symposia Pure Mathematics, vol. 35, Part 2, pp. 233–267. American Mathematical Society, Providence (1979)
Gowrisankaran, K.: Extreme harmonic functions and boundary value problems. Ann. Inst. Fourier 13(2), 307–356 (1963)
Gowrisankaran, K.: Fatou–Naïm–Doob limit theorems in the axiomatic system of Brelot. Ann. Inst. Fourier 16(2), 455–467 (1966)
Grandi, L.G.: Quadratura Circuli et Hyperbolæ per Infinitas Hyperbolas, & Parabolas Geometricè exhibita. Pisa (1703)
Hansen, W.: Konstruktion von Halbgruppen und Markoffschen Prozessen. Invent. Math. 3, 179–214 (1967)
Hardy, G.H., Littlewood, J.E.: Contributions to the arithmetic theory of series. London M. S. Proc. 2(11), 411–478 (1913)
Hardy, G.H., Littlewood, J.E.: Tauberian theorems concerning power series and Dirichlet’s series whose coefficients are positive. Proc. Lond. Math. Soc. Ser. 2 13(1), 174–191 (1914). https://doi.org/10.1112/plms/s2-13.1.174
Hardy, G.H., Littlewood, J.E.: Abel’s theorem and its converse (II). Proc. Lond. Math. Soc. s2-22(1), 254–269 (1924)
Hardy, G.H., Littlewood, J.E.: A maximal theorem with function-theoretic applications. Acta Math. 54, 81–116 (1930)
Hartogs, F.: Zur Theorie der analytischen Funktionen mehrerer unabhängiger Veränderlichen, insbesondere über die Darstellung derselber durch Reihen, welche nach Potentzen einer Veränderlichen fortschreiten. Math. Ann. 62, 1–88 (1906)
Hausdorff, F.: Grundzüge der Mengenlehre. Verlag Von Veit & Comp, Leipzig (1914)
Helms, L.L.: Potential Theory. Springer, New York (2009)
Hörmander, L.: \(L^p\) estimates for (pluri-) subharmonic functions. Math. Scand. 20, 65–78 (1967)
Hunt, R.A., Wheeden, R.L.: On the boundary values of harmonic functions. Trans. Am. Math. Soc. 132(2), 307–322 (1968)
Hunt, R.A., Wheeden, R.L.: Positive harmonic functions on Lipschitz domains. Trans. Am. Math. Soc. 147(2), 507–527 (1970)
Jech, T.: Set Theory. Academic Press, New York (1978)
Jerison, D.S., Kenig, C.E.: Boundary behavior of harmonic functions in non-tangentially accessible domains. Adv. Math. 46, 80–147 (1982)
Jessen, B.: The theory of integration in a space of an infinite number of dimensions. Acta Math. 63, 249–323 (1934)
Jones, P.: A geometric localization theorem. Adv. Math. 46, 71–79 (1982)
Kakutani, S.: Two-dimensional Brownian motion and harmonic functions. Proc. Imp. Acad. 20(10), 700–708 (1944)
Kakutani, S.: Markoff process and the Dirichlet problem. Proc. Jpn. Acad. 21(4), 227–233 (1945)
Keldych, M.V.: On the solubility and the stability of Dirichlet’s problem. Uspekhi Mat. Nauk. 8, 171–231 (1941) (Russian)
Kelley, J.L.: General Topology. Van Nostrand, New York (1955)
Kellogg, O.D.: Unicité de fonctions harmoniques. C.R. Acad. Sci. Paris 187, 526–527 (1928)
Kellogg, O.D.: Foundations of Potential Theory. Springer, Berlin (1929)
Knopp, K.: Theory and Application of Infinite Series. Blackie & Son Limited, London (1954)
Kolmogorov, A.: Sur les fonctions harmoniques conjuguées et les séries de Fourier. Fund. Math. 7, 24–29 (1925)
Korányi, A.: The Poisson integral for generalized halfplanes and bounded symmetric domains. Ann. Math. 82, 332–350 (1965)
Korányi, A.: Harmonic functions on Hermitian hyperbolic space. Trans. Am. Math. Soc. 135, 507–516 (1969)
Korányi, A.: Holomorphic and harmonic functions on bounded symmetric domains (Corso tenuto ad Urbino dal 5 al 13 luglio 1967). In: Vesentini, E. (ed.) Geometry of Homogeneous Bounded Domains. C.I.M.E. Summer Schools, vol 45. Springer, Berlin (2011)
Král, J.: The Fredholm method in potential theory. Trans. Am. Math. Soc. 125, 511–547 (1966)
Krantz, S.G.: Invariant metrics and the boundary behavior of holomorphic functions on domains in \(\mathbb{C}^n\). J. Geom. Anal. 1, 71–97 (1991)
Krantz, S.G.: Function Theory of Several Complex Variables. American Mathematical Society, Providence (2001)
Krantz, S.G.: The boundary behavior of holomorphic functions: global and local results. Asian J. Math. 11, 179–199 (2007)
Krantz, S.G.: The Besicovitch covering lemma and maximal functions. Rocky Mountain J. Math. 49, 539–555 (2019)
Krantz, S.G., Li, S.-Y.: Duality theorems for Hardy and Bergman spaces on convex domains of finite type in \(C^n\). Ann. Inst. Fourier (Grenoble) 45, 1305–1327 (1995)
Kunen, K.: Set Theory. An Introduction to Independence Proofs. North-Holland, New York (1980)
Lebesgue, H.: Leçons sur l’intégration et la recherche des fonctions primitives, professées au Collège de France. Gauthier-Villars, Paris (1904). http://www.archive.org
Lebesgue, H.: Sur le problème de Dirichlet. Rend. Circ. Mat. Palermo 24, 371–402 (1907)
Lebesgue, H.: Sur l’intégration des fonctions discontinues Ann. Sci. Ecole Norm. Sup. Ser. 3(27), 361–450 (1910)
Lebesgue, H.: Sur des cas d’impossibilité du problème de Dirichlet. (Séance du 27 Novembre 1912), p. 17. C. R. Soc. Math. de France (1913)
Lebesgue, H.: Conditions de règularitè, conditions d’irrègularitè, conditions d’impossibilitè dans les problème de Dirichlet. C. R. Acad. Sci. Paris 178, 349–354 (1924)
Leibniz, G.W.: Epistola G.G.L. ad V. Cl. Christianum Wolfium. Acta Eruditorum Suppl. V(6), 264–270 (1713). http://www.digitale.beic.it/primo_library/libweb/action/search.do
Leibniz, G.W.: In: Gerhardt, C.I. (ed.) Mathematischen Schriften, vol. 5, pp. 382–387, Halle (1858). http://www.archive.org
Lempert, L.: Boundary behaviour of meromorphic functions of several variables. Acta Math. 144, 1–25 (1980)
Lévy, P.: Propriétés asymptotiques des sommes de variables aléatoires enchainées. Bull. Sci. Math. 59(84–96), 109–128 (1935)
Lévy, P.: Théorie de l’addition des variables aléatoires. Gauthier-Villars, Paris (1937)
Littlewood, J.E.: The converse of Abel’s theorem on power series. Proc. Lond. Math. Soc. Ser. 2–9, 434–448 (1911)
Littlewood, J.E.: On a theorem of Fatou. J. Lond. Math. Soc. s-2, 172–176 (1927)
Littlewood, J.E.: Mathematical Notes (9): On functions subharmonic in a circle (III). Proc. Lond. Math. Soc. 2(32), 222–234 (1931)
Littlewood, J.E., Paley, R.E.A.C.: Theorems on Fourier Series and Power Series (II). Proc. Lond. Math. Soc. (2) 42(1), 52–89 (1937)
Lohwater, A.J., Piranian, G.: The boundary behaviour of functions analytic in a disk. Ann. Acad. Sci. Fenn. Ser. A. I. 1957(239), 1–17 (1957)
Lusin, N.: Sur une propriété des fonctions à carré sommable. Bull. Calcutta Math. Soc. 20, 139–154 (1930)
Mac Lane, S.: Categories for the Working Mathematicians, 2nd edn. Springer, Berlin (1978)
Mair, B.A., Singman, D.: A generalized Fatou theorem. Trans. Am. Math. Soc. 300(2), 705–719 (1987)
Mair, B.A., Philipp, S., Singman, D.: A converse Fatou theorem. Mich. Math. J. 36(1), 3–9 (1989)
Mair, B.A., Philipp, S., Singman, D.: A converse Fatou theorem on homogeneous spaces. Ill. J. Math. 33, 643–656 (1989)
Mair, B.A., Philipp, S., Singman, D.: Generalized local Fatou theorems and area integrals. Trans. Am. Math. Soc. 321, 401–413 (1990)
Malliavin, P.: Cooperation with Hélène Airault, Leslie Kay, Gérard Letac. In: Integration and Probability. Springer, Berlin (1995)
Marcinkiewicz, J., Zygmund, A.: A theorem of Lusin. Duke J. 4, 473–485 (1938)
Mazliak, L.: How Paul Lévy saw Jean Ville and Martingales. Electron. J. Hist. Probab. Stat. 5(1), 1–24 (2009)
McMillan, J.E.: Asymptotic values of functions holomorphic in the unit disc. Mich. Math. J. 12, 141–154 (1965)
Nagel, A., Stein, E.M.: On certain maximal functions and approach regions. Adv. Math. 54, 83–106 (1984)
Nagel, A., Stein, E.M., Wainger, S.: Boundary behavior of holomorphic functions in domains of finite type. Proc. Natl Acad. Sci. U.S.A. 78(11), 6596–6599 (1981)
Nagel, A., Stein, E.M., Wainger, S.: Balls and metrics defined by vector fields I: Basic properties. Acta Math. 155, 103–147 (1985)
Netuka, I.: The Dirichlet problem for harmonic functions. Am. Math. Mon. 87(8), 621–628 (1980)
Nikišin, E.M.: Resonance theorems and superlinear operators. Russ. Math. Surv. 25, 125–187 (1970)
Noshiro, K.: Cluster Sets. Springer, Berlin (1960)
Osgood, W.F.: Note über analytische Funktionen mehrer Veränderlicher. Math. Ann. 52, 462–464 (1899)
Osgood, W.F.: On functions of several complex variables. Trans. Am. Math. Soc. 17, 1–8 (1916)
Paley, R.E.A.C.: A remerkable system of orthogonal functions. I. Proc. Lond. Math. Soc. 34, 241–264; II. 265–279 (1932)
Paley, R.E.A.C., Zygmund, A.: A note on analytic functions inthe unit circle. Math. Proc. Camb. Philos. Soc. 28(1932), 266–272 (1932)
Perron, O.: Eine neue Behandlung der ersten Randwertaufgabe für \(\Delta u=0\). Math. Z. 18, 42–54 (1923)
Plessner, A.: Über das Verhalten analytischer Funktionen am Rande ihres DefinitionsbereichesÜber das Verhalten analytischer Funktionen am Rande ihres Definitionsbereiches. J. Reine Angew. Math. 158, 219–227 (1927)
Pommerenke, Ch.: Boundary Behaviour of Conformal Maps. Springer, Berlin (1992)
Pringsheim, A.: Ueber die Divergenz gewisser Potenzreihen an der Convergenzgrenze. Sitzungsberichte der mathematisch-physicalischen Classe der k.b., vol. 31, pp. 505–524. Akademie der Wissenschaftenzu München, Munich (1901)
Privalov, I.I.: Intégrale de Cauchy Saratov. PhD Thesis (1919)
Privalov, I.I.: Sur une généralisation du théorème de Fatou. Mat. Sb. 31(2), 232–235 (1923)
Privalov, I.I.: Randeigenschaftern analytischer Funktionen. VEB Deutscher Verlag der Wissenschaften, Berlin (1956)
Privalov, I.I., Kouznetzoff, P.: Sur les problèmes limites et les classes différentes de fonctions harmoniques et subharmoniques definies dans un domaine arbitraire. Rec. Math. Moscou Ser. 6, 345–376 (1939)
Prym, F.E.: Zur Integration der Differentialgleichung \(\frac{\partial ^2 u}{\partial {x}^2}+\frac{\partial ^2 u}{\partial {y}^2}=0\). J. Reine Angew. Math. 73, 340–364 (1871)
Remak, R.: Über potentialkonvexe Funktionen. Math. Z. 20, 126–130 (1924)
Riemann, B.: Gründlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse (Inaugural dissertation Göttingen 1851). In: Narasimhan, R. (ed.) Collected Papers, pp. 35–80. Springer, Berlin (1980)
Riesz, F.: Über die Randwerte einer analytischen Funktion. Math. Z. 18, 87–95 (1923)
Riesz, F., Riesz, M.: Über Randwerte einer analytischen Funktion, pp. 27–44. Quatrième Congrès des mathématiciens scandinaves, Stockholm (1916)
Rudin, W.: Inner function images of radii. Math. Proc. Camb. Philos. Soc. 85, 357–360 (1979)
Saks, S.: Sur les nombres derives des fonctions. Fundam. Math. 5, 98–104 (1924)
Samuel, P.: Ultrafilter and compactification of uniform spaces. Trans. Am. Math. Soc. 64(1), 100–132 (1948)
Sawyer, S.: Maximal inequalities of weak type. Ann. Math. 84, 157–173 (1966)
Sparre-Andersen, E., Jessen, B.: Some limit theorems on integrals in an abstract set. Det Kgl. Danske Vidensabernes Selskab Mat. Fys. Medd. 22(14), 1–29 (1946)
Sparre-Andersen, E., Jessen, B.: On the introduction of measures in infinite product sets. Det Kgl. Danske Vidensabernes Selskab Mat. Fys. Medd. 25(4), 1–7 (1948)
Sparre-Andersen, E., Jessen, B.: Some limit theorems on set-functions. Det Kgl. Danske Vidensabernes Selskab Mat.-Fys. Medd. 25(5), 1–8 (1948)
Spencer, D.C.: A function-theoretic identity. Am. J. Math. 65(1), 147–160 (1943)
Stein, E.M.: On the functions of Littlewood–Paley, Lusin, and Marcinkiewicz. Trans. Am. Math. Soc. 88, 430–466 (1958)
Stein, E.M.: Correction on a previous paper. Trans. Am. Math. Soc. 98, 186 (1961)
Stein, E.M.: On the behavior of harmonic functions at the boundary: II. Acta Math. 106, 137–174 (1961)
Stein, E.M.: On limits of sequences of operators. Ann. Math. 74, 140–170 (1961)
Stein, E.M.: Note on the boundary values of holomorphic functions. Ann. Math. 82, 351–353 (1965)
Stein, E.M.: Singular Integrals and Differentiability Properties of Functions. Princeton University Press, Princeton (1970)
Stein, E.M.: Topics in Harmonic Analysis Related to the Littlewood-Paley Theory. Princeton University Press, Princeton (1970)
Stein, E.M.: Boundary Behavior of Holomorphic Functions of Several Complex Variables. Princeton University Press, Princeton (1972)
Stein, E.M.: The development of square functions in the work of Zygmund. Bull. Am. Math. Soc. 7, 359–376 (1982)
Stein, E.M.: Singular integrals: the roles of Calderón and Zygmund. Not. Am. Math. Soc. 45, 1130–1140 (1998)
Stein, E.M.: The analogues of Fatou’s theorem and estimates for maximal functions (Corso tenuto ad Urbino dal 5 al 13 luglio 1967). In: Vesentini, E. (ed.) Geometry of Homogeneous Bounded Domains. C.I.M.E. Summer Schools, vol. 45. Springer, Berlin (2011)
Stein, E.M., Weiss, G.: Fourier Analysis on Euclidean Spaces. Princeton University Press, Princeton (1971)
Stoilow, S.: Leçons sur les principes topologiques de la théorie des fonctions analytiques Paris, (1938)
Stolz, O.: Beweis einiger Sätze über Potenzenreihen. Zeitschr. Math. Phys. 20, 369–376 (1875)
Sueiro, J.: On maximal functions and Poisson–Szegö integrals. Trans. Am. Math. Soc. 298, 653–669 (1986)
Sueiro, J.: A note on maximal operators of Hardy–Littlewood type. Math. Proc. Camb. Philos. Soc. 102, 131–134 (1987)
Sueiro, J.: Tangential boundary limits and exceptional sets for holomorphic functions in Dirichlet-type spaces. Math. Ann. 286, 661–678 (1990)
Tauber, A.: Ein Satz aus der Theorie der unendlichen Reihen. Monat. Math. Phys. 8, 273–277 (1897). https://doi.org/10.1007/BF01696278
Tsuji, M.: On Fatou’s theorems on Poisson integrals. Jpn. J. Math. 15, 13–18 (1939)
Tsuji, M.: On the boundary value of a harmonic function in space. Jpn. J. Math. 19(1), 111–137 (1944)
Vasilesco, F.: La notion de capacité. Hermann, Paris (1937)
Vesentini, E. (ed.): Geometry of Homogeneous Bounded Domains. C.I.M.E. Summer Schools, vol. 45. Springer, Berlin (2011)
Ville, J.: Sur la notion de Collectif. C. R. Acad. Sci. Paris 203, 26–27 (1936)
Ville, J.: Étude Critique de la Notion de Collectif. Gauthier-Villars, Paris (1939)
Vitali, G.: Sull’integrazione per serie. Rend. Circ. Mat. Palermo 23, 137–155 (1907)
von Koch, H.: Une méthode géométrique élémentaire pour l’étude de certain questions de la théorie des courbes planes. Acta Math. 30, 145–174 (1906)
Weierstrass, K.: Über das sogenannte Dirichletsche Princip. Mathematische Werke Mayer & Müller, Berlin, 1894. Read to the Royal Academy of Sciences on July 14, 1870
Widman, K.-O.: On the boundary values of functions harmonic in \(\mathbb{R}^3\) Ark. Mat. 5(3–4), 221–230 (1964)
Wiener, N.: Certain notions in potential theorem. J. Math. Phys. Mass. Inst. Technol. 3, 127–146 (1924). Reprinted in Masani, P. (ed.) Collected Works. MIT Press, Cambridge (1976)
Zaremba, S.: Sur le principe de Dirichlet. Atti del IV Congresso intenazionale dei matematici (Roma, 6–11 aprile 1908) Tip. della R. Accademia dei Lincei, Roma (1909)
Zaremba, S.: Sur le principe de Dirichlet. Acta Math. 34, 293–316 (1911)
Zygmund, A.: On a theorem of Littlewood. Summa Brasil. Math. 2(5), 51–57 (1949)
Zygmund, A.: Notes on the history of Fourier series. In: Ash, J.M. (ed.) Studies in Harmonic Analysis. The Mathematical Association of America, Washington (1976)
Zygmund, A.: Trigonometric Series, 2nd edn. Cambridge University Press, Cambridge (1988)
Acknowledgements
This study was supported by Università degli Studi G. d’Annunzio Chieti - Pescara and Indam.
Funding
Open access funding provided by Università degli Studi G. D’Annunzio Chieti Pescara within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
We were unable to find a self-contained reference where all the results in Sect. 5.4 are stated and proved. In particular, the existence of amenable nets in Theorem 5.25, proved in Sect. 11.7 and in Sect. 11.8, appears to be new. Hence we offer such a presentation that differs from the available treatments because the only tools we use are maximal operators, coupled with the standard method of Sect. 5.2.5, and because the boundedness of the maximal operator does not depend on delicate covering theorems. We recall here the statement of Theorem 5.25 that yields a differentiation theorem which does not rely on covering theorems.
Theorem 5.25 If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a measure space of finite measure and at least one of the following holds:
- (1):
-
The \(\sigma \)-algebra \(\varvec{\mathcal {S}}\) is countably generated.
- (2):
-
\( L^{1}( {X} ) \) is separable as a metric space.
Then there exists an amenable net \({{\mathbf {\mathsf{{c}}}}}={\{{\mathsf {C}}_{j}\}}_{{j}}\) in \( {X} \) such that for each \(f\in \mathcal {L}^{1}( {X} )\), the sequence of conditional expectations  converges to \(f\) a.e. and in \(L^1\).
converges to \(f\) a.e. and in \(L^1\).
We prove that amenable nets exist in great generality. This result yields a differentiation theorem which does not depend on delicate covering theorems and has the potential of producing new results in applications to the boundary behavior in several complex variables, as well as to that part of probability theory connected with martingale convergence theorems [21]. We plan to return to these matters in the near future.
For brevity, we include in this Appendix only those proofs which are not routine. Full details will appear elsewhere.
The hierarchy \(\{\text {semirings}\} \subset \{\text {rings}\} \subset \{\text {algebras}\} \subset \{\sigma \text {-algebras}\}\), and its relation to the notion of partition, provide the basis for a good understanding of these matters.
1.1 Rings, Algebras, \(\varvec{\sigma }\)-Algebras, Semirings, Finite Semirings, and Partitions
Let \( {X} \) be a nonempty set. A ring in \( {X} \) is a nonempty collection \(\mathcal {C}\subset \varvec{\mathcal {P}}( {X} ) \) with the following properties:
- (R 1):
-
If \(Q\in \mathcal {C}\) and \(R\in \mathcal {C}\), then \(Q\cup R\in \mathcal {C}\) [\(\mathcal {C}\) is closed under finite unions].
- (R 2):
-
If \(Q\in \mathcal {C}\), \(R\in \mathcal {C}\), and \(R\subset Q\), then \(Q\setminus R\in \mathcal {C}\) [\(\mathcal {C}\) is closed under proper differences].
A ring in \( {X} \) necessarily contains the empty set. Every ring is closed under differences, symmetric differences, and finite intersections, The intersection of a nonempty collection of rings in \( {X} \) is a ring in \( {X} \). If \(\mathcal {C}\subset \varvec{\mathcal {P}}( {X} ) \) is nonempty, the ring generated by \(\mathcal {C}\), denoted by \( {{\mathbf {\mathsf{{R}}}}}(\mathcal {C}) \), is the intersection of all rings which contain \(\mathcal {C}\). An algebra in \( {X} \) is a nonempty collection \(\mathcal {C}\subset \varvec{\mathcal {P}}( {X} ) \) with the following properties:
- (A 1):
-
\(\mathcal {C}\) is closed under finite unions.
- (A 2):
-
If \(Q\in \mathcal {C}\), then \( {X} \setminus Q\in \mathcal {C}\) [\(\mathcal {C}\) is closed under complementation].
An algebra in \( {X} \) necessarily contains the empty set and \( {X} \). Every algebra in \( {X} \) is a ring in \( {X} \).
Lemma 11.1
If \(\mathcal {C}\) is a ring in \( {X} \), then \(\mathcal {C}\) is an algebra in \( {X} \) if and only if \( {X} \in \mathcal {C}\).
If \(\mathcal {C}\subset \varvec{\mathcal {P}}( {X} ) \) is nonempty, the algebra generated by \(\mathcal {C}\), denoted by \( {{\mathbf {\mathsf{{A}}}}}(\mathcal {C}) \), is the intersection of all rings which contain \(\mathcal {C}\). A \(\varvec{\sigma }\)-algebra in \( {X} \) is an algebra which is closed under countable unions. Observe that any finite algebra is a \(\sigma \)-algebra. If \(\mathcal {C}\subset \varvec{\mathcal {P}}( {X} ) \) is nonempty, the \(\varvec{\sigma }\)-algebra generated by \(\mathcal {C}\), denoted by \(\sigma (\mathcal {C})\), is the intersection of all rings which contain \(\mathcal {C}\). Hence \(\mathcal {C}\subset \sigma (\mathcal {C})\subset \varvec{\mathcal {P}}( {X} ) \) and
A \(\sigma \)-algebra \(\varvec{\mathcal {S}}\) in \( {X} \) is countably generated if \(\varvec{\mathcal {S}}=\sigma ( \mathcal {D} )\) for some countable \( \mathcal {D} \subset \varvec{\mathcal {P}}( {X} ) \), and it is finitely generated if \(\varvec{\mathcal {S}}=\sigma ( \mathcal {D} )\) for some finite collection \( \mathcal {D} \subset \varvec{\mathcal {P}}( {X} ) \). If \(\mathcal {C}\subset \varvec{\mathcal {P}}( {X} ) \), define
and \(\varvec{ \mathcal {C}}^* {{\mathop {=}\limits ^{\mathrm{def}}}} \{\varvec{Q\in \varvec{\mathcal {P}}( {X} ) : Q} \hbox { may be written as union of finitely many elements of } \mathcal {C}\}\). The empty set belongs to both \(\mathcal {C}^\sharp \) and \(\mathcal {C}^*\). Observe that \(\mathcal {C}\subset \mathcal {C}^{\sharp } \subset \mathcal {C}^* \subset \varvec{\mathcal {P}}( {X} ) \).
Lemma 11.2
If \(\mathcal {C}\subset \varvec{\mathcal {P}}( {X} ) \), then \( \mathcal {C}^* \) is closed under finite unions, and \({(\mathcal {C}^*)}^*=\mathcal {C}^*\). If \(\mathcal {C}_1\subset \mathcal {C}_2\), then \(\mathcal {C}_1^*\subset \mathcal {C}_2^*\). Moreover, \(\sigma (\mathcal {C})=\sigma (\mathcal {C}^*)\).
The length of \(Q\in \mathcal {C}^\sharp \) is the smallest integer k such that \(Q\) may be written as disjoint union of k sets in \(\mathcal {C}\). A similar definition is given for \(Q\in \mathcal {C}^* \). The empty set has length equal to zero.
A nonempty collection \(\mathcal {C}\subset \varvec{\mathcal {P}}( {X} ) \) is called a semiring if it has the following properties:
- (SR 1):
-
If \(Q_1,Q_2\in \mathcal {C}\), then \(Q_1\cap Q_2\in \mathcal {C}\) [\(\mathcal {C}\) is closed under finite intersections].
- (SR 2):
-
If \(Q_1,Q_2\in \mathcal {C}\) and \(Q_2\subset Q_1\), then \(Q_1\setminus Q_2\in \mathcal {C}^\sharp \) [we write that \(\mathcal {C}-\mathcal {C}\subset \mathcal {C}^\sharp \)].
A semiring necessarily contains the empty set. The intersection of a collection of semirings in \( {X} \) is not necessarily a semiring in \( {X} \). For example, if \( {X} =\{1,2,3\}\), \(\mathcal {C}_1{\mathop {=}\limits ^{\mathrm{def}}}\{\emptyset , {X} ,\{1\},\{2,3\}\}\), and \(\mathcal {C}_2{\mathop {=}\limits ^{\mathrm{def}}}\{\emptyset , {X} ,\{1\},\{2\},\{3\}\}\), then \(\mathcal {C}_1\cap \mathcal {C}_2=\{\emptyset , {X} ,\{1\}\}\), which is not a semiring. This example should be interpreted in terms of the relation between semirings and partitions, which will be now illustrated. Recall that a nonempty collection \(\mathcal {C}\subset \varvec{\mathcal {P}}( {X} ) \) has the inclusion–exclusion property if for any pair of sets in \(\mathcal {C}\), the two sets are either disjoint or one of them is contained in the other. If \(\mathcal {C}\) has the inclusion–exclusion property and it contains the empty set, then it satisfies (SR 1). Every partition of \( {X} \) has the inclusion–exclusion property. All partitions mentioned in this work are finite, even without further explicit mention. A finite partition of a nonempty set \( {X} \) is a nonempty and finite collection \(\mathsf {C}\subset \varvec{\mathcal {P}}_{\bullet }( {X} ) \) such that each point \(q\in {X} \) belongs to one and only one set in \(\mathsf {C}\). The sets in \(\mathsf {C}\) are called tiles of the partition \(\mathsf {C}\). The tile of \(\mathsf {C}\) which contains \(q\in {X} \) is denoted by \(\varvec{\mathsf {C}[q]}\). The collection of all finite partitions of \( {X} \) is denoted by \(\varvec{\Pi ( {X} )}\). We associate a partition \([Q]\in \Pi ( {X} )\) to every subset \(Q\subset {X} \) as follows:
The set \(\Pi ( {X} )\) is endowed with a partial order (based on reverse inclusion) which makes it a directed set. The partition \(\mathsf {C}_2\) is nested in the partition \(\mathsf {C}_1\) if each tile of \(\mathsf {C}_2\) is contained in a tile of \(\mathsf {C}_1\). We then write \(\mathsf {C}_1{\preceq }\mathsf {C}_2\) and say that \(\mathsf {C}_2\) is finer than \(\mathsf {C}_1\), and that \(\mathsf {C}_1\) is coarser than \(\mathsf {C}_2\).
Definition 11.3
Given any \(\mathsf {C}_1,\mathsf {C}_2\in \Pi ( {X} )\), define \(\varvec{\mathsf {C}_1\vee \mathsf {C}_2\in \Pi ( {X} )}\) as the partition of which tiles are the nonempty sets of the form \(Q_1\cap Q_2\) where \(Q_{j}\in \mathsf {C}_{j}\), \(j=1,2\).
Observe that
and
Recall that \(\mathsf {C}_1{\preceq }\mathsf {C}_2\) means that each tile of \(\mathsf {C}_2\) is contained in a tile of \(\mathsf {C}_1\).
Lemma 11.4
The operation \((\mathsf {C}_1,\mathsf {C}_2)\mapsto \mathsf {C}_1\vee \mathsf {C}_2\), is associative and commutative, and, if \(\mathcal {Q}\subset \Pi ( {X} )\) is finite, then \({\bigvee _{\mathsf {C}\in \mathcal {Q}}\mathsf {C}}{\mathop {=}\limits ^{\mathrm{def}}}\mathsf {C}_1\vee \mathsf {C}_2\vee \ldots \vee \mathsf {C}_n\), where \({\{\mathsf {C}_j\}}_{j=1}^n\) is any ordering of \(\mathcal {Q}\), is well defined.
Lemma 11.5
If \(\mathsf {C}\) is a finite partition of \( {X} \), then \(\{\emptyset \}\cup \mathsf {C}\) is a semiring, \( \mathsf {C}^* =\mathsf {C}^\sharp \), \( \mathsf {C}^* \) is a finite algebra, and \( \mathsf {C}^* = {{\mathbf {\mathsf{{R}}}}}(\mathsf {C}) = {{\mathbf {\mathsf{{A}}}}}(\mathsf {C}) =\sigma (\mathsf {C})\).
Lemma 11.5 is a special case of a more general result, given in Theorem 11.13. Hence if \(\mathsf {C}\) is a finite partition of \( {X} \), then we define \( \mathsf {C}^* \) as the algebra generated by \(\mathsf {C}\), while \(\{\emptyset \}\cup \mathsf {C}\) is called the semiring associated to \(\mathsf {C}\).
Lemma 11.6
If \(\mathsf {C}_1,\mathsf {C}_2\in \Pi ( {X} )\) and \(\mathsf {C}_1{\preceq }\mathsf {C}_2\), then \( \mathsf {C}_{1}^* {\subset } \mathsf {C}_{2}^* \)
If \( \mathcal {D} \subset \varvec{\mathcal {P}}( {X} ) \) is finite, we define \(\mathsf {C}_{ \mathcal {D} }\in \Pi ( {X} )\) using Lemma 11.4 as follows: \(\mathsf {C}_{ \mathcal {D} } {\mathop {=}\limits ^{\mathrm{def}}}\bigvee _{Q\in \mathcal {D} }[Q]\). Hence, if \( \mathcal {D} =\{Q_1,Q_2,\ldots ,Q_n\}\) is any ordering of \( \mathcal {D} \), then \(\mathsf {C}_{ \mathcal {D} }=[Q_1]\vee [Q_2]\vee \ldots \vee [Q_n]\) (recall Definition 11.3).
Lemma 11.7
If \( \mathcal {D} \subset \varvec{\mathcal {P}}( {X} ) \) is finite, then \({(\mathsf {C}_{ \mathcal {D} })}^*= {{\mathbf {\mathsf{{A}}}}}( \mathcal {D} ) =\sigma ( \mathcal {D} )\). In particular, \(\sigma ( \mathcal {D} )\) is finite.
Theorem 11.8
If \( {X} \) is a nonempty set and \(\varvec{\mathcal {S}}\subset {X} \), then the following conditions are equivalent:
- (1):
-
There exists a finite partition \(\mathsf {C}\) of \( {X} \) such that \(\varvec{\mathcal {S}}=\mathsf {C}^*\).
- (2):
-
There exists a finite set \( \mathcal {D} \subset \varvec{\mathcal {P}}( {X} ) \) such that \(\sigma ( \mathcal {D} )=\varvec{\mathcal {S}}\).
- (3):
-
\(\varvec{\mathcal {S}}\) is a finite \(\sigma \)-algebra.
1.2 Structure Theorem for Finite Semirings and Finite Algebras
Proposition 11.9
If \(\varvec{\mathcal {S}}\subset \varvec{\mathcal {P}}( {X} ) \) is a finite semiring, then there is a partition \(\mathsf {C}\) of \( {X} \) such that \(\varvec{\mathcal {S}}\subset \mathsf {C}^*\).
The following result is contained in Theorem 11.8. However, it also follows from Proposition 11.9.
Corollary 11.10
If \(\varvec{\mathcal {S}}\subset \varvec{\mathcal {P}}( {X} ) \) is a finite algebra, then there is a partition \(\mathsf {C}\) of \( {X} \) such that \(\varvec{\mathcal {S}}=\mathsf {C}^*\).
1.3 Rings, Algebras Generated by Semirings, Nets, and Countable Semirings
Lemma 11.11
If \(\mathcal {C}\) is a semiring in \( {X} \), then if \(Q\in \mathcal {C}\), \(R\in \mathcal {C}^\sharp \), and \(R\subset Q\), then there exists \(Z\in \mathcal {C}^\sharp \) disjoint from \(R\) such that \(Q=R\cup Z\).
We informally express the conclusion of Lemma 11.11 by writing that “\(\mathcal {C}-\mathcal {C}^\sharp \subset \mathcal {C}^\sharp \)”.
Proposition 11.12
If \(\mathcal {C}\) is a semiring in \( {X} \), then \( \mathcal {C}^* =\mathcal {C}^\sharp \). Moreover, if \(Q=\bigcup _{j=1}^kQ_j\) where \(Q_j\in \mathcal {C}\), then there exist disjoint sets \(R_j\in \mathcal {C}^\sharp \) such that \(Q=\bigcup _{j=1}^kR_j\) and \(R_j\subset Q_j\) for each j.
Theorem 11.13
If \(\mathcal {C}\subset \varvec{\mathcal {P}}( {X} ) \) is a semiring, then \( \mathcal {C}^* \) is a ring, and \( \mathcal {C}^* = {{\mathbf {\mathsf{{R}}}}}(\mathcal {C}) \). If \( \mathcal {C}^* \) contains \( {X} \), then \( \mathcal {C}^* \) is an algebra and \( {{\mathbf {\mathsf{{R}}}}}(\mathcal {C}) = {{\mathbf {\mathsf{{A}}}}}(\mathcal {C}) = \mathcal {C}^* \).
We have seen that finite semirings are associated to finite partitions. We will now show that countable semirings are associated to nets. A sequence \(\mathsf {C}_1, \mathsf {C}_2,\ldots , \mathsf {C}_k,\ldots \) of partitions of \( {X} \) is called a net in \( {X} \) if the partitions are nested: \(\mathsf {C}_k{\preceq }\mathsf {C}_{k+1}\) for each \(k\ge 1\). If \({{\mathbf {\mathsf{{c}}}}}={\{\mathsf {C}_{j}\}}_{j\in \mathbb {N}}\) is a net in \( {X} \), a set which is equal to \(\mathsf {C}_{j}[q]\), for some \(j\in \mathbb {N}\) and \(q\in {X} \), is called a tile of the net. The partitions \(\mathsf {C}_{j}\) are called the partitions of the net \({{\mathbf {\mathsf{{c}}}}}\). The collection of all the tiles of \({{\mathbf {\mathsf{{c}}}}}\) is denoted by \( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}\). Hence \( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}{\mathop {=}\limits ^{\mathrm{def}}}\bigcup _{j\in \mathbb {N}}{\mathsf {C}_{j}}\).
Theorem 11.14
If \({{\mathbf {\mathsf{{c}}}}}\) is a net in \( {X} \), then \(\{\emptyset \}\cup \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}\) is a countable semiring, \( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}^*\) is a countable algebra in \( {X} \), and \( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}^*= {{\mathbf {\mathsf{{R}}}}}( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}) = {{\mathbf {\mathsf{{A}}}}}( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}) \).
\( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}^*\) is called the algebra generated by the net \({{\mathbf {\mathsf{{c}}}}}\). It is a countable algebra. We will see below that every countable algebra is the algebra generated by a net (Proposition 11.18).
Observe that \(\sigma ( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}^*)=\sigma ( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}})\), by Lemma 11.2, and that \(\sigma ( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}})\) is a countably generated \(\sigma \)-algebra, called the \(\varvec{\sigma }\)-algebra generated by the net \({{\mathbf {\mathsf{{c}}}}}\). We will see below that every countably generated \(\sigma \)-algebra is the \(\sigma \)-algebra generated by a net (Theorem 11.19).
Lemma 11.15
If \({{\mathbf {\mathsf{{c}}}}}\) is a net in \( {X} \) and \(L\subset \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}\), then there exists a unique subset \(L_{c}\subset {}L\) such that
-
1.
the elements of \(L_{c}\) are disjoint;
-
2.
\({\bigcup _{Q\in {}L_{c}}Q=\bigcup _{Q\in {}L}Q}\).
1.4 Structure Theorem for Countably Generated \(\varvec{\sigma }\)-Algebras
We give a more general version of the results of Sect. 11.2.
Lemma 11.16
If \( \mathcal {D} \subset \varvec{\mathcal {P}}( {X} ) \) is countable, then there exists a net \({{\mathbf {\mathsf{{c}}}}}\) in \( {X} \) such that
Proof
Let \( \mathcal {D} =\{Q_{j}:k\in \mathbb {N}\}\). Define inductively \(\mathsf {C}_1{\mathop {=}\limits ^{\mathrm{def}}}[Q_1]\) and, for \(j\ge 2\), \(\mathsf {C}_{j}{\mathop {=}\limits ^{\mathrm{def}}}\mathsf {C}_{j-1}\vee \, [Q_{j}]\). We claim that, for each \(j\ge 1\),
Observe that (11.6) implies (11.5), since \( \mathsf {C}_{j}^* \subset { \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}}^*\). We now prove (11.6). The fact that \(Q_1\in \mathsf {C}_1^* \) follows from the fact that \(Q\in [Q]^* \) for each \(Q\subset {X} \). In particular, \(Q_{j}\in [Q_{j}]^* \) for each \(j\). If \(j\ge 2\), then (11.4) implies that \([Q_{j}]{\preceq }\mathsf {C}_{j}\), and Lemma 11.6 implies that \( [Q_{j}]^* {\subset } \mathsf {C}_{j}^* \). Hence \(Q_{j}\in [Q_{j}]^* {\subset } \mathsf {C}_{j}^* \). \(\square \)
Corollary 11.17
If \( \mathcal {D} \subset \varvec{\mathcal {P}}( {X} ) \) is countable, then \( {{\mathbf {\mathsf{{R}}}}}( \mathcal {D} ) \) and \( {{\mathbf {\mathsf{{A}}}}}( \mathcal {D} ) \) are countable.
Proposition 11.18
If \(\mathcal {Q}\subset \varvec{\mathcal {P}}( {X} ) \) is a countable algebra in \( {X} \), then there exists a net \({{\mathbf {\mathsf{{c}}}}}\) in \( {X} \) such that \(\mathcal {Q}= \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}^*\)
Theorem 11.19
If \(( {X} ,\varvec{\mathcal {S}})\) is a measurable space, where \(\varvec{\mathcal {S}}\) is a \(\sigma \)-algebra of subsets of the space \( {X} \), then the following conditions are equivalent:
- (1):
-
\(\varvec{\mathcal {S}}\) is countably generated.
- (2):
-
\(\varvec{\mathcal {S}}\) is the \(\sigma \)-algebra generated by a net, i.e., there exists a net \({{\mathbf {\mathsf{{c}}}}}\) with \( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}\subset \varvec{\mathcal {S}}\) and \(\sigma ( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}})=\varvec{\mathcal {S}}\).
1.5 Density Results
If \(\mathcal {C}\subset \varvec{\mathcal {P}}( {X} ) \) is nonempty, then \(\mathbb {R}[\mathcal {C}] \subset \mathbb {R}^{ {X} } \quad ({\mathbb Q}[\mathcal {C}] \subset \mathbb {R}^{ {X} })\) denotes the collection of finite linear combinations with real (rational, resp.) coefficients of functions of the form \(1_{Q}\), where \(Q\in \mathcal {C}\). Observe that \(\mathbb {R}[\mathcal {C}]\) and \({\mathbb Q}[\mathcal {C}]\) are vector spaces.
Proposition 11.20
If \(\mathcal {C}\subset \varvec{\mathcal {P}}( {X} ) \) is a semiring, then
-
1.
Each function in \(\mathbb {R}[\mathcal {C}]\) may be written as a finite linear combination of indicator functions of disjoint elements of \(\mathcal {C}\).
-
2.
If \(\mathrm{f}\in \mathbb {R}[\mathcal {C}]\), then \(|\mathrm{f}|\in \mathbb {R}[\mathcal {C}]\).
-
3.
\(\mathbb {R}[\mathcal {C}]=\mathbb {R}[ \mathcal {C}^* ]\).
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a probability space, where \(\varvec{\mathcal {S}}\) is a \(\sigma \)-algebra of subsets of \( {X} \) and \(\omega \) is a measure on \(\varvec{\mathcal {S}}\), and \(\mathcal {D}\subset \varvec{\mathcal {S}}\), the \(\omega \)-closure in measure in \(\varvec{\mathcal {S}}\) of \(\mathcal {D}\) is the collection:
Observe that
and that
We say that \(\mathcal {D}\) is dense in measure in \((\varvec{\mathcal {S}},\omega )\) if \(\varvec{\mathcal {S}}= {CL} _{\varvec{\mathcal {S}}}^{\omega }\{\mathcal {D}\} \). A probability space \(( {X} ,\varvec{\mathcal {S}},\omega )\) is said to be separable in measure if there exists a countable subset \(\mathcal {D}\subset \varvec{\mathcal {S}}\) which is dense in measure in \((\varvec{\mathcal {S}},\omega )\).
The definition of separability given above only applies to measure spaces of finite measure: A slightly different definition (of which Proposition 11.23 gives a hint) is required for measure spaces of possibly infinite measure. If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a measure space, we denote by \(\varvec{\mathcal {S}}\cap L^1\) the collection of sets in \(\varvec{\mathcal {S}}\) which have finite measure. Hence \(\varvec{\mathcal {S}}\cap L^1\subset \varvec{\mathcal {S}}\), and \(\mathbb {R}[\varvec{\mathcal {S}}\cap L^1]\) is the collection of finite linear combinations of functions of the form \(1_{Q}\), where \(Q\in \varvec{\mathcal {S}}\) has finite measure. If \(\omega ( {X} )<\infty \) then \(\varvec{\mathcal {S}}\cap L^1=\varvec{\mathcal {S}}\). Observe that \(\varvec{\mathcal {S}}\cap L^1\) is a ring but not an algebra, unless \(\omega ( {X} )<\infty \). A measure space \(( {X} ,\varvec{\mathcal {S}},\omega )\) is separable in measure if there exists a countable collection \( \mathcal {D} \subset \varvec{\mathcal {S}}\cap L^1\) such that for each \(Q\in \varvec{\mathcal {S}}\cap L^1\), \({\inf \{ \omega (Q\triangle R):R\in \mathcal {D} \}=0}\).
Proposition 11.21
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a measure space, then \(\mathbb {R}[\varvec{\mathcal {S}}\cap L^1]\) is dense in \(L^1\).
Proof
[63, p. 176] \(\square \)
Corollary 11.22
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a measure space and \((\varvec{\mathcal {S}},\omega )\) is separable in measure, then \(L^1( {X} )\) is separable as a metric space.
Proposition 11.23
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a measure space and \(\mathcal {C}\subset \varvec{\mathcal {S}}\cap L^1\) is a semiring, then the following conditions are equivalent:
- (1):
-
\( \mathcal {C}^* \) is dense in \(\varvec{\mathcal {S}}\cap L^1\), i.e., for each \(Q\in \varvec{\mathcal {S}}\cap L^1\), \(\inf \{\omega (Q\triangle R): R\in \mathcal {C}^* \}=0\).
- (2):
-
\(\mathbb {R}[\mathcal {C}]\) is dense in \(L^1( {X} )\).
Proof
If (1) holds, Proposition 11.21 implies that in order to prove that \(\mathbb {R}[\mathcal {C}]\) is dense in \(L^1( {X} )\), it suffices to show that \(\mathbb {R}[\varvec{\mathcal {S}}\cap L^1]\) is contained in the closure of \(\mathbb {R}[\mathcal {C}]\) in the topology of \(L^1\). This fact follows at once from the hypothesis and from (11.8), since Proposition 11.20 implies that \(\mathbb {R}[ \mathcal {C}^* ]=\mathbb {R}[\mathcal {C}]\).
If (2) holds, let \(Q\in \varvec{\mathcal {S}}\cap L^1\) and \(\epsilon >0\). Then there exists a sequence of functions \(g_{j}\in \mathbb {R}[\mathcal {C}]\) which converges to \(1_{Q}\) in \(L^1\). Each function \(g_{j}\) may be written as \(g_{j}=\sum _{j=1}^{n}c_j1_{A_j}, \, c_j\in \mathbb {R}, A_j\in \mathcal {C}, \, \text { the sets } A_j\text { are disjoint}\). We may assume, without loss of generality that for each \({j}\) at least one coefficient \(c_j\) satisfies the condition \(c_j\ge \frac{1}{2}\), for otherwise, it would impossible for \(g_{j}\) to be close to \(1_{Q}\) in the \(L^1\) norm. Hence the set \(Q_{j}{\mathop {=}\limits ^{\mathrm{def}}}\{q\in {X} :g_{j}(q)\ge 1/2\}\) is nonempty for each \({j}\). Observe that
since \(Q_{j}\) is union of some of the sets \(A_j\). Observe that \(Q\triangle Q_{j} {\subset } \left\{ | 1_{Q} -g_{j}|\ge {1}/{2}\right\} \). Indeed, if \(q\in Q\triangle Q_{j}\), then either \(q\in Q\setminus Q_{j}\) (and in this case the expression in the right-hand side is equal to \(1-g_{j}(q)\ge 1/2\), since \(g_{j}(q)<1/2\)), or \(q\in Q_{j}\setminus Q\) (and in this case, the expression in the right-hand side is equal to \(g_{j}(q)\ge 1/2\)). It follows that
There exists n such that, if \(k>n\), the right-hand side of (11.10) is smaller than \(\epsilon \). Now, apply (11.9). \(\square \)
If one of the conditions of Proposition 11.23 holds, \(\mathcal {C}\) is called a determining semiring in \((\varvec{\mathcal {S}},\omega )\).
Lemma 11.24
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a probability space and \(\mathcal {D}\subset \varvec{\mathcal {S}}\) is an algebra, then \( {CL} _{\varvec{\mathcal {S}}}^{\omega }\{\mathcal {D}\} \) is a \(\sigma \)-algebra.
Proof
In order to show that \( {CL} _{\varvec{\mathcal {S}}}^{\omega }\{\mathcal {D}\} \) is closed under finite unions and complements, it suffices to apply the relations \(Q\triangle R= ( {X} \setminus Q)\triangle ( {X} \setminus R)\) and \( (Q_1\cup Q_2) \triangle (R_1\cup R_2) \subset (Q_1\triangle R_1) \cup (Q_2\triangle R_2)\), and the hypothesis that \(\mathcal {D}\) is an algebra. Assume that, for each \(j\in \mathbb {N}\), \(Q_k\in {CL} _{\varvec{\mathcal {S}}}^{\omega }\{\mathcal {D}\} \), and let \(Q{\mathop {=}\limits ^{\mathrm{def}}}\bigcup _{j\in \mathbb {N}}Q_k\). We may assume, without loss of generality that the sets \(Q_k\) are disjoint. Let \(Q^{-}(n){\mathop {=}\limits ^{\mathrm{def}}}\bigcup _{j=1}^{n}Q_{j}\) and \(Q^{+}(n){\mathop {=}\limits ^{\mathrm{def}}}\bigcup _{j=n+1}^{\infty }Q_{j}\) Hence given \(\epsilon >0\), there exists \(n\in \mathbb {N}\) such that \( { \sum _{j=n+1}^{\infty } \omega (Q_{j})<\epsilon }\). Since \(Q^{-}(n) \in {CL} _{\varvec{\mathcal {S}}}^{\omega }\{\mathcal {D}\} \), there exists \(R\in \mathcal {D}\) such that \(\omega (R\triangle Q^{-}(n))<\epsilon \). Hence \(\omega (R\triangle Q)<2\epsilon \) follows from the fact that \({ R\triangle Q\subset (R\triangle Q^{-}(n)) \cup (Q^{+}(n))}\). \(\square \)
Theorem 11.25
If \(\mathcal {C}\subset \varvec{\mathcal {P}}( {X} ) \), then \({\sigma (\mathcal {C}) {\subset } {CL} _{\varvec{\mathcal {S}}}^{\omega }\{ {{\mathbf {\mathsf{{A}}}}}(\mathcal {C}) \} }\).
Corollary 11.26
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a probability space and \({{\mathbf {\mathsf{{c}}}}}\) is a net in \( {X} \), then \(\sigma ( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}})\subset {CL} _{\varvec{\mathcal {S}}}^{\omega }\{ \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}^*\} \).
Corollary 11.27
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a probability space and \(\varvec{\mathcal {S}}\) is countably generated, then \((\varvec{\mathcal {S}},\omega )\) is separable in measure.
1.6 Amenable Nets, Maximal Operators, and Martingales
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a probability space, a finite partition of \( {X} \) is called measurable if all of its tiles are measurable. It is called amenable if all of its tiles are measurable and have strictly positive measure. A measurable net (amenable net) in a probability space \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a net \({{\mathbf {\mathsf{{c}}}}}\) in \( {X} \) such that each partition of \({{\mathbf {\mathsf{{c}}}}}\) is measurable (amenable, resp.). If \({{\mathbf {\mathsf{{c}}}}}\) is a measurable net in \(( {X} ,\varvec{\mathcal {S}},\omega )\), then \(\mathbb {R}[ \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}]\subset L^1( {X} )\). Theorem 11.14 implies that \(\{\emptyset \}\cup \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}\) is a countable semiring, and \( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}^*= {{\mathbf {\mathsf{{A}}}}}( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}) \) is a countable algebra contained in \(\varvec{\mathcal {S}}\). We say that a measurable net \({{\mathbf {\mathsf{{c}}}}}\) is dense in measure in \((\varvec{\mathcal {S}},\omega )\) if \( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}^*\) is dense in measure in \((\varvec{\mathcal {S}},\omega )\).
Proposition 11.28
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a measure space, and \(L^1( {X} )\) is separable, then
- (1):
-
\((\varvec{\mathcal {S}},\omega )\) is separable in measure.
- (2):
-
If \(\omega ( {X} )<\infty \), then there exists a measurable net in \( {X} \) which is dense in measure in \((\varvec{\mathcal {S}},\omega )\).
Proof
We first prove (1). Let \({\{f_k\}}_k\) be dense in \(L^1( {X} )\). Since \(\mathbb {R}[\varvec{\mathcal {S}}\cap L^1]\) is dense in \(L^1( {X} )\), for each \(j\in \mathbb {N}\), there is a sequence \({\{\varphi _{(k,j)}\}}_{k\in \mathbb {N}}\) with \(\varphi _{(k,j)}\in \mathbb {R}[\varvec{\mathcal {S}}\cap L^1]\) such that \({\lim _{k\rightarrow +\infty }\int _{ {X} }|f_{k}- \varphi _{(k,j)} |\,\mathrm{d}~\omega =0}\). Each function \(\varphi _{(k,j)}\) may be written as a finite linear combination of functions of the form \(1_{Q}\), \(Q\in L(j,k)\), where \(L(j,k)\subset \varvec{\mathcal {S}}\cap L^1\) and the set L(j, k) is finite. Let \({ \mathcal {D} {\mathop {=}\limits ^{\mathrm{def}}}\bigcup _{j,k}L(j,k)}\). Then \( \mathcal {D} \) is countable and \( \mathcal {D} \subset \varvec{\mathcal {S}}\cap L^1\). Since \(\varvec{\mathcal {S}}\cap L^1\) is a ring, \( {{\mathbf {\mathsf{{R}}}}}( \mathcal {D} ) \subset \varvec{\mathcal {S}}\cap L^1\). Lemma 11.17 implies that \( {{\mathbf {\mathsf{{R}}}}}( \mathcal {D} ) \) is countable. Thus, \({\{\varphi _{(k,j)}:j,k\in \mathbb {N}\} \subset \mathbb {R}[ \mathcal {D} ] \subset \mathbb {R}[ {{\mathbf {\mathsf{{R}}}}}( \mathcal {D} ) ] \subset \mathbb {R}[\varvec{\mathcal {S}}\cap L^1]}\). Hence \(\mathbb {R}[ {{\mathbf {\mathsf{{R}}}}}( \mathcal {D} ) ]\) is dense in \(L^1( {X} )\), and Proposition 11.23 (applied to \(\mathcal {C}= {{\mathbf {\mathsf{{R}}}}}( \mathcal {D} ) \)) implies that \( {{\mathbf {\mathsf{{R}}}}}( \mathcal {D} ) ^* = {{\mathbf {\mathsf{{R}}}}}( \mathcal {D} ) \) is dense in measure in \((\varvec{\mathcal {S}},\omega )\).
Under the hypothesis of (2), \(\varvec{\mathcal {S}}\cap L^1=\varvec{\mathcal {S}}\), and, as in (1), we obtain a countable collection \( \mathcal {D} \) with \( \mathcal {D} \subset \varvec{\mathcal {S}}\) and \(\mathbb {R}[ \mathcal {D} ]\) dense in \(L^1( {X} )\). Lemma 11.16 implies that there exists a net \({{\mathbf {\mathsf{{c}}}}}={\{\mathsf {C}_{j}\}}_{j\in \mathbb {N}}\) such that \( \mathcal {D} \subset { \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}}^*\) and \( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}\subset {{\mathbf {\mathsf{{A}}}}}( \mathcal {D} ) \subset \varvec{\mathcal {S}}\) (since \(\varvec{\mathcal {S}}\) is an algebra, because \(\omega ( {X} )<\infty \)). Hence \( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}\subset \varvec{\mathcal {S}}\). It follows that \({\{\varphi _{(k,j)}:j,k\in \mathbb {N}\} \subset \mathbb {R}[ \mathcal {D} ] \subset \mathbb {R}[ \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}^*] = \mathbb {R}[ \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}]}\). Hence \(\mathbb {R}[ \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}]\) is dense in \(L^1\), and Proposition 11.23 implies that \( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}^*\) is dense in \(\varvec{\mathcal {S}}\). \(\square \)
Corollary 11.29
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a measure space, then \(L^1( {X} )\) is separable as a metric space if and only if \((\varvec{\mathcal {S}},\omega )\) is separable in measure.
Consider the following conditions, which a probability space \(( {X} ,\varvec{\mathcal {S}},\omega )\) may or may not satisfy:
- (CG.1):
-
\(\varvec{\mathcal {S}}\) is countably generated.
- (CG.2):
-
There exists a measurable net \({{\mathbf {\mathsf{{c}}}}}\) in \( {X} \) such that \(\sigma ( \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}})=\varvec{\mathcal {S}}\).
- (S.1):
-
\((\varvec{\mathcal {S}},\omega )\) is separable in measure.
- (S.2):
-
There exists an amenable net \({{\mathbf {\mathsf{{c}}}}}\) in \(( {X} ,\varvec{\mathcal {S}})\) which is dense in measure in \((\varvec{\mathcal {S}},\omega )\).
- (S.3):
-
There exists a measurable net \({{\mathbf {\mathsf{{c}}}}}\) in \(( {X} ,\varvec{\mathcal {S}})\) which is dense in measure in \((\varvec{\mathcal {S}},\omega )\).
- (S.4):
-
There exists a measurable net \({{\mathbf {\mathsf{{c}}}}}\) in \(( {X} ,\varvec{\mathcal {S}})\) such that \(\mathbb {R}[ \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}]\) is dense in \(L^1( {X} )\).
- (S.5):
-
\(L^1( {X} )\) is separable as a metric space.
Theorem 11.30
The conditions described above satisfy the following hierarchy:
If \({{\mathbf {\mathsf{{c}}}}}={\{\mathsf {C}_{j}\}}_{j\in \mathbb {N}}\) is an amenable net in a probability space \(( {X} ,\varvec{\mathcal {S}},\omega )\), then the maximal operator \({{\mathbf {\mathsf{{c}}}}}_*\) associated to \({{\mathbf {\mathsf{{c}}}}}\) is defined by

where \(f\in L^1\) and \(q\in {X} \). Lemma 11.15 implies at once the following result.
Proposition 11.31
If \({{\mathbf {\mathsf{{c}}}}}\) is an amenable net in a probability space \(( {X} ,\varvec{\mathcal {S}},\omega )\), then \({{\mathbf {\mathsf{{c}}}}}_*\) is of weak type (1, 1).
Proposition 11.31 also holds for measurable (not necessarily amenable) nets, by a slight modification of the definition given in (11.11). We will now dwell on this issue since we prove that the existence of a dense measurable net is equivalent to the existence of an amenable net, and that both follow from the hypothesis that \((\varvec{\mathcal {S}},\omega )\) is separable in measure. If \({{\mathbf {\mathsf{{c}}}}}\) is an amenable net in a probability space \(( {X} ,\varvec{\mathcal {S}},\omega )\), \(\mathrm{f}\in L^1( {X} )\), and \(q\in {X} \), we define, for each \(j\in \mathbb {N}\)

Lemma 11.32
If \({{\mathbf {\mathsf{{c}}}}}\) is a net in the probability space \(( {X} ,\varvec{\mathcal {S}},\omega )\), then for each \(\mathrm{f}\in L^1( {X} )\), the collection \({\{{{\mathbf {\mathsf{{c}}}}}_{j}\mathrm{f}\}}_{j}\) is uniformly integrable.
Theorem 11.33
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a probability space for which at least one of the following conditions holds:
- (CG):
-
\((\varvec{\mathcal {S}},\omega )\) is countably generated.
- (S):
-
\((\varvec{\mathcal {S}},\omega )\) is separable in measure.
and if \({{\mathbf {\mathsf{{c}}}}}\) is an amenable net which is dense in measure in \((\varvec{\mathcal {S}},\omega )\), then for each \(f\in \mathcal {L}^1( {X} )\)
and
Proof
Observe that Theorem 11.30 says that \({\mathbf{(CG)}}\) implies \({\mathbf{(S)}}\). Hence we assume \({\mathbf{(S)}}\), which is the weaker hypothesis. If \(f\in \mathbb {R}[ \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}]\), then there is \(j_0\) such that
hence
Proposition 11.23 implies that \(\mathbb {R}[ \mathcal {T} _{{{\mathbf {\mathsf{{c}}}}}}]\) is dense in \(L^1( {X} )\). Hence (11.12) follows from (11.14), coupled with Proposition 11.31, by the standard method. Lemma 11.32 and (11.12) imply (11.13), by Vitali’s theorem [182]. \(\square \)
In the following two sections, we show that each of the two hypotheses of Theorem 11.33 separately implies the existence of an amenable net which is dense in measure.
1.7 On the Existence of Amenable and Dense Nets (I)
Through this section, \(( {X} ,\varvec{\mathcal {S}},\omega )\) denotes a probability space and \( \mathcal {D} \subset \varvec{\mathcal {S}}\) denotes a nonempty collection of measurable sets. We know from Corollary 11.10 that, for each finite \(\sigma \)-algebra \(\varvec{\mathcal {S}}\) in \( {X} \), there exists a finite partition \(\mathsf {C}\) of \( {X} \) such that \(\varvec{\mathcal {S}}=\mathsf {C}^*\). Something more can be said. Recall that the subsets \(Q,R\in \varvec{\mathcal {S}}\) are a.e. equal, if the quantity
is equal to 0. We then write  .
.
Lemma 11.34
For each \(Q_1,Q_2,Q_3\in \varvec{\mathcal {S}}\)
and
Lemma 11.35
If \(Q,R\in \varvec{\mathcal {S}}\) and  , then \(\omega (Q)=\omega (R)\).
, then \(\omega (Q)=\omega (R)\).
Proof
Apply (11.16) and observe that \({|\omega (Q)-\omega (R)| \le d_{\omega }(Q,R)=0}\) implies that \(\omega (Q)=\omega (R)\). \(\square \)
Proposition 11.36
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a probability space and \( \mathcal {D} \) is a finite subset of \(\varvec{\mathcal {S}}\) such that \(\sigma ( \mathcal {D} )=\varvec{\mathcal {S}}\), then
- (1):
-
there exists an amenable finite partition \(\mathsf {C}\) of \( {X} \) whose algebra \(\mathsf {C}^*\) is dense in measure in \(\varvec{\mathcal {S}}\).
- (2):
-
there exists an amenable net in \(( {X} ,\varvec{\mathcal {S}},\omega )\) which is dense in measure in \((\varvec{\mathcal {S}},\omega )\).
Proof
(2) follows from (1), since the net whose partitions are all equal to the partition obtained in (1) satisfies (2). In order to prove (1), let \(\mathsf {C}\) be the partition obtained in Corollary 11.10. In general, it is neither true that this partition is amenable, nor that there is an amenable partition \(\mathsf {C}\) such that \(\mathsf {C}^*=\varvec{\mathcal {S}}\). If \(\mathsf {C}\) is amenable, then it satisfies (1), since \(\mathsf {C}^*\) is equal to \(\varvec{\mathcal {S}}\). If \(\mathsf {C}\) is not amenable, assume that \(\mathsf {C}=\{Q_1,Q_2,\ldots ,Q_k, Q_{k+1},\ldots ,Q_{k+n}\}\), where \(Q_1,Q_2,\ldots ,Q_k\) are the only null sets of \(\mathsf {C}\). Define the partition \(\mathsf {D}\) as \(\mathsf {D}{\mathop {=}\limits ^{\mathrm{def}}}\{R_1,R_2,\ldots ,R_n\}\) where \(R_1{\mathop {=}\limits ^{\mathrm{def}}}Q_1\cup Q_2\cup \ldots \cup Q_k\cup Q_{k+1}\) and \(R_{j}=Q_{k+j}\) for \(2\le {}j\le {}n\). Then \(\mathsf {D}\) is an amenable partition of \( {X} \). Observe that \(\mathsf {D}^*\subsetneq \mathsf {C}^*=\varvec{\mathcal {S}}\). We claim that \(\mathsf {D}^*\) is dense in measure in \(\varvec{\mathcal {S}}\). Hence \(\mathsf {D}\) satisfies (1). In order to prove the claim, observe that if \(Q\in \varvec{\mathcal {S}}\) is a null set, then  and \(\emptyset \in \mathsf {D}^*\). Let \(Q\in \varvec{\mathcal {S}}\) and assume that it is not a null set. Since \(\varvec{\mathcal {S}}=\mathsf {C}^*\), there exists sets \(R\in {\{Q_1,Q_2,\ldots ,Q_k\}}^*\), \(Z\in {\{Q_{k+1}\}}^*\), \(T\in {\{Q_{k+2},\ldots ,Q_{k+n}\}}^*\), with \(Z\cup T\not =\emptyset \), such that \(Q=R\cup Z\cup T\). If \(Z=\emptyset \), then \(T\in \mathsf {D}^*\) and
and \(\emptyset \in \mathsf {D}^*\). Let \(Q\in \varvec{\mathcal {S}}\) and assume that it is not a null set. Since \(\varvec{\mathcal {S}}=\mathsf {C}^*\), there exists sets \(R\in {\{Q_1,Q_2,\ldots ,Q_k\}}^*\), \(Z\in {\{Q_{k+1}\}}^*\), \(T\in {\{Q_{k+2},\ldots ,Q_{k+n}\}}^*\), with \(Z\cup T\not =\emptyset \), such that \(Q=R\cup Z\cup T\). If \(Z=\emptyset \), then \(T\in \mathsf {D}^*\) and  . If \(Z\not =\emptyset \) let \(Q^{\prime }{\mathop {=}\limits ^{\mathrm{def}}}R_1\cup T\). Then \(Q^{\prime }\in \mathsf {D}^*\) and
. If \(Z\not =\emptyset \) let \(Q^{\prime }{\mathop {=}\limits ^{\mathrm{def}}}R_1\cup T\). Then \(Q^{\prime }\in \mathsf {D}^*\) and  . \(\square \)
. \(\square \)
Under the hypothesis of Proposition 11.36, it is not necessarily the case that there exists an amenable partition \(\mathsf {C}\) such that \(\varvec{\mathcal {S}}=\mathsf {C}^*\). The conclusion of Proposition 11.36 also holds under a weaker hypothesis.
Theorem 11.37
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a probability space and \( \mathcal {D} \) is a finite subset of \(\varvec{\mathcal {S}}\) which is dense in measure in \((\varvec{\mathcal {S}},\omega )\), then
- (1):
-
there exists an amenable finite partition \(\mathsf {C}\) of \( {X} \) whose algebra \(\mathsf {C}^*\) is dense in measure in \(\varvec{\mathcal {S}}\).
- (2):
-
there exists an amenable net in \(( {X} ,\varvec{\mathcal {S}},\omega )\) which is dense in measure in \((\varvec{\mathcal {S}},\omega )\).
Observe that if the hypothesis of Proposition 11.36 is satisfied, then the hypothesis of Theorem 11.37 is also satisfied. Indeed, if \(\varvec{\mathcal {S}}=\sigma ( \mathcal {D} )\) and \( \mathcal {D} \) is finite, then \(\varvec{\mathcal {S}}\) is finite, and \( {CL} _{\varvec{\mathcal {S}}}^{\omega }\{\varvec{\mathcal {S}}\} =\varvec{\mathcal {S}}\). In fact, the proof of the former result, based on a stronger hypothesis, is simpler than the proof of the latter, which we will give in the following section. Theorem 11.37 is contained in Theorem 11.49 below. We find it useful to prove it separately, since in so doing, we will introduce results and notions that are needed in the proof of the more general result, and which have independent interest. The proof of Theorem 11.49 will be given at the end of this section, after we introduce some preliminary results and notions which have independent interest. If \(\mathcal {C}\subset \varvec{\mathcal {S}}\), we define \(\widetilde{\mathcal {C}}{\mathop {=}\limits ^{\mathrm{def}}}\{Q\in \mathcal {D} :0<\omega (Q)<1\}\) and say that \(( {X} ,\varvec{\mathcal {S}},\omega )\) is trivial if \(\widetilde{\varvec{\mathcal {S}}}=\emptyset \). In order to prove (1) in Theorem 11.37, we introduce the following notion. An \(\omega \) atom of \((\varvec{\mathcal {S}},\omega )\) is a set \(Q\in \varvec{\mathcal {S}}\) such that
where \(\omega (R|Q){\mathop {=}\limits ^{\mathrm{def}}}\frac{\omega (R\cap Q)}{\omega (Q)}\). Observe that \(Q\in \varvec{\mathcal {S}}\) is an \(\omega \) atom if and only if

Cf. (4.1). Hence either \(Q\) is a.e. disjoint from \(R\) (if  ), or \(Q\) is a.e. contained in \(R\) (if \( Q\subset _{\omega }R \)).
), or \(Q\) is a.e. contained in \(R\) (if \( Q\subset _{\omega }R \)).
We denote by \( {{\mathsf {Atoms}}_{\omega } }\) the collection of all \(\omega \) atoms of \(( {X} ,\varvec{\mathcal {S}},\omega )\). Observe that
Lemma 11.38
If \(Q_1\) and \(Q_2\) are \(\omega \) atoms, then the following conditions are equivalent:
- (1):
-
\(Q_1\) and \(Q_2\) are not a.e. equal.
- (2):
-
\(Q_1\) and \(Q_2\) are a.e. disjoint.
Lemma 11.39
If \( \mathcal {D} \) is finite and dense in measure in \((\varvec{\mathcal {S}},\omega )\), then for each \(Q\in \varvec{\mathcal {S}}\), there exists \(Q^{\prime }\in \mathcal {D} \) such that  and \(\omega (Q^{\prime })=\omega (Q)\).
and \(\omega (Q^{\prime })=\omega (Q)\).
Lemma 11.40
If  and
and  , where \(Q_1\), \(Q_2\), \(R_1\), \(R_2\) belong to \(\varvec{\mathcal {S}}\), then
, where \(Q_1\), \(Q_2\), \(R_1\), \(R_2\) belong to \(\varvec{\mathcal {S}}\), then
- (1):
-
For each \(R\in \varvec{\mathcal {S}}\),
 .
. - (2):
-
For each \(R\in \varvec{\mathcal {S}}\), \(\omega (\,R|Q_1) =\omega (\,R|Q_2)\) provided that \(\omega (Q_1)>0\).
- (3):
-
For each \(Q\in \varvec{\mathcal {S}}\), \(\omega (\,R_1|Q)=\omega (\,R_2|Q)\) provided that \(\omega (Q)>0\).
- (4):
-
 .
.
Corollary 11.41
- (1):
-
If \(Q_1\) is an \(\omega \) atom and
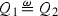 , then \(Q_2\) is an \(\omega \) atom.
, then \(Q_2\) is an \(\omega \) atom. - (2):
-
If \( \mathcal {D} \) is finite and dense in measure in \((\varvec{\mathcal {S}},\omega )\) and if \( {{\mathsf {Atoms}}_{\omega } }\not =\emptyset \) then \( \mathcal {D} \cap {{\mathsf {Atoms}}_{\omega } }\not =\emptyset \).
Lemma 11.42
If \( \mathcal {D} \) is finite and dense in measure in \((\varvec{\mathcal {S}},\omega )\), then, for every set \(T\in \varvec{\mathcal {S}}\) that is not an \(\omega \)-atom and which has positive measure,
- (1):
-
there exists \(R\in \mathcal {D} \) such that
$$\begin{aligned} \omega (T|R)=1 \text { and } 0<\omega (R)<\omega (T); \end{aligned}$$(11.21) - (2):
-
there exists \(R\in \mathcal {D} \) such that
$$\begin{aligned} \omega (T|R)=1, \, 0<\omega (R)<\omega (T), \, \text {and } R\text { is an } \omega \text { atom}. \end{aligned}$$(11.22)
Proof
Since \(T\) is not an \(\omega \) atom, there exists a set \(Z\in \varvec{\mathcal {S}}\) such that \({0<\omega (Z|T)<1}\). This means that \(0<\omega (Z\cap T) <\omega (T)\). Lemma 11.39 implies that there exists \(R\in \mathcal {D} \) such that  and \(\omega (R) =\omega (Z\cap T)\). Hence \(0<\omega (R)<\omega (T)\). Lemma (11.40) implies that \(\omega (T|R) = \omega (T|Z\cap T)=1\).
and \(\omega (R) =\omega (Z\cap T)\). Hence \(0<\omega (R)<\omega (T)\). Lemma (11.40) implies that \(\omega (T|R) = \omega (T|Z\cap T)=1\).
In order to prove (2), it suffices to apply (1) and observe that, since \( \mathcal {D} \) is finite, the selection process in (1) cannot continue indefinitely and when it stops we have reached an \(\omega \) atom. \(\square \)
Proposition 11.43
If \( \mathcal {D} \) is finite and dense in measure in \((\varvec{\mathcal {S}},\omega )\), then \( {{\mathsf {Atoms}}_{\omega } }\not =\emptyset \).
In view of the importance of Proposition 11.43, we give two proofs, one of which is constructive.
Proof
First proof. Apply Lemma 11.42 to \( {X} \). Then (2) in Lemma 11.42 yields the result.
Second proof. If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is trivial, then \( {X} \) is an \(\omega \) atom of \(( {X} ,\varvec{\mathcal {S}},\omega )\): Cf. (11.20). If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is not trivial, then let \(Q_{\diamondsuit }\) be an element of \(\widetilde{ \mathcal {D} }\) of minimal measure, i.e., \(\omega (Q_{\diamondsuit })\le \omega (Q)\) for each \(Q\in \widetilde{ \mathcal {D} }\). We claim that \(Q_{\diamondsuit }\) is an \(\omega \)-atom. Indeed, if \(Q_{\diamondsuit }\) were not an \(\omega \)-atom, the statement in (1) in Lemma 11.42 would imply the existence of a set \(R\in \widetilde{ \mathcal {D} }\), such that \(0<\omega (R)<\omega (Q_{\diamondsuit })\), which is incompatible with the choice of \(Q_{\diamondsuit }\). \(\square \)
If \(R\subset {X} \) is measurable, an a.e. partition of \(R\) is a finite collection \(\mathcal {C}\subset \varvec{\mathcal {S}}\) of sets that are pairwise a.e. disjoint, and such that the set \(\bigcup _{Q\in \mathcal {C}}Q\) is a.e. equal to \(R\). An a.e. partition is called amenable if all its elements have strictly positive measure. It is called \(\varvec{\omega }\)-atomic if all its elements are \(\omega \)-atoms. The rank of an a.e. partition \(\mathcal {C}\) is the number of elements of \(\mathcal {C}\).
Lemma 11.44
If \( \mathcal {D} \) is finite and dense in measure in \((\varvec{\mathcal {S}},\omega )\), then there exists an a.e.-partition \(\mathcal {C}\) of \( {X} \) which is \(\omega \) atomic, and \(\mathcal {C}\subset \mathcal {D} \cap {{\mathsf {Atoms}}_{\omega } }\).
Proof
We partition \( \mathcal {D} \cap {{\mathsf {Atoms}}_{\omega } }\) into equivalence classes according to the equivalence relation  and form \(\mathcal {C}\) by selecting one element from each equivalence class. Lemma 11.38 implies that the sets in the collection \(\mathcal {C}\) obtained in this way are pairwise a.e. disjoint. Observe that if \( {X} \) is an \(\omega \) atom, then \(( {X} ,\varvec{\mathcal {S}},\omega )\) is trivial and \( \mathcal {D} \cap {{\mathsf {Atoms}}_{\omega } }\) only contains sets of full measure, which are pairwise a.e. equal. In this case, \(\mathcal {C}\) contains only one element. If \( {X} \) is not an \(\omega \) atom, then \( \mathcal {D} \) contains at least two elements.
and form \(\mathcal {C}\) by selecting one element from each equivalence class. Lemma 11.38 implies that the sets in the collection \(\mathcal {C}\) obtained in this way are pairwise a.e. disjoint. Observe that if \( {X} \) is an \(\omega \) atom, then \(( {X} ,\varvec{\mathcal {S}},\omega )\) is trivial and \( \mathcal {D} \cap {{\mathsf {Atoms}}_{\omega } }\) only contains sets of full measure, which are pairwise a.e. equal. In this case, \(\mathcal {C}\) contains only one element. If \( {X} \) is not an \(\omega \) atom, then \( \mathcal {D} \) contains at least two elements.
Let \(T\) be the complement in \( {X} \) of the set \(\bigcup _{Q\in \mathcal {C}}Q\). We claim that \(\omega (T)=0\). In order to prove the claim, assume that \(\omega (T)>0\). Then Lemma 11.42 implies the existence of \(R\in {{\mathsf {Atoms}}_{\omega } }\) such that \(\omega (T|R)=1\). Lemma 11.39 and Corollary 11.41 imply that there exists an \(\omega \) atom \(R^{\prime }\in \mathcal {D} \cap {{\mathsf {Atoms}}_{\omega } }\) such that  . Let \(R^{\prime \prime }\) be the element of \(\mathcal {C}\) which is a.e. equal to \(R^{\prime }\). Now, \(R^{\prime \prime }\subset {X} \setminus T\),
. Let \(R^{\prime \prime }\) be the element of \(\mathcal {C}\) which is a.e. equal to \(R^{\prime }\). Now, \(R^{\prime \prime }\subset {X} \setminus T\),  , and \(\omega (T|R)=1\) lead to a contradiction. Hence the set \(\bigcup _{Q\in \mathcal {C}}Q\) is a.e. equal to \( {X} \) \(\square \).
, and \(\omega (T|R)=1\) lead to a contradiction. Hence the set \(\bigcup _{Q\in \mathcal {C}}Q\) is a.e. equal to \( {X} \) \(\square \).
The relevance of a.e. partitions can be gathered from the following two results.
Lemma 11.45
If \(\mathcal {C}\) is an amenable a.e.-partition of \( {X} \) then, for every \(R\in \varvec{\mathcal {S}}\),
Lemma 11.46
If \(\mathcal {C}\) is an amenable a.e.-partition of \( {X} \) and if \(R\in \varvec{\mathcal {S}}\) has the property that for every \(Q\in \mathcal {C}\) the value of \(\omega (R|Q)\) is either 0 or 1, then there exists \(Q\in \mathcal {C}^*\) such that  .
.
Proof
If \(\omega (R|Q)=0\) for each \(Q\in \mathcal {C}\), then (11.23) implies that \(\omega (R)=0\), i.e.,  , and the conclusion holds, since \(\emptyset \in \mathcal {C}^*\). If \(\omega (R)>0\), then (11.23) implies that the set \(\mathcal {C}^{\prime } {\mathop {=}\limits ^{\mathrm{def}}}\{Q:Q\in \mathcal {C}\, \text { and }\omega (R|Q)=1\}\) is nonempty. Our assumption implies that \(\omega (R|Q)=0\) for each \(Q\in \mathcal {C}\setminus \mathcal {C}^{\prime }\). Let \({ Q^{\prime }{\mathop {=}\limits ^{\mathrm{def}}}\bigcup _{Q\in \mathcal {C}^{\prime }}Q}\). Observe that \(Q^{\prime }\in \mathcal {C}^*\). We claim that
, and the conclusion holds, since \(\emptyset \in \mathcal {C}^*\). If \(\omega (R)>0\), then (11.23) implies that the set \(\mathcal {C}^{\prime } {\mathop {=}\limits ^{\mathrm{def}}}\{Q:Q\in \mathcal {C}\, \text { and }\omega (R|Q)=1\}\) is nonempty. Our assumption implies that \(\omega (R|Q)=0\) for each \(Q\in \mathcal {C}\setminus \mathcal {C}^{\prime }\). Let \({ Q^{\prime }{\mathop {=}\limits ^{\mathrm{def}}}\bigcup _{Q\in \mathcal {C}^{\prime }}Q}\). Observe that \(Q^{\prime }\in \mathcal {C}^*\). We claim that  . Indeed, let \(\mathcal {C}^{\prime \prime } {\mathop {=}\limits ^{\mathrm{def}}}\mathcal {C}\setminus \mathcal {C}^{\prime }\), apply (1) and (4) in Lemma 11.40, and observe that \(\omega (R|Q)=0\) implies
. Indeed, let \(\mathcal {C}^{\prime \prime } {\mathop {=}\limits ^{\mathrm{def}}}\mathcal {C}\setminus \mathcal {C}^{\prime }\), apply (1) and (4) in Lemma 11.40, and observe that \(\omega (R|Q)=0\) implies  and \(\omega (R|Q)=1\) implies \( Q\subset _{\omega }R \), i.e.,
and \(\omega (R|Q)=1\) implies \( Q\subset _{\omega }R \), i.e.,  . Hence
. Hence

\(\square \).
Proposition 11.47
If \(\mathcal {C}\) is an \(\omega \) atomic a.e. partition of \( {X} \) then
- (1):
-
For every \(R\in \varvec{\mathcal {S}}\), there exists \(Q\in \mathcal {C}^*\) such that
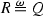 .
. - (2):
-
\(\mathcal {C}^*\) is dense in \((\varvec{\mathcal {S}},\omega )\).
Proposition 11.48
If there exists an amenable a.e. partition \(\mathcal {C}\) of \( {X} \), then there exists an amenable partition \(\mathsf {C}\) of \( {X} \) of the same rank, such that for each \(Q\in \mathcal {C}\), there exists \(R\in \mathsf {C}\) with  .
.
Proof
Let \(\mathcal {C}=\{Q_1,Q_2,\ldots ,Q_n\}\). Define \(\mathsf {C}{\mathop {=}\limits ^{\mathrm{def}}}\{R_1,R_2, \ldots ,R_n\}\) where the tiles \(R_k\) are defined as follows: \(R_1{\mathop {=}\limits ^{\mathrm{def}}}Q_1\), \(R_2{\mathop {=}\limits ^{\mathrm{def}}}Q_2\setminus Q_1\), \(R_3{\mathop {=}\limits ^{\mathrm{def}}}Q_3\setminus (Q_1\cup Q_2)\), \(\ldots \) \(R_{n-1} {\mathop {=}\limits ^{\mathrm{def}}}Q_{n-1}\setminus (\cup _{j=1}^{n-2}Q_{j})\), and
Now, observe that the sets \(R_j\) are disjoint, and that  for each \(j=1,2,\ldots ,n\). \(\square \)
for each \(j=1,2,\ldots ,n\). \(\square \)
Proof of Theorem 11.37
In Lemma 11.44, we proved the existence of an a.e. partition \(\mathcal {C}\) of \( {X} \) which is \(\omega \) atomic. Observe that Proposition 11.47 implies that for every \(R\in \varvec{\mathcal {S}}\), there exists \(Q\in \mathcal {C}^*\) such that  . Proposition 11.48 implies the existence of an amenable partition \(\mathsf {C}\) of \( {X} \) of the same rank as \(\mathcal {C}\) such that for each \(Q\in \mathcal {C}\), there exists \(R\in \mathsf {C}\) with
. Proposition 11.48 implies the existence of an amenable partition \(\mathsf {C}\) of \( {X} \) of the same rank as \(\mathcal {C}\) such that for each \(Q\in \mathcal {C}\), there exists \(R\in \mathsf {C}\) with  . Thus, for every \(R\in \varvec{\mathcal {S}}\), there exists \(Q\in \mathsf {C}^*\) such that
. Thus, for every \(R\in \varvec{\mathcal {S}}\), there exists \(Q\in \mathsf {C}^*\) such that  . Hence (1) in Theorem 11.37 has been proved. Now, (2) follows from (1), since the net \({{\mathbf {\mathsf{{c}}}}}\) of which partitions are all equal to the partition \(\mathsf {C}\) obtained in (1) satisfies the statement in (2). \(\square \)
. Hence (1) in Theorem 11.37 has been proved. Now, (2) follows from (1), since the net \({{\mathbf {\mathsf{{c}}}}}\) of which partitions are all equal to the partition \(\mathsf {C}\) obtained in (1) satisfies the statement in (2). \(\square \)
1.8 On the Existence of Amenable and Dense Nets (II)
Through this section, \(( {X} ,\varvec{\mathcal {S}},\omega )\) denotes a probability space and \( \mathcal {D} \subset \varvec{\mathcal {S}}\) denotes a nonempty collection of measurable sets.
The goal of this section is to present a proof of the following result.
Theorem 11.49
If \(( {X} ,\varvec{\mathcal {S}},\omega )\) is a probability space and \((\varvec{\mathcal {S}},\omega )\) is separable in measure, then there exists an amenable net in \(( {X} ,\varvec{\mathcal {S}},\omega )\) which is dense in measure in \((\varvec{\mathcal {S}},\omega )\).
Recall from Corollary 11.27 that if \(\varvec{\mathcal {S}}\) is countably generated, then \((\varvec{\mathcal {S}},\omega )\) is separable in measure.
In Sect. 11.1, we defined the binary operation \((\mathsf {C}_1,\mathsf {C}_2)\mapsto \mathsf {C}_{1}\vee \mathsf {C}_2\) in the set \(\Pi ( {X} )\) of finite partitions of the set \( {X} \). Unfortunately, this operation may yield partitions which are not amenable, even when \(\mathsf {C}_1\) and \(\mathsf {C}_2\) are amenable. Indeed, it may happen that the partition \(\{R\cap Q,R\setminus Q\}\) of \(R\) is binary but not amenable. Observe that \(\{R\cap Q,R\setminus Q\}\) is a binary and amenable partition of \(R\) if and only if \(0<\omega (Q|R)<1\). Our variant of the \(\vee \) operation preserves amenability and is general enough for our goals.
Let \(\Pi _{\omega }( {X} )\) be the set of amenable partitions of \( {X} \). Recall that \(\widetilde{\varvec{\mathcal {S}}}{\mathop {=}\limits ^{\mathrm{def}}}\{Q:Q\in \varvec{\mathcal {S}}\text { and } 0<\omega (Q)<1\}\).
We define an operation \(\widetilde{\varvec{\mathcal {S}}}\times \Pi _{\omega }( {X} )\rightarrow \Pi _{\omega }( {X} )\) denoted by \((Q,\mathsf {C})\mapsto Q*\mathsf {C}\), as follows. If \(Q\in \widetilde{\varvec{\mathcal {S}}}\) and \(\mathsf {C}\in \Pi _{\omega }( {X} )\), we define \(\mathsf {C}^{\sharp }_{Q} {\mathop {=}\limits ^{\mathrm{def}}}\{ R: R\in \mathsf {C}\text { and } \omega (Q|R)\in (0,1)\}\) and
Hence \(\mathsf {C}^{\sharp }_{Q} \subset \mathsf {C}\) and \(\mathsf {C}^{\prime \prime }_{Q} \subset \mathsf {C}\) are disjoint and \(\mathsf {C}=\mathsf {C}^{\sharp }_{Q}\cup \mathsf {C}^{\prime \prime }_{Q}\). We then define
Lemma 11.50
If \(Q\in \widetilde{\varvec{\mathcal {S}}}\) and \(\mathsf {C}\in \Pi _{\omega }( {X} )\), then

Proof
The first statement in (11.24) is immediate, since each tile in \(Q*\mathsf {C}\) is either a tile of \(\mathsf {C}\) or is obtained from a tile \(R\) of \(\mathsf {C}\) by the binary partition \(\{R\cap Q,R\setminus Q\}\).
First case. \(\mathsf {C}_{Q}^{\sharp }=\emptyset \). Then \(\mathsf {C}_{Q}^{\prime \prime }=\mathsf {C}\) and \(Q*\mathsf {C}=\mathsf {C}\). The fact that \(\mathsf {C}_{Q}^{\sharp }=\emptyset \) means that \(\omega (Q|R)\) is either 0 or 1 for each \(R\in \mathsf {C}\). Lemma 11.46 implies that there exists \(Z\in {\mathsf {C}}^*\) such that  . Since in this case, \(Q*\mathsf {C}=\mathsf {C}\), the proof of (11.24) is complete.
. Since in this case, \(Q*\mathsf {C}=\mathsf {C}\), the proof of (11.24) is complete.
Second case. \(\mathsf {C}_{Q}^{\prime \prime }=\emptyset \). This means that \(0<\omega (Q|R)<1\) for each \(R\in \mathsf {C}\). Hence
Hence \(\mathsf {C}\preceq Q*\mathsf {C}\). Since \({ Q= \bigcup _{R\in \mathsf {C}}Q\cap R}\) and the sets \(R\cap Q\) are tiles of \(Q*\mathsf {C}\), we obtain \(Q\in {(Q*\mathsf {C})}^*\).
Third case. \(\mathsf {C}_{Q}^{\sharp }\not =\emptyset \) and \(\mathsf {C}_{Q}^{\prime \prime }\not =\emptyset \). Consider the sets
Then \({ \mathsf {C}_{Q}^{\prime \prime } = \mathsf {C}_{Q}^{0} \cup \mathsf {C}_{Q}^{1}}\), and \(Q= \bigcup _{R\in \mathsf {C}_{Q}^{\sharp }} Q\cap R\cup \bigcup _{R\in \mathsf {C}_{Q}^{\prime \prime }} Q\cap R= \bigcup _{R\in \mathsf {C}_{Q}^{0}} Q\cap R\cup \bigcup _{R\in \mathsf {C}_{Q}^{1}} Q\cap R\cup \bigcup _{R\in \mathsf {C}_{Q}^{\sharp }} Q\cap R\).
Observe that \(R\in \mathsf {C}_{Q}^{0}\) implies that  , and \(R\in \mathsf {C}_{Q}^{1}\) implies that
, and \(R\in \mathsf {C}_{Q}^{1}\) implies that  . Hence
. Hence

Finally, observe that \( { \bigcup _{R\in \mathsf {C}_{Q}^{1}} R\cup \bigcup _{R\in \mathsf {C}_{Q}^{\sharp }} Q\cap R\in {(Q*\mathsf {C})}^*}\). \(\square \)
Proof of Theorem 11.49
Let \( \mathcal {D} \subset \varvec{\mathcal {S}}\), \( \mathcal {D} \) countable, and \( {CL} _{\varvec{\mathcal {S}}}^{\omega }\{ \mathcal {D} \} =\varvec{\mathcal {S}}\). We may assume, without loss of generality that for every pair \(Q,R\) of distinct sets in \( \mathcal {D} \), \(Q\) is not a.e. equal to \(R\). Indeed, it suffices to partition \( \mathcal {D} \) into equivalence classes under the equivalence relation  and then select one element from each equivalence class. Since \( {X} \) and \(\emptyset \) belong to the algebra of any net, we also assume that \(0<\omega (Q)<1\) for each \(Q\in \mathcal {D} \), by simply removing from \( \mathcal {D} \) the sets \(Q\) for which \(\omega (Q)=0\) or \(\omega (Q)=1\), if any. Let \( \mathcal {D} ={\{Q_k\}}_{k\in \mathbb {N}}\), and define \(\mathsf {C}_1{\mathop {=}\limits ^{\mathrm{def}}}\{Q_1, {X} \setminus Q_1\}\). Observe that \(\mathsf {C}_1\) is an amenable net, since \(0<\omega (Q)<1\), and that \(Q_1\in \mathsf {C}^*\). Then define \(\mathsf {C}_2{\mathop {=}\limits ^{\mathrm{def}}}Q_{2}*\mathsf {C}_1\). Lemma 11.50 implies that \(\mathsf {C}_2\) is amenable and that there exists \(Z_2\in \mathsf {C}_2^*\) such that
and then select one element from each equivalence class. Since \( {X} \) and \(\emptyset \) belong to the algebra of any net, we also assume that \(0<\omega (Q)<1\) for each \(Q\in \mathcal {D} \), by simply removing from \( \mathcal {D} \) the sets \(Q\) for which \(\omega (Q)=0\) or \(\omega (Q)=1\), if any. Let \( \mathcal {D} ={\{Q_k\}}_{k\in \mathbb {N}}\), and define \(\mathsf {C}_1{\mathop {=}\limits ^{\mathrm{def}}}\{Q_1, {X} \setminus Q_1\}\). Observe that \(\mathsf {C}_1\) is an amenable net, since \(0<\omega (Q)<1\), and that \(Q_1\in \mathsf {C}^*\). Then define \(\mathsf {C}_2{\mathop {=}\limits ^{\mathrm{def}}}Q_{2}*\mathsf {C}_1\). Lemma 11.50 implies that \(\mathsf {C}_2\) is amenable and that there exists \(Z_2\in \mathsf {C}_2^*\) such that  , and that \(\mathsf {C}_1\preceq \mathsf {C}_2\). Hence Lemma 11.6 implies that \(\mathsf {C}_1^*\subset \mathsf {C}_2^*\), and therefore, \(Q_1\in \mathsf {C}_2^*\). Repeat the process, and define inductively \(\mathsf {C}_{k}{\mathop {=}\limits ^{\mathrm{def}}}Q_{k}*\mathsf {C}_{k-1}\). Lemma 11.50 implies that, for each \(k\in \mathbb {N}\), \(\mathsf {C}_k\) is amenable , and that there exists a set \(Z_k\in \mathsf {C}_k^*\) such that
, and that \(\mathsf {C}_1\preceq \mathsf {C}_2\). Hence Lemma 11.6 implies that \(\mathsf {C}_1^*\subset \mathsf {C}_2^*\), and therefore, \(Q_1\in \mathsf {C}_2^*\). Repeat the process, and define inductively \(\mathsf {C}_{k}{\mathop {=}\limits ^{\mathrm{def}}}Q_{k}*\mathsf {C}_{k-1}\). Lemma 11.50 implies that, for each \(k\in \mathbb {N}\), \(\mathsf {C}_k\) is amenable , and that there exists a set \(Z_k\in \mathsf {C}_k^*\) such that  . Since the collection \( \mathcal {D} \) is dense in measure in \((\varvec{\mathcal {S}},\omega )\), it follows that \({\bigcup _{k\in \mathbb {N}}\mathsf {C}_k^*}\) is also dense in measure in \((\varvec{\mathcal {S}},\omega )\). Hence \({\{\mathsf {C}_k\}}_{k\in \mathbb {N}}\) is an amenable net which is dense in \((\varvec{\mathcal {S}},\omega )\).
. Since the collection \( \mathcal {D} \) is dense in measure in \((\varvec{\mathcal {S}},\omega )\), it follows that \({\bigcup _{k\in \mathbb {N}}\mathsf {C}_k^*}\) is also dense in measure in \((\varvec{\mathcal {S}},\omega )\). Hence \({\{\mathsf {C}_k\}}_{k\in \mathbb {N}}\) is an amenable net which is dense in \((\varvec{\mathcal {S}},\omega )\).
Summary. Stein never ceased to emphasize that differentiation theorems on the boundary are useful to obtain results on the boundary behavior of functions. A typical example of this fact, which is a precise instance of Abel’s heuristic principle, can be found in Theorem 6.2. A more sophisticated version can be found in [165, p. 33]. The need for differentiation theorems also arises in [32]. Usually, differentiation theorems are obtained using delicate covering theorems, coupled with the doubling condition for the underlying measure. In this appendix, we have proved the differentiation theorems that were stated in Sect. 5.4 (Theorems 5.25 and 5.26), which do not depend on those tools, but only on the standard method of Sect. 5.2.5 and on Lemma 5.10. These differentiation theorems depends on the existence of an amenable net: In this appendix, we proved that amenable nets exist for a large class of measure spaces, which includes those which arise as boundaries of bounded domains. Hence these results have the potential of forming the groundwork for applications to the study of the boundary behavior of holomorphic functions. \(\square \)
Miscellaneous Notes
Section 1. An overview of the history of the Romanian school of Potential theory can be found in [6].
Section 3.3. The quotation from Leibniz (1713) comes from a public letter that Leibniz wrote to Christian Wolff, published in Actorum Eruditorum Supplementa, [107, 108]. The original Latin is transitu a finito ad infinitum simul fiat transitus a disjunctivo [...] ad unum [...] positivum, inter disjuntiva medium. “the passage from finite to infinite is similar to that from an alternative [between two different options] to a definite choice, which is the average between them.”
Section 2.5.8. Recall that it is possible to reconstruct a topology from the knowledge of its convergent (topological) nets (not to be confused with the measure-theoretic nets defined in Sect. 11.6) [87]. If \(\tau _1\) and \(\tau _2\) are topologies on a set \( \mathbf {Y} \), a more stringent condition for a net in \( \mathbf {Y} \) to be convergent in a topology is given by a set-theoretically larger topology: If \(\tau _1\subset \tau _2\), then every \(\tau _2\)-convergent net is also \(\tau _1\) convergent to the same limiting value. Hence if we think of a topology as a sieve which lets only convergent nets pass through, then a (set-theoretically) smaller topology yields a coarser sieve, which lets more nets pass through, and indeed \(\tau _{1}\) is called coarser than \(\tau _2\).
Filters behave contrariwise, since they act on the domain of functions rather than on the codomain. Thus, if \( \Phi _1, \Phi _2\in \mathsf {Filters}( {Y} ) \), a more stringent condition on a filter for a function \(u\in \mathbb {C}^{ {Y} }\) to be convergent along a filter is given by a set-theoretically smaller filter: If \( \Phi _1\subset \Phi _2\), then every function \(u: {Y} \rightarrow \mathbb {C}\) for which \(\lim _{ \Phi _1}u\) exists, the limiting value \(\lim _{ \Phi _2}u\) also exists and is equal to \(\lim _{ \Phi _1}u\). Hence the situation is reversed, and a (set theoretically) smaller filter corresponds to a finer sieve (not to a coarser one). For this reason, keeping in mind that filters associated to broader approach regions are set theoretically smaller, if \( \Phi _1\subset \Phi _2\), we call \( \Phi _1\) broader than \( \Phi _2\), rather than coarser, since the latter terminology would be confusing.
Section 4.4. Calderón’s real-variable proof of the local Fatou theorem of Privalov, with its clever use of a point-of-density argument related to the geometric properties of the sawtooth region (6.8), as well as of its variants, lies at the root of Theorem 4.2 and of its extensions, such as Theorem 7.7. Observe, however, which Calderón’s proof involves harmonic functions, while Theorems 4.2 and 7.7 are valid for any function. Cf. [42, Theorem 2.9], [119,120,121,122]. See also A generalized Local Fatou Theorem by R. Wittmann (unpublished).
Section 5.1. In 1935 [110, p. 93], Paul Levy introduced a technical property (that would now be called a martingale), which he called Condition \((\mathcal {C})\), and that he also used in 1937 [111, Théorèm 68]. In 1936, Jean André Ville introduced the general concept, motivated by the lively dispute about mathematical foundations of probability that was ongoing at that time, where the axioms proposed by R. von Mises, and made more precise by Wald, had been sharply criticized by some of the leading probabilists. Ville had been exposed to Wald’s ideas while participating in Karl Menger’s Vienna Colloquium in 1935, and in 1936 pointed out a flaw in that approach, first in a short note [180, 181] that received little attention, and later in his thesis [180] published in 1939 that immediately caught the attention of Doob, who wrote an enthusiastic and prescient review [48]. Ville used the term martingale as a synonym for système de jeu [gambling strategy], as it had been used in this sense since at least the 18th Century, when Giacomo Casanova, recounting his gambling adventures, wrote the following lines:
Je continuais à jouer à la martingale, mais ce fut avec tant de malheur que je ne tardai pas à me trouver sans un sequin. [I kept playing the martingale but with such a bad luck that I was soon left penniless.]
Further information can be found in the work of Bienvenue et al. and Mazliak [10, 125].
Results which are closely related to Theorem 5.26 can be found, in various renditions, in the work of Levy [110, p. 129], Sparre Andersen and Jessen [154,155,156], and Doob [49, 50, Chapter VII]. This is how Sparre–Andersen and Jessen introduce their result:
The present paper deals with two limit theorems on integrals on an abstract set. The first limit theorem is a generalization of the well-known theorem on differentiation on a net, the net being replaced by an increasing sequence of \(\sigma \)-fields.
The “well known theorem on differentiation on a net” in the quotation given above appears to be due to de la Vallée Poussin [39, 40].
Section 5.2.6. S. Sawyer and E. M. Nikišin have generalized Theorem 5.7 in various directions [65, 131, 153].
Section 6.10. A regularity hypothesis in a theorem is one which is not formally necessary to give meaning to its conclusion. In 1916, William Fogg Osgood had the following to say about regularity conditions:
It is unsatisfactory, in stating an important theorem, not to know whether a given hypothesis is needed merely for convenience of proof, or whether the theorem would be false if it were omitted. The situation is still more annoying when it is conceivable that the theorem could be proven with about the same ease without the hypothesis, if one were only able to see more clearly.[134]
Some theorems, originally proved under some regularity condition, also hold without: In this case, the regularity condition is not essential. A notable example of this kind is given by the boundedness hypothesis in Osgood’s theorem on the holomorphicity of separately holomorphic functions [133]. Indeed, Hartogs proved that the conclusion holds even if this hypothesis is omitted [74]. Among the other examples of this kind, we mention one due to Stein [163, p. 251], and one due to Saks [151]. Other theorems do fail if we omit the regularity condition from the hypothesis. An example of this kind is the countability hypothesis in Egorov’s theorem on pointwise convergence [13, p. 198], [16, Theorem 2, INT IV.64]. There seems to be no general way to understand a priori whether a given regularity hypothesis is essential or not. Theorem 6.23 shows that the regularity condition (6.19) in Theorem 6.21 is neither essential nor inessential [43, 53, 80, 101].
Section 8.1.3. If \(E\subset \partial \Omega \), then \(E\in {\widehat{\varvec{\mathcal {B}}}}_{\omega } \) if and only if the indicator function \(1_E\) is resolutive, in the sense of classical potential theory [52, Chapter 1.VIII].
Section 6.8. Plessner’s theorem has the flavor of a zero-one law in probabilistic settings, where certain “tail” \(\sigma \)-algebras are trivial. For this point of view, see [54] and references therein.
Section 9. In 1967, Hórmander published a paper (submitted on November 1966) where a lucid geometric description of the metric \(\delta \) appears [77]. In July of the same year, Korányi and Stein gave lectures at the Centro Internazionale Matematico Estivo Summer School organized by Edoardo Vesentini in Urbino (Italy) [179]. In the notes of those lectures, both authors make a reference to a “joint paper” they had in preparation, but which apparently never appeared [168, p. 298], [94, p. 171], [92, 162].
Deep contributions to the subject have been given by L. Lempert and S. R. Barker [7, 109].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Di Biase, F., Krantz, S.G. Foundations of Fatou Theory and a Tribute to the Work of E. M. Stein on Boundary Behavior of Holomorphic Functions. J Geom Anal 31, 7184–7296 (2021). https://doi.org/10.1007/s12220-021-00618-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12220-021-00618-z




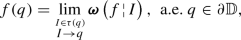
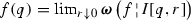 a. e.
a. e.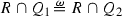 .
.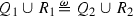 .
.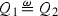 , then
, then 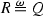 .
.