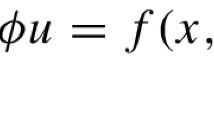Abstract
In this paper, we consider the following Gross–Pitaevskii equation describing Bose–Einstein condensation of trapped dipolar quantum gases:
where \(\lambda >0\), \(Q\in C({\mathbb {R}}^{3},{\mathbb {R}})\) is a potential well, \(\star \) denotes the convolution, \(K(x)=\frac{1-3\cos ^{2}\theta }{|x|^{3}}\) and \(\theta =\theta (x)\) is the angle between the dipole axis determined by the vector x and the vector (0, 0, 1). When \((\omega _{1},\omega _{2})\in {\mathbb {R}}^{2}\) lies in the defined unstable regime, under some suitable conditions on Q, the existence and concentration of nontrivial solutions to problem (0.1) are proved by using variational methods. In particular, the trapping potential is allowed to be sign-changing. Moreover, when \((\omega _{1},\omega _{2})\in {\mathbb {R}}^{2}\) lies in the stable regime, we show that problem (0.1) with small bounded sign-changing potential has only trivial solutions.
Similar content being viewed by others
References
Antonelli, P., Sparber, C.: Existence of solitary waves in dipolar quantum gases. Physica D 240, 426–431 (2011)
Bao, W., Cai, Y., Wang, H.: Efficient numerical method for computing ground states and dynamic of dipolar Bose–Einstein condensates. J. Comput. Phys. 229, 7874–7892 (2010)
Bartsch, T., Pankov, A., Wang, Z.-Q.: Nonlinear Schrödinger equations with steep potential well. Commun. Contemp. Math. 3, 549–569 (2001)
Bartsch, T., Tang, Z.: Multibump solutions of nonlinear Schrödinger equations with steep potential well and indefinite potential. Discrete Contin. Dyn. Syst. 33, 7–26 (2013)
Bartsch, T., Wang, Z.-Q.: Existence and multiplicity results for superlinear elliptic problems on \({\mathbb{R}}^N\). Commun. Partial Differ. Equ. 20, 1725–1741 (1995)
Bellazzini, J., Jeanjean, L.: On dipolar quantum gases in the unstable regime. SIAM J. Math. Anal. 48, 2028–2058 (2017)
Brézis, H., Lieb, E.: A relation between pointwise convergence of functions and convergence of functionals. Proc. Am. Math. Soc. 88, 486–490 (1983)
Carles, R., Hajaiej, H.: Complementary study of the standing wave solutions of the Gross–Pitaevskii equation in dipolar quantum gases. Bull. Lond. Math. Soc. 47, 509–518 (2015)
Carles, R., Markowich, P., Sparber, C.: On the Gross–Pitaevskii equation for trapped dipolar quantum gases. Nonlinearity 21, 2569–2590 (2008)
Deng, Y., Peng, S., Shuai, W.: Existence and asymptotic behavior of nodal solutions for the Kirchhoff-type problems in \({\mathbb{R}}^{3}\). J. Funct. Anal. 269, 3500–3527 (2015)
Ding, Y., Szulkin, A.: Bound states for semilinear Schrödinger equations with sign-changing potential. Calc. Var. Partial Differ. Equ. 29, 397–419 (2007)
Ekeland, I.: Convexity Methods in Hamiltonian Mechanics. Springer, Berlin (1990)
Feng, B., Wang, Q.: Strong instability of standing waves for the nonlinear Schrödinger equation in trapped dipolar quantum gases. J. Dyn. Differ. Equ. (2020). https://doi.org/10.1007/s10884-020-09881-0
He, Y., Luo, X.: Concentrating standing waves solutions for the Gross–Pitaevskii equation in trapped dipolar quantum gases. J. Differ. Equ. 266, 600–629 (2019)
Li, G., Ye, H.: Existence of positive ground state solutions for the nonlinear Kirchhoff type equations in \({\mathbb{R}}^{3}\). J. Differ. Equ. 257, 566–600 (2014)
Li, L., Sun, J.: Existence and multiplicity of solutions for the Kirchhoff equations with asymptotically linear nonlinearities. Nonlinear Anal. Real World Appl. 26, 391–399 (2015)
Lushnikov, P.: Collapse of Bose–Einstein condensates with dipole–dipole interactions. Phys. Rev. A 66, 051601(R) (2002)
Lushnikov, P.: Collapse and stable self-trapping for Bose–Einstein condensates with \(1/{r^b}\) type attractive interatomic interaction potential. Phys. Rev. A 82, 023615 (2010)
Rabinowitz, P.: Minimax methods in critical point theory with applications to differential equations. In: CBMS Regional Conference Series in Mathematics, vol. 65 (1986)
Santos, L., Shlyapnikov, G., Zoller, P., Lewenstein, M.: Bose–Einstein condensation in trapped dipolar gases. Phys. Rev. Lett. 85, 1791–1797 (2000)
Stuart, C., Zhou, H.: Global branch of solutions for nonlinear Schrödinger equations with deepening potential well. Proc. Lond. Math. Soc. 92, 655–681 (2006)
Triay, A.: Derivation of the dipolar Gross–Pitaevskii energy. SIAM J. Math. Anal. 50, 33–63 (2018)
Wang, Z., Zhou, H.: Positive solutions for nonlinear Schrödinger equations with deepening potential well. J. Eur. Math. Soc. 11, 545–573 (2009)
Willem, M.: Analyse harmonique réelle. Hermann, Paris (1995)
Willem, M.: Minimax theorems. In: Progress Nonlinear Differential Equations and Their Applications, vol. 24 (1996)
Yi, S., You, L.: Trapped atomic condensates with anisotropic interactions. Phys. Rev. 61, 041604 (2000)
Yi, S., You, L.: Trapped condensates of atoms with dipole interactions. Phys. Rev. 63, 053607 (2001)
Zhao, L., Zhao, F.: On the existence of solutions for the Schrödinger Poisson equations. J. Math. Anal. Appl. 346, 155–169 (2008)
Acknowledgements
The authors are very grateful to Professor Daomin Cao whose comments on the first version of this work have permitted us to improve our manuscript and to avoid including a wrong proof. The authors also thank Professor Gongbao Li for helpful discussions on the whole paper and constant encouragements over the past few years.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Huifang Jia is supported by NNSF of China (Nos. 12001126 and 11771166), Xiao Luo is supported by NNSF of China (No. 11901147) and the Fundamental Research Funds for the Central Universities of China (Nos. JZ2019HGBZ0156 and JZ2020HGTB0030)
Rights and permissions
About this article
Cite this article
Jia, H., Luo, X. Existence and concentration of solutions to the Gross–Pitaevskii equation with steep potential well. Z. Angew. Math. Phys. 72, 71 (2021). https://doi.org/10.1007/s00033-021-01510-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-021-01510-0