Abstract
Low-rank Krylov methods are one of the few options available in the literature to address the numerical solution of large-scale general linear matrix equations. These routines amount to well-known Krylov schemes that have been equipped with a couple of low-rank truncations to maintain a feasible storage demand in the overall solution procedure. However, such truncations may affect the convergence properties of the adopted Krylov method. In this paper we show how the truncation steps have to be performed in order to maintain the convergence of the Krylov routine. Several numerical experiments validate our theoretical findings.
Similar content being viewed by others
1 Introduction
We are interested in the numerical solution of general linear matrix equations of the form
where \(A_{i}\in \mathbb {R}^{n_{A}\times n_{A}}\), \(B_{i}\in \mathbb {R}^{n_{B}\times n_{B}}\) are large matrices that allow matrix-vector products Aiv, Biw to be efficiently computed for all i = 1,…,p, and any \(v\in \mathbb {R}^{n_{A}}\), \(w\in \mathbb {R}^{n_{B}}\). Moreover, C1, C2 are supposed to be of low rank, i.e., \(C_{1}\in \mathbb {R}^{n_{A}\times q}\), \(C_{2}\in \mathbb {R}^{n_{B}\times q}\), q ≪ nA,nB. For sake of simplicity we consider the case of nA = nB ≡ n in the following, so that the solution \(X\in \mathbb {R}^{n\times n}\) is a square matrix, but our analysis can be applied to the rectangular case, with nA≠nB, as well.
Many common linear matrix equations can be written as in (1.1). For instance, if p = 2 and B1 = A2 = In, In identity matrix of order n, we get the classical Sylvester equations. Moreover, if B2 = A1, A2 = B1, and C1 = C2, the Lyapunov equation is attained. These equations are ubiquitous in signal processing and control and systems theory. See, e.g., [1,2,3]. The discretization of certain elliptic PDEs yields Lyapunov and Sylvester equations as well. See, e.g., [4, 5].
Generalized Lyapunov and Sylvester equationsFootnote 1 amount to a Lyapunov/Sylvester operator plus a general linear operator:
See, e.g., [6, 7]. These equations play an important role in model order reduction of bilinear and stochastic systems, see, e.g., [6, 8, 9], and many problems arising from the discretization of PDEs can be formulated as generalized Sylvester equations as well. See, e.g., [4, 10, 11].
General multiterm linear matrix equations of the form (1.1) have been attracting attention in the very recent literature because they arise in many applications like the discretization of deterministic and stochastic PDEs, see, e.g., [12, 13], PDE-constrained optimization problems [14], data assimilation [15], matrix regression problems arising in computational neuroscience [16], fluid-structure interaction problems [11], and many more.
Even when the coefficient matrices Ai’s and Bi’s in (1.1) are sparse, the solution X is, in general, dense and it cannot be stored for large scale problems. However, for particular instances of (1.1), as the ones above, and under certain assumptions on the coefficient matrices, a fast decay in the singular values of X can be proved and the solution thus admits accurate low-rank approximations of the form \(S_{1}{S_{2}^{T}}\approx X\), S1, \(S_{2}\in \mathbb {R}^{n\times t}\), t ≪ n, so that only the low-rank factors S1 and S2 need to be computed and stored. See, e.g., [6, 7, 17, 18].
For the general multiterm linear equation (1.1), robust low-rank approximability properties of the solution have not been established so far even though X turns out to be numerically low-rank in many cases. See, e.g., [14, 15]. In the rest of the paper we thus assume that the solution X to (1.1) admits accurate low-rank approximations.
The efficient computation of the low-rank factors S1 and S2 is the task of the so-called low-rank methods and many different algorithms have been developed in the last decade for both generalized and standard Lyapunov and Sylvester equations. A non complete list of low-rank methods for such equations includes projection methods proposed in, e.g., [7, 13, 19,20,21], low-rank (bilinear) ADI iterations [6, 22, 23], sign function methods [24, 25], and Riemannian optimization methods [26, 27]. We refer the reader to [28] for a thorough presentation of low-rank techniques.
To the best of our knowledge, few options are present in the literature for the efficient numerical solution of general equations (1.1): A greedy low-rank method by Kressner and Sirković [29], and low-rank Krylov procedures (e.g., [6, 14, 15, 30]) which are the focus of this paper.
Krylov methods for matrix equations can be seen as standard Krylov subspace schemes applied to the n2 × n2 linear system
where ⊗ denotes the Kronecker product and \(\text {vec}:\mathbb {R}^{n\times n}\rightarrow \mathbb {R}^{n^{2}}\) is such that vec(X) is the vector obtained by stacking the columns of the matrix X one on top of each other.
These methods construct the Krylov subspace
and compute an approximate solution of the form vec(Xm) = Vmym ≈vec(X), where \(V_{m}=[v_{1},\ldots ,v_{m}]\in \mathbb {R}^{n^{2}\times m}\) has orthonormal columns and it is such that \(\text {Range}(V_{m})=\mathbf {K}_{m}(\mathcal {A},\text {vec}(C_{1}{C_{2}^{T}}))\) with \(y_{m}\in \mathbb {R}^{m}\). The vector ym can be computed in different ways which depend on the selected Krylov method. The most common schemes are based either on a (Petrov-)Galerkin condition on the residual vector or a minimization procedure of the residual norm; see, e.g., [31].
The coefficient matrix \(\mathcal {A}\) in (1.2) is never assembled explicitly in the construction of \(\mathbf {K}_{m}(\mathcal {A},\text {vec}(C_{1}{C_{2}^{T}}))\) but its Kronecker structure is exploited to efficiently perform matrix-vector products. Moreover, to keep the memory demand low, the basis vectors of \(\mathbf {K}_{m}(\mathcal {A},\text {vec}(C_{1}{C_{2}^{T}}))\) must be stored in low-rank format. To this end, the Arnoldi procedure to compute Vm has to be equipped with a couple of low-rank truncation steps. In particular, a low-rank truncation is performed after the “matrix-vector product” \(\mathcal {A}v_{m}\) where vm denotes the last basis vector, and during the orthogonalization process. See, e.g., [14, Section 3], [30, Section 2], [15, Section 3] and Section 2.
In principle, the truncation steps can affect the convergence of the Krylov method and the well-established properties of Krylov schemes (see, e.g., [31]) may no longer hold. However, it has been numerically observed that Krylov methods with low-rank truncations often achieve the desired accuracy, even when the truncation strategy is particularly aggressive. See, e.g., [14, 15].
In this paper we establish some theoretical foundations to explain the converge of Krylov methods with low-rank truncations. In particular, the full orthogonalization method (FOM) [31, Section 6] and the generalized minimal residual method (GMRES) proposed in [32] are analyzed.
We assume that two different truncation steps are performed within our routine and, to show that the convergence is maintained, we deal with these truncations in two distinct ways. First, the truncation performed after the matrix-vector product \(\mathcal {A}v_{m}\) is seen as an inexact matrix-vector product and results coming from [33] are employed. The low-rank truncations that take place during the Gram-Schmidt procedure provide us with basis vectors with lower ranks and they are thus very advantageous from a storage demand perspective. However, these truncations lead to a computed basis that is no longer orthogonal in general. We propose to perform a second orthogonalization step that takes place only in the space generated by the columns of the low-rank matrix representing the newly generated basis vector. Since this subspace is very low-dimensional in general, the extra orthogonalization step can be performed exactly, namely no truncations are computed afterwards. In addition to retrieve the orthogonality of the basis, our new procedure maintains the benefits in terms of memory allocation coming from the previously computed low-rank truncations. The additional orthogonalization leads to some modifications in the procedure adopted to compute the vector ym and we show how the projected problem formulation can be adjusted accordingly.
We would like to underline the fact that the schemes studied in this paper significantly differ from tensorized Krylov methods analyzed in, e.g., [34]. Indeed, our \(\mathcal {A}\) is not a Laplace-like operator in general, i.e., \(\mathcal {A}\neq {\sum }_{i=1}^{p}I_{n_{1}}\otimes \cdots \otimes I_{n_{i-1}}\otimes A_{i}\otimes I_{n_{i+1}}\otimes \cdots \otimes I_{n_{p}} \).
The following is a synopsis of the paper. In Section 2 we review the low-rank formulation of FOM and GMRES and their convergence is proved in Section 3. In particular, in Section 3.1 and 3.2 the two different low-rank truncation steps are analyzed, respectively. Some implementation aspects of these low-rank truncations are discussed in Section 4. It is well known that Krylov methods must be equipped with effective preconditioning techniques in order to achieve a fast convergence in terms of number of iterations. Due to some peculiar aspects of our setting, the preconditioners must be carefully designed as we discuss in Section 5. Short recurrence methods like CG, MINRES and BICGSTAB can be very appealing in our context due to their small memory requirements and low computational efforts per iteration. Even though their analysis can be cumbersome since the computed basis is not always orthogonal (e.g., the orthogonality may be lost in finite precision arithmetic), their application to the solution of (1.1) is discussed in Section 6. Several numerical examples reported in Section 7 support our theoretical analysis. The paper finishes with some conclusions given in Section 8.
Throughout the paper we adopt the following notation. The matrix inner product is defined as 〈X,Y 〉F = trace(YTX) so that the induced norm is \(\|X\|_{F}= \sqrt {\langle X, X\rangle _{F}}\). In the paper we continuously use the identity vec(Y )Tvec(X) = 〈X,Y 〉F so that \(\|\text {vec}(X)\|_{2}^{2}=\|X\|_{F}^{2}\). Moreover, the cyclic property of the trace operator allows for a cheap evaluation of matrix inner products with low-rank matrices. Indeed, if \(M_{i},N_{i}\in \mathbb {R}^{n\times r_{i}}\), ri ≪ n, i = 1,2, \(\langle M_{1}{N_{1}^{T}},M_{2}{N_{2}^{T}}\rangle _{F}=\text {trace}(N_{2}{M_{2}^{T}}M_{1}{N_{1}^{T}})=\text {trace}(({M_{2}^{T}}M_{1})({N_{1}^{T}}N_{2}))\) and only matrices of small dimensions ri are involved in such a computation. Therefore, even if it is not explicitly stated, we will always assume that matrix inner products with low-rank matrices are cheaply computed without assembling any dense n × n matrix. For the sake of simplicity we will omit the subscript in ∥⋅∥F and write only ∥⋅∥.
The k th singular value of a matrix \(M\in \mathbb {R}^{m_{1}\times m_{2}}\) is denoted by σk(M), where the singular values are assumed to be ordered in a decreasing fashion. The condition number of M is denoted by κ(M) = σ1(M)/σp(M), \(p=\text {rank}(M)=\arg \min \limits _{i}\lbrace \sigma _{i}(M)\neq 0\rbrace \).
As already mentioned, In denotes the identity matrix of order n and the subscript is omitted whenever the dimension of I is clear from the context. The i th canonical basis vector of \(\mathbb {R}^{n}\) is denoted by ei while 0m is a vector of length m whose entries are all zero.
The brackets [⋅] are used to concatenate matrices of conforming dimensions. In particular, a Matlab-like notation is adopted and [M,N] denotes the matrix obtained by stacking M and N one next to the other whereas [M;N] the one obtained by stacking M and N one of top of each other, i.e., [M;N] = [MT,NT]T. The notation diag(M,N) is used to denote the block diagonal matrix with diagonal blocks M and N.
2 Low-rank FOM and GMRES
In this section we revise the low-rank formulation of FOM (LR-FOM) and GMRES (LR-GMRES) for the solution of the multiterm matrix equation (1.1).
Low-rank Krylov methods compute an approximate solution Xm ≈ X of the form
In the following we will always assume the initial guess x0 to be the zero vector \(\mathbf {0}_{n^{2}}\) and in Remark 3.1 such a choice is motivated. Therefore, the m orthonormal columns of \(V_{m}=[v_{1},\ldots ,v_{m}]\in \mathbb {R}^{n^{2}\times m}\) in (2.1) span the Krylov subspace (1.3) and \(y_{m}\in \mathbb {R}^{m}\).
One of the peculiarities of low-rank Krylov methods is that the basis vectors must be stored in low-rank format. We thus write \(v_{j}=\text {vec}(\mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T})\) where \(\mathcal {V}_{1,j},~\mathcal {V}_{2,j}\in \mathbb {R}^{n\times s_{j}}\), sj ≪ n, for all j = 1,…,m.
The basis Vm can be computed by a reformulation of the underlying Arnoldi process (see, e.g., [31, Section 6.4]) that exploits the Kronecker structure of \(\mathcal {A}\) and the low-rank format of the basis vectors. In particular, at the m th iteration, the n2-vector \(\widehat v=\mathcal {A}v_{m}\) must be computed. For sparse matrices Ai, Bi, a naive implementation of this operation costs \(\mathcal {O}(\mathtt {nnz}(\mathcal {A}))\) floating point operations (flops) where \(\mathtt {nnz}(\mathcal {A})\) denotes the number of nonzero entries of \(\mathcal {A}\). However, it can be replaced by the linear combination \(\widehat {V}={\sum }_{i=1}^{p} \left (A_{i}\mathcal {V}_{1,j}\right )\left (B_{i}\mathcal {V}_{2,j}\right )^{T}\), \(\text {vec}(\widehat {V})=\widehat v\), where 2psj matrix-vector products with matrices of order n are performed. The cost of such operation is \(\mathcal {O}((\max \limits _{i}\mathtt {nnz}(A_{i})+\max \limits _{i}\mathtt {nnz}(B_{i}))ps_{j})\) flops and it is thus much cheaper than computing \(\widehat v\) naively via the matrix-vector product by \(\mathcal {A}\) since \(\mathtt {nnz}(\mathcal {A})=\mathcal {O}(\max \limits _{i}\mathtt {nnz}(A_{i})\cdot \max \limits _{i}\mathtt {nnz}(B_{i}))\), sj is supposed to be small and p is in general moderate. A similar argumentation carries over when (some of) the matrices Ai, Bi are not sparse but still allow efficient matrix vector products.
Moreover, since
the low-rank format is preserved in the computation of \(\widehat {V}\). In order to avoid an excessive increment in the column dimension psj of \(\widehat {V}_{1},\widehat {V}_{2}\), it is necessary to exercise a column compression of the factors \(\widehat {V}_{1}\) and \(\widehat {V}_{2}\), i.e., the matrices \((\overline {V}_{1}, \overline {V}_{2})=\mathtt {trunc}(\widehat {V}_{1},I,\widehat {V}_{2},\varepsilon _{\mathcal {A}})\) are computed. With (L,M,N,εtrunc) we denote any routine that computes low-rank approximations of the product LMNT with a desired accuracy of order ε, so that, the matrices \(\overline {V}_{1}\), \(\overline {V}_{2}\) are such that \(\|\overline {V}_{1} \overline {V_{2}^{T}}- \widehat {V}_{1} \widehat {V_{2}^{T}}\|/\|\widehat {V}_{1} \widehat {V_{2}^{T}}\|=\varepsilon _{\mathcal {A}}\) with \(\overline {V}_{1}\), \(\overline {V}_{2}\in \mathbb {R}^{n\times \overline {s}}\), \(\overline {s}\leq ps_{j}\). Algorithm 1 illustrates a standard approach for such compressions that is based on thin QR-factorizations and a SVD thereafter; see, e.g., [30, Section 2.2.1], and used in the remainder of the paper. Some alternative truncation schemes are discussed in Section 4.

The vector \(\text {vec}(\overline {V}_{1}\overline {V_{2}^{T}})\approx \widehat v\) returned by the truncation algorithm is then orthogonalized with respect to the previous basis vectors \(\text {vec}(\mathcal {V}_{1,j}\mathcal {V}_{1,j}^{T})\), j = 1,…,m. Such orthogonalization step can be implemented by performing, e.g., the modified Gram-Schmidt procedure and the low-rank format of the quantities involved can be exploited and maintained in the result. The vector formulation of the orthogonalization step is given by
and, since \(\text {vec}(\mathcal V_{1,j}\mathcal V_{2,j}^{T})^{T}\text {vec}(\overline {V}_{1}\overline {V_{2}^{T}})=\langle \mathcal V_{1,j}\mathcal V_{2,j}^{T},\overline {V}_{1}\overline {V_{2}^{T}}\rangle _{F}\), we can reformulate (2.2) as
where \({\Theta }_{m}=\text {diag}(I_{\overline {s}},-h_{1,m}I_{s_{1}},\ldots ,-h_{m,m}I_{s_{m}})\), \(\text {vec}(\widetilde V)=\widetilde v\), and the m coefficients hj,m are collected in the m th column of an upper Hessenberg matrix \(H_{m}\in \mathbb {R}^{m\times m}\).
Obviously, the resulting \(\widetilde V\) has factors with increased column dimension so that a truncation of the matrix \([\overline {V}_{1},\mathcal V_{1,1},\ldots ,\mathcal V_{1,m}]{\Theta }_{m}[\overline {V}_{2},\mathcal V_{2,1},\ldots ,\mathcal V_{2,m}]^{T}\) becomes necessary. In particular, if ε is a given threshold, we compute
The result in (2.3) is then normalized to obtained the (m + 1)th basis vector, namely \(\mathcal {V}_{1,m+1}=\widetilde V_{1}/\sqrt {\|\widetilde V_{1}\widetilde {V}_{2}^{T}\|}\) and \(\mathcal {V}_{2,m+1}=\widetilde V_{2}/\sqrt {\|\widetilde V_{1}\widetilde {V}_{2}^{T}\|}\). The upper Hessenberg matrix \(\underline {H}_{m}\in \mathbb {R}^{(m+1)\times m}\) is defined such that its square principal submatrix is given by Hm and \(e_{m+1}^{T} \underline {H}_{m}e_{m}=h_{m+1,m}:=\|\widetilde V_{1}\widetilde {V}_{2}^{T}\|\).
The difference between FOM and GMRES lies in the computation of the vector ym in (2.1). In FOM a Galerkin condition on the residual vector
is imposed. If no truncation steps are performed during the Arnoldi procedure, the Arnoldi relation
is fulfilled and it is easy to show that imposing the Galerkin condition (2.4) is equivalent to solving the m × m linear system
for \(y_{m}=y_{m}^{fom}\). Moreover, in the exact setting where (2.5) holds, the norm of the residual vector \(\text {vec}(C_{1}{C_{2}^{T}})+\mathcal {A}\text {vec}(X_{m})\) can be cheaply computed as
See, e.g., [31, Proposition 6.7].
In GMRES, the vector \(y_{m}=y_{m}^{gm}\) is computed by solving a least squares problem
which corresponds to the Petrov-Galerkin orthogonality condition
If (2.5) holds, \(y_{m}^{gm}\) can be computed as
By following, e.g., [31, Section 6.5.3] the vector \(y_{m}^{gm}\) and the related residual norm can be computed at low cost.
If at the m th iteration the residual norm \(\|\text {vec}(C_{1}{C_{2}^{T}})+\mathcal {A}V_{m}y_{m}\|\) is sufficiently smallFootnote 2, we recover the solution Xm. Clearly, the full Xm is not constructed explicitly as this is a large, dense matrix. However, since we have assumed that the solution X to (1.1) admits accurate low-rank approximations, we can compute low-rank factors S1, \(S_{2}\in \mathbb {R}^{n\times t}\), t ≪ n, such that \(S_{1}{S_{2}^{T}}\approx X\). Also this operation can be performed by exploiting the low-rank format of the basis vectors. In particular, if \({\Upsilon }=\text {diag}(({e_{1}^{T}}y_{m})I_{s_{1}},\ldots ,({e_{m}^{T}}y_{m})I_{s_{m}})\), then
The low-rank FOM and GMRES procedures are summarized in Algorithm 2. For sake of simplicity, we decide to collect the two routines in the same pseudo-algorithm as they differ only in the computation of ym and the convergence check.

At each iteration step m of Algorithm 2 we perform three low-rank truncationsFootnote 3 and these operations substantially influence the overall solution procedure. If the truncation tolerances \(\varepsilon _{\mathcal {A}}\) and ε are chosen too large, the whole Krylov method my break down. Therefore, in the following sections we discuss how to adaptively choose the truncation tolerances \(\varepsilon _{\mathcal {A}}\) and ε along with a novel procedure which ensures the orthogonality of the computed, low-rank basis. Moreover, the low-rank truncation does have its own computational workload which can be remarkable, especially if the ranks of the basis vectors involved is quite large. In Section 4 we discuss some computational appealing alternatives to Algorithm 1.
3 A convergence result
In this section we show that the convergence of LR-FOM and LR-GMRES is guaranteed if the thresholds \(\varepsilon _{\mathcal {A}}\) and ε for the low-rank truncations in lines 4 and 10 of Algorithm 2 are properly chosen and if a particular procedure which guarantees the orthogonality of the basis is adopted.
The truncation that takes place in line 17, after the iterative process terminated, to recover the low-rank factors of the approximate solution is not discussed. Indeed, this does not affect the convergence of the Krylov method and it is justified by assuming that the exact solution X admits low-rank approximations.
3.1 Inexact matrix-vector products
We start by analyzing the truncation step in line 4 of Algorithm 2 assuming, for the moment, that the one in line 10 is not performed. In this way the generated basis Vm is ensured to be orthogonal. In Section 3.2 we will show how to preserve the orthogonality of the constructed basis when the truncations in line 10 of Algorithm 2 are performed so that the results we show here still hold.
The low-rank truncation performed in line 4 of Algorithm 2 can be understood as an inexact matrix-vector product with \(\mathcal {A}\). Indeed, at the m th iteration, we can write
where Em is the matrix discarded when \(\mathtt {trunc}(\widehat {V}_{1},I,\widehat {V}_{2},\varepsilon _{\mathcal {A}})\) is applied so that \(\|E_{m}\|/\|\widehat {V}_{1}\widehat {V}_{2}^{T}\|\leq \varepsilon _{\mathcal {A}}\). Therefore, we have
and the vector \(\text {vec}(\overline {V}_{1}\overline {V}_{2}^{T})\) can thus be seen as the result of an inexact matrix-vector product by \(\mathcal {A}\).
Following the discussion in [33], the Arnoldi relation (2.5) must be replaced by the inexact counterpart
and Range(Vm) is no longer a Krylov subspace generated by \(\mathcal {A}\).
The vectors \(y_{m}^{fom}\) and \(y_{m}^{gm}\) can be still calculated as in (2.6) and (2.8), respectively, but these are no longer equivalent to imposing the Galerkin and Petrov-Galerkin conditions (2.4)–(2.7) since the Arnoldi relation (2.5) no longer holds; different constraints must be taken into account.
Proposition 3.1 (See [33])
Let (3.1) hold and define \(W_{m}=\mathcal {A}V_{m}-[\text {vec}(E_{1}),\ldots ,\text {vec}(E_{m})]\). If \(y_{m}^{gm}\) is computed as in (2.8), then \(q_{m}^{gm}:=W_{m}y_{m}^{gm}\) is such that
Similarly, if \(y_{m}^{fom}\) is computed as in (2.6), then \(q_{m}^{fom}:=W_{m}y_{m}^{fom}\) is such that
Consequently, Hm is not a true Galerkin projection of \(\mathcal {A}\) onto Range(Vm). One may want to compute the vectors \(y_{m}^{fom}\) and \(y_{m}^{gm}\) by employing the true projection \(T_{m}:={V_{m}^{T}}\mathcal {A}V_{m}=H_{m}+{V_{m}^{T}}[\text {vec}(E_{1}),\ldots ,\text {vec}(E_{m})]\) in place of Hm in (2.6)–(2.8) so that the reduced problems represent a better approximation (cf. [35]) of the original equation and the orthogonality conditions imposed are in terms of the true residual. However, the computation of Tm requires to store the matrix [vec(E1),…,vec(Em)] and this is impracticable as the benefits in terms of memory demand coming from the low-rank truncations are completely lost due to the allocation of both Vm and [vec(E1),…,vec(Em)]. A different option is to store the matrix \(\mathcal {A}V_{m}\) and compute an explicit projection of \(\mathcal {A}\) onto the current subspace, but also this strategy leads to an unfeasible increment in the memory requirements of the overall solution process as the storage demand grows of a factor p. Therefore, in all the numerical experiments reported in Section 7, the matrix Hm arising from the orthonormalization procedure is employed in the computation of \(y_{m}^{fom}\) and \(y_{m}^{gm}\).
If (3.1) holds and vec(Xm) = Vmym is the approximate solution to (1.2) computed by projection onto Range(Vm), then, at the m th iteration, the true residual vector can be expressed as
where \(\widetilde r_{m}\) is the computed residual vector.
In [33, Section 4] it has been shown that the residual gap \(\delta _{m}:=\|r_{m}-\widetilde r_{m}\|\) between the true residual and the computed one can be bounded by
Since \(|{e_{j}^{T}}y_{m}|\) decreases as the the iterations proceed (see, e.g., [33, Lemma 5.1–5.2]), ∥Em∥ is allowed to increase while still maintaining a small residual gap and preserving the convergence of the overall solution process. This phenomenon is often referred to as relaxation.
Theorem 3.1 (See 33)
Let ε > 0 and let \(r_{m}^{gm}:=\text {vec}(C_{1}{C_{2}^{T}})+\mathcal {A}V_{m}y_{m}^{gm}\) be the true GMRES residual after m iterations of the inexact Arnoldi procedure. If for every k ≤ m,
then \(\|r_{m}^{gm}-\widetilde r_{m}^{gm}\|\leq \varepsilon \). Moreover, if
then \(\|(V_{m+1}\underline {H}_{m})^{T}r_{m}^{gm}\|\leq \varepsilon \).
Similarly, if \(r_{m}^{fom}:=\text {vec}(C_{1}{C_{2}^{T}})+\mathcal {A}V_{m}y_{m}^{fom}\) is the true FOM residual after m iterations of the inexact Arnoldi procedure, and if for every k ≤ m,
then \(\|r_{m}^{fom}-\widetilde r_{m}^{fom}\|\leq \varepsilon \) and \(\|{V_{m}^{T}}r_{m}^{fom}\|\leq \varepsilon \).
The quantities involved in the estimates (3.3), (3.4) and (3.5) are not available at iteration k < m making the latter of theoretical interest only. To have practically usable truncation thresholds, the quantities in (3.3), (3.4) and (3.5) must be approximated with computable values. Following the suggestions in [33], we can replace m by the maximum number \(m_{\max \limits }\) of allowed iterations, \(\sigma _{m_{\max \limits }}(\underline {H}_{m_{\max \limits }})\) is replaced by \(\sigma _{n^{2}}(\mathcal {A})\), and we approximate \(\sigma _{1}(\underline {H}_{m_{\max \limits }})\) by \(\sigma _{1}(\mathcal {A})\) when computing \(\kappa (\underline {H}_{m_{\max \limits }})\) in (3.4). The extreme singular values of \(\mathcal {A}\) can be computed once and for all at the beginning of the iterative procedure, e.g., by the Lanczos method that must be carefully designed to avoid the construction of \(\mathcal {A}\) and to exploit its Kronecker structure. Approximations of \(\sigma _{1}(\mathcal {A})\) and \(\sigma _{n^{2}}(\mathcal {A})\) coming, e.g., from some particular features of the problem of interest, can be also employed. To conclude, we propose to use the following practical truncation thresholds \(\varepsilon _{\mathcal {A}}^{(k)}\) in line 4 of Algorithm 2 in place of \(\varepsilon _{\mathcal {A}}\):
for LR-GMRES, and
for LR-FOM.
Allowing ∥Ek∥ to grow is remarkably important in our setting, especially for the memory requirements of the overall procedure. Indeed, if the truncation step in line 4 of Algorithm 2 is not performed, the rank of the basis vectors increases very quickly as, at the m th iteration, we have
Therefore, at the first iterations the rank of the basis vectors is low by construction and having a very stringent tolerance in the computation of their low-rank approximations is not an issue. When the iterations proceed, the rank of the basis vectors increases but, at the same time, the increment in the thresholds for computing low-rank approximations of such vectors leads to more aggressive truncations with consequent remarkable gains in the memory allocation.
The interpretation of the truncation in line 4 of Algorithm 2 in terms of an inexact Krylov procedure has been already proposed in [36] for the more general case of GMRES applied to (1.2) where \(\mathcal {A}\) is a tensor and the approximate solution is represented in the tensor-train (TT) format. However, also in the tensor setting, the results in Theorem 3.1 hold if and only if the matrix Vm has orthonormal columns. In general, the low-rank truncation in line 10 can destroy the orthogonality of the basis. In the next section we show that Vm has orthogonal columns if the truncation step is performed in an appropriate way.
We first conclude this section with a couple of remarks.
Remark 3.1
We have always assumed the initial guess \(x_{0}\in \mathbb {R}^{n^{2}}\) in (2.1) to be zero. This choice is motivated by the discussion in, e.g., [33, Section 3], [37], where the authors show how this is a good habit in the framework of inexact Krylov methods.
Remark 3.2
Since
where \(\varepsilon _{\mathcal {A}}^{(j)}\) denotes one of the values in (3.6) and (3.7) depending on the selected procedure, the quantity \(\|\widetilde r_{m}\|+{\sum }_{j=1}^{m} \varepsilon _{\mathcal {A}}^{(j)}\cdot |{e_{j}^{T}}y_{m}|\) must be computed to have a reliable stopping criterion in Algorithm 2.
3.2 An orthogonality safeguard
In this section we show how to preserve the orthogonality of the basis while maintaining the benefits in terms of memory requirements coming from the low-rank truncations performed during the Gram-Schmidt procedure in line 10 of Algorithm 2. Thanks to the orthogonality of the basis Vm, the results presented in Section 3.1 are still valid.
At the m th iteration, the (m + 1)th basis vector is computed by performing (2.3) and then normalizing the result. In particular, if \({\Theta }_{m}=\text {diag}(I_{\overline {s}},-h_{1,m}I_{s_{1}},\ldots ,-h_{m,m}I_{ s_{m}})\), then
that is
where \(F_{1,m}F_{2,m}^{T}\) is the matrix discarded during the application of Algorithm 1.
If \(Q_{1}^{(m)}R_{1}=[\overline {V}_{1},\mathcal V_{1,1},\ldots ,\mathcal V_{1,m}]\), \(Q_{2}^{(m)}R_{2}=[\overline {V}_{2},\mathcal V_{2,1},\ldots ,\mathcal V_{2,m}]\) denote the skinny QR factorizations performed during and \(U{\Sigma } W^{T}=R_{1}{\Theta }_{m}{R_{2}^{T}}\) is the SVD with \(U=[u_{1},\ldots ,u_{\mathfrak {s}_{m}}]\), \(W=[w_{1},\ldots ,w_{\mathfrak {s}_{m}}]\), \({\Sigma }=\text {diag}(\sigma _{1},\ldots ,\sigma _{\mathfrak {s}_{m}})\), \(\mathfrak {s}_{m}:=\overline {s}+{\sum }_{j=1}^{m} s_{j}\), then we consider the partitions
where \(U_{k_{m}}\), \(W_{k_{m}}\), \({\Sigma }_{k_{m}}\) contain the leading km singular vectors and singular values, respectively, and km is the smallest index such that \(\sqrt {{\sum }_{i=k_{m}+1}^{\mathfrak {s}_{m}}{\sigma _{i}^{2}}}\leq \varepsilon _{\mathtt {orth}}\|{\Sigma }\|\). We can write
and, since \(Q_{1}^{(m)}\), \(Q_{2}^{(m)}\), W and U are orthogonal matrices,
However, the rank truncation destroys the orthogonality of the expanded basis, in general, so that \(\langle \mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T}, \widetilde V_{1}\widetilde {V}_{2}^{T} \rangle _{F}\neq 0\) for all j = 1,…,m.
To retrieve the orthogonality of the basis we propose to perform an extra Gram-Schmidt step without rank truncation in order to reorthogonalize \(\widetilde V_{1}\widetilde {V}_{2}^{T}\) with respect to
Since the vectors \(\text {vec}(\widetilde V_{1}\widetilde {V}_{2}^{T})\) and \(\text {vec}(Q_{1}^{(m)}U_{k_{m}}(Q_{1}^{(m)}U_{k_{m}})^{T}\mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T}(Q_{2}^{(m)}W_{k_{m}})\) \((Q_{2}^{(m)}W_{k_{m}})^{T})\) both live in \(\text {Range}(Q_{2}^{(m)}W_{k_{m}})\otimes \text {Range}(Q_{1}^{(m)}U_{k_{m}})\), the extra orthogonalization step can be carefully implemented in order to involve only matrices of order km. Indeed, if \(\{{\Xi }^{(m)}_{j}, j=1,\ldots ,t_{m}\}\), \({\Xi }_{j}^{(m)}\in \mathbb {R}^{k_{m}\times k_{m}}\), tm ≤ m, is an orthonormal basis for \(\text {span}\{ (Q_{1}^{(m)}U_{k_{m}})^{T}\mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T}(Q_{2}^{(m)}W_{k_{m}}), j=1,\ldots ,m\}\), then we have \(\mathbb {V}_{m}=\text {span}\{Q_{1}^{(m)}U_{k_{m}}{\Xi }^{(m)}_{j}(Q_{2}^{(m)}W_{k_{m}})^{T}\}_{j=1,\ldots ,t_{m}}\) and we can thus write

where

so that the overall workload of Algorithm 2 does not remarkably increase. Notice that also the computation of the matrices \({\Xi }^{(m)}_{j}\)’s can be implemented such that only thekm × km matrices \((Q_{1}^{(m)}U_{k_{m}})^{T}\mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T}(Q_{2}^{(m)}W_{k_{m}})\) are manipulated. Morevover, such a reorthogonalization procedure does not increase the ranks of the results because 
We must mention that if \(\dim (\mathbb {V}_{m})={k_{m}^{2}}\), then  . However, such a scenario is very unlikely since tm ≤ m and m ≪ km in general; see, e.g., Section 7. Moreover, if the dimension of \(\mathbb {V}_{m}\) turns out to be \({k_{m}^{2}}\), we can always make a step back and consider a larger value of \(k_{m}\leq \mathfrak {s}_{m}\) in the construction of \(\widetilde V_{1}\), \(\widetilde V_{2}\) to be able to compute
. However, such a scenario is very unlikely since tm ≤ m and m ≪ km in general; see, e.g., Section 7. Moreover, if the dimension of \(\mathbb {V}_{m}\) turns out to be \({k_{m}^{2}}\), we can always make a step back and consider a larger value of \(k_{m}\leq \mathfrak {s}_{m}\) in the construction of \(\widetilde V_{1}\), \(\widetilde V_{2}\) to be able to compute  . Notice that we can always find such a km since for \(k_{m}=\mathfrak {s}_{m}\) we can set
. Notice that we can always find such a km since for \(k_{m}=\mathfrak {s}_{m}\) we can set  and this is orthogonal to \(\mathcal {V}_{1,j} \mathcal {V}_{2,j}^{T}\) for all j = 1,…,m by construction.
and this is orthogonal to \(\mathcal {V}_{1,j} \mathcal {V}_{2,j}^{T}\) for all j = 1,…,m by construction.
By defining  , then \(\mathcal {V}_{1,m+1}\mathcal {V}_{2,m+1}^{T}\) has unit norm and it is orthogonal with respect to \(\mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T}\) for all j = 1,…,m. Indeed, each \(\mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T}\) can be written as
, then \(\mathcal {V}_{1,m+1}\mathcal {V}_{2,m+1}^{T}\) has unit norm and it is orthogonal with respect to \(\mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T}\) for all j = 1,…,m. Indeed, each \(\mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T}\) can be written as
and, since
we have

The overall procedure is illustrated in Algorithm 3. To preserve the orthonormality of the computed basis, Algorithm 3 should be used in line 10 of Algorithm 2 in place of Algorithm 1.

We thus have shown the following proposition.
Proposition 3.2
The matrix \(V_{m+1}=[\text {vec}(\mathcal {V}_{1,1}\mathcal {V}_{2,1}^{T}),\ldots ,\text {vec}(\mathcal {V}_{1,m+1}\mathcal {V}_{2,m+1}^{T})]\in \mathbb {R}^{n^{2}\times (m+1)}\) computed by performing m iterations of Algorithm 2, where the low-rank truncations in line 10 are carried out using Algorithm 3, has orthonormal columns.
We would like to underline that the matrices \(\widetilde V_{1}\widetilde {V}_{2}^{T}\) and \(F_{1,m}F_{2,m}^{T}\) we compute are block-orthogonal to each other, i.e., \((\widetilde V_{1}\widetilde {V}_{2}^{T})^{T}F_{1,m}F_{2,m}^{T}=0\), see, e.g., [38], an not only orthogonal with respect to the matrix inner product 〈⋅,⋅〉F. This property is due to the QR-SVD-based truncation we perform which directly provides us with an orthonormal basis for the space \(\text {Range}(Q_{2}^{(m)}W_{k_{m}})\otimes \text {Range}(Q_{1}^{(m)}U_{k_{m}})\) where the second, exact orthogonalization step is carried out. Further computational efforts may be necessary if different truncation strategies are adopted.
The matrix \(\widetilde V_{1}\widetilde {V}_{2}^{T} =Q_{1}^{(m)}U_{k_{m}}{\Sigma }_{k_{m}}(Q_{2}^{(m)}W_{k_{m}})^{T}\) can be numerically orthogonal to \(\mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T}\), j = 1,…,m, if ε is very small and \(\text {span}(\widetilde V_{1}\widetilde {V}_{2}^{T})\approx \text {span}(\widetilde V_{1}\widetilde {V}_{2}^{T} +F_{1,m}F_{2,m}^{T})\). In this case, the second orthogonalization step is no longer necessary. Therefore, once the matrices \((Q_{1}^{(m)}U_{k_{m}})^{T}\mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T}Q_{2}^{(m)}W_{k_{m}}\) in line 4 of Algorithm 3 are computed, we suggest to calculate \(\langle {\Sigma }_{k},(Q_{1}^{(m)}U_{k_{m}})^{T}\mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T}Q_{2}^{(m)}W_{k_{m}}\rangle _{F}\) and perform the extra orthogonalization step only with respect those matrices for which a loss of orthogonality is detected.
We would like to mention that if the procedure presented in this section is not performed, the computed basis is not guaranteed to be orthogonal and the theory developed in, e.g., [39] may be exploited to estimate the distance of Vm to orthogonality and such a value can be incorporated in the bounds (3.3), (3.4) and (3.5) to preserve the convergence of the overall iterative scheme.
In spite of Proposition 3.2, in finite precision arithmetic the computed basis Vm+ 1 may fall short of being orthogonal and the employment of a modified Gram-Schmidt procedure with reorthogonalization—as outlined in Algorithm 2—is recommended. See, e.g., [40, 41] for some discussions about the loss of orthogonality in the Gram-Schmidt procedure.
The truncations performed during the Gram-Schmidt procedure consist in another source of inexactness that must be taken into account. Moreover, also the exact reorthogonalization step in Algorithm 3 introduces an extra factor in the Arnoldi relation (3.1).
Collecting all the steps presented in this section, we can write

so that the Arnoldi relation (3.1) becomes
where the matrix \(T_{m}\in \mathbb {R}^{n^{2}\times m}\) takes into account the extra orthogonalization step in Algorithm 3 and its j th column is given by

Therefore, we can write
and in the next section we show how to deal with the extra terms \(F_{1,k}F_{2,k}^{T}\) and Tm. In particular, the latter can be handled by modifying the inner problem formulation (2.6)–(2.8) whereas one can derive results similar to the ones in Theorem 3.1 to obtain estimates for \(\|E_{k}+ F_{1,k}F_{2,k}^{T}\|\).
3.2.1 Modified inner problem formulations
Since we are still looking for a solution of the form vec(Xm) = Vmym, by using the inexact Arnoldi relation (3.12) we can write
If we compute \(y_{m}^{fom}\) as the solution of the linear system
namely
then we are not imposing a Galerkin condition on the residual but a result similar to the one in Proposition 3.1 can be stated. Similarly, if we compute
i.e., \(y_{m}^{gm}\) is the solution of the normal equations
Proposition 3.3
Let (3.12) hold and define \(W_{m}=\mathcal {A}V_{m}-[\text {vec}(E_{1}+F_{1,1}F_{2,1}^{T}),\ldots ,\text {vec}(E_{m}+F_{1,m}F_{2,m}^{T})]\). If \(y_{m}^{gm}\) is computed as in (3.14) then \(q_{m}^{gm}:=W_{m}y_{m}^{gm}\) is such that
Similarly, if \(y_{m}^{fom}\) is computed as in (3.13) then \(q_{m}^{fom}:=W_{m}y_{m}^{fom}\) is such that
Proof
The proof follows exactly the same steps as the proof of [33, Proposition 3.2–3.3]. □
To make the overall scheme feasible also in terms of number of operations, the computation of the vectors \(y_{m}^{fom}\) and \(y_{m}^{gm}\) in (3.13)–(3.14) should not remarkably increase the workload of the iterative procedure. To this end, we first show that the matrix \({V_{m}^{T}}T_{m}\) in (3.13) can be computed at reasonable extra cost.
The j th column of Tm, j ≤ m, is given in (3.11) and we can thus write

Following the same argument of Section 3.2, we write
so that

Recalling that \(\text {span}\{ {\Xi }_{i}^{(j)}, i=1,\ldots ,t_{j}\}=\text {span}\{ (Q_{1}^{(j)}U_{k_{j}})^{T} \mathcal {V}_{1,i}\mathcal {V}_{2,i}^{T}(Q_{2}^{(j)}W_{k_{j}})\), i = 1,…,j}, then there exists a matrix \(\mathcal {R}_{j}\in \mathbb {R}^{t_{j}\times j}\) such that
If the matrices \((Q_{1}^{(j)}U_{k_{j}})^{T}\mathcal {V}_{1,i}\mathcal {V}_{2,i}^{T}(Q_{2}^{(j)}W_{k_{j}})\), i = 1,…,j, are linearly independent, the relation above corresponds to a skinny QR factorization and tj = j.
We can write

which means that the upper triangular part of \({V_{m}^{T}}T_{m}\) can be easily computed at low cost. Moreover, it easy to show that the first subdiagonal of \({V_{m}^{T}}T_{m}\) is zero. Indeed, for all j = 1,…,m − 1, \(\mathcal {V}_{1,j+1}\mathcal {V}_{2,j+1}^{T}=Q_{1}^{(j)}U_{k_{j}} {\Delta }_{k_{j}}(Q_{2}^{(j)}W_{k_{j}})^{T}\) so that
and \(\mathcal {V}_{1,j+1}\mathcal {V}_{2,j+1}\) is orthogonal to \(\text {span}\{{\Xi }^{(j)}_{i}\}_{i=1,\ldots ,t_{j}}\) by construction. We are thus left with computing the last m − j − 1 entries of \({V_{m}^{T}}T_{m}e_{j}\). These entries have to be explicitly computed via

This operation does not significantly increase the computational efforts of the overall procedure because it amounts to m − j − 1 matrix inner products with kj × kj matrices. This task has to be performed for all of the m columns of \({V_{m}^{T}}T_{m}\) so that we have to compute m ⋅ (m − j − 1) matrix inner products with small dimensional matrices. However, the computational cost can be reduced by exploiting the recursive structure of \({V_{m}^{T}}T_{m}\), namely

so that only the vector \(\text {vec}(\mathcal {V}_{1,m}\mathcal {V}_{2,m}^{T})^{T}T_{m-2}\) has to be computed at the m th iteration.
From a storage perspective, the computation of \({V_{m}^{T}}T_{m}\) first requires the allocation of \(Q_{1}^{(j)}U_{k_{j}}, Q_{2}^{(j)}W_{k_{j}}\) for all j = 1,…,m. This does not remarkably increase the memory requirements of the overall procedure if the basis vectors are represented by means of a LDU format, namely \(\mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T}=Q_{1}^{(j)}U_{k_{j}}{\Delta }_{j}(Q_{2}^{(j)}W_{k_{j}})^{T}\). Additionally, the matrices  have to be stored for all j = 1,…,m, but this introduces again reasonable extra costs since kj is supposed to be small.
have to be stored for all j = 1,…,m, but this introduces again reasonable extra costs since kj is supposed to be small.
If \(y_{m}^{gm}\) is computed as in (3.14), the exact same procedure as before can be applied to compute the terms \(\underline {H}_{m}^{T}V_{m+1}^{T}T_{m}\) and \({T_{m}^{T}}\text {vec}(C_{1}{C_{2}^{T}})=\beta {T_{m}^{T}}V_{1}\) in the normal equations formulation (3.15). A similar approach can be also adopted to compute the symmetric matrix \({T_{m}^{T}}T_{m}\) whose (ℓ,j)th entry is given by

3.2.2 Dealing with further inexactness
In contrast to what we have shown in the previous section for the term Tm in (3.12) that can be included in the formulation of the projected problem, the matrix \([\text {vec}(F_{1,1}F_{2,1}^{T}),\ldots ,\text {vec}(F_{1,m}F_{2,m}^{T})]\) is completely neglected to fully take advantage of the low-rank truncations we perform. On the other hand, by disregarding such term we introduce a further inexactness in our scheme.
Since
it may be interesting to study how to distribute the allowed inexactness between the truncation steps.
Since the rank of the iterates grows less dramatically during the orthogonalization step compared to what happens after the multiplication with \(\mathcal {A}\), we allow 2∥Ek∥ to grow in accordance with Theorem 3.1, while \(\| F_{1,k}F_{2,k}^{T}\|\) is maintained sufficiently small. Indeed, the matrix \([\overline {V}_{1},\mathcal {V}_{1,1},\ldots ,\mathcal {V}_{1,m}]{\Theta }_{m}[\overline {V}_{2},\mathcal {V}_{2,1}\ldots ,\mathcal {V}_{2,m}]^{T}\) in line 10 of Algorithm 2 is, in general, very rank-deficient and a significant reduction in the number of columns to be stored takes place even when the function is applied with a small threshold.
In particular, at the m th iteration, we can set
where ε is the desired accuracy of the final solution in terms of relative residual norm. This means that \(\|E_{k}+ F_{1,k}F_{2,k}^{T}\|\) fulfills the estimates in (3.3), (3.4) and (3.5) and the convergence is thus preserved.
The true relative residual norm can be written as
and following the discussion in Remark 3.2 we have
so that the right-hand side in the above expression must be computed to check convergence.
We would like to point that the norm of the computed residual \(\|\widetilde r_{m}\|\) can no longer be calculated as illustrated in Section 2 since the formulation of the inner problem is now changed. See Section 3.2.1. For LR-FOM we can write
so that also at the m th LR-FOM iteration the matrices \({T_{m}^{T}} T_{m}\) and the vector \({T_{m}^{T}}\text {vec}(\mathcal {V}_{1,m+1}\mathcal {V}_{2,m+1}^{T})\) have to be computed. Similarly, for LR-GMRES, we have
4 Alternative truncation strategies
As we discussed above, to keep the low-rank Krylov methods computationally feasible, the quantities involved in the solution process have to be compressed so that their rank, i.e., the sizes of the low-rank factors, is kept small. Let NMLT with factors \(N,L\in \mathbb {R}^{n\times m}\), \(M\in \mathbb {R}^{m\times m}\), be the quantity to be compressed, and assume that rank(NMLT) = m. So far we have used a direct approach using QR and SVD decompositions in Algorithms 1 and 3 which essentially computes a partial SVD of NMLT corresponding to all m nonzero singular values. This whole procedure relies heavily on dense linear algebra computations and can, hence, become quite expensive. This is especially due to the QR decompositions which will be expensive if the rectangular factors N,L have many columns. Moreover, if NMLT has a very small numerical numerical rank, say k ≪ m, then Algorithms 1 and 3 will generate a substantial computational overhead because m − k singular vectors will be thrown away. Nevertheless, thanks to the complete knowledge of all singular values, this procedure is able to correctly assess the truncation error in the Frobenius norm so that the required accuracy of the truncation is always met.
Following the discussion in, e.g., [14, 42, 43], a more economical alternative could be to compute only a partial SVD \(NML^{T}\approx U_{k}{\Sigma }_{k}{W_{k}^{T}}\) associated to the k singular values that are larger than the given truncation threshold. If also the (k + 1)th singular value is computed, one has the truncation error in the 2-norm: \(\|NML^{T}-U_{k}{\Sigma }_{k}{W_{k}^{T}}\|_{2}\leq \sigma _{k+1}(NML^{T})\).
Obviously, the results of the previous section are still valid if this form of truncation is used.
Approximations of the dominant singular values and corresponding singular vectors can be computed by iterative methods for large-scale SVD computations as, e.g., Lanczos bidiagonalization [44,45,46] or Jacobi-Davidson methods [47]. To apply these methods, only matrix vector products N(M(LTx)) and L(MT(NTx)) are required. For achieving the compression goal one could, e.g., compute \(k_{\max \limits }\geq k\) triplets and, if required, neglect any singular vectors corresponding to singular value below a certain threshold. However, we do in general not know in advance how many singular values will be larger than a given threshold. Picking a too small value of \(k_{\max \limits }\) can lead to very inaccurate truncations that do not satisfy the required thresholds (3.3)–(3.5), and (3.16) and, therefore, endanger the convergence of the low-rank Krylov method. Some of the aforementioned iterative SVD methods converge theoretically monotonically, i.e., the singular values are found in a decreasing sequence starting with the largest one. Hence, the singular value finding iteration can be kept running until a sufficiently small singular value approximation, e.g., \(\tilde \sigma < \varepsilon _{\text {trunc}}\|NML^{T}\|_{2}\), is detected. In the practical situations within low-rank Krylov methods, the necessary number of singular triplets can be \(\mathcal {O}(10^{2})\) or larger and it may be difficult to ensure that the iterative SVD algorithms do not miss some of the largest singular values or that no singular values are detected several times. Due to the sheer number of occurrences where compression is required in Algorithm 2, preliminary tests with iterative SVD methods did not yield any substantial savings compared to the standard approach used in Algorithms 1 and 3.
Compression algorithms based on randomized linear algebra might offer further alternative approaches with reduced computational times. See, e.g., [48,49,50].
5 Preconditioning
It is well-known that Krylov methods require preconditioning in order to obtain a fast convergence in terms of number of iterations and low-rank Krylov methods are no exception. However, due to the peculiarity of our framework, the preconditioner operator must possess some supplementary features with respect to standard preconditioners for linear systems. Indeed, in addition to be effective in reducing the number of iterations at a reasonable computational cost, the preconditioner operator must not dramatically increase the memory requirements of the solution process.
Given a nonsingular operator \(\mathcal {P}\) or its inverse \(\mathcal {P}^{-1}\), if we employ right preconditioning, the original system (1.2) is transformed into
so that, at each iteration m, we have to apply \(\mathcal {P}^{-1}\) to the current basis vector \(\text {vec}(\mathcal {V}_{1,m}\mathcal {V}_{2,m}^{T})\). Note that we restrict ourselves here to right preconditioning because this has the advantage that one can still monitor the true unpreconditioned residuals without extra work within the Krylov routine. Of course, in principle also left and two-sided preconditioning can be used.
The preconditioning operation must be able to exploit the low-rank format of \(\mathcal {V}_{1,m}\mathcal {V}_{2,m}^{T}\). Therefore, a naive operation of the form \(\mathcal {P}^{-1}\text {vec}(\mathcal {V}_{1,m}\mathcal {V}_{2,m}^{T})\) is not admissible in our context as this would require the allocation of the dense n × n matrix \(\mathcal {V}_{1,m}\mathcal {V}_{2,m}^{T}\). One way to overcome this numerical difficulty is to employ a preconditioner operator \(\mathcal {P}\) which can be represented as a Kronecker sum:
This means that the operation \(z_{m}=\mathcal {P}^{-1}\text {vec}(\mathcal {V}_{1,m}\mathcal {V}_{2,m}^{T})\) is equivalent to solving the matrix equation
In our setting, the operator \(\mathcal {P}\) often amounts to an approximation to \(\mathcal {A}\) in (1.2) obtained by either dropping some terms in the series or replacing some of them by a multiple of the identity. See, e.g., [4, 13, 51]. Another option that has not been fully explored in the matrix equation literature so far is the case of polynomial preconditioners (see, e.g., [52, 53]) where \(\mathcal {P}^{-1}\) resembles a fixed low-degree polynomial evaluated in \(\mathcal {A}\). Alternatively, we can formally set \(\mathcal {P}=\mathcal {A}\) in (5.2) and inexactly solve (5.3) by few iterations of another Krylov method (e.g., Algorithm 2) leading to an inner-outer or nested Krylov method; see, e.g., [54].
Clearly, (5.3) must be easy to solve. For instance, if ℓ = 1, then \(Y_{m}=(T_{1}^{-1}\mathcal {V}_{1,m})(P_{1}^{-1}\mathcal {V}_{2,m})^{T}\) and an exact application of the preconditioner can be carried out. Similarly, when ℓ = 2 and a fixed number of ADI iterations are performed at each Krylov iteration m, then it is easy to show that we are still working in an exact preconditioning framework. See, e.g., [6, 9]. In all these cases, the results presented in the previous sections still hold provided \(\mathcal {A}\) is replaced by the preconditioned matrix \(\mathcal {A}\mathcal {P}^{-1}\).
Equation (5.3) is often iteratively solved and, in general, this procedure leads to the computation of a low-rank approximation \(\mathcal {Z}_{1,m}\mathcal {Z}_{2,m}^{T}\) to Ym that has to be interpreted as a variable preconditioning scheme with a different preconditioning operator at each outer iteration. In these cases, a flexible variant of Algorithm 2 must be employed which consists in a standard flexible Krylov procedure equipped with the low-rank truncations presented in the previous sections. See, e.g., [55, Section 10] for some details about flexible Krylov methods and [31, Section 9.4.1; 56] for a discussion about flexible GMRES.
We must mention that the employment of a flexible procedure doubles, at least, the memory requirements of the solution process. Indeed, both the preconditioned and unpreconditioned bases must be stored and \(\text {rank}(\mathcal {Z}_{1,m}\mathcal {Z}_{2,m}^{T})\geq \text {rank}(\mathcal {V}_{1,m}\mathcal {V}_{2,m}^{T})\) for all m. This aspect must be taken into account when designing the preconditioner. See Example 1.
At a first glance, the presence of a variable preconditioning procedure can complicate the derivations illustrated in Sections 3.1–3.2 for the safe selection of the low-rank truncation thresholds that guarantees the convergence of the solution method. Indeed, if at iteration m, \(\mathcal {Z}_{1,m}\mathcal {Z}_{2,m}^{T}\) is the result of the preconditioning step (5.3), we still want to truncate the matrix
in order to moderate the storage demand and one may wonder if the inexactness of step (5.3) plays a role in such a truncation. Thanks to the employment of a flexible strategy, we are going to show how the tolerances for the low-rank truncations, namely \(\varepsilon _{\mathcal {A}}\) and ε in Algorithm 2, can be still computed as illustrated in Sections 3.1–3.2.
Flexible Krylov methods are characterized not only by having a preconditioner that changes at each iteration but also from the fact that the solution is recovered by means of the preconditioned basis. In particular,
see, e.g., [56]; this is a key ingredient in our analysis.
We start our discussion by considering flexible Krylov methods with no truncations. For this class of solvers the relation
holds, see, e.g., [31, Equation (9.22)], and \(\text {span}\{\text {vec}(\mathcal {Z}_{1,1}\mathcal {Z}_{2,1}^{T}),\ldots ,\text {vec}(\mathcal {Z}_{1,m}\mathcal {Z}_{2,m}^{T})\}\) is not a Krylov subspace in general. Therefore, also for the flexible Krylov methods with no low-rank truncations we must consider constrains different from the ones in (2.4)–(2.7) and results similar to the ones in Proposition 3.1 with \(W_{m}=\mathcal {A}Z_{m}\) hold. See, e.g., [31, Proposition 9.2].
If we now introduce a low-rank truncation of the matrix
at each iteration m, that is we compute
then the relation (5.4) becomes
where the matrices Ek’s are the ones discarded when (5.5) is performed. If ∥Ek∥ satisfies the inequalities in Theorem 3.1, then the convergence of the low-rank flexible Krylov procedure is still guaranteed in the sense that the residual norm keeps decreasing as long as \(\text {span}\{\text {vec}(\mathcal {Z}_{1,1}\mathcal {Z}_{2,1}^{T}),\ldots ,\text {vec}(\mathcal {Z}_{1,m}\mathcal {Z}_{2,m}^{T})\}\) grows. However, the matrix Hm no longer represents an approximation of \(\mathcal {A}\) onto the current subspace and approximations of \(\sigma _{m_{\max \limits }}(\underline {H}_{m_{\max \limits }})\) and \(\sigma _{1}(\underline {H}_{m_{\max \limits }})\) in the right-hand side of (3.3)–(3.4)–(3.5) via the corresponding singular values of \(\mathcal {A}\) may no longer be effective. In our numerical experience, approximating \(\sigma _{m_{\max \limits }}(\underline {H}_{m_{\max \limits }})\) and \(\sigma _{1}(\underline {H}_{m_{\max \limits }})\) by the smallest and largest singular values of the preconditioned matrix \(\mathcal {A}\mathcal {P}^{-1}\), i.e., mimicking what is done in case of exact applications of \(\mathcal {P}\), provides satisfactory results. Obtaining computable approximations to \(\sigma _{m_{\max \limits }}(\underline {H}_{m_{\max \limits }})\) and \(\sigma _{1}(\underline {H}_{m_{\max \limits }})\) for the inner-outer approach is not straightforward. In this case, a practical approach may be to still approximate \(\sigma _{m_{\max \limits }}(\underline {H}_{m_{\max \limits }})\) and \(\sigma _{1}(\underline {H}_{m_{\max \limits }})\) by \(\sigma _{n^{2}}(\mathcal {A})\) and \(\sigma _{1}(\mathcal {A})\), respectively. These approximations may be very rough as they completely neglect the role of the preconditioner so that they may lead to quite conservative truncation thresholds. However, at the moment, we do not see any another possible alternatives.
The introduction of the low-rank truncations that lead to (5.6) implies that the constraints imposed on the residual vector are no longer in terms of the space spanned by Zm and the results presented in Proposition 3.1 with \(W_{m}=\mathcal {A}Z_{m}-[\text {vec}(E_{1}),\ldots ,\text {vec}(E_{m})]\) hold.
In flexible Krylov methods, the orthogonalization procedure involves only the unpreconditioned basis Vm so that the truncation step in line 10 of Algorithm 2 is not really affected by the preconditioning procedure and the results in Propositions 3.2–3.3 are still valid. The truncation threshold ε can be still selected as proposed in Section 3.2.
6 Short recurrence methods
Short recurrence Krylov methods can be very appealing in our context as only a fixed, usually small, number of basis vectors have to be stored. In case of symmetric problems, i.e., (1.1) where all the coefficient matrices Ai’s and Bi’s are symmetric, the low-rank MINRES algorithm proposed in [57] can be employed in the solution process.
If \(\mathcal {A}\) in (1.2) is also positive definite, the low-rank CG method illustrated in [58] is a valid candidate for the solution of (1.1). Notice that, in general, it is not easy to characterize the spectral distribution of \(\mathcal {A}\) in terms of the spectrum of the coefficient matrices Ai’s and Bi’s. However, it can be shown that if Ai and Bi are positive definite for all i, then also \(\mathcal {A}\) is positive definite.
Short recurrence methods can be appealing also in case of a nonsymmetric \(\mathcal {A}\) and low-rank variants of BICGSTAB [59], QMR [60] or other methods can be employed to solve (1.1). See, e.g., [6, 14] for an implementation of low-rank MINRES, CG and BICGSTAB.
In many short recurrence Krylov methods, the constructed basis Vm is not orthogonal in practice and this loss of orthogonality must be taken into account in the bounds for the allowed inexactness proposed in Theorem 3.1. In [33, Section 6], the authors propose to incorporate the smallest singular value of the computed basis, namely σm(Vm), in the right-hand side of (3.3), (3.4) and (3.5) to guarantee the convergence of the method. However, no practical approximation to σm(Vm) is proposed in [33].
A different approach that can be pursued is the one illustrated in [61]. In this paper the authors propose to select bounds of the form
where \(\widetilde r_{k}\) is the current computed residual vector, and in [62] the authors studied the effects of such a choice on the convergence of a certain class of inexact Krylov methods. In particular, in [62] it is shown how the residual gap δm remains small if ∥Ek∥ fulfills (6.1) for all k ≤ m. Even though the true residual and the computed one are close, this does not imply that the residual norm is actually always small and we thus have to assume that the norm of the computed residual goes to zero as it is done in [62].
7 Numerical examples
In this section we present some numerical results that confirm the theoretical analysis derived in the previous sections. To this end we consider some general multiterm linear matrix equations of the form (1.1) stemming from the discretization of certain deterministic and stochastic PDEs.
We apply the LR-GMRES variant of Algorithm 2 in the solution process and we always select Algorithm 1 and 3 for the low-rank truncations as previously explained.
We report the number of performed iterations, the rank of the computed solution, the computational time needed to calculate such a solution together with the relative residual norm achieved, and the storage demand. For the latter, we document the number of columns \(\mathfrak {s}={\sum }_{j=1}^{m+1}s_{j}\) of the matrix \([\mathcal {V}_{1,1},\ldots ,\mathcal {V}_{1,m+1}]\), where m is the number of iterations needed to converge. Similarly, if a flexible strategy is adopted, we also report the number of columns \(\mathfrak {z}\) of \([\mathcal {Z}_{1,1},\ldots ,\mathcal {Z}_{1,m}]\).
This means that, for equations of the form (1.1) where nA = nB = n, we have to allocate \(2\mathfrak {s}\) (\(2(\mathfrak {s}+\mathfrak {z})\)) vectors of length n. If nA≠nB, the memory requirements amount to \(\mathfrak {s}\) (\(\mathfrak {s}+\mathfrak {z}\)) vectors of length nA and \(\mathfrak {s}\) (\(\mathfrak {s}+\mathfrak {z}\)) vectors of length nB.
The solution process is stopped as soon as the upper bound on the residual norm in (3.17), normalized by \(\|C_{1}{C_{2}^{T}}\|\), gets smaller than 10− 6.
As already mentioned, we always assume that the exact solution X admits accurate low-rank approximations. Nevertheless, if S1,S2 are the low-rank factors computed by Algorithm 2, we report also the real relative residual norm \(\|{\sum }_{i=1}^{p}A_{i}S_{1}{S_{2}^{T}}{B_{i}^{T}}+C_{1}{C_{2}^{T}}\|/\|C_{1}{C_{2}^{T}}\|\) in the following to confirm the reliability of our numerical procedure. Once again, the real residual norm can be computed at low cost by exploiting the low rank of \(S_{1}{S_{2}^{T}}\) and the cyclic property of the trace operator.
All results were obtained with Matlab R2017b [63] on a Dell machine with 2.4GHz processors and 250 GB of RAM.
Example 7.1
We consider a slight modification of Example 4 in [4]. In particular, the continuous problem we have in mind is the convection-diffusion equation
where ν > 0 is the viscosity parameter and the convection vector \(\vec {w}\) is given by
The centered finite differences discretization of (7.1) yields the following matrix equation
where \(T\in \mathbb {R}^{n\times n}\) is the negative discrete laplacian, \(B\in \mathbb {R}^{n\times n}\) corresponds to the discretization of the first derivative, Φi and Ψi are diagonal matrices collecting the nodal values of the corresponding functions ϕi, ψi, i = 1,2, and \(\mathbf {1}\in \mathbb {R}^{n}\) is the vector of all ones. See [4] for more details.
Equation (7.2) can be seen as a generalized Lyapunov equation since the overall operator we need to invert can be viewed as the sum of a Lyapunov operator \({\mathscr{M}}(X)=\nu TX+\nu XT\) and a linear operator \(\mathcal {N}(X)={\Phi }_{1}BX{\Psi }_{1}+{\Phi }_{2}XB^{T}{\Psi }_{2}\). However, the solution schemes available in the literature and tailored to this kind of problems cannot be applied to (7.2) in general. Indeed, to the best of our knowledge, all the existing methods for large-scale generalized equations rely on the existence of a convergence splitting of the overall discrete operator, namely \(\rho ({\mathscr{M}}^{-1}\mathcal {N})<1\), where ρ(⋅) denotes the spectral radius. See, e.g., [6, 7, 21]. The latter property may be difficult to meet in case of the convection-diffusion equation, especially for dominant convection.
We would like to mention that also different solution procedures based on, e.g., a low-rank multigrid method tailored to (7.2) which exploits the possible data-sparse format of the involved coefficient matrices can be employed as well. See, e.g., [64, 65].
We interpret (7.2) as a general multiterm matrix equation of the form (1.1) and we solve it by the preconditioned LR-GMRES. Following the discussion in [4], we use the operator
as preconditioner, where \(\overline {\psi }_{1},\overline {\phi }_{2}\in \mathbb {R}\) are the mean values of ψ1(y) and ϕ2(x) on (0,1), respectively.
At each LR-GMRES iteration, we approximately invert \({\mathscr{L}}\) by performing 10 iterations of the extended Krylov subspace method for Sylvester equationsFootnote 4 derived in [5]. Since this scheme gives a different preconditioner every time it is called, we must employ the flexible variant of LR-GMRES. To avoid an excessive increment in the memory requirements due to the allocation of both the preconditioned and unpreconditioned bases, we do not apply \({\mathscr{L}}\) to the current basis vector, i.e., at iteration k, we do not compute \(\mathcal {Z}_{1,k}\mathcal {Z}_{2,k}^{T}\approx {\mathscr{L}}^{-1}(\mathcal {V}_{1,k}\mathcal {V}_{2,k}^{T})\). We first truncate the low-rank factors \(\mathcal {V}_{1,k},\mathcal {V}_{2,k}\), namely we compute \((\mathcal {\widehat {V}}_{1,k},\mathcal {\widehat {V}}_{2,k})=\mathtt {trunc}(\mathcal {V}_{1,k},I,\mathcal {V}_{2,k},\varepsilon _{\mathtt {precond}})\), and then define \(\mathcal {Z}_{1,k},\mathcal {Z}_{2,k}\) such that \(\mathcal {Z}_{1,k}\mathcal {Z}_{2,k}^{T}\approx {\mathscr{L}}^{-1}(\mathcal {\widehat {V}}_{1,k}\mathcal {\widehat {V}}_{2,k}^{T})\). This procedure leads to a lower storage demand of the overall solution process and to less time consuming preconditioning steps. On the other hand, the effectiveness of the preconditioner in reducing the total iteration count may get weakened, especially for large ε. In the results reported in the following we have always set ε= 10− 3.
In Table 1 we report the results for different values of n and ν.
We notice that the number of iterations is very robust with respect to the problem dimension n, and thus the mesh-size, confirming the quality of the preconditioner \({\mathscr{L}}\). Unfortunately, this does not lead to a storage demand that is also independent of n. The rank of the basis vectors, i.e., the number of columns of the matrices \([\mathcal {V}_{1,1},\ldots ,\mathcal {V}_{1,m+1}]\) and \([\mathcal {Z}_{1,1},\ldots ,\mathcal {Z}_{1,m}]\) increases with the problem size. This trend is probably inherited from some intrinsic properties of the continuous problem but further studies in this direction are necessary. A similar behavior is observed when decreasing the viscosity parameter ν as well.
A growth in the rank of the basis vectors determines also a remarkable increment in the computational time as illustrated in Table 1. Indeed, the computational cost of basically all the steps of Algorithm 2, from the Arnoldi procedure and the low-rank truncations, to the preconditioning phase, depends on the rank of the basis vectors.
We also underline the fact that the true relative residual norm turns out to be always smaller than the normalized computed bound (3.17) validating the reliability of (3.17) as convergence check.
In Fig. 1 (left) we report the normalized bound (3.17) together with the truncation threshold \(\varepsilon _{\mathcal {A}}^{(j)}/\|C_{1}{C_{2}^{T}}\|_{F}\) for the case n = 5000 and ν = 0.5. We can appreciate how the tolerance for the low-rank truncations increases as the residual norm decreases. As already mentioned, this is a key element to obtain a solution procedure with a feasible storage demand. Moreover, in Fig. 1 (right) we document the increment in the rank of the vectors of the preconditioned and unpreconditioned bases as the iterations proceed. We also plot the rank of the unpreconditioned basis we would obtain if no truncations (and no preconditioning steps) were performed, i.e., 4j. We can see how we would obtain full-rank basis vectors after very few iterations with consequent impracticable memory requirements of the overall solution process.
Example 7.1, n = 5000, ν = 0.5. Left: Normalized bound (3.17) and \(\varepsilon _{j}^{(\mathcal {A})}/\|C_{1}{C_{2}^{T}}\|_{F}\) for j = 1,…,9. Right: Rank of the matrix representing the j th vector of the preconditioned and unpreconditioned basis
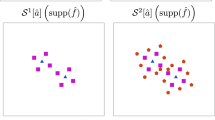
To conclude, in Fig. 2, we report the inner product between the last basis vector we have computed and the previous ones, namely we report \(\langle \mathcal {V}_{1,9}\mathcal {V}_{2,9}^{T},\mathcal {V}_{1,j}\mathcal {V}_{2,j}^{T}\rangle _{F}\) for j = 1,…,9. This numerically confirms that the strategy illustrated in Section 3.2 is able to maintain the orthogonality of the basis.
Example 7.2
In the second example we consider the algebraic problem stemming from the discretization of stochastic steady-state diffusion equations. In particular, given a sufficiently regular spatial domain D and a sample space Ω associated with the probability space \(({\Omega },\mathcal {F},\mathbb {P})\), we seek an approximation to the function \(u:D\times {\Omega }\rightarrow \mathbb {R}\) which is such that \(\mathbb {P}\)-almost surely
We consider D = [− 1,1]2 and we suppose a to be a random field of the form
where \(\sigma _{i}:{\Omega }\rightarrow {\Gamma }_{i}\subset \mathbb {R}\) are real-valued independent random variables (RVs).
In our case, a(x,ω) is a truncated Karhunen-Loève (KL) expansion
See, e.g., [66] for more details.
The stochastic Galerkin method discussed in, e.g., [13, 51, 67,68,69], leads to a discrete problem that can be written as a matrix equation of the form
where \(K_{i}\in \mathbb {R}^{n_{x}\times n_{x}}\), \(G_{i}\in \mathbb {R}^{n_{\sigma }\times n_{\sigma }}\), and \(f_{0} \in \mathbb {R}^{n_{x}}\), \(g_{0} \in \mathbb {R}^{n_{\sigma }}\). See, e.g., [13, 69].
We solve (7.5) by LR-GMRES and the following operators
are selected as preconditioners. \(\mathcal {P}_{\mathtt {mean}}\) is usually referred to as mean-based preconditioner, see, e.g., [13, 69] and the references therein, while Ullmann proposed \(\mathcal {P}_{\mathtt {Ullmann}}\) in [51].
Both \(\mathcal {P}_{\mathtt {mean}}\) and \(\mathcal {P}_{\mathtt {Ullmann}}\) are very well-suited for our framework as their application amounts to the solution of a couple of linear systems so that the rank of the current basis vector does not increase. See the discussion in Section 5. Moreover, supposing that these linear systems can be solved exactly by, e.g., a sparse direct solver, there is no need to employ flexible GMRES so that only one basis has to be stored. In particular, in all our tests, we precompute once and for all the LU factors of the matricesFootnote 5 which define the selected preconditioner so that only triangular systems are solved during the LR-GMRES iterations.
We generate instances of (7.5) with the help of the S-IFISSFootnote 6 package version 1.04; see [70]. The S-IFISS routine stoch_diff_testproblem_pc is executed to generate two instances of (7.5). The first equation (Data 1) is obtained by using a spatial discretization with 27 points in each dimension, r = 2 RVs in (7.4) which are approximated by polynomial chaos expansions of length ℓ = 100 leading to nx = 16129, nσ = 5151, and r + 1 = 3. The second instance (Data 2) was generated with 28 grid points, r = 5, and chaos expansions of length ℓ = 10 resulting in nx = 65025, nσ = 3003, and r + 1 = 6.
Table 2 summarizes the results and apparently problem Data 2 is much more challenging than Data 1. This is meanly due to the number of terms in (7.5). Indeed, the effectiveness of the preconditioners may deteriorate as r increases even though the actual capability of \(\mathcal {P}_{\mathtt {mean}}\) and \(\mathcal {P}_{\mathtt {Ullmann}}\) in reducing the iteration count is related to the coefficients of the KL expansion (7.4). See, e.g., [69, Theorem 3.8] and [51, Corollary 5.4]. Moreover, r + 1 terms are involved in the products in line 3 of Algorithm 2 and a sizable r leads, in general, to a faster growth in the rank of the basis vectors so that a larger number of columns are retained during the truncation step in line 4. As a result, the computational cost of our iterative scheme increases as well leading to a rather time consuming routine.
If the discrete operator stemming from the discretization of (7.3) is well posed, then it is also symmetric positive definite and the CG method can be employed in the solution process. See, e.g., [69, Section 3]. We thus try to apply the (preconditioned) low-rank variant of CG (LR-CG) to the matrix (7.5). To this end, we adopt the LR-CG implementation proposed in [6]. With the notation of [6, Algorithm 1] we truncate all the iterates Xk+ 1, Rk+ 1, Pk+ 1 and Qk+ 1. In particular, the threshold for the truncation of Xk+ 1 is set to 10− 12 while the value on the right-hand side of (6.1) is used at the k th LR-CG iteration for the low-rank truncation of all the other iterates. We want to point out that in the LR-CG implementation proposed in [6], the residual matrix Rk+ 1 is explicitly calculated by means of the current approximate solution Xk+ 1. We compute the residual norm before truncating Rk+ 1 so that what we are actually evaluating is the true residual norm and not an upper bound thereof.
The results are collected in Table 3 where the column “Mem.” reports the maximum number of columns that had to be stored in the low-rank factors of all the iterates Xk+ 1, Rk+ 1, Pk+ 1, Qk+ 1, and Zk+ 1.
Except for Data 1 with \(\mathcal {P}_{\mathtt {Ullmann}}\) as a preconditioner where LR-GMRES and LR-CG show similar results especially in terms of memory requirements, LR-CG allows for a much lower storage demand with a consequent reduction in the total computational efforts while achieving the prescribed accuracy. However, for Data 2, LR-CG requires a rather large number of iterations to converge regardless of the adopted preconditioner. This is due to a very small reduction of the residual norm, almost a stagnation, from one iteration to the following one we observe in the final stage of the algorithm. See Fig. 3 (left). This issue may be fixed by employing a more robust, possibly more conservative, threshold for the low-rank truncations. Alternatively, a condition of the form ∥Xk − Xk+ 1∥F ≤ ε can be included in the convergence check as proposed in [13].
We conclude by mentioning a somehow surprising behavior of LR-CG. In particular, in the first iterations the rank of all the iterates increases as expected, while it starts decreasing from a certain \(\overline {k}\) on until it reaches an almost constant value. See Fig. 3 (right). This trend allows for a feasible storage demand also when many iterations are performed as for Data 2. We think that such a phenomenon deserves further studies. Indeed, it seems that the truncation strategy we employed may be able to overcome a severe issue detected in previously studied Krylov methods for linear matrix equations like a possibly excessive increment of the ranks of the iterates during the transient phase of the adopted scheme. See, e.g., [71].
8 Conclusions
Low-rank Krylov methods are one of the few options for solving general linear matrix equations of the form (1.1), especially for large problem dimensions. An important step of these procedures consists in truncating the rank of the basis vectors to maintain a feasible storage demand of the overall solution process. In principle, such truncations can severely impact on the converge of the adopted Krylov routine.
In this paper we have shown how to perform the low-rank truncations in order to maintain the convergence of the selected Krylov procedure. In particular, our analysis points out that not only the thresholds employed for the truncations are important, but further care has to be adopted to guarantee the orthogonality of the computed basis. In particular, we propose to perform an auxiliary, exact Gram-Schmidt procedure in a low dimensional subspace which is able to retrieve the orthogonality of the computed basis—if lost—while preserving the memory-saving features of the latter. This additional orthogonalization step leads to a modified formulation of the inner problems and we have shown how this is still feasible in terms of computational efforts.
Notes
We note that also for p = 2, the equations we get when B1≠In, A2≠In are sometimes referred to as generalized Sylvester (Lyapunov) equations. In this work the term generalized always refers to the case p > 2 consisting of a Lyapunov/Sylvester operator plus a linear operator.
\(y_{m}=y_{m}^{fom}\) or \(y_{m}=y_{m}^{gm}\).
One after the application of \(\mathcal {A}\) in line 4, and two during the orthogonalization procedure in line 10, at the end of each of the two loops of the modified Gram-Schmidt method.
A Matlab implementation is available at http://www.dm.unibo.it/~simoncin/software.html.
The computational time of such decompositions is always included in the reported results.
References
Antoulas, A.C.: Approximation of large-scale dynamical systems, Advances in Design and Control, vol. 6. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2005)
VanDooren, P.M.: Structured linear algebra problems in digital signal processing. In: Numerical linear algebra, digital signal processing and parallel algorithms (Leuven, 1988), NATO Adv. Sci. Inst. Ser. F Comput. Systems Sci., vol. 70, pp 361–384. Springer, Berlin (1991)
Benner, P., Ohlberger, M., Cohen, A., Willcox, K.: Model reduction and approximation. Society for Industrial and Applied Mathematics, Philadelphia (2017)
Palitta, D., Simoncini, V.: Matrix-equation-based strategies for convection-diffusion equations. BIT 56(2), 751–776 (2016)
Breiten, T., Simoncini, V., Stoll, M.: Low-rank solvers for fractional differential equations. Electron. Trans. Numer. Anal. 45, 107–132 (2016)
Benner, P., Breiten, T.: Low rank methods for a class of generalized Lyapunov equations and related issues. Numer. Math. 124(3), 441–470 (2013)
Jarlebring, E., Mele, G., Palitta, D., Ringh, E.: Krylov methods for low-rank commuting generalized sylvester equations. Numer. Linear Algebra Appl. 25(6). e2176 (2018)
Benner, P., Damm, T.: Lyapunov equations, energy functionals, and model order reduction of bilinear and stochastic systems. SIAM J. Control Optim. 49(2), 686–711 (2011)
Damm, T.: Direct methods and ADI-preconditioned Krylov subspace methods for generalized Lyapunov equations. Numer. Linear Algebra Appl. 15 (9), 853–871 (2008)
Ringh, E., Mele, G., Karlsson, J., Jarlebring, E.: Sylvester-based preconditioning for the waveguide eigenvalue problem. Linear Algebra Appl. 542, 441–463 (2018)
Weinhandl, R., Benner, P., Richter, T.: Low-rank linear fluid-structure interaction discretizations. Z. Angew Math. Mech. Early View, e201900205 (2020)
Baumann, M., Astudillo, R., Qiu, Y., M.Ang, E.Y., van Gijzen, M.B., Plessix, R-E: An MSSS-preconditioned matrix equation approach for the time-harmonic elastic wave equation at multiple frequencies. Comput. Geosci. 22(1), 43–61 (2018)
Powell, C.E., Silvester, D., Simoncini, V.: An efficient reduced basis solver for stochastic Galerkin matrix equations. SIAM J. Sci. Comput. 39(1), A141–A163 (2017)
Stoll, M., Breiten, T.: A low-rank in time approach to PDE-constrained optimization. SIAM J. Sci. Comput. 37(1), B1–B29 (2015)
Freitag, M.A., Green, D.L.H.: A low-rank approach to the solution of weak constraint variational data assimilation problems. J. Comput. Phys. 357, 263–281 (2018)
Kürschner, P., Dolgov, S., Harris, K.D., Benner, P.: Greedy low-rank algorithm for spatial connectome regression. J. Math. Neurosci. 9 (2019)
Penzl, T.: Eigenvalue decay bounds for solutions of Lyapunov equations: the symmetric case. Systems Control Lett. 40(2), 139–144 (2000)
Baker, J., Embree, M., Sabino, J.: Fast singular value decay for Lyapunov solutions with nonnormal coefficients. SIAM J. Matrix Anal. Appl. 36 (2), 656–668 (2015)
Druskin, V., Simoncini, V.: Adaptive rational Krylov subspaces for large-scale dynamical systems. Systems Control Lett. 60(8), 546–560 (2011)
Simoncini, V.: A new iterative method for solving large-scale Lyapunov matrix equations. SIAM J. Sci. Comput. 29(3), 1268–1288 (2007)
Shank, S.D., Simoncini, V., Szyld, D.B.: Efficient low-rank solution of generalized Lyapunov equations. Numer. Math. 134(2), 327–342 (2016)
Benner, P., Li, R.-C., Truhar, N.: On the ADI method for Sylvester equations. J. Comput. Appl. Math. 233(4), 1035–1045 (2009)
Li, J.-R., White, J.: Low-rank solution of Lyapunov equations. SIAM Rev. 46(4), 693–713 (2004)
Baur, U., Benner, P.: Factorized solution of Lyapunov equations based on hierarchical matrix arithmetic. Computing 78(3), 211–234 (2006)
Baur, U.: Low rank solution of data-sparse Sylvester equations. Numer. Linear Algebra Appl. 15(9), 837–851 (2008)
Kressner, D., Steinlechner, M., Vandereycken, B.: Preconditioned low-rank Riemannian optimization for linear systems with tensor product structure. SIAM J. Sci. Comput. 38(4), A2018–A2044 (2016)
Vandereycken, B., Vandewalle, S.: A Riemannian optimization approach for computing low-rank solutions of Lyapunov equations. SIAM J. Matrix Anal. Appl. 31(5), 2553–2579 (2010)
Simoncini, V.: Computational methods for linear matrix equations. SIAM Rev. 58(3), 377–441 (2016)
Kressner, D., Sirković, P.: Truncated low-rank methods for solving general linear matrix equations. Numer. Linear Algebra Appl. 22(3), 564–583 (2015)
Kressner, D., Tobler, C.: Low-rank tensor Krylov subspace methods for parametrized linear systems. SIAM J. Matrix Anal. Appl. 32(4), 1288–1316 (2011)
Saad, Y.: Iterative methods for sparse linear systems, 2nd edn. SIAM, Society for Industrial and Applied Mathematics, Philadelphia (2003)
Saad, Y., Schultz, M.H.: GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Statist. Comput. 7(3), 856–869 (1986)
Simoncini, V., Szyld, D.B.: Theory of inexact Krylov subspace methods and applications to scientific computing. SIAM J. Sci. Comput. 25(2), 454–477 (2003)
Kressner, D., Tobler, C.: Krylov subspace methods for linear systems with tensor product structure. SIAM J. Matrix Anal. Appl. 31(4), 1688–1714 (2009/10)
Güttel, S.: Rational Krylov methods for operator functions. Ph.D. Thesis, Technische Universität Bergakademie Freiberg. Available online from the Qucosa server (2010)
Dolgov, S.V.: TT-GMRES: solution to a linear system in the structured tensor format. Russian J. Numer. Anal. Math. Modell. 28(2), 149–172 (2013)
Liesen, J., Strakos, Z.: Krylov subspace methods: Principles and analysis. Oxford University Press (2012)
Gutknecht, M.H.: Krylov subspace algorithms for systems with multiple right hand sides: an introduction. In: Siddiqi, A.H., Duff, I., Christensen, O. (eds.) Modern mathematical models, methods and algorithms for real world systems. Available at http://www.sam.math.ethz.ch/~mhg/pub/delhipap.pdf. Anshan Ltd (2007)
Kandler, U.: Inexact methods for the solution of large scale Hermitian eigenvalue problems. Ph.D. Thesis, Technische Universität Berlin (2019)
Giraud, L., Langou, J., Rozložník, M., vanden Eshof, J.: Rounding error analysis of the classical Gram-Schmidt orthogonalization process. Numer. Math. 101(1), 87–100 (2005)
Giraud, L., Langou, J., Rozloznik, M.: The loss of orthogonality in the Gram-Schmidt orthogonalization process. Comput. Math. Appl. 50(7), 1069–1075 (2005)
Benner, P., Onwunta, A., Stoll, M.: Low-rank solution of unsteady diffusion equations with stochastic coefficients. SIAM/ASA J. Uncertain. Quant. 3(1), 622–649 (2015)
Onwunta, A.: Low-rank iterative solvers for stochastic Galerkin linear systems. Dissertation, OVGU (2016)
Larsen, R.: Lanczos bidiagonalization with partial reorthogonalization. DAIMI Rep. Ser. 27, 537 (1998)
Baglama, J., Reichel, L.: Augmented implicitly restarted Lanczos bidiagonalization methods. SIAMSciComp 27(1), 19–42 (2005)
Stoll, M.: A Krylov-Schur approach to the truncated SVD. LinAlgapp 436(8), 2795–2806 (2012)
Hochstenbach, M.E.: A Jacobi–Davidson type SVD method. SIAMSciComp 23(2), 606–628 (2001)
Halko, N., Martinsson, P., Tropp, J.: Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions. SIAM Rev. 53(2), 217–288 (2011)
Kressner, D., Periša, L: Recompression of Hadamard products of tensors in Tucker format. SIAM J. Sci. Comput. 39(5), A1879–A1902 (2017)
Che, M., Wei, Y.: Randomized algorithms for the approximations of Tucker and the tensor train decompositions. Adv. Comput. Math. 45(1), 395–428 (2019)
Ullmann, E.: A Kronecker product preconditioner for stochastic Galerkin finite element discretizations. SIAM J. Sci. Comput. 32(2), 923–946 (2010)
van Gijzen, M.B.: A polynomial preconditioner for the GMRES algorithm. J. Comput. Appl. Math. 59(1), 91–107 (1995)
Liu, Q., Morgan, R.B., Wilcox, W.: Polynomial preconditioned GMRES and GMRES-DR. SIAM J. Sci. Comput. 37(5), S407–S428 (2015)
Simoncini, V., Szyld, D.B.: Flexible inner-outer Krylov subspace methods. SIAM J. Numer. Anal. 40(6), 2219–2239 (2003) (2002)
Simoncini, V., Szyld, D.B.: Recent computational developments in Krylov subspace methods for linear systems. Numer. Linear Algebra Appl. 14 (1), 1–59 (2007)
Saad, Y.: A flexible inner-outer preconditioned GMRES algorithm. SIAM J. Sci. Comput. 14(2), 461–469 (1993)
Paige, C.C., Saunders, M.A.: Solutions of sparse indefinite systems of linear equations. SIAM J. Numer. Anal. 12(4), 617–629 (1975)
Hestenes, M.R., Stiefel, E.: Methods of conjugate gradients for solving linear systems. J. Res. Nat. Bur. Stand. 49, 409–436 (1953) (1952)
vander Vorst, H.A.: Bi-CGSTAB: a fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems. SIAM J. Sci. Statist. Comput. 13(2), 631–644 (1992)
Freund, R.W., Nachtigal, N.M.: QMR: a quasi-minimal residual method for non-Hermitian linear systems. Numer. Math. 60(3), 315–339 (1991)
Bouras, A., Frayssé, V.: Inexact matrix-vector products in Krylov methods for solving linear systems: a relaxation strategy. SIAM J. Matrix Anal. Appl. 26(3), 660–678 (2005)
vanden Eshof, J., Sleijpen, G.L.G.: Inexact Krylov subspace methods for linear systems. SIAM J. Matrix Anal. Appl. 26(1), 125–153 (2004)
MATLAB: version 9.3.0 (r2017b). The MathWorks Inc., Natick (2017)
Grasedyck, L., Hackbusch, W.: A Multigrid Method to Solve Large Scale Sylvester Equations. SIAM J. Matrix Anal. Appl. 29(3), 870–894 (2007)
Elman, H.C., Su, T.: A Low-Rank Multigrid Method for the Stochastic Steady-State Diffusion Problem. SIAM J. Matrix Anal. Appl. 39(1), 492–509 (2018)
Lord, G.J., Powell, C.E., Shardlow, T.: An introduction to computational stochastic PDEs, Cambridge Texts in Applied Mathematics. Cambridge University Press (2014)
Babuška, I., Tempone, R., Zouraris, G.E.: Galerkin finite element approximations of stochastic elliptic partial differential equations. SIAM J. Numer. Anal. 42(2), 800–825 (2004)
Deb, M.K., Babuška, I.M., Oden, J.T.: Solution of stochastic partial differential equations using Galerkin finite element techniques. Comput. Methods Appl. Mech. Engrg. 190(48), 6359–6372 (2001)
Powell, C.E., Elman, H.C.: Block-diagonal preconditioning for spectral stochastic finite-element systems. IMA J. Numer. Anal. 29(2), 350–375 (2009)
Silvester, D.J., Bespalov, A., Powell, C.E.: S-IFISS version 1.04 (2017)
Kressner, D., Plešinger, M., Tobler, C.: A preconditioned low-rank CG method for parameter-dependent Lyapunov matrix equations. Numer. Linear Algebra Appl. 21(5), 666–684 (2014)
Acknowledgments
We thank Hussam Al Daas for insightful comments on earlier versions of the manuscript and the two anonymous reviewers for their constructive remarks.
The first author is a member of the Italian INdAM Research group GNCS. Part of this work was carried out while the second author was affiliated with the Max Planck Institute for Dynamics of Complex Technical Systems in Magdeburg, Germany.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Palitta, D., Kürschner, P. On the convergence of Krylov methods with low-rank truncations. Numer Algor 88, 1383–1417 (2021). https://doi.org/10.1007/s11075-021-01080-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-021-01080-2