Abstract
Fuzzy extractor (FE) extracts and reproduces a uniform string from a fuzzy source. Robustly reusable fuzzy extractor (rrFE) considers reusability and robustness simultaneously. Reusability of rrFE allows multiple extractions of pseudorandom strings from the same source and robustness detects active attacks. To achieve reusability and robustness, the existing constructions of rrFE make heavy use of perfect random coins (which are uniformly distributed and independent of each other), besides the fuzzy source. However, efficiently sampling unbiased random bits only exists in the ideal world. In this paper, we show how to construct rrFE resorting to imperfect randomness (non-uniform but of high entropy), which is easy to sample in practice. We propose two generic constructions of rrFE in the CRS model, with one construction dealing with perfect randomness and the other dealing with imperfect randomness. We also present two instantiations of rrFE from the DDH and LPN assumptions working with perfect randomness, and another two instantiations of rrFE from DDH and LPN working with imperfect randomness. All instantiations support linear fraction of errors between samples of the fuzzy source.
-
Our DDH-based rrFE (both rrFE with perfect randomness and rrFE with imperfect randomness) are the first tightly secure rrFEs in the standard model, i.e., the reusability and robustness are tightly reduced to the DDH assumption. Compared with the DDH-based rrFE scheme in PKC2019 by Wen et al., our rrFE enjoys tighter security, better efficiency, and support of usage of imperfect randomness.
-
Our LPN-based rrFE (both rrFE with perfect randomness and rrFE with imperfect randomness) are the first rrFEs from the LPN assumption in the standard model.
















Similar content being viewed by others
Notes
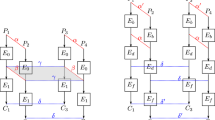
Indeed, the integration of \(\mathsf {Ext}\), \(\mathsf {Ext}'\) and \(\textsf { SKEM}\) (in the dashed frame in Fig. 5) can be regarded as a computational, unbounded non-malleable two-source extractor, but the correlation between w and \({w}_i\) is limited to adversary-chosen perturbations \(\delta _i\).
In an information-theoretic setting, the cryptographic scheme is secure means that, for any all-powerful adversary \(\mathcal {A}\), it implements a successful attack on the scheme with probability \(\zeta _A\) at most \(2^{-\varOmega (\lambda )}\). We can always consider \(\zeta _A=0+2^{-\varOmega (\lambda )}\), which means the security loss is 0. Hence, information-theoretical cryptographic scheme like [11] always enjoys tight security.
Vadhan showed the relationship between strong seeded extractor and average strong seeded extractor in [28] (Problem 6.8), and we extend the proof to deal with two-source extractor.
The definition of truncated source \({\hat{R}}_{\textsf {truncate}}\) can be found in Remark 9.
The definition of truncated source \({\hat{R}}_{\textsf {truncate}}\) can be found in Remark 9.
References
Alamélou Q., Berthier P., Cachet C., Cauchie S., Fuller B., Gaborit P., Simhadri S.: Pseudoentropic isometries: a new framework for fuzzy extractor reusability. In: Proceedings of the 2018 on Asia Conference on Computer and Communications Security, AsiaCCS 2018, Incheon, Republic of Korea, 04–08 June 2018, pp. 673–684 (2018).
Apon D., Cho C., Eldefrawy K., Katz J.: Efficient, reusable fuzzy extractors from LWE. In: Cyber Security Cryptography and Machine Learning—First International Conference, CSCML 2017, Beer-Sheva, Israel, June 29-30, 2017, Proceedings, pp. 1–18 (2017).
Bennett C.H., Shor P.W.: Quantum information theory. IEEE Trans. Inf. Theory 44(6), 2724–2742 (1998).
Boyen X.: Reusable cryptographic fuzzy extractors. In: Proceedings of the 11th ACM Conference on Computer and Communications Security, CCS 2004, Washington, DC, USA, 25–29 October 2004, pp. 82–91 (2004).
Boyen X., Dodis Y., Katz J., Ostrovsky R., Smith A.D.: Secure remote authentication using biometric data. In: Advances in Cryptology—EUROCRYPT 2005, 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Aarhus, Denmark, 22–26 May 2005, Proceedings, pp. 147–163 (2005).
Canetti R., Fuller B., Paneth O., Reyzin L., Smith A.D.: Reusable fuzzy extractors for low-entropy distributions. In: Advances in Cryptology–EUROCRYPT 2016—35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, 8–12 May 2016, Proceedings, Part I, pp. 117–146 (2016).
Cherkaoui A., Bossuet L., Marchand C.: Design, evaluation, and optimization of physical unclonable functions based on transient effect ring oscillators. IEEE Trans. Inf. Forensics Security 11(6), 1291–1305 (2016).
Cramer R., Dodis Y., Fehr S., Padró C., Wichs D.: Detection of algebraic manipulation with applications to robust secret sharing and fuzzy extractors. In: Advances in Cryptology - EUROCRYPT 2008, 27th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Istanbul, Turkey, 13–17 April 2008. Proceedings, pp. 471–488 (2008).
Daugman J.: How iris recognition works. IEEE Trans. Circuits Syst. Video Technol. 14(1), 21–30 (2004).
Dodis Y., Elbaz A., Oliveira R., Raz R.: Improved randomness extraction from two independent sources. In: Approximation, Randomization, and Combinatorial Optimization, Algorithms and Techniques, 7th International Workshop on Approximation Algorithms for Combinatorial Optimization Problems, APPROX 2004, and 8th International Workshop on Randomization and Computation, RANDOM 2004, Cambridge, MA, USA, 22–24 August, 2004, Proceedings, pp. 334–344 (2004).
Dodis Y., Reyzin L., Smith A.D.: Fuzzy extractors: How to generate strong keys from biometrics and other noisy data. In: Advances in Cryptology—EUROCRYPT 2004, International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004, Proceedings, pp. 523–540 (2004).
Dodis Y., Katz J., Reyzin L., Smith A.D.: Robust fuzzy extractors and authenticated key agreement from close secrets. In: Advances in Cryptology—CRYPTO 2006, 26th Annual International Cryptology Conference, California, USA, 20–24 August 2006, Proceedings, pp. 232–250 (2006).
Dodis Y., Ostrovsky R., Reyzin L., Smith A.D.: Fuzzy extractors: How to generate strong keys from biometrics and other noisy data. SIAM J. Comput. 38(1), 97–139 (2008).
Fuller B., Meng X., Reyzin L.: Computational fuzzy extractors. In: Advances in Cryptology—ASIACRYPT 2013—19th International Conference on the Theory and Application of Cryptology and Information Security, Bengaluru, 1–5 December 2013, Proceedings, Part I, pp. 174–193 (2013).
Gilbert H., Robshaw M.J.B., Seurin Y.: How to encrypt with the LPN problem. In: Automata, Languages and Programming, 35th International Colloquium, ICALP 2008, Reykjavik, Iceland, 7–11 July 2008, Proceedings, Part II—Track B: Logic, Semantics, and Theory of Programming & Track C: Security and Cryptography Foundations, pp. 679–690 (2008).
Guruswami V., Håstad J., Sudan M., Zuckerman D.: Combinatorial bounds for list decoding. IEEE Trans. Inf. Theory 48(5), 1021–1034 (2002).
Han S., Liu S., Lyu L.: Efficient KDM-CCA secure public-key encryption for polynomial functions. In: Advances in Cryptology—SIACRYPT 2016—22nd International Conference on the Theory and Application of Cryptology and Information Security, Hanoi, Vietnam, 4–8 December 2016, Proceedings, Part II, pp. 307–338 (2016).
Herder C., Yu M.M., Koushanfar F., Devadas S.: Physical unclonable functions and applications: a tutorial. Proc. IEEE 102(8), 1126–1141 (2014).
Herder C., Ren L., van Dijk M., Yu M.M., Devadas S.: Trapdoor computational fuzzy extractors and stateless cryptographically-secure physical unclonable functions. IEEE Trans. Dependable Sec. Comput. 14(1), 65–82 (2017).
Jain A.K., Ross A., Prabhakar S.: An introduction to biometric recognition. IEEE Trans. Circuits Syst. Video Technol. 14(1), 4–20 (2004).
Kanukurthi B., Reyzin L.: An improved robust fuzzy extractor. In: Security and Cryptography for Networks, 6th International Conference, SCN 2008, Amalfi, Italy, 10–12 September 2008. Proceedings, pp. 156–171 (2008).
Marasco E., Ross A.: A survey on antispoofing schemes for fingerprint recognition systems. ACM Comput. Surv. 47(2), 28:1–28:36 (2014).
Nisan N., Zuckerman D.: Randomness is linear in space. J. Comput. Syst. Sci. 52(1), 43–52 (1996).
Shaltiel R.: Recent developments in explicit constructions of extractors. Bull. EATCS 77, 67–95 (2002).
Shoup V.: A Computational Introduction to Number Theory and Algebra. Cambridge University Press, Cambridge (2006).
Sun X., Li B., Lu X.: Cramer-shoup like chosen ciphertext security from LPN. In: López, J., Wu, Y. (eds.) Information Security Practice and Experience—11th International Conference, ISPEC 2015, Beijing, China, 5–8 May 2015. Proceedings. Lecture Notes in Computer Science, vol. 9065, pp. 79–95. Springer, Cham (2015).
Ta-Shma A., Zuckerman D., Safra S.: Extractors from Reed–Muller codes. J. Comput. Syst. Sci. 72(5), 786–812 (2006).
Vadhan S.P.: Pseudorandomness. Found. Trends Theor. Comput. Sci. 7(1–3), 1–336 (2012).
Wen Y., Liu S.: Reusable fuzzy extractor from LWE. In: Information Security and Privacy—23rd Australasian Conference, ACISP 2018, Wollongong, NSW, Australia, 11–13 July 2018, Proceedings, pp. 13–27 (2018)
Wen Y., Liu S.: Robustly reusable fuzzy extractor from standard assumptions. In: Advances in Cryptology—ASIACRYPT 2018—24th International Conference on the Theory and Application of Cryptology and Information Security, Australia, 2–6 December 2018, Proceedings, Part III, pp. 459–489 (2018).
Wen Y., Liu S., Han S.: Reusable fuzzy extractor from the decisional Diffie–Hellman assumption. Des. Codes Cryptogr. 86(11), 2495–2512 (2018).
Wen Y., Liu S., Gu D.: Generic constructions of robustly reusable fuzzy extractor. In: Public-Key Cryptography - PKC 2019 - 22nd IACR International Conference on Practice and Theory of Public-Key Cryptography, Beijing, China, 14–17 April 2019, Proceedings, Part II, pp. 349–378 (2019).
Yu Y., Steinberger J.P.: Pseudorandom functions in almost constant depth from low-noise LPN. In: Fischlin, M., Coron, J. (eds.) Advances in Cryptology—EUROCRYPT 2016—35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, 8–12 May 2016, Proceedings, Part II. Lecture Notes in Computer Science, vol. 9666, pp. 154–183. Springer (2016).
Acknowledgements
Special thanks go to the anonymous reviewers who give us helpful comments and insightful observations. Shengli Liu and Nan Cui were partially supported by National Natural Science Foundation of China (NSFC No. 61925207) and Guangdong Major Project of Basic and Applied Basic Research (2019B030302008). Dawu Gu were partially supported by NSFC No. 61932014. Jian Weng was partially supported by National Natural Science Foundation of China under Grant Nos. U1736203, 61825203 and 61732021, Major Program of Guangdong Basic and Applied Research Project under Grant No. 2019B030302008.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Padro.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Proofs of Lemmas 7, 8, 9
1.1 A.1 Proof of Lemma 7
Proof
The proof is similar to the proof of Lemma 4. By Proposition 1, we have \(||(\mathsf {Ext}(\mathsf {w},\tilde{\mathsf {r}}),\tilde{\mathsf {r}},\mathsf {s}=\mathsf {SS.Gen}(\mathsf {w}))-(U,\tilde{\mathsf {r}},\mathsf {s}=\mathsf {SS.Gen}(\mathsf {w}))||\le \zeta _1+2^{-\omega (\log \lambda )}.\)
Assume there exists an adversary \(\mathcal {A}\) such that \(|\Pr [\mathbf{G_2}\Rightarrow 1]-\Pr [\mathbf{G_1}\Rightarrow 1]|=\zeta _1+2^{-\omega (\log \lambda )}\), then we can construct an all-powerful adversary \({\mathcal {B}}\) to distinguish \((\mathsf {Ext}(\mathsf {w},\tilde{\mathsf {r}}),\tilde{\mathsf {r}},\mathsf {s}=\mathsf {SS.Gen}(\mathsf {w}))\) from \(({ U},\tilde{\mathsf {r}},\mathsf {s}=\mathsf {SS.Gen}(\mathsf {w}))\) with advantage \(\zeta _1+2^{-\omega (\log \lambda )}\). The powerful adversary \({\mathcal {B}}\) simulates \(\mathbf{G_2/G_1}\) for \(\mathcal {A}\) as follows.
-
On receiving (\(\textsf {X},{\tilde{\mathsf {r}}},\mathsf {s})\) where \(\mathsf X\) is either \(\mathsf {Ext}(\mathsf {w},\tilde{\mathsf {r}})\) or U, \({\mathcal {B}}\) invokes \(\mathsf {pp}_{\mathsf {skem}}\leftarrow {\textsf {SKEM.Setup}}(1^{\lambda })\), sets \(\mathsf {pp}=(\tilde{\mathsf {r}}, \mathsf {pp}_{\mathsf {skem}})\) and returns \(\mathsf {pp}\) to the adversary \(\mathcal {A}\).
-
Upon receiving the ith challenge query \(\delta _i\) from \(\mathcal {A}\) with \({\textsf {dis}}(\delta _i)\le t\), \({\mathcal {B}}\) simulates \({\mathcal {O}}_{\mathtt{rob}}(\delta _i)\) for \(\mathcal {A}\) as follows:
-
Compute \(\mathsf {s}_i=\mathsf {s}+\mathsf {SS.Gen}(\delta _i)\), \(\mathsf {k}_i=\textsf {X}+\mathsf {Ext}(\delta _i,\tilde{\mathsf {r}})\) and set \(\mathsf {k}_i:=(\mathsf {k}_{i1},\mathsf {k}_{i2})\).
-
Choose \(\hat{\mathsf {r}}_i\leftarrow {\hat{R}}\) and compute \(\mathsf {r}_i=\mathsf {Ext}^\prime (\hat{\mathsf {r}}_i, \mathsf {k}_{i2})\).
-
Compute \((\mathsf {K}_i,\mathsf {C}_i)\leftarrow \mathsf {SKEM.Encap}(\mathsf {k}_{i1};\mathsf {r}_i)\) and parse \(\mathsf {K}_i=(\mathsf {K}_{i1},\mathsf {K}_{i2})\).
-
Set \(\sigma _i:=\mathsf {K}_{i1}\), \(\mathsf {R}_i:=\mathsf {K}_{i2}\), \(\mathsf {P}_i:=(\mathsf {s}_i,\mathsf {C}_i, \sigma _i)\) and \(\mathcal {Q}:= \mathcal {Q}\cup \{\mathsf {P}_i\}\).
-
Return \((\mathsf {P}_i,\mathsf {R}_i)\).
-
-
Upon receiving \(\mathcal {A}\)’s forgery \((\mathsf {P}^*,\delta ^*)\) with \(\mathsf {P}^*=(\mathsf {s}^*,\mathsf {C}^*,{\sigma }^*)\). If \({\textsf {dis}}(\delta ^*)>t\) or \(\mathsf {P}^*\in \mathcal {Q}\), return 0. Otherwise, \({\mathcal {B}}\) calculates \(\tilde{\delta }^*=g(\delta ^*, \mathsf {s}, \mathsf {s}^*)\), \(\tilde{\mathsf {k}}=\textsf {X}+\mathsf {Ext}(\tilde{\delta }^*,\tilde{\mathsf {r}})\), sets \(\tilde{\mathsf {k}}:=(\tilde{\mathsf {k}}_1,\tilde{\mathsf {k}}_2)\) and invokes \(\tilde{\mathsf {K}}\leftarrow \mathsf {SKEM.Decap}(\tilde{\mathsf {k}}_1,\mathsf {C}^*)\). After that, \({\mathcal {B}}\) parses \(\tilde{\mathsf {K}}=(\tilde{\mathsf {K}}_1,\tilde{\mathsf {K}}_2)\) and sets \(\tilde{{\sigma }}:=\tilde{\mathsf {K}}_1\). If \({\sigma }^*=\tilde{{\sigma }}\), return 1. Else, return 0.
If \(\textsf {X}=\textsf {Ext}(\mathsf {w},{\tilde{\mathsf {r}}})\), \({\mathcal {B}}\) perfectly simulates \(\mathbf{G}_1\); if \(\textsf {X}=U\), \({\mathcal {B}}\) perfectly simulates \(\mathbf{G}_2\). Hence, we can get
\(\square \)
1.2 A.2 Proof of Lemma 8
Proof
The proof is similar to the proof of Lemma 5, we prove the lemma by a series of games \(\mathbf{G}_{2.i}\), \(i\in [0,Q]\). The specific description of \(\mathbf{G}_{2.i}\) is shown below.
-
I.
Challenger \({\mathcal {C}}\) samples \(\tilde{\mathsf {r}}\leftarrow {\hat{R}}\), \(\mathsf {w}\leftarrow W\), invokes \(\mathsf {pp}_{\mathsf {skem}}\leftarrow {\textsf {SKEM.Setup}}(1^{\lambda })\), initializes \(\mathcal {Q}=\emptyset \). It computes \(\mathsf {s}\leftarrow \mathsf {SS.Gen}(\mathsf {w})\), chooses \(\mathsf {k}\leftarrow _{\$}\mathcal {S}\), sets \(\mathsf {k}:=(\mathsf {k}_1,\mathsf {k}_2)\). It sets \(\mathsf {pp}:=(\tilde{\mathsf {r}}, \mathsf {pp}_{\mathsf {skem}})\) and sends \(\mathsf {pp}\) to the adversary.
-
II.
Upon receiving the jth challenge query \(\delta _j\) from \(\mathcal {A}\) with \({\textsf {dis}}(\delta _j)\le t\), \({\mathcal {C}}\) does as follows.
-
1.
Compute \(\mathsf {s}_j=\mathsf {s}+\mathsf {SS.Gen}(\delta _j)\) and \(\mathsf {k}_{j1}=\mathsf {k}_1+\varDelta _{j1}\).
-
2.
-
If \(j<i\), \(\mathsf {r}_j\leftarrow _{\$}{\mathcal {R}}\).
-
If \(j=i\), \(\mathsf {k}_{j2}=\mathsf {k}_2+\varDelta _{j2}\), \(\mathsf {r}_j\leftarrow _{\$}{\mathcal {R}}\).
-
If \(j>i\), \(\mathsf {k}_{j2}=\mathsf {k}_2+\varDelta _{j2}\), \(\hat{\mathsf {r}}_j\leftarrow {\hat{R}}\), \(\mathsf {r}_j\leftarrow \mathsf {Ext}'(\hat{\mathsf {r}}_j,\mathsf {k}_{j2})\).
-
-
3.
Compute \((\mathsf {K}_j,\mathsf {C}_j)\leftarrow \mathsf {SKEM.Encap}(\mathsf {k}_{j1};\mathsf {r}_j)\) and parse \(\mathsf {K}_j=(\mathsf {K}_{j1},\mathsf {K}_{j2})\).
-
4.
Set \(\sigma _j:=\mathsf {K}_{j1}\), \(\mathsf {R}_j:=\mathsf {K}_{j2}\), \(\mathsf {P}_j:=(\mathsf {s}_j,\mathsf {C}_j, \sigma _j)\) and \(\mathcal {Q}:= \mathcal {Q}\cup \{\mathsf {P}_j\}.\)
-
5.
Return \((\mathsf {P}_j,\mathsf {R}_j)\).
-
1.
-
III.
Upon receiving \(\mathcal {A}\)’s forgery \((\mathsf {P}^*,\delta ^*)\) with \(\mathsf {P}^*=(\mathsf {s}^*,\mathsf {C}^*,{\sigma }^*)\). If \({\textsf {dis}}(\delta ^*)>t\) or \(\mathsf {P}^*\in \mathcal {Q}\), return 0. Otherwise, \({\mathcal {B}}\) calculates \(\tilde{\delta }^*=g(\delta ^*,\mathsf {s},\mathsf {s}^*)\), \(\tilde{\mathsf {k}}=\mathsf {k}+\mathsf {Ext}(\tilde{\delta }^*,\tilde{\mathsf {r}})\), sets \(\tilde{\mathsf {k}}:=(\tilde{\mathsf {k}}_1,\tilde{\mathsf {k}}_2)\), and invokes \(\tilde{\mathsf {K}}\leftarrow \mathsf {SKEM.Decap}(\tilde{\mathsf {k}}_1,\mathsf {C}^*)\). After that, \({\mathcal {B}}\) parses \(\tilde{\mathsf {K}}=(\tilde{\mathsf {K}}_1,\tilde{\mathsf {K}}_2)\) and sets \(\tilde{{\sigma }}:=\tilde{\mathsf {K}}_1\). If \({\sigma }^*=\tilde{{\sigma }}\), return 1. Else, return 0.
Clearly, \(\mathbf{G}_{2.0}\) is identical to \( \mathbf{G}_2\) and \(\mathbf{G}_{2.Q}\) is identical to \( \mathbf{G}_3\), so we have
Proposition 4
\(|\Pr [\mathbf{G}_{2.i-1}\Rightarrow 1]-\Pr [\mathbf{G}_{2.i}\Rightarrow 1]|\le \zeta _2\) for \(i\in [Q]\).
Recall that \({\hat{R}}\) is \((\hat{{\mathcal {R}}},Q+1,b_{\hat{\mathsf {r}}})\)-correlated source, so \(\tilde{H}_{\infty }(\hat{\mathsf {r}}_{i}|\{\hat{\mathsf {r}}_{j}\}_{j\in [i-1]},\tilde{\mathsf {r}})\ge b_{\hat{\mathsf {r}}}\). Meanwhile, \(\mathsf {Ext}'\) is a \((b_{\hat{\textsf {r}}},\zeta _2)\)-strong seeded extractor, then by Definition 10,
where \({\textsf {U}}\leftarrow _{\$}{\mathcal {R}}\), \(\bar{\textsf {k}}\) is uniformly chosen. Assume there exists an adversary \(\mathcal {A}\) such that \(|\Pr [\mathbf{G}_{2.i-1}\Rightarrow 1]-\Pr [\mathbf{G}_{2.i}\Rightarrow 1]|=\zeta \), then we can construct an all-powerful algorithm \({\mathcal {B}}\) who can distinguish \((\mathsf {Ext}'(\hat{\mathsf {r}}_i,\bar{\mathsf {k}}),\bar{\mathsf {k}})\) from \(({\textsf {U}},\bar{\mathsf {k}})\) with the same advantage \(\zeta \). Given \((\textsf {X}, \bar{\mathsf {k}})\), where \(\textsf {X}\) is either \(\mathsf {Ext}'(\hat{\mathsf {r}}_i,\bar{\mathsf {k}})\) or \({\textsf {U}}\), \({\mathcal {B}}\) simulates the experiment \(\mathbf{G}_{2.i-1}'/\mathbf{G}_{2.i}\) for \(\mathcal {A}\) as follows.
-
Given the pair \((\textsf {X},\bar{\mathsf {k}})\), algorithm \({\mathcal {B}}\) samples \(\mathsf {w}\leftarrow W\), \(\tilde{\mathsf {r}}\leftarrow {\hat{R}}\) and invokes \(\mathsf {pp}_{\mathsf {skem}}\leftarrow {\textsf {SKEM.Setup}}(1^{\lambda })\). It sets \(\mathsf {pp}:=(\tilde{\mathsf {r}},\mathsf {pp}_{\mathsf {skem}})\), samples \(\mathsf {k}\leftarrow _{\$}{\mathcal {R}}\), sets \(\mathsf {k}:=(\mathsf {k}_1,\mathsf {k}_2)\), and returns \(\mathsf {pp}\) to \(\mathcal {A}\).
-
Upon receiving the jth challenger query \(\delta _j\) from \(\mathcal {A}\) with \({\textsf {dis}}(\delta _j)\le t\), algorithm \({\mathcal {B}}\) does as follows:
-
Compute \(\mathsf {s}_j=\mathsf {SS.Gen}(\mathsf {w})+\mathsf {SS.Gen}(\delta _j)=\mathsf {s}+\mathsf {SS.Gen}(\delta _j)\).
-
Parse \(\mathsf {Ext}(\delta _j,\tilde{\mathsf {r}})=(\varDelta _{j1},\varDelta _{j2})\).
-
Compute \(\mathsf {k}_{j1}=\mathsf {k}_1+\varDelta _{j1}\).
-
-
If \(j<i\), randomly choose \(\mathsf {r}_j\leftarrow _{\$}{\mathcal {R}}\);
-
If \(j=i\), set \(\mathsf {k}_{j2}=\bar{\mathsf {k}}\), \(\mathsf {r}_j=\textsf {X}\);
-
If \(j>i\), compute \(\mathsf {k}_{j2}=\bar{\mathsf {k}}-\varDelta _{i2}+\varDelta _{j2}\), choose \(\hat{\mathsf {r}}_j\leftarrow {\hat{R}}\), and compute \(\mathsf {r}_j\leftarrow \mathsf {Ext}'(\hat{\mathsf {r}}_j,\mathsf {k}_{j2})\).
-
-
Compute \((\mathsf {K}_j,\mathsf {C}_j)\leftarrow \mathsf {SKEM.Encap}(\mathsf {k}_{j1};\mathsf {r}_j)\) and parse \(\mathsf {K}_j=(\mathsf {K}_{j1},\mathsf {K}_{j2})\).
-
Set \(\sigma _j:=\mathsf {K}_{j1}\), \(\mathsf {R}_j:=\mathsf {K}_{j2}\), \(\mathsf {P}_j:=(\mathsf {s}_j,\mathsf {C}_j, \sigma _j)\), and \(\mathcal {Q}:= \mathcal {Q}\cup \{\mathsf {P}_j\}.\)
-
Return \((\mathsf {P}_j,\mathsf {R}_j)\).
-
-
Upon receiving \(\mathcal {A}\)’s forgery \((\mathsf {P}^*,\delta ^*)\) with \(\mathsf {P}^*=(\mathsf {s}^*,\mathsf {C}^*,{\sigma }^*)\). If \({\textsf {dis}}(\delta ^*)>t\) or \(\mathsf {P}^*\in \mathcal {Q}\), return 0. Otherwise, \({\mathcal {B}}\) calculates \(\tilde{\delta }^*=g(\delta ^*, \mathsf {s}, \mathsf {s}^*)\), \(\tilde{\mathsf {k}}=\mathsf {k}+\mathsf {Ext}(\tilde{\delta }^*,\tilde{\mathsf {r}})\), sets \(\tilde{\mathsf {k}}:=(\tilde{\mathsf {k}}_1,\tilde{\mathsf {k}}_2)\), and invokes \(\tilde{\mathsf {K}}\leftarrow \mathsf {SKEM.Decap}(\tilde{\mathsf {k}}_1,\mathsf {C}^*)\). After that, \({\mathcal {B}}\) parses \(\tilde{\mathsf {K}}=(\tilde{\mathsf {K}}_1,\tilde{\mathsf {K}}_2)\) and sets \(\tilde{{\sigma }}:=\tilde{\mathsf {K}}_1\). If \({\sigma }^*=\tilde{{\sigma }}\), return 1. Else, return 0.
Here, \({\mathcal {B}}\) implicitly sets \(\mathsf {k}_2=\bar{\mathsf {k}}-\varDelta _{i2}\). According to Lemma 1, \(\mathsf {k}_2\) is uniformly distributed and independent of \(\varDelta _{i2}\) due to the fact that \(\bar{\mathsf {k}}\) is uniformly distributed and independent of \(\varDelta _{i2}\).
If \((\textsf {X}, \bar{\mathsf {k}})=(\mathsf {Ext}'(\hat{\mathsf {r}}_i,\bar{\mathsf {k}}),\bar{\mathsf {k}})\), then \(\mathsf {k}_{j2}=\bar{\mathsf {k}}-\varDelta _{i2}+\varDelta _{j2}=\mathsf {k}_{2}+\varDelta _{j2}\) for \(j\ge i\). Hence, \({\mathcal {B}}\) perfectly simulates \(\mathbf{G}_{2.i-1}\). If \((\textsf {X}, \bar{\mathsf {k}})=({\textsf {U}},\bar{\mathsf {k}})\), then \(\mathsf {k}_{j2}=\bar{\mathsf {k}}-\varDelta _{i2}+\varDelta _{j2}=\mathsf {k}_{2}+\varDelta _{j2}\) for \(j> i\). Hence, \({\mathcal {B}}\) perfectly simulates \(\mathbf{G}_{2.i}\).
Consequently, \(|\Pr [\mathbf{G}_{2.i-1}\Rightarrow 1]-\Pr [\mathbf{G}_{2.i}\Rightarrow 1]|=|\Pr [{\mathcal {B}}(\bar{\mathsf {k}},\mathsf {Ext}'(\hat{\mathsf {r}}_i,\bar{\mathsf {k}}))\Rightarrow 1]-\Pr [{\mathcal {B}}(\bar{\mathsf {k}},{\textsf {U}})\Rightarrow 1]|\le \zeta _2.\)
From Proposition 4 and Eq.(11), Lemma 8 follows. \(\square \)
1.3 A.3 Proof of Lemma 9
Proof
The proof is similar to the proof of Lemma 6. Assume there exists a PPT adversary \(\mathcal {A}\) such that \(|\Pr [\mathbf{G_4}\Rightarrow 1]-\Pr [\mathbf{G_3}\Rightarrow 1]|=\zeta \), then we can construct a PPT algorithm \({\mathcal {B}}\) who can implement the key shift pseudorandom attack for SKEM with the same advantage \(\zeta \). The algorithm \({\mathcal {B}}\) is given \(\mathsf {pp}_{\mathsf {skem}}\) and oracle access to \({\mathcal {O}}_{\textsf {ksp}}(\cdot )\). Then it simulates \(\mathbf{G_3}/\mathbf{G_4}\) for \(\mathcal {A}\) as follows.
-
\({\mathcal {B}}\) samples \(\tilde{\mathsf {r}}\leftarrow {\hat{R}}\), \(\mathsf {w}\leftarrow W\), sets \(\mathsf {pp}=(\tilde{\mathsf {r}}, \mathsf {pp}_{\mathsf {skem}})\) and returns \(\mathsf {pp}\) to \(\mathcal {A}\).
-
Upon receiving the ith query \(\delta _i\) from \(\mathcal {A}\) with \({\textsf {dis}}(\delta _i)\le t\), \({\mathcal {B}}\) replies as follows.
-
Compute \(\textsf {s}_i={\textsf {SS.Gen}}(\mathsf {w})+{\textsf {SS.Gen}}(\delta _i)\).
-
Parse \(\mathsf {Ext}(\delta _i,\tilde{\mathsf {r}})=(\varDelta _{i1},\varDelta _{i2})\).
-
\({\mathcal {B}}\) asks its own \({\mathcal {O}}_{\textsf {ksp}}(\cdot )\) oracle with \(\varDelta _{i1}\), and receives a pair \((\mathsf {X}_i, \mathsf {Y}_i)\).
-
Parse \(\mathsf {X}_i=(\mathsf {X}_{i1},\mathsf {X}_{i2})\).
-
Set \(\sigma _i=\mathsf {X}_{i1}\), \(\mathsf {R}_i=\mathsf {X}_{i2}\), \(\mathsf {P}_i:=(\mathsf {s}_i,\mathsf {Y}_i, \sigma _i)\), and \(\mathcal {Q}:= \mathcal {Q}\cup \{\mathsf {P}_j\}.\)
-
Return \((\mathsf {P}_i,\mathsf {R}_i)\).
-
-
Upon receiving \(\mathcal {A}\)’s forgery \((\mathsf {P}^*,\delta ^*)\) with \(\mathsf {P}^*=(\mathsf {s}^*,\mathsf {C}^*,{\sigma }^*)\). If \({\textsf {dis}}(\delta ^*)>t\) or \(\mathsf {P}^*\in \mathcal {Q}\), return 0. Otherwise, \({\mathcal {B}}\) calculates \(\tilde{\delta }^*=g(\delta ^*, \mathsf {s}, \mathsf {s}^*)\), \(\tilde{\mathsf {k}}=\mathsf {k}+\mathsf {Ext}(\tilde{\delta }^*,\tilde{\mathsf {r}})\), sets \(\tilde{\mathsf {k}}:=(\tilde{\mathsf {k}}_1,\tilde{\mathsf {k}}_2)\), and invokes \(\tilde{\mathsf {K}}\leftarrow \mathsf {SKEM.Decap}(\tilde{\mathsf {k}}_1,\mathsf {C}^*)\). After that, \({\mathcal {B}}\) parses \(\tilde{\mathsf {K}}=(\tilde{\mathsf {K}}_1,\tilde{\mathsf {K}}_2)\) and sets \(\tilde{{\sigma }}:=\tilde{\mathsf {K}}_1\). If \({\sigma }^*=\tilde{{\sigma }}\), return 1. Else, return 0.
If \((\mathsf {X}_i, \mathsf {Y}_i)\) is the output of \(\mathsf {SKEM.Encap}(\mathsf {k}_{i1};\mathsf {r}_i)\), \({\mathcal {B}}\) perfectly simulates \(\mathbf{G_3}\) for \(\mathcal {A}\). If \((\mathsf {X}_i, \mathsf {Y}_i)\leftarrow _{\$}\mathcal {K}\times {\mathcal {C}}\), \({\mathcal {B}}\) perfectly simulates \(\mathbf{G_4}\) for \(\mathcal {A}\).
Hence, \(|\Pr [\mathbf{G_4}\Rightarrow 1]-\Pr [\mathbf{G_3}\Rightarrow 1]|\le \textsf {Adv}_{\textsf {SKEM}}^{\textsf {ksp}}({\lambda }).\) \(\square \)
Appendix B: Two instantiations of rrFE working with perfect randomness
In this section, we give two instantiations of robustly reusable fuzzy extractor working with perfect randomness.
Instantiation \(\overline{\textsf {rrFE}}_{\textsf {DDH}}\). Taking instantiations of SS in Sect. 5.2.1, \({\textsf {SKEM}}_{\textsf {DDH}}\) in 5.1.1, and \(\overline{\mathsf {Ext}}\) in Sect. 5.2.2 together, we obtain a specific rrFE scheme \(\overline{\textsf {rrFE}}_{\textsf {DDH}}\). The \(\overline{\textsf {rrFE}}_{\textsf {DDH}}\) scheme is depicted in Fig. 17. According to Theorem 1, we have the following corollary.
Corollary 1
Let \(\zeta _1=\zeta _2=2^{-\omega (\log \lambda )}\). Let q be a prime with \(q\approx 2^{\lambda +\omega (\log \lambda )}\). Let \(m=\lambda +\omega (\log \lambda ).\) Let \(n=\varTheta (\lambda )\), \(n_\mathsf {w}=\varTheta (\lambda )\), \(b_\mathsf {w}=\varTheta (\lambda )\) such that \(b_\mathsf {w}-m>\omega (\log \lambda )\) and \(n_\mathsf {w}-b_\mathsf {w}>\varTheta (\lambda )+\omega (\log \lambda )\).
In the generic construction of \(\overline{\textsf {rrFE}}\) in Fig. 8, suppose that SS is instantiated with the \((\{0,1\}^n, n_\mathsf {w},b_\mathsf {w}+\omega (\log \lambda ),t)\)-secure sketch given in Sect. 5.2.1, \(\overline{\mathsf {Ext}}:\{0,1\}^n\times \{0,1\}^{nm}\rightarrow \{0,1\}^m\) is instantiated with the \((b_\mathsf {w},2^{-\omega (\log \lambda )})\text {-}\overline{\mathsf {Ext}}\) given in Sect. 5.2.2, and \({\mathsf {SKEM}}\) is instantiated with the \({\mathsf {SKEM}}_{\textsf {DDH}}\) over \(\mathbb {G}\) of order q, which is given in Fig. 13. If W is a \((\{0,1\}^n,n_\mathsf {w})\)-source, then the resulting \(\overline{\textsf {rrFE}}_{\textsf {DDH}}\) scheme in Fig. 17 is a \((\{0,1\}^n,n_\mathsf {w},\{0,1\}^\lambda ,t,\epsilon _1,\epsilon _2)\)-robustly reusable fuzzy extractor with
Performance analysis The secure sketch in Sect. 5.2.1 is a \((\{0,1\}^n, n_\mathsf {w},b_\mathsf {w}+\omega (\log \lambda ),t)\text {-}\textsf {SS}\). Since \(n=\varTheta (\lambda ), n_\mathsf {w}=\varTheta (\lambda ), b_\mathsf {w}=\varTheta (\lambda )\), the syndrome \(\mathsf {s}\) can leak about \(n_\mathsf {w}-(b_\mathsf {w})+\omega (\log \lambda )=\varTheta (\lambda )\) bits of entropy about \(\mathsf {w}\). There is no further limits about the length of \(\mathsf {s}\), so the length of \(\mathsf {s}\) can be as large as a linear fraction of that of \(\mathsf {w}\), which implies it can correct linear fraction of errors, which implies \(\overline{\textsf {rrFE}}_{\textsf {DDH}}\) can tolerate linear fraction of errors in the fuzzy source.
Instantiation \(\overline{\textsf {rrFE}}_{\textsf {LPN}}\) Now, taking instantiations of SS in Sect. 5.2.1, \({\textsf {SKEM}}_{\textsf {LPN}}\) in Sect. 5.1.2, and \(\overline{\mathsf {Ext}}\) in Sect. 5.2.2 together, we obtain a specific rrFE scheme \(\overline{\textsf {rrFE}}_{\textsf {LPN}}\). The \(\overline{\textsf {rrFE}}_{\textsf {LPN}}\) scheme is depicted in Fig. 18, and we have the following corollary.
Corollary 2
Let \(\zeta _1=\zeta _2=2^{-\omega (\log \lambda )}\). Choose \(\eta \in (0,1/2)\). Let \(\mathfrak {t}=\varTheta (\lambda )\), and \(\mathfrak {m},\mathfrak {k},d=\varTheta (\lambda )(\mathfrak {m}>\mathfrak {k})\) s.t. \([\mathfrak {m},\mathfrak {k},d]~(d=2\mathfrak {t}+1)\) is an error-correcting code with correction capacity \(\mathfrak {t}\) and \(\eta \mathfrak {m}<\mathfrak {t}\). Let \(m=\mathfrak {n}\cdot \mathfrak {m}=\varTheta (\lambda ^2).\) Let \(n=\varTheta (\lambda ^2)\), \(n_\mathsf {w}=\varTheta (\lambda ^2)\), \(b_\mathsf {w}=\varTheta (\lambda ^2)\) such that \(b_\mathsf {w}-m>\omega (\log \lambda )\) and \(n_\mathsf {w}-b_\mathsf {w}>\varTheta (\lambda ^2)+\omega (\log \lambda )\).
In the generic construction of \(\overline{\textsf {rrFE}}\) in Fig. 8, suppose that SS is instantiated with the \((\{0,1\}^n, n_\mathsf {w},b_\mathsf {w}+\omega (\log \lambda ),t)\text {-}\textsf {SS}\) given in Sect. 5.2.1, \(\overline{\mathsf {Ext}}:\{0,1\}^n \times \{0,1\}^{nm} \rightarrow \{0,1\}^m\) is instantiated with the \((b_\mathsf {w},2^{-\omega (\log \lambda )})\text {-}\overline{\mathsf {Ext}}\) given in Sect. 5.2.2, and \({\mathsf {SKEM}}\) is instantiated with the \({\mathsf {SKEM}}_{\textsf {LPN}}\) (see Fig. 14) with the internal \([\mathfrak {m},\mathfrak {k},d]\) error-correcting code \(\mathfrak {C}:\{0,1\}^{\mathfrak {k}}\rightarrow \{0,1\}^{\mathfrak {m}}\) (i.e., encoding algorithm \({\mathcal {E}}\), decoding algorithm \({\mathcal {D}}\)), and secret key space \(\mathbb {Z}_2^{\mathfrak {n}\times \mathfrak {m}}\), and Bernoulli randomness extractor \(\textsf {Ber}_{\eta }^\mathfrak {m}:\{0,1\}^{2\eta \mathfrak {m}\log \mathfrak {m}}\rightarrow \{0,1\}^{\mathfrak {m}}\). If W is a \((\{0,1\}^n,n_\mathsf {w})\)-source, then the resulting \(\overline{\textsf {rrFE}}_{\textsf {LPN}}\) scheme in Fig. 18 is a \((\{0,1\}^n,n_\mathsf {w},\{0,1\}^\lambda ,t,\epsilon _1,\epsilon _2)\)-robustly reusable fuzzy extractor with
where Q denotes the number of oracle queries.
Performance analysis The secure sketch in this instantiation is a \((\{0,1\}^n, n_\mathsf {w},b_\mathsf {w}+\omega (\log \lambda ),t)\text {-}{\textsf {SS}}\). Since \(n=\varTheta (\lambda ^2), n_\mathsf {w}=\varTheta (\lambda ^2), b_\mathsf {w}=\varTheta (\lambda ^2)\), the syndrome \(\mathsf {s}\) can leak about \(n_\mathsf {w}-(b_\mathsf {w})+\omega (\log \lambda )=\varTheta (\lambda ^2)\) bits of entropy about \(\mathsf {w}\). There is no further limits about the length of \(\mathsf {s}\), so the length of \(\mathsf {s}\) can be as large as a linear fraction of that of \(\mathsf {w}\), which implies it can correct linear fraction of errors, which implies \(\overline{\textsf {rrFE}}_{\textsf {LPN}}\) can tolerate linear fraction of errors in the fuzzy source.
Appendix C: Two instantiations of rrFE working with imperfect randomness
Instantiation \({\textsf {rrFE}}_{\textsf {DDH}}\). Taking instantiations of SS in Sect. 5.2.1, \({\textsf {SKEM}}_{\textsf {DDH}}\) in Sect. 5.1.1, Ext in Sect. 5.2.3, and \(\mathsf {Ext}'\) in Sect. 5.2.4 together, we obtain a specific rrFE scheme \({\textsf {rrFE}}_{\textsf {DDH}}\). The \({\textsf {rrFE}}_{\textsf {DDH}}\) scheme is depicted in Fig. 19. According Theorem 2, we know that the \({\textsf {rrFE}}_{\textsf {DDH}}\) scheme is a robustly reusable fuzzy extractor, as shown in the following corollary.
Corollary 3
Let \(\zeta _1=\zeta _2=2^{-\omega (\log \lambda )}\). Let q be a prime with \(q\approx 2^{\lambda +\omega (\log \lambda )}\). Let \(k_2=\omega (\log \lambda )\), \(m=\lambda +\omega (\log \lambda )\), \(n=\varTheta (\lambda ^3)\) and \(b_{\hat{\mathsf {r}}}=\varOmega (\lambda ^{2.5}\cdot \log \lambda )\). Let \(n_\mathsf {w}=\varTheta (\lambda )\), \(b_\mathsf {w}=\varTheta (\lambda )\) such that \(n_\mathsf {w}-b_\mathsf {w}>\varTheta (\lambda )+\omega (\log \lambda )\). Let \(k=\log q+k_2=\lambda +\omega (\log \lambda )\) and let \(b_\mathsf {w},b_{\tilde{\mathsf {r}}}, \ell =\varTheta (\lambda )\) satisfy \(b_\mathsf {w}+b_{\tilde{\mathsf {r}}}-\ell >\lambda +\omega (\log \lambda )\).
In the generic construction of \({\textsf {rrFE}}\) in Fig. 10, suppose that SS is instantiated with the \((\{0,1\}^\ell , n_\mathsf {w},b_\mathsf {w}+\omega (\log \lambda ),t)\text {-}\textsf {SS}\) given in Sect. 5.2.1, \(\mathsf {Ext}:\{0,1\}^\ell \times \{0,1\}^\ell \rightarrow \{0,1\}^k\) is instantiated with the \((b_\mathsf {w},b_{\tilde{\mathsf {r}}},\zeta _1)\)-\(\mathsf {Ext}\) associated with matrices \(\mathbf{A}_i,i\in [k]\), defined in Fig. 15, \(\mathsf {Ext}':\{0,1\}^n\times \{0,1\}^{k_2}\rightarrow \{0,1\}^m\) is instantiated with the \((b_{\hat{\mathsf {r}}},\zeta _2)\)-\(\mathsf {Ext}'\) with the internal parameters \(\alpha =\beta \approx \frac{\zeta _2}{2(m+1)}\), \(h\!=\!\lceil 3\!\sqrt{n/\log n}\rceil \), \(q'\!\ge \!\varOmega (\frac{h}{\alpha ^4\beta ^4})\), \(y\!=\!\log q'\), \(\bar{y}\!=\!\mathsf {poly}(\alpha ^{-1},\!\beta ^{-1})\) and the encoding algorithm \(\mathbf{C}:\{0,1\}^y\rightarrow \{0,1\}^{\bar{y}}\) given in Fig. 16, and \({\mathsf {SKEM}}\) is instantiated with the \({\mathsf {SKEM}}_{\textsf {DDH}}\) over \(\mathbb {G}\) of order q, which is given in Fig. 13. If W is a \((\{0,1\}^\ell ,n_\mathsf {w})\)-source, \({\hat{R}}\) is a \((\{0,1\}^n,Q+1,b_{\hat{\mathsf {r}}})\)-correlated source and the truncated source \({\hat{R}}_{\textsf {truncate}}\)Footnote 4 is a \((\{0,1\}^\ell ,b_{\tilde{\mathsf {r}}})\)-source, then the resulting \({\textsf {rrFE}}_{\textsf {DDH}}\) scheme in Fig. 19 is a \(((\{0,1\}^\ell ,n_{\mathsf {w}}),(\{0,1\}^\ell ,Q+1,b_{\hat{\mathsf {r}}}),\{0,1\}^\lambda ,t,\epsilon _1, \epsilon _2)\)-robustly reusable fuzzy extractor with
where Q is the number of oracle queries.
Performance analysis Gen is dominated by only two modular exponentiations over \(\mathbb {G}\) and Rep is dominated by only one modular exponentiation over \(\mathbb {G}\).
The syndrome-based secure sketch in Sect. 5.2.1 is a \((\{0,1\}^\ell , n_\mathsf {w},b_\mathsf {w}+\omega (\log \lambda ),t)\text {-}\textsf {SS}\). Since \(\ell =\varTheta (\lambda ), n_\mathsf {w}=\varTheta (\lambda ), b_\mathsf {w}=\varTheta (\lambda )\), the syndrome \(\mathsf {s}\) can leak about \(n_\mathsf {w}-(b_\mathsf {w})+\omega (\log \lambda )=\varTheta (\lambda )\) bits of entropy about \(\mathsf {w}\). There is no further limits about the length of \(\mathsf {s}\), so the length of \(\mathsf {s}\) can be as large as a linear fraction of that of \(\mathsf {w}\). That means it can correct linear fraction of errors. As a result, our \({\textsf {rrFE}}_{\textsf {DDH}}\) scheme can tolerate linear fraction of errors in the fuzzy source.
Parameters in \({\textsf {rrFE}}_{\textsf {DDH}}\) Our aim is to extract \(\lambda \) bits from a fuzzy source, i.e., \(|\mathsf {R}|=|\mathsf {K}_2|=\lambda \). For \(\epsilon _2\)-robustness to be negligible, we set \(\epsilon _2:=2^{-\omega (\log \lambda )}\). Then a necessary condition is \(|\sigma |=|\mathsf {K}_1|={\omega (\log \lambda )}\) bits (which is used for authentication). Recall that \(\mathsf {K}=(\mathsf {K}_1, \mathsf {K}_2)=(\sigma , \mathsf {R})\in \mathbb {G}\). Hence, the order q of \(\mathbb {G}\) should be as large as \(2^{\lambda +\omega (\log \lambda )}\). We set \(q\approx 2^{\lambda +\omega (\log \lambda )}\), hence \(m=\log q=\lambda +\omega (\log \lambda )\).
Set \(\zeta _1=\zeta _2:=2^{-\omega (\log \lambda )}\), \(n:=\varTheta (\lambda ^3)\) and \(b_{\hat{\mathsf {r}}}:=\varOmega (\lambda ^{2.5}\cdot \log \lambda )\). Then it holds that \(3m\sqrt{n}\log (\frac{n}{\zeta _2})\le b_{\hat{\mathsf {r}}}\le n\). Hence, \(k_2=\log n+O(\log m)+O(\log \frac{1}{\zeta _2})=\omega (\log \lambda )\) and \(k=\log q+k_2=\lambda +\omega (\log \lambda )\).
As for \(\mathsf {Ext}\), \(\zeta _1=2^{-\omega (\log \lambda )}\) implies \(2^{-\frac{b_w+b_{\tilde{\mathsf {r}}}+2-(\ell +k)}{2}}\le 2^{-\omega (\log \lambda )}\). We set \( b_\mathsf {w}=\varTheta (\lambda ), b_{\tilde{\mathsf {r}}}=\varTheta (\lambda ), \ell =\varTheta (\lambda )\) such that \(b_\mathsf {w}+b_{\tilde{\mathsf {r}}}-\ell >\lambda +\omega (\log \lambda )\).
Finally, given \(\ell =\varTheta (\lambda )\) and \(b_\mathsf {w}=\varTheta (\lambda )\), we can set \(n_\mathsf {w}:=\varTheta (\lambda )\) such that \(n_\mathsf {w}-\varTheta (\lambda )>b_{\mathsf {w}}+\omega (\log \lambda )\). Then \(\textsf {SS}\) is just a \((\{0,1\}^\ell , n_\mathsf {w},b_\mathsf {w}+\omega (\log \lambda ),t)\)-secure sketch that can correct linear fraction of errors. This completes the choice of parameters.
These above choices of parameters are just for illustration. We stress there are flexible choices of parameters, which result in different tradeoffs among performance, entropy loss and security level.
Instantiation \({\textsf {rrFE}}_{\textsf {LPN}}\) Taking instantiations of SS in Sect. 5.2.1, \({\textsf {SKEM}}_{\textsf {LPN}}\) in Sect. 5.1.2, Ext in Sect. 5.2.3, and \(\mathsf {Ext}'\) in Sect. 5.2.4 together, we obtain a concrete rrFE scheme \({\textsf {rrFE}}_{\textsf {LPN}}\) shown in Fig. 20.
According Theorem 2, we know that the \({\textsf {rrFE}}_{\textsf {LPN}}\) scheme is a robustly reusable fuzzy extractor, as shown in Corollary 4.
Subroutines and parameters
-
1.
Let \(\zeta _1=\zeta _2=2^{-\omega (\log \lambda )}\), \(c_1, c_2\) are constants with \(c_1>1\) and \(c_2=c_1+1\).
-
2.
Let \(\mathfrak {k}=\lambda +\omega (\log \lambda )\), \(\mathfrak {n}=\lambda \), \(\mathfrak {m}=\textsf {poly}(\lambda )=\varTheta (\lambda ^{c_1})(\mathfrak {m}>\mathfrak {k})\) and \(\mathfrak {t}\approx \varTheta (\lambda ^{c_1})\) such that \([\mathfrak {m},\mathfrak {k},d]\) \((d=2t+1)\) is an error-correcting code with error correction capacity \(\mathfrak {t}\).
-
3.
Let \(\eta \in (0,1/2)\) such that \(\eta \mathfrak {m}<\mathfrak {t}\).
-
4.
Let \(k_1=|{\mathsf {k}}_1|=\mathfrak {n}\cdot \mathfrak {m}=\varTheta (\lambda ^{c_2})\), \(m=\mathfrak {k}+\mathfrak {n}+2\eta \mathfrak {m}\log \mathfrak {m}=\varTheta (\lambda ^{c_1}\log \lambda )\), \(n=\varTheta (\lambda ^{2c_1+2}\cdot \omega (\log ^2\lambda ))\), \(k_2=|{\mathsf {k}}_2|=\omega (\log \lambda )\) and \(b_{\hat{\mathsf {r}}}=\varOmega (\lambda ^{2c_1+1}\cdot \omega (\log \lambda ))\).
-
5.
Let \(n_{\mathsf {w}}=\varTheta (\lambda ^{c_2})\), and \(b_{\mathsf {w}}=\varTheta (\lambda ^{c_2})\) such that \(n_{\mathsf {w}}-b_{\mathsf {w}}>\varTheta (\lambda ^{c_2})+\omega (\log \lambda )\).
-
6.
Let \(k=k_1+k_2=\varTheta (\lambda ^{c_2})+\omega (\log \lambda )\) and \(b_{\mathsf {w}}, b_{\tilde{\mathsf {r}}}, \ell =\varTheta (\lambda ^{c_2})\) satisfy \(b_{\mathsf {w}}+b_{\tilde{\mathsf {r}}}-\ell >\varTheta (\lambda ^{c_2})+\omega (\log \lambda )\).
-
7.
We setup the SS with the \((\{0,1\}^\ell , n_\mathsf {w},b_\mathsf {w}+\omega (\log \lambda ),t)\text {-}\textsf {SS}\) given in Sect. 5.2.1.
-
8.
We setup the \(\mathsf {Ext}:\{0,1\}^\ell \times \{0,1\}^\ell \rightarrow \{0,1\}^k\) with the \((b_\mathsf {w},b_{\tilde{\mathsf {r}}},\zeta _1)\)-\(\mathsf {Ext}\) associated with matrices \(\mathbf{A}_i,i\in [k]\), defined in Fig. 15.
-
9.
We setup the internal parameters for \((b_{\hat{\mathsf {r}}},\zeta _2)\)-\(\mathsf {Ext}'\!:\!\{0,1\}^n\!\times \!\{0,1\}^{k_2}\!\rightarrow \!\{0,1\}^m\) in Fig. 16 as follows.
-
a.
Let \(\alpha =\beta \approx \frac{\zeta _2}{2(m+1)}\), \(h\!=\!\lceil 3\!\sqrt{n/\log n}\rceil \), \(q'\!\ge \!\varOmega (\frac{h}{\alpha ^4\beta ^4})\), \(y\!=\!\log q'\) and \(\bar{y}\!=\!\textsf {poly}(\alpha ^{-1},\!\beta ^{-1})\).
-
b.
Let \(\mathbf{C}:\{0,1\}^y\rightarrow \{0,1\}^{\bar{y}}\) be the encoding algorithm.
-
a.
-
10.
We setup the parameters for \({\textsf {SKEM}}_{\textsf {LPN}}\) in Fig. 14 as follows.
-
a.
Let secret key space be \({\mathbb {Z}}_2^{\mathfrak {n}\times \mathfrak {m}}\) and random space be \(\mathbb {Z}_2^{\mathfrak {k}+\mathfrak {n}+2\eta \mathfrak {m}\log \mathfrak {m}}\).
-
b.
Let \(\mathfrak {C}:\{0,1\}^{\mathfrak {k}}\rightarrow \{0,1\}^{\mathfrak {m}}\) be the \([\mathfrak {m},\mathfrak {k},d]\) error-correcting code (i.e., encoding algorithm \({\mathcal {E}}\) and decoding algorithm \({\mathcal {D}}\)).
-
c.
Let \(\textsf {Ber}_{\eta }^\mathfrak {m}:\{0,1\}^{2\eta \mathfrak {m}\log \mathfrak {m}}\rightarrow \{0,1\}^{\mathfrak {m}}\) be the Bernoulli randomness extractor.
-
a.
Corollary 4
If W is a \((\{0,1\}^\ell ,n_\mathsf {w})\)-source, \({\hat{R}}\) is a \((\{0,1\}^n,Q+1,b_{\hat{\mathsf {r}}})\)-correlated source, the truncated source \({\hat{R}}_{\textsf {truncate}}\)Footnote 5 is a \((\{0,1\}^\ell ,b_{\tilde{\mathsf {r}}})\)-source is a \((\{0,1\}^\ell ,b_{\tilde{\mathsf {r}}})\)-source, and parameters and subroutines are chosen as above, then the resulting \({\textsf {rrFE}}_{\textsf {LPN}}\) scheme in Fig. 20 is a \(((\{0,1\}^\ell ,n_{\mathsf {w}}),(\{0,1\}^\ell ,Q+1,b_{\hat{\mathsf {r}}}),\{0,1\}^\lambda ,t,\epsilon _1, \epsilon _2)\)-robustly reusable fuzzy extractor with
where Q is the number of oracle queries.
Performance analysis The syndrome-based secure sketch in Sect. 5.2.1 is a \((\{0,1\}^\ell ,n_{\mathsf {w}},b_{\mathsf {w}}+\omega (\log \lambda ),t)-\textsf {SS}\). Since \(n=\varTheta (\lambda ^{c_2}), n_\mathsf {w}=\varTheta (\lambda ^{c_2}), b_\mathsf {w}=\varTheta (\lambda ^{c_2})\), the syndrome \(\mathsf {s}\) can leak about \(n_\mathsf {w}-(b_\mathsf {w})+\omega (\log \lambda )=\varTheta (\lambda ^{c_2})\) bits of entropy about \(\mathsf {w}\). There is no further limits about the length of \(\mathsf {s}\), so the length of \(\mathsf {s}\) can be as large as a linear fraction of that of \(\mathsf {w}\). Hence, the secure sketch can correct linear fraction of errors, which implies \({\textsf {rrFE}}_{\textsf {LPN}}\) scheme can tolerate linear fraction of errors.
Parameters in \({\textsf {rrFE}}_{\textsf {LPN}}\) Similar to the choice before, our aim is to extract \(\lambda \) bits from a fuzzy source, i.e., \(|\mathsf {R}|=|\mathsf {K}_2|=\lambda \). For \(\epsilon _2\)-robustness to be negligible, we set \(\epsilon _2:=2^{-\omega (\log \lambda )}\). Then a necessary condition is \(|\sigma |=|\mathsf {K}_1|={\omega (\log \lambda )}\) bits (which is used for authentication). Recall that \(\mathfrak {k}=|\mathsf {K}|=|(\mathsf {K}_1, \mathsf {K}_2)|=|(\sigma , \mathsf {R})|=\lambda +\omega (\log \lambda )\), then we set \(\mathfrak {m}=\textsf {poly}(\lambda )=\varTheta ( \lambda ^{c_1})(c_1>1~\text {is~a~constant}, \mathfrak {m}>\mathfrak {k})\), and \(\mathfrak {t}\approx \varTheta (\lambda ^{c_1})\) s.t. \([\mathfrak {m},\mathfrak {k},d]\) \((d=2\mathfrak {t}+1)\) is an error-correcting code with correction capacity \(\mathfrak {t}\). For the sake of correctness of \({\textsf {SKEM}}_{\textsf {LPN}}\), we require \(\eta \in (0,1/2)\) and \(\eta \mathfrak {m}<\mathfrak {t}\). Recall that \(\mathfrak {n}=\lambda \), \(2\eta \mathfrak {m}\log \mathfrak {m}=\varTheta (\lambda ^{c_1}\log \lambda )\), hence \(m=\mathfrak {k}+\mathfrak {n}+2\eta \mathfrak {m}\log \mathfrak {m}=\varTheta (\lambda ^{c_1}\log \lambda )\).
Set \(\zeta _1=\zeta _2:=2^{-\omega (\log \lambda )}\), \(n:=O(\lambda ^{2c_1+2}\cdot \omega (\log ^2\lambda ))\) and \(b_{\hat{\mathsf {r}}}:=\varOmega (\lambda ^{2c_1+1}\cdot \omega (\log \lambda ))\), then \(3m\sqrt{n}\log (\frac{n}{\zeta _2})\le b_{\hat{\mathsf {r}}}\le n\) can be satisfied. Hence, \(k_2=\log n+O(\log m)+O(\log \frac{1}{\zeta _2})=\omega (\log \lambda )\) and \(k=k_1+k_2=\mathfrak {n}\cdot \mathfrak {m}+\omega (\log \lambda )\approx \varTheta (\lambda ^{c_2})(c_2>2~\text {is~a~constant})\).
For \(\mathsf {Ext}\), \(\zeta _1=2^{-\omega (\log \lambda )}\) implies \(2^{-\frac{b_w+b_{\tilde{\mathsf {r}}}+2-(\ell +k)}{2}}\le 2^{-\omega (\log \lambda )}\). We can set \(b_\mathsf {w}=\varTheta (\lambda ^{c_2}), b_{\tilde{\mathsf {r}}}=\varTheta (\lambda ^{c_2}), \ell =\varTheta (\lambda ^{c_2})\) such that \(b_\mathsf {w}+b_{\tilde{\mathsf {r}}}-\ell >\varTheta (\lambda ^{c_2})+\omega (\log \lambda )\).
Finally, given that \(\ell =\varTheta (\lambda ^{c_2})\), \(b_\mathsf {w}=\varTheta (\lambda ^{c_2})\), we can set \(n_\mathsf {w}:=\varTheta (\lambda ^{c_2})\) such that \(n_\mathsf {w}-\varTheta (\lambda ^{c_2})>b_{\mathsf {w}}+\omega (\log \lambda )\). Then \(\textsf {SS}\) is a \((\{0,1\}^\ell , n_\mathsf {w},b_\mathsf {w}+\omega (\log \lambda ),t)\)-secure sketch that can correct linear fraction of errors. This completes the choice of parameters.
Rights and permissions
About this article
Cite this article
Cui, N., Liu, S., Gu, D. et al. Robustly reusable fuzzy extractor with imperfect randomness. Des. Codes Cryptogr. 89, 1017–1059 (2021). https://doi.org/10.1007/s10623-021-00843-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10623-021-00843-1