1 Introduction

Approximate Bayesian Computation (ABC) is a broad class of methods allowing Bayesian inference on parameters governing complex models. For such models, computing the likelihood, either analytically or numerically, is typically unfeasible. To overcome this critical problem, ABC dispenses with exact likelihood computation, and only requires the ability of simulating pseudo-data by sampling observations from a generative model, as detailed in Sect. 2.

In the literature, a variety of ABC methods have been proposed, see Sisson et al (2018, Ch. 4), and for recent reviews Lintusaari et al. (2017), Karabatsos et al. (2018). In the vast majority of these methods, the approximate likelihood function takes positive values only when the distance between the simulated and the observed data is lower than a predefined threshold. In other words, most ABC schemes involve—implicitly or explicitly—a rejection step, which often leads to discarding a huge number of proposals. This results in a waste of computational resources and/or in an inadequate sample size, that is, in sample degeneracy. Sample degeneracy may also cause serious distortions in the form of the approximate posterior distribution, at least when the number of iterations is not large enough. Indeed, accepting poor parameter proposals, i.e., those producing simulated data very rarely resembling the observed data, is a rare event. In the lack of accepted values, the posterior probability of such proposals will be approximated just as zero, in turn resulting in a distortion in the tails. This may be especially problematic for posterior distributions with long tails.

Our idea is to mitigate the problem of sample degeneracy by improving the approximation of the likelihood function. In particular, we speculate that taking into account the positive, however small, probability of rare events, i.e., poor proposals leading to simulated data resembling the observed data, allows avoiding the rejection step altogether and weighting all parameter proposals. To this end, we resort to the theory of Large Deviations (LDT). Our aim is to show how LDT provides a convenient way to define an approximate likelihood, as well as guarantees of its convergence to the true likelihood as the size of pseudo-datasets goes to infinity. In order to make the incorporation of LDT into ABC as smooth as possible, we rely on one of the less general formulations of Sanov’s theorem. Accordingly, we only consider models for discrete i.i.d. random variables which, despite their apparent simplicity, will be shown to be of interest in several applications of ABC. This allows adopting a straightforward information theoretic formulation of LDT known as the method of types (Csiszár 1998; Cover and Thomas 2006).

Related work In the literature, there have been many proposals aimed at improving the computational efficiency of basic ABC. Prangle (2016) proposed Lazy ABC, which saves computing time by abandoning simulations likely to lead to a poor match between the simulated and the observed data. To this end, at each iteration, the simulation is given up with a probability depending on the probability of its acceptance and on the expected required time for its completion. Unlike our method, Lazy ABC does not avoid rejection, but rather accelerates the process leading to discarding a proposal.

Another way to improve computational efficiency is to consider proposal distributions closer to the posterior on the parameter space, employing sophisticated sampling methods, such as MCMC (Marjoram et al. 2003), Population Monte Carlo (Beaumont et al. 2009) and Sequential Monte Carlo (Del Moral et al. 2012). In the same vein, Chiachio et al. (2014) proposed a sequential way of achieving computational efficiency by overcoming the difficulties in getting samples resembling the observed data. This latter was the first attempt to improve the acceptance rate by adopting a rare-event approach. In particular, Chiachio et al. (2014) combine the ABC scheme with a rare-event sampler that draws conditional samples from a nested sequence of subdomains. However, even this method cannot completely avoid rejections, and only partially mitigates the sample degeneracy problem.

In order to tackle the problem more systematically, clever proposal distributions should be combined with better approximations to the likelihood. Accordingly, Prangle et al. (2018) also resorted to a sequential approach, but explicitly considering a likelihood estimate that takes into account the probability of rare events. As a comparison, our method evaluates the probabilities of rare events based on theoretical results (LDT), rather than on Monte Carlo estimates of tail probabilities. Moreover, they focus on continuous data by showing that extensions to discrete data can be challenging and require application-specific solutions; in contrast, the method of types provides a natural way of dealing with discrete random variables by summarizing data via empirical distributions, thus avoiding the common practice of summarizing data by selecting ad hoc summary statistics.

Other methods have been proposed avoiding the selection of summary statistics and relying on empirical distributions. In particular, Park et al. (2016) rely on the maximum mean discrepancy between the embeddings of the simulated and the observed empirical distributions. They avoid rejection by weighting each parameter proposal by means of a kernel function defined on a non-compact support. Other interesting methods involve the Wasserstein distance (Bernton et al. 2019) or the Kullback–Leibler divergence (Jiang 2018) as measures of the discrepancy between observed and simulated data. In particular, Jiang (2018) approximates the likelihood by means of an estimator of the Kullback–Leibler divergence between the unknown distribution of the data given the true parameter, and given the parameter sampled at the current iteration. Exploiting the fact that the maximum likelihood estimator is the one minimizing that Kullback–Leibler divergence, they prove that their approximate posterior distribution converges to a restriction of the prior distribution on the region in which the above mentioned divergence is smaller than a predefined threshold. Although most of the above mentioned methods apply to continuous data, we note that ABC applications to discrete data appear frequently in population genetics, epidemiology, ecology and system biology (see Beaumont (2010) for an overview of the applications of ABC in these fields). In particular, in population genetics, discrete (possibly i.i.d.) data representing the genotyping at a few loci of different (unrelated) individuals have often been summarized through their empirical distributions (Marjoram et al. 2003; Buzbas and Rosenberg 2015, among others).

A very different way of bypassing the selection of summary statistics relies on the random forest method (Raynal et al. 2019). Here, regression random forests are trained by using a training-set composed of a large number of parameter proposals and pseudo-datasets sampled from the prior distribution and the generative model, respectively. Since all the summary statistics are involved as covariates, summary selection is avoided. The output of the algorithm is the predicted expected value of an arbitrary function of interest on the parameter space, conditional on the observed data.

Structure of the paper The rest of this paper is structured as follows. Section 2 contains background and preliminaries on ABC, focusing on the importance sampling scheme and the sample degeneracy issue. In Sect. 3 we introduce LDT by adopting the method of types. We also show how LDT allows poor parameter proposals to contribute to the representation of the approximate posterior distribution. Section 4 gives the LDW-ABC algorithm and compares it with R-ABC. In Sect. 5 we present the results of a toy example and an experiment conducted on a real world dataset. Section 6 contains some concluding remarks and ideas for future research. The Appendices contain the proofs, technical materials, and additional results from experiments.

2 Background on ABC

Let \({\varvec{x}}\in {\mathcal {X}}^n\) be the observed data, which will be assumed to be drawn from a probability distribution in the family \({\mathcal {F}}{\mathop {=}\limits ^{\triangle }}\{P(\cdot |\theta ): \theta \in \varTheta \}\).

In principle, given a prior distribution \(\pi (\theta )\) on \(\varTheta \), the aim of Bayesian inference is to provide information about the uncertainty on \(\theta \) by deriving the posterior distribution \(\pi (\theta |{\varvec{x}}) \propto \pi (\theta )P({\varvec{x}}|\theta )\) via Bayes’ Theorem. When the likelihood function is intractable, ABC allows simulated inference providing a conversion of samples from the prior to samples from the posterior distribution, through comparisons between the observed data and the pseudo-datasets generated from a simulator. A simulator can be thought of as a probabilistic computer program taking as input a parameter value (or a vector thereof) \(\theta \in \varTheta \) and returning a sample from the distribution \(P(\cdot |\theta )\). In general, no knowledge of the analytical form of the likelihood is necessary to write down such a program. More specifically, in the primal rejection sampling algorithm, whose origins can be traced back to Rubin (1984), Tavaré et al. (1997), Pritchard et al. (1999), the following actions are taken:

  1. 1.

    \(S\ge 1\) parameter values from the prior distribution \(\pi (\cdot )\) are generated;

  2. 2.

    for each \(s\in \{1,\ldots ,S\}\), given the parameter proposal \(\theta ^{(s)}\) as input, the simulator generates a realization of a random variable \({\varvec{Y}}\in {\mathcal {X}}^n\) distributed according to \(P(\cdot |\theta ^{(s)})\);

  3. 3.

    only parameter values leading to a pseudo-dataset equal to the observed data are accepted, thereby samples from the exact posterior are derived by conditioning on the event \(\{{\varvec{Y}}={\varvec{x}}\}\).

Introducing a twofold approximation scheme, as illustrated in Algorithm 1, might increase the efficiency of the algorithm outlined above. First, one introduces a summary statistic, \(s(\cdot )\), which is a function from the sample space \({\mathcal {X}}^n\subseteq \mathbb {R}^n\) to a lower-dimensional space \({\mathcal {S}}\subset \mathbb {R}^k\), with \(k\ll n\). Second, exact matching of the simulated and the observed data is relaxed to similarity, expressed in terms of a predefined distance function \(d(\cdot ,\cdot )\) and tolerance threshold \(\epsilon >0\).

figure a

Abbreviating \(\mathrm {s}({\varvec{x}})\) by \(\mathrm {s}_{{\varvec{x}}}\) and \(\mathrm {s}({\varvec{y}})\) by \(\mathrm {s}_{{\varvec{y}}}\), the output of Algorithm 1 is a sample of pairs \( (\theta ^{(s)}, \mathrm {s}_{{\varvec{y}}}^{(s)})\) from the following approximate joint posterior distribution

$$\begin{aligned} {\tilde{\pi }}(\theta , \mathrm {s}_{{\varvec{y}}}|\mathrm {s}_{{\varvec{x}}}) \propto \pi (\theta )\,P(\mathrm {s}_{{\varvec{y}}}|\theta )\, \mathbb {1}\{d(s_{{\varvec{y}}},\mathrm {s}_{{\varvec{x}}})\le \epsilon \} \end{aligned}$$
(1)

where \(\mathbb {1}\{d(\mathrm {s}_{{\varvec{y}}},\mathrm {s}_{{\varvec{x}}})\le \epsilon \}\), the indicator function assuming the value 1 if \(d(\mathrm {s}_{{\varvec{y}}},\mathrm {s}_{{\varvec{x}}})\le \epsilon \) and 0 otherwise, corresponds to the acceptance/rejection step. Marginalizing out \(\mathrm {s}_{{\varvec{y}}}\) in (1), that is, ignoring the simulated summary statistics, the output of the algorithm becomes a sample from the marginal posterior distribution \(\Pr (\theta |d(\mathrm {s}_{{\varvec{Y}}},\mathrm {s}_{{\varvec{x}}})\le \epsilon )\). Indeed, abbreviating \(\mathrm {s}({\varvec{Y}})\) by \(\mathrm {s}_{{\varvec{Y}}}\),

$$\begin{aligned} {\tilde{\pi }}(\theta |\mathrm {s}_{{\varvec{x}}})&\propto \int _{{\mathcal {S}}} \pi (\theta )\,P(\mathrm {s}_{{\varvec{y}}}|\theta )\, \mathbb {1}\{d(\mathrm {s}_{{\varvec{y}}},\mathrm {s}_{{\varvec{x}}})\le \epsilon \}\,d \mathrm {s}_{{\varvec{y}}}\\&= \pi (\theta )\int _{{\mathcal {S}}} P(\mathrm {s}_{{\varvec{y}}}|\theta )\,\mathbb {1}\{d(\mathrm {s}_{{\varvec{y}}},\mathrm {s}_{{\varvec{x}}})\le \epsilon \}\,d \mathrm {s}_{{\varvec{y}}}\\&=\pi (\theta ) \cdot \Pr \big (d(\mathrm {s}_{{\varvec{Y}}},\mathrm {s}_{{\varvec{x}}})\le \epsilon |\theta \big )\\&\propto \Pr (\theta |d(\mathrm {s}_{{\varvec{Y}}},\mathrm {s}_{{\varvec{x}}})\le \epsilon ). \end{aligned}$$

Here \(\Pr \big (d(\mathrm {s}_{{\varvec{Y}}},\mathrm {s}_{{\varvec{x}}})\le \epsilon |\theta \big )\) is called the ABC approximate likelihood.

Remark 1

(Marginal samplers) Some ABC sampling schemes (Sisson et al. 2007; Marjoram et al. 2003, among others) allow directly sampling from the approximate marginal posterior distribution \({\tilde{\pi }}(\theta |\mathrm {s}_{{\varvec{x}}}) \). The key idea is that \({\tilde{\pi }}(\theta |\mathrm {s}_{{\varvec{x}}}) \) can be estimated pointwise by

$$\begin{aligned} \pi (\theta ^{(s)}) \cdot \frac{1}{M}\sum \limits _{i=1}^M \mathbb {1}\{d(\mathrm {s}_{{\varvec{y}}}^{(i)},\mathrm {s}_{{\varvec{x}}})\le \epsilon \}\;\;\;\;\;\;\;\;\;\ \forall s \in \{1,\ldots ,S\} \end{aligned}$$
(2)

by simulating M pseudo-datasets from \(P(\cdot |\theta ^{(s)})\) and computing \(\mathrm {s}_{{\varvec{y}}}^{(i)}\) for \(i\in {1,\ldots ,M}\) at each iteration s. As is apparent, the second term in (2) provides a Monte Carlo estimate of the ABC approximate likelihood.

Note that marginalizing the output of Algorithm 1 corresponds to the implementation of a marginal sampler with \(M=1\). In such a case, the indicator function represents a crude Monte Carlo estimate of the probability \(\Pr \big (d(\mathrm {s}_{{\varvec{Y}}},\mathrm {s}_{{\varvec{x}}})\le \epsilon |\theta \big )\).

As pointed out by Sisson et al. (2018, Ch. 1), the use of the indicator function does not enable one to discriminate between whether the pseudo-dataset \({\varvec{y}}\) coincides with the observed data and whether the pseudo-dataset just is close enough. This may lead to a waste of information. For this reason, the indicator function in (1) is often replaced by a kernel function:

$$\begin{aligned} K_{\epsilon }\big (d(\mathrm {s}_{{\varvec{y}}},\mathrm {s}_{{\varvec{x}}})\big ) = {\left\{ \begin{array}{ll} \kappa \big ( d(\mathrm {s}_{{\varvec{y}}},\mathrm {s}_{{\varvec{x}}})\big )\,\,\,\,\,\,\, &{}\text {if } d(\mathrm {s}_{{\varvec{y}}},\mathrm {s}_{{\varvec{x}}})\le \epsilon \\ 0 \,\,\,\,\,\,\, &{}\text {if } d(\mathrm {s}_{{\varvec{y}}},\mathrm {s}_{{\varvec{x}}})>\epsilon \end{array}\right. } \end{aligned}$$
(3)

where \(\kappa \big ( \cdot \big )\) is a kernel function (e.g., triangular, Epanechnikov, Gaussian, etc.) defined on a compact support and decaying continuously from 1 to 0, see e.g. Beaumont et al. (2002). Now the ABC approximate likelihood becomes the convolution of the true model with the kernel \(K_\epsilon \) (Prangle et al. 2018):

$$\begin{aligned} \tilde{{\mathcal {L}}}_{\epsilon ,d}(\theta ;\mathrm {s}_{{\varvec{x}}})=\int _{{\mathcal {S}}} P(\mathrm {s}_{{\varvec{y}}}|\theta )\,K_\epsilon (\,d(\mathrm {s}_{{\varvec{y}}},\mathrm {s}_{{\varvec{x}}})\,)\,d\mathrm {s}_{{\varvec{y}}}. \end{aligned}$$
(4)

Note that this general setting encompasses also the case when R-ABC employs the uniform kernel as \(\kappa (\cdot )\). The accuracy of the posterior distribution approximation depends both on how much information about the parameters is preserved by the summary statistics and on the magnitude of the threshold \(\epsilon \). In fact, as \(\epsilon \rightarrow 0\), the approximate likelihood \(\tilde{{\mathcal {L}}}(\theta ;{\varvec{x}})\) converges to the true likelihood (Prangle et al. 2018, Appendix A) and, whenever sufficient summary statistics for \(\theta \) have been chosen, the approximate posterior distribution \({\tilde{\pi }}(\cdot |\mathrm {s}_{{\varvec{x}}})\) converges to the true posterior \(\pi (\cdot |{\varvec{x}})\) (Sisson et al. 2018, Ch. 1). On the other hand, as \(\epsilon \rightarrow \infty \), the probability \(\Pr \big (d(\mathrm {s}_{{\varvec{Y}}},\mathrm {s}_{{\varvec{x}}})\le \epsilon |\theta \big )\) approaches 1 and samples are generated from the prior distribution. This establishes a trade-off between the statistical bias and the computational efficiency (Lintusaari et al. 2017): as the tolerance level \(\epsilon \) decreases, the error of the approximation of the ABC posterior vs. the true posterior decreases at the cost of higher computational effort.

2.1 Importance sampling ABC and sample degeneracy

In the ABC literature, a great variety of methods to sample from \({\tilde{\pi }}(\theta , \mathrm {s}_{{\varvec{y}}}|\mathrm {s}_{{\varvec{x}}})\) have been proposed that go beyond the rejection scheme. Hereafter, we will adopt an importance sampling scheme (IS-ABC) which, as outlined by Karabatsos et al. (2018), encompasses R-ABC and most of the other ABC algorithms.

figure b

Like the standard importance sampling, see Robert and Casella (2013, Ch. 3), IS-ABC consists of sampling pairs \((\theta ^{(s)}, \mathrm {s}_{{\varvec{y}}}^{(s)})\) from an importance distribution and weighting each pair, avoiding the computation of the acceptance probabilities. More formally, let \(h: (\varTheta \times {\mathcal {S}})\rightarrow \mathbb {R}\) be a function of interest and let \(E_p[h(\theta ,\mathrm {s}_{{\varvec{Y}}})]\) denote its expected value w.r.t. a probability distribution p over \(\varTheta \times {\mathcal {S}}\). Suppose that we are interested in estimating \(E_{{\tilde{\pi }}}[h(\theta ,\mathrm {s}_{{\varvec{Y}}})]\), where \({\tilde{\pi }}\) is our target distribution, i.e., the joint approximate posterior. In particular, by choosing \(h(\cdot )\) to be a kernel function, this formulation also enables a kernel density estimation for the joint approximate posterior, a case which will be considered in Sect. 5.

Now it is a standard fact that

$$\begin{aligned} E_{{\tilde{\pi }}}[h(\theta ,\mathrm {s}_{{\varvec{Y}}})]=E_{q}[{\bar{\omega }}(\theta ,\mathrm {s}_{{\varvec{Y}}}) h(\theta ,\mathrm {s}_{{\varvec{Y}}})] \end{aligned}$$
(5)

where \(q(\theta , \mathrm {s}_{{\varvec{y}}})\) is the importance distribution on \(\varTheta \times {\mathcal {S}}\) and \({\bar{\omega }}(\theta , \mathrm {s}_{{\varvec{y}}})=\dfrac{{\tilde{\pi }}(\theta ,\mathrm {s}_{{\varvec{y}}}|\mathrm {s}_{{\varvec{x}}})}{q(\theta , \mathrm {s}_{{\varvec{y}}})}\) are the importance weights. In particular, in the ABC framework, the importance distribution can be

$$\begin{aligned} q(\theta , \mathrm {s}_{{\varvec{y}}})=q(\theta ) P(\mathrm {s}_{{\varvec{y}}}|\theta ) \end{aligned}$$

and, denoting by Z the normalizing constant for the joint posterior, the resulting importance weights \({\bar{\omega }}(\theta ^{(s)},\mathrm {s}_{{\varvec{y}}}^{(s)})\), \({\bar{\omega }}_s\) for short, are

$$\begin{aligned} {\bar{\omega }}_s&=\dfrac{\pi (\theta ^{(s)})\,\ P(\mathrm {s}_{{\varvec{y}}}^{(s)}|\theta ^{(s)})\,\ K_{\epsilon }\big (d(\mathrm {s}_{{\varvec{y}}}^{(s)},\mathrm {s}_{{\varvec{x}}})\big )}{ Z\, q(\theta ^{(s)}) \,\ P(\mathrm {s}_{{\varvec{y}}}^{(s)}|\theta ^{(s)})}\\&= \dfrac{K_{\epsilon }\big (d(\mathrm {s}_{{\varvec{y}}}^{(s)},\mathrm {s}_{{\varvec{x}}})\big )}{Z} \cdot \dfrac{\pi (\theta ^{(s)})}{q(\theta ^{(s)})}\;\;\;\;\;\; \;\;\;\;\;\;\; \forall s\in \{1,\ldots ,S\} \end{aligned}$$

By computing, at each iteration s, the following unnormalized weight

$$\begin{aligned} \omega _s=K_{\epsilon }\big (d(\mathrm {s}_{{\varvec{y}}}^{(s)},\mathrm {s}_{{\varvec{x}}})\big ) \cdot \dfrac{\pi (\theta ^{(s)})}{q(\theta ^{(s)})}, \end{aligned}$$
(6)

an approximation for the constant Z is obtained:

$$\begin{aligned} Z&=\int \limits _{\varTheta }\int \limits _{{\mathcal {S}}} \pi (\theta )\,\ P(\mathrm {s}_{{\varvec{y}}}|\theta )\, K_{\epsilon }\big (d(\mathrm {s}_{{\varvec{y}}},\mathrm {s}_{{\varvec{x}}})\big )\,d\mathrm {s}_{{\varvec{y}}}d\theta \\&= \int \limits _{\varTheta }\int \limits _{{\mathcal {S}}}\omega (\theta ,\mathrm {s}_{{\varvec{y}}})\,q(\theta ,\mathrm {s}_{{\varvec{y}}})\, d\mathrm {s}_{{\varvec{y}}}d\theta \approx \frac{1}{S}\sum \limits _{s=1}^S \omega _s \end{aligned}$$

where the second equality is obtained by multiplying and dividing by \(q(\theta ,\mathrm {s}_{{\varvec{y}}})\). It follows that from the output of Algorithm 2 we can estimate (5) as

$$\begin{aligned} \frac{1}{S \, Z}\sum \limits _{s=1}^S\omega _s \,h(\theta ^{(s)}, \mathrm {s}_{\varvec{y}}^{(s)})\approx \sum \limits _{s=1}^S \tilde{\omega }_s\,h(\theta ^{(s)}, \mathrm {s}_{\varvec{y}}^{(s)}) \end{aligned}$$
(7)

where each \({\tilde{\omega }}_s=\omega _s/\sum \nolimits _{r=1}^S \omega _r\) is a normalized weight.

Unlike the standard importance sampling scheme, IS-ABC implicitly involves a rejection step. In fact, usually the kernel density function, \(K_{\epsilon }(\cdot )\), is such that a strictly positive weight is given to a pair \((\theta ^{(s)}, \mathrm {s}_{{\varvec{y}}}^{(s)})\) only when \(d(\mathrm {s}_{{\varvec{y}}}^{(s)},\mathrm {s}_{{\varvec{x}}})\le \epsilon \). For example, looking at Algorithm 1, it is apparent that the primal rejection scheme is a special case of Algorithm 2 where the marginal importance distribution, \(q(\theta )\), is the prior distribution and the resulting importance weights are

$$\begin{aligned} \omega _s= K_{\epsilon }\big (d(\mathrm {s}_{{\varvec{y}}}^{(s)},\mathrm {s}_{{\varvec{x}}})\big )=\mathbb {1}\{d(\mathrm {s}_{{\varvec{y}}}^{(s)},\mathrm {s}_{{\varvec{x}}}))\le \epsilon \} \end{aligned}$$
(8)

meaning that each pair is implicitly rejected or accepted depending on the value of \(\omega _s\in \{0,1\}\).

In order to evaluate the efficiency of an importance sampling method, a widespread “rule of thumb” is to evaluate the Effective Sample Size (ESS), see Liu (2008, Ch 2). ESS represents the number of samples from the target distribution needed to get a Monte Carlo estimate with the same variance as the IS estimate in (7) given a budget of S iterations, and is defined by

$$\begin{aligned} \text {ESS} {\mathop {=}\limits ^{\triangle }}\dfrac{S}{1+var[{\bar{\omega }}]}. \end{aligned}$$
(9)

One of the major drawbacks of the importance sampling scheme is that the resulting Monte Carlo estimate in (7) is highly variable due to the problem of sample degeneracy, already mentioned previously, which in this context means that only a few of the proposed pairs \((\theta ,\mathrm {s}_{{\varvec{y}}})\) have relatively high weights resulting in a small ESS. Generally speaking, sample degeneracy is caused by an importance distribution far from its target. In this case, parameter values from regions with a low target posterior density are very likely to be drawn under the importance distribution, so that they are often proposed and associated with very small weights.

In the ABC framework as well, an importance density \(q(\theta )\) far from the marginal target \({\tilde{\pi }}(\theta |\mathrm {s}_{{\varvec{x}}})\) can lead to sample degeneracy. In this setting, an additional issue is that the weights also depend on the distance \(d(\mathrm {s}_{{\varvec{Y}}},\mathrm {s}_{{\varvec{x}}})\), hence on the random variableFootnote 1\(\mathrm {s}_{{\varvec{Y}}}\) (Sisson et al. 2018). This implies that when a parameter \(\theta ^{*}\) is proposed such that \(\Pr (\mathrm {s}_{{\varvec{Y}}}=\mathrm {s}_{{\varvec{x}}}|\theta ^{*})\) is close to zero, usually a very large number of zero-weighted pairs \((\theta ^*, \mathrm {s}_{{\varvec{y}}})\) will be generated before a distance smaller than \(\epsilon \) will be observed, especially when \(\epsilon \) is small.

In the next two sections we propose a method to define a kernel \(K_{\epsilon }(\cdot )\) that improves the efficiency of IS-ABC in terms of ESS.

3 ABC and the theory of large deviations

Recall that in R-ABC, at each iteration s, the indicator function represents a crude estimate for the probability \(\Pr ( d(\mathrm {s}_{{\varvec{Y}}},\mathrm {s}_{{\varvec{x}}})\le \epsilon |\,\theta ^{(s)})\) (see Remark 1). A possible approach to mitigate sample degeneracy is to provide a finer estimate for the ABC likelihood by evaluating that probability. In order to deal with rare events, we resort to LDT, which studies the exponential decay of the probability of rare events. We speculate that taking into account the positive probability of a large deviation event allows one to avoid rejection at all. This might provide a higher ESS, thus making the algorithm more efficient.

From now on we will confine our attention to discrete random variables, and adopt an information theoretic point of view based on the method of types (Csiszár 1998; Cover and Thomas 2006). In particular, we will assume that \({\mathcal {X}}=\{r_1,\ldots ,r_{|{\mathcal {X}}|}\}\) is a finite, nonempty set. Moreover, \({\mathcal {F}}{\mathop {=}\limits ^{\triangle }}\{P(\cdot |\theta ): \theta \in \varTheta \}\) is a family of distributions on \({\mathcal {X}}\), where each \(P(\cdot |\theta )=P_\theta \) has full support: \(\mathrm {supp}(P(\cdot |\theta )){\mathop {=}\limits ^{\triangle }}\{r: P(r|\theta )>0\}={\mathcal {X}}\) for each \(\theta \in \varTheta \).

We will let \( {\varvec{X}}^n=\{X_i\}_{i=1}^n\), \({\varvec{Y}}^m=\{Y_i\}_{i=1}^m\) and so on denote sequences of i.i.d. random variables, distributed according to an (intractable) probability distribution \(P_\theta \in {\mathcal {F}}\).

3.1 LDT via the method of types

Let \({\varvec{x}}^n\) be a sequence of n symbols drawn from \({\mathcal {X}}\), say \({\varvec{x}}^n=(x_1,\ldots ,x_n)\). The method of types moves the focus from the sequence \({\varvec{x}}^n\) itself to its type, defined as follows.

Definition 1

(Type) Let \({\varvec{x}}^n=(x_1,\ldots ,x_n)\in {\mathcal {X}}^n\). The type of \({\varvec{x}}^n\), written \(T_{{\varvec{x}}^n}\), is the probability distribution on \({\mathcal {X}}\) defined by

$$\begin{aligned} T_{{\varvec{x}}^n}(r)&{\mathop {=}\limits ^{\triangle }}\dfrac{|\{i: x_i=r\}|}{n} \;\;\;\; \forall r \in {\mathcal {X}}. \end{aligned}$$
(10)

We let \({\mathcal {T}}^n\) denote the set of n-types, that is, types with denominator n.

Note that the superscript n keeps track of the length of the sequence, which is also the denominator of the type. As is apparent, type is a function summarizing the information included in the observed sequence \({\varvec{x}}^n\) by mapping the n-dimensional observed sequence onto a \(|{\mathcal {X}}|\)-dimensional summary statistic.

The following quantities play a crucial role in the method of types. Below, we stipulate that \(0\cdot \log \frac{0}{r}{\mathop {=}\limits ^{\triangle }}0\) and that \(r\cdot \log \frac{r}{0}{\mathop {=}\limits ^{\triangle }}+\infty \) if \(r>0\), where \(\log \) denotes the logarithm to base 2. Given two probability distributions on \({\mathcal {X}}\), P and Q, we consider

  • the entropy of P, defined as

    $$\begin{aligned} H(P){\mathop {=}\limits ^{\triangle }}-\sum \limits _{r\in {\mathcal {X}}} P(r) \log P(r)\,; \end{aligned}$$

  • the Kullback–Leibler divergence between P and Q, defined as

    $$\begin{aligned} D(P||Q) {\mathop {=}\limits ^{\triangle }}\sum \limits _{r\in {\mathcal {X}}} P(r)\;\ \log \dfrac{P(r)}{Q(r)}\,. \end{aligned}$$

    With an abuse of notation, whenever the first argument of \(D(\cdot ||Q)\) is a set of probability distributions, say E, D(E||Q) stands for \(\inf _{P \in E} D(P||Q)\). When \(P^*=\mathop {\mathrm{argmin}}\nolimits _{P \in E} D(P||Q)\) exists, it is called the information projection of Q onto E.

Let \({\varvec{X}}^n=\{X_i\}_{i=1}^n\) be a sequence of i.i.d. random variables, distributed according to \(P_{\theta }{\mathop {=}\limits ^{\triangle }}P(\cdot |\theta )\), for some \(\theta \in \varTheta \). In what follows, we let \(\Pr (\cdot |\theta )\) be the probability measure on sequences induced by \(P_\theta \). The joint probability of n i.i.d. extractions \({\varvec{x}}^n\) according to \(P_\theta \), can be written as

$$\begin{aligned} \Pr ({\varvec{X}}^n={\varvec{x}}^n|\theta )=2^{n\,\big (-D(T_{{\varvec{x}}^n}||P_\theta )-H(T_{{\varvec{x}}^n})\big )}. \end{aligned}$$
(11)

See Cover and Thomas (2006, Ch.11) for a proof. It follows from the Neyman–Fisher theorem (Cox and Hinkley 1979, Ch. 2.2) that types are always sufficient statistics for \(\theta \), whatever \(P_\theta \).

Remark 2

(Types and ABC) While the number of sequences of length n is exponential in n, it is easy to show that the cardinality of \({\mathcal {T}}^n\) is polynomial in n; in fact, \(|{\mathcal {T}}^n|\le (n+1)^{|{\mathcal {X}}|}\), see Cover and Thomas (2006, Ch.11). From an ABC perspective, it follows that using types as summary statistics could mitigate the computational problems related to the comparison between the observed dataset and the pseudo-dataset, especially for large n. Furthermore, summarizing data through their empirical distributions is a way of overcoming the difficulties in finding sufficient statistics when \(P_\theta \) is unknown (and \(\Pr (\cdot |\theta )\) as well). Indeed, even when confined to discrete random variables, \(P(\cdot |\,\theta )\) is an unknown model, not necessarily a Multinomial model, see Sect. 5 for examples. With no knowledge of the analytical form of the likelihood, finding a sufficient summary statistic for \(\theta \), the vector of parameters given as an input to the simulator, is a central issue. In the literature there are several examples of models for conditionally independent discrete data in which the likelihood is analytically intractable and the required ABC method concerns empirical distributions. Examples are the ABC methods proposed by Joyce et al. (2012) and Buzbas and Rosenberg (2015) to make inference on the mutation and selection parameters governing the Fisher–Wright model (Fisher 1930). There, despite the conditional independence and the discretness of the observations, the likelihood function is difficult to evaluate since the normalizing constant depends on the parameters: for small values of the selection parameter, numerical solutions have been found by Genz and Joyce (2003), in other cases, likelihood-free methods are required.

Noting from (11) that the probability of the observed sequence decreases exponentially at a rate given by the Kullback–Leibler divergence between \(T_{{\varvec{x}}^n}\) and \(P_{\theta }\), we can say (informally) that a sequence \({\varvec{x}}^n\) is typical if \(D(T_{{\varvec{x}}^n}||P_\theta )<\delta \) for some small \(\delta >0\).

The Law of Large Numbers (LLN) states that as the length of a typical sequence goes to infinity, its type converges in probability to \(P_\theta \), see Cover and Thomas (2006, Ch 11.2.1) for formulation of the LLN in terms of the method of types presented below.

Theorem 1

(Law of Large Numbers) Let \({\varvec{X}}^n=\lbrace X_i\rbrace _{i=1}^n\) be a sequence of i.i.d. random variables with \(X_i\sim P_{\theta }\). Then for each \(\delta >0\)

$$\begin{aligned} \Pr \big (D(T_{{\varvec{X}}^n}||P_\theta )\le \delta |\theta \big )\ge 1-2^{-n(\delta -|{\mathcal {X}}| \frac{\log (n+1)}{n})}. \end{aligned}$$
(12)

Moreover, under \(\Pr (\cdot |\theta )\), as \(n\rightarrow \infty \), \(D(T_{{\varvec{X}}^n}||P_\theta )\rightarrow 0\) with probability 1.

On the other hand, observing a sequence whose type is far from \(P_\theta \), called a non-typical sequence, is a rare event, and its probability obeys a fundamental result in LDT, Sanov’s theorem; see Cover and Thomas (2006, Th.11.4.1).

Theorem 2

(Sanov’s Theorem) Let \(\varvec{X}^n=\{X_i\}_{i=1}^n\) be i.i.d. random variables on \({\mathcal {X}}\) such that each \(X_i\sim P_{\theta }\). Let \(\varDelta ^{|{\mathcal {X}}|-1}\) be the simplex of probability distributions over \({\mathcal {X}}\) and let \( {E}\subseteq \varDelta ^{|{\mathcal {X}}|-1}\). Then

$$\begin{aligned} \Pr \big (T_{{\varvec{X}}^n}\in {E}\,|\,\theta \big )\le (n+1)^{|{\mathcal {X}}|}2^{-nD(P^*||P_{\theta })}, \end{aligned}$$
(13)

where \(P^*= \mathop {\mathrm{argmin}}\limits _{P\in {E}} D(P||P_\theta )\) is the information projection of \(P_\theta \) onto E. Furthermore, if E is the closure of its interior,

$$\begin{aligned} \lim \limits _{n\rightarrow \infty } \frac{1}{n}\log \Pr (T_{{\varvec{X}}^n}\in E\,|\,\theta )=-D( E||P_{\theta })=-D(P^*||P_{\theta }). \end{aligned}$$

Suppose that E is composed of types of non-typical sequences. Then Sanov’s theorem characterizes the exponential decrease rate of the probability of E. Taking into account this probability may provide a finer ABC approximation of the likelihood, as discussed in the next section.

3.2 LDT in ABC

In this section we provide a formal explanation of what is meant by poor parameter proposals and how they can contribute to the representation of the approximate posterior distribution by means of LDT. We are interested in obtaining an approximation of the posterior distribution, \({\tilde{\pi }}(\theta |{\varvec{x}}^n)\), via R-ABC or an equivalent IS-ABC by assuming as given: (a) the marginal importance density \(q(\theta )\) to be the prior distribution on \(\varTheta \); (b) \(\epsilon >0\) as a threshold; (c) types as summary statistics; (d) the Kullback–Leibler divergence as distance function. For the sake of simplicity, from now on we will also assume \(T_{{\varvec{x}}^n}\) to be full support.

Given a budget of S iterations, both R-ABC and IS-ABC generate a sequence of pairs \((T_{{\varvec{y}}^m}^{(s)},\theta ^{(s)})\) with \(s\in \{1,\ldots ,S\}\). Each \(T_{{\varvec{y}}^m}^{(s)}\) is an m-type resulting from a sequence of i.i.d. random variables, \({\varvec{Y}}^m=\{Y_j\}_{j=1}^m\), distributed according to \(P\big (\cdot |\, \theta ^{(s)}\big )\). We stress that the length of the simulated sequence, m, need not be equal to n, the length of the observed data sequence. Note also that, because of the independence assumption, choosing \(m=M\cdot n\) with \(M\in \mathbb {N}\) means that the algorithm simulates M pseudo-datasets at each iteration, like a marginal sampler (see Remark 1).

Looking at Algorithms 1 and 2, being the whole pair \((\theta ^{(s)},T_{{\varvec{y}}^m}^{(s)})\) accepted or rejected, one can define the joint acceptance region for these algorithms on the space \(\varTheta \times {\mathcal {T}}^m \). However, as the acceptance rule is based only on the simulated type, regardless of the proposed parameter value, the acceptance region can be projected onto the probability simplex \(\varDelta ^{|{\mathcal {X}}|-1}\supset {\mathcal {T}}^m\).

Definition 2

(Acceptance region) Let \(\varDelta ^{|{\mathcal {X}}|-1}\) be the simplex of probability distributions over \({\mathcal {X}}\) and let \(T_{{\varvec{x}}^n}\) be the type of the observed sequence \({\varvec{x}}^n\). The acceptance region \({\mathcal {B}}_\epsilon (T_{{\varvec{x}}^n})\), referred to as \({\mathcal {B}}_{\epsilon }\) for short, is defined for any \(\epsilon \ge 0\), as

$$\begin{aligned} {\mathcal {B}}_{\epsilon }{\mathop {=}\limits ^{\triangle }}\big \{P\in \varDelta ^{|{\mathcal {X}}|-1}: D(P||T_{{\varvec{x}}^n})\le \epsilon \big \}. \end{aligned}$$

Now we can define a poor parameter proposal as a parameter \(\theta ^{(s)}\) such that \(T_{{\varvec{x}}^n}\) and the other types in the acceptance region are types of non-typical sequences w.r.t. \(P(\cdot \,|\,\theta ^{(s)})\).

Accordingly, sampling a poor parameter means that there is a large divergence between \(T_{{\varvec{x}}^n}\) and \(P(\cdot |\theta ^{(s)})\). On the other hand, with m large enough, \(T_{{\varvec{y}}^m}^{(s)}\) is very likely to be close to \(P(\cdot |\theta ^{(s)})\), due to the Law of Large Numbers. Heuristically, this implies that the probability of simulating a sequence \({\varvec{y}}^m\) whose type is in the acceptance region is very small. Recalling that in R-ABC and in IS-ABC outlined at the beginning of this section a crude Monte Carlo estimate of the probability \(\Pr (T_{{\varvec{Y}}^m}\in {\mathcal {B}}_{\epsilon }|\,\theta ^{(s)})\) is given by the indicator function \(\mathbb {1}\{D(T_{{\varvec{y}}^m}^{(s)}||T_{{\varvec{x}}^n})\le \epsilon \}\), the vast majority of the poor parameter proposals are discarded altogether. We propose to mitigate this problem by assigning strictly positive weights to each proposal \(\theta ^{(s)}\), even if \(T_{{\varvec{y}}^m}^{(s)}\) is outside the acceptance region. To this end, we want to replace the indicator function with a finer estimate of the probability \(\Pr (T_{{\varvec{Y}}^m}\in {\mathcal {B}}_{\epsilon }|\,\theta ^{(s)})\).

In principle, Sanov’s theorem implies that, for m large enough, that probability can be approximated at each iteration by

$$\begin{aligned} \Pr \big ( T_{{\varvec{Y}}^m}\in {\mathcal {B}}_{\epsilon }\,| \,\theta ^{(s)}\big ) \approx 2^{-mD({\mathcal {B}}_{\epsilon }||P_{\theta ^{(s)}})}. \end{aligned}$$
(14)

By replacing the indicator function in (1) with (14), the approximate posterior becomes

$$\begin{aligned} {\tilde{\pi }}(\theta , T_{{\varvec{y}}^m}|T_{{\varvec{x}}^n})\propto \pi (\theta )P(T_{{\varvec{y}}^m}|\theta ) 2^{-mD({\mathcal {B}}_{\epsilon }||P_\theta )}\,. \end{aligned}$$
(15)

Unfortunately, the computation of the probability in (14) is still not feasible when the model \({\mathcal {F}}=\{P_\theta : \theta \in \varTheta \}\) is unknown, as we do not know how to compute \(D({\mathcal {B}}_{\epsilon }||P_{\theta ^{(s)}})\). The following theorem provides an asymptotic approximation to circumvent the problem. A proof is provided in “Appendix A”.

Theorem 3

Let \({\mathbf {Y}}^m=\{Y_j\}_{j=1}^m\) be a sequence of i.i.d. random variables taking values on the finite set \({\mathcal {X}}=\{r_1,\ldots ,r_{|{\mathcal {X}}|}\}\), with each \(Y_j\sim P_{\theta }\). Then under the measure \(\Pr (\cdot |\theta )\)

$$\begin{aligned} \lim \limits _{m\rightarrow \infty } D({\mathcal {B}}_{\epsilon }||T_{{\varvec{Y}}^m})=D({\mathcal {B}}_{\epsilon }||P_\theta )\;\;\;\;\; a.s. \end{aligned}$$
(16)

In essence, this result says that, as m increases and the type \(T_{{\varvec{y}}^m}\) converges to the distribution \(P_\theta \) that has generated \({\varvec{y}}^m\), the information projection of \(T_{{\varvec{y}}^m}\) onto \({\mathcal {B}}_{\epsilon }\) converges to that of \(P_\theta \) onto \({\mathcal {B}}_{\epsilon }\) (see Fig. 1). From (14) and Theorem 3, for m large enough, \(2^{-mD({\mathcal {B}}_{\epsilon }||T_{{\varvec{y}}^m})}\) provides a feasible asymptotic estimate for the acceptance probability, \(\Pr (T_{{\varvec{Y}}^m}\in {\mathcal {B}}_{\epsilon }\,|\,\theta )\). Replacing the indicator function in the ABC approximate posterior (1) with this estimate, we obtain the following new joint approximate posterior distribution:

$$\begin{aligned} {\tilde{\pi }}(\theta , T_{{\varvec{y}}^m}|T_{{\varvec{x}}^n})\propto \pi (\theta )P(T_{{\varvec{y}}^m}\,|\,\theta ) 2^{-mD({\mathcal {B}}_{\epsilon }||T_{{\varvec{y}}^m})}. \end{aligned}$$
(17)
Fig. 1
figure 1

Acceptance region, \({\mathcal {B}}_{\epsilon }\), types, \(T_{{\varvec{x}}^n}\) and \(T_{{\varvec{y}}^m}\), and the probability distribution \(P_\theta \) that generated \({\varvec{y}}^m\). Asymptotically (as \(m\rightarrow \infty \)) \(T_{{\varvec{y}}^m}\) converges to \(P_\theta \) and the distance \(D({\mathcal {B}}_{\epsilon }||T_{{\varvec{y}}^m})\) (red) converges to \(D({\mathcal {B}}_{\epsilon }||P_\theta )\) (green) (color figure online)

Full size image

4 Weighted approximate Bayesian computation

The discussion in the previous section indicates that IS-ABC can be improved by resorting to a better approximation for the likelihood. In particular, the (implicit) rejection step can be avoided by evaluating the positive probability of rare events via Sanov’s theorem. Indeed, an easy way of sampling from (17) is a large deviations version of IS-ABC, which we will call the weighted approximate Bayesian computation (LDW-ABC).

Starting from the definition of an acceptance region satisfying the hypothesis of Sanov’s theorem, as in Definition 2, a sample from the approximate posterior distribution \({\tilde{\pi }}(\theta ,T_{{\varvec{y}}^m}|T_{{\varvec{x}}^n})\) can be obtained as described in Algorithm 3.

figure c

Looking at Algorithm 3, it is apparent that LDW-ABC is a specialization of the more general IS-ABC. More specifically, the sufficient summary statistics involved are the types, the distance function is the Kullback–Leibler divergence, and the kernel density function is defined as follows:

$$\begin{aligned} K_{\epsilon ,m}\big (T_{{\varvec{y}}^m}\big )= {\left\{ \begin{array}{ll} 1 &{} \text {if } D(T_{{\varvec{y}}^m}||T_{{\varvec{x}}^n})\le \epsilon \\ 2^{-mD({\mathcal {B}}_{\epsilon }||T_{{\varvec{y}}^m})}\; &{}\text {if } D(T_{{\varvec{y}}^m}||T_{{\varvec{x}}^n})> \epsilon \end{array}\right. }. \end{aligned}$$
(18)

At each iteration a positive weight is assigned to the proposed \(\theta ^{(s)}\). More precisely, the weight equals 0 only when \(D({\mathcal {B}}_{\epsilon }||T_{{\varvec{y}}^m})=\infty \). Each \(\omega _s\) is computed by approximating the divergence \(D({\mathcal {B}}_{\epsilon }||T_{{\varvec{y}}^m})\) as described in “Appendix B”.

As a special case of the general IS-ABC, the output of Algorithm 3 is a weighted sample from the following approximate joint posterior distribution:

$$\begin{aligned} {\tilde{\pi }}(\theta , T_{{\varvec{y}}^m}|T_{{\varvec{x}}^n})\propto \pi (\theta )\,K_{\epsilon ,m}\big (T_{{\varvec{y}}^m}\big ) \;P_\theta (T_{{\varvec{y}}^m}) \end{aligned}$$
(19)

which, by marginalizing out simulated types, becomes

$$\begin{aligned} {\tilde{\pi }}(\theta |T_{{\varvec{x}}^n})\propto \pi (\theta )\sum \limits _{T_{{\varvec{y}}^m}\in {\mathcal {T}}^m}K_{\epsilon ,m}\big (T_{{\varvec{y}}^m}\big ) \;P_\theta (T_{{\varvec{y}}^m}) \end{aligned}$$
(20)

where \({\mathcal {T}}^m\) denotes the set of the m-types. Hence, the likelihood approximated by LDW-ABC is

$$\begin{aligned} \tilde{{\mathcal {L}}}_{\epsilon ,m}(\theta ;T_{{\varvec{x}}^n}){\mathop {=}\limits ^{\triangle }}\sum \limits _{T_{{\varvec{y}}^m}\in {\mathcal {T}}^m}K_{\epsilon ,m}\big (T_{{\varvec{y}}^m}\big )\,P_\theta (T_{{\varvec{y}}^m}). \end{aligned}$$
(21)

Note that the quality of the approximation depends both on the threshold \(\epsilon \) and on the size of pseudo-dataset, m. More precisely, the adjustment w.r.t. the likelihood approximate by R-ABC,Footnote 2 here denoted by \(\tilde{{\mathcal {L}}}^R_{\epsilon ,m}(\theta ;T_{{\varvec{x}}^n}){\mathop {=}\limits ^{\triangle }}\!\! \sum \limits _{T_{{\varvec{y}}^m}\in {\mathcal {B}}_{\epsilon }}\!P_\theta (T_{{\varvec{y}}^m})\), depends on m and \(\epsilon \). In fact, from (18) and Definition 2, the approximate likelihood in (21) can be written as

$$\begin{aligned} \tilde{{\mathcal {L}}}_{\epsilon ,m}(\theta ;T_{{\varvec{x}}^n})&= \sum \limits _{T_{{\varvec{y}}^m}\in {\mathcal {B}}_{\epsilon }}\!\!P_\theta (T_{{\varvec{y}}^m})+\!\!\sum \limits _{T_{{\varvec{y}}^m}\in {\mathcal {B}}_{\epsilon }^c}\!\!2^{-m D({\mathcal {B}}_{\epsilon }||T_{{\varvec{y}}^m})}P_\theta (T_{{\varvec{y}}^m})\\&=\tilde{{\mathcal {L}}}_{\epsilon ,m}^R(\theta ;T_{{\varvec{x}}^n})+\alpha _{\epsilon ,m}(\theta ) \end{aligned}$$

where the term \(0\le \alpha _{\epsilon ,m}(\theta )\le 1\) is the adjustment. The following lemma gives an upper bound for that adjustment \(\alpha _{\epsilon ,m}(\theta )\), in two cases depending on \(P_\theta \). The proof is in “Appendix A”.

Proposition 1

(The adjustment upper bound) Let \(\alpha _{\epsilon ,m}(\theta )=\tilde{{\mathcal {L}}}_{\epsilon ,m}(\theta ;T_{{\varvec{x}}^n})-\tilde{{\mathcal {L}}}_{\epsilon ,m}^R(\theta ;{\mathcal {B}}_{\epsilon })\) be the difference between the two likelihood functions approximated by LDW-ABC and R-ABC. Let \({\mathcal {B}}_{\epsilon }\) be the ABC acceptance region and \(\mathring{{\mathcal {B}}_{\epsilon }}\) its interior. We have the following upper bounds, depending on \(\theta \), which hold for all \(m\ge 1\).

  1. (a)

    \(P_\theta \in \mathring{{\mathcal {B}}_{\epsilon }}\). Then \(D({\mathcal {B}}_{\epsilon }^c||P_{\theta })>0\) and \(\alpha _{\epsilon ,m}(\theta )\le (m+1)^{|{\mathcal {X}}|} 2^{-mD({\mathcal {B}}_{\epsilon }^c||P_{\theta })}\);

  2. (b)

    \(P_\theta \in {\mathcal {B}}_{\epsilon }^c\). Let \(\gamma {\mathop {=}\limits ^{\triangle }}D({\mathcal {B}}_{\epsilon }||P_\theta )>0\). Then there exists \(0<\delta <\gamma \) s.t. \(\alpha _{\epsilon ,m}(\theta )\le (m+1)^{|{\mathcal {X}}|} 2^{-m \delta }\).

From Proposition 1 it follows that as m goes to infinity, \(\alpha _{\epsilon ,m}(\theta )\rightarrow 0\) for almost all \(\theta \in \varTheta \). Therefore, the approximate likelihood from LDW-ABC achieves the approximate likelihood from R-ABC and preserves its asymptotic properties. Moreover, we speculate that LDW-ABC improves the efficiency by mitigating the sample degeneracy. An evaluation of ESS might be a way of appreciating the improvement induced by avoiding the implicit rejection.

Since the term ESS in (9) involves the evaluation of the variance of the normalized weights, \(var[{\bar{\omega }}]\), its exact computation is infeasible, as it depends on the unknown target normalizing constant. For this reason, we adopt the following estimate derived by Kong (1992) and Elvira et al. (2018):

$$\begin{aligned} \widehat{\text {ESS}}&{\mathop {=}\limits ^{\triangle }}\dfrac{\bigg (\sum \nolimits _{s=1}^S\omega _s\bigg )^2}{\sum \nolimits _{s=1}^S \omega ^2_s} \end{aligned}$$
(22)

(with the proviso that \(\widehat{\text {ESS}}{\mathop {=}\limits ^{\triangle }}0\) if all \(\omega _s\)’s are zero). Let \(\widehat{\text {ESS}}_{IS}\) and \(\widehat{\text {ESS}}_{LD}\) be, respectively, the value of ESS achieved by S iterations of IS-ABC and LDW-ABC by setting the same tuning parameters, distance function and importance density \(q(\theta )\). Explicitly, let us assume that the kernel function for IS-ABC is 1 within the acceptance region \({\mathcal {B}}_{\epsilon }\) and 0 outside. Heuristically, adding positive weights increases the numerator more than the denominator in (22), suggesting that a non null weight assigned by LDW-ABC to a parameter proposal rejected by IS-ABC is enough to have \(\widehat{\text {ESS}}_{LD}>\widehat{\text {ESS}}_{IS}\). This is confirmed by the following simple result, whose proof is given in “Appendix A”.

Proposition 2

(Empirical ESS) It holds that \(\widehat{\text {ESS}}_{LD}\ge \widehat{\text {ESS}}_{IS}\). Moreover this inequality is strict, provided that in at least one iteration of the algorithm there is generated a full support \(T_{{\varvec{y}}^m}\) falling outside \({\mathcal {B}}_{\epsilon }\).

A tedious but straightforward analysis shows in fact that the event mentioned in the statement, upon which strict inequality holds, occurs with probability 1 as \(S\longrightarrow +\infty \). The above result will be empirically validated in the experiments of Sect. 5, thus providing further evidence that LDW-ABC achieves an improvement in terms of efficiency.

Below, we sum up the technical development so far with a discussion of the role of the parameters m and \(\epsilon \).

Remark 3

(On the role of the tuning parameters) Concerning the role of m, the size of pseudo-dataset, and \(\epsilon \), the tolerance, we can sum up the content of Propositions 1 and 2 as follows:

  1. 1.

    large m and small \(\epsilon \) point to low \(\widehat{\text {ESS}}\) and low \(\alpha _{\epsilon ,m}\);

  2. 2.

    small m and large \(\epsilon \) point to high \(\widehat{\text {ESS}}\) and high \(\alpha _{\epsilon ,m}\).

If one regards \(\widehat{\text {ESS}}\) as a measure of efficiency, and \(\alpha _{\epsilon ,m}\) as a measure of (lack of) accuracy w.r.t. the R-ABC likelihood, (but see also below), 1 and 2 above indicate how to trade off one for the other.

In particular, as Theorem 3 requires a relatively large m in order to get a good approximation for the posterior probability, 1 above says we can increase the tolerance \(\epsilon \) to mitigate the resulting inefficiency. On the other hand, in cases where a small tolerance parameter \(\epsilon \) is required, 2 above offers room to mitigate the resulting inefficiency by decreasing m.

Note, however, that when considering accuracy w.r.t. the target posterior density \(\pi (\theta |T_{{\varvec{x}}^n})\), the adjustment \(\alpha _{\epsilon ,m}\) cannot simply be regarded as a measure of imprecision: rather, it represents a compensation for those \(\theta \)’s that would be assigned a too low probability by pure R-ABC. In this case, a sounder measure of precision can be obtained by directly comparing a kernel-estimated density (obtained with LDW-ABC weights) and the target posterior density, e.g., in terms of the mean integrated squared error (MISE). This measure is, however, impossible to evaluate analytically, since its calculation presupposes the knowledge of the target posterior density. From a more empirical point of view, further discussion of the consequences of different choices of \(\epsilon \) and m on the performances of the posterior estimators is presented in Sect. 5, illustrated by a number of examples.

5 Experiments

In order to evaluate the performance of the proposed method, we have put a proof-of-concept implementation of LDW-ABC at work on two examples. We compare the results obtained from LDW-ABC with those obtained from R-ABC. For both examples, there is a MCMC method for sampling from the exact posterior distribution, and the resulting posterior inference is taken as a reference for comparison.

5.1 Example 1: mixture of binomial distributions

Let \({\varvec{X}}^n=\{X_i\}_{i=1}^n\) be a sequence of i.i.d. discrete random variables distributed according to the following parametric finite mixture model:

$$\begin{aligned} \lambda Bin(\theta _1, N=4)+ (1-\lambda ) Bin(\theta _2, N=4). \end{aligned}$$
(23)

Here we assume a uniform prior distribution on the mixture weight \(\lambda \) and that \((\theta _1,\theta _2)\) are uniformly distributed on the set \(\{(\theta _1,\theta _2):0\le \theta _2\le \theta _1\le 1\}\) by imposing the following identifiability constraint:

$$\begin{aligned} \theta _1\ge \theta _2. \end{aligned}$$

An analytical computation of the posterior distribution requires the evaluation of the likelihood

$$\begin{aligned}&P({\varvec{x}}^n| \lambda , \theta _1, \theta _2) \nonumber \\&\quad =\prod \limits _{i=1}^n {N\atopwithdelims ()x_i} \bigg [\lambda \theta _1^{x_i}(1-\theta _1)^{N-x_i}+(1-\lambda )\theta _2^{x_i}(1-\theta _2)^{N-x_i}\bigg ]. \end{aligned}$$
(24)

The direct computation of (24) is infeasible, as even with a few hundred observations, it involves the expansion of the likelihood into \(2^n\) terms. In the literature, there are several methods to deal with this problem, which allow sampling from the parameters’ posterior distributions, see Marin et al. (2005). A widespread method is a Gibbs Sampling handling the finite mixtures issue as a missing data problem, see Diebolt and Robert (1994). Samples from the joint posterior distribution are obtained by means of a hierarchical model involving a vector of latent random variables, \({\varvec{Z}}^n=\{Z_i\}_{i=1}^n\), where each \(Z_i\sim Bernoulli(1-\lambda )\) indicates to which component the i-th observation belongs:

$$\begin{aligned} \left\{ \begin{array}{ll} X_i\sim Bin (\theta _1, N) \,\,\,\,\ \text {if } z_i=0\\ X_i\sim Bin (\theta _2, N) \,\,\,\,\ \text {if } z_i=1.\\ \end{array}\right. \end{aligned}$$
(25)
figure d

Here the generative model consists of simulating each of the n values from one of the two binomials according to the result of a Bernoulli(1-\(\lambda )\) experiment. The same generative model has been run by a plug-in of the true values of the parameters displayed in Table 1 (LHS) to obtain the observed data. We ran Algorithm 4 as detailed in Table 1 (RHS), and after burn-in and thinning we got 5000 values for each parameter regarded as drawn independently from the true posterior distributions. The posterior means and variances are displayed in Table 2.

Table 1 Details for the simulation of the dataset and for the Gibbs implementation
Full size table
Table 2 Posterior estimates derived via Gibbs sampling
Full size table

In order to compare performance of LDW-ABC with that of R-ABC, the marginal importance distributions are set equal to the prior distributions.

Fig. 2
figure 2

Posterior distributions corresponding to four different pairs of tuning parameters \((m,\epsilon )\). Each panel refers to one of the three model parameters. Red lines represent the posterior density estimates provided via R-ABC. The blue lines represent the estimates provided via LDW-ABC. The dashed black lines are the output of the Gibbs sampler. The gray dashed lines are the ratios \(\tilde{{\mathcal {L}}}_{\epsilon ,m}(\theta ;T_{{\varvec{x}}^n})/\tilde{{\mathcal {L}}}_{\epsilon ,m}^{R}(\theta ;T_{{\varvec{x}}^n})\) providing a representation of the adjustment \(\alpha _{\epsilon ,m}\) (color figure online)

Full size image
Fig. 3
figure 3

Posterior cumulative density functions for \(\theta _2\). Each plot shows in blue the output of LDW-ABC, in red the output of R-ABC and in black the true cumulative density function for a pair \((m,\epsilon )\). For \(\theta _2>0.5\) both the cumulative density functions equal 1. \(90\%\) intervals over 100 runs of each algorithm are also shown (color figure online)

Full size image

We ran Algorithms 1 and 3 with \(S=100{,}000\) and with four different pairs (m, \(\epsilon \)). Since our speculation is that introducing the evaluation of the probability of rare events provides a better approximation in the tails of the distributions, we are interested in comparing the shape of the posterior distributions obtained by LDW-ABC and by R-ABC taking the Gibbs posterior distributions as reference. Accordingly, besides the posterior estimates of the means and variances, we also reconstruct the posterior densities by means of a Gaussian kernel density estimation.

The point estimates are compared via the MSE, and the kernel density estimates via the MISE. In particular, the corresponding estimates, \(\widehat{\text {MSE}}\) and \(\widehat{\text {MISE}}\), are computed by averaging over 100 runs the squared errors and the integrated squared errors w.r.t. the output of the Gibbs sampler. The results are summarized in Table 3.

Table 3 Squared errors and integrated squared errors w.r.t. the output of the Gibbs sampler averaged over 100 runs
Full size table

First, we note that both the \(\widehat{\text {MSE}}\) and the \(\widehat{\text {MISE}}\) achieved by LDW-ABC are always lower for LDW-ABC than for R-ABC. Hence, in our example, taking into account the probability of large deviation events has improved both the point estimates and the approximation of the posterior distributions. Moreover, as already pointed out in Sect. 4, LDW-ABC mitigates the sample degeneracy by achieving an \(\widehat{\text {ESS}}\) up to more than five times that achieved by R-ABC (see Table 4).

Table 4 ESS and normalized perplexity averaged over 100 runs for each pair of tuning parameters
Full size table

In order to evaluate the sample degeneracy, Table 4 (RHS) also displays the normalized perplexity, which equals \(2^{H(\tilde{\varvec{\omega }})}/S\), where \(H(\tilde{\varvec{\omega }})\) denotes the entropy of the normalized weights. Cappé et al. (2008) show that the normalized perplexity represents an estimate of \(2^{-D\big ({\tilde{\pi }}(\theta ,T_{{\varvec{y}}^m}|T_{{\varvec{x}}^n})||q(\theta ,T_{{\varvec{y}}^m})\big )}\), meaning that when the perplexity is larger, the sample degeneracy is smaller.

The following comments are consistent with Remark 3. Concerning the role of the tuning parameters, m and \(\epsilon \), we note that by fixing a large m (e.g., 5000), as \(\epsilon \) increases both \(\widehat{\text {ESS}}\) and the perplexity increase. Moreover, both \(\widehat{\text {MSE}}\) and \(\widehat{\text {MISE}}\) decrease. The same happens by reducing m with \(\epsilon \) fixed to a small value (e.g., 0.005). This provides guidance on how to set the tuning parameters. In Fig. 2 three matrices of plots, one for each parameter, show the posterior densities: the size of the pseudo-dataset, m, equals 500 in the plots on the LHS of each panel, and 5, 000 on the RHS. The topmost plots show the approximate distributions with \(\epsilon =0.01\), the others the distributions corresponding to \(\epsilon =0.005\). According to Remark 3, we note that as m increases the blue lines (LDW-ABC) overlap the red ones (R-ABC). In principle, we would expect that both the algorithms achieve a better approximation of the posterior shapes with \(\epsilon =0.005\) than \(\epsilon =0.01\). However, in the case of R-ABC, we see a deviation from the true posterior distributions (dotted lines), when moving from the first to the second row of each matrix. The same deviation occurs for LDW-ABC, but only in the second column, when \(m=5{,}000\). This suggests that the quality of the R-ABC approximation is affected by a low value of the ESS which is in turn determined by a too exacting value of \(\epsilon \) and m. In fact, when \(m=500\), LDW-ABC manages to mitigate the effect of a small \(\epsilon \), but it fails when a large value of m causes a too small ESS for the LDW-ABC as well. In the figures we also superimposed the ratio \(\tilde{{\mathcal {L}}}_{\epsilon ,m}(\theta ;T_{{\varvec{x}}^n})/\tilde{{\mathcal {L}}}_{\epsilon ,m}^{R}(\theta ;T_{{\varvec{x}}^n})=1+\alpha _{\epsilon ,m}(\theta ;T_{{\varvec{x}}^n})/\tilde{{\mathcal {L}}}_{\epsilon ,m}^{R}(\theta ;T_{{\varvec{x}}^n})\) evaluated pointwise and shown by the gray dashed lines. This quantity depends on the contribution of the adjustment w.r.t. the R-ABC likelihood and shows how the adjustment acts in modifying this latter when the R-ABC posterior density is underestimated (gray areas). Figure 3 shows the posterior cumulative density functions for \(\theta _2\). The posterior cumulative density functions for the other two parameters are given in “Appendix C”, Fig. 4. We also show the \(90\%\) credible intervals for the estimated cumulative density functions. The red areas are always larger than the blue areas, meaning that the estimates provided by R-ABC exhibit greater variability. This is more significant when \(\epsilon =0.005\), due to the small acceptance probability.

To wrap up, as suggested by the \(\widehat{\text {MISE}}\)’s, the posterior distributions approximated by LDW-ABC appear more faithful to the true shapes. Moreover, the ESS and the variability of the estimates are less sensitive to small values of \(\epsilon \).

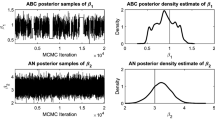
5.2 Example 2: learning from anonymized data

The second example is aimed at comparing LDW-ABC and R-ABC at work on a real-world dataset. We consider a scenario in which the dataset contains microdata that have been anonymized in order to protect the privacy of the individuals involved. More specifically, our data are a subset of 5692 rows from the Adult dataset extracted by Barry Becker from the 1994 US Census database and available from the UCI machine learning repository (Kohavi and Becker 1996). The anonymizaton method we have adopted, Anatomy (Xiao and Tao 2006), is a group based anonymization scheme. Given a dataset consisting of a collection of rows, each one corresponding to an individual and containing his/her sensitive (e.g., disease, income) and nonsensitive attributes (e.g., gender, nationality, ZIP code), a group-based anonymization algorithm produces an obfuscated version of itself by partitioning the rows into groups. The idea is to process the set of rows in each group so that even knowing the nonsensitive attribute of an individual, one cannot identify his/her sensitive values. To reach this goal, Anatomy vertically and randomly permutes the nonsensitive features within each group, thus breaking the link between the sensitive and nonsensitive attributes.

Table 5 Cleartext and anonymized tables
Full size table

An example of group based anonymization is in Table 5, adapted from Wong et al. (2011). The LHS table is the original table collecting medical data from eight individuals; here, Disease is considered as the only sensitive attribute. The RHS table is an example of an application of the Anatomy scheme: within each group, the nonsensitive part of the rows is vertically and randomly permuted, thus breaking the link between the sensitive and nonsensitive values. Generally speaking, the obfuscated table can be seen as the output of a generative mechanism: given the population parameters as input, the mechanism first generates a cleartext table by drawing a number of rows i.i.d., then applies the anonymization algorithm to this table and outputs the result. One is interested in the posterior distribution of the population parameters, given an observation of the obfuscated table. Clearly, the likelihood function involved in this mechanism is highly nontrivial, and also depends on the details of the anonymization algorithm. Below we make this precise by adopting the model proposed by Boreale et al. (2020).

Let a row of the original (cleartext) dataset be a pair \((s,r)\in {\mathcal {S}}\times {\mathcal {R}}\), for finite, nonempty sets \({\mathcal {S}}\) and \({\mathcal {R}}\). Here, s and r represent the sensitive and nonsensitive attributes (or vectors of attributes). Given a multiset of n rows, \(d=\{\!|(s_1,r_1),\ldots ,(s_n,r_n)|\!\}\), Anatomy will first arrange d into a sequence of groups, \({\varvec{x}}= g_1,\ldots ,g_k\), the cleartext table. Each group in turn is a sequence of \(n_i\) rows, \(g_i=(s_{i,1},r_{i,1}),\ldots ,(s_{i,n_i},r_{i,n_i})\). The obfuscated table is then obtained as the sequence \({\varvec{x}}^*=g^*_1,\ldots ,g^*_k\), where the obfuscation of each group \(g_i\) is a pair \(g_i^*=(\sigma _i,\rho _i)\). Here, each \(\sigma _i=s_{i,1},\ldots ,s_{i,n_i}\) is the sequence of sensitive values occurring in \(g_i\); each \(\rho _i\), called the generalized nonsensitive value, is the multiset of \(g_i\)’s nonsensitive values: \(\rho _i=\{\!| r_{i,1},\ldots ,r_{i,n_i}|\!\}\)—i.e., \(\rho _i\) includes all those and only those values, with multiplicities, found in \(g_i\).

The model consists of the following random variables:

  • \(\varvec{\theta }=(\theta _S,\varvec{\theta }_{R|S})\), where \(\varvec{\theta }_{R|S}=\{\theta _{R|s}: s\in {\mathcal {S}}\}\). Here, \(\varvec{\theta }\) takes values on the set of full support probability distributions \({\mathcal {D}}\) over \( {\mathcal {S}}\times {\mathcal {R}}\) and represents the joint probability distribution of the sensitive and nonsensitive attributes in the population.

  • \({\varvec{X}}=G_1,\ldots ,G_k\), which takes values in the set of cleartext tables \({\mathcal {X}}\). Each group \(G_i\) is in turn a sequence of \(n_i\ge 1\) consecutive rows in \({\varvec{X}}\), \(G_i=(S_{i,1},R_{i,1}),\ldots ,(S_{i,n_i},R_{i,n_i})\) with \(S_{i,j}\sim \theta _S\) and \(R_{i,j}\sim \theta _{R|s_{i,j}}\). The number of groups k is not fixed, but depends on the anonymization scheme and on the specific tuples in d.

  • \({\varvec{X}}^*=G^*_1,\ldots ,G^*_k\), which takes values in the set of obfuscated tables \({\mathcal {X}}^*\).

We assume that \({\varvec{X}}^*\) solely depends on the table \({\varvec{X}}\) and the underlying obfuscation algorithm, thus the above three random variables form a Markov chain:

$$\begin{aligned} \varvec{\theta }\longrightarrow \; {\varvec{X}}\; \longrightarrow {\varvec{X}}^*. \end{aligned}$$
(26)

Here, our aim is to derive the posterior distribution for the population parameters \(\varvec{\theta }\) by observing an instance of the anonymized table, \({\varvec{x}}^*\). There is no tractable analytical expression for the likelihood \({\mathcal {L}}(\varvec{\theta }; {\varvec{x}}^*)\). In Kifer (2009) and Boreale et al. (2020) this problem is circumvented by defining an MCMC scheme for sampling from the joint posterior \(\pi (\varvec{\theta }, {\varvec{x}}| {\varvec{x}}^*)\) and then discarding the cleartext tables (further details on the MCMC scheme are in Boreale et al. (2020, Section 5). Here we pursue an alternative solution based on ABC. Specifically, we simulate the anonymized tables \({\varvec{y}}^*\) according to the following generative model:

  1. 1.

    Generate a table of n i.i.d. rows \((s,r)\in {\mathcal {S}}\times {\mathcal {R}}\) distributed according to the \(\varvec{\theta }\) given as input;

  2. 2.

    Partition the table into k groups of dimensions \(\{n_i\}_{i=1}^k\);

  3. 3.

    Randomly permute the values of the nonsensitive attributes, \(r_{1},\ldots ,r_{n_i}\), within each group \(g_i\).

Here, n is the number of rows and k is the number of groups in the observed anonymized table \({\varvec{x}}^*\), while \(n_i\) is the number of rows in \(g^*_i\). In our example, the observed data \({\varvec{x}}^*\) consists of an obfuscated table composed of \(k=1423\) groups, with \(n_i=4\) for each group \(g_i\). We take race (four possible values) as a nonsensitive attribute and workclass (four possible values) as the sensitive attribute. As in Boreale et al. (2020), we assume that \(\theta _S\) and the \(\theta _{R|s}\)’s are independently distributed according to non-informative Dirichlet prior distributions. The output of the ABC algorithms will be a sample from the approximate joint posterior distribution \({\tilde{\pi }}(\varvec{\theta }_{R|S}, T_{{\varvec{y}}^*}|T_{{\varvec{x}}^*})\) since the sensitive part is not changed by the anonymization algorithm and the posterior distribution for \(\theta _S\) exists in closed form.Footnote 3 Note that in order to satisfy the assumptions of Sanov’s theorem, the m simulated rows must be independent and identically distributed. Recalling that the m pairs (s, r)’s are generated independently and that the permutation is completely at random, we conjecture that the i.i.d. assumption is satisfied. We have positively verified this assumption empirically via the permutation test based on the periodicity test statistic described in the National Institute of Standards and Technology Special Publication 800-90B (Turan et al. 2018).

As in the previous experiment, we consider the output of 100, 000 MCMC runs as a reference, in order to compute the \(\widehat{\text {MSE}}\)’s and \(\widehat{\text {MISE}}\)’s, and thus comparing the accuracy of LDW-ABC and R-ABC. The posterior means derived via MCMC are displayed in “Appendix C” (Table 8).

Table 6 The leftmost table shows the squared errors integrated over the 3-simplex and averaged over 100 runs of ABC
Full size table

By setting \(m=100\) and \(\epsilon =1\), as far as point estimations are concerned, both LDW-ABC and R-ABC perform quite similarly. The results are displayed in “Appendix C” (Table 9). Nevertheless, the \(\widehat{\text {MSE}}\)’s achieved by LDW-ABC are almost always smaller than the ones achieved by R-ABC. Concerning the approximations of the multivariate posterior distributions, looking at \(\widehat{\text {MISE}}\) we can conclude that LDW-ABC outperforms R-ABC (see Table 6). Moreover, by focusing on the improvement in efficiency, we note that the value of \(\widehat{\text {ESS}}\) for LDW-ABC is more than twice that for R-ABC.

6 Conclusions and future research

We have put forward an approach to address sample degeneracy in methods of approximate Bayesian computation (ABC). Our proposal consists in the definition of a convenient kernel function which, via the theory of large deviations, takes into account the probability of rare events—a poor parameter proposal generating pseudo-data close to those observed. By adopting the information theoretic method of types, which involves summarizing data via their empirical distributions, we also by-pass the issue of selecting summary statistics. The proposed kernel function, being defined on a non-compact support, avoids any implicit or explicit rejection step, thus effectively increasing the effective sample size, as empirically verified in Sect. 5. Moreover, the resulting approximate ABC likelihood leads to a better approximation of the tails of the posterior distributions, that is, poor parameter proposals are assigned small but nonzero probability. We also provide formal guarantees of the convergence of our ABC approximate likelihood to the true likelihood.

The proposed method deals with the inefficiency in ABC algorithms by focusing on the kernel function. Although a variety of ABC sampling schemes addressing the same problem have been proposed, most of them (e.g., MCMC-ABC, SMC-ABC, PMC-ABC, SIS-ABC, etc.) handle the problem of finding a good marginal importance distribution, \(q(\theta )\), completely ignoring the choice of the kernel \(K_{\epsilon }(\cdot )\). We speculate that these two approaches can be combined by adopting those sampling schemes rather than the involved IS-ABC. Finally, further research is called for in order to apply the proposed method to sequences of dependent random variables, such as Markov chains, and to continuous data. This will in turn require considering more sophisticated versions of the theory of large deviations, where the i.i.d. assumption is relaxed. Such extensions are required to make the algorithm applicable to more complex situations in which no other ways of sampling from the posterior distribution are available. However we want to emphasize that at the current stage, the method is already applicable in contexts in which the other available sampling methods (e.g., MCMC) can be computationally demanding. For example, an efficient ABC algorithm may be usefully applied to models involving high-dimensional latent variables even when an MCMC algorithm exists. In fact, ABC algorithms can be run in parallel, leading to a computational gain when many of the existing MCMC algorithms suffer from a slow mixing of the chain.